1. Introduction
Schlieren methods provide qualitative and quantitative visualization of gas density gradients in compressible flow and are widely used in a wide range of ground test facilities. Conventional reflector- or refractor-based schlieren systems typically use a mirror or an achromatic doublet field lens and a light source with a small pinhole or a short single slit with a typical width of 100–500
m. The light beam within the test section is nearly collimated [
1]. A second mirror or lens is used to focus the light onto a knife edge or an absorbing edge. Light sources with pinholes and slits are distributed light sources and usually require that a relay lens be focused to provide a sharp image of the schlieren object plane. However, out-of-focus regions are only weakly blurred in conventional schlieren systems because the light source is narrow. Conventional schlieren methods yield approximately path-integrated images of index-of-refraction gradients, including window defects, shear layers, boundary layers, and any other index-of-refraction gradient within the field of view. This type of schlieren system is usually not capable of recognizing specific spanwise flow features because the blurring of objects away from the object plane is weak [
2].
Focusing schlieren methods use an array of light source slits, and because the distributed light source is much wider than the single slit in conventional methods, the achievable out-of-focus blur is much greater [
2,
3,
4]. As noted by Ref. [
5], “focusing schlieren” is a poor name for this method because all schlieren systems with distributed light sources are focusing; a more accurate name could be “multiple-source schlieren”. Traditional focusing schlieren methods use two grids, namely a source grid forming the distributed light source and a second cutoff grid formed in the image of the source grid and acting as the multiple knife edges (one for each slit) with a photographic lens forming an image of the source grid on the cutoff grid. However, constructing the cutoff grid in a perfect image of the source grid and properly aligning these grids relative to each other is challenging and has prevented the widespread use of focusing schlieren systems.
The self-aligned focusing schlieren (SAFS) method of Bathel and Weisberger [
6,
7,
8] circumvents the issue of constructing and aligning a separate cutoff grid by using a photographic lens to create an image of a cutoff grid on a retroreflector located at the source grid location. This cutoff grid image, functioning as the source grid, is then re-imaged back onto the same cutoff grid. In this manner, the system is “self-aligning” and requires only that the lens be focused so that the cutoff grid image is reasonably sharp. This technique was used in a hypersonic boundary-layer study to focus on the surface of a cone in a Mach 6 free jet facility [
9].
In SAFS, as well as most traditional focusing schlieren methods, a single-field lens is used to form an image of the source grid on the cutoff grid. The field of view of these single-field lens focusing schlieren systems is analogous to conventional schlieren systems using a single-field lens or mirror rather than the more common dual achromatic doublet systems or z-type systems with two parabolic mirrors. Single-field lens focusing schlieren systems have the advantage that the field of view can be larger than the entrance pupil of the field lens. However, single-field lens focusing schlieren systems (as well as single-lens/mirror conventional schlieren systems) are much less applicable to direct-connect facilities than free jet facilities because the field of view of a single lens increases with increasing distance from the lens, and the converging/diverging light rays are cut off by the test section walls, greatly reducing the visibility of the near-wall region of the upper and lower test-section walls.
One of the earliest focusing schlieren systems designed by Kantrowitz and Trimpi [
10] used two field lenses, but the field of view was small, and the method was apparently not developed further. A traditional single-lens focusing schlieren method was used in a direct-connect facility with visibility of both upper and lower near-wall regions, but extensive image processing was required to produce a useful visualization result [
11] and the field of view of the post-processed image remained significantly distorted. A single-field lens system was used to visualize the near-wall region of a single wall with good results, but the single wall was placed near the center line of the optical system, and the system was as long as about 5 m (16 ft) in overall length [
12]. Interestingly, a three-field lens SAFS system was created by Weisberger and Bathel [
13], with potential applications to direct-connect tunnels, but the focus of that work was on a combined-focused laser differential interferometer (FLDI), and the additional two-field lenses were apparently used only to couple the SAFS and FLDI systems.
There are many techniques for measuring gas velocity in high-speed ground test facilities, including particle image velocimetry (PIV) [
14], laser Doppler velocimetry (LDV) [
15], femtosecond laser electronic excitation tagging (FLEET) [
16], krypton tagging velocimetry (KTV) [
17], schlieren image velocimetry (SIV) [
18], and laser spark velocimetry (LSV) [
19,
20]. However, PIV techniques in supersonic flows suffer from issues with seeding and particle slip. The accuracy of laser-based tagging techniques is often poor, and the technique requires specialized equipment. Because conventional schlieren methods yield approximately path-integrated images of index-of-refraction gradients, cross-correlation based SIV techniques using conventional schlieren systems are complicated by the need to distinguish the free-stream velocity from the convective velocity in the window boundary layers or jet shear layer. While LSV has poor spatial resolution, it can be readily applied for measurement of free-stream flow velocity.
In LSV, sometimes also called a thermal mark method, a laser-induced plasma, referred to as a laser spark, is generated in the flow and convects downstream. The plasma luminescence can be tracked directly [
19], or the hot gas kernel created by the plasma can be tracked using schlieren visualization [
20]. In the creation of the laser spark, the high electric field at the waist of a focused laser beam ionizes the neutral gas, which then absorbs a fraction of the laser energy, creating a hot plasma that expands outward with a strong concomitant shock wave [
21,
22]. Due to the elongated shape of the laser-beam waist, the hot plasma and the resulting shock wave are first elongated rather than spherical. The initial dynamics of the shock wave and hot gas kernel can be approximated using the Sedov–Taylor [
23,
24] self-similarity solution for a strong blast. Because the Sedov–Taylor solution assumes a strong shock, it is only approximately valid when the Mach number of the shock wave is
[
21]. In the weak shock limit, an extended blast-wave solution is required, such as that proposed in Ref. [
25]. While the shock wave continues expanding and gradually decays to an acoustic wave, the hot gas kernel reaches a final radius when the hot gas pressure equals that of the surrounding gas.
In this work, a self-aligned focusing schlieren system is designed with two field lenses to improve near-wall visibility of both upper and lower test-section walls of a direct-connect wind tunnel. A pulsed LED is used for high-speed image acquisition with a pulse width sufficiently short to freeze the flow. The SAFS system has a compact footprint for implementation in facilities with restricted available space. The SAFS system is demonstrated in the following three test cases: a wall-normal cylinder in supersonic crossflow, laser spark velocimetry, and schlieren image velocimetry in supersonic flow. Analytical forms are derived for the defocus blur and vignetting of two field lens systems.
2. Experimental Method
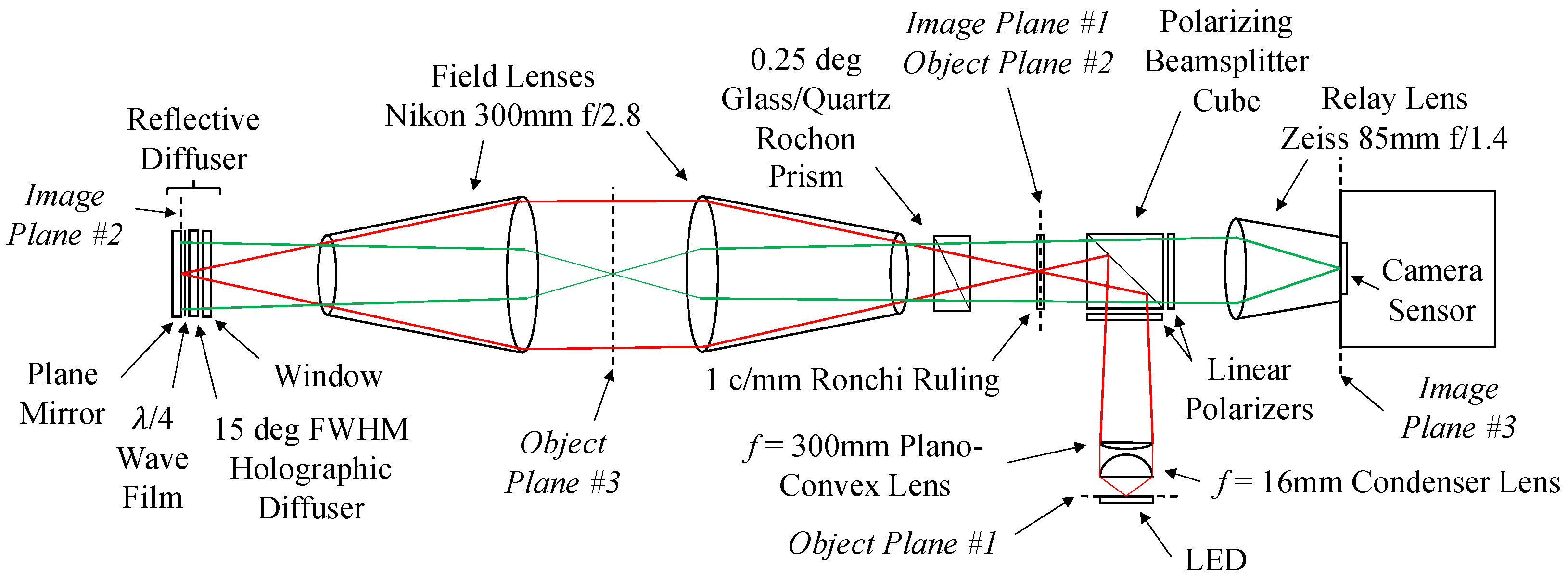
The focused schlieren system is schematically illustrated in
Figure 1, and a photo of the system is shown in
Figure 2. A high-power LED (Luminus Devices CBT-90-RX-L15-BM100) is powered by a pulsed diode driver (PicoLAS LDP-V 240-100 V3.3). The optical pulse width is 150–200 ns FWHM for 50–100 A peak electrical current pulse, and the pulse repetition rate is up to 1 MHz. The light from the LED is collected by an
mm aspheric condenser lens, and an
mm plano-convex lens is used to form an approximately
mm image of the
mm light-emitting surface of the LED onto a 1 c/mm Ronchi ruling (Applied Image RR1-24-CG), which is the cutoff grid. The LED is an incoherent source with a 631 nm center wavelength and 20 nm line width, which reduces the combined effects of diffraction softening and chromatic aberrations. The light is passed through a linear polarizer to create vertically linearly polarized light that is reflected by a 50 mm polarizing beam-splitter cube to illuminate the Ronchi ruling. The light then passes through a 0.25 deg glass/quartz Rochon prism (United Crystals), which has been shown to transmit diffuse light in both directions without polarization changes [
26]. The Rochon prism is oriented so that the vertically polarized light passes through undeflected. The light is then approximately collimated by the first field lens (Nikon Nikkor ED Ai-S 300 mm f/2.8), passes through the test section, and is re-focused by a second field lens onto the reflective diffuser assembly with about
magnification. The field of view is set by the entrance pupil of the first field lens, which is 107 mm in diameter.
The reflective diffuser assembly consists of wave film (Edmund Optics #14-725) oriented at 45 deg to produce circular polarized light and placed between a 15 deg FWHM holographic diffuser (Edmund Optics #47-677) and a plane mirror. The reflective diffuser components are installed in a rotation mount, and a window is placed in front of the holographic diffuser to ensure that the components are in close contact. Upon reflection, the polarization of the light is rotated to horizontal. Because the wave film is ∼50 m thick, the cutoff grid image remains adequately sharp. By placing the wave film between the holographic diffuser and the mirror, all surface reflections between the polarizing beam-splitter cube and the reflective diffuser have the original vertical polarization and are rejected, decreasing glare and improving image contrast.
The cutoff grid (Ronchi ruling) image on the reflective diffuser is re-imaged by the field lenses onto the same Ronchi ruling. On the reverse pass through the Rochon prism, the light is deflected by 0.25 deg, and the image of the Ronchi ruling is displaced slightly when it is re-imaged onto the ruling. In this manner the physical Ronchi ruling cuts off the re-imaged Ronchi ruling and acts as a knife edge for each individual source. The distance between the Rochon prism and the Ronchi ruling adjusts the degree of cutoff, analogous to adjusting the degree of cutoff using a knife edge in a conventional schlieren system. Because the field lens has no optical elements near the lens mount, the lens mount and rear ∼65 mm of the field lens are removed to make room for the Rochon prism, which gives greater adjustability and the flexibility to use either the 1 c/mm Ronchi ruling or a 2 c/mm Ronchi ruling for greater sensitivity at higher stagnation temperature and lower free-stream density. The light then passes through the polarizing beam-splitter cube and a second linear polarizer to ensure good contrast. Images are recorded by a synchronized high-speed camera (Phantom v2512) with a 260 ns gate using a relay lens (Zeiss 85 mm f/1.4). The position of the schlieren focal plane is set by adjusting the focus of the relay lens. The total length of the system, from the rear of the camera to the back of the reflective diffuser, is 1.2 m (4 ft).
By using a holographic diffuser rather than a ground glass diffuser, light is diffused only enough to be re-imaged by the second field lens, reducing light loss. Because the LED surface is imaged directly onto the Ronchi ruling, a diffuser is not necessary for the light source, which also reduces light loss. However, when the Ronchi ruling is placed normal to the optical axis, a portion of the glare from the chrome bands on the Ronchi ruling is focused by the relay lens onto a small area on the camera sensor. This light passes through the polarizing beam-splitter cube and the linear polarizer in front of the relay lens because the reflected light has an elliptical polarization rather than linear polarization, and the horizontal component is transmitted through the polarizing components. The Ronchi ruling is rotated slightly to move this focused glare to the side of the sensor, and the Rochon prism is rotated slightly in the same direction to compensate. When a diffuser is placed between the light source and polarizing beam-splitter cube, glare from the Ronchi ruling is diffuse, and rotating the Ronchi ruling has little effect.
In
Figure 1, red lines denote the ray bundle of first-pass light that travels from a point at the center of the light-emitting surface of the LED, passes near the edges of the field lenses, and is focused again as a point on the reflective diffuser. If this ray bundle were to originate near the edge of the LED surface, it would be focused near the edge of the Ronchi ruling. After passing through the linear polarizer, this light is vertically polarized. Green lines denote the ray bundle of second-pass light that originates at the edges of the source grid, passes through a point in the schlieren object plane, and is focused by the field lens at a point on the camera sensor. This light has horizontal polarization. There are three object/image conjugate planes, namely the LED surface and the Ronchi ruling (denoted object/image plane #1), the Ronchi ruling and the reflective diffuser (object/image plane #2), and the schlieren object plane and the camera sensor (object/image plane #3).
The defocus blur of the schlieren system is qualitatively shown in
Figure 3 by translating a tube with a blowing jet of saturated room-temperature difluoroethane vapor
between the two field lenses in quiescent lab air. The inner diameter of the tube is 1.4 mm, and the outer diameter is 3.1 mm. The field lenses are separated by 160 mm, and the displacement of the difluoroethane jet in
Figure 3 is measured from the schlieren object plane, which is placed halfway between the field lenses, with positive displacement away from the camera. The difluoroethane jet is in sharp focus when placed on the schlieren object plane, and when the jet is placed
mm from the object plane, the defocus blur is sufficient to almost completely blend the jet image into the background. The defocus blur appears to be symmetric about the schlieren object plane.
3. Mathematical Model
The degree to which a focusing schlieren system can blur regions outside of the schlieren object plane is referred to as the depth of field of the system. The depth of field can be quantified by relation to application-specific parameters, such as the depth at which the image remains sharp at a given pixel level (sometimes referred to as “depth of sharp focus”) or the depth required to blur an object of a certain size (sometimes referred to as “depth of unsharp focus”). However, the former is dependent on pixel size, and the latter is somewhat qualitative. A more general definition of defocus blur should be independent of pixel size and specifics of the object being imaged. As noted by Boedeker [
27], defocus blur can be quantified by the height (
h) on the sensor plane of a ray bundle originating from a point near the schlieren object plane, which is also referred to as the circle of confusion. For a point on the schlieren object plane, the rays are focused to a point on the sensor plane, and
. For a point off the schlieren object plane,
h increases with increasing distance (
x) from the object plane. This definition of defocus blur can be easily used to obtain other depth-of-field values of interest. For example, the depth of sharp focus is simply the distance (
x) required to yield a ray-bundle height on the sensor plane (
h) equal to the pixel pitch.
Consider the focusing schlieren system shown in
Figure 4 consisting of two thin field lenses, one thin relay lens, and a distributed light source of width
w. The relay lens has a focal length of
, an f-number of
, a flange-focal distance of
, and a throat width of
t and is placed a distance of
g from the light source. The field lens has a focal length of
and an f-number of
and is placed a distance of
q from the light source. Note that the effective lens distance for a thin lens should be used for
q, not the actual distance of the photographic lens to the light source. The effective lens distance can be found using the compound lens focal distance set point in the thin lens equation and adding the distance from the lens design image plane to the light source. The distance from the field lens to the schlieren object plane is
s. Using the thin lens equation and similar triangles, the distance from the relay lens to the schlieren image plane, corresponding to the camera sensor plane distance, is
and the resulting image magnification is
Combining Equations (
1) and (
2) and simplifying, the relay-lens focal length required to yield image magnification (
m) is
For
, Equations (
1)–(
3) are equivalent to the equations presented by Settles [
2].
In the design of a focusing schlieren system, the desired image magnification (
m) is found by knowing the schlieren field of view and the camera sensor size. The desired relay-lens focal length is then calculated from Equation (
3). However, low-f-number relay lenses are usually required in focusing schlieren systems, and low-f-number photographic lenses usually have a fixed focal length and are only available in certain discrete focal lengths. Therefore, once the relay-lens focal length is chosen from among the available options, the distance from the relay lens to the schlieren image plane is calculated using Equation (
1), and the actual image magnification is calculated using Equation (
2).
The ray-bundle height at the schlieren image plane is
where
is the difference in schlieren image-plane distance for a point a distance of
x from the schlieren object plane, and
a is the ray-bundle height at the relay lens. The apparent height of the ray bundle in the schlieren object plane is then
. The ray-bundle height at the relay lens found using similar triangles is
where
is the ray-bundle height at the field lens. For
, the ray-bundle height at the field lens is limited by the field-lens entrance pupil, and
b in Equation (
5) should be replaced by the field-lens entrance pupil diameter (
). For
, the ray-bundle height at the relay lens is limited by the relay-lens entrance pupil, and
a in Equation (
4) should be replaced by the relay-lens entrance pupil diameter (
).
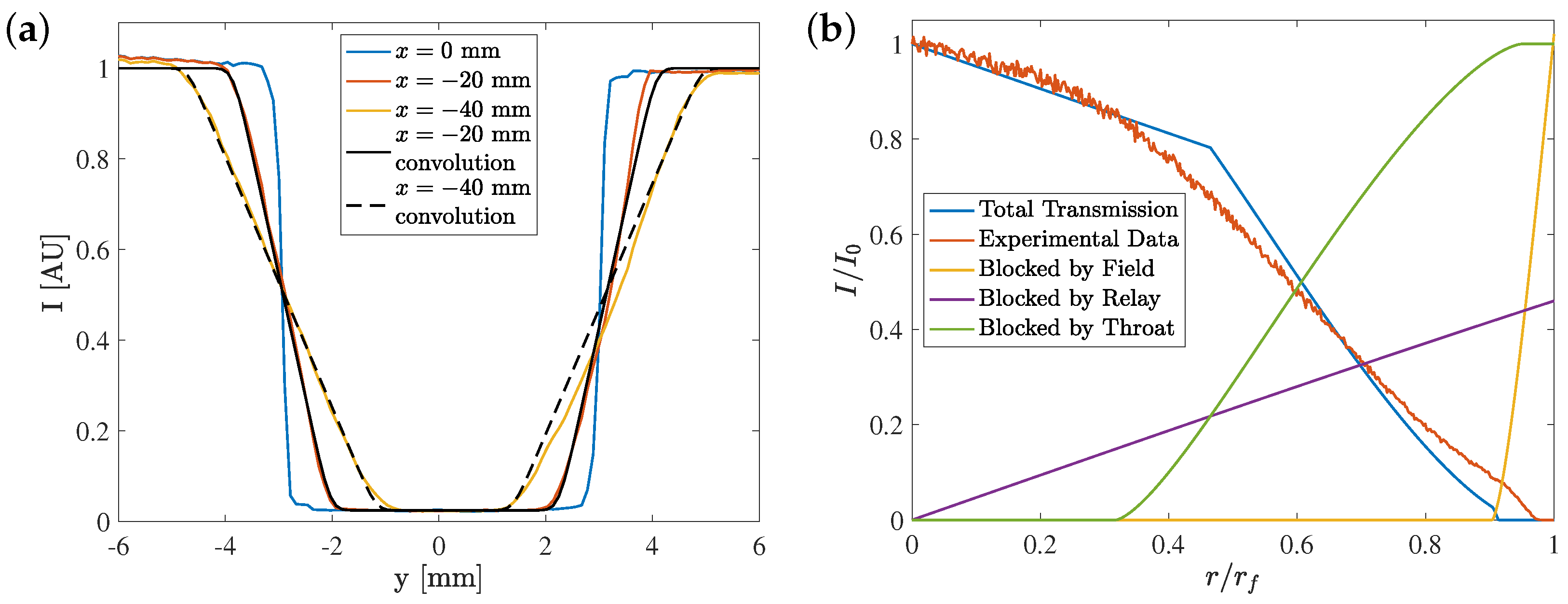
The optical parameters of the present SAFS system are 300 mm, 85 mm, 1.4, 2.8, 80 mm, 43 mm, 105 mm, and 347 mm. However, a 49 mm lens filter adapter is used on the relay lens as a rudimentary light block to prevent glare from the light source, so the relay-lens entrance pupil is limited to 48.25 mm rather than 60.7 mm, which somewhat reduces the ray-bundle height. The theoretical ray-bundle height using the above mathematical model is as , and the ratio is approximately constant with x.
Because point light sources become circles with an apparent diameter of
when displaced from the object plane, the defocused image can be considered a convolution of the in-focus image with a step function of diameter
. The ray-bundle height of the present SAFS system is determined by translating a 6 mm diameter horizontal rod between the field lenses and summing along pixel rows to determine the image intensity profile. When the rod is located at the object plane (
mm), the intensity profile is approximately a square wave, with lens aberrations softening the profile slightly. When displaced from the object plane, the intensity profile has sloped boundaries rather than a step change at the edge of the rod. The actual intensity profile of the defocused rod is compared to the convolution of a 6 mm wide square wave with a square wave of width
. The product of this convolution is then convolved with a narrow Gaussian profile to account for lens aberrations. As shown in
Figure 5a, when the rod is located at the schlieren object plane, it appears in the image as a square wave with 6 mm width. When displaced from the schlieren object plane, the rod appears as the convolution of a 6 mm square wave and a square wave of width
. The width of the convolving square wave is
, which is in reasonable agreement with the above theoretical apparent ray-bundle height of
.
When a point on the schlieren object plane is displaced from the optical center line by a distance of
, the corresponding point in the image plane is displaced by a distance of
. At the field lens, the center line of the ray bundle is displaced by a distance of
, and the height of the ray bundle is
b. At the relay lens, the center line of the ray bundle is displaced from the optical center line by a distance of
, and the height of the ray bundle is
a. At the relay-lens throat, the center line of the ray bundle is displaced from the optical center line by a distance of
and the height of the ray bundle is
. As the ray bundle is displaced from the center line, the edge of the ray bundle can pass over the edge of the field-lens entrance pupil, relay-lens entrance pupil, or relay-lens throat and be blocked. Light rays that are blocked do not contribute to the corresponding region in the image plane, and the light intensity of that location in the image plane is decreased, which is known as vignetting. Only light rays that pass through the field-lens entrance pupil, relay-lens entrance pupil, and relay-lens throat are present in the image plane and detected by the camera sensor. The vignetting of the present SAFS system is shown in
Figure 5b, along with the theoretical total light transmission and the amount of light blocked by the field-lens entrance pupil, relay-lens entrance pupil, and relay-lens throat (note that regions of the ray bundle that are blocked by one region can also be blocked by another region, so the three blocked curves do not sum to the total blocked light). The theoretical light transmission curve is in reasonable agreement with the experimental data. It is seen that vignetting in the present SAFS system is primarily due to the relay lens.
4. Wall-Normal Cylinder
The SAFS system was used for visualization of Mach 2 flow at the University of Notre Dame’s SBR-50, which is a supersonic direct-connect blowdown wind tunnel. The exit of the planar nozzle has a cross-section of mm and is attached directly to the test section. The upper and lower walls of the test section have a 1 deg half-angle expansion to account for boundary-layer growth. Quartz windows on both sides of the test section provide optical access. For the presented data, the stagnation pressure is bar, and the stagnation temperature is K. A single 2.5 mm diameter, 25.4 mm height cylinder is installed on the top wall. The pin is offset from the center line by 6 mm towards the camera.
Single-pulse SAFS images are presented in
Figure 6. The schlieren object plane is placed on the cylinder, and a raw, unprocessed schlieren image is shown in
Figure 6a. This raw image is subject to about three stops of light falloff, and the light intensity at the edges of the image is reduced by a factor of about
. This vignetting is due primarily to light cut off by the relay lens, as discussed above. There is also some sensor pattern noise. To correct these issues, the schlieren image is normalized by a no-flow condition image, with solid wall regions omitted from the normalizing image. No other image processing is applied. The normalized image is shown in
Figure 6b.
A bow shock is formed in front of the cylinder and continues around the tip of the pin as an oblique shock. A separation shock is visible near the base of the cylinder with unstable shock wave–boundary layer interaction. The turbulent boundary layer is well-visualized as well. Not visible in this image are the turbulent boundary layers on the windows or window defects such as scratches, chips, or inclusions.
When the relay lens is focused on the near-window boundary layer, another shock comes into focus, as shown in
Figure 6c. This is the unsteady footprint of the curved bow shock from the cylinder reflecting off the near window. Now, the turbulent boundary layer on the near window is also visible. The shocks near the cylinder are blurred because they are outside of the schlieren object plane.
When the relay lens is focused on the far-window boundary layer, the unsteady footprint of the bow-shock reflection off the far window comes into focus, as shown in
Figure 6d, and the near-window shock footprint is blurred. Because the pin is not placed on the center line but rather 6 mm closer to the near window, the far-window shock footprint occurs further downstream than the near-window shock footprint.
5. Laser Spark Velocimetry
Laser spark velocimetry was performed in Mach 2 flow at the SBR-50 facility using SAFS imaging [
28]. The stagnation conditions remain the same, and the pin insert on the upper test section wall is removed and replaced with a window. The second harmonic of a ns-pulsed 100 Hz Nd:YAG laser (Solar Laser Systems LQ 629-100) at 532 nm is expanded from a beam diameter of 4.6 mm to 12.3 mm and focused onto the test-section center line using an f = 75 mm lens. The pulse energy is 70 mJ/pulse as measured by a thermopile power meter. Beyond a certain threshold pulse energy, the electric field at the focal point is sufficiently high such that the neutral gas is ionized. This ionized gas then absorbs a fraction of the laser energy, creating a hot plasma and a strong shock wave. The hot gas kernel reaches a final radius when the hot gas pressure equals that of the surrounding gas, and the shock wave decays to an acoustic wave.
SAFS images of the laser spark 16.7
s after laser emission are shown in
Figure 7a,b. The schlieren object plane in
Figure 7a is on the test-section center line, and the hot gas kernel and shock wave are in focus. In
Figure 7b, the schlieren object plane is placed 5 mm from the far-window surface. The hot gas kernel and shock wave are out of focus, and the far-window turbulent boundary layer is in focus. When the schlieren object plane is placed on the test-section center line, both near-window and far-window turbulent boundary layers are blurred, improving the visibility of the hot gas kernel and shock wave and facilitating their tracking.
Figure 7c is a composite time series of the laser spark evolution and advection, where
x is the streamwise direction measured from the laser focal point and
t is the time after laser emission. These are 256 × 64 pixel images taken at 500 kHz from 2.7 to 22.7
s after laser emission, with 2
s between frames. At 2.7
s, the plasma emission is strong, and most of the laser spark is obscured because the sensor is saturated. Plasma emission remains relatively strong at 4.7
s, and the hot gas kernel is still saturated, but the shock wave is now visible. At 6.7
s, the hot gas kernel has reached its final size, and plasma emission is only weakly visible. Throughout the time series, the shockwave radius continues increasing, and both the hot gas kernel and shock wave continue advecting downstream.
The hot gas kernel displacement with time for the laser spark in
Figure 7c is shown in
Figure 8a. The slope of this line is the convective speed, which is
m/s. The spherical shock wave is tracked by finding the least-squares best-fit circle to the shock wave. The derivative of the shockwave radius (
) with time yields the shockwave speed, which is shown in
Figure 8b. The shock wave is initially supersonic and decays to a nearly constant speed within the cropped SAFS image, indicating that the shockwave speed is close to the acoustic limit. The experimental shock speed is fit with an analytical solution for point blast waves [
25] by using the energy deposition as a fitting parameter. An initial guess for the laser energy deposition is found using the final diameter of the hot gas kernel [
29]. By combining this analytical solution with the isentropic relations for the one-dimensional flow of a calorically perfect ideal gas and using the known stagnation pressure of
bar, the Mach number is found to be
, and the stagnation temperature is
K, in reasonable agreement with the previously measured Mach number of M = 2.07 and stagnation temperature of
K [
28]. The best-fit energy deposition is 13.5 mJ, indicating that under these experimental conditions, the plasma absorbs about 20% of the total laser pulse energy.
6. Schlieren Image Velocimetry
Because of the blurring of perturbations out of the schlieren object plane, focusing schlieren visualization is a powerful method of analyzing natural flow perturbations. Flow perturbation dynamics from a SAFS line of observation can be used to retrieve the convective flow velocity, which is referred to as schlieren image velocimetry [
30,
31], as well as the spectra of flow disturbances. In the case of conventional schlieren or background-oriented schlieren techniques, there is still a debate as to which portion of the flow field contributes to the result. The boundary layer in wall-bounded flows or the shear layer in free jet flows usually has the largest magnitude of gas density disturbances, leading to some unknown underestimate of the flow velocity when based on conventional schlieren imaging. However, a SAFS system can be used to focus on one a plane of interest; regions outside the schlieren object plane are blurred, reducing their influence on the calculated convective flow velocity and spectra.
The SAFS system described above was used for analysis of flow perturbations in the SBR-50 facility. The data were collected at two positions on the schlieren object plane, namely at the test-section center line and
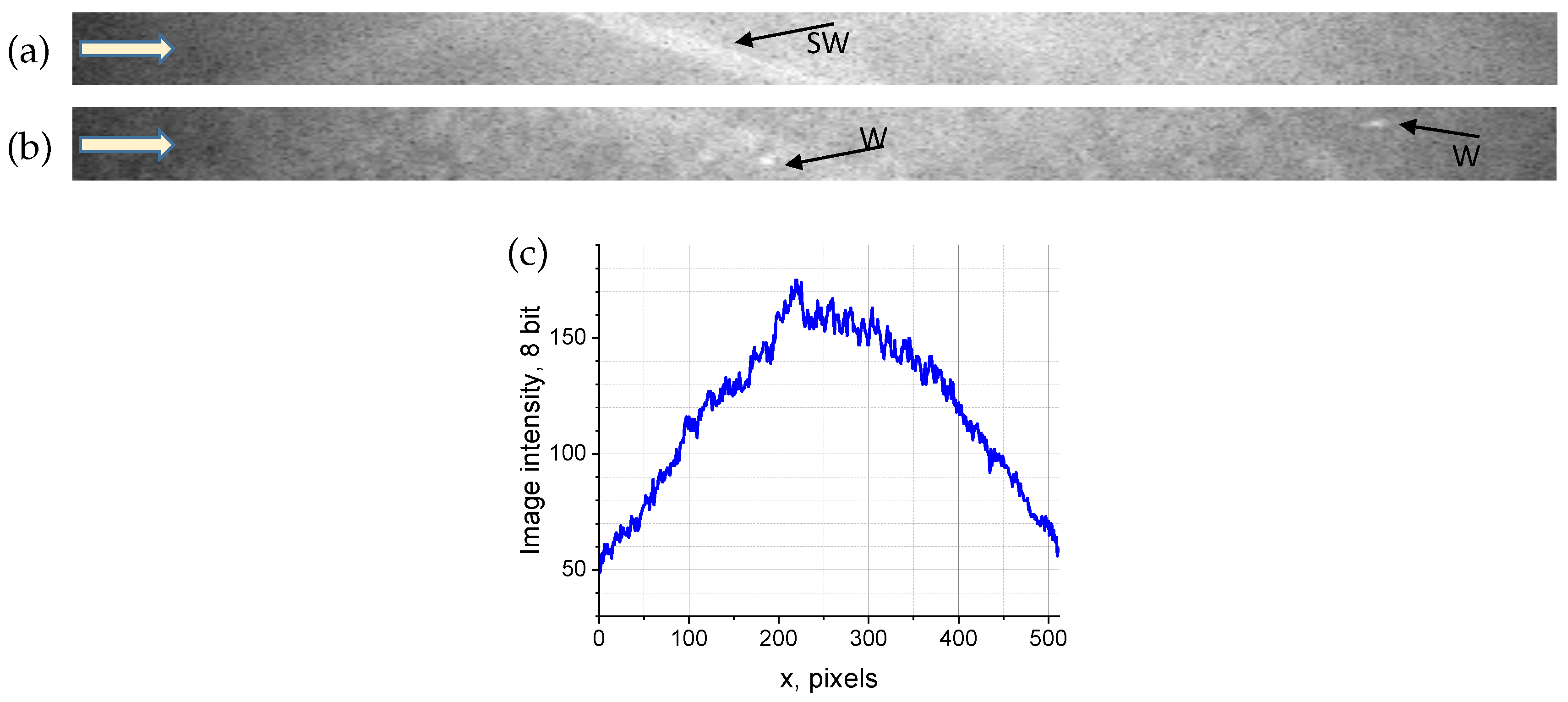
mm from the near-side window, which is within the boundary layer. The SAFS frame rate was 500 kHz in bursts consisting of 200 frames per burst, with a burst repetition rate of 100 Hz. Each image has dimensions of 512 × 32 pixels. Typical unprocessed schlieren images for centerline and boundary-layer positions are shown in
Figure 9a,b, respectively. In the raw images, the flow perturbations are not easily recognizable. Weak oblique shock waves (SWs) are seen in
Figure 9a, while multiple window imperfections (W) are easily visible in
Figure 9b. Also present in
Figure 9b is the turbulent boundary layer on the near-side window visible in
Figure 6c. The images are then processed; the intensity profiles are extracted from each image using a 512 × 10 pixel sub-image with 10-pixel vertical binning. A typical intensity profile is shown in
Figure 9c for the boundary-layer case. The flow density perturbations cannot be properly identified based on a single intensity profile. The intensity profiles from all burst images are then stacked into a single data matrix (
, where
i represents the pixel number along the frame (distance) and
j indicates the image number).
Consequent processing includes double data normalization to remove the SAFS vignetting and reduction of the light source intensity during the pulse burst.
where
is the number of images in the burst (
in this case), and
is the number of pixels in the longitudinal intensity profile (
in this case).
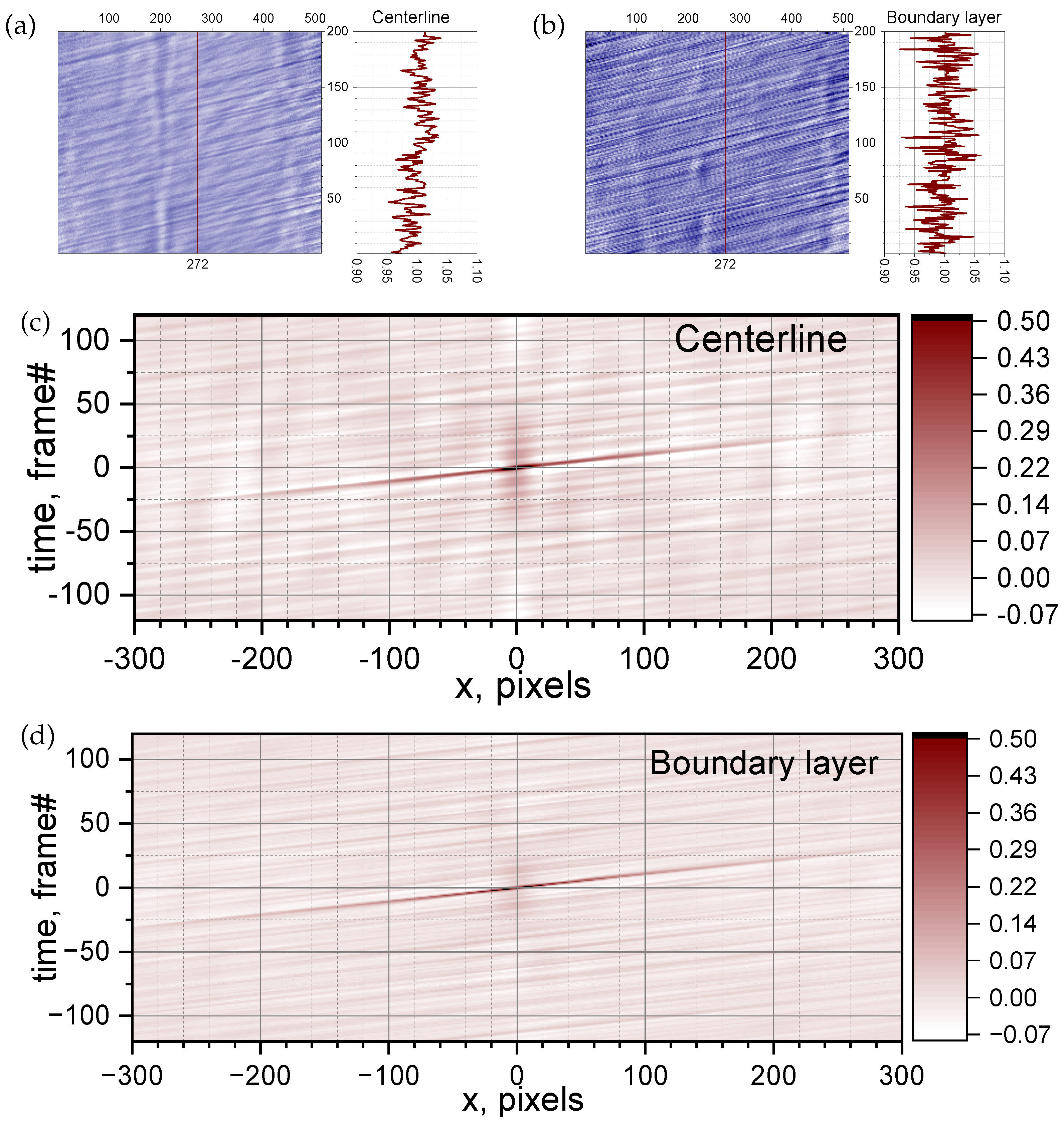
A visual form of the
matrix after normalization is shown in
Figure 10a for the centerline case and in
Figure 10b for the boundary-layer case. These images represent the artificial streak visualization of easily recognizable downstream propagating flow perturbations. As shown in the time sequences of image intensity on the right side of each image, the magnitude of the perturbations is up to
% for the centerline case and more than
% for the boundary-layer case. Visually,
Figure 10a appears significantly smoother, reflecting a lower perturbation magnitude.
The 2D self-correlation of the
matrix is shown in
Figure 10c for the centerline case and in
Figure 10d for the boundary-layer case. The inclined straight line going through
represents the moving flow disturbances. The amplitude of the correlation function is high (up to 0.5), indicating the high accuracy of the calculated flow velocity. Applying the scale coefficients for a frame rate of 2
s/frame and a spacial scale of 0.1087 mm/pixel for the centerline images and 0.1093 mm/pixel for the near-window images, the convective flow speed is calculated to be
m/s for the core flow and
m/s for the near-wall focus position. The core flow speed is in reasonable agreement with the laser spark velocimetry data. Closer to the window, the flow speed is measured to be about 4% lower than in the core flow. Because the magnitude of flow perturbations is higher in the boundary layer, it can be expected that a conventional schlieren system will underestimate the core flow speed.
The
matrix is stacked into a single column (
), and the spectral function (
) of the signal in the time domain (
) is
which is found using an FFT algorithm. The amplitude of the spectral function is
where
n is the number of samples. Then, the power spectral density (
) is
where
kHz is the sampling frequency. The power spectra of the
time sequence for two considered cases are shown in
Figure 11. In the frequency domain, the magnitude of the flow perturbations is practically the same for the centerline case and the boundary-layer case for
Hz. These perturbations likely have a spatial scale of
mm and are attributed to the flow of large-scale disturbances originating from the facility’s plenum section, similar to those visualized in Ref. [
32]. However, there is a significant difference of up to eight times, between the flow perturbation magnitude in the frequency range of
Hz
Hz. These frequencies correspond to special scales of 2 mm
10 mm and are attributed to large eddy structures in the boundary layer.
7. Conclusions
A self-aligned focusing schlieren (SAFS) system with two field lenses is developed to resolve specific spanwise flow structures and to improve the visibility of the upper and lower near-wall regions in direct-connect wind tunnels. It is shown that the depth of field of this system is sufficiently shallow to separate specific spanwise features in supersonic flow of a wall-normal slim cylinder installed with cross-flow in a 76.2 mm wide test section, blurring the boundary layers on the windows and window-surface imperfections. The system is compact for use in facilities with restricted space, with a total length of 1.2 m. However, the current schlieren system has several known flaws. Vignetting is appreciable, reducing the signal intensity near the edge of the field by about a factor of eight as compared to the center of the field. Analytical forms derived for depth of field and vignetting show that vignetting is primarily caused by the limited aperture and throat width of the relay lens. Apparently, vignetting can be effectively reduced through the use of a larger format, low-f-number relay lens. Another known issue is that glare from the chrome bands on the Ronchi ruling is focused by the relay lens onto the camera sensor, saturating the image at this location and preventing the Ronchi ruling from being placed normal to the optical axis. This issue can be resolved through the implementation of an absorptive Ronchi ruling. However, as shown in this work, the majority of the above issues can be mitigated by simple data post processing.
In this work, for the purpose of demonstration of the capabilities of SAFS, flow velocimetry was performed in two ways, namely using the method of thermal mark (laser spark) tagging and by analysis of natural flow perturbation dynamics using an SAFS system with a 500 kHz image acquisition rate and 200 ns optical pulse width. The shock wave from a laser spark in flow was accurately tracked. The Mach number and stagnation temperature were calculated by comparison of the experimental shockwave location and speed with an analytical blast-wave solution. The core flow speed was measured to be m/s, corresponding to a flow Mach number of M = 2.05. Schlieren image velocimetry was performed by analyzing natural flow perturbations using a self-correlation method. The convective flow velocity was calculated to be m/s for the core flow and m/s for the near-wall focus position. Because the magnitude of flow perturbations is higher in the boundary layer, it can be expected that a conventional schlieren system will underestimate values for the flow speed. Power spectra of flow perturbations indicate a significantly higher prevalence of high-frequency perturbations in the boundary layer than in the core flow.
In this study, an improved SAFS system was demonstrated to have impressive capabilities for measuring supersonic flow parameters and for visualization of flow features. In addition, the authors see considerable room for further enhancement in terms of spatial resolution and the ability to retrieve quantitative data in a wide range of ground test facilities.