Abstract
The integrated design of waverider forebodies and inlets is considered a critical challenge in high Mach number vehicle development. To facilitate the rapid construction of integrated geometrical models for waverider forebodies and inlets during the conceptual design phase, a method based on discrete point cloud reconstruction has been proposed. In this method, the geometries of the waverider body and inlet are used as inputs and decomposed into the point cloud under discrete rules. This point cloud is refitted to generate new section lines, which are then lofted into an integrated shape under the constraints of guide curves. By modifying the coordinates of the point cloud positions, the geometric configuration of the integrated shape can be rapidly adjusted, providing initial support for subsequent aerodynamic optimization and thermal protection. Using this method, an integrated approach was applied to a waverider forebody and inward-turning inlet in a tandem configuration. This achieved body-inlet matching and integration, resulting in a 15.6% improvement in the inlet’s total pressure recovery coefficient. The integration time was reduced to just 3.18% of the time required for traditional manual adjustments. Additionally, optimization based on the discrete point cloud enhanced the lift-to-drag ratio by 7.83%, demonstrating the feasibility of the proposed method.
1. Introduction
High Mach number vehicles possess advantages such as high speed, strong penetration capability, good stealth, and rapid deployment, offering significant benefits and application prospects in many fields [1,2,3,4,5]. As a critical technology in the design of high Mach number vehicles, the integrated design of waverider forebody/inlet has become a current research focus [6,7,8].
Using a waverider as the forebody of a high Mach number vehicle can achieve pre-compression of the incoming flow, thereby improving the inlet’s flow coefficient and total pressure recovery coefficient, as well as enhancing the vehicle’s lift-to-drag ratio [9]. Depending on the reference flow field, the waverider has evolved through several stages: wedge waverider, cone-derived waverider, wedge-cone waverider, osculating-cone waverider, osculating axisymmetric waverider, and osculating flowfield waverider. As waverider theory has developed, its geometric configuration and aerodynamic flow field have become increasingly complex, adding to the challenges of integrating the waverider forebody and inlet. Simultaneously, high Mach number inlets have transitioned from two-dimensional to three-dimensional designs. Current inlet configurations primarily include two-dimensional planar compression inlet, axisymmetric inlet, sidewall compression inlet, and three-dimensional inward-turning inlet. This trend towards complexity and diversity demands greater adaptability and flexibility in integration methods [10].
In the conceptual design phase of high Mach number vehicles, efficiently conducting forebody/inlet integrated design is crucial [11]. A flexible, adjustable, and efficient integration method can shorten the development cycle and enhance the iteration speed of design schemes. Numerous researchers have already studied the integrated design of waverider forebody/inlet. Li et al. applied the osculating cone waverider theory to propose a dual-waverider integrated configuration, integrating pre-designed 3D shock waves with the shape of the inward-turning inlet exit, improving the lift-to-drag ratio of the body and the air intake performance of the inlet [7]. Ding et al. generated an integrated configuration including the body, wings, and inlet directly based on cone-derived reference flow fields and validated the method’s effectiveness through numerical calculations [12]. These studies demonstrate that integration based on reference flow fields can produce configurations with excellent aerodynamic performance and controllable flow fields. However, the design process requires reverse-designing geometric surfaces based on coupled internal and external flow fields, making integrated design challenging. Wang et al. used the Class Shape Transformation (CST) parameterization method to develop a wing-body integrated shape with a high lift-to-drag ratio and uniform inlet flow field [13]. Alkaya et al. designed a high Mach number transport aircraft featuring a Sears-Haack body and supercritical airfoil from the perspective of the conceptual design process [14]. This approach supports designing a vehicle that meets specified requirement by proposing a new integrated shape, considering various factors such as aerodynamics and layout. However, this process is time-consuming and challenging to generalize for new design requirement. To overcome the low precision of data-driven optimization and the difficulty of extending geometric parameterization methods to complex configurations, Fu et al. proposed a global search multi-objective optimization framework. This framework uses directly extracted vehicle parameters to optimize a two-dimensional high Mach number forebody/inlet [15]. Zhang et al. introduced a multidisciplinary performance analysis model, completing the multidisciplinary optimization of an X-43a-like vehicle, including aerodynamics, propulsion, and stealth, based on 86 design parameters using a concurrent subspace optimization method [16]. The current parameterization methods for integrated configuration optimization require an initial rough design, inadvertently increasing the workload of iterative optimization.
Through the analysis of the above studies, it is evident that the current research on waverider forebody/inlet integration faces several issues. Most studies overlook the geometric integration of the forebody and inlet, typically relying on manual adjustments to construct integrated Computer-Aided Design (CAD) model, resulting in suboptimal geometric characteristics. The design process often involves complex aerodynamic calculations for reverse integration, making the coupled design of the forebody and inlet challenging. Integrated design needs to consider multiple factors such as aerodynamics, thermal protection, and layout, leading to lengthy design cycles. Additionally, the integrated geometric model requires a preliminary modeling followed by parameterization, which reduces the efficiency of iterative reconstruction.
To address the aforementioned issues, this paper proposes an Integrated waverider forebody/inlet Fusion method based on Discrete point cloud reconstruction (IFD). This method connects and fits the discrete point cloud generated from the geometric model using parametric curves, thereby resolving the geometric integration problem. It provides a means to decouple the design of the forebody and inlet, reducing the complexity of integrated design. During the construction of the integrated forebody/inlet shape, this method allows flexible adjustments of the discrete scheme based on time constraints and geometric information, achieving controllable shape construction cycles and precision. The final shape can be adjusted and optimized by performing operations such as displacement and reduction on the discrete point cloud, simplifying the complexity of shape adjustments and optimization. The simulation results of the integrated reconstruction model of the waverider forebody and inward-turning inlet validate the reasonableness, practicality, and superiority of this method.
2. Method
2.1. Overview
The concept definition of IFD, referred to as , is as follows:
where represents the positioning rule, which aims to adjust the forebody and inlet to their appropriate positions. represents the discretization rule, which aims to break down the shapes of the forebody and inlet into the point cloud. represents the reconstruction rule, which aims to reconstruct the point cloud into an integrated shape. represents the adjustment rule, which aims to optimize the shape based on the discrete point cloud. Specifically, refers to the discretization of surfaces in the discretization rule, refers to the discretization of lines in the discretization rule, refers to the reconstruction of surfaces in the reconstruction rule, and refers to the reconstruction of lines in the reconstruction rule.
The relationships between the above concepts are illustrated in Figure 1. The individually designed waverider and inlet geometric models, along with their relative positions, are taken as inputs. Supported by the discretization method based on feature points and feature sections, these models are decomposed into the point cloud. This point cloud is then lofted to form an integrated shape based on reconstruction rules. The resulting integrated shape can be further optimized using adjustment rules.
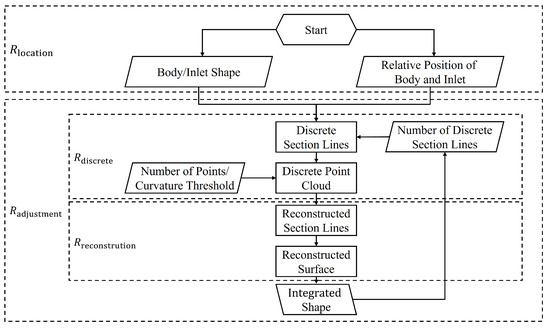
Figure 1.
Method flow.
2.2. Positioning Rule
When positioning the geometric models of the waverider body and the inlet, both models can be treated as rigid bodies during the geometric modeling phase. Their relative positions can be determined based on the positions of leading edge points and the axis system relationship of these points. Six relative position control parameters are utilized to uniquely determine the relative positions of the waverider body and the inlet, laying the foundation for their geometric integration. The specific rule is as follows:
where , , , and represent the coordinates of the body leading edge point, the angles of the body axis system, the coordinates of the inlet leading edge point, and the angles of the inlet axis system, respectively.
2.3. Discretization Rules
The primary objective of geometric discretization is to extract geometric features of the input waverider and inlet according to discretization rules, ensuring the maximization of preserved geometric information even with a limited number of extracted features.
2.3.1. Discretization of Surfaces
The discretization of surfaces involves slicing the geometric surfaces to extract section lines that capture the shape features. The surface discretization rule is defined as follows:
First, feature sections must be identified based on the current geometric characteristics. Feature sections refer to cross-sections with significant geometric features. The rule for defining feature sections is as follows:
where represents the starting position of the inlet and body integration; represents the position of the cowl-lip; represents the ending position of the body and inlet integration.
Once the feature sections are identified, the determination of section positions begins. The determination of section positions needs to consider the complexity and symmetry of the distribution. When opting for a simple symmetric distribution, the rule for section distribution is as follows:
where the prescribed positions for the feature sections are , , while the coordinates for section distribution are . Assuming , the distribution for the above configuration is illustrated in Figure 2.
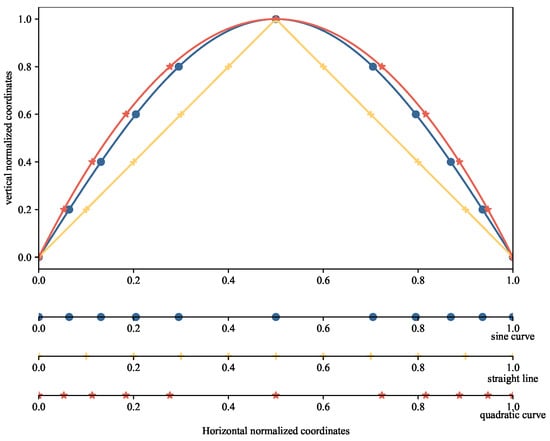
Figure 2.
Example of cross sections distribution between feature sections.
From Figure 2, it can be observed that a linear distribution function can generate an equidistant configuration, whereas a non-linear distribution function can produce a configuration with denser spacing near the feature sections and sparser spacing further away from the feature sections. The aforementioned distribution functions are straightforward to solve but do not consider the geometric features of the body/inlet shape, making them suitable for scenarios with high configuration generation time requirements and low precision demands.
In order to further ensure the accuracy of discretization, it is necessary to determine the section positions based on the geometric information of the shape itself. The shape of the sections is constrained by guide curves, and the variation in section can be characterized by the variation in guide curves. Therefore, it is proposed to set the section distribution based on the absolute variation in guide curve projection (as shown in Figure 3), resulting in a discretization rule between feature sections based on geometric features:
where and (, m is the number of guide curves) serve as the projection functions of guide curves between feature sections, while represents the coordinate change function of the guide curves.
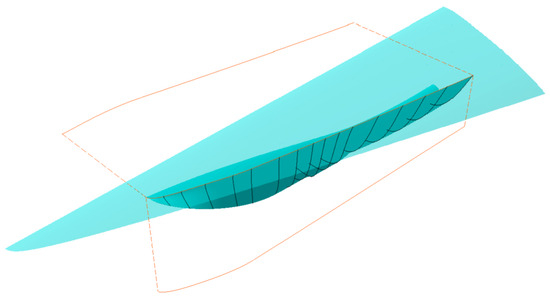
Figure 3.
The section distribution under the constraint of the guide curve.
2.3.2. Discretization of Lines
The line discretization rule requires the extraction of the key point cloud from the sections to ensure the geometric model’s accuracy during subsequent reconstruction. The rule is defined as follows:
The discretization of lines is similar to the discretization of surfaces and requires identifying the feature points on the section lines. The rule for determining the feature points is as follows:
where represents the inflection points of the section lines, while represents the points with the maximum and minimum coordinates on the section. After determining the feature points, candidate points between the feature points are obtained by equally dividing the coordinate differences between them. The final discrete points are then selected based on curvature. The specific rule is as follows:
where and are the y-coordinates of adjacent feature points, is the section line function, (where is the number of discrete points to be inserted between two adjacent feature points) represents the coordinates of the discrete points, s is the curvature, is the distance between points , and S is the specified curvature threshold.
Given a waverider forebody/inlet half-section, with 10 discrete points set between feature points and a curvature threshold of 0.00025 for discretization, the example of the resulting discrete points after removing the internal points is shown in Figure 4.
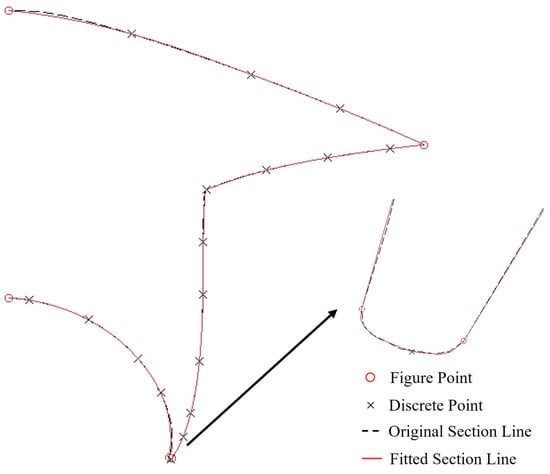
Figure 4.
Semi-section discretization and reconstruction.
2.4. Reconstruction Rule
2.4.1. Reconstruction of Lines
The line reconstruction rule employs the discrete point cloud to reconstruct the section lines, facilitating subsequent integrated shape reconstruction and optimization. The rule is defined as follows:
where denotes the need for segmentation at feature points to ensure geometric similarity between the reconstructed section lines and the original ones. Meanwhile, indicates the requirement for tangency between adjacent lines to prevent abrupt changes in shape that could compromise aerodynamic performance.
The current fitting parameterized curves mainly include polynomial curves, CST curves, and Non-Uniform Rational B-Splines (NURBS) curves. NURBS curves have advantages such as high precision and flexible adjustment [17]. Moreover, they have been recognized by the International Organization for Standardization (ISO) as the sole mathematical description method for defining the geometric shape of industrial products [18]. Setting this curve as the fitting rule for connecting discrete points facilitates the direct construction and analysis of geometric models in CAD software [19]. The parametric expression of NURBS curves is given by [17]:
where are called weighting factors, determined by the control points . The first and last weights , while the remaining weights . The polygon formed by sequentially connecting the control vertices is known as the control polygon of the NURBS curve. are the basis functions of the B-spline curve, defined by the knot vector using the Cox-DeBoor recursion formula for the k-th order normalized B-spline basis functions [17]:
The fitting results of the NURBS curve using 5 discrete points and 17 intermediate discrete points are shown in Figure 4. It can be visually observed that the NURBS fitted curve has a minimal fitting error compared to the original section line, effectively capturing the essential geometric features.
2.4.2. Reconstruction of Surfaces
The integrated shape surface reconstruction rule is based on the lofting method. The inputs required for lofting include fitted section lines, guide curves, and adjacent surfaces. The fitted section lines are NURBS parametric curves corresponding to the lofting sections; the guide curves connect the feature points of each section, serving as boundaries for the lofting; and the adjacent surfaces constrain the tangents at the ends of the integrated surfaces, ensuring a smooth transition between the integrated surfaces and the adjacent surfaces. The specific rule is defined as follows:
The guide curves refer to the boundary lines that control the generation of the surface in the lofting command. Different guide curves will produce different transition surfaces. Therefore, the key to drawing a transition surface is to define one or a set of guide curves [20]. These guide curves need to pass through feature points and should be smooth and simple. NURBS curves can also be used for fitting these guide curves:
After constructing the guide curves, all section lines need to be evenly divided into points. The method for evenly dividing the points is as follows:
where m represents the number of node vectors in the set of section line node vectors . Suppose the node vectors for two section lines are and , then the final point selection rule is . By connecting the evenly divided points at corresponding positions in the node vectors using the rule , a NURBS curve can be generated, forming the wireframe supporting the lofted surface.
Interpolation based on the wireframe allows for obtaining all the points on the final lofted surface, completing the lofting operation. The interpolation rule is defined as follows:
where and represent the NURBS curve equations of the two end section lines, while and denote the NURBS curve equations of the two guide curves. a and b represent the proportional positions of the interpolation points in the lofting direction and the section direction, respectively.
2.5. Adjustment Rule
The adjustment rule is defined as follows:
During the design phase of integrated shapes, adjustments and optimizations are often required. The adjustment rule should be constructed based on the specific requirements of integration. Here, blunt leading edge modification is taken as an example to illustrate the ease of use and efficiency of the discrete point cloud reconstruction rule during adjustment iterations.
In high Mach number flight, shock waves and viscous blocking effects cause the flow kinetic energy at the leading edge to transform into thermal energy, leading to a sharp increase in the leading edge temperature, necessitating a blunt treatment of the intake leading edge [21]. Common methods for leading edge bluntness include blunting surface completion and cross-sectional cutting.
The principle of the blunting surface rule involves directly displacing the surface of the inlet to blunt the radius, followed by filling in relevant defects with fillets, as illustrated in Figure 5. The corresponding rule formula is as follows:
where R represents the blunting radius, and denotes the new coordinates of the blunted inlet point cloud. represents the formula for the leading edge fillet curve, and represents the coordinates of the leading edge point.
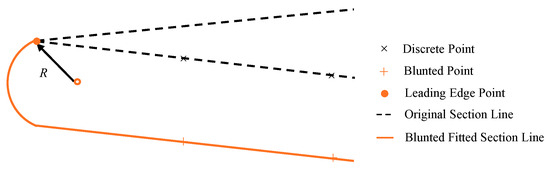
Figure 5.
The principle of the blunting surface rule.
The principle of the cross-sectional cutting rule involves taking the angle bisectors of the upper and lower surfaces, setting the leading edge radius, determining the center of the blunting fillet on the angle bisector line based on the length of the leading edge radius, and then blunting and removing the excess surface, as illustrated in Figure 6. The corresponding rule is as follows:
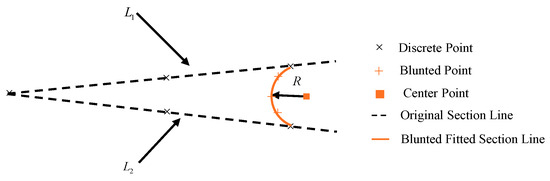
Figure 6.
The principle of the cross-sectional cutting rule.
3. Application Example
3.1. Validation of Numerical Method
In this study, ANSYS Fluent (2022 R1) was employed to simulate the flow field. During the numerical simulations, the AUSM (Advection Upstream Splitting Method) flux scheme was utilized, and the Navier-Stokes equations were solved using a second-order upwind spatial discretization. The SST (Shear Stress Transport) turbulence model and standard wall functions were adopted to obtain viscous information. Throughout the simulations, air was assumed to be a perfect calorically gas, and the fluid viscosity was determined using Sutherland’s law. Freestream conditions were applied at the far field, with the outflow conditions specified via extrapolation. Additionally, adiabatic and no-slip conditions were applied to the wall regions. The computational domain was discretized using an unstructured tetrahedral mesh.
To evaluate the numerical simulation accuracy of the methods and conditions used in this study, the Agard-B model was selected for validation. Zhang et al. [22] provides the shape of the test model and the related aerodynamic information obtained from wind tunnel experiments. The numerical simulation results for the aerodynamic performance of Agard-B as a function of Mach number, with the angle of attack fixed at 0°, are shown in Figure 7. It is clearly evident that, under high Mach number conditions, the numerically obtained lift and drag coefficients have an average error of 3.29% compared to the experimental data. This demonstrates that the numerical methods employed in this study can simulate high Mach number flow fields within an acceptable error range, ensuring the reliability of the subsequent results.
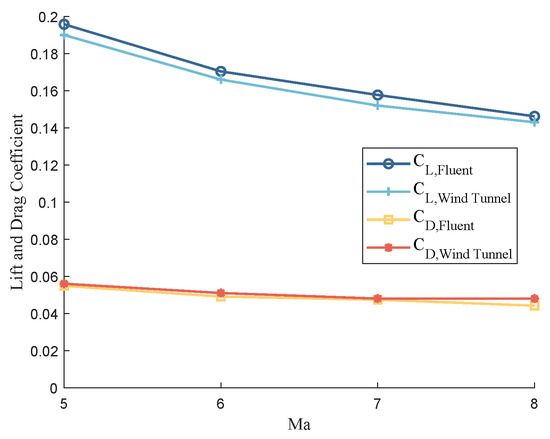
Figure 7.
Comparison between numerical simulation results and experimental data of Agard-B.
3.2. Integrated Shape Generation
The method was validated using a layout where a waverider forebody is combined with an inward-turning inlet in a tandem configuration along the flow direction. The relative positioning of this layout is determined by the symmetric surface shock wave closure. The integrated model is generated following the steps of surface discretization, point discretization, section line reconstruction and surface reconstruction.
The input for the integrated method is a cone-derived waverider forebody produced by the inverse design method [23]. The upper surface is generated using the free streamline method, while the lower surface is created by stream tracing the leading-edge line in the external cone flow field, as illustrated in Figure 8. The inlet is an inward-turning design created for a specified baseline flow field [24], as shown in Figure 8.

Figure 8.
Inputs used for integration. (a) Waverider. (b) Inlet.
The shock angle of the waverider forebody’s symmetry plane is calculated separately under free-stream conditions of Ma = 6 and a 0° angle of attack. Based on the positioning rule, the position parameters are adjusted so that the inlet cowl-lip is located on the waverider forebody’s symmetry plane shock, achieving a two-dimensional “shock closure’’ effect, as shown in Figure 9. The goal is to minimize the impact of the inlet on the waverider forebody’s shock and to prevent complex interactions between the waverider forebody shock and the inward-turning shock reflections within the inlet.
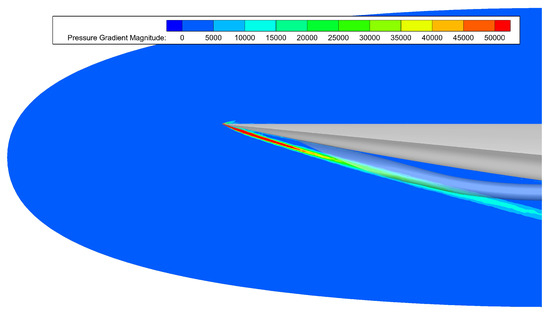
Figure 9.
Forebody/inlet matching based on waverider symmetry plane shock wave.
In accordance with the discrete rule , the feature sections are set at the cowl-lip, the beginning of integration, and the end of integration. Sections between two feature sections are established based on the function, with the section coordinates listed in Table 1. Feature points are designated at the maximum and minimum heights, the farthest points on the lateral side, intersections of lines, and the inlet’s leading edge, guided by the function. 10 alternative points between feature points are determined based on , with discrete points selected through curvature filtering, establishing the sequence of discrete points for subsequent section line reconstruction. Lastly, the function is applied to introduce a displacement to the surface point cloud of the inlet, achieving thickening of the inlet wall and leading-edge blunting, thus completing the point cloud discretization of the integrated shape.

Table 1.
Discrete cross section positions.
The transition angle between the inward-turning inlet and the waverider is significant, and the fitting target curve is complex. Utilizing the rule, the point cloud within the same section is reconstructed into section lines. During reconstruction, segments are categorized based on feature points into: upper surface segment of waverider (1), lower surface segment of waverider (2), tangential transition segment (3), fusion segment (4), leading-edge blunting segment (5), and inlet inner wall segment (6). The reconstructed section lines are illustrated in Figure 10. Given the current configuration, the generation of discrete section outlines necessitates consideration of the fusion segment adjustment rule:
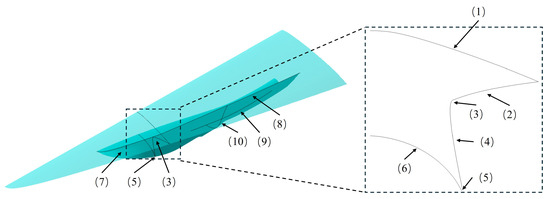
Figure 10.
Adjusted positions of the fusion lines.
- : The cross-section line of the fusion segment (4) should be tangent to the cross-section line of the lower surface segment of waverider (2), as shown in Figure 10 (3). This ensures a smooth configuration.
- : The leading edge of the inlet adopts the blunting surface rule, as shown in Figure 10 (5).
- : When transitioning to the shockwave body, the guide curves of the merging segment should be positioned closer to the symmetry plane than the inlet leading edge, particularly before reaching the maximum area of the inlet, as illustrated at Figure 10 (7). This positioning allows for the merging segment surface to contract inwardly, aiming to prevent significant resistance caused by the merging segment surface directly facing the incoming flow direction. Additionally, this facilitates smooth displacement of the uncaught airflow.
- : After the maximum area of the inlet, the guide curves of the merging segment on the waverider body should gradually move away from the symmetry plane in the direction of the airflow, as shown in Figure 10 (8). This adjustment aims to prevent excessive pressure drag.
- : The inlet wall and the fusion segment wall should maintain a certain structural distance, as shown in Figure 10 (9).
- : The shape of the fusion segment after the cowl-lip should be convex to prevent excessive pressure drag, as shown in Figure 10 (10).
Upon completing the reconstruction, the coordinates of the feature points on each section line are extracted. is used to generate the bounding loft guide curves, which close at the common leading-edge point. The final discrete wireframe is illustrated in Figure 11. Using the section lines and guide curves as inputs, is applied to generate the final integrated shape. The discretely reconstructed integrated shape, including the forebody, inlet and integrated fusion segment, is shown in Figure 12.

Figure 11.
Discrete wire frame of the integrated shape.
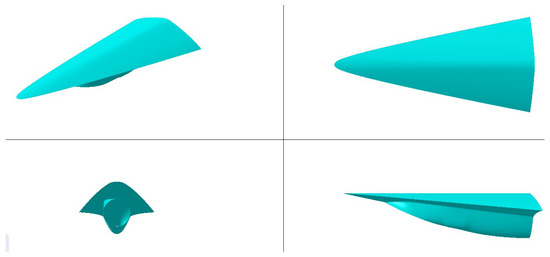
Figure 12.
Integrated shape.
3.3. Geometric Analysis
To verify the geometric accuracy of the integrated method, a comparison was performed using sampled points. Random coordinates in the X and Y directions were selected within the range of the integrated shape. The Z-coordinate values were compared to determine the surface error, as shown in Table 2. The average fusion error for each segment is 0.13%, demonstrating that the integrated method effectively merges the inlet and waverider geometric models while maintaining minimal deviation in the primary aerodynamic surfaces. This ensures that optimal aerodynamic performance is preserved.

Table 2.
Geometric error before and after integration.
3.4. Aerodynamic Analysis
The validated numerical method was used to perform the aerodynamic assessment of the inlet, waverider, and integrated shape. The computational settings are detailed in Table 3. Figure 13 illustrates the unstructured grid and the inflow and outflow boundary conditions used in the computational test of the integrated vehicle. The pressure far field is set as the boundary condition for inlet 1, while a pressure outlet is used for outlet 1 and outlet 2. The grids are refined in the vicinity of the forebody and within the inlet. Due to the symmetry of the geometric configuration, only half of the flow field needed to be solved, resulting in 26,942,691 unstructured grid cells. The first layers of grids all meet the requirement of .

Table 3.
Calculation setting.
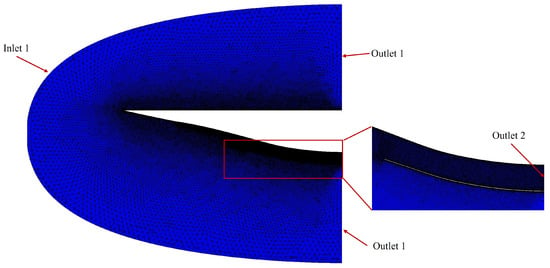
Figure 13.
Computational grid for integrated shape.
A comparison of the aerodynamic performance between the integrated shape and the waverider before integration is presented in Table 4. The data reveals that the lift-to-drag ratio of the waverider decreases after the integration with the inlet. Figure 14 illustrates the pressure coefficient contour under free-stream conditions of Ma = 6 and a 0° angle of attack. Apart from some overflow at the waverider’s leading edge due to viscosity and other factors, the high-pressure gas behind the shock wave is largely confined between the lower surface of the shape and the surface of the first oblique shock wave. This demonstrates that the integrated shape retains favorable waverider characteristics. The shock waves induced by the inlet lip and the waverider body are well-matched, positively impacting the vehicle’s performance. Firstly, there are no complex shock interactions and reflections ahead of the forebody, which prevents additional drag. Secondly, the high flow quality is maintained in front of the inlet, making the actual flow field within the inlet similar to the reference flow field. This provides a stable operating environment for the engine.

Table 4.
Comparison of performance before and after integration.
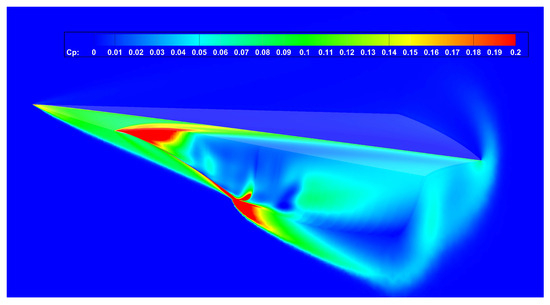
Figure 14.
Pressure coefficient contour of the integrated shape.
The performance comparison between the integrated inlet and the pre-integration inlet is shown in Table 3. The data indicates that the total pressure recovery coefficient of the inlet improves by 15.6% due to the pre-compression effect of the waverider forebody. Figure 15 and Figure 16 presents a comparison of the total pressure contour before and after integration. The pre-compression effect of the integrated forebody reduces the intensity of the first internal turning shock wave in the inlet, significantly decreasing total pressure loss. As a result, high-energy gases are effectively retained within the isolator section of the inlet.
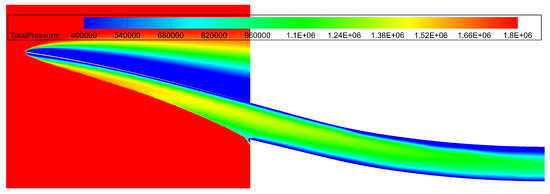
Figure 15.
Total pressure contour of the inlet.
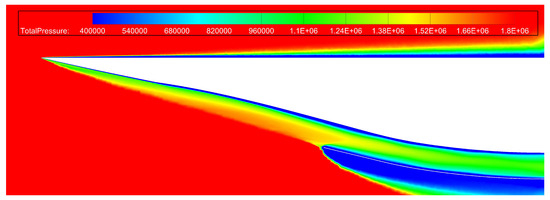
Figure 16.
Total pressure contour of the integrated shape.
The Mach number distribution is uniform in the middle of the throat and the isolator exit, as shown in Figure 17. This ideal phenomenon indicates that the shock wave from the waverider forebody does not degrade the flow quality ahead of the inlet. The internal flow field of the inlet remains largely unchanged, with shock interactions creating a uniformly low Mach number region. This demonstrates that the smooth transition of the integrated shape effectively reduces the interaction between the inlet and the forebody.
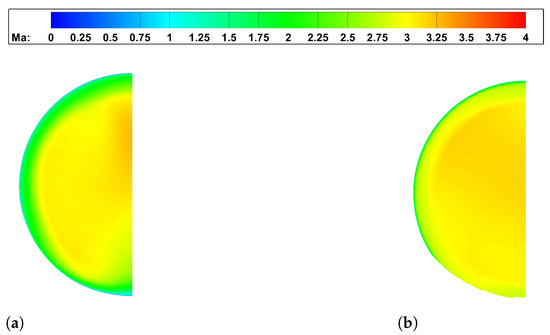
Figure 17.
Mach number contours of inlet. (a) Throat. (b) Isolator exit.
Figure 18 shows the pressure coefficient contour on the symmetry plane at Mach 6 and 0° angle of attack. The analysis indicates that due to viscous effects and the two-dimensional design of the symmetry plane shock wave closure, the internal compression shock wave slightly deviates from the lip position. However, the shock wave generated by the integrated configuration primarily impacts the inlet lip, achieving a shoulder point shock attenuation effect and reducing the intensity of the stabilization section shock wave. The shock wave closure characteristics of the internal compression shock wave and the waveriding characteristics of the waverider are effectively retained in the integrated configuration. This unifies the high lift characteristics and excellent inlet performance of the integrated configuration.
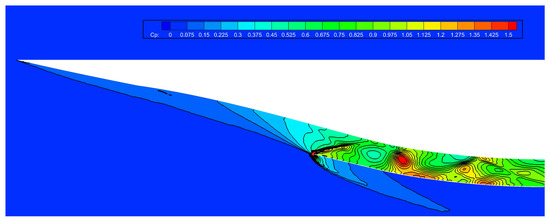
Figure 18.
Pressure coefficient contour of symmetric plane.
3.5. Optimization Analysis
To validate the ease of use of the discrete point cloud method during optimization, the integrated configuration’s blending section was optimized through point cloud displacement. Before optimization, the pressure near the throat and isolator exit significantly dropped due to the large angle with the airflow direction. To improve the lift-to-drag ratio, the point clouds of the throat and the isolator exit were displaced along the gravitational direction. This adjustment resulted in the reconstruction of new section lines and an integrated shape, as shown in Figure 19.
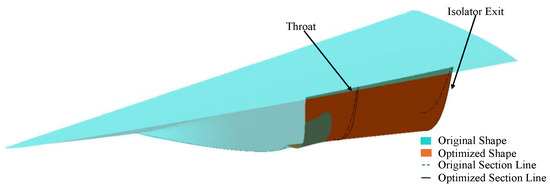
Figure 19.
Shape before/after optimization.
The aerodynamic performance before and after optimization was validated using the previously described mesh generation and computational settings. The results are presented in Table 5, showing a 7.83% improvement in the lift-to-drag ratio after optimization. A comparison of the pressure coefficient contours on the windward surface before and after optimization is depicted in Figure 20. Additionally, the pressure coefficient distribution along the blending section cross-section is illustrated in Figure 21. Due to the small angle between the blending section and the freestream direction, an increase in wall pressure results in a slight increase in drag coefficient and a significant increase in lift coefficient. Consequently, there is an overall improvement in the lift-to-drag ratio.

Table 5.
Comparison of lift/drag ratio before/after optimization.
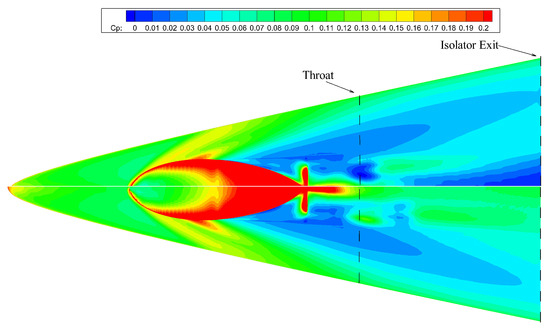
Figure 20.
Comparison of windward surface pressure coefficient contour before/after optimization (The upper half: Original; The lower half: Optimized).
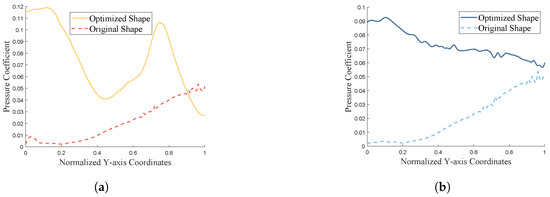
Figure 21.
Pressure coefficient distribution of fusion surface before/after optimization. (a) (throat). (b) (isolator exit).
3.6. Time Analysis
To verify the efficiency of IFD in generating proposals during the conceptual design phase, the waverider forebody/inward-turning inlet aircraft was discretely reconstructed and optimized at coarse (10 cross-sections, 5 discrete points between feature points), medium (16 cross-sections, 10 discrete points between feature points, as previously described), and fine (20 cross-sections, 15 discrete points between feature points) levels of discretization. A comparison was made with the time taken for manual fusion of shapes, and the results are presented in the Table 6 below. Regardless of the coarse, medium, or fine discretization levels, IFD reconstruction significantly outpaced the traditional manual adjustment reconstruction speed. Utilizing IFD as a foundation for rapidly generating integrated matching schemes enables a more efficient iterative optimization process for high Mach number aircraft conceptual design phases, thereby reducing the design and development cycle of high Mach number aircraft.

Table 6.
Comparison of time consumption.
4. Conclusions
IFD employs rules such as point cloud discretization and geometric reconstruction adjustments to rapidly merge individually designed waveriders and inlets into integrated shapes, supporting subsequent optimization iterations. Based on IFD, a tandem fusion of the waverider and inward-turning inlet was constructed, with the geometric error compared to the original pre-fusion shape being only 0.13%. This preservation of excellent aerodynamic and inlet performance was further optimized based on discrete point clouds, resulting in a 7.83% increase in lift-to-drag ratio. Notably, the entire process took only 3.18% of the time required for manual adjustments, demonstrating the significant efficiency of the IFD methodology. This case demonstrates that IFD can efficiently complete the geometric construction and optimization of integrated shapes while preserving the individual performance of waveriders and inlets, providing a powerful tool for conceptual design of high Mach number aircraft in the design phase. Subsequent research will consider more high Mach number flow characteristics, establish corresponding fusion adjustment rules to enhance aerodynamic performance, and utilize artificial intelligence techniques to identify and apply patterns in point cloud distributions.
Author Contributions
Conceptualization, Z.L. and M.L.; methodology, Z.L. and G.Y.; software, Z.L., J.Z. and C.H.; validation, Z.L.; formal analysis, Z.L.; investigation, Z.L.; resources, G.Y.; data curation, Z.L. and G.Y.; writing—original draft preparation, Z.L.; writing—review and editing, Z.L. and M.L.; visualization, Z.L.; supervision, M.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available from the corresponding author upon request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sziroczak, D.; Smith, H. A review of design issues specific to hypersonic flight vehicles. Prog. Aerosp. Sci. 2016, 84, 1–28. [Google Scholar] [CrossRef]
- Ding, Y.; Yue, X.; Chen, G.; Si, J. Review of control and guidance technology on hypersonic vehicle. Chin. J. Aeronaut. 2022, 35, 1–18. [Google Scholar] [CrossRef]
- Jiang, Y.; Ling, Y.; Zhang, S. Investigation of the Inverse Magnus Effect on a Rotating Sphere in Hypersonic Rarefied Flow. Appl. Sci. 2024, 14, 1042. [Google Scholar] [CrossRef]
- Ma, J.; Chen, H.; Wang, J.; Zhang, Q. Real-Time Trajectory Planning for Hypersonic Entry Using Adaptive Non-Uniform Discretization and Convex Optimization. Mathematics 2023, 11, 2754. [Google Scholar] [CrossRef]
- Lu, Q.; Sun, R.; Lu, Y.; Liu, X. Finite-Time Extended State Observer-Based Attitude Control for Hypersonic Vehicles with Angle-of-Attack Constraint. Mathematics 2024, 12, 1061. [Google Scholar] [CrossRef]
- Ding, F.; Liu, J.; Huang, W.; Zhou, Y.; Guo, S. Boundary-layer viscous correction method for hypersonic forebody/inlet integration. Acta Astronaut. 2021, 189, 638–657. [Google Scholar] [CrossRef]
- Li, Y.; Zheng, X.; Shi, C.; You, Y. Integration of inward-turning inlet with airframe based on dual-waverider concept. Aerosp. Sci. Technol. 2020, 107, 106266. [Google Scholar] [CrossRef]
- Yu, Z.; Huang, G.; Xia, C. 3D inverse method of characteristics for hypersonic bump-inlet integration. Acta Astronaut. 2020, 166, 11–22. [Google Scholar] [CrossRef]
- Ding, F.; Liu, J.; Shen, C.b.; Huang, W. Novel approach for design of a waverider vehicle generated from axisymmetric supersonic flows past a pointed von Karman ogive. Aerosp. Sci. Technol. 2015, 42, 297–308. [Google Scholar] [CrossRef]
- Ma, Y.; Guo, M.; Tian, Y.; Le, J. Recent advances and prospects in hypersonic inlet design and intelligent optimization. Aerosp. Sci. Technol. 2024, 146, 108953. [Google Scholar] [CrossRef]
- Dai, Y.; Fan, Z.; Xu, J.; He, Y.; Yu, X. A Rapid Method of Integrated Aeropropulsive Analysis for the Conceptual Design of Airbreathing Hypersonic Aircraft. Aerospace 2024, 11, 89. [Google Scholar] [CrossRef]
- Ding, F.; Liu, J.; Shen, C.b.; Huang, W. Novel inlet–airframe integration methodology for hypersonic waverider vehicles. Acta Astronaut. 2015, 111, 178–197. [Google Scholar] [CrossRef]
- Wang, J.; Cai, J.; Liu, C.; Duan, Y.; Yu, Y. Aerodynamic configuration integration design of hypersonic cruise aircraft with inward-turning inlets. Chin. J. Aeronaut. 2017, 30, 1349–1362. [Google Scholar] [CrossRef]
- Alkaya, C.; Alex Sam, A.; Pesyridis, A. Conceptual Advanced Transport Aircraft Design Configuration for Sustained Hypersonic Flight. Aerospace 2018, 5, 91. [Google Scholar] [CrossRef]
- Fu, J. Multi-objective aerodynamic optimization of two-dimensional hypersonic forebody-inlet based on the heuristic algorithm. Aerosp. Sci. Technol. 2022, 123, 107470. [Google Scholar] [CrossRef]
- Zhang, D.; Tang, S.; Che, J. Concurrent subspace design optimization and analysis of hypersonic vehicles based on response surface models. Aerosp. Sci. Technol. 2015, 42, 39–49. [Google Scholar] [CrossRef]
- Dimas, E.; Briassoulis, D. 3D geometric modelling based on NURBS: A review. Adv. Eng. Softw. 1999, 30, 741–751. [Google Scholar] [CrossRef]
- Starly, B.; Lau, A.; Sun, W.; Lau, W.; Bradbury, T. Direct slicing of STEP based NURBS models for layered manufacturing. Comput.-Aided Des. 2005, 37, 387–397. [Google Scholar] [CrossRef]
- Hughes, T.; Cottrell, J.; Bazilevs, Y. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput. Methods Appl. Mech. Eng. 2005, 194, 4135–4195. [Google Scholar] [CrossRef]
- Piegl, L.; Tiller, W. The NURBS Book; Monographs in Visual Communication; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar] [CrossRef]
- Guo, L.; Fang, S. Study on aerodynamic force and aerothermal effect of two-dimensional wedge wave rider with different passivation shape of the head. J. Phys. Conf. Ser. 2022, 2403, 012002. [Google Scholar] [CrossRef]
- Zhang, T.; Ye, R.; Jiang, W.; Chen, X. Aerodynamic test data of HSCM calibration models in hypersonic wind tunnel. Phys. Gases 2021, 6, 57–65. [Google Scholar] [CrossRef]
- Sobieczky, H.; Dougherty, F.C.; Jones, K. Hypersonic Waverider Design from Given Shock Waves. In Proceedings of the First International Hypersonic Waverider Symposium, College Park, MD, USA, 17–19 October 1990; pp. 17–19. [Google Scholar]
- Xiong, B.; Fan, X.q.; Wang, Y. Parameterization and optimization design of a hypersonic inward turning inlet. Acta Astronaut. 2019, 164, 130–141. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).