Abstract
The safety of airport runways is important to guarantee aircraft taking-off, landing, and taxiing, and the comparison of the mechanical response of pavement structures under dynamic and static loading by LS-DYNA has rarely been studied. The purpose of this work is to separate two analysis methods to investigate the mechanical response of rigid airport pavements. Firstly, a tire–road coupling model of an airfield was established to evaluate the suitability of dynamic and static analyses. Then, the effects of landing pitch angles, sinking speeds, and tire pressures on the effective stress, effective strain, and z-displacement of the runway were investigated for both dynamic and static analysis. Finally, the significance of influence factors was analyzed by regression analysis in Statistical Product and Service Solutions (SPSS). The results indicated that the effective stress, effective strain, and z-displacement of the runway increased with a decrease in the landing pitch angle, which also increased with an increase in the sinking speed and tire pressure. It was demonstrated that the difference in pavement mechanical response between dynamic and static analyses progressively widened at high tire pressure and sinking speed. In other words, the static analysis method can be adopted to assess the dynamic mechanical behavior when the landing pitch angle is large and the tire pressure is small. Among the various factors of mechanical response, the effect of tire pressure was the most obvious, followed by sinking speed and landing pitch angle. The work proposes a new approach to understanding the mechanical behavior of runways under complicated and varied conditions, evaluates the applicability of the dynamic and static mechanical analysis methods, identifies key factors in the dynamic and static mechanical analysis of rigid runways, and provides technical support for improving and maintaining the impact resistance of pavement facilities.
1. Introduction
With the rapid development of air transport, the safety and durability requirements of airport pavements are increasing. It is well known that the pavement is subjected to both static and dynamic loads generated by aircraft taking off, taxiing, and parking during the process of airport operations, contributing to stresses and displacements produced on the surface and within the pavement structure that affect the safety of aircraft operations. The results can be employed to identify potential safety hazards, determine the risk level of existing problems, formulate reasonable and targeted maintenance plans, optimize resource allocation, and promote the sustainable development of airport facilities by implementing a systematic mechanical response assessment of the runway [1,2,3]. Currently, tests including the Charpy Impact test, the Falling Weight Deflectometer (FWD), and the Hopkinson Bar and simulations containing ANSYS (Canonsburg, PA, USA), COMSOL (Stockholm, Sweden), and ABAQUS (Dassault Systèmes, France) are used to evaluate the mechanical response of airport pavement [4,5,6]. However, However, the experiments are time-consuming and costly, with specific test conditions and large experimental errors that affect the accurate characterization of the evolution of pavement performance [7]. Simulations, on the other hand, can replicate a wide variety of operating conditions at any time with lower costs and higher safety. Among the methods for analyzing pavement mechanical response, finite element analysis (FEA) is a traditional approach that can simulate diverse operating conditions, reveal the interactions between aircraft and pavement at a lower cost, and further predict pavement deformations, stress distributions, and potential failure modes [8].
It is widely recognized that the mechanical response of airport pavement to loads is mainly influenced by the method of static and dynamic loads. As the most typical static load, gravity has a long duration and is consistently and uniformly applied to the pavement through aircraft landing gear tires, which also possess the characteristics of stable magnitude and direction. The dynamic processes involve mass, velocity, acceleration, and other factors, and the value and direction of the dynamic loads are also variable. Moreover, it is suggested that the pavement structures are in an extremely unstable state within a short period after experiencing the unpredictable and destructive impact effects of dynamic loads, exhibiting significantly different mechanical behaviors from those under static loading conditions [9]. Existing static analysis methods can be used to calculate mechanical properties at low speeds and weights [10]. Consequently, most researchers often simplify dynamic loads as concise and stable static loads in order to reduce design steps and calculation volume [11,12,13]. However, to further investigate the change in airport pavement structure during daily operation, the characteristics of impact and vibration under dynamic loads are essential. The differences in the mechanical response of pavement structures under dynamic and static loading need to be considered separately [14].
At present, the impact load of aircraft is simplified into a periodic function to analyze the pavement’s mechanical response in airport operations. Alternatively, the static load can be multiplied by an empirical amplification factor to account for the effects of the dynamic action of the aircraft [15]. Huang pointed out that the efficiency calculations could be improved by transferring the load variation curve into a semi-sine function to simulate pavement stress [16]. Based on this, Kim, Wang, and other researchers utilized harmonic loads to characterize the mechanical effects of vehicles on the pavement and to study the mechanical response of the pavement [17,18]. With the exception of simple harmonics, Saad and others converted loads into triangular waves in order to explore the mechanical response and damage process under cyclic action [15,19]. Otherwise, Zeng constructed a three-dimensional model of an airport runway by FEA. In his study, the effect of complex aircraft landing gear on pavement mechanics has been simplified by converting loads using the dynamic load coefficient [20]. Moreover, the influence of dynamic loads on the pavement was also worthy of attention. Zeng utilized FWD to determine the relationship between impact load and flexural deformation, while Gu and other researchers developed a virtual prototype model by Automatic Dynamic Analysis of Mechanical Systems (ADAMS) to simulate the impact behavior [21,22,23,24,25]. In addition, Cui and Zhang employed the Runge–Kutta method and an artificial intelligence algorithm to study the mechanical response of pavement under dynamic load [26,27,28]. To ensure safety and reliability, researchers have worked to improve the impact resistance and durability of airport pavements through experimentation and simulation. However, it is challenging to fully replicate complex loads in real-world environments through compression testing, FWD, and vibration testing, which are easily influenced by human factors [29]. Furthermore, the existing simulation methods mostly transform dynamic problems into static ones by directly multiplying them with an amplification factor, which lacks scientific validity and applicability for modern large aircraft [26,30]. Therefore, we propose a method to distinguish the applicability of dynamic and static analysis methods, with a further view to understanding the mechanical behavior of pavement.
In this paper, Workbench is used to establish a tire-runway coupling model for the rigid pavement of an airport, which is imported into LS-DYNA to develop a comparative study of the mechanical response of the pavement under both static and dynamic methods. Additionally, the effects of landing pitch angle, sinking speed, and tire pressure on the effective stress, effective strain, and z-displacement of the pavements were evaluated, and the significance of these variables on the mechanical response indicators was determined by significance analysis in SPSS. Importantly, it is expected that this work can provide a useful approach to the construction and repair of airport pavements to further develop runway quality.
2. Methodology
2.1. Finite Element Analysis in ANSYS (ANSYS 2021 R1)
For static analysis, Workbench was used to characterize the equilibrium state, excluding structural inertia and damping. In addition, structural statics problems are limited to the stiffness matrix , which provides a highly efficient solution. The comprehensive balance equation is as follows [31]:
where is the stiffness matrix, is the displacement vector, and is the external force vector.
During the simulation of impact processes, a common approach to applying loads is to attach a mass to a structure and then apply the initial velocity. This method can provide a more accurate representation of the dynamic mechanical response and energy conversion during the impact of an aircraft landing under the influence of gravity, providing valuable references for runway safety assessment. LS-DYNA was selected as the dynamic analysis tool to describe the instantaneous behavior of the structure, explore the dynamic effects including impacts and collisions, and calculate the mechanical response under time-varying loads, taking into account the inertia and damping effects. The relevant dynamic equation is as follows [32]:
where is the mass matrix, is the damping matrix, is the stiffness matrix, is the external force vector, is the acceleration vector, is the velocity vector, and is the displacement vector.
2.2. Significance Analysis in SPSS
Regression analysis is a statistical method used to investigate the relationships between variables, including the landing pitch angle, sinking speed, and tire pressure. The least-squares method and maximum likelihood estimation are used to construct an optimally fitting equation to predict the pattern of the dependent variable in relation to the independent variable [33]. In this study, the optimally fitting equations of the variables were developed separately to perform causal analysis, and the degree of response of the mechanical performance was also considered. To identify extreme values and variations in the data, a heatmap format with color intensity was chosen to visually represent the degree of correlation [34].
In this paper, variables such as the landing pitch angle, sinking speed, and tire pressure were considered. The mechanical response indexes, such as effective stress, effective strain, and z-displacement, were used as the control parameters for the color. The intensity of the color in each quadrangle was directly proportional to the magnitude of the corresponding mechanical response.
2.3. Developing a Finite Element Model
The construction of an airport pavement tire–road-coupled model typically involves five steps, namely, the model geometry, material properties, meshing and boundary conditions, vibration frequency, and model validation. The flowchart is shown in Figure 1.
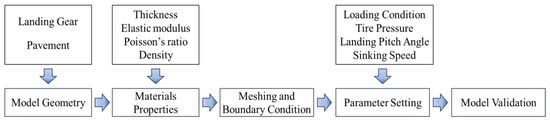
Figure 1.
Flowchart of the model.
2.3.1. Model Geometry
All of the loads exerted by an aircraft on the runway are transmitted through the wheels of the landing gear, which would have a significant effect on the magnitude of the loads experienced by the runway. One of the main landing gears derived from the Boeing 737–800 was used as a model, and the geometry model is shown in Figure 2a. It is well known that aircraft tires are composed of multiple layers of rubber and cord fabric, with a simple vertical tread pattern and a thickness of 20 mm. An aircraft radial tire was selected with structures such as the inner liner, carcass fabric layer, belt layer, reinforcement layer, sidewall, tread, steel bead, tread compound, and bead heel. To ensure the quality of the mesh, the parts were integrated into five components: tire bead, sidewall, carcass, tread compound, and tread. The composition of the tire is illustrated in Figure 2b. It is suggested that the overall structure of the tire was highly symmetrical, suggesting that the cross-section of the aircraft tire rotated around the central axis of the tire for one revolution, which could be considered a three-dimensional tire geometry model. The primary purpose of an airport runway is to facilitate diverse ground operations of aircraft, including takeoff, landing, taxiing, and parking. The structural stability and functional characteristics of the runway are essential to the safe operation of aircraft. Some research has indicated that the mechanical response of the runway is negligible when the distance from the aircraft impact load area is more than 15 m [35]. Consequently, the geometric dimensions of the runway were determined to be 15 m × 15 m with a thickness of 5 m. The constructed coupling geometric model is shown in Figure 2c.
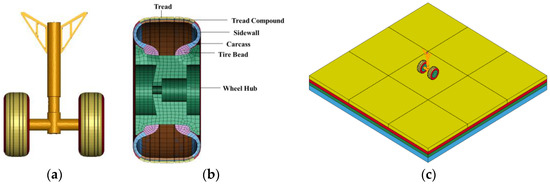
Figure 2.
Geometry of (a) landing gear, (b) tire, and (c) coupling model.
2.3.2. Material Properties
The materials for the aircraft landing gear and tires were defined using structural steel and the Yeoh model. The C10, C20, C30, and density parameters for each component of the tire, including the bead, sidewall, carcass, tread compound, and tread, are presented in Table 1 [36]. A rigid pavement structure was selected, consisting of a cement concrete layer, cement-stabilized upper and lower base layers, and a subgrade. The thickness parameters of the airport pavement, as listed in Table 2, are derived from typical pavement structures, which are also adopted in the engineering project. The material parameters, including the elastic modulus, Poisson’s ratio, and density, were sourced from an engineering laboratory in order to facilitate the connection between the model and the engineering project.

Table 1.
Material constants for different segments of the tire’s rubber.

Table 2.
Performance characteristic metrics of airport runway structure.
2.3.3. Meshing and Boundary Conditions
The model’s mesh density affects the efficiency and accuracy of finite element calculations. In order to improve precision, different mesh methods for different parts were used to balance the central processing unit (CPU) performance and computation time. The wheel hub and buffer system in the landing gear structure were set as the rigid bodies, and the multizone and tetrahedrons mesh methods were adopted with element sizes of 15 mm and 20 mm, respectively. In the case of the aircraft tire, a hex-dominant approach with a 10 mm mesh size was applied, and the mesh size in the contact area between the tire and the wheel hub was smaller. For the runway structure, the tetrahedron mesh method was used with a unit size of 20 mm.
With the exception of the upper surface of the concrete in the pavement structure, the remaining surfaces were configured with displacement constraints. Meanwhile, the surfaces should be set as non-reflecting boundary conditions to simulate an infinite domain, ensuring the mechanical response without reflection and refraction. For the rigid parts of the landing gear, the vertical displacement was free while all other directions were fixed, and the axial rotation of the wheel hub was set to be free.
2.3.4. Parameter Setting and Vibration Frequency
The mechanical response of pavements under different conditions is influenced by many factors, including aircraft type, load, tire pressure, aircraft angle, sinking speed, runway materials, structures, and so on. Due to the limitations of space and content, this paper will focus on the loading condition, tire pressure, sinking speed, and landing pitch angle in relation to the response of pavement.
① Loading Condition
In this study, static analysis applied stress directly to the structures, while dynamic analysis required the input of parameters of velocity, acceleration, and mass. The Boeing 737–800 uses a dual-wheel landing gear structure with a maximum landing weight of 663.80 kN and a tire pressure of 213.21 psi. The conversion coefficients of the main landing gear and buffer system were 95% and 85%, respectively [37]. It was determined that the weight of each landing gear should be 47.30 kN. In addition, the dynamic coefficient was set to 1.25 [38], and we converted the gravity of each landing gear to a pressure of 59.13 kN. For dynamic analysis, a mass point was placed on the landing gear surface with a weight of 4.83 t, and the whole structure was subjected to a gravitational acceleration of 9.8 m/s2 in order to simulate the dynamic effects on the runway during aircraft landings. The mechanical response of the pavement under dynamic and static loading was studied to determine the applicability of the two methods.
② Tire Pressure
Aircraft tires are in direct contact with the runway during takeoff, landing, and taxiing, and require stability, high-temperature resistance, and wear resistance. Aircraft tires are usually filled with nitrogen at a pressure of 190 psi to 230 psi, which provides adequate support and stability and reduces tire wear as well. Tire pressure requirements for different aircraft types depend on factors such as weight, flight speed, and altitude. The objective of this study was to investigate the effect of tire pressure on pavement mechanical response for the B737-800 aircraft model at three specific tire pressures: 1.14 MPa, 1.47 MPa, and 1.57 MPa, corresponding to the A320, B737-800, and B787-800 aircraft, respectively.
③ Landing Pitch Angle
The landing pitch angle refers to the angle of the aircraft relative to its horizontal flight attitude. As for the B737-800, the theoretical upper limit for the pitch angle is 11°, while the lower limit is −0.7° during the landing process [39]. Beyond this range, accidents such as the tail strike, excessive taxiing distance, and sinking speed would occur, potentially causing damage to the structure and discomfort to passengers. It is typical for the landing pitch angle of aircraft to be controlled within the range of 3° to 6° in order to ensure a safe, stable, and comfortable landing [40]. In this study, landing pitch angles of 3°, 4°, 5°, and 6° were selected for subsequent calculations to analyze the influence on the mechanical response of rigid airport pavements. The diagram of aircraft attitude angle is shown in Figure 3.
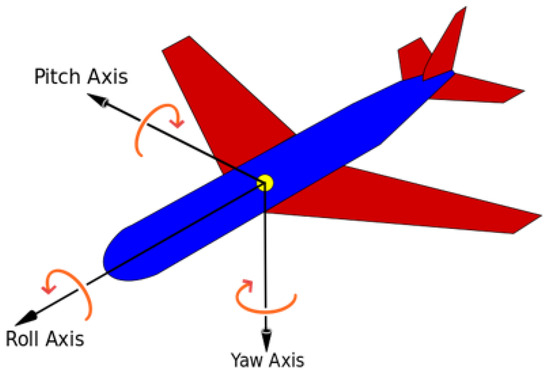
Figure 3.
Aircraft attitude angle diagram.
④ Sinking Speed
The sinking speed of an aircraft refers to the vertical speed at which an aircraft descends during takeoff. During the descent phase, an appropriate sinking speed is crucial to ensure a smooth landing and to reduce the impact force on the runway. The sinking speed of a commercial aircraft should be ≤3.05 m/s and ≤1.83 m/s, respectively, when the maximum landing weight and the maximum take-off weight are considered separately in accordance with Article 25.473 of the “China Civil Aviation Regulations: Part 25”. In this paper, the maximum landing weight of the aircraft was adopted for the subsequent calculations, and the sinking speeds were set to 1 m/s, 2 m/s, and 3 m/s to investigate the influence on the mechanical response of the runway.
2.3.5. Model Validation
In this study, the FWD test was performed on an existing rigid airport pavement to validate the accuracy of the tire–road-coupled mechanical model [41]. The 4E rigid airport runway was used as the sample, with a concrete structure thickness of 400 mm, an average PCI value of 88, and a damage level of “excellent”. The FWD test was performed with a 450 mm diameter load plate, using a dynamic load with a peak value of 250 kN [42]. Based on the thin-wall theory, the tire pressure is approximately equal to the ground pressure. In addition, the ground pressure on the load plate can be considered equivalent to the tire pressure, both of which are 1.57 MPa. The drop hammer of FWD was oriented perpendicular to the runway and was in free fall. During the simulation process, the landing pitch angle and the sinking speed were set to 0° and 0 m/s, respectively, based on the actual FWD tests, and the distance between measurement points in the model was 300 mm. Validation of the tire–road-coupled mechanical model was achieved by comparing the measured data from the FWD test and the simulation results. Figure 4a,b represents the results of the FWD test and the model calculation, respectively. The origin point of the drop hammer was defined as d01, with a distance of 300 mm between each adjacent point. By comparing the results, the accuracy of the model was validated, as shown in Figure 5.
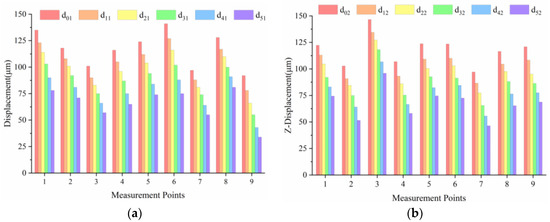
Figure 4.
Runway displacement results: (a) FWD test results, (b) model calculation results.
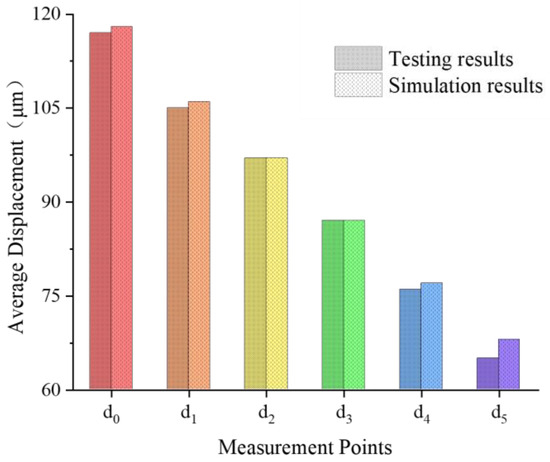
Figure 5.
Comparison of test and simulation average results.
Figure 5 illustrates that the displacement of the runway decreased as the measurement points moved away from the impact point in both the test and the simulation. To validate the accuracy of the model, a two-sample t-test was performed on the average displacements at 18 different points located at different distances. At the 0.05 significance level, there was no significant difference between the FWD test and the simulation results, indicating that the model can accurately characterize the actual displacement state of the pavement. Therefore, the calculation results under different conditions based on this model have a certain reference value for future studies.
3. Results and Discussion
The four kinds of landing pitch angles, three sorts of sinking speeds, and tire pressures were selected as the research objects to conduct separate dynamic and static analysis studies, resulting in a total of 36 operating conditions. The corresponding relationship between the numbers and the conditions is presented in Table 3.

Table 3.
Calculation conditions.
3.1. Dynamic and Static Analysis
The differences in the mechanical response of airport rigid pavements subjected to different load application methods, as well as the variations in dynamic and static analysis response, are shown in Figure 6, Figure 7 and Figure 8.
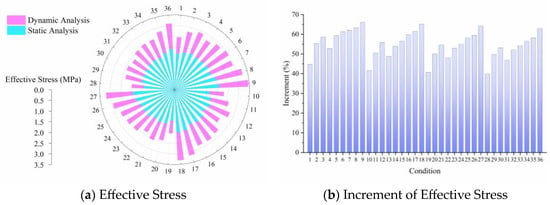
Figure 6.
Effective stress in dynamic and static analyses.
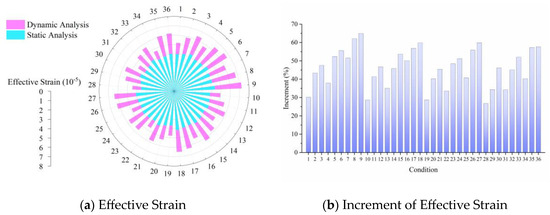
Figure 7.
Effective strain in dynamic and static analyses.
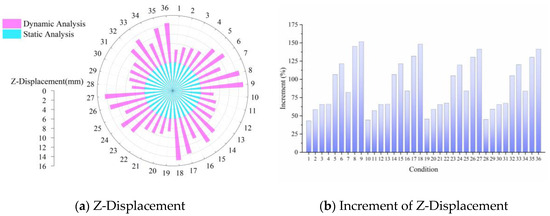
Figure 8.
Z-Displacement in dynamic and static analyses.
Figure 6 depicts the effective stress under various conditions in dynamic and static analyses of airport rigid pavements. From Figure 6a, it is clear that the effective stress in dynamic analysis exceeded those calculated in the static method. It is apparent that the result obtained from the dynamic analysis was notably higher than that of the static under the condition of considering stress, strain, and z-displacement, which was in agreement with the results obtained from the FWD and load plate tests [29,43,44]. Nevertheless, the variation trend of the effective stress from dynamic and static analysis methods was similar when the landing pitch angle, sinking speed, and tire pressure were different. The effective stress of pavements gradually decreased as the landing pitch angle increased in the case in which the tire pressure and sinking speed were constant. The dynamic method promoted that the effective stress at 3° was approximately 1.05 times, 1.13 times, and 1.17 times that of 4°, 5°, and 6°, respectively, which was approximately 1.03 times that of the static one. At a constant landing pitch angle and sinking speed, the effective stress of the dynamic and static analysis increased by 8.7% and 14.1%, respectively, with increasing tire pressure. Furthermore, with a constant landing pitch angle and tire pressure, the effective pavement stress increased by 9.8% and 19.6%, respectively, as the sinking speed increased, indicating that the sinking speed had a more significant effect on the effective pavement stress.
In Figure 6b, the incremental effective stress of the dynamic and static calculation methods is compared. The average incremental effective stress at landing pitch angles of 4°, 5°, and 6° decreased by 5.8%, 7.9%, and 9.7%, respectively, in comparison with that at 3° under the constant sinking speed and tire pressure. This implies that the difference in stress between the dynamic and static loads decreased with the increase in the landing pitch angle, as at last it tended to stabilize. The average incremental effective stress at sinking speeds of 2 m/s and 3 m/s increased by 17.7% and 41.7%, respectively, in comparison to that at 1 m/s with the same landing pitch angle and tire pressure. It can be inferred that the difference between the dynamic and static loads also increases with the sinking speed increasing, while the effect of the sinking speed on the effective stress is more significant than that of the landing pitch angle under the dynamic and static analysis methods. Moreover, the average incremental effective stress at tire pressures of 1.47 MPa and 1.57 MPa increased by 12.2% and 19.3%, respectively, compared to that at 1.14 MPa, indicating that the difference in effective stress is more obvious as the tire pressure increases. In summary, the calculation of effective stress in both dynamic and static analyses is first influenced by the sinking speed, followed by the tire pressure and landing pitch angle. The greater the tire pressure and sinking speed, the greater the diversity that can be observed in the two analysis methods.
The effective strain and increment under the two analysis methods for rigid airport pavements are illustrated in Figure 7. From Figure 7a, it can be seen that the effective strain of the dynamic method was larger than that of the static one. Concrete, as a rigid material, exhibits elastic behavior and shows a linear relationship between stress and strain when subjected to small loads before damage occurs [45]. Therefore, the changes in landing pitch angle, sinking speed, and tire pressure are similar to the variation laws of the effective stress, which would increase with the decrease in the landing pitch angle, and also increase with the increase in sinking speed and tire pressure. Importantly, the effective strain results of the dynamic analysis were 1.01 times, 1.34 times, and 1.82 times those of the static analysis for various landing pitch angles, tire pressures, and sinking speeds.
Figure 7b exhibits the increase in effective strain under the two analysis methods, indicating that the increment rules of the effective strain are similar to those of effective stress. The difference between the dynamic and the static analysis results became more apparent when the landing pitch angle decreased, while the sinking speed and tire pressure increased. Furthermore, the order of influence factors for the gap between the dynamic and the static analyses of airport rigid pavements is as follows: sinking speed > tire pressure > landing pitch angle.
Figure 8 demonstrates the z-displacement and incremental changes in rigid airport pavements under dynamic and static analyses. From Figure 7a, it can be seen that the z-displacement of the pavement was independent of factors such as landing pitch angle, sinking speed, and tire pressure under the static analysis method. However, the z-displacement of the pavement changed slightly by approximately 1% with the landing pitch angle in the dynamic analysis, which was insignificant. The z-displacement of the pavement at sinking speeds of 2 m/s and 3 m/s exhibited an improvement of 15.3% and 27.2%, respectively, compared to that at 1 m/s, when the landing pitch angle and tire pressure were both stable. Similarly, the runway z-displacement at tire pressures of 1.47 MPa and 1.57 MPa increased by 19.1% and 25.7%, respectively, compared to that at 1.14 MPa. This indicates that the sinking speed has a more significant effect on pavement deformation than tire pressure.
In Figure 8b, the incremental changes in z-displacement under different analysis methods are shown. It can be observed that the z-displacement increments under the two analysis methods remained stable when the sinking speed and tire pressure were constant. However, the increment of the average z-displacement at sinking speeds of 2 m/s and 3 m/s was 54.2% and 93.7%, respectively, compared to 1m/s. Meanwhile, the increase in the average z-displacement at the tire pressure of 1.14 MPa exceeded 67.1% and 60.1% compared with that of at 1.47 MPa and 1.57 MPa, respectively, which was less than the sinking speed. In conclusion, dynamic analysis has a more significant effect on z-displacement compared to effective stress and strain, and the sinking speed has a greater influence on the z-displacement growth rate in dynamic and static analyses.
3.2. Significance Analysis
The relationship between the landing pitch angle, tire pressure, sinking speed, and mechanical indexes of rigid airport pavements is depicted in Figure 9, Figure 10 and Figure 11.
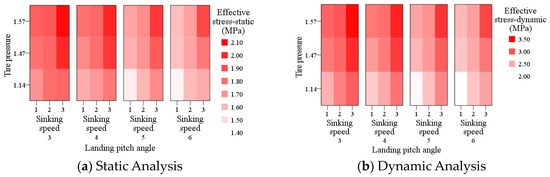
Figure 9.
Effective stress in significance analysis.
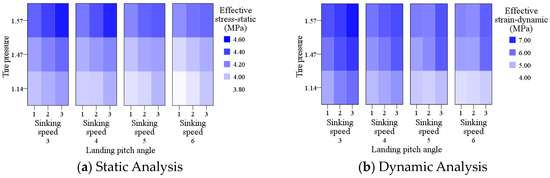
Figure 10.
Effective strain in significance analysis.
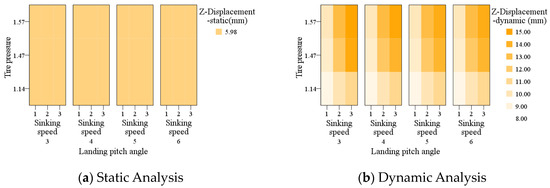
Figure 11.
Z-displacement in significance analysis.
The correlation between the landing pitch angle, sinking speed, tire pressure, and effective stress under the dynamic and static analysis is presented in the heat map shown in Figure 9. The deeper the shade of red, the higher the values of effective stress.
Figure 9a depicts the relationship between the influence factors and effective stress under static analysis. The results of the regression analysis were combined to yield an adjusted R2 of 0.923, indicating a high degree of fit between the equation and the data. The significance level (p < 0.001) confirmed the overall significance of the equation, with at least one independent variable having a significant effect on the dependent variable. The regression coefficients of the tire pressure, landing pitch angle, and sinking speed were 0.381, −0.074, and 0.111, respectively, demonstrating the negative impact of the landing pitch angle on effective stress, while tire pressure and sinking speed showed positive effects. Simultaneously, the significance levels of these factors were all less than 0.001, indicating a significant influence on effective stress. Among them, the tire pressure has the greatest influence, followed by sinking speed, and the landing pitch angle has the least influence.
Figure 9b illustrates the correlations among the landing pitch angle, tire pressure, sinking speed, and effective stress in the dynamic analysis. The regression coefficients of the factors were −0.145, 0.928, and 0.275 through regression analysis, showing that all factors significantly affect the pavement’s effective stress, which is consistent with the results of the static analysis. In contrast, the influence of tire pressure on the effective stress calculated in the dynamic analysis is more conspicuous.
The heat map in Figure 10 depicts the correlations among the landing pitch angle, sinking speed, tire pressure, and effective strain calculated by the two analysis methods. The intensity of blue in the heatmap corresponds to the value of the effective strain.
Based on Figure 10a and the regression analysis, it can be seen that the landing pitch angle, tire pressure, and sinking speed significantly affect the effective strain of pavement under the static analysis. The regression coefficients were −0.060, 0.682, and 0.076, respectively, and the order of the influence factors on pavement effective strain is the same as that for effective stress, i.e., tire pressure > sinking speed > landing pitch angle.
Figure 10b illustrates the effective strain values calculated by various factors such as landing pitch angles, sinking speeds, and tire pressures under dynamic conditions. The inverse relationship between the landing pitch angle and effective strain is shown, while tire pressure and sinking speed are positive. Tire pressure has the most significant effect on effective strain in relation to sinking speed and the landing pitch angle, with a regression coefficient of 2.634. Compared to the static analysis, the influence of effective strain in dynamic analysis is more pronounced.
The correlation between z-displacement and the landing pitch angle, sinking speed, and tire pressure is presented in Figure 11. The various shades of orange represent the z-displacement of the runway under distinct conditions.
From Figure 11a, it is evident that the influence of the landing pitch angle, sinking speed, and tire pressure on the pavement z-displacement is negligible by static analysis. Additionally, the sinking speed does not significantly affect z-displacement; in other words, this parameter may not be pivotal when performing a static analysis. Consequently, it can be concluded that the static analysis method should not be chosen to replace the dynamic mechanical research, even at low tire pressures and large landing pitch angles, due to the influence of sinking speed.
Figure 11b displays the relationship between the variables and the z-displacement under dynamic analysis. Combined with the regression analysis, the fit degree of the regression model was 92.1%. The regression coefficients of the landing pitch angle, sinking speed, and tire pressure were −0.076, 1.937, and 6.083, respectively. The sinking speed and tire pressure demonstrated a significant influence on the pavement z-displacement, with the effect of tire pressure being more apparent.
4. Conclusions
In this study, the mechanical response of rigid airport pavements during the impact process was analyzed using Workbench and LS-DYNA. First, a tire–pavement coupling model was established and validated based on the FWD test results. Then, dynamic and static analysis methods were employed to calculate the effects of the landing pitch angle, sinking speed, and tire pressure on pavement effective stress, effective strain, and z-displacement. Additionally, the differences in mechanical properties of pavement under static and dynamic analyses were compared. Finally, the relationship between factors and mechanical indexes was investigated by a regression analysis in SPSS. The conclusions are as follows:
(1) The mechanical response of the dynamic analysis is significantly larger than that of the static analysis, and the effective stress, effective strain, and z-displacement increased as the landing pitch angle decreased, and, in contrast, decreased as sinking speed and tire pressure decreased. By comparing the effective stress, effective strain, and z-displacement calculated using dynamic and static methods, it can be concluded that the static analysis may be used as an alternative approach to dynamic research under conditions of large landing pitch angles and low tire pressures. However, the results must be validated to ensure the accuracy of the data.
(2) Among the various factors that influence the differences between the dynamic and static analyses of rigid airport pavements, the first is sinking speed, followed by tire pressure, and the last is landing pitch angle. The z-displacement of the static analysis shows no significant correlation with the parameters, and in the dynamic analysis, the z-displacement of the pavement changed slightly with the landing pitch angle by approximately 1%.
(3) The landing pitch angle has a negative effect on effective stress, effective strain, and z-displacement in pavement mechanical indicators, while tire pressure and sinking speed have a positive influence. The correlation coefficients of tire pressure in the static study of effective stress and effective strain are 0.381 and 0.682, respectively. Among these factors, tire pressure has the most significant impact on pavement mechanical performance, followed by sinking speed and landing pitch angle.
(4) The correlation coefficient between the landing pitch angle and the z-displacement regression model should be −0.078, indicating that there is no significant relationship between the landing pitch angle and the z-displacement of the dynamic analysis.
In conclusion, the mechanical analysis of airport pavements provides critical information for pavement design, construction, and maintenance to assess pavement operating conditions. Nevertheless, further research with long-term monitoring data is required, as well as complex multi-factor coupling and standardized evaluation, in order to meet the growing demands of traffic and promote the sustainable development of the industry.
Author Contributions
The authors confirm contributions to the paper as follows: formal analysis, writing—original draft and data curation: Q.M.; funding acquisition and methodology: K.Z.; methodology and writing—review and editing: Y.L.; methodology: M.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by [National Key R&D Program of China], grant number [2021YFB2601200], and the APC was funded by [Ministry of Science and Technology of the People’s Republic of China].
Data Availability Statement
Dataset available on request from the authors.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, T.; Wu, Y.; Wu, H. A Study on Impact of Different Surface Treatment Agents on the Durability of Airport Pavement Concrete. Coatings 2022, 12, 162. [Google Scholar] [CrossRef]
- Gu, G.; Chen, F.; Ma, T.; Xu, F.; Yang, D. Electromagnetic and mechanical properties of soft magnetic cement composite for airport runway induction heating: Experimental and simulation analyses. J. Clean. Prod. 2022, 332, 130141. [Google Scholar] [CrossRef]
- Miah, M.T.; Oh, E.; Chai, G.; Bell, P. An overview of the airport pavement management systems (APMS). Int. J. Pavement Res. Technol. 2021, 13, 581–590. [Google Scholar] [CrossRef]
- Dong, Z.; Wang, T.; Ma, X.; Cao, C.; Sun, J. Structural performance evaluation of airport asphalt pavement based on field data measurement and finite element simulation. Measurement 2023, 210, 112553. [Google Scholar] [CrossRef]
- Senthil, K.; Pelecanos, L.; Rupali, S.; Sharma, R.; Saini, K.; Iqbal, M.A.; Gupta, N.K. Experimental and numerical investigation of transient dynamic response on reinforced concrete tunnels against repeated impact loads. Int. J. Impact Eng. 2023, 178, 104604. [Google Scholar] [CrossRef]
- Sun, J.; Chai, G.; Oh, E.; Bell, P. A Review of PCN Determination of Airport Pavements Using FWD/HWD Test. Int. J. Pavement Res. Technol. 2022, 16, 908–926. [Google Scholar] [CrossRef]
- Zegeye, E.; Le, J.; Turos, M.; Marasteanu, M. Investigation of size effect in asphalt mixture fracture testing at low temperature. Road Mater. Pavement Des. 2012, 13, 88–101. [Google Scholar] [CrossRef]
- Zhu, X.; Zhang, Q.; Chen, L.; Du, Z. Mechanical response of hydronic asphalt pavement under temperature–vehicle coupled load: A finite element simulation and accelerated pavement testing study. Constr. Build. Mater. 2021, 272, 121884. [Google Scholar] [CrossRef]
- Li, Q.; Meng, H. About the dynamic strength enhancement of concrete-like materials in a split Hopkinson pressure bar test. Int. J. Solids Struct. 2003, 40, 343–360. [Google Scholar] [CrossRef]
- Dong, Z.; Ma, X. Analytical solutions of asphalt pavement responses under moving loads with arbitrary non-uniform tire contact pressure and irregular tire imprint. Road Mater. Pavement Des. 2017, 19, 1887–1903. [Google Scholar] [CrossRef]
- JTG D40-2011; Specifications for Design of Highway Cement Concrete Pavement. Ministry of Transport of the People’s Republic of China: Beijing, China, 2011.
- JTG D50-2017; Specifications for Design of Highway Asphalt Pavement. Ministry of Transport of the People’s Republic of China: Beijing, China, 2017.
- MH/T 5004-2010; Specifications for Airport Cement Concrete Pavement Design. CAAC: Beijing, China, 2010.
- Cao, D.; Zhao, Y.; Liu, W.; Li, Y.; Ouyang, J. Comparisons of asphalt pavement responses computed using layer properties backcalculated from dynamic and static approaches. Road Mater. Pavement Des. 2018, 20, 1114–1130. [Google Scholar] [CrossRef]
- Du, L. Simulation Analysis on Performance Degradation of Airfield Pavement Structure under Aircraft Load. Master’s Thesis, Southeast University, Nanjing, China, 2021. [Google Scholar]
- Huang, Y. Pavement Analysis and Design; China Communication Press: Beijing, China, 1998. [Google Scholar]
- Kim, S. Influence of horizontal resistance at plate bottom on vibration of plates on elastic foundation under moving loads. Eng. Struct. 2004, 26, 519–529. [Google Scholar] [CrossRef]
- Wang, J.; Dou, Y.; Li, J.; Wei, M.; Zhai, Y. Dynamic Response Analysis of Jointed Concrete Pavements Under Moving Load Factors. Constr. Technol. 2018, 47, 93–97. [Google Scholar]
- Saad, B.; Mitri, H.; Poorooshasb, H. Three-dimentional dynamic analysis of flexible conventional pavement foundation. J. Transp. Eng. 2005, 131, 460–469. [Google Scholar] [CrossRef]
- Zeng, J. Research on Key Performance of Airprot Runway Pavement with Epoxy Asphalt Concrete. Master’s Thesis, Southeast University, Nanjing, China, 2013. [Google Scholar]
- Liang, L.; Gu, Q.; Liu, G.; Zhang, R.; Jiang, L. Using ADAMS to Assess Dynamic Load of Pavement during Aircraft Landing. J. Southwest Jiaotong Univ. 2012, 47, 502–508. [Google Scholar]
- Qian, J.; Pan, X.; Cen, Y.; Liu, D. Aircraft Taxiing Dynamic Load Induced by Runway Roughness. J. Vib. Shock 2022, 41, 176–184, 269. [Google Scholar] [CrossRef]
- Zhao, M.; Zhao, H.; Wu, D. Identification of Cavities Underneath Concrete Pavement Based on Pavement vibration. China J. Highw.Transp. 2020, 33, 42–52. [Google Scholar] [CrossRef]
- Fu, G.; Wang, H.; Zhao, Y.; Yu, Z.; Li, Q. Non-destructive evaluation of longitudinal cracking in semi-rigid asphalt pavements using FWD deflection data. Struct. Control Health Monit. 2022, 29, e3050. [Google Scholar] [CrossRef]
- Qin, F. Analytical Dynamic Responses of Aeroplane in Landing and Taxiing. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2011. [Google Scholar]
- Cui, Y.; Cen, G.; Liang, L. Study on the Characteristics Dynamic Load of New Aircraft Landing. Comput. Integr. Manuf. Syst. 2020, 37, 15–21. [Google Scholar]
- Bai, Z.; Liu, Y.; Yang, J.; He, S. A constitutive model for concrete subjected to extreme dynamic loadings. Int. J. Impact Eng. 2020, 138, 103483. [Google Scholar] [CrossRef]
- LeMinh, H.; Khatir, S.; AbdelWahab, M.; CuongLe, T. A concrete damage plasticity model for predicting the effects of compressive high-strength concrete under static and dynamic loads. J. Build. Eng. 2021, 44, 103239. [Google Scholar] [CrossRef]
- Shi, B.; Cao, B.; Zhang, Y.; Xu, W.; Ren, W. Test and Analysis on Bearing Capacity of Highway Runway Asphalt Pavement Based on HWD. Sci. Technol. Eng. 2015, 15, 134–140. [Google Scholar]
- Mourlas, C.; Markou, G.; Papadrakakis, M. Accurate and computationally efficient nonlinear static and dynamic analysis of reinforced concrete structures considering damage factors. Eng. Struct. 2019, 178, 258–285. [Google Scholar] [CrossRef]
- Li, J.; Yang, J. Refinement of Structural Statical Mathematical Model. ACTA Aeronaut. ET Astronaut. Sin. 1993, 14, 13–18. [Google Scholar]
- Xing, Y.; Yang, R. Application of Euler Midpoint Symplectic Integration Method for the Solution of Dynamic Equilibrium Equations. Chin. J. Theor. Appl. Mech. 2007, 39, 100–105. [Google Scholar]
- Chatterjee, S. Regression Analysis by Example; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Aldaco, J.R.; Gibert, O.; Giraldo, D.M.; Barbat, A.H. Seismic vulnerability assessment of urban areas using multi-criteria analysis and geographic information systems: A case study in Manizales, Colombia. Nat. Hazards 2020, 104, 1323–1350. [Google Scholar]
- Xue, H. Analysis on Vibration Frequency Response of Rigid Pavement in Conditions of Aircraft Taxing. Master’s Thesis, Civil Aviation University of China, Tianjin, China, 2014. [Google Scholar]
- Luo, R. Nonlinear Finite Element Analysis of 34*10.75-16 Tire of Aircraft in ABAOUS. Master’s Thesis, Guilin University of Electronic Technology, Guilin, China, 2015. [Google Scholar]
- HB 8498-2014; Test Requirement for Landing Gear System Performance of Civil Aircraft. Avic China Aero-Polytechnology Establishment: Beijing, China, 2014.
- Weng, X. Airport Pavement Design; China Communication Press: Beijing, China, 2017. [Google Scholar]
- Meng, Q.; Zhong, K.; Sun, M. Dynamic Response Analysis of Airport Pavement under Impact Loading. Appl. Sci. 2023, 13, 5723. [Google Scholar] [CrossRef]
- Zhu, L. Simulation and Expression of Dynamic Behavior of Rigid Pavement Based on Large Aircraft Virtual Prototype. Doctor’s Thesis, Tongji University, Shanghai, China, 2017. [Google Scholar]
- JTG E60—2008; Field Test Methods of Subgrade and Pavement for Highway Engineering. China Communications Press: Beijing, China, 2008.
- MH/T 5110-2015; In-situ Measurement Specification for Pavement and Subgrade of Civil Airports. Civil Aviation Administration of China: Beijing, China, 2015.
- Zhao, J.; Wang, H. Dynamic pavement response analysis under wide-base tyre considering vehicle-tyre–pavement interaction. Road Mater. Pavement Des. 2021, 23, 1650–1666. [Google Scholar] [CrossRef]
- Xie, N.; Lv, S.; He, Y.; Lei, W.; Pu, C.; Meng, H.; Ma, H.; Peng, X. Load response and fatigue life of cement-stabilized macadam base structure considering dynamic and static load differences and tension-compression modulus differences. Constr. Build. Mater. 2023, 394, 132060. [Google Scholar] [CrossRef]
- Ameen, M. Computational Elasticity. Theory of Elasticity and Finite and Boundary Element Methods; Alpha Science International Ltd.: Oxford, UK, 2005. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).