Optimization Study of Steady-State Aerial-Towed Cable Circling Strategy Based on BP Neural Network Prediction
Abstract
1. Introduction
2. Modeling and Calculation Methods
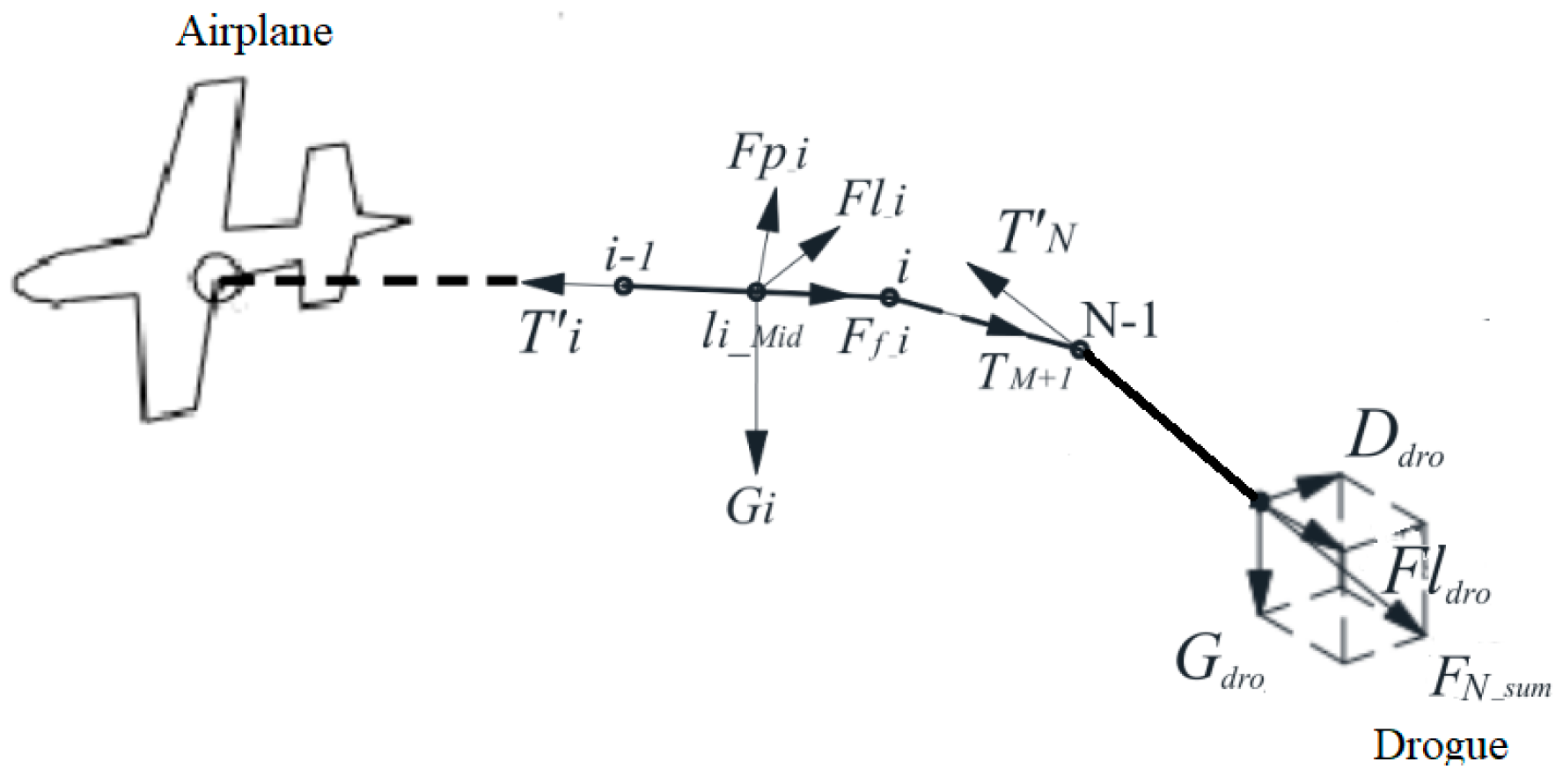
2.1. Steady-State Trailing Cable Model
2.1.1. Quasi-Stationary Circling Aircraft Model for Unconstrained Trailing Cable
- The towing cable is considered a flexible structure that exhibits high flexibility while maintaining inextensible.
- The aircraft maintains a constant altitude while circling uniformly.
- This paper mainly considers the circling of a towed carrier in a stabilized environment. The wind speed profile in the environment is not taken into consideration, and only the relative wind speed in the circling is taken into account as one of the variables.
- In the following section, the computational results of the model in this paper will be verified against the existing literature to verify that the assumptions made in paper do not affect the computational results.
2.1.2. Quasi-Stationary Circling Aircraft Model for Fixed-End Trailing Cable
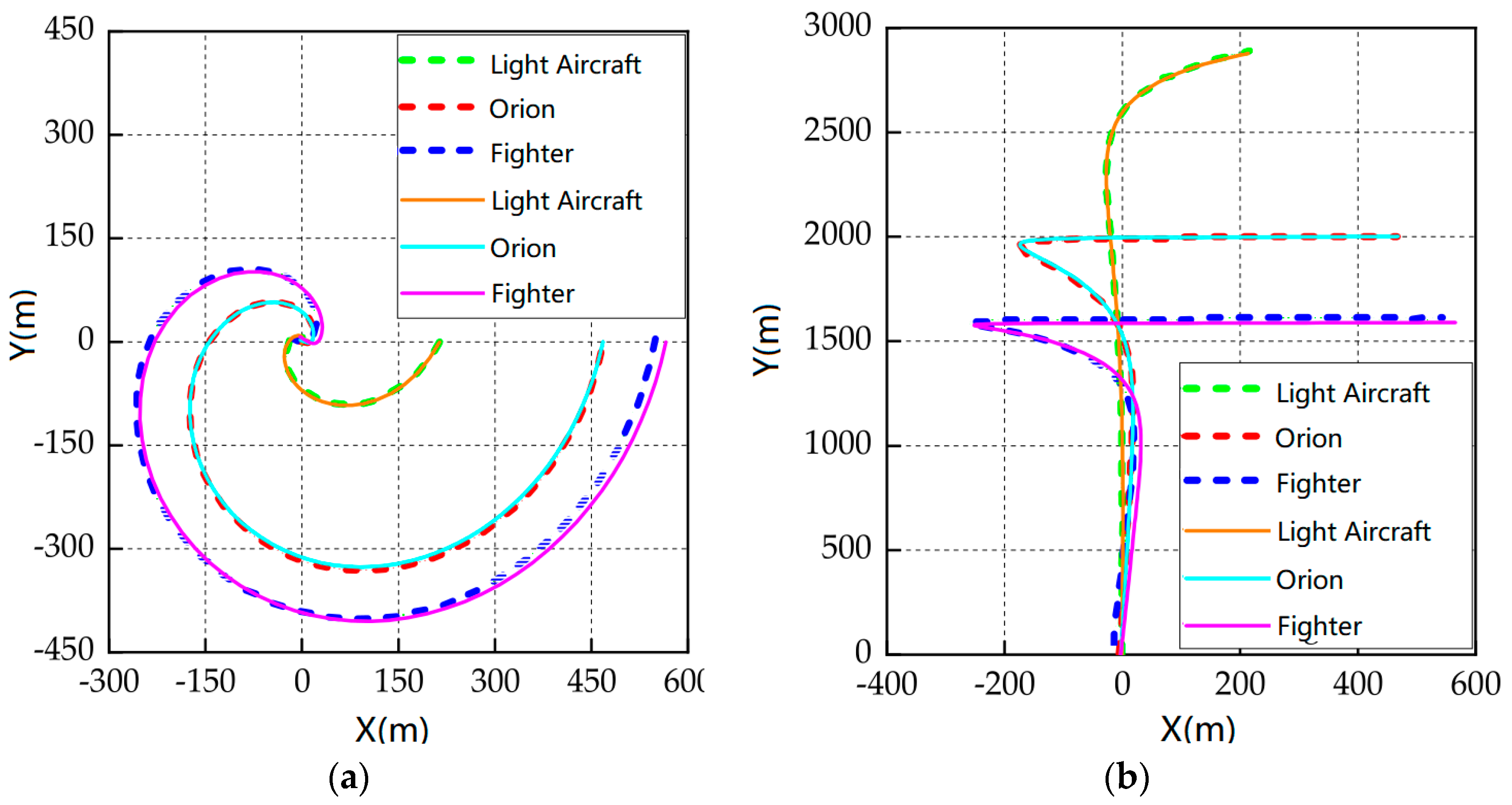
2.1.3. Model Accuracy Validation
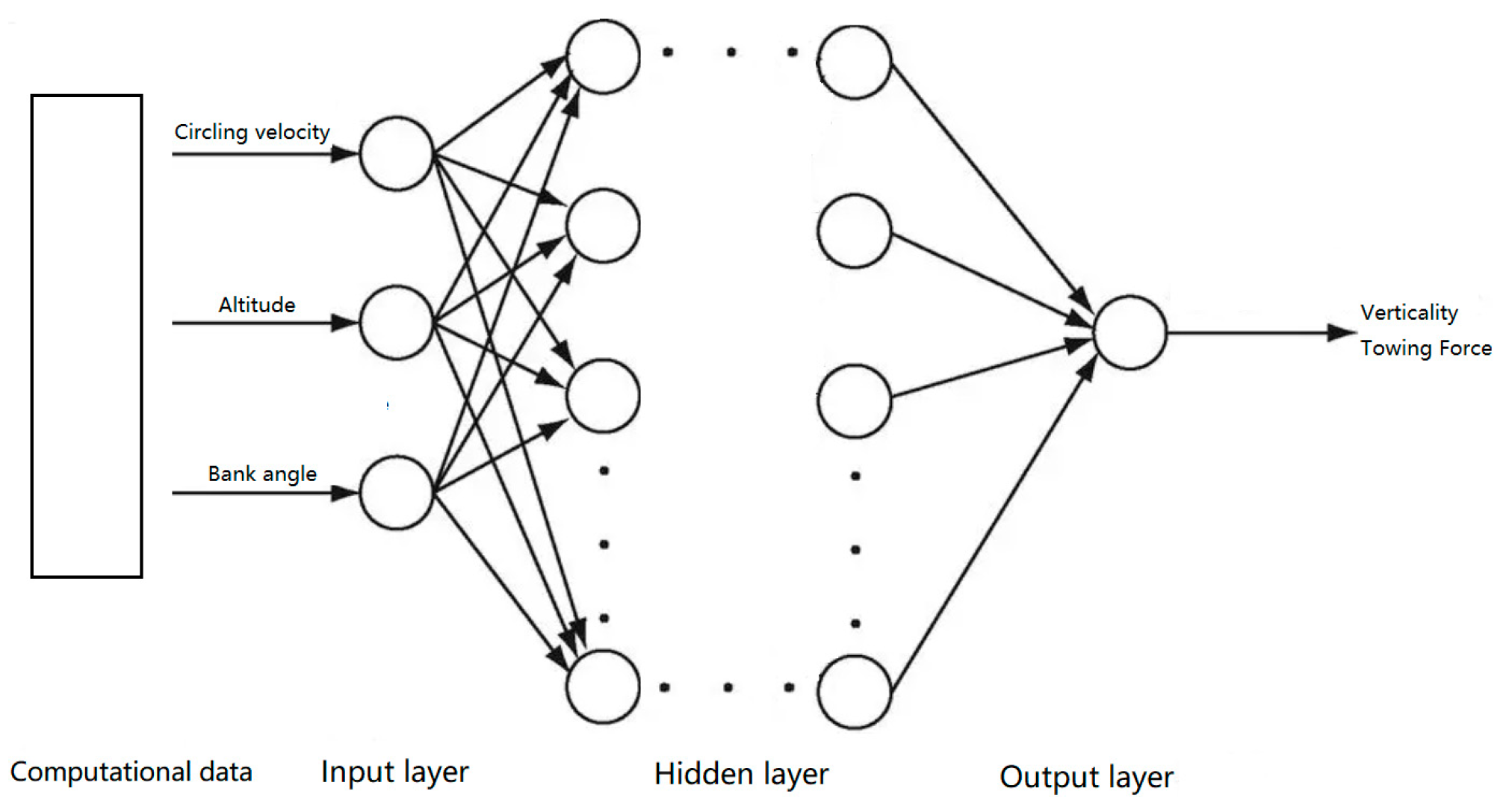
2.2. Neural Network Prediction Methods
2.2.1. Prediction Method Introduction
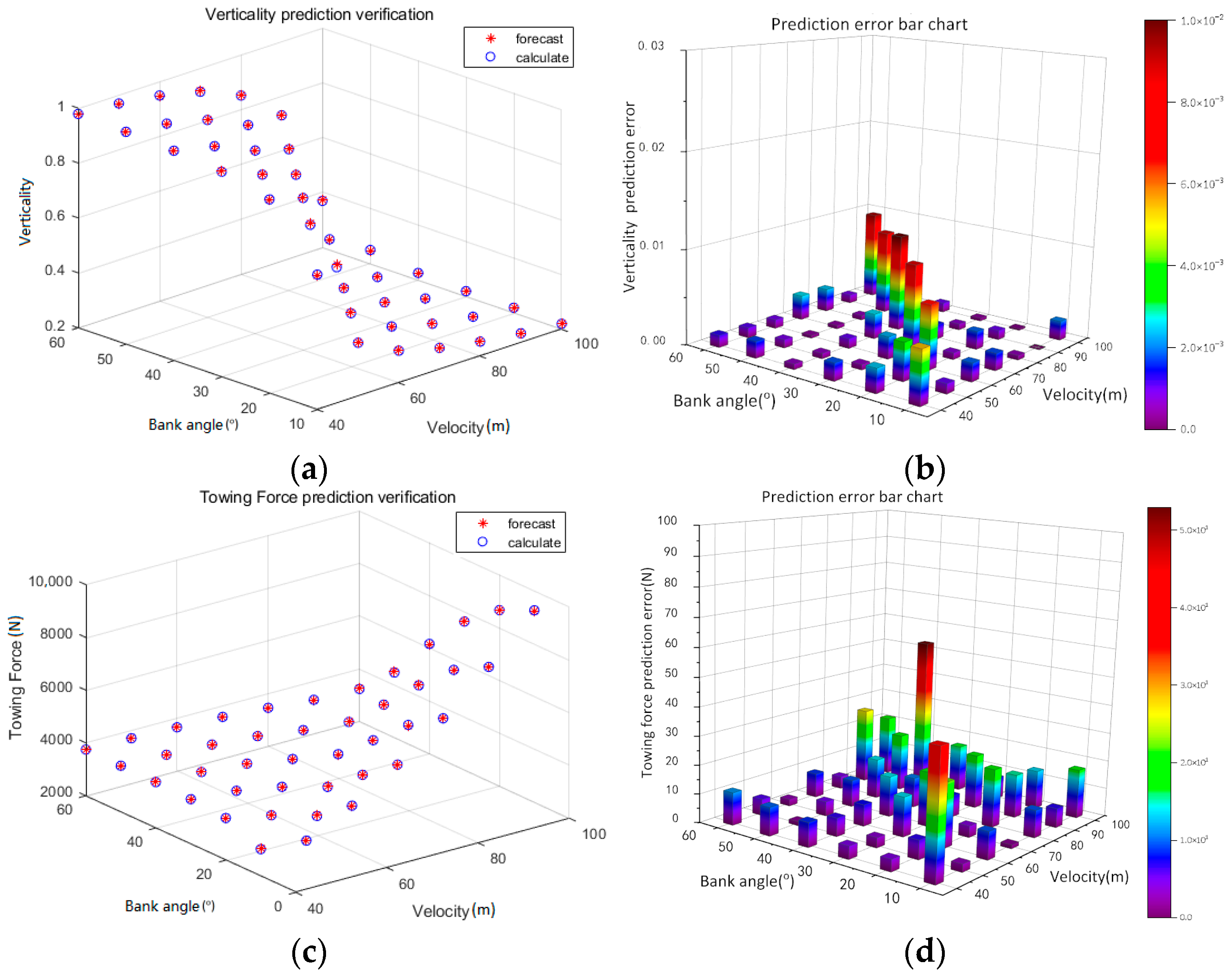
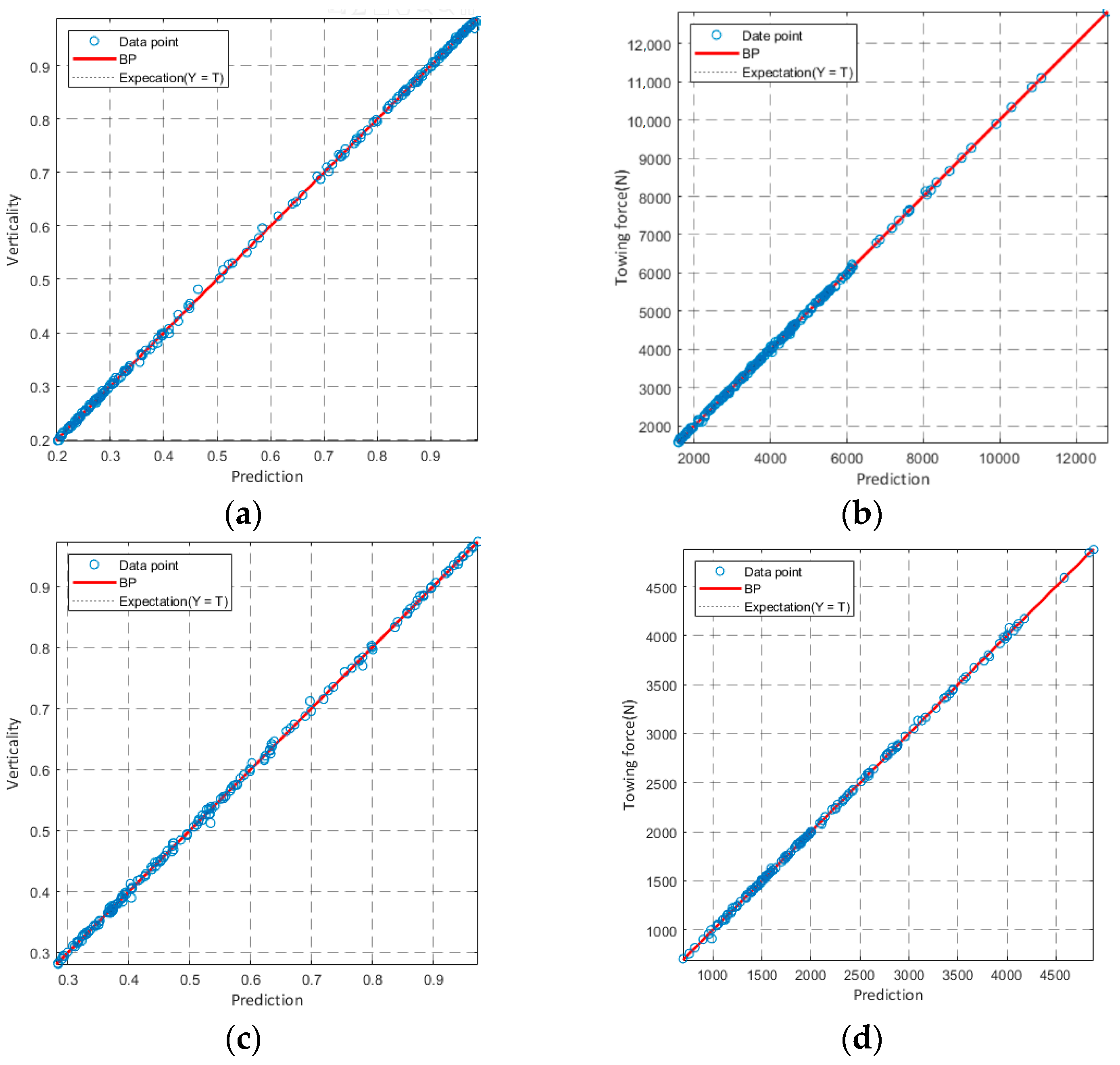
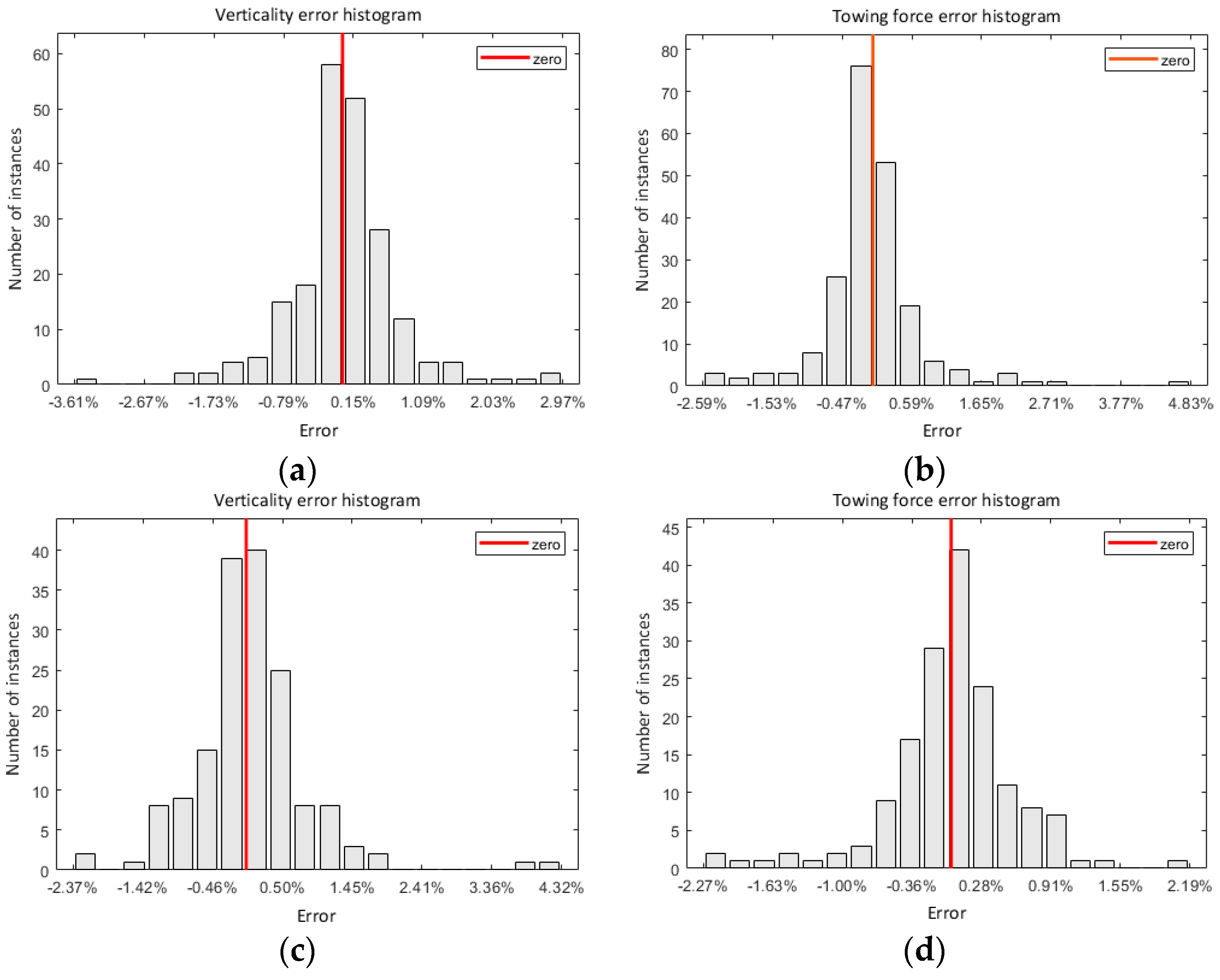
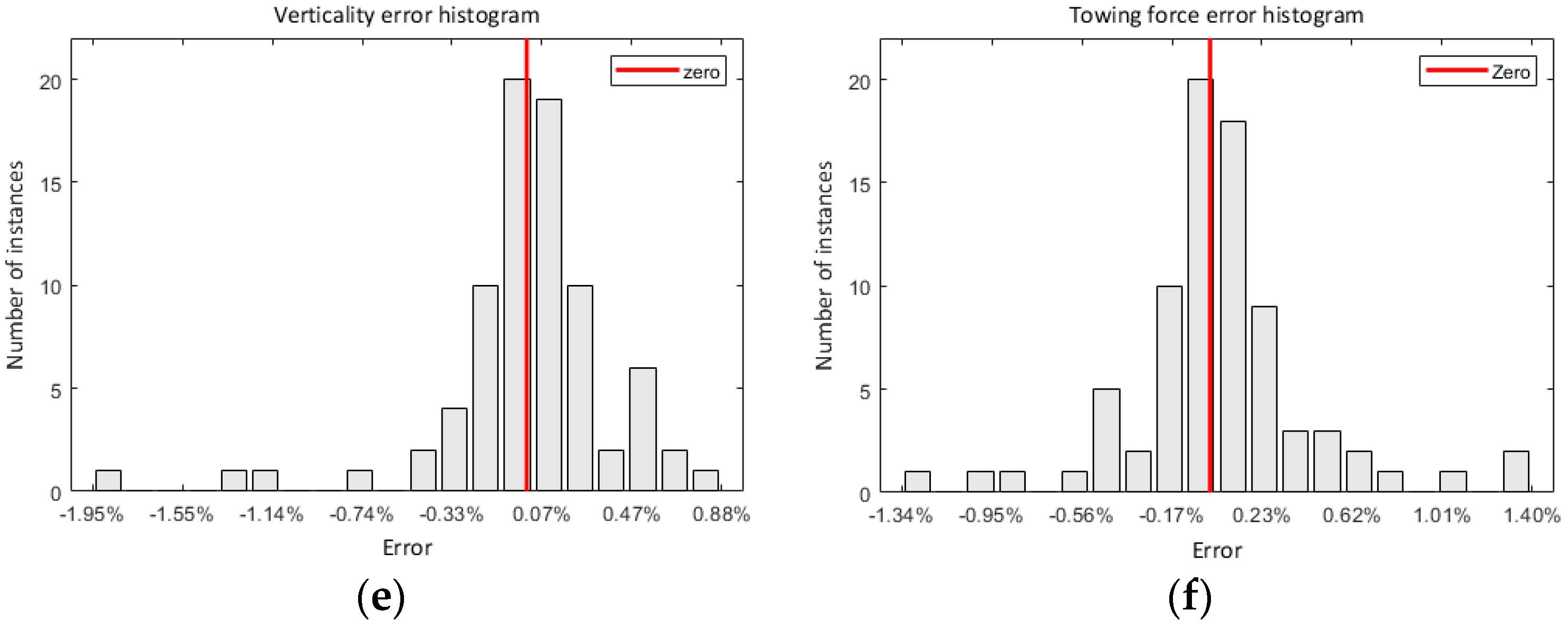
2.2.2. Neural Network Prediction Accuracy Validation
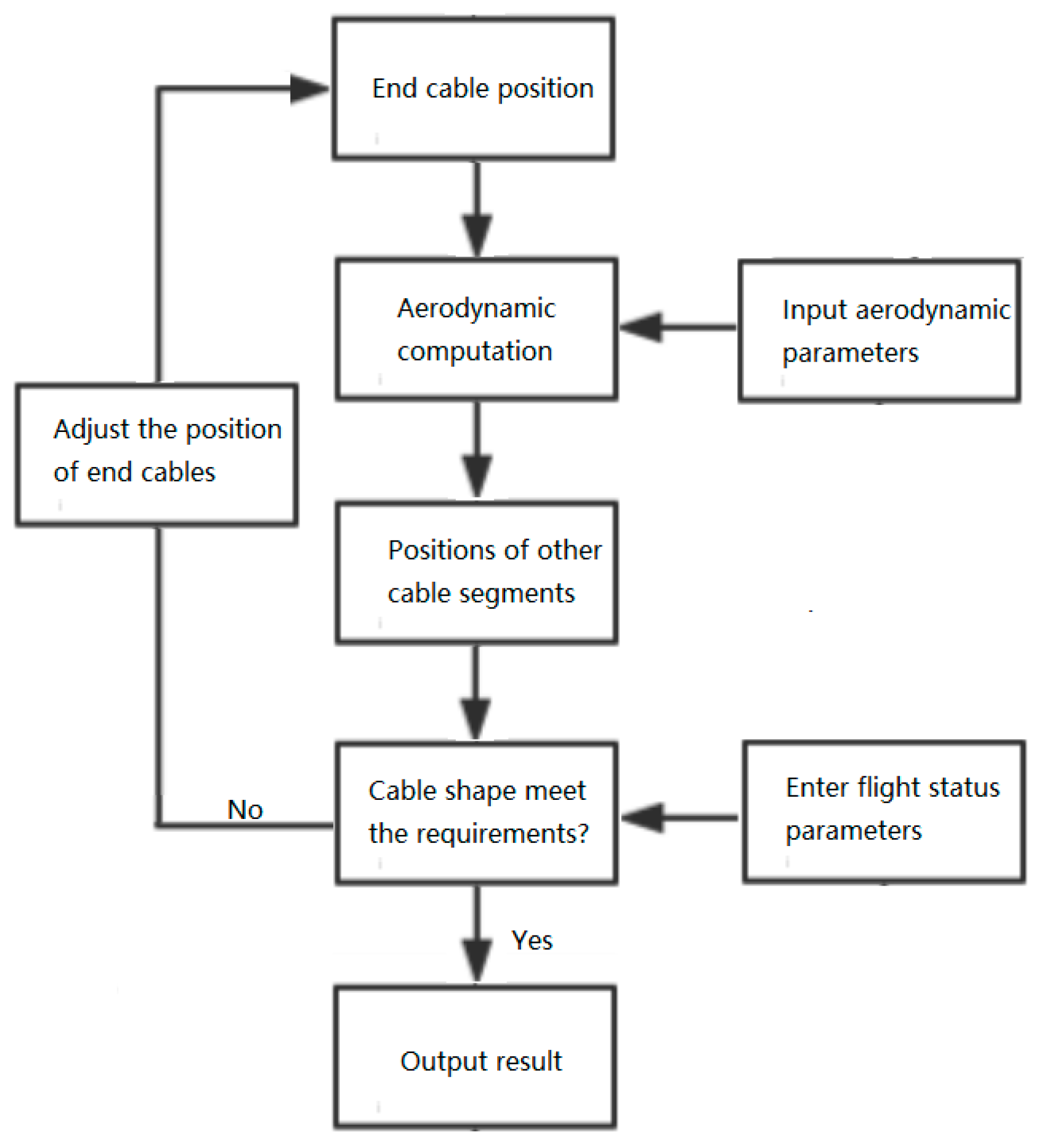
2.3. Optimization Methods
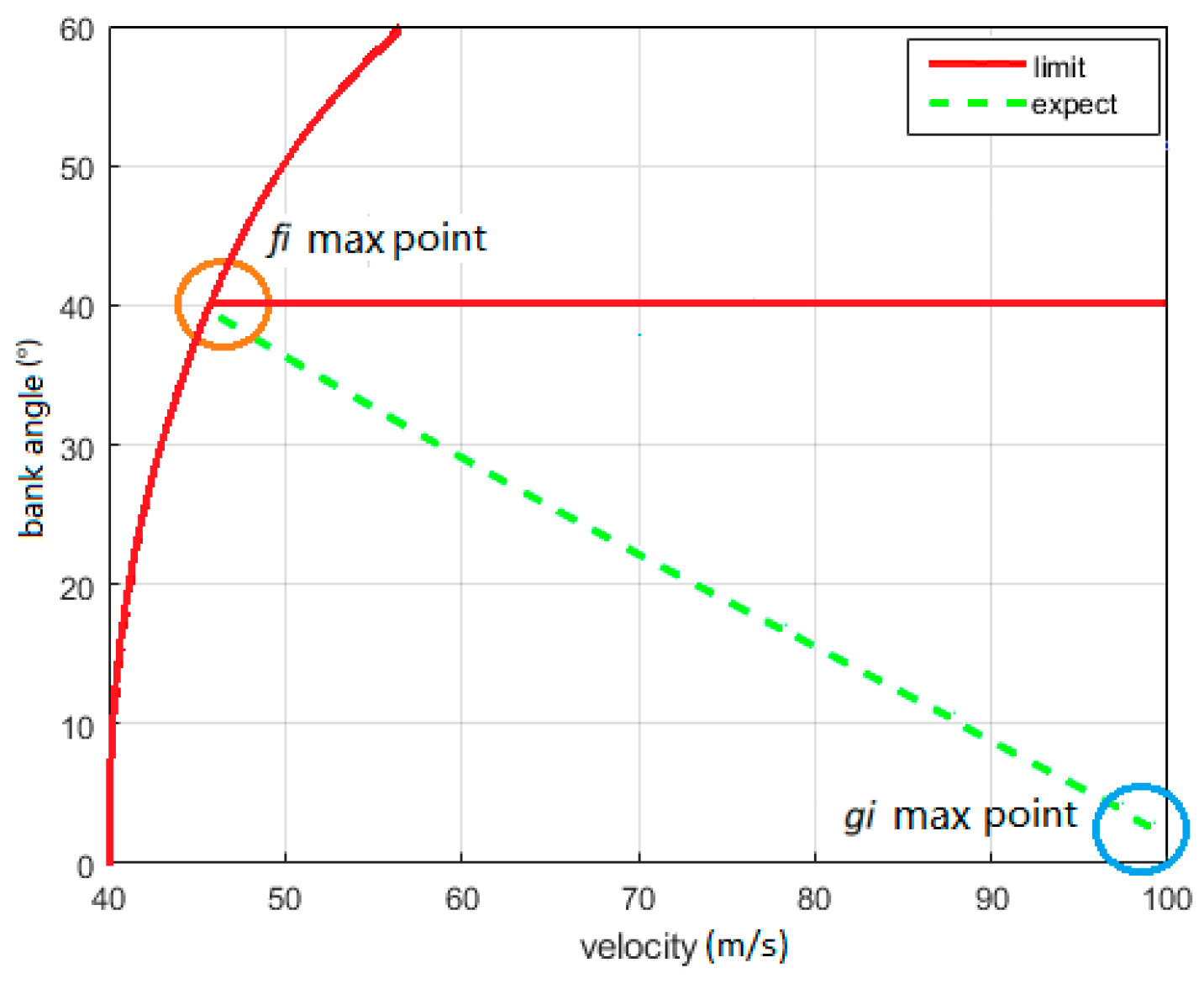
2.3.1. Segmentation of the Search Area
2.3.2. Towed Cable Performance Evaluation Function
- (1)
- Although cable verticality in the search region exceeds 65%, a margin should be allowed due to differing flight conditions. To ensure cable stability, verticality should be prioritized over towing force.
- (2)
- After the cable verticality reaches a certain degree, a further increase in the verticality has a minimal effect on the cable. At this point, the cable’s lower towing force results in a smaller impact on the aircraft. Therefore, the focus should be on minimizing the towing force exerted by the cable on the aircraft accordingly.
- (3)
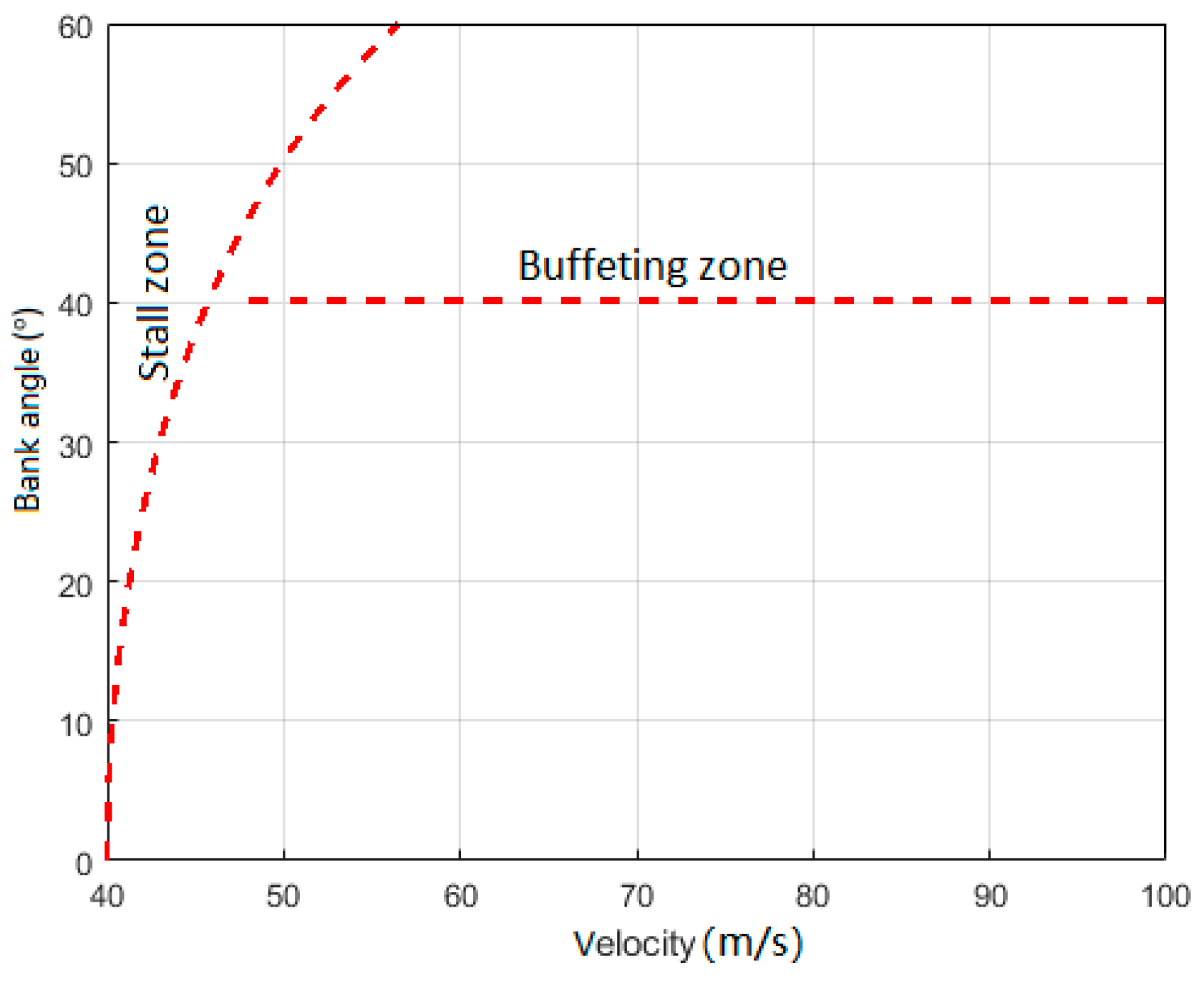
- When both verticality and towing force meet specific conditions, it is crucial to maintain a significant buffer from stall and vibration boundaries to enhance the towing aircraft’s aerodynamic performance. This buffer zone ensures that the aircraft operates well within safe aerodynamic limits.
3. Calculation Results
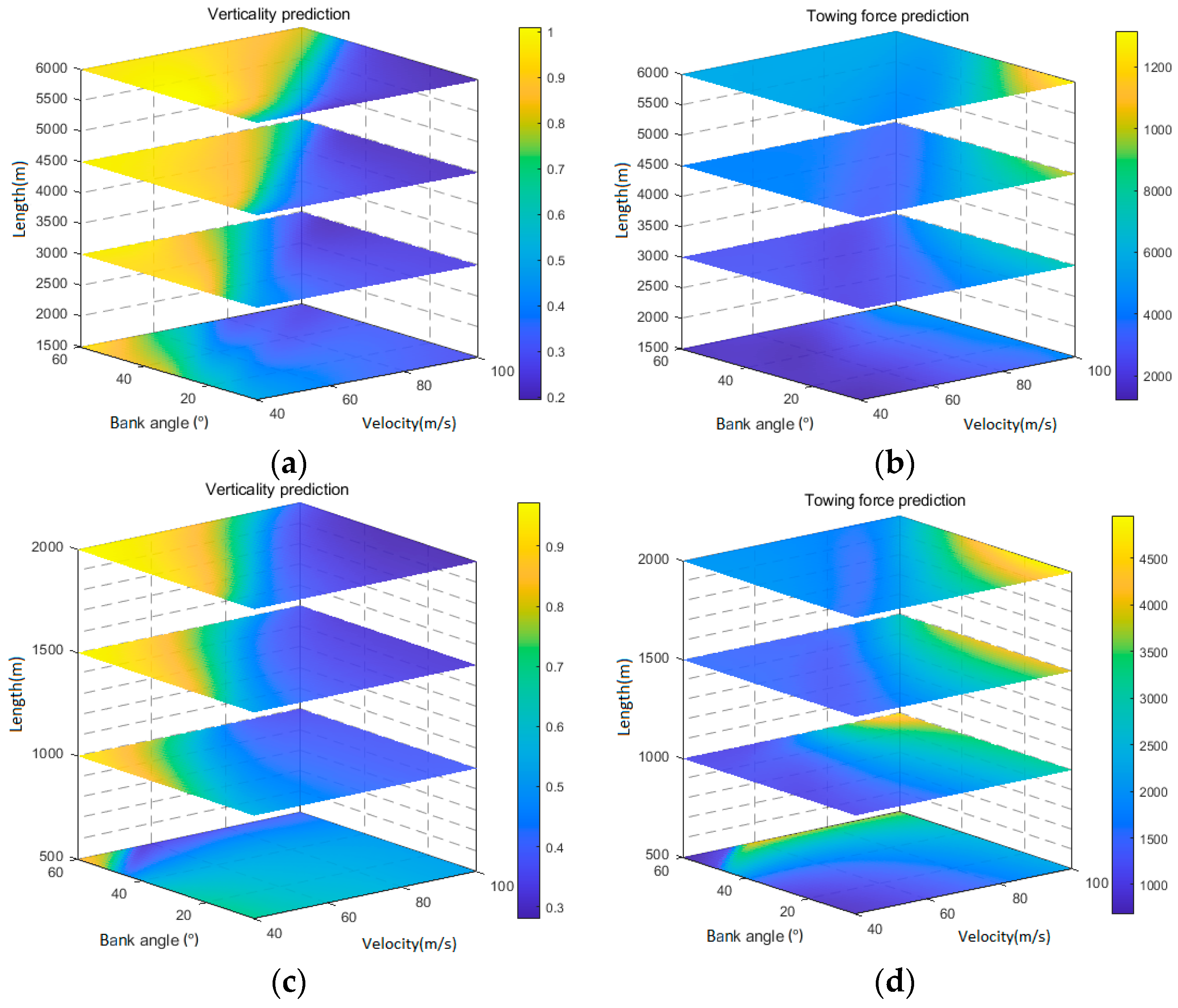
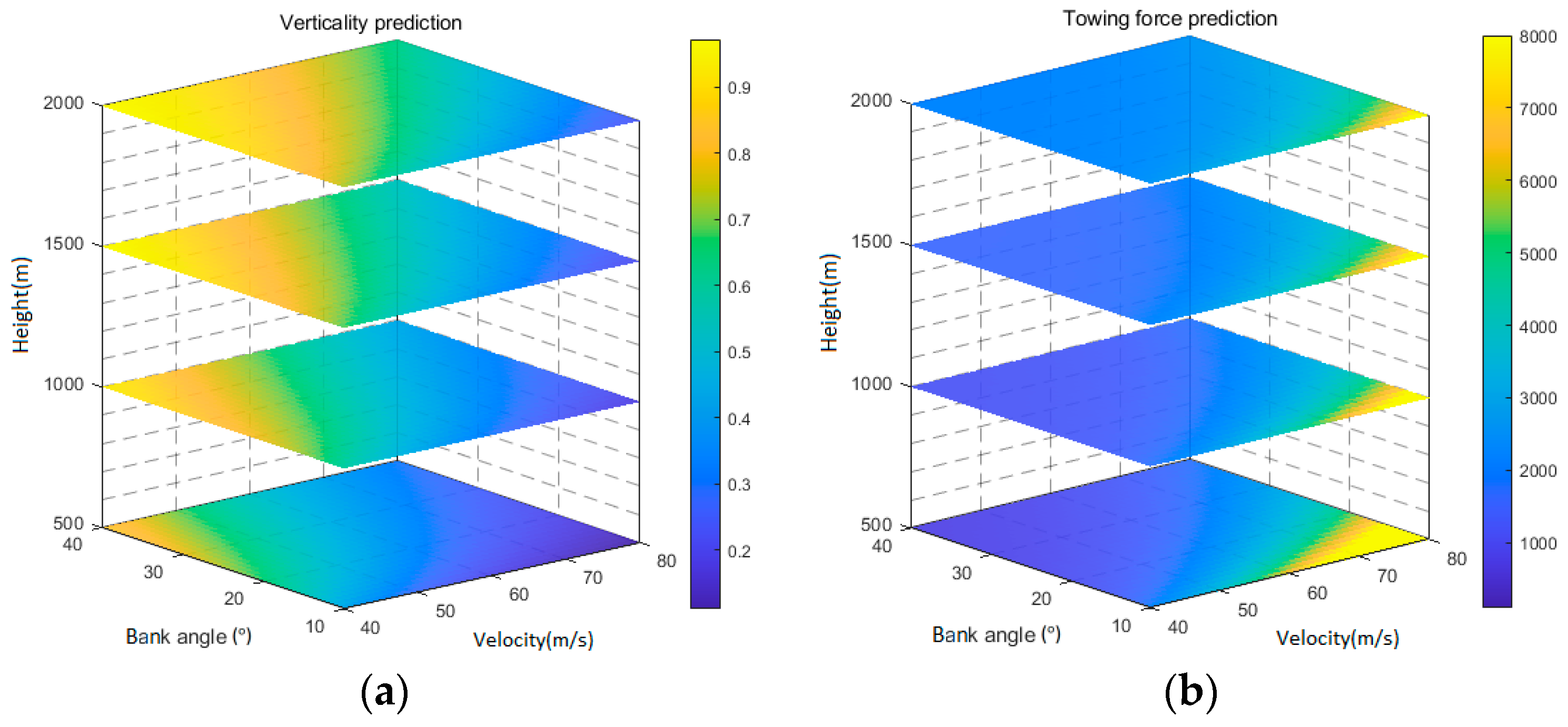
3.1. Different Circling Altitudes
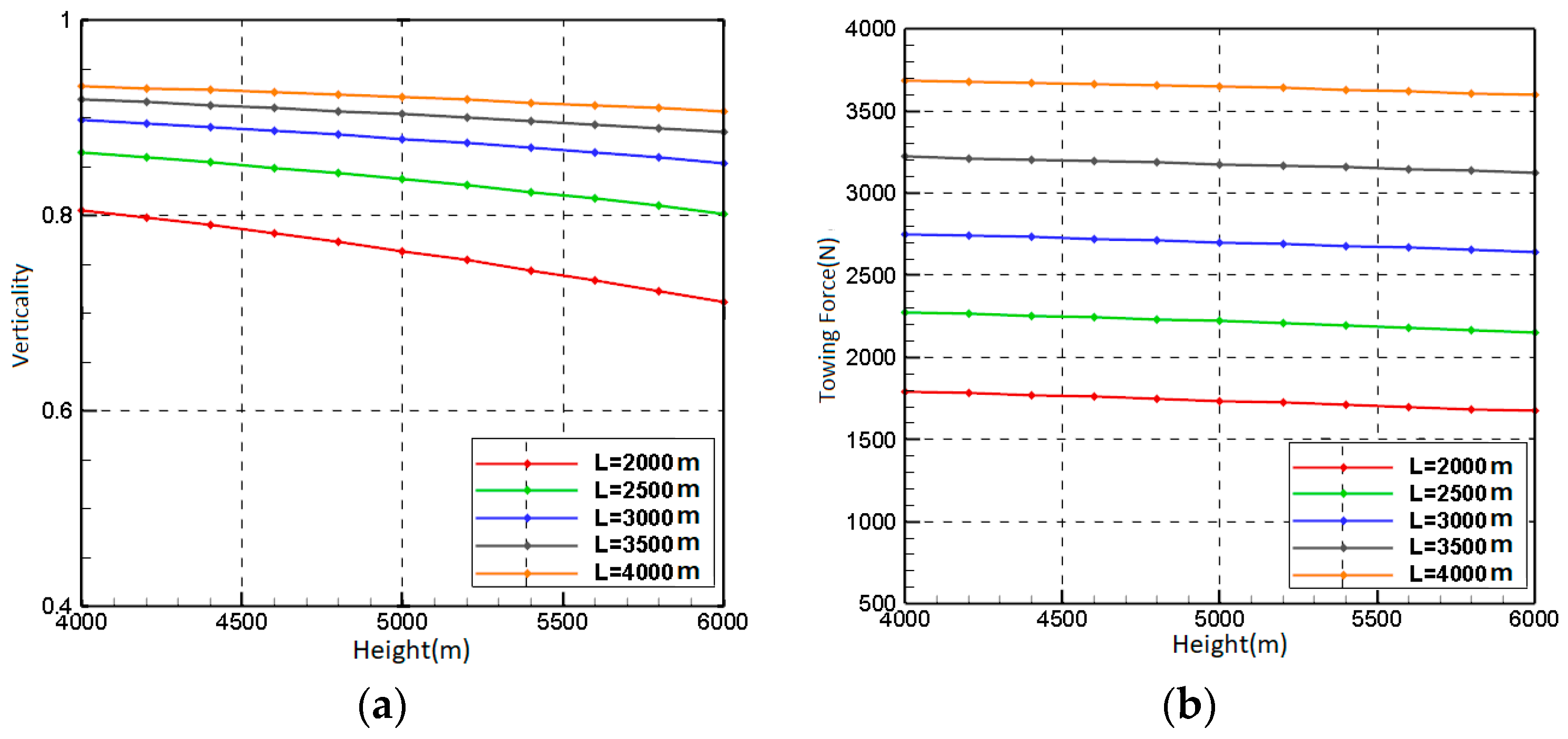
3.1.1. End-Free State CABLE
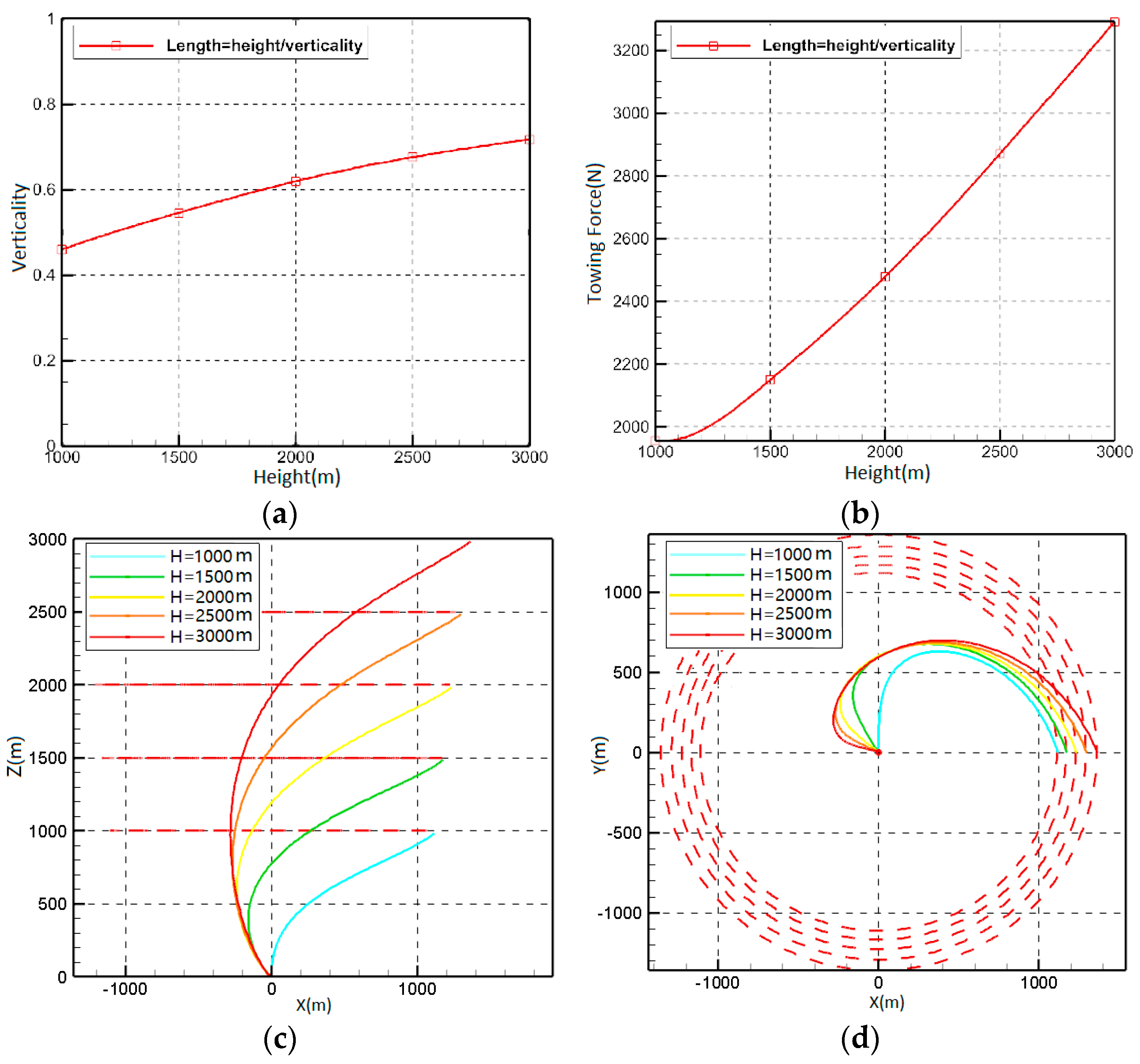
3.1.2. Fixed-End State Cable
3.2. Neural Network Training
3.3. PSO Search Results
3.3.1. PSO Search Results for End-Free Condition
3.3.2. PSO Search Results for Fixed-End Condition
4. Conclusions
- Under free-end conditions, the shape of the towing cable progressively enhances with an increase in the bank angle of the aircraft coupled with a decrease in circling velocity. Moreover, increasing the length of the cable within the same circling condition results in better vertical alignment, although it also results in an increase in towing force, requiring consideration and the balancing of the trade-off between vertical alignment and towing force. Within the range of 2000 m to 6000 m, lowering the altitude further improves the cable’s shape under identical circling conditions. Moreover, a reduced altitude enhances the aerodynamic efficiency of the aircraft. Consequently, it is advisable to minimize circling altitude whenever feasible.
- Under fixed-end conditions, the transition of the cable’s verticality changes gradually, similar to the trend observed in free-end scenarios. However, the towing force exhibits more drastic changes when the cable is fixed at the end. Under this setup, the orbiting aircraft must carefully maintain a specific circling altitude and cable length while ensuring that the circling velocity remains within acceptable limits. Otherwise, a rapid increase in towing force may occur, demanding greater attention to the material properties and structural integrity of the aircraft.
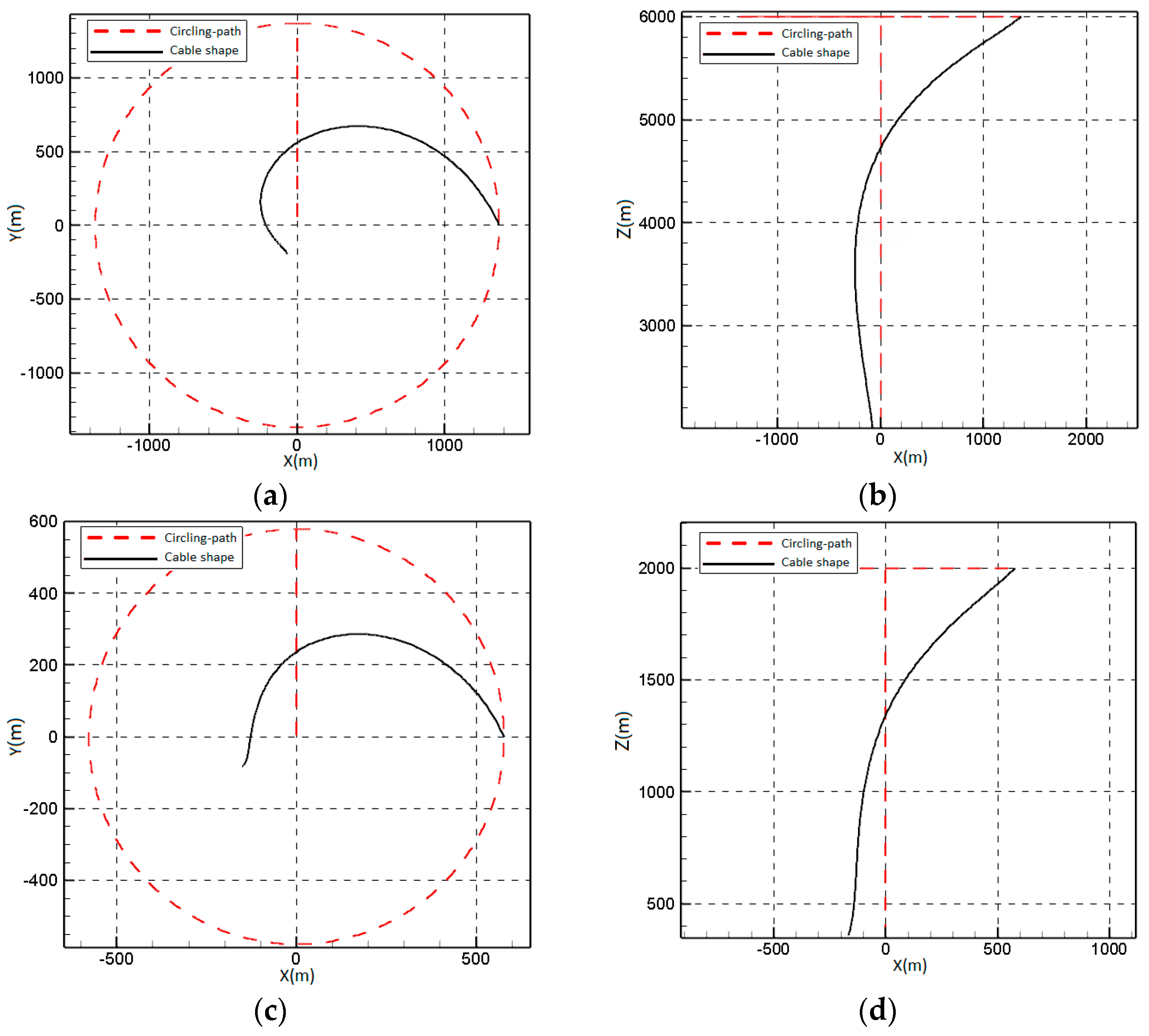
- Under free-end conditions at an altitude of 6000 m, the evaluation function reaches its optimal state with a cable length of 5258 m, a circling velocity of 62 m/s and a bank angle of 28°, where the cable verticality is 79% and the towing force is 4400 N.
- Under free-end conditions at an altitude of 2000 m, the evaluation function reaches its optimal condition when the cable length is 2052 m, the circling velocity of the orbiting aircraft is 55 m/s and the bank angle is 33°. At this point, the cable verticality is 81% and the towing force is 1800 N.
- Under fixed-end conditions, the evaluation function reaches the optimal state when the circling altitude is 2470 m. Here, the cable extends over 3758 m, with the orbiting aircraft maintaining a consistent circling velocity of 55 m/s, accompanied by a bank angle of 29°. This setup results in a cable verticality of 84%, demanding a towing force of 2546 N.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, D. The Research of the Dual Trailing Wire Antenna (DTWA) on the Aircraft in Application to the Submarine Communication. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 2009. [Google Scholar]
- Ma, T.; Wei, Z.; Chen, H.; Wang, X. Research on parameters of the trailing VLF antenna using lumped-mass method. In IOP Conference Series: Materials Science and Engineering, proceedings of the 2018 2nd International Conference on Advanced Technologies in Design, Mechanical and Aeronautical Engineering (ATDMAE 2018), Dalian, China, 1–3 July 2018; IOP Publishing Ltd.: Bristol, UK, 2018. [Google Scholar]
- Ma, D.L.; Wang, S.Q.; Yang, M.Q.; Dong, Y. Dynamic simulation of aerial towed decoy system based on tension recurrence algorithm. Chin. J. Aeronaut. 2016, 29, 1484–1495. [Google Scholar] [CrossRef]
- Zhu, Y.J.; Luo, D. Dynamic modeling and analysis of tow cable for aircraft circling. J. Tong Ji Univ. 2018, 1, 46. [Google Scholar]
- Merz, M.; Johansen, T.A. Feasibility study of a circularly towed cable-body system for uav applications. In Proceedings of the 2016 International Conference on Unmanned Aircraft Systems, Arlington, VA, USA, 7–10 June 2016. [Google Scholar]
- Merz, M.; Johansen, T.A. Optimal path of a UAV engaged in wind-influenced circular towing. In Proceedings of the 2017 Workshop on Research, Education and Development of Unmanned Aerial Systems, Linköping, Sweden, 3–5 October 2017. [Google Scholar]
- Williams, P.; Trivailo, P. Stability and equilibrium of a circularly-towed aerial cable system with an attached wind-sock. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, San Francisco, CA, USA, 15–18 August 2005. [Google Scholar]
- Murray, R.M. Trajectory generation for a towed cable system using differential flatness. IFAC Proc. Vol. 1996, 29, 2792–2797. [Google Scholar] [CrossRef]
- Wang, L.X.; Li, H.; Liu, Y.X.; Ai, J.L. Design and Realization of a Cable-Drogue Aerial Recharging Device for Small Electric Fixed-Wing UAVs. In Proceedings of the 2023 International Conference on Unmanned Aircraft Systems, Warsaw, Poland, 6–9 June 2023. [Google Scholar]
- Zheng, X.H.; Hou, Z.Q.; Han, W.; Li, J.X. Research on the Steady Dynamic of VLF Trailing Antenna on an Aircraft. J. Mech. Eng. 2012, 48, 166–171. [Google Scholar] [CrossRef]
- Cheng, J.F.; Liu, X.Q.; Deng, F. Numerical Study on Parameters of the Airborne VLF Antenna by Quasi-Stationary Model. Aero 2022, 10, 29. [Google Scholar] [CrossRef]
- Wu, C.L. Study on Dynamic Characteristics of In-Flight Refueling Hose-Cone Sleeve System. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2009. [Google Scholar]
- Liu, Y.H.; Wang, H.L.; Su, Z.K. Deep learning based trajectory optimization for UAV aerial refueling docking under bow wave. Aerosp. Sci. Technol. 2018, 80, 392–402. [Google Scholar] [CrossRef]
- Mohsan, S.A.H.; Othman, N.Q.H.; Khan, M.A.; Amjad, H.; Żywiołek, J. A Comprehensive Review of Micro UAV Charging Techniques. Micromachines 2022, 13, 977. [Google Scholar] [CrossRef] [PubMed]
- Pereira, J.A.; Camacho, E.A.; Marques, F.D. Flapping Airfoil Aerodynamics using Recurrent Neural Network. In Proceedings of the AIAA Scitech 2024 Forum, Orlando, FL, USA, 8–12 January 2024. [Google Scholar]
- Faller, W.E.; Schreck, S.J. Neural networks: Applications and opportunities in aeronautics. Prog. Aerosp. Sci. 1996, 32, 433–456. [Google Scholar] [CrossRef]
- Buscema, M. Back propagation neural networks. Subst. Use Misuse 1998, 33, 233–270. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995. [Google Scholar]
- Venter, G.; Sobieszczanski-Sobieski, J. Particle swarm optimization. AIAA J. 2003, 41, 1583–1589. [Google Scholar] [CrossRef]
- Zountouridou, E.; Kiokes, G.; Dimeas, A.; Prousalidis, J. A guide to unmanned aerial vehicles performance analysis—The MQ-9 unmanned air vehicle case study. J. Eng. 2023, 6, e12270. [Google Scholar] [CrossRef]
- Mohsan, S.A.H.; Khan, M.A.; Noor, F.; Ullah, I. Towards the unmanned aerial vehicles (UAVs): A comprehensive review. Drones 2022, 6, 147. [Google Scholar] [CrossRef]
- Guo, R.; Bai, Y.; Qiao, Z.; Pei, X.; Wu, G. Numerical investigation on buffeting and lock-in phenomenon for biplane airfoils at α = 40°. Int. J. Mech. Sci. 2022, 219, 107120. [Google Scholar] [CrossRef]
- Pasandideh, F.; da Costa, J.P.J.; Kunst, R.; Islam, N.; Hardjawana, W. A review of flying ad hoc networks: Key characteristics, applications, and wireless technologies. Remote Sens. 2022, 14, 4459. [Google Scholar] [CrossRef]






| Cable Length (m) | Bank Angle (°) | Velocity (m/s) | Radius (m) | Verticality (V1) | Verticality (V2) |
|---|---|---|---|---|---|
| 8404.6 | 31 | 112.9 | 2165.3 | 76.63% | 78.52% |
| 7962.0 | 31 | 113.4 | 2194.8 | 73.14% | 75.24% |
| 7519.8 | 32 | 114.5 | 2139.0 | 74.14% | 73.26% |
| 7077.5 | 35 | 116 | 1960.4 | 73.29% | 74.03% |
| 6635.2 | 35 | 116 | 1960.4 | 73.12% | 70.06% |
| Example | R (m) | ω (rad/s) | d (mm) |
|---|---|---|---|
| Light Aircraft | 213.78 | 0.246 | 1.27 |
| Orion | 468.05 | 0.240 | 1.39 |
| Fighter | 565.61 | 0.218 | 1.28 |
| Parameters | Values | Unit |
|---|---|---|
| Antenna Diameter | 4 | mm |
| Material Density | 0.0915 | kg/m |
| Antenna pressure coefficient | 1.15 | ~ |
| Antenna friction coefficient | 0.05 | ~ |
| Drogue’s mass | 30 | kg |
| Drogue’s drag coefficient | 0.6 | ~ |
| Drogue’s area | 0.5 | m2 |
| Altitude | 6000 | m |
| Air density | 0.66 | kg/m3 |
| Minimum stall speed | 40 | m/s |
| UAV Model | Wing Area (m2) | Take-Off Weight (kg) | Stall Speed (m/s) |
|---|---|---|---|
| MQ-9 Reaper | 41.76 | 4760 | 66.6 |
| RQ-4 Global Hawk | 65.5 | 14,628 | 61.1 |
| Heron TP | 52 | 4500 | 42.3 |
| CH-4 Rainbow | 18 | 1330 | 30.8 |
| Triton MQ-4C | 39.6 | 14,628 | 59.0 |
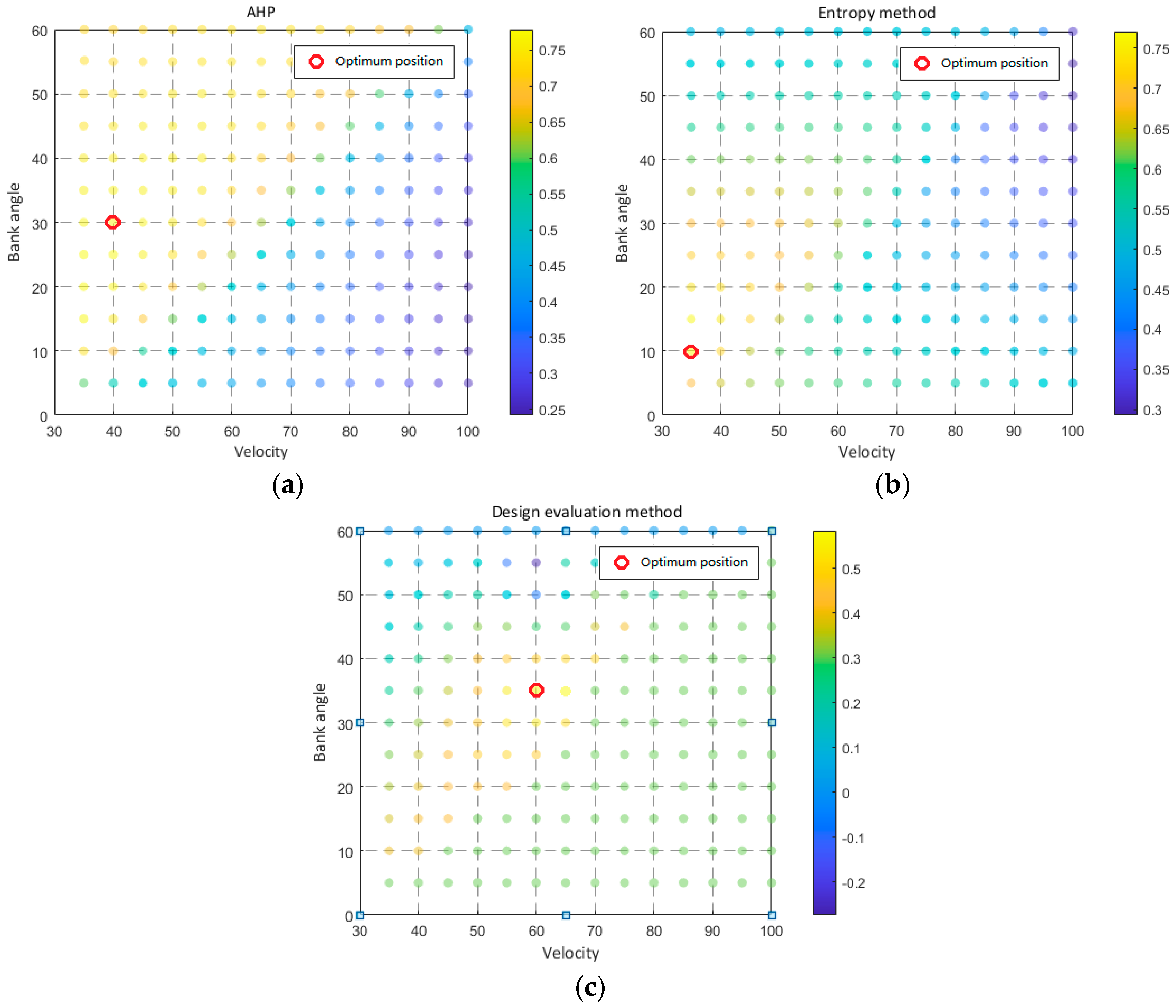
| Parameters | Analytic Hierarchy Process | Entropy Weighting |
|---|---|---|
| Verticality | 0.500 | 0.1112 |
| Towing force | 0.250 | 0.3947 |
| Velocity | 0.125 | 0.1435 |
| Bank angle | 0.125 | 0.3506 |
| Parameters | Design Methods | Analytic Hierarchy Process | Entropy Weighting |
|---|---|---|---|
| Verticality | 0.8241 | 0.9325 | 0.8329 |
| Towing force | 3397.6 | 3664.6 | 3294.6 |
| Velocity | 60.00 | 40.00 | 35.00 |
| Bank angle | 35.00 | 25.00 | 10.00 |
| Altitude | Length of Cable (m) |
|---|---|
| 1000 | 2272 |
| 1500 | 2830 |
| 2000 | 3225 |
| 2500 | 3703 |
| 3000 | 4166 |
| Parameters | R-Squared | Test Error Norm | Maximum Error |
|---|---|---|---|
| H = 6000 m | |||
| Towing Force | 0.9995 | 327.12 N | 114.07 N (4.83%) |
| Verticality | 0.9993 | 0.0471 | 0.0124 (2.97%) |
| H = 2000 m | |||
| Towing Force | 0.9951 | 164.81 N | 78.56 N (1.8%) |
| Verticality | 0.9995 | 0.0510 | 0.0221 (2.19%) |
| L = 500–2000 m | |||
| Towing Force | 0.9994 | 68.1349 N | 23.85 N (1.4%) |
| Verticality | 0.9995 | 0.0230 | 0.0064 (0.8%) |
| H = 6000 m (Initial State: Velocity = 60 m/s, Bank Angle = 20°, Length = 3500 m) | |||
| Parameters | Parameter Variation Range | Change in Verticality Evaluation (Absolute Value) | Change in Drag Force Evaluation (Absolute Value) |
| Velocity | ±10 (m/s) | 0.01991 (Δ1 m/s) | 52.94 (Δ1 m/s) |
| Bank angle | ±10° | 0.01799 (Δ1°) | 40.36 (Δ1°) |
| Length | ±500 (m) | 0.00401 (Δ100 m) | 10.74 (Δ100 m) |
| H = 2000 m (Initial state: velocity = 60 m/s, bank angle = 20°, length = 1500 m) | |||
| Parameters | Parameter variation range | Change in verticality evaluation (absolute value) | Change in drag force evaluation (absolute value) |
| Velocity | ±10 (m/s) | 0.00777 (Δ1 m/s) | 45.36 (Δ1 m/s) |
| Bank angle | ±10° | 0.00443 (Δ1°) | 25.10 (Δ1°) |
| Length | ±500 (m) | 0.00211 (Δ100 m) | 9.85 (Δ100 m) |
| H-L (Initial state: velocity = 60 m/s, bank angle = 20°, length = 1500 m) | |||
| Parameters | Parameter variation range | Change in verticality evaluation (absolute value) | Change in drag force evaluation (absolute value) |
| Velocity | ±10 (m/s) | 0.01479 (Δ1 m/s) | 51.68 (Δ1 m/s) |
| Bank angle | ±10° | 0.01624 (Δ1°) | 110.96 (Δ1°) |
| Height | ±500 (m) | 0.01596 (Δ100 m) | 51.98 (Δ100 m) |
| Number of Iterations | Optimal Point Position (Length, Speed, Bank Angle) | Optimum Value |
|---|---|---|
| 50 | [55.03792, 33.04564, 2049.5392] | 0.57853 |
| 80 | [54.436105, 33.456913, 1957.7764] | 0.57819 |
| 100 | [55.067775, 33.029162, 2052.9438] | 0.57856 |
| 120 | [55.06784, 33.029106, 2052.9256] | 0.57856 |
| H = 6000 m | ||||||
| Parameters | Length (m) | Circling Velocity (m/s) | Bank Angle (°) | Towing Force (N) | Verticality | Comprehensive Evaluation Function, F |
| Predicted value | 5258.72 | 62.08 | 28.07 | 4419.2 | 0.799 | 0.529 |
| Calculated value | 5259.00 | 65.00 | 28.00 | 4325.9 | 0.803 | ~ |
| H = 2000 m | ||||||
| Parameters | Length (m) | Circling Velocity (m/s) | Bank Angle (°) | Towing force (N) | Verticality | Comprehensive evaluation function, F |
| Predicted value | 2052.93 | 55.067 | 33.03 | 1833.8 | 0.8042 | 0.579 |
| Calculated value | 2053.00 | 55.00 | 33.00 | 1797.1 | 0.802.0 | ~ |
| H-L | ||||||
|---|---|---|---|---|---|---|
| Ki min | Height (m) | Circling Velocity (m/s) | Bank Angle (°) | Towing Force (N) | Verticality | Comprehensive Evaluation Function, F |
| 0.2 | 2053.4 | 52.22 | 32.34 | 2128.1 | 0.8697 | 0.7601 |
| 0.25 | 2470.1 | 55.45 | 28.75 | 2546.4 | 0.8395 | 0.7291 |
| 0.3 | 2921.9 | 58.57 | 25.41 | 3034.4 | 0.8031 | 0.7052 |
| 0.35 | 3288.4 | 61.03 | 22.92 | 3473.8 | 0.7666 | 0.6871 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, L.; Liu, X.; Nio, Z.F. Optimization Study of Steady-State Aerial-Towed Cable Circling Strategy Based on BP Neural Network Prediction. Aerospace 2024, 11, 594. https://doi.org/10.3390/aerospace11070594
Feng L, Liu X, Nio ZF. Optimization Study of Steady-State Aerial-Towed Cable Circling Strategy Based on BP Neural Network Prediction. Aerospace. 2024; 11(7):594. https://doi.org/10.3390/aerospace11070594
Chicago/Turabian StyleFeng, Luqi, Xueqiang Liu, and Zi Feng Nio. 2024. "Optimization Study of Steady-State Aerial-Towed Cable Circling Strategy Based on BP Neural Network Prediction" Aerospace 11, no. 7: 594. https://doi.org/10.3390/aerospace11070594
APA StyleFeng, L., Liu, X., & Nio, Z. F. (2024). Optimization Study of Steady-State Aerial-Towed Cable Circling Strategy Based on BP Neural Network Prediction. Aerospace, 11(7), 594. https://doi.org/10.3390/aerospace11070594






