Figure 1.
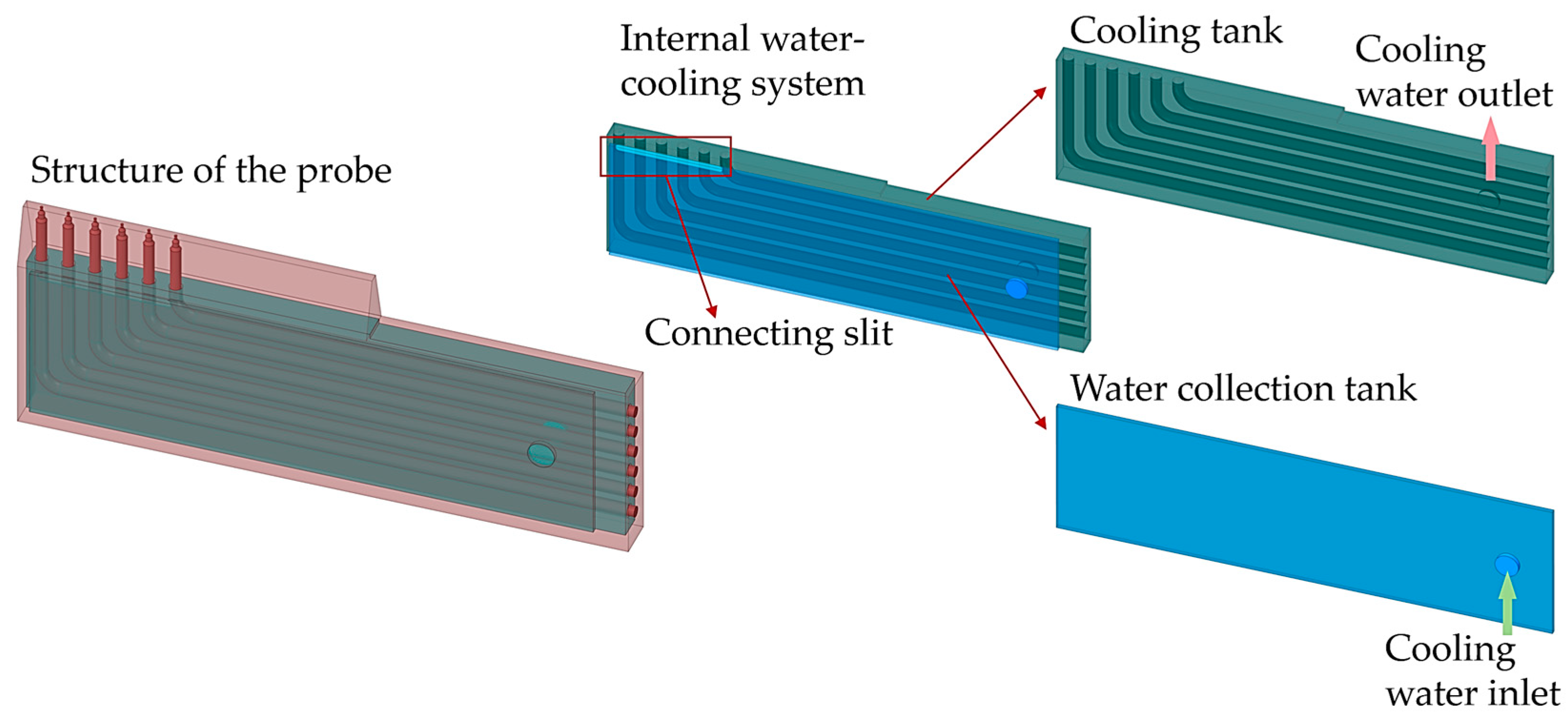
Structure of the probe head.
Figure 1.
Structure of the probe head.
Figure 2.
Internal water-cooling system.
Figure 2.
Internal water-cooling system.
Figure 3.
Solving model and meshing.
Figure 3.
Solving model and meshing.
Figure 4.
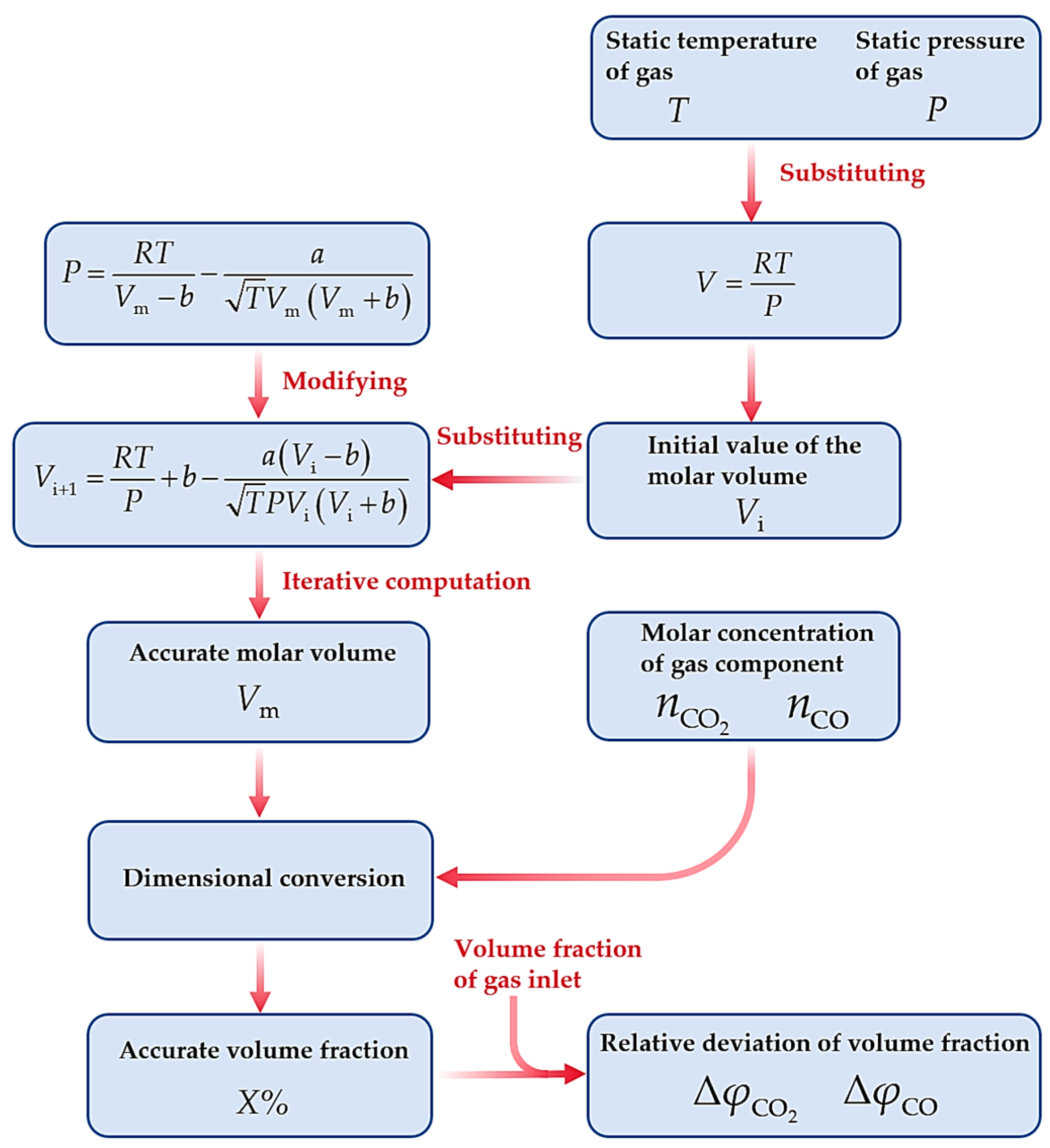
Procedure of solving relative deviation of volume fractions.
Figure 4.
Procedure of solving relative deviation of volume fractions.
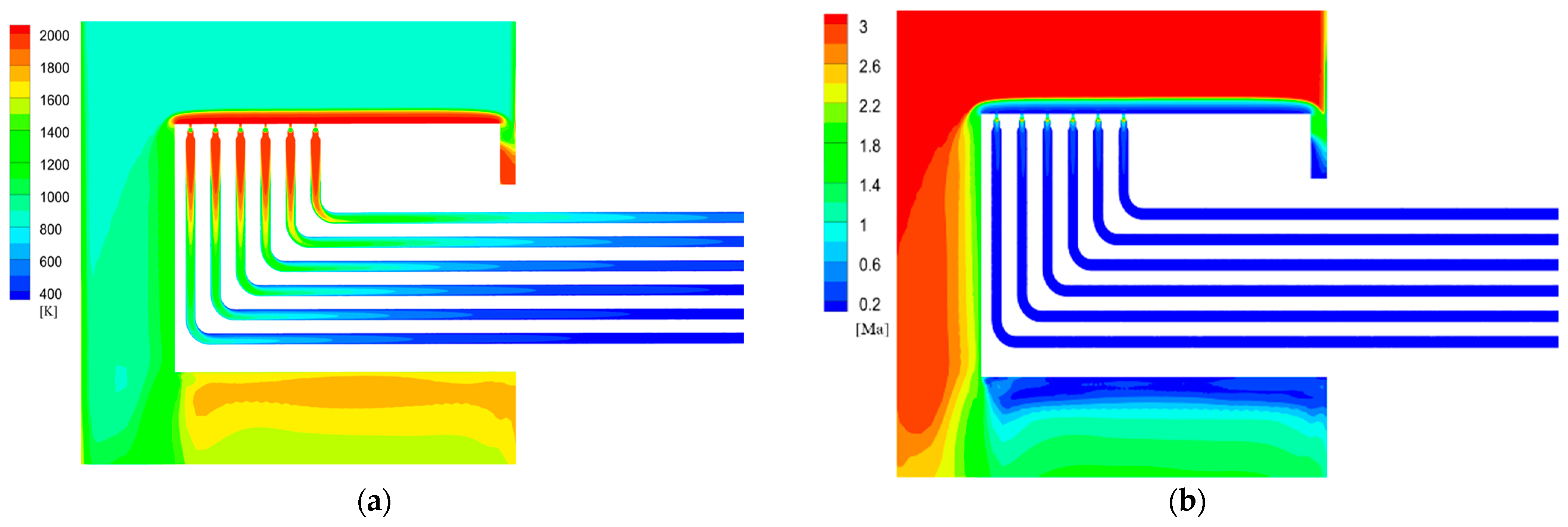
Figure 5.
Static temperature distribution of initial simulation test.
Figure 5.
Static temperature distribution of initial simulation test.
Figure 6.
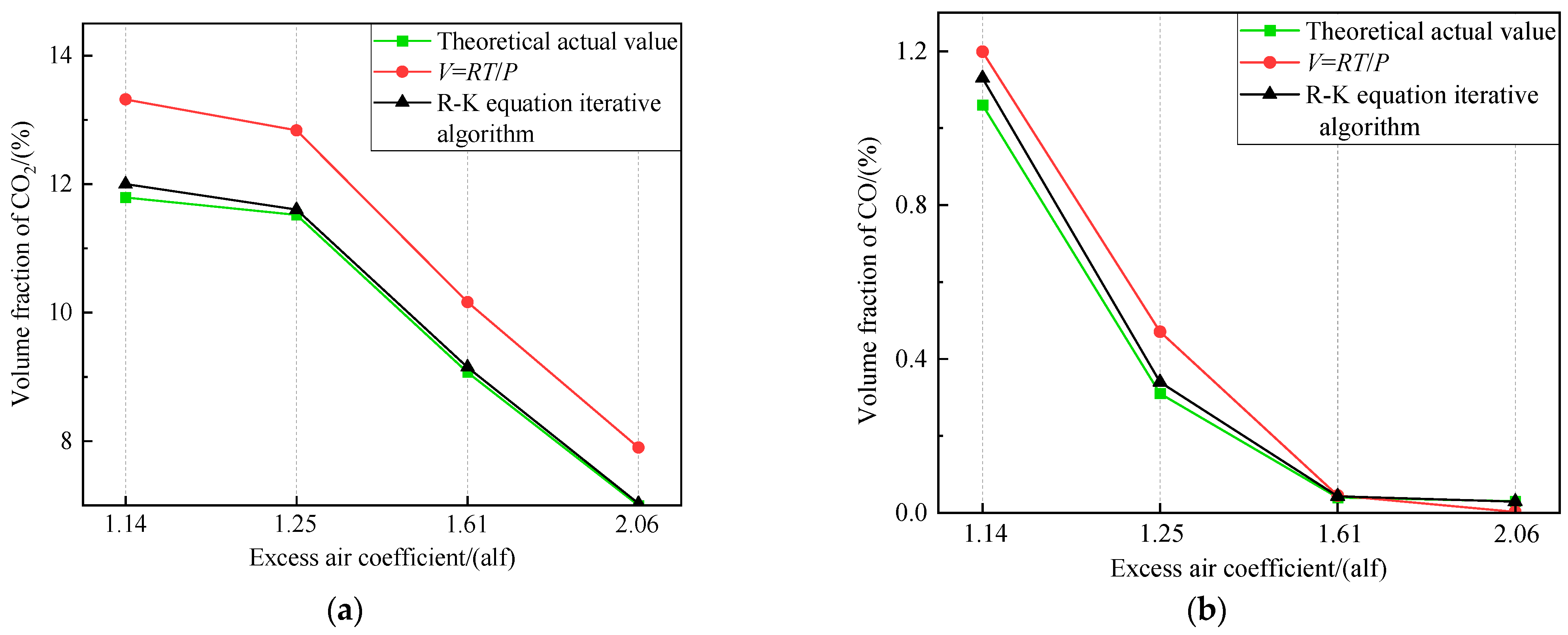
Calculation of component volume fractions at different excess air coefficients. (a) Volume fraction of CO2. (b) Volume fraction of CO.
Figure 6.
Calculation of component volume fractions at different excess air coefficients. (a) Volume fraction of CO2. (b) Volume fraction of CO.
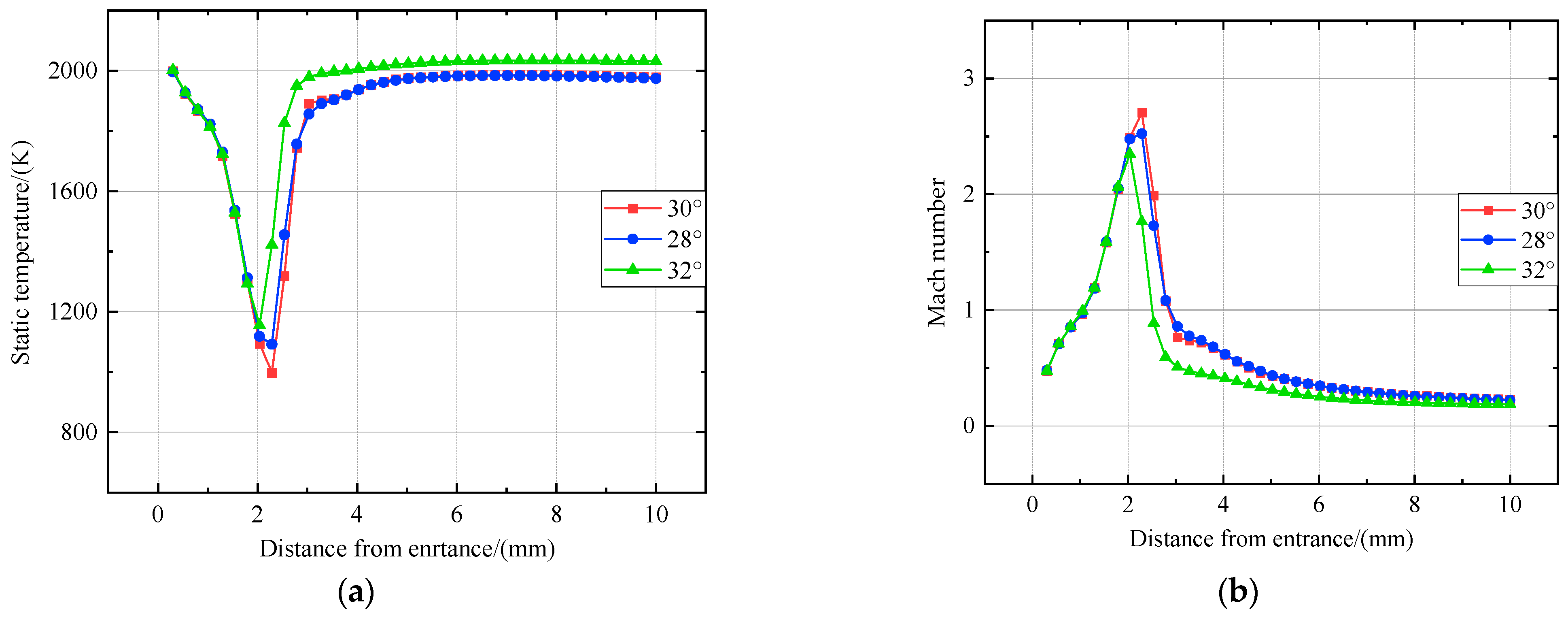
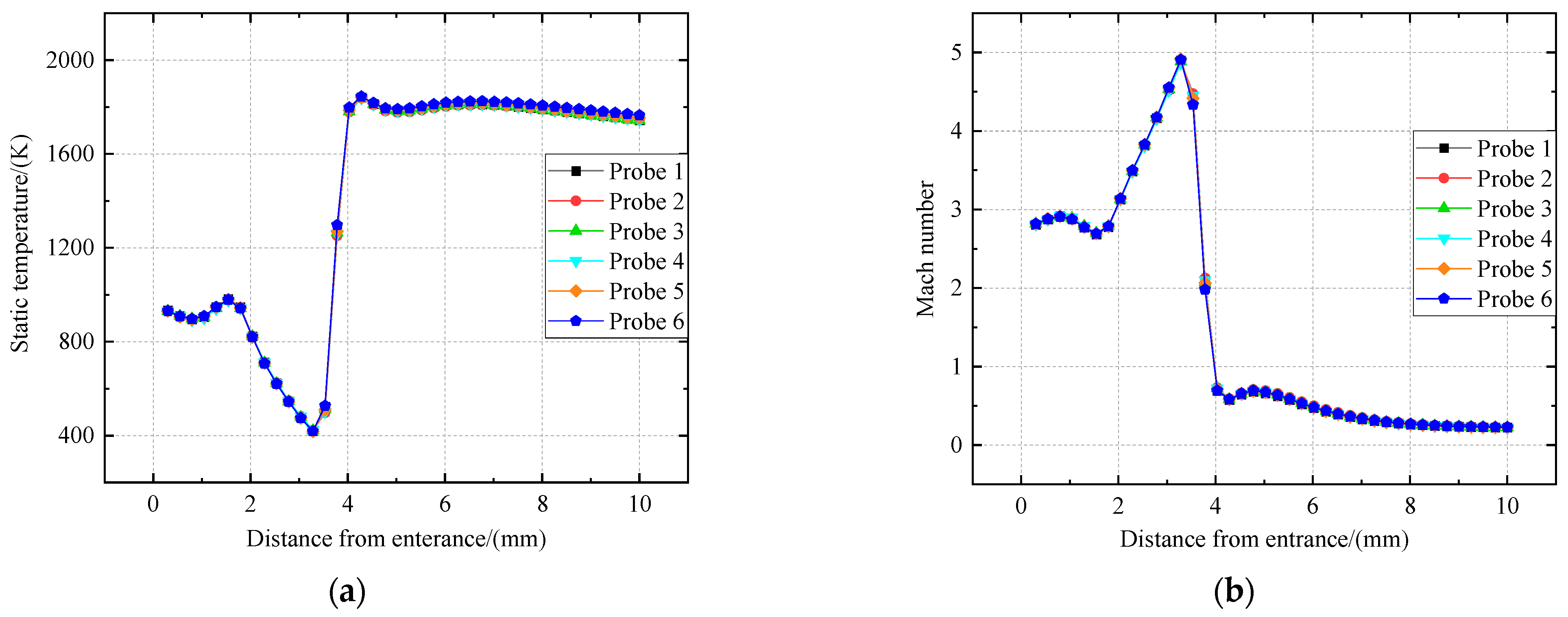
Figure 7.
Distribution of static temperature and Mach number of probe sampling in a supersonic environment. (a) Distribution of static temperature. (b) Distribution of Mach number.
Figure 7.
Distribution of static temperature and Mach number of probe sampling in a supersonic environment. (a) Distribution of static temperature. (b) Distribution of Mach number.
Figure 8.
Distribution of head temperature in different clamping angle probes.
Figure 8.
Distribution of head temperature in different clamping angle probes.
Figure 9.
Variation in gas flow parameters in the expansion section in different clamping angle probes. (a) Variation in static temperature. (b) Variation in Mach number.
Figure 9.
Variation in gas flow parameters in the expansion section in different clamping angle probes. (a) Variation in static temperature. (b) Variation in Mach number.
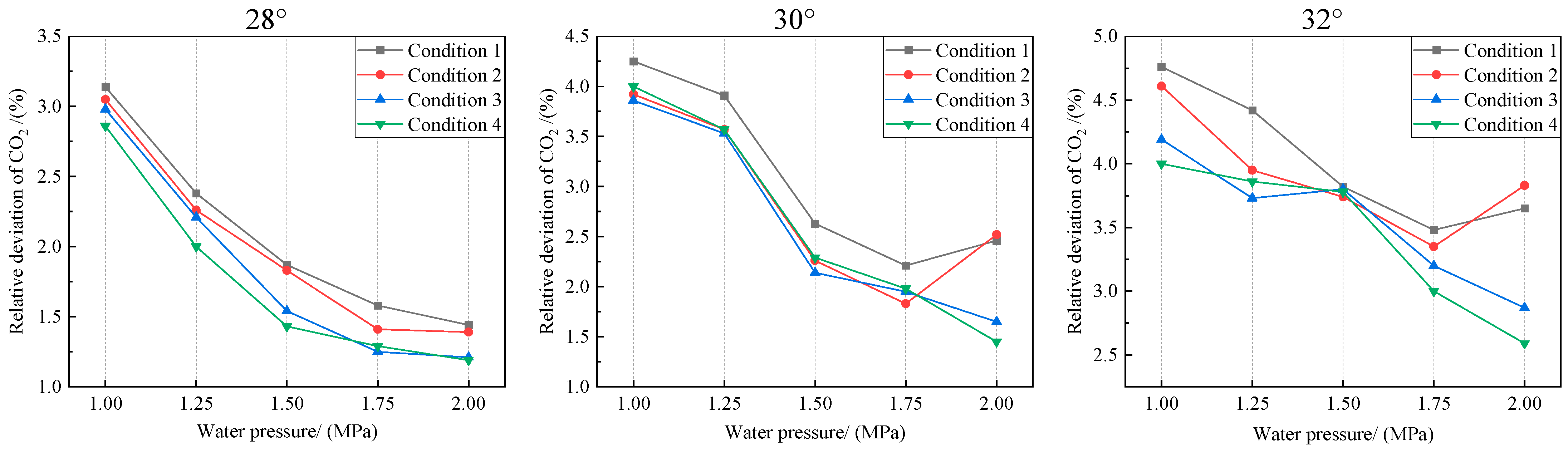
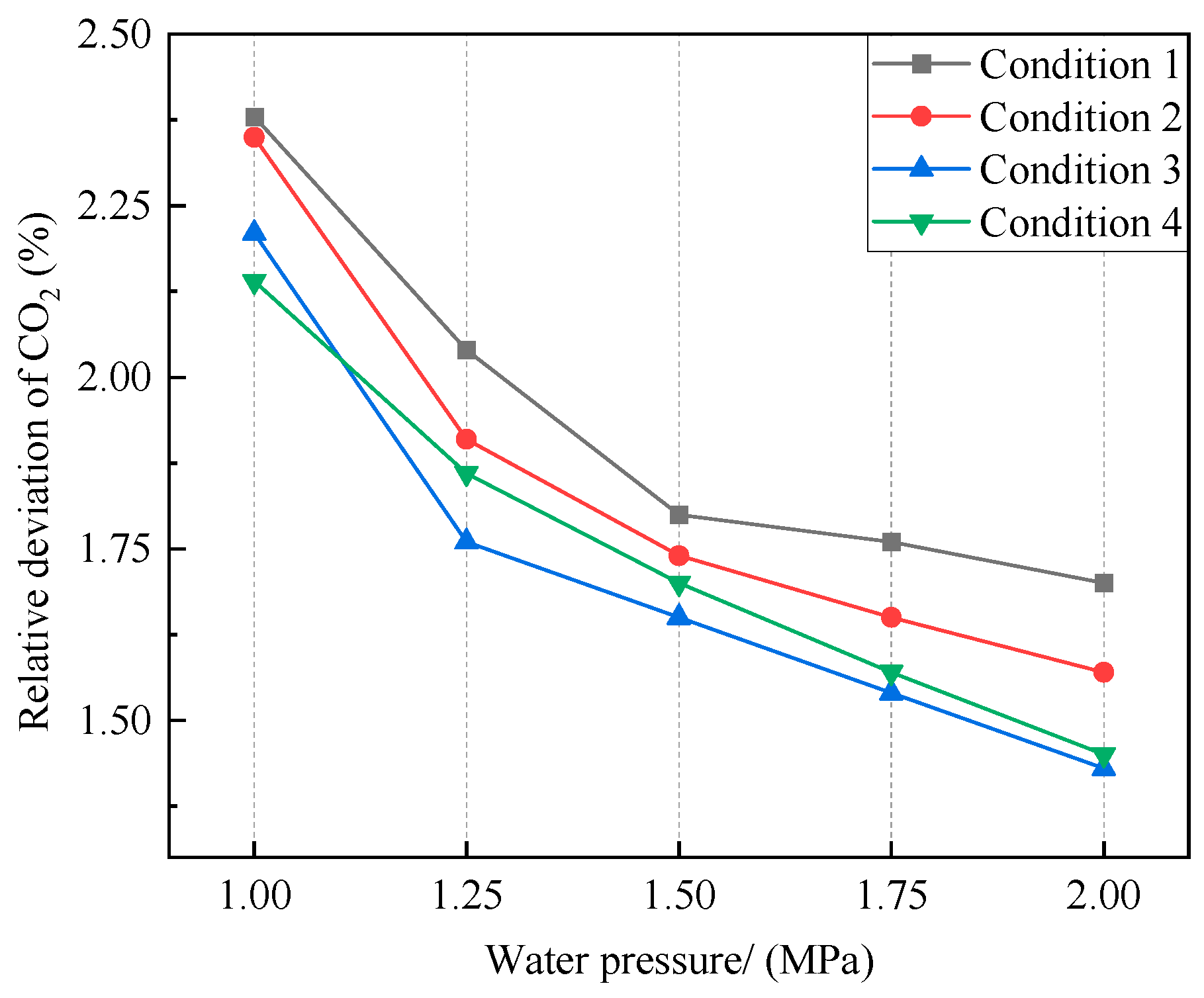
Figure 10.
Effect of water pressure on CO2 sampling relative deviation.
Figure 10.
Effect of water pressure on CO2 sampling relative deviation.
Figure 11.
Optimized probe structure.
Figure 11.
Optimized probe structure.
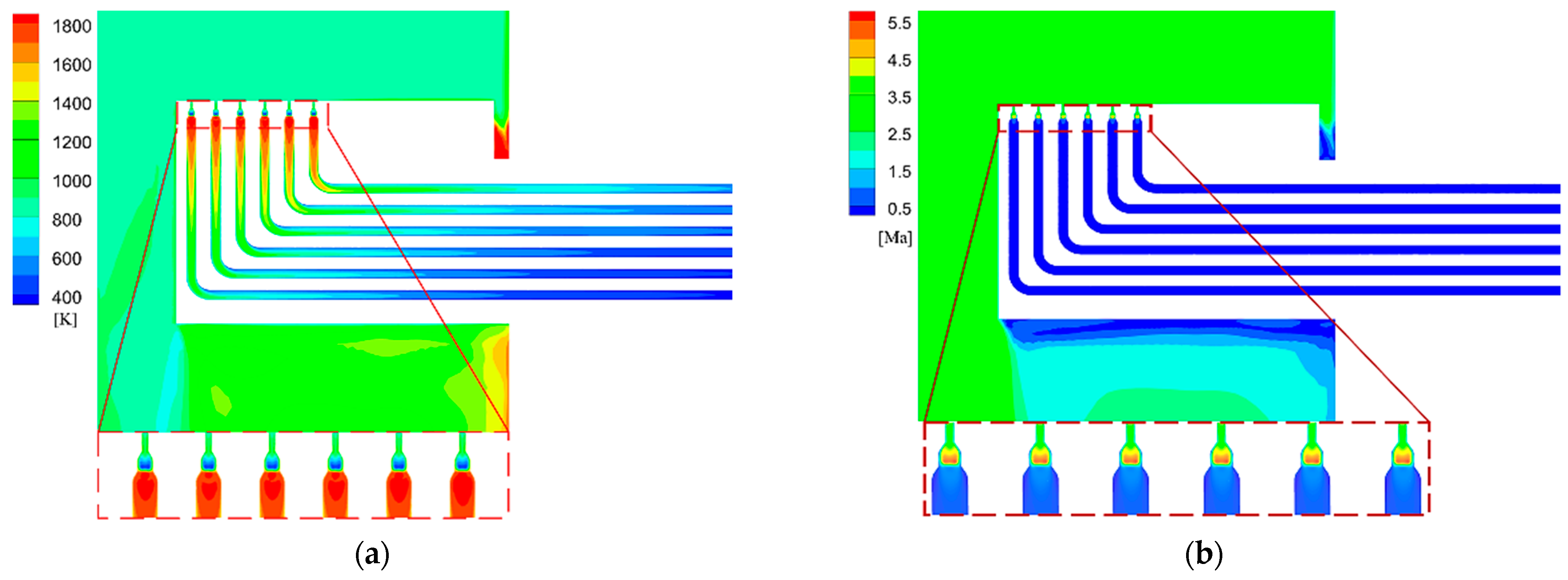
Figure 12.
Static temperature and Mach number distribution of the optimized probe. (a) Distribution of static temperature. (b) Distribution of Mach number.
Figure 12.
Static temperature and Mach number distribution of the optimized probe. (a) Distribution of static temperature. (b) Distribution of Mach number.
Figure 13.
The gas flow velocity distribution before and after optimization. (a) Before optimization. (b) After optimization.
Figure 13.
The gas flow velocity distribution before and after optimization. (a) Before optimization. (b) After optimization.
Figure 14.
Variation in static temperature and Mach number in the expansion section (optimized probe). (a) Variation in static temperature. (b) Variation in Mach number.
Figure 14.
Variation in static temperature and Mach number in the expansion section (optimized probe). (a) Variation in static temperature. (b) Variation in Mach number.
Figure 15.
Impact of cooling water pressure on CO2 relative deviation (optimized probe).
Figure 15.
Impact of cooling water pressure on CO2 relative deviation (optimized probe).
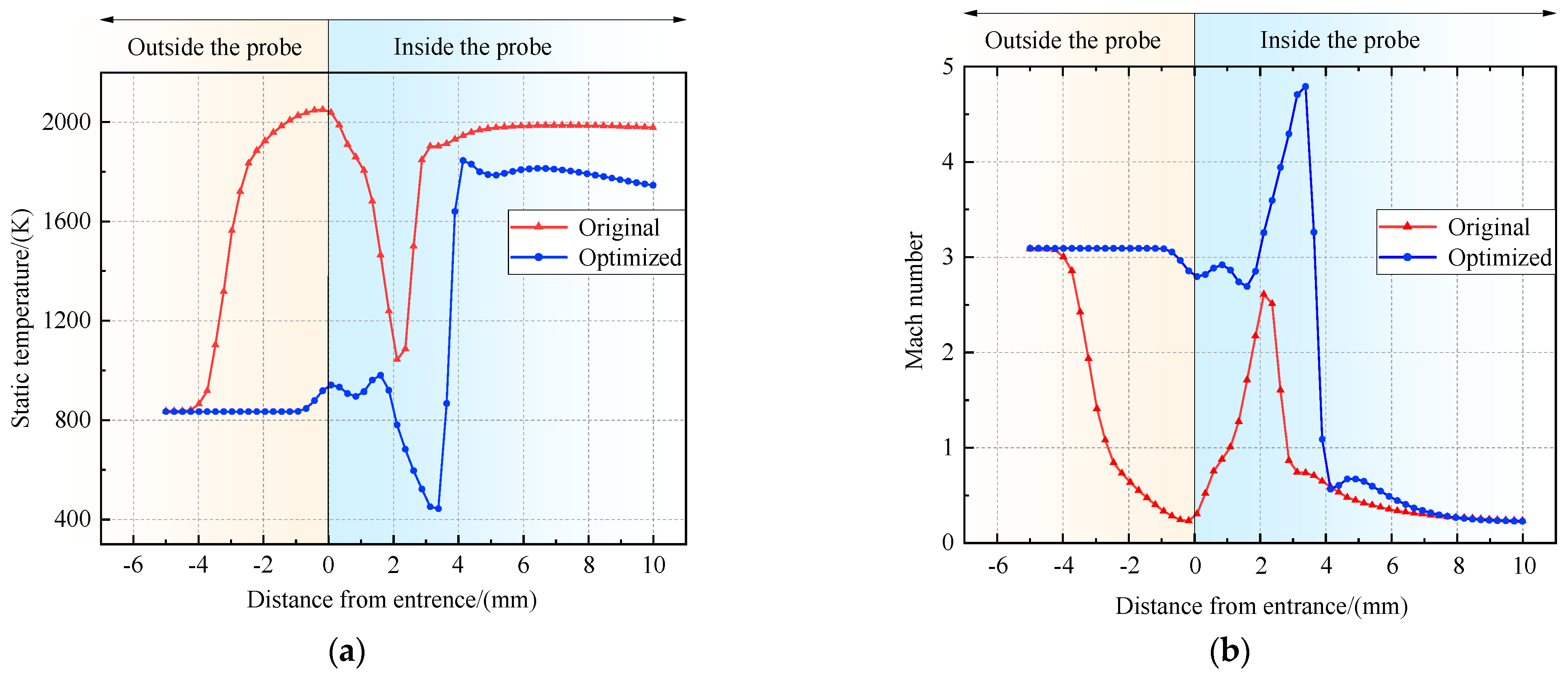
Figure 16.
Variation in static temperature and Mach number before and after optimization. (a) Variation in static temperature. (b) Variation in Mach number.
Figure 16.
Variation in static temperature and Mach number before and after optimization. (a) Variation in static temperature. (b) Variation in Mach number.
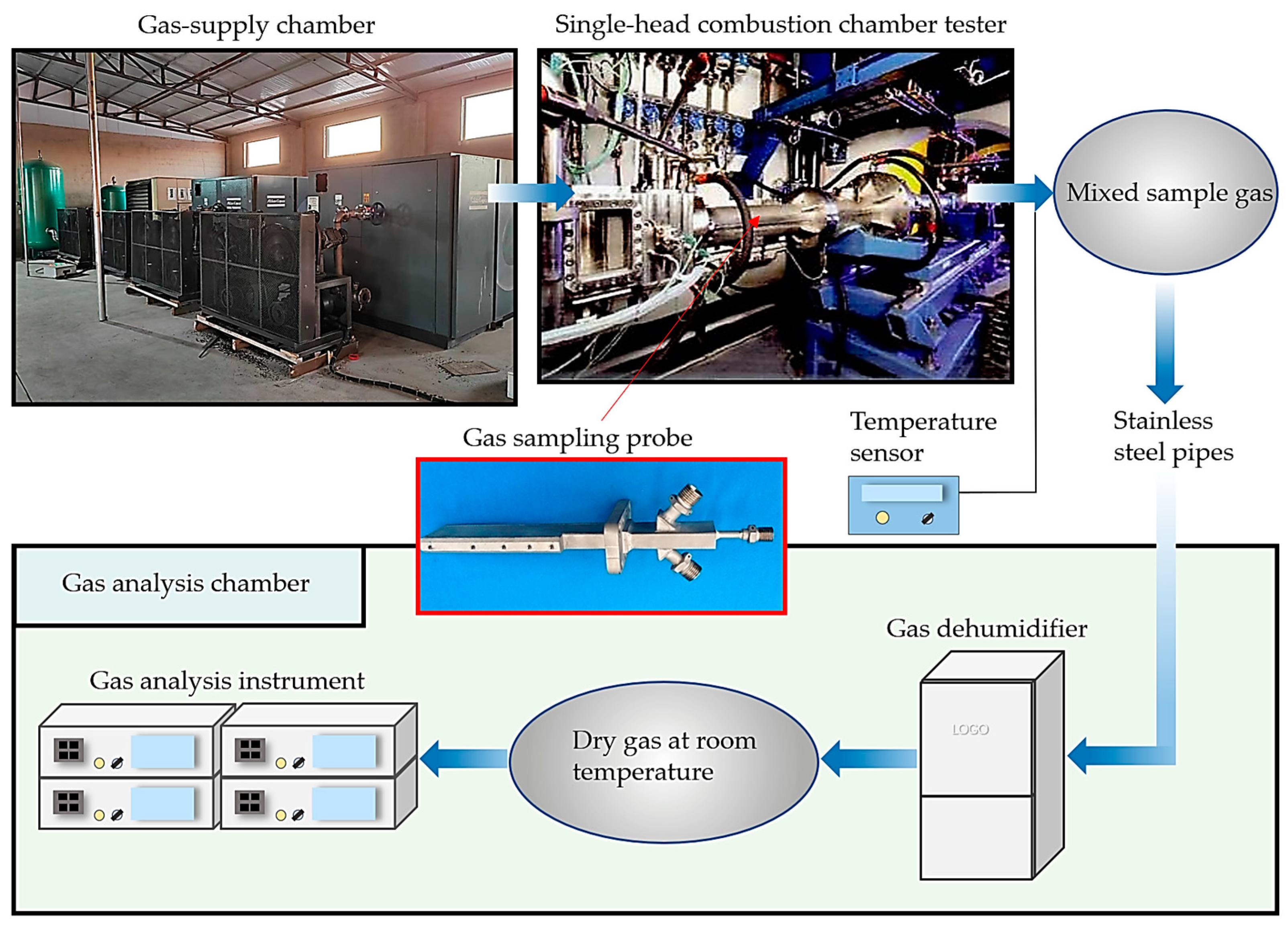
Figure 17.
Test operation process.
Figure 17.
Test operation process.
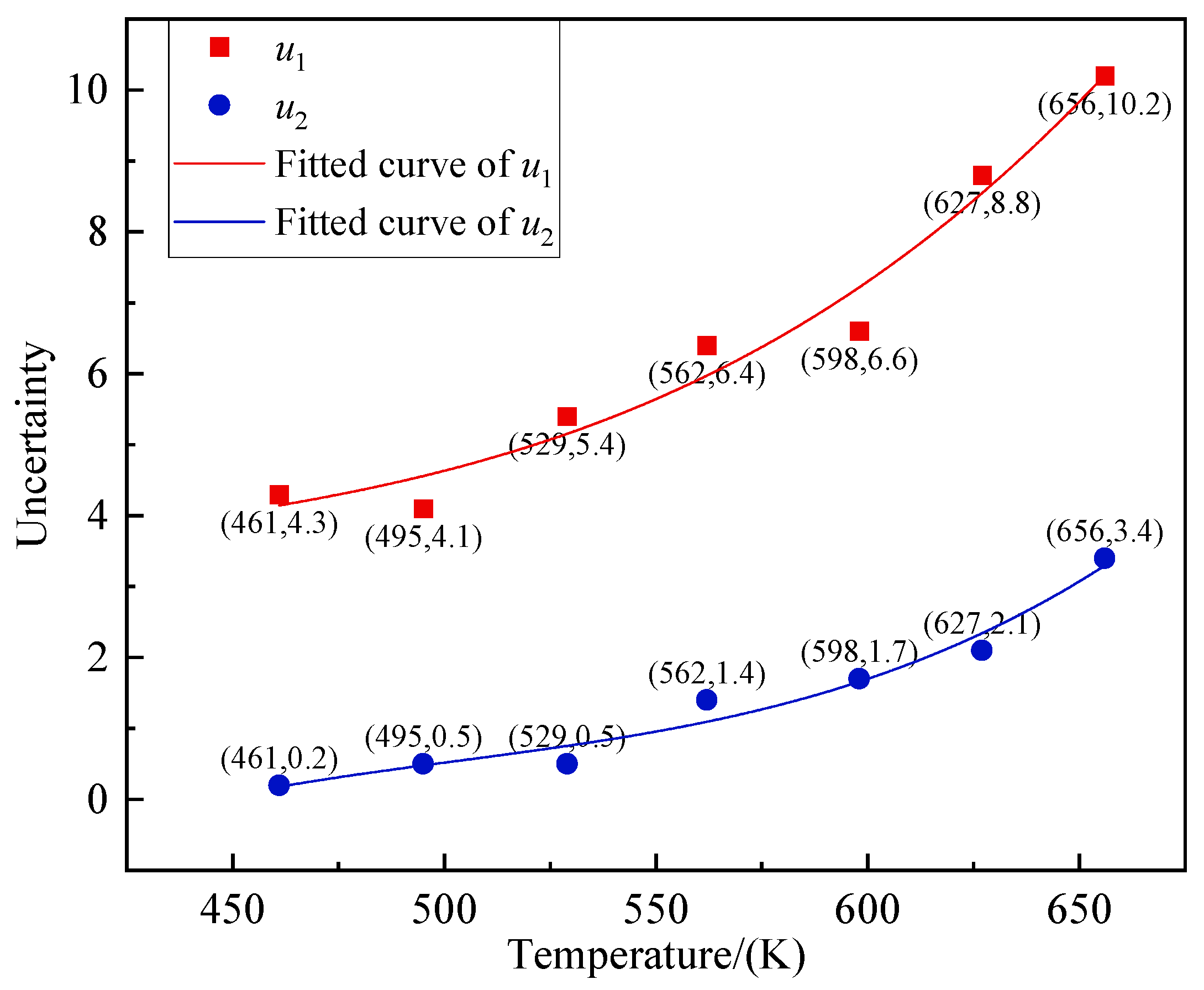
Figure 18.
Uncertainty at different temperature measuring points.
Figure 18.
Uncertainty at different temperature measuring points.
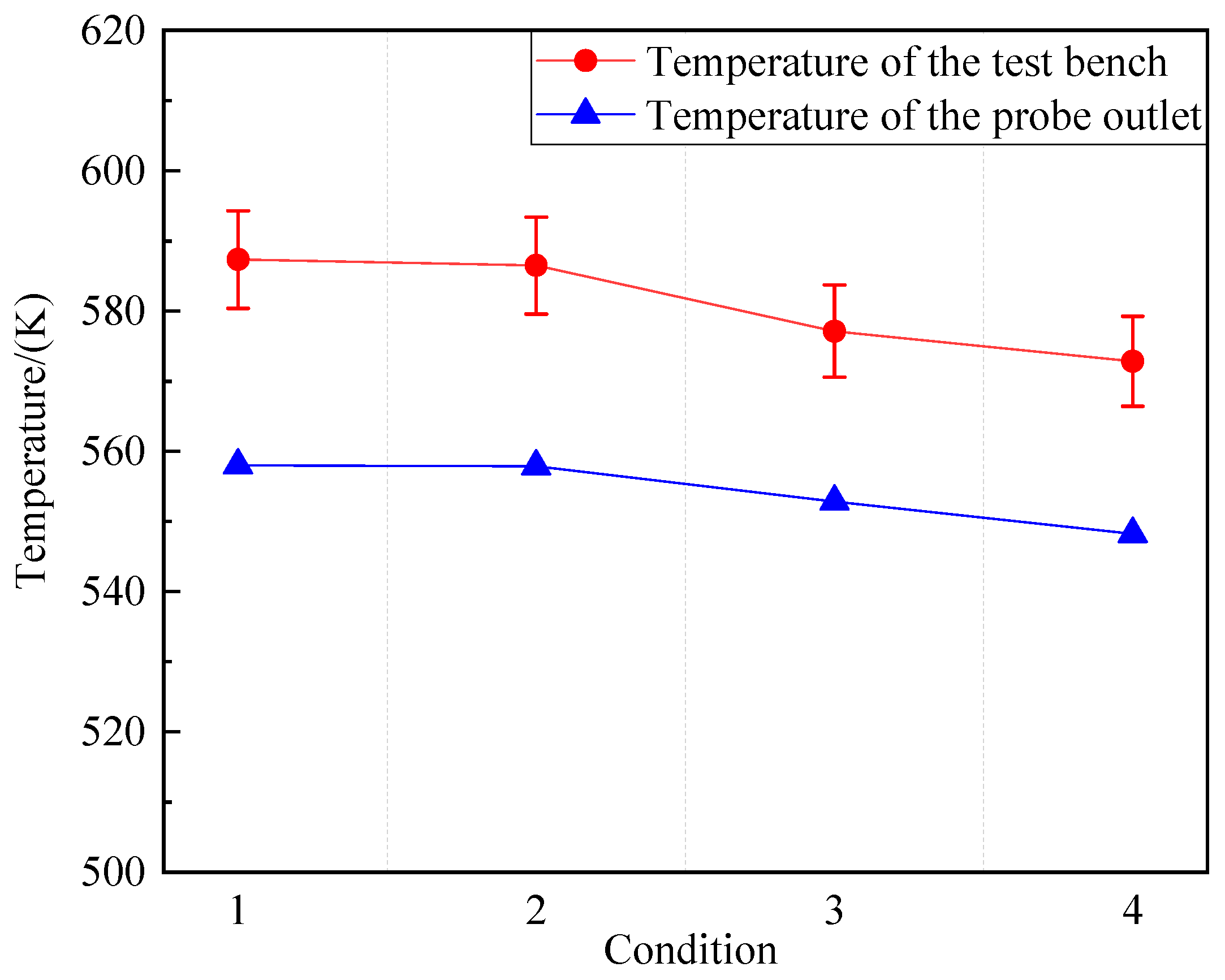
Figure 19.
Comparison of test bench data with simulation results.
Figure 19.
Comparison of test bench data with simulation results.
Table 1.
Structural parameters of the probe head.
Table 1.
Structural parameters of the probe head.
| Structural Parameter | Numerical Value |
|---|
| L1, L2, L4 | 1 mm |
| L3 | 1.5 mm |
| P1 | 0.8 mm |
| P2 | 2 mm |
| P3 | 3.2 mm |
| R1, R2 | 60 ± 1° |
| R3 | 30° |
Table 2.
Boundary conditions.
Table 2.
Boundary conditions.
| Boundary | Total Temperature/Backflow Temperature (K) | Total Pressure/Gauge Pressure (MPa) | Initial Gauge Pressure (MPa) |
|---|
| Gas inlet | 2000 | 2.4 | 0.0485 |
| Gas outlet | 290 | 0.101 | --- |
| Probe outlet | 290 | 0.0075 | --- |
| Cooling inlet | 290 | Adjustable | --- |
| Cooling outlet | 290 | 0.101 | --- |
Table 3.
Comparison of CO2 volume fraction.
Table 3.
Comparison of CO2 volume fraction.
| Excess Air Coefficient (alf) | Theoretical Actual Value (%) | Calculated Molar Volume of V = RT/P (m3/mol) | Calculated Volume Fraction of V = RT/P (%) | Calculated Molar Volume of R-K Equation Iterative Algorithm (m3/mol) | Calculated Volume Fraction of R-K Equation Iterative Algorithm (%) |
|---|
| 1.14 | 11.79 | 165.57 × 10−3 | 13.32 | 149.19 × 10−3 | 12.00 |
| 1.25 | 11.52 | 162.63 × 10−3 | 12.83 | 146.29 × 10−3 | 11.6 |
| 1.61 | 9.07 | 161.15 × 10−3 | 10.16 | 143.88 × 10−3 | 9.15 |
| 2.06 | 7.00 | 160.92 × 10−3 | 7.9 | 143.17 × 10−3 | 7.03 |
Table 4.
Comparison of CO volume fraction.
Table 4.
Comparison of CO volume fraction.
| Excess Air Coefficient (alf) | Theoretical Actual Value (%) | Calculated Molar Volume of V = RT/P (m3/mol) | Calculated Volume Fraction of V = RT/P (%) | Calculated Molar Volume of R-K Equation Iterative Algorithm (m3/mol) | Calculated Volume Fraction of R-K Equation Iterative Algorithm (%) |
|---|
| 1.14 | 1.06 | 165.57 × 10−3 | 1.1985 | 156.10 × 10−3 | 1.1311 |
| 1.25 | 0.31 | 162.63 × 10−3 | 0.4707 | 150.73 × 10−3 | 0.3422 |
| 1.61 | 0.04 | 161.15 × 10−3 | 0.0448 | 143.39 × 10−3 | 0.0431 |
| 2.06 | 0.03 | 160.92 × 10−3 | 0.027 | 137.84 × 10−3 | 0.0295 |
Table 5.
Relative deviation of volume fractions.
Table 5.
Relative deviation of volume fractions.
| Condition | Water Pressure (MPa) | (%) | (%) |
|---|
| 1 | 0.5 | 5.52 | 5.67 |
| 2 | 0.5 | 5.31 | 5.43 |
| 3 | 0.5 | 5.07 | --- |
| 4 | 0.5 | 5.14 | --- |
Table 6.
Calculation error of combustion efficiency.
Table 6.
Calculation error of combustion efficiency.
| Condition | (%) | (%) | Δδ (%) |
|---|
| 1 | 0.201 | 0.201 | 0.284 |
| 2 | 0.08046 | 0.0808 | 0.114 |
| 3 | 0.007359 | --- | <0.1 |
| 4 | 0.009663 | --- | <0.1 |
Table 7.
The lowest relative deviation of volume fractions (28°).
Table 7.
The lowest relative deviation of volume fractions (28°).
| Condition | Optimum Water Pressure (MPa) | (%) | (%) |
|---|
| 1 | 2 | 1.44 | 1.42 |
| 2 | 1.75–2 | 1.39 | 1.36 |
| 3 | 1.75–2 | 1.21 | --- |
| 4 | 2 | 1.14 | --- |
Table 8.
The lowest relative deviation of volume fractions (30°).
Table 8.
The lowest relative deviation of volume fractions (30°).
| Condition | Optimum Water Pressure (MPa) | (%) | (%) |
|---|
| 1 | 1.75 | 2.21 | 2.27 |
| 2 | 1.75 | 1.83 | 1.9 |
| 3 | 2 | 1.65 | --- |
| 4 | 2 | 1.29 | --- |
Table 9.
The lowest relative deviation of volume fractions (32°).
Table 9.
The lowest relative deviation of volume fractions (32°).
| Condition | Optimum Water Pressure (MPa) | (%) | (%) |
|---|
| 1 | 1.75 | 3.48 | 3.4 |
| 2 | 1.75 | 3.22 | 3.26 |
| 3 | 2 | 2.87 | --- |
| 4 | 2 | 2.57 | --- |
Table 10.
The lowest calculation error of combustion efficiency (28°).
Table 10.
The lowest calculation error of combustion efficiency (28°).
| Condition | (%) | (%) | Δδ (%) |
|---|
| 1 | 0.05258 | 0.05015 | 0.07266 |
| 2 | 0.02110 | 0.01910 | 0.02846 |
| 3 | 0.00176 | --- | --- |
| 4 | 0.002147 | --- | --- |
Table 11.
The lowest calculation error of combustion efficiency (32°).
Table 11.
The lowest calculation error of combustion efficiency (32°).
| Condition | (%) | (%) | Δδ (%) |
|---|
| 1 | 0.1268 | 0.1204 | 0.17486 |
| 2 | 0.04884 | 0.04584 | 0.06698 |
| 3 | 0.004160 | --- | --- |
| 4 | 0.004831 | --- | --- |
Table 12.
Relative deviation of volume fractions (optimized probe).
Table 12.
Relative deviation of volume fractions (optimized probe).
| Condition | Water Pressure (MPa) | (%) | (%) |
|---|
| 1 | 0.5 | 4.25 | 3.31 |
| 2 | 0.5 | 4.18 | 3.26 |
| 3 | 0.5 | 3.97 | --- |
| 4 | 0.5 | 4 | --- |
Table 13.
The lowest relative deviation of volume fractions (optimized probe).
Table 13.
The lowest relative deviation of volume fractions (optimized probe).
| Condition | Optimum Water Pressure (MPa) | (%) | (%) |
|---|
| 1 | 2 | 1.7 | 1.61 |
| 2 | 2 | 1.57 | 1.63 |
| 3 | 2 | 1.43 | --- |
| 4 | 2 | 1.43 | --- |
Table 14.
Calculation error of combustion efficiency (optimized probe).
Table 14.
Calculation error of combustion efficiency (optimized probe).
| Condition | (%) | (%) | Δδ (%) |
|---|
| 1 | 0.1547 | 0.117 | 0.194 |
| 2 | 0.06331 | 0.04584 | 0.07816 |
| 3 | 0.005759 | --- | <0.01 |
| 4 | 0.007516 | --- | <0.01 |
Table 15.
The lowest calculation error of combustion efficiency (optimized probe).
Table 15.
The lowest calculation error of combustion efficiency (optimized probe).
| Condition | (%) | (%) | Δδ (%) |
|---|
| 1 | 0.06186 | 0.05684 | 0.084 |
| 2 | 0.02374 | 0.02294 | 0.033 |
| 3 | 0.002080 | --- | <0.01 |
| 4 | 0.002684 | --- | <0.01 |
Table 16.
Concentration data of gas components of the test bench.
Table 16.
Concentration data of gas components of the test bench.
| Excess Air Coefficient (alf) | CO2 (%) | CO (ppm) | Temperature of the Test Bench (K) | HUC (ppm) | NOx (ppm) |
|---|
| 1.14 | 11.79 | 10,611.91 | 587.35 | 97.51 | 163.39 |
| 1.25 | 11.52 | 3685.24 | 586.47 | 43.90 | 162.83 |
| 1.61 | 9.07 | 407.93 | 577.12 | 45.40 | 103.25 |
| 2.06 | 7.03 | 283.66 | 572.84 | 75.11 | 67.15 |
| 2.56 | 5.54 | 889.36 | 567.34 | 389.56 | 61.29 |
Table 17.
Uncertainty of temperature measurement.
Table 17.
Uncertainty of temperature measurement.
| | Temperature (K) | 567.34 | 572.84 | 577.12 | 586.47 | 587.35 |
|---|
| Uncertainty | |
|---|
| u1 | 6.127 | 6.299 | 6.440 | 6.768 | 6.805 |
| u2 | 1.160 | 1.234 | 1.300 | 1.445 | 1.466 |
| uc | 6.235 | 6.418 | 6.565 | 6.920 | 6.961 |
Table 18.
Simulated test data and temperature deviation.
Table 18.
Simulated test data and temperature deviation.
| Excess Air Coefficient (alf) | CO2 (%) | CO (%) | Temperature of the Probe Outlet (K) | Temperature Deviation | Condition |
|---|
| 1.14 | 11.79 | 1.0611 | 557.98 | 5.00% | 1 |
| 1.25 | 11.52 | 0.3685 | 557.87 | 4.88% | 2 |
| 1.61 | 9.07 | 0.0408 | 552.85 | 4.21% | 3 |
| 2.06 | 7.03 | 0.0284 | 548.21 | 4.30% | 4 |