New Data-Driven Models of Mass Flow Rate and Isentropic Efficiency of Dynamic Compressors
Abstract
1. Introduction
2. Existing Empirical Models of Compressor Mass Flow Rate and Isentropic Efficiency
2.1. Basic Parameters of Dynamic Compressors
- Parameters regarding mass flow rate
- 2.
- Compressor isentropic efficiency
2.2. Existing Empirical Formulas for Compressor Mass Flow Rate
2.3. Existing Empirical Formulas for Compressor Efficiency
3. Evaluation of the Reviewed Models for Applications to Aero Engine and ECS Compressors
3.1. Criteria for Evaluation
3.2. Description of Dynamic Compressors
3.3. Performance Maps of Dynamic Compressors
3.3.1. Performance Maps of BIGFAN Compressors
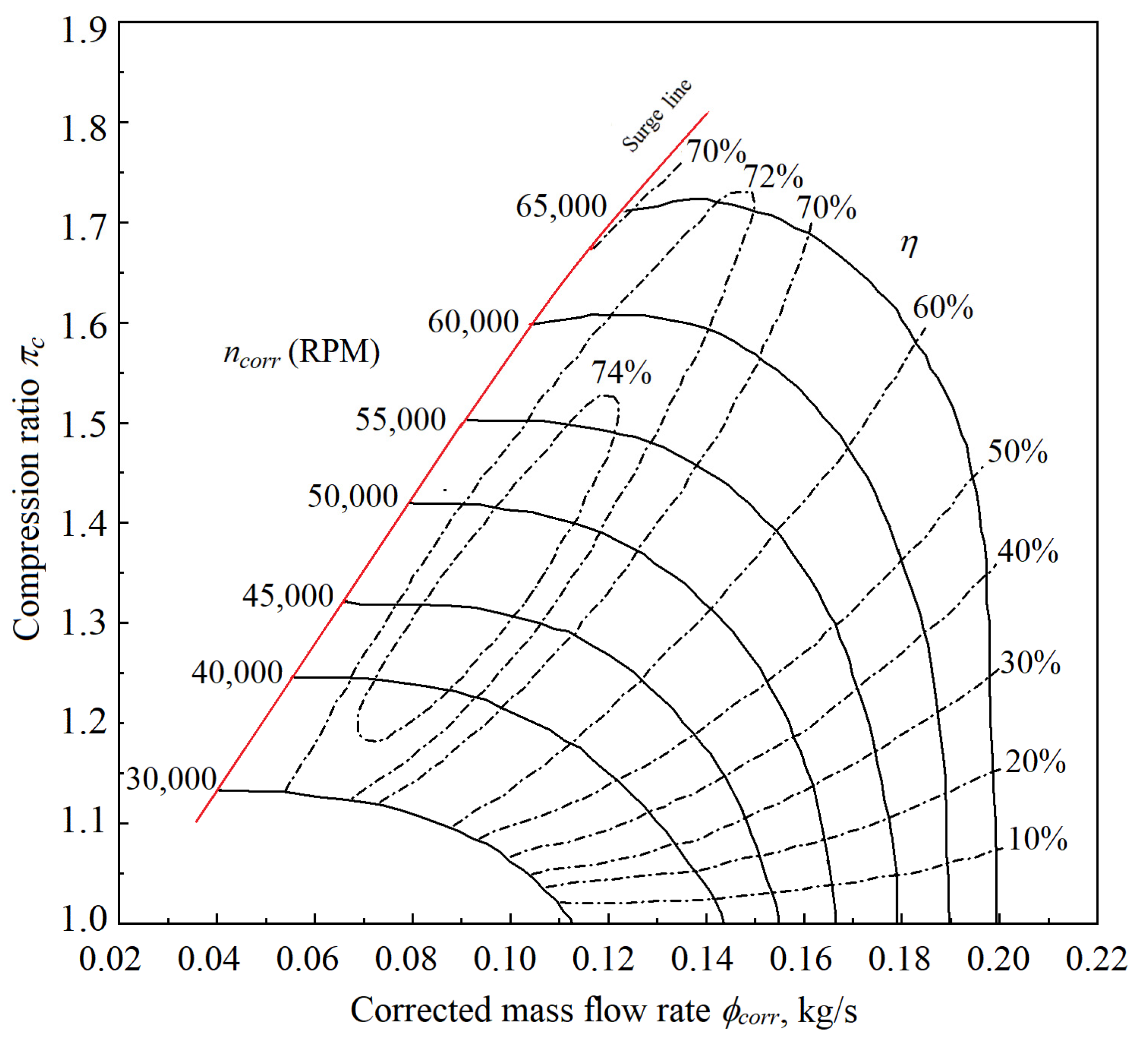
3.3.2. Performance Map of Aircraft ECS Compressor
3.4. Evaluation of the Existing Mass Flow Models
- None of the evaluated existing mass flow models has an MAD less than 2.0%, indicating the need to develop new models with high accuracy.
- The Tian [44] model has the highest prediction accuracy for the BIGFAN LPC and the ECS compressor, with MADs of 2.0% and 2.4%, respectively, while it predicts poorly for the BIGFAN HPC, with an MAD of 11.0%. The Orkisz and Stawarz [42] model has the highest prediction accuracy for the BIGFAN HPC, with MAD = 2.1%, and a moderate prediction accuracy for the BIGFAN LPC, with an MAD of 3.5%, while it predicts poorly for the ECS compressor, with an MAD of 15%.
- The BIGFAN LPC is a multi-stage axial compressor, with ϕcorr = 19.2–107.8 kg/s and πc = 1.07–1.96. The BIGFAN HPC is a multi-stage axial compressor, with ϕcorr = 20–65.7 kg/s and πc = 1.21–16.82. The ECS compressor is a centrifugal compressor, with ϕcorr = 0.04–0.2 kg/s and πc = 1.02–1.73. Comparing the compressor type, mass flow rate, and the compression ratio, from the prediction accuracy of the Tian [44] model and the Orkisz and Stawarz [42] model to the three compressors, it may be reasoned that, among the three factors, the compression ratio and the compressor type rank in the first and the second places as to the effect on model applicability, and a single mass flow rate model may not be adequate to variety of applications.
- For evaluating the applicability of compressors, the MAD is much better than Rc2. This can be seen by comparing the prediction accuracy of the Tian [44] model and that of Jensen et al. [13]. For the BIGFAN LPC and the ECS compressor, the Jensen et al. [13] model has higher Rc2 values than the Tian [44] model, but actually the predictions of the Jensen et al. [13] model has much larger deviation from the map values than the Tian [44] model has.
3.5. Evaluation of the Existing Isentropic Efficiency Models
- The Tian [44] model has the highest prediction accuracy for all the three compressors, with MAD = 1.8% for the BIGFAN LPC, MAD = 0.8% for the BIGFAN HPC, and MAD = 3.2% for the ECS compressor, suggesting that it is possible to propose a single efficiency model for a wide range of applications.
- For the ECS compressor, the highest prediction accuracy of the existing models is MAD = 3.2% and, for the BIGFAN LPC, the highest prediction accuracy of the existing models is MAD = 1.8%, indicating a need to develop a highly accurate efficiency model.
4. Development of New Empirical Models for Dynamic Compressor Performance
4.1. New Empirical Models of Mass Flow Rate
4.1.1. Developing New Models
Method 1
- Choose a k value. For example set k = 3.
- Construct sub-functions f1(πc, ncorr), f2(πc, ncorr), and f3(πc, ncorr). The simplest practice is to use polynomial forms.
- Based on the above-mentioned three performance maps of mass flow rate, conduct extensive computational trial and error using different data-driven methods. Those yielding superior results are selected to refine the sub-functions in the next step. In this step, the tested data-driven methods include the Levenberg–Marquardt method, the Powell Optimization method, the Quasi-Newton method, the Simplex method, the Gold Rush Optimizer, the Python curve fit tool, and the Genetic Algorithm (GA). The Levenberg–Marquardt method, the Python curve fit tool, and GA show superior performance, and are selected to refine the sub-functions in the next step.
- Use MAD as the criterion to tune the sub-functions using the data-driven methods selected in the above step. In this step, add or remove terms in the sub-functions one by one to determine which terms should be included. If removing a term does not increase MAD, this term should be removed. If adding a term does not reduce MAD, this term should not be added. The general model form include all terms for the three compressors.
- If the result obtained in the above step is unsatisfactory, go to step 1 and repeat the processes of trial and error in steps 1–4, until a satisfied result is obtained.
Method 2
4.1.2. Comparison of the New Models with the Best Existing Models
4.2. New Empirical Model of Isentropic Efficiency
4.2.1. Developing New Model
4.2.2. Comparison of the New Model with the Best Existing Models
5. Conclusions and Discussion
- For three dynamic compressors, none of the existing empirical models of mass flow rate has an MAD less than 2.0%, and the smallest MAD of the existing isentropic efficiency models is 3.4%, indicating the need to develop new models with high accuracy.
- As to the effect on the applicability of mass flow rate models, compression ratio and compressor type rank in the first and the second places among the three factors of compressor type, mass flow rate, and the compression ratio. A single mass flow rate model may not be adequate to a variety of applications.
- A compressor efficiency model is less sensitive to compressor type, mass flow rate, and the compression ratio than a mass flow rate model. The Tian [44] model was developed for aircraft ECS centrifugal compressors with low compression ratio and small mass flow rate, but it has the highest prediction accuracy for multi-stage axial compressors in wide ranges of compression ratio and mass flow rate among the existing models.
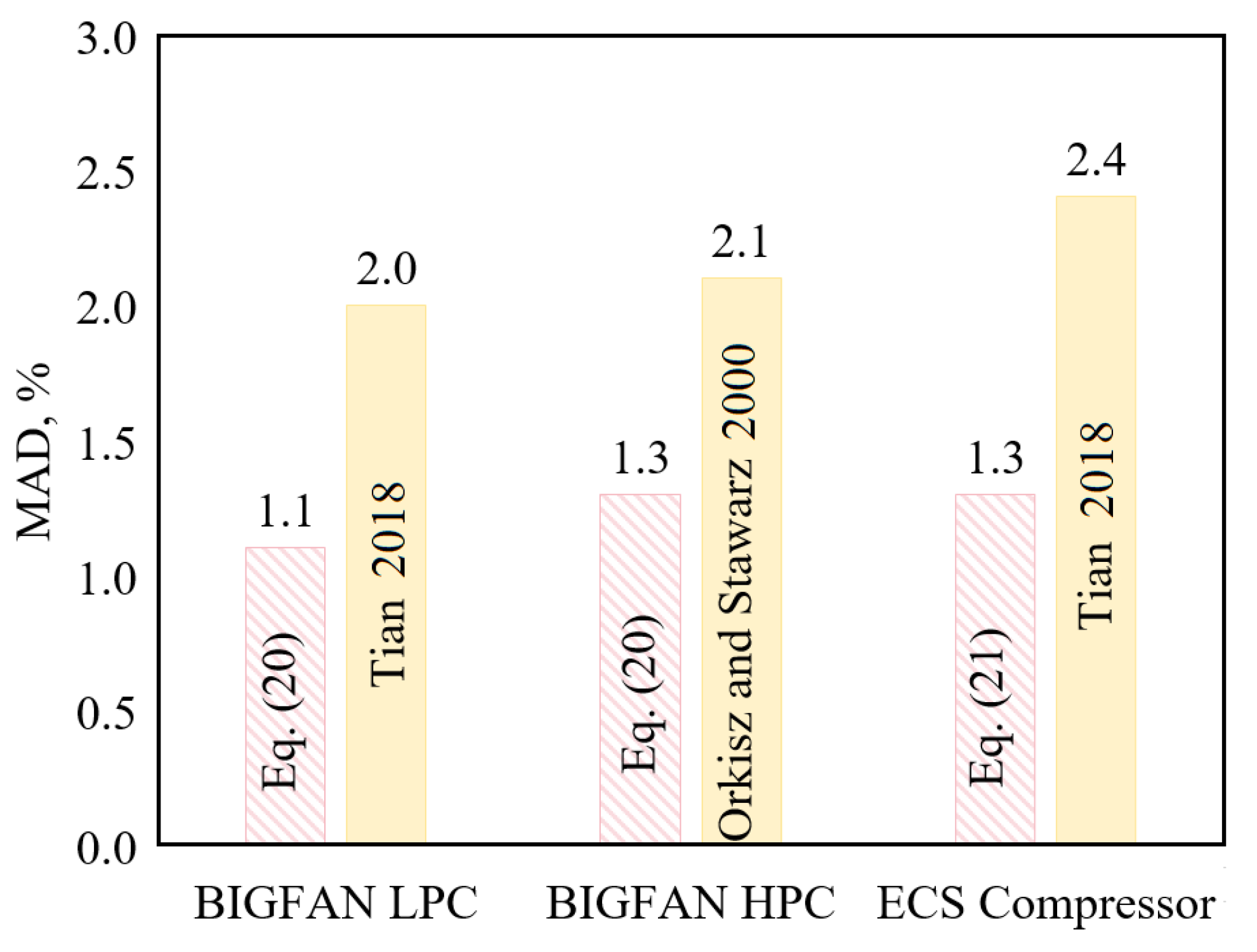
- The data-driven method is used to develop new models of mass flow rate and isentropic efficiency for dynamic compressors, for which two empirical formulas (Equations (20) and (21)) for the mass flow rate and one (Equation (22)) for the isentropic efficiency are developed.
- The new models have much higher prediction accuracy than the best existing models. The new mass flow rate models predict the three compressors with MAD ≤ 1.3%, while the best existing models all have MAD > 2.0%. The new efficiency model predicts the BIGFAN LPC, BIGFAN HPC, and ECS compressor, with MAD of 1.0%, 0.4%, and 1.9%, respectively, while the best existing one predicts the BIGFAN LPC, BIGFAN HPC, and ECS compressor with MAD of 1.8%, 0.8%, and 3.2%, respectively.
- For evaluating the applicability of compressors, the criterion MAD is much better than Rc2, while Rc2 is preferred to refining a general form, with some terms needing to be removed or added.
- Most of the existing empirical models of mass flow rate and isentropic efficiency of dynamic compressors relate to dimensional parameters, which limits the model robustness. Modeling the characteristics by relying on the fundamentals of the theory of dynamic compressors may have potential to solve the problem.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| ai | constant (i = 0, 1, 2, …) |
| bi | constant (i = 0, 1, 2, …) |
| cp | constant pressure specific heat, J/kg K |
| d | blade wheel diameter, m |
| G | mass flow rate, kg/s |
| k | isentropic exponent |
| Ma | Mach number |
| n | rotational speed, rev/s (RPS) |
| ncorr | corrected rotational speed, , RPS |
| nr | non-dimensional speed, n/nref |
| nt | rotational speed parameter, , rev/s K1/2 |
| p | pressure, Pa |
| Q | volume flow rate, m3/s |
| R | gas constant, J/kg K |
| R2 | coefficient of determination |
| Rc2 | corrected coefficient of determination |
| s2 | residual mean square |
| T | temperature, K |
| U | blade tip speed, m/s |
| W | compression work, W |
| Z | coefficient of relative stability margin |
| Greek symbols | |
| γ | polytropic exponent |
| η | isentropic efficiency |
| πc | compression ratio |
| ρ | density, kg/m3 |
| ϕ | normalized mass flow rate |
| ϕcorr | corrected mass flow parameter, kg/s |
| ψ | dimensionless head parameter |
| Subscripts | |
| corr | corrected parameter |
| exp | experimental |
| in | inlet |
| max | maximum |
| out | outlet |
| pred | predicted |
| ref | value at a reference point |
| top | maximum value on a speedline |
| s | isentropic |
References
- Yang, B.; Fang, X.; Zhang, L.; Zhuang, F.; Bi, M.; Chen, C.; Li, G.; Wang, X. Applicability of empirical models of isentropic efficiency and mass flow rate of dynamic compressors to jet engines. Prog. Aerosp. Sci. 2019, 106, 32–42. [Google Scholar] [CrossRef]
- Fang, X. Aircraft Environmental Control and Refrigeration; Beihang Press: Beijing, China, 2023. [Google Scholar]
- Meira, R.L.; Costa, G.M.N.; Kalid, R.A.; Martins, M.A.F. Improving the centrifugal compressor map through rigorous thermodynamic modeling: An analysis on a natural gas compression station pipeline. J. Nat. Gas Sci. Eng. 2021, 92, 104006. [Google Scholar] [CrossRef]
- Molière, M. The fuel flexibility of gas turbines: A review and retrospective outlook. Energies 2023, 16, 3962. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, X.; Yang, S.; Hooman, K.; Yang, X. Assessment evaluation of a trigeneration system incorporated with an underwater compressed air energy storage. Appl. Energy 2021, 303, 117648. [Google Scholar] [CrossRef]
- Wang, Z.; Xiao, Y.; Li, X.; Ren, X.; Gu, C.; Li, Y. Experiment and numerical simulation of the performance on scaled compressor cascade and development of a prediction model. Int. J. Heat. Fluid. Flow. 2024, 105, 109243. [Google Scholar] [CrossRef]
- Li, Z.; Agarwal, R.K. Numerical simulations and design optimization of compressor cascade flow using one equation and Wray-Agarwal turbulence model. Int. J. Comput. Fluid Dyn. 2022, 36, 705–718. [Google Scholar] [CrossRef]
- Nicolas, V.; Sdanghi, G.; Mozet, K.; Schaefer, S.; Maranzana, G.; Celzard, A.; Fierro, V. Numerical simulation of a thermally driven hydrogen compressor as a performance optimization tool. Appl. Energy 2022, 323, 119628. [Google Scholar] [CrossRef]
- Tsujikawa, G.S. Digital Controlled Closed Loop Air Cycle Development; SAE 851319; Society of Automobile Engineers, Inc.: Warrendale, PA, USA, 1985. [Google Scholar]
- He, J.; Zhao, J.Q.; Sun, W. Dynamic simulation of bootstrap air cycle refrigeration components for aircraft environmental control system. J. Syst. Simul. 2004, 16, 727–729. [Google Scholar]
- Yang, Y.; Chen, S.; Sheng, C.; Xie, H.; Luo, G.; Hou, Y. Study on coupling performance of turbo-cooler in aircraft. Energy 2021, 224, 120029. [Google Scholar] [CrossRef]
- Jennions, I.; Ali, F.; Miguez, M.E.; Escobar, I.C. Simulation of an aircraft environmental control system. Appl. Therm. Eng. 2020, 172, 114925. [Google Scholar] [CrossRef]
- Jensen, J.P.; Kristensen, A.F.; Sorenson, S.C.; Houbak, N.; Hendricks, E. Mean Value Modeling of a Small Turbocharged Diesel Engine; SAE 910070; Society of Automobile Engineers, Inc.: Warrendale, PA, USA, 1991. [Google Scholar]
- Mueller, M. Mean Value Modeling of Turbocharged Spark Ignition Engines. Master′s Thesis, DTU, Kgs Lyngby, Denmark, 1997. [Google Scholar]
- Canova, M.; Midlam-Mohler, S.; Guezennec, Y.; Rizzoni, G. Mean value modeling and analysis of HCCI diesel engines with external mixture formation. J. Dyn. Syst. Meas. Control. 2009, 131, 011002. [Google Scholar] [CrossRef]
- Liu, M.; Wang, B.; Liu, D. A digital twin modeling method for turbofan engine real-time test data analysis and performance monitoring. In Proceedings of the 2020 11th International Conference on Prognostics and System Health Management (PHM-2020), Virtual Meeting, 16–18 October 2020. [Google Scholar]
- Zhang, Z.J.; Duraisamy, K. Machine learning methods for data-driven turbulence modeling. In Proceedings of the 22nd AIAA Computational Fluid Dynamics Conference, Dallas, TX, USA, 22–26 June 2015. [Google Scholar]
- Ahmad, T.; Chen, H.; Guo, Y.; Wang, J. A comprehensive overview on the data driven and large scale based approaches for forecasting of building energy demand: A review. Energy Build. 2018, 165, 301–320. [Google Scholar] [CrossRef]
- Pulpeiro Gonzalez, J.; Hall, C. Equation-Based Compressor and Turbine Modeling for Variable Geometry Turbochargers; SAE Technical Paper 2018-01-0966; SAE: Warrendale, PA, USA, 2018. [Google Scholar] [CrossRef]
- Sun, J.; Li, C.; Liu, C.; Gong, Z.; Wang, R. A data-driven health indicator extraction method for aircraft air conditioning system health monitoring. Chin. J. Aeronaut. 2019, 32, 409–416. [Google Scholar] [CrossRef]
- Fang, X.; Dai, Q. Modeling of turbine mass flow rate performances using the Taylor expansion. Appl. Therm. Eng. 2010, 30, 1824–1831. [Google Scholar] [CrossRef]
- Fang, X.; Xu, Y. Development of an empirical model of turbine efficiency using the Taylor expansion and regression analysis. Energy 2011, 36, 2937–2942. [Google Scholar] [CrossRef]
- Nikiforov, A.; Popova, D.; Soldatova, K. A network application for modeling a centrifugal compressor performance map. IOP Conf. Ser. Mater. Sci. Eng. 2017, 232, 012046. [Google Scholar] [CrossRef]
- Fei, J.; Zhao, N.; Shi, Y.; Feng, Y.; Wang, Z. Compressor performance prediction using a novel feed-forward neural network based on Gaussian kernel function. Adv. Mech. Eng. 2016, 8, 1–14. [Google Scholar] [CrossRef]
- Uzun, M.; Demirezen, M.U.; Inalhan, G. Physics guided deep learning for data-driven aircraft fuel consumption modeling. Aerospace 2021, 8, 44. [Google Scholar] [CrossRef]
- Tu, H.; Chen, H. Modeling of a compressor’s performance map by fitting function methodology. Adv. Mater. Res. 2013, 779–780, 1194–1198. [Google Scholar] [CrossRef]
- Li, X.; Yang, C.; Wang, Y.; Wang, H. A prediction model of compressor with variable-geometry diffuser based on elliptic equation and partial least squares. R. Soc. Open Sci. 2018, 5, 171468. [Google Scholar] [CrossRef]
- Yang, H.; Yang, C. Application of scaling-endoreversible thermodynamic analysis model to aircraft environmental control system-methodology development. Int. J. Refrig. 2020, 112, 90–99. [Google Scholar] [CrossRef]
- Chen, S.; Zuo, S.; Wu, Z. Aerodynamic performance modeling of the centrifugal compressor and stability analysis of the compression system for fuel cell vehicles. SAE Int. J. Adv. Curr. Pract. Mobil. 2021, 3, 2325–2336. [Google Scholar] [CrossRef]
- Canova, M. Development and validation of a control-oriented library for the simulation of automotive engines. Int. J. Engine Res. 2004, 5, 219–228. [Google Scholar] [CrossRef]
- Fang, X.; Chen, W.; Zhou, Z.; Xu, Y. Empirical models for efficiency and mass flow rate of centrifugal compressors. Int. J. Refrig. 2014, 41, 190–199. [Google Scholar] [CrossRef]
- Andersson, P. Air Charge Estimation in Turbocharged Spark Ignition Engines. Ph.D. Thesis No. 989, Department of Electrical Engineering, Linkoping University, Linkoping, Sweden, 2005. [Google Scholar]
- Kolmanovsky, I.V.; Moraal, P.E.; van Nieuwstadt, M.J.; Criddle, M.; Wood, P. Modeling and Identification of a 2.0 L Turbocharged DI Diesel Engine; Ford Internal Technical Report SR-97-039; Ford: Dearborn, MI, USA, 1997. [Google Scholar]
- Moraal, P.; Kolmanovsky, I. Turbocharger modeling for automotive control application. SAE Trans. 1999, 108, 1324–1338. [Google Scholar]
- Tsoutsanis, E.; Meskin, N.; Benammar, M.; Khorasani, K. A component map tuning method for performance prediction and diagnostics of gas turbine compressors. Appl. Energy 2014, 135, 572–585. [Google Scholar] [CrossRef]
- Tsoutsanis, E.; Meskin, N.; Benammar, M.; Khorasani, K. Transient gas turbine performance diagnostics through nonlinear adaptation of compressor and turbine maps. J. Eng. Gas Turbines Power 2015, 137, 091201. [Google Scholar] [CrossRef]
- Biteus, J. Mean Value Engine Model of a Heavy Duty Diesel Engine; LITH-ISY-R-2666; Department of Electrical Engineering, Linkopings Universitet: Linkoping, Sweden, 2004. [Google Scholar]
- Eriksson, L.; Nielsen, L.; Brugard, J.; Bergstriim, J.; Pettersson, F.; Andersson, P. Modeling of a turbocharged SI engine. Annu. Rev. Control. 2002, 26, 129–137. [Google Scholar] [CrossRef]
- Guzzella, L.; Amstutz, A. Control of diesel engines. IEEE Control. Syst. Mag. 1998, 18, 53–71. [Google Scholar]
- Jiang, H.; Dong, S.; Liu, Z.; He, Y.; Ai, F. Performance prediction of the centrifugal compressor based on a limited number of sample data. Math. Probl. Eng. 2019, 2019, 5954128. [Google Scholar] [CrossRef]
- Park, Y.; Park, I.; Min, K.; Sunwoo, M. Model-based feedforward control of the VGT in a diesel engine based on empirical models of compressor and turbine efficiencies. Int. J. Automot. Technol. 2015, 16, 561–570. [Google Scholar] [CrossRef]
- Orkisz, M.; Stawarz, S. Modeling of turbine engine axial-flow compressor and turbine characteristics. J. Propuls. Power 2000, 16, 336–339. [Google Scholar] [CrossRef]
- Sieros, G.; Stamatis, A.; Mathioudakis, K. Jet engine component maps for performance modeling and diagnosis. J. Propuls. Power 1997, 13, 665–674. [Google Scholar] [CrossRef]
- Tian, L. Research on Mathematical Modeling of Fault Prediction of Aircraft Environmental Control System. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2018. [Google Scholar]
- Yang, Y. Simulation Research on Mean Value Model of Air Circulation Machine and Aircraft Environmental Control System. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2020. [Google Scholar]
- NLR. Program GSP 11; National Aerospace Laboratory NLR: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Yang, B. Research on Adaptive Control of Turbofan Engine Based on Data Driven. Ph.D. Thesis, Beihang University, Beijing, China, 2021. [Google Scholar]
- Sun, P.; Fang, X.; Zhuang, F.; Chen, C.; Shang, H.; Liu, Y.; Yang, B. Evaluation of applicability of empirical models of turbine performance to aircraft engine. Aerosp. Sci. Technol. 2021, 117, 106953. [Google Scholar] [CrossRef]
- Jones, K.; Claeys, H. The Continuing Evolution of the C-130 Environmental Control System; SAE 1999-01-2163; Society of Automobile Engineers, Inc.: Warrendale, PA, USA, 1999. [Google Scholar]
- Ryan, S.K. F-15 Environmental System Improvements; SAE 901235; Society of Automobile Engineers, Inc.: Warrendale, PA, USA, 1990. [Google Scholar]
- Wiegand, C.; Bullick, B.A.; Catt, J.A.; Hamstra, J.W.; Walker, G.P.; Wurth, S. F-35 air vehicle technology overview. In Proceedings of the AIAA Aviation Forum, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar]

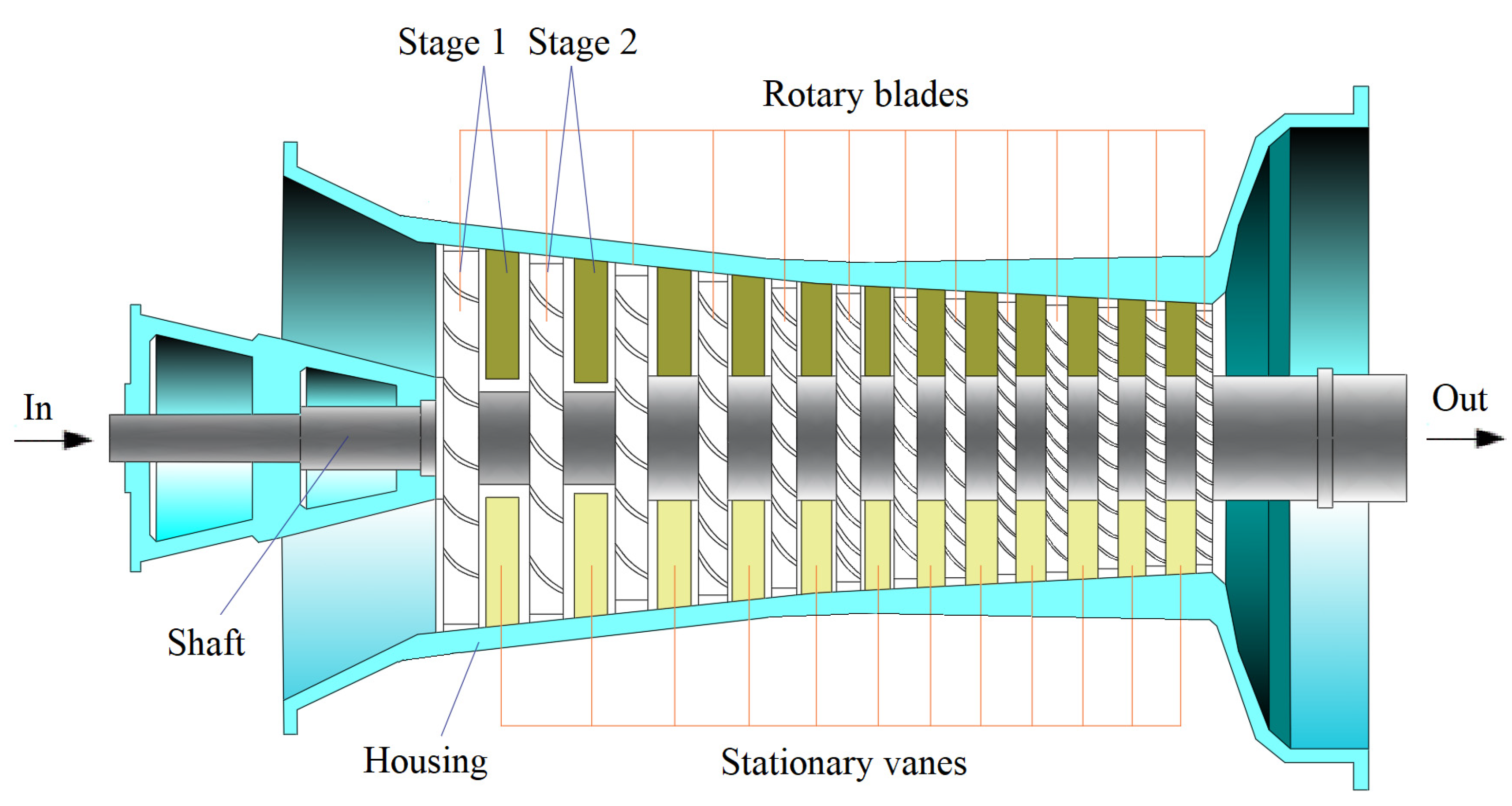
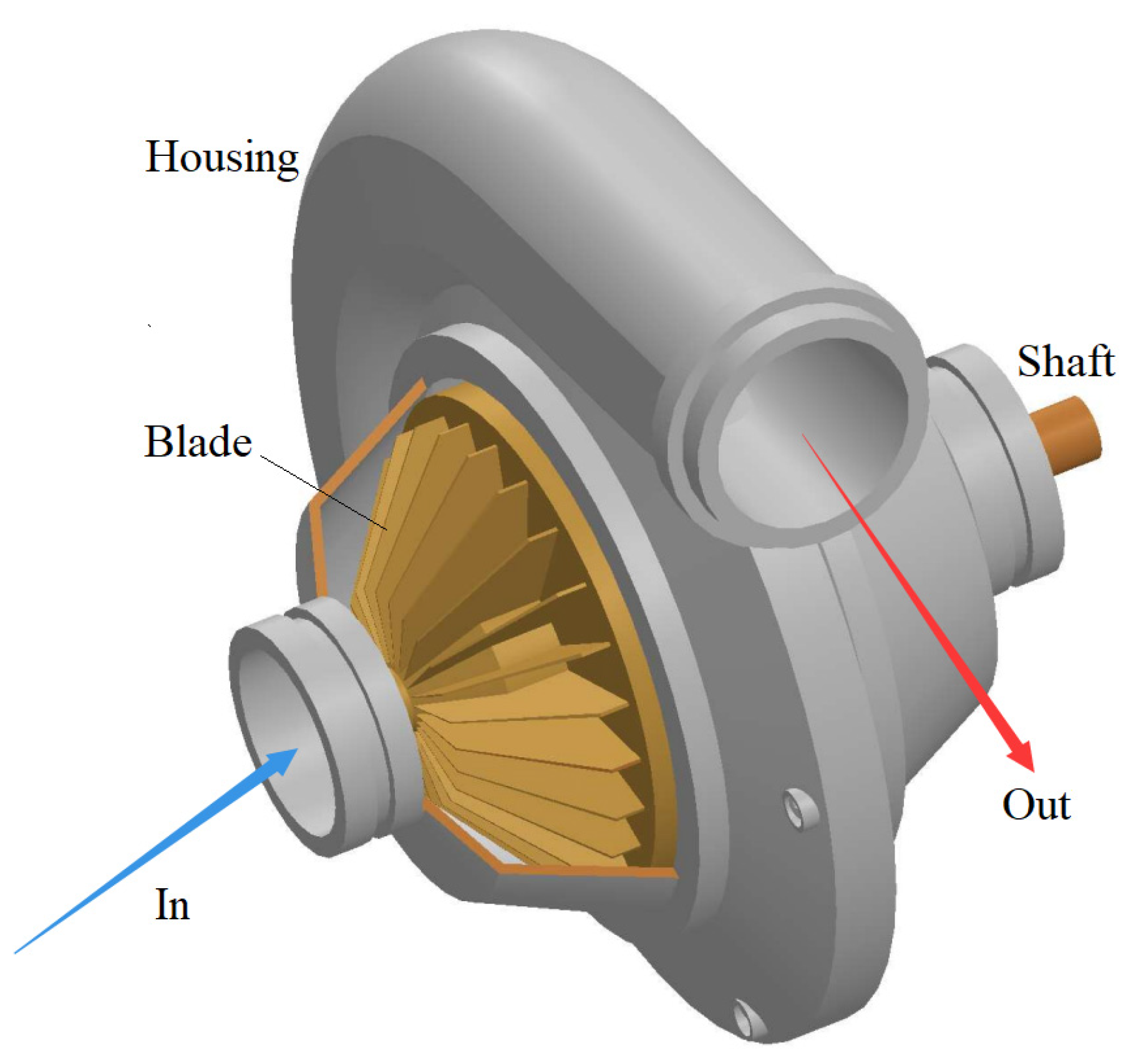
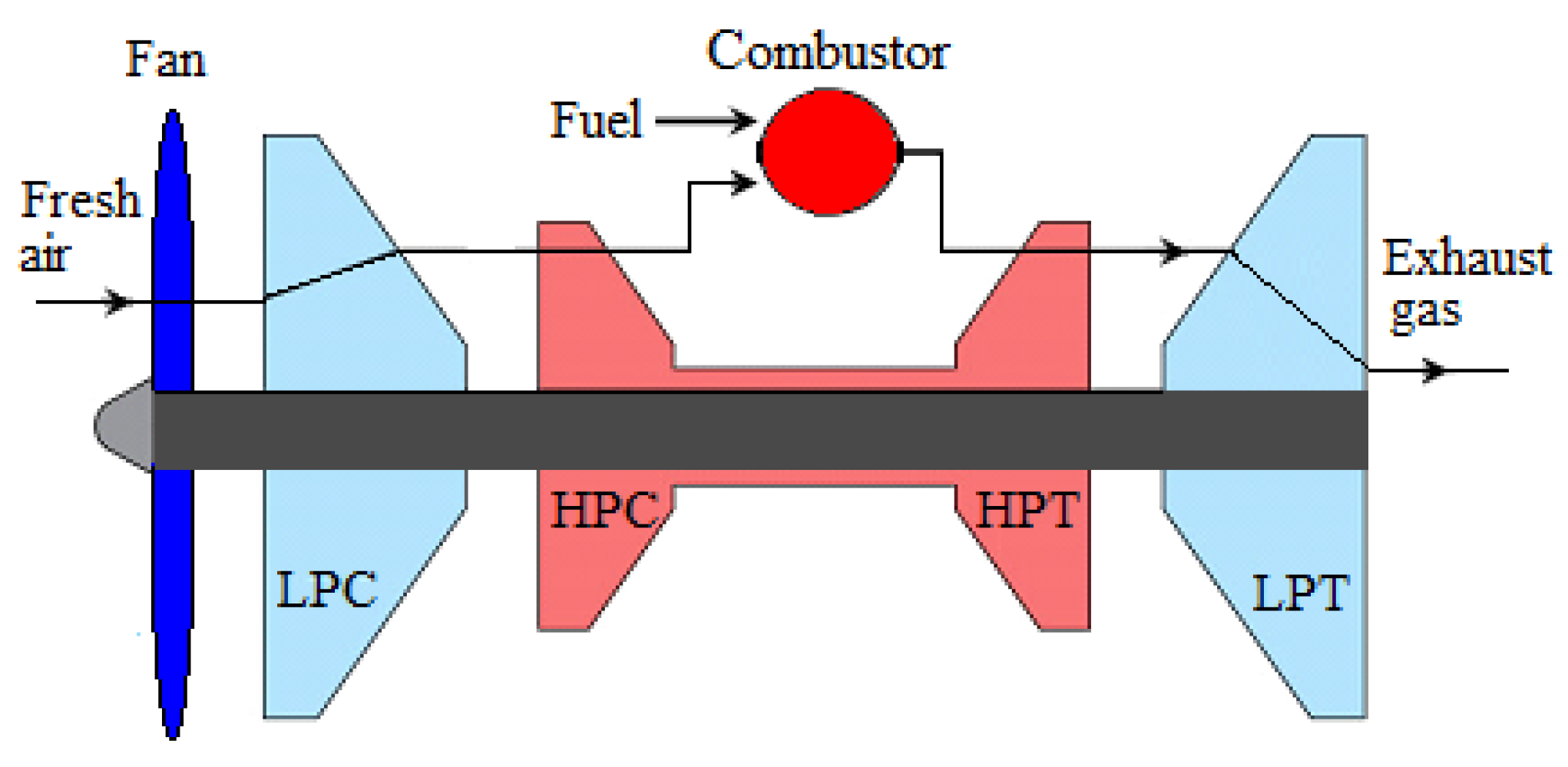

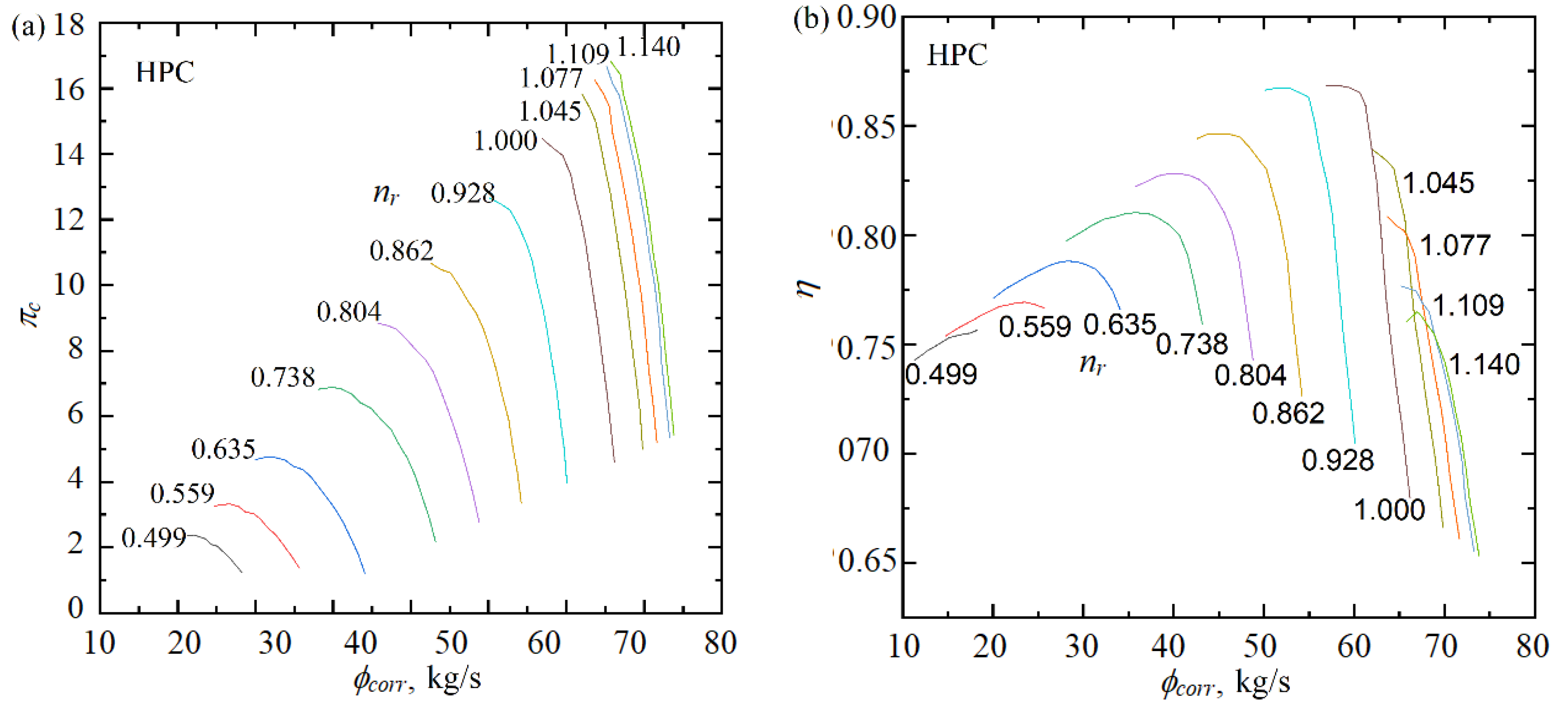


| Sources | Models | Remarks |
|---|---|---|
| Jensen et al. [13] | where coefficients aij are determined through the least square fit on experimental data, and the Mach number Ma is defined as where R is the gas constant. | They proposed the model when studying the compressor of a 1.6 L turbocharged indirect injection diesel engine. |
| Mueller [14] | Mueller proposed the polynomial model to simulate the compressor of turbocharged spark ignition (SI) engines. | |
| Tu and Chen [26] | where the coefficients a, b, c are fitted by polynomial function of the Mach number Ma as in the following: where the order of the polynomials m, n, l are obtained from the actual curve fitting. | They proposed the exponential model and implemented a case study of a compressor map for the TCA88 turbocharger to verify it. |
| Andersson [32] | where . | Andersson reasoned that the normalized mass flow rate could be described using only the head parameter and thus proposed a model for the compressor of turbocharged SI engines. |
| Kolmanovsky et al. [33,34] | where ϕtop is the maximum normalized mass flow rate on each speedline, and πc,top is the compression ratio corresponding to ϕc,top. | They proposed the model for compressors used in automobile turbocharged diesel engines. |
| Tsoutsanis et al. [35,36] | where and denote the semi-major and the semi-minor axes of the ellipse, respectively, and ϕcorr0 and πc0 denote the corrected mass flow rate and the compression ratio when the ellipse center is fixed at (0, 0). Taking into consideration that each ellipse is free to rotate at an angle θ, then the ellipse’s new coordinates (ϕcorr, πc) are given by The coefficients and are expressed as | They proposed a compressor map tuning method to improve the accuracy and fidelity of gas turbine engine performance models. Axial compressor performance maps were used in their study. |
| Biteus [37] | The model was proposed for heavy duty diesel engine compressors. | |
| Eriksson et al. [38] | where . | They developed the model for turbocharged SI engine compressors. |
| Guzzella and Amstutz [39] | where Ai (i = 1, 2, 3) depend on the shaft speed n only, and can be parameterized as polynomial functions. | They proposed the compressor model in studying the model-based control of diesel engines. |
| Jiang et al. [40] | The model was proposed for centrifugal compressors. | |
| Orkisz and Stawarz [42] | where Z is the coefficient of relative stability margin of the compressor. | They rescaled a traditional axial compressor performance map in a coordinate system of (nt, Z, ϕ), based on which they proposed their model. |
| Sieros et al. [43] | 1. Non-linear model, which can be reduced to
2. Simple linear model, which can be reduced to 3. Generalized linear model 1 The simplest form of the generalized linear models is 4. Generalized linear model 2 A further increase in accuracy may be achieved by using the following second-degree polynomial form: | They proposed four types of mass flow models for jet engine compressors: Non-linear model, simple linear model, generalized linear model 1, and generalized linear model 2. All of them incorporate the rotational speed ratio nr. The simple linear model, generalized linear model 1, and generalized linear model 2 are implicit, which are not convenient for use. since iteration is needed during the calculations. |
| Tian [44] | The model was proposed to fit the performance map of an ECS compressor. |
| Sources | Models | Remarks |
|---|---|---|
| Jensen et al. [13] | They proposed the model when studying the compressor of a 1.6 L turbocharged indirect injection diesel engine. | |
| Canova et al. [15] | where Wcorr is difined as and it is obtained by where the coefficients Ai (i = 1, 2, 3, 4) are linear functions of the corrected speed ncorr and can be obtained by fitting the compressor maps. | They proposed the model for automotive diesel engine compressors, where the corrected compression work Wcorr is treated as the function of the corrected mass flow rate ϕcorr. |
| Tu and Chen [26] | where Q is the volume flow rate. | They proposed the polynomial model and implemented a case study of a compressor map for the TCA88 turbocharger to verify it. |
| Andersson [32] | Andersson proposed the model for the compressor of turbocharged SI engines by modifying the Guzzella and Amstutz model [39] with πc replaced by 1 + (πc − 1)0.5. | |
| Tsoutsanis et al. [35,36] | where and denote the semi-major and the semi-minor axes of the ellipse, respectively, and ϕcorr0 and η0 denote the corrected mass flow rate and the efficiency when the ellipse center is fixed at (0, 0). The coefficients and are expressed as Taking into consideration that each ellipse is free to rotate at an angle θ, then the compressor isentropic efficiency η is given by | They proposed a compressor map tuning method to improve the accuracy and fidelity of gas turbine engine performance models. Axial compressor performance maps were used in their study. |
| Eriksson et al. [38] | where a1, a2, a3, b1, …, b5 are constants needing to be determined based on the available data. | They described a component-based modeling method for turbocharged engines and developed the model for turbocharged SI engine compressors. |
| Guzzella and Amstutz [39] | where ϕcorr,ηmax and πc,ηmax are the corrected mass flow parameter and the compression ratio corresponding to the maximum efficiency ηmax, respectively. This model requires ηmax and its location in terms of ϕcorr,ηmax and πc,ηmax. This data point may not be included in the measured data, in which case ηmax, ϕcorr,ηmax and πc,ηmax need to be determined using curve fitting or similar methods. | They proposed the compressor model in studying the model-based control of diesel engines. |
| Jiang et al. [40] | The model was proposed for centrifugal compressors. | |
| Park et al. [41] | where c1–c6 are the fitted constants. | They proposed the model when studying the control of the variable geometry turbocharger in a diesel engine. |
| Orkisz and Stawarz [42] | where Z is the coefficient of relative stability margin of the compressor. | They rescaled a traditional axial compressor performance map in a coordinate system of (nt, Z, ϕ), based on which they proposed the model. |
| Sieros et al. [43] | 1. Simple linear model Y = a1 + a2X 2. Generalized linear model 1 3. Generalized linear model 2 | They proposed the simple linear and generalized linear models for the isentropic efficiency of jet engine compressors. They indicated that the generalized linear model 2 has the same accuracy as the generalized linear model 1, while reducing the regression constants from six to five. The simple linear model is implicit, which is not convenient for use, since the iteration is needed during the calculation. |
| Tian [44] | The model was proposed to fit the performance map of an ECS compressor. |
| Model | MAD (%) | Rc2 |
|---|---|---|
| Tian [44] | 2.0 | 0.954 |
| Jiang et al. [40] | 2.2 | 0.930 |
| Guzzella and Amstutz [39] | 2.9 | 0.938 |
| Orkisz and Stawarz [42] | 3.5 | 0.988 |
| Eriksson et al. [38] | 5.2 | 0.974 |
| Jensen et al. [13] | 6.3 | 0.962 |
| Tsoutsanis et al. [35,36] | 12.7 | 0.870 |
| Tu and Chen [26] | 12.8 | 0.865 |
| Model | MAD (%) | Rc2 |
|---|---|---|
| Orkisz and Stawarz [42] | 2.1 | 0.997 |
| Jensen et al. [13] | 4.1 | 0.989 |
| Tsoutsanis et al. [35,36] | 4.9 | 0.988 |
| Eriksson et al. [38] | 5.1 | 0.989 |
| Tu and Chen [26] | 7.5 | 0.966 |
| Jiang et al. [40] | 10.2 | 0.827 |
| Tian [44] | 11.0 | 0.893 |
| Model | MAD (%) | Rc2 |
|---|---|---|
| Tian [44] | 2.4 | 0.960 |
| Jiang et al. [40] | 3.0 | 0.994 |
| Tu and Chen [26] | 4.5 | 0.945 |
| Sieros et al. [43] model 1 | 5.2 | 0.922 |
| Jensen et al. [13] | 8.1 | 0.986 |
| Biteus [37] | 10.9 | 0.748 |
| Kolmanovsky et al. [33,34] | 11.0 | 0.741 |
| Model | MAD (%) | Rc2 |
|---|---|---|
| Tian [44] | 1.8 | 0.911 |
| Jiang et al. [40] | 2.4 | 0.657 |
| Park et al. [41] | 2.5 | 0.815 |
| Orkisz and Stawarz [42] | 3.1 | 0.724 |
| Guzzella and Amstutz [39] | 3.2 | 0.654 |
| Tsoutsanis et al. [35,36] | 3.4 | 0.667 |
| Sieros et al. [43] model 3 | 4.6 | 0.540 |
| Eriksson et al. [38] | 5.7 | 0.542 |
| Model | MAD (%) | Rc2 |
|---|---|---|
| Tian [44] | 0.8 | 0.956 |
| Park et al. [41] | 1.6 | 0.902 |
| Orkisz and Stawarz [42] | 1.7 | 0.911 |
| Jiang et al. [40] | 1.8 | 0.852 |
| Tsoutsanis et al. [35,36] | 2.0 | 0.828 |
| Eriksson et al. [38] | 2.4 | 0.796 |
| Sieros et al. [43] model 3 | 2.8 | 0.744 |
| Guzzella and Amstutz [39] | 3.5 | 0.779 |
| Model | MAD (%) | Rc2 |
|---|---|---|
| Tian [44] | 3.2 | 0.982 |
| Sieros et al. [43] model 2 | 7.0 | 0.954 |
| Sieros et al. [43] model 3 | 8.5 | 0.871 |
| Park et al. [41] | 8.5 | 0.935 |
| Compressor | MAD (%) | Rc2 | Terms Removed from Equation (20) |
|---|---|---|---|
| BIGFAN LPC | 1.1 | 0.9981 | a6, a13 |
| BIGFAN HPC | 1.3 | 0.9988 | a7, a11, a14 |
| ECS compressor | 2.8 | 0.9827 | a4, a5, a6, a13 |
| Compressor | MAD (%) | Rc2 |
|---|---|---|
| ECS compressor | 1.3 | 0.9808 |
| BIGFAN LPC | 2.0 | 0.9992 |
| BIGFAN HPC | 5.6 | 0.9952 |
| Compressor | MAD (%) | Rc2 | Terms Removed from Equation (22) |
|---|---|---|---|
| BIGFAN LPC | 1.0 | 0.9633 | a6, a13 |
| BIGFAN HPC | 0.4 | 0.9922 | a12 |
| ECS compressor | 1.9 | 0.9967 | a13, a15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, X.; Fang, Y.; Yang, Y.; He, Z.; Yang, B. New Data-Driven Models of Mass Flow Rate and Isentropic Efficiency of Dynamic Compressors. Aerospace 2024, 11, 589. https://doi.org/10.3390/aerospace11070589
Fang X, Fang Y, Yang Y, He Z, Yang B. New Data-Driven Models of Mass Flow Rate and Isentropic Efficiency of Dynamic Compressors. Aerospace. 2024; 11(7):589. https://doi.org/10.3390/aerospace11070589
Chicago/Turabian StyleFang, Xiande, Yuxiang Fang, Yang Yang, Zhiqiang He, and Bei Yang. 2024. "New Data-Driven Models of Mass Flow Rate and Isentropic Efficiency of Dynamic Compressors" Aerospace 11, no. 7: 589. https://doi.org/10.3390/aerospace11070589
APA StyleFang, X., Fang, Y., Yang, Y., He, Z., & Yang, B. (2024). New Data-Driven Models of Mass Flow Rate and Isentropic Efficiency of Dynamic Compressors. Aerospace, 11(7), 589. https://doi.org/10.3390/aerospace11070589







