Numerical Simulation of the Transient Thermal Load of a Sightseeing Airship Cockpit
Abstract
1. Introduction
2. Numerical Calculation Method and Verification
2.1. Numerical Calculation Method
2.1.1. Computational Assumption
- In order to facilitate the division of the grid, the structure was reasonably simplified when the physical model was established;
- The internal temperature of the cockpit was assumed to be 299 K after being cooled down by the environmental control system;
- The free-flow velocity was considered to be the same at different altitudes when calculating the thermal load within the flight envelope.
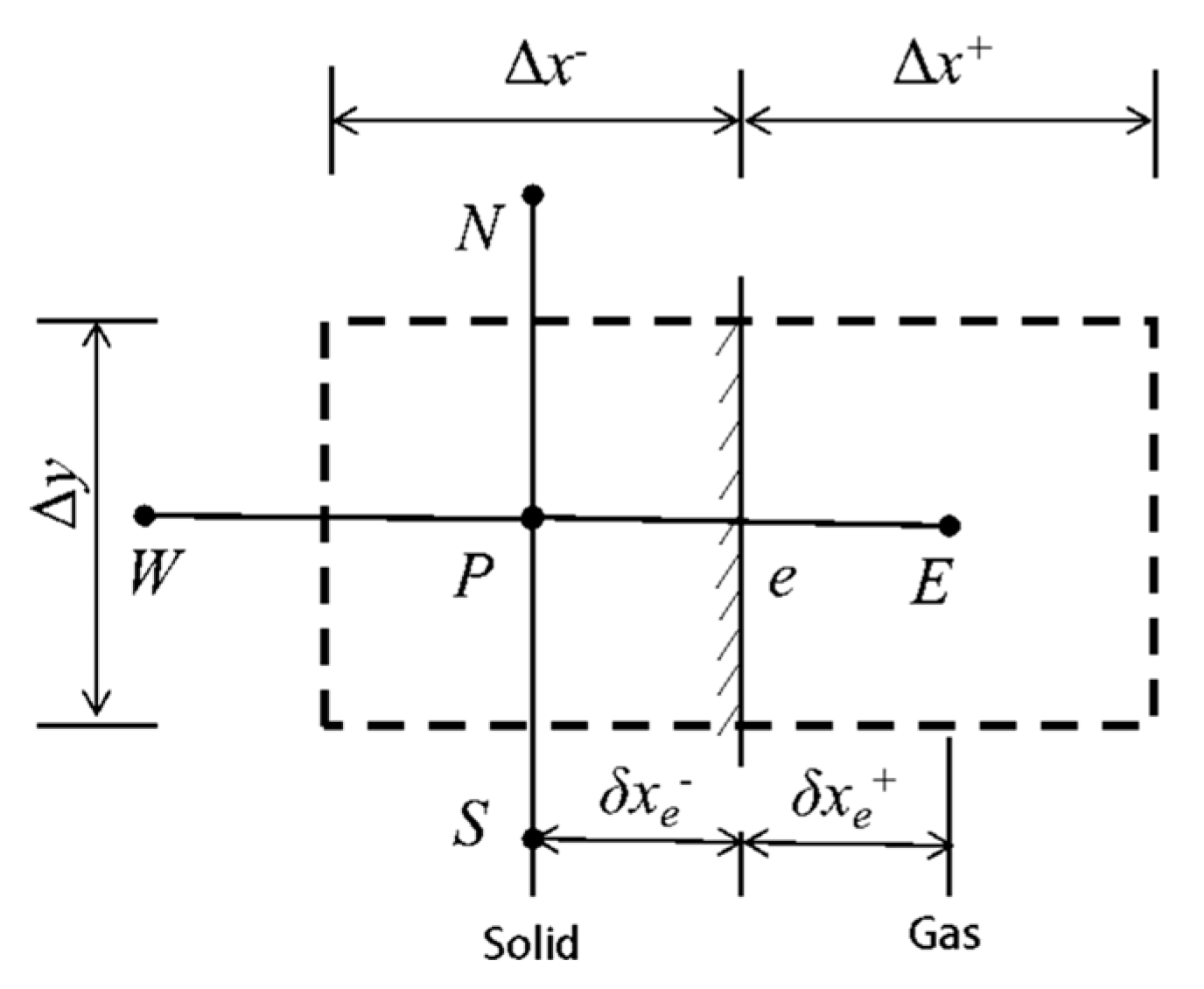
2.1.2. Governing Equation and Turbulence Model
2.1.3. Radiation Model
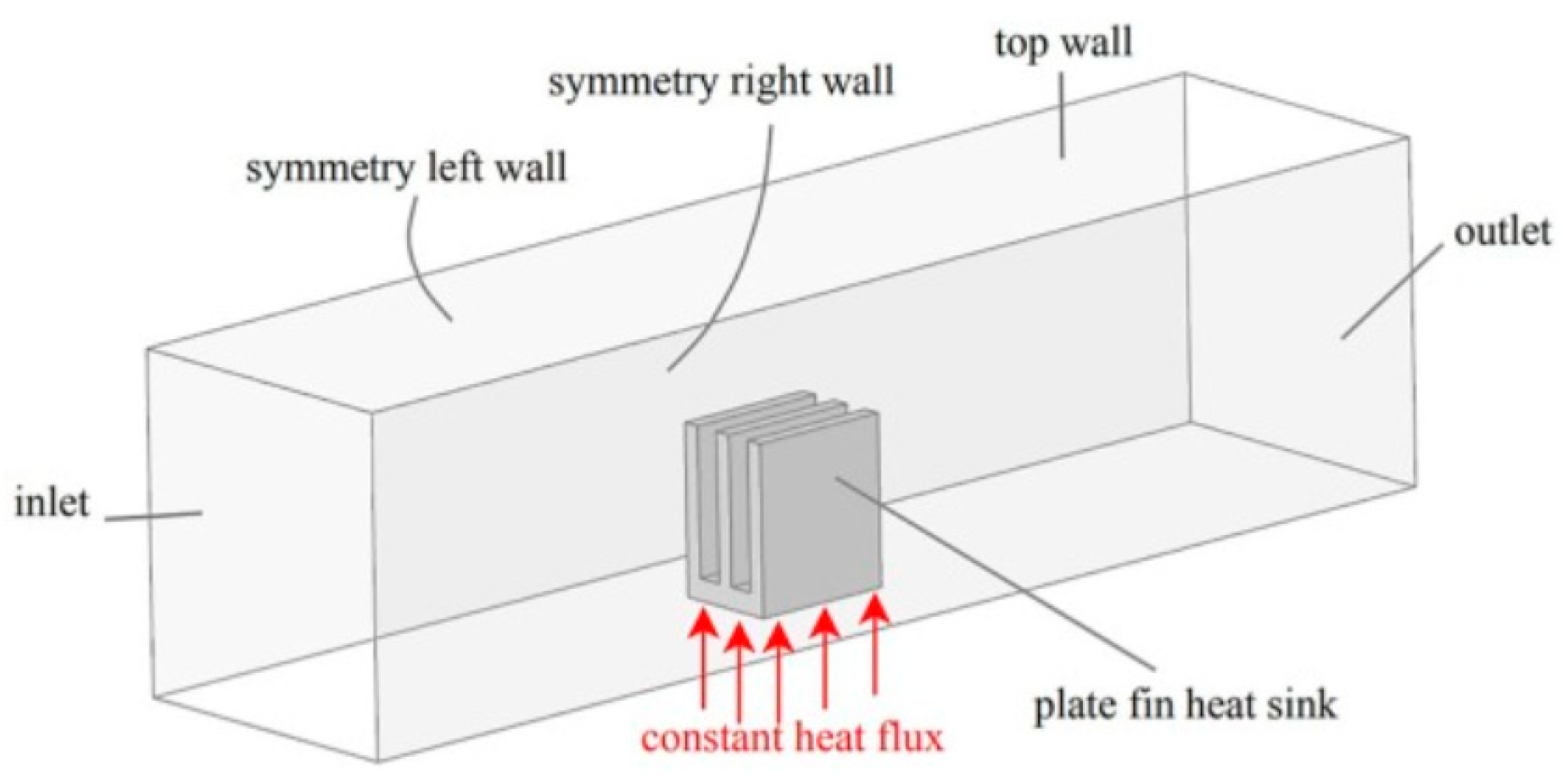
2.2. Models and Grids
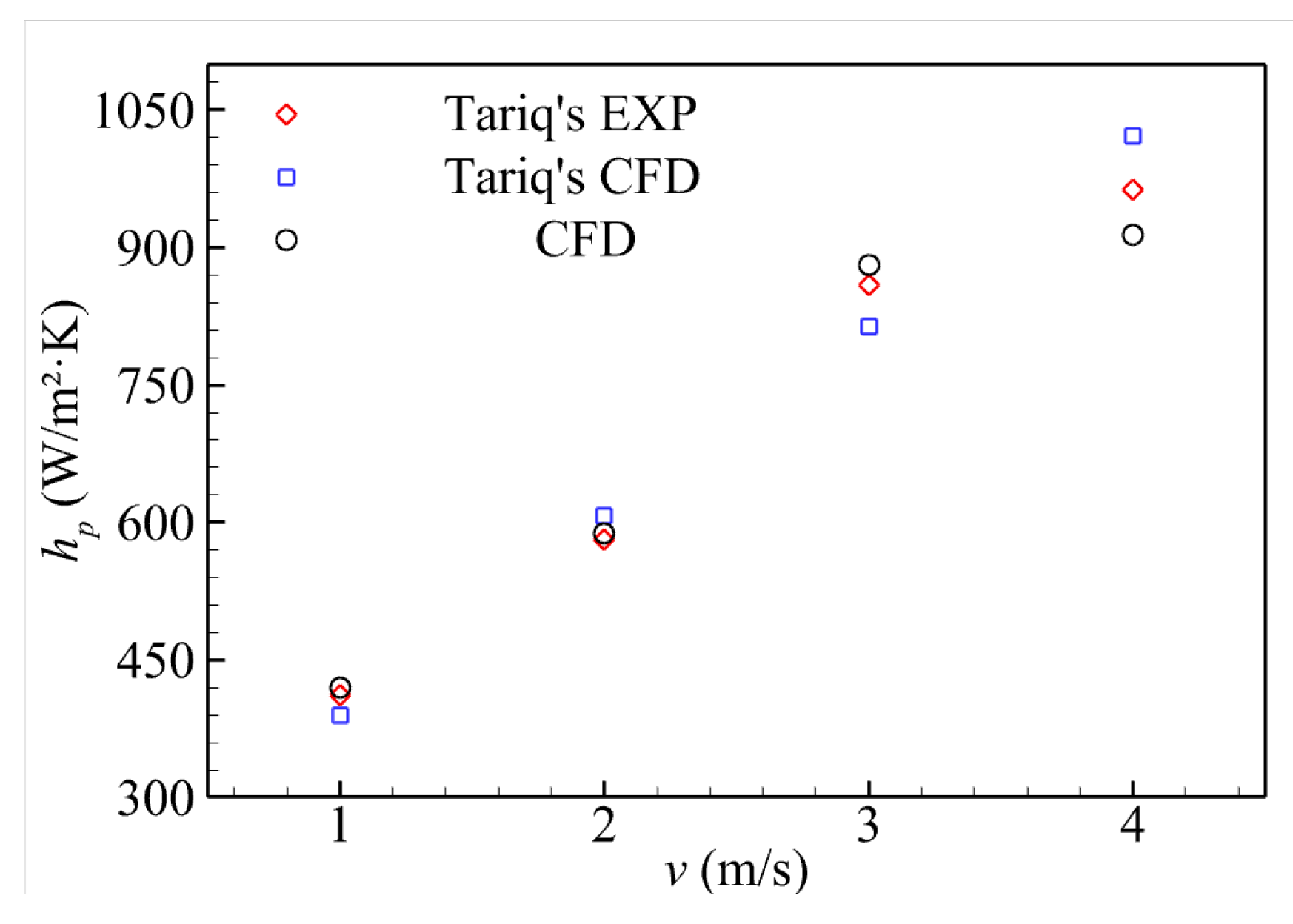
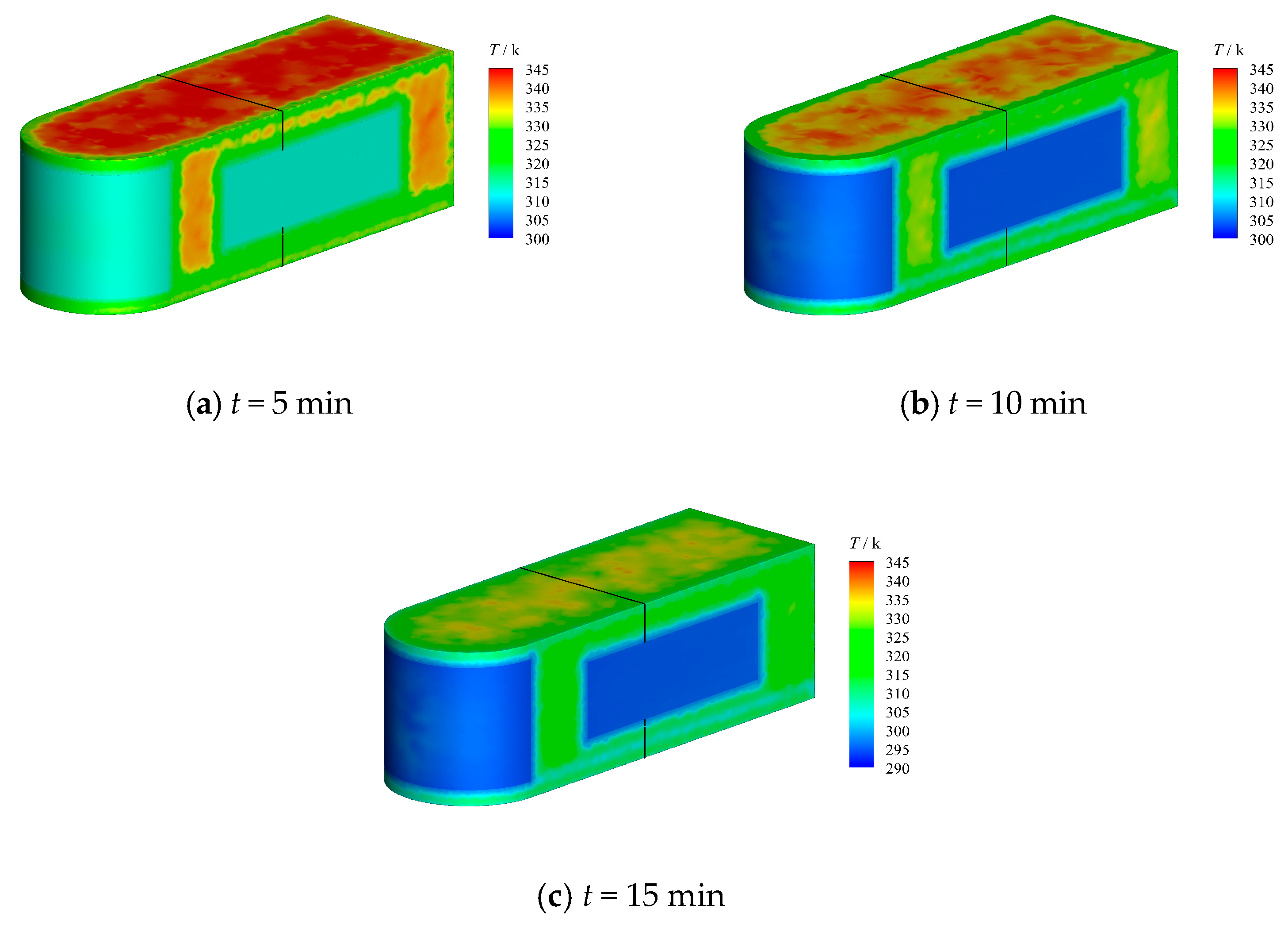
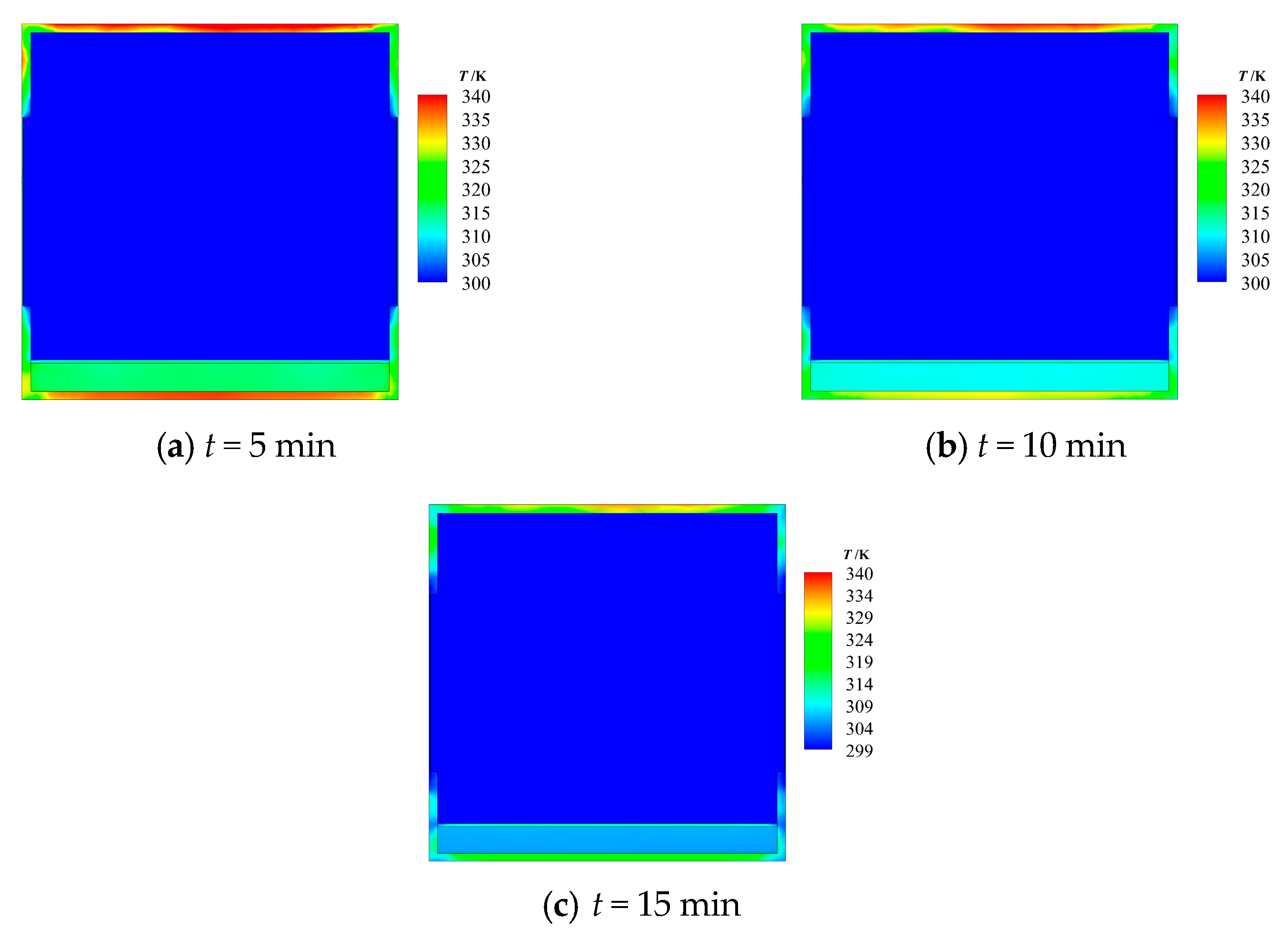
2.3. Simulation Model Verification
3. Results and Analysis
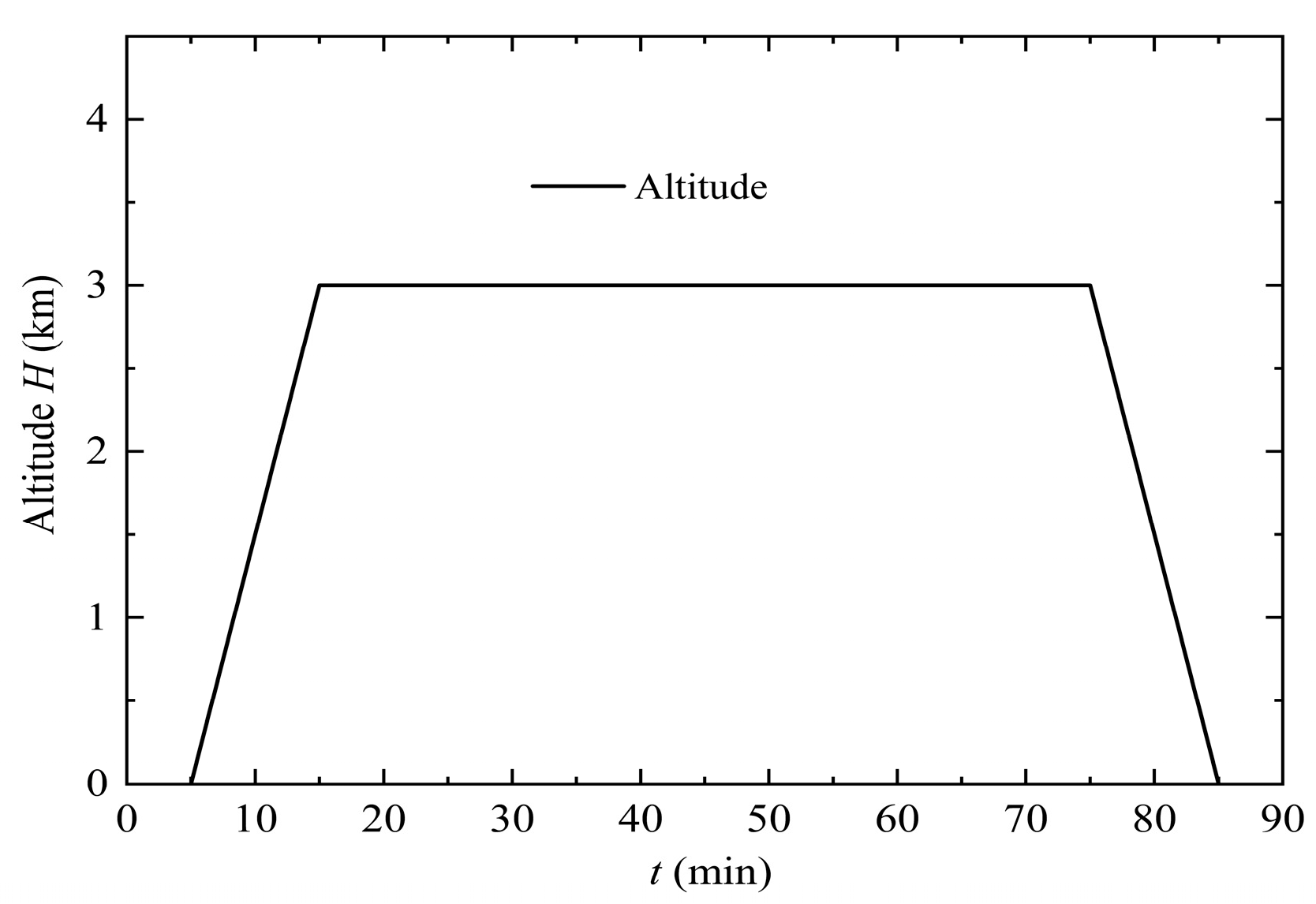
3.1. Flight Mission Envelope
3.2. Results and Discussion
3.2.1. The Influence of Altitudes
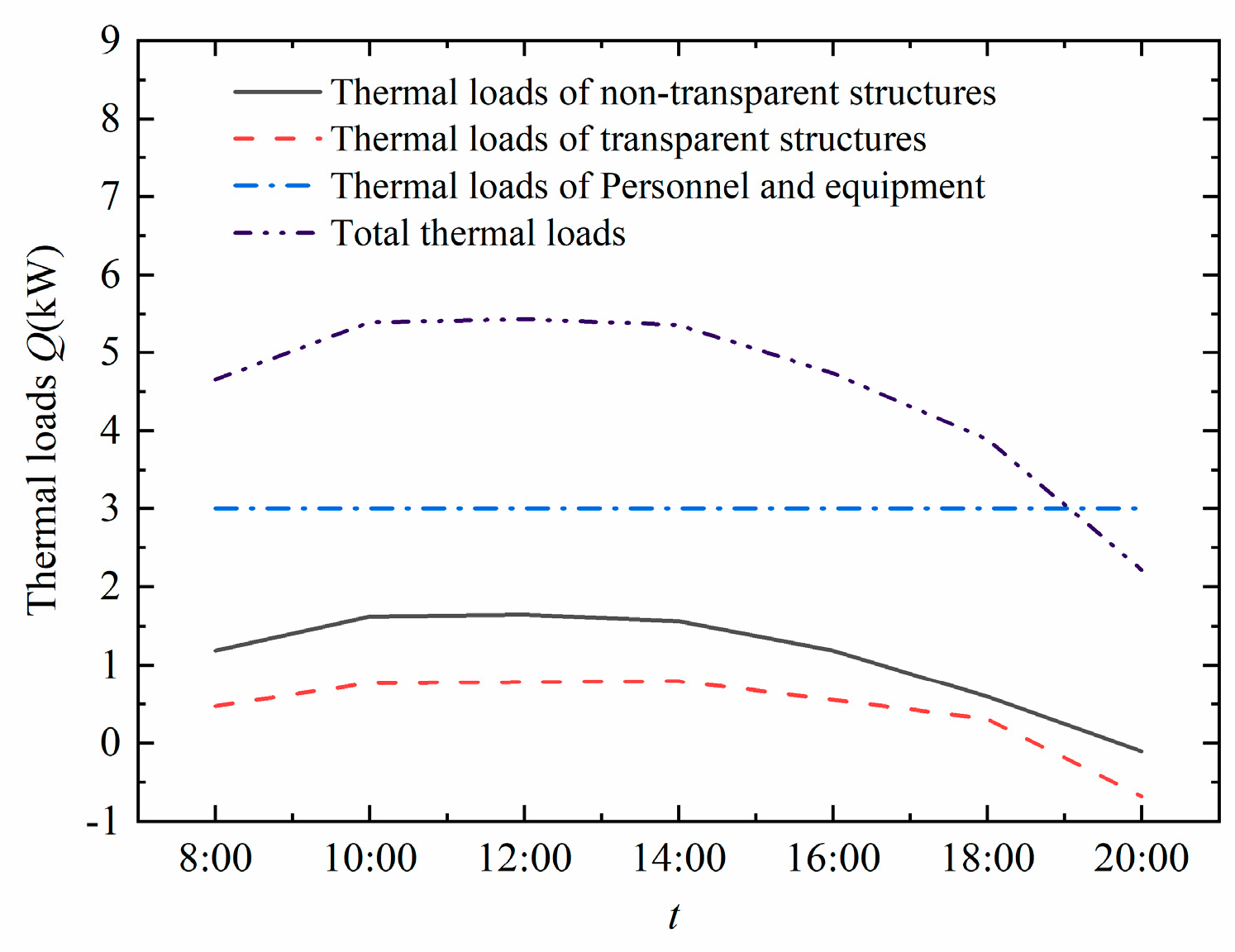
3.2.2. Influence of Solar Radiation
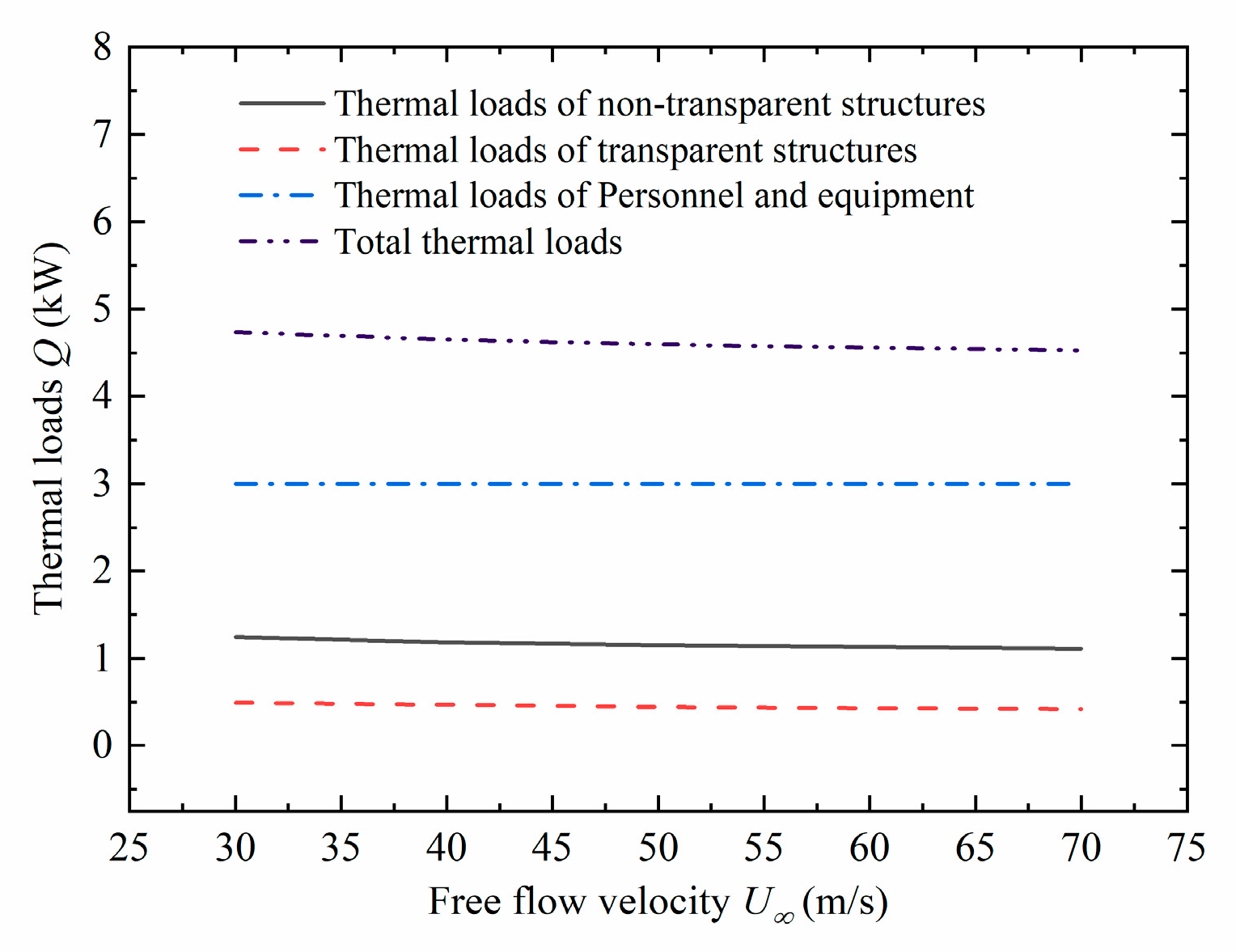
3.2.3. Influence of the Free-Flow Velocity
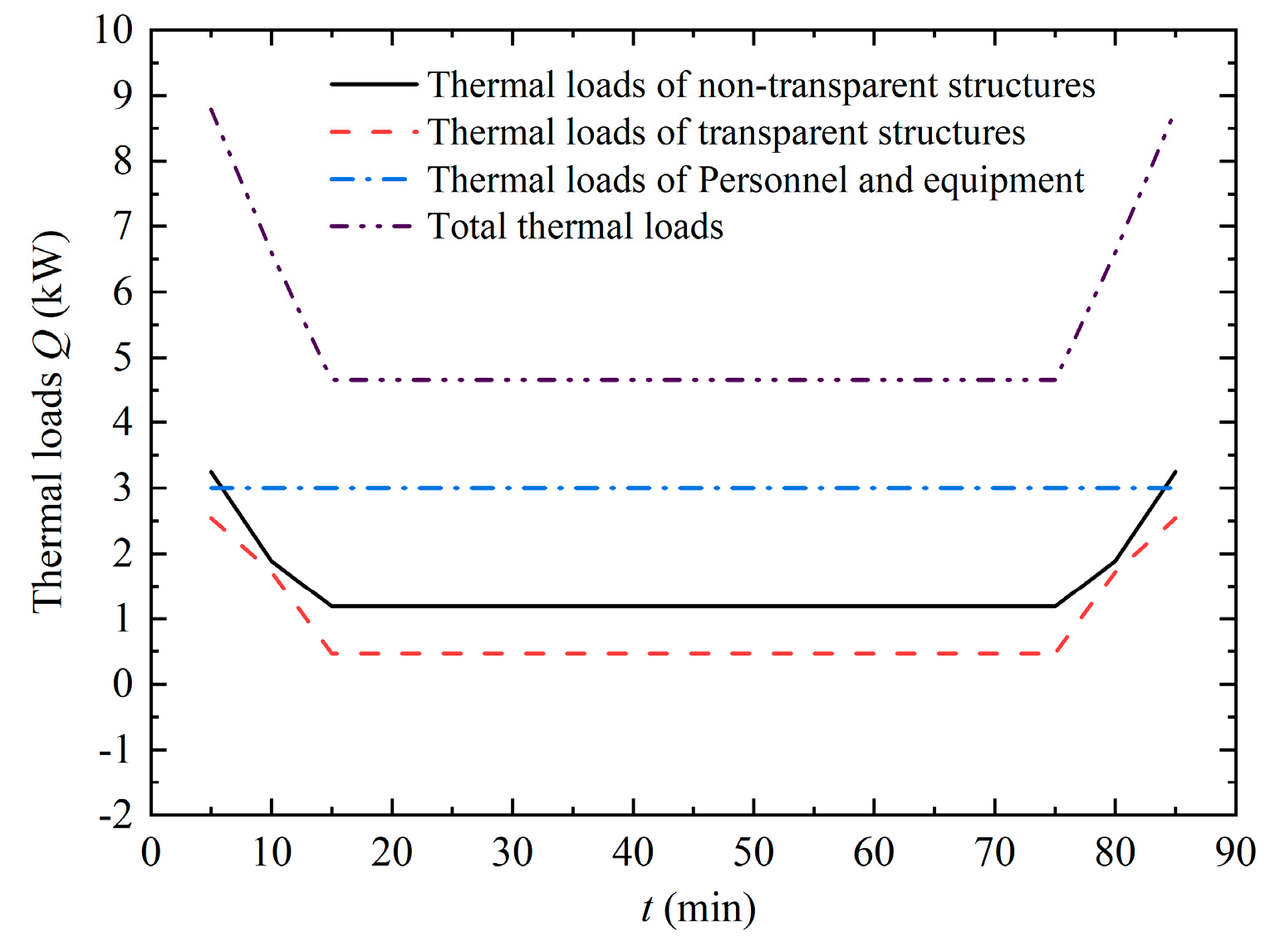
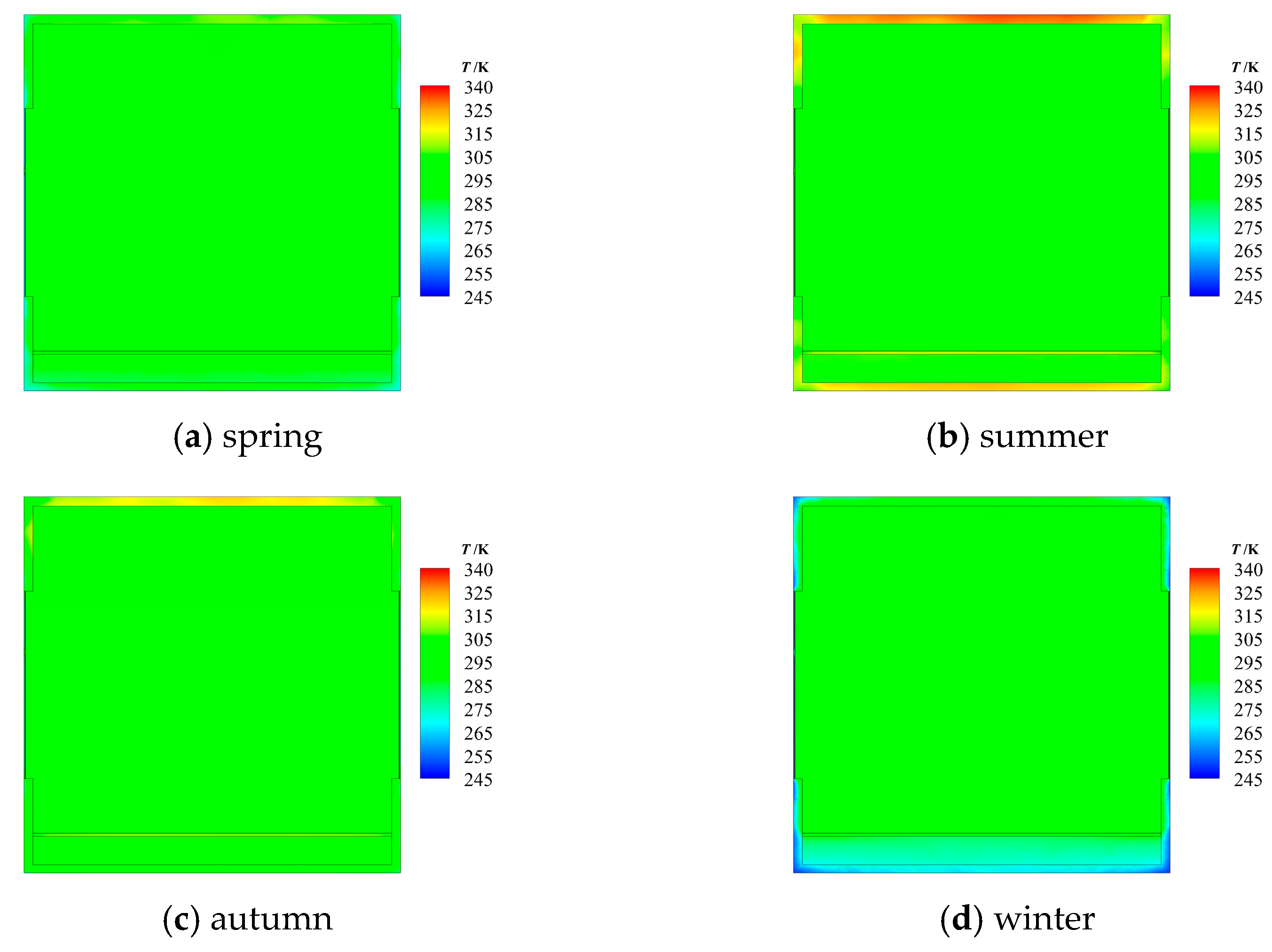
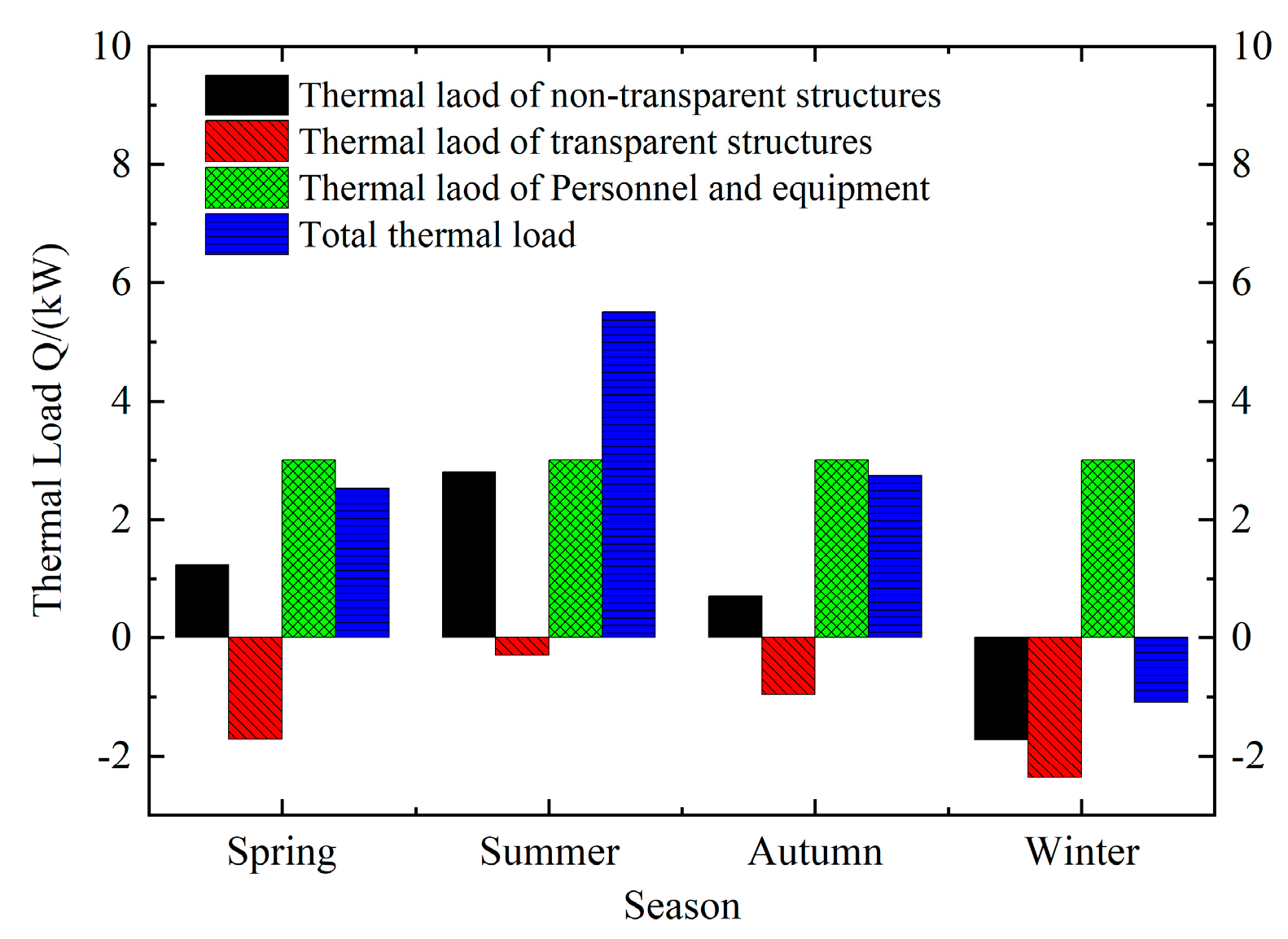
3.2.4. Influence of the Season
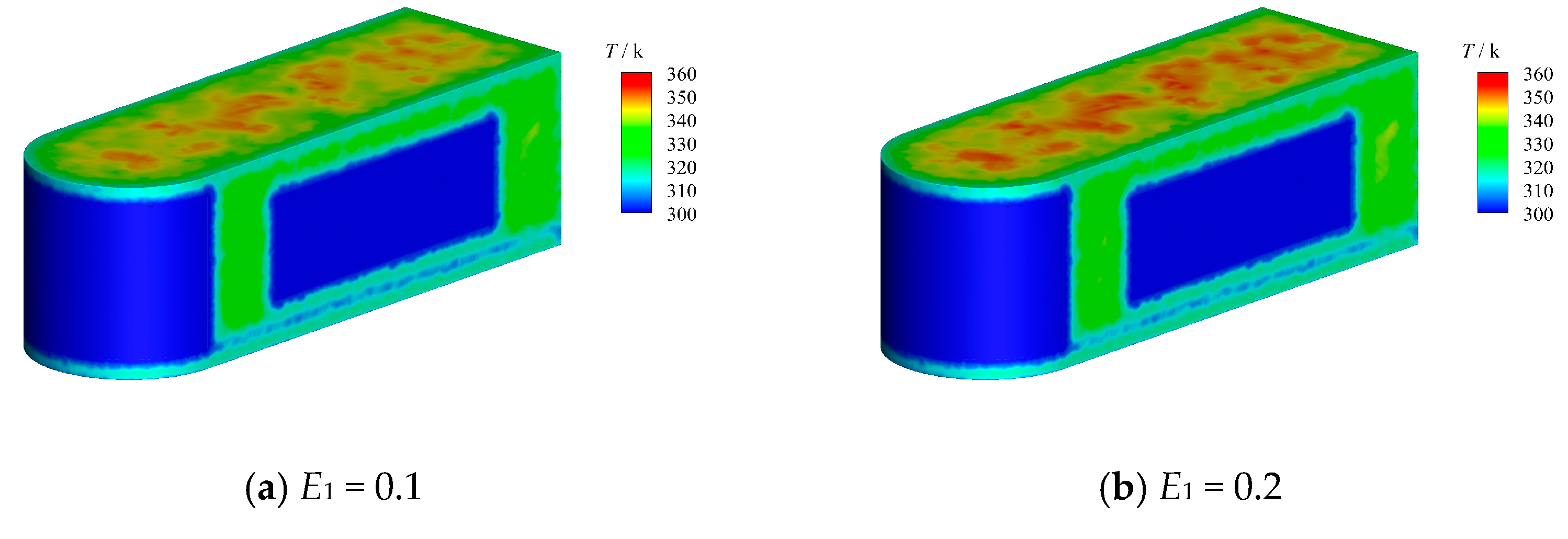
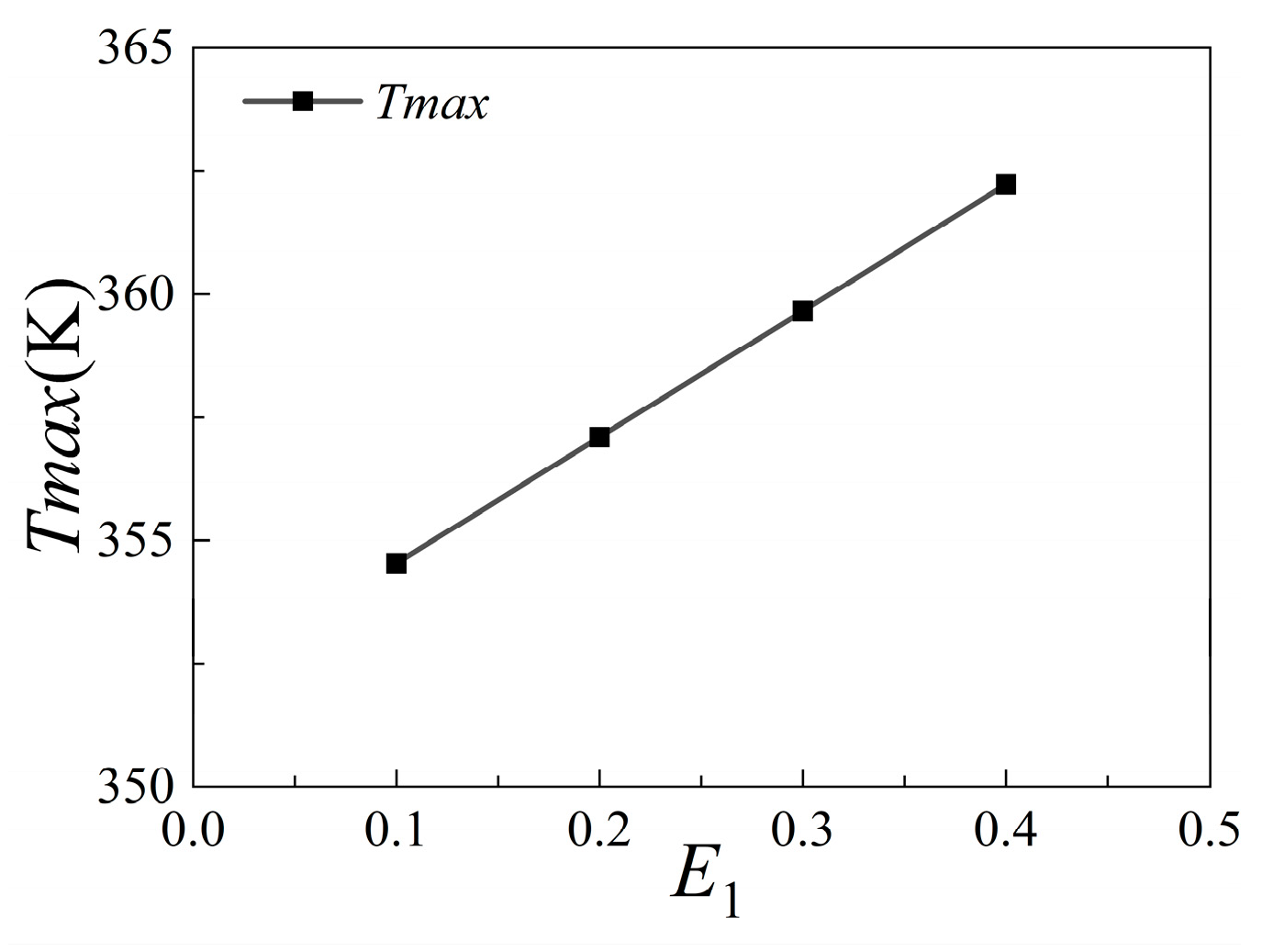
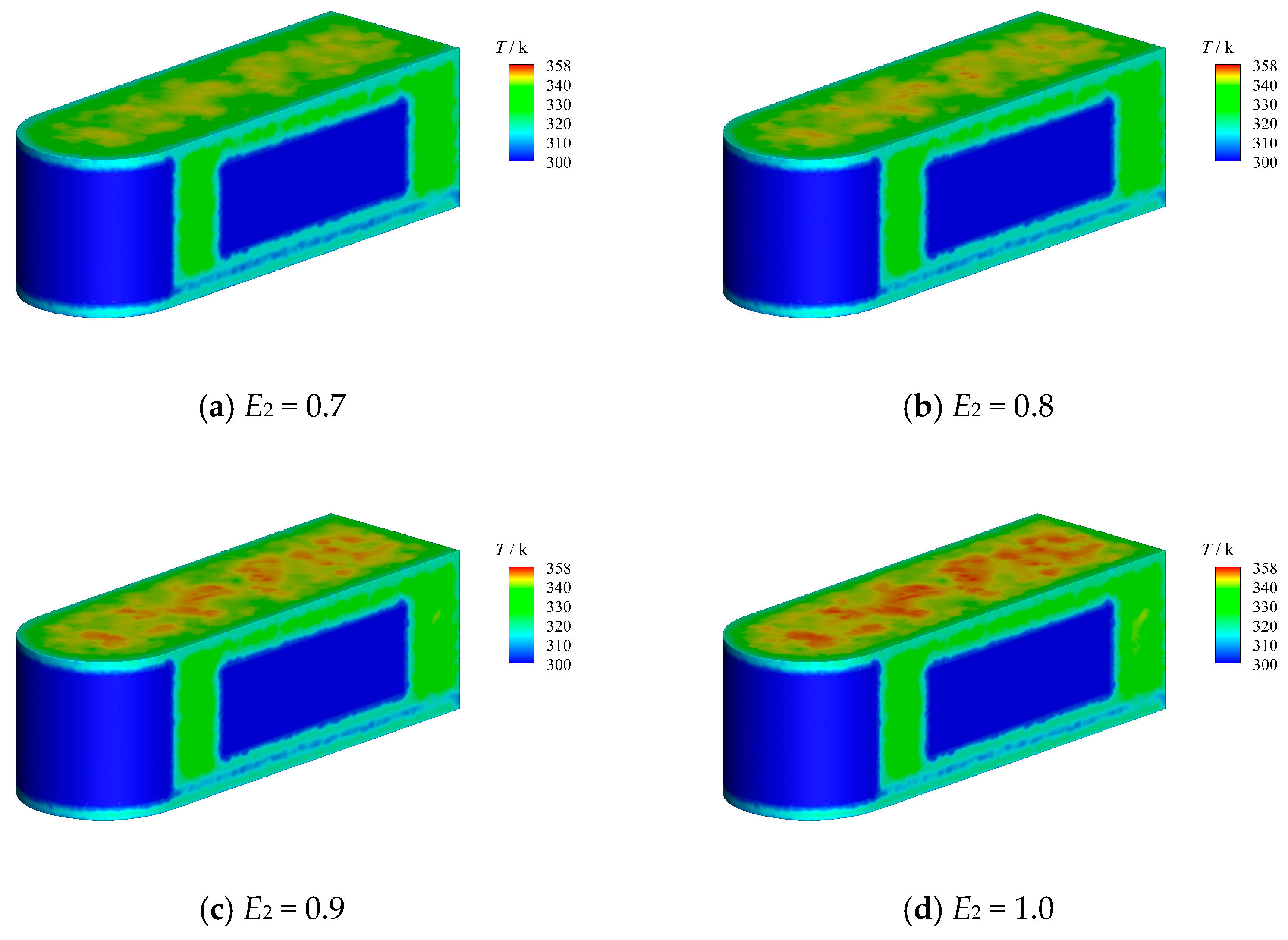
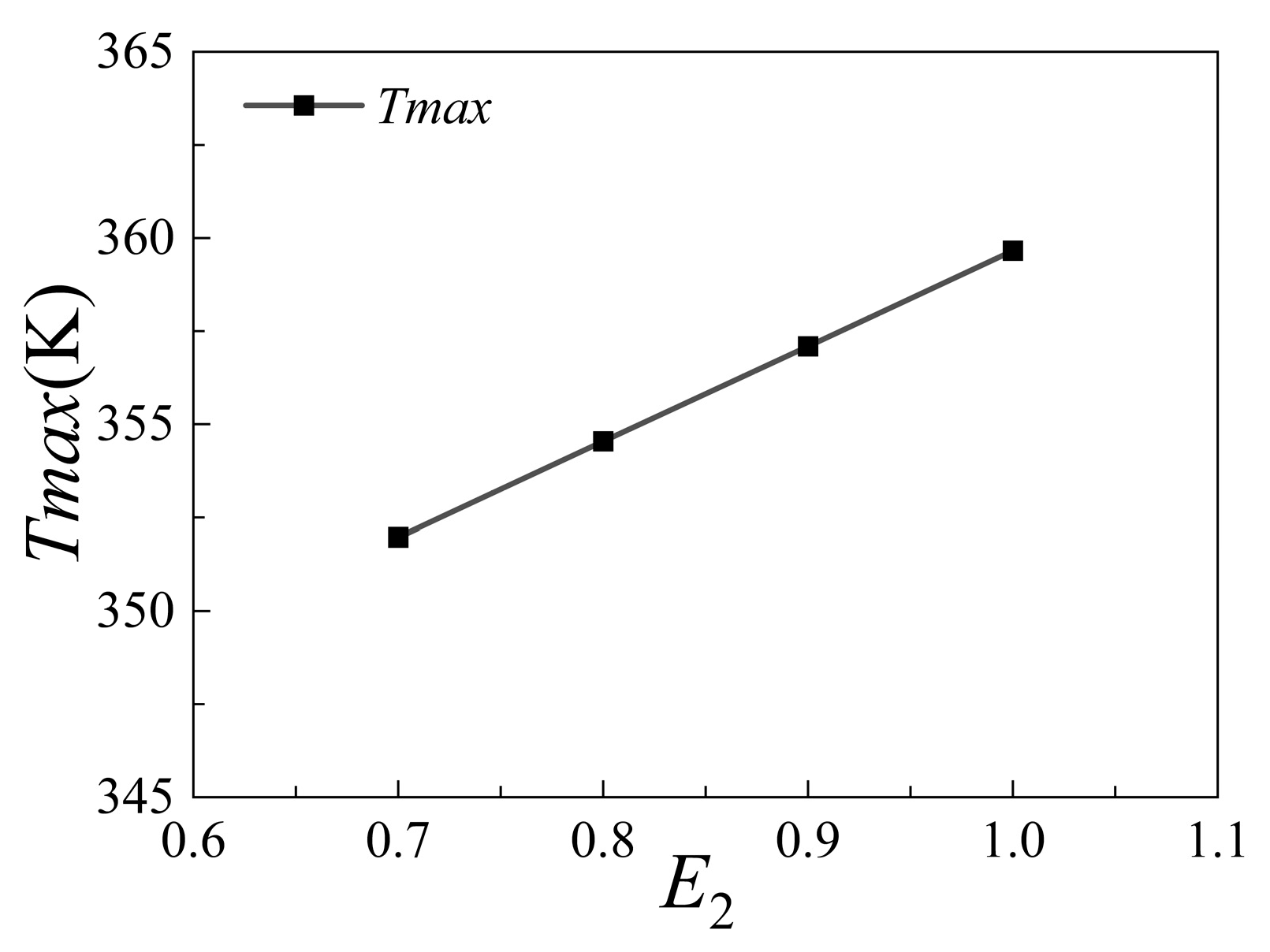
3.2.5. Influence of the Solar Absorptivity and Infrared Emissivity
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jian, X.; Li, N. Research on the Calculation Method of Transient Heat Load for Aircraft Cabin. Civ. Aircr. Des. Res. 2010, 3, 30–33. [Google Scholar]
- Shou, R.; He, H. Aircraft Environment Control; Beijing University of Aeronautics and Astronautics Press: Beijing, China, 2004; pp. 1–5. [Google Scholar]
- Hu, S. Calculation of Helicopter Cabin Thermal Conductivity. Helicopter Technol. 2017, 1, 36–38. [Google Scholar]
- Wang, L.; Zhao, J.Q. Numerical Simulation of Heat Transfer in Aircraft Cabins. Comput. Simul. 2008, 5, 44–46+142. [Google Scholar]
- Fan, W.; Zhuang, D.; Yuan, X.; Li, D. Calculation and Simulation of Transient Heat Load for Cabins. J. Beijing Univ. Aeronaut. Astronaut. 2001, 27, 654–657. [Google Scholar]
- Zhang, X.; Yang, C.; Yuan, X. Engineering estimation methods of thermal load of airplane. J. Beijing Univ. Aeronaut. Astronaut. 2009, 35, 1503–1506. [Google Scholar]
- Liu, Z.; Dong, S.; Zhou, Y.Y.; Zhang, S.; Fu, Y. Parameter Identification and Simulation Method of 2-Node Thermal Network Model of Aircraft Cabin. IET Conf. Proc. 2022, 7, 151–156. [Google Scholar]
- Rezanova, E.A.; Merkulovb, V.I.; Rossovac, K.V.; Tishchenko, I.V. The Comparative Analysis of External Heat Transfer Calculation Methods for a Solar Aircraft Spacesui. MATEC Web Conf. 2020, 324, 03007–03009. [Google Scholar] [CrossRef]
- Wu, J.; Jiang, F.; Song, H.; Liu, C.; Lu, B. Analysis and validation of transient thermal model for automobile cabin. Appl. Therm. Eng. 2017, 122, 91–102. [Google Scholar] [CrossRef]
- Omle, I.; Kovács, E.; Bolló, B. Applying recent efficient numerical methods for long-term simulations of heat transfer in walls to optimize thermal insulation. Results Eng. 2023, 20, 101476. [Google Scholar] [CrossRef]
- Frank, P.I.; David, P.D. Introduction to Heat Transfer, 3rd ed.; John Wiley and Sons: Hoboken, NJ, USA, 1996. [Google Scholar]
- Shaheed, R.; Mohammadian, A.; Gildeh, H.K. A comparison of standard k–ε and realizable k–ε turbulence models in curved and confluent channels. Environ. Fluid Mech. 2019, 19, 543–568. [Google Scholar] [CrossRef]
- Yang, S.; Tao, W. Heat Transfer; Higher Education Press: Beijing, China, 2019. [Google Scholar]
- Tao, W. Numerical Heat Transfer; Xi’an Jiaotong University Press: Xi’an, China, 2001. [Google Scholar]
- Tariq, A.; Altaf, K.; Ahmad, S.W.; Hussain, G.; Ratlamwala, T.A.H. Comparative numerical and experimental analysis of thermal and hydraulic performance of improved plate fin heat sinks. Appl. Therm. Eng. 2021, 182, 115949. [Google Scholar] [CrossRef]
- ANSYS® Fluent 19.2, Release 19.0, Help System, ANSYS Fluent User’s Guide, ANSYS, Inc. 2018. Available online: https://pdfcoffee.com/ansys-fluent-tutorial-guide-2019-pdf-free.html (accessed on 3 December 2023).
- Yang, S.; Tao, W. Heat Transfer Science; Higher Education Press: Beijing, China, 2019. [Google Scholar]




| Thermal Conductivity (W/(m·K)) | Density (kg/m3) | Specific Heat Capacity (J/kg·K) | |
|---|---|---|---|
| Fiberglass | 1.09 | 2600.00 | 794.20 |
| PVC Foam | 0.04 | 1380.00 | 1200.00 |
| Inner Wall | 0.11 | 1300.00 | 10.00 |
| Roof Inner Wall | 0.04 | 1000.00 | 28.00 |
| Average Thermal Conductivity (W/(m·K)) | Average Density (kg/m3) | Average Specific Heat Capacity(J/kg·K) | |
|---|---|---|---|
| Roof | 0.05 | 1578.79 | 1033.50 |
| Bulkhead | 0.06 | 1508.51 | 1031.24 |
| Floor | 0.04 | 1086.54 | 1034.55 |
| Windshield | 0.22 | 1180.00 | 200.00 |
| Window | 0.22 | 1180.00 | 200.00 |
| Number of Cells (Million) | Tmax (K) |
|---|---|
| 2.44 | 345.07 |
| 3.23 | 339.33 |
| 3.60 | 339.37 |
| 8:00 | 10:00 | 12:00 | 14:00 | 16:00 | 18:00 | 20:00 | |
|---|---|---|---|---|---|---|---|
| Direct Normal Solar Irradiation [W/m2] | 371.0 | 425.8 | 439.5 | 430.7 | 388.4 | 216.7 | 0 |
| Diffuse Solar Irradiation—vertical surface: [W/m2] | 114.4 | 99.9 | 77.48 | 94.4 | 114.4 | 74.8 | 0 |
| Diffuse Solar Irradiation—horizontal surface [W/m2] | 100.5 | 115.4 | 119.2 | 116.7 | 105.3 | 58.7 | 0 |
| Ground Reflected Solar Irradiation—vertical surface [W/m2] | 50.4 | 84.1 | 98.1 | 88.7 | 58.5 | 15.6 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Lin, X.; Xu, C.; Li, Z. Numerical Simulation of the Transient Thermal Load of a Sightseeing Airship Cockpit. Aerospace 2024, 11, 127. https://doi.org/10.3390/aerospace11020127
Li X, Lin X, Xu C, Li Z. Numerical Simulation of the Transient Thermal Load of a Sightseeing Airship Cockpit. Aerospace. 2024; 11(2):127. https://doi.org/10.3390/aerospace11020127
Chicago/Turabian StyleLi, Xiaoyang, Xiaohui Lin, Changyue Xu, and Zhuopei Li. 2024. "Numerical Simulation of the Transient Thermal Load of a Sightseeing Airship Cockpit" Aerospace 11, no. 2: 127. https://doi.org/10.3390/aerospace11020127
APA StyleLi, X., Lin, X., Xu, C., & Li, Z. (2024). Numerical Simulation of the Transient Thermal Load of a Sightseeing Airship Cockpit. Aerospace, 11(2), 127. https://doi.org/10.3390/aerospace11020127






