Preliminary Sizing of High-Altitude Airships Featuring Atmospheric Ionic Thrusters: An Initial Feasibility Assessment
Abstract
1. Introduction
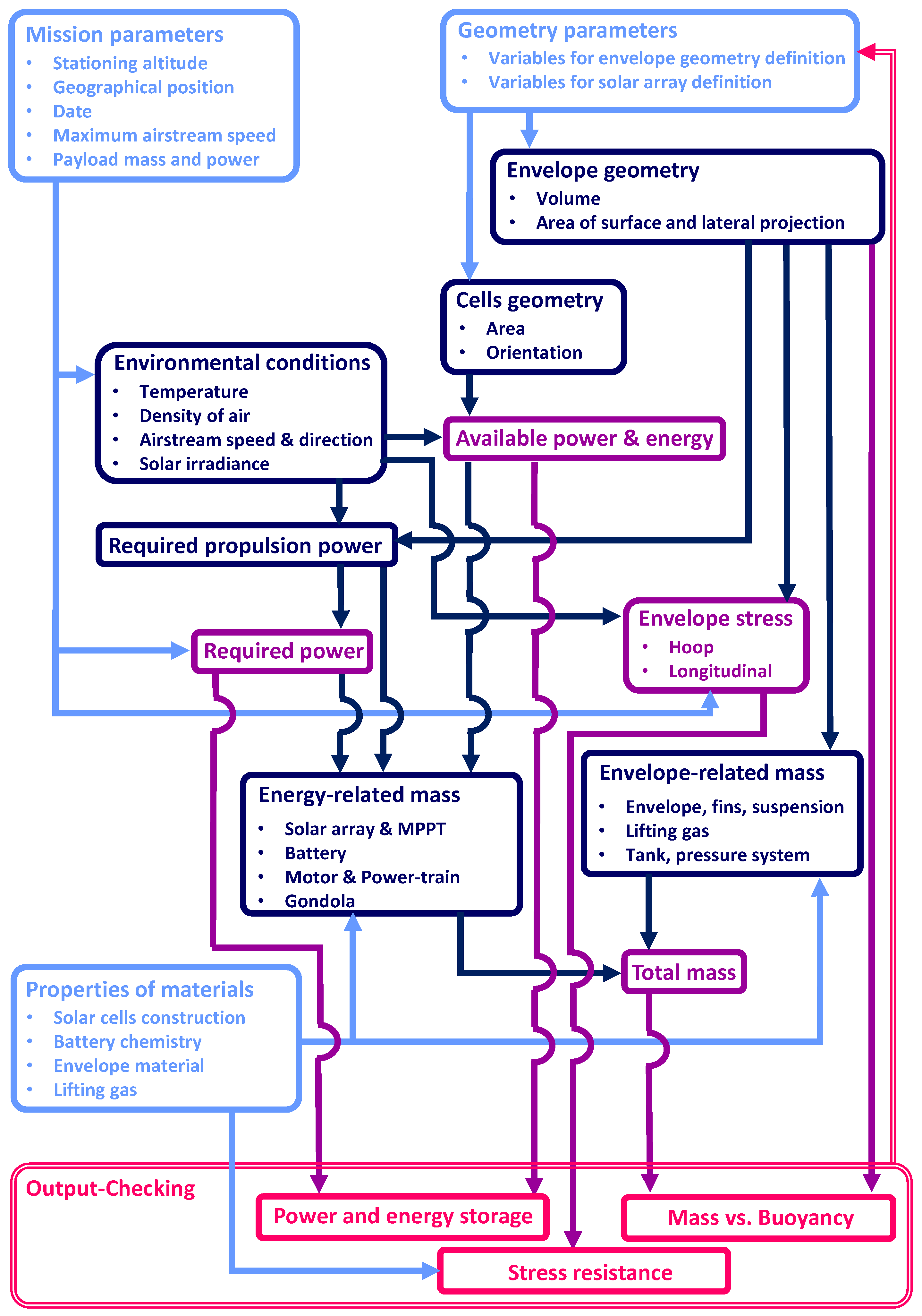
2. Baseline Sizing Methodology for an Airship Featuring Standard Electric Propulsion
- Mission parameters. These are first the stationing altitude and geographical position (coordinates) on the start date of the mission. These features influence the thermodynamic state of the atmosphere, as well as wind (including its intensity and direction) and solar irradiance (including daylight time and radiation direction) along the mission profile. A reference profile with altitude for these characteristics has been worked out, obtained by weighting and averaging the values corresponding to geographical and temporal samples over the surface of the Earth and the time of the year. Such a profile can be employed to uncorrelate the sizing of the airship from a specific location and the start time of the mission. Further flight mechanics quantities include the buoyancy ratio at altitude, the climb/descent angle and velocity, and the cruise velocity with respect to the ground (typically null for a station-keeping mission).
- Payload parameters. Payload mass and related power supply.
- Envelope and systems parameters. Maximum acceptable wind speed for envelope sizing, envelope material (specified through its mass density as well as top-stress characteristics), and lifting gas (including purity level). Characteristics of the fins, septa, and stringers. Characteristics of the ballonet system.
- Power system parameters. Battery chemistry (yielding specific energy and specific power characteristics), solar cell material (specified through its mass density and energy conversion efficiency), and motor characteristics (including the conversion efficiency of the electric motor and the propulsive efficiency of the propeller).
2.1. Sizing Loop
- Geometrical sizing of envelope and solar cells. Through the assignment of the parameters in , it is immediately possible to build the complete geometry of the airship envelope, thus computing, in particular, its volume, area of the external surface, and area of the front and longitudinal sections. Correspondingly, the exact size of the solar cells and their orientation in space (dictated by the local orientation of the envelope surface) can be computed. An estimation of the zero-lift drag coefficient and drag due to lift coefficient K, configuring a classical parabolic polar for the airship, can be carried out based on regressions for the envelope, in particular involving its fineness ratio [27]. In the same fashion, it is possible to obtain estimations for the sensitivities and (the latter representing that of the aerodynamic side force vs. the sideslip angle). Refinements of this preliminary estimation can be carried out based on the size of the fins and gondola (if any) [30], themselves in turn obtained from regressions of statistical data, given the size of the envelope (or payload and energy system for the case of the gondola).
- Environmental conditions at stationing altitude and during climb. Through the assignment of the position on Earth and time of the year for the ascent, it is possible to compute from dedicated models the temperature, pressure, and density of air, the wind intensity and direction at altitude, and the solar irradiance (in terms of both intensity and direction). In particular, the International Standard Atmosphere (ISA) model can be employed for static air characteristics [31], whereas the Horizontal Wind Model (HWM) can be employed for obtaining the wind characteristics [32,33]. The SMARTS model can be adopted for the computation of direct and diffused irradiance at altitude [34].As pointed out earlier in this section, alternatively to the selection of a location and time of the year for the mission and to the corresponding explicit computation of all quantities just mentioned through models accounting for such information, it is possible to carry out this step in the sizing procedure employing an averaged model for the state of the atmosphere, as well as for the wind and solar irradiance, where each output quantity is only a function of the altitude. This averaged model has been prepared to start from the original ones [32,33,34], sampling the profile with altitude at nodal positions on Earth and time-wise along a yearly period. This choice is especially interesting for making comparisons among concurrent designs (for instance, design solutions obtained by changing the value of some parameters) without binding the solution to a specific location or time of the year for the start of the mission.
- Computation of total power and energy required. Having assigned the target stationing altitude and having computed the wind characteristics along the climb and at altitude, it is possible to define the power (and the corresponding peak power ) and energy E required for a mission profile, composed of an ascent, stationing phase at altitude for a certain time, and descent.In particular, it is assumed that the airship is flying in climb/descent with a given climb angle with an assigned heading and course. The angle of attack is computed correspondingly, considering the actual intensity of the horizontal wind to compute the angle of attack and the sideslip angle. Conversely, when at the stationing altitude, the airship is hypothesized to be always oriented with the wind so that, in particular, non-sideslip occurs. With these assumptions, it is possible to estimate the lift coefficient , the side force coefficient , and correspondingly, the drag coefficient , the latter being a function of both and (as well as bound to a constant component independent of the two) through the polar of the airship. The computation of power for propulsion is therefore possible in climb/descent by further assigning the climb speed , and at the stationing altitude as well, having computed the wind speed and having assigned a cruise speed with respect to the ground (i.e., a ground speed in cruise). The latter may be null, typically in casein the case that the mission is that of station-keeping (yet in that case the velocity of the wind will not be null, and the power required for propulsion in cruise will be correspondingly non-null). The value of power can be computed at any time as , as usual for flight performance computations, where drag D is obtained from dynamic pressure at each considered altitude along the flight profile, and the drag coefficient has been computed as just mentioned.Power for propulsion is complemented by the power required for the payload and by the power required for other plants on board, including losses (estimated via regressions). Once the time history of power along the mission profile is known, peak power and the energy required for the mission are easily obtained.
- Computation of available power and energy. Available power and energy are estimated starting from the geometry of solar cells and from the mission profile. The latter provides a flight trajectory and the orientation of the airship along it (through the assumptions introduced at the previous point). This knowledge can be employed to define the power capture based on the irradiance data coming from the corresponding model. By comparing the power available and the power required (previous point), a power balance can be carried out, yielding the size of the batteries required for covering the mission.In particular, the energy quotas considered for battery sizing are obtained by integrating the difference between the power available from solar irradiance and the power required by the airship (for propulsion and systems operation), considering those conditions where this difference is negative. This means that when the power from irradiance exceeds the power required, as typical in daylight at cruising altitude, the airship is powered by solar energy. Conversely, at night and during climb and descent, the airship is typically fed by the batteries.Considering all segments in the mission profile where the power required exceeds the power available, corresponding values of energy quotas are obtained. The maximum among them (namely ) is selected within the sizing algorithm. Additionally, since batteries are associated with a top value of power that they can treat, the top value of the power flow from the batteries is considered to be well, as a possible constraint for battery sizing. The sizing operation can be, therefore, written in mathematical terms as the problemIn Equation (1), the values of and represent the specific energy and power of the battery, the battery discharge efficiency, the efficiency of the motors and the efficiency of the propeller. The values of and are typically related to one another through a specific choice of the chemistry of the battery [35].
- Mass of power system. The power required for flight allows the assignment of the power of the motors and propellers . These are turned into corresponding masses and complemented by those of the power-trains and sub-plants (cables, power electronics, etc.), wrapped in . Finally, the mass of the power system includes that of the batteries and solar cells , obtained starting from their respective sizing (see previous points).
- Stress analysis on envelope. With a knowledge of the dynamic pressure along the mission and of the maximum wind speed to sustain, as well as of the external pressure, it is possible to compute the pressure differential and its corresponding maximum along the mission profile, and from it the hoop stress and longitudinal stress on the envelope from regressions. It should be noted that, in the presence of inflatable ballonets, the pressure differential is typically constant during any altitude change. Conversely, when the ballonets are not present, like for almost-constant altitude missions, or when the airship is operating above its target altitude and ballonets are empty, the differential may indeed change with the altitude. When present, ballonets will be associated with a weight , computed via statistical regressions from their volume, in turn, intended to allow reaching the target altitude without increasing the stress on the envelope.
- Mass of envelope. From the knowledge of the sizing of the envelope, its mass can be readily computed. It is noteworthy that the thickness of the envelope is assigned a priori since it is not considered to be a continuous variable, being based on the number of layers of the same material that are superimposed, hence not being practical to change in an optimization algorithm. In other words, the number of layers and their corresponding thickness are assigned among the constant parameters, and the sizing of the envelope is carried out accordingly. The mass of the lifting gas and of the pressure system required to fill and pressurize the envelope are computed at this step as well, together with the masses of structural parts like the fins () and inner diaphragms (), which are functions of the size of the envelope.
2.2. Optimum-Seeking Loop
- Buoyancy. The buoyancy ratio of the airship should be over an assigned minimum. The latter is typically chosen very close to unity for HAAs for safety reasons unless the wind is expected to provide a steady and sufficiently predictable contribution to lift. This analytically yieldswhere the target buoyancy ratio needs to be matched by that obtained from computations in the sizing loop, in particular considering the buoyancy force found at the cruising altitude of the airship (), which is the lowest encountered value, hence making the satisfaction of the constraint more requiring.
- Envelope stress. The stress values on the envelope computed in the previous procedure are compared to the nominal stress values , which the material adopted for the envelope can sustain (as obtained from a corresponding characterization). This yieldswhere the value of measured along the mission profile has been obtained from the sizing loop, starting from the pressure differential .
- Battery power flow. Within the sizing loop, the sizing of the power system (including, in particular, the battery) is carried out without considering the ability of the system to reload the battery in preparation for covering the energy requirement of those phases of the flight where the power harvested from the solar cells is lower than the power required. A corresponding constraint is therefore added, imposing that the energy stored in the batteries during those time frames when the power harvested is larger than that required to be at least equal to the energy released by the battery when the power flow from the solar cells is incapable of covering the requirements of the airship.In analytic terms, this constraint can be written by conceptually defining three time instants. First, a time instant corresponds to the start of a phase where solar power is recharging the battery, meaning sufficient power is harvested for that task and for covering the power required by the airship. Second, a time instant corresponds to inversion of the power flow, which is no longer charging the battery but where power is flowing from it since the harvested power is no longer sufficient to cover the power required by the airship. Finally, corresponds to the end of the latter discharging phase and corresponds to a new recharge-discharge cycle. It is possible to find this triple of time instant for each of the recharge-discharge cycles during a mission, thus allowing the identification of time boundaries for evaluating the integral of power. Additionally, for clarity, we introduce the power harvested by the solar cells as and that flowing from the batteries as . All these definitions allow the construction of the following constraint
3. Airship Sizing Methodology Accounting for Atmospheric Ionic Thrusters
3.1. Atmospheric Ionic Thrusters for Airships
3.2. A Sizing Methodology for Atmospheric Ionic Thrusters on Airships
3.2.1. Assigned Geometrical and Technological Parameters
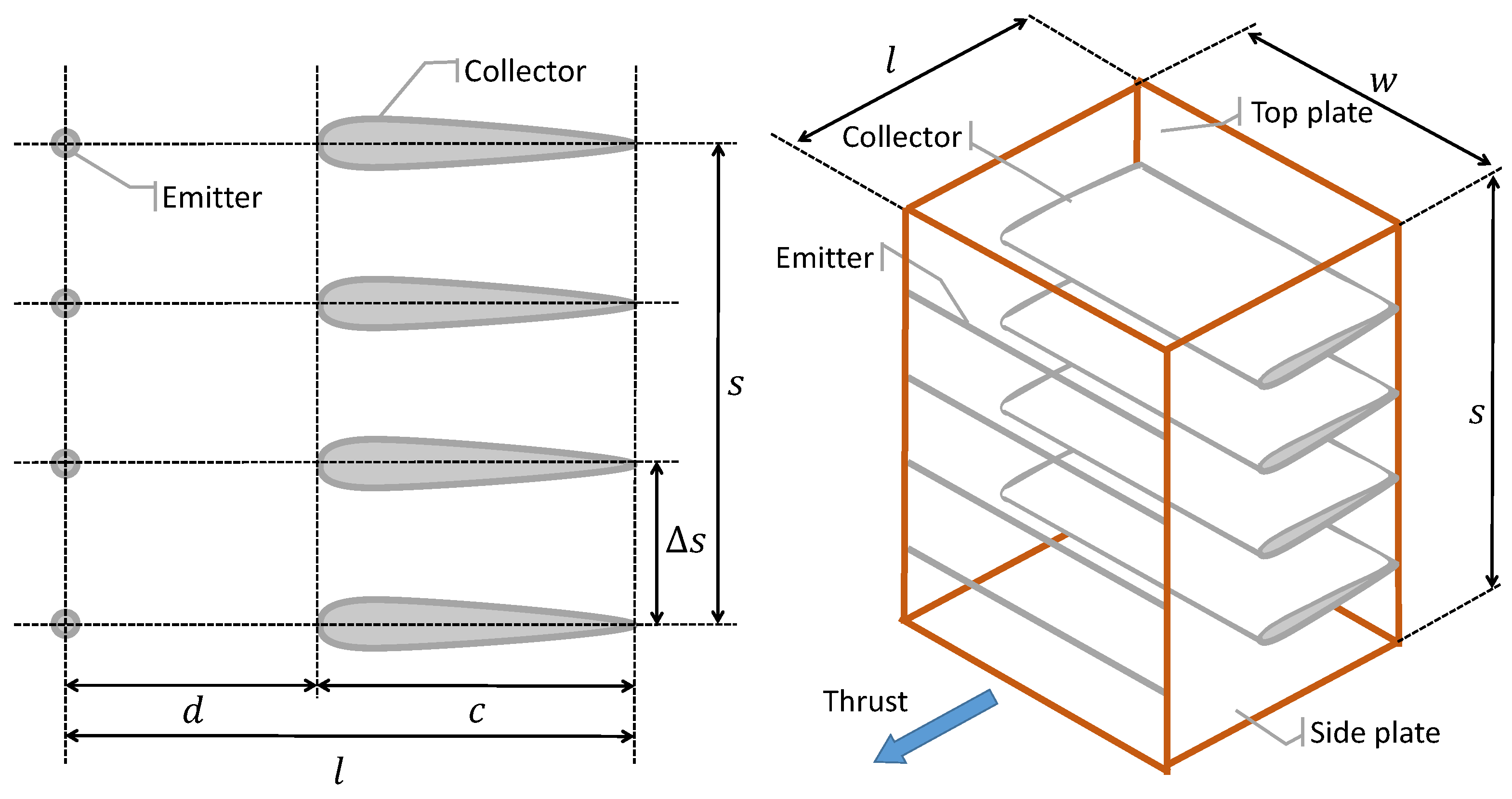
- Geometrical features of each thruster. In particular, referring to Figure 2, quantities l, w, and s are assigned (they are optimized in the laboratory, starting from basic theoretical models, currently being employed at Politecnico di Milano in conjunction with practical testing). This yields an a priori knowledge of the geometrical sizing of each thruster unit. In particular, it is assumed for simplicity that implying a square front section of each thruster.
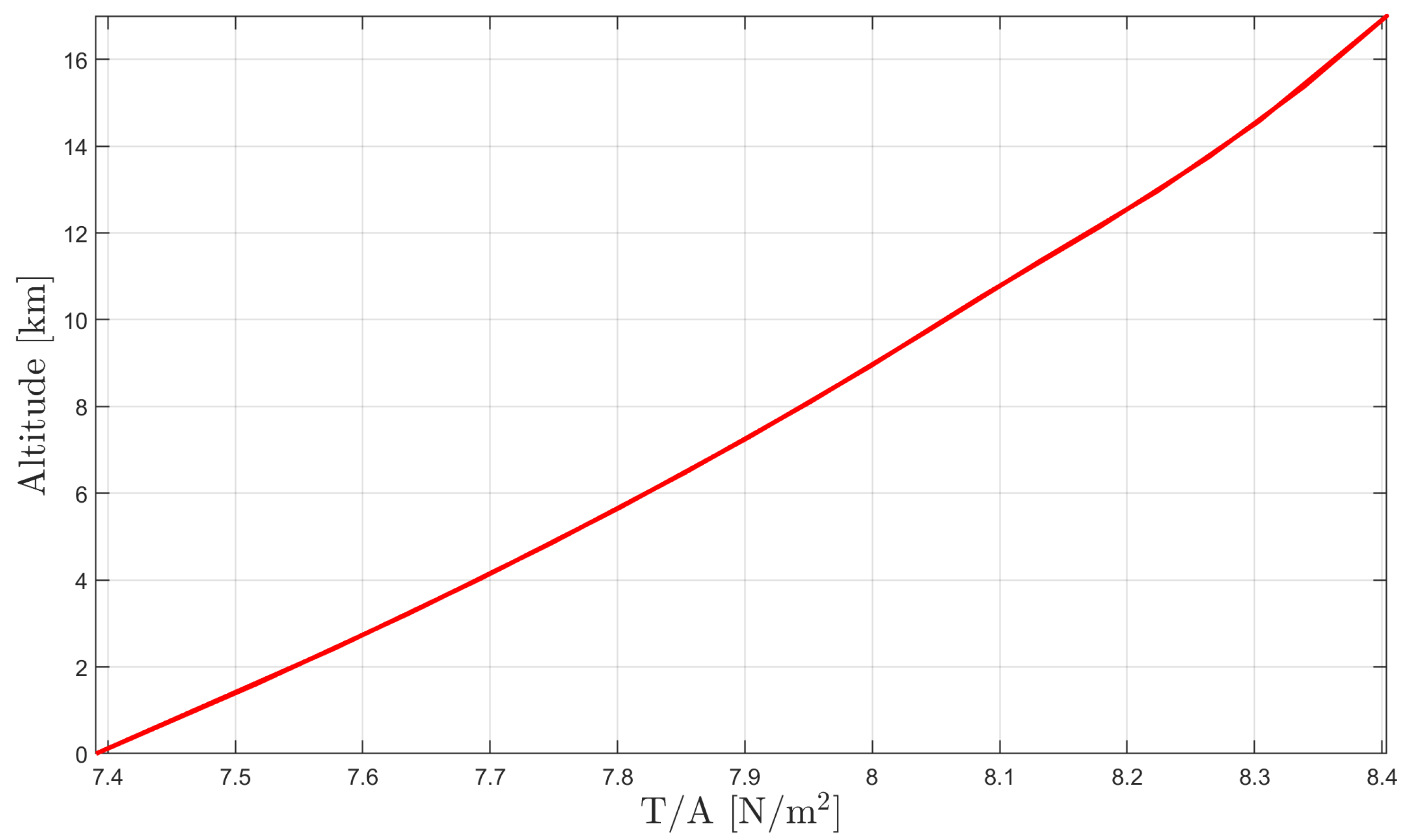
- Thrust-to-frontal area. The value of the ratio follows an assigned behavior with the altitude (similar to geometrical characteristics of the thruster, experimentation on the optimization of this value through a selection of the thruster configuration, supported by a dedicated theoretical model, is well underway within project IPROP). This relevant assumption is supported by the adoption of a certain geometry and general arrangement of the components within the thrusters (e.g., the relative numbers and positioning of emitters and collectors, the sizing of the basic components like c, d and , etc.). This behavior shows an increasing trend, yielding an increasing value of the ratio with the altitude [24,36], according to the law displayed in Figure 4. It can be observed that the ratio is generally increasing with the altitude.
- Thrust-to-power. The ratio is a measure of the efficiency of the thruster, and it might bear an impact on the actual value of power required from the electrical system (and batteries in particular). The behavior of this quantity with altitude is currently a matter of investigation (among the aims of project IPROP). For the present work, assumptions on the behavior of the thermodynamic state of the atmosphere at altitude, known to bear an impact on the ratio, have been employed to feed a preliminary first-principle model [24,36], thus producing the behavior in Figure 5.From the figure, it is immediate to check that is decreasing with the altitude, yielding a less efficient conversion of the power fed to the thrusters into thrust when the airship approaches higher layers of the atmosphere.
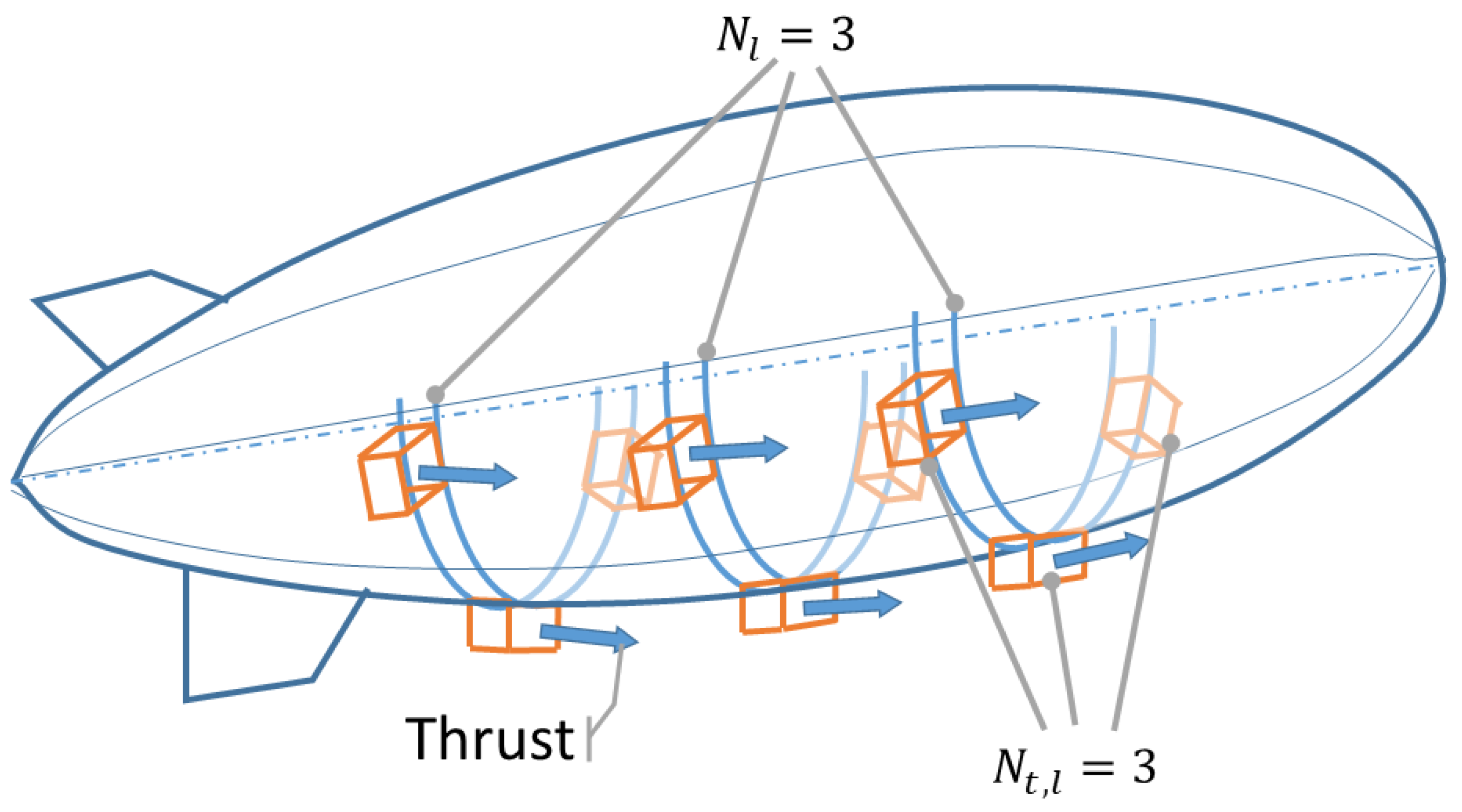
- Arrangement and number of thrusters. Based on the assumed size of the frontal area, in particular, considering the width w, it is possible to compute the maximum number of thrusters to put on a longitudinal station of the airship hull by simply considering the bottom half-circumference of that station and dividing it by the width of each thruster. However, it is interesting to study the effect of the placement of the thrusters, also considering reducing the top number of units that can be arranged on a longitudinal station (a dedicated paragraph is correspondingly included in the application section). To this aim, we introduce a blockage parameter , considered to be assigned and constant and representing the share of the bottom half-circumference of a longitudinal station that can be taken over by the thrusters. When 1, the entire bottom half-circumference is available for the thrusters. Conversely, when (for example) 0.5, only half of the bottom half-circumference is available for placing thrusters, and correspondingly, gaps will appear between thrusters on the same longitudinal station.
- Voltage booster. The voltage booster is associated with a technological figure, namely a ratio of the power over weight and to a voltage level. These quantities are considered to be assigned and constant.
3.2.2. Amendments to the Baseline Sizing Procedure
- Compute the drag coefficient associated with the configuration of the thrusters. This can be performed starting from the drag coefficient value obtained for the airship without thrusters and estimating the additional contribution due to the nacelles of the thrusters. This step can be performed based on a model of the nacelle sides as flat plates. The drag coefficient of the plate is obtained as a function of the relative velocity and viscosity of air and of the length of the plate, which compose the Reynolds number. Then, the drag coefficient obtained for one nacelle can be multiplied by to obtain the total additional drag , hence the actual value of .
- Compute the drag for each node along the mission profile. From this time series of values, the maximum drag encountered over the mission as can be computed.
- Compute the nominal available thrust. Based on the number of thrusters on board , assumed in the current run of the sizing loop, and based on the value of the thrust-to-area ratio , it is possible to compute the actual value of thrust at the altitude corresponding to each time node along the mission, multiplying the total front area of all thrusters by that ratio, thus yielding
- Check the minimum difference of the thrust available vs. drag. Following the computation of the thrust available at every altitude and, correspondingly, the drag, it is possible to check whether the installed thrust is sufficient to compensate for the drag, especially in the worst conditions encountered along the profile. In analytic terms, that check corresponds to the evaluation of the constraintIn case the constraint in Equation (8) is not satisfied, thrusters are added on a further longitudinal station, increasing the number by 1 and restarting from point 1. of this cycle, with a new total number of thrusters . Conversely, if the inequality in Equation (8) is satisfied, the procedure is over.
- Wires employed as emitters. Due to their very limited diameter, these components are associated with a negligible weight.
- Collectors. Depending on the material employed and structural sizing (i.e., hollow or filled structure), the weight may vary significantly.
- Load-bearing structure. Thanks to the relatively low value of force exerted by each thruster, its load-bearing structure can be manufactured with relatively light and flexible material. The cage structure naturally resulting from the setup of this type of thruster allows the obtaining of overall good levels of rigidity at the price of a mild global weight of the structure.
- Nacelle. The material of the nacelle may be the same as the load-bearing structure. The sides of the nacelle may be actually part of it. The structural role of the nacelle top is typically not relevant; hence, this component can be manufactured from very light material.
- Voltage booster. As pointed out, this component is typically not to be found in powerplants for aviation, and its corresponding weight-to-power figure may be somewhat penalizing, albeit already compatible with airship flight operations at the current level of technology. Ways to obtain a better value of this parameter are currently under study (within project IPROP).
4. Application Studies
4.1. Baseline Mission Characteristics and Payload
4.2. Comparison of Design Solutions on Baseline Mission
4.3. Effect of Mission and Technology Parameters on the Design Solution
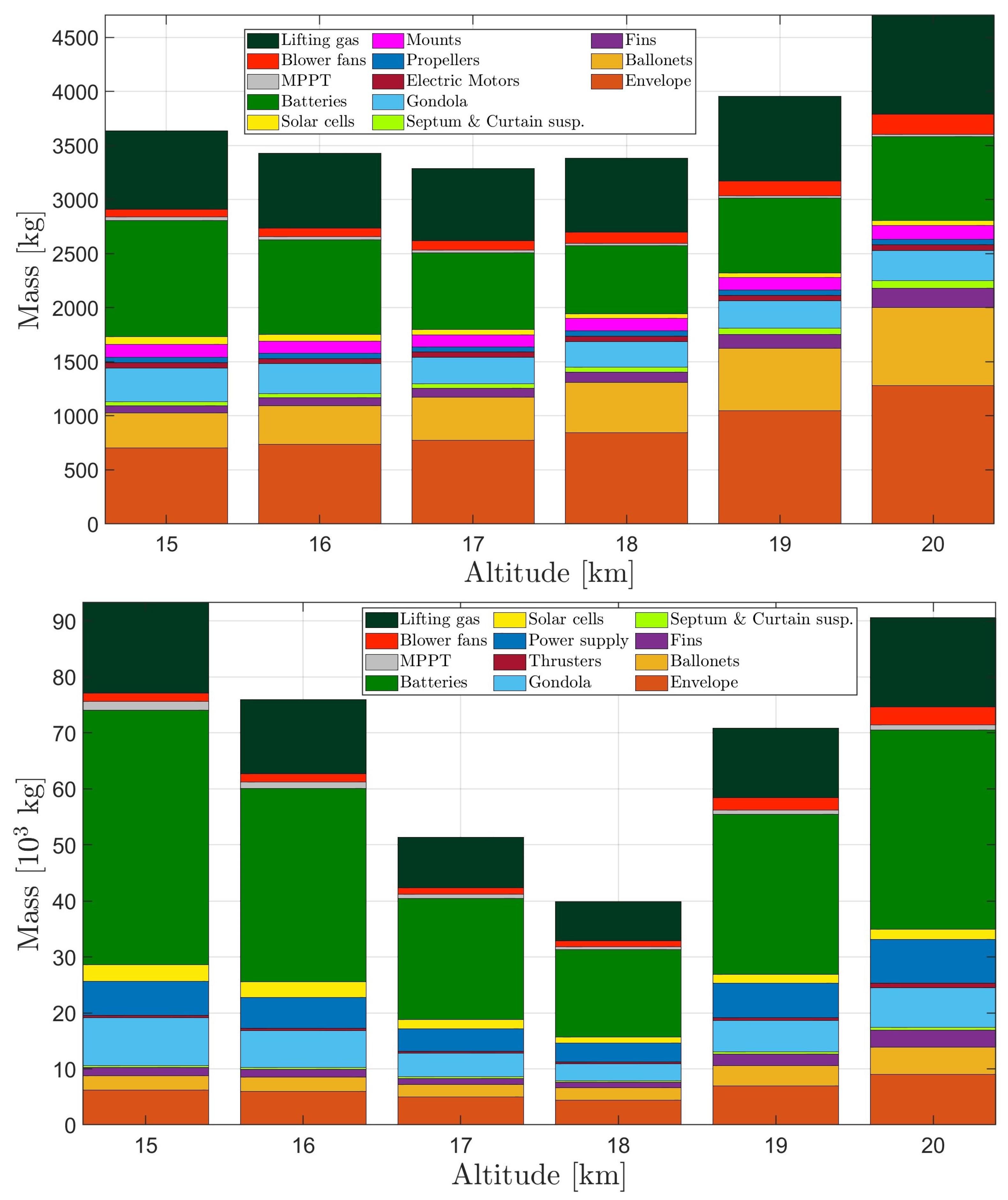
4.3.1. Effect of Stationing Altitude on the Design Based on Conventional and Atmospheric Ionic Thrusters
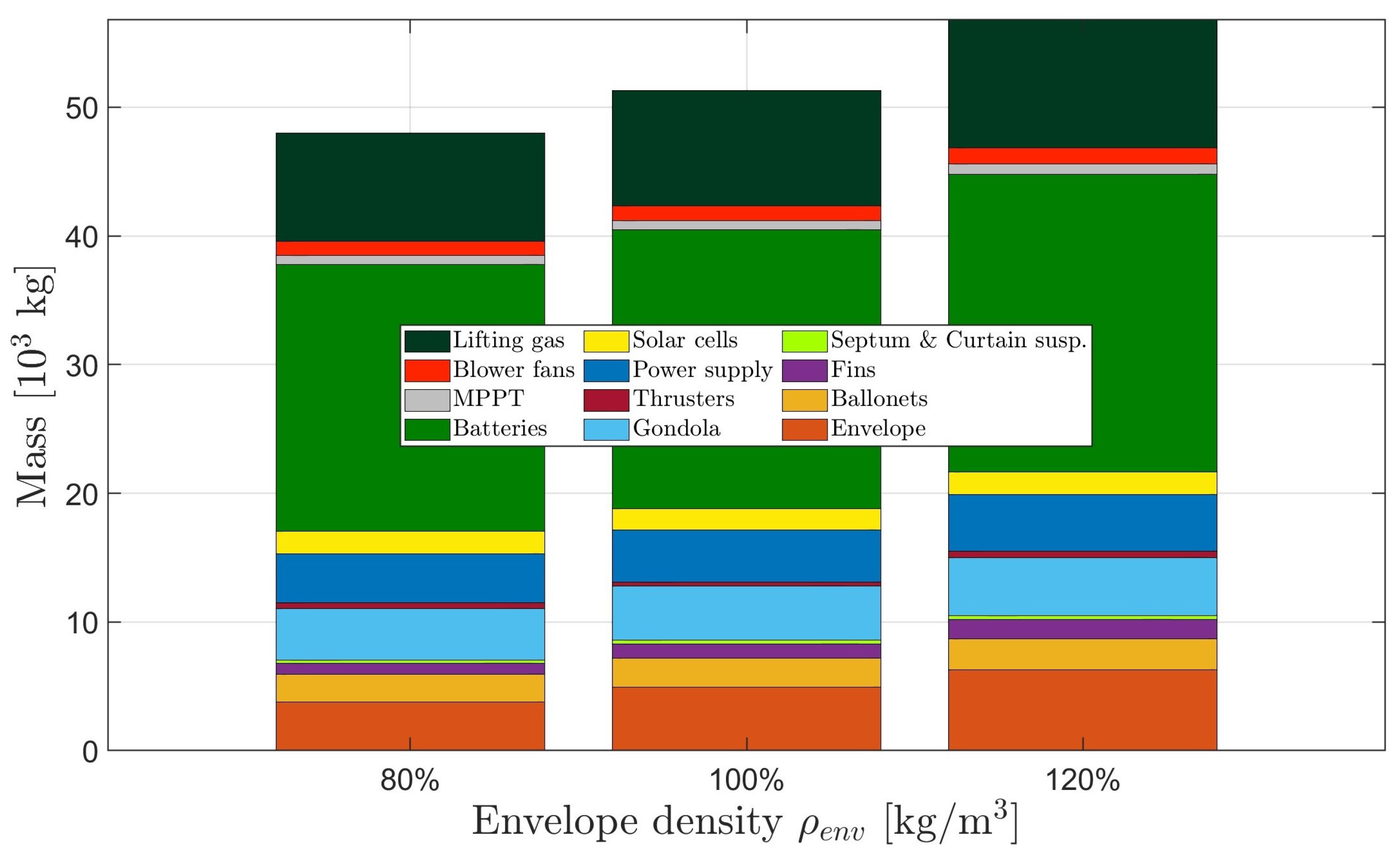
4.3.2. Effect of Envelope Density on the Design Based on Atmospheric Ionic Thrusters
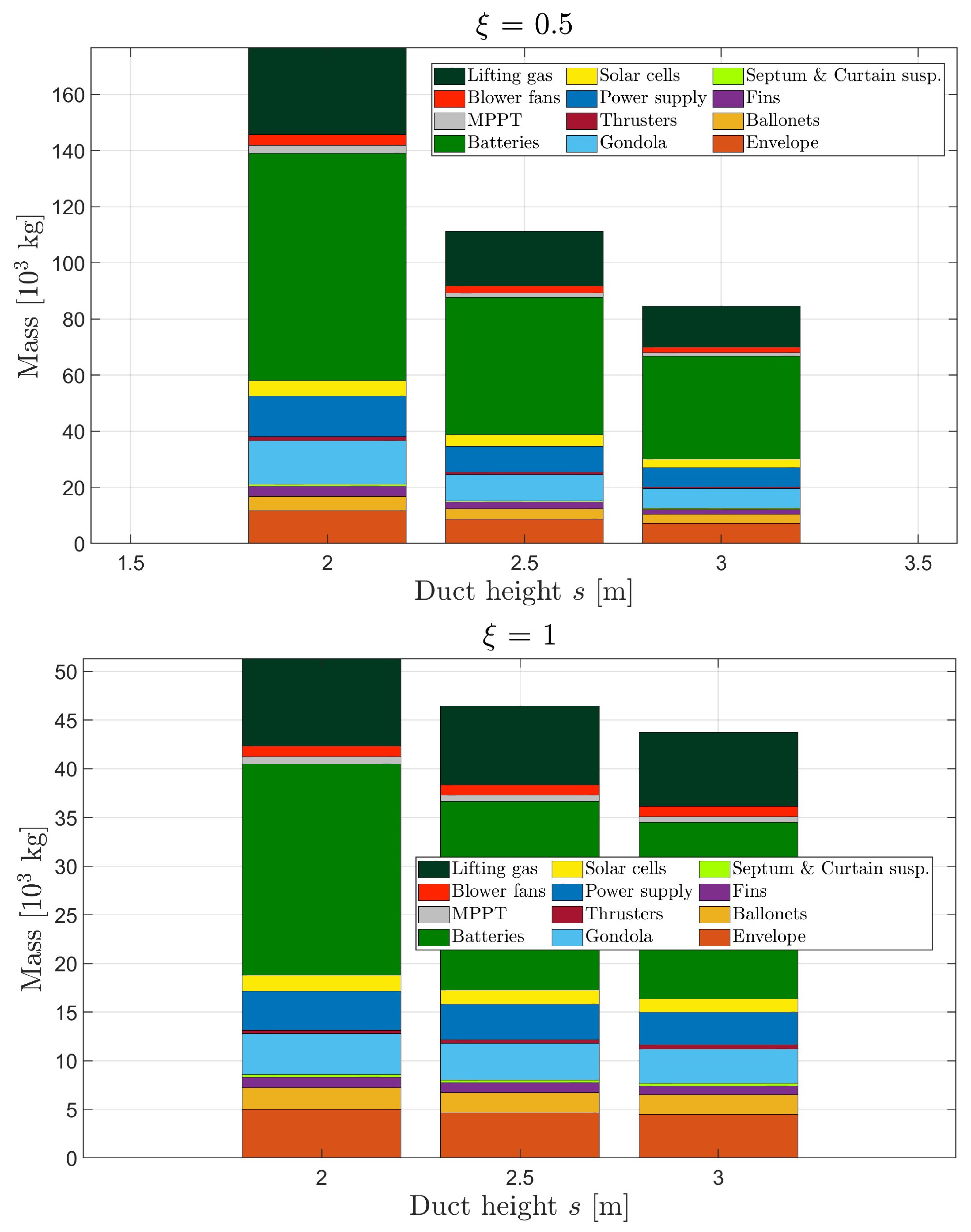
4.3.3. Effect of the Sizing of Atmospheric Ionic Thrusters
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- HyLight. 2022. Available online: https://www.hylight.aero (accessed on 27 June 2024).
- Kelluu Oy. 2023. Available online: https://kelluu.com (accessed on 27 June 2024).
- Colozza, A. Initial Feasibility Assessment of a High Altitude Long Endurance Airship; Technical Report NASA/CR–2003-212724; Analex Corp.: Fairfax, VA, USA, 2003. [Google Scholar]
- Chen, Q.; Zhu, M.; Sun, K. Analysis to Effects on Conceptual Parameters of Stratospheric Airship with Specified Factors. J. Comput. 2011, 6, 1055–1062. [Google Scholar] [CrossRef]
- Riboldi, C.E.D.; Rolando, A.; Regazzoni, G. On the feasibility of a launcher-deployable high-altitude airship: Effects of design constraints in an optimal sizing framework. Aerospace 2022, 9, 210. [Google Scholar] [CrossRef]
- Nagabhushan, B.L.; Tomlinson, N.P. Dynamics and control of a heavy lift airship hovering in a turbulent cross wind. J. Aircr. 1982, 19, 826–830. [Google Scholar] [CrossRef]
- Riboldi, C.E.D.; Rolando, A. Layout Analysis and Optimization of Airships with Thrust-Based Stability Augmentation. Aerospace 2022, 9, 393. [Google Scholar] [CrossRef]
- Riboldi, C.E.D.; Rolando, A. Thrust-based stabilization and guidance for airships without thrust-vectoring. Aerospace 2023, 10, 344. [Google Scholar] [CrossRef]
- Riboldi, C.E.D.; Rolando, A. Autonomous flight in near hover and hover for thrust controlled unmanned airships. Drones 2023, 7, 545. [Google Scholar] [CrossRef]
- Dubourg, V.; Raizonville, P.; Vargas, A.; Louvel, S. French balloon activities 2018–2021: National report. In Proceedings of the 43rd COSPAR Scientific Assembly, Sydney, Australia, 28 January–4 February 2021. [Google Scholar]
- Dubourg, V.; Louvel, S.; Venel, S.; Vacher, F.; Thomieux, F.; Deschamps, A. An update of the CNES stratospheric balloon activities. In Proceedings of the Aerospace Europe Conference 2023-10th EUCASS-9th CEAS, Lausanne, Switzerland, 9–13 July 2023. [Google Scholar]
- Involve Space. 2024. Available online: https://www.involvespace.eu (accessed on 27 June 2024).
- Wang, Q.; Chen, J.; Fu, G.; Duan, D.; Zhao, H. A methodology for optimisation design and analysis of stratosphere airship. Aeronaut. J. 2009, 113, 533–540. [Google Scholar] [CrossRef]
- Yu, D.; Lv, X. Configurations analysis for high-altitude/long-endurance airships. Aircr. Eng. Aerosp. Technol. 2010, 82, 48–59. [Google Scholar] [CrossRef]
- Baraniello, V.R.; Persechino, G. Conceptual Design of a Stratospheric Hybrid Platform for Earth Observation and Telecommunications. In Proceedings of the Aerospace Europe CEAS 2017 Conference, Bucharest, Romania, 16–20 October 2017. [Google Scholar]
- Gonzalo, J.; López, D.; Domínguez, D.; García, A.; Escapa, A. On the capabilities and limitations of high altitude pseudo-satellites. Prog. Aerosp. Sci. 2018, 98, 37–56. [Google Scholar] [CrossRef]
- Zhang, L.; Zhu, W.; Du, H.; Lv, M. Multidisciplinary design of high altitude airship based on solar energy optimization. Aerosp. Sci. Technol. 2021, 110, 106440. [Google Scholar] [CrossRef]
- Chu, A.; Blackmore, M.; Oholendt, R.G.; Welch, J.V.; Baird, G.; Cadogan, D.P.; Scarborough, S.E. A novel concept for stratospheric communications and surveillance: Star Light. In Proceedings of the AIAA Balloon Systems Conference, Williamsburg, VA, USA, 21–24 May 2007. [Google Scholar] [CrossRef]
- Smith, S.; Fortenberry, M.; Lee, M.; Judy, R. HiSentinel80: Flight of a High Altitude Airship. In Proceedings of the 11th AIAA Aviation Technology, Integration, and Operations (ATIO) Conference, Virginia Beach, VA, USA, 20–22 September 2011. [Google Scholar] [CrossRef]
- Yang, X.; Liu, D. Conceptual Design of Stratospheric Airships Focusing on Energy Balance. J. Aerosp. Eng. 2018, 31. [Google Scholar] [CrossRef]
- Belan, M.; Arosti, L.; Polatti, R.; Maggi, F.; Fiorini, S.; Sottovia, F. A parametric study of electrodes geometries for atmospheric electrohydrodynamic propulsion. J. Electrost. 2021, 113, 103616. [Google Scholar] [CrossRef]
- Belan, M.; Terenzi, R.; Trovato, S.; Usuelli, D. Effects of the emitters density on the performance of an atmospheric ionic thruster. J. Electrost. 2022, 120, 103767. [Google Scholar] [CrossRef]
- Kahol, O.; Belan, M.; Pacchiani, M.; Montenero, D. Scaling relations for the geometry of wire-to-airfoil atmospheric ionic thrusters. J. Electrost. 2023, 123, 103815. [Google Scholar] [CrossRef]
- Gomez-Vega, N.; Brown, A.; Xu, H.; Barrett, S.R.H. Model of Multistaged Ducted Thrusters for High-Thrust-Density Electroaerodynamic Propulsion. AIAA J. 2023, 61, 767–779. [Google Scholar] [CrossRef]
- Gomez-Vega, N.; Barrett, S.R.H. Order-of-Magnitude Improvement in Electroaerodynamic Thrust Density with Multistaged Ducted Thrusters. AIAA J. 2024, 62, 1342–1353. [Google Scholar] [CrossRef]
- Grant ID: HORIZON-EIC-2022-PATHFINDEROPEN-01, No. 101098900, IPROP-Ionic Propulsion in the Atmosphere. 2023–2027. Available online: https://pat.polimi.it/iprop-project/ (accessed on 27 June 2024).
- Carichner, G.E.; Nicolai, L.M. Fundamentals of Aircraft and Airship Design; AIAA Education Series; American Institute of Aeronautics and Astronautics, Inc.: Reston, VA, USA, 2013. [Google Scholar]
- Riboldi, C.E.D.; Belan, M.; Cacciola, S.; Terenzi, R.; Trovato, S.; Usuelli, D.; Familiari, G. Preliminary sizing of a low-altitude airship including ion-plasma thrusters. In Proceedings of the 34th Congress of the International Council of the Aeronautical Sciences (ICAS2024), Florence, Italy, 9–13 September 2024. [Google Scholar]
- Riboldi, C.E.D.; Rolando, A.; Cacciola, S.; Regazzoni, G.; Spadafora, I. On the Optimal Preliminary Design of High-Altitude Airships: Automated Procedure and the Effect of Constraints. In Proceedings of the Aerospace Europe Conference 2023-10th EUCASS-9th CEAS, Lausanne, Switzerland, 9–13 July 2023. [Google Scholar]
- Kämpf, B. Flugmechanik und Flugregelung von Luftschiffen. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 2004. [Google Scholar] [CrossRef]
- U.S. Standard Atmosphere; Technical Report NOAA-S/T 76-1562; NOAA-NASA-USAF: Washington, DC, USA, 1976.
- Drob, D.P.; Emmert, J.T.; Crowley, G.; Picone, J.; Shepherd, G.G.; Skinner, W.; Hays, P.; Niciejewski, R.J.; Larsen, M.; She, C.Y.; et al. An empirical model of the Earth’s horizontal wind fields: HWM07. J. Geophys. Res. Space Phys. 2008, 113, 1–18. [Google Scholar] [CrossRef]
- Drob, D.P.; Emmert, J.T.; Meriwether, J.W.; Makela, J.J.; Doornbos, E.; Conde, M.; Hernandez, G.; Noto, J.; Zawdie, K.A.; McDonald, S.E.; et al. An update to the Horizontal Wind Model (HWM): The quiet time thermosphere. Earth Space Sci. 2015, 2, 301–319. [Google Scholar] [CrossRef]
- Gueymard, C. SMARTS2, a Simple Model of the Atmospheric Radiative Transfer of Sunshine: Algorithms and Performance Assessment; Technical Report FSEC-PF-270-95; Florida Solar Energy Center: Cocoa, FL, USA, 1995. [Google Scholar]
- Riboldi, C.E.D.; Gualdoni, F. An integrated approach to the preliminary weight sizing of small electric aircraft. Aerosp. Sci. Technol. 2016, 58, 134–149. [Google Scholar] [CrossRef]
- Gilmore, C.K.; Barrett, S.R. Electroaerodynamic Thruster Performance as a Function of Altitude and Flight Speed. AIAA J. 2018, 56, 1105–1117. [Google Scholar] [CrossRef]
- Li, A.; Vallabh, R.; Bradford, P.D.; Kim, D.; Seyam, A.F.M. Development of hull material for high-altitude airship: A parametric study. J. Reinf. Plast. Compos. 2022, 41, 444–458. [Google Scholar] [CrossRef]
- Riboldi, C.E.D. An optimal approach to the preliminary design of small hybrid-electric aircraft. Aerosp. Sci. Technol. 2018, 81, 14–31. [Google Scholar] [CrossRef]

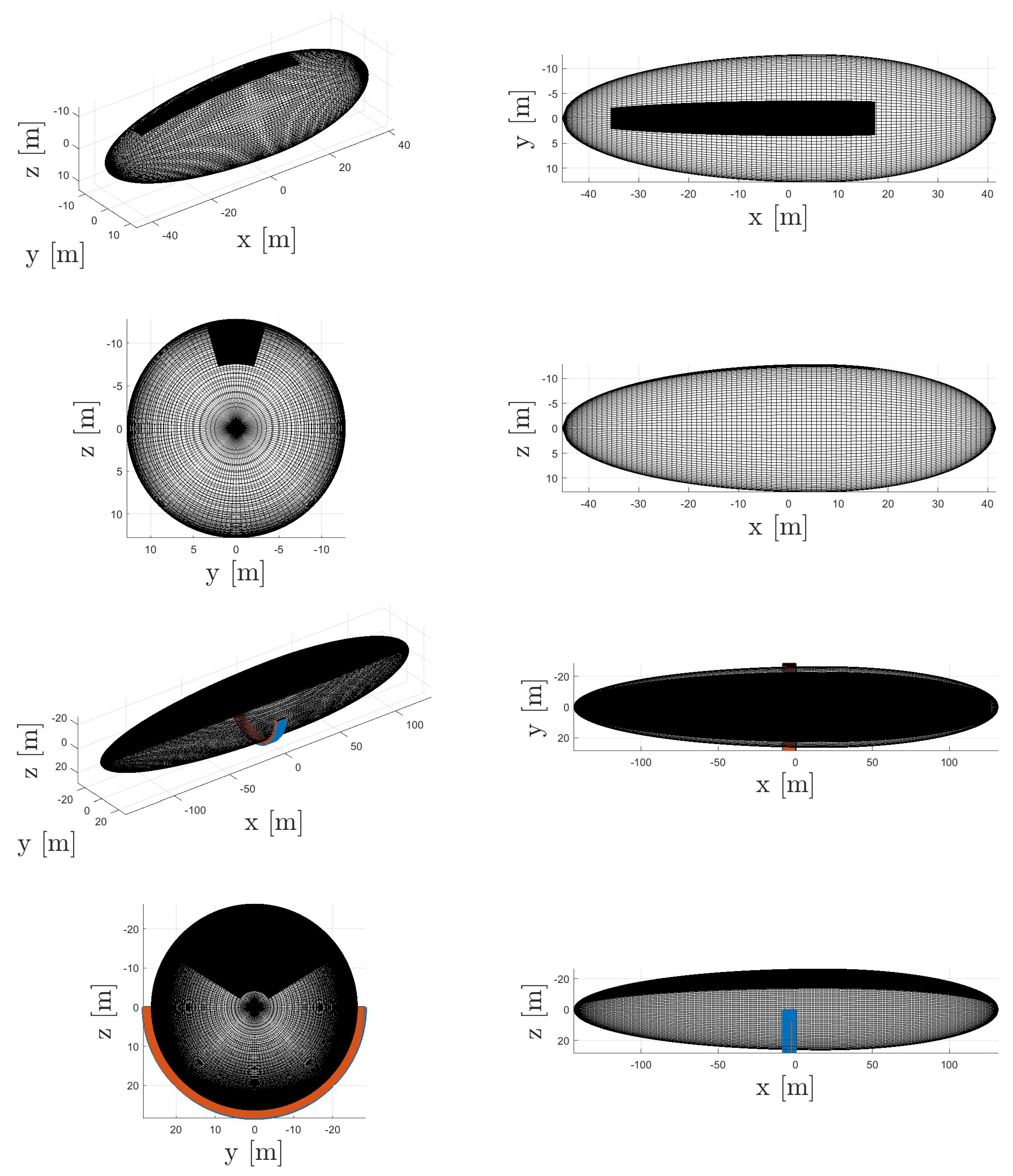
| Mission Parameter | Value |
|---|---|
| Flight time | 48 h |
| Climb and descent ground speed | 6 m/s |
| Top altitude (above ground) | 17 km |
| Climb and descent angle (absolute value) | 30 deg |
| System | Weight [kg] | Power [kW] |
|---|---|---|
| Data links & Computers | 10 | 0.1 |
| ELM-2022A | 95 | 3.3 |
| AJCN | 227 | 9.7 |
| MS-177 | 244 | 1.75 |
| Component | Technological Parameter | Value |
|---|---|---|
| Envelope | Surface density | 113 g/cm2 |
| Maximum tensile strength | 970 N/cm | |
| Battery | Energy density | 450 Wh/kg |
| Power density | 1800 W/kg | |
| Charge/Discharge efficiency | 96% | |
| Cables | Volumetric energy density | 1150 J/m3 |
| Quantity | Conventional | Ionic |
|---|---|---|
| Envelope length [m] | 87.0 | 275.7 |
| Fineness ratio | 3.40 | 5.23 |
| Total weight W [kg] | 3864 | 51,889 |
| Envelope [kg] | 772 | 4943 |
| Ballonet [kg] | 399 | 2257 |
| Lifting gas [kg] | 668 | 8975 |
| Support structures, tail [kg] | 124 | 1370 |
| Thruster [kg] | 207 | 313 |
| Voltage booster [kg] | 0 | 4052 |
| Battery [kg] | 712 | 21,674 |
| Solar cells, MPPT [kg] | 72 | 2358 |
| Gondola [kg] | 247 | 4213 |
| Payload [kg] | 576 | 576 |
| Altitude | |||
|---|---|---|---|
| 15 km | 43 | 43 | 1849 |
| 16 km | 37 | 43 | 1591 |
| 17 km | 30 | 41 | 1230 |
| 18 km | 24 | 42 | 1008 |
| 19 km | 32 | 55 | 1760 |
| 20 km | 35 | 64 | 2240 |
| Frontal Area Side [m] | Blockage Parameter | ||||
|---|---|---|---|---|---|
| 2.0 | 0.5 | 80 | 146 | 30 | 4380 |
| 2.0 | 1 | 80 | 30 | 41 | 1230 |
| 2.5 | 0.5 | 100 | 86 | 20 | 1720 |
| 2.5 | 1 | 100 | 22 | 32 | 704 |
| 3.0 | 0.5 | 120 | 60 | 15 | 900 |
| 3.0 | 1 | 120 | 18 | 26 | 468 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Riboldi, C.E.D.; Belan, M.; Cacciola, S.; Terenzi, R.; Trovato, S.; Usuelli, D.; Familiari, G. Preliminary Sizing of High-Altitude Airships Featuring Atmospheric Ionic Thrusters: An Initial Feasibility Assessment. Aerospace 2024, 11, 590. https://doi.org/10.3390/aerospace11070590
Riboldi CED, Belan M, Cacciola S, Terenzi R, Trovato S, Usuelli D, Familiari G. Preliminary Sizing of High-Altitude Airships Featuring Atmospheric Ionic Thrusters: An Initial Feasibility Assessment. Aerospace. 2024; 11(7):590. https://doi.org/10.3390/aerospace11070590
Chicago/Turabian StyleRiboldi, Carlo E.D., Marco Belan, Stefano Cacciola, Raffaello Terenzi, Stefano Trovato, Davide Usuelli, and Giuseppe Familiari. 2024. "Preliminary Sizing of High-Altitude Airships Featuring Atmospheric Ionic Thrusters: An Initial Feasibility Assessment" Aerospace 11, no. 7: 590. https://doi.org/10.3390/aerospace11070590
APA StyleRiboldi, C. E. D., Belan, M., Cacciola, S., Terenzi, R., Trovato, S., Usuelli, D., & Familiari, G. (2024). Preliminary Sizing of High-Altitude Airships Featuring Atmospheric Ionic Thrusters: An Initial Feasibility Assessment. Aerospace, 11(7), 590. https://doi.org/10.3390/aerospace11070590








