Abstract
A rapid trajectory-planning method based on an analytical predictor–corrector design of drag acceleration profile and a bank-reversal logic based on double-stage adaptive adjustment is proposed to solve the entry issue under time and full-state constraints. First, an analytical predictor–corrector algorithm is used to design the profile parameters to satisfy the terminal of altitude, velocity, range, time, and flight-path angle constraints. Subsequently, an adaptive lateral planning algorithm based on heading adjustment and maintenance is proposed to achieve the flight stage adaptive division and determination of the bank-reversal point, thereby satisfying the terminal position and heading angle constraints. Concurrently, a rapid quantification method is proposed for the adjustable capacity boundary of the terminal heading angle. On this basis, a range-and-time correction strategy is designed to achieve high precision and the rapid generation of a three-degree-of-freedom entry trajectory under large-scale lateral maneuvering. The simulation results demonstrated that compared with the existing methods, the proposed method can adaptively divide flight stages, ensuring better multitask applicability and higher computational efficiency.
1. Introduction
As a key technology for entry vehicles [1], rapid entry trajectory planning represents a crucial strategy for enhancing flight autonomy, task adaptability, and intelligence level. Conventional entry trajectory planning only considers path and partial terminal state constraints, such as position, altitude, velocity, and heading-angle errors. However, with the proposal of coordinated flight and the flight-formation concept [2,3], the entry vehicle must be capable of controlling the flight time and terminal attack angles. At this point, the issue of entry trajectory planning comprises the path, time, and terminal full-state constraints, which reduce the feasible region and further complicate entry trajectory design.
However, the existing methods considering the time and terminal angle constraints mainly focused on the terminal guidance phase [4,5], which are generally based on the constant velocity assumption, and cannot consider the path constraint. Moreover, the traditional entry trajectory-planning methods based on the standard trajectory design [6,7,8], predictor–corrector [9,10], and quasi-equilibrium glide condition (QEGC) [11,12] cannot consider the time and terminal angle constraints. On the basis of the above methods, numerous entry trajectory-planning methods considering complex constrains have been recently proposed.
In terms of time constraints, methods were mainly based on the standard profile design [13,14,15,16], predictor–corrector method [17,18,19,20], neural network design [21], and reinforcement learning [22]. As a representative of the standard profile method, Wang et al. [13] designed an altitude–velocity profile with dual parameters and corrected the profile parameter through numerical method to satisfy the range and time constraints. Qiao et al. [15] demonstrated the correlation between an actual trajectory length and flight time based on the maneuver coefficient and designed a segmented linear drag acceleration profile to satisfy the range and time constraints. In terms of the predictor–corrector, Li et al. [18] introduced adjustable parameters into longitudinal and lateral profiles, thereby enhancing the range of flight-time adjustment. Additionally, to improve the computational efficiency of the algorithm, Yu et al. [19] simplified the lift–drag ratio model to a quadratic polynomial and controlled flight time by an analytical predictor–corrector algorithm. The above methods adjusted the flight time by correcting the longitudinal profile parameters. Regarding lateral planning, Fang et al. [21] employed a neural network to predict the time to go and controlled the flight time by adjusting the width of the heading-angle-error corridor. Zhang et al. [22] abstracted lateral guidance as a Markov decision problem and designed the time-controllable entry guidance by a lateral intelligent maneuver decision maker based on Deep Q-learning Network (DQN).
To consider the terminal angle constraints, Liang et al. [23] proposed a multi-waypoint entry guidance method, iteratively solving for double bank-reversal points using a numerical algorithm to satisfy the waypoint and heading angle constraints. Following reference [23], Liang et al. [24] improved and proposed a lateral guidance logic based on aiming points. Compared to the waypoint method, aiming points are only employed to determine the reversal timing of bank angles without passing through, thus reducing the number of bank reversals. Additionally, Wang et al. [25] proposed an entry trajectory-planning method considering terminal full-state constraints based on the altitude–velocity profile design. Although the above methods can individually solve the entry trajectory-planning problem involving flight time or angle constraint, they generally rely on numerical integration for range and time prediction, which are time consuming and cannot simultaneously consider the terminal time and full-state constraints.
On the basis of the above methods, several entry trajectory-planning methods considering both time and terminal full-state constraints have been proposed. These methods were mainly based on trajectory optimization [26] and the predictor–corrector algorithm [27,28]. Liu et al. [26] proposed a trajectory-planning method based on the improved sequential convex optimization algorithm, but this method has a strong dependence on initial reference trajectory, making it difficult to ensure efficient and reliable convergence. To improve the computational efficiency, reference [27] designed a predictor–corrector guidance method based on range and generalized heading-angle analytical prediction, and they introduced a bias-explicit guidance method at the terminal guidance stage to enhance terminal accuracy. Additionally, reference [28] proposed a multistage entry guidance method, dividing the entry trajectory into lateral maneuvering, longitudinal maneuvering, and a terminal guidance stage, which can simultaneously satisfy the flight time and terminal-angle constraints. However, this method mainly introduced QEGC and divided the entry trajectory into multiple stages, which is not conducive to quickly quantifying the adjustable range of flight time, range, and heading angle, limiting the adjustable range of them.
In tasks such as omni-directional arrival and coordinated capture, the inclusion of terminal time and full-state constraints significantly increases the complexity of trajectory planning. Reference [28] addresses the reentry guidance problem with these constraints through a segmented trajectory design approach. However, this method restricts maneuverability and adjustment capabilities and is designed for offline trajectory planning, thus not addressing computational efficiency. To overcome these limitations, this paper proposes a rapid trajectory-planning method that satisfies both time and terminal full-state constraints. This method effectively circumvents the drawbacks of traditional techniques, such as numerical prediction–correction, multiple bank angle reversal iterations, and segmented trajectory design, in terms of computational efficiency and adjustability. By meeting the time and terminal full-state constraints, it further enhances computational efficiency. The main innovations are summarized as follows:
- (1)
- An analytical predictor–corrector design of the drag acceleration profile: Unlike the existing profile-based methods [13,14,15], an analytical predictor–corrector method is used to design the dual-parameter drag acceleration profile, thereby avoiding numerical integration and QEGC [28], improving the accuracy and computational efficiency, and satisfying the terminal altitude, velocity, range, time, and flight path angle constraints.
- (2)
- Phased adaptive lateral planning based on a heading adjustment and maintenance strategy: Compared with the previous approaches [23,24], this paper designs an adaptive lateral-planning algorithm based on the double stage of heading adjustment and maintenance to achieve the adaptive division of the flight stage and determine the bank-reversal points, ensuring accuracy while avoiding the multi-parameter iteration, which can also rapidly quantify the adjustable range of the terminal heading angle and fully exploit the lateral maneuverability of the vehicle.
- (3)
- Multitask adaptive iterative correction for three-dimensional (3D) trajectory: Dissimilar to the existing 3D trajectory correction methods, such as Evolved Acceleration Guidance Logic for Entry (EAGLE) [7], this paper considers the lateral large-scale maneuvering situation and extends the applicability of trajectory-correction methods, thereby improving the applicability of multitasking.
The rest of this paper is organized as follows: Section 2 introduces the entry trajectory-planning problem. Section 3 designs the rapid entry trajectory-planning method considering the terminal time and full-state constraints. Section 4 verifies the effectiveness of the method and the advantage of the terminal time and full-state control. Finally, Section 5 concludes the study.
2. Entry Trajectory-Planning Problem
2.1. Motion Model
The non-dimensional three degrees of freedom (3DOF) equations of motion for an entry vehicle over a spherical rotating earth with respect to energy can be expressed as follows [29]:
The left side of Equation (1) represents the derivatives of the dimensionless-state variables, , with respect to the dimensionless energy . The meanings of the variables mentioned in Equation (1) are shown in Table 1. In these equations, lengths are scaled by , time is scaled by , and velocity is scaled by . The Coriolis terms , and Centripetal terms , corresponding to the Earth’s rotation have been described in [29]. The dimensionless lift acceleration () and drag acceleration () are scaled by , namely
where is the dimensional mass of the vehicle, is the dimensional aerodynamic reference area, and and are the lift and drag coefficients, respectively. The dimensional atmospheric density is uniformly calculated using , where is the atmospheric density at sea level, is dimensional flight altitude, and = 7200 m.

Table 1.
The meanings of variables mentioned in Equation (1).
It is noteworthy that can be solved at any given and by
Additionally, for the convenience of the subsequent profile design, the dimensionless energy is normalized () as follows:
where ; and are the initial and terminal energies of entry, respectively; .
2.2. Constraints
2.2.1. Path Constraints
The path constraints mainly comprise the heating rate , dynamic pressure , and overload as follows:
where is the dimensional Earth-relative velocity magnitude, is a constant; and , and represent the maximum heating rate, maximum dynamic pressure, and maximum overload, respectively, as determined by the characteristics of the vehicle’s structure and control mechanisms.
The quasi-equilibrium glide condition (QEGC) [11] assumes that when the vehicle is gliding in the atmosphere without propulsion, it is in a state of force equilibrium in the longitudinal direction at every point along the trajectory, namely
At this point, both the flight-path angle and its rate of change for the vehicle are very small and can be approximated as .
To ensure the controllability of the trajectory, it is necessary to ensure that the maximum lift the vehicle can generate during flight can always balance the other forces, namely
where is the bank angle during quasi-equilibrium glide.
Next, the constraints in Equations (5) and (7) are converted into functional relationships between and , corresponding to the boundary of heating rate , the boundary of dynamic pressure , the boundary of overload and the boundary of equilibrium-entry . The specific expressions are reported in reference [8]. Consequently, the D–E entry-corridor boundary is obtained as follows:
where and are the upper and lower boundaries of the D–E corridor, respectively.
Therefore, the path constraints in Equation (5) can be transformed into corridor constraints, as follows:
2.2.2. Control Constraints
To facilitate trajectory control and tracking, the following control constraints are introduced. The control variables include attack angle and bank angle . For the bank angle, upper and lower bounds are imposed on its magnitude as follows:
where and represent the upper and lower limits of the attack angle , respectively; represents the maximum rate of change in ; and represent the upper and lower limits of the bank angle magnitude, respectively; and represents the maximum rate of change in .
Considering the range-capability and thermal-protection requirements, the profile is preset as a three-segment linear form, specifically as follows:
where and are the maximum attack angle and the maximum - ratio of attack angle, respectively; and and are the segment parameters of the profile.
2.2.3. Terminal Constraints
The terminal constraints of the entry phase include the terminal altitude, velocity, longitude, latitude, flight-path angle, heading angle, and flight time, as follows:
where is the terminal line-of-sight angle and , , , , , , , and represent the corresponding terminal constraints.
Since the angle of attack profile is also based on the preset velocity, both drag acceleration and energy are functions of altitude and velocity only, namely
Therefore, the terminal altitude and velocity constraints can be transformed into drag acceleration constraints at the terminal energy as follows:
The terminal longitude and latitude constraints are transformed into the terminal remaining range as follows:
where and are the constraint values of terminal drag acceleration and remaining range, respectively.
Gliders use the bank-to-turn (BTT) technology with its control variables typically being the attack angle and the bank angle. Therefore, the rapid trajectory-planning problem for gliders studied in this paper can be described as follows: by designing appropriate commands for attack angle and bank angle, rapidly generate a 3DOF gliding trajectory that meets dynamic equations, process constraints, control constraints, time constraints, and terminal full-state constraints. In this context, the attack angle command is predetermined based on range and thermal requirements. Thus, the bank angle is the only control variable for the aircraft. Adjusting the magnitude of the bank angle enables longitudinal trajectory modifications, while designing the sign of the bank angle can control the aircraft’s heading and position.
3. Trajectory-Planning Algorithm
Considering the aerodynamic control capability and computational burden, the initial descent phase adopts a constant bank angle control and transitions to the entry phase at , where is the initial drag acceleration in glide phase.
Figure 1 shows the three core modules of the entry trajectory rapid planning method. Longitudinal trajectory planning rapidly generates the D–E profile and the magnitude command of the bank angle to consider the terminal altitude, velocity, flight-path angle, time, and range constraints through the profile analytical predictor–corrector design method. Lateral planning comprises the double-stage adaptive planning algorithm based on heading adjustment and maintenance as well as the bank-reversal logic to satisfy the terminal heading and position constraints. Additionally, considering lateral large-scale maneuvers, a 3DOF entry trajectory correction and generation algorithm framework considering longitudinal and lateral coupled motion is designed, further enhancing the terminal full-state accuracy and multitask applicability of the trajectory. The specific design methods for the three modules are presented below.
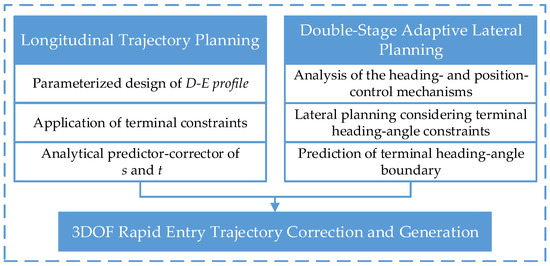
Figure 1.
Content arrangement.
3.1. Longitudinal Trajectory Planning
Longitudinal trajectory planning is aimed at designing a reference trajectory that satisfies the path, terminal altitude, velocity, range, flight time, and flight-path angle constraints. To achieve this, a parameterized dual-parameter D–E profile with corridor-boundary interpolation is presented in this section, and the analytical predictor–corrector of the profile parameters is designed. The analytical predictor–corrector process for the profile dual-parameter is shown in Figure 2.
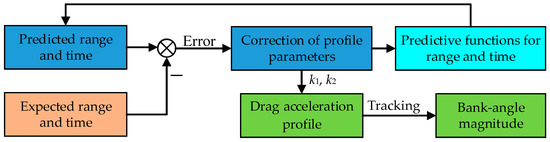
Figure 2.
Analytical predictor–corrector of the profile parameters.
3.1.1. Parameterized Design of the Drag Acceleration Profile
First, the upper and lower boundaries of the entry corridor should be fitted. The upper boundary of the corridor comprises the heating rate, dynamic pressure, and overload constraints, which can be fitted as a four-segment quadratic function curve , and the lower boundary of the corridor is the QEGC, which can be fitted as a double-segment quadratic function curve . The specific fitting method is discussed in reference [16]. Concurrently, the fitted corridor must be inside the original corridor to ensure the safety of the flight path.
Based on the analysis of flight dynamics, the vehicle achieves the minimum range when it flies along the upper boundary of the corridor , and the corresponding flight time is also minimized. Conversely, it achieves the maximum range when it flies along the lower boundary of the corridor , and the corresponding flight time will be maximized. Therefore, by interpolating between and , a reference D–E profile can be designed, which ensures the safe flight of the vehicle within the entry corridor while maximizing the range and flight time adjustment range. Figure 3 shows a comparison of the shapes of the actual and fitted corridor boundaries.
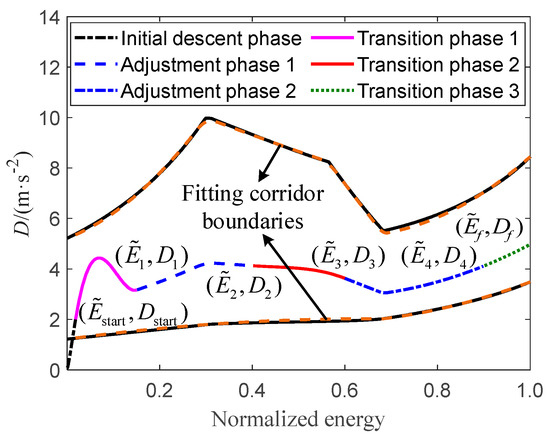
Figure 3.
Sketch map of the D–E profile.
Therefore, considering the time, range, terminal altitude, velocity, and flight-path angle constraints and ensuring the continuity and smoothness of the profile, the reference D–E profile is designed with the five-segment form (Figure 3) with specific expressions as follows:
where and are the undetermined dual-parameters of the drag acceleration profile. These parameters are used to enforce range and time constraints to ensure that the drag acceleration profile remains within the corridor, which should satisfy the constraints as follows:
where is at the start of the entry and , , , and are at the preset segment points, which can be determined considering the ability to adjust the range and time as well as the continuity and smoothness of the profile. Furthermore, , and correspond to the double adjustment phases, which can be obtained by fitting the interpolation of the upper and lower boundaries of the corridor. , , and correspond to three transition phases, and their polynomial coefficients , , , () can be determined by the function values and first-order derivative continuous conditions at the left and right endpoints to ensure the continuity and smoothness of the designed profile.
3.1.2. Application of Terminal Constraints
The design of the terminal transition segment is taken as a case to provide the solution method for the polynomial coefficients , , , and satisfying the terminal altitude, velocity, and flight-path angle constraints.
First, the coefficients of transition segment , , , and can be determined by the continuity and differentiability conditions of the function at points and , where the constraints at point are given as follows:
where represents the derivative constraint of terminal D–E profile, which can be expressed as functions of , , and . The derivative of with respect to can be expressed as follows:
where each derivative is given by
Substituting Equation (20) into (19) yields the following:
Afterward, substituting the terminal constraint values of each state yields the following:
Therefore, the terminal altitude, velocity, and flight-path angle constraints can be imposed. Combined with the continuity and derivative conditions of the profile at point , the polynomial coefficients , , , and can be solved. Therefore, the polynomial coefficients of the other segments can be calculated similarly.
After determining the coefficients of the above transition segments, are only related to parameter and , both of which can be determined by the range and time constraints.
3.1.3. Analytical Predictor–Corrector of Range and Time
Existing research studies [13,14,15] are generally based on numerical integration methods for prediction. To further improve the efficiency of range and time prediction and thus enhance the rapidity of profile design, this section proposes an analytical prediction algorithm for range and time to go based on polynomial profile as follows.
The range s is defined as the projected length of the 3D trajectory on the Earth’s surface. Therefore, the derivatives of range and energy with respect to time are given as follows [16]:
where and is the dimensionless angular velocity of the Earth’s rotation.
Assuming that and , the derivatives of and with respect to are given by
where ; is related to the Earth’s rotation and can be simplified as a linear function of , namely
where
where and are corresponding to the initial and terminal states; is the initial longitude; and is the weighted average of the heading angles. Assuming that the flight trajectory is near the great circle, can be approximately represented by the current target azimuth , that is . Therefore, the coefficients and are all known parameters.
Assuming , the range and time corresponding to the D–E profile under the influence of the Earth’s rotation can be obtained by integrating Equation (24). The specific expression is as follows
where .
Thus, the right-hand side of Equation (27) is the integral function with respect to . The analytical prediction equation for the range and time to go can be obtained by integrating this equation. The derivation processes of the corresponding analytical prediction functions for the range and time are described below.
- (1)
- Range Prediction
Assume that within interval , and satisfy the quadratic function as follows:
By analytical derivation, the range-prediction function can be obtained as follows:
where .
Assume that within the interval , and satisfy the cubic function as follows:
The range-prediction function can be obtained by analytical derivation as follows:
The solution of the equation can be obtained by the cubic root equation without requiring the numerical methods.
- (2)
- Time Prediction
If and satisfy the quadratic function relationship in Equation (28), the analytical derivation would yield the time-prediction equation as follows:
where
Assuming and satisfy the cubic function relationship in Equation (30), the analytical derivation would yield the time-prediction equation as follows:
where , , , and are the intermediate variables expressed as follows:
The roots of the equation can be converted into a cubic equation for the solution. Therefore, based on the proposed analytical prediction method, the profile parameters and can be rapidly obtained using the double-parameter correction method [13]. Additionally, combined with the profile-tracking algorithm [8], the command can be generated to simultaneously satisfy the path, terminal altitude, velocity, flight-path angle, range, and time constraints.
3.2. Double-Stage Adaptive Lateral Planning
Lateral planning is aimed at controlling the lateral motion of the vehicle by designing the sign of , thereby satisfying the terminal position and heading angle constraints, which constitute the focus of this study. Reference [23] proposed a method based on the iterative design of bank-reversal points, which can satisfy the terminal heading angle constraints. However, the iterative process requires multiple numerical integrations for heading-angle prediction, and strong coupling exists between the reversal points, which decreases the convergence efficiency. Conversely, although the classic method based on the heading-angle-error corridor [6] avoids numerical integration, it cannot satisfy the terminal heading angle constraints. Thus, in this section, a double-stage adaptive planning method based on heading adjustment and maintenance is proposed for bank-reversal. This method comprises two main parts: (1) an iterative algorithm for bank reversal considering heading adjustment and (2) the design of a heading-angle-error corridor considering heading maintenance.
3.2.1. Lateral Reduced-Order Motion Model
Considering the effect of the Earth’s rotation, is assumed, and the following is defined:
Thereafter,
Subsequently, the following second-order lateral motion equation is derived from Equation (1) as follows:
where , , , and can be obtained by tracking , and can be obtained using and . Furthermore, = / is related to the Earth’s rotation.
Therefore, after tracking the longitudinal profile, the terminal lateral states , , and can be rapidly predicted by integrating the above equation.
3.2.2. Analysis of the Heading- and Position-Control Mechanisms
In lateral planning, the primary method of controlling the heading of an aircraft is through bank reversals. Accordingly, this paper defines the energy corresponding to the moment of bank reversal as the bank-reversal points . Designing the bank-reversal points to satisfy terminal heading angle constraints is therefore crucial in lateral planning.
To simultaneously satisfy the terminal heading and position constraints, the lateral-maneuvering capability must be reasonably allocated. Analyzing the expression for the derivative of the heading angle with respect to time reveals that exhibits a significantly positive correlation with and . Therefore, adjusting the magnitude and sign of under different energy can achieve the heading and position adjustments. Considering the lack of energy in the later stage of the entry phase and the necessity of focusing on the accuracy of the handover point position, the vehicle is allowed to conduct large-scale lateral maneuvers in the early entry stage to bring its line-of-sight angle close to the desired terminal heading , thus achieving a wide-range adjustment of heading and initial alignment. In the later stage, a lateral planning method based on the heading-error corridor is used to control the vehicle to fly toward the target area along the desired heading while ensuring high terminal-position accuracy.
Based on the above analysis, lateral planning is divided into two stages: large-scale maneuvering heading adjustment (LMHA) and heading maintenance with terminal-position correction (HMPC). LMHA controls the vehicle to face the target heading through a single bank reversal, completing a wide-range adjustment of the heading and initial alignment, which corresponds to adjusting the position of the vehicle relative to the target so that the line-of-sight angle gradually approaches the desired value for the terminal heading angle . HMPC, based on the heading-error corridor method, adjusts the heading angle toward the terminal line-of-sight angle and , achieving position-accuracy correction and angle fine-tuning.
Figure 4 shows the double-stage bank-reversal adaptive planning principle based on heading adjustment and maintenance. Here, represents the deviation between the heading angle and line-of-sight angle, is corresponding to the bank-reversal point in LMHA, and is at the entry point of HMPC, which can be adaptively determined based on the timing of the vehicle entering the heading-error corridor. The change in the line-of-sight angle = at the segment point relative to the entry point depends on . A larger corresponds to the prolonged lateral maneuvering of the vehicle in one direction, resulting in an increased lateral distance and a larger change in the line-of-sight angle. Therefore, is monotonically related to . As the change in the line-of-sight angle in the later stage is small, HMPC can converge the heading angle to the vicinity of the line-of-sight angle through heading fine-tuning, i.e., a small deviation between and . Therefore, can be iteratively solved to satisfy the terminal heading angle constraint. The specific lateral guidance algorithm is described below.
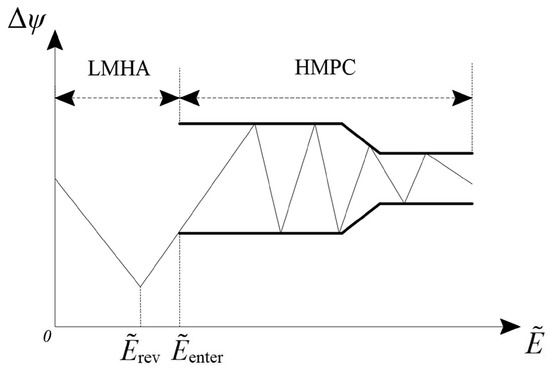
Figure 4.
Schematic of lateral planning.
3.2.3. Lateral Planning Considering Terminal Heading-Angle Constraints
- (1)
- Bank-Reversal Adaptive Planning Algorithm
From the above analysis, is a function of the bank-reversal point . Therefore, assuming = , the deviation of can be expressed as follows:
where is a nonlinear function of the independent variable .
To satisfy the terminal heading angle constraint, let
The equation above can be rapidly solved using Newton’s iteration method as follows.
Assuming the iteration step is j, the update algorithm for the reversal point will be given by
where is the partial derivative, which can be approximated by a finite difference as follows:
where is a small quantity, can be obtained by integrating Equation (38).
The iteration is repeatedly until the following termination condition is satisfied:
where is the convergence error tolerance. As aforementioned, is monotonically related to . Thus, the proposed iterative algorithm exhibits good convergence within the adjustable heading range and is not sensitive to the initial iterative value. To ensure the feasibility of the obtained bank-reversal point , it must satisfy , where is corresponding to the maximum bank reversal, which can be determined based on the lateral maneuverability before and after the reversal, which is generally expressed as .
- (2)
- Bank-Reversal Logic Design
Based on the above analysis and planning algorithm design, the double-stage bank-reversal logic is expressed as follows:
① At , the vehicle is in LMHA, and the sign of can be determined by the following equation:
where is the sign of the initial bank angle.
② At , the vehicle enters HMPC. Afterward, the sign of can be determined by the heading-angle-error corridor, and the corresponding bank-reversal logic is given as follows:
where is the sign of at the previous moment and is the boundary of the heading-angle-error corridor, which can be predesigned as a segmented linear function of the velocity, as reported in reference [28]. To ensure the accuracy of , must be less than .
Remark 1.
Dissimilar to reference [28], which divides the entire trajectory into lateral maneuvering, longitudinal adjustment, and end-guidance correction segments, although the lateral guidance method in this study comprises two stages, the segment point is determined adaptively by the moment of entering the heading-angle-error corridor. Based on the previous analysis, the bank-reversal point can be limited to a certain range , so that it can smoothly enter the heading-angle-error corridor after the first bank reversal, realizing the adaptive segmented adjustment of the bank reversal. Therefore, compared with the existing methods, the method reported in this paper will not limit the maneuverability and adjustment capability of entry flights.
3.2.4. Prediction of Terminal Heading-Angle Boundary
Assuming that and are monotonically related, double extreme ground tracks would exist (Figure 5) under a fixed D–E profile. At , corresponding to the situation shown in Figure 5a, increases with , reaching its maximum value at , where also approximately reaches its maximum value, . At , corresponding to the situation shown in Figure 5b, decreases with , reaching its minimum value at , where also approximately reaches its minimum value .
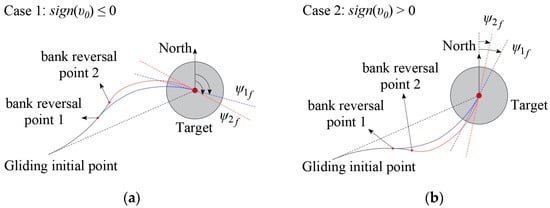
Figure 5.
Schematic diagram of the heading adjustment pattern: (a) case 1; (b) case 2.
Based on the above analysis, the adjustable range of under a fixed D–E profile can be determined; the specific algorithm is as follows:
Step 1: Assuming and , the lateral descent motion Equation (38) is integrated to obtain .
Step 2: Assuming and , the lateral descent motion Equation (38) is integrated to obtain .
Step 3: The adjustment range of can be determined as .
The above mechanism and algorithm are based on the condition where the initial heading angle faces the target point, and the other general conditions can be discussed similarly.
Since the attack angle is predetermined based on range and thermal requirements, the bank angle is the only control variable. To prevent the aircraft from excessively yawing over extended periods (i.e., continuously turning in one direction), bank reversals are necessary to alter the lateral force direction, thereby controlling the aircraft’s heading and position. Prior to a bank angle reversal, the aircraft continues turning in one direction, causing changes in the line-of-sight angle. Therefore, within a certain range, the later the first bank reversal occurs, the greater the change in line-of-sight angle compared to its initial value, which consequently results in a larger variation in heading angle. As shown in Figure 5a, the change in line-of-sight angle corresponding to bank reversal point 2 is greater than that of bank reversal point 1; hence, .
3.3. Three-Degree-of-Freedom Rapid Entry Trajectory Correction and Generation
The conventional 3DOF trajectory generation methods are mostly based on the EAGLE algorithm [7]. In the iterative process between longitudinal and lateral planning, the range is corrected by the deviation of the great circle arc length to improve the accuracy of the terminal position. However, regarding large lateral maneuvers, applying only the conventional EAGLE algorithm cannot guarantee the accuracy of range correction and may even fail to converge to the desired solution. Therefore, the following section proposes a suitable range correction method for large lateral maneuvers to enhance the applicability of the algorithm to multiple tasks.
As shown in Figure 6, let the azimuth angle between the entry point and target be , the great circle trajectory-arc length be , the arc length of the great circle between the predicted trajectory terminal and entry point be , and the distance between the predicted trajectory terminal and target be . When the deviation between and is large, , utilizing only the deviation of the great circle arc length will be insufficient to correct the target-trajectory-arc length. In this case, must be used as the correction quantity for the target-trajectory-arc length. However, as is often greater than 0, using it as a correction quantity will cause the continuous increase in the target-trajectory-arc length, making it impossible for the trajectory terminal to converge near the target point. Therefore, the sign of must be adaptively determined based on the relative position relationship between the predicted trajectory terminal and target point, and the specific method is expressed as follows:
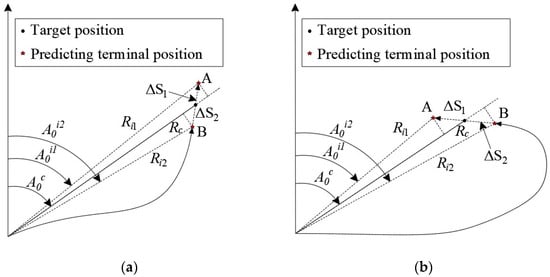
Figure 6.
Schematic of the lateral maneuvering trajectory: (a) case 1; (b) case 2.
In the i-th iteration, the projection of the great circle length on the surface is given by . Based on the spherical triangle equation, the following equation can be obtained:
where , represents the azimuth angle between the trajectory terminal point and the initial entry point.
Combined with Figure 6, it is observed that the sign of is related to the terminal point and target heading angle :
- (1)
- At , two situations corresponding to Figure 6a are observed. Among them, point A represents the situation where the trajectory overshoots. According to the relative position relationship between the predicted trajectory terminal and target, it is confirmed that and < 0; conversely, regarding Point B, , and > 0, which implies = .
- (2)
- At , two situations corresponding to Figure 6b are observed. Among them, point A represents the situation where the trajectory overshoots. According to the relative position relationship between the predicted trajectory terminal and target, it is confirmed that and < 0; conversely, regarding Point B, and > 0, indicating that = .
Based on the above analysis, the sign of can be represented by the following equation:
Additionally, to reduce the number of corrections to the target-trajectory-arc length and reduce the computation time, a maneuver coefficient is introduced to adjust the initial target-trajectory-arc length, following reference [15].
Overall, Figure 7 shows the flowchart of the 3DOF trajectory-planning algorithm, and its basic steps are as follows:
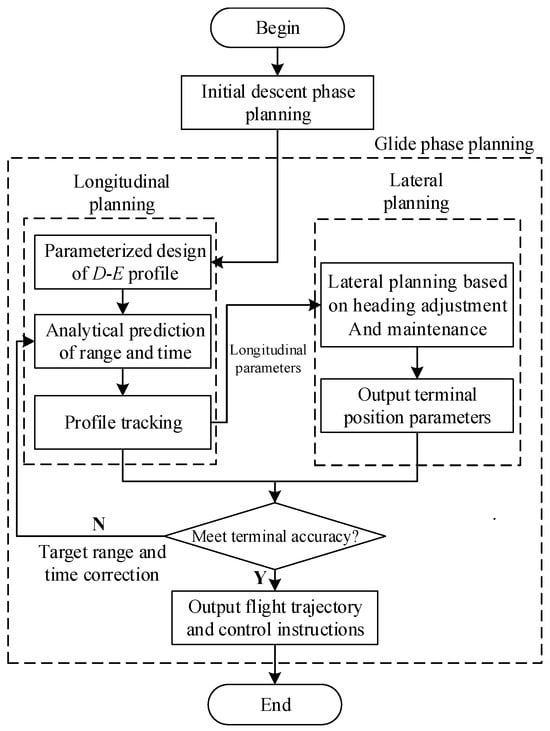
Figure 7.
Algorithm flow of trajectory planning.
Step 1: Determine based on the terminal heading angle constraint, , and complete the initial descent-phase trajectory planning.
Step 2: Let = 0, , , where and are the target-trajectory arc length and flight time for step i, respectively;
Step 3: Based on the requirements of range and time constraints, simultaneously correct parameters and based on the algorithm of the analytical design of the D–E profile, obtaining the reference profile .
Step 4: Track the reference profile to obtain the longitudinal trajectory parameters; the magnitude of bank angle ; and the total flight time .
Step 5: According to the terminal position and heading angle constraints, iteratively solve the bank-reversal point to obtain the lateral trajectory parameters; the sign of bank angle ; and the terminal position.
Step 6: Calculate deviations and based on the terminal position.
Step 7: Set as the error limit of terminal-trajectory-arc length and determine the validity of the current , . If yes, the algorithm ends, and the 3DOF trajectory is output; otherwise, proceed to step 8.
Step 8: Update the total trajectory-arc length of the target as = + , and the target flight time as = + , allowing , followed by the repetition of Steps 3–7.
Remark 2.
The numerical iterative process of lateral planning only requires the integration of lateral reduced-order equations, effectively avoiding the extensive numerical integration prediction calculations of conventional methods and further improving the computational efficiency of the algorithm.
Remark 3.
The proposed 3DOF trajectory generation method directly corrects the target-trajectory-arc length and time with the terminal parameter deviation obtained through lateral planning, thereby avoiding the outer-loop-integration correction process of the conventional EAGLE method and further improving the computational efficiency of the planning algorithm.
4. Simulation Analysis
4.1. Simulation Conditions
The CAV-H model [30] is adopted for the simulations. The initial- and terminal-state constraints are set as follows: = 80 km, = 6500 m/s, = 0°, = 25 km, = 2000 m/s, , = 0 km. The path constraints are set as follows: , , . The control constraints are set as follows: = 80°, = 5°, = 5°. The preset profile is shown in Equation (11) with the related parameters set as follows: , , = 5000 m/s, and = 4000 m/s. The parameters of the heading-error corridor are set as follows: = 2600 m/s, = 2000 m/s, = 15°, = 0.8°. The preset parameters for the D–E profile are set as follows: = 2 m/s2, , , , and . All simulations are performed on a desktop computer equipped with an Intel Core i7-8700 3.20 GHz and using the Visual Studio 2019 platform.
4.2. Rapid Prediction of Heading Adjustability
In this section, the terminal heading angle adjustable capability boundary is simulated based on the proposed lateral planning algorithm to verify the advantages of the proposed algorithm in rapid quantification. The simulation conditions are set as follows: , , = 100°, , and with other simulation conditions consistent with the discussion in Section 4.1. Figure 8 shows the simulation results. The blue solid and red dashed lines represent the parameter curves corresponding to the trajectories with the maximum and minimum heading angles, respectively.
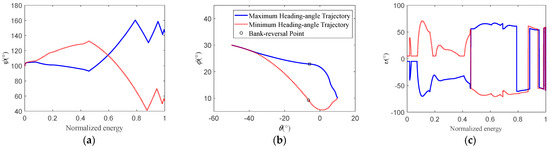
Figure 8.
Predictive diagram of terminal heading angle boundary: (a) the curve of heading angle; (b) the curve of ground trajectory; (c) the curve of bank angle.
Based on the statistics, the average prediction time is 595 ms, whereas the existing trajectory optimization methods typically operated at the second level, indicating that the proposed method exhibits a higher computational efficiency advantage. As shown in Figure 8a, the adjustable boundary values of terminal heading angle are and , with an adjustable range of , indicating that the proposed lateral planning algorithm can fully facilitate the heading-adjustment capability of the vehicle to achieve a wide range of heading adjustments. As shown in Figure 8b,c, the initial sign of the inclination corresponding to is ; thus, gradually decreased before the lateral reversal, causing the vehicle to move northeast of the target, thereby increasing the line-of-sight angle. After the reversal point, the heading angle turned toward the direction of the target, and in the final stage, it entered the heading-angle-error corridor until it reached the target, corresponding to a phenomenon similar to . As shown in Figure 8b, both trajectories corresponding to and must exhibit large-scale lateral maneuvers to achieve a wider range of heading adjustments.
4.3. Simulation of the Multitasking Applicability
The multitasking simulation conditions are presented in Table 2, with the target longitude and latitude set to and , respectively, while other simulation conditions remained consistent with the discussion in Section 4.1. Table 3 and Figure 9 present the simulation results.

Table 2.
Multitask simulation condition settings.

Table 3.
Terminal parameters deviation corresponding to different task conditions.
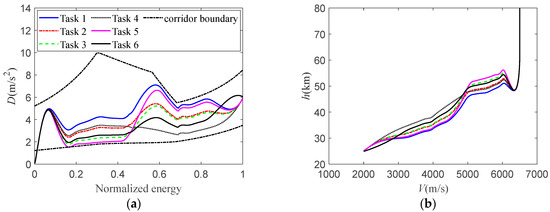
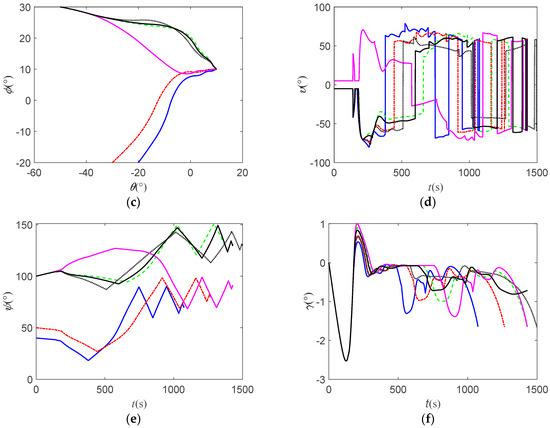
Figure 9.
Simulation result curves under different constraints: (a) drag acceleration profile; (b) the curve of altitude–velocity; (c) the curve of ground trajectory; (d) the curve of bank angle; (e) the curve of heading angle; (f) the curve of flight-path angle.
Table 3 presents the terminal-parameter deviations and computational times from Tasks 1 to 6. The terminal altitude, velocity, longitude, latitude, flight-path angle, heading angle, and flight time deviations are <150 m, <0.5 m/s, <0.012°, <0.006°, <0.25°, <1.0°, and <1.0 s, respectively, and the computational time for generating a single trajectory is within 1.6 s.
Figure 9 shows the simulation result curves corresponding to Tasks 1 to 6. Figure 9a,b show that the D–E profile is smooth, continuous, and satisfied the path constraints. Among them, Tasks 1 and 2 verified the applicability of the proposed algorithm to different range constraints. With the increase in target range, the overall D–E profile decreased, and the flight altitude increased to enhance the range capability of the vehicle, thereby achieving the task requirements. Tasks 3 and 4 further verified the control ability of the algorithm regarding the flight time under the same range conditions. Compared with Task 4, in segment k1 is smaller in Task 3 but larger in segment k2. This is because of the inverse correlation of the flight time with and velocity. Moreover, the parameter corresponds to a smaller flight velocity in the k2 adjustment segment, indicating that the time-adjustment ability in this segment is stronger. Therefore, reducing in this segment can extend the flight time.
Figure 9c–e show that the vehicle performed large-scale lateral maneuvers in the early stage before first bank reversal to transition the heading angle toward meeting the terminal constraint. In the later stage, multiple bank reveals are performed to converge the ground track and heading angle to the target. According to the statistics, the total number of bank reveals is five to seven times. Additionally, compared with Task 3, Figure 9b,f show that as the terminal flight-path angle constraint is set to −0.5° in Task 6, its altitude rapidly decreased in the later stage, after which it gradually became flat, thereby increasing the normal overload by increasing the atmospheric density to increase the terminal flight-path angle.
4.4. Comparison Simulation of Lateral Planning Methods
To further demonstrate the accuracy and efficiency of the method, comparative simulations of the methods reported in this paper and the existing literature are performed. Method 1 represents this paper, whereas Methods 2 and 3 adopt longitudinal planning methods consistent with Method 1. However, the difference lay in the lateral planning algorithms: Method 2 is based on double-bank-reversal iteration from reference [23], whereas Method 3 is based on the heading-error corridor from reference [6]. We set = 108° and = 1450 s, respectively. The other simulation conditions are consistent with Task 4 in Table 2. Table 4 and Figure 10 present the simulation results of the three methods.

Table 4.
Terminal parameters deviation corresponding to different methods.
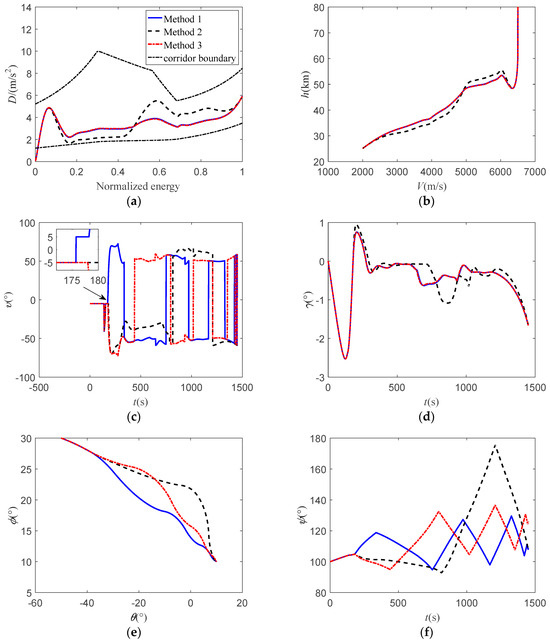
Figure 10.
Simulation result curves under different methods: (a) drag acceleration profile; (b) the curve of altitude–velocity; (c) the curve of bank angle; (d) the curve of flight-path angle; (e) the curve of ground trajectory; (f) the curve of heading angle.
According to Table 4, it can be found that the errors in the terminal altitude, velocity, flight-path angle, and flight time are relatively small. Compared with Method 3, Methods 1 and 2 exhibited smaller deviations. However, compared with Method 1, Method 2 exhibited a longer planning time, as it must simultaneously iterate the double bank-reversal-point parameters. Conversely, Method 1 only iterates one bank-reversal-point parameter, and the relationship between this parameter and is more monotonic. Therefore, Method 1 ensured better convergence and required shorter planning time.
Figure 10 shows the partial simulation result curves for the three methods. Figure 10a–d show that the longitudinal trajectory and control parameters corresponding to Methods 1 and 3 are the same. However, owing to the lateral method based on double bank-reversal points in Method 2, its trajectory arc is longer. Consequently, the corresponding drag acceleration profile is smaller in segment k1 and larger in segment k2, respectively, to ensure an increased trajectory-arc length under a consistent flight time. Figure 10a,b,d show that the flight path angle for Method 2 is larger in segment k1, causing the aircraft to ascend to a higher altitude to reduce drag. However, just before entering segment k2, the flight path angle decreases rapidly, leading to a quick descent and an increase in drag. Figure 10b,c show that the altitude for Method 2 is higher in the initial phase, resulting in lower air density. Therefore, the bank angle magnitude is smaller to achieve balanced gliding flight. Additionally, Figure 10e,f as well as Table 4 show that the range of heading angle variation and trajectory curvature of Method 1 are relatively small, which is closer to the initial trajectory arc length. Therefore, the outer loop iteration correction times are fewer, and the calculation efficiency is higher.
4.5. Summary
Table 5 shows the proposed method in this paper can rapidly generate a trajectory that satisfies time and terminal full-state constraints under various task conditions. Compared to other methods, the proposed method effectively combined the advantages of an iterative design method based on bank-reversal point with the heading-angle-error corridor method, balancing terminal accuracy and computational efficiency.

Table 5.
Summary table of the results from different tasks and methods.
5. Conclusions
To satisfy the entry problem under the time and terminal full-state constraints, a rapid trajectory-planning method based on the D–E profile and adaptive lateral planning algorithm based on the double-stage adjustment of heading-adjustment and -maintenance is proposed. The theoretical analysis and simulation results demonstrate the following:
- (1)
- Owing to the analytical predictor–corrector design of the profile, the phased adaptive planning of bank reversal, and trajectory outer-loop iterative correction, the proposed method achieved higher accuracy regarding the time and terminal full-state constraints as well as higher computational efficiency. It could adaptively divide the flight stages according to the task conditions, demonstrating better applicability in multitasking.
- (2)
- Compared with the existing lateral methods, the proposed lateral method achieved higher computational efficiency while maintaining comparable accuracy regarding the terminal position and heading angle; it could also achieve the rapid quantification of the adjustable range of .
- (3)
- The proposed method can achieve the rapid generation of gliding trajectories with spatiotemporal full-state constraints under a certain precision, making it suitable for aircraft formation networking and mid-course coordination tasks. If further enhanced with model predictive static planning and convex optimization techniques, the terminal full-state accuracy and optimality of the trajectories can be improved. Additionally, in near-space defense operations, this method can be used to provide benchmark trajectories with complex terminal constraints for cooperative guidance of multiple interceptors, ensuring effective mid-course and terminal phase coordination. This will also be the focus of future research.
Author Contributions
Conceptualization, W.X. and P.W.; methodology, W.X. and X.Y.; software, W.X. and P.W.; validation, W.X., P.W. and X.Y.; formal analysis, W.X. and X.Y.; investigation, B.H.; resources, B.H. and X.L.; data curation, B.H. and X.L.; writing—original draft preparation, W.X. and P.W.; writing—review and editing, X.Y. and X.L.; visualization, W.X. and P.W.; supervision, W.X. and P.W.; Project Administration, X.Y.; Funding Acquisition, X.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 11602296 and the Open Fund of Intelligent Control Laboratory, grant number ICL-2023-0402.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Li, Z.; Hu, C.; Ding, C.; Liu, G.; He, B. Stochastic gradient particle swarm optimization based entry trajectory rapid planning for hypersonic glide vehicles. Aerosp. Sci. Technol. 2018, 76, 176–186. [Google Scholar] [CrossRef]
- Song, J.; Xu, X.; Tong, X.; Zhao, K. A Time Cooperation Guidance for Multi-Hypersonic Vehicles Based on LSTM Network and Improved Artificial Potential Field Method. Aerospace 2022, 9, 562. [Google Scholar] [CrossRef]
- Dong, X.; Ren, Z. Finite-Time Distributed Leaderless Cooperative Guidance Law for Maneuvering Targets under Directed Topology without Numerical Singularities. Aerospace 2022, 9, 157. [Google Scholar] [CrossRef]
- Kim, T.H.; Lee, C.H.; Jeon, I.S.; Tahk, M.J. Augmented polynomial guidance with impact time and angle constraints. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 2806–2817. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, W.; Yu, W. Impact-Angle and Terminal-Maneuvering-Acceleration Constrained Guidance against Maneuvering Target. Aerospace 2022, 9, 22. [Google Scholar] [CrossRef]
- Harpold, J.C.; Graves, C.A. Shuttle entry guidance. J. Astronaut. Sci. 1979, 27, 239–268. [Google Scholar]
- Saraf, A.; Leavitt, J.A.; Chen, D.T.; Mease, K.D. Design and evaluation of an acceleration guidance algorithm for entry. J. Spacecr. Roc. 2004, 41, 986–996. [Google Scholar] [CrossRef]
- Xie, Y.; Liu, L.; Tang, G.; Zheng, W. Highly constrained entry trajectory generation. Acta Astronaut. 2013, 88, 44–60. [Google Scholar] [CrossRef]
- Lu, P. Entry guidance: A unified method. J. Guid. Control Dyn. 2014, 37, 713–728. [Google Scholar] [CrossRef]
- Lu, P. Predictor-corrector entry guidance for low-lifting vehicles. J. Guid. Control Dyn. 2008, 31, 1067–1075. [Google Scholar] [CrossRef]
- Shen, Z.; Lu, P. Onboard generation of three-dimensional constrained entry trajectories. J. Guid. Control Dyn. 2003, 26, 111–121. [Google Scholar] [CrossRef]
- Lu, P. Asymptotic analysis of quasi-equilibrium glide in lifting entry flight. J. Guid. Control Dyn. 2006, 29, 662–670. [Google Scholar] [CrossRef]
- Wang, X.; Guo, J.; Tang, S.; Qi, S. Time-cooperative entry guidance based on analytical profile. Acta Aeronaut. Astronaut. Sin. 2018, 40, 322565. [Google Scholar]
- Wang, H.; Guo, J.; Wang, X.; Li, X.; Tang, S. Time-coordination entry guidance using a range-determined strategy. Aeroap. Sci. Technol. 2022, 129, 107842. [Google Scholar] [CrossRef]
- Qiao, H.; Li, S.; Li, X. Static cooperative entry guidance method for multi-hypersonic vehicles. J. Astronaut. 2020, 41, 541–552. [Google Scholar]
- Wang, P.; Yan, X.; Nan, W.; Li, X. A Rapid and Near Analytic Planning Method for Entry Trajectory under Time Constraints. Available online: http://kns.cnki.net/kcms/detail/11.2176.TJ.20230918.1049.004.html (accessed on 14 April 2023).
- Liang, Z.; Yu, J.; Zhang, R.; Li, Q. Trajectory planning for cooperative flight of two hypersonic entry vehicles. In Proceedings of the 21st AIAA International Space Planes and Hypersonic Systems and Technologies Conferences, Xiamen, China, 6–9 March 2017. [Google Scholar]
- Li, Z.; He, B.; Wang, M.; Lin, H.; An, X. Time-coordination entry guidance for multi-hypersonic vehicles. Aerosp. Sci. Technol. 2019, 89, 123–135. [Google Scholar] [CrossRef]
- Yu, W.; Chen, W.; Jiang, Z.; Zhang, W.; Zhao, P. Analytical entry guidance for coordinated flight with multiple no-fly-zone constraints. Aerosp. Sci. Technol. 2019, 84, 273–290. [Google Scholar] [CrossRef]
- Liang, Z.; Lv, C.; Zhu, S. Lateral Entry Guidance with Terminal Time Constraint. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 2544–2553. [Google Scholar] [CrossRef]
- Fang, K.; Zhang, Q.; Ni, K.; Cheng, L.; Huang, Y. Time-coordinated entry guidance law for hypersonic vehicle. Acta Aeronaut. Astronaut. Sin. 2018, 39, 197–212. [Google Scholar]
- Zhang, W.; Yu, W.; Li, J.; Cheng, W. Cooperative entry guidance for intelligent lateral maneuver of hypersonic vehicle based on downrange analytical solution. Acta Armamentarii 2021, 42, 1400–1411. [Google Scholar]
- Liang, Z.; Li, Q.; Ren, Z. Waypoint constrained guidance for entry vehicles. Aerosp. Sci. Technol. 2016, 52, 52–61. [Google Scholar] [CrossRef]
- Liang, Z.; Long, J.; Zhu, S.; Xu, R. Entry guidance with terminal approach angle constraint. Aerosp. Sci. Technol. 2020, 102, 105876. [Google Scholar] [CrossRef]
- Wang, X.; Guo, J.; Tang, S.; Qi, S.; Wang, Z. Entry trajectory planning with terminal full states constraints and multiple geographic constraints. Aerosp. Sci. Technol. 2019, 84, 620–631. [Google Scholar] [CrossRef]
- Liu, Z.; Zheng, W.; Wang, Y.; Wen, G.; Zhou, X.; Li, Z. A cooperative guidance method for multi-hypersonic vehicles based on convex optimization. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6 November 2020. [Google Scholar]
- Yu, W.; Yao, Y.; Chen, W. Analytical cooperative entry guidance for rendezvous and formation flight. Acta Astronaut. 2020, 171, 118–138. [Google Scholar] [CrossRef]
- Yu, J.; Dong, X.; Li, Q.; Ren, Z.; Lv, J. Cooperative guidance strategy for multiple hypersonic entry vehicles system. Chin. J. Aeronaut. 2020, 33, 990–1005. [Google Scholar] [CrossRef]
- Guo, J.; Wu, X.; Tang, S. Autonomous gliding entry guidance with geographic constraints. Chin. J. Aeronaut. 2015, 28, 1343–1354. [Google Scholar] [CrossRef]
- Phillips, T.H. A Common Aero Vehicle (CAV) Model, Description, and Employment Guide; Schafer Corporation for AFRL and AFSPC; Schafer Corporation: Arlington, VA, USA, 2003; pp. 1–12. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).