A Parametrical Study on Hypervelocity Impact of Orbital Debris

Abstract

A numerical method has been presented to simulate hypervelocity impacts on metal targets. The target is a rectangular prism and is positioned at various inclined angles relative to the impact direction, while four different projectiles such as square prism, triangular prism, truncated cone, and ogival shape are chosen. This numerical model employs an open-source code, MPM3D-F90, which is based on the Material Point Method. In order to enhance flexibility of the code for defining projectiles and target bodies in the material domain, a preprocessor is developed to create a variety of geometrical shapes for a given volume. In addition to supplementing and defining various geometrical bodies, this tool also simplifies the preprocessing process to create the user’s specific preferences for the problem. To demonstrate the utility of the preprocessor tool and investigate the influence of geometry on hypervelocity impacts, simulations are conducted using various projectile and target configurations. The analysis results reveal that the structure of the debris cloud formations, scattering behavior of the ejected particle from both front and rear faces, and penetration depth measures are significantly influenced by the projectile shape and impact angles.

1. Introduction

The increase in space activities has resulted in a buildup of orbital debris, which poses a significant threat to spacecraft and satellites in Earth’s orbit. This debris includes man-made components like spent satellites, discarded rocket stages, fragments originating from collisions, and paint chips, capable of causing hypervelocity impacts with speeds of up to 15 km/s [1,2,3,4]. The outcomes of such impacts range from material ablation to the release of spacecraft material as debris clouds. A great deal of effort has been devoted to the hypervelocity impact simulations to comprehend how materials and structures behave under such extreme circumstances [5,6,7,8,9,10,11,12,13].

Hypervelocity impacts from micrometeoroids and orbital debris pose a significant threat, as they can damage spacecraft and satellite components [14]. Evaluating the survivability of Earth satellites against these impacts is crucial. Even millimeter-sized objects moving at orbital velocities can have catastrophic consequences for space structures [15]. Recent incidents, like a small piece of debris puncturing a robotic arm on the International Space Station in May 2021, highlight this vulnerability [accessed on 15 May 2024, https://www.cbsnews.com/news/space-junk-damage-international-space-station/]. As Figure 1 illustrates, these impacts can leave lasting marks on various space structures, from windows to solar cells [16].

Understanding the intricate dynamics of hypervelocity impact phenomena is of great importance to mitigating the risk posed by orbital debris and to developing spacecraft protection strategies, ensuring the structural integrity of space structures against potential damage. In this context, hypervelocity impact experiments play a pivotal role. However, conducting experimental studies on hypervelocity impacts presents several challenges. These include difficulties in accurately replicating real-world conditions [17], logistical complexities and high costs [18], and limited capability to capture detailed data during impact events [19].

Due to these challenges, while experimental research has been the primary focus in the past, the complexity of impact dynamics and the growing number of potential shielding designs have underscored the need for improved computer-aided design tools. These tools are essential for efficiently evaluating a wide range of candidate shielding concepts, characterizing three-dimensional performance, and addressing the challenges posed by impact velocity, obliquity, and material failure effects. Additionally, the shift towards faster and cost-effective spacecraft designs emphasizes the importance of simulation-based approaches over traditional experimental methods, especially given the diverse impact velocities and kinetic energies encountered in hypervelocity scenarios [20].

As a result, several numerical methods such as Smoothed Particle Hydrodynamics (SPH) and Discrete Particle Method (DPM) [21,22,23,24] are developed and employed in the study of hypervelocity impacts, aiding in understanding hypervelocity impact phenomena and optimizing protective measures. One prominent numerical method in hypervelocity impact research is the Material Point Method (MPM). This method emerges as a powerful computational tool that combines the advantages of both Lagrangian and Eulerian methods, making it well-suited for modeling large deformation and fragmentation phenomena during hypervelocity impacts. MPM was introduced by Sulsky et al. [25] as an extension of particle-in-cell methods, initially employed for modeling highly distorted fluid flow. MPM primarily discretizes media into Lagrangian material points which move with the material, carrying essential information such as velocities, strain, and stresses [26,27]. This feature makes MPM particularly suitable for modeling highly distorted fluid flow and complex material behaviors. Alongside other numerical methods, MPM is proven to be a versatile and effective tool in hypervelocity impact research, enabling researchers to simulate impact phenomena. Additionally, for exploring a detailed comparison between MPM and SPH, one could refer to [28].

Within this context, this study presents a computational framework, utilizing the Material Point Method (MPM) to assess the risk of orbital debris impacting space structures. By incorporating various parameters, including projectile size and shape, the framework aims to enhance protection strategies against hypervelocity impacts.

Previous research has demonstrated the significant influence of projectile size and shape on shield response. Schonberg and Williamsen [29] investigated hypervelocity impacts of various non-spherical projectiles, demonstrating that projectile shape significantly affects penetration ability, with longer shapes being more effective. Morrison [30] studied the effects of cylindrical projectiles on double-sheet structures, concluding that cylinders impacting axially are more effective penetrators than spheres of equal mass. Carrasquilla and Miller [31] presented numerical simulations that predicted shield performance for spherical and prolate ellipsoid impactors, but overestimated performance for oblate ellipsoid impactors. Buyuk et al. [32] conducted parametric studies on ellipsoidal projectiles with equivalent radar cross-sections and mass, finding that spherical projectiles are not always the most dangerous threat. Williamsen et al. [33] also highlighted the importance of incorporating the effects of mass and shape in mission risk assessments before the first flight of any spacecraft. For an investigation of NASA’s research on the effects of orbital debris’ shape for mitigating risks, one could refer to [20].

To investigate the effects of various projectile sizes and shapes, we conducted numerical simulations using an open-source MPM-based code [34,35,36]. An in-house preprocessor developed in MATLAB R2017b was used to prepare the configuration setup file. This preprocessor simplifies the configuration setup process by enabling the generation of input files for diverse scenarios involving different projectile and target geometry configurations. To explore the geometric influences on hypervelocity impact, four distinct projectile shapes (square prism, triangular prism, cone, and ogival) were simulated, along with three different inclined positions (θ = 0°, 30°, and 60°) of the rectangular prism target. Employing the Johnson-Cook plasticity model and Mie-Grüneisen equation of state (EOS) [37,38], several simulations were performed, and the influence of projectile shape and oblique impact angles on debris formation and target damage were investigated. The results reveal significant variations in debris cloud morphology on both the front and rear faces of the target, influenced by the shape and impact angle of the projectiles.

2. The Numerical Method

The numerical model employed in this study adopts the Material Point Method (MPM), which was originally developed in Refs. [34,35,36]. In this method, a continuum body is discretized using Lagrangian material points, also referred to as particles, which track the material properties throughout the deformation process. Each material point in MPM is associated with properties such as position, mass, density, velocity, deformation gradient, stress tensor, temperature, and other internal variables required for the constitutive model, collectively providing a Lagrangian description of the continuum body. The MPM approach ensures mass conservation as each material point maintains a fixed mass throughout the simulation [34].

The discretization is made in the material domain $\mathit{\Omega }$ using a collection of material particles, moving through an Eulerian background grid. Each particle has a subdomain ${\mathit{\Omega }}_{\mathbf{P}}$ along with all its associated attributes such as mass, momentum, energy, strain, stress, and internal state variables essential for history-dependent constitutive modeling. A typical discretization for the MPM is sketched in Figure 2 [34].

The MPM utilizes the updated Lagrangian approach in which the stress and strain measures are defined based on the current configuration, specifically using the Cauchy stress and rate of deformation, while derivatives and integrals are calculated using the Eulerian coordinate $\mathit{x}$. According to this approach the weak form for the momentum equation and the traction boundary condition is given as [34].

$$\underset{\Omega }{{\displaystyle \int }}\mathit{\rho }{\ddot{\mathit{u}}}_{\mathit{i}}\mathit{\delta }d\mathit{V}+\underset{\Omega }{{\displaystyle \int }}\mathit{\rho }{\mathit{\sigma }}_{\mathit{i}\mathit{j}}^{\mathit{s}}\mathit{\delta }{\mathit{u}}_{\mathit{i},\mathit{j}}d\mathit{V}-\underset{\Omega }{{\displaystyle \int }}\mathit{\rho }{\mathit{b}}_{\mathit{i}}\mathit{\delta }{\mathit{u}}_{\mathit{i}}d\mathit{V}-\underset{{\Gamma }_{\mathit{t}}}{{\displaystyle \int }}\mathit{\rho }{\overline{\mathit{t}}}_{\mathit{i}}^{\mathit{s}}\mathit{\delta }{\mathit{u}}_{\mathit{i}}d\mathit{A}=0$$

(1)

Here, $u_{\mathit{i}}$ is the displacement field, $\Omega$ is the deformed configuration, ${\Gamma }_{\mathit{t}}$ is the traction boundary, $\mathit{\sigma }$ is the Cauchy stress tensor, ρ is the current density given by Equation (2) and $\mathit{b}$ is the body force per unit mass.

$$\mathit{\rho }\left(\mathit{x}\right)={\displaystyle \sum }_{\mathit{p}=1}^{\mathit{n}}{\mathit{m}}_{\mathit{p}}\mathit{\delta }\left(\mathit{x}-{\mathit{x}}_{\mathit{p}}\right)$$

(2)

Here, the particle is denoted by subscript $\mathit{p}$, the mass of the particle is ${\mathit{m}}_{\mathit{p}}$, while the spatial coordinate of the particle is ${\mathit{x}}_{\mathit{p}}$. $\mathit{n}$ is the total number of the particles, and $\mathit{\delta }\left(\mathit{x}\right)$ is the Dirac delta function. When the approximated material density given in Equation (2) is substituted in the weak form of momentum equation, we reach [34]

$${\displaystyle \sum }_{\mathit{p}=1}^{\mathit{n}}{\mathit{m}}_{\mathit{p}}{\ddot{\mathit{u}}}_{\mathit{i}\mathit{p}}\mathit{\delta }{\mathit{u}}_{\mathit{i}\mathit{p}}+{\displaystyle \sum }_{\mathit{p}=1}^{\mathit{n}}{\mathit{m}}_{\mathit{p}}{\mathit{\sigma }}_{\mathit{i}\mathit{j}\mathit{p}}^{\mathit{s}}\mathit{\delta }{\mathit{u}}_{\mathit{i}\mathit{p},\mathit{j}}-{\displaystyle \sum }_{\mathit{p}=1}^{\mathit{n}}{\mathit{m}}_{\mathit{p}}{\mathit{b}}_{\mathit{i}\mathit{p}}\mathit{\delta }{\mathit{u}}_{\mathit{i}\mathit{p}}-{\displaystyle \sum }_{\mathit{p}=1}^{\mathit{n}}{\mathit{m}}_{\mathit{p}}{\overline{\mathit{t}}}_{\mathit{i}\mathit{p}}^{\mathit{s}}{\mathit{h}}^{-1}\mathit{\delta }{\mathit{u}}_{\mathit{i}\mathit{p}}=0$$

(3)

where ${\mathit{u}}_{\mathit{i}\mathit{p}}={\mathit{u}}_{\mathit{i}}\left({\mathit{x}}_{\mathit{p}}\right)$, ${\mathit{\sigma }}_{\mathit{i}\mathit{j}\mathit{p}}^{\mathit{s}}={\mathit{\sigma }}_{\mathit{i}\mathit{j}}^{\mathit{s}}\left({\mathit{x}}_{\mathit{p}}\right)$, ${\mathit{u}}_{\mathit{i}\mathit{p},\mathit{j}}={\mathit{u}}_{\mathit{i},\mathit{j}}\left({\mathit{x}}_{\mathit{p}}\right)$, ${\mathit{b}}_{\mathit{i}\mathit{p}}={\mathit{b}}_{\mathit{i}}\left({\mathit{x}}_{\mathit{p}}\right)$, ${\overline{\mathit{t}}}_{\mathit{i}\mathit{p}}^{\mathit{s}}={\overline{\mathit{t}}}_{\mathit{i}}^{\mathit{s}}\left({\mathit{x}}_{\mathit{p}}\right)$ and $\mathit{h}$ is the thickness of the fictitious layer used for conversion of a surface integral to a volume integral, noting that the displacement of the particle $\mathit{p}$ is ${\mathit{u}}_{\mathit{i}\mathit{p}}$ and its derivative is ${\mathit{u}}_{\mathit{i}\mathit{p},\mathit{j}}$.

In MPM, the grid is used transiently for gradient and divergence calculations, without retaining permanent information. This flexibility allows for the grid to be fixed in space while particles transport material properties, minimizing errors. During the convective phase, the grid is reset to its original position, while particles maintain their current positions. Velocity reconstruction on the new grid can be achieved using consistent and lumped grid mass matrices [39].

In the original MPM formulation by Sulsky [25], the method functions as an updated Lagrangian scheme. The simulated body’s space during deformation is discretized by a background grid where the momentum balance equation is solved. The use of a grid in MPM offers several advantages. It eliminates the need for direct computation of particle-particle interactions, simplifies collision treatment through the background Eulerian grid, and enables efficient momentum equation solution due to fewer grid points compared to particles. Typically, a fixed regular Cartesian grid is employed throughout the simulation for computational efficiency [39].

In order to compute the hypervelocity response of the projectile-target system, the MPM uses a constitutive model selected for the particular simulation. In the simulations Johnson-Cook plasticity model with failure is used which is a suitable constitutive model for hypervelocity impact. This model is employed with Mie-Grüneisen’s equation of state (EOS) which is used to determine the pressure within a shock-compressed solid [37,38]. The parameters for the selected constitutive model and variables for the equation of state and the material properties are given in

Table 1. Properties of target and projectile [34].

		Aluminum	Lead
Mechanical properties	Density, ρ (kg/m3)	2700	11,350
	Elasticity modulus, E (GPa)	69	22.4
	Poisson ratio, ν	0.3	0.42
Johnson-Cook plasticity model	A (MPa)	262	125
	B (MPa)	52.1	12
	n	0.41	1.0
	C	0	0
	εfail	1.6	3.0
Mie-Grüneisen EOS	c0 (m/s)	2092	5350
	S1	1.45	1.34

.

3. Results and Discussion

We investigate the hypervelocity impact response of several projectile-target configurations at high speeds using various projectile shapes and oblique scenarios. By analyzing impact dynamics and the morphology of the debris cloud, we aim to provide valuable insights into the behavior of hypervelocity impacts and their relevance to the protection of space structures.

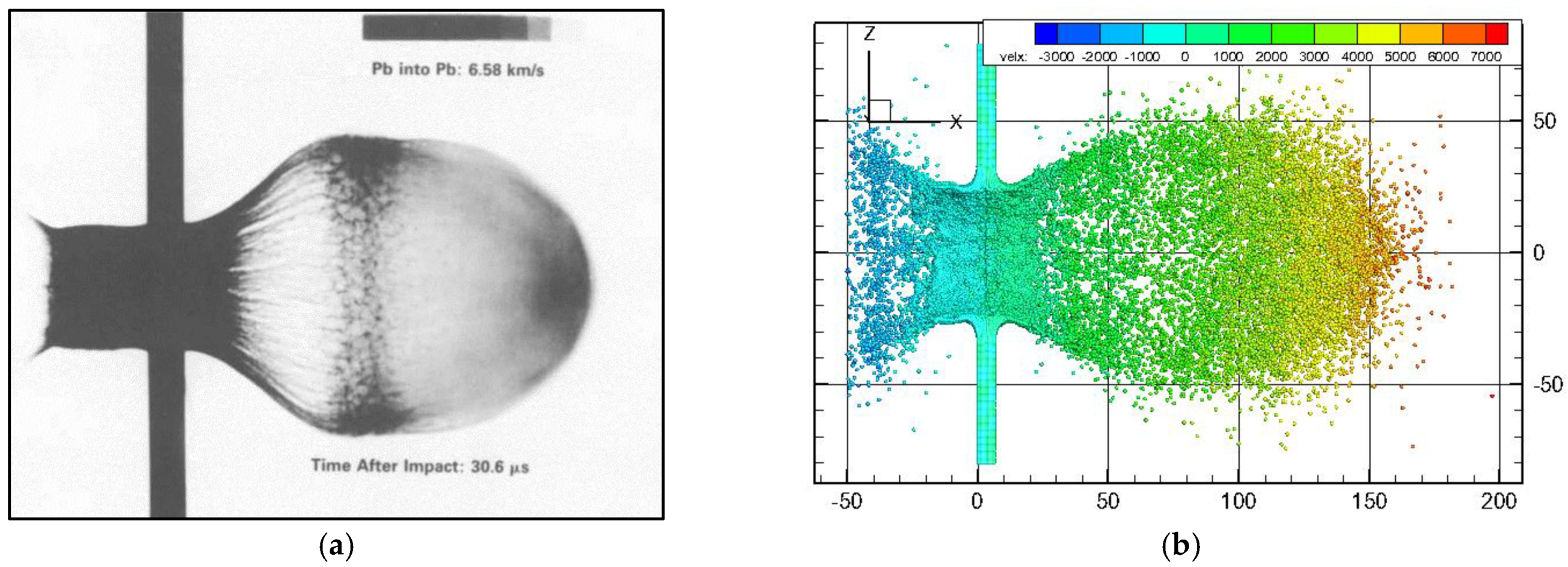
We first present a comparison between our results and those of an experiment conducted by Anderson et al. [37]. In this experiment, the impact of a lead spherical projectile into a lead target at an angle of 90° was captured by a high-speed camera, shown in Figure 3a. The diameter of the spherical projectile was approximately 2.4 times of the plate thickness, and its initial velocity was set to 6580 m/s. Using the same physical parameters and geometrical configuration, we carry out a hypervelocity impact simulation and display the deformation result in Figure 3b. It is important to note that for this validation study, as well as all simulations conducted throughout the study, the deformation measurements are reported in millimeters (mm).

Anderson et al. [37] reported that a spherical lead projectile impacting a lead target produced a diffused debris cloud. This cloud consisted of liquid-like streamers connecting the main cloud to the plate, with no distinct solid particles in the forward portion. When comparing the morphology of the debris cloud, our simulations show a general alignment with these experimental findings, albeit with some variations. Specifically, the experimental radiograph in Figure 3a indicates a depth of 200 mm and a width of 145 mm, whereas our simulations measured approximately 175 mm in depth and 125 mm in width. The observed discrepancies could be attributed to factors such as a slight mismatch in simulation time (0.0306 ms in the experiment versus 0.030 ms in our simulation) and the initial particle and grid spacing used in our model. In our simulations, the domain was discretized into 1,101,540 particles, with an initial particle spacing of 0.53 mm and a grid spacing of 1.0 mm. A referenced study [40] has demonstrated that reducing the particle size (to 0.21 mm) and increasing the number of particles (to 13,542,030) can significantly enhance the accuracy of debris cloud simulations. Despite these minor discrepancies, the overall agreement between our simulation results and the experimental data are considered to be satisfactory.

Prior to demonstrating the simulation results, an important aspect of this study worth mentioning is the development of an in-house preprocessor to generate input files for simulations of each projectile-target configuration. This preprocessor simplifies the process by allowing users to create the necessary input files required to execute the code and to outline the user’s specific preferences for the problem. It is developed using MATLAB and comprises three key elements: the solver setup, grid files for both projectile and target, and physical definitions including boundary conditions.

The current version of MPM3D-F90 [34,35,36] has built-in functions to define three bodies: block, sphere, and particles. To enhance the ability of the current code, bodies with a variety of shapes are included within this tool. These shapes include prisms (triangular, square, pentagonal, and hexagonal), spheres (solid and hollow), cones (truncated cone), and ogivals. Among these shapes, a square prism, a triangular prism, a truncated cone, and an ogival shape are chosen according to their relevance to simulate an orbital debris impact.

In addition to the inclusion of a variety of shapes, the relative location of the projectile and target can be adjusted within this tool, making the oblique impact preprocessing step quite easy. To manage computational costs effectively, symmetry boundary conditions can also be imposed using this tool. This enables users to conveniently set up the problem for either the entire domain or just the half of it. Upon selection, the projectile and target are divided into their respective halves along the pertinent symmetry plane.

By using this preprocessor, the generation of input files for various physical cases and projectile-target combinations becomes straightforward. In the forthcoming sections, including the previously presented validation study, all input files are generated for various combinations of projectile shapes and target configurations via this preprocessor.

3.1. The Influence of Projectile Shapes

The influence of shape on the impact of orbital debris and the ballistic performance of the shield system is a critical aspect of space structure design. The shape and orientation of debris significantly affect the ballistic performance of shielding systems. The variations in projectile geometry can influence the distribution of impact forces and the formation of shock waves within the target material, thereby affecting the overall damage profile. In order to explore these effects, we simulate the hypervelocity impacts using three different lead projectile shapes.

The selection of projectile shapes aims to showcase distinct impact behaviors. The square prism represents a blunt-nosed projectile, while the triangular prism and truncated cone exemplify the behavior of sharp-nosed projectiles. Notably, the triangular prism itself is formed by an obtuse-angled triangle, further diversifying the category of sharp-nosed projectiles.

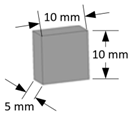
To ensure a fair comparison, we selected projectile geometries and materials similar to those used in experiments [41,42]. All projectiles had the same mass, approximately 5.675 g for lead (500 mm³ × 0.01135 g/mm³) and 1.35 g for aluminum (500 mm³ × 0.0027 g/mm³). By maintaining a constant volume of 500 mm³ for all projectiles, we ensured that they had the same mass and were subjected to identical impact conditions, allowing for a direct comparison of the effects of projectile shape.

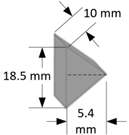
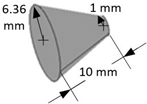
The geometrical properties of these projectiles are presented in detail in

Table 2. Projectile and target geometry specifications.

Projectile Geometry	Square Prism	Triangular Prism	Truncated Cone
	Volume = 500.0 mm3	Volume = 499.6 mm3	Volume = 500.7 mm3
# of material points	234,651	237,323	234,476

. The target material is aluminum and has dimensions of 200 mm × 100 mm with a thickness of 5 mm. The initial impact velocity is set to 4000 m/s. Material failure is considered to occur when the equivalent plastic strain reaches 1.6 mm/mm for the target and 3.0 mm/mm for the projectile, indicating an inability to sustain deviatoric stress. The total number of model particles for each projectile-target configuration is also provided in Table 2.

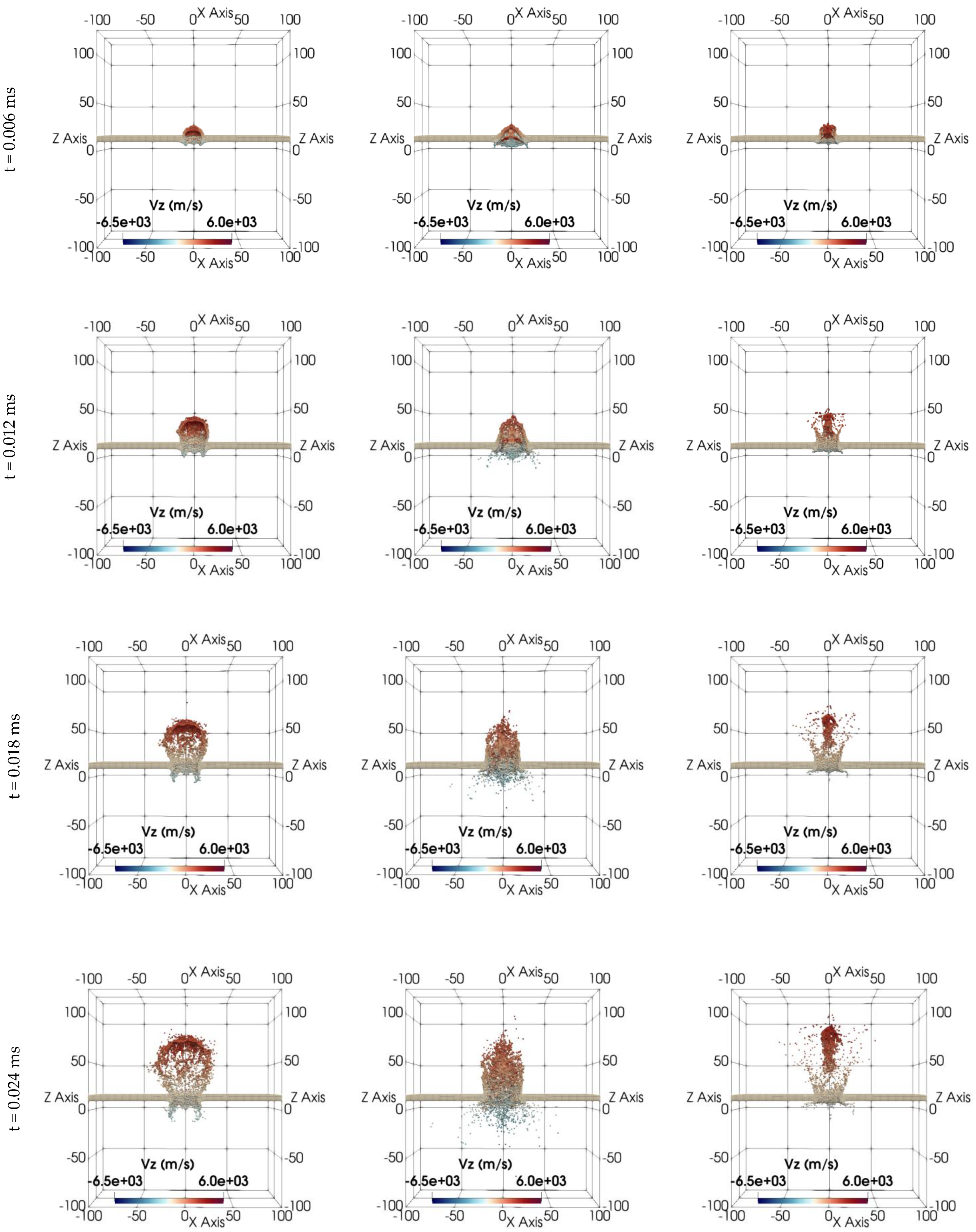
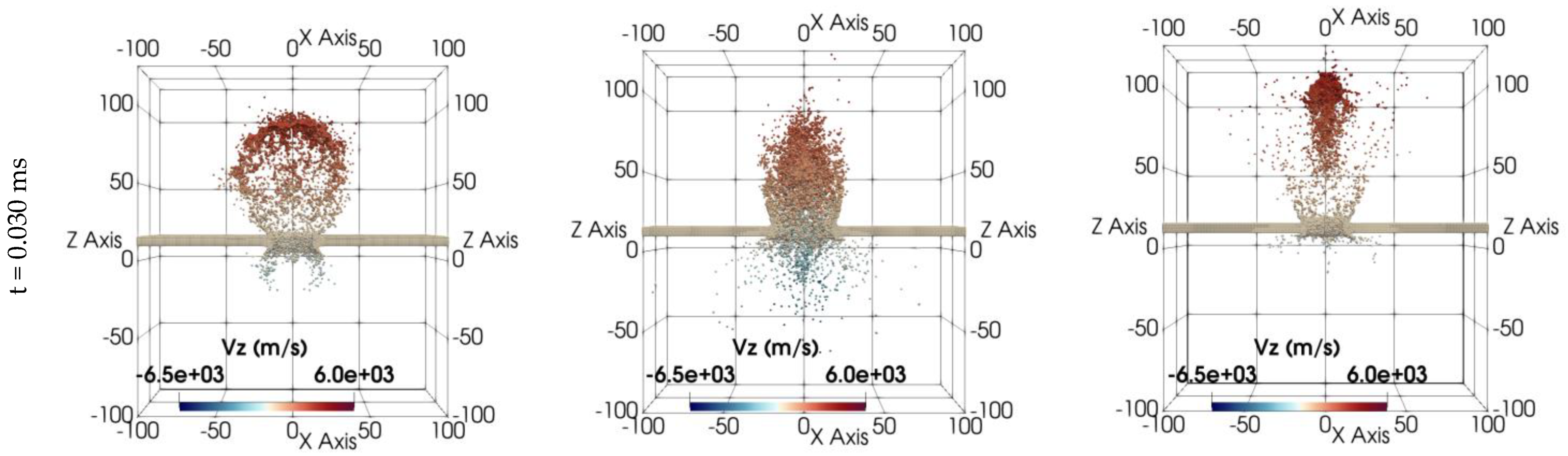
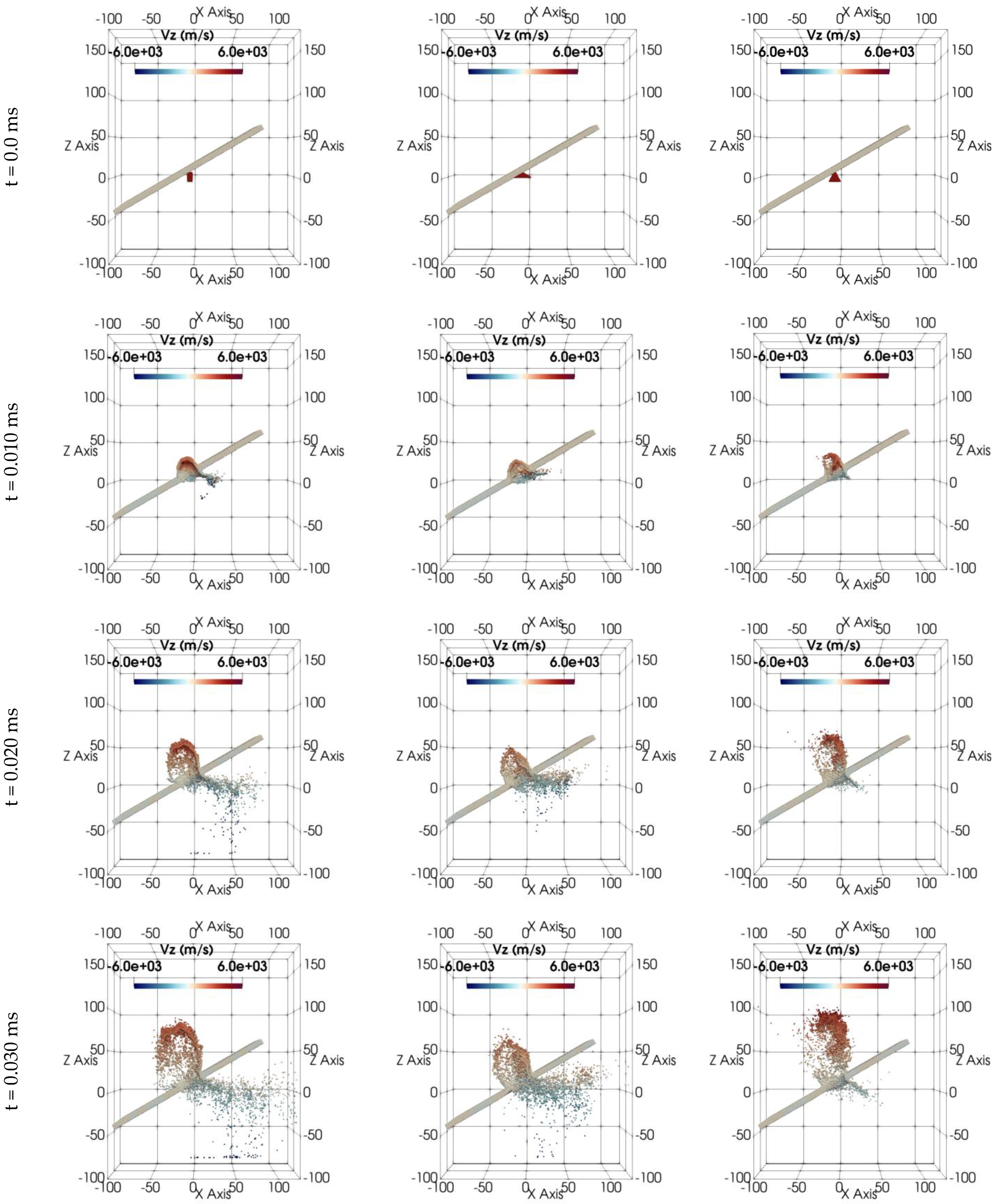
The deformation results are captured at distinct time intervals, t = 0.000, 0.006, 0.018, 0.024, and 0.030 ms, respectively, and are plotted in Figure 4. Each column within this matrix of figures represents sequential snapshots that plot the impact scenarios involving square prism-, triangular prism-, and truncated cone-shaped projectiles. Notably, the color gradient employed in these figures displays the velocity variations along the z direction. For clarity, the face initially struck by the projectile is referred to as the “rear face” or “back face.” The opposing face, across the target’s thickness, is called the “front face.”

Each projectile has approximately the same volume of 500 mm³ and is made of lead. The rectangular target is hit from the center at an impact angle of 90°. To quantify impact damage from these projectiles, we primarily analyzed the debris cloud, focusing on its formation and velocity distribution on both the front and rear faces of the target. Our simulations revealed significant variations in these metrics depending on the projectile geometry and impact angle. As evident from these figures, the projectile’s shape significantly influences the structure of the debris cloud, showing distinct variations from impact initiation to 0.030 ms post-impact. This influence becomes increasingly pronounced as the impact event progresses.

In the first column of the results, corresponding to the square prism impact, a typical debris cloud formation is observed, while the debris clouds resulting from impacts of triangular prism and truncated cone-shaped projectiles, shown in the second and third columns, exhibit distinct formations. The scattering behavior of debris on the front formation aligns with the shape of the projectiles. Although the overall structures of the debris cloud vary for different-shaped projectiles, a consistent external bubble is maintained for all projectile types during the early stages of impact (t < 0.012 ms). However, beyond t > 0.012 ms, the external bubble of the major debris structure becomes scattered, particularly for the sharp-nosed projectiles.

Notably, projectiles with sharp noses, such as those of the triangular prism and truncated cone, induce deeper penetration compared to blunt shapes. Following perforation, the impact of the triangular prism projectile results in particle movements that resemble a bubble with a sharp tip. In contrast, the truncated cone projectile generates a motion characterized by the formation of a debris cloud with a central rod-like structure. These front face debris structures are not evident in the initial stages of impact, and yet they become progressively more pronounced over time.

Upon investigating the rear formation of the debris clouds, Figure 4 reveals distinct rear debris cloud formations for each projectile shape, consistent with their behavior in the front formation. The square prism projectile exhibits minimal radial scattering, with its rear debris cloud evolving into a rounded shape similar to the front. In contrast, the triangular prism projectile exhibits significantly more radial scattering, ejecting the greatest amount of debris from the rear face than other projectiles. This trend is evident even in the early stages of the impact. Compared to triangular and square prism projectiles, the truncated cone projectile produces the least amount of ejected debris, demonstrating minimal scattering behavior.

Furthermore, the angle at which debris is ejected from the rear surface of the target becomes increasingly visible and distinct as the impact progresses for each projectile shape. Notably, for sharp-nosed projectiles, the ejection angles are sharper compared to those of blunt-shaped projectiles.

The simulation reveals that the truncated cone projectile imparts the highest velocities to particles. This is evident from the central concentration of red dots in the graph, indicating a focused ejection of debris with greater speeds. While the square prism also exhibits fast-moving particles, unlike the triangular prism, it experiences more significant scattering. This difference in scattering behavior likely explains why the square prism’s particles appear slower than those of the triangular prism.

Overall, investigating debris cloud formations from the perpendicular impacts by different projectiles reveals unique debris dispersion patterns for each projectile type. Sharp-nosed projectiles, like the triangular prism and truncated cone, penetrate deeper into the target material compared to the square prism. This deeper penetration results in the formation of larger craters and potentially more extensive damage. Additionally, sharp-nosed projectiles exhibit more directional scattering at the front face, focusing the ejected debris particles away from the impact zone. Conversely, the blunt square prism causes isotropic scattering, dispersing debris in all directions. Additionally, the rear face debris formation of the triangular prism also exhibits isotropic scattering.

3.2. Oblique Impact Simulations

The oblique impact involve debris striking a target surface at an angle and poses significant challenges for space structures and spacecraft that requires special attention. Understanding the effects of oblique impacts is crucial for designing effective shielding and protective measures in space environments [10,13]. We investigate the effects of oblique impact angles on the structural integrity and damage patterns of a target material subjected to high-speed projectile impacts.

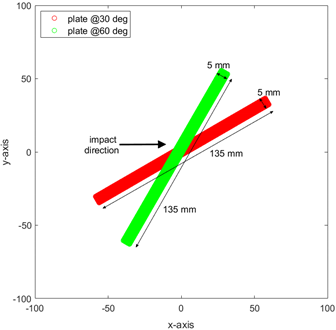
Two distinct oblique impact scenarios are explored: one with the target oriented at a 30° angle relative to the impact direction, and the other at a 60° angle. To comprehensively understand the impact behavior, two main sets of analyses are conducted. For both sets of analyses simulations are conducted using a projectile velocity of 4000 m/s, which represents typical hypervelocity conditions encountered in space structures.

The first set of analysis focuses on understanding how projectile shape affects target behavior in oblique impacts. To achieve this, simulations are conducted using three previously analyzed projectiles: square prism, triangular prism, and truncated cone. This allows us to compare the combined effect of impact obliquity and projectile shape on the target response. Following the first set, an additional simulation is conducted using a projectile with an ogival shape to explore its behavior under oblique impact conditions.

3.2.1. The Influence of Projectile Shapes in Oblique Impact

The first set demonstrates the oblique impact simulations for previously used projectiles, including square and triangular prisms, as well as a truncated cone. The in-house preprocessor previously mentioned simplifies this process by rotating the same target plate to the desired angles (30° and 60° in this set). Using this processor, six simulation cases are generated, encompassing the three projectile shapes and two target angle configurations. 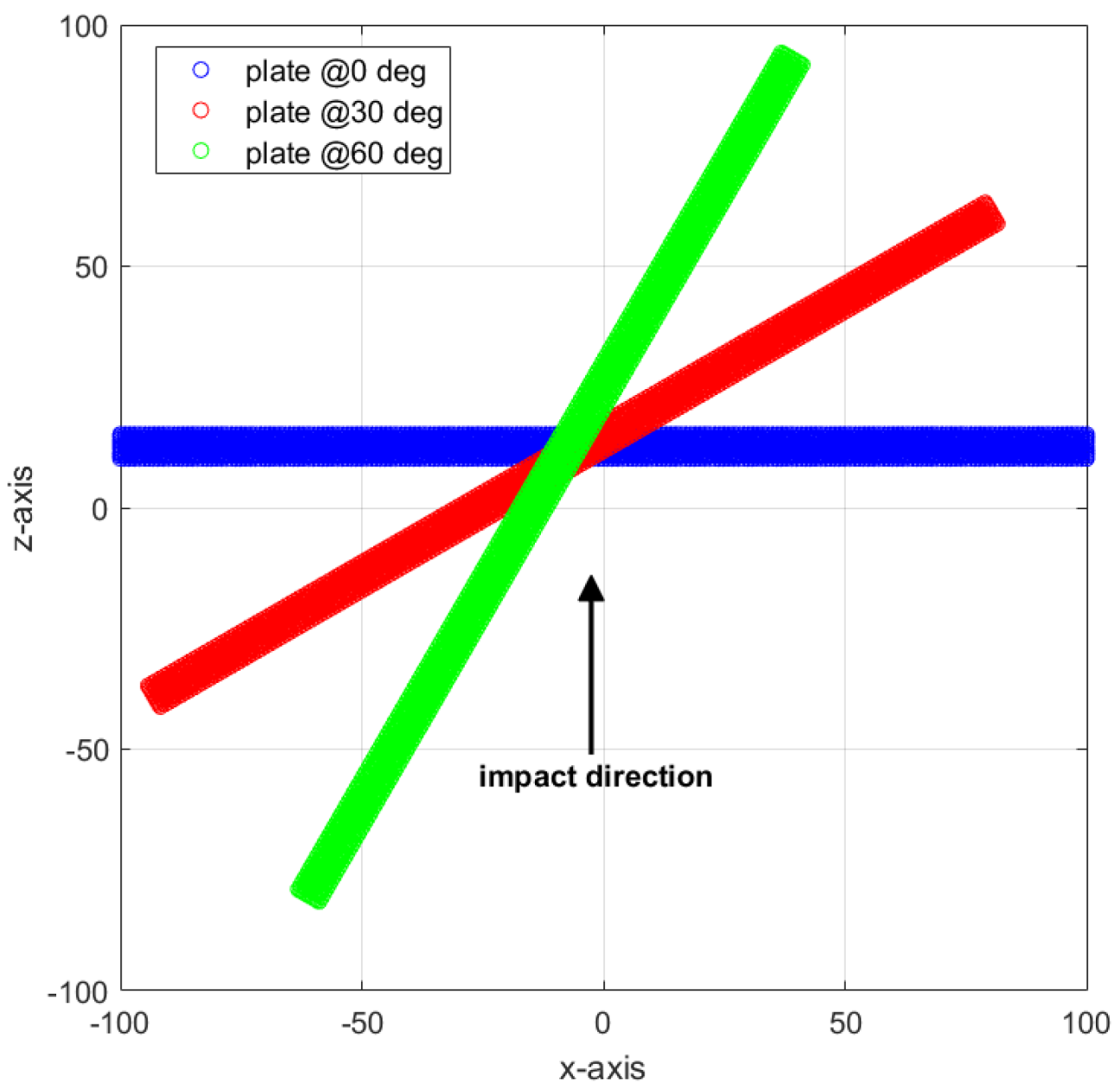The geometric details of the projectiles are provided in Table 2 and, along with this, Figure 5 presents the target geometries for this set of oblique impact scenarios.

Snapshots for the 30° and 60° impact angle scenarios are captured and displayed at t = 0, 10, and 30 μs, in Figure 6 and Figure 7, respectively. As presented in these figures, color gradient visualizes the velocity variations along the z-direction, with red representing higher positive velocities and blue representing higher negative velocities. To facilitate a direct comparison, an identical color map range is employed for both projectile simulations.

Initial observations from Figure 6 (30° impact) reveal that the debris cloud expands from both the front and back faces of the target as the simulation progresses (t = 10 μs and 30 μs). The impact creates shockwaves that travel through both the projectile and target, initiating the fragmentation of both materials. This fragmentation is significant for all projectile-target configurations, but with distinct behaviors.

For the truncated cone projectile, the target’s front face fragments in the early stages of impact. In contrast, targets impacted by the square and triangular prism projectiles show initial fragmentation only on their back faces. However, as the simulation progresses, the front face of the target fragments for all projectiles.

For the truncated projectile, as coherent with the perpendicular impact case, the front face scattering is very profound, while minimal particle ejection is observed from the back face of the plate. This trend is non-existent for square and triangular prisms, and their debris cloud on the front and back faces are more evenly distributed. Also, this behavior observed in the truncated cone projectile leads to a focused ejection of debris with greater speeds, displayed with dark red color.

Following the initial impact (t = 0), the analysis of the plot in Figure 6 (row 1, column 2) reveals a trend in particle velocities at the front face of the target: truncated cone > square prism > triangular prism. Interestingly, the triangular prism exhibits the slowest particles. This behavior directly relates to the projectile shape and the target configuration. The triangular prism case presents a noteworthy behavior. Due to its side base being parallel to the target’s rear face, as the projectile moves forward (z-direction), the target thickness acts as a barrier, hindering its penetration. In this specific target-projectile configuration, essentially, the triangular prism effectively functions as a blunt projectile during the initial stages of impact, despite its inherently sharp edges.

Similar to the 30° impact scenario (Figure 6), initial observations from Figure 6 (60° impact) reveal that fragmentation begins only on the back faces of the targets for all of the projectiles. The front faces of the targets impacted by the square prism and truncated cone projectiles remain unfragmented nearly until t = 20 μs.

Intriguingly, the front face of the target impacted by the triangular prism projectile exhibits no fragmentation, even at later stages (Figure 7). This can be explained by the previously discussed behavior: due to the projectile’s shape and the 60° impact angle, it travels along the z-direction, nearly skimming the target’s rear face, explaining the lack of fragmentation on the front face and large scattering in the back face.

Similar to the triangular prism at 30° impact case, the truncated cone in the 60° impact case exhibits reduced penetration due to its side being parallel to the target’s rear face. This configuration translates to a less-severe impact and, consequently, fewer ejected particles compared to other projectiles.

3.2.2. Oblique Impact of Ogival Projectile

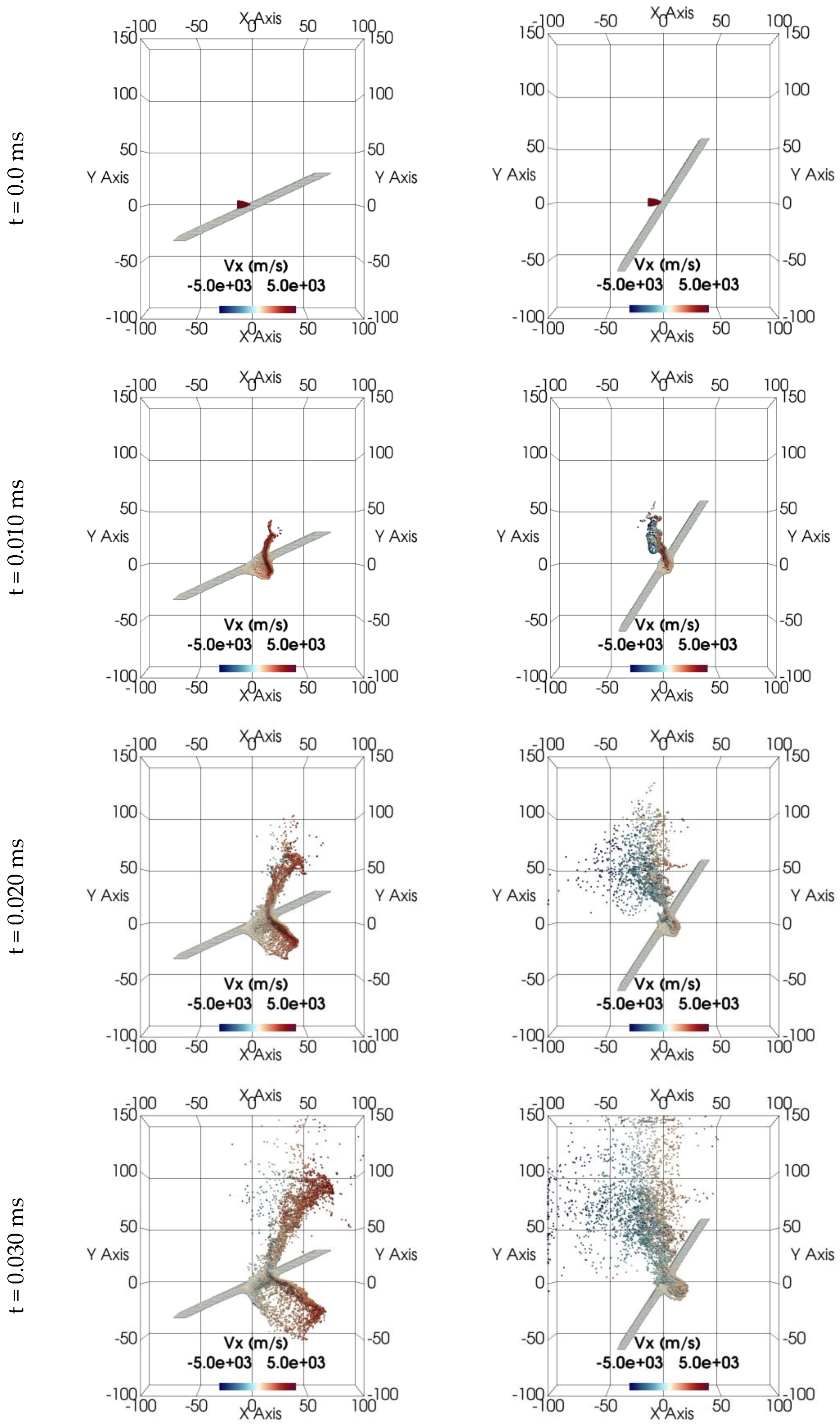
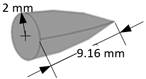
The second set of oblique impact results are conducted for an ogival shape projectile, characterized by a pointed nose and streamlined geometry. The details of the projectile and target geometries are tabulated in

Table 3. Projectile and target geometry specifications for oblique impact.

Projectile Geometry	Ogival Shape
	Volume = 62.2 mm3
Plate Geometry
	Dimensions = 135 mm × 5 mm × 50 mm
Angle of impact	30°	60°
# of material points	298,802	217,406

. The snapshots for the both impact scenarios are plotted at t = 0, 10, and 30 μs, and are presented in Figure 8.

This case is generated to demonstrate the versatility of the in-house preprocessor in generating more intricate projectile shapes and target configurations. Unlike the previous analysis, this simulation utilizes a projectile impacting in the x-direction. The velocity of the projectile is set 4000 m/s.

The analysis of hypervelocity oblique impact simulations, particularly those focusing on 30° and 60° impact angles with an ogival projectile, revealed significant effects on impact dynamics and resulting damage patterns. Analysis of the debris cloud suggests distinct characteristics for the two scenarios. A 30° impact likely exhibits partial penetration with localized deformation and material ejection confined to the impact zone. In contrast, a 60° impact angle resulted in a deeper penetration and more widespread fragmentation, especially in the front faces of the target.

Additionally, the projectile shape plays a pivotal role in determining the penetration mechanics and resultant damage patterns. The ogival shape, characterized by a pointed nose and smooth curvature, enhances aerodynamic efficiency and kinetic energy transfer upon impact.

Upon impact, the projectile imparts energy to the target material, causing localized deformation and material ejection primarily towards the impact direction. This ejection predominantly occurs in the impact direction. However, the target’s angled position in oblique impacts diverts the ejection path. The 30° impact scenario clearly demonstrates this diversion, with ejected material forming a dispersion angle relative to the target.

The distributions of debris clouds from the front and rear faces differ significantly between the 30° and 60° impact scenarios. In the 30° case, the rear face exhibits a more scattered debris cloud concentrated in the upper right region. In contrast, the front face forms a well-defined, nearly rectangular cloud. The 60° impact simulation shows a broader scattering of debris in the upper region of the rear face, accompanied by more significant fragmentation. Interestingly, the rear face consistently experiences greater localized fragmentation and material ejection compared to the front face.

4. Conclusions

This study presents a numerical method for simulating the hypervelocity impacts of various shaped projectiles into metal targets, and incorporates a rectangular prism target positioned at different oblique angles relative to the impact direction. Four distinct projectile shapes were investigated: square prism, triangular prism, truncated cone, and ogival. The simulations were performed using the open-source code MPM3D-F90 based on the Material Point Method (MPM). A preprocessing tool was developed to simplify the definition of complex projectile and target geometries within the material domain. This tool allows users to define various projectile and target configurations, adjust their relative positions, and select symmetry boundary conditions, and, overall, one can easily customize impact scenarios based on their specific needs.

This investigation focuses on the influence of projectile shape and oblique impact angles on debris formation and target damage. The simulations reveal significant variations in debris cloud formation, propagation depending on the projectile geometry and impact angle, scattering behavior of ejected particles from both the target’s front and rear faces, and penetration depth.

• Sharp-nosed projectiles (triangular prism and truncated cone) produced a debris cloud with more directional scattering at the front face, focusing ejected particles away from the impact zone. In contrast, the debris cloud from blunt (square prism) projectiles exhibited isotropic scattering, dispersing debris in all directions.
• Sharp-nosed projectiles penetrate deeper, forming larger craters and causing more localized damage, while blunt shapes scatter debris more uniformly.
• In the 30° impact angle scenario, the debris cloud scattering behavior becomes more balanced between the front and rear faces for ogival, square, and triangular prisms projectiles as the impact progressed, while the scattering remained unbalanced, with the rear face experiencing greater material ejection than the front face for the truncated cone projectile.
• In the 60° impact angle scenario, square and truncated cone projectiles exhibited a relatively balanced debris cloud scattering behavior between the front and rear faces. In contrast, ogival and triangular prism projectiles displayed with the rear face ejected more particles for ogival projectiles and the front face for triangular prism projectiles.

Overall, the presented framework offers a valuable tool for researchers to assess the risk of orbital debris impacting space structures. It could also be used to design and optimize shield systems for spacecraft protection against hypervelocity impacts encountered in space missions.