Abstract
This study introduces an advanced dual-mode compound attitude control framework for reusable launch vehicles (RLVs), underpinned by an enhanced particle swarm optimization (PSO) algorithm. This innovative strategy is tailored to meet the stringent demands for precision and robust anti-interference capabilities across the entire flight envelope of RLVs. The research commences with the formulation of a comprehensive attitude dynamics model and diverse heterogeneous actuator representations, meticulously crafted to reflect the distinct phases of RLV flight. Building upon this foundation, a synergistic control paradigm is engineered, integrating PID and fuzzy PID controllers and dynamically adjusting the inertia weights and learning factors of the PSO algorithm to achieve the balance between global and local optimization performance, complemented by a refined fitness evaluation function. The crux of the study is the application of an upgraded PSO algorithm to fine-tune the controllers’ weighting coefficients, culminating in an optimized dual-mode compound attitude control system. A series of comparative simulation analyses are thoroughly executed to appraise the system’s responsiveness, stability, precision, and resilience to interference. The simulation outcomes demonstrate an average reduction of 42.21% in step response overshoot, an 18.52% decrease in settling time, a 53.18% decline in steady-state error, a 56.80% drop in the maximum deviation value, a 55.82% improvement in recovery speed, and a 75.61% enhancement in tracking precision for the proposed controller. The findings clearly verify the superior performance of the proposed control system, affirming its contribution to the advancement of RLV attitude control. The proposed controller holds promising potential for real application in attitude control systems and is poised to augment the reliability and mission success rate of RLVs under intricate flight scenarios.
1. Introduction
The reusable launch vehicle (RLV) represents a novel space transportation tool that incorporates minor modifications to the basic configuration of conventional launch vehicles, enabling it to possess the capability of landing and returning. This advanced system offers several advantages, including reduced requirements for landing sites, a smaller technological leap, and relatively lower research and development costs [1]. Typically, the RLV undergoes seven distinct flight segments, which include the active phase, attitude adjustment phase, trajectory correction phase, high-altitude unpowered descent phase, powered deceleration descent phase, unpowered deceleration descent within the atmosphere, and the landing phase, as illustrated in Figure 1. To effectively control the vehicle’s attitude during these varied flight stages, the RLV must coordinate the operation of various heterogeneous actuation systems, such as the swiveling engines, grid fins, and the reaction control system (RCS) thrusters [2]. The complexities presented by the extensive airspace and velocity envelopes, significant changes in dynamic characteristics, and high environmental uncertainties [3] during the entire flight mission make it challenging to establish clear and precise kinematic laws and mathematical models for the RLV. Consequently, the design of a high-precision and robust anti-interference attitude control system for the RLV, which is subject to the influence of multiple heterogeneous actuators, and the unified description of all flight stages within a single control framework, are pivotal research directions in the field of aerospace launch vehicles [2].
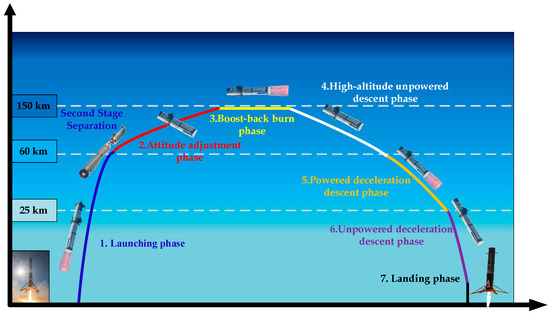
Figure 1.
RLV flight profile.
As a core function of the launch vehicle control system, attitude control utilizes data from sensitive devices, guidance signals, and navigation computations to generate control commands that manipulate the vehicle’s rotational motion around its center of mass. This ensures stable flight and effective command tracking even under various disturbances and potential faults [4]. As depicted in Figure 2, the attitude control system computes pitch, roll, and yaw angle commands (), which subsequently undergo meticulous comparison with instantaneous attitude telemetry furnished by a measurement device (); then, error signals () are generated. The controller, leveraging these error signals and tailored control algorithms, outputs control signals (), activating multiple heterogeneous actuators responsible for generating the requisite control moments () to effect dynamic compensation; this process rectifies and stabilizes the vehicle’s triaxial orientation (), guaranteeing in-flight stability and trajectory precision. Undoubtedly, the controller and multiple heterogeneous actuators are crucial to the effectiveness of RLV attitude control. Inaccurate or delayed attitude control during the vehicle’s return phase can lead to unsuccessful rocket recovery, which in turn affects the reusability and economic efficiency of the vehicle. Consequently, the selection of an appropriate control strategy and the design of a reasonable controller are crucial elements for the successful implementation of RLV attitude control.
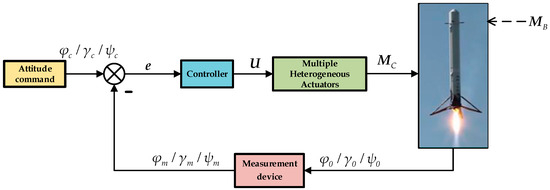
Figure 2.
Basic principle of RLV attitude control system.
Over the past half-century, the majority of launch vehicles have employed traditional PID control, combined with the use of Lyapunov-based models [5], correction networks [6], and reference models [7] to enhance the performance in attitude control. However, with the enhancement of launch vehicle performance and control requirements, the vehicle body experiences greater disturbances, more severe parameter perturbations, and larger deviations during the execution of complex flight missions. The PID controllers designed based on classical control theory use a single-tuned control gain with a limited adjustable range, making the design overly conservative and insufficient to meet the control requirements of launch vehicles [8]. To enhance the adaptability of launch vehicles to changes in the flight environment, researchers, both domestically and internationally, have started to focus on modern control methods and intelligent control strategies, aiming to optimize the performance of launch vehicle attitude control systems. Virtually all classic and modern control methods have been applied to some extent in the design of attitude control systems. Among them, fuzzy control, as a simple and efficient intelligent control method, is particularly advantageous in launch vehicle attitude control due to its flexibility in handling non-precision, nonlinearity, and time-varying complexities without relying on precise mathematical models of the system. It translates expert control experience into concise and easily understandable linguistic control rules, making it easier to leverage its advantages in simplicity, anti-interference, and robustness [9]. However, fuzzy controllers are rarely used as a standalone solution for vehicle attitude control due to limitations in control precision, cumbersome debugging, and excessive reliance on expert experience. Instead, fuzzy control is often combined with other control methods. Wang Pei et al. [10] proposed an anti-interference attitude controller based on fuzzy logic and PD control for launch vehicles, aiming to enhance the effectiveness and robustness of launch vehicle attitude control. R. Sumathi et al. [11] designed a fuzzy–PID hybrid controller for launch vehicle engine attitude control, demonstrating that this controller completely eliminates overshoot and provides substantial stability. Chan-oh Min et al. [12] introduced a control scheme using a Mamdani-type fuzzy PD controller for attitude control during the approach and landing phases of reentry vehicles, showing that this controller exhibits good control performance and robustness. Vladimir Melnic [13] proposed a hybrid attitude controller for spacecraft that simultaneously utilizes fuzzy and PID controllers, adjusting the outputs of both controllers through a predetermined combination function. This approach integrates the robustness and rapidity of fuzzy control with the accuracy of PID control, although it is constrained by the fixed combination function and cannot fully exploit the individual advantages of the two controllers.
Furthermore, the simultaneous use of multiple control methods inevitably leads to an increase in the number of controller parameters and complicates the tuning process. Therefore, selecting an appropriate parameter optimization method is crucial for rapidly designing controller parameters and ensuring system performance during intensive launch missions. Particle swarm optimization (PSO) is a modern intelligent bio-inspired algorithm based on population search; it was proposed by Kennedy et al. [14] in 1995 and developed through the simulation of bird flock foraging behavior. PSO and its improved algorithms have demonstrated excellent performance in solving various complex optimization tasks, particularly for the intricate and critical task of optimizing controller parameters. In recent years, they have been widely applied in the aerospace and control fields. Shi Qi et al. [15] introduced PSO to determine the specific values of various controller parameters based on adaptive augmented control technology for launch vehicles, providing an effective approach for determining controller parameters. Remya S et al. [16] tuned PID controller parameters based on an improved PSO algorithm, optimizing the RLV servo drive system. S. Bouallègue et al. [17] proposed a parameter tuning strategy for PID-type fuzzy controllers using an improved PSO algorithm, and simulations verified the effectiveness and superiority of the proposed PSO-based PID–fuzzy control method. Housny H et al. [18] introduced an adaptive multi-dimensional improved PSO algorithm and applied it to optimize the parameters of fuzzy controllers, enhancing the performance of fuzzy PID attitude controllers in quadrotor aircraft.
Current research predominantly favors standalone fuzzy PID controllers or PID linked with fuzzy controllers by fixed combination functions, overlooking adaptive parameter tuning; this limits the exploitation of the complementary strengths of both controllers across varying operational conditions, leading to the restraint of the controllers’ dynamic responsiveness and precision. In terms of algorithmic improvements, the existing work tends to integrate particle swarm optimization (PSO) with advanced auxiliary optimization techniques, resulting in significant performance enhancements at the cost of increased computational complexity, undermining PSO’s inherent simplicity and efficiency in some degrees. Building upon current studies, this paper proposes a novel control architecture that synergistically combines a PID controller with a fuzzy PID controller, aiming to maximize their complementary advantages and to combine the high precision of PID with the strong adaptability of fuzzy control. Furthermore, the paper introduces linear and nonlinear functions to dynamically adjust PSO’s inertia weights and learning factors, striking a balance between global and local search capabilities and optimizing the fitness evaluation function to enhance assessment capability. This approach simultaneously maintains the elegance of the algorithm and enhances its comprehensive optimization efficiency.
The remainder of this paper is structured as follows: Section 2 establishes the launch vehicle attitude dynamics model based on the flight characteristics of RLV and individually models the various heterogeneous actuators in different flight segments. Section 3 designs the basic structure of the RLV compound attitude controller through the coordination of fuzzy PID and traditional PID for dual-mode combined control. Section 4 optimizes the output weight parameters of the controller using the improved PSO algorithm and adds an integral term of time multiplied by the absolute value of the second derivative of the error to the fitness evaluation function to assess the system’s relative stability, addressing issues such as minor oscillations in the optimization results. Section 5 conducts comparative simulation tests on the RLV flight states during the attitude adjustment and unpowered deceleration within the atmosphere phases to verify the comprehensive performance of the dual-mode compound attitude controller based on improved PSO. Finally, the research work presented in this paper is summarized.
2. Modeling of Reusable Launch Vehicle
2.1. Dynamics Modeling of Launch Vehicle Attitude
Neglecting the influence of the elastic vibrations of the vehicle body, this paper treats the launch vehicle as a rigid body, with its rotational dynamics equation around the center of mass as follows [2]:
In Equations (1) and (2), represents angular momentum; represents the angular velocity of the vehicle body, including the angular velocities along the x, y, and z axes , , ; represents the vehicle’s inertia tensor; , , represent the moment of inertia of the vehicle in the x, y, and z axes; represents the roll angle; represents the yaw angle, and represents the pitch angle; represents the moment term generated by the rocket engine thrust; represents the moment term generated by the reaction control system (RCS) actuators; represents the moment term generated by the grid fins; and represents the disturbance moment term.
Based on the rotational dynamics equation of the vehicle body around the center of mass, the attitude dynamics model of the RLV can be derived as follows:
where , , represents the control matrix, represents the control variables, and represents the transformation matrix between attitude angles and angular velocities.
Throughout the entire flight process of the launch vehicle, significant changes in flight conditions and various disturbances occur. However, the aforementioned modeling process does not consider these complex state changes. Therefore, based on the previously obtained attitude dynamics model, the influence of internal parameter uncertainties and external disturbances on the vehicle’s attitude must be introduced [19,20]. Consequently, the final form of the launch vehicle’s attitude dynamics model should be as follows:
where represents the uncertainty term in the moment of inertia, including the uncertainties in the moment of inertia of the vehicle in the x, y, and z axes, represented as , , ; represents the disturbance torque term, with the derivation process and specific form provided in the literature [21].
2.2. Modeling of Various Heterogeneous Actuators
Throughout the seven flight segments of the RLV’s takeoff and landing, various heterogeneous actuation systems, including the swiveling engines, reaction control system (RCS), and grid fins, need to switch their operations, and each system operates on different principles [2]. Therefore, the specific forms of the control matrix and control variables in Equation (5) will also differ.
- (1)
- During the active phase, flight attitude stability is controlled through swiveling engines, with their control matrix and control variables given as:
- (2)
- During the attitude adjustment phase/high-altitude unpowered descent phase, in order to achieve large-scale and significant attitude reversals, direct force control is employed. The reaction control system (RCS) is installed at a location far from the center of mass as the actuation mechanism, with its control matrix and control variables expressed as:
- (3)
- In the trajectory correction phase, the powered descent phase, and the landing phase, a single swiveling engine controls the pitch and yaw channels, while the RCS controls the roll channel. In this configuration, the control matrix and control variables are expressed as:
- (4)
- During the atmospheric flight phase, attitude adjustments are made using the aerodynamic moments generated by the grid fins, with the control matrix and control variables expressed as:
Table 1 presents the actuators employed during each flight phase of the RLV; along with Equations (1) and (6)–(13), it can be observed that although the various heterogeneous actuators operate on different principles, the ultimate control variables for the launch vehicle’s attitude dynamics model are in the form of combined external moments; that is, they provide control moments to achieve control over the vehicle’s motion around its center of mass. Therefore, a unified control framework can be established, where the attitude angles serve as control commands, and the combined external moments act as the control variables for the vehicle’s attitude, thereby achieving attitude control of the RLV.

Table 1.
Actuators and shift conditions of every flight phase of RLV.
3. Attitude Controller Design
3.1. Fuzzy PID Attitude Controller
PID control is renowned for its reliability and simplicity in terms of parameters in aerospace attitude control. Despite these advantages, its intricate calibration, substantial offline design efforts, and lack of dynamic parameter adaptation hinder its capability to effectively manage the sophisticated disturbances and strong uncertainties encountered by RLV. Fuzzy controllers rooted in fuzzy logic principles, mirror human intuition by associating input variables with fuzzy sets and conducting inference based on a rule library; then, the defuzzification transforms the derived output into a clear action, conferring the controller with a strong adaptive capacity to accommodate fluctuating environmental conditions.
The fuzzy PID control strategy emerged with the development of fuzzy control theory and has been widely applied in engineering fields. A fuzzy PID controller integrates both a fuzzy logic controller and a traditional PID controller. It relies on expert control experience to perform fuzzy inference through an internal fuzzy controller and then defuzzifies the results to obtain correction values for the PID control parameters, enabling adaptive adjustment of parameters during the control process and further enhancing system stability and response speed. The RLV attitude control system exhibits time-varying and nonlinear characteristics, and the use of a fuzzy PID controller allows comprehensive adjustment of the control parameters in response to uncertainties and disturbances at various mission stages, thereby improving the system’s control performance.
As shown in Figure 3, based on the flight characteristics of the RLV, this paper designs a Mamdani-type fuzzy controller with attitude angle error and attitude angle error rate as dual inputs, and the correction values of the three PID parameters as triple outputs. The membership functions for the input and output variables are selected as Gaussian functions, and the centroid method is used for defuzzification. The fuzzy controller quantifies the deviation and deviation rate by scaling factors and converts them into fuzzy variables. After the membership functions allocate appropriate membership degrees, the controller performs fuzzy reasoning and decision making according to predefined fuzzy rules. Following defuzzification, the controller obtains clear values for the outputs, which are the adjustment values for the three outputs. This process ultimately allows the adaptive optimization of the PID control parameters.
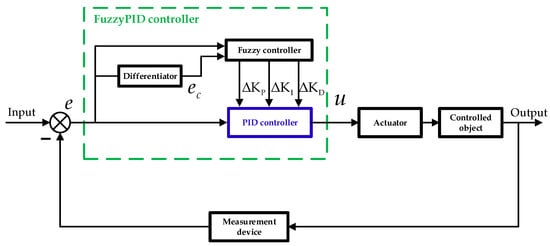
Figure 3.
Schematic diagram of fuzzy PID controller.
The fuzzy PID attitude controller, while capable of enhancing the overall system performance to some extent, suffers from a reliance on expert experience to determine output values and the absence of integral action, which results in poorer control accuracy and the presence of control blind spots near equilibrium points [22]. This is also one of the reasons why fuzzy control is less widely used in the attitude control of launch vehicles at present.
3.2. Dual-Mode Compound Attitude Controller
To further improve the control performance, it is common to study the combination of fuzzy control with various control methods, aiming to overcome the limitations of the basic fuzzy controller while effectively utilizing the advantages of fuzzy control [23]. In the literature [22], a dual-mode switching controller composed of a PI controller and a fuzzy controller was designed. This controller employs the fuzzy controller when the deviation is large, enhancing the system’s response speed, and switches to the PI controller when the deviation is small, eliminating the control blind spots of the fuzzy controller and improving the system’s steady-state accuracy. The dual-mode switching controller combines the strengths of both controllers, although it may lead to a frequent oscillation range at the critical point during mode switching [24,25]. If applied to attitude control of the vehicle body, the mode switching may introduce significant uncertainty in the response, leading to an unstable state of the vehicle body.
In response to this issue, this paper, based on the compound controller given in literature [23,25], the hybrid controller given in literature [13], and the dual-mode switching controller given in literature [22], designs a fuzzyPID–PID dual-mode compound controller, as shown in Figure 4. As depicted in Figure 4, this controller collaborates with both the PID controller and the fuzzy PID controller (shown in Figure 3) for joint control. It sets the appropriate working weight coefficients for the two controllers using the compound control strategy and sums the outputs of each controller after weighting to obtain the final output of the dual-mode compound controller. This approach combines the advantages of fuzzy PID and PID control methods, enhancing both the dynamic performance and the steady-state accuracy of the system, while avoiding the adverse effects of mode switching, thereby maximizing the performance of the controller.
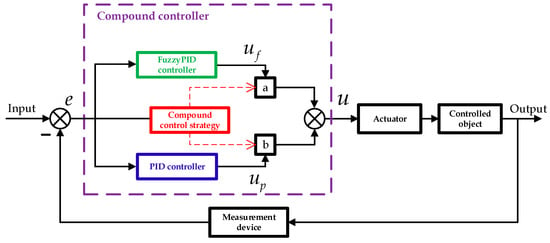
Figure 4.
Schematic diagram of dual-mode compound controller.
From the analysis above, it can be observed that selecting appropriate working weight parameters and evaluation functions is particularly crucial for the dual-mode compound attitude control strategy, and it also has a decisive influence on the tuning and optimization of the output of the dual-mode compound attitude controller.
4. Dual-Mode Compound Attitude Controller Based on Improved PSO
4.1. Improved Particle Swarm Optimization Algorithm
The core idea of the particle swarm optimization (PSO) algorithm is to continuously iterate and optimize by sharing information, aiming to find the global optimal solution [26]. The algorithm randomly initializes particles throughout the entire space and adjusts their velocity vectors and solution positions based on individual and global best solutions. The update formulas for the velocity and position of the particles are as follows:
where represents the current iteration number; represents the current inertia weight; represents the current individual learning factor; represents the current group learning factor; , represent the random numbers generated; represents the current velocity of the i-th particle; represents the current individual best position of the i-th particle; represents the current position of the i-th particle; represents the current group best position; and represents the current group position.
From Equation (14), it becomes evident that the inertia weight and the learning factors , directly influence the velocity of the particles throughout the iterations, subsequently affecting their searching capabilities and convergence speed. During the initial stages of iteration, a larger , combined with a larger and a smaller , promotes global exploration of the solution space, effectively preventing premature convergence. Conversely, as the iterations progress, to enhance the algorithm’s local convergence abilities, the inertia weight should gradually decrease, while a smaller and a larger help the particles’ convergence towards the optimal solution. During the iterative process of the particle swarm optimization algorithm, to balance the global search capability and local convergence ability [27], it is recommended to use a linear or nonlinear decreasing function to update the algorithm’s inertia weight , individual learning factor , and group learning factor . The improved calculation formulas are as follows:
where represents the maximum inertia weight; represents the minimum inertia weight; represents the current iteration number; represent the maximum iteration number; , represent the maximum and minimum values of the individual learning factor; and , represent the maximum and minimum values of the group learning factor.
Referring to the aforementioned core formulas, this paper employs the improved PSO algorithm to optimize the working weight parameters of the controller, as shown in Figure 5.
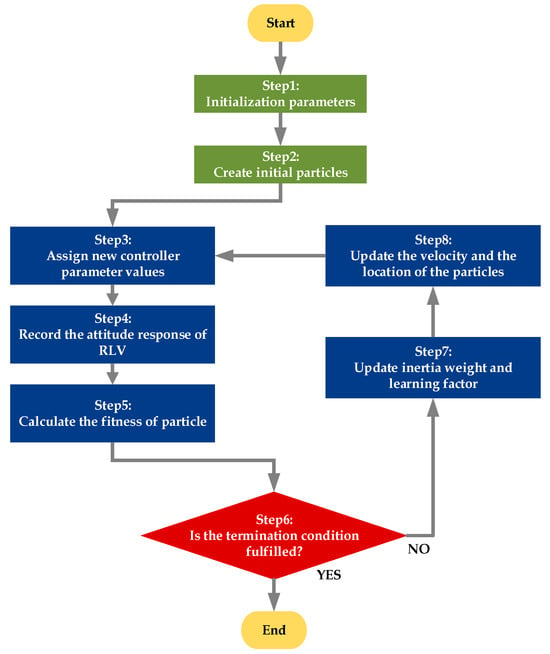
Figure 5.
Optimization flowchart of improved PSO algorithm.
As illustrated in Figure 5, the optimization process begins with the system initializing parameters. After initialization, an initial population is randomly generated. The improved PSO algorithm records each particle as a controller parameter and calculates the deviation between the response result of the vehicle’s attitude angle and the target attitude angle. Based on the fitness evaluation function, the algorithm selects the best particle in the population. The algorithm then determines whether the particle meets the convergence condition (i.e., whether the response result of the vehicle’s attitude angle reaches the predefined target requirements) and whether it meets the iteration termination condition (i.e., whether it reaches the maximum iteration number). If the conditions are met, the particle is used as the working weight coefficients of the RLV dual-mode compound attitude controller. Otherwise, the algorithm updates the inertia weight and learning factors, continues the iteration based on the velocity and position update formulas of the particles, and seeks a better solution.
Based on the dual-mode compound attitude controller designed in Section 3.2 (Figure 4), the dual-mode compound attitude controller based on the improved PSO algorithm can be derived, as shown in Figure 6. The output equation of the dual-mode compound attitude controller in the figure is:
where represents the output of the dual-mode compound attitude controller based on the improved PSO; represents the output of the fuzzy PID attitude controller; represents the output of the PID attitude controller; a represents the working weight coefficient of the fuzzy PID attitude controller; and b represents the working weight coefficient of the PID attitude controller.
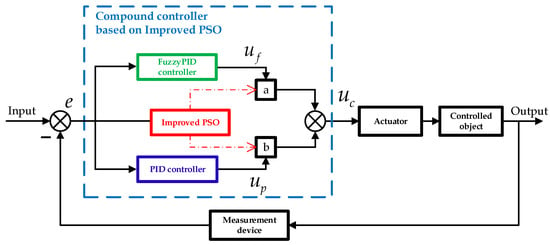
Figure 6.
Schematic diagram of dual-mode compound controller based on improved PSO.
4.2. Optimization of Fitness Evaluation Function
The “fitness” mentioned in Step 5 of the optimization process (Figure 5) in Section 4.1 is a reference value used to evaluate the quality of the particles. Most of the literature currently selects the ITAE (integral of time-weighted absolute error) index as the fitness evaluation function for the algorithm [18,26], which evaluates the comprehensive performance of the system by integrating the product of time and the absolute value of the error, with its expression being:
where represents the time during which the system operates; represents the error of the system.
The dual-mode compound controller under the control strategy of the RLV is evaluated for fitness using Equation (20), with the pitch angle response curve of the attitude adjustment phase selected as the reference, as shown in Figure 7a. It is evident from Figure 7a that, although the dual-mode compound controller based on the improved PSO outperforms the traditional PID controller in terms of rapidity (convergence speed) and accuracy (error magnitude), the RLV’s attitude still exhibits slight oscillations during the response process and after the system stabilizes. Such response results are also considered unsatisfactory. This indicates that the ITAE evaluation index has a flaw in determining the fitness of the particles, i.e., it fails to identify the oscillation in the response curve, leading to poor system response stability.
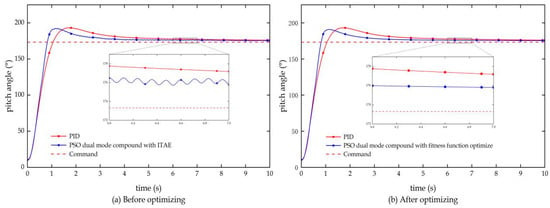
Figure 7.
Pitch angle response results before and after optimizing the fitness evaluation function.
Sudden changes in the RLV’s angular acceleration often trigger oscillatory attitude responses. For the RLV’s angular position, its second derivative physically represents the angular acceleration. Hence, the oscillation in an RLV’s attitude response can be characterized using the second derivative of the attitude response error. This paper introduces a term that evaluates the system’s oscillation by integrating the absolute value of the second derivative of the error multiplied by time and then weights and sums these terms to construct an optimized fitness evaluation function. The specific form of this function is:
where represents the time during which the system operates; represents the system error, with its second derivative used to characterize the degree of system oscillation.
The attitude response of the RLV under the dual-mode compound control strategy is recalculated for fitness using Equation (21), with the pitch angle response curve of the attitude adjustment phase selected as the reference, as shown in Figure 7b. From Figure 7b, it can be observed that the optimized attitude angle response curve has significantly improved, not only suppressing the slight oscillations present before optimization, enhancing the stability of the response, but also maintaining good rapidity and accuracy.
5. System Simulation Test
5.1. System Step Response Test
After the first and second stages of the RLV undergo thermal separation, the first stage of the carrier enters the return phase. To alleviate the attitude control pressure in subsequent flight segments, the vehicle body must perform a 180° attitude reversal and maintain a stable attitude for a certain period of time during the attitude adjustment phase [28]. Therefore, this paper selects the attitude adjustment segment with significant changes in the vehicle’s flight attitude for system step tracking comparative tests, which can better verify the control effect of the designed dual-mode compound controller.
According to the flight state of the RLV attitude adjustment segment, the initial pitch angle is set to 10.54°, the initial roll angle is set to 4.89°, and the initial yaw angle is set to 0°. The commanded pitch angle is 173.31°, the commanded roll angle is 1.00°, and the commanded yaw angle is 1.29°. Figure 8, Figure 9 and Figure 10 show the attitude angle response test curves of the vehicle body in the attitude adjustment segment, and Table 1, Table 2 and Table 3 provide the corresponding attitude angle tracking test indicators.
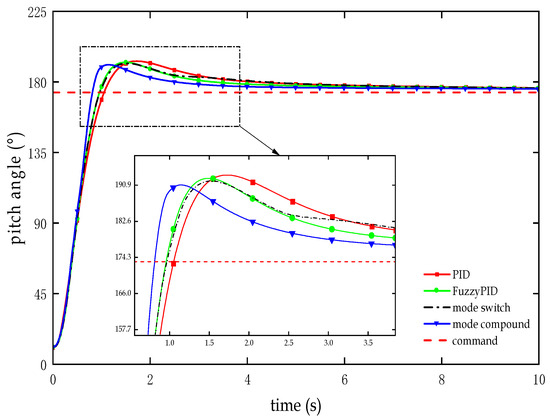
Figure 8.
Test curve of pitch angle response in the attitude adjustment section.
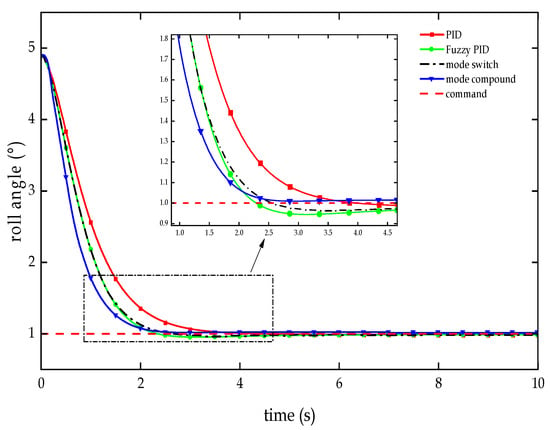
Figure 9.
Test curve of roll angle response in the attitude adjustment phase.
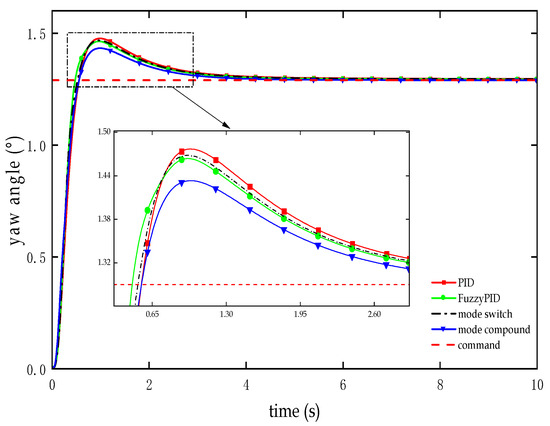
Figure 10.
Test curve of yaw angle response in the attitude adjustment phase.

Table 2.
Step tracking test indicators for pitch angle channel.

Table 3.
Step tracking test indicators for roll angle channel.
As observed from Figure 8 and Table 2, in the control of the RLV’s pitch angle during the attitude adjustment segment, the dual-mode compound controller based on the improved PSO demonstrates a faster response speed, reducing adjusting time by 35.7% relative to conventional PID, 22.96% compared to fuzzy PID, and 23.79% against the dual-mode switching controller. Furthermore, it exhibits enhanced behavior with significantly reduced overshoot (average reduction of 27.48%) and steady-state error (average decrease of 25.9%).
As illustrated in Figure 9 and Table 3, in the control of the RLV’s roll angle during the attitude adjustment segment, the dual-mode compound controller based on the improved PSO achieves effective control of the roll attitude; it not only preserves the zero-overshoot characteristic of conventional PID controllers, but also achieves a 34.57% reduction in adjusting time. While inheriting the rapid response of fuzzy PID controllers, it surpasses them with a 45.80% decrease in steady-state error. This controller demonstrates good stability, rapidity, and accuracy.
As indicated in Figure 10 and Table 4, in the control of the RLV’s yaw angle during the attitude adjustment segment, the dual-mode compound controller based on the improved PSO outperforms the other three controllers. It exhibits reduced overshoot of 15.21% to 21.20% and shortened adjusting time of 8.97% to 10.75% and eliminates steady-state errors; in contrast, non-zero steady-state errors persist with the remaining controllers.

Table 4.
Step tracking test indicators for yaw angle channel.
Overall, the tests indicate that, in terms of attitude control during the RLV’s attitude adjustment segment, the dual-mode compound attitude controller based on the improved PSO holds certain advantages in terms of stability (stability), response speed (rapidity), and control precision (accuracy). It is better suited for the task of achieving substantial and high-precision attitude adjustments of the vehicle body during flight.
5.2. System Anti-Interference Test
To alleviate the guidance and control pressure during the vertical landing phase, the RLV should satisfy various terminal constraints on position, velocity, and attitude after entering the unpowered descent phase within the atmosphere. This requires precise adjustment of the vehicle’s attitude using the grid fins to ensure an accurate handover from the end position to the start of the landing phase [28]. However, due to the fact that the first stage of the rocket reenters the atmosphere at this stage, it experiences a complex external environment, severe external disturbances, and a significant increase in aerodynamic characteristic deviations. Therefore, this paper selects the most severe environmental conditions and the most complex flight characteristics of the unpowered descent segment within the atmosphere for anti-interference comparative tests, which can better validate the anti-interference characteristics of the designed dual-mode compound controller.
According to the flight state of the RLV’s unpowered descent segment within the atmosphere, the initial pitch angle of the vehicle body is set to 120.14°, the initial roll angle is set to 1.77°, and the initial yaw angle is set to 3.89°. The commanded pitch angle is 84.41°, the commanded roll angle is 15.00°, and the commanded yaw angle is 12.56°. After the simulation runs for 6 s, a pulse interference signal in the form of a disturbance moment is added to simulate the disturbances the RLV may encounter during flight. Figure 11, Figure 12 and Figure 13 show the anti-interference test curves of the vehicle body’s attitude angles in the unpowered descent segment within the atmosphere, and Table 4, Table 5 and Table 6 provide the corresponding anti-interference test indicators for the attitude angles.
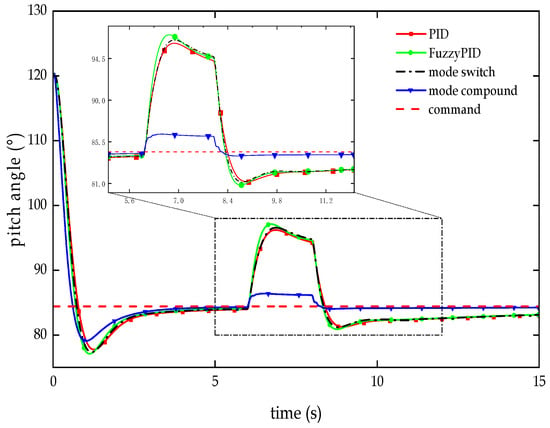
Figure 11.
Test curve of anti-interference in the pitch angle channel.
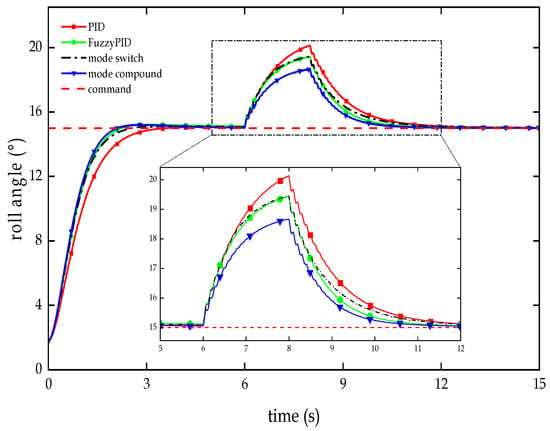
Figure 12.
Test curve of anti-interference in the roll angle channel.
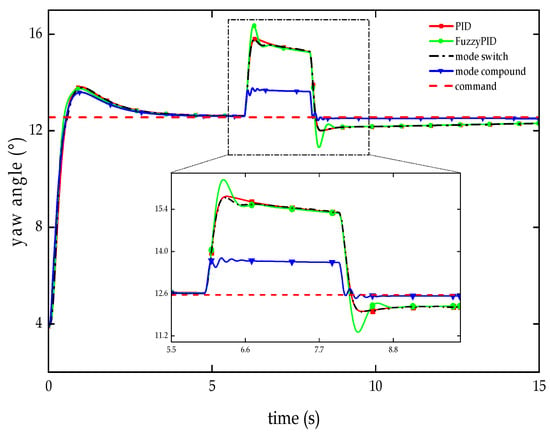
Figure 13.
Test curve of anti-interference in the yaw angle channel.

Table 5.
Anti-interference test indicators for pitch angle channel.

Table 6.
Anti-interference test indicators for roll angle channel.
As depicted in Figure 11 and Table 5, in the anti-interference test of the RLV’s pitch angle during the unpowered descent segment within the atmosphere, after the interference signal is introduced, unlike the pitch angles of the traditional PID controller, fuzzy PID controller, and dual-mode switching controller, which deviate significantly from the target angle, the dual-mode compound controller based on the improved PSO exhibits a smaller deviation (with a maximum deviation of only 1.880°) from the target angle, representing an decrease of over 84% compared to the other methods. Moreover, after the interference disappears, the controller is able to quickly (with a recovery time of only 0.256 s) and accurately (with a tracking deviation of only 0.281°) resume the tracking of the target signal and is nearly 78% faster than the alternatives.
As illustrated in Figure 12 and Table 6, in the anti-interference test of the RLV’s roll angle during the unpowered descent segment within the atmosphere, when faced with equal amplitude interference, all the controllers essentially suppress the interference signal. Compared to the other three controllers, the dual-mode compound controller reduces the maximum deviation by a factor of 1.2 to 1.4, accelerates the recovery speed by 1.17 to 1.59 times, and diminishes the tracking deviation by 2 to 5.5 times, demonstrating exceptional disturbance rejection capabilities.
As indicated in Figure 13 and Table 7, in the anti-interference test of the RLV’s yaw angle during the unpowered descent segment within the atmosphere, during the period when the interference signal is active, the arrow body’s yaw angle controlled by traditional PID controllers, fuzzy PID controllers, and dual-mode switching controllers would experience significant deviations. However, the maximum deviation for the dual-mode compound controller based on the improved PSO is significantly reduced by more than 63%. After the interference signal disappears, compared to the other three controllers, the dual-mode compound controller based on the improved PSO tracking speed improves by 54.45% to 65.74%, and the tracking accuracy sees a notable boost of over 80%.

Table 7.
Anti-interference test indicators for yaw angle channel.
In summary, the tests indicate that, in terms of anti-interference for the attitude angles during the RLV’s unpowered descent segment within the atmosphere, the dual-mode compound attitude controller based on the improved PSO can significantly suppress external interference factors and quickly resume the tracking of the target signal. It possesses excellent anti-interference capability.
6. Conclusions
This study addresses the imperative for high-precision and robust anti-interference attitude control in the operational profile of reusable launch vehicles (RLVs) by proposing an integrated control strategy that harmonizes PID with fuzzy PID controllers. Utilizing an advanced particle swarm optimization (PSO) algorithm and enhancing its search performance and strengthening its evaluative capabilities by refining the inertia weight, learning factors, and fitness evaluation function, the research optimizes the output weight coefficients of these controllers, culminating in the development of an enhanced PSO-driven dual-mode compound attitude controller. This controller is adept at managing the intricate demands of the entire RLV flight spectrum.
To substantiate the efficacy of the proposed control system, this paper meticulously selects the attitude adjustment phase and the unpowered descent phase within the atmospheric re-entry as representative flight stages. A suite of step tracking and anti-interference tests are conducted and compared against traditional PID, fuzzy PID, and dual-mode switching controllers. The simulation outcomes are compelling, revealing that the dual-mode compound attitude controller, underpinned by the refined PSO, surpasses its counterparts across the metrics of stability, agility, accuracy, and interference mitigation. In the step response tracking tests, the dual-mode compound controller exhibits an average 42.21% reduction in overshoot across all three attitude channels, a mean 18.52% decrease in adjusting time, and an average 53.18% decline in steady-state error; it achieves a no-overshoot response in the roll channel and a zero-error response in the yaw channel. In the anti-interference test, the controller displays exceptional disturbance tolerance, with an average 56.80% decrease in maximum deviations, a 55.82% average increase in recovery speed, and an average 75.61% improvement in tracking precision. This controller significantly bolsters the overall performance of the RLV’s attitude control system, empowering it to adeptly navigate the complexities of multi-stage flight missions.
While the dual-mode compound controller based on the improved PSO proposed in this study demonstrates superior performance in simulated scenarios, its current design relies heavily on a specific RLV attitude dynamics model. The complexities and variations in real flight environments pose significant challenges to the controller’s performance. Hence, it is crucial to validate its control efficiency under actual operating conditions in subsequent research. A comprehensive analysis of system stability and a thorough assessment of safety must be conducted to ensure the practical engineering applicability of the proposed controller. This will contribute to advancing the development of reusable launch vehicle attitude control technology.
Author Contributions
Software, S.Y.; Validation, L.Y.; Formal analysis, E.Z.; Investigation, T.W. and E.Z.; Resources, H.C.; Data curation, S.Y.; Writing—original draft, S.Y.; Writing—review & editing, L.G. and H.C.; Supervision, L.G. and H.C.; Project administration, T.W., L.Y. and H.C.; Funding acquisition, H.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Natural Science Foundation of Jiangsu Province grant number [BK20220911] and Fundamental Research Funds for the Central Universities grant number [NS2024065].
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Cui, N.; Wu, R.; Wei, C.; Xu, D. Double-order power fixed-time convergence sliding mode control method for launch vehicle vertical returning. J. Harbin Inst. Technol. 2020, 52, 15–24. [Google Scholar]
- Zhang, L.; Li, D.; Cui, N.; Li, Y. Full flight profile prescribed performance control for vertical take-off and vertical landing reusable launch vehicle. Acta Aeronaut. Astronaut. Sin. 2023, 44, 179–195. [Google Scholar]
- Bao, W. A review of reusable launch vehicle technology development. Acta Aeronaut. Astronaut. Sin. 2023, 44, 8–33+3. [Google Scholar]
- Wu, Y. Review and prospect of attitude control technologies for China’s launch vehicle. J. Astronaut. 2023, 44, 509–518. [Google Scholar]
- Nair, A.P.; Selvaganesan, N.; Lalithambika, V. Lyapunov based PD/PID in model reference adaptive control for satellite launch vehicle systems. Aerosp. Sci. Technol. 2016, 51, 70–77. [Google Scholar] [CrossRef]
- Silva, A.G.; Leite Filho, W.C. Launch vehicle attitude control system using PD plus phase lag. IFAC Proc. Vol. 2013, 46, 48–53. [Google Scholar] [CrossRef]
- Abdallah, Y.M.; Leite Filho, W.C. An adaptive tuning strategy of PID attitude control system. IFAC Proc. Vol. 2004, 37, 1009–1014. [Google Scholar] [CrossRef]
- He, F. Research on Model Reference Adaptive Augmenting Control of Heavy Lift Launch Vehicle; Harbin Institute of Technology: Harbin, China, 2018. [Google Scholar]
- Zhou, R. The Application of Fuzzy Control Theory in Attitude Control of Launch Vehicle; National University of Defense Technology: Changsha, China, 2004. [Google Scholar]
- Pei, W.; Bo, L.M.; Lei, G.Z.; Shan, X. Fuzzy adaptive attitude controller design for launch vehicle. In Proceedings of the 2017 International Conference on Robotics and Automation Sciences (ICRAS), Hong Kong, China, 26–29 August 2017; pp. 58–63. [Google Scholar]
- Sumathi, R.; Usha, M. Pitch and yaw attitude control of a rocket engine using hybrid fuzzy-PID controller. Open Autom. Control Syst. J. 2014, 6, 29–39. [Google Scholar] [CrossRef][Green Version]
- Min, C.; Lee, D.; Cho, K.; Jo, S.; Yang, J.; Lee, W. Control of approach and landing phase for reentry vehicle using fuzzy logic. Aerosp. Sci. Technol. 2011, 15, 269–282. [Google Scholar] [CrossRef]
- Mao, Q.; Dou, L.; Zong, Q.; Ding, Z. Attitude controller design for reusable launch vehicles during reentry phase via compound adaptive fuzzy H-infinity control. Aerosp. Sci. Technol. 2018, 72, 36–48. [Google Scholar] [CrossRef]
- James, K.; Russell, E. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Shi, Q.; She, Y.; Hu, C.; Qi, R. Optimization and tuning method of adaptive augmenting control parameters for launch vehicles. Aerosp. Control 2023, 41, 18–23. [Google Scholar]
- Remya, S.; Priya, C.; Priyanka, C. PID controller design using particle swarm optimization for servo actuation system of reusable launch vehicle. Int. J. Adv. Res. Electr. Electron. Instrum. Eng. 2015, 4, 7226–7236. [Google Scholar]
- Bouallègue, S.; Haggège, J.; Ayadi, M.; Benrejeb, M. PID-type fuzzy logic controller tuning based on particle swarm optimization. Eng. Appl. Artif. Intell. 2012, 25, 484–493. [Google Scholar] [CrossRef]
- Housny, H.; El Fadil, H. Fuzzy PID control tuning design using particle swarm optimization algorithm for a quadrotor. In Proceedings of the 2019 5th International Conference on Optimization and Applications (ICOA), Kenitra, Morocco, 25–26 April 2019; pp. 1–6. [Google Scholar]
- Qian, M.; Xiong, K.; Wang, H. Sliding mode dynamic surface control in precise recovery phase for reusable launch vehicle. J. Astronaut. 2018, 39, 879–888. [Google Scholar]
- Xu, Q.; Xiang, Y.; Wang, Z.; Tang, S. Attitude control method for vertical rocket recovery based on nonlinear model predictive control. Flight Dyn. 2024, 42, 8–15. [Google Scholar]
- Wu, R. Return Guidance and Control Methods of Vertical Takeoff Vertical Landing Reusable Launch Vehicle; Harbin Institute of Technology: Harbin, China, 2019. [Google Scholar]
- Chai, J.; Chen, X.; Yu, Y.; Cui, E. Research on pressure control algorithm of gas generator based on Fuzzy-PI dual mode controller. J. Propuls. Technol. 2018, 39, 1151–1156. [Google Scholar]
- Chen, M.; Yu, D. Improved fuzzy PID dual-mode compound controller. Modul. Mach. Tool Autom. Manuf. Technol. 2020, 7, 102–103+108. [Google Scholar]
- Zhang, R.; Guo, Y. Application study on composite fuzzy controller applied to aero-engine control. Mach. Des. Manuf. 2006, 9, 64–66. [Google Scholar]
- Gao, X.; Wang, Q.; Xue, Z.; Liu, J. Application of Fuzzy-PID composite controller based on PSO in pintle adjustment engine pressure control. J. Propuls. Technol. 2023, 1–14. [Google Scholar] [CrossRef]
- Liu, J.; Wu, H.; Ji, M.; Li, Z. Multi-strategy improved particle swarm optimization AGV fuzzy PID control. Mach. Tool Hydraul. 2024, 9, 1–10. [Google Scholar]
- Dileep, M.; Kamath, S.; Nair, V.G. Particle swarm optimization applied to ascent phase launch vehicle trajectory optimization problem. Procedia Comput. Sc. 2015, 54, 516–522. [Google Scholar] [CrossRef][Green Version]
- Wei, C.; Ju, X.; Xu, D.; Wu, R.; Cui, N. Guidance and control for return process of vertical takeoff vertical landing reusable launching vehicle. Acta Aeronaut. Astronaut. Sin. 2019, 40, 322782. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).