Summary of Lunar Constellation Navigation and Orbit Determination Technology
Abstract
1. Introduction
2. Current Status of Lunar Relay Navigation Satellite Networks
2.1. U.S. Lunar Navigation and Communication Plan
- LunaNet
- (1)
- Universal stable time and frequency reference source for achieving time synchronization between all elements of the entire network;
- (2)
- Key measurement information obtained from each observable communication link, such as radiance or optimization;
- (3)
- Observability of GNSS signals;
- (4)
- Angle measurement of stars and celestial bodies for determining relative positions;
- (5)
- Images of surface features nearby for relative terrain navigation;
- (6)
- Broadcasting signals that transmit navigation data throughout the lunar environment, similar to GPS signals on Earth.
- 2.
- CommStar-1
- (1)
- Receive/distribute radio frequency and optical (laser) communications from the Moon, Earth, and cislunar space;
- (2)
- Fully enable integration and interoperability with other space and terrestrial infrastructure—lunar, terrestrial, and cislunar space;
- (3)
- Cloud-based data distribution, open architecture, software definition, and end-to-end user management;
- (4)
- Realize communication between users and space;
- (5)
- User data are distributed directly to different cloud storage facilities (hosts), corporate sites, and universities/laboratories through existing interconnections between space stations and ground stations.
2.2. ESA Lunar Navigation and Communication Program
2.3. China’s Lunar Navigation and Communication Plan
- (1)
- Phase I of the project (around 2030): Build a pilot constellation to support the fourth phase of the lunar exploration project, the international lunar scientific research station and other tasks.
- (2)
- Phase II of the project (before 2040): Complete the basic constellation to realize regional navigation. It will serve manned lunar exploration, international lunar exploration, as well as the exploration of Mars and Venus.
- (3)
- Phase III of the project (before 2050): Build an expanded constellation to achieve communication and navigation coverage on Mars and Venus, and serve the exploration of Mars, Venus, giant planets and the edge of the solar system.
2.4. Other Countries
3. Overview of Single-Satellite Navigation and Orbit Determination Methods
3.1. Radio Measurement Orbit Determination Technology
- Radio velocity measurement
- 2.
- Radio ranging
- 3.
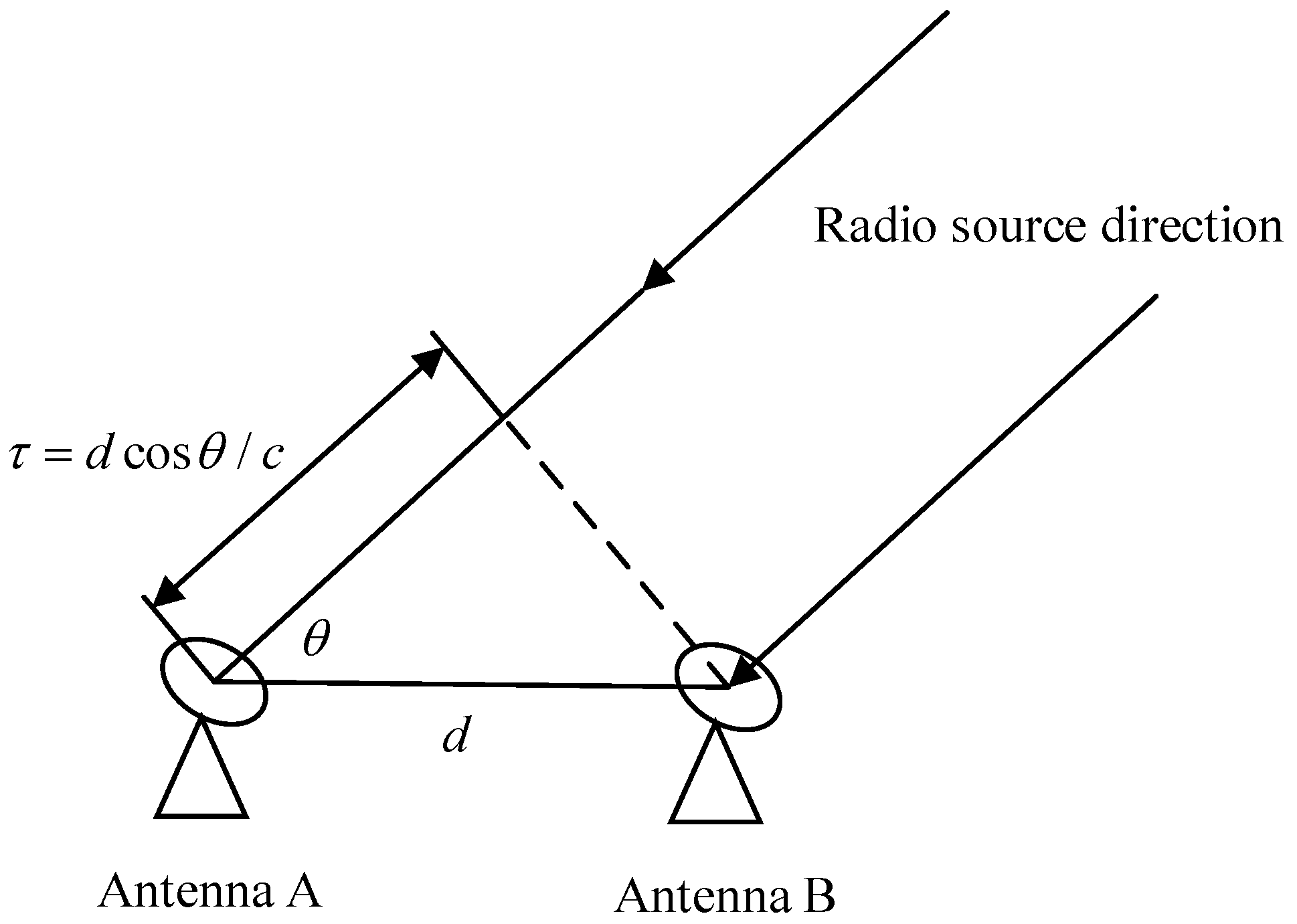
- Very long baseline interferometry (VLBI)
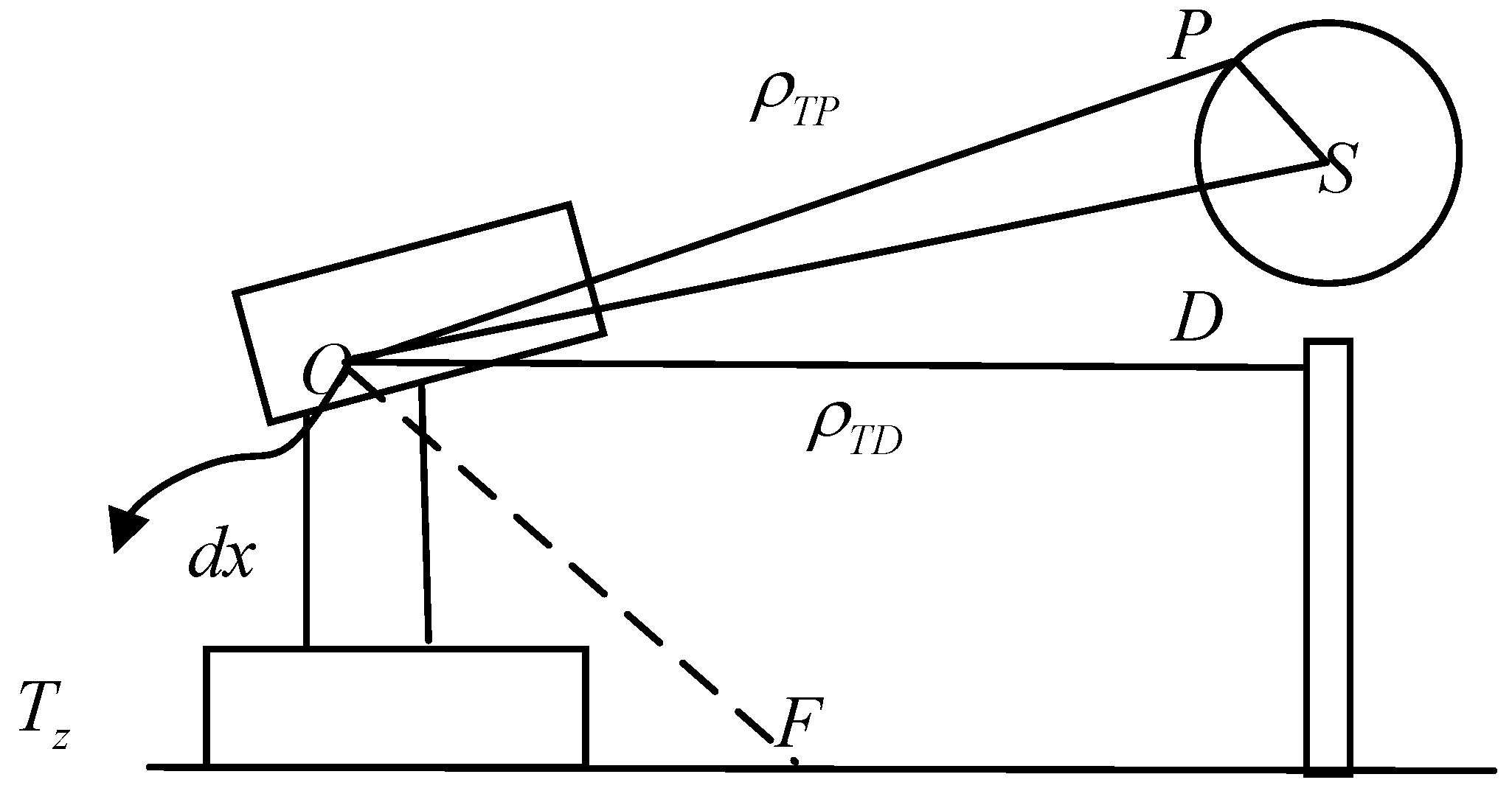
3.2. Astronomical Navigation Technology
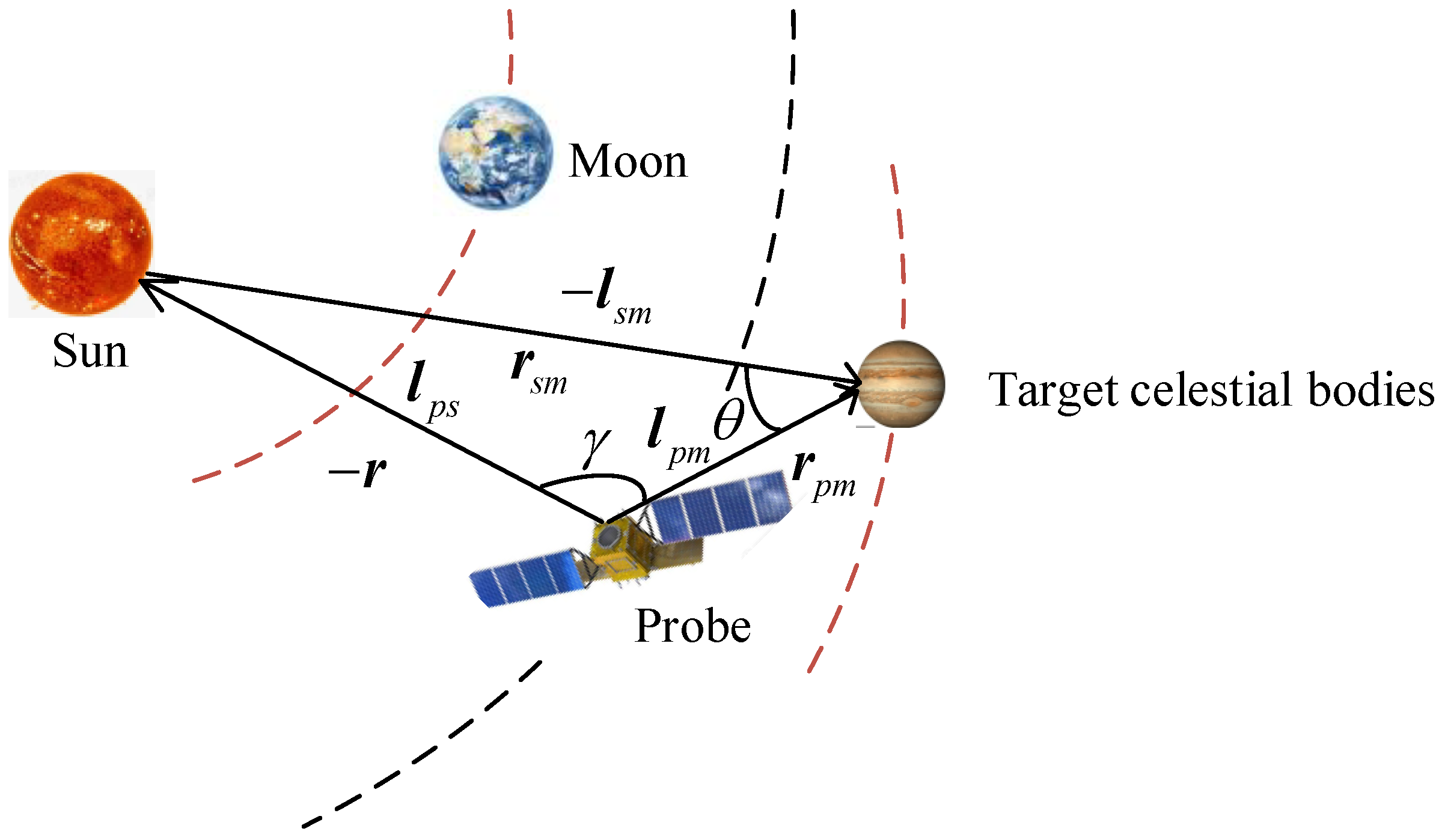
- Astronomical angle measurement navigation
- 2.
- Astronomical ranging navigation
- 3.
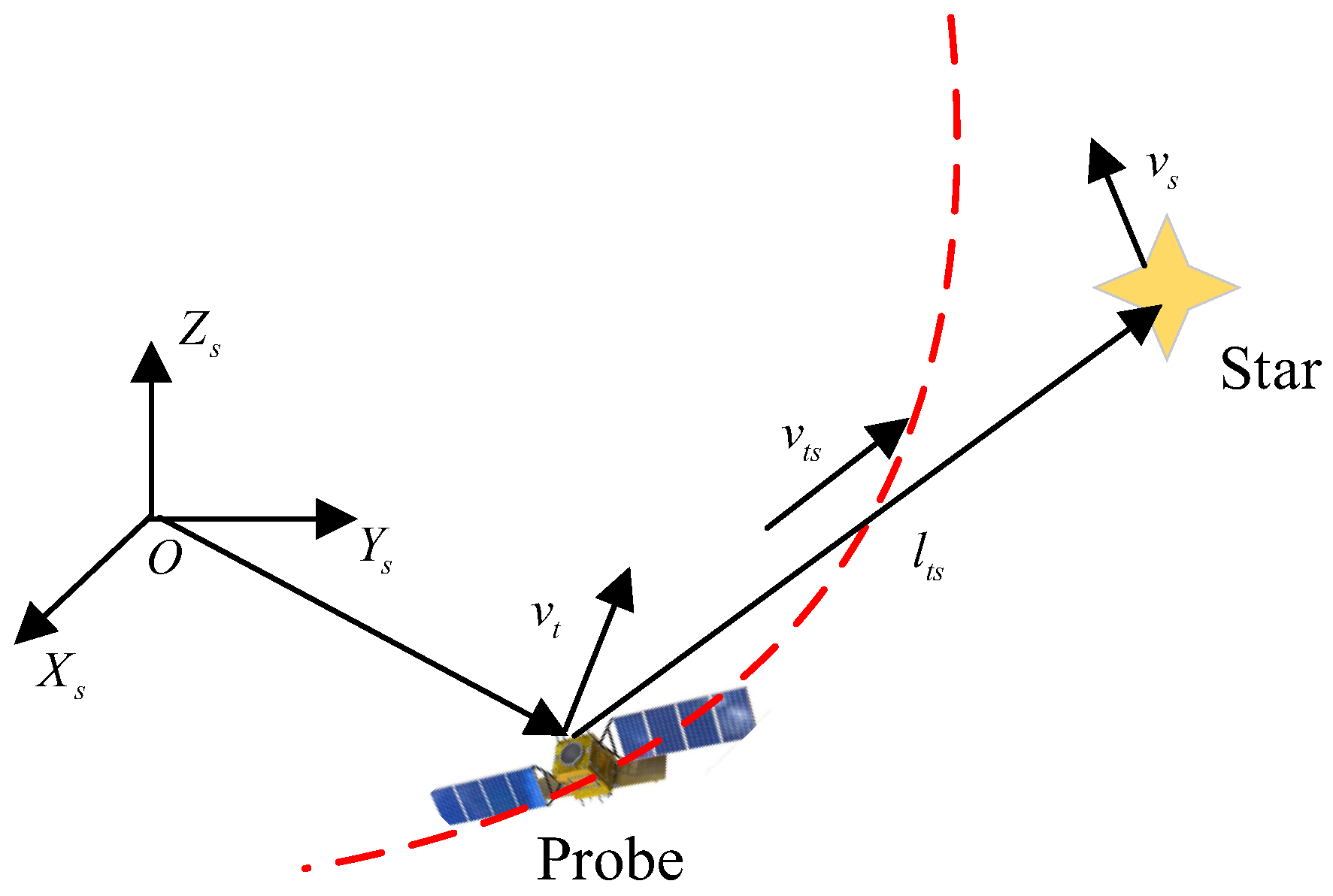
- Astronomical velocity navigation
3.3. Satellite-to-Ground Laser Measurement Technology
3.4. GNSS Orbit Determination Technology
- (1)
- Satellite signal transmission: GNSS satellites emit signals that contain information about the satellite’s own position and time. These signals travel through the air via radio waves and are picked up by ground-based receivers.
- (2)
- Signal receiving and processing: After the ground receiver receives the signal transmitted by the satellite, it will process the signal. This includes amplifying, filtering, demodulating and other operations on the signal to extract useful information.
- (3)
- Signal time difference measurement: By measuring the time difference between signals received from multiple satellites, the ground receiver can calculate its distance from each satellite. This is accomplished by comparing the difference in the time it takes for the signal to arrive at the receiver.
- (4)
- Positioning calculation: By measuring the distance between four or more known satellites and the GNSS receiver, the position of the receiver can be determined through distance intersection. Therefore, the positional information of the satellite which is equipped with the GNSS receiver can be obtained. There are many methods for calculating position, among which the triangulation method and the least squares method are the most commonly used.
3.5. Navigation Data Processing Technology
4. Constellation Navigation and Orbit Determination Technology
4.1. Multi-Constellation GNSS Lunar Satellite Orbit Determination Method
4.2. Inter-Satellite Measurement Autonomous Navigation Method
4.3. LiAISON Autonomous Navigation Method
5. Outlook on Key Technologies for Lunar Constellation Navigation and Orbit Determination
5.1. Moon Reference Frames and Time Scales
5.2. High-Precision Dynamic Model
5.3. Multi-Source Ranging Fusion Technology
5.4. Quantity Measurement Error Propagation Mechanism and Suppression
5.5. Data Processing Filter Algorithm
5.6. Multi-Source Navigation Information Fusion and System Optimization
5.7. Libration Point Constellation Design
5.8. Systematic Design for Deeper Space
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Angelopoulos, V. The ARTEMIS Mission; Springer: Berlin/Heidelberg, Germany, 2014; pp. 3–25. [Google Scholar]
- Johnson, S.K.; Mortensen, D.J.; Chavez, M.A.; Woodland, C.L. Gateway—A communications platform for lunar exploration. In Proceedings of the 38th International Communications Satellite Systems Conference (ICSSC 2021), Arlington, WV, USA, 27–30 September 2021; IET: London, UK, 2021; Volume 2021. [Google Scholar]
- Köpping, A.H. The moon village and space 4.0: The ‘open concept’ as a new way of doing space? Space Policy 2019, 49, 101323. [Google Scholar] [CrossRef]
- Zhou, C.; Jia, Y.; Liu, J.; Li, H.; Fan, Y.; Zhang, Z.; Liu, Y.; Jiang, Y.; Zhou, B.; He, Z.; et al. Scientific objectives and payloads of the lunar sample return mission—Chang’E-5. Adv. Space Res. 2022, 69, 823–836. [Google Scholar] [CrossRef]
- Sun, X.; Chao, H.; Chen, P. Real-time precise orbit determination of LEO satellites using a single-frequency GPS receiver: Preliminary results of Chinese SJ-9A satellite. Adv. Space Res. 2017, 60, 1478–1487. [Google Scholar] [CrossRef]
- Montenbruck, O.; Swatschina, P.; Markgraf, M.; Santandrea, S.; Naudet, J.; Tilmans, E. Precision spacecraft navigation using a low-cost GPS receiver. GPS Solut. 2012, 16, 519–529. [Google Scholar] [CrossRef]
- Yang, Y.; Yue, X.; Dempster, A.G. GPS-based onboard real-time orbit determination for LEO satellites using consider Kalman filter. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 769–777. [Google Scholar] [CrossRef]
- Montenbruck, O.; Hackel, S.; Wermuth, M.; Zangerl, F. Sentinel-6A precise orbit determination using a combined GPS/Galileo receiver. J. Geod. 2021, 95, 109. [Google Scholar] [CrossRef]
- Hauschild, A.; Montenbruck, O. Precise on-board navigation of LEO satellites with GNSS broadcast ephemerides. In Proceedings of the 33rd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2020), Online, 22–25 September 2020. [Google Scholar]
- Israel, D.J.; Mauldin, K.D.; Roberts, C.J.; Mitchell, J.W.; Pulkkinen, A.A.; La Vida, D.C.; Johnson, M.A.; Christe, S.D.; Gramling, C.J. Lunanet: A flexible and extensible lunar exploration communications and navigation infrastructure. In Proceedings of the 2020 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2020; IEEE: Piscataway, NJ, USA, 2020. [Google Scholar]
- Giordano, P.; Malman, F.; Swinden, R.; Zoccarato, P.; Ventura-Traveset, J. The Lunar Pathfinder PNT experiment and Moonlight navigation service: The future of lunar position, navigation and timing. In Proceedings of the 2022 International Technical Meeting of The Institute of Navigation, Long Beach, CA, USA, 25–27 January 2022. [Google Scholar]
- Zini, E.E. Precise Orbit Determination Techniques for a Lunar Satellite Navigation System. Master’s Thesis, Politecnico di Torino, Torino, Italy, 2021. [Google Scholar]
- Offord Harle, N.; Oates, C.; Bywater, S.; Cranstoun, C.; Friend, J.; Lay, G.; Schwarz, B.; Stevens, P.; Hufenbach, B.; Liuicci, F.; et al. Lunar comms and nav infrastructure–first data relay orbiter Lunar Pathfinder, operational in 2024, paves the way for full constellation by 2030s. ASCEND 2021, 2021, 4132. [Google Scholar]
- Commstar Space Communications. Intention to Deploy Next-Generation Hybrid Data Relay Satellite Between the Earth and the Moon by 2023. 2020. Available online: https://commstar.space/news/commstar-space-communications-launch-announcement/ (accessed on 10 October 2020).
- Ma, L.; Xie, P.; Liu, D.; Wu, Y. Research on the Influence of China’s Commercial Spaceflight on the Economic and Social Development of the Regions Along the Belt and Road. New Space 2019, 7, 223–234. [Google Scholar] [CrossRef]
- Palmerini, G.B.; Sabatini, M.; Perrotta, G. En route to the Moon using GNSS signals. Acta Astronaut. 2009, 64, 467–483. [Google Scholar] [CrossRef]
- Flanegan, M.; Gal-Edd, J.; Anderson, L.; Warner, J.; Ely, T.; Lee, C.; Shah, B.; Vaisnys, A.; Schier, J. NASA lunar communication and navigation architecture. In Proceedings of the SpaceOps 2008 Conference, Heidelberg, Germany, 12–16 May 2008. [Google Scholar]
- Xu, M.; Wang, S.; Zhao, W. Why did Chang’e build a Magpie Bridge before exploring the moon? Nanfang Daily 2024, A08. [Google Scholar] [CrossRef]
- Moyer, T.D. Formulation for Observed and Computed Values of Deep Space Network Data Types for Navigation; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Lin, K. Lectures on Space Geodesy—Lecture 8 Very Long Baseline Interferometry (Part 1). Bull. Surv. Mapp. 1983, 02, 43–47. [Google Scholar]
- Hornig, A.; Homeister, M. TYCHO: Demonstrator and operational satellite mission to Earth–Moon-Libration point EML-4 for communication relay provision as a service. Acta Astronaut. 2015, 108, 156–170. [Google Scholar] [CrossRef]
- Chen, X.; Xu, J.; Zhang, X.; Zhang, W. Research on the filter algorithm for integrated autonomous navigation based on angle and velocity measurementin deep space. Sci. Sin. Phys. Mech. Astron. 2022, 52, 214509. [Google Scholar] [CrossRef]
- Xue, X.; Zhang, H.; Kong, D. A review of astronomical autonomous navigation technology for deep space exploration. Astron. Res. Technol. 2017, 14, 382–391. [Google Scholar]
- Battin, R.H. An Introduction to the Mathematics and Methods of Astrodynamics; Aiaa: Reston, VA, USA, 1999. [Google Scholar]
- Duxbury, T.C.; Born, G.H.; Jerath, N. Viewing phobos and deimos for navigating mariner 9. J. Spacecr. Rocket. 1974, 11, 215–222. [Google Scholar] [CrossRef]
- Bhaskaran, S.; Desai, S.; Dumont, P.; Kennedy, B.; Null, G.; Owen, W., Jr.; Riedel, J.; Synnott, S.; Werner, R. Orbit Determination Performance Evaluation of the Deep Space 1 Autonomous Navigation System; NASA: Washington, DC, USA, 1998.
- Mastrodemos, N.; Kubitschek, D.G.; Synnott, S.P. Autonomous navigation for the deep impact mission encounter with comet tempel 1. Space Sci. Rev. 2005, 117, 95–121. [Google Scholar] [CrossRef]
- Ma, P.B.; Baoyin, H.X.; Mu, J.S. Autonomous navigation of Mars probe based on optical observation of Martian moon. Opt. Precis. Eng. 2014, 22, 863–869. [Google Scholar]
- You, W. Multi-Vector Fusion Mechanism and Estimation Method for Astronomical Velocity Measurement and Navigation in Deep Space Exploration. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2020. [Google Scholar]
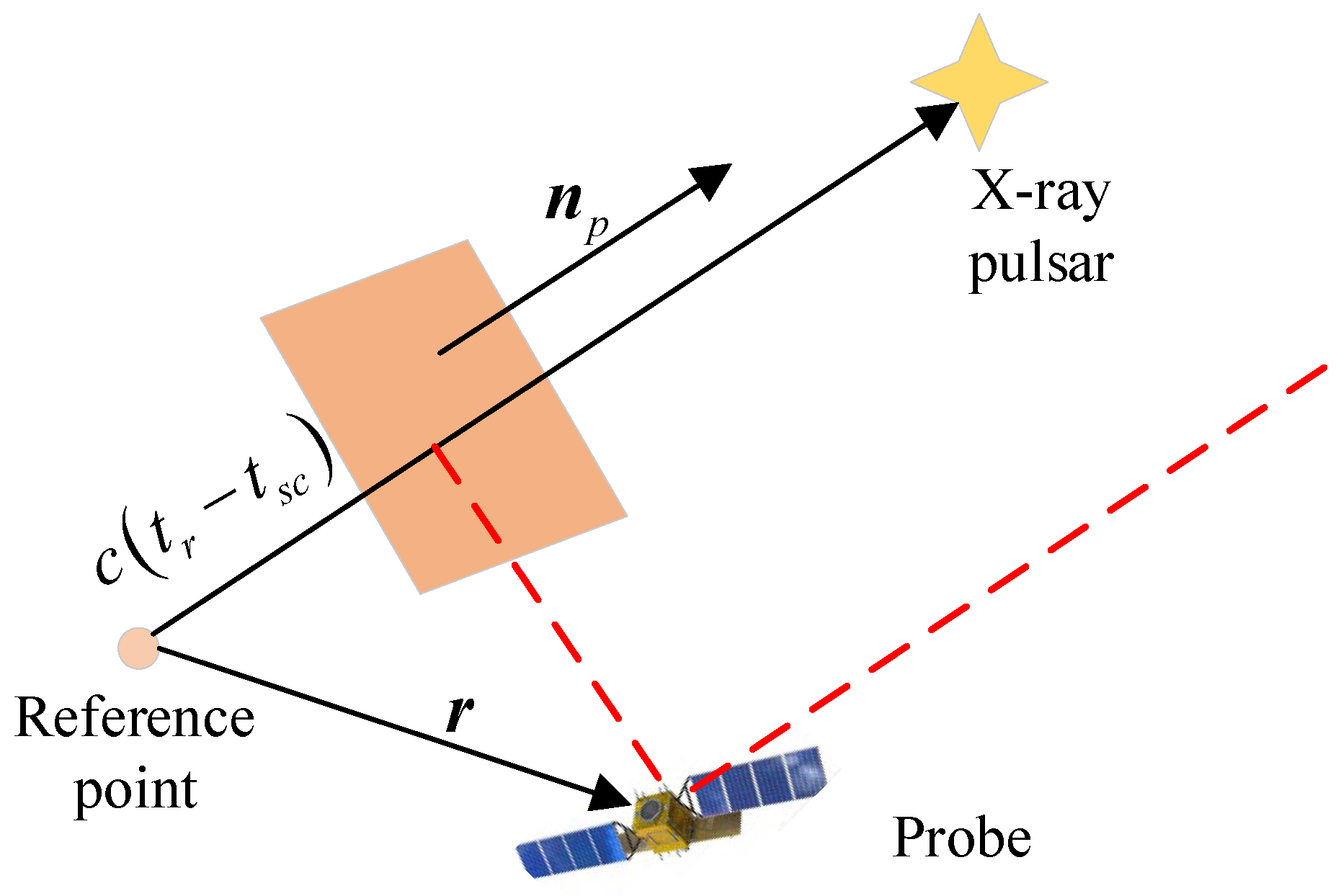
- Downs, G.S. Interplanetary Navigation Using Pulsating Radio Sources; No. JPL-TR-32-1594; NASA: Washington, DC, USA, 1974.
- Sheikh, S.I. The Use of Variable Celestial X-Ray Sources for Spacecraft Navigation; University of Maryland: College Park, MD, USA, 2005. [Google Scholar]
- Wang, H. NASA has completed the world’s first space validation of XNAV. Chin. J. Space Sci. 2018, 38, 277–278. [Google Scholar]
- Zheng, S.; Ge, M.; Han, D.; Wang, W.; Chen, Y.; Lu, F.; Bao, T.; Chai, J.; Dong, Y.; Feng, M.; et al. Test of pulsar navigation with POLAR on TG-2 space station. Sci. Sin. Phys. Mech. Astron. 2017, 47, 099505. [Google Scholar] [CrossRef]
- Lin, Q.; Huang, L.; Shuai, P. TOA estimation methods for the observation data based on the X-ray Pulsar-based Navigation-1 (XPNAV-1) satellite. Chin. Space Sci. Technol. 2017, 38, 1–7. [Google Scholar]
- Zheng, S.J.; Zhang, S.N.; Lu, F.J.; Wang, W.B.; Gao, Y.; Li, T.P.; Song, L.M.; Ge, M.Y.; Han, D.W.; Chen, Y.; et al. In-orbit demonstration of X-ray pulsar navigation with the Insight-HXMT satellite. Astrophys. J. Suppl. Ser. 2019, 244, 1. [Google Scholar] [CrossRef]
- Shuai, P.; Chen, S.; Wu, Y.; Zhang, C.; Li, M. Navigation principles using X-ray pulsars. J. Astronaut. 2007, 06, 1538–1543. [Google Scholar]
- Zhang, W.; Chen, X.; You, W.; Zhang, W.; Fang, X. New autonomous navigation method based on redshift. Shanghai Aerosp. 2013, 30, 32–33+38. [Google Scholar]
- Franklin, R.G.; Birx, D.L. A study of natural electromagnetic phenomena for space navigation. Proc. IRE 1960, 48, 532–541. [Google Scholar] [CrossRef]
- Guo, Y. Self-contained autonomous navigation system for deep space missions. Spacefl. Mech. 1999, 1999, 1099–1113. [Google Scholar]
- Yim, J.; Crassidis, J.; Junkins, J. Autonomous orbit navigation of interplanetary spacecraft. In Proceedings of the Astrodynamics Specialist Conference, Denver, CO, USA, 14–17 August 2000. [Google Scholar]
- Liu, J.; Fang, J.C.; Yang, Z.H.; Kang, Z.W.; Wu, J. X-ray pulsar/Doppler difference integrated navigation for deep space exploration with unstable solar spectrum. Aerosp. Sci. Technol. 2015, 41, 144–150. [Google Scholar] [CrossRef]
- Ning, X.; Gui, M.; Fang, J.; Liu, G.; Dai, Y. A novel differential Doppler measurement-aided autonomous celestial navigation method for spacecraft during approach phase. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 587–597. [Google Scholar] [CrossRef]
- Zhang, H. Research and Implementation of Key Technologies for Improving Space Target Laser Ranging Capability. Master’s Thesis, Shandong University of Science and Technology, Qingdao, China, 2020. [Google Scholar]
- Verhagen, S.; Teunissen, P.J. Least-squares estimation and Kalman filtering. In Handbook of Global Navigation Satellite Systems; Springer: Berlin/Heidelberg, Germany, 2017; pp. 639–660. [Google Scholar]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Bucy, R.S.; Senne, K.D. Digital synthesis of non-linear filters. Automatica 1971, 7, 287–298. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K. Unscented filtering and nonlinear estimation. Proc. IEEE 2004, 92, 401–422. [Google Scholar] [CrossRef]
- Witternigg, N.; Obertaxer, G.; Schönhuber, M.; Palmerini, G.B.; Rodriguez, F.; Capponi, L.; Soualle, F.; Floch, J.J. Weak GNSS signal navigation for Lunar exploration missions. In Proceedings of the 28th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2015), Tampa, FL, USA, 14–18 September 2015. [Google Scholar]
- Zhang, C. Research on adaptive filter methods. Chin. J. Aeronaut. 1998, S1, 97–100. [Google Scholar]
- Wei, W.; Qin, Y.; Zhang, X.; Zhang, Y. Improvement of Sage-Husa algorithm. J. Chin. Inert. Technol. 2012, 20, 678–686. [Google Scholar]
- Xia, Q.; Sun, Y.; Zhou, C. Optimal adaptive algorithm of vanishing Kalman filter and its application. J. Autom. 1990, 03, 210–216. [Google Scholar]
- Qian, H.; Ge, L.; Yu, P. Multi-evanescent factor Kalman filter and its application in SINS initial alignment. J. Chin. Inert. Technol. 2012, 20, 287–291. [Google Scholar]
- Duan, S.; Sun, W.; Wu, Z. Application of error-resistant adaptive EKF in INS/GNSS tight combination. J. Univ. Electron. Sci. Technol. China 2019, 48, 216–220. [Google Scholar]
- Yang, Y.; He, H.; Xu, T. On dynamic adaptive filter. Acta Geod. Cartogr. Sin. 2001, 04, 293–298. [Google Scholar]
- Yang, Y.; Ren, X.; Xu, Y. Main progress in the theory and application of adaptive robust filter. J. Navig. Position. 2013, 1, 9–15. [Google Scholar]
- Sage, A.P.; Husa, G.W. Adaptive filter with unknown prior statistics. In Proceedings of the Tenth Joint Automatic Control Conference, Boulder, CO, USA, 5–7 August 1969. No. 7. [Google Scholar]
- Fagin, S.L. Recursive linear regression theory, optimal filter theory, and error analysis of optimal systems. In IEEE International Convention Record; No. Part 1; IEEE: Piscataway, NJ, USA, 1964; Volume 12. [Google Scholar]
- Yang, Y. Adaptive Dynamic Navigation and Positioning; Surveying and Mapping Press: Beijing, China, 2006; pp. 10–40. [Google Scholar]
- Mohamed, A.H.; Schwarz, K.P. Adaptive Kalman filter for INS/GPS. J. Geod. 1999, 73, 193–203. [Google Scholar] [CrossRef]
- Qiao, D.; Zhou, X.; Li, X. Analytical configuration uncertainty propagation of geocentric interferometric detection constellation. Astrodynamics 2023, 7, 271–284. [Google Scholar] [CrossRef]
- Le, L. Star selection algorithm for GNSS/pseudolite combined positioning. Electron. Test 2020, 13, 41–43+73. [Google Scholar]
- Feng, B.; Chai, H.; Pan, Z.; Wang, M.; Yang, K. An improved star selection algorithm for integrated navigation systems. Eng. Surv. Mapp. 2018, 27, 26–31. [Google Scholar]
- Peng, S.; Guo, C.; Liu, F. Research on fast star selection algorithm in Beidou/GPS dual-mode positioning. GNSS World China 2017, 42, 11–14. [Google Scholar]
- Wang, E.; Jia, C.; Qu, P.; Huang, Y.; Pang, T.; Bie, Y.; Jiang, Y. Beidou/GPS integrated navigation star selection algorithm based on chaotic particle swarm optimization. J. Beijing Univ. Aeronaut. Astronaut. 2019, 45, 259–265. [Google Scholar]
- Zhang, J.; Li, J.; Hu, C. Satellite navigation and positioning solution method based on Cubature Kalman filter. J. Univ. Chin. Acad. Sci. 2021, 38, 532–537. [Google Scholar]
- Zhang, J.; Yang, Y.; Qian, F. Research on GNSS/INS error feedback correction based on Kalman filter-neural network prediction. Electron. Des. Eng. 2015, 23, 103–105. [Google Scholar]
- Carlson, N.A. Federated square root filter for decentralized parallel processors. IEEE Trans. Aerosp. Electron. Syst. 1990, 26, 517–525. [Google Scholar] [CrossRef]
- Wu, L.; Sun, Y.; Chen, C. Multi-constellation integrated navigation adaptive information fusion filter algorithm. Aerosp. Control 2010, 28, 38–42+62. [Google Scholar]
- Zhang, Y.; Jiang, X.; Yang, W.; Liu, J.; Wei, Y. Research on joint positioning technology of GNSS systems based on Kalman filter. Electron. Meas. Technol. 2021, 44, 109–113. [Google Scholar]
- Menn, M.D.; Bernstein, H. Ephemeris observability issues in the global positioning system (GPS) autonomous navigation (AUTONAV). In Proceedings of 1994 IEEE Position, Location and Navigation Symposium-PLANS’94; IEEE: Piscataway, NJ, USA, 1994. [Google Scholar]
- Guo, S.; Cai, H.; Meng, Y.; Geng, C.; Jia, X.; Mao, Y.; Geng, T.; Mao, Y.; Zhang, Y.; Xie, X. Beidou-3 navigation and positioning technology system and service performance. Acta Geod. Cartogr. Sin. 2019, 48, 810–821. [Google Scholar]
- Li, Z.; Xin, J.; Guo, R.; Li, X.; Tang, C.; Tian, Y. Feasibility analysis of autonomous satellite navigation based on Beidou inter-satellite link. Geomat. Inf. Sci. Wuhan Univ. 2022, 47, 55–60. [Google Scholar]
- Shao, R.; Chang, J.; Lin, X.; Tan, S.; Gong, W.; Lin, B. An orbit determination algorithm suitable for extended users between Beidou-3 satellites. Chin. Space Sci. Technol. 2024, 44, 106–113. [Google Scholar]
- Yang, Y.; Yang, Y.; Hu, X.; Tang, C.; Zhao, L.; Xu, J. Comparative analysis of the accuracy of two orbit determination modes of Beidou-3 satellite. Acta Geod. Cartogr. Sin. 2019, 48, 831–839. [Google Scholar]
- Zhou, Y. Research on Key Technologies for Autonomous Orbit Determination of User Spacecraft Based on the Beidou Interstellar Link. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2020. [Google Scholar]
- Zhang, W.; Wang, X.; Cui, W.; Zhao, Z.; Chen, S. Self-induced collision risk of the Starlink constellation based on long-term orbital evolution analysis. Astrodynamics 2023, 7, 445–453. [Google Scholar] [CrossRef]
- Abusali, P.A.M.; Tapley, B.D.; Schutz, B.E. Autonomous navigation of global positioning system satellites using cross-link measurements. J. Guid. Control. Dyn. 1998, 21, 321–327. [Google Scholar] [CrossRef]
- Lin, L.; Liu, Y. On the problem of deficient rank in autonomous orbit determination with star-to-star relative measurements. J. Spacecr. TTC Technol. 2000, 19, 1–4. [Google Scholar]
- Chen, J.; Jiao, W.; Ma, J.; Song, X. Research on autonomous orbit determination of navigation satellites based on inter-satellite ranging/orbit orientation parameter constraints. Geomat. Inf. Sci. Wuhan Univ. 2005, 05, 439–443. [Google Scholar]
- Tang, C. Fusion of Multiple Observation Data to Calculate High-Precision Broadcast Ephemeris of Beidou Navigation Satellites. Master’s Thesis, University of Chinese Academy of Sciences, Beijing, China, 2016. [Google Scholar]
- Gong, X. Research on Centralized Autonomous Real-Time Orbit Determination and Time Synchronization Method of Beidou System. Ph.D. Thesis, Wuhan University, Wuhan, China, 2013. [Google Scholar]
- Zhang, W.; Liu, W.; Gong, X. Analysis of the impact of EOP forecast errors on autonomous orbit determination results. J. Geod. Geodyn. 2011, 31, 106–110. [Google Scholar]
- Zhao, Q.; Liu, J.; Ge, M. Research on precision orbit determination theory and software of GPS navigation constellations and low-orbit satellites. Geomat. Inf. Sci. Wuhan Univ. 2005, 30, 1. [Google Scholar]
- Liu, W. Method Research and Simulation Calculation of Navigation Satellite Autonomous Orbit Determination and Satellite-Ground Joint Orbit Determination. Ph.D. Thesis, Wuhan University, Wuhan, China, 2008. [Google Scholar]
- Zhao, D.; Zhou, H.; Wang, Z. Joint orbit determination data fusion modeling and optimal weighting algorithm based on multi-source observations. J. Syst. Simul. 2008, 10, 2515–2519. [Google Scholar]
- Song, X. Research on Orbit Determination of COMPASS Navigation Satellite. Ph.D. Thesis, Chang’an University, Xi’an, China, 2008. [Google Scholar]
- Li, Z.; Huang, J. GPS Measurement and Data Processing; Wuhan University: Wuhan, China, 2005; pp. 40–42. [Google Scholar]
- Cai, Z.; Han, C.; Chen, J. Constellation rotation error analysis and control of long-term autonomous orbit determination of navigation satellites. J. Astronaut. 2008, 02, 522–528. [Google Scholar]
- Ruan, R.; Feng, L.; Jia, X. Equipment delay estimation method in navigation satellite-ground/inter-satellite link joint orbit determination. Acta Geod. Cartogr. Sin. 2014, 43, 137–142+157. [Google Scholar]
- Shuai, P.; Qu, G. Time synchronization technology for autonomous navigation of navigation constellations. Acta J. Astronaut. 2005, 06, 768–772. [Google Scholar]
- Chen, Z. Research on Key Technologies for Autonomous Operation of Navigation Satellite Constellations Based on Inter-Satellite Links. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2012. [Google Scholar]
- Hill, K.; Born, G.H.; Lo, M.W. Linked, Autonomous, Interplanetary Satellite Orbit Navigation(LiAISON) in Lunar Halo Orbits. Adv. Astronaut. Sci. 2006, 123, 2369–2388. [Google Scholar]
- Hill, K.; Parker, J.; Born, G.; Demandante, N. A lunar L2 navigation, communication, and gravity mission. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Keystone, CO, USA, 21–24 August 2006. [Google Scholar]
- Hill, K.; Parker, J.; Born, G.H.; Lo, M.W. Low-cost lunar communication and navigation. In CCAR White Paper 5; 2006. Available online: https://www.researchgate.net/publication/237404072_LOW-COST_LUNAR_COMMUNICATION_AND_NAVIGATION (accessed on 17 June 2024).
- Hill, K.A.; Born, G.H. Autonomous orbit determination from lunar halo orbits using crosslink range. J. Spacecr. Rocket. 2008, 45, 548–553. [Google Scholar] [CrossRef]
- Parker, J.; Anderson, R.; Born, G.; Fujimoto, K.; Leonard, J.; McGranaghan, R. Navigation between geosynchronous and lunar L1 orbiters. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference, Keystone, CO, USA, 21–24 August 2006. [Google Scholar]
- Parker, J.S.; Leonard, J.M.; Anderson, R.L.; Born, G.H. LiAISON-supplemented navigation of a crewed vehicle in a lunar halo orbit. In Proceedings of the AAS/AIAA Astrodynamics Specialist Conference, Hilton Head, SC, USA, 11–15 August 2013. No. AAS 13-776. [Google Scholar]
- Hesar, S.G.; Parker, J.S.; Leonard, J.M.; McGranaghan, R.M.; Born, G.H. Lunar far side surface navigation using linked autonomous interplanetary satellite orbit navigation (LiAISON). Acta Astronaut. 2015, 117, 116–129. [Google Scholar] [CrossRef]
- Du, L. Inter-satellite ranging and orbit determination of Halo-lunar orbit under circular restricted three-body problem. Acta Geod. Cartogr. Sin. 2013, 42, 184–190. [Google Scholar]
- Liu, P.; Hou, X.Y.; Tang, J.S.; Liu, L. Application of two special orbits in the orbit determination of lunar satellites. Res. Astron. Astrophys. 2014, 14, 1307. [Google Scholar] [CrossRef]
- Huang, Y.; Yang, P.; Chen, Y.; Li, P.; Zhou, S.; Tang, C.; Hu, X. Interstellar ranging and autonomous orbit determination of the Earth-Moon space probe. Sci. Sin. (Phys. Mech. Astron.) 2023, 53, 132–144. [Google Scholar]
- Cheetham, B.; Gardner, T.; Forsman, A.; Kayser, E.; Clarkson, M. Capstone: A unique CubeSat platform for a navigation demonstration in cislunar space. In Proceedings of the ASCEND 2022, Las Vegas, NV, USA, 24–26 October 2022; p. 4382. [Google Scholar]
- Li, X. Research on Precise Orbit Determination of Lunar Probes Using Combined Orbit Measurement VLBI, USB and Space VLBI Technology. Ph.D. Thesis, Wuhan University, Wuhan, China, 2016. [Google Scholar]
- Qi, Y. Anton de Ruiter. Trajectory correction for lunar flyby transfers to libration point orbits using continuous thrust. Astrodynamics 2022, 6, 285–300. [Google Scholar] [CrossRef]
- Muralidharan, V.; Howell, K.C. Stretching directions in cislunar space: Applications for departures and transfer design. Astrodynamics 2023, 7, 153–178. [Google Scholar] [CrossRef]

| Project Name | Leading Institution | Project Objectives | Navigation Communication Criteria | Orbit |
|---|---|---|---|---|
| LunaNet | NASA | A flexible and scalable lunar communications and navigation architecture | Providing network services, positioning, navigation and timing services, and scientific utilization services near the Moon | Earth–Moon space |
| CommStar-1 | CSC | Real-time relay optical laser communications between the Moon and Earth | It will provide real-time advanced data services within a distance of 360,000 km, via microwave and laser communications. | Orbit between Earth and the Moon |
| Moonlight | ESA | Establishing a lunar shared communication and navigation network | For manned missions, the target positioning accuracy at any location on the Moon can reach less than 50 m. | Orbit around the Moon |
| Lunar Pathfinder | ESA | The first dedicated navigation and communication satellite of Project Moonlight | For unmanned exploration missions 1: Achieve 100 m positioning accuracy 2: Communication to the Moon: UHF, S-band 3: Ground relay: X-band 4: Data rate: 0.5–2048 kbps 5: Communication protocol: CCSDS Proximity-1 | Frozen large elliptical orbit around the Moon |
| Queqiao | China | Provide lunar relay, communication and navigation services | In view of the communication and navigation capability requirements of the fourth phase of lunar exploration, the International Lunar Research Station and subsequent lunar exploration missions will carry out research on the lunar communication and navigation satellite system, complete critical technologies such as lunar relay navigation satellite constellation planning, relay navigation network architecture and navigation algorithms, and establish an interoperable lunar relay navigation constellation to provide general relay communication and navigation services for targets on the lunar surface. | Circum Moon+ Libration point+ GEO Constellation |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Sun, Z.; Chen, X.; Pan, L.; Zhong, Y. Summary of Lunar Constellation Navigation and Orbit Determination Technology. Aerospace 2024, 11, 497. https://doi.org/10.3390/aerospace11060497
Zhang X, Sun Z, Chen X, Pan L, Zhong Y. Summary of Lunar Constellation Navigation and Orbit Determination Technology. Aerospace. 2024; 11(6):497. https://doi.org/10.3390/aerospace11060497
Chicago/Turabian StyleZhang, Xiao, Zhaowei Sun, Xiao Chen, Linxin Pan, and Yubin Zhong. 2024. "Summary of Lunar Constellation Navigation and Orbit Determination Technology" Aerospace 11, no. 6: 497. https://doi.org/10.3390/aerospace11060497
APA StyleZhang, X., Sun, Z., Chen, X., Pan, L., & Zhong, Y. (2024). Summary of Lunar Constellation Navigation and Orbit Determination Technology. Aerospace, 11(6), 497. https://doi.org/10.3390/aerospace11060497







