Comprehensive Measurement of Position and Velocity in the Transverse Direction Using the Crab Pulsar

Abstract

Traditional X-ray pulsar ranging and velocity measurement methods only estimate the radial position and velocity information of the pulsar. For non-linear orbits, errors in the transverse position and velocity of the pulsar lead to errors in the radial velocity of the pulsar, leading to distortion of the X-ray pulsar profile. Based on this, we propose using the distortion of the pulsar profile to infer the transverse position and velocity information of the pulsar. First, a model of the distortion of the pulsar profile due to errors in the transverse position and velocity is established, and the observable directions of the transverse position and velocity are given separately. Then, considering that the distortions in the pulsar profile caused by errors in the transverse position and velocity are indistinguishable, we establish a reactive motion state measure related to the observable directions for the transverse position and velocity errors as a new observable measure in X-ray pulsar navigation. The experimental results show that the precision of the reactive motion state measure reaches 0.57, equivalent to a position error of 284.50 m or a velocity error of 0.57 m/s.

1. Introduction

X-ray pulsar navigation, as a new type of astronomical navigation system, provides crucial support for deep space exploration, autonomous spacecraft operations, and comprehensive navigation in near-Earth space. Pulsars are rapidly rotating neutron stars, and their highly periodic and stable signals can be utilized to identify changes in a spacecraft’s spatial position, allowing for high-precision navigation and positioning of spacecraft [1,2,3,4,5].

Research on pulsars has been ongoing for over half a century, leading to numerous breakthroughs. Countries such as the United States and Russia have conducted extensive surveys and studies on various aspects of pulsars and have established a complete pulsar navigation technology system [6,7,8]. In 2017, NASA installed the NICER detector on the International Space Station and carried out in-orbit demonstration experiments and verification of X-ray millisecond pulsar navigation technology [9,10]. Despite its late start in X-ray pulsar observation activities due to limitations in the X-ray sensor hardware technology, China has rapidly developed in recent years and successfully launched several independently developed X-ray pulsar observation satellites, such as XPNAV-1 and Tiangong 2, validating the feasibility of practical applications of pulsar navigation [11,12,13].

X-ray pulsar positioning utilizes the periodic signals emitted by pulsars and the time differences between multiple receivers on Earth to determine positions. In theory, measurements of spacecraft spatial positions can be derived by observing three pulsars in different directions. Combined with spacecraft orbital dynamics models [14], spacecraft’s spatial positions can be estimated using navigation filters. The estimation of a spacecraft’s radial velocity using X-ray pulsars is achieved based on the Doppler effect, through short-term observations of the pulsar period by the spacecraft [15,16]. In terms of navigation filtering, the methods include robust filtering algorithms for model uncertainties [17], the Augmented Sigma-point Kalman Filter algorithm for addressing pulsar direction errors [18], and the Unscented Kalman Filter algorithm based on multi-mode adaptive estimation [19]. Li N, Kang Z W, and others have combined Empirical Mode Decomposition (EMD) with an extended Kalman filter (EKF) to propose an adaptive extended Kalman filter method based on EMD [20].

High-speed spacecraft flight and pulsar period leaps can cause cumulative distortion in the pulsar profile, leading to a shift in the pulsar time of arrival (TOA) [21]. The estimation of the Doppler shift in the pulsar velocity utilizes the accumulated distortion of the X-ray pulsar profile to provide navigation information. The basic principle is as follows: first, the pulsar signal is folded according to different periods to obtain a series of accumulated profiles with different distortions. Then, these accumulated profiles are analyzed to identify the profile with the least distortion, and the corresponding period is determined as the intrinsic period of the pulsar [22]. Therefore, pulsar period estimation is also an important topic. In the field of period estimation, numerous experts and scholars have conducted in-depth research and achieved significant results. Currently, the typical methods include time-domain methods, Fourier spectrum methods [23], and others. Song M Z and Wang Y D improved the fast folding algorithm by introducing the post-order traversal of a binary tree, which can be used to estimate the spin period of an X-ray pulsar under low signal-to-noise ratio conditions. [24]. Shen L R et al. used the Fast Lomb Periodogram to estimate the initial value of the pulsar’s rotation frequency and implemented fine frequency division based on a criterion of layer-by-layer overlap in a small domain around the initial frequency value, calculating continuous Lomb periodograms at a fine frequency, thus achieving high-precision pulsar period estimation with low computational cost [25]. Liu J proposed a rapid pulsar period estimation method based on compressed sensing, leveraging the strong sparse signal processing capability of compressed sensing and the concentration of the pulsar profile energy in the low-frequency part, developing a low-frequency Fourier transform matrix into a measurement matrix. Super-resolution sparse recovery algorithms have been used to achieve period estimation for X-ray pulsars [26].

However, for pulsars in orbit, they may be significantly affected by the effects of gravitational fields, and the non-uniformity of the gravitational field can cause a pulsar’s orbit to twist and deform, affecting its position in the line of sight. In addition, disturbances from other celestial bodies may also affect a pulsar’s orbit and position [27]. For example, close interactions with other celestial bodies may alter a pulsar’s trajectory, leading to positional drift. This drift could cause accumulated distortion in the pulsar’s profile, necessitating modeling and correction of these positional drifts to obtain accurate observational results. Wang Y D utilized satellite orbital dynamics to approximate pulsar phase evolution and proposed the use of on-orbit pulsar timing algorithms for X-ray pulsar navigation correction [28]. Wang Y D introduced a framework called on-orbit epoch folding, which, through steps that eliminate the effects of spacecraft orbit motion, can transform the TOA with the original photon TOA corrected according to the Solar System Barycenter (SSB). This enables the search for the period of the transformed photons’ TOAs and estimation of the initial phase [29]. Wu D L introduced the concept of quantum computing and proposed a fast pulsar positioning and velocity estimation method based on sparrow-optimized quantum compressed sensing, capable of simultaneously providing position and velocity information [30]. Sun Haifeng proposed the grouped bi-chi-squared technique inversion method based on a significant enhancement in orbital dynamics pulse profiles, which can reduce the orbital elements in the distorted information in X-ray pulse profiles [31]. Su J Y studied the distribution characteristics of significant data and proposed using the variance in pulsar profile significance data as the basis for the optimal estimation of orbital elements, achieving the estimation of orbital elements under the presence of deviations in all six orbital parameters [32].

The traditional methods for measuring the velocity and distance of pulsars have focused primarily on radial velocity or position information, presenting several limitations. Firstly, if a pulsar possesses velocity components in directions other than radial, traditional methods, by only considering the radial velocity, may lead to misconceptions about the pulsar’s overall motion state. Additionally, the traditional distance measurement techniques typically calculate the distance by measuring the time it takes for a pulse signal emitted by a pulsar to be received by a receiver [33]. In reality, slight variations in a pulsar’s position due to various factors may affect the accuracy of distance calculations. Moreover, these methods do not provide information on the relative velocity between the pulsar and the receiver, which may be required in certain application scenarios. Jia Y Z utilized the cyclic cross-correlation method to solve for the arrival time of pulsars in the radial direction, established a model for pulsar profile distortion under transverse position errors, and thereby determined the observable directions in the transverse plane; finally, this method has been used to calculate position errors in the observable directions on the pulsar’s transverse surface [34]. Liu J employed singular value decomposition to study the directions of observable velocity components, estimating the two Doppler velocity components corresponding to the largest and middle singular values, while also proposing the Dictionary Folding (DF) method to reduce computational requirements [35].

In non-linear orbits, even velocity or position errors for pulsars in the perpendicular plane can lead to radial velocity errors, subsequently causing deformations in the pulsar profile. Experiments have shown that for pulsars with low flux, the signal-to-noise ratio of their profiles is too low, allowing only for the detection of phase shifts; effective detection of profile distortions is possible only for high-flux pulsars [36]. A combined estimate of velocity and distance measurements can provide a more accurate estimation of the target position than using distance measurements alone. Integrating pulsar distance and velocity measurements can offer a more precise target position estimation. By combining the results of both measurements, certain errors can be eliminated, enhancing the accuracy of the target position estimation. For these reasons, we utilize the accumulated profile distortions of the high-flux Crab pulsar to infer transverse position and velocity, proposing a method to achieve comprehensive measurement of position and velocity information using a single pulsar. This method, in principle, determines the observable position-reactive directions and velocity-reactive directions on the transverse surface of the pulsar. Then, given that the pulsar profile distortions caused by transverse position and velocity errors are indistinguishable, we establish a reactive motion state measure concerning transverse position and velocity errors in the observable directions, serving as a new motion observational metric in X-ray pulsar navigation.

2. The Orbital Dynamics Equations and Pulsar Profile Distortion

Currently, autonomous positioning of spacecraft using pulsars primarily relies on filtering algorithms based on orbital dynamics. For spacecraft in orbit, short-term forecasts of their position, velocity, and other state information can be accomplished by adhering to the laws of orbital dynamics. For Earth satellites, the geocentric inertial coordinate system (J2000.0) is typically selected. The state model of the autonomous navigation system for Earth satellites can be described using a general state equation.

$$\stackrel{•}{\mathit{X}}(t)=f(\mathit{X},t)+w(t)$$

(1)

In Equation (1), the state vector components $\mathit{X}={[x,y,z,v_x,v_y,v_z]}^{\mathrm{T}}$, $\mathit{p}=\left[x,y,z\right]$, and $v=\left[v_x,v_y,v_z\right]$ correspond to the spacecraft’s position and velocity vectors, respectively. $f\left(•\right)$ denotes the orbital dynamics model, and w denotes the noise.

The Pulsar Profile Distortion

During its flight, a spacecraft continuously collects photons from pulsars and processes them according to a predicted period (or frequency) through Epoch Folding (EF), thereby reconstructing the real-time accumulated profile of the pulsar. Due to the unknown pulsar period, the accumulated pulsar profile obtained through the predicted period may exhibit certain distortions when compared to the standard pulsar profile.

Let the normalized standard profile of the pulsar be denoted by $h(\phi )$. Herein, $\phi$ signifies the pulse phase; the cumulative pulsar profile $\tilde{h}(\tilde{\phi })$ is represented as the average of all the accumulated sub-profiles of the pulsar and can be articulated as follows:

$$\tilde{h}(\tilde{\phi })=\frac{1}{N}{\displaystyle {\sum }_{n=0}^{N-1}h(\phi +\Delta {\phi }_n)}=\frac{1}{N}{\displaystyle {\sum }_{n=0}^{N-1}h\left(\phi +\frac{\delta r_n^{\mathrm{r}}}{c·T}\right)}$$

(2)

where c represents the speed of light; $T$ signifies the intrinsic period of the pulsar; $\Delta {\phi }_n$ denotes the phase error for the $n\left(n=0,1,2,\dots ,N-1\right)$ period; N stands for the number of pulsar periods within the cumulative observation time.

From Equation (2), it is evident that the cumulative profile of a pulsar is a superposition of pulsar sub-profiles at different phases, inevitably leading to distortions. According to the literature [28], the pulsar profile results from the superposition of sub-profiles at various phases; to prevent distortions in the cumulative pulsar profile, the radial error must always be zero. Based on the properties of error propagation, for the radial error to remain consistently zero, the transverse position and velocity errors must also be zero.

For non-linear orbits, our method is predicated upon the time-domain ${\chi }^2$ estimation technique, with the ${\chi }^2$ value serving as the criterion for assessing the extent of the distortion in the cumulative profile. Theoretically, the highest ${\chi }^2$ value denotes the minimum degree of distortion. This is attributable to the fact that compared to distorted profiles, the standard pulsar profile exhibits the sharpest peaks [37].

3. Comprehensive Measurement of Position and Velocity in the Transverse Direction

In this section, we propose a method that exclusively utilizes the Crab pulsar to comprehensively measure the transverse position and velocity. Contrary to traditional methods of pulsar-based positioning and velocity determination using X-rays, this approach employs the observable transverse reactive direction as a physical measure, focusing on the transverse position and velocity information. Due to the strong correlation between position and velocity, which typically results in significant errors in an ordinary dimensionless directional search for position and velocity, we introduce a reactive motion state measure related to both position and velocity to enhance the search accuracy. The method outlined in this paper comprises three modules: (1) searching for the position- and velocity-reactive directions in the transverse plane; (2) solving for the adjustment coefficients of position and velocity, constructing a reactive motion state measure; (3) comprehensively measuring position and velocity transversely.

3.1. The Reactive Direction in the Transverse Plane

Velocity and position errors can be decomposed into three perpendicular components in three-dimensional space. The error component in the line-of-sight direction is readily estimable, whereas the two mutually perpendicular error components in the plane in the transverse plane are challenging to assess. Our research has found that in the transverse plane, distortions exhibit varying sensitivities to the two error components, with the degree of pulsar profile distortion caused by errors in different directions varying accordingly. The greater the distortion induced in the pulsar profile, the better the observability in that transverse direction.

Based on the methodology described in reference [34], it is known that on the pulsar’s perpendicular plane, the distortion profiles of different radial and tangential positions or velocity errors form a “ridge”. The peak of this ridge, representing the maximum ${\chi }^2$ value, signifies the pulsar profile with the minimal positional error. In the “ridge direction”, ${\chi }^2$ values of the pulsar’s distortion profiles are nearly identical, that is, based on the pulsar’s distortion profiles with the same ${\chi }^2$ values. In contrast, perpendicular to the “ridge”, the ${\chi }^2$ values of the pulsar’s distortion profiles vary significantly, enabling the differentiation of positions along this direction based on ${\chi }^2$ of the pulsar’s distortion profiles. The variation in the distortion degree of the pulsar profile is more reactive along the perpendicular to the ridge. 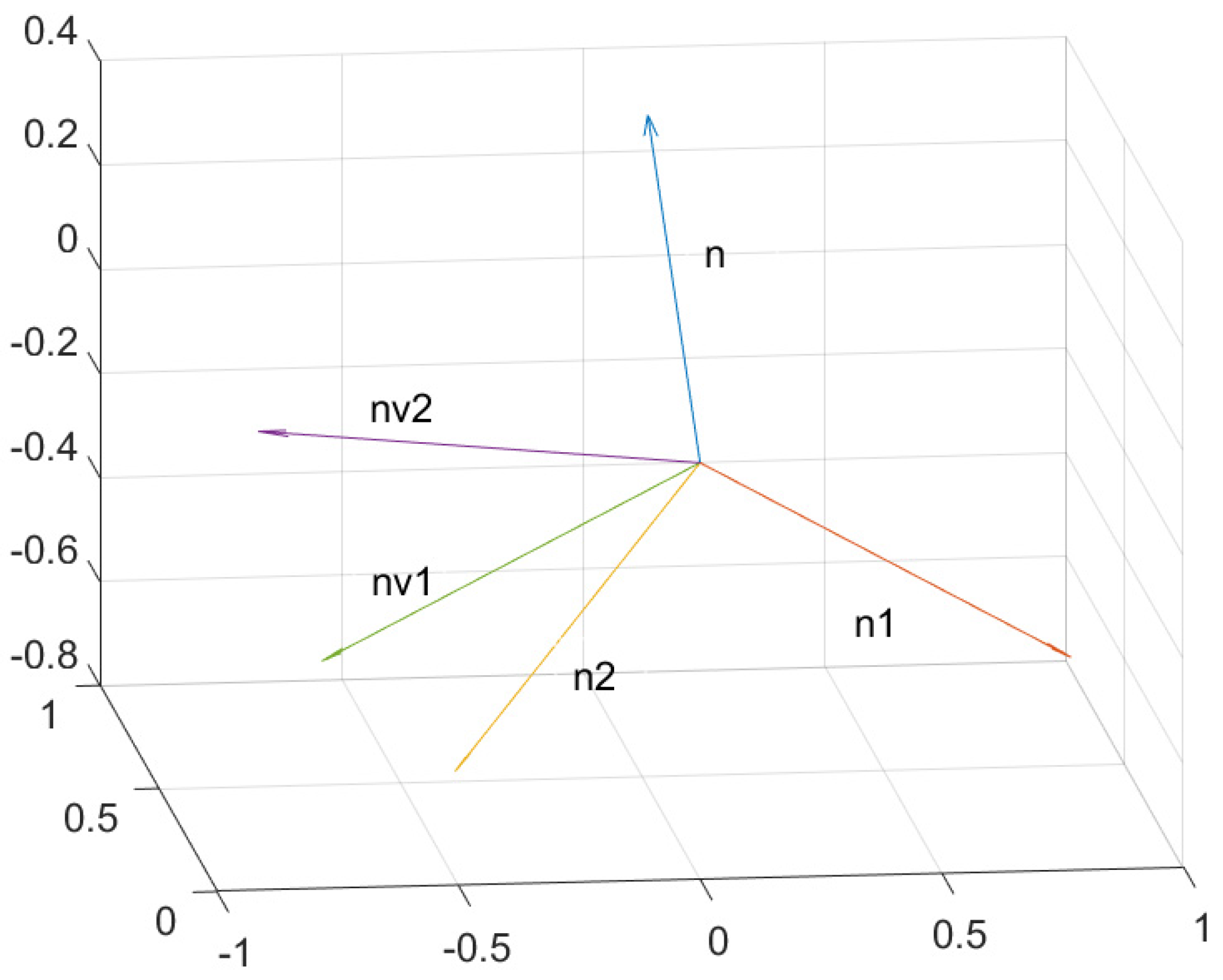As seen in Figure 1, the reactive direction is a specific radial direction of the orbital projection on the pulsar’s perpendicular plane. The reactive direction indicates that velocity errors and positional errors in this direction can easily lead to positional errors in the radial direction. Since the reactive direction can be regarded as the radial direction at a specific time within the observation period, it is termed the Reactive Radial Direction (RRD).

After constructing the model for pulsar profile distortion, based on the “ridge line direction”, the observable transverse direction perpendicular to it can be calculated. After obtaining the slope $p_r$ of the “ridge line”, the RRD can be obtained through the following set of equations:

$$\alpha =\arctan p_r$$

(3)

$$\beta =\alpha +\frac{\pi }{2}$$

(4)

$$\mathit{A}=\mathit{n}{\mathit{n}}^T$$

(5)

$$\mathit{B}=\left[\begin{array}{ccc}0& -\mathit{n}(3)& \mathit{n}(2)\\ \mathit{n}(3)& 0& -\mathit{n}(1)\\ -\mathit{n}(2)& \mathit{n}(1)& 0\end{array}\right]$$

(6)

$$\mathit{C}=\cos \beta ·{\mathit{I}}_{3\times 3}+(1-\cos \beta ){\mathit{A}}^2+\sin \beta ·\mathit{B}$$

(7)

$${\mathit{n}}_{rrd}=\mathit{C}·{\mathit{n}}_s$$

(8)

where $\alpha$ is the angle between the direction of the “ridge line” and the velocity direction at the initial position, and $\beta$ is the angle between the RRD and the velocity direction at the initial position. $\mathit{n}$ represents the direction of the pulsar, while $\mathit{n}(1)$, $\mathit{n}(2)$, $\mathit{n}(3)$, respectively, denote the three components of $\mathit{n}$. $\mathit{A}$ is a matrix formed by $\mathit{n}$, $\mathit{B}$ is an antisymmetric matrix, and $\mathit{C}$ is the rotation matrix from the velocity direction at the initial position to the RRD. ${\mathit{n}}_s$ is the vertical direction of the initial position’s projection onto the transverse plane, and ${\mathit{n}}_{rrd}$ is the RRD being solved for.

We aim to comprehensively measure the velocity and position perpendicular to the transverse direction of the pulsar, thus necessitating separate determination of the position-reactive direction $p_{rrd}$ and the velocity-reactive direction $v_{rrd}$.

Figure 1 provides a schematic illustration concerning the pulsar’s radial direction and orbital plane, orbital projection, and initial position, as well as the position-reactive and velocity-reactive directions. Herein, the vector $\mathit{n}$ denotes the direction of the pulsar; vector ${\mathit{n}}_1$ represents the projection of the initial position vector of the detector onto the transverse plane. ${\mathit{n}}_2$ is perpendicular to ${\mathit{n}}_1$; $\mathit{n}{\mathit{v}}_1$ is the position-reactive direction; $\mathit{n}{\mathit{v}}_2$ is the velocity-reactive direction; ${\mathit{n}}_1$, ${\mathit{n}}_2$, $\mathit{n}{\mathit{v}}_1$, and $\mathit{n}{\mathit{v}}_2$ are all on the same plane, that is, the transverse plane.

3.2. The Solution for Adjustment Coefficients for Position and Velocity

Due to the correlation between the distortion caused by position and velocity offsets, they mutually influence each other, resulting in lower accuracy in the dimensionless directional search for position and velocity. In this section, an attempt is made to demonstrate that with the same orbital error, it is impossible to differentiate whether it is caused by an initial positional error or an initial velocity error. Additionally, it may be assumed that there exists a linear relationship between position and velocity. Subsequently, this linear relationship may be theoretically solved and termed the adjustment coefficient. Finally, a reactive motion state measure concerning the position and velocity on the transverse plane is established as a new observable in X-ray pulsar navigation.

3.2.1. The Indistinguishability of the Offsets in Position and Velocity

In this subsection, we explore whether the orbital errors caused by initial position errors and initial velocity errors can be distinguished.

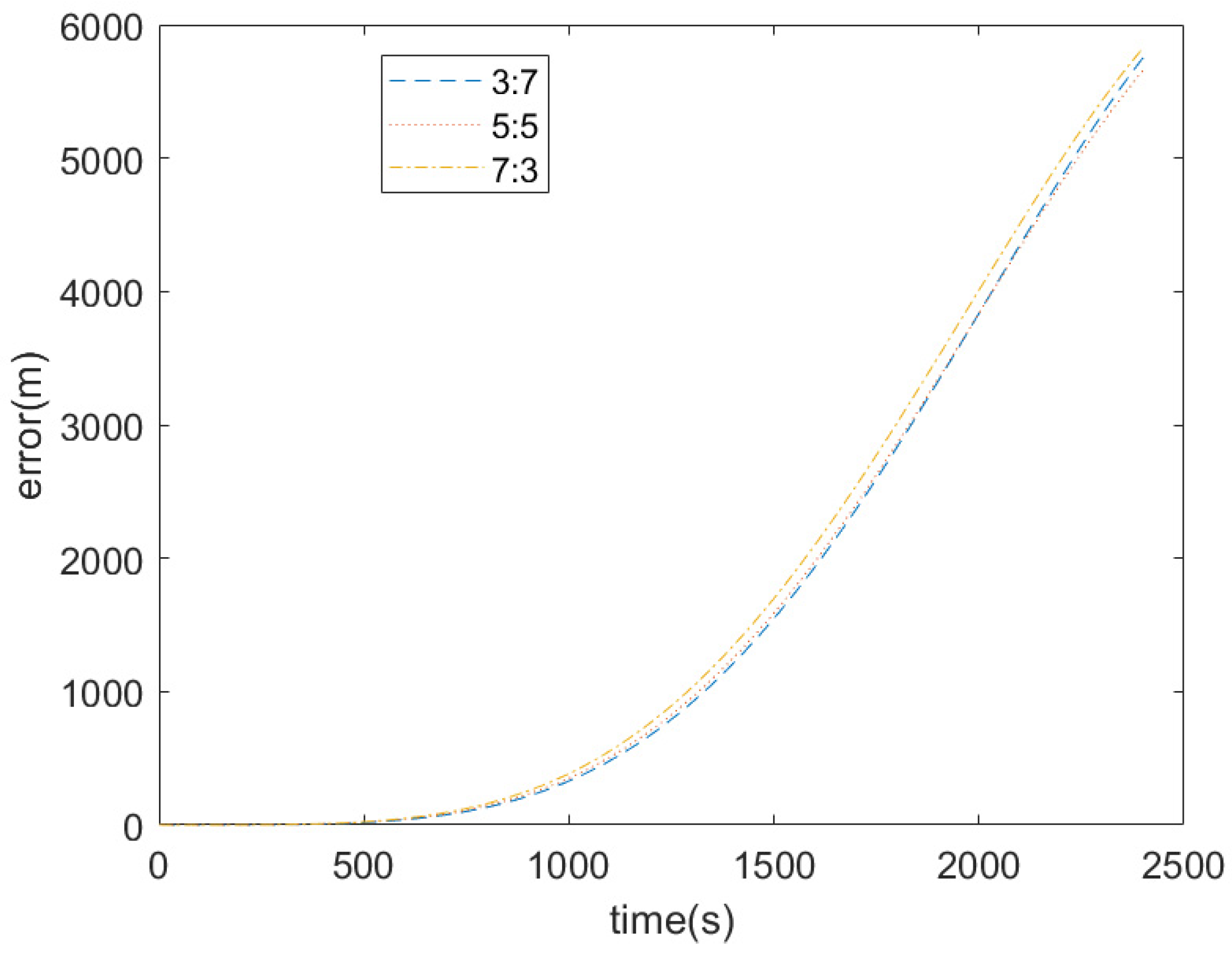
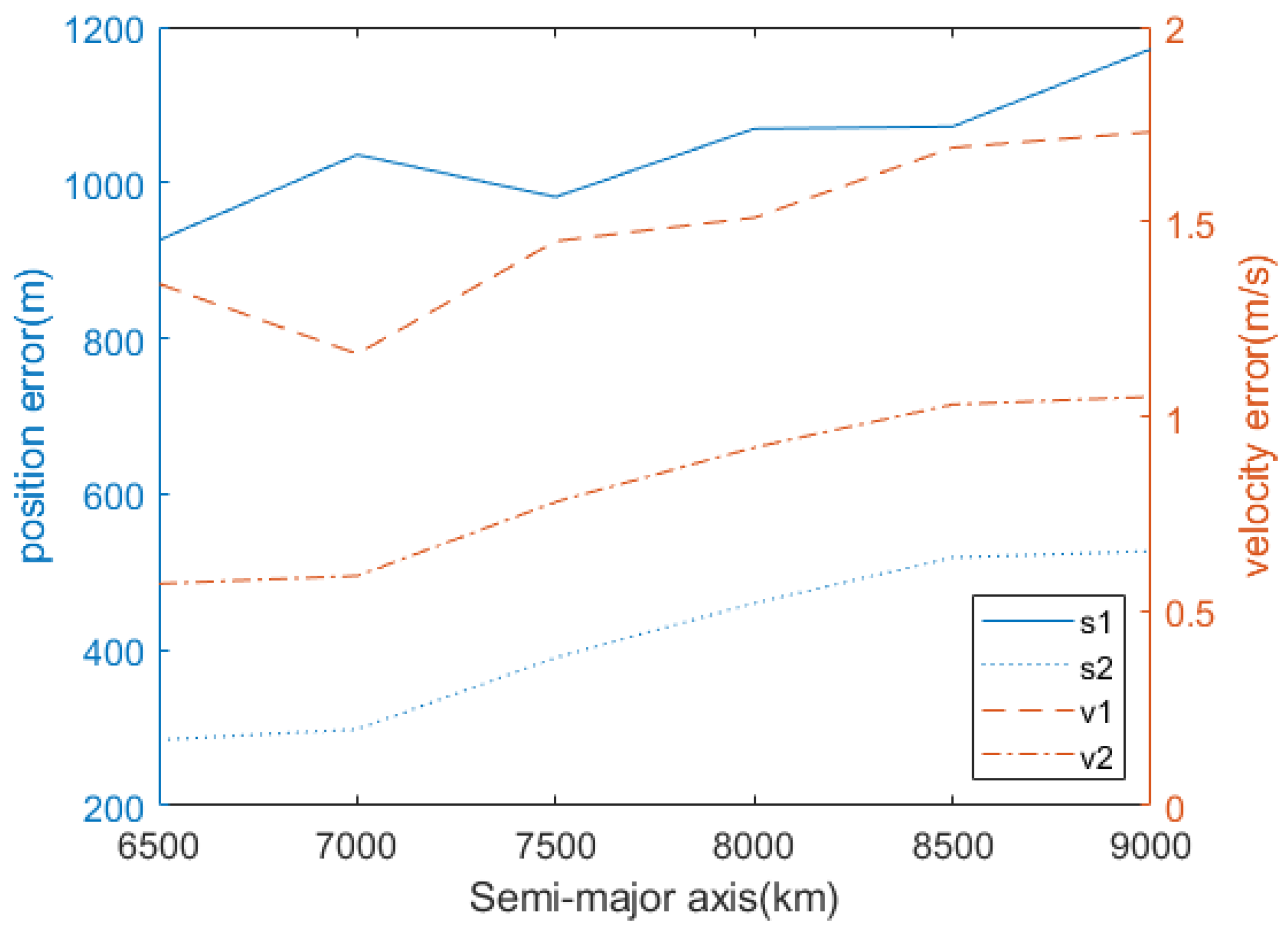
As shown in Figure 2, the position error curves of curves s1, s2, and s3 are quite similar, and the difference in the trajectory prediction error caused by them is very small with an increase in time. Among them, curve s1 has an initial position error of only 735 m, curve s2 has an initial velocity error of only 1 m/s, and curve s3 has both an initial position error of 410 m and a velocity error of 1 m/s. Curve s4 has both an initial position error of −410 m and a velocity error of 1 m/s. Curves s3 and s4 indicate that errors caused by velocity and position can either cancel each other out or accumulate, demonstrating that errors caused by position and velocity are indistinguishable. As mentioned in the previous section, if the initial velocity error and position error are set according to a certain linear relationship, curves similar to the above can be obtained, and it is impossible to distinguish whether the trajectory prediction error is caused by the initial position error or the velocity error.

3.2.2. The Adjustment Coefficients for Position and Velocity

In Section 2, we have already introduced that initial positional errors and velocity errors can cause orbital errors, leading to profile distortion. It is assumed that if there exists a positional error in the direction of $p_{rrd}$, there must be a velocity error in $v_{rrd}$ such that the positional error caused by the pulsar’s line of sight can be approximately canceled out.

We use the fourth-order Runge–Kutta method to obtain the next orbit recursive position error by computing multiple slopes using weighted averaging. According to the fourth-order Runge–Kutta method, we can predict the state of the spacecraft at time t. The approximate state at time t is shown in the equation.

$${\mathit{x}}_t={\mathit{x}}_0+\frac{1}{6}(d_1+2d_2+2d_3+d_4)$$

(9)

where $d_1$ represents the slope at the beginning of the time interval, $d_2$ and $d_3$ represent the slopes at the midpoints of the time interval, and $d_4$ represents the slope at the end of the time interval.

Let the initial state of ${\mathit{x}}_0$ be:

$${\mathit{x}}_0=\left[\begin{array}{c}\mathit{p}\\ \mathit{v}\end{array}\right]$$

(10)

Through the orbital dynamics equations and the Runge–Kutta method, the spacecraft’s position ${\mathit{r}}_t$ can be derived, which can be simplified as follows:

$${\mathit{r}}_t=F({\mathit{r}}_0,t)$$

(11)

Assuming only an initial positional error $\Delta r_p=(\Delta \mathit{p},0)$ is introduced, with $\Delta \mathit{p}={\mathit{p}}_{rrd}·\Delta p$, we obtain the orbital propagation error $\Delta \mathit{P}(t)$ caused by the initial positional error:

$$\Delta \mathit{P}(t)=F_{\mathrm{r}}({\mathit{r}}_0+\Delta {\mathit{r}}_p,t)-F_{\mathrm{r}}({\mathit{r}}_0,t)$$

(12)

Assuming only an initial velocity error $\Delta r_v=(0,\Delta \mathit{v})$ is introduced, with $\Delta \mathit{v}={\mathit{v}}_{rrd}·\Delta v$, we obtain the orbital propagation error $\Delta \mathit{V}(t)$ caused by the initial velocity error:

$$\Delta \mathit{V}(t)=F_{\mathrm{r}}({\mathit{r}}_0+\Delta {\mathit{r}}_v,t)-F_{\mathrm{r}}({\mathit{r}}_0,t)$$

(13)

We assume that the orbital recursive error caused by the initial position error and the orbital recursive error caused by the initial velocity error in the direction of the pulsar’s line of sight are linearly related since the line of sight of the pulsar $\mathit{n}$ and the initial position $\mathit{p}$ of the spacecraft orbit are approximately perpendicular and $\mathit{n}$ is perpendicular to the equatorial plane. After simplification, we can derive Equation (14):

$$k·\mathit{n}[\frac{{(\frac{\mathit{v}}{2}t)}^{\mathrm{T}}(\frac{\mathit{v}}{2}t)}{\left|\mathit{p}+\frac{\mathit{v}}{2}t\right|}+\frac{{(\frac{\mathit{v}}{2}t)}^{\mathrm{T}}(\frac{\mathit{v}}{2}t)(\mu \frac{t^2}{4}\frac{1}{{\left|p\right|}^3}+1)}{\left|\mathit{p}+\frac{\mathit{v}}{2}t+\mu \frac{t^2}{4}\frac{\mathit{p}}{{\left|p\right|}^3}\right|}]\Delta \mathit{p}=\mathit{n}[\frac{{(\frac{\mathit{v}}{2}t)}^T(\frac{\mathit{v}}{2}t)\frac{t}{2}}{\left|\mathit{p}+\frac{\mathit{v}}{2}t\right|}+\frac{{(\frac{\mathit{v}}{2}t)}^T(\frac{\mathit{v}}{2}t)\frac{t}{2}}{\left|\mathit{p}+\frac{\mathit{v}}{2}t+\mu \frac{t^2}{4}\frac{\mathit{p}}{{\left|p\right|}^3}\right|}]\Delta \mathit{v}$$

(14)

Formula (14) is simplified into Formula (15).

$$k·n\Delta {\mathit{P}}_t=n\Delta {\mathit{V}}_t$$

(15)

Given that the orbital propagation error varies over time, we attempt to find the most suitable $k$ using the least squares method. Least squares analysis provides a standard method for obtaining approximate solutions. Within the overall solution, the least squares calculation results in the equation’s output and minimizes the sum of the squares of residuals. Let $\mathit{n}\Delta {\mathit{P}}_t$ be ${\mathit{P}}_t$ and $\mathit{n}\Delta {\mathit{V}}_t$ be ${\mathit{V}}_t$, as shown in Equation (16):

$$k=\frac{\overline{{\mathit{P}}_t{\mathit{V}}_t}-\overline{\mathit{P}}·\overline{\mathit{V}}}{\overline{{\mathit{P}}_t^2}-{(\overline{\mathit{P}})}^2}$$

(16)

To demonstrate the effectiveness of $k$, Equation (17) is provided. Let $e=k{\mathit{P}}_t-{\mathit{V}}_t$:

$$s^2=\frac{{\displaystyle \sum _{t=1}^{T/2}(e_t}-\overline{e}{)}^2}{\left(T/2\right){\displaystyle \sum _{t=1}^{T/2}\widehat{e}}}$$

(17)

where $s$ represents the standard deviation, $T$ stands for the orbital period, $\overline{e}$ denotes the mean, and $\widehat{e}$ represents the true value.

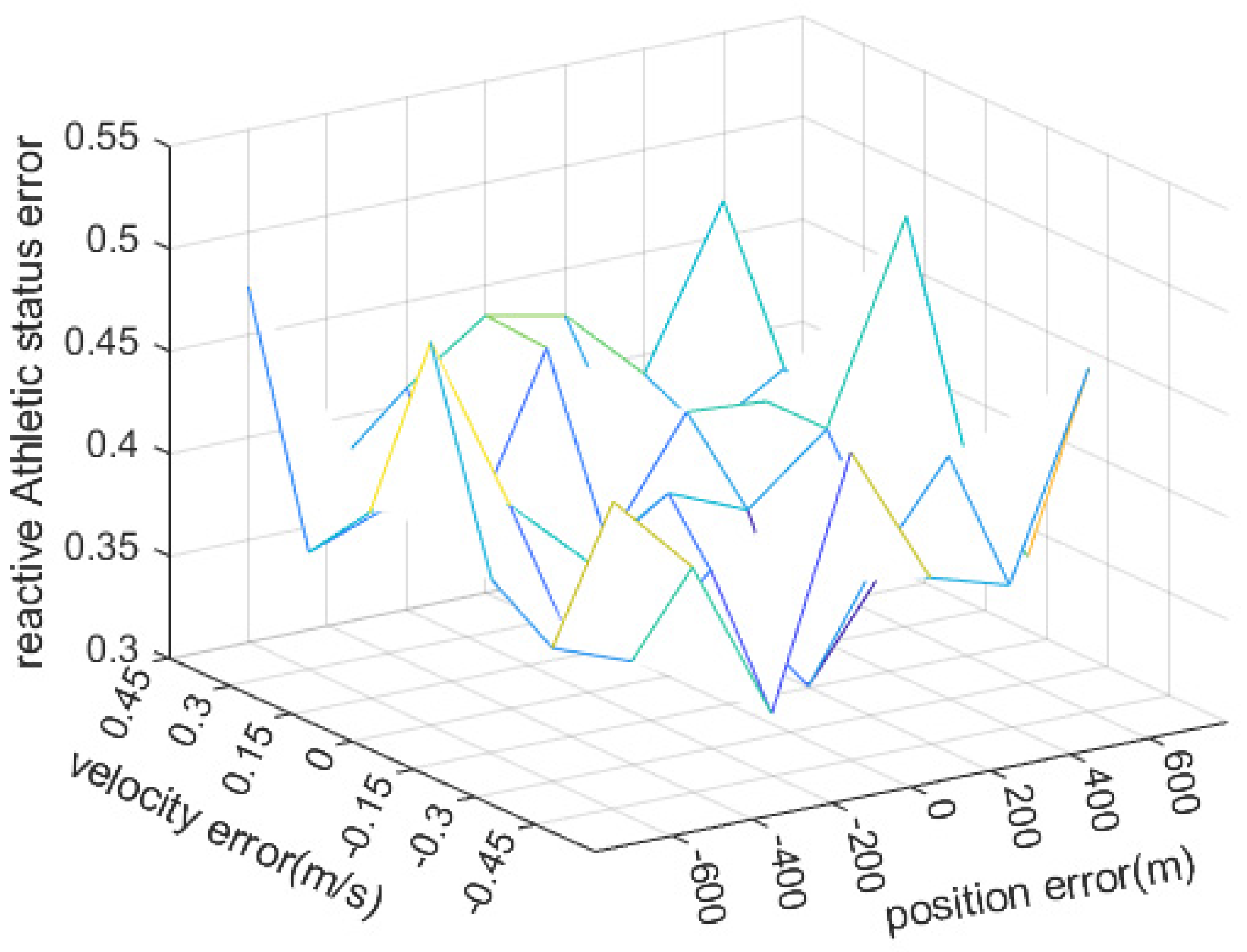
Based on Equation (17), we obtain the normalization result of the standard deviation, as shown in Figure 3. From Figure 3, it can be observed that when the initial velocity error in the $v_{rrd}$ direction and the initial position error in the $p_{rrd}$ direction change, the corresponding adjustment coefficients are determined through the least squares method and then substituted into the equation. Considering the nature of straight lines, after normalization, the standard deviation of the orbit propagation error over the entire observation period is generally around 17, proving the position error and velocity error can be fitted into a new observation direction using the adjustment coefficient k.

3.2.3. Construction of the Reactive Motion State Measure for Position and Velocity

Due to the indistinguishability of the distortion of pulsar contours caused by the offset between position and velocity, this distinguishes traditional two-dimensional position and velocity searches, suffering from low precision. Consequently, we utilize Equation (16) to determine the adjustment coefficient $k$ for position and velocity, thereby synthesizing a reactive motion state measure that encapsulates both. To standardize the units and normalize the process, the positional error and velocity error are divided by their respective sampling intervals, as shown in Equation (18).

$${\varphi }_{\mathrm{i}}=\frac{{\widehat{v}}_0·{\mathit{v}}_{rrd}}{\delta r_v}+k·\frac{{\widehat{p}}_0·{\mathit{p}}_{rrd}}{\delta r_p}$$

(18)

The reactive motion state measure represents, when the initial positional error is zero, approximately the velocity error in direction ${\varphi }_{\mathrm{i}}·\delta r_v$, and when the initial velocity error is zero, approximately the positional error in direction ${\varphi }_{\mathrm{i}}·\delta r_p$.

Due to the displacement of position and velocity, pulsar distortion can be caused. The measure of the reactive motion state ${\varphi }_{\mathrm{i}}$ is a dimensionless quantity. This measurement is obtained by fitting the position error and velocity error using the least squares method. We can sample the position and velocity parts together according to different proportions of sampling steps.

3.3. The Comprehensive Measurement of Position and Velocity

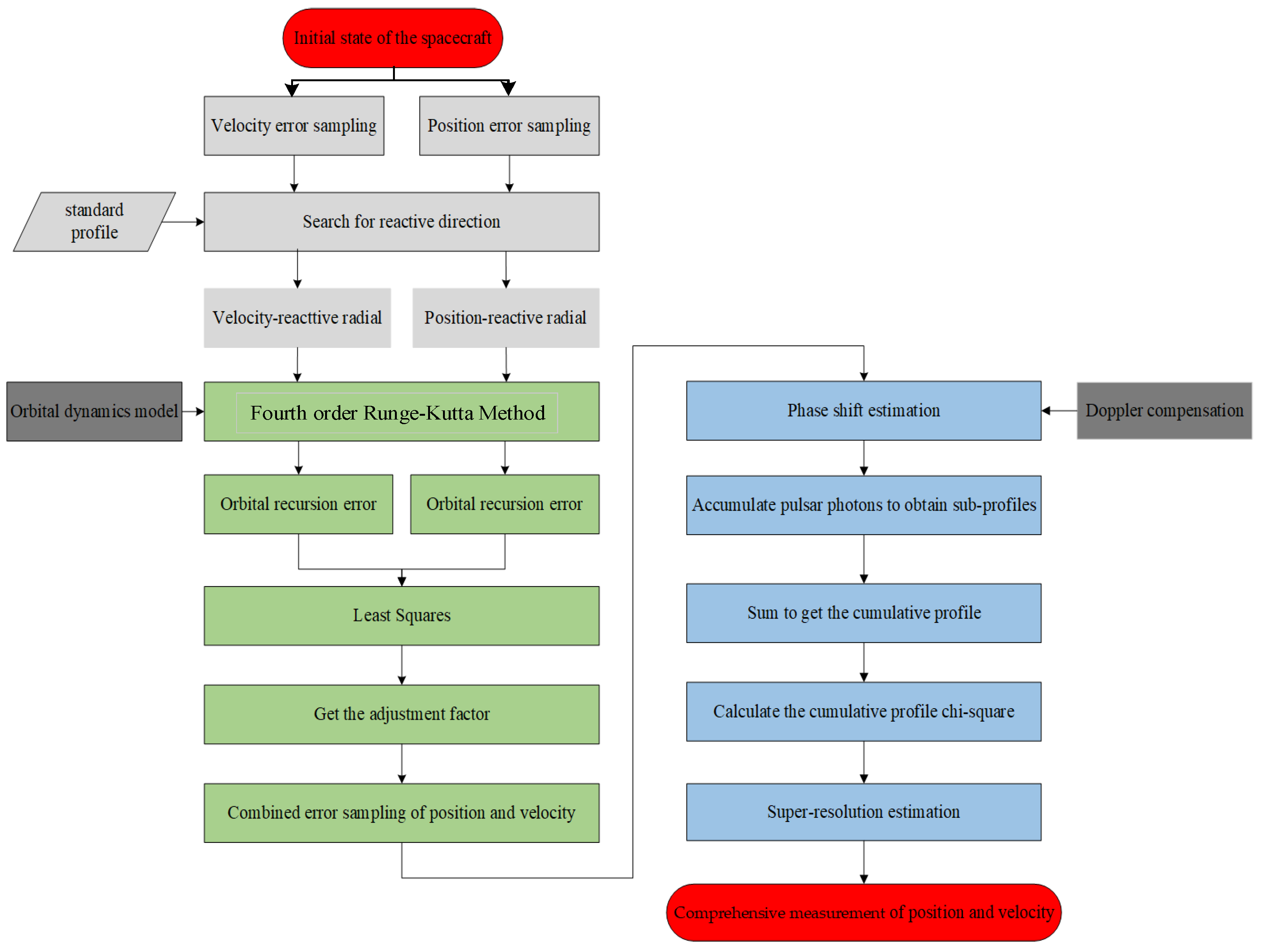
The flowchart of the Comprehensive Measurement of Position and Velocity is shown in Figure 4. The specific steps are as follows:

Step 1: Solve the position–velocity adjustment coefficient. Combining the orbital dynamics model and the fourth-order Runge–Kutta method, we also solve for the adjustment coefficient k in the discovered reactive directions $p_{rrd}$ and $v_{rrd}$ according to Equation (16).

Step 2: Sample the reactive motion state measure. Given the indistinguishability between position and velocity, we set the error ratio to 5 to 5, defining a reactive motion state measure for the joint position–velocity. The combined initial error is expressed as follows:

$$\Delta r_m^{sv}=\frac{k\Delta \mathit{p}[m-(N_{obs}+1)/2]}{\delta {{\displaystyle r}}_p}{f}_1+\frac{\Delta \mathit{v}[m-(N_{obs}+1)/2]}{\delta {{\displaystyle r}}_v}{f}_2$$

(19)

where $\delta r_v$ and $\delta r_p$ represent the sampling interval; $N_{\mathrm{obs}}$ denotes the number of samples; $m$ is a variable, $\mathrm{m}=1,2,\dots ,N_{\mathrm{obs}}$. $f_1$ and $f_2$ are proportional coefficients. $\Delta p$ and $\Delta v$ are the errors in $p_{rrd}$ and $v_{rrd}$, respectively.

Step 3: Estimate the phase shift. Due to the presence of combined initial errors, it inevitably causes a phase drift. Based on the nature of error propagation, errors on the transverse plane can induce positional errors in the radial direction of the pulsar. By incorporating the combined errors into the orbital dynamics model, the radial position at moment $uT/U\left(u=0,1,2,\dots ,U-1\right)$ can be estimated as ${\tilde{r}}_n^{\mathrm{r}}$. At this point, the phase shift of the pulsar is as follows:

$${\omega }_n={\tilde{r}}_n^{\mathrm{r}}/\left(c·T_0\right)$$

(20)

where c is the speed of light, and $T_0$ is the intrinsic period of the pulsar.

Step 4: Accumulate the pulsar profiles. Let $h({\omega }_{k,m})$ be the sub-profile of the pulsar accumulated over a time period. The accumulated pulsar profile ${\tilde{h}}_k\left(\tilde{\omega }\right)$ is the result of shifting and superimposing all the accumulated sub-profiles of the pulsar, which can be represented as follows:

$${\tilde{h}}_k(\tilde{\omega })=\frac{1}{U}{\displaystyle {\sum }_{u=0}^{U-1}h(\omega +{\omega }_{k,m})}$$

(21)

Step 5: Calculate the accumulated profiles. Calculate the value of ${\chi }^2$ for a total of $N_{obs}$ profiles generated in Step 4.

Step 6: Perform comprehensive super-resolution measurement [38]. Perform a comprehensive measurement with super-resolution estimation to significantly improve the estimation accuracy. The super-resolution expression for a one-dimensional matrix is as follows:

$$\widehat{l}=l_{\max }-\frac{0.5({\chi }_{l_{\max }+1}^2-{\chi }_{l_{\max }-1}^2)}{{\chi }_{l_{\max }+1}^2+{\chi }_{l_{\max }-1}^2-2{\chi }_{l_{\max }}^2}$$

(22)

In the expression, element ${\chi }_{l_{\max }}^2$ represents the maximum element, and $l_{\max }$ is the index of the maximum element, while ${\chi }_{l_{\max }+1}^2$ and ${\chi }_{l_{\max }-1}^2$ denote the elements immediately to the right and left of the maximum element, respectively. From Equation (22), it follows that $\widehat{l}$ is the sampling point for super-resolution, and $\left[\widehat{l}-(N_{obs}+1)/2\right]·\delta r_v$ is the error in the reactive motion state measure that we seek.

4. Simulations and Analysis of Their Results

In this section, we validate the feasibility and effectiveness of our proposed method for comprehensive measurement of position and velocity in the transverse directions through simulations. Initially, we demonstrate that the use of a reactive motion state measure enhances the robustness of the estimation. By considering various orbital parameters, such as the semi-major axis of the orbit and the angle between the orbital plane and the pulsar’s radial direction, we analyze the impact of these elements on the accuracy of the comprehensive measurement of position and velocity. Furthermore, we compare the precision differences between the traditional dimensionless directional search method for position and velocity and the one-dimensional search method using the reactive motion state measure, verifying the superiority of our approach. Finally, we contrast our method with other common methods, such as the singular direction two-dimensional velocity measurement method and the dual one-dimensional ranging method, further demonstrating the effectiveness and advantages of our approach.

4.1. The Simulation Conditions

The orbital elements of a low-Earth orbit satellite used in this paper are shown in

Table 1. The six orbital elements of a satellite.

Orbital Elements	Value
Semi-Major Axis/(km) Eccentricity	6500
	0.0005983
Orbital Inclination/($°$)	70
Argument of Periapsis/($°$)	150
Right Ascension of Ascending Node/($°$)	170
True Anomaly/($°$)	0

. Due to the high signal-to-noise ratio of the Crab pulsar (PSR B0531+21), the Crab pulsar is chosen as the navigation star. The simulation parameters and X-ray detector parameters are provided in

Table 2. Parameters related to the Crab pulsar and X-ray sensors.

Parameter Name	Value
Pulsar Period/(ms)	33
Radiation Photon Flux Density/(ph/cm2/s)	1.54
Background Noise Flux Density/(ph/cm2/s)	0.005
Number of Pulsar Intervals	330,000
Detector Area/(m2)	0.5
Time Resolution/(μs)	0.1
Profile Accumulation Time/(s)	2600
Number of Pulsar Accumulation Time Segments	100
Sampling Points	41
Position Sampling Step Length/(m)	500
Velocity Sampling Step Length/(m/s)	1

. The working platform is a laptop with an i7-12700H @ 2.3 GHz CPU and 16 G of RAM.

4.2. The Reactive Motion State Measure Sampling

In this subsection, we delve into the influence of different sampling ratios of position and velocity on the outcomes under the conditions of a constant magnitude and an invariant reactive motion state measure. According to Equation (19), when using reactive-motion-state-measure-combined error sampling, it is necessary to set the position error proportional coefficient $f_1$ and the velocity error proportional coefficient $f_2$. Figure 5 illustrates the orbital extrapolation error curves resulting from different ratios under a constant reactive motion state measure. The figure reveals that the three orbital extrapolation error curves are very close to each other, indicating that under the premise of an unchanged reactive motion state measure magnitude, the error from different position and velocity ratios has a minimal impact on the orbital extrapolation error.

Table 3. The impact of different ratios on reactive motion state measure.

Ratio	${\mathit{\chi }}^2$ Value	Reactive Motion State Measure Error
7:3	195.1652389	0.582
5:5	195.1650181	0.569
3:7	195.1651573	0.587

shows that the ${\chi }^2$ value error is around 0.0001, and the error of the reactive motion state measure is also within the error range, with the minimum error when the ratio of $f_1$ and $f_2$ is 5 to 5.

Figure 6 depicts the orbital extrapolation error curves resulting from varying the magnitude of the reactive motion state measure while keeping the sampling ratio of position to velocity constant. The figure indicates that the value of the reactive motion state measure is affected by positive and negative influences, leading to a symmetrical relationship in the induced orbital extrapolation error. The gap between the three orbital extrapolation error curves is more pronounced under different ratios, suggesting that the magnitude of the reactive motion state measure has a significant impact on the orbital extrapolation error.

Using the previously mentioned ratio of 5 to 5 for the reactive motion state measure, denoted as $f_1$ and $f_2$ as a baseline, denoted as ${\varphi }_0$, Figure 5 shows the trajectory recursion error curve caused by changing the size of the sensitive motion state measure (as shown in

Table 4. The impact of different reactive motion state measures on the results.

Relative Size of the Reactive Motion State Measure	${\mathit{\chi }}^2$ Value	Reactive Motion State Measure Error
0.6	195.1931075	0.733
1	195.1650181	0.569
1.4	195.1499452	0.408
−0.6	195.1931356	0.766
−1	195.1650458	0.581
−1.4	195.1503526	0.394

, which is compared to the size of ${\varphi }_0$) when the sampling ratio of position and velocity remains unchanged. From Figure 6, it is evident that the values of the reactive motion state measure are influenced by positive and negative factors. However, it is not possible to distinguish between positive and negative solely based on the calculated ${\chi }^2$ values, as the resulting orbit propagation error curves exhibit an almost symmetrical relationship. Nevertheless, according to Table 4, the difference in search errors for reactive motion state measures of opposite magnitudes is minimal. In contrast, under different proportions, the three orbit propagation error curves show more noticeable differences, indicating that the magnitude of the reactive motion state measure has a significant impact on the orbit propagation error.

4.3. Robustness of the Reactive Motion State Measure

In the insensitive direction, the velocity and position errors in this direction do not easily lead to position errors in the radial direction. Figure 7 shows the impact of adding position and velocity errors in the unreactive direction on the reactive motion state measure. As shown in the figure, with an increase in the velocity and position errors, the search accuracy slightly decreases but still maintains a good level, demonstrating the robustness of the method proposed in this paper.

4.4. The Angle between the Orbit and the Radial Direction of a Pulsar

In this section, we investigate the impact of the angle between the orbital and pulsar radial directions on the comprehensive measurement method, as shown in

Table 5. The precision of comprehensive measurement at different angles.

Angle/°	Dimensionless Directional Search		Adjustment Coefficient	Reactive Motion State Measure Error
	Position Error/m	Velocity Error/(m/s)
20	1087.87	4.07	−3.0579	0.392
30	1418.76	3.69	−4.0937	0.352
40	1164.26	3.68	−3.0818	0.385
50	1278.59	3.77	−3.6037	0.365
60	1190.04	3.64	−3.8461	0.345
70	1335.58	4.02	0.8496	0.293
80	1729.22	3.15	8.2413	0.312

.

Table 5 indicates that the error in the dimensionless directional search for position and velocity is large, with position errors above 1000 m and velocity errors around 4 m/s, rendering it unsuitable for pulsar navigation. The accuracy of the reactive motion state measure for different degrees is around 0.3. Taking an angle of 20 degrees as an example, the accuracy of the reactive motion state measure is 0.392, which corresponds to a position error of approximately 196 m and a velocity error of 0.392 m/s, significantly higher than the accuracy of the dimensionless directional search for position and velocity. The angle between the orbit and the pulsar radial direction has a minor impact on the accuracy of the comprehensive measurement of position and velocity, indicating that by using the reactive motion state measure, we not only achieve great computational convenience but also maintain high estimation accuracy. This proves the universality and accuracy of the comprehensive measurement method for position and velocity in the transverse directions using a single pulsar.

4.5. The Impact of the Semi-Major Axis

In this section, we explore the impact of the semi-major axis on the accuracy of the comprehensive measurement method for position and velocity. Figure 8 shows the performance of the comprehensive measurement of position and velocity for different semi-major axes. As can be seen from Figure 8, as the semi-major axis gradually increases, curves s1 and v1, which represent the search accuracy of the dimensionless directional search for position and velocity, have larger errors and cannot be used for navigation; the errors for velocity measurement (curve v2) and range measurement (curve s2) in the comprehensive measurement show an increasing trend. This is because the position error and the velocity error lead to a decrease in the positional error along the line of sight of the pulsar, thereby causing a very small cumulative profile distortion of the pulsar. That is, the sensitivity of the pulsar’s cumulative profile distortion to the position error and velocity error is low, leading to an increase in the comprehensive measurement error. However, overall, the accuracy of the comprehensive measurement is good. With a semi-major axis of 9000 km, the velocity error is maintained below 1.2 m/s, and the position error is maintained below 550 m.

4.6. The Impact of Adjustment Coefficients

From the construction process of the reactive motion state measure, it is known that the key factor determining the accuracy of the comprehensive measurement is the slope k, which is determined by the initial state of the spacecraft and the search step length. Given a certain orbit, we explore the impact of different search step lengths on the search results.

Table 6. The impact of different search step sizes on reactive motion state measure.

Position Search Step Size/m	Velocity Search Step Size/(m/s)	Reactive Motion State Measure Error	Time/s
500	1	0.392	23.842
500	2	0.318	23.922
1000	1	0.375	24.002

compares the effects of different search step sizes on the results. From Table 6, we can observe that in the transverse directions ${\mathit{p}}_{rrd}$ and ${\mathit{v}}_{rrd}$, the proportions between the position search step size and the velocity search step size vary, resulting in different outcomes. However, the position error remains below 400 m, and the velocity error stays under 0.7 m/s. Furthermore, compared to thousands of seconds of observation time, the use of a one-dimensional search for 25 s is shorter, adequately demonstrating the feasibility and real-time capability of the method.

4.7. Comparison with Other Methods

To highlight the superiority of the comprehensive measurement of position and velocity in the transverse direction using only the Crab pulsar, it is compared with the two-dimensional Doppler velocimetry approach, which only measures velocity, and the dual one-dimensional range measurement method, which only measures distance, as shown in

Table 7. Precision comparison for different search methods.

Measurement Method	Position Error/m	Velocity Error/(m/s)
Comprehensive measurement method	284.51	0.57
Two-dimensional Doppler velocimetry approach method	-	0.69
Dual one-dimensional ranging method	321.14	-

.

Under the parameters of the low-orbit satellite as shown in Table 1, compared to the two-dimensional Doppler velocimetry approach [35], the comprehensive measurement method achieves a higher velocity measurement accuracy. Compared to the dual one-dimensional range measurement method [34], the comprehensive measurement method achieves a higher range measurement accuracy, and the search efficiency is significantly improved. The reason lies in the comprehensive measurement method’s use of both position and velocity information and its reduction in the mutual impact of position and velocity through the reactive motion state measure, thereby improving the positioning accuracy. The comprehensive measurement method uses only a one-dimensional search, reducing the computational load and time compared to a dimensionless directional search for position and velocity.

5. Conclusions

In comparison to traditional pulsar distance and velocity measurement methods that consider only the radial direction to the pulsar, we propose a method that uses a single pulsar to comprehensively measure the position and velocity offsets of the observer in the transverse directions. This method is based on the estimation of the RRD on the transverse plane and creates a new physical measure. The method proposed in this paper has the following advantages:

• High accuracy in comprehensive measurement positioning. By constructing a reactive motion state measure, the accuracy of the comprehensive measurement in the RRD direction is high, meeting the requirements for positioning accuracy in spacecraft autonomous navigation.
• Real-time capability. The total calculation time for this method is less than 25 s, which is very small compared to the cumulative time, ensuring the real-time nature of the navigation system. Furthermore, this method uses a one-dimensional search, which significantly reduces the computational load compared to a dimensionless directional search for position and velocity.
• Low resource consumption. Traditional X-ray pulsar navigation requires at least three pulsars to achieve three-dimensional positioning. This method only uses the Crab pulsar to achieve comprehensive measurement of position and velocity, undoubtedly greatly reducing the navigation system’s burden.
• Strong robustness. For different reactive directions, this method can maintain a high positioning accuracy. For errors in other directions, the accuracy slightly decreases.

In the future, this method has certain reference and application prospects in the field of X-ray pulsar navigation.