Abstract
High-fidelity computations are often used in predicting the tonal and broadband noise of propellers and rotors associated with Advanced Air Mobility Vehicles (AAMVs). But LES is both CPU and storage intensive. We present here an investigation of the feasibility of reduction methods such as Proper Orthogonal Decomposition as well as Dynamic Mode Decomposition for reduction of data obtained via LES to be used further to obtain additional parameters. Specifically, we investigate how accurate reduced models of the high-fidelity computations can be used to predict the far-field noise. It is found that POD is capable of accurately reconstructing the parameters of interest with 15–40% of the total mode energies, whereas the DMD can only reconstruct primitive parameters such as velocity and pressure loosely. A rank truncation convergence criterion > 99.8% is needed for better performance of the DMD algorithm. In the far-field spectra, DMD can only predict the tonal contents in the lower and mid frequencies, while the POD can reproduce all frequencies of interest.
1. Introduction
A great deal of research has been performed on the prediction of open rotor/propeller noise. These methods range from low-fidelity simplifications to high-fidelity computations. Some of the earliest theories in this field include Gutin’s theory of the noise produced by the rotating pressure field of propellers, developed in 1937 [1], and that by Deming [2]. These approaches could predict some tonal noise but missed higher harmonics and the broadband noise entirely. Some advances have been seen in the hydroacoustic prediction of propeller noise using solutions coupled with acoustic analogies [3,4]. The higher-fidelity methods such as LES or Hybrid LES better predict the broadband, but they are computationally expensive.
Once LES is obtained, it is expensive to run it again and it is expensive to store for subsequent use. As such, approaches have been explored to find ways to replace the original set of data with a reduced model, to enable easy use of the data. Recently, advances in data science and machine learning have provided opportunities to apply these relatively new technologies to CFD. Using modal decomposition, we can approximate the resulting flow field using Proper Orthogonal Decomposition (POD) [5,6], Spectral POD [7], and Dynamic Mode Decomposition (DMD) [8]. Traditionally, such methods have been used to reconstruct flow fields with inputs either from experiments or CFD. Several researchers have utilized POD methods to understand the physics of various flows such as cavity flows [9] and pitching airfoils [10], to name a couple. Towne and Schmitz utilized Spectral POD methods to investigate the coherent structures of a jet. Countless researchers have utilized DMD for various studies. Rowley and Dawson [11] provide an extensive review of these models and their utilization in great detail. Generally, reduced-order models are used for either an interpolation-type case, usually PODs [12,13], or an extrapolation type case, usually DMDs, with very few extensions of POD for extrapolation over the years [14,15]. In this work, we attempt to investigate the capabilities of both POD and DMD in aeroacoustics.
Currently, little work has been performed using these reduced-order methods in predicting the acoustics of rotor systems. In this work, we consider the aeroacoustics field of an isolated airfoil as obtained by Hybrid LES [16]. Our objective is to represent the resulting aeroacoustics field by applying a reduced-order method and assess the feasibility of this method, the trade-off errors, and the computational cost benefits.
2. Modeling Approach
As mentioned in the introduction, several options for model reduction are available in the literature. We explore two of these methods for their level of accuracy after reduction of the original data has been performed:
2.1. Proper Orthogonal Decomposition (POD)
POD originates from the field of turbulence and was first introduced by Lumley [5,6]. This technique attempts to decompose a random vector field into a set of deterministic functions that capture some fractions of the original data. It essentially reduces the order of the fidelity while attempting to retain the “important” features of the flow. POD attempts to find spatial correlations in the flow and to find a low-rank number of modes to reconstruct the original data. One of the advantages of POD is the ability to provide a straightforward ranking of the weight of each mode of the dataset. However, this method typically struggles to resolve heavy time-dependent structures of the flow. The general formulation is to decompose a field vector into a set of spatial functions and its random set of time coefficients :
We implement the snapshot method of the POD, which allows us to interchange the temporal and spatial variables, such that we have deterministic temporal modes with random spatial coefficients. The general algorithm is as follows, when setting :
- We extract the fluctuating components of the flow by subtracting the mean: ;
- We then find the correlation matrix of the snapshot matrix ;
- We then find the eigenvalue and vectors of the correlation matrix such thatwhere are the temporal modes;
- The spatial modes are reconstructed as ;
- The reconstructed field .
Another approach to the algorithm involves the use of the singular value decomposition (SVD) method, where the correlation matrix and eigenvalue steps can be replaced by
And is redefined as
2.2. Dynamic Mode Decomposition (DMD)
DMD is a data-driven reduction algorithm developed by Schmitz [17]. DMD computes the set of dynamic modes, which are each associated with a frequency and a decay/growth rate. It is useful for finding correlations with coherent structures in the domain and has the ability to consider the temporal dimension as well in the form of an FFT (see Figure 1). We first start the algorithm by splitting the snapshot matrix into two—the first runs from to , and the second matrix is from to .

Figure 1.
Overview of DMD for vortex shedding of a cylinder. “Reprinted/adapted with permission of The Licensor through PLSclear, 2024” [18].
Next, the following equations are used for the development of the DMD:
- a.
- The equation that relates each snapshot to the next:
- b.
- We then take a singular value decomposition of X:
- c.
- Given the rank or number of modes for reconstruction, r, are truncated from 1 to r. The low-rank subspace matrix .
- d.
- Next, the eigenvalues and eigenvectors are obtained:
- e.
- The real-space DMD mode is computed as
- f.
- The reconstructed reduced-order model is then given as
Here, x(t) represents the variables of interest, say pressure or velocity. With this reconstruction, we can extend the dataset for different variables.
2.3. Choice of Mode Truncation
The general goal of these reduction methods is to identify the minimum number of modes that can describe a system without significant loss of information. This usually requires a metric for specifying the truncation. For the POD case, the algorithm allows for a simple method of ranking the weights of each mode by comparing the singular values to the original data. For DMD, however, this is not so straightforward as there is no longer a singular matrix for comparison. To remedy this, two approaches can be utilized. The first is to define a hard limit called the optimal hard threshold, , for the singular value truncation such that [18]
- If then
- If and then is replaced by the aspect ratio :where is a known noise magnitude of the system. If the noise of the system is not known, as in most real-world applications, the median singular value can be used to estimate the system. The equation for this estimation is discussed by Gavish and Donoho [19].
The second, more common approach is the energy truncation method. In the singular value decomposition approach, the singular value matrix is used to gain insights into the total energy of the system, such that
We define the truncation value r to be the minimum of ( convergence value), where we specify for the POD case that there is a convergence value of 95% of the total energy of the system.
3. Inputs and Data to Be Reduced
We consider here the flow and acoustic fields associated with an isolated propeller of a UAV. In the computational domain, the unsteady flow field and the acoustic near field are directly resolved numerically. A Hybrid LES-URANS (HLES) approach is adopted here, like the one used previously by Mankbadi et al. [16], in which URANS is used near the solid surfaces, while LES is used elsewhere. The governing equations for the entire computational domain are the compressible, unsteady Favre-averaged Navier–Stokes equations [20]:
where is the total energy, is the heat flux, and is the total laminar and turbulent stresses, with the turbulence kinetic energy defined as . The Spalart–Allmaras turbulence model with rotation/curvature correction is utilized [21,22,23]. For this study, we use the two-bladed-type 9450 propeller of the DJI Phantom III drone.
OpenFOAM open-source finite volume code is used in the HLES computation. Mesh rotation is achieved using the arbitrary mesh interface (AMI) method. Using baffles (duplicate mesh interfaces), the flow variables are translated from the rotating interface to the static nonrotating interface at the boundary of the rotating cell zone.
The transient compressible PIMPLE solver is employed. The PIMPLE algorithm is a combination of the pressure implicit with splitting of operator (PISO) and semi-implicit method for pressure-linked equations (SIMPLE) algorithms. The PIMPLE solver is used with five corrector loops per time step and three pressure corrections per loop, allowing for convergence of flow parameters per time step.
Spatial differencing is performed using the second Gauss linear scheme, which is a second-order central differencing scheme with low dissipation. A second-order accurate Crank–Nicolson temporal discretization scheme is used. The Crank–Nicolson scheme includes an off-centering coefficient that can be modified to increase stability at the cost of the overall scheme order. For numerical stability, an off-centering coefficient of 0.4 is employed. A physical time step of 1.5 × 10−6 s, corresponding to about 0.05° rotor rotation at 6000 RPM, is performed. This is used to initialize the URANS solution. After ~10 rotor revolutions, the HLES turbulence model is switched on. The time step is reduced to 7.5 × 10−7 s. To ensure solution convergence, a convergence criterion is specified (∼1 × 10−9), and inner corrector loops are run until convergence is achieved. This ensures convergence of the LES section of the computation, as well as accurate resolution of the fluctuations in the flow and the acoustic field. More details on the computational setup can be found in Mankbadi et al. [16].
Inputs
Our overarching goal is to explore the feasibility of these decomposition methods to predict the far-field noise. Since resolving the acoustic field requires high resolution, it is more practical to compute the near-field unsteady flow and acoustic solution and then use another technique to extend the near field to the far field. Therefore, we use the FWH formulation [24] as the acoustic extension technique in the current work. Farassat’s 1A formulation of the FWH equation developed by Brentner and Farassat [25] is utilized in this study. The far field noise is computed using Farassat’s 1A formulation of Ffowcs–Williams–Hawkings equations (FWHs) [26]:
where
Note that for permeable surfaces in hover, .
So, Equation (19) reduces to
To solve this, we interpolate values of pressure, velocity, and their time derivatives onto a porous top-capped control surface, as shown in Figure 2.

Figure 2.
Control surface for integration.
The interpolation process is carried out in OpenFOAM v1912, and data are output as a series of VTK files. These are then imported into MATLAB v2019a using the vtk toolbox [27].
For validation, we choose the case with an rpm of 6000 [16]. Spectral results are compared with experimental work by Intaratep et al. [28], with the observer point shown in Figure 3.

Figure 3.
Observer location point [28].
The general workflow of the computations and framework is shown in Figure 4.
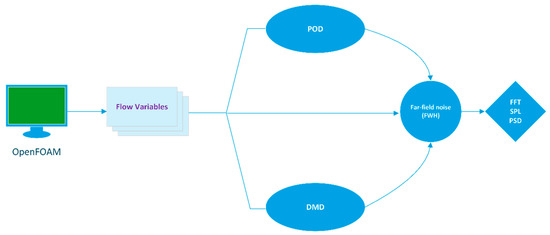
Figure 4.
Schematic showing the workflow.
4. Results
4.1. High-Fidelity Data
We utilized high-fidelity computations of a single rotor in hover, at 6000 rpm. We show results from the computation of the near-field dilatation rate of the single isolated propeller [16] in Figure 5.

Figure 5.
Vertical slice (left) and horizontal slice (right) of the dilatation field [16].
It can be seen that there are contributions both from the blades and the wake. To compute the far-field noise, we utilize a top-capped control surface encompassing both blade and wake noise sources (see Figure 2). Next, we show the far-field noise spectra when compared with the experiments in Figure 6. A frequency resolution of () of 8 Hz, which corresponds to samples, was utilized in charting the power spectral density plot.
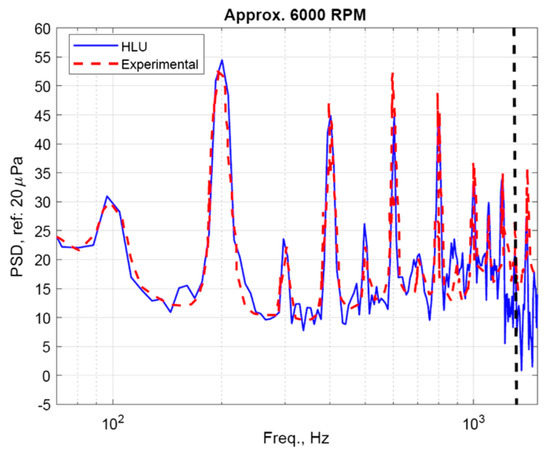
Figure 6.
Power spectral density plot compared with experimental data [28].
The spectral data above required about 600 CPU hours on an HPC with 360 processors using OpenFOAM. This is prohibitively expensive as it takes a lot of computational time and storage without an option to re-run for a different observer location after the fact.
4.2. Near-Field Data Reduction
As mentioned earlier, the data are extracted and interpolated onto a cylindrical surface in OpenFOAM. The desired primitive variables of interest for the eventual FWH computations are velocity, pressure, and their time derivatives. Data are collected at a sample rate of s, where 6755 samples were collected in this case and utilized for the reduced-order analyses.
To verify the performance of the models, we utilize an integral metric:
where X is the variable of interest.
- i.
- POD Results
For the POD case, we elected to use the energy truncation method to define the mode cut-off needed for the singular value decomposition. A convergence criterion of % was selected.
In the contour plots in Figure 7, there is a great reconstruction of the near-field parameters. The results show that the velocity can be reconstructed with the first 15% of the modes, which corresponds to over 95% of the total energy of the system. For pressure, however, due to the increased fluctuations, significantly more modes are required to properly represent the system at about 40% of the energy. Inherently, POD in its native form is a sort of linearization of a system and can struggle to represent higher-order systems. With the optimization approach for selecting the truncation modes, we note that the time derivatives of velocity and pressure both require a significantly larger number of modes to properly represent the system, at about 46–50% of the total number of modes.
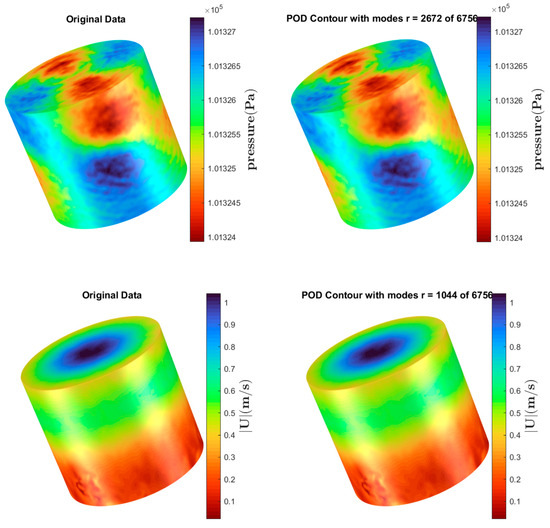

Figure 7.
Instantaneous snapshot surface contours of variables at t = 0.01 s. (Left): Original data. (Right): Reduced data (POD).
Using the integral metric specified in Equation (21), we investigated the accuracy of the POD reconstruction over the entire time history.
Overall, great reconstruction of the data was seen across all timesteps. Looking at the pressure plot (Figure 8a), it can be noted that there was a slight underprediction, with a room mean square error (rmse) of . Similarly, for velocity magnitude (Figure 8b), there was an rmse of . There were larger deviations for the time derivatives, and the pressure derivative (Figure 8c) had the largest rmse of 223.93, while acceleration had the lowest (Figure 8d) with an rmse of 0.3564. One merit of the POD method is that it can be used to model the parameters of interest as an input to a neural network architecture for control within the specified design space. It can also be used as a quick interpolation for different sampling times, for comparison with any experimental result. The major demerit of this method is that it cannot, in its default form, be used as an extrapolation or future prediction method, and thus it cannot be used to extend the time series for a better FFT resolution.
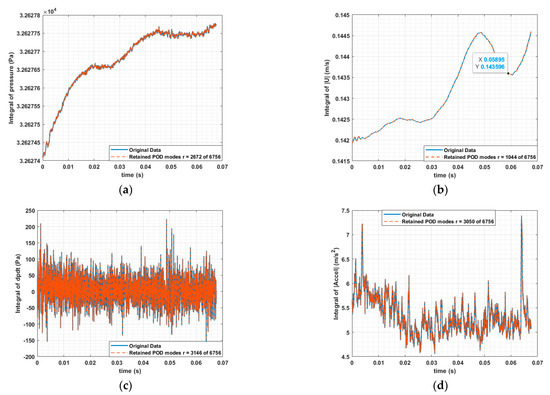
Figure 8.
Integral metric for performance of POD reconstruction. (a) Metric for pressure; (b) Velocity magnitude; (c) Derivative of pressure; (d) Derivative of velocity magnitude.
- ii.
- DMD Results
For the DMD case, we first elected to use the optimal hard threshold approach for the mode truncation. We utilized case #2 (Equations (11) and (12)) for the computation of the mode truncation.
Looking at the contour plots in Figure 9, it can be noted that there was a good reconstruction of the velocity magnitude, as well as the pressure, though the results from the POD case were not as good. In particular, there was a loss of fluctuation in the case of the pressure contours, which may have affected the broadband aspect of the noise. Also, we can see that there was a very poor reconstruction of the time derivatives. The reconstruction of the time coefficients is based on an initial estimate of the original data rather than all the modes like in the POD, and this causes severe deviations from the original data if mode truncation is not performed well. We took a closer look by plotting the integral metric for the desired parameters (see Figure 10).
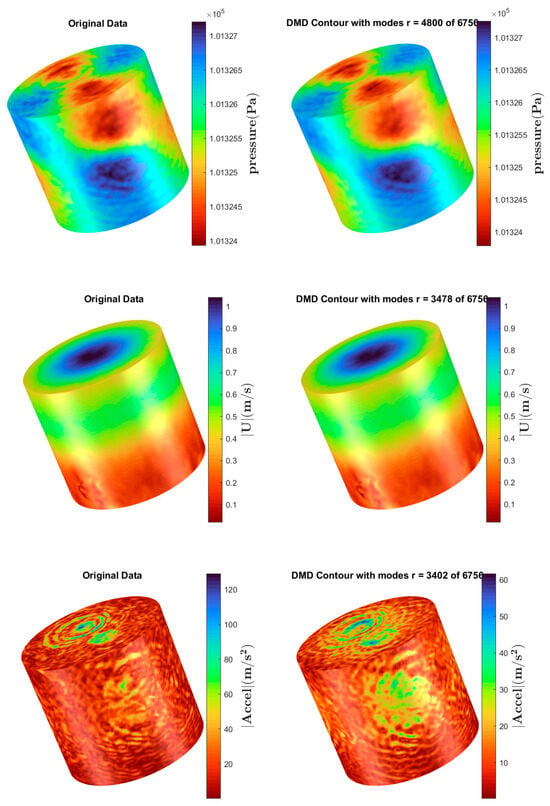

Figure 9.
Instantaneous snapshot surface contours of variables at t = 0.01 s. (Left): Original data. (Right): Reduced data (DMD).
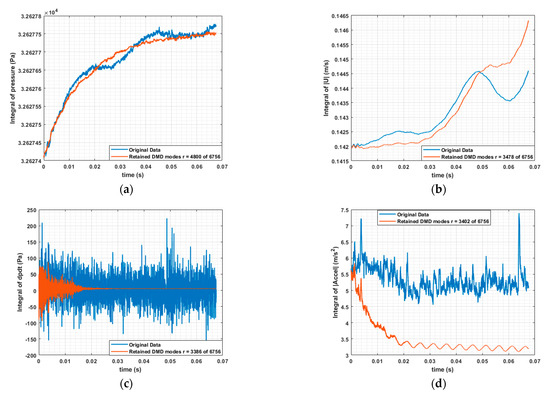
Figure 10.
Integral metric for performance of DMD reconstruction (optimal hard threshold). (a) Metric for pressure; (b) Velocity magnitude; (c) Derivative of pressure; (d) Derivative of velocity magnitude.
Here, we can see a good trend for the pressure, although there was some loss of unsteadiness, which may have translated into a loss of broadband content in the far-field noise. A reported rmse of 0.0033 was obtained for pressure. The velocity magnitude shows there was a good reconstruction in the first few time steps, but it deviates quite significantly afterwards, with an rmse of 0.0074. Both the time derivatives were predicted extremely poorly and were not usable for further computations. To remedy this, we applied the energy truncation approach with a convergence criterion of % (Figure 11). Comparable improvements were seen in the pressure and velocity time derivatives at the expense of a significantly increased number of modes required. It is important to note that using all of the modes does not automatically improve the reconstruction accuracy and does cause the mode amplitudes for the time coefficients to grow exponentially to unreasonably large values. As such, the cut-off criterion has to be chosen carefully. In this study, the root mean square error of the initial mode was used as a tuning parameter, such that the error was minimized for a given convergence criterion.
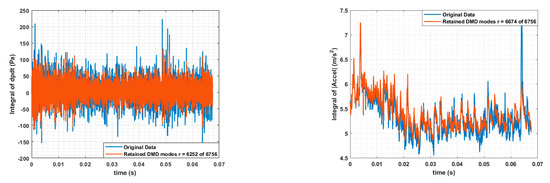
Figure 11.
Integral metric for performance of DMD reconstruction for time derivatives (energy truncation approach).
A merit of the DMD approach is that it can be used for future prediction or forecasting of the time series via the time coefficient reconstruction in the algorithm. However, the accuracy of the prediction may need to be investigated, and a predictor–corrector method could be used to increase its fidelity. This could then be implemented in a control system for active noise control of rotors.
4.3. Far-Field Acoustic Pressure and Spectral Reconstruction
The reconstruction parameters were used as inputs to the Ffowcs–Williams–Hawkings equations [24] (Equations (17) and (18)). The resulting far-field acoustic pressure time history was compared with the original HLU computations, as shown in Figure 12. For clarity, we show the results for only one blade rotation, that is, for a 6000 rpm case, with a time window of 0.01 s.
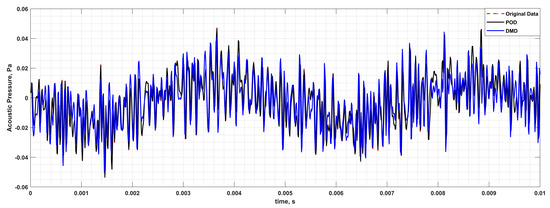
Figure 12.
Far-field acoustic pressure time history comparison between reduced-order models and HLU over one rotor rotation.
Very good reproduction was seen in the POD case when compared with the HLU results, with some slight underpredictions in the fluctuations (an rmse of 0.0018). For the DMD case, however, there were notable variations in the pressure, with some under-resolution of the fluctuations seen, which may again have resulted in poor broadband reproduction. The general peaks and troughs were, however, captured quite well. A reported rmse of 0.0145 was obtained.
Spectral Reconstruction
The resulting power spectral density (PSD) plot from the HLU computations (Figure 6) was obtained using a frequency resolution () of 8 Hz. The reduced-order models could only be resolved to () of 16 Hz due to the smaller sample size. To better compare them, we first re-computed the PSD of the HLU to match that of the reduced-order models, for better comparison of their performance. In Figure 13, we compare the two resolutions of the HLU case with the experimental data [28]. We note that there is a slight overprediction of the low-frequency broadband, mainly because there is a low resolution there and thus the prediction misses those points. However, the general trends are sufficient for comparison with the reduced-order models.
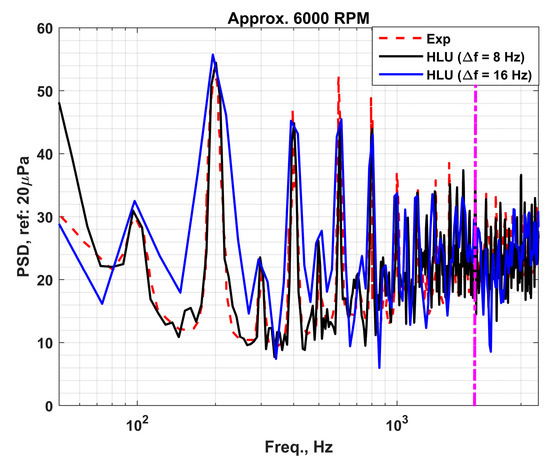
Figure 13.
PSD plot comparing effect of frequency resolution of HLU to experimental data [28].
Next, we compare the results of the POD and DMD spectral reconstructions with those of the comparably resolved original HLU dataset. Figure 14 shows that unsurprisingly the POD is able to reproduce the spectra quite well, almost matching those of the original data. With the DMD case, it can capture the tonal levels for the first few harmonics perfectly, but it completely misses the broadband content. Additionally, it does not capture the shaft rate harmonics or the sub-harmonics, which indicates that it does not capture the contribution of the wake sources, which have been proven to be the source of the sub-harmonics [16].
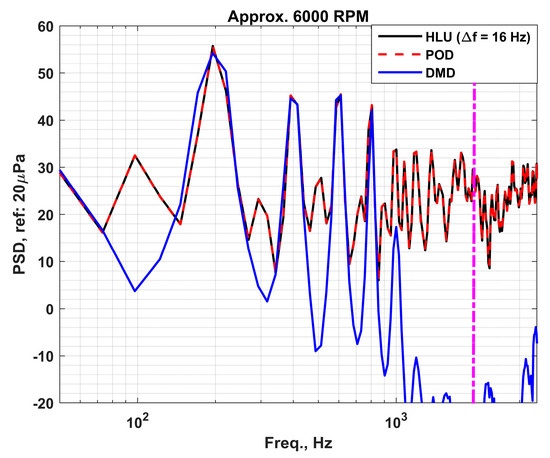
Figure 14.
PSD plot comparing original data with the reduced-order models.
Also, note that the cut-off frequency for the DMD case seems to drop off sooner than that of the original dataset. This may be due to the linearization performed in the time coefficient reconstruction.
5. Conclusions
In sum, two data reduction techniques have been explored, and their application to acoustic pressure prediction has been discussed. The input parameters were pressure, velocity, and their time derivatives. The test case selected was an isolated UAV rotor [16], with a rotational rate of 6000 rpm. Snapshots of the data mapped onto a cylindrical surface were utilized in the POD and DMD reconstructions, with an eventual FFT performed to ascertain their spectral performance. A critical step in the development of the data reduction was the choice of the mode truncation. Two methods were mentioned—the mode energy truncation approach, and the optimal hard threshold method.
The POD method utilized was the snapshot method using the singular value decomposition approach. The truncation method used was mode energy truncation. The results showed near-perfect data reconstruction, with as low as only 15% of the mode energies needed in the case of the velocity magnitudes, while the time derivatives needed slightly higher percentages for good reconstruction. The spectral performance showed matching reproduction with the original dataset. The POD reduced model can be utilized for interpolation of the dataset for various sampling times, for FFT computations at a significantly lower computational cost.
The model can also be used for multiple acoustic computations at different observer locations without re-running high-fidelity computations. An added benefit of this model is that multiple cases can be made and used as inputs into a more sophisticated neural network architecture for acoustic predictions.
The DMD method is the significantly more complicated of the two methods. Because it attempts to reconstruct the time coefficients using an initial guess from the modes, the mode truncation becomes critical to the success of the model. The optimal hard threshold method was first tested with some successes when using the primitive variables pressure and velocity, but it failed in the time derivatives. Using the mode energy truncation method with a convergence >99.8% increased the accuracy of the predictions significantly. However, this resulted in a very large number of modes needed for reconstruction.
A look at the spectral performance showed that it is only capable of reconstructing and predicting the tonal content, while completely misses out on the broadband. This is in part due to the algorithm not being able to resolve fluctuations in the data, as evident in Figure 14. However, for frameworks requiring only tonal predictions, this model would work excellently, and it can be used for forecasting data, which may be useful for active control applications.
In the future, there is a need to investigate more novel DMD approaches such as the extended DMD [29] and the forward–backward DMD [30], with some extensions to account for control systems [31]. Additionally, extensions to the POD method can be investigated for extrapolation of the data, such as the Krylov-based POD [32]. These approaches show promise in terms of using a reduced-order-model-based acoustic prediction system, which may result in a faster turnaround time for design.
Author Contributions
Conceptualization, S.A. and R.M.; methodology, S.A.; software, S.A.; validation, S.A.; formal analysis, S.A.; investigation, S.A.; resources, S.A.; data curation, S.A.; writing—original draft preparation, S.A.; writing—review and editing, S.A. and R.M.; visualization, S.A.; supervision, R.M.; project administration, R.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author due to propriety.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gutin, L. On the Sound Field of a Rotating Propeller. 1948. Available online: https://ntrs.nasa.gov/citations/20030068996 (accessed on 3 August 2022).
- Deming, A.F. Propeller Rotation Noise Due to Torque and Thrust. J. Acoust. Soc. Am. 1940, 12, 173–182. [Google Scholar] [CrossRef]
- Kim, S.; Kinnas, S.A. Numerical Prediction of Underwater Noise on a Flat Hull Induced by Twin or Podded Propeller Systems. J. Sound Vib. 2022, 539, 117256. [Google Scholar] [CrossRef]
- Belibassakis, K.; Prospathopoulos, J. A 3d-BEM for Underwater Propeller Noise Propagation in the Ocean Environment Including Hull Scattering Effects. Ocean Eng. 2023, 286, 115544. [Google Scholar] [CrossRef]
- Lumley, J.L. Coherent Structures in Turbulence. Transit. Turbul. 1981, 1981, 215–242. [Google Scholar] [CrossRef]
- Berkooz, G.; Holmes, P.; Lumley, J.L. The Proper Orthogonal Decomposition in the Analysis of Turbulent Flows. Annu. Rev. Fluid Mech. 2003, 25, 539–575. [Google Scholar] [CrossRef]
- Towne, A.; Schmidt, O.T.; Colonius, T. Spectral Proper Orthogonal Decomposition and Its Relationship to Dynamic Mode Decomposition and Resolvent Analysis. J. Fluid Mech. 2018, 847, 821–867. [Google Scholar] [CrossRef]
- Peters, N.J.; Wissink, A.; Ekaterinaris, J. A Mode Based Reduced Order Model for Rotorcraft Store Separation. In Proceedings of the AIAA SciTech Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar] [CrossRef]
- Cabell, R.H.; Kegerise, M.A.; Cox, D.E.; Gibbs, G.P. Experimental Feedback Control of Flow-Induced Cavity Tones. AIAA J. 2012, 44, 1807–1815. [Google Scholar] [CrossRef]
- Brunton, S.L.; Rowley, C.W.; Williams, D.R. Reduced-Order Unsteady Aerodynamic Models at Low Reynolds Numbers. J. Fluid Mech. 2013, 724, 203–233. [Google Scholar] [CrossRef]
- Rowley, C.W.; Dawson, S.T.M. Model Reduction for Flow Analysis and Control. Annu. Rev. Fluid Mech. 2017, 49, 387–417. [Google Scholar] [CrossRef]
- Valbuena, M.; Sarabia, D.; de Prada, C. A Reduced-Order Approach of Distributed Parameter Models Using Proper Orthogonal Decomposition. Comput. Aided Chem. Eng. 2011, 29, 26–30. [Google Scholar]
- Dehghan, M.; Abbaszadeh, M. A Combination of Proper Orthogonal Decomposition–Discrete Empirical Interpolation Method (POD–DEIM) and Meshless Local RBF-DQ Approach for Prevention of Groundwater Contamination. Comput. Math. Appl. 2018, 75, 1390–1412. [Google Scholar] [CrossRef]
- Fic, A.; Białecki, R.A.; Kassab, A.J. Solving Transient Nonlinear Heat Conduction Problems by Proper Orthogonal Decomposition and the Finite-Element Method. Numer. Heat Transfer Part B Fundam. 2005, 48, 103–124. [Google Scholar] [CrossRef]
- Wang, Z.; Xiao, D.; Fang, F.; Govindan, R.; Pain, C.C.; Guo, Y. Model Identification of Reduced Order Fluid Dynamics Systems Using Deep Learning. Wiley Online Libr. 2017, 86, 255–268. [Google Scholar] [CrossRef]
- Mankbadi, R.R.; Afari, S.O.; Golubev, V.V. High-Fidelity Simulations of Noise Generation in a Propeller-Driven Unmanned Aerial Vehicle. AIAA J. 2021, 59, 1020–1039. [Google Scholar] [CrossRef]
- Schmid, P.J. Dynamic Mode Decomposition of Numerical and Experimental Data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef]
- Brunton, S.L.; Steven, L.; Kutz, J.N. Data-Driven Science and Engineering: Machine Learning, Dynamical Systems, and Control; Cambridge University Press: Cambridge, UK, 2022; Volume 472. [Google Scholar]
- Gavish, M.; Donoho, D.L. The Optimal Hard Threshold for Singular Values Is 4/√3. arXiv 2013, arXiv:1305.5870. [Google Scholar] [CrossRef]
- Mankbadi, R.R. Transition, Turbulence, and Noise; Springer: Boston, MA, USA, 1994; ISBN 978-0-7923-9481-5. [Google Scholar]
- Shur, M.L.; Strelets, M.K.; Travin, A.K.; Spalart, P.R. Turbulence Modeling in Rotating and Curved Channels: Assessing the Spalart-Shur Correction. AIAA J. 2000, 38, 784–792. [Google Scholar] [CrossRef]
- Spalart, P.; Allmaras, S. A One-Equation Turbulence Model for Aerodynamic Flows. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1992. [Google Scholar]
- Spalart, P.R.; Jou, W.-H.; Strelets, M.; Allmaras, S.R. Comments on the Feasibility of LES for Wings, and on a Hybrid RANS/LES Approach; Advances in DNS/LES: Direct Numerical Simulation and Large Eddy Simulation; Greyden Press: Dayton, OH, USA, 1997; Volume 1, ISBN 1570743657. [Google Scholar]
- Ffowcs Williams, J.E.; Hawkings, D.L. Sound Generation by Turbulence and Surfaces in Arbitrary Motion. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1969, 264, 321–342. [Google Scholar] [CrossRef]
- Brentner, K.S. Modeling Aerodynamically Generated Sound: Recent Advances in Rotor Noise Prediction. In Proceedings of the 38th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2000; American Institute of Aeronautics and Astronautics Inc.: Reston, VA, USA, 2000. [Google Scholar]
- Brentner, K.S.; Farassat, F. Analytical Comparison of the Acoustic Analogy and Kirchhoff Formulation for Moving Surfaces. AIAA J. 1998, 36, 1379–1386. [Google Scholar] [CrossRef]
- VtkToolbox—File Exchange—MATLAB Central. Available online: https://www.mathworks.com/matlabcentral/fileexchange/94993-vtktoolbox (accessed on 3 August 2022).
- Intaratep, N.; Alexander, W.N.; Devenport, W.J.; Grace, S.M.; Dropkin, A. Experimental Study of Quadcopter Acoustics and Performance at Static Thrust Conditions. In Proceedings of the 22nd AIAA/CEAS Aeroacoustics Conference, Lyon, France, 30 May–1 June 2016. [Google Scholar] [CrossRef]
- Williams, M.O.; Kevrekidis, I.G.; Rowley, C.W. A Data–Driven Approximation of the Koopman Operator: Extending Dynamic Mode Decomposition. J. Nonlinear. Sci. 2015, 25, 1307–1346. [Google Scholar] [CrossRef]
- Dawson, S.T.M.; Hemati, M.S.; Williams, M.O.; Rowley, C.W. Characterizing and Correcting for the Effect of Sensor Noise in the Dynamic Mode Decomposition. Exp. Fluids 2015, 57, 42. [Google Scholar] [CrossRef]
- Proctor, J.L.; Brunton, S.L.; Kutz, J.N. Dynamic Mode Decomposition with Control. SIAM J. Appl. Dyn Syst. 2014, 15, 142–161. [Google Scholar] [CrossRef]
- Liu, X.; Wang, H.; Yu, X.; Wang, C. A Krylov-Based Proper Orthogonal Decomposition Method for Elastodynamics Problems with Isogeometric Analysis. Eng. Anal. Bound Elem. 2021, 133, 71–83. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).