Transformer Encoder Enhanced by an Adaptive Graph Convolutional Neural Network for Prediction of Aero-Engines’ Remaining Useful Life
Abstract
1. Introduction
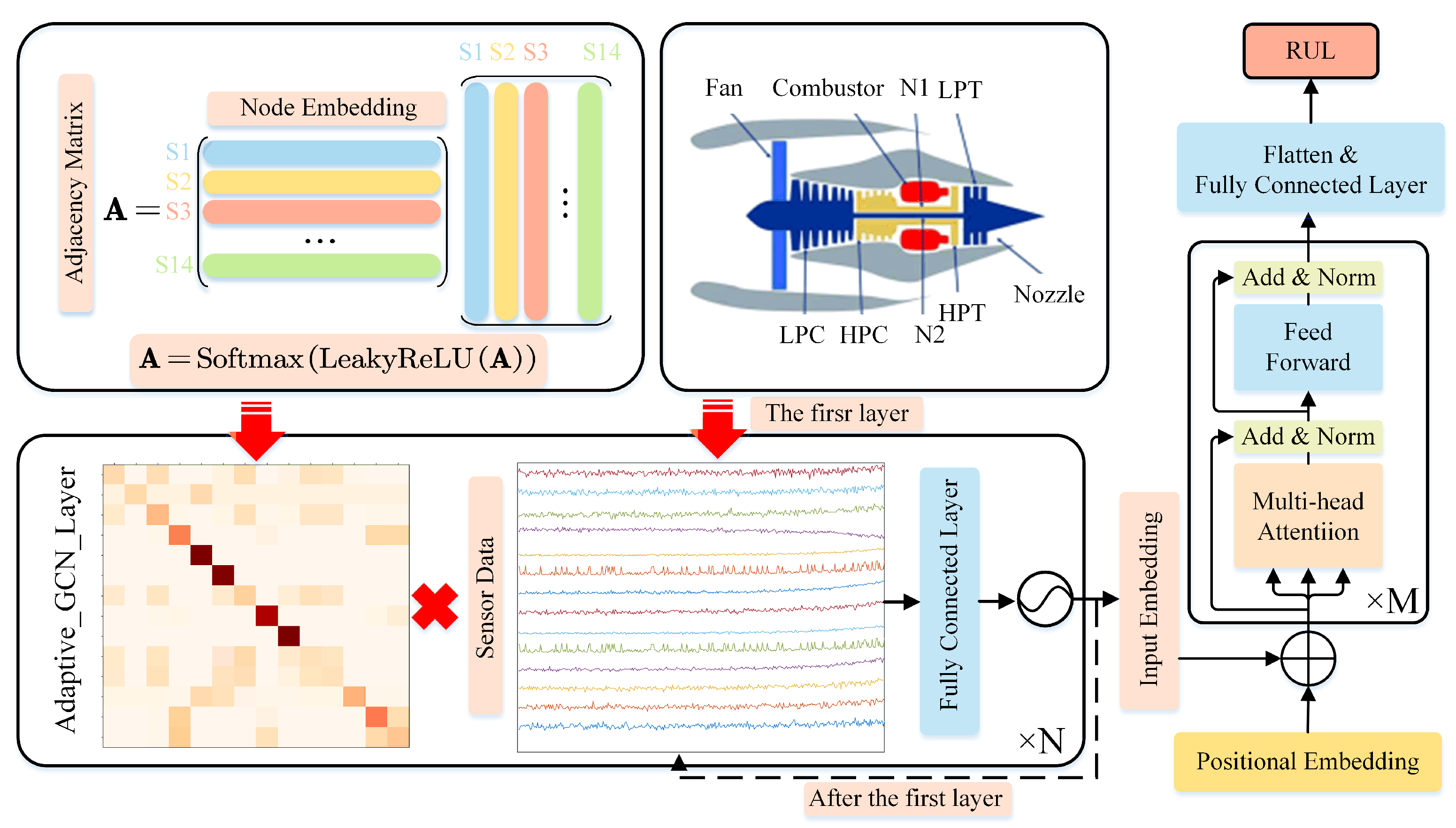
2. Methodology
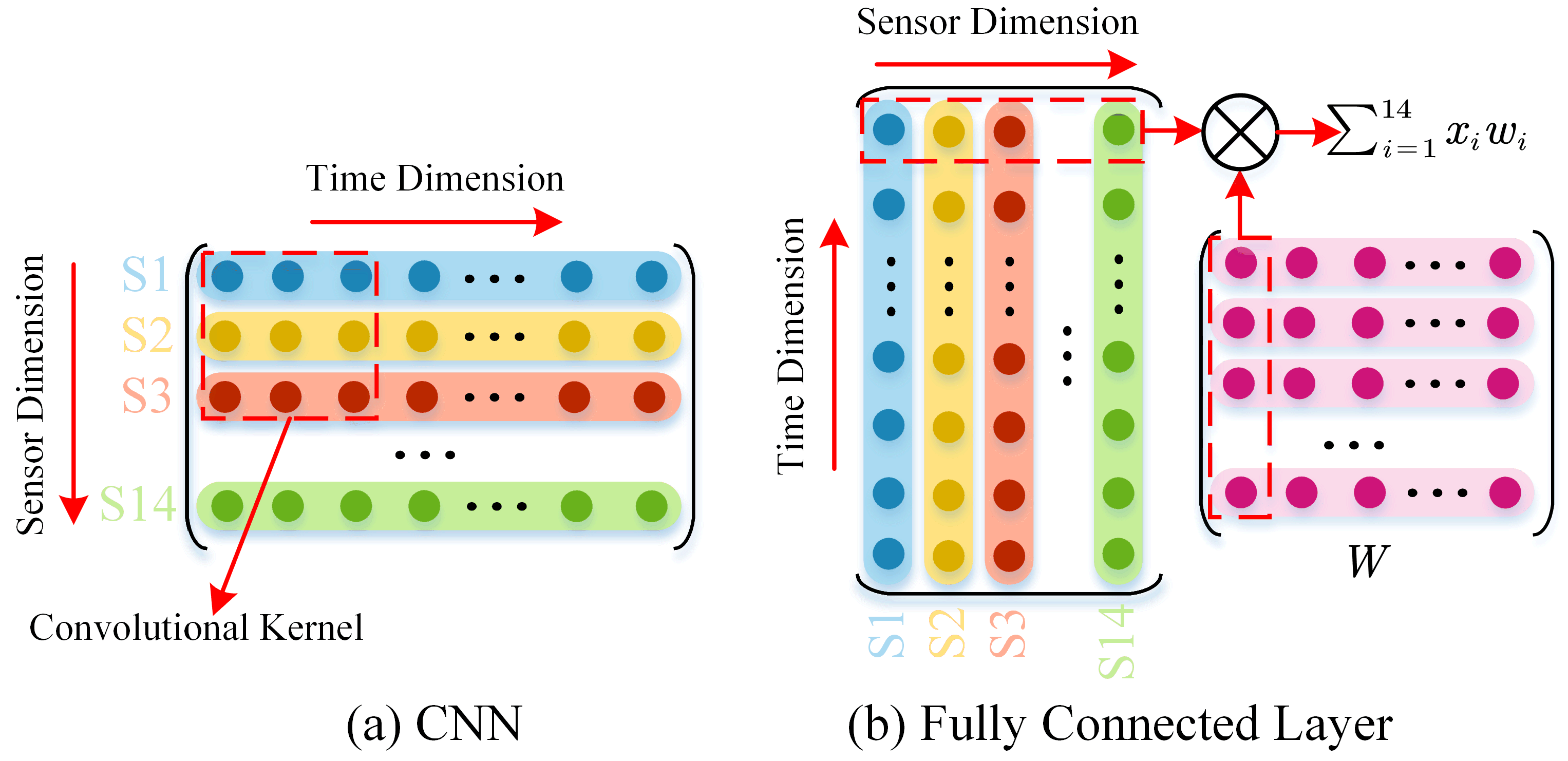
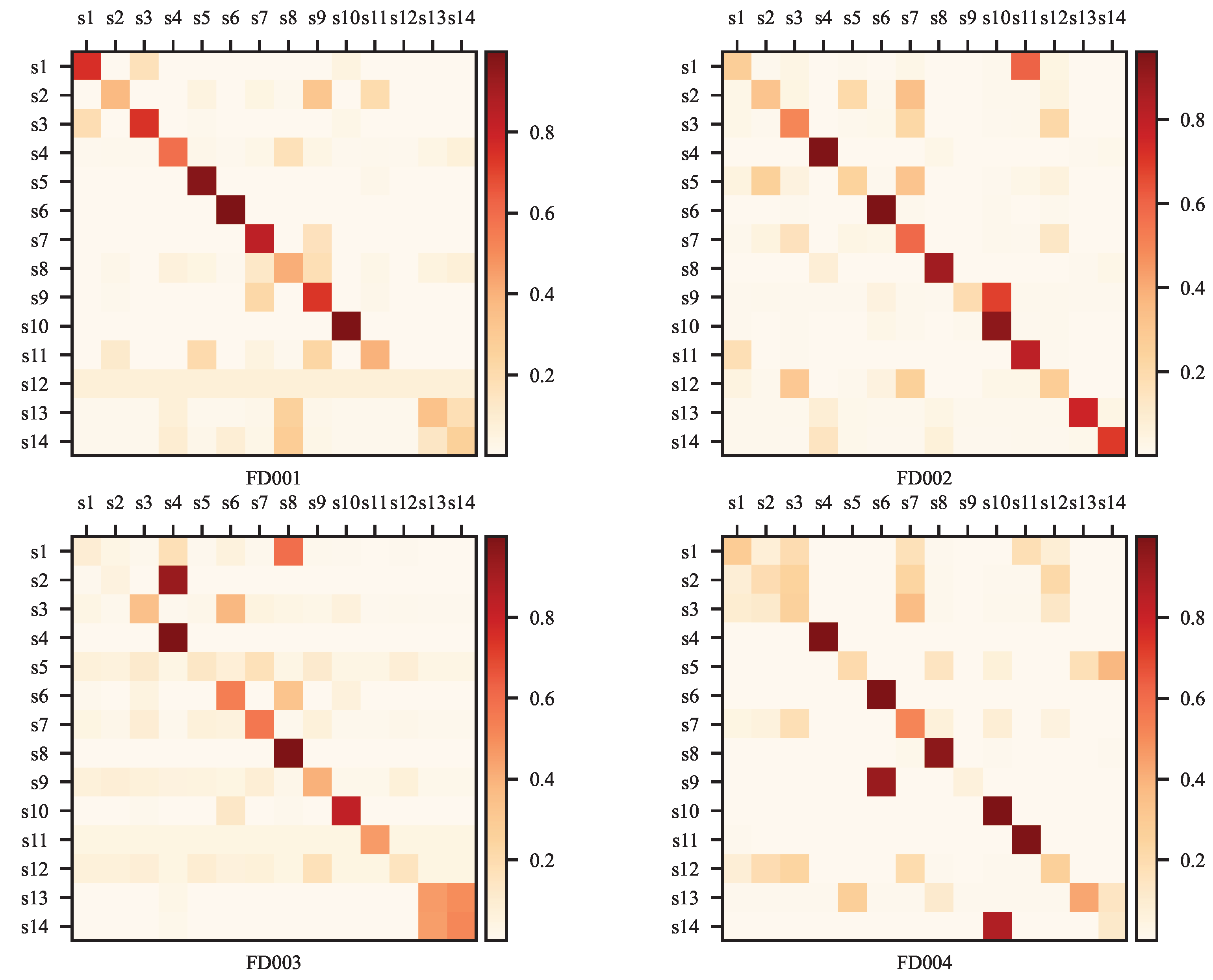
2.1. Adaptive GCN Layers
2.2. Transformer Encoder
2.2.1. Input Embedding
2.2.2. Positional Embedding
2.2.3. Multi-Head Attention
2.2.4. Feed-Forward Function
2.2.5. Skip Connection and Layernormalization
3. Experiment
3.1. Dataset Description
3.2. Data Preprocessing
3.3. Evaluation Metrics
3.4. Implementation Details
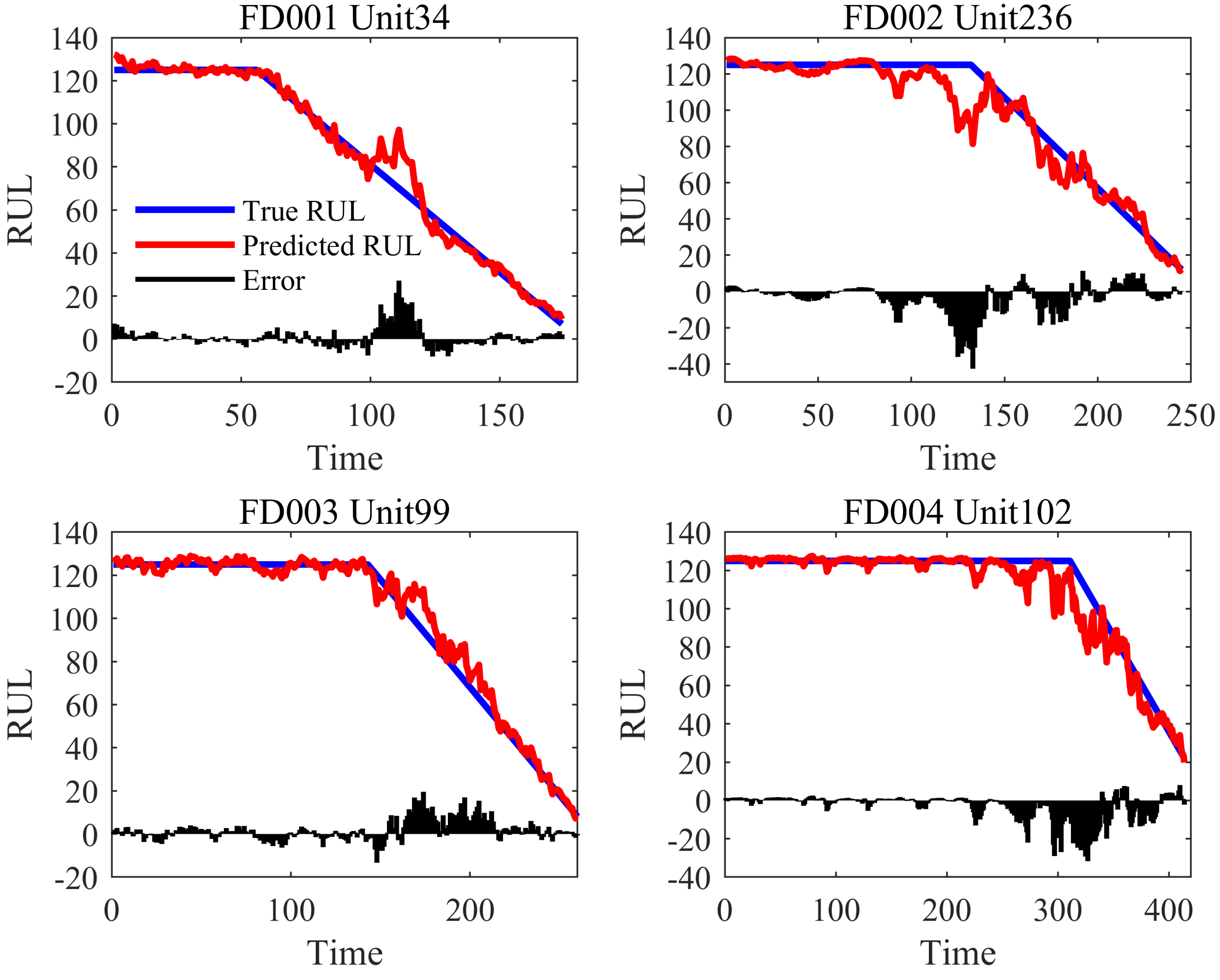
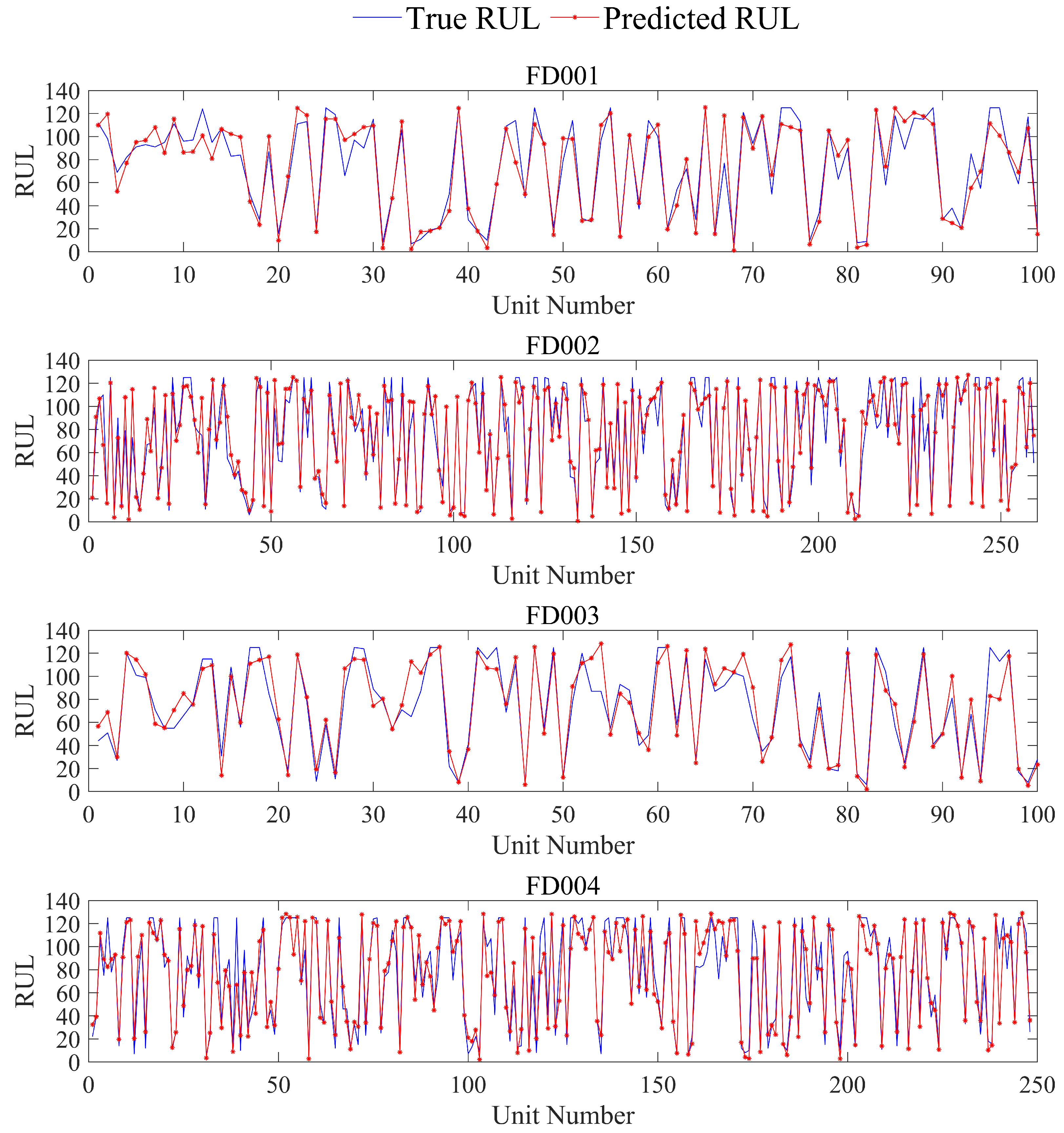
4. Results and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, H.; Zhang, Z.; Li, X.; Deng, X.; Jiang, W. Comprehensive Dynamic Structure Graph Neural Network for Aero-engine Remaining Useful Life Prediction. IEEE Trans. Instrum. Meas. 2023, 72, 3533816. [Google Scholar] [CrossRef]
- Chen, J.; Shen, C.; Jing, Z.; Wu, Y.; Chen, R. Remaining useful life prediction of aircraft flap control system with mode transition. AIAA J. 2022, 60, 1104–1115. [Google Scholar] [CrossRef]
- Wang, H.; Ma, X.; Zhao, Y. An improved Wiener process model with adaptive drift and diffusion for online remaining useful life prediction. Mech. Syst. Signal Proc. 2019, 127, 370–387. [Google Scholar] [CrossRef]
- Chiachío, J.; Jalón, M.L.; Chiachío, M.; Kolios, A. A Markov chains prognostics framework for complex degradation processes. Reliab. Eng. Syst. Saf. 2020, 195, 106621. [Google Scholar] [CrossRef]
- Li, Y.; Li, J.; Wang, H.; Liu, C.; Tan, J. Knowledge enhanced ensemble method for remaining useful life prediction under variable working conditions. Reliab. Eng. Syst. Saf. 2024, 242, 109748. [Google Scholar] [CrossRef]
- Li, T.; Zhao, Z.; Sun, C.; Yan, R.; Chen, X. Hierarchical attention graph convolutional network to fuse multi-sensor signals for remaining useful life prediction. Reliab. Eng. Syst. Saf. 2021, 215, 107878. [Google Scholar] [CrossRef]
- Zhang, X.; Kang, J.; Jin, T. Degradation modeling and maintenance decisions based on Bayesian belief networks. IEEE Trans. Reliab. 2014, 63, 620–633. [Google Scholar] [CrossRef]
- Benkedjouh, T.; Medjaher, K.; Zerhouni, N.; Rechak, S. Health assessment and life prediction of cutting tools based on support vector regression. J. Intell. Manuf. 2015, 26, 213–223. [Google Scholar] [CrossRef]
- Bezerra Souto Maior, C.; das Chagas Moura, M.; Didier Lins, I.; Lopez Droguett, E.; Henrique Lima Diniz, H. Remaining useful life estimation by empirical mode decomposition and support vector machine. IEEE Latin Am. Trans. 2016, 14, 4603–4610. [Google Scholar] [CrossRef]
- Li, X.; Ding, Q.; Sun, J.-Q. Remaining useful life estimation in prognostics using deep convolution neural networks. Reliab. Eng. Syst. Saf. 2018, 172, 1–11. [Google Scholar] [CrossRef]
- Sayah, M.; Guebli, D.; Noureddine, Z.; Al Masry, Z. Deep LSTM enhancement for RUL prediction using Gaussian mixture models. Autom. Control Comp. Sci. 2021, 55, 15–25. [Google Scholar] [CrossRef]
- Chen, D.; Qin, Y.; Wang, Y.; Zhou, J. Health indicator construction by quadratic function-based deep convolutional auto-encoder and its application into bearing RUL prediction. ISA Trans. 2021, 114, 44–56. [Google Scholar] [CrossRef] [PubMed]
- Kamei, S.; Taghipour, S. A comparison study of centralized and decentralized federated learning approaches utilizing the transformer architecture for estimating remaining useful life. Reliab. Eng. Syst. Saf. 2023, 233, 109130. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Philip, S.Y. A comprehensive survey on graph neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4–24. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Li, X.; He, D. A directed acyclic graph network combined with CNN and LSTM for remaining useful life prediction. IEEE Access 2019, 7, 75464–75475. [Google Scholar] [CrossRef]
- Kong, Z.; Jin, X.; Xu, Z.; Zhang, B. Spatio-temporal fusion attention: A novel approach for remaining useful life prediction based on graph neural network. IEEE Trans. Instrum. Meas. 2022, 71, 1–12. [Google Scholar] [CrossRef]
- Liu, N.; Guo, J.; Chen, S.; Zhang, X. Aero-Engines Remaining Useful Life Prognostics Based on Multi-Hierarchical Gated Recurrent Graph Convolutional Network. In Proceedings of the 2023 International Conference on Cyber-Physical Social Intelligence (ICCSI), Xi’an, China, 20–23 October 2023; pp. 642–647. [Google Scholar]
- Gilmer, J.; Schoenholz, S.S.; Riley, P.F.; Vinyals, O.; Dahl, G.E. Neural message passing for quantum chemistry. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 1263–1272. [Google Scholar]
- Deng, A.; Hooi, B. Graph neural network-based anomaly detection in multivariate time series. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; pp. 4027–4035. [Google Scholar]
- Zhang, X.; Leng, Z.; Zhao, Z.; Li, M.; Yu, D.; Chen, X. Spatial-temporal dual-channel adaptive graph convolutional network for remaining useful life prediction with multi-sensor information fusion. Adv. Eng. Inform. 2023, 57, 102120. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Ogunfowora, O.; Najjaran, H. A Transformer-based Framework For Multi-variate Time Series: A Remaining Useful Life Prediction Use Case. arXiv 2023, arXiv:2308.09884. [Google Scholar]
- Mo, Y.; Wu, Q.; Li, X.; Huang, B. Remaining useful life estimation via transformer encoder enhanced by a gated convolutional unit. J. Intell. Manuf. 2021, 32, 1997–2006. [Google Scholar] [CrossRef]
- Devlin, J.; Chang, M.-W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv 2018, arXiv:1810.04805. [Google Scholar]
- Dong, Y.; Cordonnier, J.-B.; Loukas, A. Attention is not all you need: Pure attention loses rank doubly exponentially with depth. In Proceedings of the International Conference on Machine Learning, Virtual, 18–24 July 2021; pp. 2793–2803. [Google Scholar]
- Saxena, A.; Goebel, K.; Simon, D.; Eklund, N. Damage propagation modeling for aircraft engine run-to-failure simulation. In Proceedings of the 2008 International Conference on Prognostics and Health Management, Denver, CO, USA, 6–9 October 2008; pp. 1–9. [Google Scholar]
- Sateesh Babu, G.; Zhao, P.; Li, X.-L. Deep convolutional neural network based regression approach for estimation of remaining useful life. In Proceedings of the Database Systems for Advanced Applications: 21st International Conference, DASFAA 2016, Dallas, TX, USA, 16–19 April 2016; Proceedings, Part I 21. pp. 214–228. [Google Scholar]
- Zheng, S.; Ristovski, K.; Farahat, A.; Gupta, C. Long short-term memory network for remaining useful life estimation. In Proceedings of the 2017 IEEE international conference on prognostics and health management (ICPHM), Dallas, TX, USA, 19–21 June 2017; pp. 88–95. [Google Scholar]
- Ellefsen, A.L.; Bjørlykhaug, E.; Æsøy, V.; Ushakov, S.; Zhang, H. Remaining useful life predictions for turbofan engine degradation using semi-supervised deep architecture. Reliab. Eng. Syst. Saf. 2019, 183, 240–251. [Google Scholar] [CrossRef]
- Liu, X.; Xiong, L.; Zhang, Y.; Luo, C. Remaining Useful Life Prediction for Turbofan Engine Using SAE-TCN Model. Aerospace 2023, 10, 715. [Google Scholar] [CrossRef]
- Mo, H.; Iacca, G. Evolutionary neural architecture search on transformers for RUL prediction. Mater. Manuf. Process. 2023, 38, 1881–1898. [Google Scholar] [CrossRef]
- Wang, L.; Cao, H.; Xu, H.; Liu, H. A gated graph convolutional network with multi-sensor signals for remaining useful life prediction. Knowl.-Based Syst. 2022, 252, 109340. [Google Scholar] [CrossRef]


| Dataset | FD001 | FD002 | FD003 | FD004 |
|---|---|---|---|---|
| Training EU | 100 | 260 | 100 | 249 |
| Testing EU | 100 | 259 | 100 | 248 |
| Working Conditions | 1 | 6 | 1 | 6 |
| Fault types | 1 | 1 | 2 | 2 |
| Number | Symbol | Description | Units |
|---|---|---|---|
| 1 | T2 | Total temperature at fan inlet | °R |
| 2 | T24 | Total temperature at LPC outlet | °R |
| 3 | T30 | Total temperature at HPC outlet | °R |
| 4 | T50 | Total temperature at LPT outlet | °R |
| 5 | P2 | Pressure at fan inlet | psia |
| 6 | P15 | Total pressure in bypass-duct | psia |
| 7 | P30 | Total pressure at HPC outlet | psia |
| 8 | Nf | physical fan speed | rpm |
| 9 | Nc | physical core speed | rpm |
| 10 | epr | Engine pressure ratio (P50/P2) | - |
| 11 | Ps30 | Static pressure at HPC outlet | psia |
| 12 | phi | Ratio of fuel flow to Ps30 | pps/psi |
| 13 | NRf | Corrected fan speed | rpm |
| 14 | NRc | Corrected core speed | rpm |
| 15 | BPR | Bypass ratio | - |
| 16 | farB | Burner fuel-air ratio | - |
| 17 | htBleed | Bleed Enthalpy | - |
| 18 | Nf_dmd | Demanded fan speed | rpm |
| 19 | PCNfR_dmd | Demanded corrected fan speed | rpm |
| 20 | W31 | HPT coolant bleed | lbm/s |
| 21 | W32 | LPT coolant bleed | lbm/s |
| Methods | FD001 | FD002 | FD003 | FD004 | |
|---|---|---|---|---|---|
| CNN [28] | 18.45 | 30.29 | 19.82 | 29.16 | 24.43 |
| DCNN [10] | 12.61 | 22.36 | 12.64 | 23.31 | 17.73 |
| LSTM-FNN [29] | 16.14 | 24.49 | 16.18 | 28.17 | 21.25 |
| RBM-LSTM-FNN [30] | 12.56 | 22.73 | 12.10 | 22.66 | 17.51 |
| DSAE-TCN [31] | 18.01 | - | - | - | - |
| GCU-Transformer [24] | 11.27 | 22.81 | 11.42 | 24.86 | 17.59 |
| Transformer-1 [13] | 13.52 | 16.11 | 17.10 | 19.77 | 16.63 |
| Transformer-2 [32] | 11.50 | 16.14 | 11.35 | 20.00 | 14.75 |
| DAG [15] | 11.96 | 20.34 | 12.46 | 22.43 | 16.80 |
| STFA [16] | 11.35 | 19.17 | 11.64 | 21.41 | 15.89 |
| CDSG [1] | 11.26 | 18.13 | 12.03 | 19.73 | 15.29 |
| GGCN [33] | 11.82 | 17.24 | 12.21 | 17.36 | 14.66 |
| AGCTE (this paper) | 12.46 | 13.7 | 12.95 | 15.83 | 13.74 |
| Methods | FD001 | FD002 | FD003 | FD004 | Avg. |
|---|---|---|---|---|---|
| CNN [28] | 1287 | 13,570 | 1596 | 7886 | 6084.75 |
| DCNN [10] | 274 | 10,412 | 284 | 12,466 | 5859 |
| LSTM-FNN [29] | 338 | 445 | 852 | 5550 | 2795.5 |
| RBM-LSTM-FNN [30] | 231 | 3366 | 251 | 2840 | 1672 |
| DSAE-TCN [31] | 161 | - | - | - | - |
| GCU-Transformer [24] | - | - | - | - | - |
| Transformer-1 [13] | 287.07 | 1436.74 | 263.64 | 2784.62 | 1193.02 |
| Transformer-2 [32] | 202 | 1131 | 227 | 2298 | 964.5 |
| DAG [15] | 229 | 2730 | 535 | 3370 | 1716 |
| STFA [16] | 194.44 | 2493.09 | 224.53 | 2760.13 | 1418.05 |
| CDSG [1] | 188 | 1740 | 218 | 2332 | 1119.5 |
| GGCN [33] | 186.6 | 1493.7 | 245.19 | 1371.5 | 824.25 |
| AGCTE (this paper) | 259.37 | 833.41 | 372.44 | 1520.05 | 746.32 |
| Methods | FD001 | FD002 | FD003 | FD004 | Avg. |
|---|---|---|---|---|---|
| AGCTE | 12.46 | 13.70 | 12.95 | 15.83 | 13.74 |
| AGCTE-w/o GCN | 13.6 | 14.16 | 12.86 | 16.36 | 14.26 |
| difference | 1.14 | 0.46 | −0.09 | 0.53 | 0.51 |
| AGCTE-w/o Transformer | 13.27 | 22.83 | 12.73 | 35.94 | 21.19 |
| difference | 0.81 | 9.13 | −0.22 | 20.11 | 7.76 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, M.; Wang, Z.; Zhong, Z. Transformer Encoder Enhanced by an Adaptive Graph Convolutional Neural Network for Prediction of Aero-Engines’ Remaining Useful Life. Aerospace 2024, 11, 289. https://doi.org/10.3390/aerospace11040289
Ma M, Wang Z, Zhong Z. Transformer Encoder Enhanced by an Adaptive Graph Convolutional Neural Network for Prediction of Aero-Engines’ Remaining Useful Life. Aerospace. 2024; 11(4):289. https://doi.org/10.3390/aerospace11040289
Chicago/Turabian StyleMa, Meng, Zhizhen Wang, and Zhirong Zhong. 2024. "Transformer Encoder Enhanced by an Adaptive Graph Convolutional Neural Network for Prediction of Aero-Engines’ Remaining Useful Life" Aerospace 11, no. 4: 289. https://doi.org/10.3390/aerospace11040289
APA StyleMa, M., Wang, Z., & Zhong, Z. (2024). Transformer Encoder Enhanced by an Adaptive Graph Convolutional Neural Network for Prediction of Aero-Engines’ Remaining Useful Life. Aerospace, 11(4), 289. https://doi.org/10.3390/aerospace11040289






