Comparative Study of Numerical Schemes for Granular Combustion of Boron Potassium Nitrate
Abstract
1. Introduction
2. Closed Bomb Test
3. Compressible Multifluid Formulation for Granular Combustion
4. Numerical Schemes
4.1. HLLC
4.2. AUSM+-up
4.3. HLLC-AUSM
5. Computational Framework
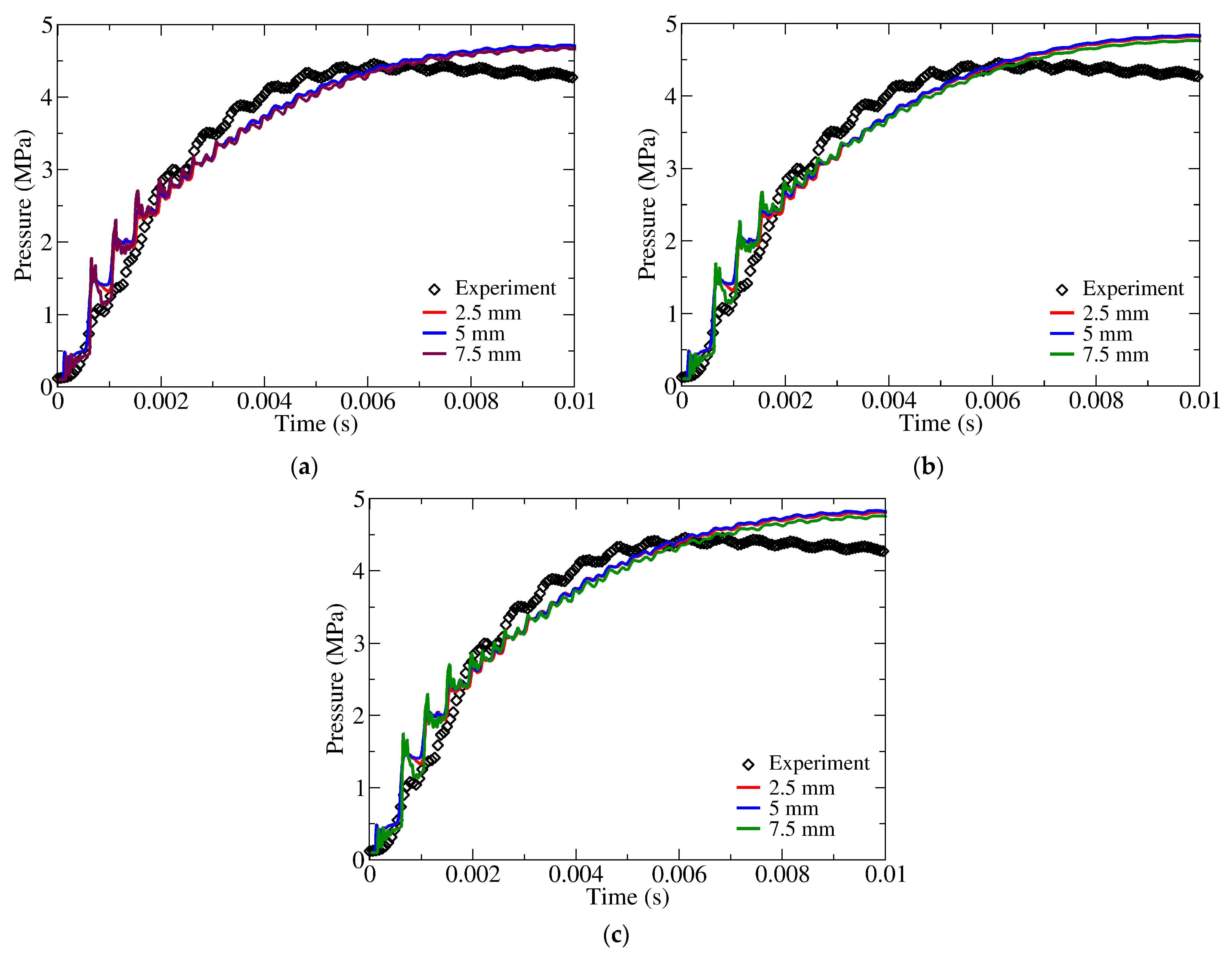
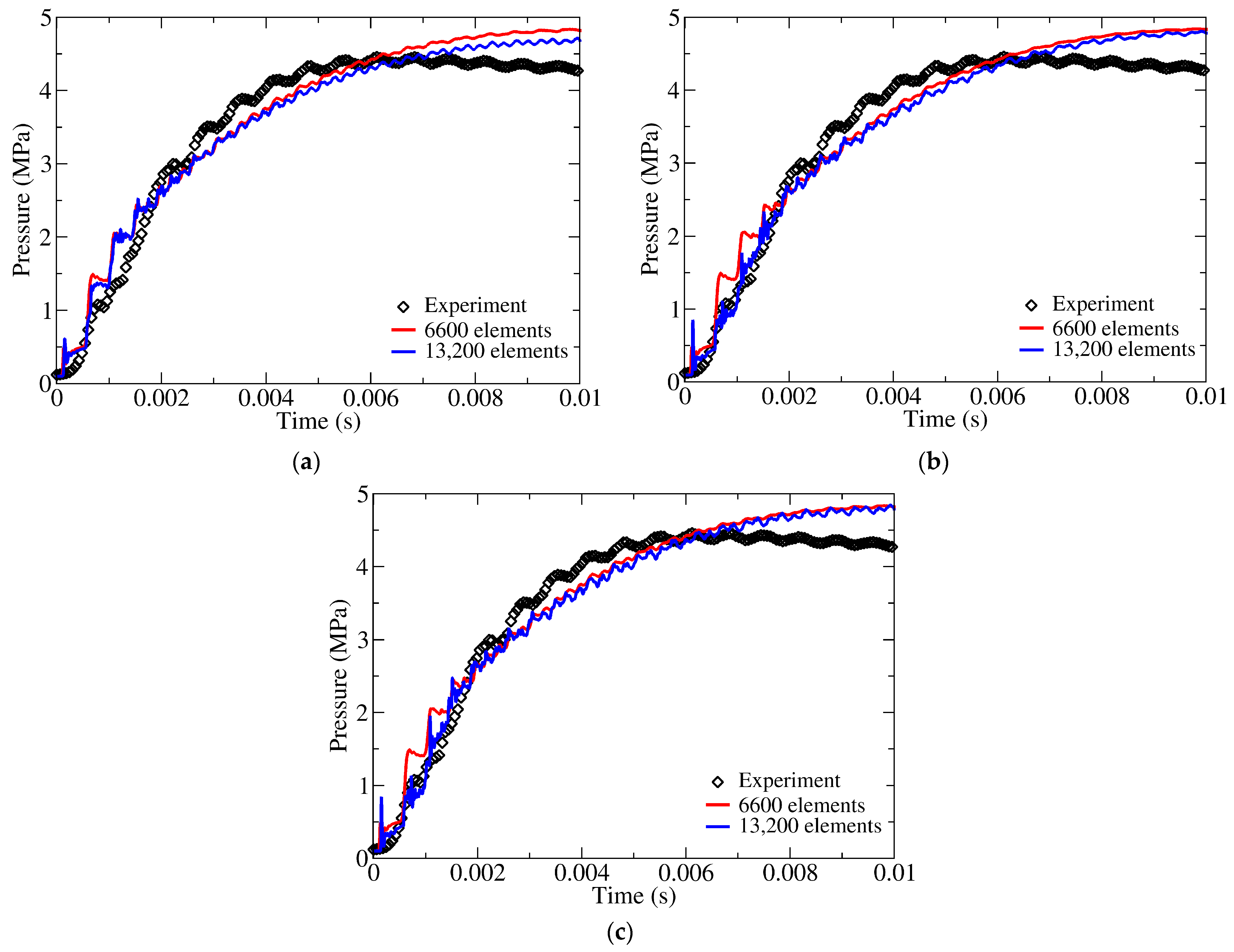
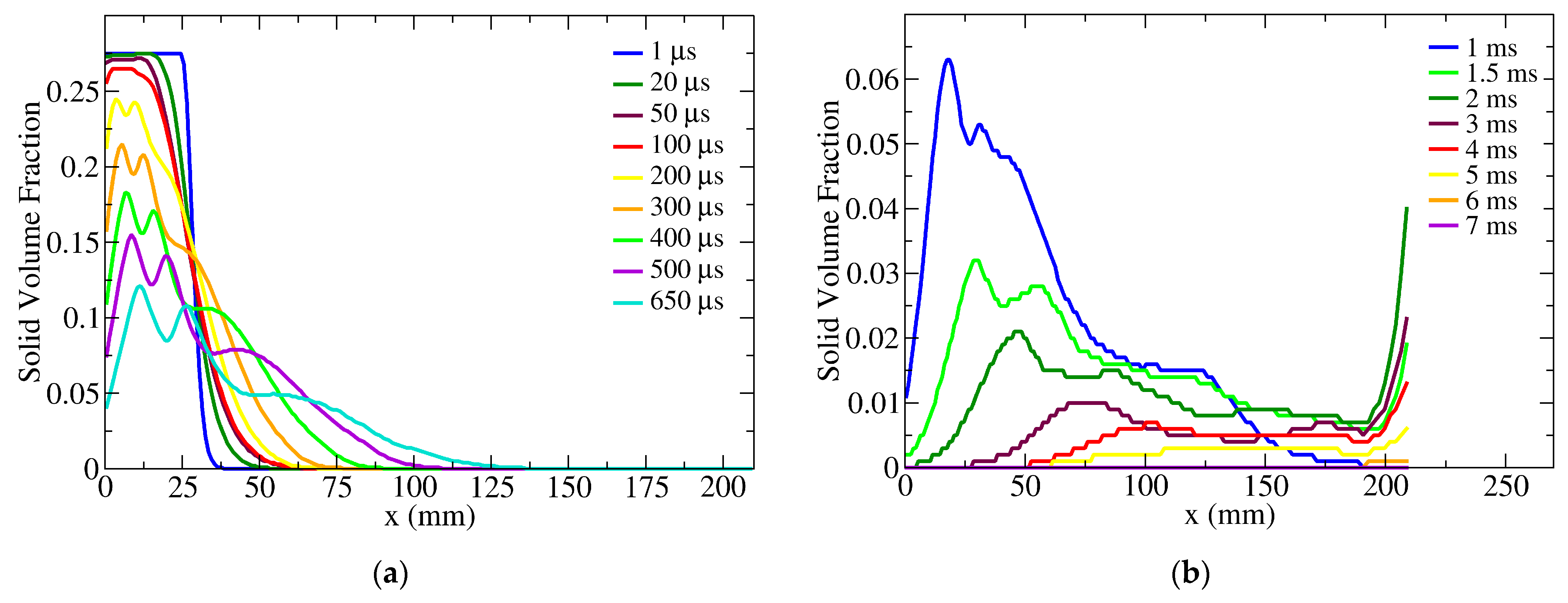
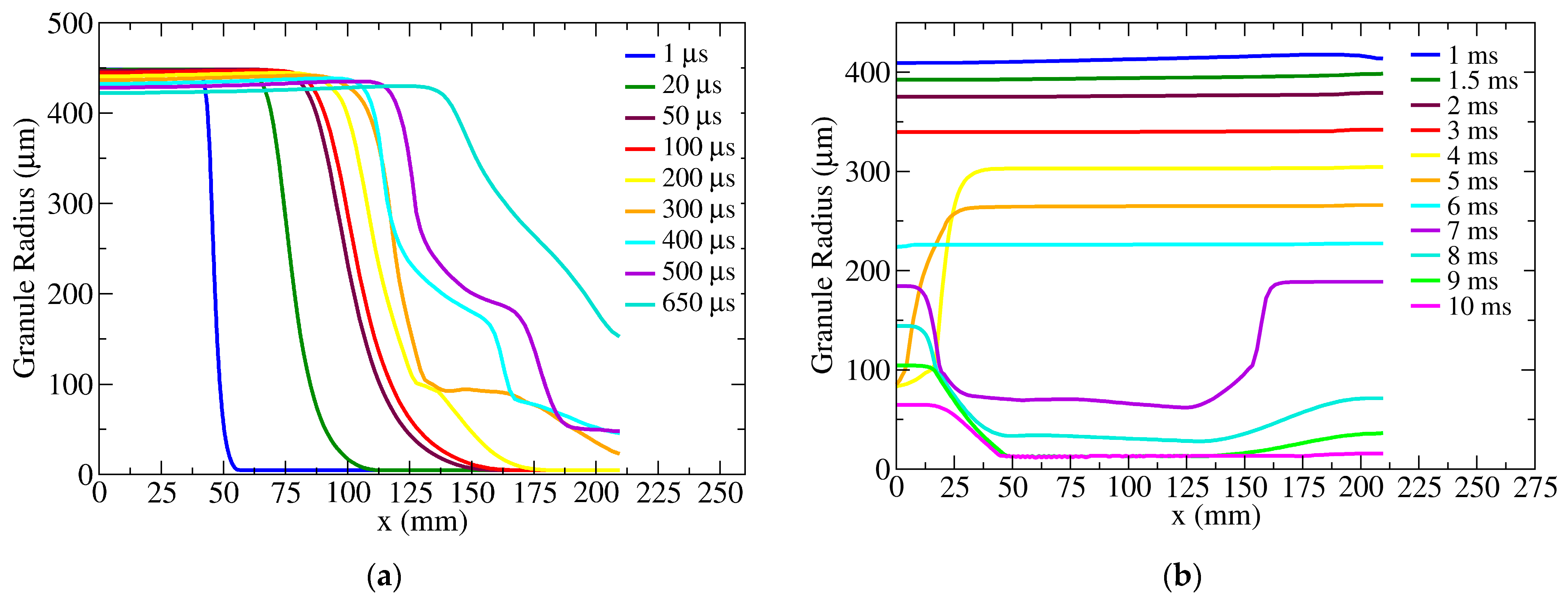
6. Results and Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| mass generated | |
| a | speed of sound |
| D | drag |
| E | total energy |
| E | total flux vector |
| e | internal energy |
| F | axial flux vector |
| G | radial flux vector |
| Hc | heat of combustion |
| N | number density per unit volume |
| P | pressure |
| Q | heat transfer |
| q | velocity vector |
| r | radial direction |
| S | source term vector |
| S | wave speed |
| t | time |
| T | temperature |
| U | conserved variables vector |
| u | axial velocity |
| v | radial velocity |
| x | axial direction |
| Y | local mass fraction |
| Greek | |
| volume fraction | |
| µ | pressure relaxation |
| γ | specific heat ratio |
| ξ | gaseous combustion products mass fraction |
| τ | pressure relaxation time |
| Ω | volume |
| density | |
| Subscripts | |
| g | gas phase |
| I | interface |
| i | computational cell |
| k | gas/solid phase |
| l/L | left |
| p | solid phase |
| q | condensed phase combustion products |
| r/R | right |
| Abbreviations | |
| AUSM | advection upstream splitting method |
| BPN | boron potassium nitrate |
| CEA | chemical equilibrium compositions and applications |
| HLLC | Harten-Lax-van Leer-Contact |
References
- Kuo, K.K. Principles of Combustion, 1st ed.; Wiley-Interscience: Hoboken, NJ, USA, 1986; pp. 601–614. [Google Scholar]
- Krier, H.; Gokhale, S. Predictions of vigorous ignition dynamics for a packed bed of solid propellant grains. Int. J. Heat Mass Transf. 1976, 8, 915–923. [Google Scholar] [CrossRef]
- Kuo, K.K.; Vichnevetsky, R.; Summerfield, M. Theory of flame front propagation in porous propellant charges under confinement. AIAA J. 1973, 11, 444–451. [Google Scholar] [CrossRef]
- Powers, J.; Stewart, D.; Krier, H. Theory of two-phase detonation—Part i: Modeling. Combust. Flame 1990, 80, 264–279. [Google Scholar] [CrossRef]
- Powers, J.M.; Gonthier, K.A. Pyrotechnic modelling for the NSI driven pin puller. Intern. Fluid Mech. Div. 1992. [Google Scholar]
- Gonthier, K.A.; Powers, J.M. Formulations, predictions, and sensitivity analysis of a pyrotechnically actuated pin puller model. J. Propuls. Power 1994, 10, 501–507. [Google Scholar] [CrossRef]
- Bdzil, J.; Menikoff, R.; Son, S.; Kapila, A.; Stewart, D.S. Two-phase modeling of deflagration-to-detonation transition in granular materials: A critical examination 46 of modeling issues. Phys. Fluids 1999, 11, 378–402. [Google Scholar] [CrossRef][Green Version]
- Saurel, R.; Le Martelot, S.; Tosello, R.; Lapebie, E. Symmetric model of compressible granular mixtures with permeable interfaces. Phys. Fluids 2014, 26, 123304. [Google Scholar] [CrossRef]
- Saurel, R.; Chinnayya, A.; Carmouze, Q. Modelling compressible dense and dilute two-phase flows. Phys. Fluids 2017, 29, 063301. [Google Scholar] [CrossRef]
- Davis, T.; Kuo, K. Experimental study of the combustion processes in granular propellant beds. J. Spacecr. Rocket. 1979, 16, 203–209. [Google Scholar] [CrossRef]
- Han, D.-H.; Sung, H.-G.; Ryu, B.-T. Numerical simulation for the combustion of a zirconium/potassium perchlorate explosive inside a closed vessel. Propellants Explos. Pyrotech. 2017, 42, 1168–1178. [Google Scholar] [CrossRef]
- Ulas, A.; Risha, G.A.; Kuo, K.K. An investigation of the performance of a boron/potassium-nitrate based pyrotechnic igniter. Propellants Explos. Pyrotech. Int. J. Deal. Sci. Technol. Asp. Energ. Mater. 2006, 79, 311–317. [Google Scholar] [CrossRef]
- Yeom, G.S.; Chang, K.S. A modified HLLC-type Riemann solver for the compressible six-equation two-fluid model. Comput. Fluids 2013, 76, 86–104. [Google Scholar] [CrossRef]
- Furfaro, D.; Saurel, R. A simple HLLC-type Riemann solver for compressible non-equilibrium two-phase flows. Comput. Fluids 2015, 111, 159–178. [Google Scholar] [CrossRef]
- Kitamura, K.; Liou, M.S.; Chang, C.H. Extension and comparative study of AUSM-family schemes for compressible multiphase flow simulations. Commun. Comput. Phys. 2014, 16, 632–674. [Google Scholar] [CrossRef]
- Houim, R.W.; Oran, E.S. A technique for computing dense granular compressible flows with shock waves. arXiv 2013, arXiv:1312.1290. [Google Scholar]
- Houim, R.W.; Oran, E.S. A multiphase model for compressible granular–gaseous flows: Formulation and initial tests. J. Fluid Mech. 2016, 789, 166–220. [Google Scholar] [CrossRef]
- Gordon, S.; McBride, B.J. Computer Program for Calculation of Complex Chemical Equilibrium Compositions and Applications; NASA Reference Publication 1311; NASA Lewis Research Center: Cleveland, OH, USA, 1994. [Google Scholar]
- Yeom, G.S.; Chang, K.S. Dissipation of shock wave in a gas-droplet mixture by droplet fragmentation. Int. J. Heat Mass Transf. 2012, 55, 941–957. [Google Scholar] [CrossRef]
- Isherwood, L.; Grant, Z.J.; Gottlieb, S. Strong stability preserving integrating factor Runge–Kutta methods. SIAM J. Numer. Anal. 2018, 56, 3276–3307. [Google Scholar] [CrossRef]
- Blazek, J. Computational Fluid Dynamics: Principles and Applications, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2001; pp. 129–133. [Google Scholar]
- Michalak, K.; Ollivier-Gooch, C. Differentiability of slope limiters on unstructured grids. In Proceedings of the Fourteenth Annual Conference of the Computational Fluid Dynamics Society of Canada, Kingston, Canada, 16–18 July 2006. [Google Scholar]
- Batten, P.; Clarke, N.; Lambert, C.; Causon, D.M. On the choice of wavespeeds for the HLLC Riemann solver. SIAM J. Sci. Comput. 1997, 18, 1553–1570. [Google Scholar] [CrossRef]
- Liou, M.S. A sequel to AUSM, Part II: AUSM+-up for all speeds. J. Comput. Phys. 2006, 214, 137–170. [Google Scholar] [CrossRef]
- Kim, B.; Jang, S.-G.; Yoh, J.J. A full-scale hydrodynamic simulation of energetic component system. Comput. Fluids 2017, 156, 368–383. [Google Scholar] [CrossRef]
- Wang, L.; Feng, C.; Han, C. Experimental study on boron-potassium nitrate initiated by shock. J. Propuls. Power 1998, 14, 416–420. [Google Scholar] [CrossRef]
- Ding, D. A study on the ignition of boron/potassium nitrate mixture. Sci. Technol. Energ. Mater. 2006, 67, 23. [Google Scholar]
- Wu, J.; Liu, J.; Yang, L.; Li, Y.; Chen, L. Numerical simulation of the metal bridge foil explosion plasma ignition of B/KNO3. Phys. Plasmas 2020, 27, 033509. [Google Scholar] [CrossRef]

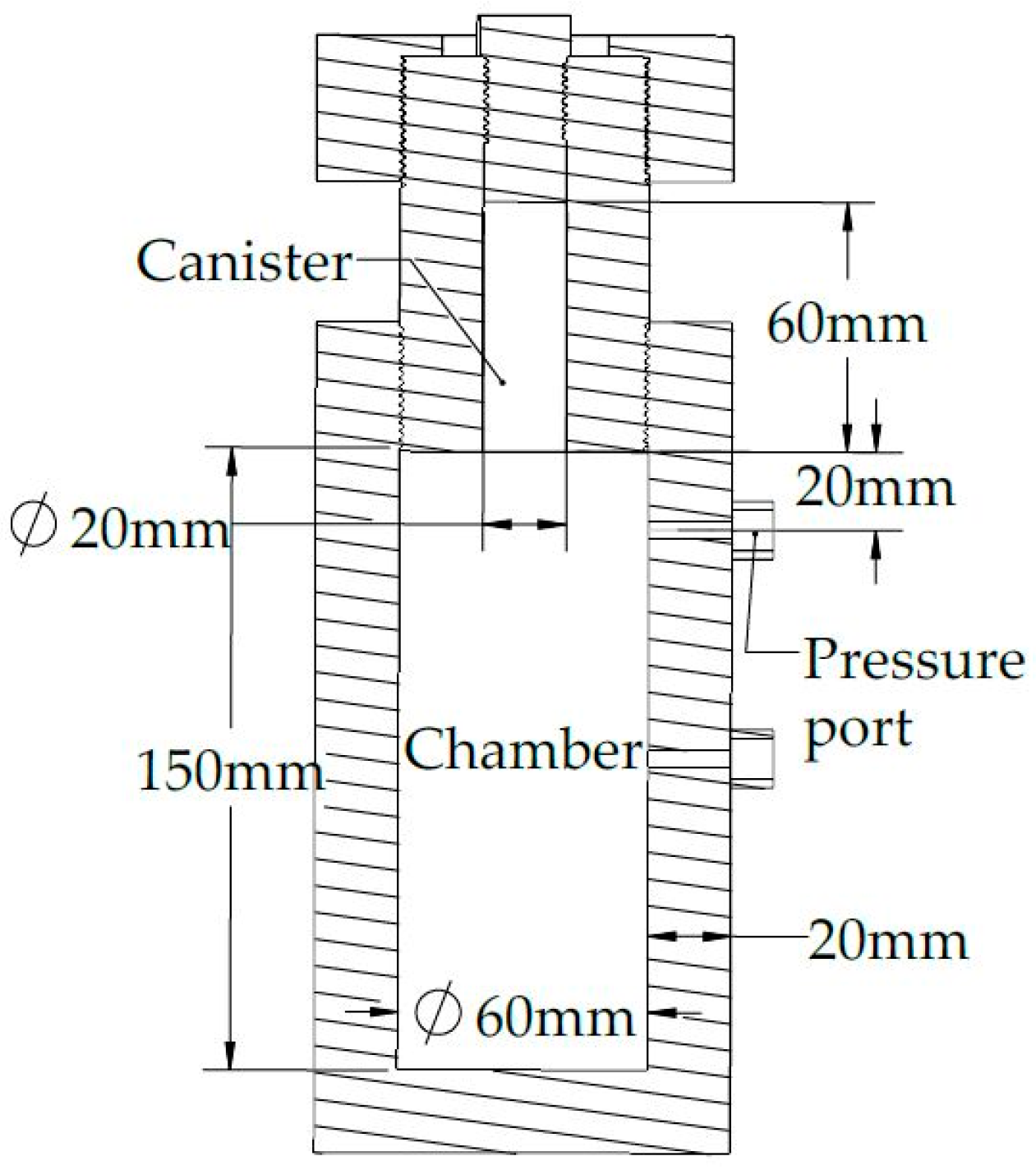

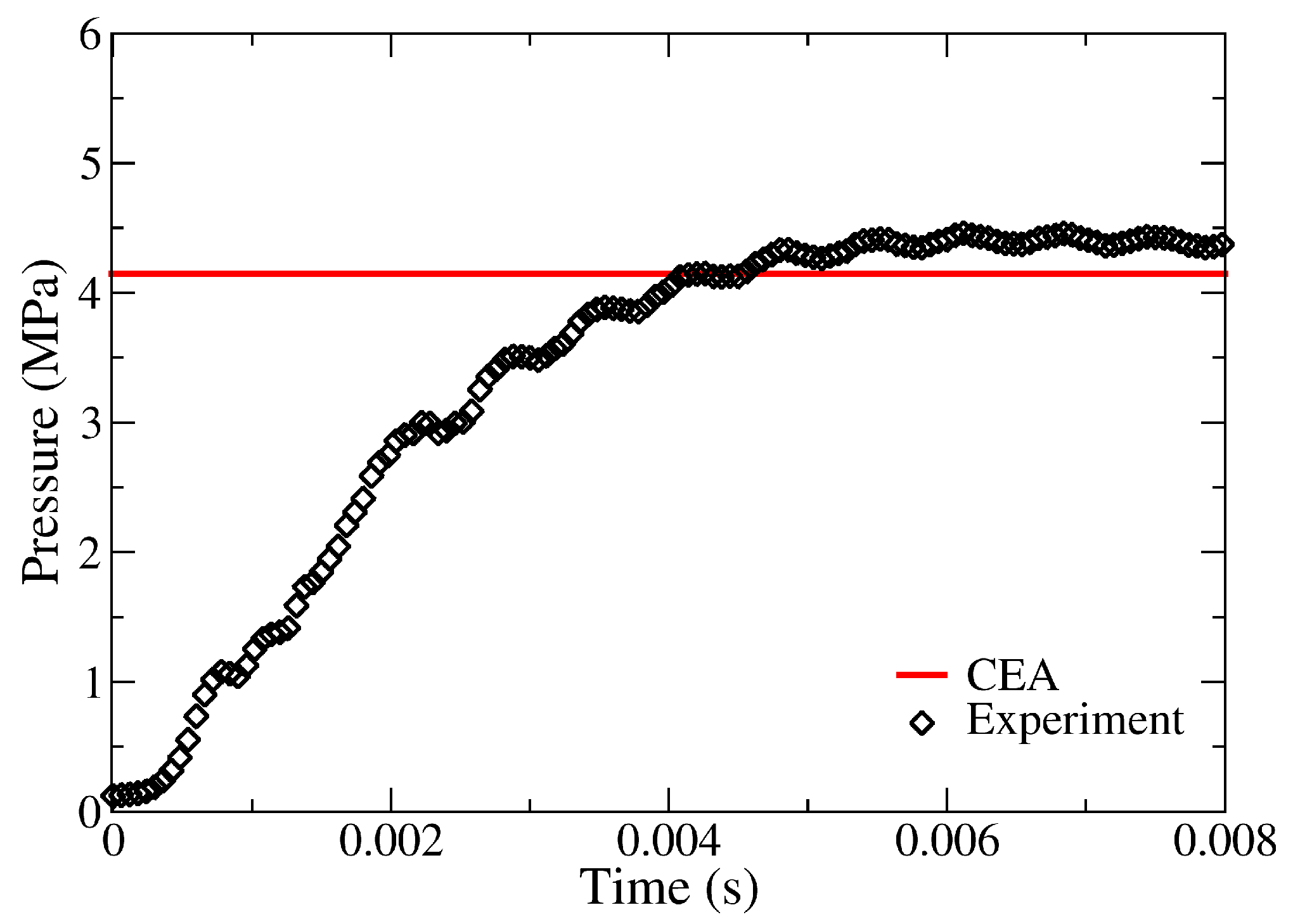
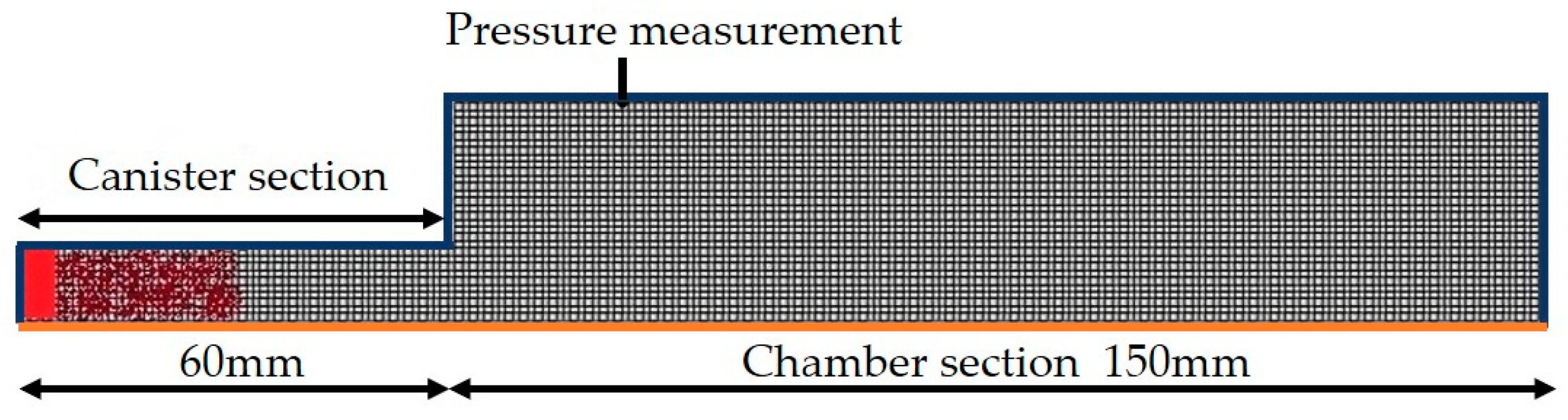
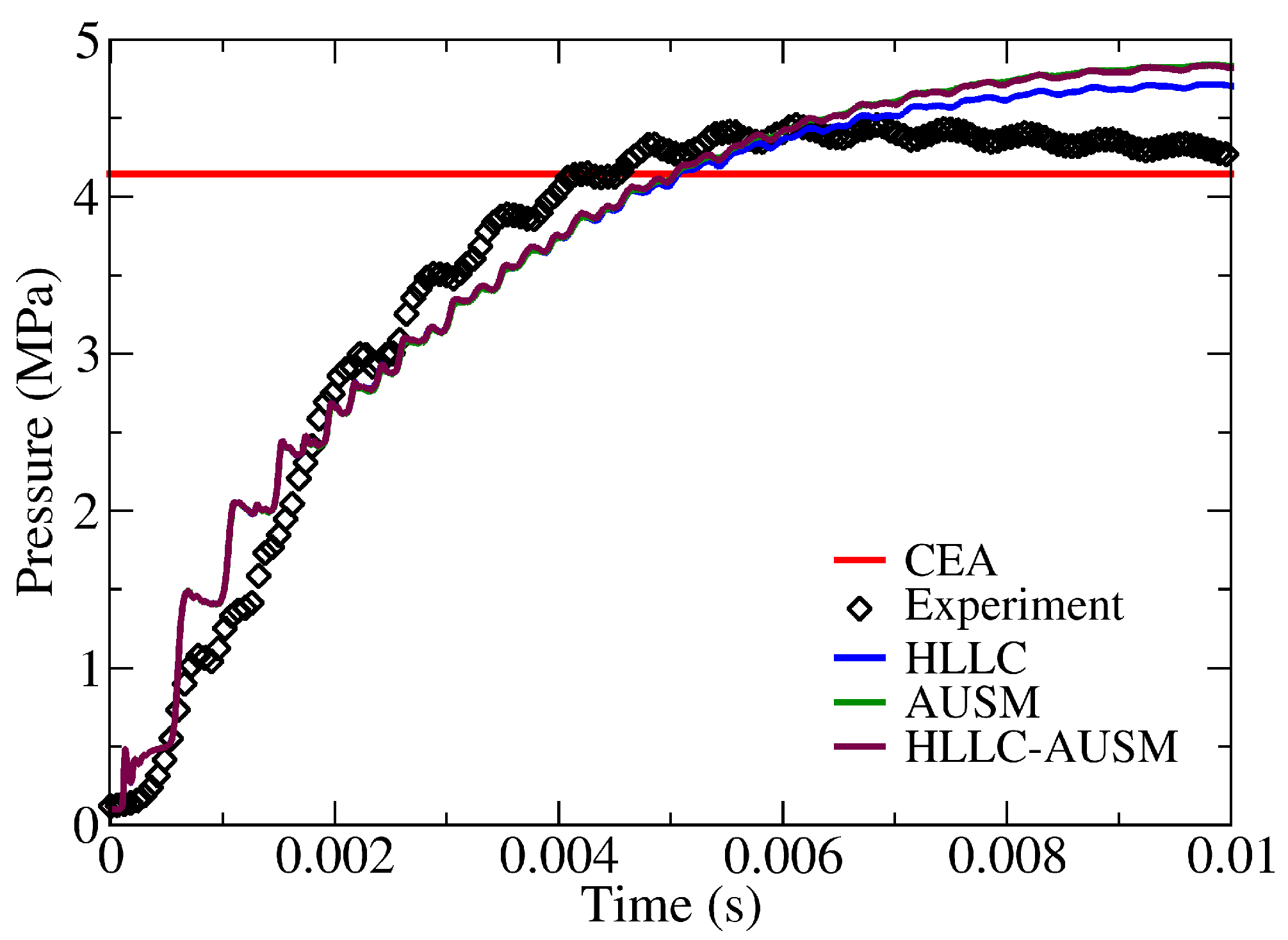
| Parameters | Value |
|---|---|
| Make and model number | Kulite; EWCTV 312(M) |
| Pressure range | 140 bar |
| Operating temperature range | 297 to 1366 K |
| Residual unbalance | 0.5 V ± 100 mV |
| Uncertainty in pressure measurement | 0.1% of full scale (FS) |
| Parameters | Value | Source |
|---|---|---|
| Density (kg/m3) | 2000 | measured |
| Diameter (µm) | 897 | measured |
| Volume of one granule | 0.3779 | calculated |
| Surface area–volume relation | 4.836Vol0.67 | sphere correlation |
| Burn rate law (mm/s; P in bar) | 19.75P0.19 | measured |
| Speed of sound (m/s) | 2463 | Kim et al. [25] |
| BPN specific heat ratio | 2.2023 | computed from Wang et al. [26] |
| (GPa) | 6.075 | computed from Wang et al. [26] |
| Initial solid volume fraction | 0.275 | calculated |
| Length occupied in the canister (mm) | 29 | measured |
| Initial pressure (bar) | 1 | ambient condition |
| Initial temperature (K) | 308.15 | ambient condition |
| Ignition temperature (K) | 834 | Dayu [27] |
| Flame temperature (K) | 3011.5 | CEA analysis [18] |
| Heat of combustion (kJ/kg) | 7773.2 | Wu et al. [28] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elizabeth, A.R.; Sarma, S.; Jayachandran, T.; Ramakrishna, P.A.; Borthakur, M. Comparative Study of Numerical Schemes for Granular Combustion of Boron Potassium Nitrate. Aerospace 2024, 11, 251. https://doi.org/10.3390/aerospace11040251
Elizabeth AR, Sarma S, Jayachandran T, Ramakrishna PA, Borthakur M. Comparative Study of Numerical Schemes for Granular Combustion of Boron Potassium Nitrate. Aerospace. 2024; 11(4):251. https://doi.org/10.3390/aerospace11040251
Chicago/Turabian StyleElizabeth, Annie Rose, Sumit Sarma, T. Jayachandran, P. A. Ramakrishna, and Mondeep Borthakur. 2024. "Comparative Study of Numerical Schemes for Granular Combustion of Boron Potassium Nitrate" Aerospace 11, no. 4: 251. https://doi.org/10.3390/aerospace11040251
APA StyleElizabeth, A. R., Sarma, S., Jayachandran, T., Ramakrishna, P. A., & Borthakur, M. (2024). Comparative Study of Numerical Schemes for Granular Combustion of Boron Potassium Nitrate. Aerospace, 11(4), 251. https://doi.org/10.3390/aerospace11040251







