Experimental Investigation of the Shock-Related Unsteadiness around a Spiked-Blunt Body Based on a Novel DMD Energy Sorting Criterion
Abstract
1. Introduction
2. Experimental Facility and Method
2.1. Direct-Connect Wind Tunnel
2.2. Spiked-Blunt Body Model
2.3. High-Speed Schlieren System
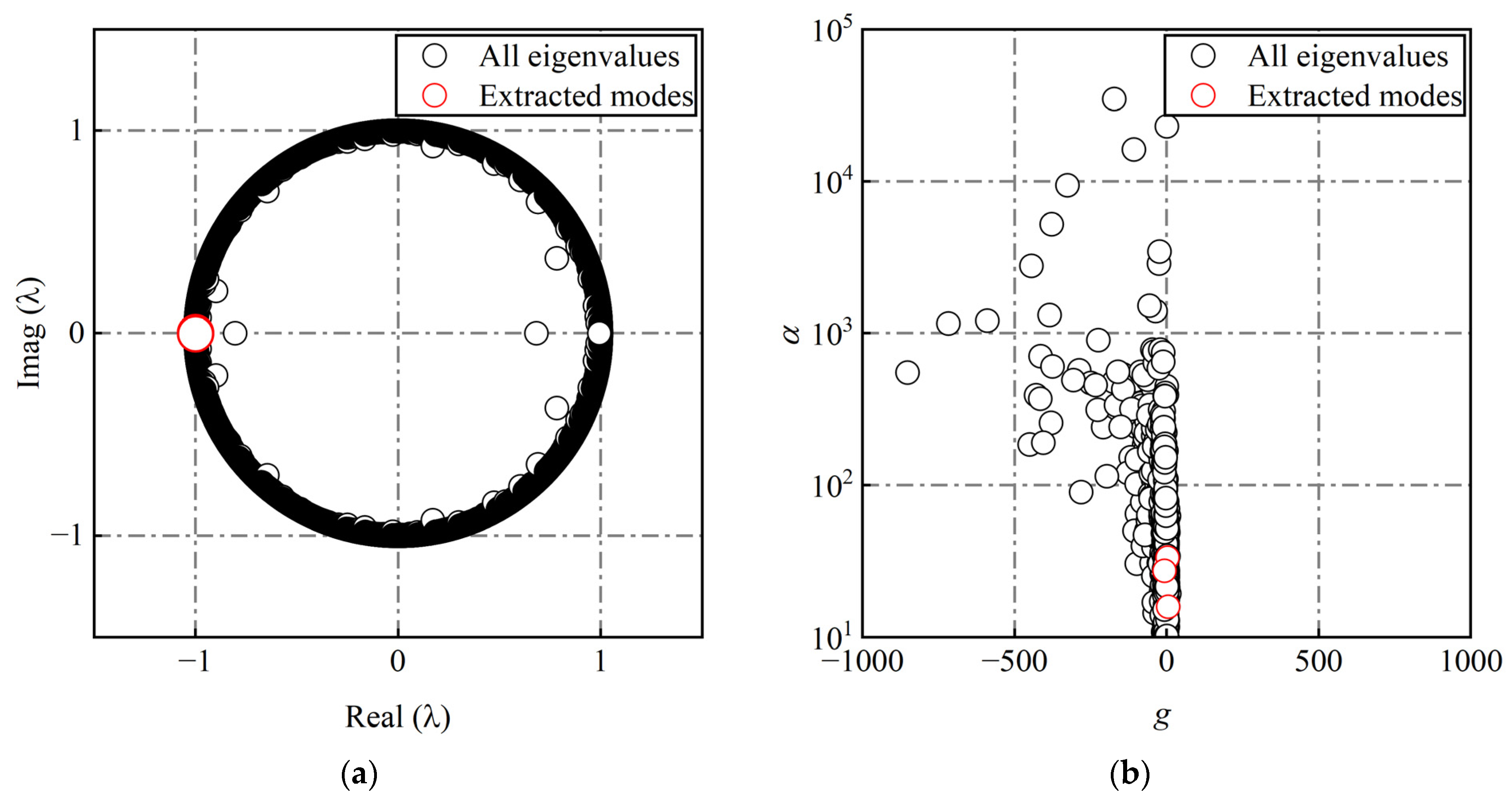
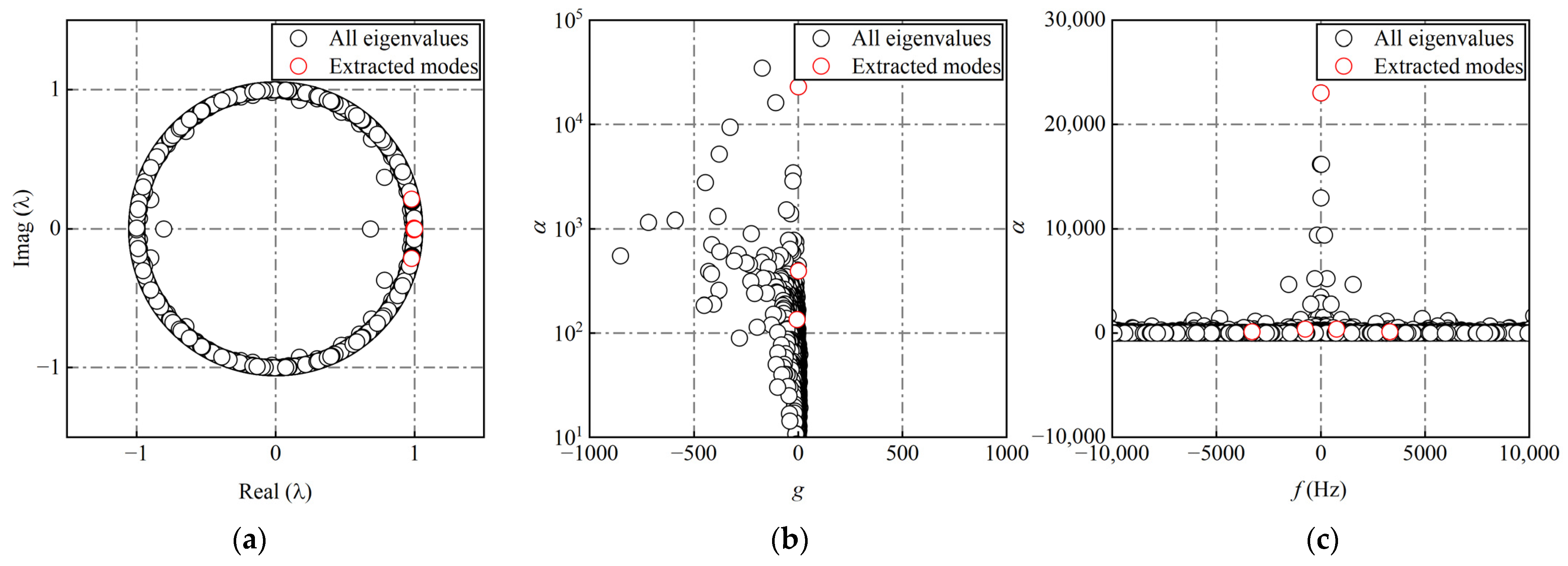
2.4. Dynamic Mode Decomposition
3. Results and Discussion
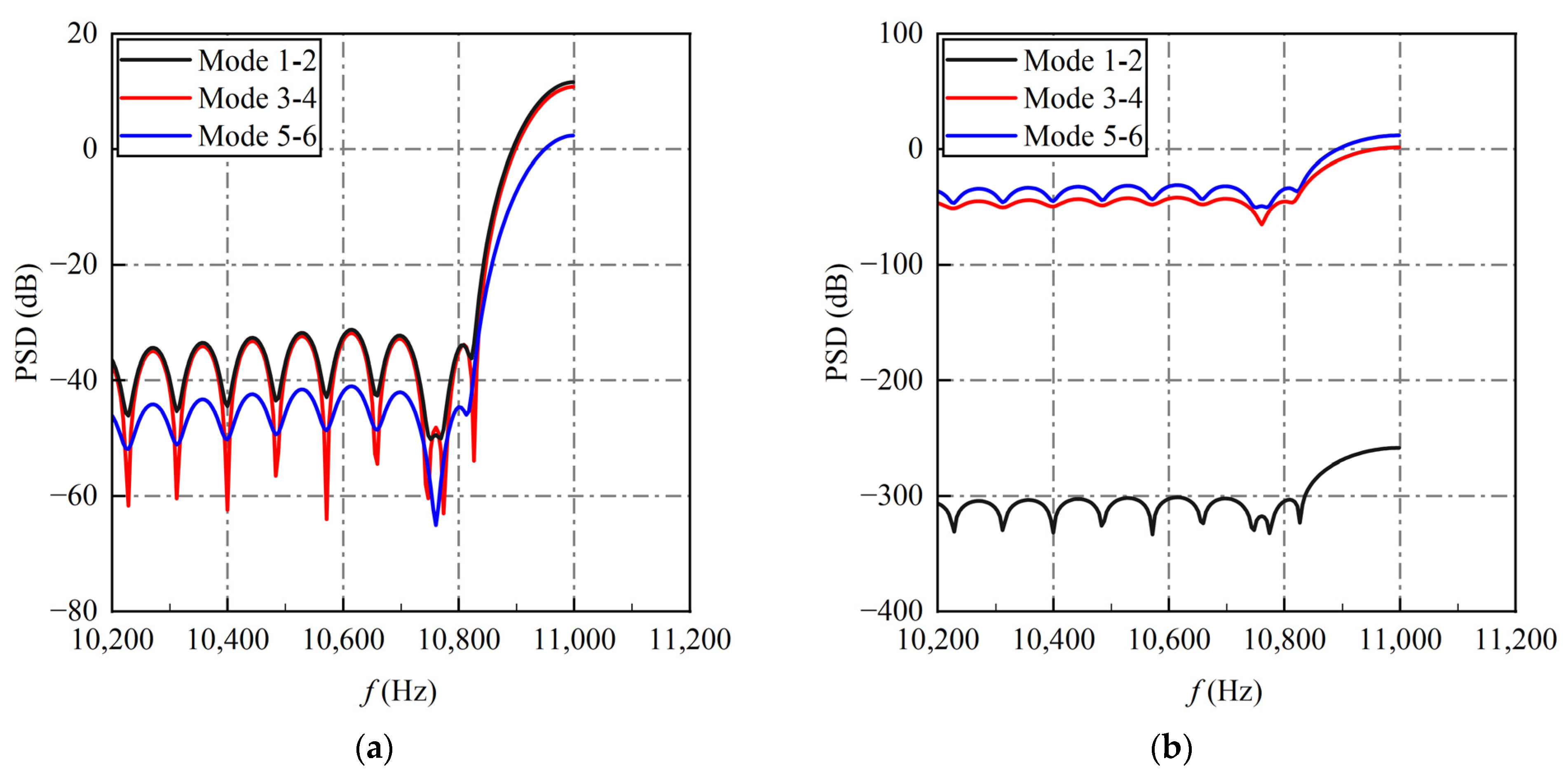
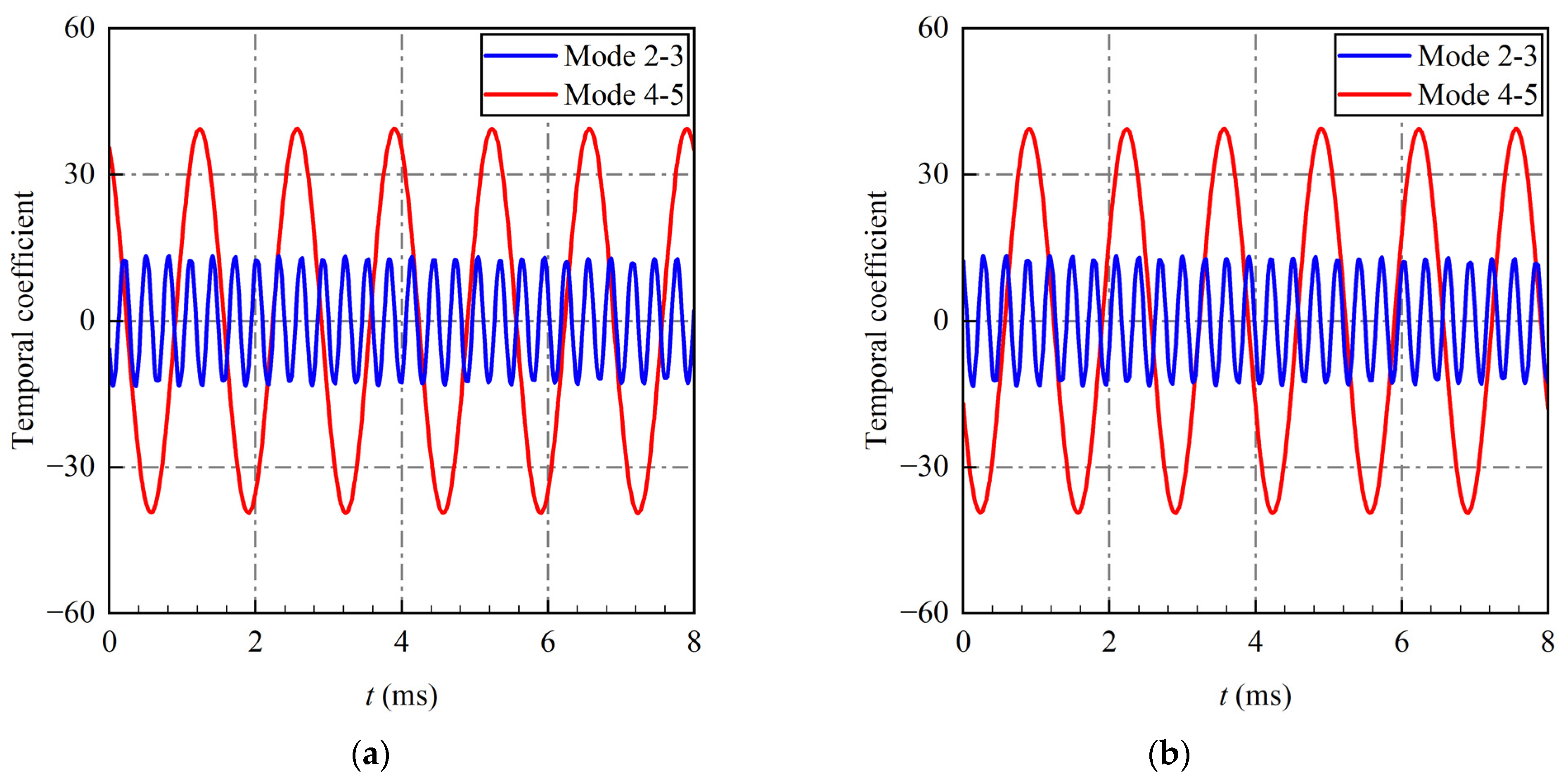
3.1. Conventional Amplitude Sorting Criterion
3.2. Conventional Frequency Sorting Criterion
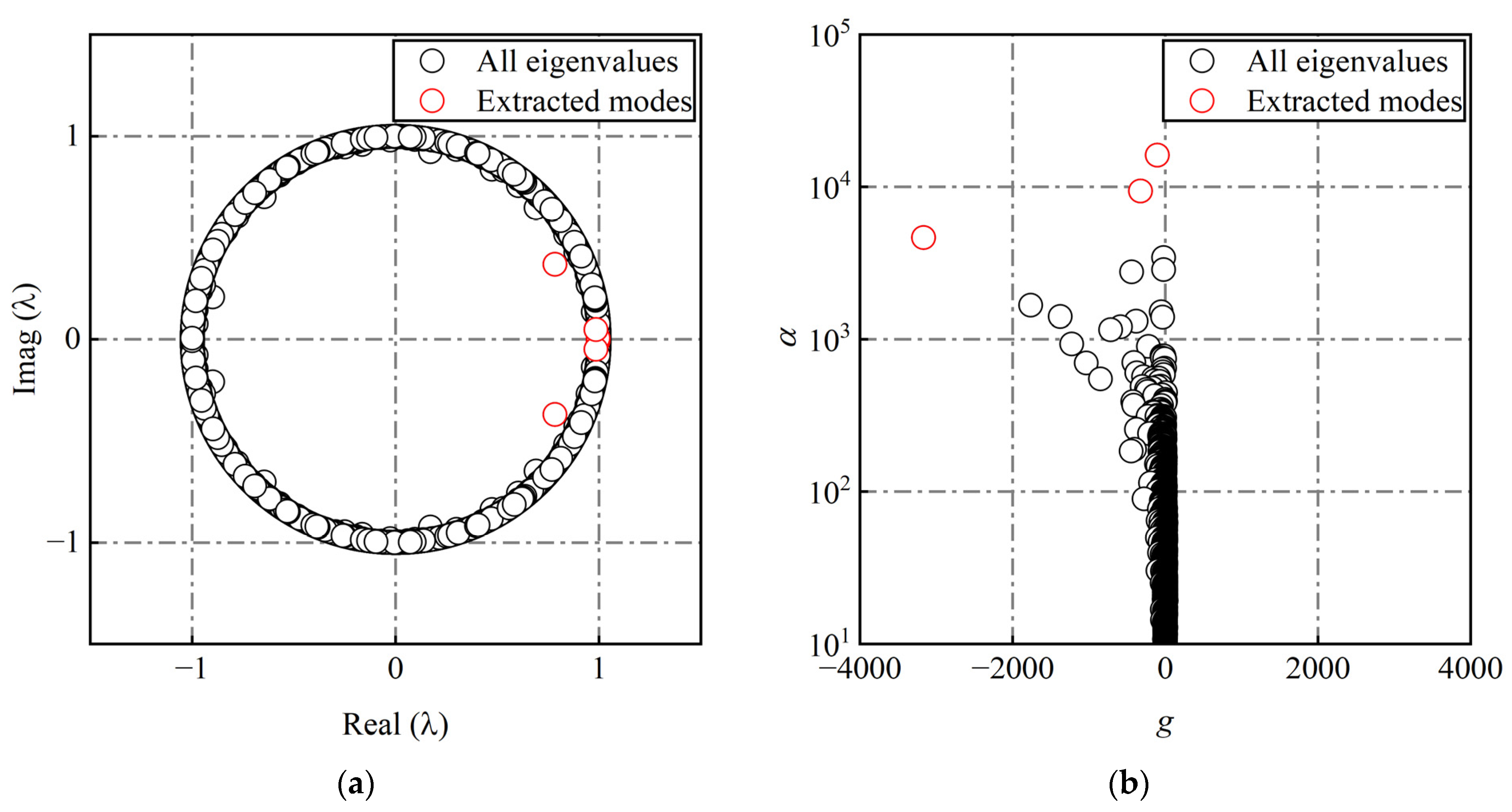
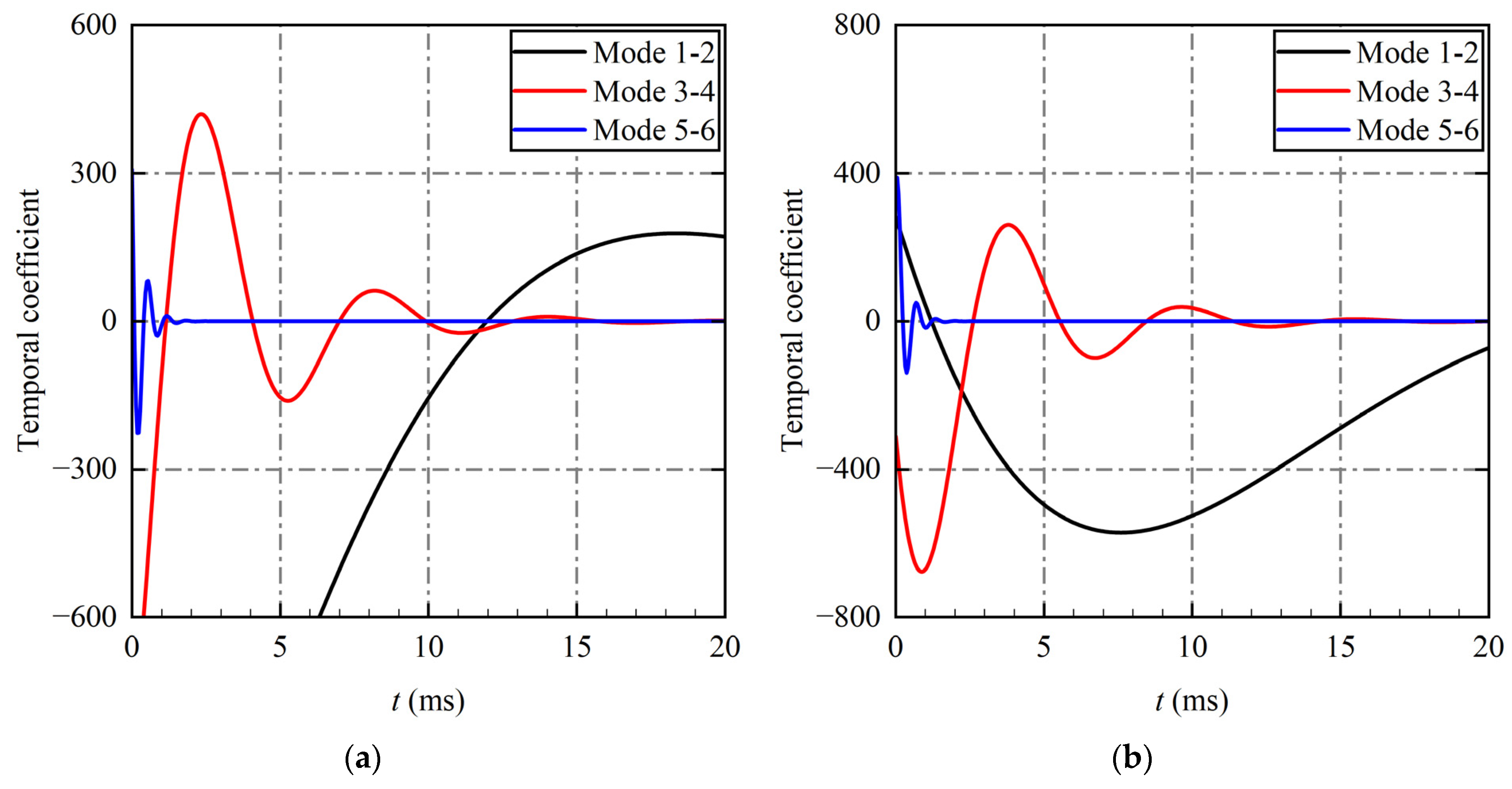
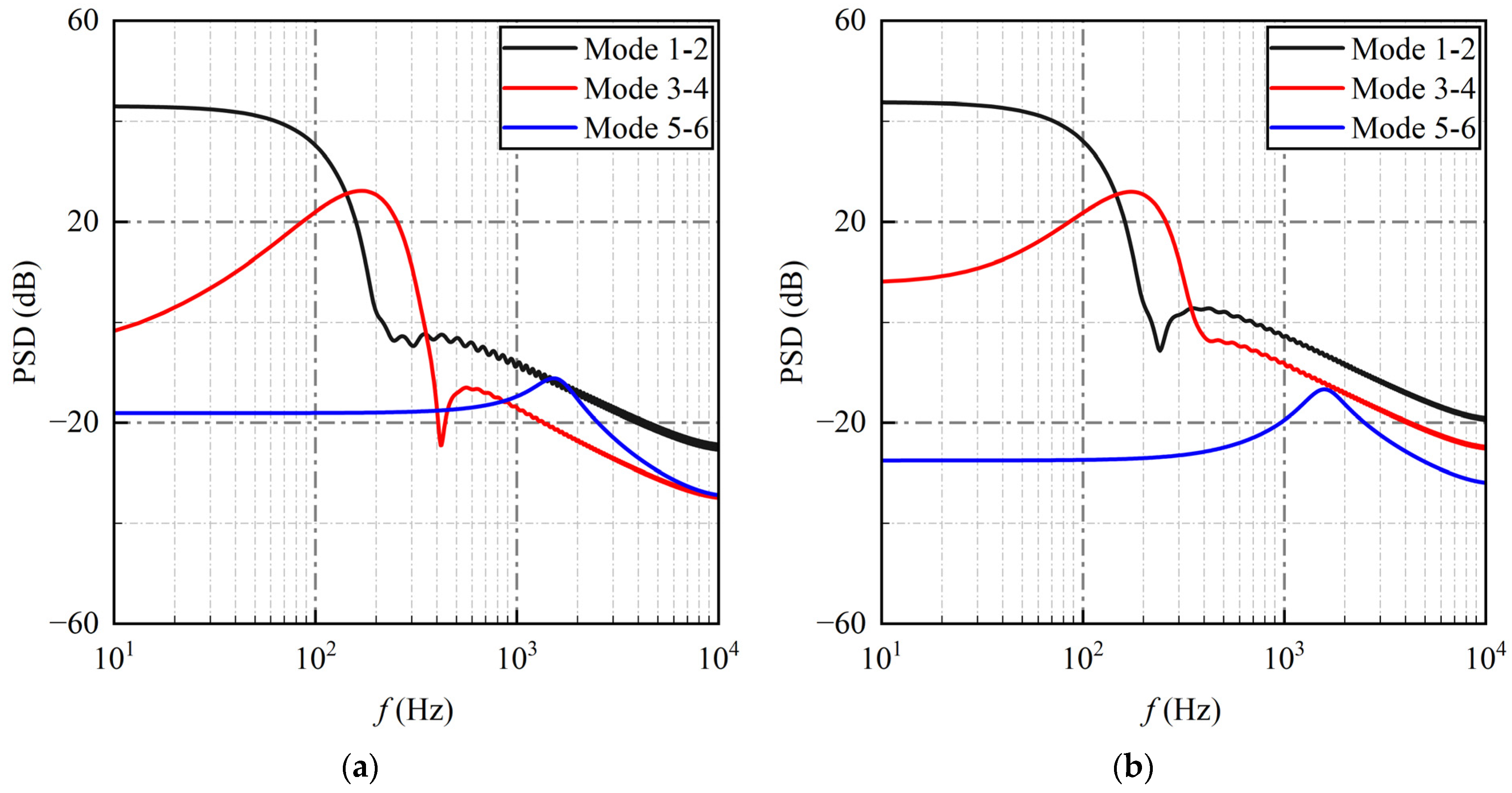
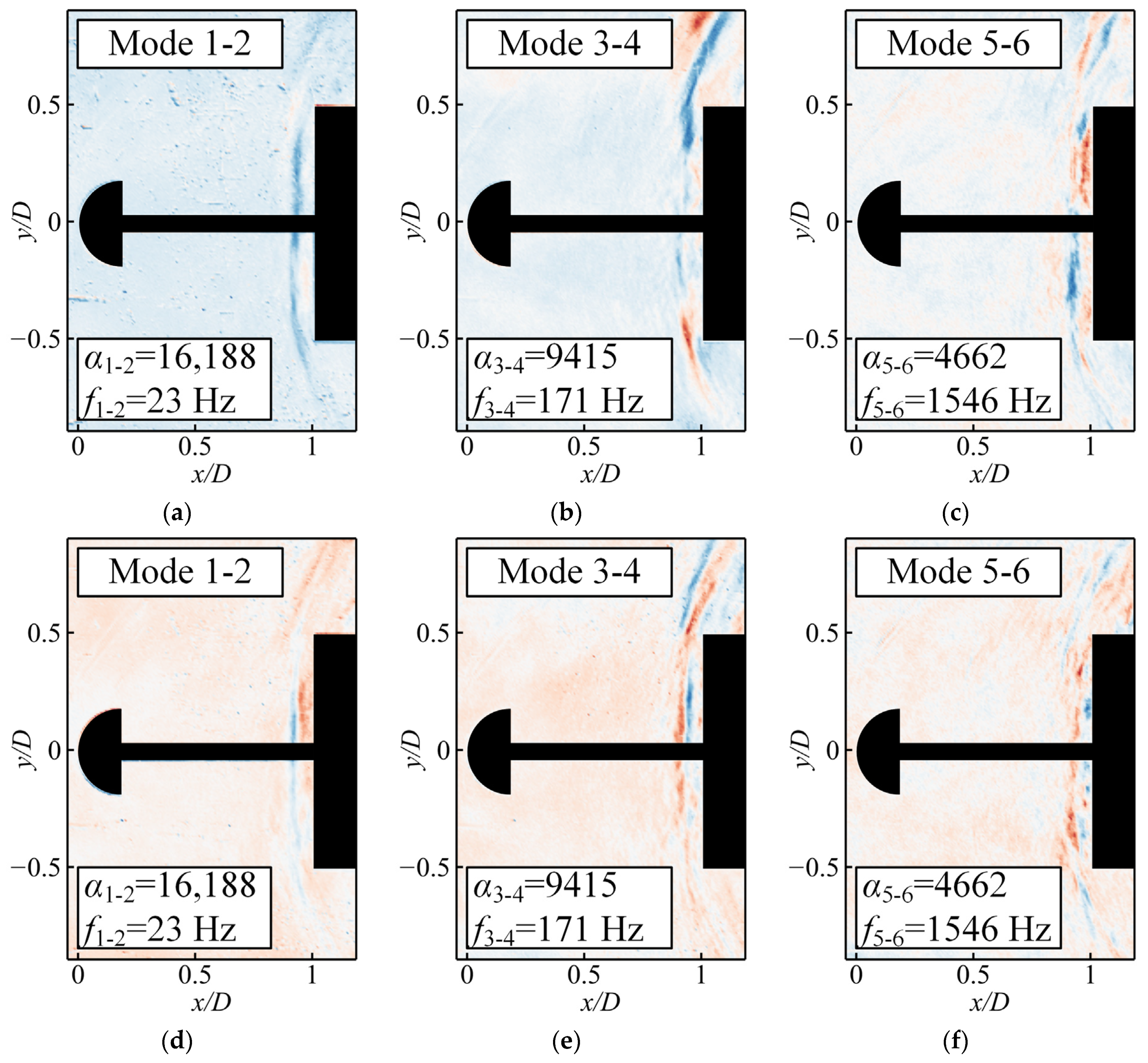
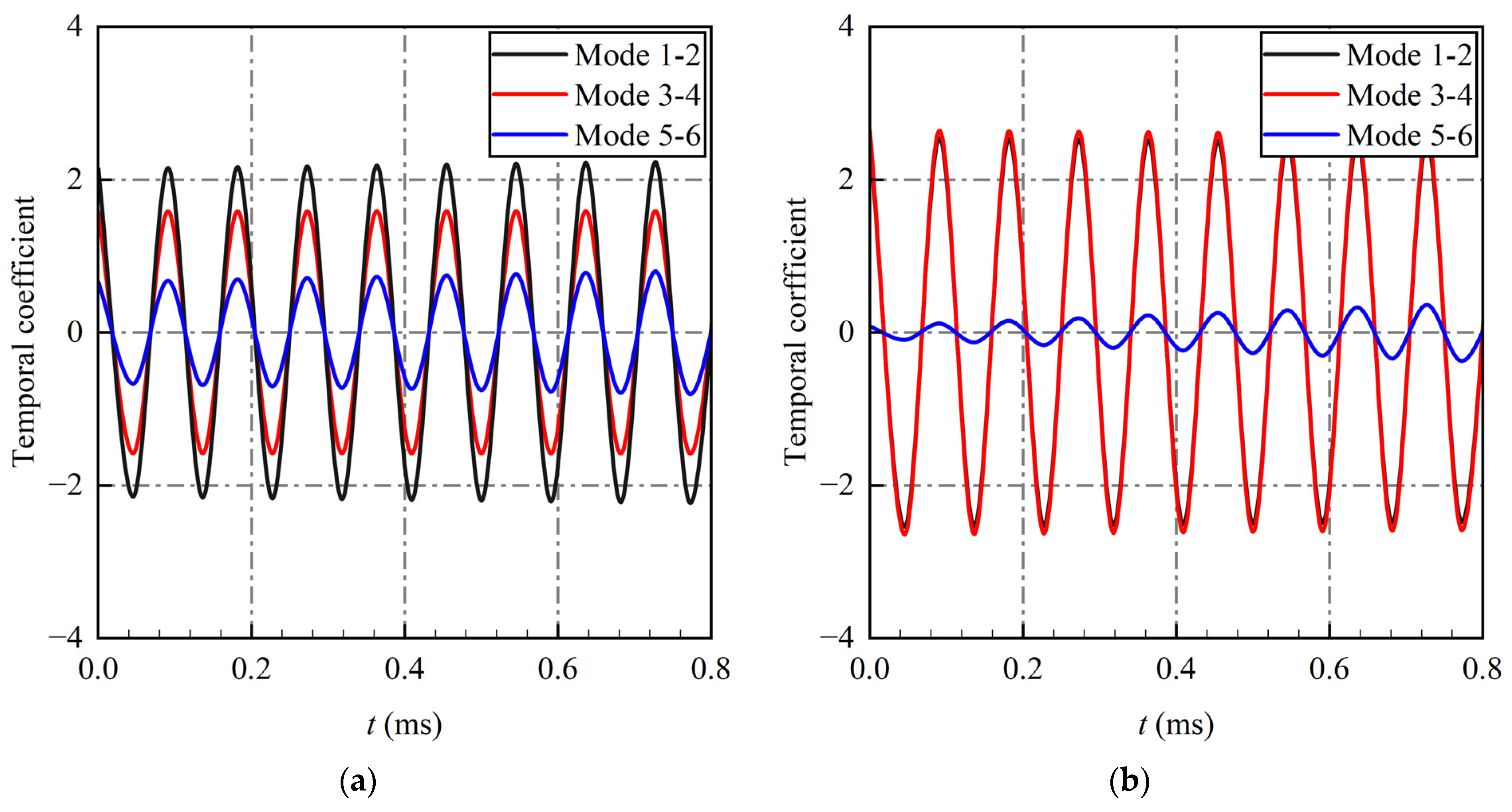
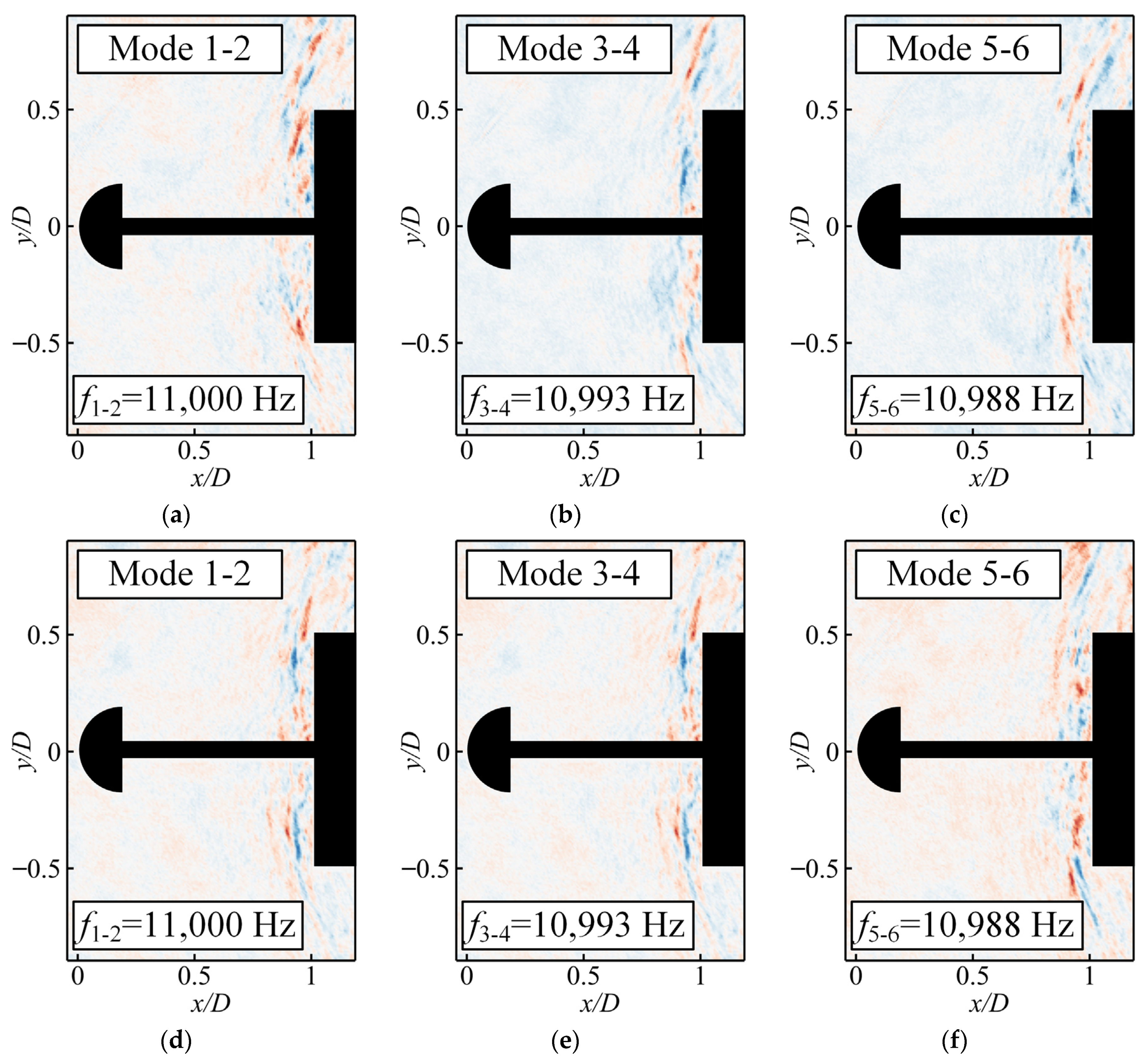
3.3. Novel Energy Sorting Criterion
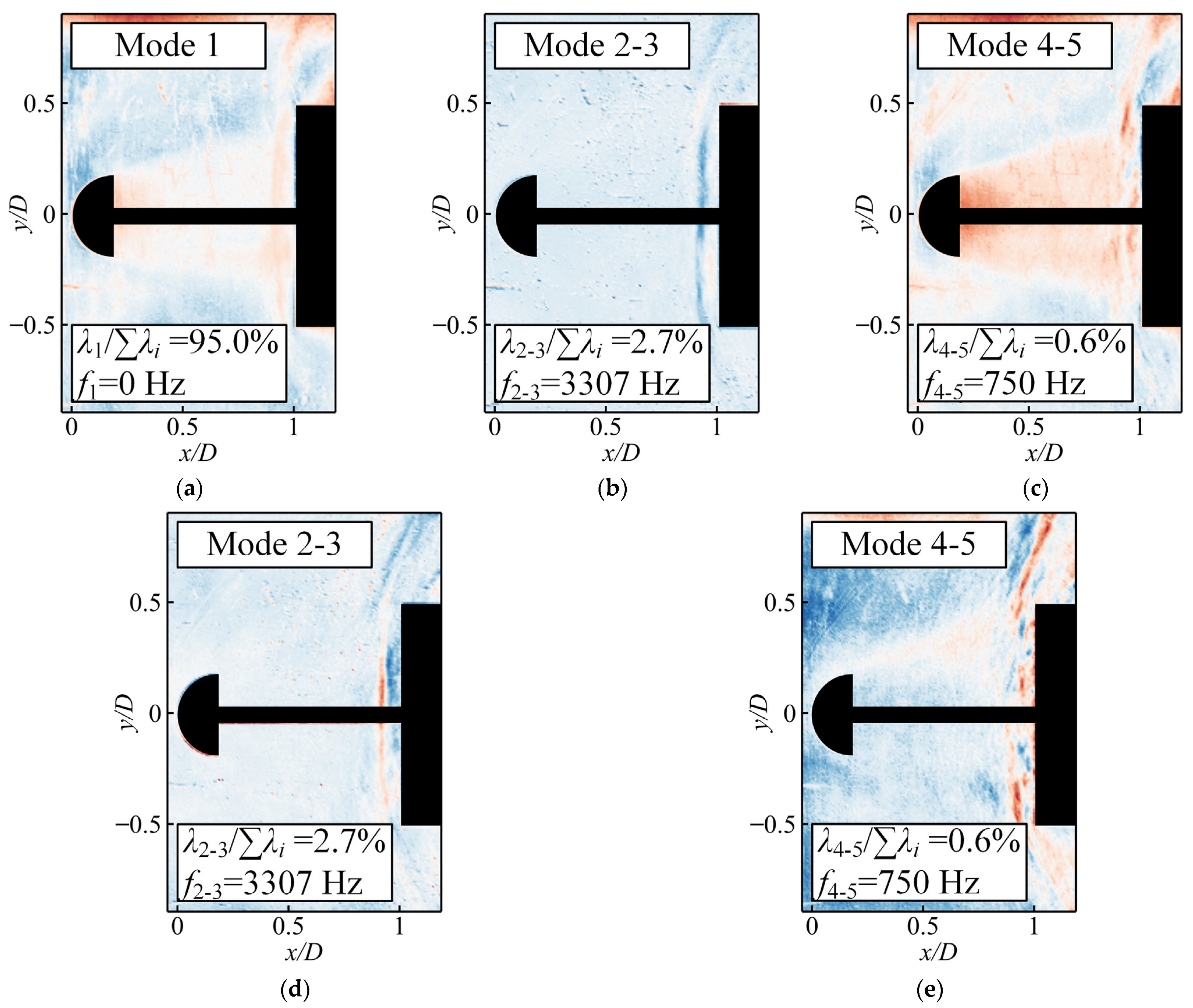
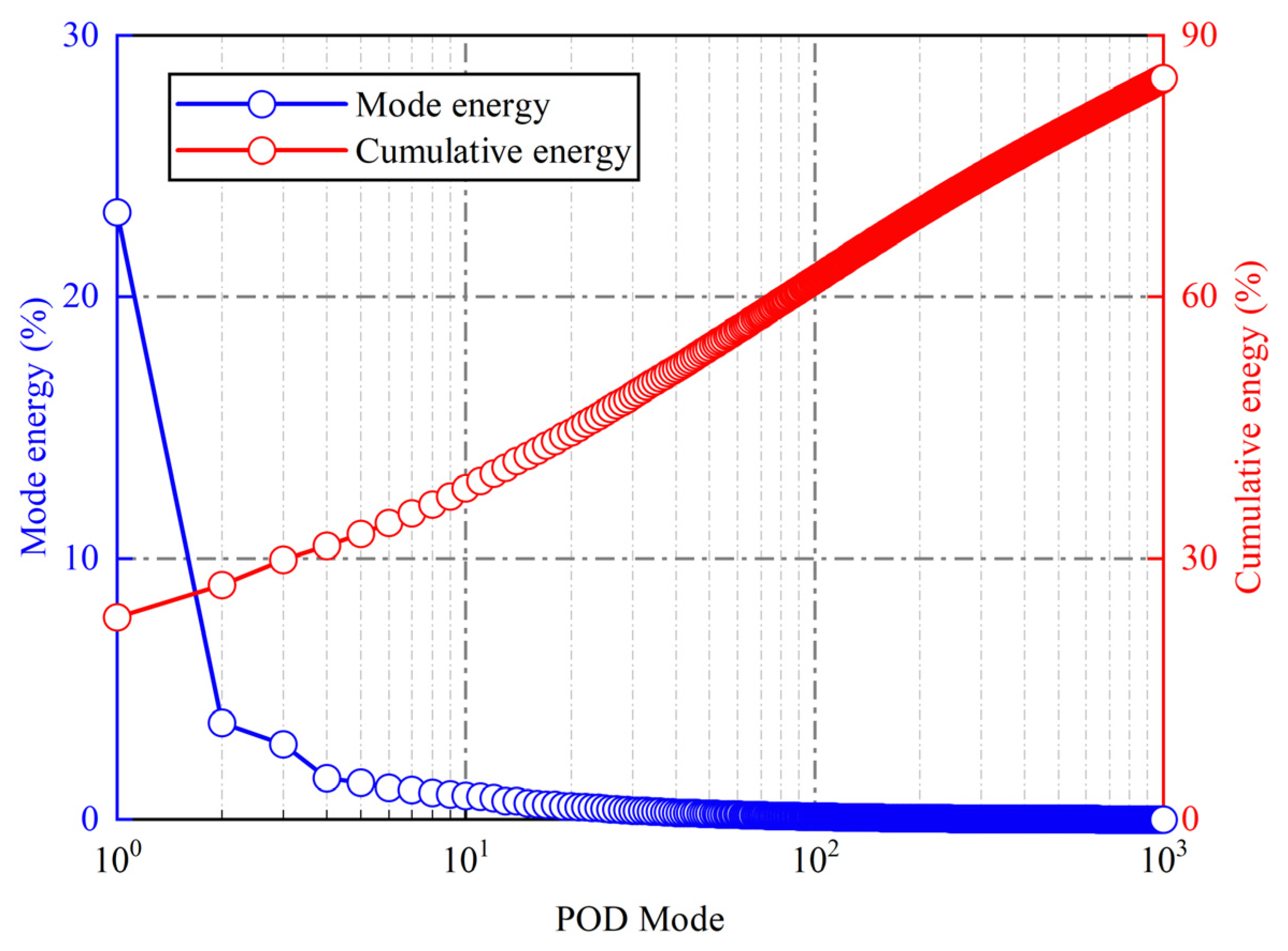
3.4. Proper Orthogonal Decomposition
- Limited data length: The length of the data series used for DMD affects the accuracy of the decomposition. Insufficient data length may result in an incomplete representation of the dynamics, leading to inaccurate pattern recognition and ordering.
- Truncation error: When truncating the SVD in DMD, a truncation error occurs, where modes with small singular values are removed. This error affects the accuracy of the decomposition, and the choice of truncation layer should be carefully considered to balance the simplicity and accuracy of the model.
- Interpretation of modes: The interpretation of the modes obtained from the DMD should be performed with caution. Although the modes represent coherent spatio-temporal patterns, they may not always correspond to physically meaningful structures. The physical interpretation of the modes should be based on domain knowledge, complementary analysis, and validation.
4. Conclusions
- DMD with the conventional amplitude–frequency sorting criterion presents substantial limitations. DMD using the amplitude sorting criterion can capture structures with large initial amplitudes from the flow field. However, these extracted modes may exhibit excessive decay rates, which make them unable to maintain stability in the flow field over extended periods. DMD using the frequency sorting criterion can extract high- and low-frequency structures from the flow field. However, this criterion has the drawback of limited differentiation amongst the extracted modes. The reason is that they essentially represent similar types of flow field structures, which results in excessive loss of flow field information.
- DMD, with the energy sorting criterion, can extract the predominant structures of unsteady pulsation in the flow field. This approach simultaneously considers spatial and temporal orthogonality, which effectively avoids the limitations of modes sorted by amplitude with high decay rates and modes sorted by frequency with low differentiation. Compared with the two other sorting criteria, the energy sorting criterion proves more suitable for the experimental dataset of unsteady flow fields.
- POD can effectively capture dominant coherent structures in the flow field by determining spatially orthogonal bases. The results from POD, along with the spectral characteristics of experimentally measured dynamic pressure signals, exhibit a strong alignment with the DMD results obtained using the energy sorting criterion. This finding substantiates the superiority of the energy sorting criterion over the two other sorting criteria when applied to unsteady experimental flow fields.
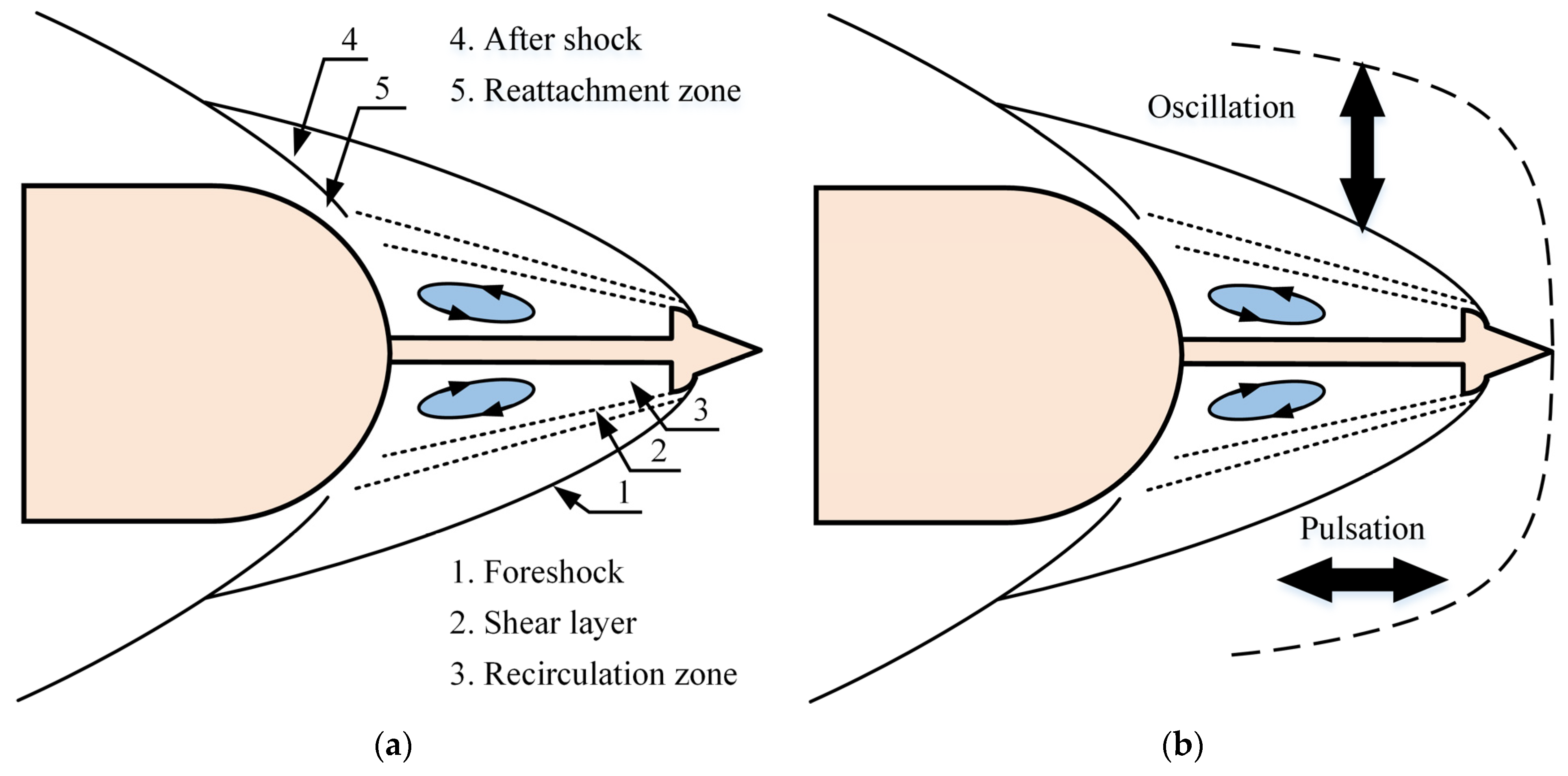
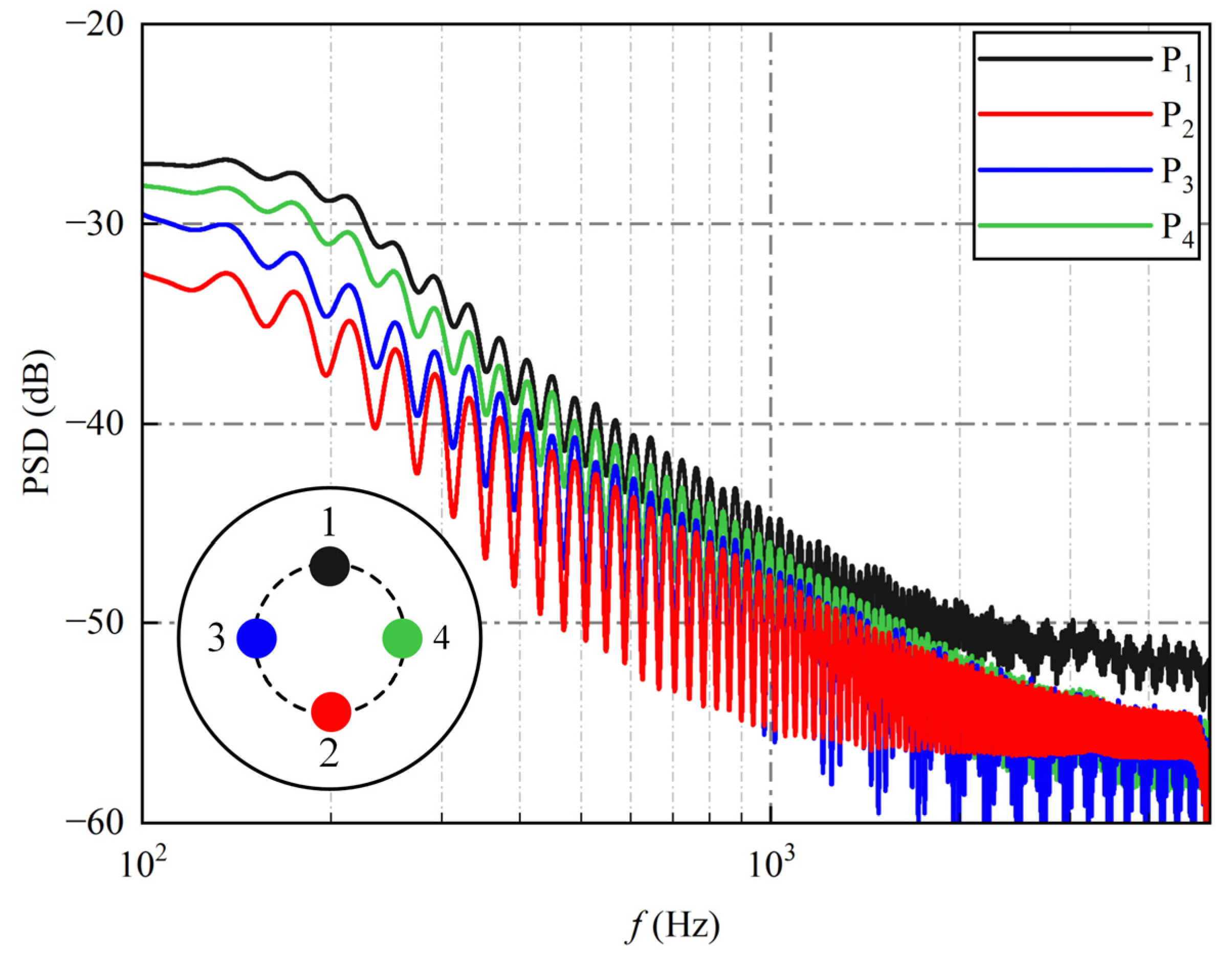
- The spatial composition of the flow field around a hemispherical aerodome and a cylindrical blunt body under supersonic inflow conditions primarily consists of several key elements: the aftershock in front of the cylindrical blunt body, the foreshock in front of the aerodome, and the shear layer and recirculation zone behind the aerodome. The unsteady flow field is predominantly influenced by the pulsation of the aftershock in front of the cylindrical, blunt body. This flow pattern exhibits multi-frequency coupling, with the primary frequency of 3.3 kHz originating from the periodic motion of the aftershock. This reciprocating motion continuously drives the compression and expansion of gas on the surface of the cylindrical, blunt body.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| English symbols: | |
| A | system matrix of the high-dimensional flow field, (-) |
| low-dimensional similar matrix, (-) | |
| C | temporal coefficient of DMD mode, (-) |
| D | diameter of blunt body, (mm) |
| E | energy of DMD mode, (-) |
| I | identity matrix, (-) |
| L | length of blunt body, (mm) |
| Ma | Mach number, (-) |
| N | number of snapshots, (-) |
| P1~4 | pressure monitoring point, (-) |
| Re | Reynolds number, (-) |
| T | temperature, (K) |
| U, V | unitary matrix, (-) |
| X, Y | adjacent snapshot matrix, (-) |
| d | diameter of spike, (mm) |
| f | frequency, (Hz) |
| g | growth rate, (-) |
| l | length of spike, (mm) |
| p | pressure, (Pa) |
| t | time series, (ms) |
| x | column vector of single flow field snapshot, (-) |
| Greek symbols: | |
| eigenvector, (-) | |
| Φ | matrix of DMD mode, (-) |
| Σ | diagonal matrix, (-) |
| α | amplitude of DMD mode, (-) |
| λ | eigenvalue of related DMD mode, (-) |
| ρ | density, (kg/m3) |
| σ | standard deviation, (-) |
| ω | frequency of DMD mode, (Hz) |
| Subscripts: | |
| (∙)A | aerodome |
| (∙)b | back pressure |
| (∙)e | exit condition |
| (∙)F | Frobenius norm |
| (∙)m | test model |
| (∙)t | total parameter |
References
- Stewartson, K. On the Linearized Potential Theory of Unsteady Supersonic Motion. Q. J. Mech. Appl. Math. 1950, 3, 182–199. [Google Scholar] [CrossRef]
- Clemens, N.T.; Narayanaswamy, V. Low-Frequency Unsteadiness of Shock Wave/Turbulent Boundary Layer Interactions. Annu. Rev. Fluid Mech. 2014, 46, 469–492. [Google Scholar] [CrossRef]
- Howlett, D.; Hunter, L. A Study of a Supersonic Axisymmetric Spiked Inlet at Angle of Attackusing the Navier-Stokes Equations. In Proceedings of the 24th Aerospace Sciences Meeting, Reno, NV, USA, 6–9 January 1986; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1986. [Google Scholar]
- Sekar, K.R.; Karthick, S.K.; Jegadheeswaran, S.; Kannan, R. On the Unsteady Throttling Dynamics and Scaling Analysis in a Typical Hypersonic Inlet–Isolator Flow. Phys. Fluids 2020, 32, 126104. [Google Scholar] [CrossRef]
- Jagadeesh, G.; Hashimoto, T.; Naitou, K.; Sun, M.; Takayama, K. Visualization of Unsteady Shock Oscillations in the High-Enthalpy Flow Field around Double Cones. J. Vis. 2003, 6, 195–203. [Google Scholar] [CrossRef]
- Gomes-Fernandes, R. Flow Features around Double Cones at Hypersonic Speed. Aeronaut. J. 2013, 117, 741–748. [Google Scholar] [CrossRef]
- Sudarshan, B.; Saravanan, S. Heat Flux Characteristics within and outside a forward Facing Cavity in a Hypersonic Flow. Exp. Therm. Fluid Sci. 2018, 97, 59–69. [Google Scholar] [CrossRef]
- Charwat, A.F.; Roos, J.N.; Dewey, F.C.; Hitz, J.A. An Investigation of Separated Flows—Part I: The Pressure Field. J. Aerosp. Sci. 1961, 28, 457–470. [Google Scholar] [CrossRef]
- Estruch-Samper, D.; Chandola, G. Separated Shear Layer Effect on Shock-Wave/Turbulent-Boundary-Layer Interaction Unsteadiness. J. Fluid Mech. 2018, 848, 154–192. [Google Scholar] [CrossRef]
- Mair, W.A. Experiments on Separation of Boundary Layers on Probes in Front of Blunt-Nosed Bodies in a Supersonic Air Stream. Philos. Mag. J. Sci. 1952, 43, 695–716. [Google Scholar] [CrossRef]
- Maull, D.J. Hypersonic Flow over Axially Symmetric Spiked Bodies. J. Fluid Mech. 1960, 8, 584–592. [Google Scholar] [CrossRef]
- Panaras, A.G.; Drikakis, D. High-Speed Unsteady Flows around Spiked-Blunt Bodies. J. Fluid Mech. 2009, 632, 69–96. [Google Scholar] [CrossRef]
- Guenther, R.A.; Reding, J.P. Fluctuating Pressure Environment of a Drag Reduction Spike. J. Spacecr. Rockets 1977, 14, 705–710. [Google Scholar] [CrossRef]
- Ahmed, M.Y.M.; Qin, N. Drag Reduction Using Aerodisks for Hypersonic Hemispherical Bodies. J. Spacecr. Rockets 2010, 47, 62–80. [Google Scholar] [CrossRef]
- Sahoo, D.; Das, S.; Kumar, P.; Prasad, J.K. Effect of Spike on Steady and Unsteady Flow over a Blunt Body at Supersonic Speed. Acta Astronaut. 2016, 128, 521–533. [Google Scholar] [CrossRef]
- Motycka, D.L.; Murphy, J.B. Experimental Investigation of Inlet-to-Inlet Shock Interference; SAE International: Warrendale, PA, USA, 1965. [Google Scholar]
- Farahani, M.; Daliri, A.; Younsi, J.S. Supersonic Inlet Buzz Detection Using Pressure Measurement on Wind Tunnel Wall. Aerosp. Sci. Technol. 2019, 86, 782–793. [Google Scholar] [CrossRef]
- D’souza, N.; Molder, S.; Moretti, G. Numerical Method for Hypersonic Internal Flow over Blunt Leading Edges and Two Blunt Bodies. AIAA J. 1972, 10, 617–622. [Google Scholar] [CrossRef]
- Ericsson, L.E. Aeroelastic Instability Caused by Slender Payloads. J. Spacecr. Rockets 1967, 4, 65–73. [Google Scholar] [CrossRef]
- Tumuklu, O.; Theofilis, V.; Levin, D. On the Unsteadiness of Shock–Laminar Boundary Layer Interactions of Hypersonic Flows over a Double Cone. Phys. Fluids 2018, 30, 106111. [Google Scholar] [CrossRef]
- Schuelein, E. Wave Drag Reduction Approach for Blunt Bodies at High Angles of Attack: Proof-of-Concept Experiments. In Proceedings of the 4th Flow Control Conference, Seattle, WA, USA, 23–26 June 2008; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2008. [Google Scholar]
- Jones, J.J. Flow Separation from Rods ahead of Blunt Noses at Mach Number 2.72; Langley Aeronautical Laboratory: Langley Field, VA, USA, 1952.
- Wood, C.J. Hypersonic Flow over Spiked Cones. J. Fluid Mech. 1962, 12, 614–624. [Google Scholar] [CrossRef]
- Kabelitz, H.-P. Zur Stabilität Geschlossener Grenzschichtablösegebiete an Konischen Drehkörpern bei Hyperschallanströmung; Abt. Wissenschaftliches Berichtswesen der Deutschen Forschungs- und Versuchsanstalt für Luft- und Raumfahrt: Berlin, Germany, 1971. [Google Scholar]
- Yamauchi, M.; Fujii, K.; Higashino, F. Numerical Investigation of Supersonic Flows around a Spiked Blunt Body. J. Spacecr. Rockets 1995, 32, 32–42. [Google Scholar] [CrossRef]
- Crawford, D.H. Investigation of the Flow over a Spiked-Nose Hemisphere-Cylinder at a Mach Number of 6.8; NASA Technical Note; National Aeronautics and Space Administration: Washington, DC, USA, 1959.
- Mehta, R.C. Numerical Analysis of Pressure Oscillations over Axisymmetric Spiked Blunt Bodies at Mach 6.80. Shock Waves 2002, 11, 431–440. [Google Scholar] [CrossRef]
- Sahoo, D.; Karthick, S.K.; Das, S.; Cohen, J. Shock-Related Unsteadiness of Axisymmetric Spiked Bodies in Supersonic Flow. Exp. Fluids 2021, 62, 89. [Google Scholar] [CrossRef]
- Schmid, P.J.; Sesterhenn, J. Dynamic Mode Decomposition of Numerical and Experimental Data. In Proceedings of the Sixty-First Annual Meeting of the APS Division of Fluid Dynamics, San Antonio, TX, USA, 23–25 November 2008. [Google Scholar]
- Schmid, P.J. Dynamic Mode Decomposition of Numerical and Experimental Data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef]
- Seena, A.; Sung, H.J. Dynamic Mode Decomposition of Turbulent Cavity Flows for Self-Sustained Oscillations. Int. J. Heat Fluid Flow 2011, 32, 1098–1110. [Google Scholar] [CrossRef]
- Duke, D.; Soria, J.; Honnery, D. An Error Analysis of the Dynamic Mode Decomposition. Exp. Fluids 2012, 52, 529–542. [Google Scholar] [CrossRef]
- Muld, T.W.; Efraimsson, G.; Henningson, D.S. Flow Structures around a High-Speed Train Extracted Using Proper Orthogonal Decomposition and Dynamic Mode Decomposition. Comput. Fluids 2012, 57, 87–97. [Google Scholar] [CrossRef]
- Sarmast, S.; Dadfar, R.; Mikkelsen, R.F.; Schlatter, P.; Ivanell, S.; Sørensen, J.N.; Henningson, D.S. Mutual Inductance Instability of the Tip Vortices behind a Wind Turbine. J. Fluid Mech. 2014, 755, 705–731. [Google Scholar] [CrossRef]
- Jovanović, M.R.; Schmid, P.J.; Nichols, J.W. Sparsity-Promoting Dynamic Mode Decomposition. Phys. Fluids 2014, 26, 024103. [Google Scholar] [CrossRef]
- Sayadi, T.; Schmid, P.J.; Richecoeur, F.; Durox, D. Parametrized Data-Driven Decomposition for Bifurcation Analysis, with Application to Thermo-Acoustically Unstable Systems. Phys. Fluids 2015, 27, 037102. [Google Scholar] [CrossRef]
- Chen, K.K.; Tu, J.H.; Rowley, C.W. Variants of Dynamic Mode Decomposition: Boundary Condition, Koopman, and Fourier Analyses. J. Nonlinear Sci. 2012, 22, 887–915. [Google Scholar] [CrossRef]
- Wynn, A.; Pearson, D.S.; Ganapathisubramani, B.; Goulart, P.J. Optimal Mode Decomposition for Unsteady Flows. J. Fluid Mech. 2013, 733, 473–503. [Google Scholar] [CrossRef]
- Dawson, S.T.M.; Hemati, M.S.; Williams, M.O.; Rowley, C.W. Characterizing and Correcting for the Effect of Sensor Noise in the Dynamic Mode Decomposition. Exp. Fluids 2016, 57, 42. [Google Scholar] [CrossRef]
- Leroux, R.; Cordier, L. Dynamic Mode Decomposition for Non-Uniformly Sampled Data. Exp. Fluids 2016, 57, 94. [Google Scholar] [CrossRef]
- Bagheri, S. Effects of Weak Noise on Oscillating Flows: Linking Quality Factor, Floquet Modes, and Koopman Spectrum. Phys. Fluids 2014, 26, 094104. [Google Scholar] [CrossRef]
- Hemati, M.S.; Williams, M.O.; Rowley, C.W. Dynamic Mode Decomposition for Large and Streaming Datasets. Phys. Fluids 2014, 26, 111701. [Google Scholar] [CrossRef]
- Tu, J.H.; Rowley, C.W.; Kutz, J.N.; Shang, J.K. Spectral Analysis of Fluid Flows Using Sub-Nyquist-Rate PIV Data. Exp. Fluids 2014, 55, 1805. [Google Scholar] [CrossRef]
- Gueniat, F.; Mathelin, L.; Pastur, L. A Dynamic Mode Decomposition Approach for Large and Arbitrarily Sampled Systems. Phys. Fluids 2015, 27, 025113. [Google Scholar] [CrossRef]
- Proctor, J.L.; Brunton, S.L.; Kutz, J.N. Dynamic Mode Decomposition with Control. SIAM J. Appl. Dyn. Syst. 2016, 15, 142–161. [Google Scholar] [CrossRef]
- Annoni, J.; Seiler, P. A Method to Construct Reduced-Order Parameter-Varying Models. Int. J. Robust. Nonlinear Control 2017, 27, 582–597. [Google Scholar] [CrossRef]
- He, G.; Wang, J.; Pan, C. Initial Growth of a Disturbance in a Boundary Layer Influenced by a Circular Cylinder Wake. J. Fluid. Mech. 2013, 718, 116–130. [Google Scholar] [CrossRef]
- Wan, Z.H.; Zhou, L.; Wang, B.F.; Sun, D.J. Dynamic Mode Decomposition of Forced Spatially Developed Transitional Jets. Eur. J. Mech.-B Fluids 2015, 51, 16–26. [Google Scholar] [CrossRef]
- Ducoin, A.; Loiseau, J.C.; Robinet, J.C. Numerical Investigation of the Interaction between Laminar to Turbulent Transition and the Wake of an Airfoil. Eur. J. Mech.-B Fluids 2016, 57, 231–248. [Google Scholar] [CrossRef]
- Statnikov, V.; Bolgar, I.; Scharnowski, S.; Meinke, M.; Kähler, C.J.; Schröder, W. Analysis of Characteristic Wake Flow Modes on a Generic Transonic Backward-Facing Step Configuration. Eur. J. Mech.-B Fluids 2016, 59, 124–134. [Google Scholar] [CrossRef]
- Qin, Q.; Guan, R.; Ma, Z.; Xu, J. Experimental Verification of Pulsation Suppression over Spiked Cylinder Using Standard/Double/Inverse Aerodome. Aerosp. Sci. Technol. 2021, 116, 106848. [Google Scholar] [CrossRef]
- Guan, R.; Qin, Q.; Wang, Y.; Xu, J. Experimental Investigation of the Pulsing Flow Field around Four Types of Spiked-Blunt Body at Mach 2.2. Aerosp. Sci. Technol. 2023, 133, 108129. [Google Scholar] [CrossRef]
- Guan, R.; Qin, Q.; Wang, Y.; Xu, J. Experimental Investigation of Flow Unsteadiness over Four Types of Spiked-Blunt Body at Mach 2.2. Aerosp. Sci. Technol. 2023, 140, 108468. [Google Scholar] [CrossRef]
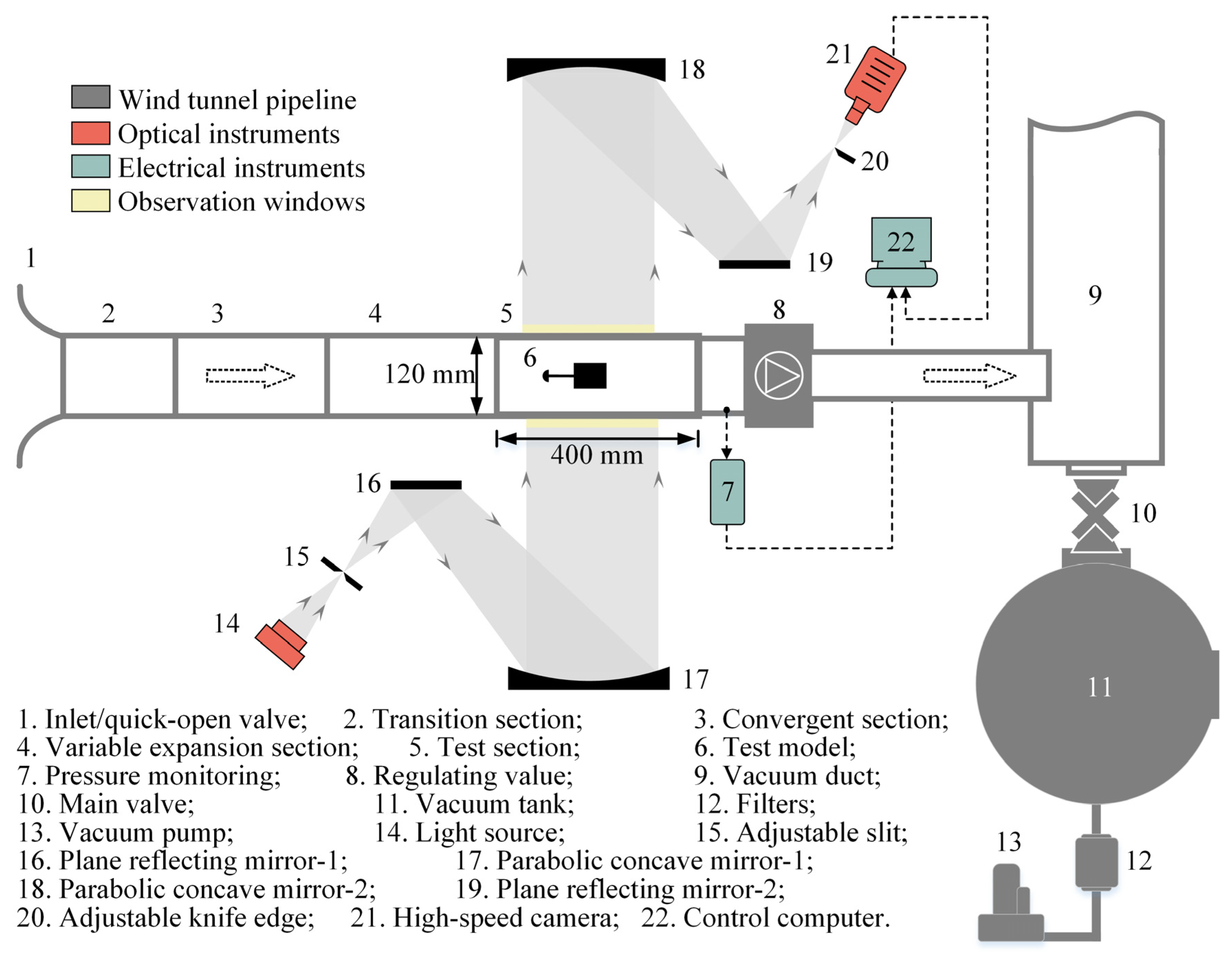





| Mae, [-] | Tt,e, [K] | pt,e, [Pa] | pb, [Pa] | ReD, [-] |
|---|---|---|---|---|
| 2.2 | 305 | 1.01 × 103 | 8.5 × 103 | 2.6 × 105 |
| Parameter | Symbol | Value [mm] |
|---|---|---|
| Diameter of blunt body | D | 40 |
| Length of blunt body | L | 40 |
| Length of spike | l | 40 |
| Diameter of spike | d | 2.6 |
| Diameter of aerodome | DA | 14.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Xu, J.; Qin, Q.; Guan, R.; Cai, L. Experimental Investigation of the Shock-Related Unsteadiness around a Spiked-Blunt Body Based on a Novel DMD Energy Sorting Criterion. Aerospace 2024, 11, 188. https://doi.org/10.3390/aerospace11030188
Wang Y, Xu J, Qin Q, Guan R, Cai L. Experimental Investigation of the Shock-Related Unsteadiness around a Spiked-Blunt Body Based on a Novel DMD Energy Sorting Criterion. Aerospace. 2024; 11(3):188. https://doi.org/10.3390/aerospace11030188
Chicago/Turabian StyleWang, Yifan, Jinglei Xu, Qihao Qin, Ruiqing Guan, and Le Cai. 2024. "Experimental Investigation of the Shock-Related Unsteadiness around a Spiked-Blunt Body Based on a Novel DMD Energy Sorting Criterion" Aerospace 11, no. 3: 188. https://doi.org/10.3390/aerospace11030188
APA StyleWang, Y., Xu, J., Qin, Q., Guan, R., & Cai, L. (2024). Experimental Investigation of the Shock-Related Unsteadiness around a Spiked-Blunt Body Based on a Novel DMD Energy Sorting Criterion. Aerospace, 11(3), 188. https://doi.org/10.3390/aerospace11030188






