1. Introduction
Aircraft survivability is defined as the ability of an aircraft to avoid and/or withstand hostile environments [
1]. Attacks from air defense and terrorist weapons can bring in-flight damage to aircraft [
2,
3,
4]. An attrition kill (the loss of aircraft) occurs when the aircraft loses one or more essential functions (i.e., structural integrity, lift, thrust, and control) for flight [
1]. To maintain such damaged aircraft in controlled flight, various technologies (including damage identification, control reconfiguration, envelope protection [
5,
6,
7,
8], etc.) have been developed. Subsequently, a successful landing [
9,
10] can prevent the attrition kill of a damaged aircraft, which actually improves its survivability.
Thrust failure is a common cause of kills/losses in military/civilian aircraft [
11,
12]. In such cases, the determination of the forced landing sites is very significant since pilots have only one chance for landing [
13]. A well-known case is a passenger aircraft landing in the Hudson River with a twin-engine failure, where all 155 people onboard survived. In the accident report, the captain’s decision to choose the Hudson River as the landing site rather than an airport was considered to provide the highest survival probability [
14]. Typically, the landing site for thrust-failed aircraft is determined in three steps [
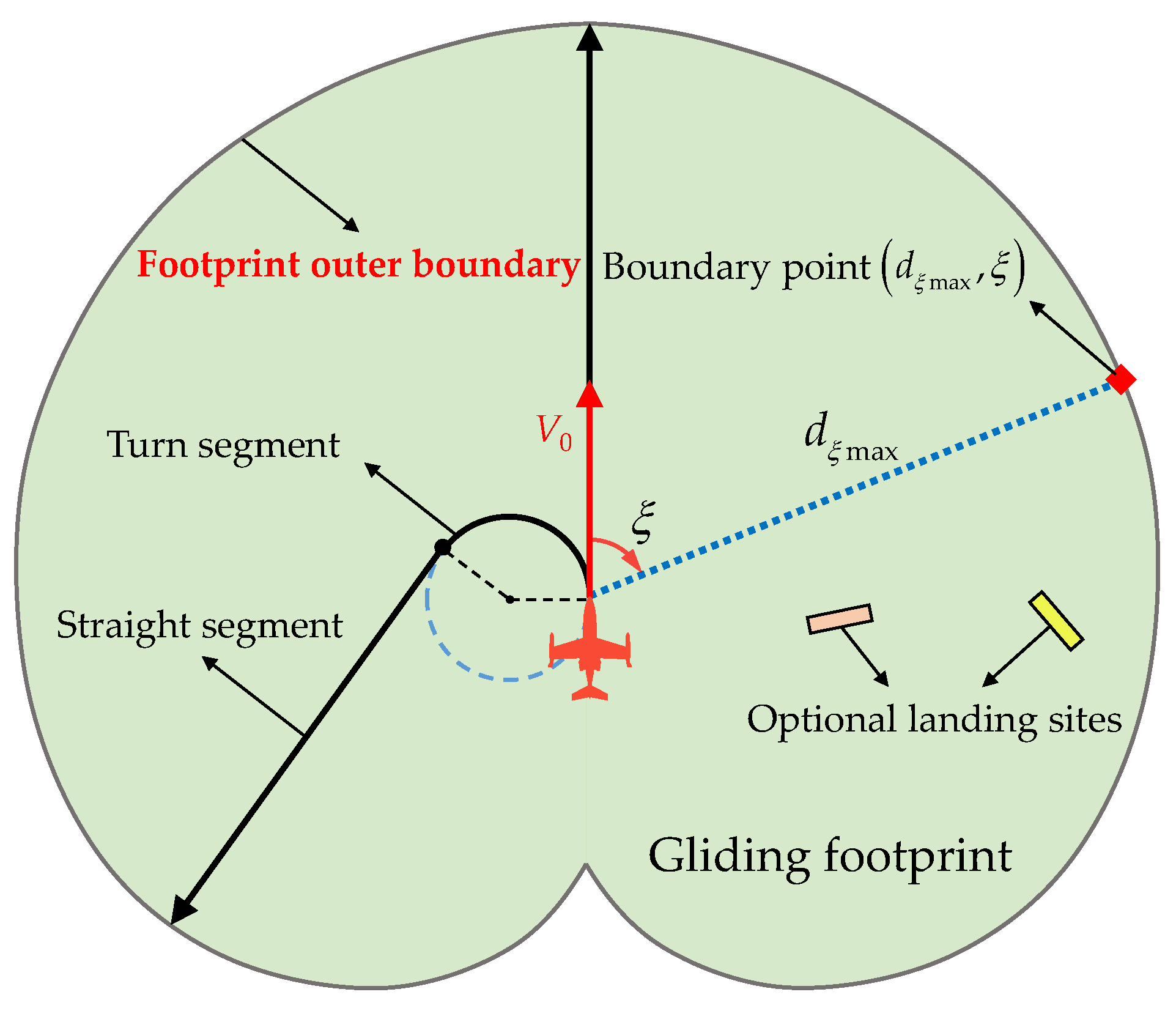
15]. First, the gliding footprint, which is the reachable region on the ground, is estimated. Then, feasible landing sites are searched within it. These sites are finally prioritized by calculating a utility function to find the top-ranked one in terms of suitability as the target landing site. Knowledge of the gliding footprint can limit the search space for landing sites [
16] and improve the efficiency of landing site determination. Therefore, the gliding footprint needs to be well developed.
To obtain the gliding footprint, a critical problem is finding the farthest gliding trajectories around the aircraft, because the footprint is encircled by corresponding landing points. Current methods can be summarized into two solutions. The first solution is based on the optimization theory. Maya et al. [
17] employed a pseudo-spectral method to compute the farthest trajectories and gliding footprint, with a cost function built using the gliding distance. The control variables were lift coefficient and roll angle. Segal et al. [
18] further calculated the footprint considering wind in the airspace, with velocity and bank angle set as control variables. Similar methods are also widely applied in the gliding footprint calculation of re-entry vehicles [
19,
20]. To follow the optimal trajectories in [
16,
17], continuous maneuvers are required in a short period of time. This is a great challenge for unpowered aircraft with degraded performance, thus compromising landing safety.
The second solution employs a segmented landing trajectory that is relatively easy for aircraft to track. This trajectory is extended from a Dubins curve [
21] and contains a steady straight segment with/without a steady turn segment. When calculating the gliding footprint under a given initial altitude, the focus is on finding the steady states that produce the farthest gliding trajectories over the entire range of maneuvering capabilities. Siegel et al. [
22] adopted a segmented trajectory that included only a straight segment and assumed the gliding footprint to be a circle. The circle center was the vertical projection of the initial position, and the radius was the forward gliding distance with the straight segment at the best-glide angle (i.e., the maximum and also shallowest flight-path angle, negative value). This angle was chosen because the corresponding gliding distance is maximum for a given altitude loss [
23]. Some other researchers used a segmented trajectory consisting of a steady turn segment and a steady straight segment, and determined the gliding footprint based on the boundary points with maximum gliding distances around the aircraft. These studies all chose the best-glide state in the straight segment and differed mainly in the turn segment. Atkins et al. [
15] predefined the turning states and obtained a circular gliding footprint based on three boundary points. Coombes et al. [
24] also specified the turning states and obtained a gliding footprint encircled by a series of boundary points. Poissant et al. [
25] established several groups of turning states and investigated the turning parameter effects on the gliding footprint. However, the determination of the best-turn states that corresponded to the farthest segmented trajectories was still unresolved. Seminal work was carried out by Di Donato et al. [
26], who utilized the unpowered-flight envelope to characterize aircraft maneuvering capabilities. The best-turn states were computed by traversing the steady turning states in the envelope.
The flight envelope in [
26] is a discrete library of attainable steady straight and steady turning states of the thrust-failed aircraft. An attainable steady state means that the aircraft can be trimmed at this state. Each steady state is characterized by a group of parameters (i.e., altitude, bank angle, and flight-path angle) which are set as known variables during the trim process. By setting proper ranges and step sizes for the characterization parameters, the flight envelope is computed and compiled into a three-dimensional matrix. Similar studies have also been conducted on powered aircraft [
27,
28,
29,
30]. Altitude, velocity, turn rate, and flight-path angle are the characterization parameters, and the flight envelope is compiled into a four-dimensional matrix. The conventional velocity–altitude flight envelope is a subset of this matrix where the turn rate and flight-path angle are zero [
31]. The method in [
26] requires extensive computations since every footprint boundary point is obtained after traversing all turning states in the flight envelope. An Artificial Neural Network (ANN) is an information-processing system inspired by biological neural networks [
32]. It can acquire knowledge by training and solve problems of the same class [
33]. The Back-Propagation Artificial Neural Network (BP-ANN) is one of the most widely applied neural networks. It has powerful computational advantages and can effectively map various nonlinear relationships [
34]. Current studies have applied ANN to reduce the computational time in computationally intensive situations. Norouzi et al. [
27] utilized ANN on an aircraft with aileron failure and predicted the flight envelope in real time. Zhang et al. [
35] further used BP-ANN to estimate the flight envelope of an aircraft with wing damage. These studies provide a good reference for gliding footprint calculation.
Although existing methods can obtain the gliding footprint well, there are still several challenges. First, all methods model the thrust-failed aircraft with point-mass flight dynamics. The aircraft is trimmed by balancing the forces only, without considering the moment equilibrium. This will lead to deviations in the flight parameters, especially the flight-path angle, which can accumulate into a considerable gliding distance error over the whole forced landing. Second, the unpowered-flight envelope contains only low-velocity steady states and does not match the aircraft’s full maneuvering capabilities. Given a group of characterization parameters for steady states, two different velocities can be computed using force equilibrium equations. When compiling the flight envelope, only the state with a smaller velocity is selected. Third, the determination of best-turn states is computationally intensive and time-consuming, making the footprint results unsuitable for direct application to in-flight damage conditions that require the footprint in real time.
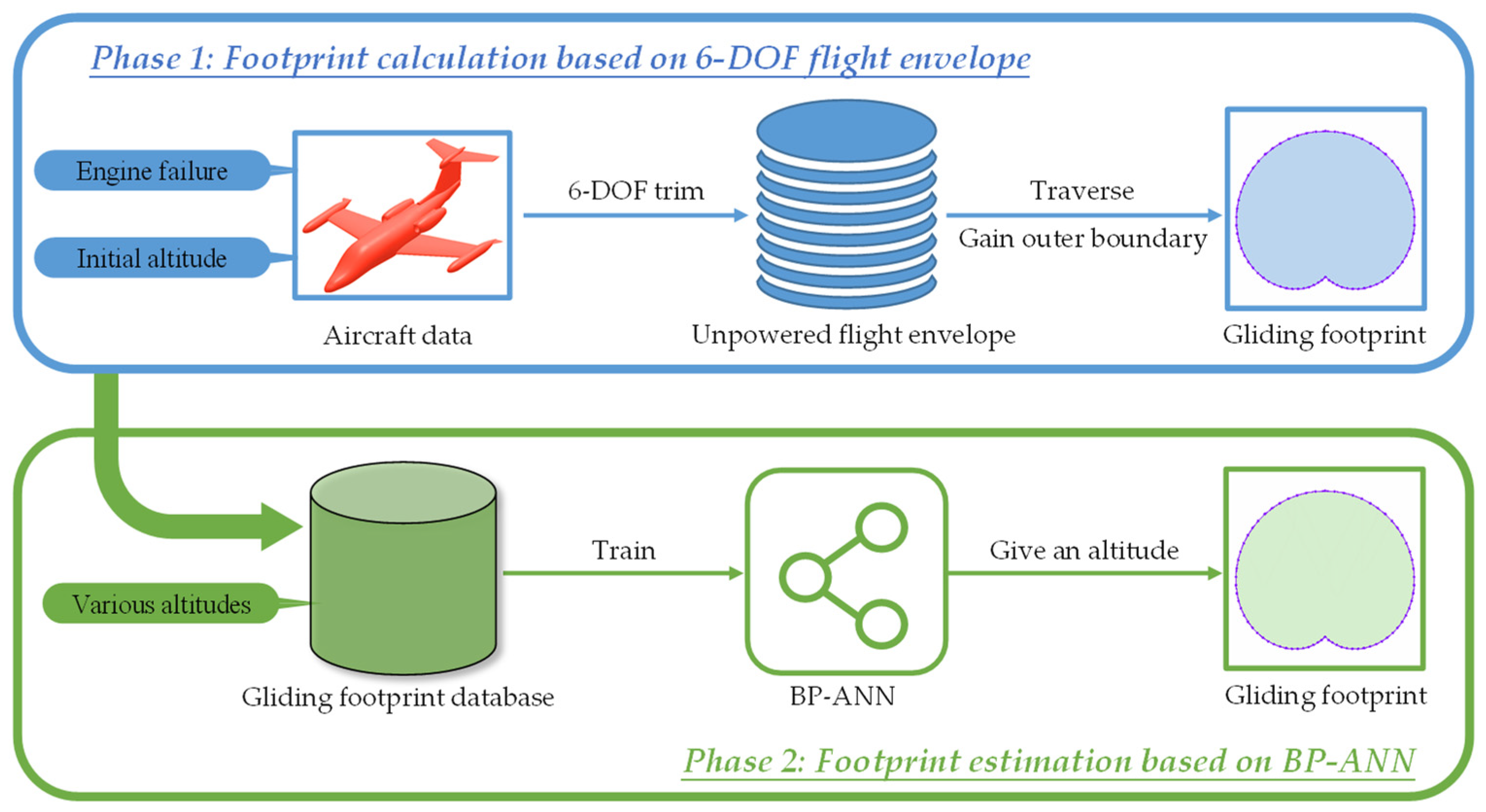
This paper proposes two methods to calculate the glide footprint of a fixed-wing aircraft with thrust failure. Method 1 extends the calculation process in [
26], with the aircraft modeled using 6-DOF flight dynamics instead of point-mass dynamics. To characterize the maneuvering capabilities of the 6-DOF thrust-failed aircraft, a novel unpowered-flight envelope model is proposed. Method 2 utilizes BP-ANN to estimate the gliding footprint, with the network trained using the gliding footprint results obtained by Method 1.
In summary, this paper makes the following contributions:
- (1)
We develop a gliding footprint calculation method based on the 6-DOF flight envelope. Compared with conventional methods that employ point-mass dynamics, this 6-DOF method considers more constraints, including the moment equilibrium, control surface saturation, and aerodynamic contributions of the control surfaces.
- (2)
We propose a 6-DOF unpowered-flight envelope model by defining three novel characterization parameters of the steady states. Each group of characterization parameters corresponds to a unique steady state. The flight envelope is compiled into a three-dimensional matrix that represents the full maneuvering capabilities of the aircraft.
- (3)
We introduce BP-ANN to estimate the gliding footprint. The trained BP-ANN effectively constructs the relationship between the initial altitude and footprint boundary points, and predicts the gliding footprint in real time.
This paper is structured as follows. In
Section 2, we describe the gliding footprint calculation problem and the research framework of this study. In
Section 3, we detail the 6-DOF unpowered-flight envelope model, the flight envelope-based footprint calculation method, and the footprint results in comparison with existing methods. In
Section 4, we present the BP-ANN model-based footprint estimation method and the footprint prediction results. Finally, we summarize our conclusions and future work in
Section 5.
3. Footprint Calculation Based on 6-DOF Flight Envelope
In this section, we detail the gliding footprint calculation based on the 6-DOF unpowered-flight envelope. First, we describe how to achieve the maximum gliding distance along segmented trajectories. Then, we show the 6-DOF flight envelope model and the 6-DOF trim process that computes attainable steady states. After this, we present a flight envelope-based calculation method that obtains the footprint by finding its boundary points. Finally, we analyze the simulation results of the flight envelope and gliding footprint.
3.1. Maximum Gliding Distance Achievement
This study employs a segmented landing trajectory that contains a straight segment with/without a turn segment. Given an initial altitude, the achievement of maximum gliding distances is presented below.
3.1.1. Gliding Distance Maximization
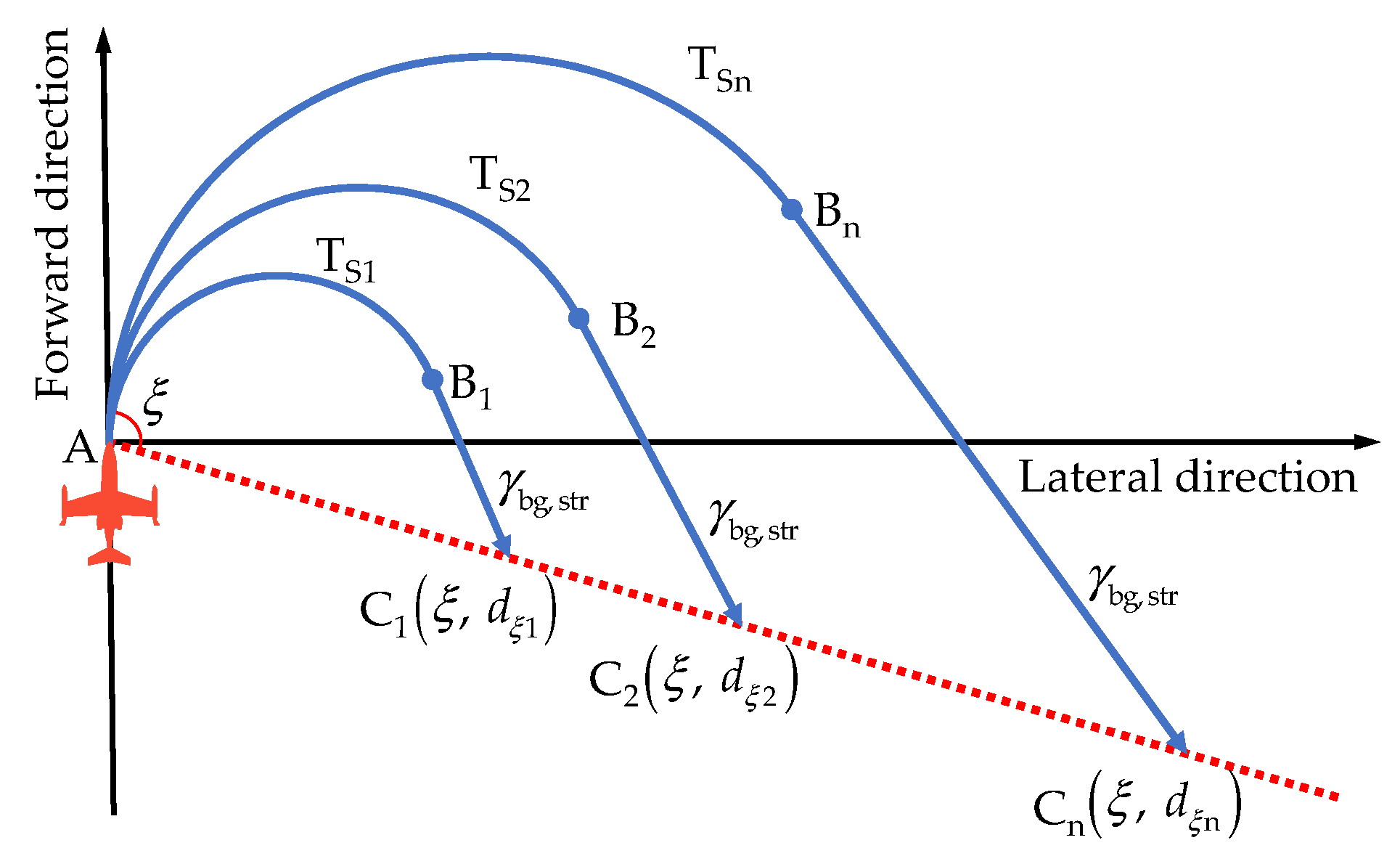
Figure 3 shows a top view of feasible segmented landing trajectories given the initial altitude and radial angle
ξ. To achieve the maximum gliding distance, the straight segments are all at the best-glide angle
. For different steady turning states (T
S1, T
S2…T
Sn) in the turn segment (AB
1, AB
2…AB
n), the landing points (C
1, C
2…C
n) can have different gliding distances (
,
…
). By extracting the maximum gliding distance, we will find the boundary point
along radial angle
ξ. If we set a step size for
ξ, then we can find a series of discrete boundary points around the aircraft.
To achieve the maximum gliding distance along a radial angel
ξ, we need
and all feasible segmented trajectories along
ξ. The value of
can be extracted from the flight-path angles of all attainable steady straight states, and the feasible segmented trajectories need all attainable steady turning states. They both require the unpowered-flight envelope (as detailed in
Section 3.2), which is a library of attainable steady turning and steady straight states of the unpowered aircraft.
3.1.2. Gliding Distance Formula Derivation
Given the initial altitude, the best-glide angle , and a steady state in the turn segment, the gliding distance of a feasible segmented trajectory landing along the radial angle ξ is derived as follows.
Figure 4 shows a top view of the segmented trajectory landing on the right-half gliding footprint along radial angle
ξ, with necessary angles and auxiliary lines added. The coordinate origin refers to the initial position when thrust failure occurs. The forward direction is consistent with the initial heading direction, while the lateral direction is perpendicular to it. The range of
ξ is [−180°, 180°], with the value positive if the landing point is on the right side of the forward direction and negative if it is on the left [
26]. The angle Δ
ψ is the angular change in the heading direction during the turn segment and is also the central angle. The lengths of the arc and straight line in the horizontal plane are denoted by
and
. The gliding distance
is the distance between the landing point and the coordinate origin.
In the turn and straight segments, the altitude loss is calculated as
where
is the flight-path angle in the turn segment, and
R is the horizontal turn radius.
Based on the geometric relationships in
Figure 4a, given an initial altitude
, we obtain [
26]
where Δ
ψ satisfies
ξ < Δ
ψ < 2
ξ. In this study, Equations (3) and (4) are verified to also be applicable for 90° ≤
ξ ≤ 180° as in
Figure 4b. In addition, if the turn segment is conducted at a left turning (−180° ≤
ξ < 0°), the value of
ξ in Equations (3) and (4) should be replaced by its absolute value.
If the parameters ξ, , , , and R are known, Δψ and can be calculated by Equations (3) and (4), respectively. Among them, the values of ξ and are known, and is extracted from the trim solutions of all attainable steady straight states. For a given steady turning state, is within the trim solution and R is computed as follows.
In the flight-path frame, the unpowered aircraft satisfies the following dynamic equation of motion:
where
m is the aircraft mass;
V is the velocity;
χ is the flight-path azimuth angle; the over-dot indicates the time derivative;
L and
Y are the lift and side forces; and
μ is the bank angle.
This study considers the difference between the bank angle
μ and roll angle
ϕ. Their values are not equal, and
μ is derived from other aerodynamic and flight-path angles [
36]:
where
α and
β are the angles of attack and sideslip, and
θ is the pitch angle.
Then, the values of μ and can be calculated with Equations (6) and (5), respectively, where α, β, ϕ, θ, L, and Y are all obtained with the trim solution of the given turning state.
Therefore, the radius
R is calculated as
3.2. Unpowered-Flight Envelope Modeling
Using point-mass dynamics, [
26] studied the unpowered-flight envelope. But the envelope contained only the low-velocity steady states. As an extension, we propose a novel model of a 6-DOF unpowered-flight envelope consisting of all attainable steady states.
3.2.1. Six-Degree-of-Freedom Flight Envelope Model
The 6-DOF nonlinear dynamic equations of motion describing the translational and rotational accelerations of an aircraft with thrust failure are given as
where
f is a vector of nonlinear functions;
x and
u are the state and control vector;
p,
q, and
r are the roll, pitch, and yaw rates;
,
, and
are the angular deflections in the elevator, aileron, and rudder.
A steady state is the condition in which all forces and moments are constant or zero. This requires all linear and angular velocity rates and aerodynamic angles rates of the thrust-failed aircraft to be zero. Then, the dynamic state vector
satisfies
with the following additional constraints according to the flight condition:
where
h is the flight altitude;
ψ is the yaw angle; and the asterisk superscript denotes the desired trimmed conditions.
Among the parameters
and
, and those in
and
, we choose
,
, and
as the characterization parameters of the steady states. Each group of
corresponds to a unique flight state (as derived in
Section 3.2.2). Then,
,
, and
are actually functions of
, which can represent the trim state families. By setting proper ranges and step sizes for them, a three-dimensional matrix will be constructed. The 6-DOF trim is used to judge whether a state
in the matrix is attainable. Then, the unpowered-flight envelope is obtained and consists of all attainable steady straight (
= 0) and turning (
≠ 0) states.
This flight envelope model differs from that of powered aircraft, which is characterized by
[
27,
28,
29,
30]. The reason is that the flight-path angle
γ is used to trim the aircraft due to the loss of engine thrust control input and is no longer independent from
,
, and
.
3.2.2. Six-Degree-of-Freedom Trim Procedure
For a specified set
, we find the trim condition through the 6-DOF trim. A general method for deriving the trim condition is to solve the nonlinear constrained optimization problem that minimizes the cost function. A typical choice of the cost function is:
where
Q is a positive definite weighting matrix describing the contribution of each variable in
to the cost function
J. For a trimmed condition,
J satisfies
To trim the thrust-failed aircraft given the set
, ten parameters in the trim vector
should be calculated. They are
α,
β,
p,
q,
r,
ϕ,
θ,
,
, and
. As with existing studies on the gliding footprint, only the coordinated flight states are considered to land in this paper. So, the value of
β is zero. Meanwhile, four of the aforementioned parameters (i.e.,
p,
q,
r, and
θ) can be derived and computed for the others:
where
γ is introduced in the trim process and
Then, six parameters, including
α,
γ,
ϕ,
,
, and
, are left to be calculated. They are set as the trim control parameters, which are directly solved by the numerical optimization method. Meanwhile, Equation (11) corresponds to six dynamic equations of motion. The number of equations equals the number of unknown trim control parameters. So, the trim problem has a unique solution if the solution exists [
37]. Moreover, the inequality constraints of the trim control parameters are
This study employs the Sequential Quadratic Programming (SQP) technique [
27,
28,
29] to solve the nonlinear optimization problem. A condition is considered to be a feasible trim condition if the cost function
J < 10
−7. After obtaining the trim solution, the value of
in Equations (12) and (13) can be computed as
During the trim process,
J is calculated using the following equations of motion [
38]:
where
D is the drag force;
,
M, and
N are the roll, pitch, and yaw moments;
g is the gravitational acceleration;
Ii is the moment of inertia, and
Iij is the product of inertia, with
i,
j =
x,
y,
z. When calculating the aerodynamic forces and moments, this study considers the effects of both the angle of attack
α and the control surface deflections
,
, and
.
3.3. Gliding Footprint Calculation Method
Conventional methods simplify the aircraft as a point mass. In this study, we develop a gliding footprint calculation method with the aircraft modeled using 6-DOF flight dynamics that considers more flight constraints.
The gliding footprint is encircled by a series of boundary points with maximum gliding distances. In this study, we define the flight parameters in steady states that produce the segmented trajectories to footprint boundary points as the best-footprint parameters, including
,
,
,
, etc. Meanwhile, when the initial altitude
is insufficient, there may exist certain unreachable areas within the footprint outer boundary. The simple connectivity of the gliding footprint is judged by the following equation [
26,
39]:
where
is the minimum turn radius, and
is the minimum horizontal projection length of the segmented trajectories arriving at the footprint outer boundary.
In [
26], the footprint boundary points are calculated based on the unpowered-flight envelope characterized by
. This study follows this idea, and the extension lies in two aspects: (1) the aircraft is modeled with 6-DOF dynamics and the steady states are computed by the 6-DOF trim; (2) a novel 6-DOF flight envelope model is developed with the steady states characterized by
. The gliding footprint calculation process of a fixed-wing aircraft is illustrated in
Figure 5, including the following steps.
Step 1. Calculate the 6-DOF unpowered-flight envelope. The envelope is discretized by setting proper ranges and step sizes for V and at given . Every steady state in the flight envelope corresponds to a set and is computed by the 6-DOF trim using the aircraft data.
Step 2. Extract the maximum flight-path angle from the trim solutions of all steady straight states in the flight envelope, and calculate the turn radius of all steady turning states using Equations (5)–(7). The minimum radius also needs to be extracted from the above turn radii.
Step 3. Compute all feasible gliding distances along different radial directions with Equations (3) and (4). The radial directions are discretized by setting proper step size for ξ within the range [0°, 180°]. During the computation, the straight segment is at and the turn segment is at every right turning state in the flight envelope.
Step 4. Extract the farthest landing point along every discrete ξ from the computed feasible gliding distances. Corresponding landing points then make up the right-half footprint outer boundary and the best-turn states are also obtained. The left-half outer boundary is determined via the symmetry along the initial heading direction.
Step 5. Identify the simple connectivity of the gliding footprint with Equation (27). If the equation is satisfied, the gliding footprint is simply connected and consists of all the points within the outer boundary. Otherwise, the inner boundary of the gliding footprint needs further calculation, which is beyond the scope of this paper.
3.4. Simulation Results and Discussion
According to above footprint calculation method, simulation results including the 6-DOF unpowered-flight envelope and gliding footprint were generated and are discussed below.
3.4.1. Simulation Setup
In this study, simulations were conducted on a Learjet-24-like subsonic business jet (SBJ) under flaps-up configuration. We performed the simulation using a workstation with 3.70 GHz Intel Xeon eight-core processor under the Windows 7 operating system. The data of the SBJ and the simulation settings were as follows.
(1) Data of the SBJ
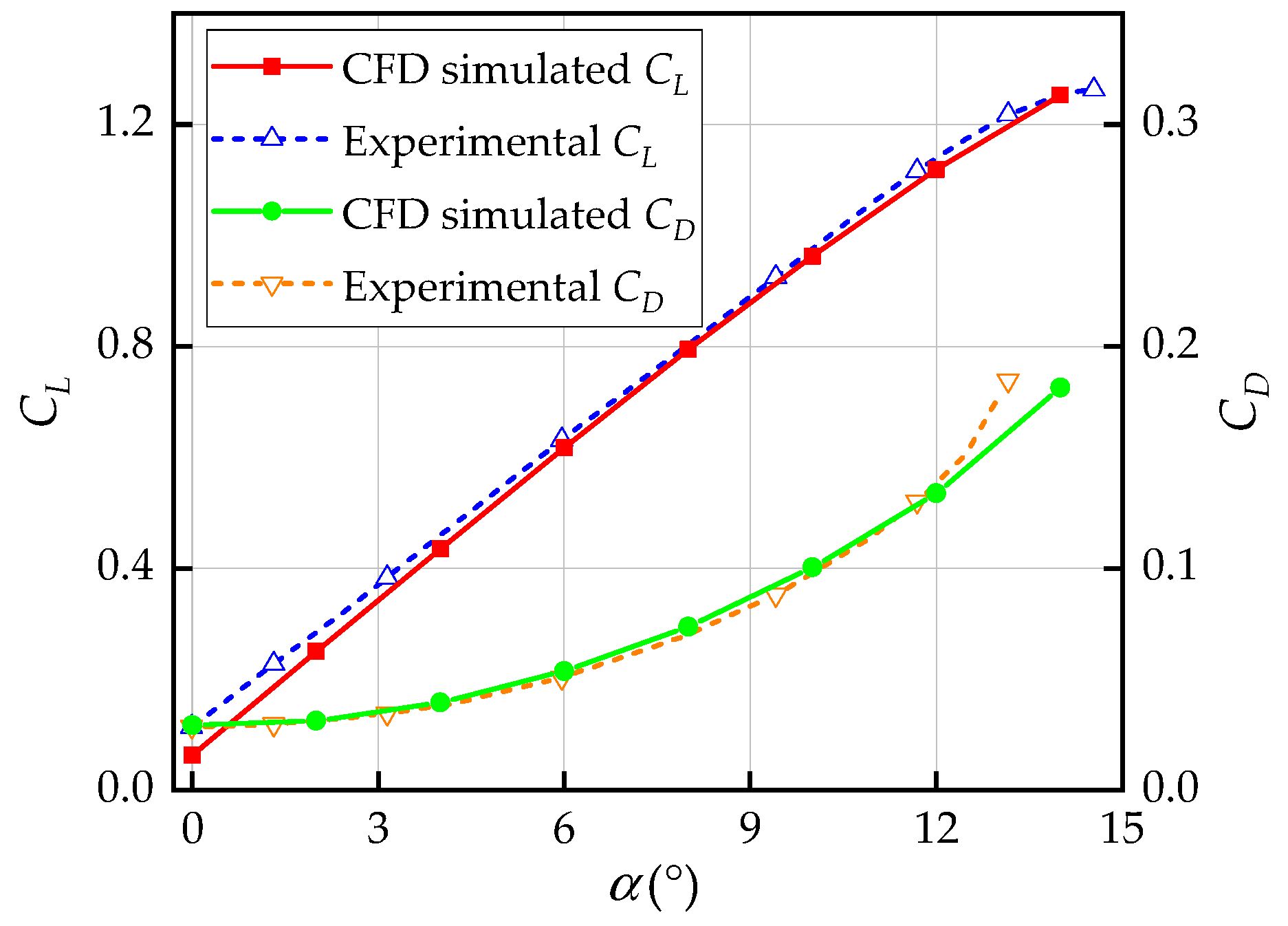
The aerodynamic data of the SBJ were calculated using the CFD method, with flight conditions set with altitudes of 0, 5, and 10 km and
Ma = 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, and 0.8, respectively. For other flight conditions, the aerodynamic data were obtained through interpolation. In [
40], the experimental data of lift coefficient
and drag coefficient
are shown with Reynolds number
Re = 8.6 × 10
6. To verify the credibility of the CFD simulated results, the experimental data were chosen for comparison, as shown in
Figure 6. Between the two groups of results, the lift curve slope error was less than 5% and the drag coefficient data were close to each other. Thus, the CFD results were considered reliable.
The geometric and inertial data of the SBJ are shown in
Table 1.
The SBJ also satisfies some physical constraints as in Equation (21). The ranges of control surface deflections are given in [
43], satisfying
15°,
18°, and
30°. The upper limit of
α is defined as the maximum
α in the linear segment of the lift coefficient to avoid aerodynamic stalls [
25,
28], being approximately 12°, as shown in
Figure 6. The lower limit of
α is mainly used to trim the SBJ and set it at −12°, which is much smaller than the trimmed solutions. Considering the structural limit represented by
nmax (
Table 1), this paper also assumes that
60° as in [
26]. Moreover, the range of
γ is assumed to be [−40°, 0°].
(2) Simulation settings
During simulations on the SBJ, the initial altitude was 0.5 km. The other settings of the flight envelope and gliding footprint are shown in
Table 2. Unless otherwise specified, the following settings will apply to all simulations.
3.4.2. Unpowered-Flight Envelope
According to the footprint calculation process in
Section 3.3, the 6-DOF unpowered-flight envelope characterized by
was computed. For a specified initial altitude
, the flight envelope is represented by a two-dimensional matrix
.
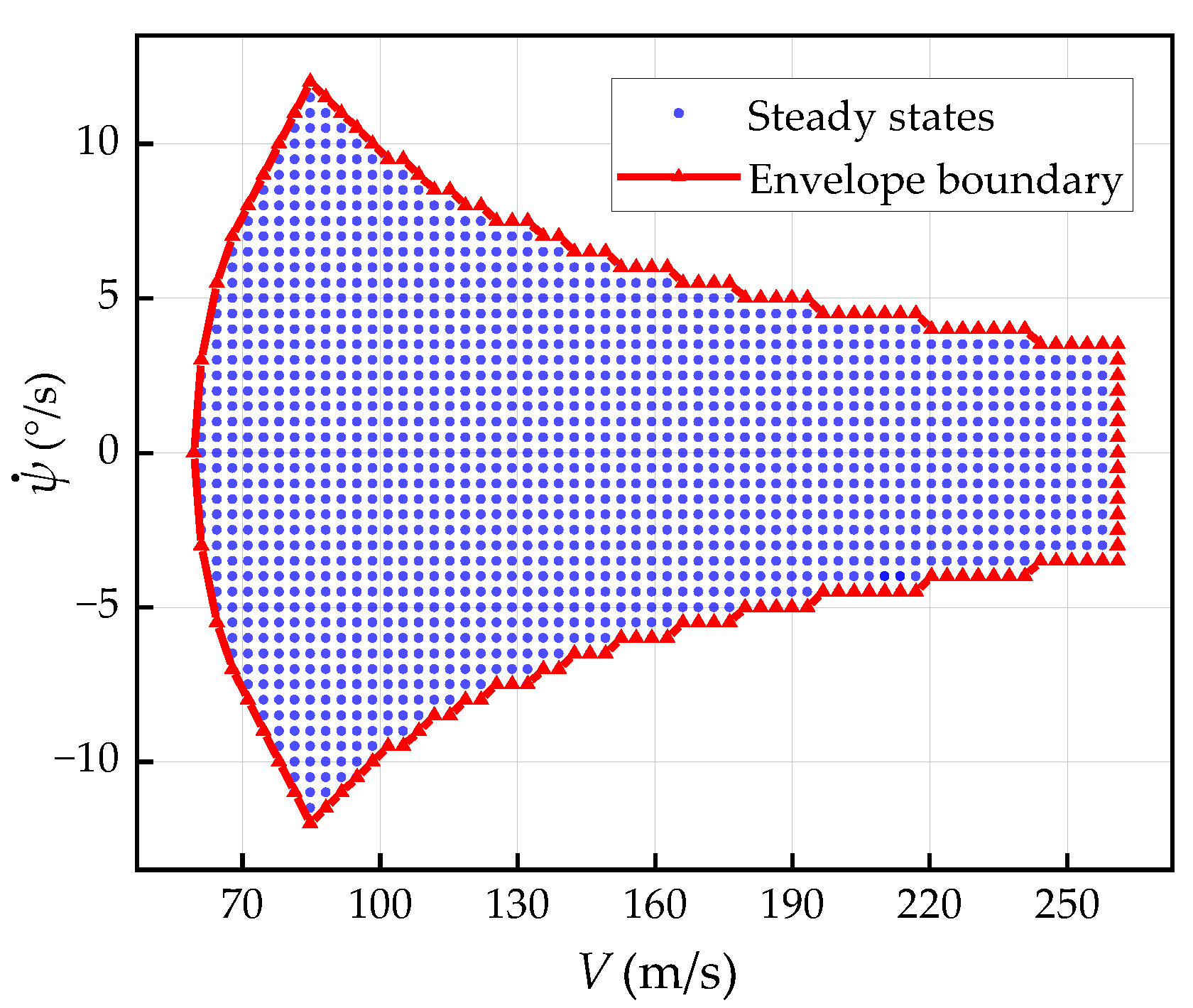
Figure 7 shows the 6-DOF unpowered-flight envelope results after sparse processing. The envelope contains a total of 752 thousand discrete steady states and is symmetrical along the zero
line, showing equivalent maneuvering capability to turn right (
) and left (
). The maximum
is 12.39 °/s at a velocity of 85.11 m/s (0.251
Ma), where the minimum turn radius
is also obtained. The velocity range of the flight envelope is 59.34–261.10 m/s (0.175~0.770
Ma). As the velocity increases, the number of corresponding steady states shows a trend of first increasing, and then, decreasing.
During the 6-DOF trim process, steady states should satisfy the inequality constraints of
α,
γ,
ϕ,
,
, and
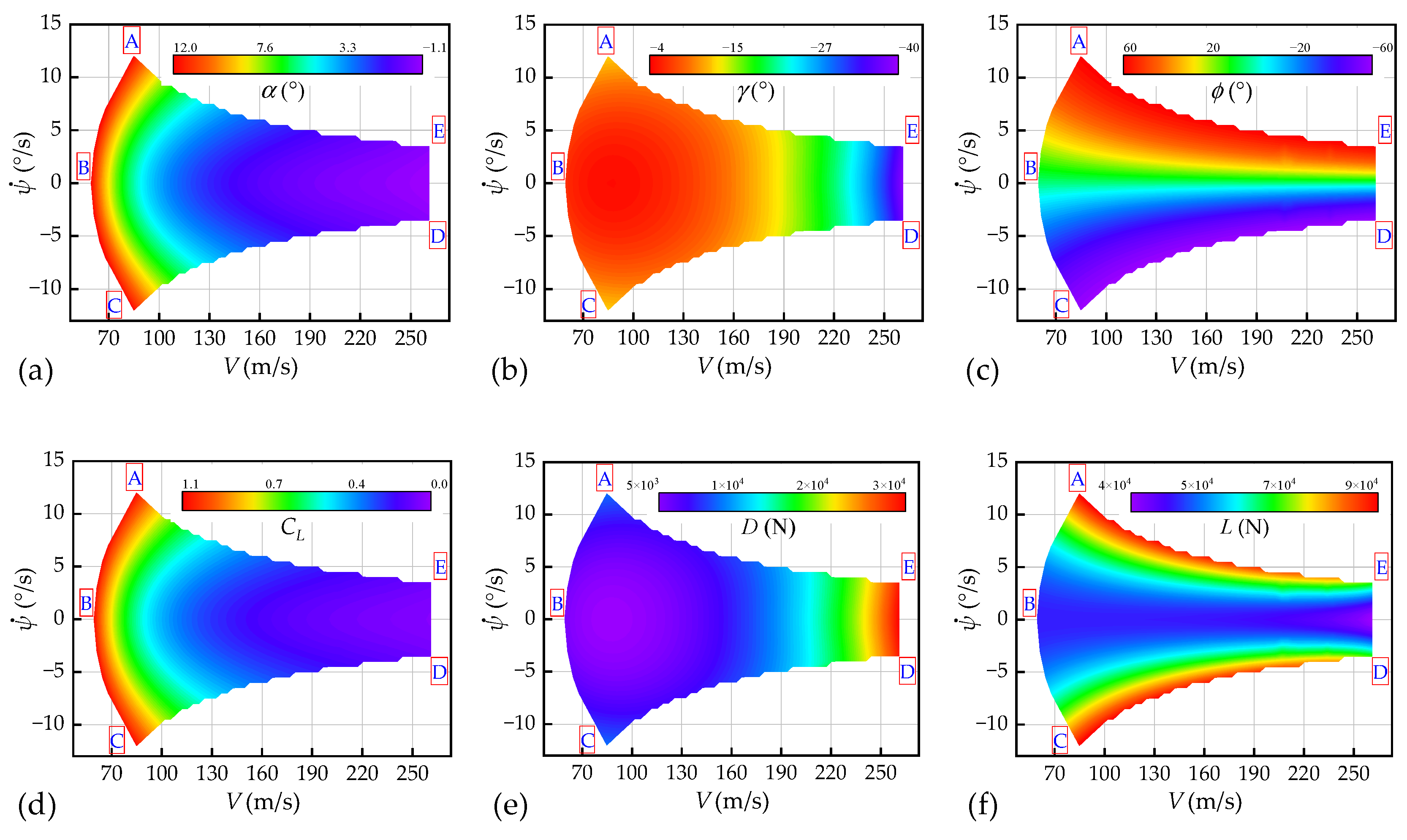
, as in Equation (21).
Figure 8 illustrates some trimmed parameters of the steady states, trying to find the parameters constraining the envelope boundary. The boundary is divided into four sections, namely ABC, CD, DE, and AE. The leftmost section, ABC, is the minimum-velocity boundary at different
and is constrained by the upper limit of
α (in
Figure 8a). The maximum lift force coefficients at different
are obtained (in
Figure 8d) in this section. For flight states with smaller velocity, the dynamic pressure will not be able to produce adequate lift force to trim the aircraft. The rightmost section DE is the maximum-velocity boundary and is limited by the lower limit of
γ (the steepest flight path in
Figure 8b). The maximum drag forces at different
are obtained (in
Figure 8e) in this section. For flight states with larger velocity, the drag force will be too great for the gravitational component along the flight-path angle to balance. The conditions of the above two sections are consistent with the conventional velocity–altitude flight envelope of powered aircraft. The remaining two sections, CD and AE, are restricted by the lower and upper limits of
ϕ, respectively (in
Figure 8c). The maximum lift forces at different velocities are gained (in
Figure 8f). For flight states with bigger
, the lift force component along
ϕ will be insufficient to provide centripetal force during the turn.
The altitude loss in the turn segment affects the total gliding distance along the segmented trajectory and is determined by
R,
, and Δ
ψ, as in Equation (1).
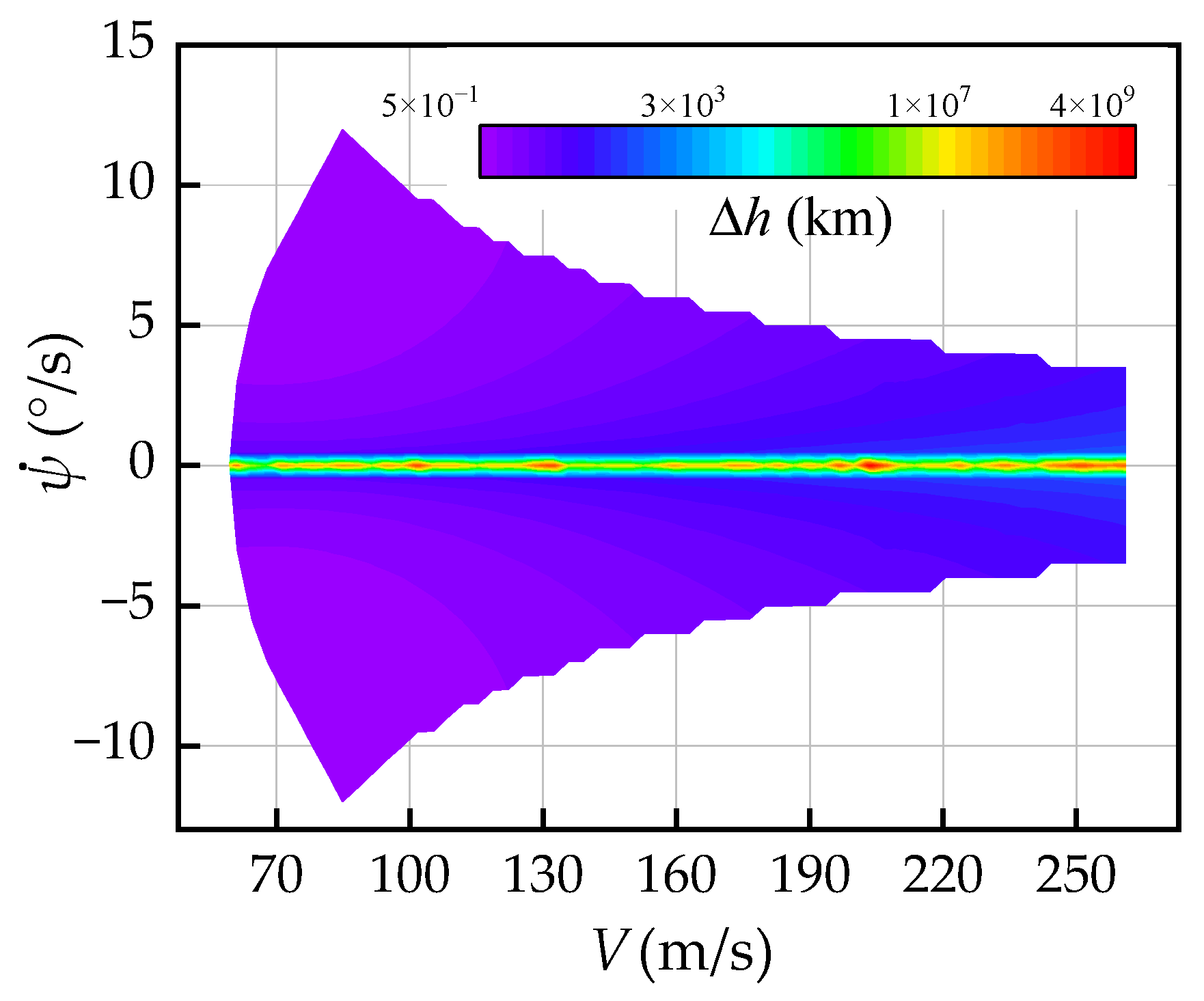
Figure 9 shows the altitude loss over a complete Δ
ψ = 360° turn for steady states in the flight envelope. For a constant velocity, the altitude loss decreases gradually with the increase in the turn rate
, when the value of
also increases (in
Figure 8c). For a constant value of
, such a trend also arises as the velocity decreases. The minimum altitude loss is 509.07 m at the steady states with maximum
, when
is also obtained simultaneously. When
is near zero, the turning descent is close to straight gliding, and magnitude of the altitude loss is rather huge.
3.4.3. Gliding Footprint
Figure 10 illustrates the segmented trajectories arriving at the footprint outer boundary, with a step size of 30° for
ξ. The gliding footprint is the area within the outer boundary that is discretized into 73 boundary points. For the right-half boundary, the turn segments are conducted with right turning, and for the left half, with left turning. The flight trajectory corresponding to zero
ξ contains only a straight segment, while the 180°
ξ has two equivalent flight trajectories with the turn segment at left and right turnings, respectively. In addition, the values of the gliding distance and altitude loss in the straight segment are larger than those of the turn segment.
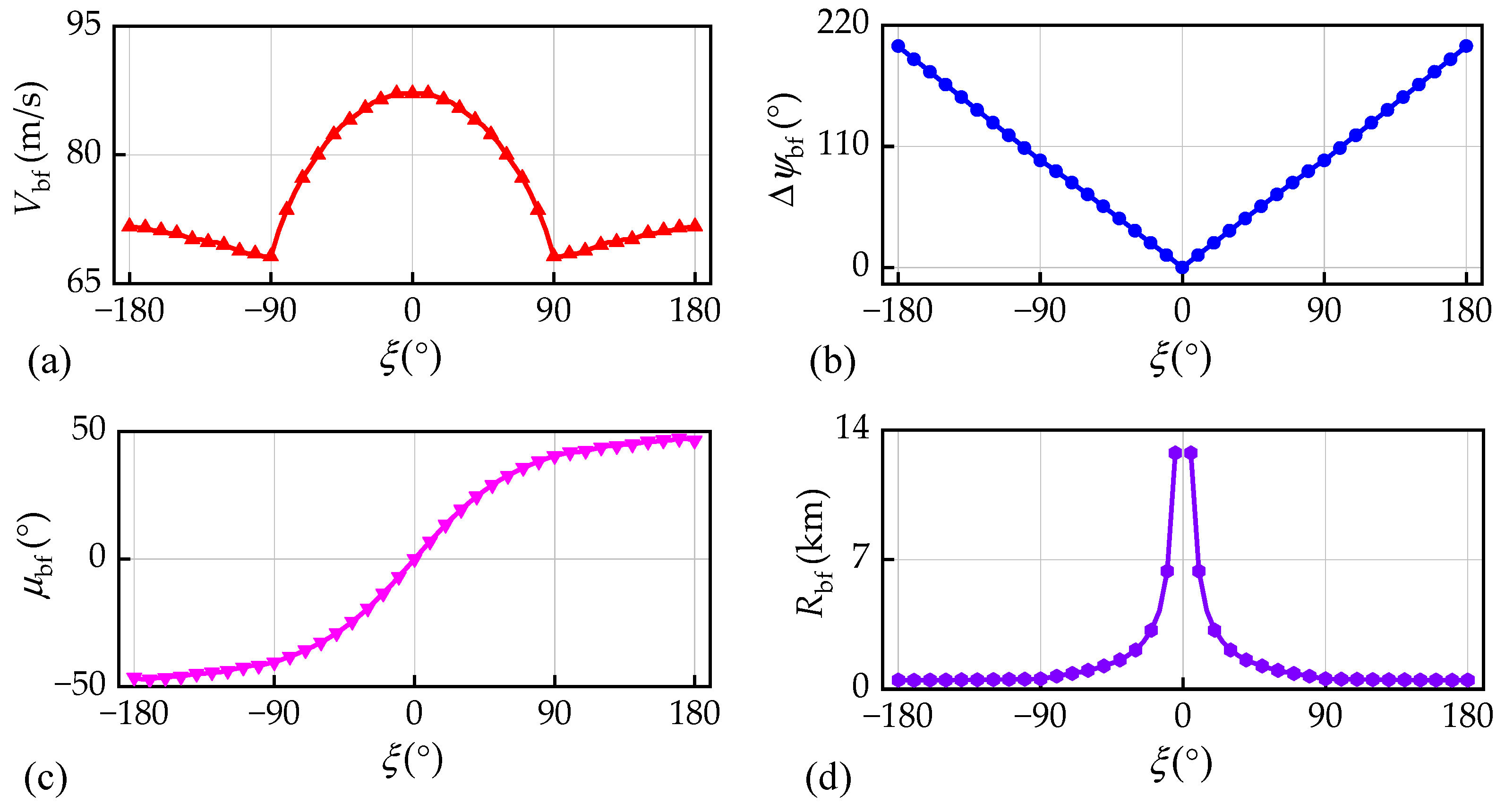
To better illustrate the above segmented trajectories, several best-footprint parameters were also analyzed.
Figure 11 shows the results of
,
,
, and
regarding the radial angle. In this figure, the values at
ξ = 0° are parameters of the best-glide state, and those at nonzero
ξ are of the best-turn states. The range of
is 68.15~87.15 m/s. Combined with the flight envelope results in
Figure 7 where the velocity range is 59.34~261.10 m/s, both the best-glide and best-turn states are found to be located in the low-velocity region of the envelope. Take the right-half footprint (positive
ξ), for example;
first decreases, and then, increases with an increase in
ξ, and the values of
increase linearly. The maximum
is obtained at zero
ξ. When
ξ = 5°, 90°, and 180°, the results of
are 5.57°, 97.23°, and 200.99°, respectively. The values of
are larger than the corresponding radial angles
ξ. As the positive
ξ increases,
becomes larger, and
becomes smaller. When
ξ = 5°, 90°, and 180°, the results of
are 12.76, 0.55, and 0.49 km. The minimum
is obtained when
ξ = 180° and is still larger than
.
To investigate the effects of 6-DOF flight dynamics on the gliding footprint, we compared the gliding footprint results between the proposed method and the method in [
26].
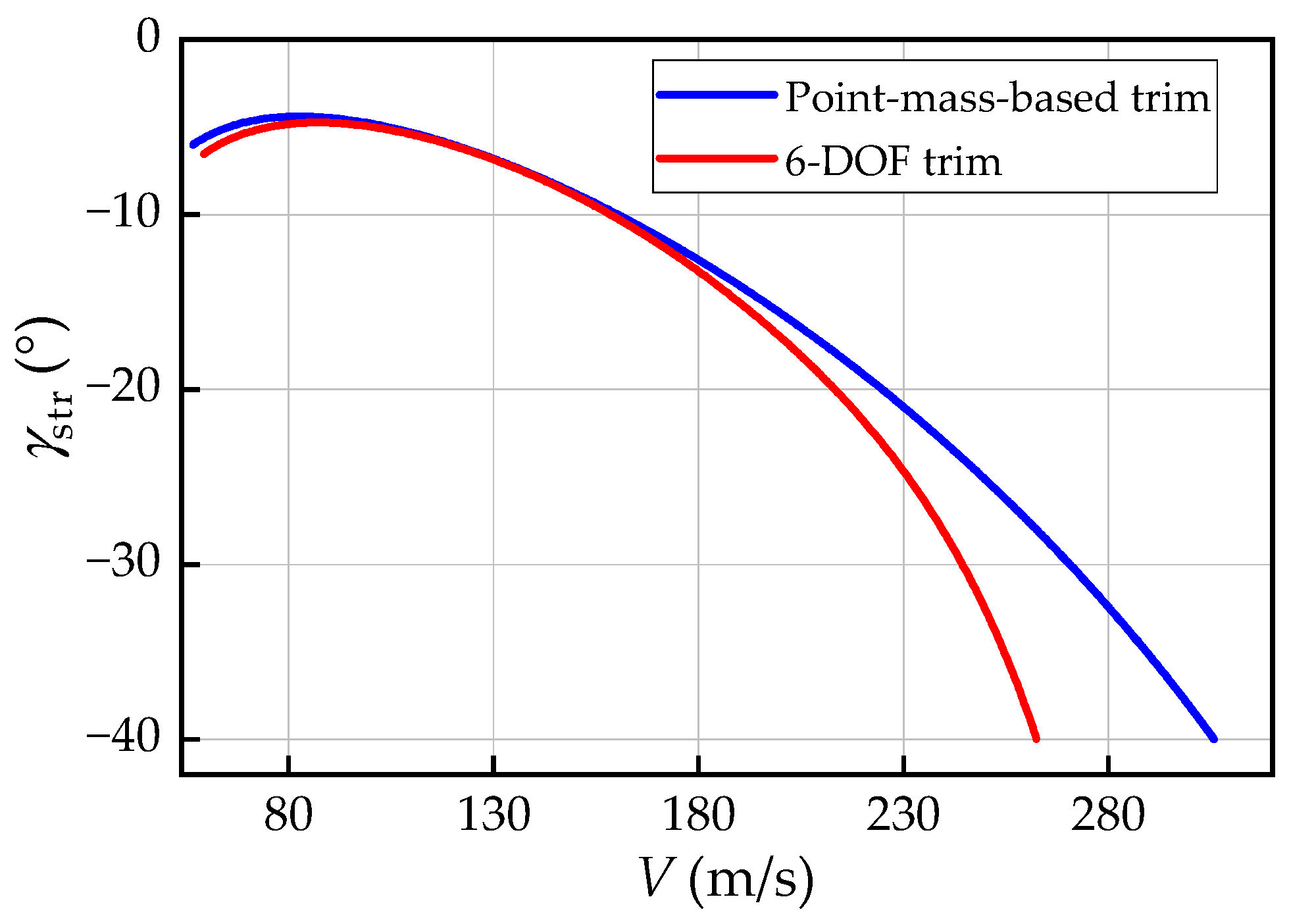
As a critical factor influencing the gliding distance, the flight-path angle was first analyzed.
Figure 12 shows the comparative results of flight-path angles in attainable steady straight states, which were computed using two trim methods. The point-mass-based trim computes
by balancing the forces, while the 6-DOF trim considers both force and moment equilibrium. The values of
in the 6-DOF trim at different velocities are all smaller than those of the former method, implying a steeper descent path. The best-glide angle
of the former method is −4.386° at a velocity of 82.64 m/s, which is larger than the value −4.738° of the latter method at a velocity of 87.15 m/s. The absolute and relative errors of
are 0.352° and 8.03%, respectively. Then, according to Equation (2), the best-glide distance in the straight segment (i.e., the maximum straight gliding distance) of the two trim methods are 13.04 and 12.07 times the altitude loss. The relative error of the maximum straight gliding distance is 7.44%. Such an error can lead to significant deviations in the gliding footprint, as demonstrated below.
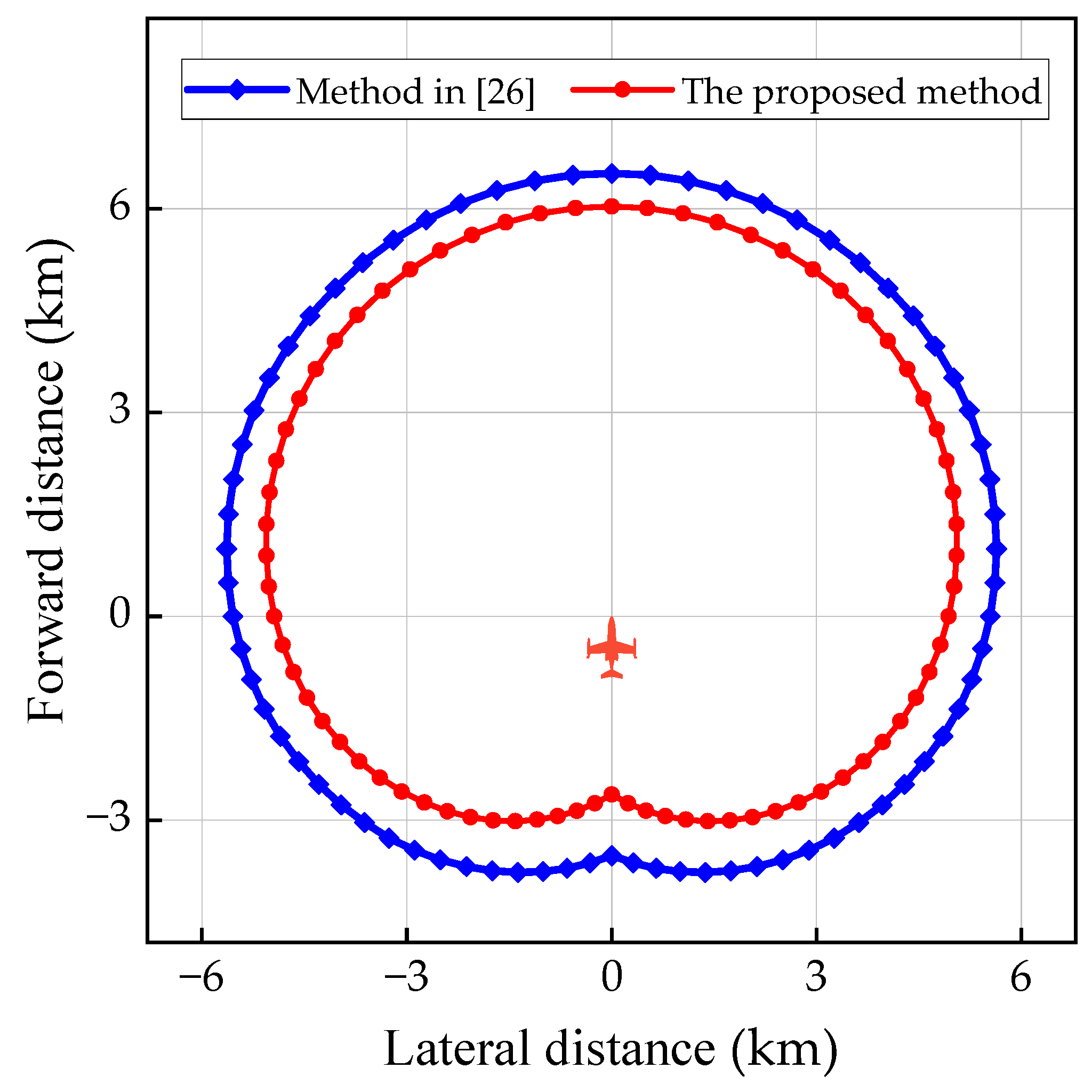
The comparative results of the gliding footprint are shown in
Figure 13 and
Table 3. According to
Table 3, the straight segment in the proposed method is steeper (
= −4.738°) than that of the method in [
26] (
= −4.386°). When
ξ = 0°, the maximum gliding distances
are 6.52 and 6.03 km, respectively. The relative error is 7.44% and is consistent with the above results in
Figure 12. With the increase in
ξ, the two groups of
both decrease obviously, which can also be seen in
Figure 13. When
ξ = 0°, 45°, 90°, 135°, and 180°, the absolute errors of
between the two methods are 0.49, 0.52, 0.61, 0.73, and 0.90 km. These errors present an increasing trend, which is the result of the combined effects of the gliding distance deviations in both the straight and turn segments. The gliding footprint areas of the two methods are 93.48 and 74.05 km
2, respectively, with a relative error of 20.79%. Therefore, there are significant deviations in both the maximum gliding distances and gliding footprints between the two methods, which cannot be ignored.
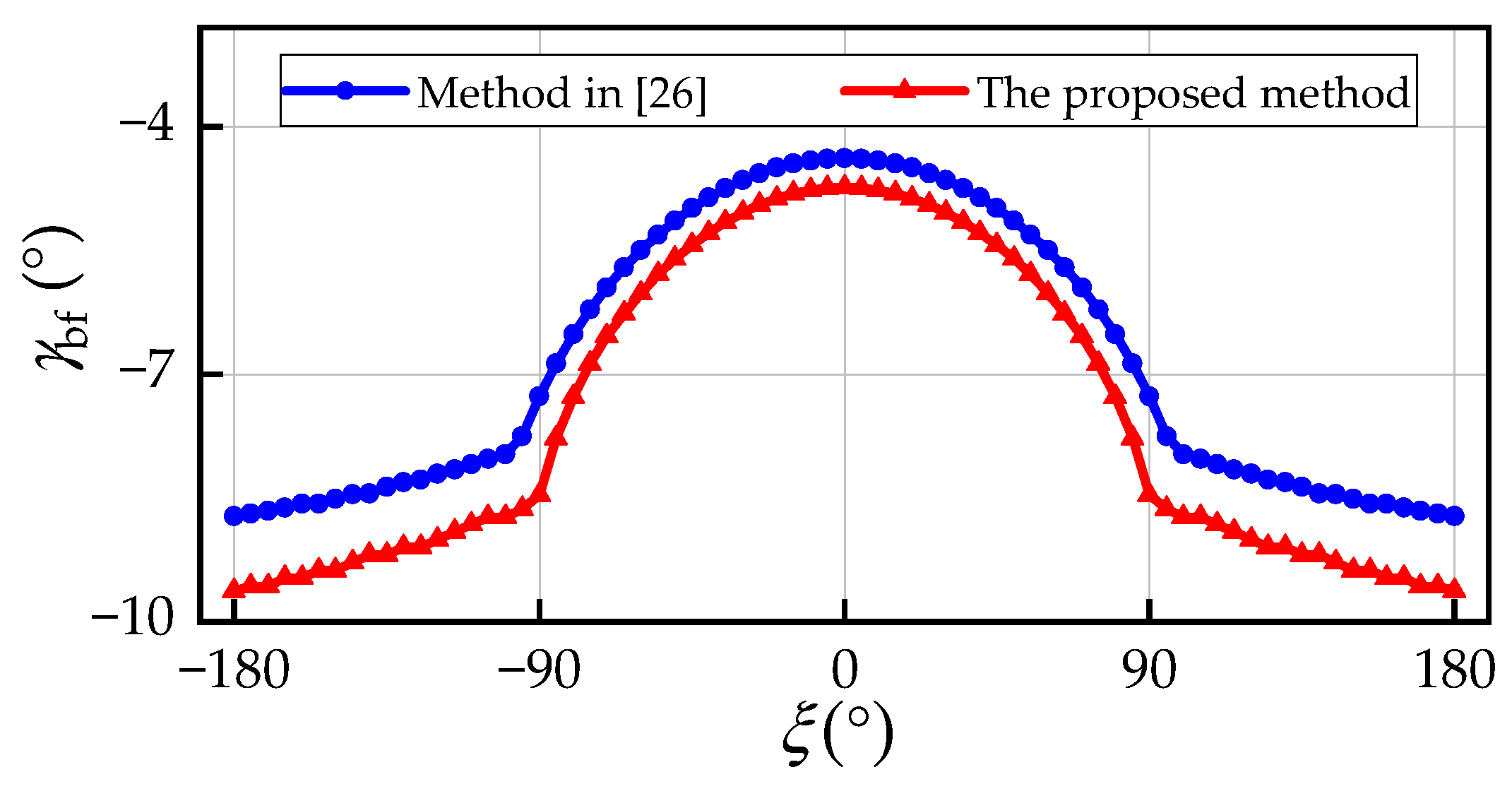
To further analyze how the trim method affects the gliding footprint, we also compared the flight-path angles in the best-turn states. The comparative results regarding the radial angle
ξ are shown in
Figure 14. With the increase in
ξ, the two groups of
show a consistent trend with each other. When
ξ = 180°, the absolute error of
between the two methods reaches 0.908°, which is considerably larger than that of the best-glide state (0.352°). The values of
in the proposed method are smaller over the whole range of
ξ. Therefore, the farthest segmented trajectories arriving at the footprint outer boundary of the proposed method are steeper in both the straight and turn segments than those of the method in [
26], which directly leads to deviations in the gliding footprint.
Combining the analysis of the results in
Figure 12,
Figure 13 and
Figure 14, it is proven that the 6-DOF flight dynamics used to model the unpowered aircraft does have a significant effect on the gliding footprint. The reason is that the 6-DOF trim considers more constraints (including the moment equilibrium, control surface saturation, and aerodynamic contributions of the control surfaces) when computing the gliding flight parameters, resulting in steeper segmented trajectories to the footprint outer boundary and a smaller gliding footprint under a given initial altitude. However, it takes about 6 h to calculate the discrete boundary points encircling the gliding footprint. Thus, the proposed method is unsuitable for direct application to in-flight damage conditions.
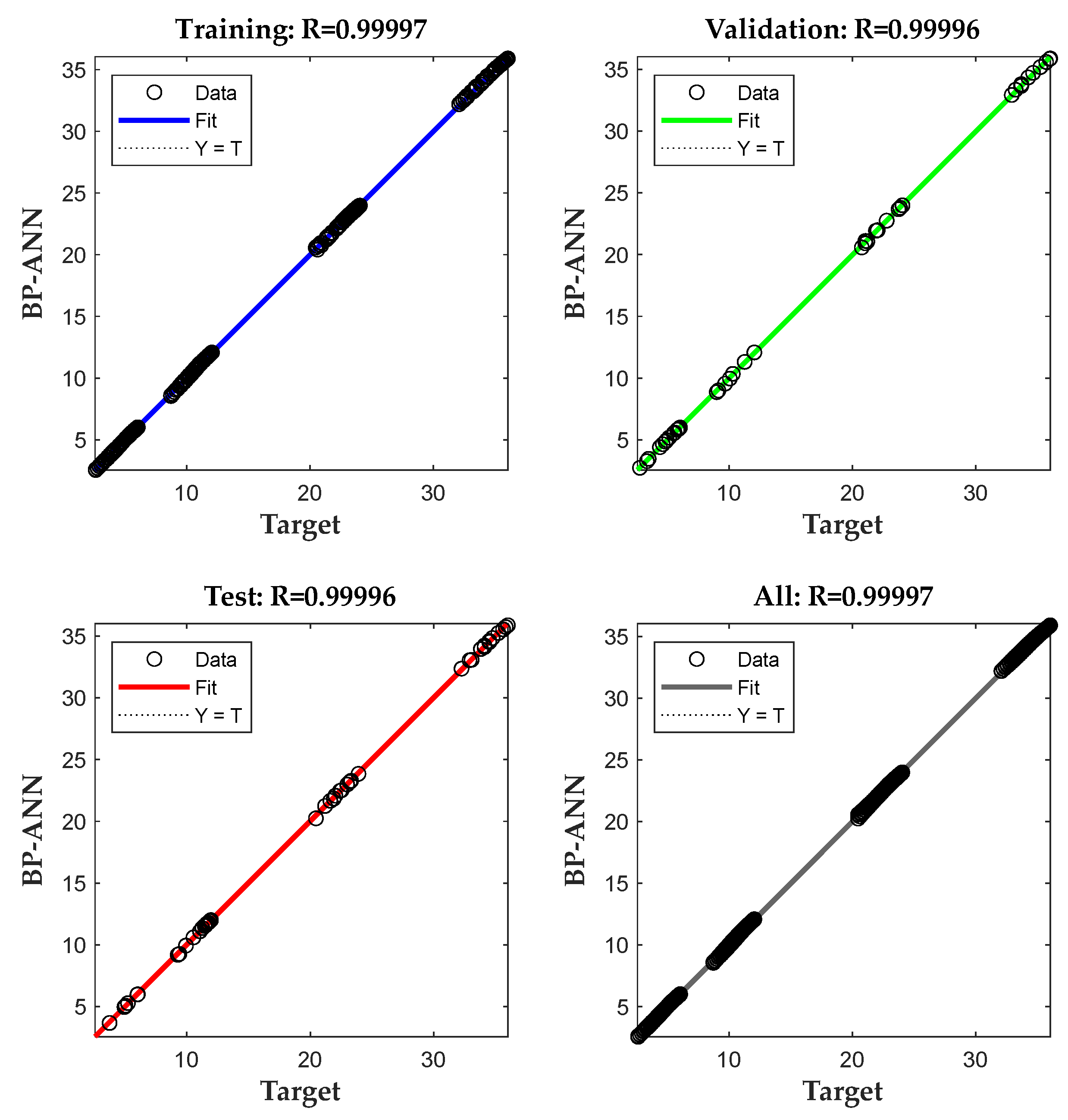
5. Conclusions
In this paper, we propose two methods to calculate the gliding footprint of an aircraft with thrust failure. Method 1 models the aircraft with 6-DOF flight dynamics and determines the footprint based on the best-glide and best-turn states that are decided within the 6-DOF unpowered-flight envelope. Method 2 is based on the BP-ANN model, which is trained by a footprint database computed using Method 1.
The simulations show that 6-DOF flight dynamics has significant effects on the gliding footprint. Compared with the conventional point-mass dynamics method, Method 1 produces steeper trajectories to the footprint outer boundary and a smaller footprint area. The deviation in footprint area is 20.79%, and that in the maximum straight gliding distance is 7.44%. The results of Method 1 are relatively conservative, which improves the safety threshold of the landing sites. Both the best-glide and best-turn states are located in the low-velocity region of the flight envelope.
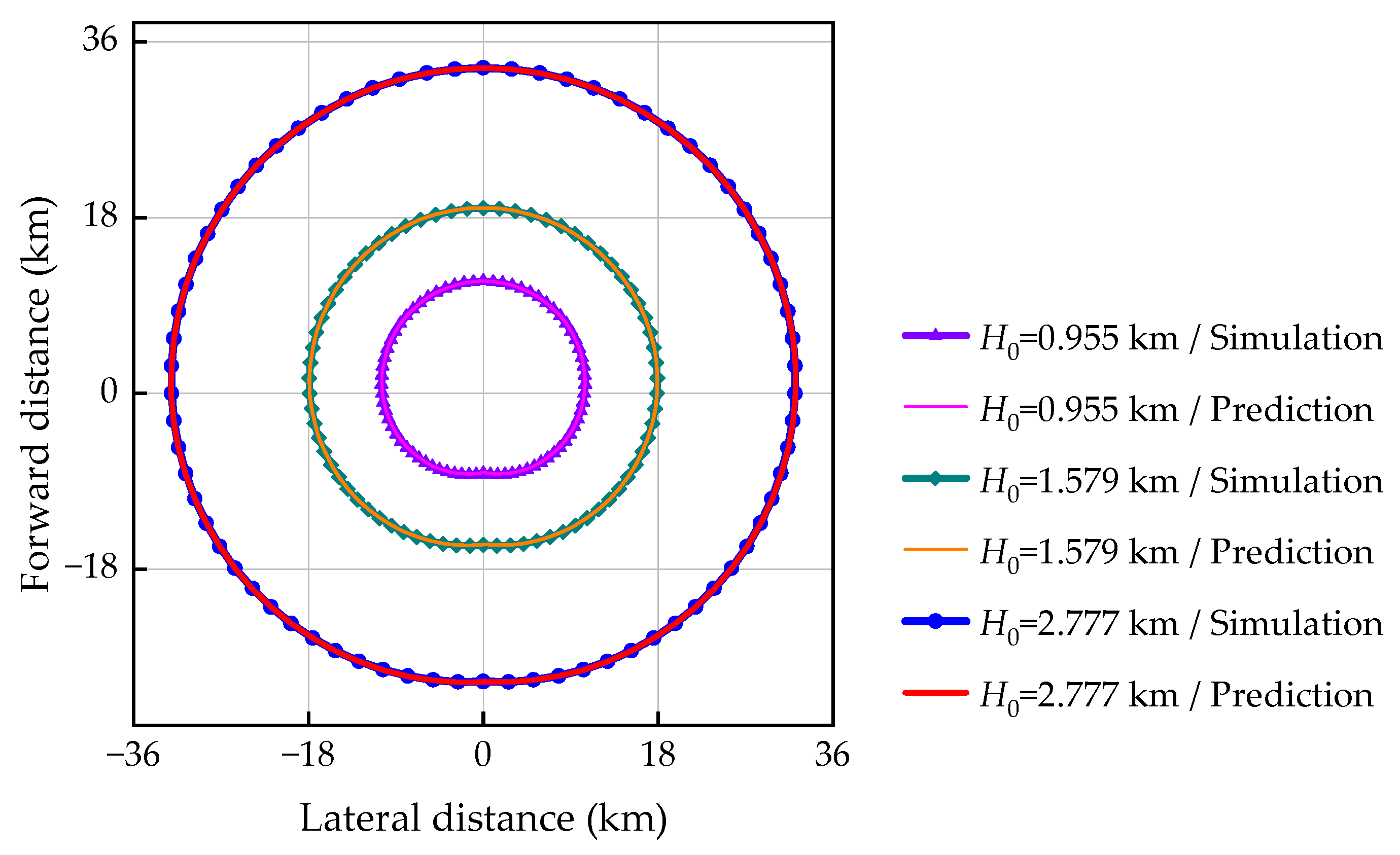
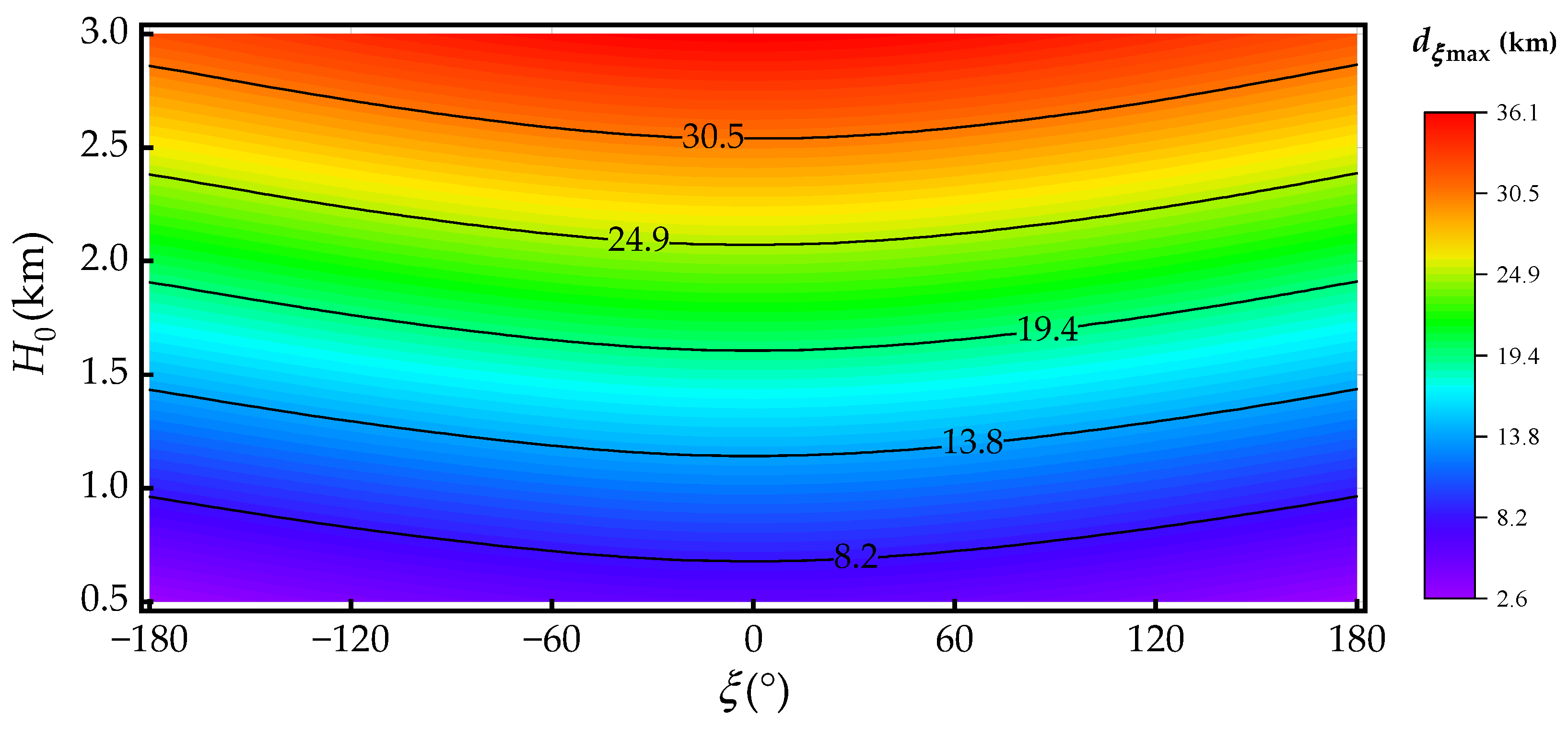
Using the BP-ANN model, Method 2 can predict the gliding footprint under the entire operational altitude and full radial direction while satisfying the real-time requirement of in-flight damage conditions. Given an initial altitude, the maximum gliding distance keeps decreasing as the radial angle increases. With the increase in the initial altitude, the decreasing trend weakens and the gliding footprint gradually becomes closer to a circle.
The proposed methods are significant for improving the forced landing capability of a thrust-failed aircraft, and hence, its survivability. Future work will include experimental flights to validate the proposed methods, gliding footprint calculation methods under additional constraints such as wind and obstacles, and effects of downward flap deflection on the gliding footprint.