Abstract
Future liquid hydrogen-powered aircraft requires the design and optimization of a large number of systems and subsystems, with cryogenic tanks being one of the largest and most critical. Considering previous space applications, these tanks are usually stiffened by internal members such as stringers, frames, and stiffeners resulting in a complex geometry that leads to an eventual reduction in weight. Cryogenic tanks experience a variety of mechanical and thermal loading conditions and are usually constructed out of several different materials. The complexity of the geometry and the loads highlights the necessity for a computational tool in order to conduct analysis. In this direction, the present work describes the development of a multi-physics finite element digital simulation, conducting heat transfer and structural analysis in a fully parametric manner in order to be able to support the investigation of different design concepts, materials, geometries, etc. The capabilities of the developed model are demonstrated by the design process of an independent-type aluminum 2219 cryogenic tank for commuter aircraft applications. The designed tank indicates a potential maximum take-off weight reduction of about 8% for the commuter category and demonstrates that aluminum alloys are serious candidate materials for future aircraft.
1. Introduction
Aiming at a more sustainable future for aviation, the 2021 Strategic Research and Innovation Agenda (SRIA) of the Clean Aviation Joint Undertaking (CAJU) of the European Union (EU) states that alternative aviation fuels are to be investigated from 2020 onwards [1]. Of the many proposed fuels, non-drop-in liquid hydrogen (LH2) is currently considered as one of the most promising, as its combustion produces no CO2 or CO emissions, and its use in fuel cells provides extremely high efficiency.
While having significant advantages like having one of the highest heating values of all fuels (about 2.8 times more energy per mass unit than hydrocarbons) and having water as the sole product of its combustion, LH2 has a low energy density (about 4 times less energy per volume unit than hydrocarbons) and has to be stored at a temperature of −253 °C [2].
The use of LH2 as an aviation fuel has been investigated in only a limited number of projects. One of the main issues of LH2-powered aircraft realization is the conflicting requirements of the large cryogenic tank, as it has to minimize heat losses and have a high strength while also being lightweight and cost efficient. The increased complexity of the design process highlights the demand for a computational tool capable of performing multi-physics analyses of several tank concepts in order to perform trade-off studies, leading to the eventual selection of an optimal solution for each case.
In this direction, the present work refers to the development of a parametric multi-physics finite element model, capable of investigating various design concepts. The developed model comprises a thermal part for the calculation of temperature distributions and heat flux and a structural part that uses the results of the thermal part as inputs and combines them with other mechanical loads in order to perform stress/strain analysis. As a fluid mechanics simulation module is not integrated yet, hydrogen is considered in two separate phases: LH2 and gas. LH2 is modeled as a temperature boundary condition and a hydrostatic pressure load, while gas is modeled as a separate constant pressure load. The simulation results are used to assess both the structural and thermal performance of the tank and its mass efficiency as a function of its design parameters, providing valuable inputs for the optimization process.
The model has a built-in geometry creation module that is capable of creating axisymmetric double-walled tanks, with the length, radius and shape of the domes being modifiable parameters. Cross-section data can also be altered, facilitating design revisions. Material properties are also introduced in a parametric manner, allowing the investigation of different materials. The digital model was developed using code written in the ANSYS parametric design language (APDL), and simulations were conducted in the ANSYS mechanical solver.
The capabilities of the model are demonstrated with the design of a cryogenic tank. The design process commences with the definition of the basic requirements, such as dimensions, capacity, and insulation efficiency. In the present work, a fuel cell-powered commuter aircraft was selected as a case study, with the requirements heavily influenced by the Embraer EMB 120 Brasilia, a typical aircraft of the class. This case study considered the selection of established and well-characterized materials, in an effort to showcase that LH2 aircraft can be developed sooner and with a relatively lower cost by utilizing existing materials and manufacturing methods. Aluminum alloy 2219-T8 was specifically selected for the structural parts of the tank, as this is a well-established material used since the 1960s for the construction of large-scale LH2 tanks of rockets, and its mechanical and thermal properties are well documented over a wide temperature range, including cryogenic temperatures. It has low hydrogen permeability and can also be welded without significant degradation of its properties, making it an extremely attractive material for the tank walls. Polyetheretherketone (PEEK), a high strength thermoplastic, was selected for the inter-tank supports, while light polyurethane (PU) foam was selected for the insulation.
A brief historical background Is provided in Section 2. Structural concepts, materials, and the state of the art are presented in Section 3, while an initial design methodology, as well as the general design parameters and requirements are described in Section 4. The heat transfer and structural analysis processes are described in Section 5 and Section 6, respectively. The functions of the model are presented in Section 7 with the analysis of the investigated tank concept, while conclusions and future work are presented in the final section.
2. Historical Background
The main contributing factor to the discovery of hydrogen as an element in the late 18th century was its flammability. It was immediately identified as a potential fuel and it was first used as such early in the 19th century [3].
The liquefaction of hydrogen was achieved late in the 19th century [4], yet due to handling issues related to the cryogenic temperatures, liquid hydrogen was not used as a fuel until 1955, when a United States Air Force (USAF) B-57B Canberra bomber was modified to carry a stainless steel LH2 tank on its wingtip that was feeding one of the two engines. The experiment was successful, with the aircraft flying for about 20 min with one engine running on LH2 [5].
The 1960s saw the first large scale use of LH2 as a rocket fuel. The first successful use of LH2 as a rocket propellant was the Atlas-Centaur, with the Centaur cryogenic upper stage used on top of the Atlas booster, with the first successful flight on 27 November 1963 [6], shown in Figure 1a. Cryogenic upper stages were also considered for the Saturn family of rockets of the Apollo program, initially with the S-IV stage of the Saturn I using the same RL-10 engines as the Centaur [6]. The RL-10 engines of the S-IV were later replaced by the J-2 engines resulting in the S-IVB upper stage, used as the second on the Saturn IB and as the third stage of the Saturn V rocket. The Saturn V, shown in Figure 1b, had a cryogenic second stage as well, the S-II, and it was powered by five J-2 engines [7]. The development of the Space Transportation System (STS), better known as the space shuttle, started before the end of the Apollo program, with the maiden flight on 12 April 1981, shown in Figure 1c. The STS comprises three main components: the space shuttle orbiter where the crew is located, the two reusable solid rocket boosters (SRB) that provide the extra thrust needed for take-off, and the external tank (ET) where the liquid hydrogen and liquid oxygen propellants for the main engines are stored [8]. The space shuttle program has laid the foundation for the development of the currently used launch vehicle for manned space exploration, the Space Launch System (SLS) of the Artemis program, shown in Figure 1d. Many space shuttle components were redesigned and repurposed for the SLS including the solid rocket boosters, with a more powerful version using five segments of fuel instead of four, the RS-25 main engines, and the external tank, which was modified to serve as the core stage. The main redesign of the ET was the replacement of the liquid oxygen tank with a cylindrical one, with the liquid hydrogen tank remaining mostly unchanged. The second stage is the same as the Delta IV rocket, again using liquid hydrogen and liquid oxygen as propellants, and it is powered by a single RL-10 engine, the same as the Centaur [9].

Figure 1.
LH2 powered rockets. (a) The first successful launch of the Atlas-Centaur [source: https://www.nasa.gov/history/centaur-americas-workhorse-in-space/ accessed on 21 July 2023]; (b) the Saturn V used for Apollo 8 being transported to launch pad 39 A [7]; (c) the first flight of the space shuttle Columbia [8]; (d) I launch of Artemis I [source: https://www.nasa.gov/image-detail/amf-nhq202211160002/ accessed on 21 July 2023].
The first major step toward the adoption of LH2 as an aviation fuel was the Tupolev Tu-155 shown in Figure 2. It is a highly modified version of the Tu-154B airliner, first flown in 1988. A large cryogenic tank was placed in the aft part of the cabin and one of the three engines was running only on LH2. The project was successful with over 100 flights completed before conversion to Liquefied Natural Gas (LNG), as it was easier to handle due to its higher storing temperature of −160 °C, its higher energy density (about 2.3 times more than liquid hydrogen), and mainly due to its significantly lower price and higher availability, especially in the Union of Soviet Socialist Republics (USSR) where the Tu-156, the planned production variant that was to be solely powered by LNG, was supposed to operate [10].
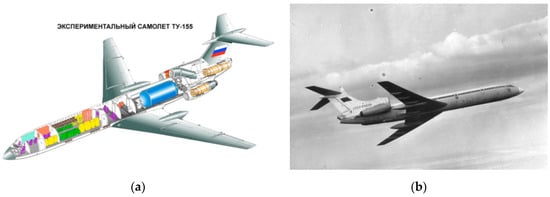
Figure 2.
Tu-155 [10]. (a) Experimental airplane Tu-155—Cutaway diagram with the large cryogenic tank visible in the aft part of the fuselage in blue color and the LH2 powered starboard engine in dark orange; (b) the Tu-155 in flight.
In 2003, Airbus designed various types of LH2-powered passenger aircraft, ranging from business jets up to long-range airliners. The cryoplane project, as it was called, showed some promising results, with the expected maximum take-off weight (MTOW) of the LH2 aircraft being lower than that of the conventional production airliners [11].
In 2008, the European Space Agency (ESA)-coordinated Long-Term Advanced Propulsion Concepts and Technologies (LAPCAT) program started the conceptual design of supersonic aircraft capable of flying from Brussels to Sydney in 2–4 h, meaning cruising Mach numbers of 4–8 [12]. The Mach 8 concept resulted in the 600 ton, LH2-fueled LAPCAT-MR1. An air turborocket propulsion system was selected for the initial acceleration up to Mach 4, and for the final acceleration up to Mach 8 and the cruising stage, a dual-mode ramjet would take over [13]. The follow-up LAPCAT II program refined the MR1 design and developed the MR2, with significant aerodynamic improvements, as well as the optimization of the propulsion system. The weight was reduced to 400 tons while LH2 remained as the selected fuel [14].
In 2009, German company H2FLY successfully tested the Antares, the first manned aircraft to be solely hydrogen powered. In 2016, an electric Pipistrel Taurus G4 was modified. Power was provided by a DLR fuel cell with compressed hydrogen stored in tanks within the fuselage. The first flight was successful, with more flights taking place in the following years. Since 2019, the company has been working on a conversion project of a Dornier 328 40-passenger regional propeller-driven aircraft to run on hydrogen fuel cells [15].
In 2012, Boeing produced the first aircraft to be powered solely by LH2, the Phantom Eye. It was a high altitude and long endurance drone that had two spherical LH2 tanks storing fuel for its two 2.3 L 150 hp (112 kW) internal combustion engines [16].
Between 2019 and 2022, the EU-funded project ‘Unifier 19’ led by Pipistrel produced a conceptual design of a 19-passenger LH2 commuter aircraft powered by fuel cells. The design showcases various innovative design solutions like distributed electric propulsion, and the ultimate goal was to provide the framework for a zero-emission and silent mini-liner capable of operating from small regional airports with short runways [17].
In 2020, Airbus launched the ZEROe initiative with the aim of introducing LH2 aircraft by 2035. Modified versions of airliners already in production are to enter service first, with other unconventional concepts like blended wing-body concepts considered for the future [18].
3. State of the Art
3.1. Insulation Concepts
LH2 is stored at −253 °C while ambient air can reach temperatures exceeding 40 °C during the summer. The difference in temperature causes heat flow from the outside environment to the LH2 stored inside the tank. This heat flow causes hydrogen to boil, increasing the pressure. The excess gas is vented in order to avoid rupture. Therefore, the heat flow toward the liquid is directly translated to a loss rate called the boil-off rate (BoR). Therefore, in order to minimize losses to an acceptable rate, the tank should be adequately insulated. The three main insulation concepts are vacuum-insulated (known as Dewar type tanks), material-insulated, and non-insulated tanks [19].
Dewar tanks have a double-wall design with a vacuum in between. They are the most thermally efficient type of tank, as heat can be transferred by radiation, while conduction is possible only through the supporting structure between the internal and the external walls that usually has the smallest possible cross section. As the main heat transfer mechanism is radiation, the walls have highly polished surfaces in order to reduce emissivity. Layers of reflective membranes (multi-layer insulation/MLI) between the two walls can further reduce the heat flux and thus the boil-off rate. Since there is a vacuum between the two walls, the structures of both walls must be reinforced, as the outer shell must withstand the atmospheric pressure loads, and the inner tank has to withstand a pressure differential increased by 1 atm. Maintaining the vacuum can also be difficult, especially for larger tanks, necessitating the use of vacuum pumps. Therefore, the main disadvantages of the Dewar concept are increased overall weight, complexity, and cost.
Material-insulated tanks are a much simpler concept as the tank is covered by layers of insulating materials with low thermal conductivity. As most insulating materials have poor mechanical properties and their properties rapidly degrade after exposure to humidity, solar radiation, etc., they are usually protected by an outer shell. The outer shell is often only used to protect the insulation, while in many cases, it can be a load bearing structure. Material-insulated tanks are usually inexpensive and lightweight, with their main disadvantage being their poor thermal insulation efficiency when compared to Dewar tanks, as the main heat transfer mechanism is conduction.
In cases like the propellant tanks of rockets, weight reduction is of utmost importance, while the filled tank is exposed to ambient conditions for only a few hours as rockets are filled on the launch pad shortly before take-off. If the operational time is short and weight reduction is critical, the tanks may not be insulated.
3.2. Structural Concepts
LH2 tanks usually have a large volume, and they are mainly cylindrical with spherical or elliptical domes in order to reduce pressure-induced stresses. The structural concept of a cryogenic tank greatly depends on the application. Stationary tanks are usually subjected to storage overpressure, the weight of the LH2, and hydrostatic pressure. For vehicle tanks, the previously mentioned loads are combined with inertia loads, as well as other structural loads depending on design and integration. The main structural concepts are the independent, the integrated, and the integral tanks [19].
When a tank is placed in a specifically designed compartment of the vehicle and is mounted in a manner such that it only receives internal and inertial loads, it is identified as an independent tank. Such tanks do not interfere with the structure of the vehicle and only cause inertial loading. They are thermally isolated from the rest of the vehicle and do not cause any thermal gradients on the structural parts. Independent tanks may be handled like cargo, and they can usually be easily removed, facilitating maintenance. The main disadvantage of this concept is the increased weight.
As the majority of insulated tanks require an outer shell, either to maintain the vacuum or to protect the insulation, some designs use a structural part of the vehicle as the outer shell. This is the integrated tank concept, which has the advantage of weight reduction and increased volume efficiency. This concept, though, may have issues, as the inner cryogenic tank, which has a temperature of around −250 °C, is directly connected to the load bearing structure via the inner tank supporting structure. This means that the load bearing structure may be subjected to low temperatures and temperature gradients, with possible thermal fatigue effects due to expansion and contraction under different thermal loading conditions. An integrated tank has to be specifically designed for the vehicle it will be placed in.
For applications where weight reduction is critical and no outer shell is used, the cryogenic tank itself may become a structural part of the vehicle. This is a common design solution for rockets, where the tank structure is the core of the vehicle with other components mounted on it. Such tanks may also be insulated like the space shuttle external tank or the core stage of the SLS rocket of the Artemis program, where foam insulation is used.
3.3. Materials
For the construction of a cryogenic tank, several materials are considered for the structural parts and the insulation. For the inner tank, the most common materials used are metals. For lightweight applications, the main material is aluminum–copper alloy 2219, which has been used since the 1960s. During the late 1980s, aluminum–copper–lithium alloy 2195 was developed. It has a higher tensile strength and a lower density than 2219 and can also be welded. Aluminum 2219 was the main material for the construction of the space shuttle external tank until 1998 when it was replaced by aluminum 2195. The new material selection significantly decreased the overall weight of the external tank, with the 2219 tank having an empty weight of 66,000 lbs (30,000 kg) and the new 2195 tank having an empty weight of 58,500 lbs (26,500 kg) [20]. Although 2195 has better properties and a significant weight reduction potential, it was not selected for the core stage of the SLS rocket due to its high cost, with friction stir welded (FSW) aluminum 2219 being selected instead. Type 304, 310, and 316 austenitic stainless steel alloys are another preferred material for cryogenic tanks due to their high strength, weldability, resistance to hydrogen embrittlement, and low cost. Fiber-reinforced polymers are also investigated as candidate materials for the inner cryogenic shells, but the difference in the thermal expansion coefficients of the matrix and fiber materials cause significant stresses, especially under cryogenic conditions [19]. Carbon fibers have a negative coefficient of thermal expansion (CTE), while most polymers have a relatively high and positive CTE. As the fibers expand, the polymer that contracts experiences severe tensile stresses that can generate cracks, which result in leaks and even structural failure. Polymers also have significantly higher hydrogen permeability when compared to metals. The long-term behavior of composites under LH2 conditions is currently under investigation, although progress is slow due to the high complexity and cost of LH2 tests.
The outer shell is generally not subjected to cryogenic temperatures and generally does not come in contact with hydrogen as much as the inner shell. If the outer shell is load bearing, materials with high strength and specific properties are preferred. Metals like aluminum and steel alloys are a common option. Since there is no exposure to cryogenic temperatures, composites may also be selected, as the temperature difference is not high enough for the different CTEs to cause an issue. Carbon fiber composites offer high specific properties, but with a cost penalty. Glass fiber composites can be a less expensive alternative at the cost of lower mechanical properties. Matrix materials can be thermoplastic or thermoset polymers.
The inner tank-supporting structure materials should have a combination of high strength and low thermal conductivity. Various materials may be considered. Metals are a common option, offering high strength. Their high thermal conductivity may be countered by selecting supports with small cross-section area and large equivalent length, increasing their thermal resistance. High-strength polymers are also common. PEEK is a thermoplastic polymer with high strength, but it has a high cost. High-density polyethylene (HDPE) is a less expensive alternative but with a lower strength. Thermoset polymers like bakelite are also viable. Ceramics may also be used due to their high strength, but their high weight renders them less suitable for vehicle applications. As the inner tank-supporting structure experiences high temperature gradients, with cryogenic temperatures on the one side and near ambient conditions on the other, composites are not usually preferred due to the CTE mismatch. A summary of the structural materials and their advantages and disadvantages is presented in Table 1.

Table 1.
Comparison of structural materials.
Several insulation materials like polymers, ceramics, and aerogels may be used. Polymer foams are inexpensive, easily applicable and have extremely low densities. Most foams, though, have poor mechanical properties that degrade after exposure to humidity and solar radiation and, therefore, a protective outer shell should be placed in order to protect them for outdoor and long-term applications. Ceramics are heavy and have higher conductivity, but they have superior mechanical properties. In some cases, ceramic insulation is capable of bearing loads, eliminating the need for an inner tank-supporting structure. Perlite powder is also a common insulator for cryogenic applications, although it has high weight and as a powder it can settle down under dynamic loads, rendering it suitable only for stationary applications. Aerogels are highly porous materials with extremely low thermal conductivity. Their mechanical properties are extremely poor, meaning they should be protected by an outer shell. Aerogels are generally expensive, and their properties are not well documented yet, but they show significant potential for future applications. A summary of the insulation materials and their advantages and disadvantages is presented in Table 2.

Table 2.
Summary of insulation concepts.
3.4. Computational Tools
Finite element methods are usually employed for the analysis of complex structures. Several digital solvers exist offering structural, thermal, and fluid mechanics simulation capabilities. During the late 2010s, finite element analyses of LH2 tanks for aircraft applications became more extensive as LH2 aircraft designs started progressing beyond the conceptual stage. Following the LAPCAT II program, the design and structural analysis of composite LH2 tanks was conducted under the EU-funded Cryogenic Hypersonic Advanced Tank Technologies (CHATT) project. Finite element simulations of the tank provided valuable information regarding the structural and damage tolerance behavior of the four-sphere composite tank [21]. The simulation results were later validated under pressure and thermal loading conditions [22].
In the same time period, there were also LH2 tank integration studies, with the development of finite element simulations of tanks within fuselage sections. A study conducted by Gomez and Smith [23] introduced two aluminum LH2 tanks in the fuselage of the MRT7-3 ‘Meridian’ concept aircraft, one forward and one aft. The developed finite element models of the tanks and fuselage sections contained structural details such as stringers and frames and were capable of estimating boil-off rates and stresses and displacements of the structures under different loading conditions such as pressure, thermal, and flights loads.
The early 2020s saw the development of computational tools capable of investigating and comparing different design concepts and geometries, as interest around independent-type tanks increased to their ability to be introduced into different aircraft. Mantzaroudis and Theotokoglou [24] developed a model capable of conducting the structural and thermal analysis of independent-type foam-insulated double-walled LH2 tanks and drawing conclusions regarding several key performance indicators such as gravimetric index and boil-off rate. The simulations consider temperature-dependent material properties and thermal and pressure loading conditions, although without the inclusion of structural details such as stringers and supports.
The present work describes the development of a computational tool that combines the parametric design approach with the inclusion of structural details such as frames and supporting structures, while also including a preliminary fluid mechanics module that can simulate the behavior of LH2 under acceleration loads. The simulated loading cases are expanded by including aircraft-induced acceleration loads, a critical load case for certification under the Federal Aviation Administration (FAA) 14 CFR or the EASA CS regulations.
4. Description of the Methodology and the Investigated Tank Concept
4.1. Methodology
The design process begins with the definition of the layout and the general requirements of the tank. Parameters such as geometry, dimensions, capacity, insulation efficiency, and integration should be considered first. In the next phase, operational requirements such as storage pressure and limit loads should be defined. In this stage, several regulations should be considered, in order to size the structural elements of the tank accordingly. Materials are selected according to the general layout, operational conditions, manufacturing techniques, and availability. Adequate documentation regarding the mechanical and thermal properties of the materials is required for the operational temperature range in order to increase the accuracy of the simulations. With the conceptual design concluded, the development of the digital simulation may commence. Geometry, material properties, and structural details are introduced to the model in a parametric manner, allowing easy revision. The operational loads and conditions are also introduced in a parametric manner, allowing the investigation of the behavior of the tank under different load scenarios.
The first module of the simulation is the non-linear FE heat transfer analysis. The geometry is meshed with thermal elements, then thermal loads and boundary conditions are introduced, and the solver produces the results of the analysis that can be used for the assessment of the insulation efficiency and calculation of the boil-off rate. The results of the heat transfer analysis are stored in a results file and will be subsequently used as inputs for the structural analysis.
After the conclusion of the heat transfer analysis, the geometry is meshed with structural elements. Structural loads and boundary conditions are introduced along with the heat transfer analysis results. The solver is conducting the structural analysis, with the stress, strain, and displacement results used for the evaluation of the tank concept, verification of the design selection, and design revision. The structural analysis also calculates the total mass of the tank. Structural analysis results may also be used as inputs for subsequent studies such as fatigue and damage tolerance. A brief explanation of the methodology is presented in Figure 3.
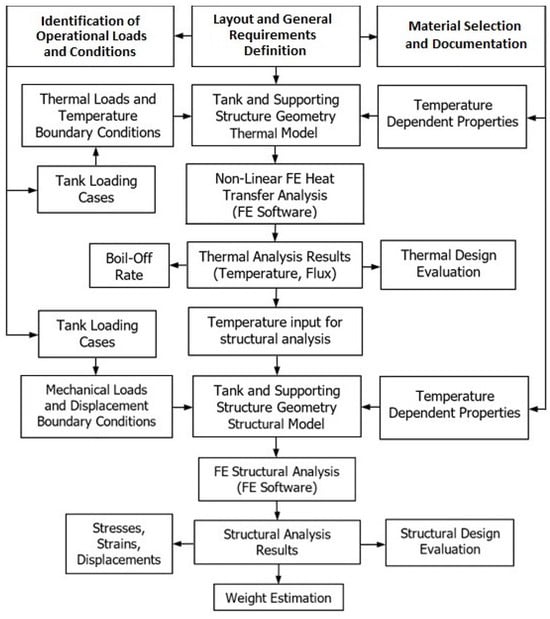
Figure 3.
Flowchart of the methodology for LH2 tank design and analysis used in the present study.
4.2. General Design Prameters
The investigated tank is designed for use in a hydrogen fuel cell-powered commuter aircraft. It is a material-insulated independent-type tank with a double-wall layout in order to protect the insulation. In order to minimize stresses, the tank is cylindrical with spherical domes and stiffened with axial and radial beams. The Embraer EMB-120 Brasilia is a representative aircraft of this category and is considered as a guideline for the design of the tank, regarding dimensions and capacity.
The fuel capacity of the EMB-120 is 2600 kg [25]. Assuming the 2.8 times higher energy density of hydrogen and the 2 times greater thermal efficiency of the hydrogen fuel cells when compared to turboprop engines (average of 60% for fuel cells, 25–35% for turboprop engines) [26,27], the required fuel mass for a similar performance fuel cell aircraft would be around 465 kg of hydrogen. With LH2 having a density of 70 kg/m3 [2] under nominal storage pressures, the tank capacity should be around 6.6 m3. A tank fully filled with a liquid may have a high chance of bursting, as liquids are incompressible, and the slightest deformation will translate to a dramatic increase in the pressure. Therefore, the tank should be filled up to 95% of the total capacity, leaving a 5% ullage volume. In order to meet the above requirements, an internal tank with a volume of 7 m3 is considered.
The fuselage of the EMB-120 has an outer diameter of 2.28 m [25]. For the tank to be able to be fitted inside a similar aircraft, the outer shell diameter should not exceed 2.2 m, leaving a clearance for the supporting structure.
At any given moment in the operation of the aircraft, power should be provided in order to keep the onboard systems operating. Conventional aircraft use an auxiliary power unit (APU) to provide electrical power in emergency cases like an engine failure or during ground operations in order to conserve fuel, as the smaller APU has lower fuel consumption. For the investigated tank concept, power is to be provided by the fuel cell at any given moment, meaning that LH2 will always be consumed during operation. A representative estimate of the minimum required power output of the fuel cell is the power output of the APU. The EMB-120 has a Hamilton-Sundstrand T-62T-40C7E1 turboshaft APU, with a power output of 95 hp (71 kW) [28]. An assumption can be made that the minimum required power output of the fuel cell of a similar performance commuter aircraft is around 70 kW. Assuming a 60% average thermal efficiency for the fuel cell with the lower heating value of hydrogen being 120 MJ/kg [2], the minimum feeding rate of the fuel cell is calculated as per Equation (1):
The tank should have adequate insulation in order to avoid venting hydrogen due to boil-off. Yet, if the loss rate is below 0.972 g/s, none of the hydrogen will be lost as it will be consumed by the fuel cell. With the previously assumed capacity of 465 kg, the maximum acceptable BoR can be calculated as per Equation (2):
Therefore, the insulation should be sized for a BoR of 18% per day, as any better insulation system will only add weight without reducing any actual losses.
According to 14 CFR part 23 § 23.561 [29], for commuter aircraft, the supporting structure of an item of mass outside the cabin that could injure occupants if it came loose must be designed to withstand inertial loads corresponding to the following ultimate load factors: upward, 3.0 g; forward, 9.0 g; sideward, 1.5 g; downward, 6.0 g. The ultimate inertial loads of the tank and its supporting structure are defined by this regulation as it should remain in place without suffering any damage in a survivable crash.
Since no aviation standards for cryogenic tanks exist as of the time of the present work, similar standards for space system applications are considered since the majority of LH2 applications come from space programs, and in both rockets and aircraft, low weight is a major requirement. According to ANSI/AIAA S-080A-2018 [30], metallic pressure vessels of space systems should have a burst factor of at least 2 and a proof factor of at least 1.5, with a minimum design safety factor of 1.4. Therefore, the inner tank should be sized to withstand a pressure of 2 times the maximum expected operational pressure (MEOP) without bursting and 1.5 times the MEOP without any plastic deformation for the temperature where the materials have the worst mechanical properties with a stress safety factor of 1.4, under the maximum inertial loads.
LH2 inside the tank should be stored at a pressure greater than the atmospheric pressure in order to avoid air ingestion and a potential explosion. The internal pressure, though, should not be high in order to avoid stress concentrations and minimize thickness, resulting in a weight reduction. The maximum expected operational internal pressure of the space shuttle external LH2 tank is 34 psia (2.35 bara) [31], meaning it experiences a pressure differential of about 1.34 bar at sea level. The same storage pressure will be considered for the investigated tank. The maximum operating altitude of the EMB-120 is 32,000 ft (9750 m) [32], where the atmospheric pressure is 0.27 bar [33]. Therefore, the MEOP of the investigated tank will be 2.08 bar, when the aircraft is cruising at maximum altitude.
A brief review of the general requirements of the investigated tank is presented in Table 3.

Table 3.
General requirements of the investigated tank.
4.3. Material Selection and Properties
4.3.1. Inner and Outer Shell
Aluminum alloy 2219-T8 is selected as the material for the inner and outer tank shells and their supporting structures. Aluminum 2219 is an aluminum–copper alloy, with some other elements also present in smaller quantities. The exact composition of aluminum 2219 is provided in Table 4.

Table 4.
Composition of aluminum alloy 2219 [34].
As aluminum alloy 2219-T8 is a well-characterized material, its mechanical and thermal properties are documented for a wide temperature range. The properties used as an input for the subsequent simulation are provided in Table 5, Table 6 and Table 7.

Table 5.
Elastic properties of aluminum alloy 2219 [34].

Table 6.
Strength properties of aluminum alloy 2219 [34].

Table 7.
Thermal properties of aluminum alloy 2219 [34].
Friction stir welding (FSW) is the selected welding technique for the investigated tank, as the lower temperatures experienced by the material affect the thermal tempering less than techniques that result in the base metal reaching temperatures above the melting point. This results in increased weld strength. According to a study by Kang et al. [35], the ultimate tensile strength of the 2219-T8 FSW is 353–373 MPa, while the tensile yield strength is 200–217 MPa. When stresses exceed 225 MPa, there is crack initiation which could lead to leaks.
Aluminum alloys are generally resistant to hydrogen embrittlement, yet they can be susceptible under specific conditions. Hydrogen embrittlement can be an issue in the presence of water or humidity mainly at ambient conditions, as aluminum is electrochemically charged in an aqueous environment [36]. However, for a cryogenic tank application, any significant amount of water would solidify at LH2 temperatures and get caught by filters before entering the tank. In dry hydrogen and cryogenic conditions hydrogen embrittlement effects are expected to be negligible [36]. Furthermore, the selected aluminum 2219 alloy has undergone the T8 temper treatment of solution heat treatment, cold working, and artificial ageing; thus, increased resistance to hydrogen embrittlement is to be expected [37,38]. Surface treatment or coatings may also be considered as an additional protective barrier if deemed necessary [37].
4.3.2. Inner Tank Supports
The high-strength thermoplastic PEEK is selected for inner tank supports due to its high strength and low conductivity combination. PEEK is a relatively expensive material, yet it will only be used in small quantities; therefore, it is not expected to have a great impact in the overall cost. Plain Solvay (Brussels, Belgium) KetaSprite® KT-820 NT PEEK is selected, as any reinforcing material would lead to stresses induced by the CTE mismatch as well as increased thermal conductivity. The properties provided by the manufacturer are listed in Table 8.

Table 8.
Solvay KetaSprite® KT-820 NT PEEK properties [39].
The thermal conductivity of PEEK is a function of temperature. The thermal conductivity variation with temperature for plain PEEK is summarized in Table 9.

Table 9.
Thermal conductivity of plain PEEK [40].
4.3.3. Insulation
Low density polyurethane foam is selected as the insulating material as it combines low thermal conductivity, low density, and low cost with easy application. The lowest practical density is the PU32 grade at 32 kg/m3, with the mechanical and thermal properties summarized in Table 10.

Table 10.
Properties of PU32 [41].
5. Heat Transfer Analysis Methodology
The non-linear heat transfer finite element analysis is the first module of the numerical model. The tank geometry is created by a parametric code, with design parameters such as diameter, length, insulation thickness, etc. being variables. The model supports any axisymmetric shape for the tank, yet in this case, a traditional pressure vessel geometry of a cylinder with two spherical domes will be modeled. The tank geometry is subsequently meshed with elements with temperature degrees of freedom. The tank walls are meshed using the triangular options of four-node thermal thin shell elements. Inner and outer wall areas are grouped separately, allowing meshing with different section types. The supporting structure beams are meshed with two-node thermal link elements. The beams are meshed by selecting specific lines of the geometry in a parametric manner. The inner tank-supporting structure tubes and rings made of PEEK are also meshed with thermal link elements. The cross-section area is a required input for these elements, and it has to be the same as the cross-section area of the beams used. The thermal mesh is presented in Figure 4.
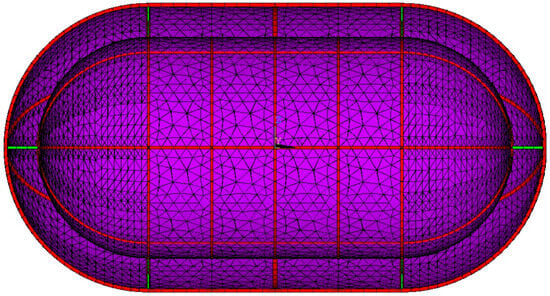
Figure 4.
Thermal mesh. Stiffening structure elements in red; inner tank-supporting structure elements in green; Shell elements in purple.
The insulation is meshed with tetrahedral options of 20-node coupled field higher-order solid elements, with displacement and temperature degrees of freedom activated, that are part of both structural and thermal analysis modules, as seen in Figure 5. Using the same elements for both modules allows the analysis to be conducted in systems with smaller memory capacity, at the expense of longer required time for the analysis process to conclude. A selection was made for 20-node solid elements instead of 8-node ones in order to increase the number of nodes for a more accurate through-the-thickness temperature distribution within the insulation, without increasing the number of elements.
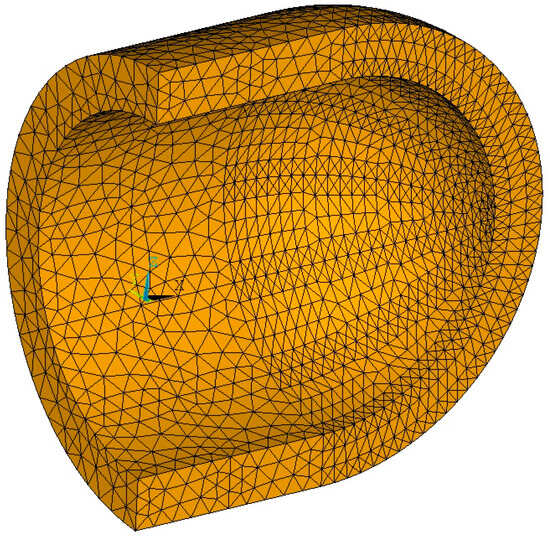
Figure 5.
Coupled field 3-D solid elements.
All the elements used by the heat transfer analysis module are presented in Figure 6.
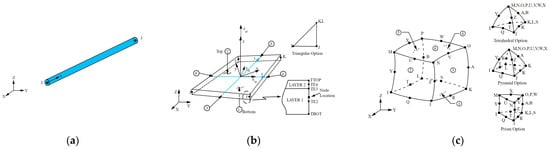
Figure 6.
Thermal module elements [42]. (a) LINK33: 2-node 3-D conduction bar; (b) SHELL131: 4-node 3-D layered thin thermal shell; (c) SOLID226: 20-node 3-D coupled field solid. Numbers in circles indicated faces were thermal loads can be applied.
The surface of the inner tank shell that is in contact with the LH2 is assumed to have the same temperature as the liquid. Therefore, all nodes belonging to elements of the inner tank shell below the surface of the liquid are selected and assigned the boiling temperature of hydrogen for each internal pressure load case as a boundary condition, as shown in Figure 7. The worst thermal load case is LH2 at atmospheric pressure, with a boiling temperature of 20 K.
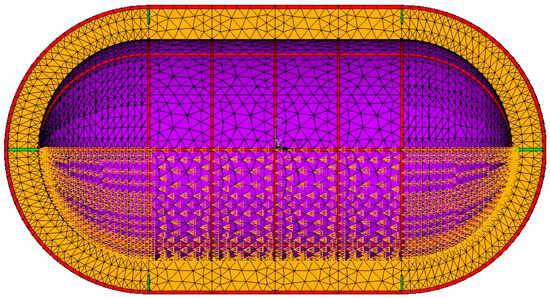
Figure 7.
Temperature boundary conditions for a 50% filing load case.
The outer shell surface is in contact with air inside the aircraft. The main heat transfer mechanism is natural convection, as a flow is induced by buoyancy forces due to temperature differences within the volume of the fluid. The flow in a free convection boundary layer depends on the relative magnitude of buoyancy and viscous forces and it is characterized by the dimensionless Grashof number (Gr), calculated as per Equation (3):
where:
- g is gravitational acceleration
- β is the CTE of the bulk fluid
- is the temperature of the surface
- is the temperature of the bulk fluid
- is the kinematic viscosity of the bulk fluid
- is the characteristic length of the surface
The dimensionless Rayleigh number (Ra) gives the ratio of buoyancy forces and thermal and momentum diffusivities. It is the product of the Grashof number and the Prandtl number (Pr), calculated as per Equation (4):
Convection phenomena are correlated by the dimensionless Nusselt number. The convection coefficient is a function of the Nusselt number (Nu), calculated as per Equation (5):
where k is the thermal conductivity of the bulk fluid.
The Nusselt number can be calculated as a function of the Rayleigh and Prandtl numbers via simple empirical correlations for a variety of known geometries [33]. The outer tank surface can be divided into two sections: the central cylinder and the two spherical domes. Nusselt number correlations are available for both geometries. For the horizontal cylinder, the Nusselt number is calculated as per Equation (6):
The Nusselt number for the sphere is calculated as per Equation (7):
For both geometries the characteristic length is the diameter. The convection coefficient is temperature dependent; therefore, it should be calculated for a certain number of surface temperatures. Air properties at the average temperature should be used when calculating the dimensionless numbers and the convection coefficients for more accurate results. Convection loads are applied on the elements of the outer tank cylinder and domes as seen in Figure 8, using the bulk fluid (ambient air) temperature of 300 K and the parametrically calculated temperature-dependent convection coefficients as inputs.
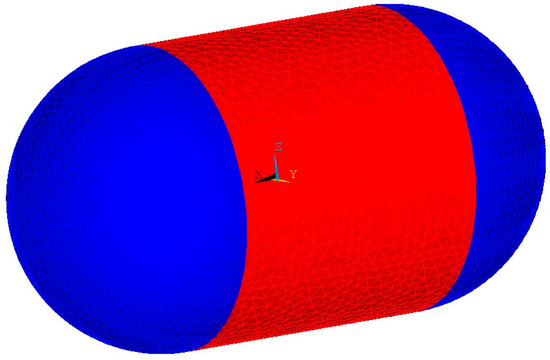
Figure 8.
Convection loads applied. Coefficient for cylinder in red; coefficient for sphere in blue.
With loads and boundary conditions defined, the non-linear heat transfer analysis is conducted. It may take several iterations for the analysis to converge, as the temperature-dependent properties are redefined for each iteration according to the previously calculated temperature. The convergence tolerance criterion is set at 0.5%, meaning the analysis is concluded when an iteration produces results with a maximum divergence in temperature and heat flux values of 0.5% or less when compared to the previous iteration. A mesh convergence study should also be conducted, examining different finite element sizes, with each iteration decreasing the element size, with the mesh assumed converged only when producing results within a 2% margin of the previous mesh. The results of the heat transfer analysis are stored in a separate results file for further use in the structural model. The heat flow toward the LH2 can be calculated by the model as a reaction, and subsequently, the BoR can be calculated. The obtained temperature distributions and heat flow results can be used in order to assess the thermal design of the tank and the efficiency of the insulation.
6. Structural Analysis Methodology
The geometry created for the heat transfer analysis is meshed with elements having structural degrees of freedom. The inner and outer tank shell are meshed using triangular options of 4-node structural thin shell elements with bending and membrane stiffness. As is the case with the thermal elements, inner and outer shell elements are grouped separately, allowing meshing with different section types of different thickness. For each specific structural shell element, the section type and section properties are the exact same as those used for the thermal mesh. The beams are meshed by selecting specific lines, as was the case in the thermal mesh. The 2-node beam elements are used, with structural degrees of freedom. The beam elements require the geometry and specific dimensions of the considered cross-section, as well as its orientation, in order to calculate bending stresses. The coupled field solid elements generated for the heat transfer analysis are retained and used for the structural analysis. The structural mesh is presented in Figure 9.

Figure 9.
Structural mesh. Stiffening structure elements in grey; inner tank-supporting structure elements in yellow; shell elements in blue.
All the elements used by the structural analysis module are presented in Figure 10.
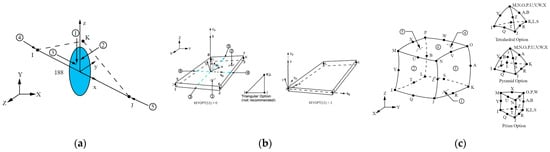
Figure 10.
Structural module elements [42]. (a) BEAM188: 2-node 3-D beam; (b) SHELL181: 4-node 3-D layered thin structural shell; (c) SOLID226: 20-node 3-D coupled field solid. Numbers in circles indicated faces were mechanical loads can be applied.
Mounting points on the outer shell surface are selected and given 0 structural degrees of freedom. The mounting points are parametrically selected, and the preferred locations are the intersections between stiffening beams, shown in Figure 11, as the beams are more capable of bearing concentrated loads.
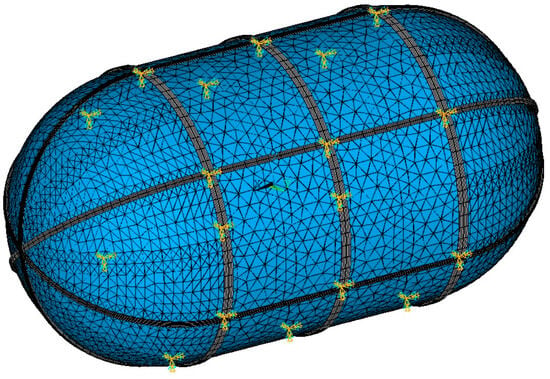
Figure 11.
Zero displacement (cyan) and rotation (orange) boundary conditions on the mounting points with the fuselage.
Acceleration values along all three axes are the first structural load inputs. Triaxial acceleration is subsequently applied to all structural elements. The density of each material is used as an input for all structural elements; therefore, their mass and inertia load under acceleration can be calculated.
Pressure is the major structural load for independent tanks, and it consists of two parts: storage overpressure and hydrostatic pressure. Storage overpressure is a design parameter and model input. However, hydrostatic pressure has to be separately calculated and applied to each element. An array with the numbers of the inner tank shell elements is first created. Each element is individually examined using a loop code. The coordinates of the element centroid are used to calculate the distance between the element and the surface of the LH2, for each specific filling case and acceleration scenario, as the surface is shifting, always remaining vertical to the total acceleration vector. The hydrostatic pressure is calculated as per Equation (8):
where:
- g is the total acceleration
- ρ is the density of the fluid
- is the distance between the element centroid and the surface of the fluid
The hydrostatic pressure is then added to the storage overpressure and, subsequently, the combined pressure is applied to the element. If an element is above the surface, only the storage overpressure is applied. An example of a hydrostatic pressure load case is presented in Figure 12. The hydrostatic pressure is also used to model the inertial load of the LH2, which is combined with the inertial loads of the rest of the structure. The model is limited to static loads; therefore, no dynamic sloshing loads are considered, as this would require a separate computational fluid mechanics module.
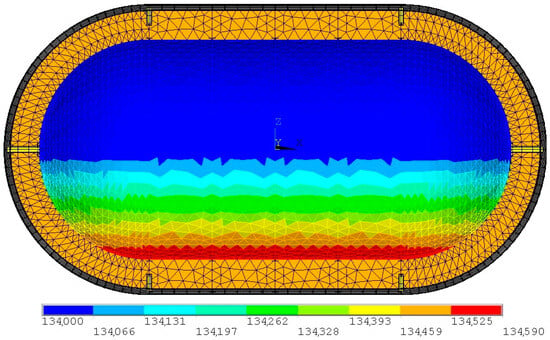
Figure 12.
Pressure loads for a 50% filled tank οf a stationary aircraft on ground. Hydrostatic pressure is affecting only the part under the LH2 surface, with the rest of the tank bearing only the storage overpressure (units in Pa).
The temperature distribution is loaded from the results file of the heat transfer analysis and is used as an input for the structural analysis. The structural and thermal meshes are identical; therefore, temperature values are available for all nodes, without any processing of the temperature distribution required. A reference temperature is defined for thermal strain calculations, and the temperature distribution is used in order to define the temperature-dependent mechanical properties.
The linear structural analysis is subsequently conducted, as the mechanical properties are not dependent on the structural degrees of freedom, since small displacements are expected and the materials are assumed to have linear elastic behavior. As was the case with the heat transfer analysis, a mesh convergence study is conducted. The resulting stresses, strains, and displacements are used in order to assess the structural design, and potential design revisions can be facilitated.
7. Analysis of the Investigated Tank Concept
The design process starts with the thermal design of the tank, which will result in the definition of the required insulation thickness for the target BoR of 18% per day. The outer tank diameter is set at the maximum value of 2.2 m, as this will result in the minimum overall length. The inner tank capacity should also remain constant at 7 m3, as this corresponds to the required amount of fuel. The inner tank-supporting structure is sized in a conservative manner by selecting a hollow circular cross-section with an outer diameter of 5 cm and a thickness of 2.5 mm made out of PEEK. The tank is supported axially by two continuous PEEK tubes and radially by a staggered arrangement of PEEK tubes on a PEEK ring with an I cross-section, with the geometry explained in Figure 13. The overall depth of the rings is 20 mm, the width of the flanges is the same as the tube diameter at 50 mm, and all elements have a thickness of 2.5 mm.
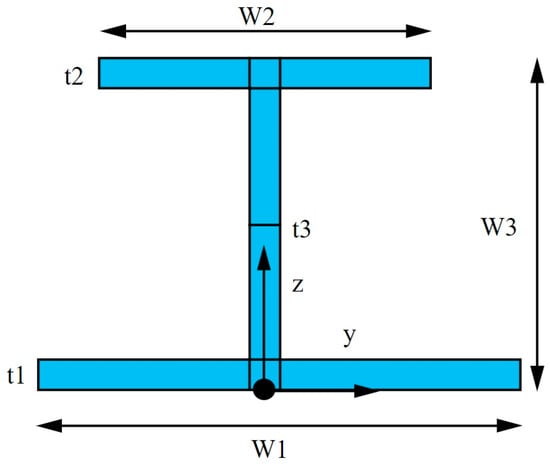
Figure 13.
I cross-section geometry. W1, W2: width of the bottom and top flanges; W3: overall depth; t1, t2: thicknesses of the bottom and top flanges; t3: thickness of the web [42].
The sizing of the aluminum components is not taken into consideration during this early design stage as even moderate changes in thickness will have a negligible impact on thermal performance due to the significantly higher thermal conductivity of aluminum when compared to PEEK or PU32.
Thermal analysis is performed for a fully filled tank at 95% of its volume capacity, as shown in Figure 14, for different insulation thicknesses. With the outer tank diameter and internal volume constant, the overall length is a function of the insulation thickness. Tanks with different insulation thicknesses are presented in Figure 15.
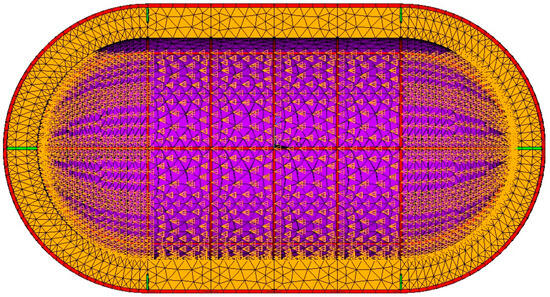
Figure 14.
Temperature boundary conditions (orange triangles) for a 95% filled tank.
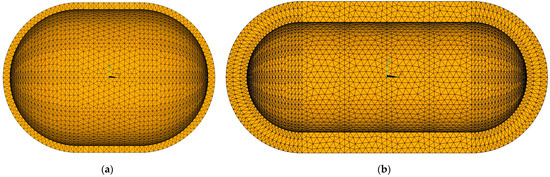
Figure 15.
Comparison of tanks with the same outer diameter and internal volume but different insulation thickness. (a) 10 cm-thick insulation; (b) 30 cm-thick insulation.
Heat flow, total length, total outer surface area, total volume, and insulation mass results are compared for the different investigated thicknesses in Table 11. The boil-off rate is a direct function of the heat flow and is calculated as per Equation (9):
where:

Table 11.
Insulation thickness investigation results.
- is the heat flow
- is the latent heat of vaporization of hydrogen with a value of 445.6 KJ/kg [43]
- is the mass of liquid hydrogen inside the tank at maximum capacity (465 kg for the investigated tank).
While increasing the insulation thickness is supposed to reduce the heat flow, it also increases the outer surface area, as the tank should be lengthened in order to retain the required volume, while compensating for the reduction in diameter. The increased outer surface area consequently increases the heat flow. Therefore, excessively increasing the insulation thickness for a fixed outer diameter and capacity does not significantly improve the thermal performance while only increasing the overall length and weight. Plots of the boil-off rate and insulation mass results from the insulation thickness trade-off study are presented in Figure 16.
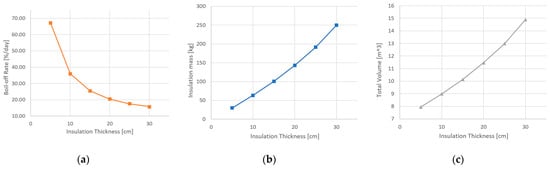
Figure 16.
Plots of the insulation thickness trade-off study results. (a) Boil-off rate; (b) insulation mass; (c) total volume.
The boil-off rate requirement is met by a 25 cm or thicker layer of PU32 insulation. As a further increase in insulation thickness will significantly increase the overall length and weight of the tank without any considerable boil-off rate reduction, the trade-off study is concluded, and a 25 cm-thick insulation layer is selected.
With the insulation thickness selection finalized, inner and outer tank dimensions can be defined next. A summary of the dimensions is provided in Table 12:

Table 12.
Inner and outer tank dimensions.
Both tanks are cylindrical with spherical domes. The domes are concentric, and as a result, both tanks have a 1.95 m long cylindrical section.
The next stage of the design process is the sizing of the inner tank and its stiffening structure. A stiffening structure comprising rings and longitudinal beams is considered in order to reduce stress concentrations resulting from the inertial loads and the shape of the supporting PEEK tubes.
Rings and beams will share the same I cross-section. An overall depth of 30 mm, width of 50 mm defined by the diameter of the supporting PEEK tubes, and a thickness of 3 mm for elements are selected. Overall, five evenly spaced rings will reinforce the cylinder that experiences higher stresses, and six evenly placed longitudinal beams will reinforce the whole inner tank structure.
The thickness of the inner tank wall sections is initially defined by an analytical calculation for thin-walled pressure vessels considering pressure as the only load and not accounting for any stiffening structure. Equations (10) and (11) define the required thickness for a cylindrical and a spherical pressure vessel, respectively.
where:
- is the thickness
- is the pressure
- is the radius
- is the maximum allowable stress of the material
The tank should be sized for a MEOP of 2.08 bar differential pressure. According to ANSI/AIAA S-080A-2018 [30], for a proof pressure of 3.12 bar, stresses should not exceed the yield strength of the Al 2219 welds divided by the stress safety factor (143 MPa). Furthermore, for a burst pressure of 4.16 bar, stresses should not exceed the ultimate strength of the Al 2219 welds divided by the stress safety factor (252 MPa). Although the material strength increases at cryogenic temperatures, the room temperature strength values are considered. The theoretical required thicknesses of the cylinder and the domes for each pressure scenario are summarized in Table 13.

Table 13.
Minimum required thickness of the inner tank wall for the pressure loads.
A thermomechanical analysis is conducted initially considering a cylindrical section of 12-gauge (2.05 mm) aluminum 2219 sheet and two spherical sections of 18-gauge (1.02 mm) aluminum 2219 sheet with the tank subjected to the combined thermal, proof pressure, and inertial loads. The resulting von Mises stress distributions are presented in Figure 17.
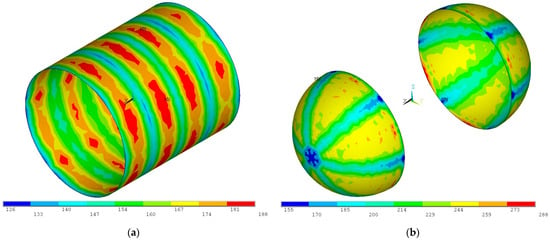
Figure 17.
Von Mises stress distribution for the proof pressure combined loads on (a) the 12-gauge (2.05 mm) cylindrical section and (b) the 18-gauge (1.02 mm) spherical domes (units in MPa).
As seen in Figure 14, the von Mises stresses on all sections of the inner tank exceed the maximum allowed of 143 MPa, as the inner tank wall was sized only for pressure, without considering the other loads. An iterative process is conducted where gradually thicker sheets are examined until the von Mises stresses are reduced to the acceptable value, below 143 MPa.
After several iterations, it has been concluded that the thinnest available aluminum sheets capable of safely bearing the loads are 8 gauge (3.26 mm) for the cylindrical part and 9 gauge (2.91 mm) for the domes, with the von Mises stress distributions presented in Figure 18.
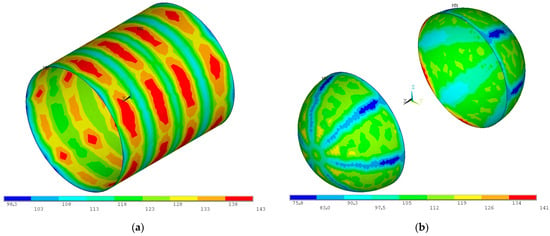
Figure 18.
Von Mises stress distribution for the proof pressure combined loads on (a) the 8-gauge (3.26 mm) cylindrical section and (b) the 9-gauge (2.91 mm) spherical domes (units in MPa).
For the same load case, the inner tank-stiffening structure experiences a maximum stress value of 130 MPa, with the von Mises stress distribution presented in Figure 19.

Figure 19.
Von Mises stress distribution for the proof pressure combined loads on the inner tank-stiffening structure (units in MPa).
With the inner tank sized for a proof pressure differential of 3.12 bar under maximum combined loads, structural analysis is conducted for the burst pressure load of 4.16 bar. As seen in Figure 20, von Mises stresses on the inner tank wall and its stiffening structure do not exceed the maximum allowable stress for burst of 252 MPa; therefore, the inner tank conforms to the ANSI/AIAA S-080A-2018 standard [30].
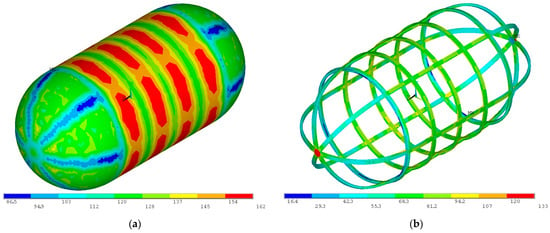
Figure 20.
Von Mises stress distribution for the burst pressure combined loads on (a) the inner tank wall and (b) the inner tank-stiffening structure (units in MPa).
With the inner tank sizing process finished, the outer tank sizing process begins. The outer tank is sized with the same stress safety factor of 1.4 as the inner tank, leading to a maximum allowed stress of 143 MPa as no plastic deformation should be present, with the combined proof pressure, acceleration, and thermal loads applied. The outer tank is stiffened by three evenly spaced rings with an I cross-section. An overall depth of 50 mm, a width of 75 mm, and a thickness of 5 mm for elements are selected. The outer tank-supporting structure also includes six evenly placed longitudinal beams with an I cross-section with an overall depth of 50 mm, a width of 50 mm, and a thickness of 5 mm for elements. After an iterative process, a 14-gauge (1.63 mm) aluminum 2219 sheet is selected for the outer tank shell. Von Mises stress distributions for the combined loads are presented in Figure 21.
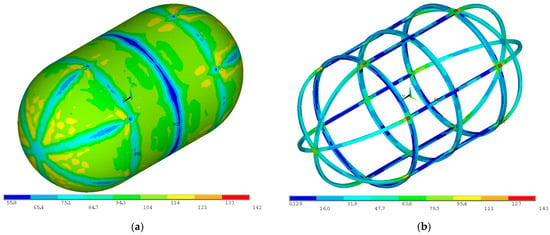
Figure 21.
Von Mises stress distribution for the proof pressure combined loads on (a) the outer tank wall and (b) the outer tank stiffening structure (units in ΜPa).
The inner tank supporting structure will be sized next. An initial analysis is performed with the supporting structure that was defined during the insulation sizing. The stress safety factor is again 1.4, resulting in a maximum allowable stress of 69 MPa. The resulting stresses are presented in Figure 22.

Figure 22.
Von Mises stress distribution for the proof pressure combined loads on the initial inner tank supporting structure (units in ΜPa).
Stresses on the axial supporting tubes are within the limit, yet the radial supports experience low stresses. Therefore, the radial supports are reduced in size, with the I cross-section ring width of the flanges reduced to 40 mm and the thickness of the elements reduced to 2 mm, while retaining the 20 mm depth. The diameter of the axial tubes is reduced to 40 mm, while their thickness is reduced to 1 mm. Since the von Mises stresses on the axial supports is close to the limit value, the axial supporting tube thickness is increased to 3 mm in order to compensate for the overall reduction in stiffness of the radial supports. Von Mises stress distributions on the new supporting structure are presented in Figure 23.
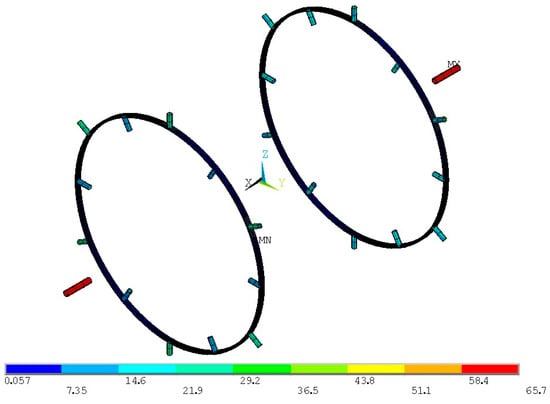
Figure 23.
Von Mises stress distribution for the proof pressure combined loads on the modified inner tank-supporting structure (units in ΜPa).
With all the structural elements sized, a final simulation is conducted with the combined proof pressure loads in order to examine the insulation and identify any potential failures in the PU32 foam that could lead to excess boil-off. As seen in Figure 24, insulation stresses are lower than the tensile strength; therefore, there is no risk of insulation damage. As insulation is not a structural element, a minor flaw will most likely not lead to a catastrophic failure, as the increased boil-off gas can be safely vented through a safety valve.
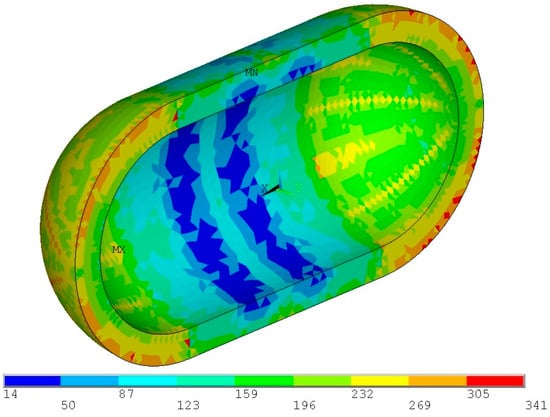
Figure 24.
Von Mises stress distribution for the proof pressure combined loads within the PU32 foam insulation (units in ΚPa).
The final design iteration leads to a heat flow of 419.1 W, which translates to a BoR of 17.48% per day, slightly reduced due to the reduction in the size of the radial supporting structure cross-section. The mesh for both thermal and structural analyses converged for an element size of 10 cm. With von Mises stresses on all structural elements for the combined loads within the limits of the regulations and with the insulation system achieving an acceptable BoR, the design process of the tank can be concluded, and the finalized tank design is presented in Figure 25.
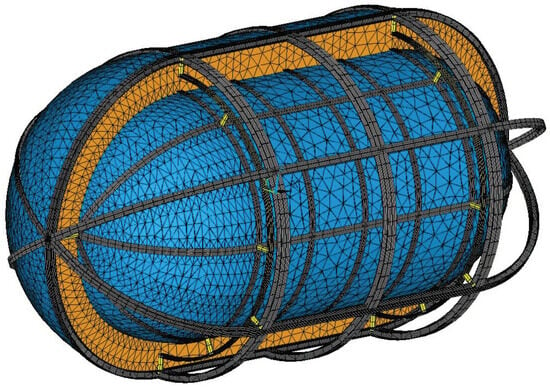
Figure 25.
Cutaway diagram of the finalized tank; tank walls in blue, stiffening members in grey, inner tank supports in yellow and PU32 foam insulation in orange.
The investigated tank concept has been designed for easy integration to commuter aircraft, with the EMB-120 used as a guideline. A conceptual EMB-120 retrofitting study has been performed, placing the LH2 tank in the cargo bay of the 19-seat combined cargo-passenger version, seen in Figure 26a. The majority of the cargo bay space is occupied by the tank, although it still leaves space in the aft for baggage. As there is no need for access to the cargo bay from the cabin, the rear cabin door has been deleted, and in its place, two additional seats have been fitted, increasing the capacity to 21 passengers. The cargo bay windows and emergency exit have also been deleted, as they are no longer needed with the tank occupying this space, contributing to a potential decrease in weight. The tank has been placed as close to the main wings as possible in order to decrease the effect of the constantly reducing fuel mass on the trim of the aircraft, although this effect is less severe with LH2 due to its low density. The 21-passenger concept is presented in Figure 26b.
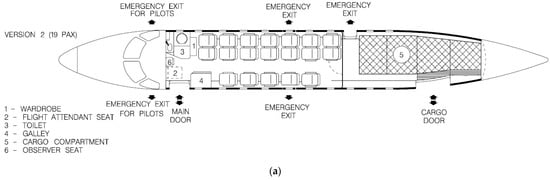
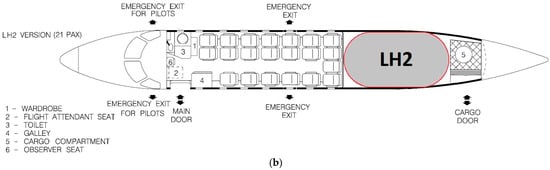
Figure 26.
Fuselage layout of (a) Embraer EMB-120 Brasilia 19-seat combined cargo–passenger version [25]; (b) the proposed concept for an LH2-powered 21-seat commuter aircraft (adapted from [25]).
8. Conclusions and Future Work
An FSW aluminum 2219 LH2 tank has been designed with the assistance of a parametric and multi-physics finite element simulation. The finalized tank has a capacity of 465 kg of LH2, enough for a hydrogen fuel cell-powered commuter passenger aircraft equivalent to the Embraer EMB-120 Brasilia. The overall mass of the tank is 674 kg, excluding piping and peripheral equipment. The cross-sections and masses of each component are described in Table A1. An indicator of the mass efficiency of a tank is the gravimetric index, calculated by dividing the mass of the stored fluid by the combined mass of the fluid and the tank. With the combined LH2 and tank mass at 1139 kg, the gravimetric index is 0.41. The combined mass of LH2 and the tank is less than half of the replaced 2600 kg of fossil fuel. Even when considering the additional mass of piping and valves, there is a significant MTOW reduction for a hydrogen fuel cell aircraft when compared to a conventional one. The weight reduction is estimated around 1 ton, accounting for about 8% of the 12-ton MTOW of the EMB-120. The designed tank indicates that LH2 is a viable aviation fuel for the future and that aluminum 2219 is a serious candidate material for the construction of aviation cryogenic tanks.
The design process was significantly aided by the developed parametric finite element model as design aspects could be easily altered and evaluated. The sizing of each component could be effectively conducted, and an optimal solution could be found after a number of iterations, while also understanding the effect that each component has on the overall performance of the tank, as it was evident that increasing the insulation thickness for a tank with set capacity and outer diameter beyond a certain extent has a minimal effect on the BoR. The simulation also allowed a better understanding of the effects of certain loads, as was the case with the inner tank, where the thickness had to be significantly increased despite being reinforced with longitudinal beams and rings due to the severity of the thermal contraction loads. Beyond component sizing, the model can also predict the behavior of the tank under different operational loading conditions and produce results that could be used for other studies, like the integration into the aircraft and fatigue life predictions.
The current version of the model is capable of applying static and quasi-static loads. Future versions will also include transient loading cases such as filling. The temperature boundary conditions on the inner tank will also be replaced with loads derived from the boiling curve of hydrogen in order to better simulate heat convection and provide more accurate results, especially for the transient loads. The structural module will also be improved with the addition of interface elements capable of simulating connections and welds, in order to improve the accuracy of the results. The geometry of the model will also be updated in order to include several peripheral equipment units that could affect the performance, like piping and endcaps. The next versions of the model will also include a third fluid mechanics module, in order to simulate dynamic phenomena like sloshing, caused by the movement of LH2 inside the tank during maneuvers. The aim of these additions and improvements is to create a digital twin of the tank, being as close to an actual built tank as possible.
Experimental data under combined mechanical and cryogenic conditions of LH2 tanks are rare or even non-existent. In order to assure that the predicted behavior by the tank FE model agrees with the behavior of the actual tank under the specified loading conditions, the results of the model have to be compared to results from experimental campaigns. The validation of the modeling techniques under realistic loading conditions is planned to be conducted in the near future by exploring the experimental data that will be derived in the EU-funded project fLHYing tank [44]. In the frame of fLHYing tank, an independent-type liquid hydrogen tank will be manufactured and flight tested in a hybrid-electric VTOL unmanned cargo aircraft. The thermo–fluid–structural digital twin of the system which is currently under development using the modeling techniques described in the present work will be validated by comparing the simulation results to the experimental data obtained during the flight testing campaign.
Author Contributions
Conceptualization, G.T.; methodology, G.T.; software, G.T.; validation, G.T., K.F. and G.L.; formal analysis, G.T.; investigation, G.T.; writing—original draft preparation, G.T.; writing—review and editing, K.F. and G.L.; visualization, G.T.; supervision, K.F. and G.L. All authors have read and agreed to the published version of the manuscript.
Funding
The present work has been funded by the flight demonstration of a Liquid HYdrogen load-bearing tank in an unmanned cargo platform project (fLHYing tank). This project has received funding from the Clean Aviation Joint Undertaking under the European Union’s Horizon Europe research and innovation program under grant agreement ID 101101946 (https://doi.org/10.3030/101101946).
Data Availability Statement
Results are not available, raw data are cited in text.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Table A1.
Cross-sections, materials, and masses of individual components of the finalized design of the LH2 tank.
Table A1.
Cross-sections, materials, and masses of individual components of the finalized design of the LH2 tank.
| Component | Number | Material | Cross-Section Type | Cross-Section Data | Mass [kg] |
|---|---|---|---|---|---|
| Inner Tank Wall | 1 | Aluminum 2219-T8 | Sheet | Cylinder: 8 gauge (3.26 mm) Domes: 9 gauge (2.91 mm) | 170.103 |
| Inner Tank Rings | 5 | Aluminum 2219-T8 | I beam | Width: 50 mm Depth: 30 mm Thickness: 3 mm | 28.000 |
| Inner Tank Beams | 6 | Aluminum 2219-T8 | I beam | Width: 50 mm Depth: 30 mm Thickness: 3 mm | 29.079 |
| Outer Tank Wall | 1 | Aluminum 2219-T8 | Sheet | 14 gauge (1.63 mm) | 131.745 |
| Outer Tank Rings | 3 | Aluminum 2219-T8 | I beam | Width: 75 mm Depth: 50 mm Thickness: 5 mm | 55.530 |
| Outer Tank Beams | 6 | Aluminum 2219-T8 | I beam | Width: 50 mm Depth: 50 mm Thickness: 5 mm | 64.019 |
| Radial Supports | 24 | PEEK | Tube | Diameter: 40 mm Thickness: 1 mm | 0.478 |
| Supporting Rings | 2 | PEEK | I beam | Width: 40 mm Depth: 20 mm Thickness: 2 mm | 3.057 |
| Axial Supports | 2 | PEEK | Tube | Diameter: 50 mm Thickness: 3 mm | 0.289 |
| Insulation | - | PU32 | Foam | Thickness: 25 cm | 191.445 |
| Total | 673.745 |
References
- Clean Aviation Strategic Research and Innovation Agenda Version December 2021. Available online: https://www.clean-aviation.eu/sites/default/files/2022-01/CAJU-GB-2021-12-16-SRIA_en.pdf (accessed on 21 July 2023).
- Boundy, B.; Diegel, S.; Wright, L.; Davis, S. Biomass Energy Databook, 4th ed.; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2011.
- Saltzman, M. The Hare-Clarke controversy over the invention of the improved gas blowpipe. Bull. Hist. Chem. 2001, 26, 106–111. [Google Scholar]
- Soulen, R. James Dewar, His Flask and Other Achievements. Phys. Today 1996, 49, 32–37. [Google Scholar] [CrossRef]
- Rao, G.A.; Yin, F.; Werij, H. Energy Transition in Aviation: The Role of Cryogenic Fuels. Aerospace 2020, 7, 181. [Google Scholar] [CrossRef]
- Dawson, V.P.; Bowles, M.B. Taming Liquid Hydrogen: The Centaur Upper Stage Rocket 1958–2002; The NASA History Series; National Aeronautics and Space Administration Office of External Relations: Washington, DC, USA, 2004.
- Sheehan, T. Apollo Program Summary Report; National Aeronautics and Space Administration, Lyndon B. Johnson Space Center: Houston, TX, USA, 1975.
- Columbia Accident Investigation Board. Available online: https://web.archive.org/web/20041109135216/http:/spaceflight.nasa.gov/shuttle/archives/sts-107/investigation/CAIB_medres_full.pdf (accessed on 23 January 2024).
- Space Launch System. Available online: https://www.nasa.gov/directorates/esdmd/space-launch-system-ftdku/ (accessed on 23 January 2024).
- PSC “Tupolev”—Cryogenic Aircraft. Available online: https://web.archive.org/web/20130218231656/http://www.tupolev.ru/English/Show.asp?SectionID=82 (accessed on 21 July 2023).
- Westenberger, A. Cryoplane—Hydrogen Aircraft. In Proceedings of the Hydrogen Technology Expo, Hamburg, Germany, 11 October 2003. [Google Scholar]
- Long-Term Advanced Propulsion Concepts and Technologies. Available online: https://cordis.europa.eu/project/id/12282 (accessed on 24 January 2024).
- Achievements Obtained within the European LAPCAT Program. Available online: https://www.esa.int/Enabling_Support/Space_Engineering_Technology/Achievements_obtained_within_the_European_LAPCAT_program (accessed on 24 January 2024).
- Steelant, J.; Langener, T. The LAPCAT-MR2 Hypersonic Cruiser Concept. In Proceedings of the 29th Congress of the International Council of the Aeronautical Sciences, Saint Petersburg, Russia, 7–12 September 2014. [Google Scholar]
- H2FLY Official Website. Available online: https://www.h2fly.de (accessed on 21 July 2023).
- Boeing Unveils Unmanned Phantom Eye Demonstrator. Available online: https://boeing.mediaroom.com/2010-07-12-Boeing-Unveils-Unmanned-Phantom-Eye-Demonstrator (accessed on 21 July 2023).
- Unifier 19 Official Website. Available online: https://www.unifier19.eu/www.unifier19.eu/index.html (accessed on 21 July 2023).
- ZEROe—Towards the World’s First Hydrogen-Powered Commercial Aircraft. Available online: https://www.airbus.com/en/innovation/low-carbon-aviation/hydrogen/zeroe (accessed on 21 July 2023).
- Mital, S.K.; Gyekenyesi, J.Z.; Arnold, S.M.; Sullivan, R.M.; Manderscheid, J.M.; Murthy, P.L. Review of Current State of the Art and Key Design Issues with Potential Solutions for Liquid Hydrogen Cryogenic Storage Tank Structures for Aircraft Applications; NASA Technical Reports Server; NASA: Washington, DC, USA, 2006.
- NASA. Facts—Super Lightweight External Tank. Available online: https://www.nasa.gov/sites/default/files/113020main_shuttle_lightweight.pdf (accessed on 21 July 2023).
- Tapeinos, I.G.; Zarouchas, D.S.; Bergsma, O.K.; Koussios, S.; Benedictus, R. Evaluation of the mechanical performance of a composite multi-cell tank for cryogenic storage: Part I—Tank pressure window based on progressive failure analysis. Int. J. Hydrogen Energy 2019, 44, 3917–3930. [Google Scholar] [CrossRef]
- Tapeinos, I.G.; Rajabzadeh, A.; Zarouchas, D.S.; Bergsma, O.K.; Koussios, S.; Benedictus, R. Evaluation of the mechanical performance of a composite multi-cell tank for cryogenic storage: Part II—Experimental assessment. Int. J. Hydrogen Energy 2019, 44, 3931–3943. [Google Scholar] [CrossRef]
- Gomez, A.; Smith, H. Liquid hydrogen fuel tanks for commercial aviation: Structural sizing and stress analysis. Aerosp. Sci. Technol. 2019, 95, 105438. [Google Scholar] [CrossRef]
- Matzaroudis, V.K.; Theotokoglou, E.E. Computational analysis of liquid hydrogen storage tanks for aircraft applications. Materials 2023, 16, 2245. [Google Scholar] [CrossRef] [PubMed]
- Embraer EMB-120 Brasilia Airport Planning Manual. Available online: https://www.flyembraer.com/irj/go/km/docs/download_center/Anonymous/Ergonomia/Home%20Page/Documents/APM_120.pdf (accessed on 21 July 2023).
- U.S. Department of Energy. Fuel Cell Fact Sheet. Available online: https://www.energy.gov/eere/fuelcells/articles/fuel-cells-fact-sheet (accessed on 21 July 2023).
- Dinc, A.; Gharbia, Y. Exergy analysis of a turboprop engine at different flight altitude and speeds using novel consideration. Int. J. Turbo Jet Eng. 2022, 39, 599–604. [Google Scholar] [CrossRef]
- Auxiliary and Ground Power Systems. Available online: http://www.gelbyson.com/documenti/new/hamilton_sundstrand_hs/Gelbyson_HS_AuxiliaryPowerUnits_APU.pdf (accessed on 21 July 2023).
- U.S. Department of Transportation, Federal Aviation Administration. Code of Federal Regulations, Title 14—Aeronautics and Space, Chapter I—Subchapter C, Part 23—Airworthiness Standards: Normal, Utility, Acrobatic and Commuter Category Airplanes; U.S. Department of Transportation, Federal Aviation Administration: Washington, DC, USA, 2011. [Google Scholar]
- ANSI/AIAA S-080A-2018; Space systems—Metallic Pressure Vessels, Pressurized Structures, and Pressure Components. American National Standards Institute, American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2018.
- READING: The External Tank. Available online: http://www.nasa-klass.com/Curriculum/Get_Training%201/ET/RDG_ET.pdf (accessed on 24 July 2023).
- European Union Aviation Safety Agency (EASA). Type—Certificate Data Sheet for EMB-120. No. EASA.IM.A.188; EASA: Cologne, Germany, 2022.
- Cengel, Y.A.; Ghajar, A.J. Heat and Mass Transfer: Fundamentals and Applications, 5th ed.; McGraw-Hill Education: New York, NY, USA, 2015; pp. 539–542, 956. [Google Scholar]
- Simon, S.; Drexler, E.; Reed, R. Review of Cryogenic Mechanical and Thermal Properties of Al-Li Alloys and Alloy 2219; National Institute of Standards and Technology: Boulder, CO, USA, 1990.
- Kang, J.; Feng, Z.C.; Li, J.C.; Frankel, G.S.; Wang, G.Q.; Wu, A.P. Friction Stir Welding of Al Alloy 2219-T8: Part II—Mechanical and Corrosion. Metall. Mater. Trans. A. 2016, 47, 4566–4577. [Google Scholar] [CrossRef]
- Lee, J.A. Hydrogen Embrittlement; National Aeronautics and Space Administration, Marshall Space Flight Center: Huntsville, AL, USA, 2016.
- Chen, Y.; Zhao, S.; Ma, H.; Wang, H.; Hua, L.; Fu, S. Analysis of Hydrogen Embrittlement on Aluminum Alloys for Vehicle-Mounted Hydrogen Storage Tanks: A Review. Metals 2021, 11, 1303. [Google Scholar] [CrossRef]
- Ishii, Y.; Safyari, M.; Kobayashi, J.; Kuramoto, S.; Itoh, G. Effect of aging treatment temperature on hydrogen embrittlement of 2219 aluminum alloy. Proc. Ibaraki Dist. Conf. 2019, 27, 411. [Google Scholar] [CrossRef]
- ANSYS. ANSYS Mechanical APDL Command Reference; ANSYS Inc.: Canonsburg, PA, USA, 2023. [Google Scholar]
- KetaSpire® KT-820 NT. Available online: https://www.solvay.com/en/product/ketaspire-kt-820-nt-1 (accessed on 24 July 2023).
- Rule, D.; Sparks, L. Low-Temperature Thermal Conductivity of Composites: Alumina Fiber/Epoxy and Alumina Fiber/PEEK; National Institute of Standards and Technology: Boulder, CO, USA, 1989.
- Arvidson, J.; Sparks, L. Thermal and Mechanical Properties of Polyurethane Foams and a Survey of Insulating Concretes at Cryogenic Temperatures; National Institute of Standards and Technology: Boulder, CO, USA, 1984.
- McCarty, R.D.; Hord, J.; Roder, H.M. Selected Properties of Hydrogen (Engineering Design Data), 1st ed.; U.S. Government Printing Office: Washington, DC, USA, 1981; pp. 1–34.
- Flight Demonstration of a Liquid HYdrogen Load-Bearing Tank in an Unmanned Cargo Platform. Available online: https://cordis.europa.eu/project/id/101101946 (accessed on 23 January 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).