Numerical Modeling of Chemical Kinetics, Spray Dynamics, and Turbulent Combustion towards Sustainable Aviation
Abstract
1. Introduction and Background
- To present a wider picture of current modeling capabilities, limitations, and strategies for jet fuels, from laminar flames and ignition to spray dynamics and turbulent combustion.
- To provide an initial discussion of alternative jet fuels in dual-mode ramjet engines based on ignition delay times.
- To present and test a new model for the liquid thermodynamic properties of jet fuels.
- Using new simulation results, to provide novel discussions of the combustion of conventional and alternative jet fuels.
2. Targeted Jet Fuels
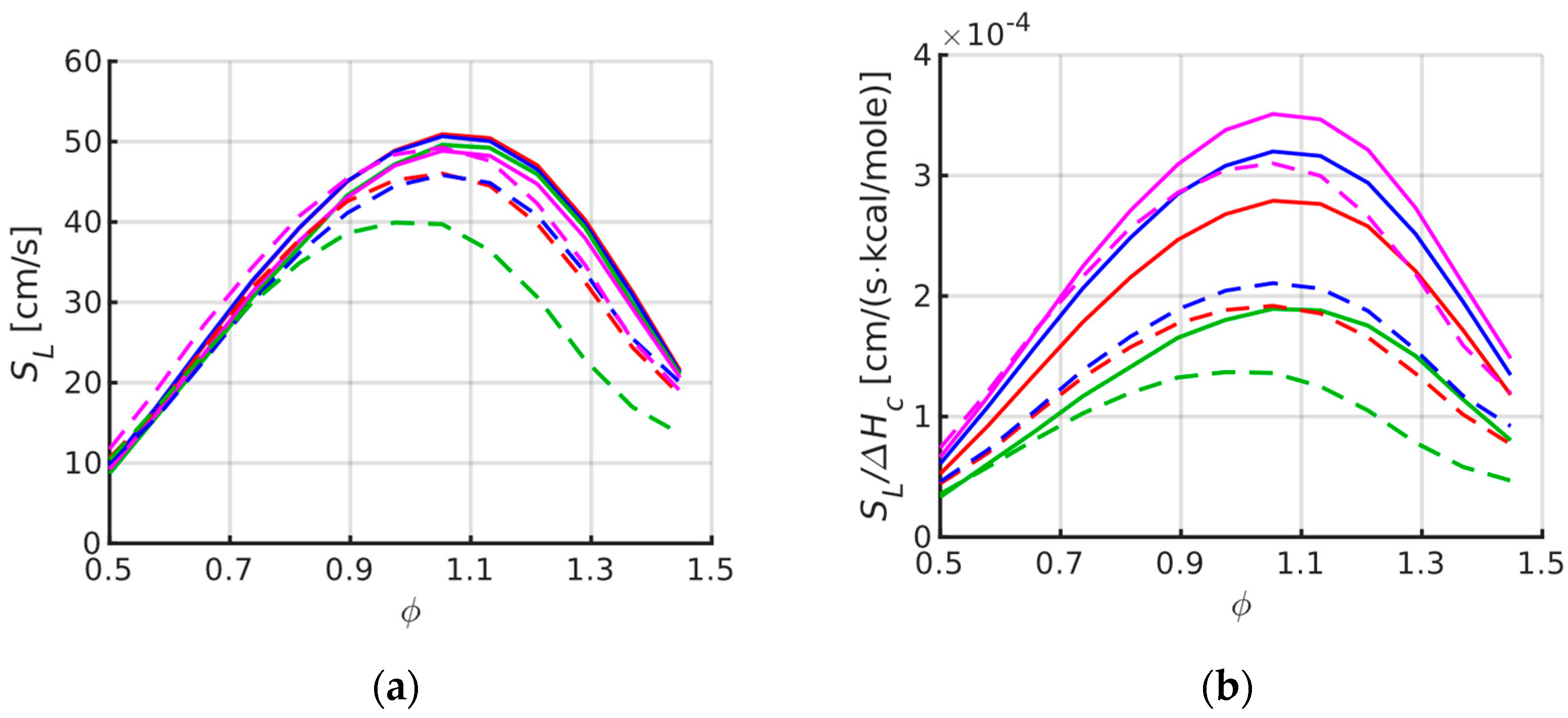
3. Laminar Burning Velocity
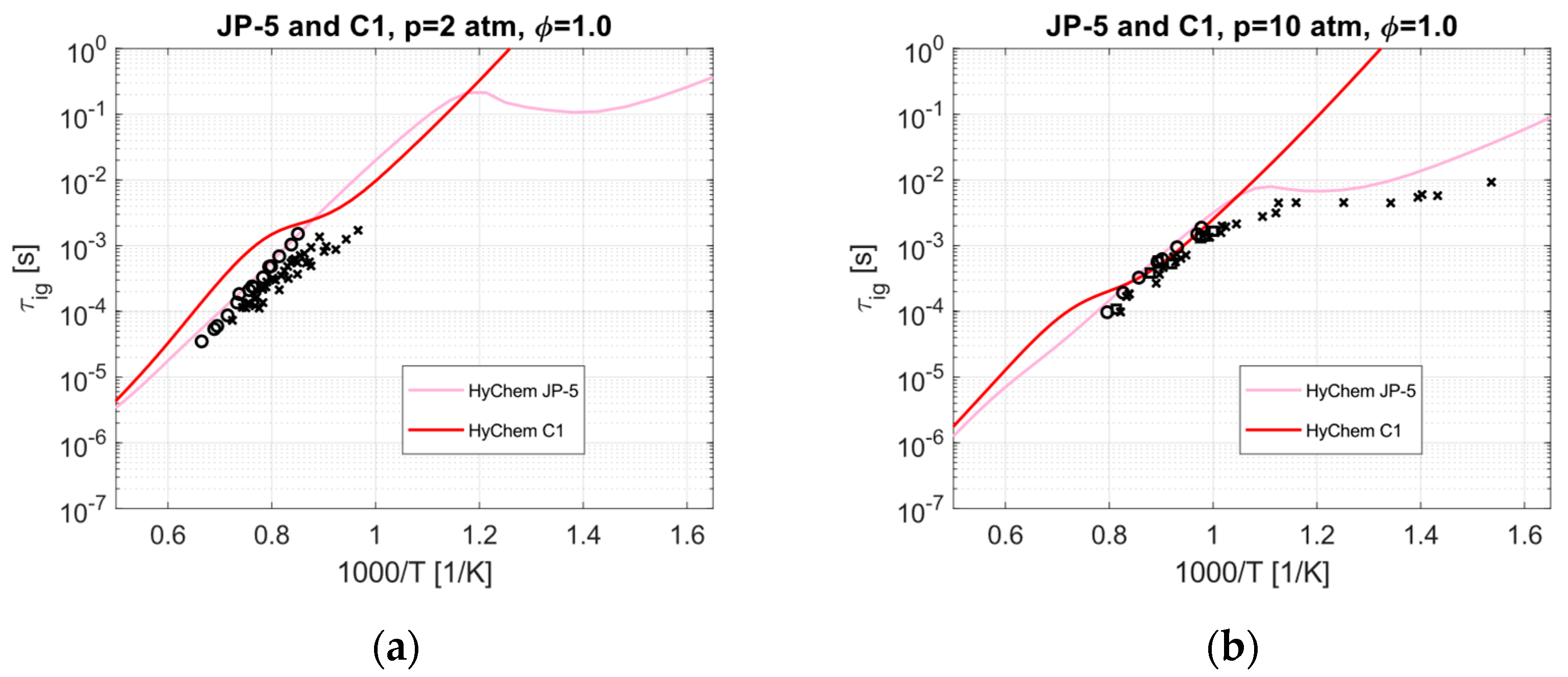
4. Alternative Jet Fuels in Dual-Mode Ramjet Engines Based on Ignition Delay Time
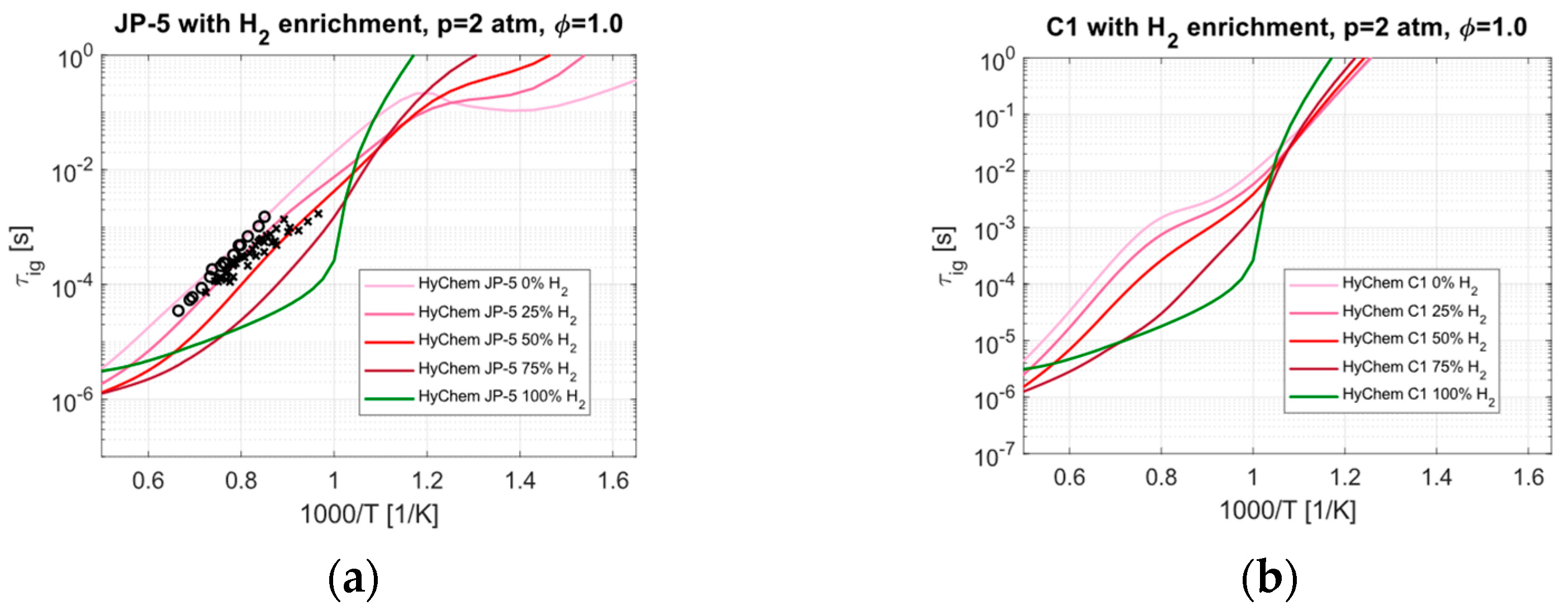
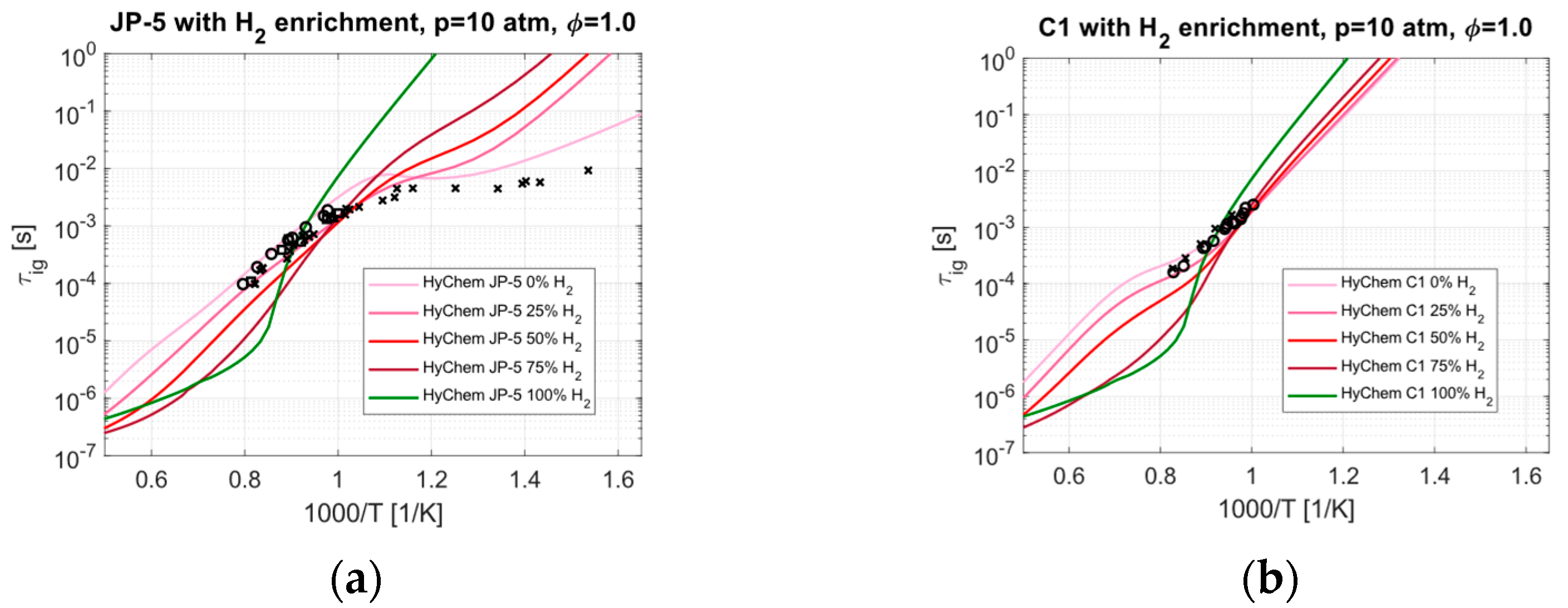
4.1. Hydrogen Enrichment
4.2. Equivalence Ratio Dependence
4.3. Concluding Remarks on Alternative Jet Fuels in Dual-Mode Ramjet Engines
5. Spray Combustion Simulation Methodology
5.1. Large Eddy Simulations
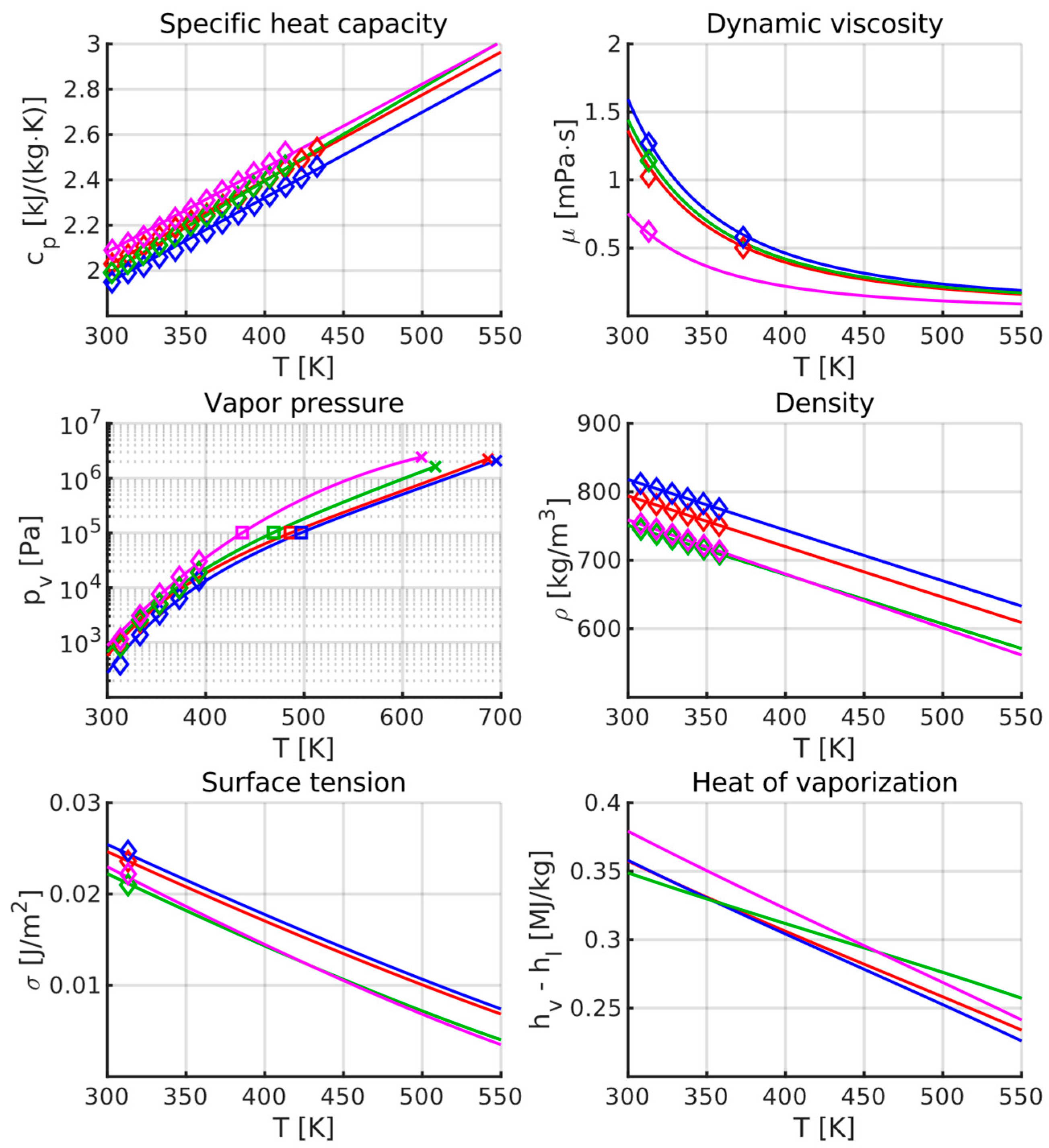
5.2. Liquid Properties Model
- For , we prefer to use identical exponential coefficients for all fuels to avoid potentially large differences as the function is extrapolated beyond the experimental measurements. Linear scaling is instead used to match each fuel to its respective experimental data.
- Esclapez et al. [30] used Watson’s method [68] to derive . This approach requires a representative value for the normal boiling temperature, and the 100% distillation point was used for this purpose in that work. Here we also employ Watson’s method, but for the representative boiling point we use the mass-averaged distillation temperature instead of the 100% distillation temperature. Our method results in a critical temperature of 686.8 K for Jet A and 695.3 K for JP-5, which is close to the critical temperatures of various fossil jet fuels as reported by Yu and Eser [69]. Due to the flat distillation curve of C5, the average and 100% distillation points are approximately the same and result in similar . This is not the case for C1, which consists of 80% C12 iso-paraffins by mass, with the remaining 20% consisting mainly of C16 iso-paraffins. This means that C1 has a flat distillation curve until the 80% mark, where it rises sharply. It is not obvious in this case which boiling temperature should be used, but since 80% of the mass boils at a temperature significantly lower than the 100% distillation point, we consider the mass-averaged boiling point to be the most logical choice. This results in a critical temperature 107 K lower than that computed by Esclapez et al. [30].
- Extrapolating from a limited range of measurements is precarious due to its exponential dependence on temperature. Here we use National Standard Reference Data Series (NSRDS) function 106 [70], which is the standard method in OpenFOAM. The coefficients were derived by curve-fitting to the experimental data, the normal boiling point (i.e., the mass-averaged distillation temperature; see the previous point), and the estimated critical point. The critical pressure, , is obtained from the literature for Jet A [69] and JP-5 [71]. For C1 and C5, it is estimated to be the mass-averaged critical pressure of the individual components of the surrogate compositions suggested by Xu et al. [38]. Although C1 is known to consist primarily of “highly-branched” C12 and C16 iso-paraffins, we were only able to find measurements for n-C12H26 and n-C16H34. This means that is likely underpredicted by up to a few bar for C1, considering the difference between e.g., n-octane ( bar [72]) and one of its highly branched isomers, 2,2,4-trimethylpentane ( bar [73]). Compared to the functions derived by Esclapez et al. [30], at 550 K, our method predicts a vapor pressure that is 5% lower for Jet A, 67% higher for C1, and 44% lower for C5. At 4 bar, it predicts the boiling temperature to be 11 K lower for Jet A, 54 K lower for C1, and 20 K higher for C5. The difference is evidently largest for C1—a consequence of the large difference between its maximum and mass-averaged distillation points.
- In OpenFOAM, and potentially other codes, the fuel vapor enthalpy , the liquid enthalpy , and the heat of vaporization are all assigned separately, forming an overdetermined equation system. The vapor enthalpy for all temperatures is provided by the reaction mechanism, in this case HyChem. The liquid enthalpy and the heat of vaporization are specified in the liquid property model. Care must be taken, then, to ensure that these three properties are consistent with each other; the difference between and must be equal to the heat of vaporization or energy will not be conserved. This also means that separate liquid properties have to be specified for separate reaction mechanisms, even if they target the same fuel. Because the HyChem mechanisms are based on the thermochemical data in Xu et al. [38], we have set the liquid formation enthalpy to be equal to , where is the heat of vaporization computed by Xu et al. [38], based on the aromatics content of each fuel. For other temperatures, the liquid enthalpy is given by the sum of the formation enthalpy and the sensible enthalpy: .
| Property | Jet A | JP-5 | Derivation |
|---|---|---|---|
[J/(kg∙K)] | Linear fit to experimental data. | ||
[kg/m3] | Linear fit to experimental data. | ||
[Pa] | Curve fit with NSRDS function 106 [70], targeting experimental data, estimated normal boiling point, and estimated critical point. | ||
[Pa∙s] | Function obtained from OpenFOAM for n-dodecane, with linear scaling between fuels. | ||
[J/m2] | Obtained from Riazi et al. [74], with linear coefficient chosen to fit experimental data. | ||
[J/kg] | Difference between the fuel vapor enthalpy provided by HyChem [21,22,23] and the liquid enthalpy . The formation enthalpy is based on the data in Xu et al. [38]. | ||
| Tcr [K] | 686.8 | 695.3 | Watson’s method [68] using the average distillation point as boiling temperature. |
| Property | C1 | C5 | Derivation |
|---|---|---|---|
[J/(kg∙K)] | Linear fit to experimental data. | ||
[kg/m3] | Linear fit to experimental data. | ||
[Pa] | Curve fit with NSRDS function 106 [70], targeting experimental data, estimated normal boiling point, and estimated critical point. | ||
[Pa∙s] | Function obtained from OpenFOAM for n-dodecane, with linear scaling between fuels. | ||
[J/m2] | Obtained from Riazi et al. [74], with linear coefficient chosen to fit experimental data. | ||
[J/kg] | Difference between the fuel vapor enthalpy provided by HyChem [21,22,23] and the liquid enthalpy . The formation enthalpy is based on the data in Xu et al. [38]. | ||
| Tcr [K] | 633.4 | 619.3 | Watson’s method [68] using the average distillation point as boiling temperature. |
5.3. Simulation Setup
5.4. Injection Model
6. Spray Combustion Results
7. Outlook on Fuel Effects in Aviation Research
8. Conclusions
- The LBV simulations indicate that in this property there are only small differences, about 5%, between the fuels studied here. LBV in itself can therefore not be exclusively used to explain significant differences between the fuels in their turbulent combustion behavior.
- The IDT predictions show the impact of the cetane number, which is correlated with the NTC effect and can vary significantly between fuels. The related timescales are typically long compared to the residence time of a dual-mode ramjet engine, but the effect could prove critical in the presence of stabilization mechanisms. H2 enrichment is predicted to be an effective method for reducing IDT but not for all temperatures.
- In the LES, the high volatility of the alternative fuels C1 and C5 result in relatively short spray penetration depths and low droplet temperatures while the radial distributions of SMD and velocity are only slightly different between all fuels.
- In the LES, C1 tends to form a flame that is stabilized quite close to the spray while the other fuels burn further away. This is consistent with previous experimental findings, lending credence to the present methodology. The trend is contingent on accurate fuel-specific models for both the liquid fuel and the gas-phase kinetics, as well as the compatibility between these.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Stratospheric Flying Opportunities for High-Speed Propulsion Concepts. Available online: https://cordis.europa.eu/project/id/769246 (accessed on 10 November 2023).
- MDO and REgulations for Low-Boom and Environmentally Sustainable Supersonic Aviation. Available online: https://cordis.europa.eu/project/id/101006856 (accessed on 10 November 2023).
- Available online: https://boomsupersonic.com/ (accessed on 14 November 2023).
- Andreadis, D. Scramjet Engines Enabling the Seamless Integration of Air and Space Operations. Ind. Phys. 2004, 10, 24. [Google Scholar]
- Harrison, R.M.; Masiol, M.; Vardoulakis, S. Civil Aviation, Air Pollution and Human Health. Environ. Res. Lett. 2015, 10, 041001. [Google Scholar] [CrossRef]
- Kärcher, B. Aviation-Produced Aerosols and Contrails. Surv. Geophys. 1999, 20, 113–167. [Google Scholar] [CrossRef]
- Blakey, S.; Rye, L.; Wilson, C.W. Aviation Gas Turbine Alternative Fuels: A Review. Proc. Combust. Inst. 2011, 33, 2863–2885. [Google Scholar] [CrossRef]
- ASTM D1655; Standard Specification for Aviation Turbine Fuels. ASTM: West Conshohocken, PA, USA, 2008.
- Kumar, K.; Sung, C.-J. An Experimental Study of the Autoignition Characteristics of Conventional Jet Fuel/Oxidizer Mixtures: Jet-A and JP-8. Combust. Flame 2010, 157, 676–685. [Google Scholar] [CrossRef]
- MIL-DTL-5624W; Turbine Fuel, Aviation, Grades JP-4 and JP-5. Military and Government Specs & Standards (Naval Publications and Form Center) (NPFC): Philadelphia, PA, USA, 2016.
- MIL-DTL-83133K; Detail Specification: Turbine Fuel, Aviation Kerosene Type, JP-8 (NATO F-34), NATO F-35, and JP-8+100 (NATO F-37). Military and Government Specs & Standards (Naval Publications and Form Center) (NPFC): Philadelphia, PA, USA, 2018.
- Braun-Unkhoff, M.; Riedel, U. Alternative Fuels in Aviation. CEAS Aeronaut. J. 2015, 6, 83–93. [Google Scholar] [CrossRef]
- Yang, J.; Xin, Z.; He, Q.; Corscadden, K.; Niu, H. An Overview on Performance Characteristics of Bio-Jet Fuels. Fuel 2019, 237, 916–936. [Google Scholar] [CrossRef]
- Kick, T.; Herbst, J.; Kathrotia, T.; Marquetand, J.; Braun-Unkhoff, M.; Naumann, C.; Riedel, U. An Experimental and Modeling Study of Burning Velocities of Possible Future Synthetic Jet Fuels. Energy 2012, 43, 111–123. [Google Scholar] [CrossRef]
- Conversion Processes. Available online: https://www.icao.int/environmental-protection/GFAAF/Pages/Conversion-processes.aspx (accessed on 18 December 2023).
- Corporan, E.; Edwards, T.; Shafer, L.; DeWitt, M.J.; Klingshirn, C.; Zabarnick, S.; West, Z.; Striebich, R.; Graham, J.; Klein, J. Chemical, Thermal Stability, Seal Swell, and Emissions Studies of Alternative Jet Fuels. Energy Fuels 2011, 25, 955–966. [Google Scholar] [CrossRef]
- Poinsot, T.; Veynante, D. Theoretical and Numerical Combustion, 2nd ed.; R.T. Edwards, Inc.: Philadelphia, PA, USA, 2005. [Google Scholar]
- Menon, S.; Fureby, C. Computational Combustion. In Encyclopedia of Aerospace Engineering; Blockley, R., Shyy, W., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Patterson, P.M.; Kyne, A.G.; Pourkashanian, M.; Williams, A.; Wilson, C.W. Combustion of Kerosene in Counterflow Diffusion Flames. J. Propuls. Power 2001, 17, 453–460. [Google Scholar] [CrossRef]
- Zettervall, N.; Fureby, C.; Nilsson, E.J.K. A Reduced Chemical Kinetic Reaction Mechanism for Kerosene-Air Combustion. Fuel 2020, 269, 117446. [Google Scholar] [CrossRef]
- Wang, H.; Xu, R.; Wang, K.; Bowman, C.T.; Hanson, R.K.; Davidson, D.F.; Brezinsky, K.; Egolfopoulos, F.N. A Physics-Based Approach to Modeling Real-Fuel Combustion Chemistry—I. Evidence from Experiments, and Thermodynamic, Chemical Kinetic and Statistical Considerations. Combust. Flame 2018, 193, 502–519. [Google Scholar] [CrossRef]
- Xu, R.; Wang, K.; Banerjee, S.; Shao, J.; Parise, T.; Zhu, Y.; Wang, S.; Movaghar, A.; Lee, D.J.; Zhao, R.; et al. A Physics-Based Approach to Modeling Real-Fuel Combustion Chemistry—II. Reaction Kinetic Models of Jet and Rocket Fuels. Combust. Flame 2018, 193, 520–537. [Google Scholar] [CrossRef]
- Wang, K.; Xu, R.; Parise, T.; Shao, J.; Movaghar, A.; Lee, D.J.; Park, J.-W.; Gao, Y.; Lu, T.; Egolfopoulos, F.N.; et al. A Physics-Based Approach to Modeling Real-Fuel Combustion Chemistry—IV. HyChem Modeling of Combustion Kinetics of a Bio-Derived Jet Fuel and Its Blends with a Conventional Jet A. Combust. Flame 2018, 198, 477–489. [Google Scholar] [CrossRef]
- Zettervall, N. Reduced Reaction Mechanisms for Aviation Fuels; FOI-D—1169—SE; FOI: Stockholm, Sweden, 2022; p. 41. [Google Scholar]
- Ranzi, E.; Cavallotti, C.; Cuoci, A.; Frassoldati, A.; Pelucchi, M.; Faravelli, T. New Reaction Classes in the Kinetic Modeling of Low Temperature Oxidation of N-Alkanes. Combust. Flame 2015, 162, 1679–1691. [Google Scholar] [CrossRef]
- Aicholtz, J.; Holland, T.; Andac, G.; Boehm, R.; Seto, S.; Lewis, R.; Williams, R.; Ludwig, D.; James, S.; Mosbacher, M. Development of Combustion Rules and Tools for the Characterization of Alternative Fuels. In Proceedings of the MACCCR 3rd Annual Fuels Summit, Princeton, NJ, USA, 20 September 2010; Available online: https://kinetics.nist.gov/RealFuels/macccr/macccr2010/MACCCR_2010_Colket.pdf (accessed on 14 November 2023).
- Colket, M.; Heyne, J.; Rumizen, M.; Gupta, M.; Edwards, T.; Roquemore, W.M.; Andac, G.; Boehm, R.; Lovett, J.; Williams, R.; et al. Overview of the National Jet Fuels Combustion Program. AIAA J. 2017, 55, 1087–1104. [Google Scholar] [CrossRef]
- Gevo. Available online: https://gevo.com/ (accessed on 14 November 2023).
- Hasti, V.R.; Kundu, P.; Som, S.; Won, S.H.; Dryer, F.L.; Gore, J.P. Computation of Conventional and Alternative Jet Fuel Sensitivity to Lean Blowout. J. Energy Inst. 2022, 101, 19–31. [Google Scholar] [CrossRef]
- Esclapez, L.; Ma, P.C.; Mayhew, E.; Xu, R.; Stouffer, S.; Lee, T.; Wang, H.; Ihme, M. Fuel Effects on Lean Blow-out in a Realistic Gas Turbine Combustor. Combust. Flame 2017, 181, 82–99. [Google Scholar] [CrossRef]
- Panchal, A.; Menon, S. LES of Fuel Sensitivity in a Realistic Spray Combustor I. Near Blowout Analysis. Combust. Flame 2022, 240, 112162. [Google Scholar] [CrossRef]
- Panchal, A.; Menon, S. LES of Fuel Sensitivity in a Realistic Spray Combustor II. Lean Blowout Analysis. Combust. Flame 2022, 240, 112161. [Google Scholar] [CrossRef]
- Guzman, F.J.; Tacina, K.M.; Hicks, Y.R.; Capil, T.; Moder, J.P. Lean Blowout Predictions of a 7-Point Swirler-Venturi Lean Direct Injector Array from Large-Eddy Simulations. In Proceedings of the AIAA Propulsion and Energy 2021 Forum, Virtual Event, 9–11 August 2021. [Google Scholar]
- Sankaran, V.; Lee, J.; Soteriou, M.C. LES Based Evaluation of Multi-Component Fuel Evaporation Effects at Aero-Engine Conditions. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- Tang, Y.; Hassanaly, M.; Raman, V.; Sforzo, B.A.; Seitzman, J. Probabilistic Modeling of Forced Ignition of Alternative Jet Fuels. Proc. Combust. Inst. 2021, 38, 2589–2596. [Google Scholar] [CrossRef]
- Ranjan, R.; Panchal, A.; Hannebique, G.; Menon, S. Towards Numerical Prediction of Jet Fuels Sensitivity of Flame Dynamics in a Swirl Spray Combustion System. In Proceedings of the 52nd AIAA/SAE/ASEE Joint Propulsion Conference, Salt Lake City, UT, USA, 25–27 July 2016. [Google Scholar]
- Edwards, J.T. Reference Jet Fuels for Combustion Testing. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar]
- Xu, R.; Wang, H.; Colket, M.; Edwards, T. Thermochemical Properties of Jet Fuels. 2015. Available online: https://web.stanford.edu/group/haiwanglab/HyChem/approach/Report_Jet_Fuel_Thermochemical_Properties_v6.pdf (accessed on 14 November 2023).
- Kee, R.J.; Miller, J.A.; Jefferson, T.H. CHEMKIN: A General-Purpose, Problem-Independent, Transportable, Fortran Chemical Kinetics Code Package; SAND—80-8003; Sandia National Laboratories: Albuquerque, NM, USA, 1980. [Google Scholar]
- Cantera. Available online: https://cantera.org/ (accessed on 14 November 2023).
- Kim, K.; Lee, W.; Wiersema, P.; Mayhew, E.; Temme, J.; Kweon, C.-B.M.; Lee, T. Effects of the Cetane Number on Chemical Ignition Delay. Energy 2023, 264, 126263. [Google Scholar] [CrossRef]
- Luning Prak, D.J.; Romanczyk, M.; Wehde, K.E.; Ye, S.; McLaughlin, M.; Luning Prak, P.J.; Foley, M.P.; Kenttämaa, H.I.; Trulove, P.C.; Kilaz, G.; et al. Analysis of Catalytic Hydrothermal Conversion Jet Fuel and Surrogate Mixture Formulation: Components, Properties, and Combustion. Energy Fuels 2017, 31, 13802–13814. [Google Scholar] [CrossRef]
- Pinkowski, N.H.; Wang, Y.; Cassady, S.J.; Davidson, D.F.; Hanson, R.K. A Streamlined Approach to Hybrid-Chemistry Modeling for a Low Cetane-Number Alternative Jet Fuel. Combust. Flame 2019, 208, 15–26. [Google Scholar] [CrossRef]
- Zhang, C.; Li, B.; Rao, F.; Li, P.; Li, X. A Shock Tube Study of the Autoignition Characteristics of RP-3 Jet Fuel. Proc. Combust. Inst. 2015, 35, 3151–3158. [Google Scholar] [CrossRef]
- Zeng, W.; Li, H.; Chen, B.; Ma, H. Experimental and Kinetic Modeling Study of Ignition Characteristics of Chinese RP-3 Kerosene. Combust. Sci. Technol. 2015, 187, 396–409. [Google Scholar] [CrossRef]
- Li, A.; Vozka, P.; Mastrean, A.; Kilaz, G.; Qiao, L. Lean flammability limits of alternative aviation fuels. Fire Saf. J. 2019, 108, 102851. [Google Scholar] [CrossRef]
- Gomez Casanova, C.A.; Othen, E.; Sorensen, J.L.; Levin, D.B.; Birouk, M. Measurement of Laminar Flame Speed and Flammability Limits of a Biodiesel Surrogate. Energy Fuels 2016, 30, 8737–8745. [Google Scholar] [CrossRef]
- Zettervall, N.; Fureby, C. A Computational Study of Ramjet, Scramjet and Dual-Mode Ramjet Combustion in Combustor with a Cavity Flameholder. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Meier, U.; Heinze, J.; Freitag, S.; Hassa, C. Spray and Flame Structure of a Generic Injector at Aeroengine Conditions. J. Eng. Gas Turbines Power 2011, 134, 031503. [Google Scholar] [CrossRef]
- Jones, W.P.; Marquis, A.J.; Vogiatzaki, K. Large-Eddy Simulation of Spray Combustion in a Gas Turbine Combustor. Combust. Flame 2014, 161, 222–239. [Google Scholar] [CrossRef]
- Andreini, A.; Bertini, D.; Mazzei, L.; Puggelli, S. Assessment of a Numerical Procedure for Scale Resolved Simulations of Turbulent Spray Flames. In Proceedings of the XXXIX Meeting of the Italian Section of the Combustion Institute, Naples, Italy, 4–6 July 2016. [Google Scholar]
- Puggelli, S.; Bertini, D.; Mazzei, L.; Andreini, A. Assessment of Scale-Resolved Computational Fluid Dynamics Methods for the Investigation of Lean Burn Spray Flames. J. Eng. Gas Turbines Power 2016, 139, 021501. [Google Scholar] [CrossRef]
- Puggelli, S.; Bertini, D.; Mazzei, L.; Andreini, A. Modeling Strategies for LES of Lean Burn Spray Flames. J. Eng. Gas Turbines Power 2017, 140, 051501. [Google Scholar] [CrossRef]
- Mazzei, L.; Puggelli, S.; Bertini, D.; Andreini, A.; Facchini, B.; Vitale, I.; Santoriello, A. Numerical and Experimental Investigation on an Effusion-Cooled Lean Burn Aeronautical Combustor: Aerothermal Field and Emissions. J. Eng. Gas Turbines Power 2018, 141, 041006. [Google Scholar] [CrossRef]
- Puggelli, S.; Paccati, S.; Bertini, D.; Mazzei, L.; Giusti, A.; Andreini, A. Multi-Coupled Numerical Simulations of the DLR Generic Single Sector Combustor. Combust. Sci. Technol. 2018, 190, 1409–1425. [Google Scholar] [CrossRef]
- Åkerblom, A.; Fureby, C. LES modeling of the DLR generic single-cup spray combustor: Validation and the impact of combustion chemistry. Flow Turbul. Combust. 2023. [Google Scholar] [CrossRef]
- Åkerblom, A.; Pignatelli, F.; Fureby, C. Numerical Simulations of Spray Combustion in Jet Engines. Aerospace 2022, 9, 838. [Google Scholar] [CrossRef]
- Kim, W.-W.; Menon, S. A New Dynamic One-Equation Subgrid-Scale Model for LES. In Proceedings of the 33rd Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 1995. [Google Scholar]
- Sabelnikov, V.; Fureby, C. LES Combustion Modeling for High Re Flames Using a Multi-Phase Analogy. Combust. Flame 2013, 160, 83–96. [Google Scholar] [CrossRef]
- Ranz, W.; Marshall, W.R. Evaporation from Drops. Chem. Eng. Prog. 1952, 48, 141–146. [Google Scholar]
- Zuo, B.; Gomes, A.; Rutland, C. Studies of Superheated Fuel Spray Structures and Vaporization in GDI Engines. Int. J. Eng. Res. 2000, 1, 321–336. [Google Scholar] [CrossRef]
- Reitz, R.D.; Diwakar, R. Effect of Drop Breakup on Fuel Sprays. SAE Technol. Pap. 1986, 95, 860469. [Google Scholar]
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A Tensorial Approach to Computational Continuum Mechanics Using Object Orientated Techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Strang, G. On the Construction and Comparison of Difference Schemes. SIAM J. Numer. Anal. 1968, 5, 506–517. [Google Scholar] [CrossRef]
- Issa, R.I. Solution of the Implicitly Discretised Fluid Flow Equations by Operator-Splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
- Hairer, E.; Wanner, G. Solving Ordinary Differential Equations II. Stiff and Differential-Algebraic Problems, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Pignatelli, F.; Passad, M.; Åkerblom, A.; Nilsson, T.; Nilsson, E.; Fureby, C. Predictions of Spray Combustion Using Conventional Category A Fuels and Exploratory Category C Fuels. In Proceedings of the AIAA SCITECH 2023 Forum, National Harbor, MD, USA, 23–27 January 2023. [Google Scholar]
- Watson, K.M. Prediction of Critical Temperatures and Heats of Vaporization. Ind. Eng. Chem. 1931, 23, 360–364. [Google Scholar] [CrossRef]
- Yu, J.; Eser, S. Determination of Critical Properties (Tc, Pc) of Some Jet Fuels. Ind. Eng. Chem. Res. 1995, 34, 404–409. [Google Scholar] [CrossRef]
- Daubert, T.E.; Danner, R.P. Data Compilation Tables of Properties of Pure Compounds; Design Institute for Physical Property Data, American Institute of Chemical Engineers: New York, NY, USA, 1985. [Google Scholar]
- Bucher, W.; Bradley, R. High Temperature Tests of a JP-5 Type Fuel; AD-A007 662; Defense Technical Information Center: Fort Belvoir, VA, USA, 1975.
- Ambrose, D.; Tsonopoulos, C. Vapor-Liquid Critical Properties of Elements and Compounds. 2. Normal Alkanes. J. Chem. Eng. Data 1995, 40, 531–546. [Google Scholar] [CrossRef]
- Daubert, T.E. Vapor-Liquid Critical Properties of Elements and Compounds. 5. Branched Alkanes and Cycloalkanes. J. Chem. Eng. Data 1996, 41, 365–372. [Google Scholar] [CrossRef]
- Riazi, M.R. Characterization and Properties of Petroleum Fractions: Solutions Manual; MNL50; ASTM International: West Conshohocken, PA, USA, 2005. [Google Scholar]
- Spalding, D.B. A Single Formula for the “Law of the Wall”. J. Appl. Mech. 1961, 28, 455–458. [Google Scholar] [CrossRef]
- Agostinelli, P.W.; Laera, D.; Boxx, I.; Gicquel, L.; Poinsot, T. Impact of Wall Heat Transfer in Large Eddy Simulation of Flame Dynamics in a Swirled Combustion Chamber. Combust. Flame 2021, 234, 111728. [Google Scholar] [CrossRef]
- Lefebvre, A.H. Airblast Atomization. Prog. Energy Combust. Sci. 1980, 6, 233–261. [Google Scholar] [CrossRef]
- Mayhew, E.K. Impact of Alternative Jet Fuels on Gas Turbine Combustion Systems. Ph.D. Thesis, University of Illinois at Urbana-Champaign, Champaign, IL, USA, 2018. [Google Scholar]
- Stouffer, S.; Hendershott, T.; Boehm, R.; Lovett, J. Referee Rig. In Fuel Effects on Operability of Aircraft Gas Turbine Combustors; Colket, M., Heyne, J., Eds.; American Institute of Aeronautics and Astronautics, Inc.: Reston, VA, USA, 2021. [Google Scholar]
- Lefebvre, A.H. Fuel Effects on Gas Turbine Combustion—Ignition, Stability, and Combustion Efficiency. J. Eng. Gas Turbines Power 1985, 107, 24–37. [Google Scholar] [CrossRef]
- Shin, D. An Investigation of Alternative Aviation Fuel Spray Characteristics at Lean Blowout Conditions Using Hybrid Air-Blast Pressure-Swirl Atomizer. Master’s Thesis, Purdue University, Indianapolis, IN, USA, 2017. [Google Scholar]
- Shin, D.; Bokhart, A.J.; Rodrigues, N.S.; Sojka, P.E.; Gore, J.P.; Lucht, R.P. Nonreacting Spray Characteristics for Alternative Aviation Fuels at Near-Lean Blowout Conditions. J. Propuls. Power 2020, 36, 323–334. [Google Scholar] [CrossRef]
- Shin, D.; Hasti, V.R.; Bokhart, A.J.; Rodrigues, N.S.; Sojka, P.E.; Lucht, R.P.; Gore, J.P.; Rizk, N.; Corber, P.A. Spray Characteristics of Conventional and Alternative Fuels. In Fuel Effects on Operability of Aircraft Gas Turbine Combustors; Colket, M., Heyne, J., Eds.; American Institute of Aeronautics and Astronautics, Inc.: Reston, VA, USA, 2021. [Google Scholar]
- Boehm, R.C.; Colborn, J.G.; Heyne, J.S. Comparing Alternative Jet Fuel Dependencies Between Combustors of Different Size and Mixing Approaches. Front. Energy Res. 2021, 9, 701901. [Google Scholar] [CrossRef]
- Muthuselvan, G.; Suryanarayana Rao, M.; Iyengar, V.S.; Pulumathi, M.; Thirumalachari, S.; Srinivasan, K. Effect of Atomization Quality on Lean Blow-Out Limits and Acoustic Oscillations in a Swirl Stabilized Burner. Combust. Sci. Technol. 2020, 192, 1028–1052. [Google Scholar] [CrossRef]
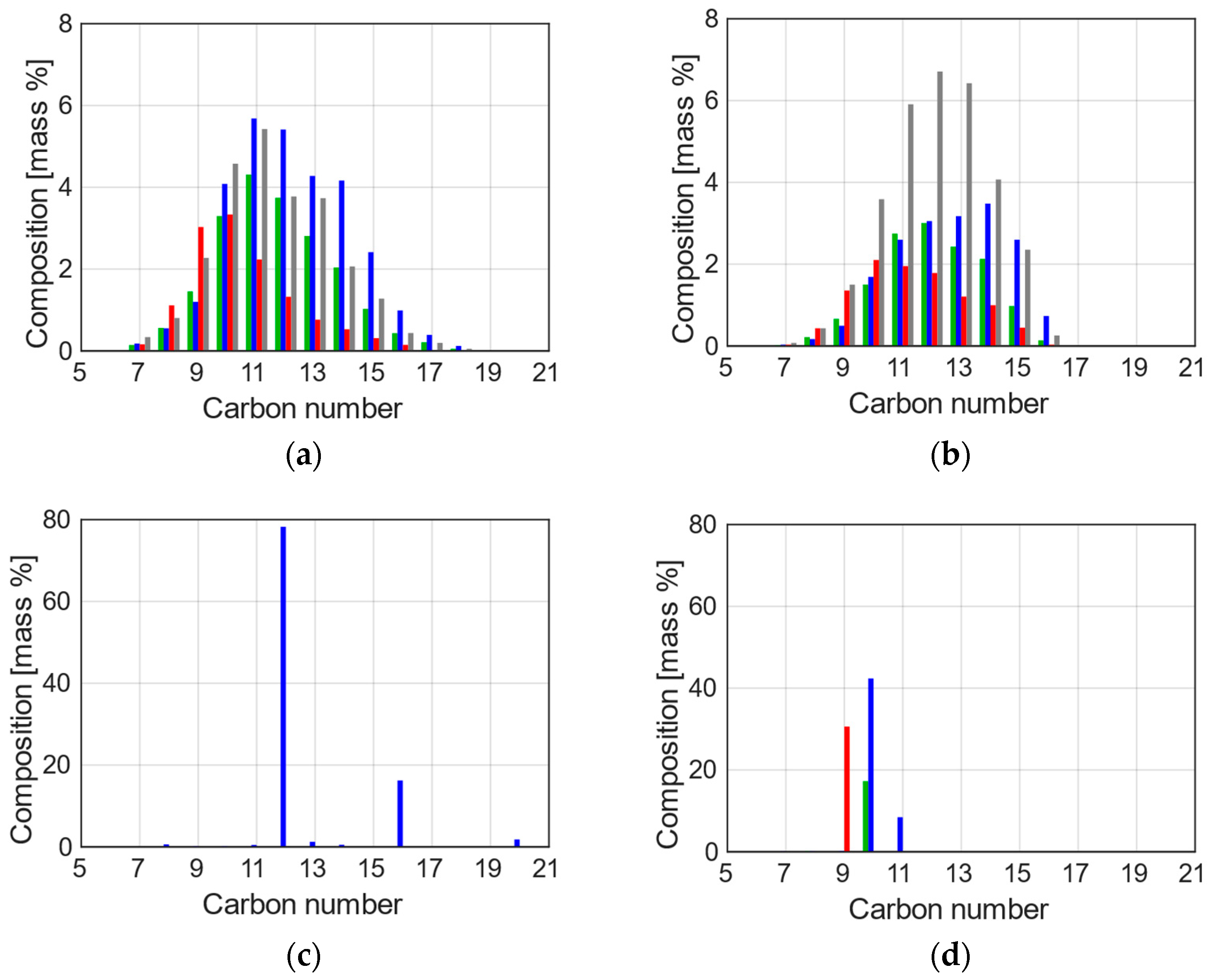






| Property | Jet A | JP-5 | C1 | C5 |
|---|---|---|---|---|
| MW [g/mol] | 158.6 | 166.1 | 178.0 | 135.4 |
| H/C [-] | 1.95 | 1.88 | 2.16 | 1.92 |
| Cetane number [-] | 48.3 | 39.2 | 17.1 | 39.6 |
| Aromatics [mol. %] | 23.42 | 27.35 | - | 34.38 |
| n-paraffins [mol. %] | 19.33 | 13.02 | - | 16.72 |
| iso-paraffins [mol. %] | 26.09 | 15.71 | 100.0 | 48.90 |
| cycloparaffins [mol. %] | 31.16 | 43.92 | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Åkerblom, A.; Passad, M.; Ercole, A.; Zettervall, N.; Nilsson, E.J.K.; Fureby, C. Numerical Modeling of Chemical Kinetics, Spray Dynamics, and Turbulent Combustion towards Sustainable Aviation. Aerospace 2024, 11, 31. https://doi.org/10.3390/aerospace11010031
Åkerblom A, Passad M, Ercole A, Zettervall N, Nilsson EJK, Fureby C. Numerical Modeling of Chemical Kinetics, Spray Dynamics, and Turbulent Combustion towards Sustainable Aviation. Aerospace. 2024; 11(1):31. https://doi.org/10.3390/aerospace11010031
Chicago/Turabian StyleÅkerblom, Arvid, Martin Passad, Alessandro Ercole, Niklas Zettervall, Elna J. K. Nilsson, and Christer Fureby. 2024. "Numerical Modeling of Chemical Kinetics, Spray Dynamics, and Turbulent Combustion towards Sustainable Aviation" Aerospace 11, no. 1: 31. https://doi.org/10.3390/aerospace11010031
APA StyleÅkerblom, A., Passad, M., Ercole, A., Zettervall, N., Nilsson, E. J. K., & Fureby, C. (2024). Numerical Modeling of Chemical Kinetics, Spray Dynamics, and Turbulent Combustion towards Sustainable Aviation. Aerospace, 11(1), 31. https://doi.org/10.3390/aerospace11010031








