Velocity Observer Design for Tether Deployment in Hamiltonian Framework

Abstract

This paper presents a nonlinear velocity observer of tether deployment using the immersion and invariance technique, and the velocity observer design problem is recast as a problem of designing an attractive and invariant manifold inside the Hamiltonian framework. The passivity-based control theory is used to define an expected Hamiltonian function, and the stability of the designed velocity observer is addressed by using the passivity-based methodology. Finally, a simple tension control law with measurable and unmeasurable states is employed for controlling the tether deployment, where the unmeasurable states use the proposed velocity observer. Numerical simulations demonstrate that the proposed velocity observer is working successfully. Sensitivity analyses are conducted to test the effectiveness and robustness of the proposed velocity observer.

1. Introduction

Space tether technology has been applied in a wide variety of applications, such as propulsion systems [1,2,3], power generation [4,5], micro-gravity experimentation [6,7], and tether transportation systems [8,9,10]. The issue of the deployment and retrieval of space tethers is crucial to space tether missions [11,12,13,14]. Many advanced control strategies have been applied to achieve a stable and fast deployment; however, it is difficult to achieve it entirely successful because the libration angle of the tether changes dramatically with high speed under the Coriolis force and other perturbed disturbances [15,16]. Meanwhile, many pieces of research have been carried out to investigate the chaotic behavior of the system, caused by the eccentricity of the orbit and out-of-orbital plane roll motion of the tether [17,18]. Unconsidered external force (atmosphere drag [19]) disturbance can also cause the instability of tethered satellites.

In past decades, many efforts have been devoted to designing the control law using different control methodologies, and they can be categorized into two parts in terms of measurable and unmeasurable states: full-state feedback [15,20,21,22] and partial-state feedback [16,23]. Among them, the tension control law with full-state feedback has been proven to be successful in realistic space missions [6,12,15]. For example, a mission function-based control law was proposed to suppress the libration motion in the tether deployment process [12]. Furthermore, a fractional-order term replacing the corresponding integer-older term inside Pradeep’s tension control law [24] has been applied to ensure a stable and fast deployment dynamic [15], and it has been theoretical proven that the fractional-order is a subset of the integer-order counterpart and has a more stable region. Recently, to ensure the explicit non-negative velocity constraint of tether length, a novel tension control law based on the invariance principle of the control system has been proposed [20], and numerical simulation results show that the tether deployment is smooth and fast and the velocity of the tether length is kept positive. The sliding mode control method [22] has also been adapted in the deployment and retrieval process to address robustness against external disturbance and the low sensitivity of model parameter uncertainties. Following that, a combination of fractional-order and sliding model controllers has also been proposed to address the unmodeled dynamics of the tether deployment [21,25]; for example, the frictional force between the loading equipment and the tether. However, it is noted that there is one assumption in the previous controller; the feedback state is directly measurable, which is challenging in a real mission due to the lack of available sensors [6]. In addition to the full-state feedback control law, a tension control law with partial-state feedback is highly desirable, as mentioned in Refs. [23,26]. Meanwhile, a simple analytical control law with partial state feedback based on the energy storage function is proposed in Ref. [16], in which only the tether length and its rate are measurable. Numerical simulation results demonstrate that a better performance is achieved against the fractional-order counterpart [15].

In addition to the controller design using different methodologies, there are also some works related to the measurement model of the measurable state. As presented in Refs. [13,27], the states of tether deployment dynamics were estimated based on the measurement data from onboard cameras and GPS. It is noted that the estimated state may be inaccurate, leading to accidental unsuccessful tether deployment. For example, the YES2 experiment was not entirely successful because of errors in estimating the tether velocity [28]. It is important that the estimation algorithm of the unmeasurable state be adopted to ensure successful tether deployment. Many efforts have been devoted to developing the estimation algorithm for the unmeasurable state of the tether system. For example, the Kalman filter algorithm has been employed to estimate the unmeasurable states of the tether system [26,29,30]. It is simple, straightforward, and easy to implement. However, the defect of this algorithm is apparent, and a significant computational load is required to process a set of sampling points [29]. The immersion and invariance (I&I) technique [31] has also been explored to estimate the unmeasurable states of the STS [32] because it is a constructive methodology that has been widely adopted in many dynamic nonlinear systems [33]. In Ref. [32], the I&I technique has been used to propose a velocity observer to estimate the libration angle (in-plane and out-of-plane) velocities of an electrodynamic tether system. It should be noted that the measurement model of the unmeasurable state can be analytically derived by solving a nonlinear partial differential equation, and this has been proven to be estimated accurately [34].

In this paper, the I&I technique is applied to design the velocity observer for tether deployment. However, compared to the work presented in [32], it is difficult and challenging to construct a Lyapunov candidate because it highly depends on the author’s experience and familiarity with the target system. In order to address the complexity of constructing a Lyapunov candidate, the velocity observer error system is converted into a generalized Hamiltonian framework. To the best of the authors’ knowledge, this is the first attempt to present a velocity observer design inside a Hamiltonian framework. Inspired by the Hamiltonian theory and passivity method [23], an attractive and invariant manifold observer is converted into an extended Hamiltonian framework. Therefore, the velocity observer design problem is recast as the problem of designing an attractive and invariant manifold inside a Hamiltonian framework, and the attractivity of the proposed manifold can be achieved by solving a formed partial differential equation [35]. Passivity-based control can be directly used to derive an expected Hamiltonian function, and the Hamiltonian storage energy function can be taken as an ideal Lyapunov candidate [36].

The rest of the paper is organized as follows: Section 2 illustrates the dynamics of tether deployment. Section 3 proposes a nonlinear velocity observer and presents the stability proof, and the proving process is explained in two parts to enhance readability. In Section 4, numerical simulations are carried out to show the effectiveness and robustness of the proposed velocity observer. Finally, Section 5 concludes the paper.

2. Dynamic System Description and Preliminaries

In this paper, as shown in Figure 1, the space tether system is supposed to be a long, thin cable with two connecting spacecraft at each end. As presented in Refs. [15,25], the system is modeled as a dumbbell model consisting of two end spacecraft connected by a straight tether with a variable length, $l$, and the spacecrafts are modelled as lumped masses without attitude dynamics. We focus on the in-plane motion since the out-of-plane motion is small compared to its counterpart [23]. The mass of the tether can be ignored compared to the mass of the spacecraft. The Lagrange’s equation is applied to derive the governing equations of the tether deployment [12,16], and they are written as

$$\begin{array}{c}{l}^{″}-l\left[{\left({\theta }^{\prime }+\Omega \right)}^2+{\Omega }^2\left(3{\cos }^2\theta -1\right)\right]=-\frac{T}{m}\\ l^2{\theta }^{″}+2l\dot{l}\left(\Omega +{\theta }^{\prime }\right)+\frac{3}{2}{l}^2{\Omega }^2\sin 2\theta =0\end{array}$$

(1)

where ${\left(\cdot \right)}^{\prime }$ represents the derivative with respect to time, $l$ indicates instantaneous tether length, $\theta$ is the in-plane (pitch) angle, $\Omega$ denotes the orbital rate of the system, and $T$ is the tension of the tether. $m=m_1{m}_2/\left(m_1+m_2\right)$ is the equivalent mass, with $m_1$ and $m_2$ being the masses of the main and the sub spacecraft, respectively.

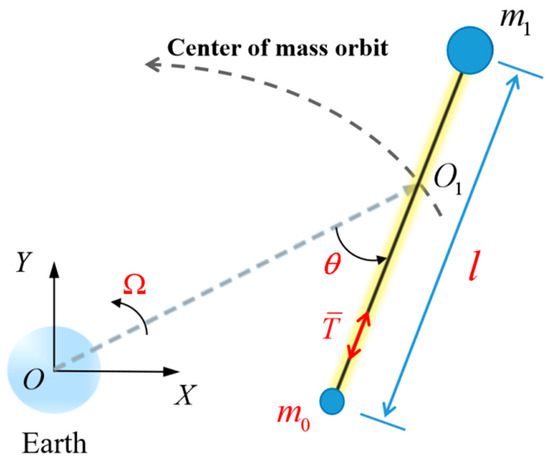
Figure 1. Schematic diagram of the space tether system.

The following non-dimensional variables are defined to non-dimensionalize Equation (1),

$$\lambda =l/l_n, \tau =\Omega t, \tilde{T}=T/\left(m{l}_n{\Omega }^2\right)$$

(2)

where $\lambda$ denotes the dimensionless tether length, with $l_n$ being the total length of the tether, and it satisfies $0<\lambda \le 1$. $\tau$ represents the dimensionless time and $\Omega$ is the angular velocity of the system.

Substituting Equation (2) into Equation (1) generates the following dimensionless equations,

$$\begin{array}{c}\ddot{\lambda }-\lambda \left[{\left(\dot{\theta }+1\right)}^2-1+3{\cos }^2\theta \right]=-\tilde{T}\\ {\lambda }^2\ddot{\theta }+2\lambda \dot{\lambda }\left(1+\dot{\theta }\right)+3{\lambda }^2\sin \theta \cos \theta =0\end{array}$$

(3)

where $\stackrel{·}{\left(\cdot \right)}$ denotes the derivative with respect to the dimensionless time, $\tau$.

Here, Equation (3) is rewriten into a compact form,

$$M\left(q\right)\ddot{q}+C\left(q,\dot{q}\right)\dot{q}+G\left(q\right)=u$$

(4)

with

$$M\left(q\right)=\left[\begin{array}{cc}1& 0\\ 0& {\lambda }^2\end{array}\right], C\left(q,\dot{q}\right)=\left[\begin{array}{cc}0& -\lambda \left(\dot{\theta }+2\right)\\ \lambda \left(\dot{\theta }+2\right)& \lambda \dot{\lambda }\end{array}\right], G\left(q\right)=\left[\begin{array}{c}-3\lambda {\cos }^2\theta \\ \frac{3}{2}{\lambda }^2\sin 2\theta \end{array}\right]$$

(5)

where $q={\left(\lambda ,\theta \right)}^T$ and $\dot{q}={\left(\dot{\lambda },\dot{\theta }\right)}^T$ are vectors of position and its rate, respectively, and $u={\left(-\tilde{T},0\right)}^T$ is the control input vector. $M\left(q\right)=M^T\left(q\right)>0$ is the generalized inertia matrix, $C\left(q,\dot{q}\right)$ is the Coriolis and Centrifugal forces matrix, and $G\left(q\right)$ is the force vector due to its gravity.

The following variables are defined to implement coordinate transform,

$$\left\{\begin{array}{l}x=R\left(q\right)\dot{q}\\ y=q\end{array}\right.$$

(6)

where $R\left(q\right)$ is an introduced factorization of the generalized inertia matrix [37], namely,

$$M\left(q\right)=R^T\left(q\right)R\left(q\right)\mathrm{and} R\left(q\right)=\left[\begin{array}{cc}1& 0\\ 0& \lambda \end{array}\right]$$

(7)

The following mappings, $L:{\mathbb{R}}^2\to {\mathbb{R}}^{2\times 2}$ and $F:{\mathbb{R}}^2\times {\mathbb{R}}^2\to {\mathbb{R}}^2$, can be defined as

$$L\left(q\right)=R^{-1}\left(q\right) \mathrm{and} F\left(q,u\right)=R^{-T}\left(q\right)\left[u-G\left(q\right)\right]$$

(8)

It is noted that the values $q$ and $u$, listed in Equation (8), are the known values, which means the above defined equations, $L\left(q\right)$ and $F\left(q,u\right)$, are the known mappings.

Taking the derivative with respect to non-dimensional time for Equation (6), the following variables with a state-space form are formed,

$$\left\{\begin{array}{l}\dot{y}=L\left(y\right)x\\ \dot{x}=S\left(x,y\right)x+F\left(y,u\right)\end{array}\right.$$

(9)

where $S\left(x,y\right)$ is a mapping matrix, and it consists of two parts: the constant part and the parameter part.

The following lemma are first given before presenting the velocity observer; the interested readers can find the detailed proofing part in [37].

Lemma 1.

The mapping matrix $S\left(x,y\right)$ is defined as

$$S\left(x,y\right)=\left[\dot{R}\left(q\right)-R^{-T}\left(q\right)C\left(q,\dot{q}\right)\right]R^{-1}\left(q\right)$$

(10)

where $S\left(x,y\right)$ decomposes into two parts, the constant part, $S_1$, and the parameter part, $S_2\left(x,y\right)$,

$$S_1=\left[\begin{array}{cc}0& 2\\ -2& 0\end{array}\right]\mathrm{and} S_2\left(x,y\right)=\left[\begin{array}{cc}0& \frac{x_2}{y_1}\\ -\frac{x_2}{y_1}& 0\end{array}\right]$$

(11)

where $S_1$ is a constant and skew-symmetric matrix. $S_2\left(x,y\right)$ has the following three properties:

(i) 

$S_2\left(x,y\right)$ is a skew-symmetric matrix, $S_2=-S_2^T$;

(ii) 

$S_2\left(x,y\right)$ is a linear function about the first argument, $S_2\left(a{x}_1+b{x}_2,y\right)=a{S}_2\left(x_1,y\right)+b{S}_2\left(x_2,y\right)$ for $x_1,x_2\in {\mathbb{R}}^2$ and  $a,b\in {\mathbb{R}}^2$;

(iii) 

There exists mapping ${\overline{S}}_2:{\mathbb{R}}^2\to {\mathbb{R}}^{2\times 2}$, $S_2\left(x,y\right)\overline{x}={\overline{S}}_2\left(\overline{x},y\right)x$ for all $y,x,\overline{x}\in {\mathbb{R}}^2$.

3. Proposed Velocity Observer

In this section, a detailed derivation process of the proposed velocity observer is presented.

Theorem 1.

Considering Equation (4), an exponentially convergent velocity observer will be presented, with unmeasurable state $x\in {\mathbb{R}}^2$, measurable output state $y\in {\mathbb{R}}^2$, and input $u\in {\mathbb{R}}^2$,

$$\dot{\chi }=A\left(\chi ,q,u\right)$$

(12)

where $\chi$ is the designed observer and $A$ denotes an existing smooth observer mapping.

3.1. Velocity Observer Design

In this paper, the immersion and invariance (I&I) theory is employed to design the velocity observer [35,38]. Here, a manifold, $\pi$, for the tether system listed in Equation (9) is given,

$$\pi :=\left\{\left(y,x,\eta ,\widehat{y},\widehat{x}\right):\eta +\beta \left(y,\widehat{y},\widehat{x}\right)-x=0\right\}\subset {\mathbb{R}}^2$$

(13)

where $\eta ,\widehat{y}\in {\mathbb{R}}^2$ denotes the dynamic part of the observer state, $\beta \left(y,\widehat{y},\widehat{x}\right):{\mathbb{R}}^2\times {\mathbb{R}}^2\times {\mathbb{R}}^2\to {\mathbb{R}}^{2\times 2}$ is a defined mapping that will be provided later, and $\widehat{x}$ is an estimate of the state $x$,

$$\widehat{x}=\eta +\beta \left(y,\widehat{y},\widehat{x}\right)$$

(14)

Then, to ensure the proposed manifold, $\pi$, is attractive and invariant, the off-the-manifold coordinate, $\psi$, is given,

$$\psi =\eta -x+\beta \left(y,\widehat{y},\widehat{x}\right)$$

(15)

where $x=\eta +\beta \left(y,\widehat{y},\widehat{x}\right)$ when $\psi$ approaches zero.

Combining Equation (9) and taking derivatives with respect to the time of Equation (15),

$$\begin{array}{c}\dot{\psi }=\dot{\eta }-\dot{x}+\dot{\beta }\left(y,\widehat{y},\widehat{x}\right)\\ =\dot{\eta }-S_1\left(x,y\right)x-S_{2}x-F\left(y,u\right)+{\nabla }_y\beta L\left(y\right)x+{\nabla }_{\widehat{y}}\beta \dot{\widehat{y}}+{\nabla }_{\widehat{x}}\beta \dot{\widehat{x}}\end{array}$$

(16)

Based on Equation (16), let the dynamics of $\eta$ be

$$\begin{array}{c}\dot{\eta }=F\left(y,u\right)-{\nabla }_y\beta L\left(y\right)\left(\eta +\beta \right)-{\nabla }_{\widehat{y}}\beta \dot{\widehat{y}}-{\nabla }_{\widehat{x}}\beta \dot{\widehat{x}}+\left(\eta +\beta \right)S_1\left(\eta +\beta ,y\right)\\ +\left(\eta +\beta \right)S_2-r^2{L}^T\left(y\right)e_y-r^2{\left[{\nabla }_y\beta L\left(y\right)\right]}^T{e}_x\end{array}$$

(17)

where ${\nabla }_y\beta$, ${\nabla }_{\widehat{y}}\beta$, and ${\nabla }_{\widehat{x}}\beta$ are Jacobian matrices of the mapping $\beta \left(y,\widehat{y},\widehat{x}\right)$ with respect to $y$, $\widehat{y}$, and $\widehat{x}$, respectively. $r$ is called the dynamic scaling factor, and it will be provided in later sections. $e_x$ and $e_y$ are the estimated error with respect to the states x and y, respectively.

$$\left\{\begin{array}{l}{e}_x=\widehat{x}-\eta -\beta \\ e_y=\widehat{y}-y\end{array}\right.$$

(18)

Substituting Equation (17) into Equation (16) generates the following equation:

$$\begin{array}{c}\dot{\psi }=S_1\left(x,y\right)\psi +{\overline{S}}_1\left(\eta +\beta ,y\right)\psi +S_2\psi -{\nabla }_y\beta L\left(y\right)\psi -r{L}^T\left(y\right)e_y\\ -r{L}^T\left(y\right)e_y-r^2{\left[{\nabla }_y\beta L\left(y\right)\right]}^T{e}_x\end{array}$$

(19)

The dynamic equations of the observer are defined as

$$\left\{\begin{array}{l}\dot{\widehat{y}}=L\left(y\right)\left(\eta +\beta \right)-{\phi }_1{e}_y\\ \dot{\widehat{x}}=\left(\eta +\beta \right)S_1\left(\eta +\beta ,y\right)+\left(\eta +\beta \right)S_2+F\left(y,u\right)-\\ {\phi }_2{e}_x-r^2{\left[{\nabla }_y\beta L\left(y\right)\right]}^T{e}_x-r^2{L}^T\left(y\right)e_y\end{array}\right.$$

(20)

where ${\phi }_1:{\mathbb{R}}^2\times {\mathbb{R}}_{+}\to {\mathbb{R}}_{+}$ and ${\phi }_2:{\mathbb{R}}^2\times {\mathbb{R}}_{+}\to {\mathbb{R}}_{+}$ are positive gains, and they will be provided in the numerical simulation section.

Taking derivatives of Equation (18) generates the following equations:

$$\left\{\begin{array}{l}{\dot{e}}_x=\dot{\widehat{x}}-\dot{\eta }-\dot{\beta }={\nabla }_y\beta L\left(y\right)\psi -{\phi }_2{e}_x\\ {\dot{e}}_y=\dot{\widehat{y}}-\dot{y}=L\left(y\right)\psi -{\phi }_1{e}_y\end{array}\right.$$

(21)

3.2. Dynamic Scaling Factor for Domination

A dynamic scaling factor, $r=\psi /z$, is introduced to transform the off-the-manifold, $\psi$, listed in Equation (19); Equation (19) is rewritten as

$$\dot{z}=z{S}_1\left(x,y\right)+z{\overline{S}}_1\left(\eta +\beta ,y\right)+z{S}_2-z{\nabla }_y\beta L\left(y\right)-r{\left[{\nabla }_y\beta L\left(y\right)\right]}^T{e}_x-r{L}^T\left(y\right)e_y-\frac{\dot{r}}{r}z$$

(22)

Also, Equation (21) is rewritten in terms of dynamics as dynamic scaling factor, $r$, as

$$\left\{\begin{array}{l}{\dot{e}}_x=\dot{\widehat{x}}-\dot{\eta }-\dot{\beta }=r{\nabla }_y\beta L\left(y\right)z-{\phi }_2{e}_x\\ {\dot{e}}_y=\dot{\widehat{y}}-\dot{y}=rL\left(y\right)z-{\phi }_1{e}_y\end{array}\right.$$

(23)

Then, a Hamiltonian form by combining Equations (22) and (23) is written as

$$\dot{X}=\left(J-R\right)\frac{\partial H}{\partial X}$$

(24)

where $X={\left(z,e_y,e_x\right)}^T$ is a new state vector of the observer dynamics. $H$ is a Hamiltonian storage energy function listed in Equation (25). $J$ and $R$ are the interconnection and damping matrices, respectively. It is noted that interconnection matrix, $J$, is a skew-symmetric matrix, $J^T=-J$, and $R$ is a damping matrix that needs to be positive definite, which means the energy is extracted out of the system.

$$H\left(z,e_y,e_x\right)=\frac{1}{2}{z}^{T}z+\frac{1}{2}{e}_y^T{e}_y+\frac{1}{2}{e}_x^T{e}_x$$

(25)

$$J=\left[\begin{array}{ccc}{S}_1\left(x,y\right)+S_2& -r{L}^T\left(y\right)& -r{\left[{\nabla }_y\beta L\left(y\right)\right]}^T\\ rL\left(y\right)& 0& 0\\ r{\nabla }_y\beta L\left(y\right)& 0& 0\end{array}\right]$$

(26)

$$R=\left[\begin{array}{ccc}-{\overline{S}}_1\left(\eta +\beta ,y\right)+{\nabla }_y\beta L\left(y\right)+\frac{\dot{r}}{r}& 0& 0\\ 0& {\phi }_1& 0\\ 0& 0& {\phi }_2\end{array}\right]$$

(27)

As noted in Equations (26) and (27), the ${\nabla }_y$ is unknown and needs to be solved. In this paper, an ideal ${\nabla }_y$ is given based on the approximation solution [39],

$${\nabla }_y\beta \left(\widehat{x},\widehat{y}\right)={\overline{S}}_1\left(\widehat{x},\widehat{y}\right)L^{†}\left(\widehat{y}\right)+k_1{L}^{†}\left(\widehat{y}\right)=\left[\begin{array}{cc}{k}_1& {\widehat{x}}_2\\ 0& k_1{\widehat{y}}_1-{\widehat{x}}_1\end{array}\right]$$

(28)

where $k_1>0$ is a positive gain to be selected and $L^{†}\left(y\right)$ is a full rank inverse of $L\left(y\right)$.

As listed in Equation (27), the first element entry inside the damping matrix, $R$, is rewritten as

$$\begin{array}{l}{R}_{1,1}=-{\overline{S}}_1\left(\eta +\beta ,y\right)+{\nabla }_y\beta L\left(y\right)+\frac{\dot{r}}{r}\\ =-{\overline{S}}_1\left(\eta +\beta ,y\right)+k_{1}I+{\overline{S}}_1\left(\widehat{x},\widehat{y}\right)-\left[{\overline{S}}_1\left(\widehat{x},\widehat{y}\right)+k_{1}I\right]\left[L^{†}\left(y\right)-L^{†}\left(\widehat{y}\right)\right]L\left(y\right)+\frac{\dot{r}}{r}\end{array}$$

(29)

where $I$ is an identity matrix with a size of $2\times 2$.

Here, an error damping, $\Delta$, is defined as

$$\Delta ={\overline{S}}_1\left(\eta +\beta ,y\right)-{\overline{S}}_1\left(\widehat{x},\widehat{y}\right)+\left[{\overline{S}}_1\left(\widehat{x},\widehat{y}\right)+k_{1}I\right]\left[L^{†}\left(y\right)-L^{†}\left(\widehat{y}\right)\right]L\left(y\right)$$

(30)

Then, the error mapping can be factorized as

$$\Delta ={\Delta }_x\left(\widehat{x},e_x\right)L\left(y\right)+{\Delta }_y\left(\widehat{y},e_y\right)L\left(y\right)$$

(31)

where ${\Delta }_x$ and ${\Delta }_y$ can be explained as the role of disturbance compensation mapping for the observer states.

$$\left\{\begin{array}{l}{\Delta }_x\left(\widehat{x},e_x\right)L\left(y\right)={\overline{S}}_1\left(\eta +\beta ,y\right)-{\overline{S}}_1\left(\widehat{x},y\right)\\ {\Delta }_y\left(\widehat{y},e_y\right)L\left(y\right)={\overline{S}}_1\left(\widehat{x},y\right)-{\overline{S}}_1\left(\widehat{x},\widehat{y}\right)+\left[{\overline{S}}_1\left(\widehat{x},\widehat{y}\right)+k_{1}I\right]\left[L^{†}\left(y\right)-L^{†}\left(\widehat{y}\right)\right]L\left(y\right)\end{array}\right.$$

(32)

where ${\Delta }_x\left(\widehat{x},e_x\right)$ and ${\Delta }_y\left(\widehat{y},e_y\right)$ can be calculated as follows,

$${\Delta }_y\left(\widehat{x},e_y\right)=\left[\begin{array}{cc}0& 0\\ 0& -k_1{e}_{y_1}\end{array}\right]\mathrm{and} {\Delta }_x\left(\widehat{x},e_x\right)=\left[\begin{array}{cc}0& -e_{x_2}\\ 0& e_{x_1}\end{array}\right]$$

(33)

where $e_{x_1}={\widehat{x}}_1-x_1$, $e_{x_2}={\widehat{x}}_2-x_2$ and $e_{y_1}={\widehat{y}}_1-y_1$. Thereby, we can obtain the following equations:

$${\Delta }_x\left(\widehat{x},0\right)=0 \mathrm{and} {\Delta }_y\left(\widehat{x},0\right)=0$$

(34)

Then, based on Equations (30)–(33), Equation (29) can be rewritten as

$$R_{1,1}=k_{1}I-\left[{\Delta }_{x}L\left(y\right)+{\Delta }_{y}L\left(y\right)\right]+\frac{\dot{r}}{r}$$

(35)

$$R=\left[\begin{array}{ccc}{k}_{1}I-\left[{\Delta }_{x}L\left(y\right)+{\Delta }_{y}L\left(y\right)\right]+\frac{\dot{r}}{r}& 0& 0\\ 0& {\phi }_1& 0\\ 0& 0& {\phi }_2\end{array}\right]$$

(36)

Remark 1.

As listed in Equation (28), the approximate solution of a partial differential equation is given. Furthermore, as listed in Equation (36), the damping matrix, $R$, has been specially converted. Note that the Hamiltonian structure is maintained, which satisfies the property of the Hamiltonian theory. Therefore, the transformed Hamiltonian function (36) will be used to prove the stability of the proposed observer.

3.3. Domination by High-Gain Injection and Stability

In this section, the introduced scaling factor, $r$, is explicitly given, and the Lyapunov stability analysis of the designed velocity observer is carried out.

Taking the time derivative of the Hamiltonian function generates the following equation,

$$\dot{H}\left(z,e_y,e_x\right)=-z^T\left[k_{1}I-\left[{\Delta }_{x}L\left(y\right)+{\Delta }_{y}L\left(y\right)\right]+\frac{\dot{r}}{r}\right]z-e_y^T{\phi }_1{e}_y-e_x^T{\phi }_2{e}_x$$

(37)

where ${\phi }_1$ and ${\phi }_2$ are defined as positive gain matrices. It is easily noted that we can obtain $\dot{H}\left(z,e_y,e_x\right)\le 0$ if the property of $k_{1}I-\left[{\Delta }_{x}L\left(y\right)+{\Delta }_{y}L\left(y\right)\right]+\frac{\dot{r}}{r}\ge 0$ is given.

$$\left\{z,e_y,e_x\in {\mathbb{R}}^2\left|\dot{H}\left(z,e_y,e_x\right)=0\right.\right\}=\left\{z,e_y,e_x\left|z=0\right.,e_y=0,e_x=0\right\}$$

(38)

Then, the scaling factor, r, is defined as,

$$\dot{r}=-\frac{k_1}{4}\tilde{r}+\frac{r}{k_1}\left({‖{\Delta }_{x}L‖}^2+{‖{\Delta }_{y}L‖}^2\right), r\left(0\right)\ge 1$$

(39)

with $\tilde{r}=r-1$, and note that the factor $r$ satisfies $\left\{r\in \mathbb{R}\left|r\ge 1\right.\right\}$ [31] and $k_1>0$, which can achieve the exponential convergence of the observer system.

Defining a positive-definite function, $V_1=\frac{1}{2}{z}^{T}z$, and its derivative with non-dimensional time is written as

$$\begin{array}{c}{\dot{V}}_1=-z^T\left[k_{1}I-\left[{\Delta }_{x}L\left(y\right)+{\Delta }_{y}L\left(y\right)\right]+\frac{\dot{r}}{r}\right]z\\ =-z^T\left(k_1+\frac{\dot{r}}{r}\right)z+z^T\left[{\Delta }_{x}L\left(y\right)+{\Delta }_{y}L\left(y\right)\right]z\\ \le -\left[\frac{k_1}{2}+\frac{\dot{r}}{r}-\frac{1}{k_1}{‖{\Delta }_{x}L\left(y\right)‖}^2+{‖{\Delta }_{y}L\left(y\right)‖}^2\right]{\left|z\right|}^2\end{array}$$

(40)

where $‖\cdot ‖$ denotes the matrix induced 2-norm, and the Young’s inequality is used to obtain the second bound.

Substituting Equation (39) into Equation (40) leads to the following equation,

$${\dot{V}}_1\le -\left[\frac{k_1}{2}-\frac{k_1}{4}\frac{\tilde{r}}{r}\right]{\left|z\right|}^2\le -\frac{k_1}{4}{\left|z\right|}^2$$

(41)

where $\tilde{r}/r\le 1$. It can be noticed that the coordinate z converges to zero exponentially.

To ensure the boundedness of the scaling function, r, listed in Equation (22), the additional positive function is defined as follows:

$$V_2=\frac{1}{2}{\tilde{r}}^2$$

(42)

Then, a proper Lyapunov candidate function for the extended system is written as

$$V=\frac{1}{2}{z}^{T}z+\frac{1}{2}{e}_y^T{e}_y+\frac{1}{2}{e}_x^T{e}_x+V_2$$

(43)

Taking the derivative leads to the following equation:

$$\begin{array}{l}\dot{V} \le -\frac{k_1}{4}{\left|z\right|}^2-e_y^T{\phi }_1{e}_y-e_x^T{\phi }_2{e}_x+\left[-\frac{k_1}{4}{\tilde{r}}^2+\frac{r\tilde{r}}{k_1}\left({‖{\Delta }_{x}L‖}^2+{‖{\Delta }_{y}L‖}^2\right)\right]\\ \le -\frac{k_1}{4}{\left|z\right|}^2-\frac{k_1}{4}{\tilde{r}}^2-\left({\phi }_1-\frac{r\tilde{r}}{k_1}{‖L‖}^2{‖{\overline{\Delta }}_y‖}^2\right){\left|e_y\right|}^2-\left({\phi }_2-\frac{r\tilde{r}}{k_1}{‖L‖}^2{‖{\overline{\Delta }}_x‖}^2\right){\left|e_x\right|}^2\end{array}$$

(44)

As listed in Equation (34), the error mappings, ${\Delta }_x\left(\widehat{x},e_x\right)$ and ${\Delta }_y\left(\widehat{x},e_y\right)$, approach zero, and the two mappings are defined as ${\overline{\Delta }}_y\ge ‖{\Delta }_y‖/\left|e_y\right|$ and ${\overline{\Delta }}_x\ge ‖{\Delta }_x‖/\left|e_x\right|$.

Here, to ensure the boundness of factor r, the gains ${\phi }_1$ and ${\phi }_2$ are chosen as

$${\phi }_1=\frac{\tilde{r}r}{k_1}{‖L‖}^2{‖{\overline{\Delta }}_y‖}^2+{\overline{\phi }}_1\mathrm{and} {\phi }_2=\frac{\tilde{r}r}{k_1}{‖L‖}^2{‖{\overline{\Delta }}_x‖}^2+{\overline{\phi }}_2$$

(45)

where ${\overline{\phi }}_1,{\overline{\phi }}_2>0$ are positive constants.

Substituting Equation (45) into Equation (44) leads to the following equations,

$$\begin{array}{c}\dot{V} \le -\frac{k_1}{4}{\left|z\right|}^2-\frac{k_1}{4}{\tilde{r}}^2-{\overline{\phi }}_1{\left|e_y\right|}^2-{\overline{\phi }}_2{\left|e_x\right|}^2\\ \le -4\delta V\left(z,e_y,e_x,\tilde{r}\right)\end{array}$$

(46)

where $\delta$ is the minimal value between the gains ${\overline{\phi }}_1$, ${\overline{\phi }}_2$, and $k_1$.

Based on Equation (46), the observer system is exponentially stable. Meanwhile, it is evident that scaling function r has a finite boundedness, and it can be used for the robustness of the observer system against disturbed mapping $\Delta$. Therefore, state error $e_x$ will exponentially converge to zero, and component $\widehat{x}$ is the estimate of state $x$.

Remark 2.

It is worth noting that the proposed observer system is converted into a Hamiltonian framework; the method for setting gain functions ${\phi }_1$ and ${\phi }_2$ is different from the method presented in [37], which needs to construct an intermediate term. In this paper, the detailed process is not presented. Meanwhile, in this work, stabilization via the I&I method is combined with the passivity-based theory, with a suitable Hamiltonian storage function.

Remark 3.

It should be noted that the defined constant gains $k_1, {\overline{\phi }}_1, {\overline{\phi }}_2:{\mathbb{R}}_{+}$ have to be explicitly and carefully chosen. Different gain parameters will significantly affect the performance of the proposed observer, which will be investigated in the numerical simulation section. Furthermore, sensitivity analysis is recommended for the proposed velocity observer with different mission requirements.

4. Numerical Cases

In this section, the proposed velocity observer is evaluated via numerical simulation. Here, the tension controller, $\tilde{T}$, proposed in Ref. [40] is used to control the tether deployment. Note that the tension controller, $\tilde{T}$, is only used as the control input for the proposed velocity observer. In this paper, the STS is in a circular orbit with an altitude of 220 km, and the initial conditions of the tether deployment are set as $\lambda =0.01$, $\dot{\lambda }=0.5$, and $\theta =\dot{\theta }=0$, and the desired state are set as ${\lambda }_f=1.00$ and $\dot{\lambda }=\theta =\dot{\theta }=0$. For simplicity, the positive gains of the proposed controller are set the same as the values presented in Ref. [40]. Figure 2 shows the time histories of the non-dimensional tether length and in-plane libration under the implemented controller when these two velocity terms, $\dot{\lambda }$ and $\dot{\theta }$, are supposed to be known. As proposed in Section 3, the velocity terms, $\dot{\lambda }$ and $\dot{\theta }$, inside the tension controller will be replaced by the proposed observed velocity, $\dot{\widehat{\lambda }}$ and $\dot{\widehat{\theta }}$, listed in Equation (24).

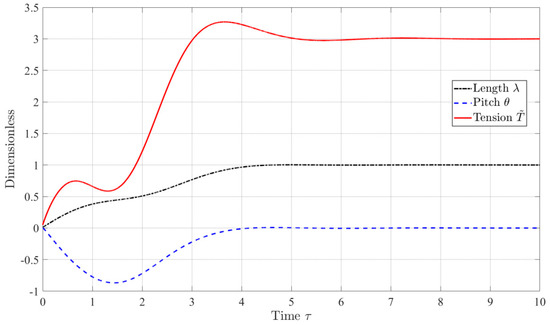
Figure 2. Time histories of non-dimensional tether length, in-plane libration angle, and input tension.

4.1. Case 1: Observer with Different Gains $k_1$

In this section, as listed in Equation (36), the velocity gain, $k_1$, affecting the performance of the proposed velocity observer, is investigated. As listed in Table 1, six different values of gain $k_1$ are considered. The simulation parameters, the gains of the observer, and the initial conditions of the STS are provided in Table 1. It should be mentioned that the relationship between the observer state ${\left(x,y\right)}^T$ and ${\left(\lambda ,\theta ,\dot{\lambda },\dot{\theta }\right)}^T$ can be found in Equation (6). The simulation results are shown in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8, and the results are illustrated by the state ${\left(\lambda ,\theta \right)}^T$ and the velocity state ${\left(\dot{\lambda },\dot{\theta }\right)}^T$ of the STS.

Table 1. Simulation parameters and initial conditions for the observer dynamics.

$k_1=0.1,0.5,1,2,5,10$	${\overline{\phi }}_1={\overline{\phi }}_2=0.175$
$y_1\left(0\right)=0.01,y_2\left(0\right)=0$	$x_1\left(0\right)=0.5,x_2\left(0\right)=0$
${\widehat{y}}_1\left(0\right)=0.05,{\widehat{y}}_2\left(0\right)=0$	${\widehat{x}}_1\left(0\right)=0.75,{\widehat{x}}_2\left(0\right)=0$
${\left.\eta \left(0\right)\right|}_{k_1=0.1,0.5,1,2,5,10}={\left.\left[\widehat{x}\left(0\right)-\beta \left(0\right)\right]\right|}_{k_1=0.1,0.5,1,2,5,10}$	$r\left(0\right)=1.5$

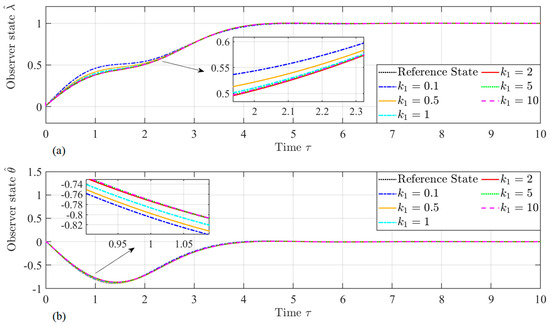
Figure 3. Time histories of the states: (a) $\widehat{\lambda }$ and (b) $\widehat{\theta }$ of the observer dynamics.

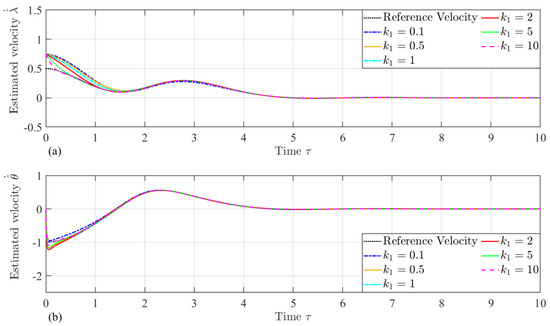
Figure 4. Time histories of the estimated velocities: (a) $\dot{\widehat{\lambda }}$ and (b) $\dot{\widehat{\theta }}$.

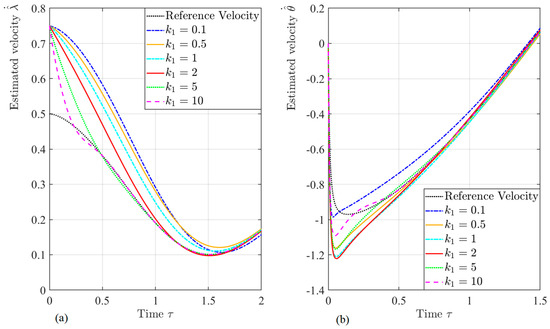
Figure 5. Time histories of the estimated velocities: (a) $\dot{\widehat{\lambda }}$ and (b) $\dot{\widehat{\theta }}$ (magnified).

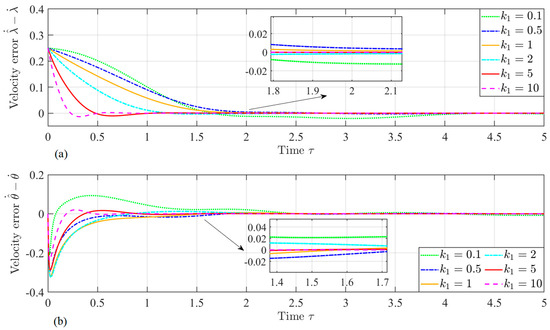
Figure 6. Time histories of the Velocity errors: (a) $\dot{\widehat{\lambda }}-\dot{\lambda }$ and (b) $\dot{\widehat{\theta }}-\dot{\theta }$.

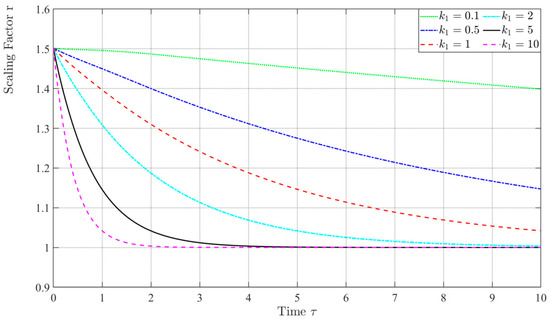
Figure 7. Time histories of the scaling factor r.

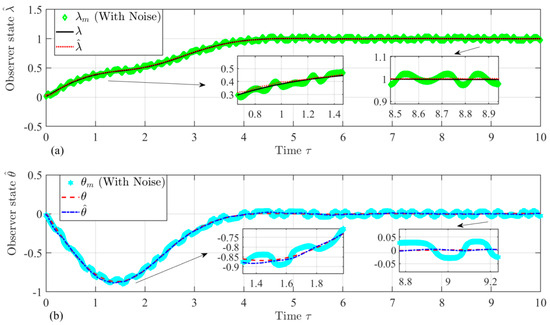
Figure 8. Time histories of real measurement states: (a) $\dot{\widehat{\lambda }}$ and (b) $\dot{\widehat{\theta }}$ with noise model.

Figure 3 and Figure 4 show the time histories of the estimated position and velocities, $\dot{\widehat{\lambda }}$ and $\dot{\widehat{\theta }}$, with different gains, $k_1$. It can be easily seen that the proposed velocity observer successfully estimates the velocity. However, it can be seen that the dynamic behavior of the tether length rate and libration rate caused by different gain, $k_1$, values are obviously different. For example, as shown in Figure 5, a larger gain makes the estimated velocity of the tether length converge to the actual value faster. However, its impact on the estimated velocity of the libration angle is inverse. Furthermore, as shown in Figure 5b, the estimated angle velocity, $\dot{\widehat{\theta }}$, has some overshoot, with both small and large gain values, such as $k_1=0.1$ and $k_1=10$. The system response is slower and prone to overshooting when the gain is too small. Conversely, when the gain is too large, the system will be too sensitive, and overshoot will also be intensified. Therefore, the dynamic behavior phenomenon suggests optimizing gain value $k_1$ to balance its effect on the estimated velocities. Figure 6 depicts the time histories of the errors of velocities $\dot{\widehat{\lambda }}-\dot{\lambda }$ and $\dot{\widehat{\theta }}-\dot{\theta }$. It is can be easily seen that the errors of velocity exponentially approach zero. In addition, Figure 7 shows the time histories of the dynamic scaling factor, $r$, under different values of gain $k_1$. It shows that the scaling factor has a boundedness of $r=1$, and it also suggests a larger gain value, making the scale, r, converge faster.

4.2. Observer with Input Measurement Noise

In this section, the measurement noise is considered for the measurable state to demonstrate the robustness of the proposed velocity observer. As listed in Equation (47), disturbance noises, $d_{\lambda }$ and $d_{\theta }$, are added to the measurement of the input states, $\lambda$ and $\theta$. The simulation parameters and the initial conditions are the same values as in Table 1. Figure 8 shows the time histories of the measurement states $\lambda$ and $\theta$ under the proposed noise model.

$$\begin{array}{l}{d}_{\lambda }\left(\tau \right)=\pi \tanh \left[\sin \left(2\tau +5\sin \left(10\tau \right)\right)\right]/100\\ d_{\theta }\left(\tau \right)=\pi \tanh \left[2\sin \left(3\tau +6\cos \left(5\tau \right)\right)\right]/100\end{array}$$

(47)

Figure 9 and Figure 10 show the time histories of the estimated velocity of the tether length, $\dot{\widehat{\lambda }}$, and the velocity of the libration angle, $\dot{\widehat{\theta }}$, under the applied disturbance. Also, the dynamic behavior of the proposed estimated velocities, $\dot{\widehat{\lambda }}$ and $\dot{\widehat{\theta }}$, with different gain value, $k_1$, are investigated. A noticeable chatting phenomenon is easily found when a large value of gain $k_1$ is chosen. Furthermore, it oscillates around the reference velocity and is not converged. Therefore, a large gain is not expected when the measurement noise model is considered. The same dynamic behavior of the pith angle velocity, $\dot{\widehat{\theta }}$ (overshoot), is also found when a small gain is applied. Figure 11 shows the rapid convergence of the estimated velocities $\dot{\widehat{\lambda }}$ and $\dot{\widehat{\theta }}$ to the referred velocities when velocity gain $k_1$ is set as 1.0, which demonstrates the robustness of the proposed observer against measurement noise. The shapes of the estimated velocity value are smooth, as expected, even when the measurement noise is considered. Therefore, the velocity gain $k_1=1.0$ will be chosen in the following simulations to illustrate the performance behavior.

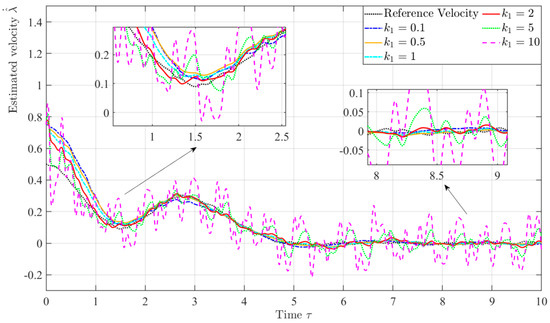
Figure 9. Time histories of estimated velocity $\dot{\widehat{\lambda }}$ with different values of the velocity gain.

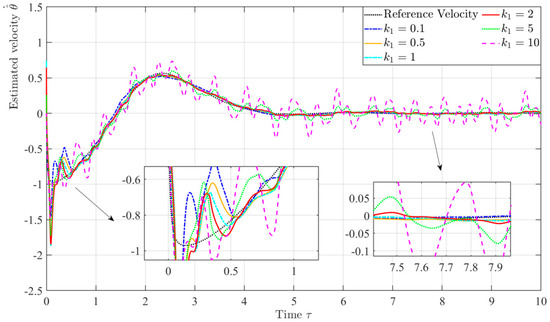
Figure 10. Time histories of estimated velocity $\dot{\widehat{\theta }}$ with different values of the velocity gain.

Figure 11. Time histories of the estimated velocities: (a) $\dot{\widehat{\lambda }}$ and (b) $\dot{\widehat{\theta }}$ with measurement noise when gain $k_1=1.0$.

4.3. Observer Under the Different Initial Conditions

In the previous section, as listed in Table 1, the initial conditions are known values. In this section, different sets of initial conditions of estimated velocities $\dot{\widehat{\lambda }}$ and $\dot{\widehat{\theta }}$ impacting the performance of the proposed velocity are investigated. Here, the velocity gain, $k_1$, is set as 1.0, and the initial value of the scale factor, $r$, is set as 1.5. The other initial conditions are set the same as the values listed in Table 1. Table 2 lists different sets of the initial conditions used in this section, and six numerical simulations are carried out. In the first three cases (i, ii, and iii), the in-plane libration rate is supposed to be zero to prevent the tether from winding up in the deployment process [17]. Figure 12 shows the time histories of the proposed observer states $\widehat{\lambda }$ and $\widehat{\theta }$, and an expected discrepancy at the initial stage between the estimated and actual states is observed due to the difference between the estimated and referred velocities. Figure 13 shows that the time histories of the proposed velocity states $\dot{\widehat{\lambda }}$ and $\dot{\widehat{\theta }}$, and it shows that the estimated velocities converging to the reference velocities in fast. It can be concluded that the effect of the initial estimated velocity of the deployment on the proposed observer is trivial.

Table 2. Initial conditions for the observer dynamics.

Value	${\mathit{x}}_1\left(0\right)$	${\mathit{x}}_2\left(0\right)$	${\widehat{\mathit{x}}}_1\left(0\right)$	${\widehat{\mathit{x}}}_2\left(0\right)$
case i	0.5	0	0.75	0
case ii	0.5	0	1	0
case iii	0.5	0	0.25	0
case iv	0.5	−0.01	0.75	0
case v	0.5	−0.01	1	0

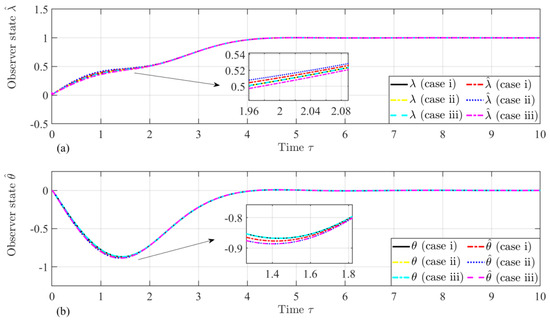
Figure 12. Time histories of the states: (a) $\widehat{\lambda }$ and (b) $\widehat{\theta }$ of the observer dynamics at different initial velocities.

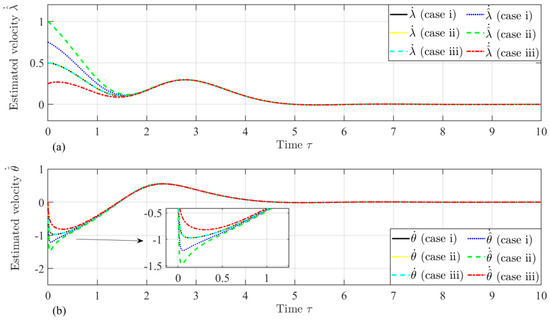
Figure 13. Time histories of the estimated velocities (a) $\dot{\widehat{\lambda }}$ and (b) $\dot{\widehat{\theta }}$ at different initial velocities.

To further validate the performance of the proposed velocity observer, the velocity of the tether libration angle, $\dot{\theta }$, is not zero, which may happen in a real mission. As listed in Table 2, another three numerical simulations are carried out. The same dynamic behavior between the observed state and the referred state is observed due to the initial difference between the estimated and referred velocities (Figure 14). Figure 15 shows that the estimated velocities also converge with the reference velocities, and their behavior is the same as that of the initial libration rate, which is zero. Finally, we can conclude that the proposed velocity observed is working well and can be applied for estimating the unmeasurable velocity terms $\dot{\lambda }$ and $\dot{\theta }$ inside the tension controller in a realistic mission analysis.

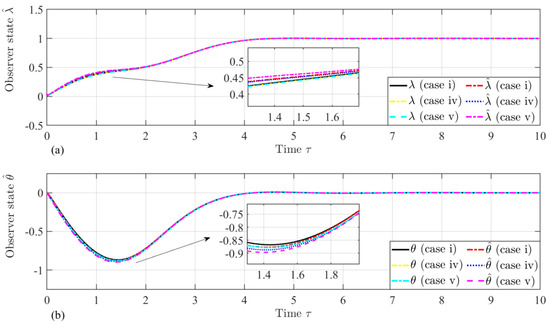
Figure 14. Time histories of the states (a) $\widehat{\lambda }$ and (b) $\widehat{\theta }$ of the observer dynamics with angle rates at different initial velocities.

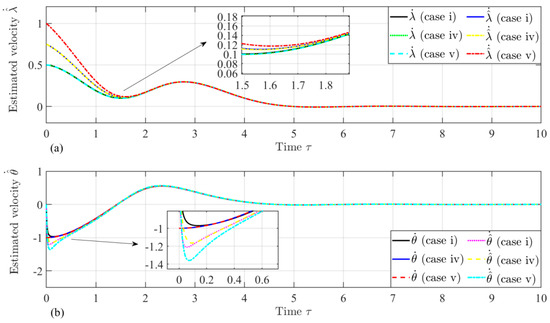
Figure 15. Time histories of the estimated velocities: (a) $\dot{\widehat{\lambda }}$ and (b) $\dot{\widehat{\theta }}$ with angle rates at different initial velocities.

5. Conclusions

This paper proposes a nonlinear velocity observer of tether deployment based on the immersion and invariance technique. The velocity observer system is transformed into an extended Hamiltonian formulation by introducing the error of the state and scaling dynamic factor. The stability of the proposed velocity observer is proven using the passivity-control methodology under a Hamiltonian framework. Furthermore, a crucial partial differential equation and a simple gain function are invoked in the design process. Finally, the proposed velocity observer is applied to simulate the tether deployment. Numerical simulations are carried out to demonstrate the effectiveness and robustness of the proposed velocity observer. Sensitivity analyses considering measurement disturbance are carried out to characterize the robustness of the proposed velocity observer.