Research on Check-In Baggage Flow Prediction for Airport Departure Passengers Based on Improved PSO-BP Neural Network Combination Model

Abstract

Accurate forecasting of passenger checked baggage traffic is crucial for efficient and intelligent allocation and optimization of airport service resources. A systematic analysis of the influencing factors and prediction algorithms for the baggage flow is rarely included in existing studies. To accurately capture the trend of baggage flow, a combined PCC-PCA-PSO-BP baggage flow prediction model is proposed. This study applies the model to predict the departing passengers’ checked baggage flow at Chengdu Shuangliu International Airport in China. First, in the preprocessing of the data, multiple interpolation demonstrates a better numerical interpolation effect compared to mean interpolation, regression interpolation, and expectation maximization (EM) interpolation in cases of missing data. Second, in terms of the influencing factors, unlike factors that affect the airport passenger flow, the total retail sales of consumer goods have a weak relationship with the baggage flow. The departure passenger flow and flight takeoff and landing sorties play a dominant role in the baggage flow. The railway passenger flow, highway passenger flow, and months have statistically significant effects on the changes in the baggage flow. Factors such as holidays and weekends also contribute to the baggage flow alternation. Finally, the PCC-PCA-PSO-BP model is proposed for predicting the baggage flow. This model exhibits superior performance in terms of the network convergence speed and prediction accuracy compared to four other models: BP, PCA-BP, PSO-BP, and PCA-PSO-BP. This study provides a novel approach for predicting the flow of checked baggage for airport departure passengers.

1. Introduction

Baggage is a fundamental element of airport operations, but it has become increasingly problematic. According to the “Baggage IT Insights 2019” released by the Society International De Tele-communications Aero-Nautiques (SITA), the global aviation industry experienced significant growth in both passenger and baggage volumes in 2019. The passenger volume reached 4.54 billion, a 5.6% increase from 2018, while the checked baggage exceeded 4.3 billion pieces, a 10% increase from the previous year. This increase also included over 20 million mishandled baggage incidents, resulting in at least USD 2.3 billion in direct losses to the civil aviation industry in a single year [1]. The COVID-19 pandemic led to a slowdown in the global civil aviation industry from 2020 to 2022. However, with the arrival of the post-pandemic era, the industry is expected to experience substantial growth, with global passenger traffic projected to double by 2040 [2]. Baggage mishandling is primarily attributed to insufficient control over baggage service resources, leading to low operational and organizational efficiency in relation to baggage handling [3]. This results in a range of negative consequences, including increased passenger complaints, greater economic losses, and heightened risks to aviation security. Currently, large and medium-sized airports face challenges related to expanding scale, increasing operational complexity, and the saturation of baggage handling system facilities. These factors place significant pressure on the efficient operation of airports. To address these challenges, accurately predicting future changes in the baggage flow is critical. This allows for the efficient allocation of baggage handling resources and improves the operational and organizational efficiency of airports and airlines. Therefore, understanding the influencing factors, changing rules, and mechanisms of baggage flow is a critical issue that requires urgent attention from civil aviation transportation management.

2. The Current Research Status on Airport Baggage Flow

2.1. Baggage Flow

The check-in baggage flow for departing passengers is summarized in Figure 1. This process begins with passengers checking in their baggage at the counter, followed by security screening, sorting, and transportation to the appropriate baggage carousel for their flight. Baggage handling staff then load the bags onto the designated aircraft. Accurate control of this flow is critical, directly impacting the allocation of check-in resources, security resources, and the optimization of the baggage sorting process. It also affects the utilization of the aircraft’s cargo hold and other resource allocation decisions. However, this has resulted in increasing economic losses due to the current lack of accurate control over baggage flow variations and characterization mechanisms.

Existing research on air traffic flows focuses mainly on passenger flows, flight flows, and cargo flows, and less on baggage flows. Yfatis mentioned in his research on the intelligent system for baggage safety inspection in terminals that specific indicators should be quantified for the checked baggage of departing passengers to facilitate classification research [4]. The software was developed to quantify the quantity, quality, and size of baggage and calibrate the location of the baggage for easy and fast retrieval. However, this study centered around software development, lacking further discussion of indicators relevant to baggage. Brunetta et al. established a model to assess the temporal behavior characteristics of terminal passenger flow and baggage flow and suggested controlling the number of check-in counters to cut down the queuing time for passengers checking in baggage [5]. Takakuwa and Oyama suggested that there was a strong correlation between baggage flow and airport passenger flow, and the prediction method for baggage flow should be applicable to passenger flow forecasting [6]. Yang investigated the characteristics and influencing factors of the demand for checked baggage in units of flights using the BP neural network [7]. The results indicate a significant correlation between baggage flow and passenger flow, and changes in baggage flow exhibit both randomness and periodicity. However, this research obtained sample data through sampling and questionnaire surveys, possessing high graininess. Li et al. created models for baggage weight and volume distribution using mathematical statistics [8]. The time required for baggage check-in exhibited a Burr distribution pattern, and the flow of checked baggage demonstrated a positive correlation with the selectivity of check-in counters. Liu et al. conducted a field study at a major Chinese airport to assess the characteristics of departure and arrival passenger flows. They evaluated terminal inbound and outbound flows through an analysis of the probability distribution of the passenger flow intensity and dwell time [9]. The check-in process for baggage occupied approximately one-third of the total dwell time for departing passengers. Additionally, the passenger and baggage flow in the arrival area exhibited a close relationship with the size of the aircraft model. Li analyzed the time distribution characteristics of checked baggage flow for departing passengers using the sample data of manual check-in passenger flow, flight numbers, and flight schedules [10]. A cross-correlation and time lag were revealed between checked baggage flow and planned departure passenger flow at different times of the day. A short-term baggage flow prediction model was constructed through the application of the seasonal autoregressive integrated moving average (SARIMA) and gradient boosting decision tree (GBDT) techniques. However, this study omitted the impact of holidays, working days, and winter and summer vacations on baggage flow and other influencing elements, such as urban economic factors, flight types, and other transportation modes. The inadequate diversity in feature vectors resulted in incomplete mapping of the relationships in the prediction model.

In summary, although some research suggests converting the predicted results of airport departure passenger flow directly into the forecast outcome of baggage flow, a scientific quantitative conversion formula has yet to be provided. Figure 2 presents a comparative analysis of the departure passenger and baggage flow at Chengdu Shuangliu International Airport during various months of 2018. The data reveal three prominent peaks in the passenger flow, occurring in March, August, and October, while the baggage flow exhibits two primary peaks in February and October. Apparently, the growth of passenger flow does not necessarily lead to an increase in baggage flow. Their changing trends have separate features. The prediction of baggage flow solely based on anticipated passenger flow may disregard the inherent characteristics of baggage flow, potentially resulting in significant discrepancies in the predictive outcomes. A comprehensive understanding of the combined effects of multiple influencing factors on baggage flow has been lacking in relevant research. Mathematical models established through traditional statistical approaches and hypothesis testing have demonstrated limitations in terms of the sample diversity, predictive accuracy, and practical utility. Therefore, it is essential to accurately and comprehensively explore baggage flow and deeply analyze its changes and mechanisms. The findings of this research possess substantial theoretical and practical significance within the current trajectory of civil aviation toward informatization and intelligence.

2.2. Traffic Prediction Algorithms

The field of traffic prediction has been subject to extensive examination, with forecasting methods conventionally classified into two categories: qualitative prediction and quantitative prediction. The former is based on “people-centered” subjective judgments, including surveys, analogy, and brainstorming. However, they are unable to quantify, have low accuracy, and are impossible to use to scientifically and accurately describe the development of things, which are conspicuous shortcomings [11]. Quantitative prediction methods rely on three distinct model types: mathematical statistical models, intelligent algorithm models, and combined algorithm models. The models based on mathematical statistics use the relationships between random variables for quantitative description, such as gray models (GMs), Kalman filter (KF), and the autoregressive integrated moving average model (ARIMA) [12]. They are simple and easy to operate. However, they have low prediction accuracy for nonlinear problems. The methods based on intelligent algorithms include support vector machines (SVMs) and artificial neural networks (ANNs) [13,14]. Among them, ANNs have excellent parallel information processing ability and nonlinear mapping ability, being widely applied in the field of prediction. Nevertheless, traditional neural networks tend to fall into local extremes when dealing with highly nonlinear problems, leading to good data fitting accompanied by possibly large deviations in the actual prediction results. Methods employing combination models integrate two or more algorithms, thereby harnessing the advantages of each, mitigating individual shortcomings, and establishing complementary benefits, ultimately leading to enhanced prediction accuracy and efficiency. Combination models have become prevalent in traffic prediction [13,15].

To address the limitations of single prediction models, this paper proposes the PCC-PCA-PSO-BP combination model. This model is based on the BP neural network prediction model, incorporating the PSO algorithm to mitigate the shortcomings of traditional BP networks, such as the slow convergence speed and susceptibility to local extrema. Meanwhile, it fully considers the correlation between the input variables of the model and introduces numerical interpolation and the Pearson correlation coefficient (PCC) method to systematically analyze the main influencing factors of departure baggage flow while retaining effective original data information. Then, PCA is used for data dimension reduction to weaken the coupling between the input variables in the BP neural network and remove redundant information, further improving the prediction accuracy of the model. Based on the data on the checked baggage flow of departing passengers at Chengdu Shuangliu International Airport in China, this article compares the proposed combination model PCC-PCA-PSO-BP with BP, PCA-BP, PSO-BP, and PCA-PSO-BP to verify its effectiveness and feasibility.

3. Baggage Flow Prediction Based on the PCC-PCA-PSO-BP Combination Model

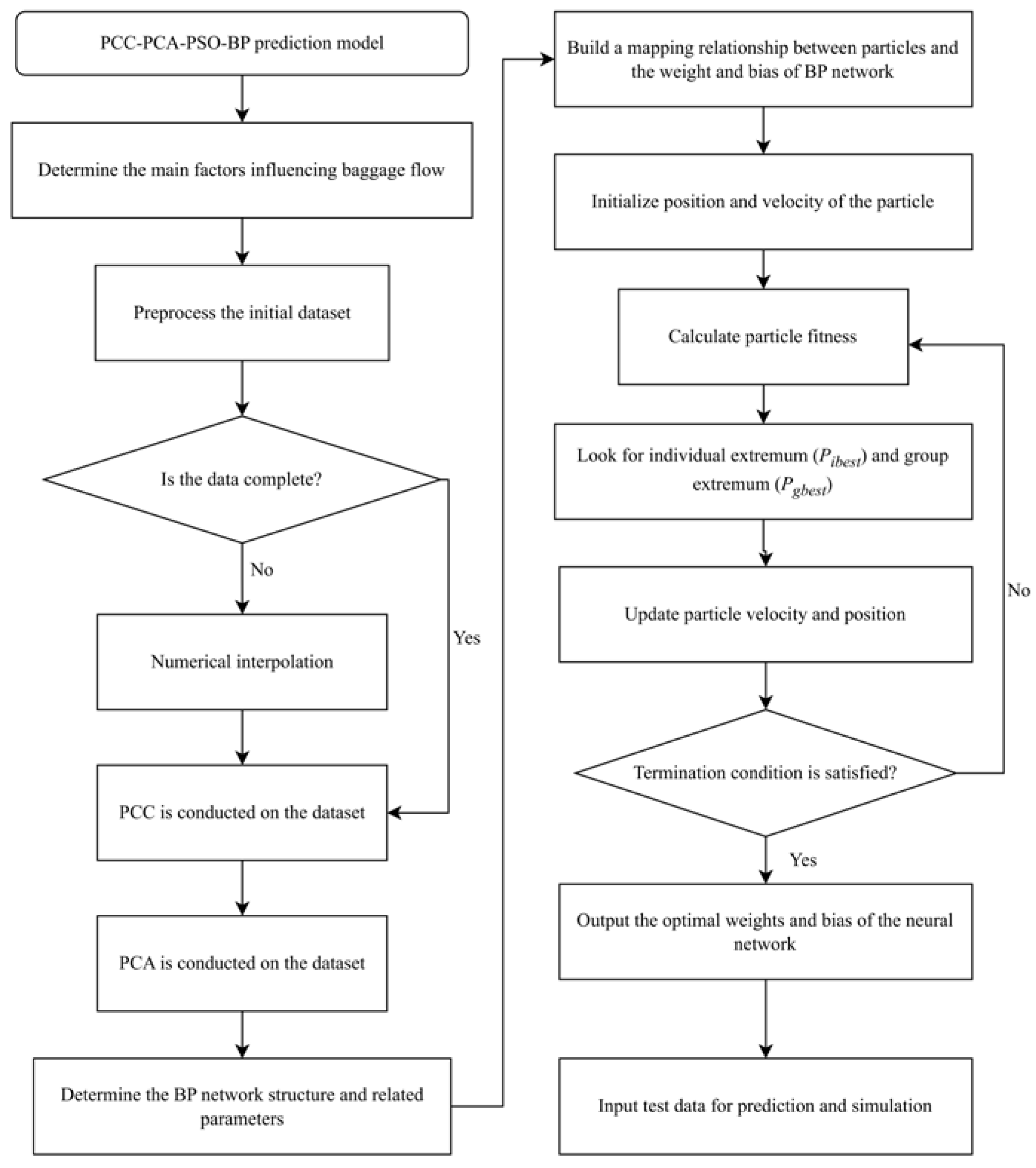
3.1. Baggage Flow: Construction of the PCC-PCA-PSO-BP Combinatorial Model

Although PSO can optimize BP neural networks to seek global optimal solutions, a large number of network parameters and significant correlations between input vectors may lead to overfitting in the network, which can adversely lower the prediction accuracy of the model [16]. Therefore, first, the PCC method is used to extract the core influencing factors of the input vectors of the neural network, effectively reducing the redundant input vector information. Second, PCA is adopted to weaken the coupling between the input variables in the BP neural network while reserving enough original data information, thus reducing the data dimension to simplify the network. Finally, by optimizing the weights and thresholds of the BP neural network through PSO, the prediction accuracy and efficiency of the neural network are further promoted. The implementation of the combination model is shown in Figure 3.

3.2. The Principle of the PCC Algorithm

PCC is used to measure the linear correlation between two datasets, X and Y, usually represented by r, with a value between −1 and 1 [17]. The larger the absolute value of r, the higher the linear correlation between the two sets of data. The expression is as follows:

$$r={\displaystyle \frac{\sum _{i=1}^n\left(x_i-\overline{x}\right)\left(y_i-\overline{y}\right)}{\sqrt{\sum _{i=1}^n{\left(x_i-\overline{x}\right)}^2}\sqrt{\sum _{i=1}^n{\left(y_i-\overline{y}\right)}^2}}}$$

(1)

In Equation (1), $x_i$ and $y_i$ are the i-th data in the two datasets with a length of n $X=\left\{x_1,x_2,{\dots ,x}_n\right\}$ and $Y=\left\{y_1,y_2,{\dots ,y}_n\right\}$, respectively, where $i=\mathrm{1,2},\dots ,n$; $\overline{x}$ and $\overline{y}$ are the mean values of the samples in X and Y, respectively; the value of r is between $\left[-1,1\right]$.

3.3. The Principle of the PCA Algorithm

As a method commonly used in multivariate statistics, PCA has the advantages of eliminating correlations between data and reducing noise and data dimensions. It can effectively address the problem of redundant data information and enhance algorithm efficiency [18]. PCA encompasses a series of steps, including data standardization, determination of principal components, calculation of the variance contribution rate and the cumulative variance contribution rate of principal components, and selection of the most significant principal components. The specific steps are as follows:

(a)

Data standardization. In a specific complex system, the original dataset $X$ consisting of n samples influenced by m variables $\left[X_1,X_2,\dots ,X_m\right]$ (referred to as influencing factors or variables in this article) is expressed as follows:

$$X=\left[\begin{array}{ccc}{x}_{11}& \cdots & x_{1m}\\ ⋮& \ddots & ⋮\\ x_{n1}& \cdots & x_{nm}\end{array}\right]$$

(2)

There may be differences in the standard between variables. In order to avoid the influence of the dimensionality and order of magnitude between data, the original dataset is mapped to [−1,1] through standardization to avoid interference from variables with large variances in the principal component analysis. The standardization formula is as follows:

$${x_{ij}}^{\prime }={\displaystyle \frac{x_{ij}-\overline{x_j}}{{\sigma }_{X_j}}}$$

(3)

The standardized matrix is obtained, expressed as follows:

$$X^{\prime }=\left[\begin{array}{ccc}{x_{11}}^{\prime }& \cdots & {x_{1m}}^{\prime }\\ ⋮& \ddots & ⋮\\ {x_{n1}}^{\prime }& \cdots & {x_{nm}}^{\prime }\end{array}\right]$$

(4)

In Equations (3) and (4), ${x_{ij}}^{\prime }$ is the standardized value of the data in the i-th row and j-th column in the original dataset $X$; $X^{\prime }$ is the standardized matrix corresponding to the original dataset $X$; $x_{ij}$ is the value in the j-th column and i-th row of $X$; and $\overline{x_j}$ and ${\sigma }_{X_j}$ are the mean and standard deviation of the influencing factors in the j-th column of $X$, respectively, ($i=\mathrm{1,2},\dots ,n$ and $j=\mathrm{1,2},\dots ,m)$.

(b)

Determination of principal components. The standardized matrix $X^{\prime }$ contains all the information of the original dataset $X$. The correlation coefficient matrix R is calculated using the standardized matrix, expressed as follows:

$$R=\left[\begin{array}{ccc}{r}_{11}& \cdots & r_{1p}\\ ⋮& \ddots & ⋮\\ r_{p1}& \cdots & r_{pp}\end{array}\right]$$

(5)

$$\mathrm{with}{\mathrm{}r}_{ij}={\displaystyle \frac{\sum _{k=1}^m\left({X_{ki}}^{\prime }-{{\overline{X}}_i}^{\prime }\right)\left({X_{kj}}^{\prime }-{{\overline{X}}_j}^{\prime }\right)}{\sqrt{\sum _{k=1}^m{\left({X_{ki}}^{\prime }-{{\overline{X}}_i}^{\prime }\right)}^2\sum _{k=1}^m{\left({X_{kj}}^{\prime }-{{\overline{X}}_j}^{\prime }\right)}^2}}}$$

(6)

In Equations (5) and (6), R is the correlation coefficient matrix of the standardized matrix $X^{\prime }$; $r_{ij}$ is the correlation coefficient of the i-th row and j-th column in $X^{\prime }$; ${X_{ki}}^{\prime }$ is the standardized value of the k-th row and i-th column in $X^{\prime }$; ${X_{kj}}^{\prime }$ is the standardized value of the k-th row and i-th column in $X^{\prime }$; and ${{\overline{X}}_i}^{\prime }$ and ${{\overline{X}}_j}^{\prime }$ are the mean values of the influencing factors in the i-th and j-th columns, respectively, ($i,j=\mathrm{1,2},\dots ,p$ and $p=m)$.

(c)

The eigenvalue λ of R and its corresponding feature vector μ are calculated. Among them, ${\lambda }_1\ge {\lambda }_2\ge \dots \ge {\lambda }_p$; feature vectors ${\mu }_1,{\mu }_2,\dots \mathrm{and}{\mu }_p$.

(d)

The variance contribution rate and cumulative variance contribution rate of the principal components are calculated. The eigenvalues of the correlation coefficient matrix are equal to the variances of the corresponding principal components, explaining the proportion of the information in each principal component to the total information in the original dataset. The expressions are as follows:

$$e_i={\displaystyle \frac{{\lambda }_i}{\sum _{i=1}^p{\lambda }_i}}$$

(7)

$$E_k={\displaystyle \frac{\sum _{i=1}^k{\lambda }_i}{\sum _{i=1}^p{\lambda }_i}}$$

(8)

In Equations (7) and (8), $e_i$ is the variance contribution rate of the i-th principal component; $E_k$ is the cumulative contribution rate of the first k principal components ($k\le p$ and $p=m$); and ${\lambda }_i$ is the eigenvalue of the i-th principal component ($i=\mathrm{1,2},\dots ,p$ and $p=m$). The ability of variables to express comprehensive information is directly proportional to the variance contribution rate. The greater the cumulative variance contribution rate of the first i principal components, the more the original information contained in the first i principal components.

(e)

Principal component selection. PCA aims to weaken the coupling between the input vectors of the BP neural network, remove redundant information, and fully retain the original data information. Generally, the number of selected principal components should not exceed six, and the cumulative variance contribution rate should be as large as possible (usually not less than 80%).

(f)

Determine input variables. The influencing factors are transformed into uncorrelated variables through linear transformation to reduce the data dimensionality. The variables after reduction can still reflect most information in the original dataset. The input variables for the BP neural network are set as $y_1,y_2,\dots \mathrm{and}{y}_p$. The principal components can be expressed as follows:

$$\left.\begin{array}{c}{y}_1=c_{11}{X}_1+c_{12}{X}_2+\dots +c_{1p}{X}_p\\ \begin{array}{c}{y}_2=c_{21}{X}_1+c_{22}{X}_2+\dots +c_{2p}{X}_p\\ \begin{array}{c}⋮\\ y_p=c_{p1}{X}_1+c_{p2}{X}_2+\dots +c_{pp}{X}_p\end{array}\end{array}\end{array}\right\}$$

(9)

In Equation (9), $y_1,y_2,\dots \mathrm{and}{y}_p$ are the 1st, 2nd, ..., and p-th principal components of the original dataset X, respectively; and $c_{ij}(i=\mathrm{1,2},\dots ,p;j=\mathrm{1,2},\dots ,p;p=m)$ is the load of X on the principal component $y_i(i=\mathrm{1,2},\dots ,pandp=m)$.

3.4. The Principle of the PSO Algorithm

PSO, a prominent algorithm within the domain of swarm intelligence, utilizes a simulation of birds’ foraging behavior to identify optimal solutions. It exhibits notable advantages in terms of the rapid convergence speed, robust performance, and strong capacity for global searching [19]. Because it does not need the feature information from the problem, it can avoid the process of requiring gradients in the gradient descent method. Compared to BP neural networks optimized by genetic algorithms, it can further shorten the training time of neural networks [20]. The basic process of the PSO algorithm is as follows. First, PSO is initialized as a group of random particles (random solutions). Then, the position and velocity of the particles are updated through iterations to search for the optimal solution. In each iteration, the particles track the individual extremum $P_{ibest}$ to find the individual optimal solution and the tail after the global extremum $P_{gbest}$ to derive the population optimal solution. The formulas for updating the position and velocity of the particles are as follows:

$$V_{id}^{k+1}=w{V}_{id}^k+c_{1}Rand()\left(P_{ibest}^k-X_{id}\right)+c_{2}rand()\left(P_{gbest}^k-X_{id}\right)$$

(10)

$$X_{id}^{k+1}=X_{id}^k+V_{id}^{k+1}$$

(11)

In Equations (10) and (11), w is the inertia weight; $c_1$ and $c_2$ are acceleration constants; $Rand\left(\right)$ and $rand\left(\right)$ are two random functions changing between $\left[\mathrm{0,1}\right]$; $X_{id}^k$ denotes the corresponding particle position of $V_{id}^k$; $V_{id}^k$ is the speed of the particle i in the d-dimensional space after the k-th iteration; $P_{ibest}$ is the optimal position experienced by the i-th particle (the optimal fitness); and $P_{gbest}$ is the optimal position experienced by all the particles.

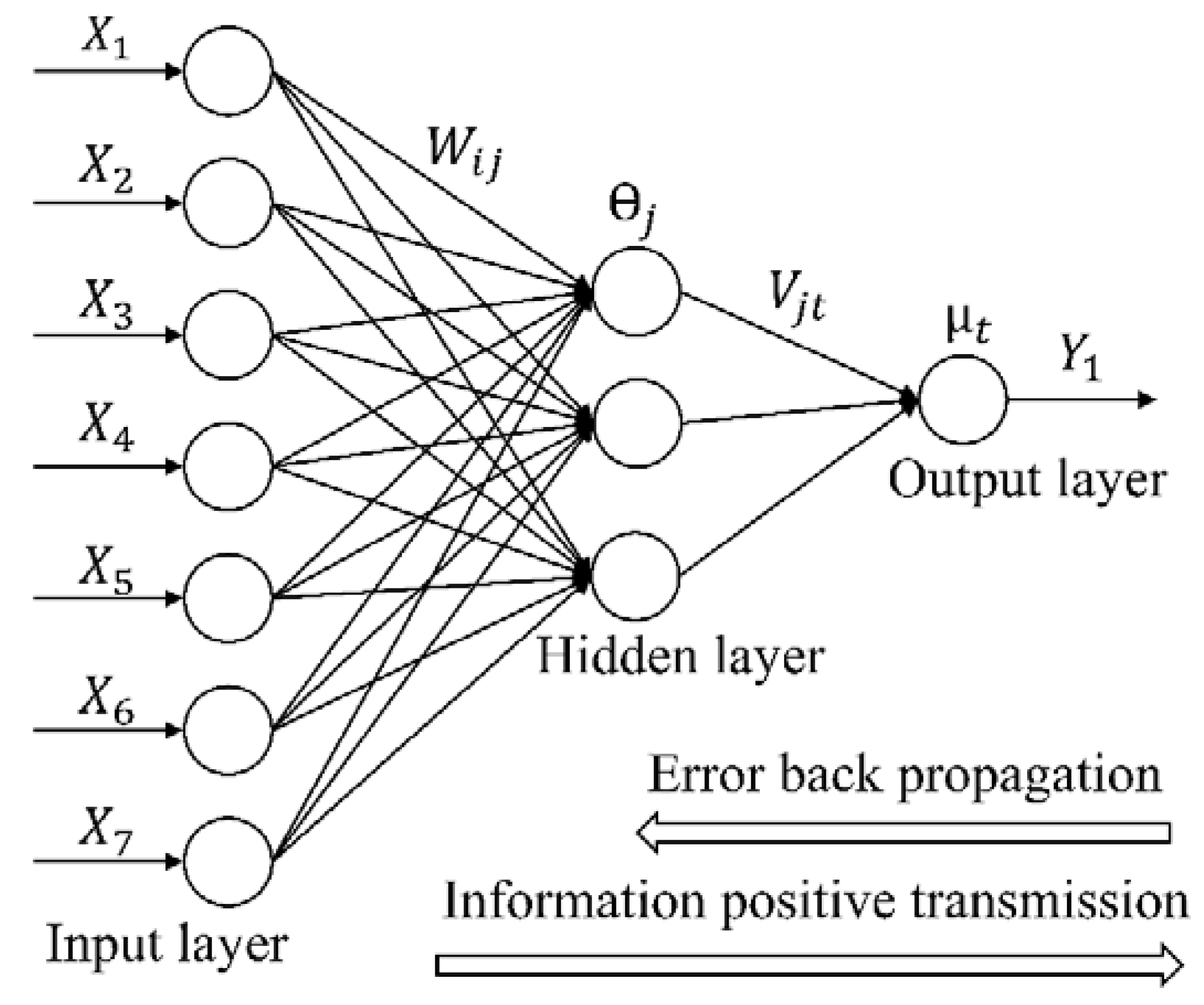
3.5. The Principle of the BP Algorithm

As an extensively used multi-layer feedforward neural network, the principle of the BP neural network is to utilize the forward transmission of information and the backward transmission of errors and to employ the gradient descent method and gradient search technology to minimize the error between the actual and the expected output values. Research has shown that a three-layer BP neural network model effectively captures complex data relationships and approximates intricate nonlinear functions, demonstrating strong nonlinear mapping and generalization capabilities. It is a leading choice for nonlinear prediction [21,22]. The algorithm model of the BP neural network (a 7-3-1 structured BP neural network serves as an illustrative example) is shown in Figure 4.

Among them, $X_1,X_2,\dots {\mathrm{and}X}_7$ are seven sets of input vectors; $Y_1$ is one set of output vectors; $W_{ij}$ is the connection weight between the input layer and the hidden layer; $V_{jt}$ is the connection weight between the hidden layer and the output layer; and ${\mathrm{\theta }}_j$ and ${\mu }_t$ are the node thresholds for the hidden layer and output layer, respectively.

Since BP neural networks are prone to falling into local minima when dealing with highly nonlinear problems, in order to make the deviation between the actual output of each neuron and the target value less than the set value, it is necessary to continuously adjust the weights and thresholds of the network. If the training sample is too large or the relationship between the input and output is complex, the convergence speed of the network will significantly drop. Therefore, BP neural networks have drawbacks, which manifest in low learning efficiency, a slow convergence speed, and susceptibility to being stuck in local minima [22]. The PSO algorithm can be used to optimize the weights and thresholds of the BP neural network, addressing the problems of the network, which are easily falling into local minima and slow convergence.

3.6. The Specific Implementation Process for the Combined Model

The specific implementation process for the combination PCC-PCA-PSO-BP model is as follows:

(a)

Determine the main influencing factors of the checked baggage flow for airport departing passengers.

(b)

Data collection and preprocessing.

(c)

Determine whether data are missing. If there are data missing, calculate the data missing rate. It is generally believed that when the ratio of missing data exceeds 20%, the analytical value of the data will drop remarkably [23]. Otherwise, proceed to step (e).

(d)

If missing data exists, perform numerical interpolation. According to different interpolation methods, the errors between the interpolation values and true values differ. This article uses four interpolation methods (regression interpolation, EM interpolation, multiple interpolation, and mean interpolation) for comparison and selection. The root mean square error (RMSE) and mean absolute percentage error (MAPE) are employed as metrics for the evaluation of the interpolation’s effectiveness:

$$RMSE=\sqrt{{\displaystyle \frac{1}{h}}\sum _{a=1}^n{\left(y_a-\widehat{y_a}\right)}^2}$$

(12)

$$MAPE={\displaystyle \frac{100\mathrm{\%}}{h}}\sum _{a=1}^n\left|{\displaystyle \frac{\widehat{y_a}-y_a}{y_a}}\right|$$

(13)

In Equations (12) and (13), $\widehat{y_{\mathrm{a}}}$ is the interpolation value for the a-th missing position; $y_a$ is the actual value of the a-th missing position ($a=\mathrm{1,2},\dots ,\mathrm{and}n$); n is the number of samples for a single influencing factor; and h is the number of missing values. The smaller the RMSE and MAPE, the better the interpolation effect.

(e)

PCC is adopted in the correlation analysis of the original dataset or interpolated dataset to extract the core influencing factors of baggage flow, reduce the dimensionality of the input vector of the BP neural network, and effectively abate redundant input vector information.

(f)

PCA is conducted on the dataset to weaken the coupling between the input variables of the BP neural network, remove the correlation interference between input vectors, and further lower the dimensionality of the input vectors of the BP neural network while retaining sufficient original data information.

(g)

Determine the topology of the BP neural network. This article uses a three-layer BP neural network structure, including one input layer, one hidden layer, and one output layer. The number of neurons in the input layer is determined by the number of principal components; the number of neurons in the output layer is one, which is the checked baggage flow of departing passengers at airports; the number of neurons in the hidden layer is obtained from the empirical Formula (14):

$$b=\sqrt{d+1}+q$$

(14)

In Equation (14), b represents the number of hidden layer neurons; d is the number of principal components; and q is an integer between $\left[\mathrm{1,10}\right]$.

(h)

Normalize the input vectors of the BP neural network to eliminate the effects of the dimensionality and order of magnitude between input vectors. The normalization formula is as follows:

$$Y_i={\displaystyle \frac{{\gamma }_i-\min \left({\gamma }_i\right)}{\max \left({\gamma }_i\right)-\min \left({\gamma }_i\right)}}$$

(15)

In Equation (15), $Y_i$ is the normalized value of the score vector ${\gamma }_i$ corresponding to the i-th principal component load; and $\max \left({\gamma }_i\right)$ and $\min \left({\gamma }_i\right)$ are the maximum and minimum values in the score vector corresponding to the i-th principal component load, where $i=\mathrm{1,2},\dots ,p$ and $p=m$.

(i)

Initialize the BP neural network and PSO algorithm, setting the parameters (number of swarms, learning factors, inertia weight, etc.) empirically. The particle dimensionality depends on the number of nodes in the BP network’s input, hidden, and output layers.

(j)

Calculate the fitness function value for each particle. By introducing weights and thresholds as particles into the PSO, the fitness function value is a key indicator of the particle quality. The minimum objective function can be derived by minimizing the fitness function. This paper uses the mean square error (MSE) of the BP neural network as the fitness function. The smaller the fitness function, the less the network error, and the better the adaptability of particles.

(k)

Determine the individual extremum and global extremum of particles. If the current particle fitness $<P_{ibest}$, update $P_{ibest}=$ the current particle fitness; otherwise, $P_{ibest}$ remains unchanged. If the current particle fitness $<P_{gbest}$, update $P_{gbest}=$ the current particle fitness; or else, $P_{gbest}$ keeps the same.

(l)

Update the velocity and position of each particle.

(m)

Assign weights and thresholds to the BP neural network based on the obtained global optimal solution.

(n)

Train the dataset using the BP neural network with optimal weights and thresholds and identify whether the training results meet the preset error. The mean absolute error (MAE) and $R^2$ (coefficient of determination) are used for judging the training effectiveness as follows:

$$MAE={\displaystyle \frac{1}{n}}\sum _{j=1}^n\left|\widehat{y_j}-y_j\right|$$

(16)

$$R^2={\displaystyle \frac{1-\sum _{j=1}^n{\left(\widehat{y_j}-y_j\right)}^2}{\sum _{j=1}^n{\left(y_j-\overline{y_j}\right)}^2}}$$

(17)

In Equations (16) and (17), $\widehat{y_j}$ is the predicted value; $y_j$ is the actual value; and $\overline{y_j}$ is the mean of the actual value ($j=\mathrm{1,2},\dots ,n$, $\mathrm{and}n$ is the number of predicted values). The smaller the MAE and the closer $R^2$ is to 1, the higher the prediction accuracy of the model.

(o)

Apply the constructed PCC-PCA-PSO-BP model to predict the flow of checked baggage of departing passengers at airports.

4. Case Study

This article analyzes the sample data of checked baggage flow of departing passengers at Chengdu Shuangliu International Airport in China from August 2017 to May 2023. The raw data were preprocessed using IBM SPSS Statistics 26. MATLAB R2019b was employed for the construction and simulation prediction of the combination model. All experimental processes were conducted on a computer with a 12th Gen Intel(R) Core(TM) i5-12490F 3.00 GHz processor and the Windows 10 Professional 64-bit operating system.

4.1. Analysis of the Main Factors That Influence Baggage Flow

Multiple factors can affect baggage flow to varying degrees. The existence of a strong correlation between baggage flow and airport passenger flow indicates that factors that exert an influence on passenger flow may also have an impact on baggage flow. From a macro perspective, factors such as the regional gross domestic product (GDP) level, the industrial structure, and the population of the airport’s service area exhibit a strong correlation with airport passenger flow. Additionally, the competitive relationship between transportation modes, such as air, railway, and highway, can impact airport passenger flow [24,25]. When predicting and modeling airport passenger flow, the regional GDP is usually regarded as the primary influencing factor. Moreover, there is multicollinearity between the GDP and variables such as the flight mileage, the population, and the proportion of the tertiary industry in the GDP [26,27]. Zhang and Xu conducted a PCA to explore the influencing factors of passenger flow at four Chinese airports with an annual passenger throughput exceeding 10 million [28]. By analyzing the regional GDP, urban population, tourist numbers, railway transportation, and highway transportation, they found that the effect of the same factor would vary with airports. However, the main influencing factors presented high consistency, including tourism resources, the regional GDP, and the competition between transportation modes. In contrast, Gao and Xiao calculated the weight ratios of seven indicators (for example, the regional GDP, the number of tourists and permanent residents) to airport passenger flow using the information entropy method [29]. It has been found that when excluding the effect of total retail sales of consumer goods (TRSCG), the weighting of the GDP based on information entropy is determined to be the least significant, while the relationship between airport passenger flow and GDP growth was weak. Using the Granger causality test method, Wang analyzed the impact of Chinese regional GDP growth on regional freight turnover. A monoidal feedback relationship was disclosed between regional logistics and regional economic growth, indicating that the regional economy could affect regional logistics, but not vice versa. Meanwhile, the impact of the GDP on freight turnover was minor [30]. Li used the gray correlation theory and found a significant promoting effect of the development of regional tourism in China on airport passenger flow [27]. For example, the flight–tourist ratio in Hainan (the ratio of airport passenger flow to the number of received tourists) is up to 69–99%. By comparison, the ratios in the Southwest and Northwest regions exceed those in North and East China. Although the number of tourists has an evident relationship with the growth of airport passenger flow, its correlation with baggage flow may not be linear. Tourists will usually not carry massive baggage. From a micro perspective, the types of flights (international and domestic), the number of routes, and the flight takeoff and landing sorties all impact passenger flow profoundly. International flight passengers have long journeys and travel times, and their baggage flow may be larger than that of domestic flight passengers [10]. Factors such as the months, weekends, and holidays have varying degrees of promoting effects on airport passenger flow [31,32,33]. Furthermore, the influence of baggage flow is also subject to a range of factors, which are difficult to quantify, including passenger psychological factors, airport service levels, checked baggage pricing, and ticket discounts. These factors can have a considerable effect. How to scientifically analyze the weights of these factors is one of the critical research directions.

In summary, it is easy to find that there are many factors that affect baggage flow. Their relationships are not simply linear but intricately nonlinear. Combining the current research status worldwide and the actual operation of the Chengdu Shuangliu International Airport, this article summarizes seven major factors that may affect baggage flow, denoted by the variables X1, X2, X3, X4, X5, X6 and X7, respectively, as listed in

Table 1. Summarizes seven key factors that may affect baggage flow.

Variables	Physicochemical Factors
X1	Different months
X2	Departure passenger flow
X3	Flight takeoff and landing frequency
X4	Total retail sales of consumer goods
X5	Non-working days
X6	Railway passenger flow
X7	Highway passenger flow

.

4.2. Data Collection and Preprocessing

After preliminarily determining the main influencing factors on the checked baggage flow of departing passengers at airports, monthly data were collected and organized into a raw dataset. Among them, data on the checked baggage flow of airport departing passengers, airport departing passenger flow, and flight takeoff and landing sorties were obtained through the baggage handling system of Chengdu Shuangliu International Airport. Data on the monthly non-working days, total retail sales of consumer goods, railway passenger flow, and highway passenger flow were derived from the official website of the Chengdu Municipal Government Statistics Bureau. The data statistics are shown in

Table 2. Missing rate of the dataset.

Variables	Physicochemical Factors	Number of Valid Data	Missing Rate (%)
X1	Different months	70	0
X2	Departure passenger flow	70	0
X3	Flight takeoff and landing frequency	70	0
X4	Total retail sales of consumer goods	70	0
X5	Non-working days	70	0
X6	Railway passenger flow	70	0
X7	Highway passenger flow	70	0
Y1	Baggage flow	59	15.71

. It should be noted that “non-working days” in Table 2 denotes the sum of weekends and legal holidays monthly. Since international flights at Shuangliu International Airport during the COVID-19 pandemic from 2020 to 2022 almost stagnated, the airport’s departure passenger flow, flight takeoff and landing sorties, baggage flow, and other data are all based on domestic flights in China as the statistical source.

Table 2 shows that the equipment of the baggage handling system can cause a partial lack of collected baggage flow data, with a calculated missing rate of 15.71%. Therefore, it is crucial to preprocess the dataset. Missing data commonly exists in practical applications, affecting the validity of research results. The larger the missing rate, the greater the impact on the research results [23]. Generally, there are two ways to handle this issue: deletion and interpolation [34]. The deletion method removes missing parts from the data as a whole, exchanging the number of samples for information integrity, which inevitably leads to information loss. The interpolation method uses known data information to construct a suitable interpolation function to interpolate missing values. Most studies have demonstrated that interpolation is more effective than deletion in processing missing data [35,36]. However, the errors between the interpolation values and the actual values vary with interpolation approaches. Therefore, this article selects four frequently used methods: mean interpolation, regression interpolation, EM interpolation, and multiple interpolation for comparison and selection. Mean interpolation divides variables in a dataset into continuous (interpolate the missing variable based on the average of its values on all other objects) and discontinuous (according to the mode principle in statistics, interpolate the missing variable using its most taken value on all other objects) variables and processes them separately [37]. In the monotonic missing data mode, regression interpolation uses the predicted regression values to substitute for missing values [38]. Based on the marginal distribution of data, EM interpolation performs maximum likelihood estimation for unknown parameters. The interpolation value is determined by maximizing the logarithmic likelihood function by alternatively executing expectation and maximization. Expectation is performed with respect to unknown underlying variables and employs the current estimation of the parameters conditioned upon the observations; maximization updates the estimation of the parameters [39]. Based on the Bayesian theory, multiple interpolation uses the Gibbs algorithm to handle missing data [40]. The specific process of numerical interpolation in this article is as follows. The data missing from the dataset belongs to univariate missing and missing completely at random. Therefore, first, complete data from 2019 and 2020 are selected as the test objects and are randomly deleted to ensure that the missing rate is similar to that of the actual baggage flow. Then, the interpolation effect is verified through four interpolation methods. The RMSE and MAPE are adopted to identify the optimal interpolation method. Finally, the optimal interpolation method is used to perform numerical interpolation on the missing data of the actual baggage flow to guarantee the reliability and stability of the interpolation effect. The comparison of the effects of interpolation methods is shown in

Table 3. Experimental comparisons among four numerical interpolation methods.

Methods	Years
	2019		2020
	Missing Rate (%)
	16.67		16.67
	RMSE	MAPE	RMSE	MAPE
Mean imputation	57,555.01	0.0825	25747.71	0.0367
Regression imputation	56,797.71	0.0933	40,088.34	0.0490
Expectation maximization	55,999.58	0.0743	25,747.71	0.0734
Multiple imputation	37,891.81	0.0649	7442.74	0.0201

.

The RMSE and MAPE of the interpolation methods in Table 3 show that in the univariate missing mode with a missing rate of 16.67%, multiple interpolation achieves the best effect, followed by mean interpolation, while regression interpolation and EM interpolation have inferior performance. Actually, the errors of the four interpolation methods are all within a reasonable range when the missing data are slight. Mean interpolation and regression interpolation both use a single method to handle missing data. As an iterative algorithm, EM interpolation arbitrarily selects initial values. However, the model is highly dependent on the selection of initial values. The quality of the initial values directly decides the training effectiveness of the model. Therefore, it has poor stability. Multiple interpolation utilizes information not only from missing variables but also from auxiliary variables. The stronger the correlation between auxiliary and missing variables, the more information can be applied, and the better the interpolation effect [40]. When using the multiple interpolation method in this article, the other two variables (departure passenger flow and flight takeoff and landing frequency) are set as auxiliary variables, generating multiple intermediate interpolation values during the calculation and providing plenty of information with which to measure the uncertainty of the estimation results. Using the variation between interpolation values to reflect the uncertainty of non-response is the reason why the multiple interpolation method has the best interpolation effect with a low data loss rate.

After numerical interpolation of the original dataset, the departure passenger flow, flight takeoff and landing frequency, and baggage flow were organized over time, as shown in Figure 5. Figure 5a,b show that the changing trends of the passenger flow and flight takeoff and landing sorties are highly consistent; the trends of the changes in the baggage flow and passenger flow in Figure 5c have similarities and significant differences; Figure 5d exhibits an overall upward trend in the total retail sales of consumer goods over time; Figure 5e illustrates a highly periodic variation in non-working days over time; and Figure 5f,g represent the railway passenger flow and highway passenger flow, respectively, and their changing trends have strong similarities to those in Figure 5a,b.

4.3. PCC Is Conducted on the Dataset

According to Table 1, baggage flow is influenced by seven physicochemical factors, including the airport departure passenger flow, flight takeoff and landing sorties, and total retail sales of consumer goods. The Pearson correlation coefficient test of these influencing factors is shown in

Table 4. PCC is conducted on the dataset.

Variables	Variables
	X1	X2	X3	X4	X5	X6	X7
Coefficient (r)	−0.321	0.793	0.759	−0.135	0.308	0.544	0.585
Significant difference (Sig.)	0.019	0.000	0.000	0.333	0.025	0.000	0.000

.

According to the validation principle of the Pearson correlation coefficient, the larger the absolute value of the correlation coefficient of two indicators, the stronger the correlation between the two; positive and negative correlation coefficients indicate corresponding positive and negative correlations between the two, respectively. Table 4 shows that besides the total retail sales of consumer goods, the Pearson correlation coefficients between each indicator and baggage flow are all greater than the absolute value |0.3|, and the significance levels are all less than 0.05, implying that each indicator is significantly correlated with baggage flow. The Pearson correlation coefficient between the total retail sales of consumer goods and baggage flow is −0.135, with a significance of 0.333, denoting a weak relationship between baggage flow at Chengdu Shuangliu International Airport and the total retail sales of consumer goods. To further verify the relationship between the total retail sales of consumer goods and baggage flow, the partial correlation coefficient method is used to verify the degree of pure correlation between the two [41]. Taking x, y, and z as examples, where z is the control variable, the partial correlation coefficient between x and y is as follows:

$$r_{xy,z}={\displaystyle \frac{r_{xy}-r_{xz}{r}_{yz}}{\sqrt{\left(1-r_{xz}^2\right)\left(1-r_{yz}^2\right)}}}$$

(18)

In Equation (18), $r_{xy}$ represents the Pearson correlation coefficient between x and y; $r_{xz}$ denotes the Pearson correlation coefficient between x and z; and $r_{yz}$ stands for the Pearson correlation coefficient between y and z.

It is generally believed that transportation is closely related to the economy, and the more developed the economy, the greater the traffic flow in the region [24,25,30,42]. With the airport departure passenger flow, railway passenger flow, and highway passenger flow as control variables, the partial correlation coefficient between the total retail sales of consumer goods and baggage flow is analyzed. The results are shown in

Table 5. The partial correlation coefficient between the TRSCG and baggage flow is analyzed.

Control Variables	Variables	Coefficient (r)	Significant Difference (Sig.)
X2	Y1 & X4	−0.024	0.844
X6
X7

.

From Table 5, it can be seen that after excluding the effects of the airport departure passenger flow, railway passenger flow, and highway passenger flow on the correlation between the total retail sales of consumer goods and baggage flow, the partial correlation coefficient between the two is −0.024, with a significance of 0.844, further verifying that the impact of the total retail sales of consumer goods on baggage flow is extremely weak. Hong et al. examined the relationship between transportation infrastructure and regional economic growth in 31 Chinese provinces and found land and water transport to have significant impacts, while air transport’s contribution was relatively minor [43]. Conversely, Hakim et al., investigating the Granger causality between air transportation and economic growth across South Asian countries, concluded that increases in air travel had no apparent impact on the economy and no reciprocal relationship existed [44]. Therefore, this article excludes the total retail sales of consumer goods and takes the remaining six physicochemical factors (months, airport departure passenger flow, flight takeoff and landing sorties, non-public days, railway passenger flow, and highway passenger flow) as the core influencing factors of baggage flow.

4.4. PCA Is Conducted on the Dataset

PCA is used to weaken the coupling between the input variables in the BP neural network, remove redundant information, decrease the input dimensionality of the BP neural network, and promote algorithm efficiency and accuracy. After normalizing the dataset of the six physicochemical factors, PCA is performed to obtain six principal components. The scree plot of the six principal components is shown in Figure 6. The eigenvalues represent the magnitude of the influence of components on the indicator variables. Therefore, principal components with an eigenvalue larger than one (λ > 1) are generally selected for discussion. The variance contribution rate and cumulative variance contribution rate of the principal components are shown in

Table 6. Eigenvalue and cumulative contribution rate of variance.

Components	Eigenvalue (λ)	Proportion of the Initial Eigenvalue’ Variance (%)	Cumulative Contribution Rate (%)
1	2.631	43.856	43.856
2	1.266	21.105	64.961
3	1.029	17.142	82.103
4	0.749	12.484	94.587
5	0.311	5.178	99.765
6	0.014	0.235	100.000

. Based on Figure 5 and Table 6, it can be seen that there are three principal components with eigenvalues greater than one: the first, second, and third principal components, of which the eigenvalues are 2.631, 1.266, and 1.029, respectively, representing 4.926 variables in total. The cumulative variance contribution rates of the three principal components are 43.856%, 64.961%, and 82.103%, respectively, indicating that the information in the first three principal components can reflect the majority of that in the six physicochemical factors.

The obtained load matrices of the first three principal components are shown in

Table 7. Load matrix of the principal components.

Variables	Components
	1	2	3
X1	0.097	−0.763	0.169
X2	0.970	0.064	0.063
X3	0.973	0.010	0.012
X5	0.133	0.292	−0.868
X6	0.414	0.662	0.444
X7	−0.738	0.395	0.214

. The coefficient of the principal component load matrix represents the degree of correlation between each indicator and the principal component. Positive and negative values indicate positive and negative correlations, respectively. The closer the absolute value of the coefficient is to 1, the higher the degree of correlation. Table 6 and Table 7 show that the variance contribution rate of the first principal component is much higher than that of the second and third principal components, indicating that the first principal component plays a dominant role in the analysis and evaluation. Moreover, the indicators with higher absolute load values in the first principal component are the airport departure passenger flow and flight takeoff and landing sorties, demonstrating their leading role in baggage flow; they are followed by the highway passenger flow, indicating that other transportation modes also significantly impact baggage flow. In the second principal component, the months and railway passenger flow have higher absolute load values, implying that other modes of transportation and months have remarkable effects on the changes in baggage flow. Regarding the third principal component, there is a high load on non-working days, indicating that vacation factors such as holidays and weekends contribute to the changes in baggage flow. From Table 7 and Equation (9), the first three principal components $y_1,y_2,\mathrm{and}{y}_3$ can be obtained, as shown in Equation (19). PCA lowers the input vectors of the BP neural network from six physicochemical factors to three, thereby abating the network input and enhancing the efficiency and quality of the algorithm.

$$\left.\begin{array}{c}{y}_1=0.097X_1+0.97X_2+0.973X_3+0.133X_4+0.414X_5-0.738X_6\\ \begin{array}{c}{y}_2=-0.763X_1+0.064X_2-0.01X_3+0.292X_4+0.662X_5+0.395X_6\\ \begin{array}{c}{y}_3=0.169X_1+0.063X_2+0.012X_3-0.868X_4+0.444X_5+0.214X_6\end{array}\end{array}\end{array}\right\}$$

(19)

4.5. The PCC-PCA-PSO-BP Model Is Used to Predict Baggage Flow

This article uses the three sets of data after the PCA and baggage flow data as the test sample dataset. The sample data are divided into training samples (the first 70%) and prediction samples (the last 30%). The MAE and $R^2$ are adopted to evaluate the fitting effect of the prediction. When selecting the BP neural network topology, in order to decrease the complexity of the neural network, this paper utilizes a network structure with a single hidden layer. According to Equation (14), the number of neurons in the hidden layer can be any integer between [3,12]. The network can be trained multiple times using the Levenberg–Marquardt (L-M) optimization algorithm [45]. Finally, the optimal fitting effect of the network is achieved when the number of neurons in the hidden layer is four. The activation function of the neural network adopts the sigmoid function, with a training frequency of 1000, a target error of 1 × 10⁻⁶, a learning rate of 0.1, a particle population of 50, a maximum population iteration of 20, a learning factor of 2, minimum and maximum limiting speeds of −1 and 1, and lower and upper boundaries of −1 and 1. The test results of the combination model in this article are compared with those of the BP neural network, PCA-BP, PSO-BP, and PCA-PSO-BP models. The performance of the trained networks is shown in Figure 7. The computational efficiencies of the five models are various. The PCC-PCA-PSO-BP model has the highest convergence speed, followed by PCA-PSO-BP, PSO-BP, PCA-BP, and BP.

Table 8. Comparison of the MAE and R2 of different forecasting models.

Prediction Model	MAE (1 × 104)	R2
BP	7.0526	0.81057
PCA-BP	5.2446	0.87192
PSO-BP	5.8072	0.83231
PCA-PSO-BP	4.8698	0.91228
PCC-PCA-PSO-BP	4.3621	0.94633

compares the predictive performance of the five models. Figure 7 and Table 8 show that among the five models, PCC-PCA-PSO-BP has the fastest convergence speed and best overall network fitting performance; its MAE and R2 are 10.43% and 3.73% higher than the PCA-PSO-BP model, 24.88% and 13.70% higher than the PSO-BP model, 16.83% and 8.53% higher than the PCA-BP model, and 38.15% and 16.75% higher than the BP neural network model. This is because PSO is used to optimize the initial weights and thresholds of the BP neural network, which can significantly shorten the training time of the neural network and enable it to converge faster. Moreover, PCC and PCA effectively decrease the redundant information of the input vectors and weaken the coupling between the input variables in the BP neural network. Due to the reduction in input nodes, the BP neural network can better handle the complexity of the model, promoting the computational efficiency and accuracy of the network. Therefore, the model in this article is superior in terms of the convergence speed and prediction accuracy to the other four models, confirming its effectiveness and feasibility.

5. Conclusions

Predicting the checked baggage flow for departing passengers at airports presents challenges due to its inherent nonlinearity and randomness. While passenger flow and baggage flow are strongly correlated, the growth of departing passengers does not always translate directly into an increase in checked baggage. This nonlinear relationship suggests that simply relying on passenger flow forecasts to predict baggage flow could overlook crucial baggage flow characteristics. Multiple factors can affect baggage flow, and their impacts are diverse. This article first analyzes and summarizes the main factors affecting baggage flow. Then, an efficient baggage flow prediction model is established, which can significantly improve the efficiency and accuracy of baggage flow prediction. The primary conclusions of this article are as follows:

• Univariate missing data exist in the dataset of factors affecting baggage flow, which belongs to the completely missing at random pattern. Under low missing rates, compared with mean interpolation, regression interpolation, and EM interpolation, multiple interpolation presents superior numerical interpolation performance.
• Unlike the factors that affect the airport departure passenger flow, the total retail sales of consumer goods have a tenuous relationship with baggage flow, and the two variables do not exhibit a reciprocal relationship. The departure passenger flow and flight takeoff and landing sorties play a dominant role in baggage flow; the railway passenger flow, highway passenger flow, and months have significant impacts on baggage flow changes; and holiday and weekend factors also contribute to baggage flow changes.
• In terms of the performance of the baggage flow prediction, the combination PCC-PCA-PSO-BP model designed in this article is compared with four models: BP, PCA-BP, PSO-BP, and PCA-PSO-BP. PCC-PCA-PSO-BP achieves a faster convergence speed and higher accuracy, which can evidently improve on the shortcomings of traditional BP neural networks. This verifies the effectiveness and feasibility of the algorithm in predicting the baggage flow of departing passengers at airports.

Predicting changes in baggage flow helps civil aviation traffic management departments implement efficient and intelligent allocation and optimization of service resources. For example, baggage check-in and security resources can be allocated more rationally by anticipating different baggage flow patterns at different times. At the baggage sorting link, pre-setting the sorting lines and the number of carousels can optimize equipment utilization rates. Accurate baggage flow prediction allows for the rational planning of aircraft belly bin utilization during baggage transport. By improving the efficiency of baggage handling, this approach reduces mishandled bags and minimizes economic losses. Meanwhile, there are limitations in the study of baggage flow in this article. For instance, how some factors that are difficult to quantify, such as passenger psychological factors, airport service levels, checked baggage prices, and ticket discounts, affects baggage flow. This raises the question of whether the model in this article still has advantages compared to other intelligent algorithms, such as SVM and artificial neural network algorithms (for example, long short-term memory networks (LSTMs) and recursive neural network (RNN). These areas constitute critical directions for future research endeavors.