Optimization of Thermal Management for the Environmental Worthiness Design of Aviation Equipment Using Phase Change Materials
Abstract
1. Introduction
2. Physical Model and Numerical Method
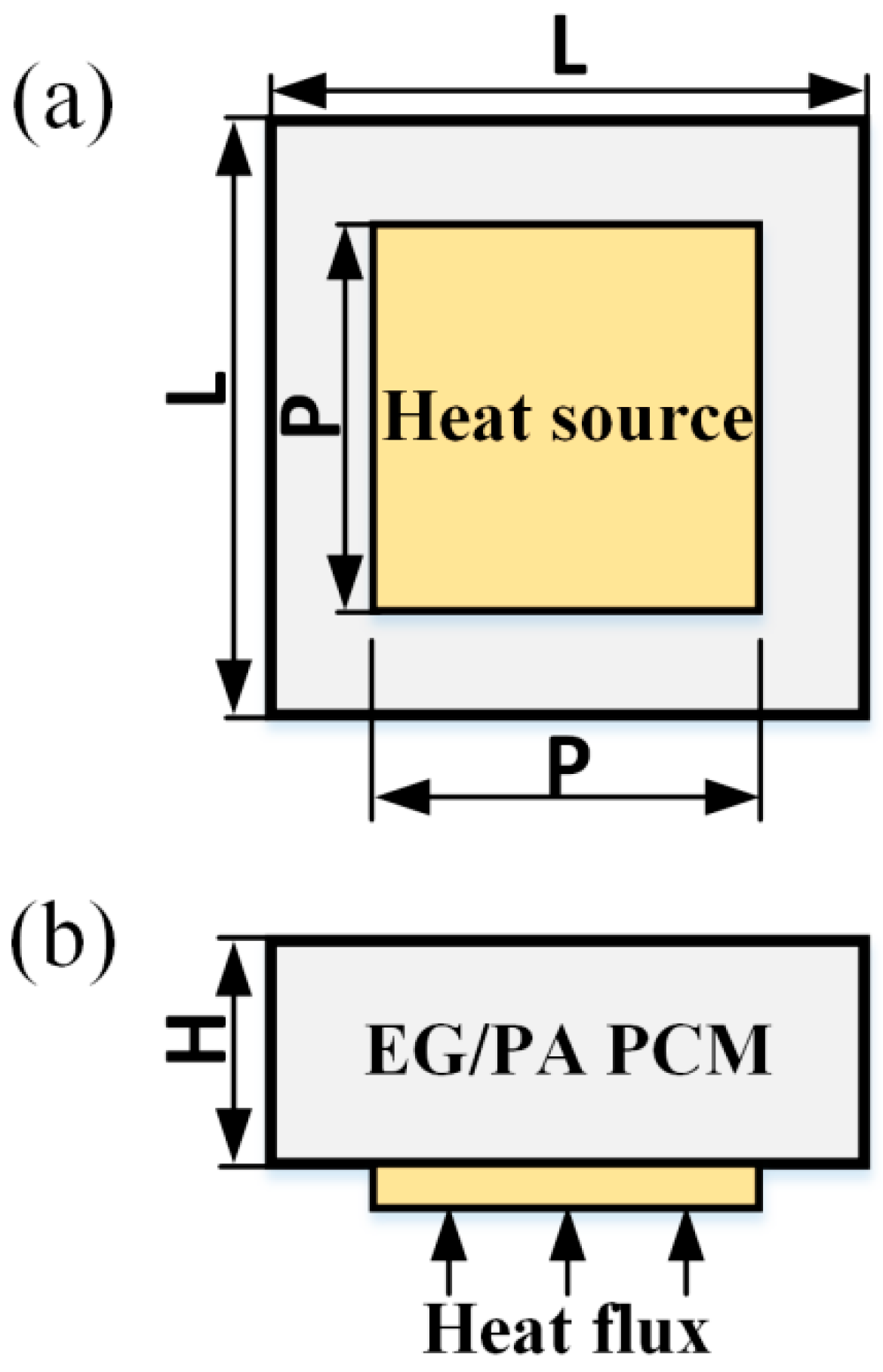
2.1. Physical Model Description
2.2. Numerical Model
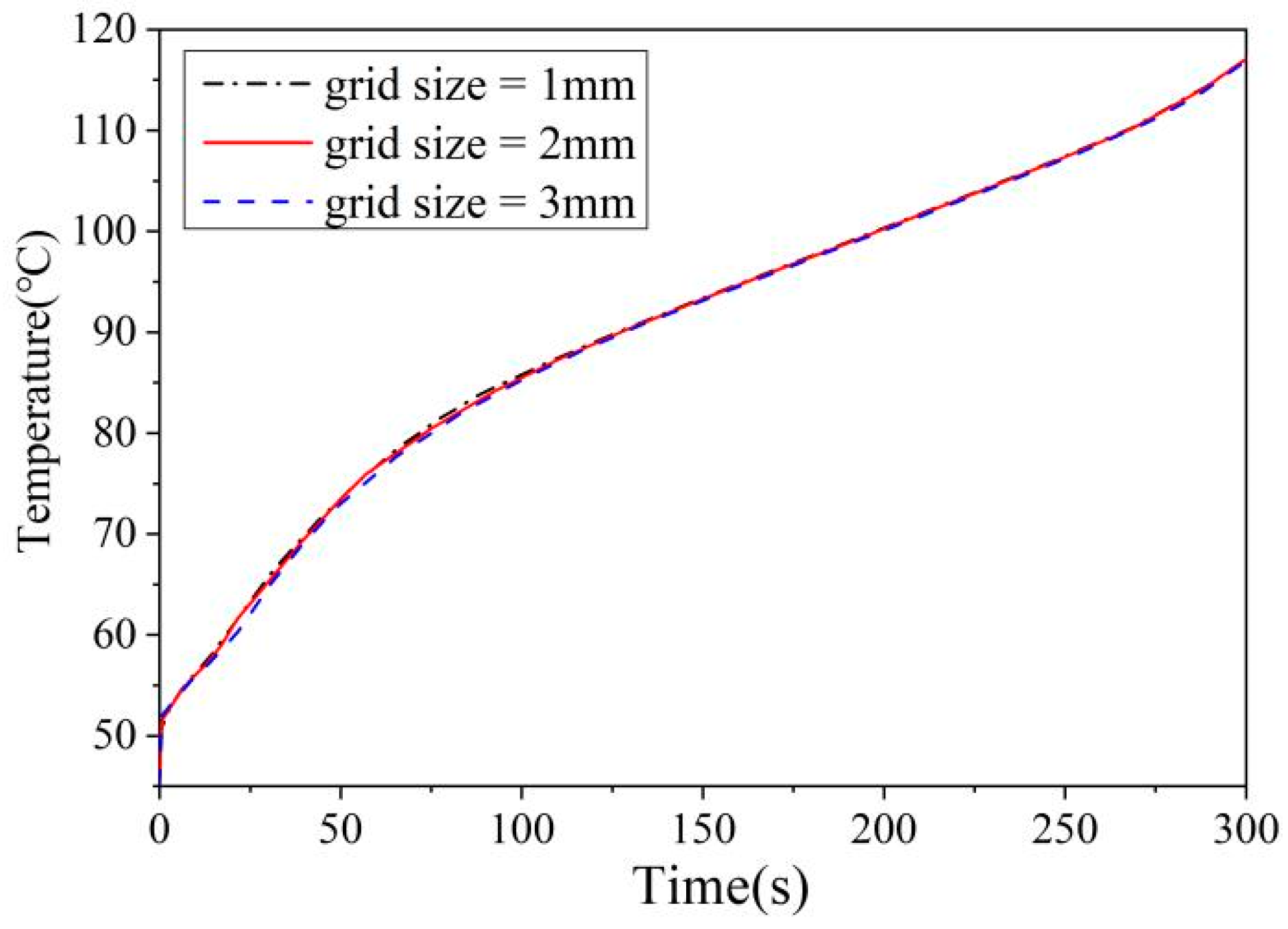
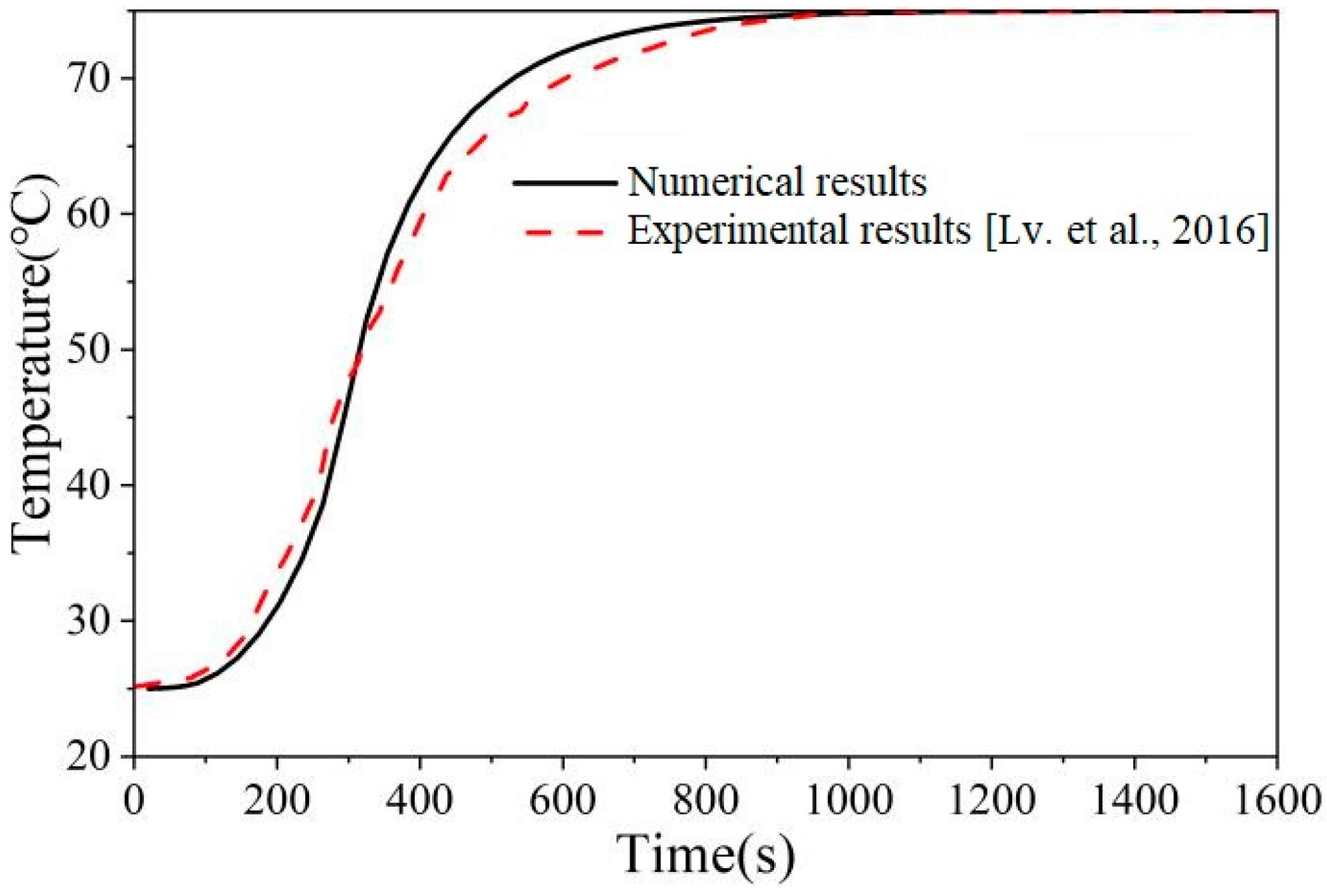
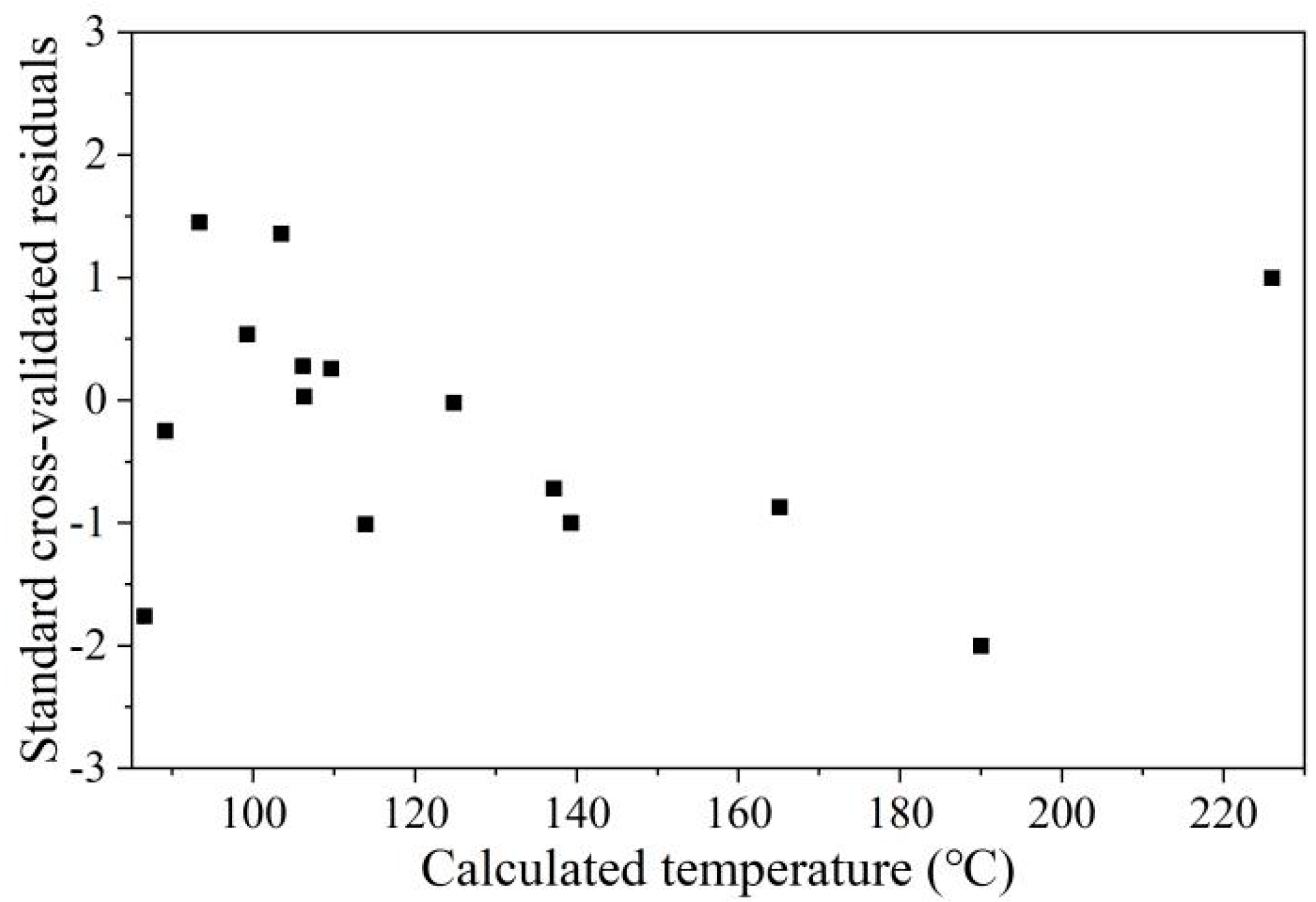
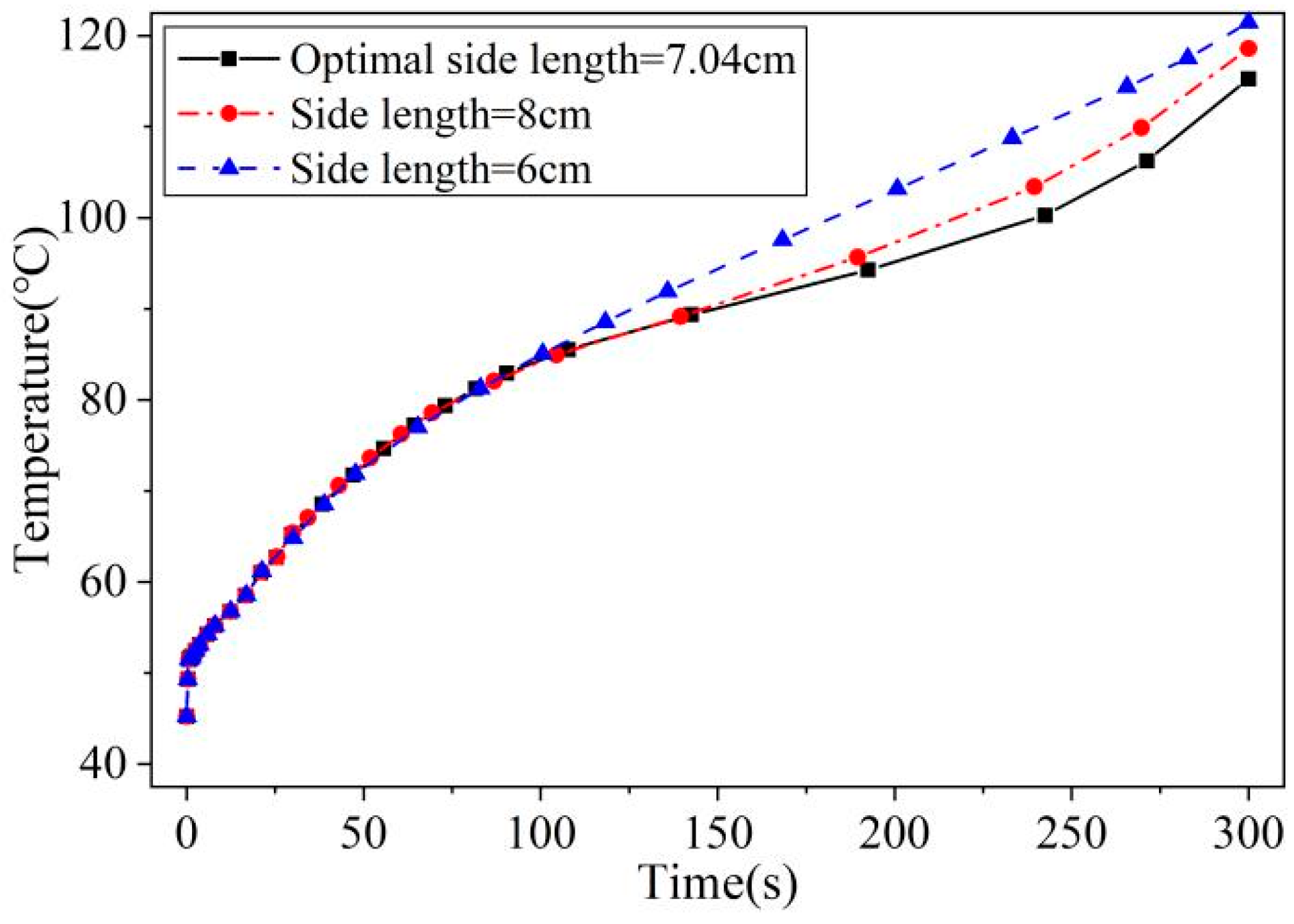
2.3. Model Validation
3. Optimization Method
3.1. Problem Description
- (1)
- The volume of the heat sink is fixed.
- (2)
- The EG mass fraction is in the interval [0, 0.5].
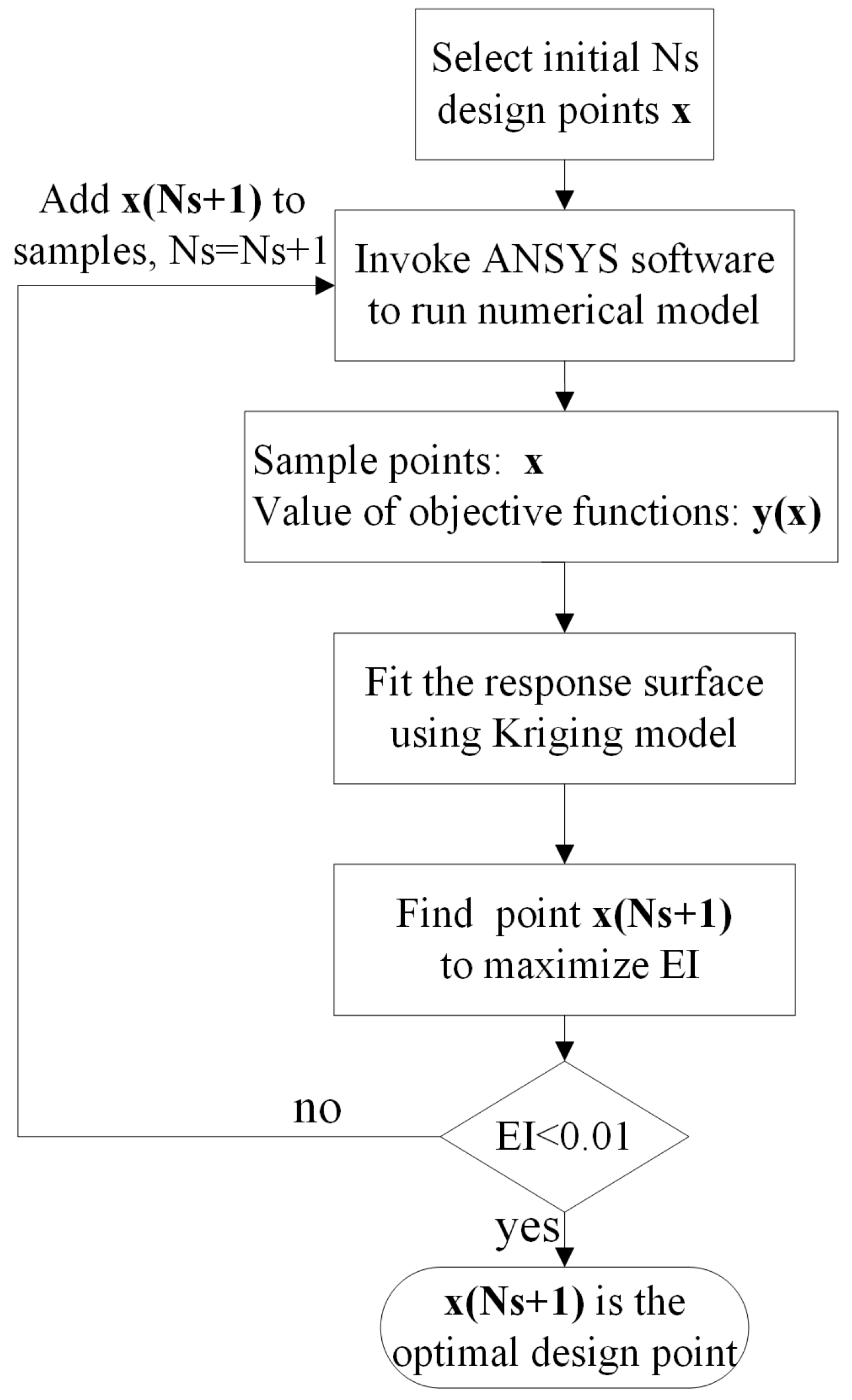
3.2. The Efficient Global Optimization (EGO) Method Using the Kriging Model
3.3. Precision of the Kriging Model
4. Results and Discussion
4.1. Results of the Optimal Design
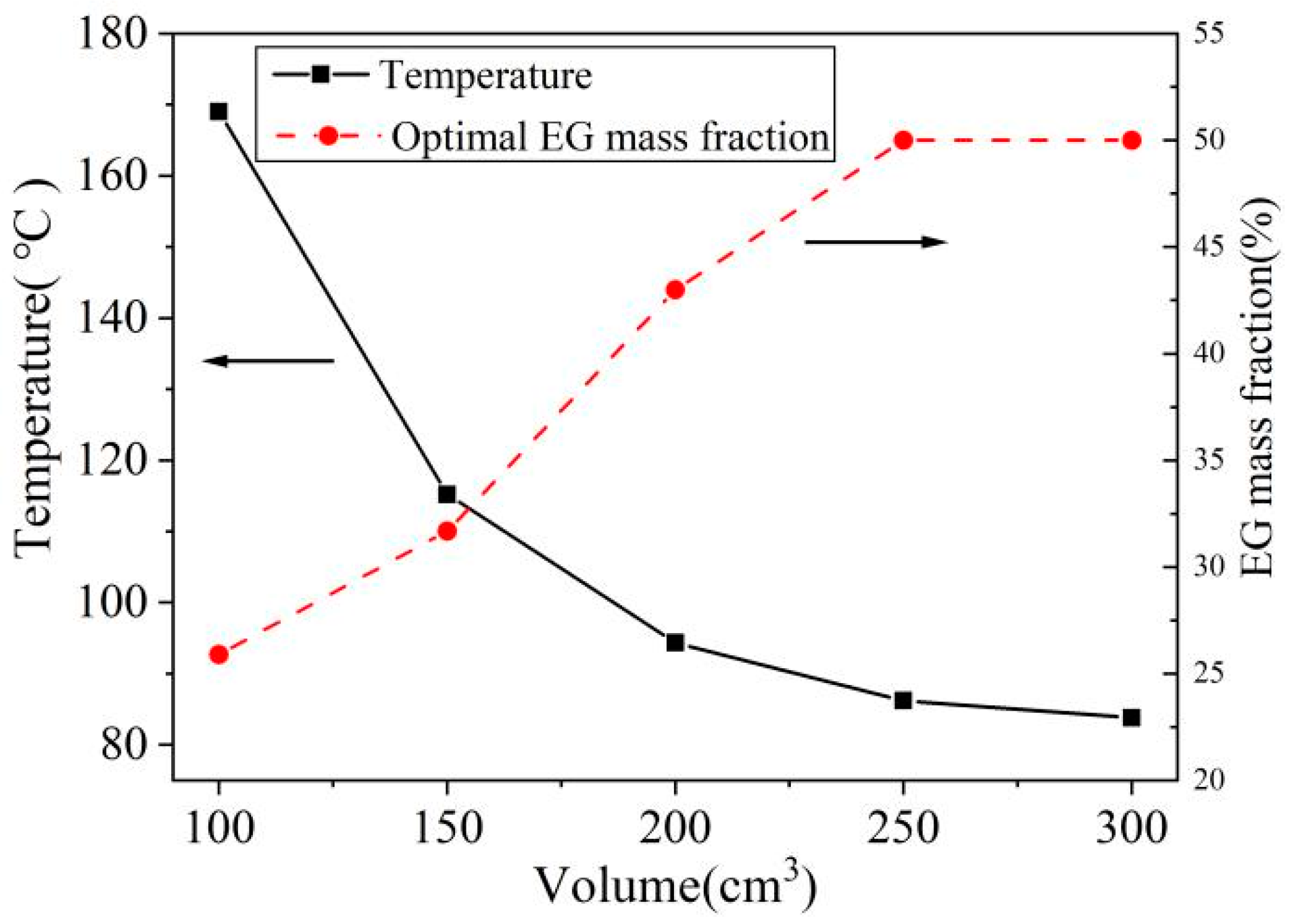
4.2. Effect of Heat Sink Volume on Optimal Parameters
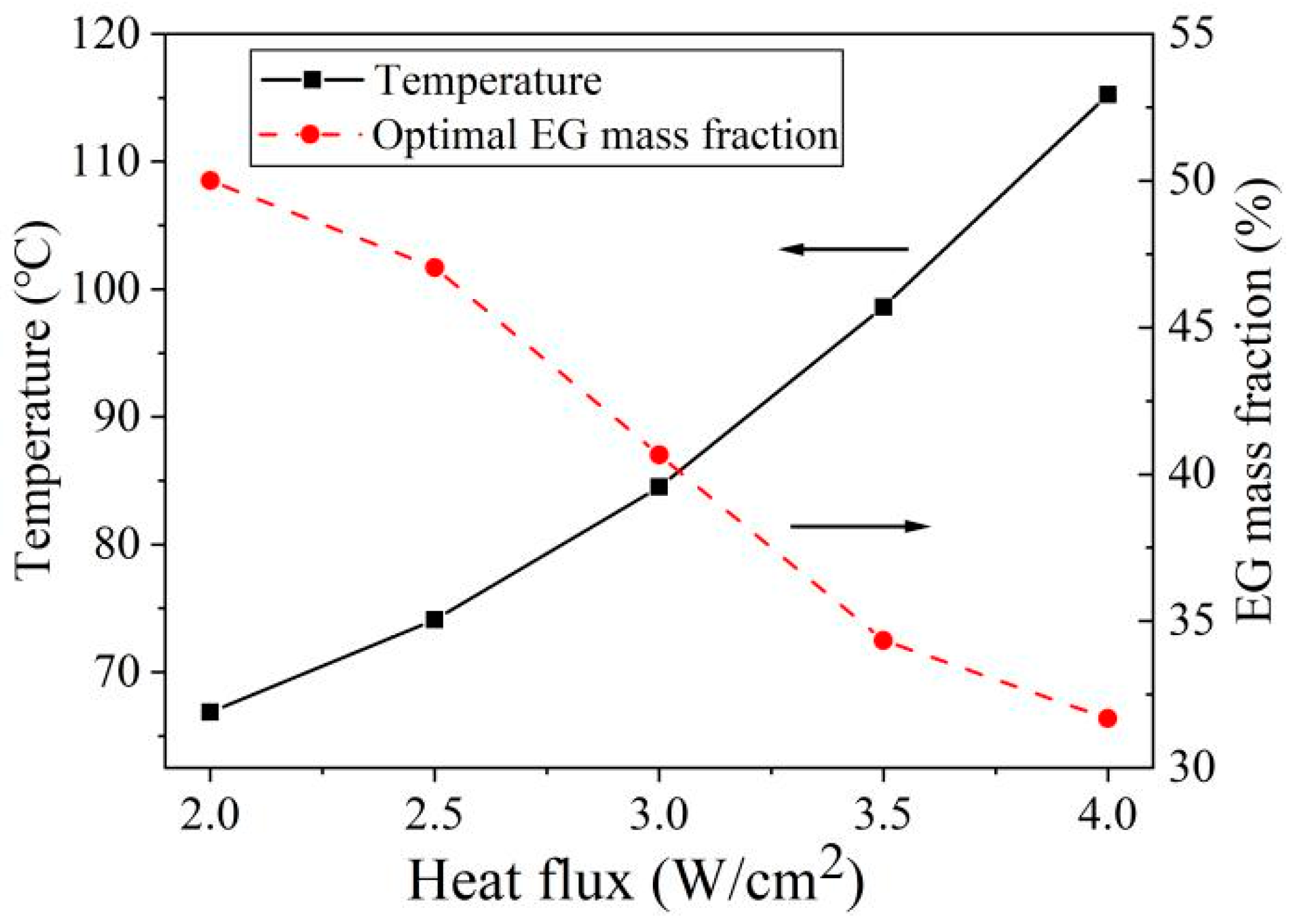
4.3. Effect of Heat Flux on Optimal Parameters
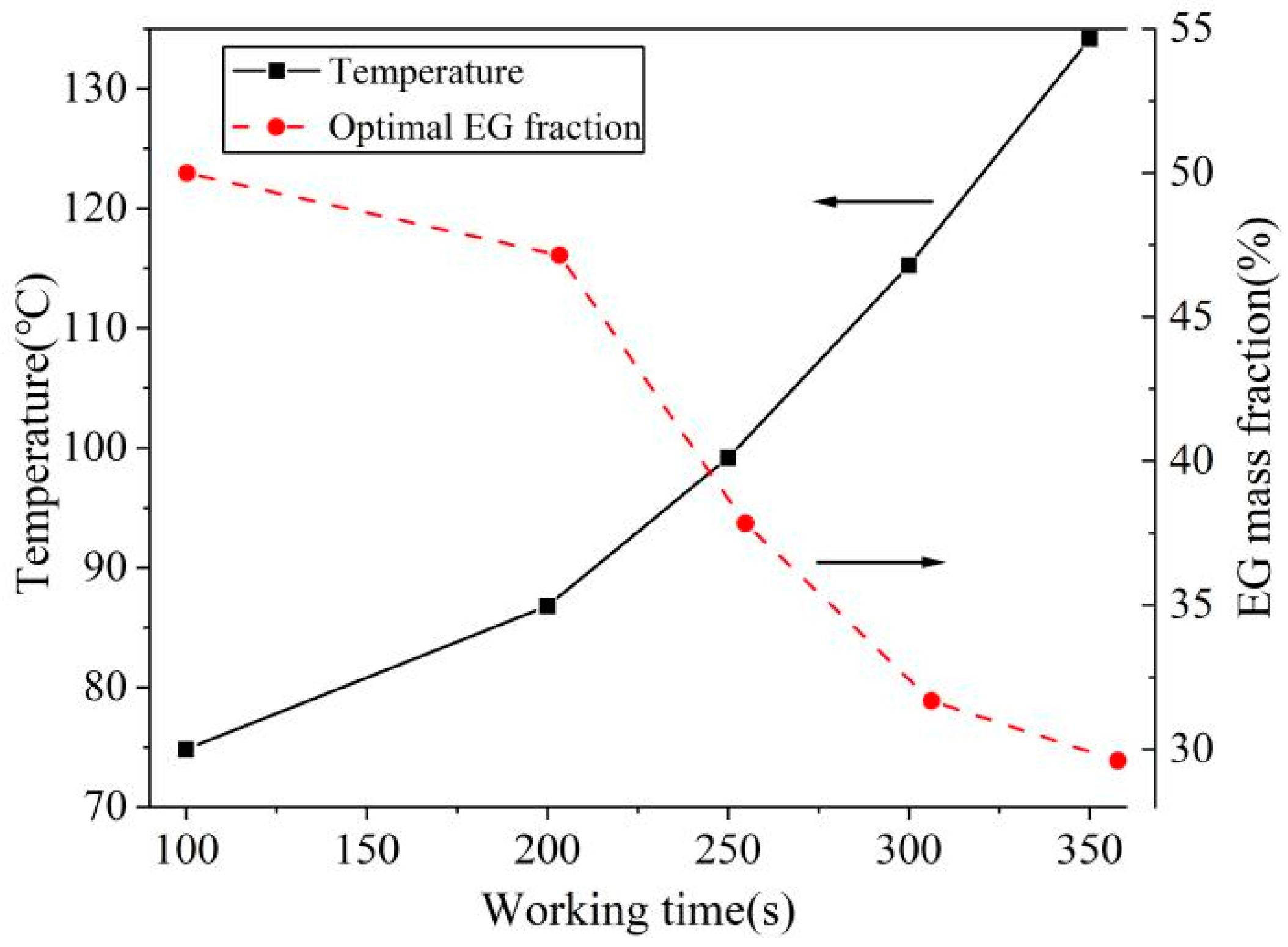
4.4. Effect of Working Time on Optimal Parameters
5. Conclusions
- (1)
- The proposed optimization method is efficiently finds the optimal parameters of the heat sink without a lot of time-consuming numerical processes.
- (2)
- The optimal EG mass fraction increases with the rise in heat sink volume and decreases with the increase in heat flux and working time.
- (3)
- The optimal ratio of the height to the length of the heat sink is 0.43.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ruoji, Z.; Zhang, J.; Zhang, J. The Impact of In-Flight Acceleration Environments on the Performance of a Phase-Change Heat Exchanger Unit with Layered Porous Media. Aerospace 2024, 11, 335. [Google Scholar] [CrossRef]
- Jouhara, H.; Żabnieńska-Góra, A.; Khordehgah, N.; Ahmad, D.; Lipinski, T. Latent thermal energy storage technologies and applications: A review. Int. J. Thermofluids 2020, 5, 100039. [Google Scholar] [CrossRef]
- Ding, C.; Zhang, C.; Ma, L.; Sharma, A. Numerical investigation on melting behaviour of phase change materials/metal foam composites under hypergravity conditions. Appl. Therm. Eng. 2022, 207, 118153. [Google Scholar] [CrossRef]
- Levin, P.P.; Shitzer, A.; Hetsroni, G. Numerical optimization of a PCM based heat sink with internal fins. Int. J. Heat Mass Transf. 2013, 61, 638–645. [Google Scholar] [CrossRef]
- Ling, Z.; Zhang, Z.; Shi, G.; Fang, X.; Wang, L.; Gao, X.; Fang, Y.; Xu, T.; Wang, S.; Liu, X. Review on thermal management systems using phase change materials for electronic components, Li-ion batteries and photovoltaic modules. Renew. Sustain. Energy Rev. 2014, 31, 427–438. [Google Scholar] [CrossRef]
- Jaguemont, J.; Omar, N.; den Bossche, P.; Mierlo, J. Phase-change materials (PCM) for automotive applications: A review. Appl. Therm. Eng. 2018, 132, 308–320. [Google Scholar] [CrossRef]
- Tomizawa, Y.; Sasaki, K.; Kuroda, A.; Takeda, R.; Kaito, Y. Experimental and numerical study on phase change material (PCM) for thermal management of mobile devices. Appl. Therm. Eng. 2016, 98, 320–329. [Google Scholar] [CrossRef]
- Huang, R.; Li, Z.; Hong, W.; Wu, Q.; Yu, X. Experimental and numerical study of PCM thermophysical parameters on lithium-ion battery thermal management. Energy Rep. 2020, 6, 8–19. [Google Scholar] [CrossRef]
- Jiang, G.; Huang, J.; Liu, M.; Cao, M. Experiment and simulation of thermal management for a tube-shell Li-ion battery pack with composite phase change material. Appl. Therm. Eng. 2017, 120, 1–9. [Google Scholar] [CrossRef]
- Sami, S.; Etesami, N. Heat transfer enhancement of microencapsulated phase change material by addition of nanoparticles for a latent heat thermal energy storage system. Energy Rep. 2021, 7, 4930–4940. [Google Scholar] [CrossRef]
- EL Hasadi, Y.M.F.; Khodadadi, J.M. Numerical simulation of solidification of colloids inside a differentially heated cavity. J. Heat Transf. 2015, 137, 072301. [Google Scholar] [CrossRef]
- Qu, Z.; Li, W.; Wang, J.; Tao, W. Passive thermal management using metal foam saturated with phase change material in a heat sink. Int. Comm. Heat Mass Transf. 2012, 39, 1546–1549. [Google Scholar] [CrossRef]
- Sar, A.; Karaipekli, A. Preparation, thermal properties and thermal reliability of palmitic acid/expanded graphite composite as form-stable PCM for thermal energy storage. Sol. Energy Mater. Sol. Cells 2009, 93, 571–576. [Google Scholar] [CrossRef]
- Zhao, C.; Wang, J.; Sun, Y.; He, S.; Hooman, K. Fin design optimization to enhance PCM melting rate inside a rectangular enclosure. Appl. Energy 2022, 321, 119368. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.; Wu, D. Microencapsulation of n-dodecane into zirconia shell doped with rare earth: Design and synthesis of bifunctional microcapsules for photoluminescence enhancement and thermal energy storage. Energy 2016, 97, 113–126. [Google Scholar] [CrossRef]
- Ao, C.; Yan, S.; Zhao, S.; Hu, W.; Zhao, L.; Wu, Y. Stearic acid/expanded graphite composite phase change material with high thermal conductivity for thermal energy storage. Energy Rep. 2022, 8, 4834–4843. [Google Scholar] [CrossRef]
- Khanna, S.; Reddy, K.S.; Mallick, T.K. Optimization of solar photovoltaic system integrated with phase change material. Sol. Energy 2018, 163, 591–599. [Google Scholar] [CrossRef]
- Yang, X.-H.; Tan, S.-C.; He, Z.-Z. Evaluation and optimization of low melting point metal PCM heat sink against ultra-high thermal shock. Appl. Therm. Eng. 2017, 119, 34–41. [Google Scholar] [CrossRef]
- Sciacovelli, F.; Gagliardi, V.; Verda, V. Maximization of performance of a PCM latent heat storage sys-tem with innovative fins. Appl. Energy 2015, 137, 707–715. [Google Scholar] [CrossRef]
- Alayil, R.; Balaji, C. Conjugate Heat Transfer in Latent Heat Thermal Storage System With Cross Plate Fins. J. Heat Transf. 2015, 137, 102302. [Google Scholar] [CrossRef]
- Augspurger, M.; Choi, K.K.; Udaykumar, H.S. Optimizing fin design for a PCM-based thermal storage device using dynamic Kriging. Int. J. Heat Mass Transf. 2018, 121, 290–308. [Google Scholar] [CrossRef]
- Pizzolato, A.; Sharma, A.; Maute, K.; Sciacovelli, A.; Verda, V. Topology optimization for heat transfer enhancement in latent heat thermal energy storage. Int. J. Heat Mass Transf. 2017, 113, 875–888. [Google Scholar] [CrossRef]
- Jiang, G.; Huang, J.; Fu, Y.; Cao, M.; Liu, M. Thermal optimization of composite phase change material/expanded graphite for Li-ion battery thermal management. Appl. Therm. Eng. 2016, 108, 1119–1125. [Google Scholar] [CrossRef]
- Wang, S.; Qin, P.; Fang, X.; Zhang, Z.; Wang, S.; Liu, X. A novel sebacic acid/expanded graphite composite phase change material for solar thermal medium-temperature applications. Sol. Energy 2014, 99, 283–290. [Google Scholar] [CrossRef]
- Li, Z.; Sun, W.G.; Wang, G.; Wu, Z.G. Experimental and numerical study on the effective thermal conductivity of paraffin/expanded graphite composite. Sol. Energy Mater. Sol. Cells 2014, 128, 447–455. [Google Scholar] [CrossRef]
- Ling, Z.; Chen, J.; Xu, T.; Fang, X.; Gao, X.; Zhang, Z. Thermal conductivity of an organic phase change material/expanded graphite composite across the phase change temperature range and a novel thermal conductivity model. Energy Convers. Manag. 2015, 102, 202–208. [Google Scholar] [CrossRef]
- Lv, Y.; Zhou, W.; Jin, W. Experimental and numerical study on thermal energy storage of polyethylene glycol/expanded graphite composite phase change material. Energy Build. 2016, 111, 242–252. [Google Scholar] [CrossRef]
- Jeong, S.; Murayama, M.; Yamamoto, K. Efficient Optimization Design Method Using Kriging Model. J. Aircr. 2005, 42, 413–420. [Google Scholar] [CrossRef]
- Jones, D.R.; Schonlau, M.; Welch, W.J. Efficient global optimization of expensive black-box functions. J. Glob. Optim. 1998, 13, 455–492. [Google Scholar] [CrossRef]
- Fan, L.; Xiang, Z.; Xue, M.; Cen, Z. Robust Optimization of Thermal–Dynamic Coupling Systems Using a Kriging Model. J. Spacecr. Rocket. 2010, 47, 1029–1037. [Google Scholar] [CrossRef]
- Ugray, Z.; Lasdon, L.; Plummer, J.; Glover, F.; Kelly, J.; Martí, R. Scatter Search and Local NLP Solvers: A Multistart Framework for Global Optimization. Inf. J. Comput. 2007, 19, 328–340. [Google Scholar] [CrossRef]

| Material | PCM | EG |
|---|---|---|
| Density (kg/m3) | 914 | 2333 |
| Thermal conductivity (W/(m·K)) | 0.305 | 129 |
| Latent heat (kJ/kg) | 226.1 | - |
| Solidus temperature (°C) | 49.7 | - |
| Liquidus temperature (°C) | 55.8 | - |
| Heat Sink Volume (cm3) | 100 | 150 | 200 | 250 | 300 |
|---|---|---|---|---|---|
| Height (cm) | 2.52 | 3.03 | 3.39 | 3.61 | 3.75 |
| Length (cm) | 6.30 | 7.04 | 7.68 | 8.32 | 8.95 |
| 0.4 | 0.43 | 0.44 | 0.43 | 0.42 |
| Heat Flux (W/cm2) | 2 | 2.5 | 3 | 3.5 | 4 |
|---|---|---|---|---|---|
| Height (cm) | 2.89 | 3.01 | 3.04 | 3.04 | 3.03 |
| Length (cm) | 7.21 | 7.06 | 7.02 | 7.03 | 7.04 |
| 0.40 | 0.43 | 0.43 | 0.43 | 0.43 |
| Working Time (s) | 100 | 200 | 250 | 300 | 350 |
|---|---|---|---|---|---|
| Height (cm) | 2.97 | 3.11 | 3.02 | 3.03 | 2.98 |
| Length (cm) | 7.11 | 6.94 | 7.05 | 7.04 | 7.10 |
| 0.42 | 0.45 | 0.43 | 0.43 | 0.42 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Li, M.; Li, H.; Fu, Y.; Cai, L. Optimization of Thermal Management for the Environmental Worthiness Design of Aviation Equipment Using Phase Change Materials. Aerospace 2024, 11, 943. https://doi.org/10.3390/aerospace11110943
Zhang J, Li M, Li H, Fu Y, Cai L. Optimization of Thermal Management for the Environmental Worthiness Design of Aviation Equipment Using Phase Change Materials. Aerospace. 2024; 11(11):943. https://doi.org/10.3390/aerospace11110943
Chicago/Turabian StyleZhang, Jianjun, Minwei Li, He Li, Yun Fu, and Liangxu Cai. 2024. "Optimization of Thermal Management for the Environmental Worthiness Design of Aviation Equipment Using Phase Change Materials" Aerospace 11, no. 11: 943. https://doi.org/10.3390/aerospace11110943
APA StyleZhang, J., Li, M., Li, H., Fu, Y., & Cai, L. (2024). Optimization of Thermal Management for the Environmental Worthiness Design of Aviation Equipment Using Phase Change Materials. Aerospace, 11(11), 943. https://doi.org/10.3390/aerospace11110943







