Impact of Target Surface Building Direction on the Heat Transfer Characteristics of Additive Manufactured Impingement Systems

Abstract

Additive manufacturing (AM) is widely recognized as a prominent tool to maximize the potential of internal cooling systems for gas turbine applications. Several past studies have been undertaken in order to assess the effect of additive manufactured components peculiar characteristics, mainly in the form of surface roughness, on heat transfer and pressure losses. On the other hand, impingement constitutes one of the most adopted solutions for turbine vane internal cooling; also, its heat transfer performance has been shown to be potentially improved through the use of roughened target surfaces in several studies. In this work, the effect of AM-generated roughness on the performance of impingement systems has been experimentally investigated. A lumped approach was used to test additive manufactured coupons reproducing an impingement array in 1:1 scale and retrieve an average heat transfer assessment. The Laser Powder Bed Fusion (L-PBF) technique was used for the manufacturing process. As one of the main parameters affecting AM-generated roughness, the building direction of the target surface was varied in order to highlight its impact on the overall performance comparing four different building directions with a smooth reference target plate made by standard CNC machining.

1. Introduction

The development of more efficient cooling systems for core engine components is still a relevant field of study within the gas turbines literature, despite the advanced technological levels that the currently adopted solutions have achieved after decades of dedicated studies. Still, the topic is widely investigated, with the goal of continuously improving the cooling efficiency and effectiveness and, in turn, cycle efficiency and specific power. Within this framework, the additive manufacturing (AM) is a potentially disruptive technology, due to its capability to unlock innovative geometries and micro-cooling features [1,2], while also allowing faster design iterations and reduced time to market [3].

In addition to these advantages, a peculiar characteristic of additive manufacturing processes is that the generated components present a surface roughness which is generally significantly higher with different characteristics with respect to traditional manufacturing techniques. Generally speaking, in the view of internal cooling systems, this characteristic can be detrimental in terms of required pressure drop, but an increase in heat transfer is also generally achieved. Beyond this qualitative and generic behavior, the assessment of roughness on the frictional and heat transfer characteristics of a certain surface or cooling architecture is a challenging task. As far as the frictional aspect is concerned, it is common practice to refer to an equivalent “$sandgrain$ $roughness$” ($k_s$), indicating the size of an ideal, uniform, roughness producing the same frictional performance of the considered one [4]. Despite the simple conceptual definition of this parameter, a large number of studies have shown that many roughness characteristics influence its value, making its prediction complex. In fact, beyond parameters describing roughness height and spacing, its actual shape can play a significant role, as demonstrated by studies that found significant relationship between $k_s$ (or in general the frictional performance) and roughness skewness [5,6,7], kurtosis and shape/density parameter [8,9]. The same parameters were also found to influence the heat transfer aspect, albeit in a different extent, further increasing the evaluation complexity [10,11,12,13]. While the quantitative impact of different roughness parameters on pressure losses and heat transfer can significantly differ for different geometries (i.e., cooling devices), its precise description goes beyond the goals of this work, and relevant reviews can be found in the works of Kadivar et al. [14] and Thole et al. [15].

On the other hand, impingement is one of the most adopted internal cooling architectures, and several past studies have pointed out that its heat transfer performance can be improved by providing some form of roughness on the target surface; in fact, it increases the wetted surface, while the heat transfer coefficient ($HTC$) can be either increased or reduced depending on the actual configuration [16]. Over the years, several kinds of surface roughening or, in general, the addition of any form of elements to the smooth surface, have been tested. In most of these studies, a smooth surface area is adopted to calculate the heat transfer coefficient from a measured heat flux, even for the rough case; therefore, even if the results are generally expressed in terms of $HTC$ ($Nu$) enhancement with respect to smooth case, $HTC/HT{C}_0$ ($Nu/N{u}_0$), the combined effect of both wetted surface and actual HTC variation is embedded in the results. Several studies have focused on macro-features added to the smooth surface, with a dimension comparable to the impingement diameter (D) [17,18], while many others, especially in recent years, have focused on micro-features or distributed roughness. Due to the goal of the present paper, a summary of the latter ones will be reported in the following. A more comprehensive review of all these solutions is reported in the work from Ekkad and Singh [19].

Chakroun et al. [20] investigated the heat transfer enhancement achieved by adding cubic elements under a single impingement jet, while a similar impingement configuration was tested by Beitelmal et al. [21], using a single ring of circular protrusion placed at a fixed radial distance from the jet. Taslim et al. [22] investigated the effect of sandpaper roughness applied on a concave target surface, resembling the internal surface of a blade leading edge, of a single row of impingement jets, while also testing macro-structures in the form of conical bumps and ribs. El-Gabry and Kaminsky [23] tested the impact of distributed roughness applied through a dedicated brazing process, under an array of impingement jets. Heat transfer enhancement under an array of impingement jets was also investigated by McInturff et al. [24] and Rao [25], using micro-elements with triangular and circular sections, respectively. Singh et al. [26] carried out a numerical and experimental activity to compare different element shapes: the circular concentric micro pin-fins were identified as the more promising solution and then extensively tested by Sundaram et al. [16].

As highlighted by these studies, beyond roughness elements characteristics, many geometrical parameters influence the heat transfer performance of the impingement system, as the jet-to-target distance (z), the pitch between jets (p), the impingement layout (single jet, row, array) and the crossflow arrangement. Also, as previously discussed, the average roughness height ($Ra$) is generally not enough to provide an exhaustive characterization and several other parameters can influence the outcome. Despite that, little can be drawn from impingement literature regarding the impact of parameters describing roughness shape, mostly because most of the studies are carried out using elements with pre-defined geometry, rather than distributed roughness. On the other hand, regarding roughness spacing characteristics, Sundaram et al. [16] showed that, for a certain micro pin fin dimension, an optimal value of pin fin spacing could be identified, while arranging the features in either more or less packed configurations resulted in reduced heat transfer performance. According to the authors, this optimal configuration corresponded to the one that constitutes the best trade-off between increasing the heat transfer surfaces and maintaining a relevant heat transfer coefficient ($HTC$); when the roughness elements are too packed between each other, they prevent the impingement flow from effectively penetrating between them and the $HTC$ is significantly reduced. When it comes to distributed roughness, the average distance between peaks is generally referred to as $Rsm$ and therefore this parameter can be expected to influence the heat transfer performance as well.

The results of the above-mentioned studies are summarized in Figure 1, in terms of equivalent Nusselt number enhancement (i.e., the global effect of a wetted surface and the actual Nusselt number), as a function of scaled average roughness ($Ra/D$) and jet pitch-to-diameter ratio ($p/D$). Results are only correlated to $Ra$, as far as the roughness parameters are concerned, because limited information regarding others, like skewness and kurtosis, can be drawn from the available impingement studies. For studies where the impact of roughness on wetted surface and actual $HTC$ was effectively distinguished, care was taken to consider their combined effect to achieve a coherent comparison with the other studies; in the following sections of this paper, Nu or $HTC$ will refer to the equivalent parameters (thus bearing also the impact of surface enhancement), while the term $actual$ $Nu$ or $HTC$ will be used to specifically refer to the purely fluid dynamic effect. Concerning the values of $Ra$, for the studies that adopted discrete roughness elements, a value equal to half of the elements height was considered, as an equivalent average roughness. Results coming from distributed roughness (El-Gabry and Kaminsky [23] and Taslim et al. [22]) are shown as crosses, while all the others are reported with a symbol denoting the shape of the adopted roughness element.

In general, a significant heat transfer enhancement is highlighted, as the scaled surface roughness is increased, up to values equal to about 2.5 times the smooth ones; while, as anticipated, the actual $HTC$ can be reduced in some cases as the roughness is increased, the wetted surface is always increased, thus resulting in a general positive correlation between the $Ra$ and $Nu/N{u}_0$. On the other hand, an opposite behavior can be noted when $Nu/N{u}_0$ is plotted against $p/D$, as a general reduction in heat transfer occurs as the geometrical parameter increases. This must be expected to occur because the stagnation areas are characterized by very thin thermal boundary layer, thus maximizing the impact of surface roughness (i.e., if the thermal boundary layer thickness is higher than $Ra$, the whole roughness elements stay in a region with hot fluid, thus reducing the capability to exchange heat); increasing $p/D$ corresponds to reducing the overall impact of these areas.

Despite the overall trends, a significant data scatter can be seen in the plots, indicating that many other parameters affect the final performance and the impossibility to identify a “general” optimal roughness configuration.

During the manufacturing process, the AM technique intrinsically produces components with a certain surface roughness; despite this, a non-negligible heat transfer enhancement could be achieved as a result of the as built surface roughness, no previous study has investigated the effect of AM on impingement surfaces. AM roughness comes as a result of several manufacturing parameters like laser power, speed, hatching (i.e., distance between laser beam passes), and printing direction. As these parameters are generally chosen for manufacturing goals, other than the optimization of the surface roughness on the heat transfer surface, the latter must be considered as a resulting characteristic. In particular, roughness parameters such as $Ra$, $Rsm$, $Rsk$, and $Rku$ cannot be independently controlled during the manufacturing. Among the printing parameters, the build direction is generally considered to be the most important factor affecting the roughness; it is increased as the considered surface moves from upskin, to vertical, to the downskin building direction, due to gravity effects on the melt pool, since downskin surfaces are unsupported ones built upon powder rather than on solidified materials [15].

In the present work, a dedicated test campaign has been performed to characterize the heat transfer performance of several AM impingement target surfaces by varying both the building direction and $p/D$ of the impingement array. The outcome of the experimental campaign allows to (1) highlight the surface roughness height and morphology achieved by a typical process adopted for gas turbine cooled components, with different building direction and (2) assess their impact on the heat transfer performance of the impingement system in order to shed light on the heat transfer enhancement that can be achieved by simply replacing the manufacturing process, rather than designing specific geometrical features. While not the primary goal of this work, an investigation of the pressure losses induced by the increased surface roughness will be discussed as a peculiar aspect of cooling system characterization.

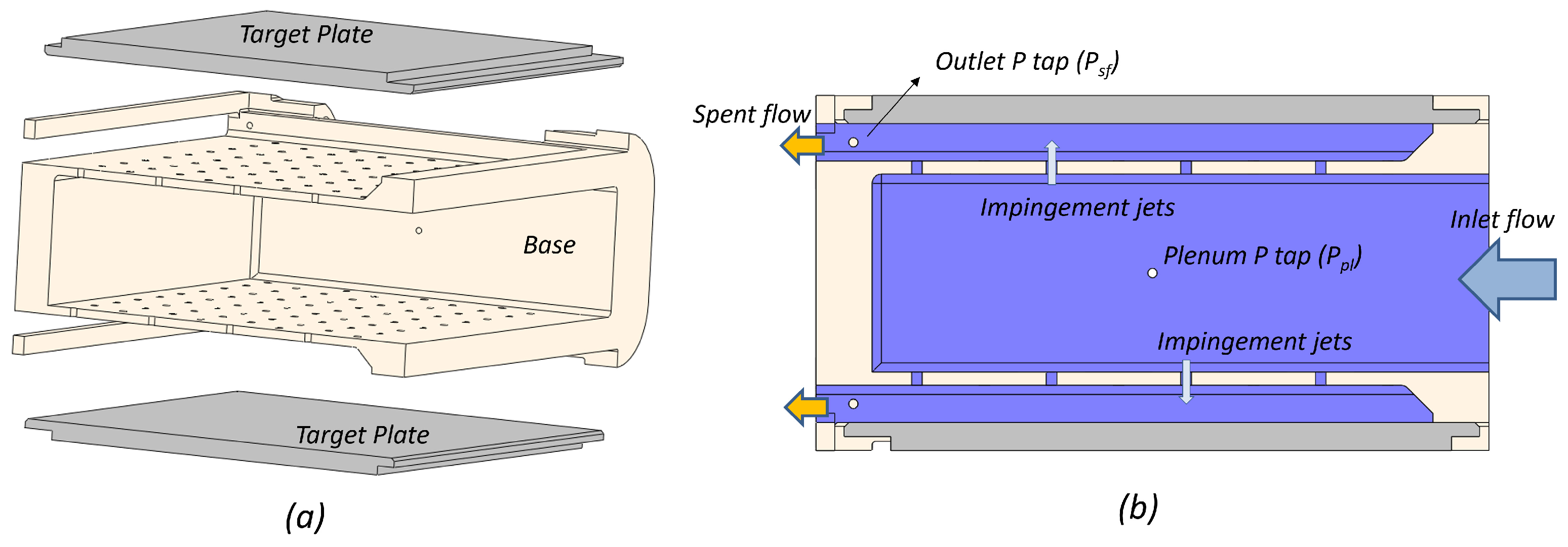
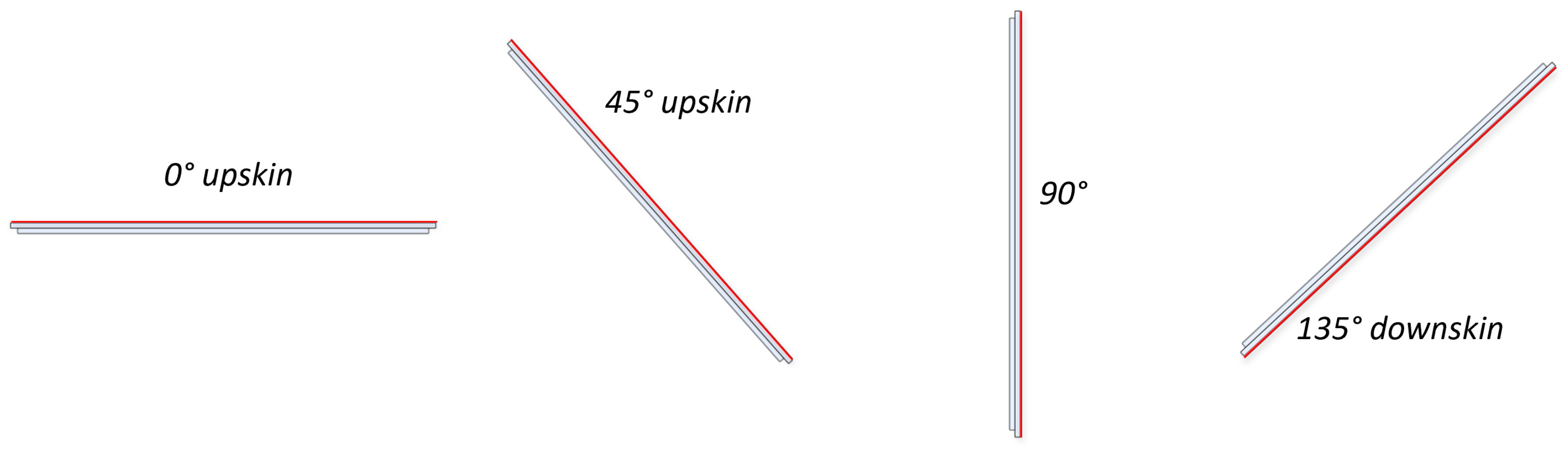
2. Test Articles

The investigated coupons were designed to mimic the behavior of impingement arrays with typical dimensions of internal cooling architectures for gas turbine vanes, in 1:1 scale. The whole coupon is made by two separate parts, as shown by the exploded CAD sketch reported in Figure 2a. The first part, which will be referred to as base, is made by the multiperforated wall, where impingement holes with a nominal diameter of 0.7 mm are realized, and the inlet plenum, which feeds the former. The second part constitutes the target surface (and will be referred to as target plate in the following); it is installed on the base part, thus creating the crossflow cavity which collects the spent flow towards the exit. For each coupon, one base part, with two perforated walls, and two target plates are necessary, in order to achieve symmetry.

The assembled coupon is shown in the sectional view of Figure 2b, together with arrows indicating the flow development; the flowpath area is highlighted in blue. Even if reported with different colors, for the sake of better understanding, all components are realized in the same nickel-based material in order to mimic real hardware printing characteristics. As shown in Figure 2b, the coupons are provided with pressure taps inside the plenum chamber ($P_{pl}$) and at the end of the spent flow cavities ($P_{sf}$) in order to record the actual inlet/outlet pressures for the impingement apparatus; an additional tiny hole, similar to the one for the pressure tap, is present in the plenum cavity, in order to insert a thermocouple and monitor the plenum air temperature to be considered as the actual impingement temperature $T_{imp}$.

Concerning AM components, two base parts and four target plates were tested, for a total of eight assembled coupons. The base parts differ for the impingement holes spacing, so to test nominal values of pitch-to-diameter ratios equal to 6 and 12; a staggered hole arrangement was adopted for both of them. Target plates differ just for the printing angle: values of printing angle equal to 0 (horizontal), 45, 90 (vertical), and 135 degrees were used. The first two were printed with an upskin target surface, while 135° indicates a downskin target surface. As a typical limitation of AM processes, it was not possible to realize the horizontal downskin configuration, which would require a completely unsupported horizontal surface. For a better understanding, the full set of AM target plates is shown in Figure 3, where the target surface to the impingement jets is highlighted in red.

Base and plates were printed on EOS^® M290 powder bed fusion system. A Baker Hughes nickel-based patented material for high temperature application was used. The layers were exposed with a hatching and contour scan strategy, one of the most common while printing functional parts. The most critical features of the components are the impingement holes in base parts; these are printed with the outlet flange surface on the building plate, thus resulting in horizontal impingement holes axes (i.e., parallel to the ground). Small holes (<1 mm) made by AM have a significant variability due to the peculiarities of the L-PBF process and downskin unsupported areas usually cause a partial collapse of the top section of horizontal holes. To compensate this phenomenon, slightly modified holes with a teardrop shape were adopted as printing geometry. An offset to the nominal diameter was applied, so to compensate the natural tendency of L-PBF processes to obtain dimensions smaller than intent, when holes with reduced are concerned. In a preliminary testing phase, the base components were differentially flow-checked, plugging the holes on one of the two perforated walls. Results showed negligible differences in the effective areas measured for the two sides of each base part.

Beside AM target surfaces, additional ones were manufactured using standard CNC machining, in order to compare the results to the ones from completely smooth impingement surfaces and understand the impact of AM-induced roughness. The whole tested parts are reported in

Table 1. List of tested parts and nominal geometric characteristics.

Base Components	D [mm]	p/D [-]	z/D [-]	L/D [-]	Manufacturing
Base 6	0.7	6	3.3	1.2	AM
Base 12	0.7	12	3.3	1.2	AM
Target plates	Manufacturing	Printing angle [°]
Target-0	AM	0 (upskin)
Target-45	AM	45 (upskin)
Target-90	AM	90 (vertical)
Target-135	AM	135 (downskin)
Target CNC	CNC	-

, where the most important geometric parameters are also summarized, with their nominal (i.e., intent) values. Parameters $z/D$ and $L/D$ represents the non-dimensional jet-to-target distance and impingement holes length, respectively. Since it was not a goal of this paper to provide a sensitivity of the results to the variation in these parameters, a fixed value representative of typical applications with impingement-cooled components was chosen for each of them.

3. Experimental Methodology

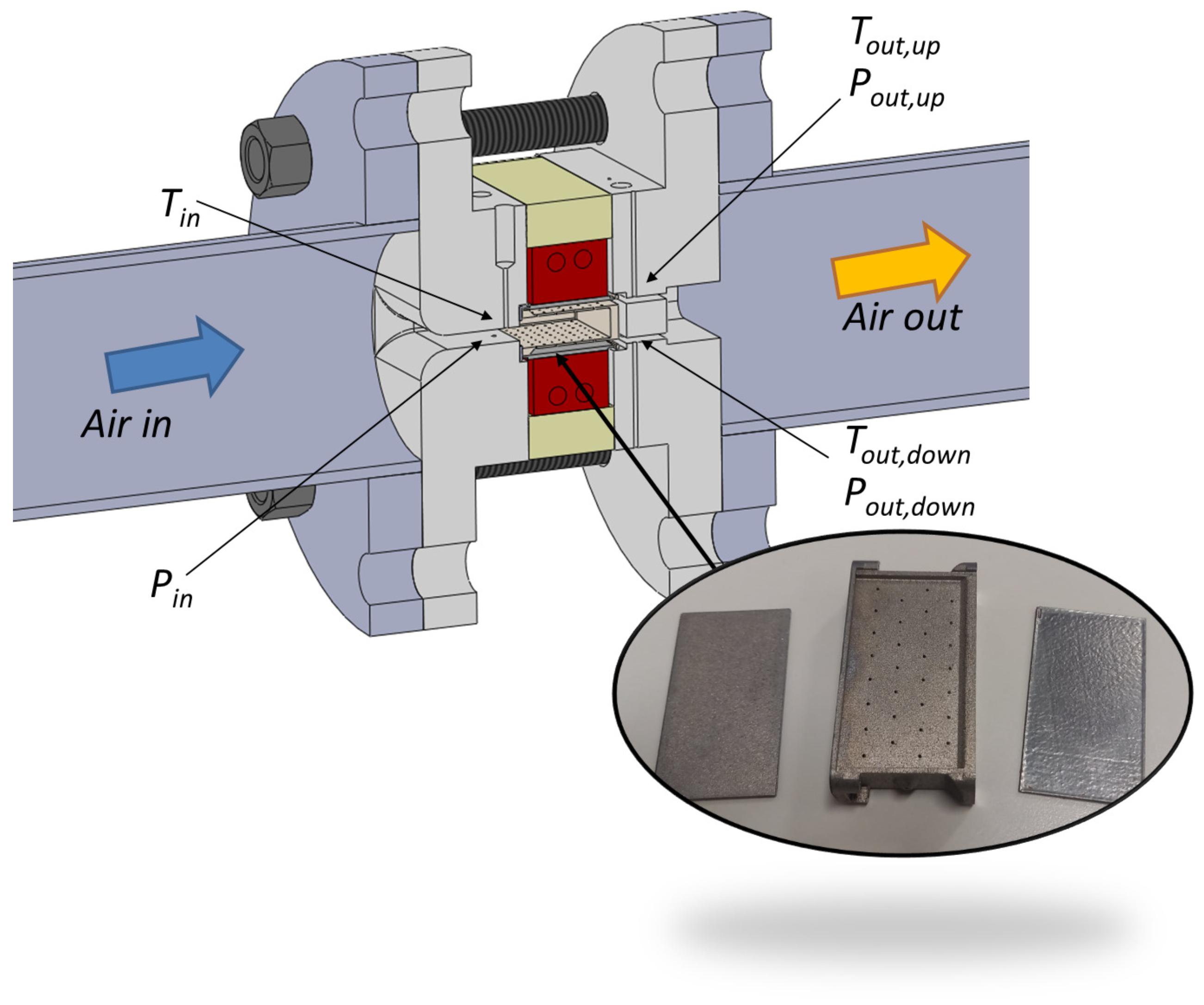
3.1. Test Rig

A description of the test rig adopted for the present investigation can be found in the works of Castelli et al. [27] and Bacci et al. [28]. A brief description is also provided in the following for the sake of a better understanding.

A sketch of the test section is reported in Figure 4, together with an image of the $p/D=6$ base part and Target-0 (right) and 90 (left) plates. The tested coupon is installed between two flanges made by low thermal conductivity material, in order to minimize thermal losses; PTFE was chosen for these components. Graphite gaskets were used to prevent air leakages. The inlet flange presents a flowpath cavity that perfectly matches the section of the coupon’s inlet cavity; three thermocouples can be inserted in this area, in order to monitor the air inlet temperature ($T_{in}$) and verify its pitchwise uniformity. Three pressure taps have been realized as well, in order to monitor and control the inlet pressure ($P_{in}$).

The outer flange, on the other hand, presents two cavities that matches position and cross-sectional area of the coupon’s exit cavities to collect the spent flow towards the rig exit. In each cavity, two thermocouples ($T_{out}$) and two pressure taps ($P_{out}$) are present. The streamwise location of inlet and outlet thermocouples and pressure taps is indicated by the arrows in Figure 4.

The coupon is installed between an upper and a bottom copper block. Two cartridge heaters are inserted in each block in order to provide the heat flux required for the experimental approach; they are fed by two separate DC supplies, one for the upper and one for the lower copper block. A thermocouple is also inserted in each block ($T_{Cu,up}$, $T_{Cu,down}$), 2.5 mm distant from the copper–coupon interface, to measure the copper temperature. The uniformity of the copper blocks temperature in the streamwise and pitchwise directions was verified by preliminary FEM evaluations, to justify the adoption of a single thermocouple for each block; also, three thermocouples for each block, spaced in the streamwise direction, were used during the rig commissioning phase, confirming the uniform temperature distribution. The whole test section is encapsulated in a casing of thermal insulating material fitting around the whole assembly in order to minimize thermal losses. Small holes were realized in order to provide passages for the heating and temperature measurement devices’ cables.

All the temperatures are measured by T-type thermocouples ($\pm 0.5$ K relative accuracy), while static pressures are sampled by means of a TE Connectivity NetScanner 9116 Pressure Scanner (150 Pa accuracy).

The mass flow rate is regulated by an automatic upstream valve, controlled through an in-house developed Labview-based software, which is also used to record all the measured variables. The mass flow values are measured by a calibrated orifice, affected by a maximum error of about 1%, within the tested range of mass flow rates, according to the standard ANSI/ASME PTC 19.1 [29] based on the Kline and McClintock method [30]. A manual valve, downstream of the test section, is used to control the rig backpressure and hence the Mach number of the impingement jets.

3.2. Measurement Technique

As anticipated, the above-described coupons have been characterized in terms of pressure losses and heat transfer performance.

For the former, the coupons installed in the rig have been flowchecked in cold condition (i.e., heaters switched off) recording the inlet/outlet pressures. The mass flow rate and the flow temperatures, which are kept at ambient value for these tests, were also recorded in order to characterize the flow conditions and relate the pressure drop to Reynolds and Mach numbers.

Concerning heat transfer characterization, a steady-state lumped approach was adopted. As anticipated, a known heat flux ($Q_{Joule}=E·I$) is provided by two cartridge heaters inserted in each copper block and fed by DC supplies, while copper temperatures ($T_{Cu,up}$, $T_{Cu,down}$) and air temperature ($T_{imp}$) are acquired. Voltage provided to upper/lower copper blocks is regulated in order to achieve approximately the same copper temperature (within 0.2 K). The heat flux actually provided to the coupon was found by subtracting the heat losses ($Q_{loss}$) to the actual provided thermal power. This term was evaluated by a preliminary steady state test, where no airflow was enforced and the provided thermal power was recorded and related to the difference between copper and ambient temperatures, to retrieve the heat dispersion through the insulating casing.

$$Q_{conv}=Q_{Joule}-Q_{loss}$$

In order to retrieve the impingement surface temperature required to scale the actual heat transfer coefficient, a 1D correction was carried out, starting from the measured copper temperature and the calculated $Q_{conv}$:

$$T_{c,s}=T_{Cu}-{\displaystyle \frac{Q_{conv}}{A}}·(R_{Cu}+Rc)$$

(1)

with $R_{Cu}$ and $R_c$ being the thermal conduction resistances of the 2.5 mm copper layer (between TC measurement position and copper–coupon interface) and the 1.5 mm target plates respectively.

The heat transfer coefficient can finally be calculated by the following:

$$HTC={\displaystyle \frac{Q_{conv}}{A·(T_{c,s}-T_{imp})}}$$

(2)

Since the HTC is scaled using the smooth surface area A, the calculated parameter must be considered as an equivalent heat transfer coefficient, bearing both the wetted surface enhancement and the actual HTC variation. The plenum air temperature is used to scale the results, as it is common practice for impingement applications [31]; in the same way, the Nusselt number is calculated using the air thermal conductivity evaluated at the film temperature, equal to the average between metal ($T_{c,s}$) and air ($T_{imp}$) temperatures.

$$Nu={\displaystyle \frac{HTC·D}{k_{film}}}$$

(3)

The process is repeated and then averaged for the two sides of the coupon; in general, negligible differences were found between them due to the symmetry of the coupons.

The uncertainty of the Nusselt number was evaluated starting from the measured variables, according to the Kline and McClintock method [30]. Uncertainty on the measured $Q_{Joule}$, starting from measured voltage–current, $Q_{loss}$ and temperatures ($T_{imp}$ and $T_{Cu}$) were considered, to retrieve an overall uncertainty within 3.5% for all cases.

Preliminary FEM calculations, imposing representative heat loads were also carried out, in order to verify the amount of the heat transfer between fluid and non-impingement solid surfaces, with respect to impingement heat transfer. Even at a lower $Re$ number, the heat flux across the non-impingement surfaces was found to be significantly lower with respect to heat flux across the target surfaces and hence negligible in the post-processing methodology.

3.3. Operating Conditions

In order to investigate engine-relevant conditions for the heat transfer performance characterization, a set of Reynolds number ranging from 4000 to 17,000 was investigated. The impingement Reynolds number is defined using a hole diameter equal to 0.7 mm:

$$Re={\displaystyle \frac{\rho VD}{\mu }}$$

Within this range of conditions, the maximum Mach number in the crossflow cavity did not exceed $0.12$ ($0.03$) for $p/D=6$ (12). The maximum value of $\rho V_{cr}/\rho V_j$ (i.e., ratio between crossflow and impingement jet momentum) reached a maximum of $0.4$ ($0.1$) for $p/D=6$ (12).

During the tests, the coupon temperature was kept at around 80 °C.

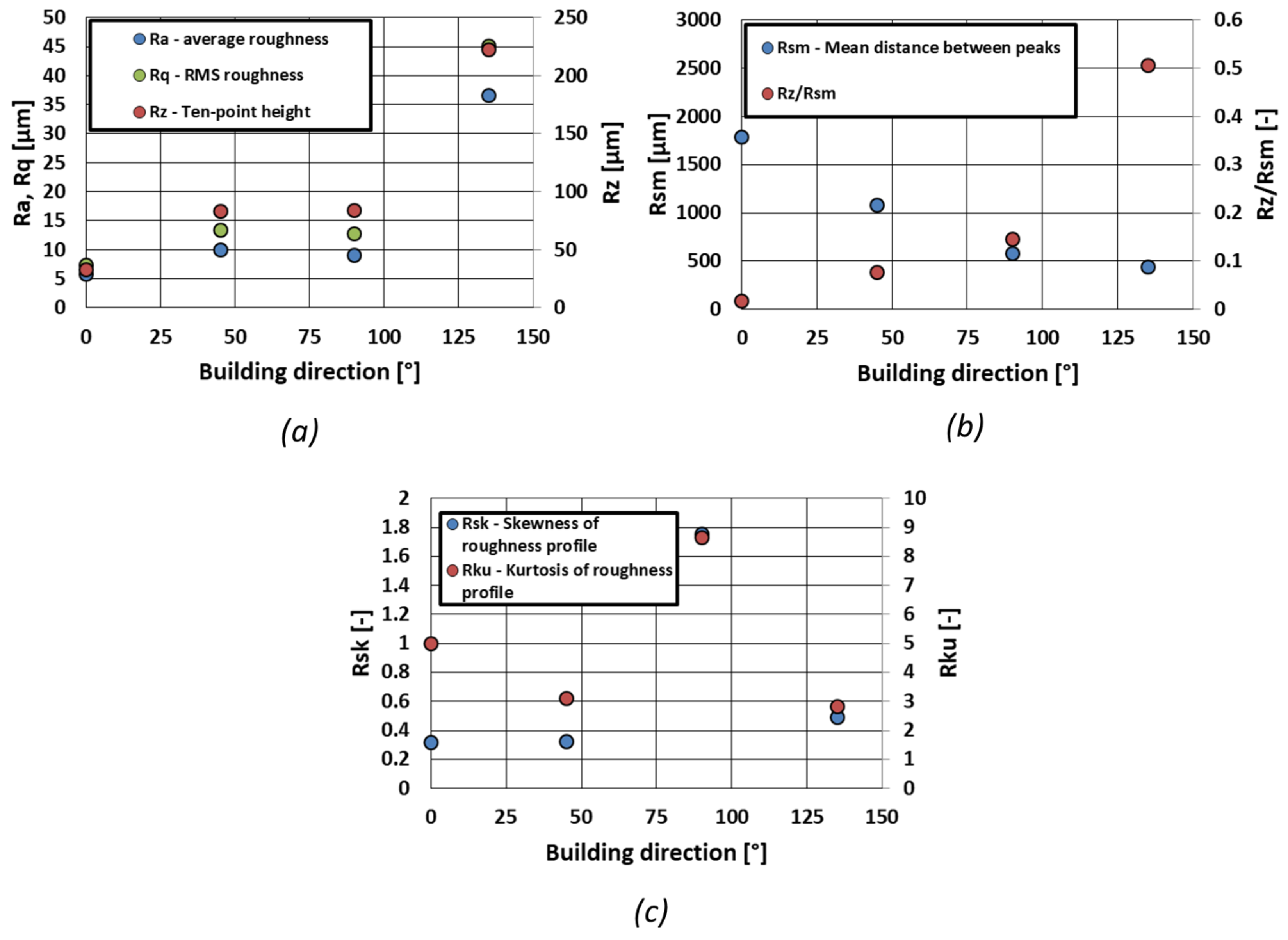
4. AM Parts Characterization

Before moving on to the results, it is necessary to provide an account of the characterization of the AM parts, since their resulting roughness is a mandatory aspect to consider in order to understand both the measured outcome and how the roughness morphology is shaped, according to the different building directions. In addition, it could help to generalize the data set since the resulting roughness is even influenced by all the best practices adopted during the printing process.

Target surface roughness was characterized using an Alicona Infinite Focus optical system. Such an optical instrument allows, with a single scan, to obtain several bi-dimensional data points about the surface topology. The results are reported in Figure 5, in terms of relevant roughness parameters; the description of each parameter is reported in the label, while their precise definition can be found in the work of Gadelmawla et al. [32]. Parameters related to roughness height, spacing, and shape are reported, so as to consider all the more relevant information regarding the roughness profile.

It can be easily seen (Figure 5a) that surface roughness increases moving from upskin to downskin surfaces, as it was expected. Albeit non-negligible, the horizontal upskin surface presents a minimum average roughness $Ra$ equal to about 6 µm, while it increases to similar values of about 10 µm, for 45° and 90° plates. A significant increase, up to more than 35 µm is then achieved for the 135° plate, which, as already explained, is printed with the target surface in a downskin position. The same trend is achieved for the RMS roughness $Rq$ and for the ten-point height $Rz$, even if with different values. At the same time, the parameter $Rsm$ (Figure 5b) shows a clear and significant reduction of the average distance between the roughness peaks, as the focus moves from upskin to downskin surfaces. This results in significantly more “packed” roughness structure for Target-135 than it is for Target-0, as it is shown from the ratio between peaks height and distance ($Rz/Rsm$). Concerning roughness shape, the Target-90 plate shows a significantly higher skewness (i.e., asperity—filled valleys and high peaks) and kurtosis (i.e., sharpness—many high peaks and low valleys), while the other configurations show similar and lower values. Summarizing, Target-0 shows a significantly different layout with respect to all the others, with a very limited surface roughness; Target-45 and Target-90 share a similar surface height and spacing, even if their shape is quite different; finally, Target-135 presents far more significant roughness height and lower spacing than all the others, while sharing a similar shape with Target-45.

As the differences are generally quite significant, both in terms of quantitative roughness height and qualitative morphology, non-negligible differences could be expected in the resulting thermal behavior, which will be detailed in the next sections.

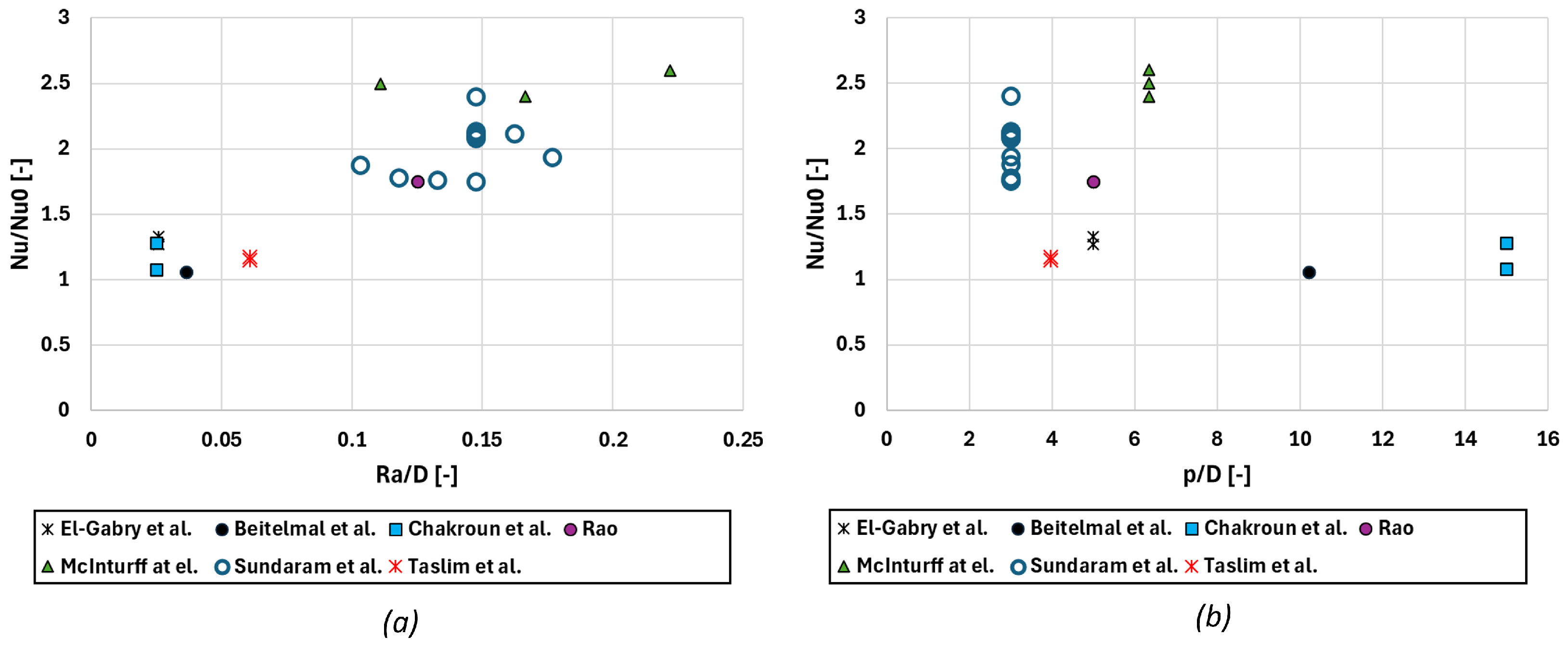
5. Experimental Results

In the next sections, results coming from the investigation of the impingement coupons will be detailed. While the main focus of this paper stays in the evaluation of the thermal performance, the attention will be firstly put on the analysis of the frictional characteristics, as a necessary evaluation in the view of considering the impact of additive manufacturing in the impingement-based cooling system.

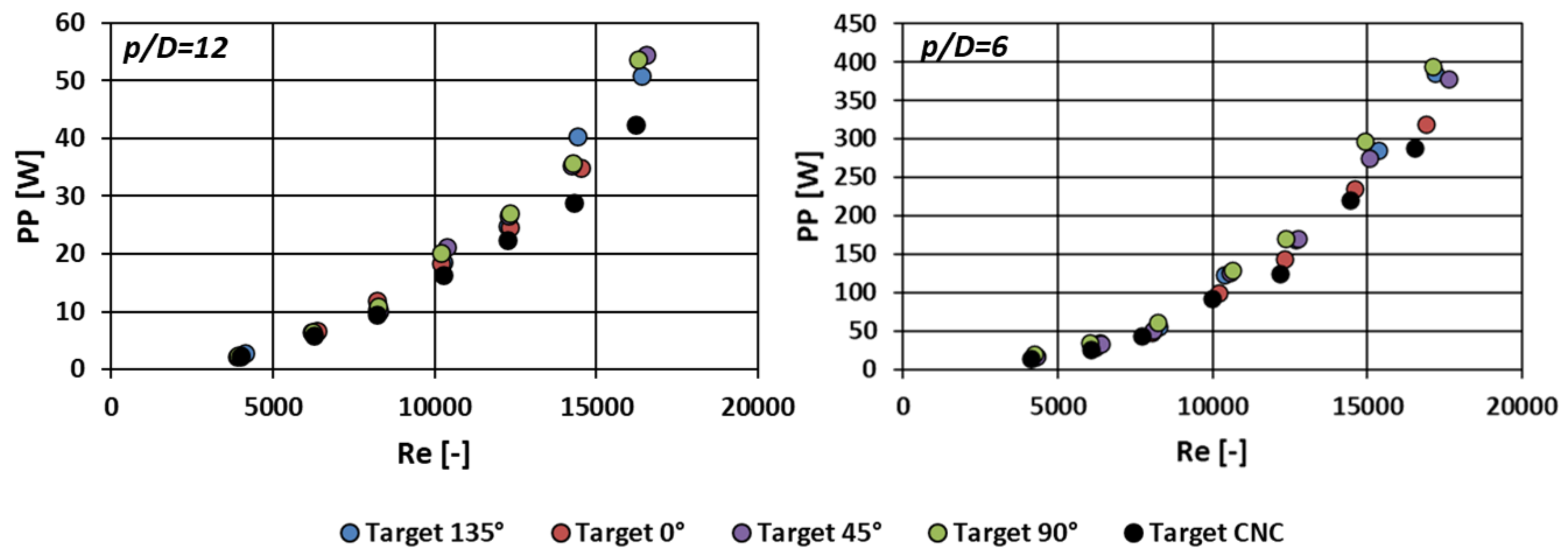
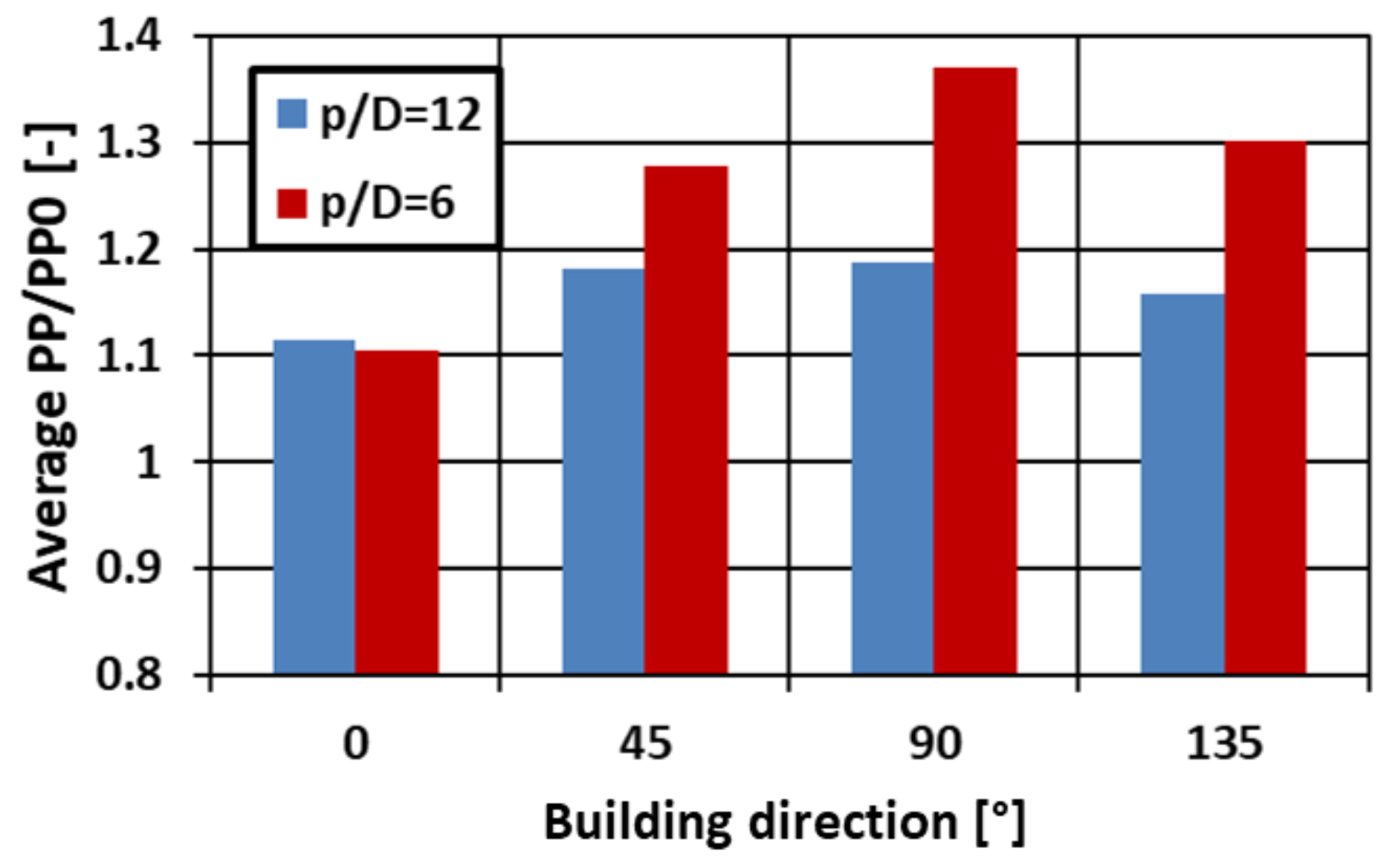
5.1. Pressure Losses

In order to characterize the pressure loss variation enforced by the increased surface roughness, the pumping power required to enforce a certain mass flow rate (i.e., Reynolds number) through the impingement system is considered, as previously adopted by Sundaram et al. [16], for similar cooling architectures, and defined as follows:

$$PP={\displaystyle \frac{\pi }{4}}·\nu ·Re·D·\Delta P·N$$

with N being the number of impingement holes.

Results are reported in Figure 6 for all the tested target plates, separately for the two impingement $p/D$ values.

Taking the configuration with the smooth (i.e., CNC) target (black dots) as a reference, it can be seen that for both hole spacing configurations, a slightly higher pumping power is enforced by the rough targets; if a fixed pumping power is considered, the Reynolds number reduction, induced by the target roughness, is limited, but far from completely negligible.

A more effective quantitative comparison can be achieved by scaling the results achieved from the AM targets by the correspondent one from the CNC target at the same Reynolds number; the latter is referred to as $P{P}_0$, being the reference value. The values of $PP/P{P}_0$, for each AM target and hole spacing is reported in Figure 7: in order to provide an effective evaluation, the calculated ratios have been averaged over the tested Reynolds number, to achieve an average $PP/P{P}_0$ for each configuration.

It can be easily seen that the rate of increase is generally higher for the case with $p/D=6$, as it could be expected due to both the higher number of jets, thus resulting in a generally thinner boundary layer, and the higher velocity in the crossflow cavity. For both layouts, the minimum increase is shown by the Target-0 configuration, in agreement with its limited roughness, while it tends to increase moving towards higher building directions. Noteworthy, a slight reduction in pumping power is measured when the focus moves from the Target-90 to the Target-135 configuration for both impingement arrangement, despite the latter featuring a higher surface roughness. The expected reasons for this behavior will be discussed together with the heat transfer results, in the next section.

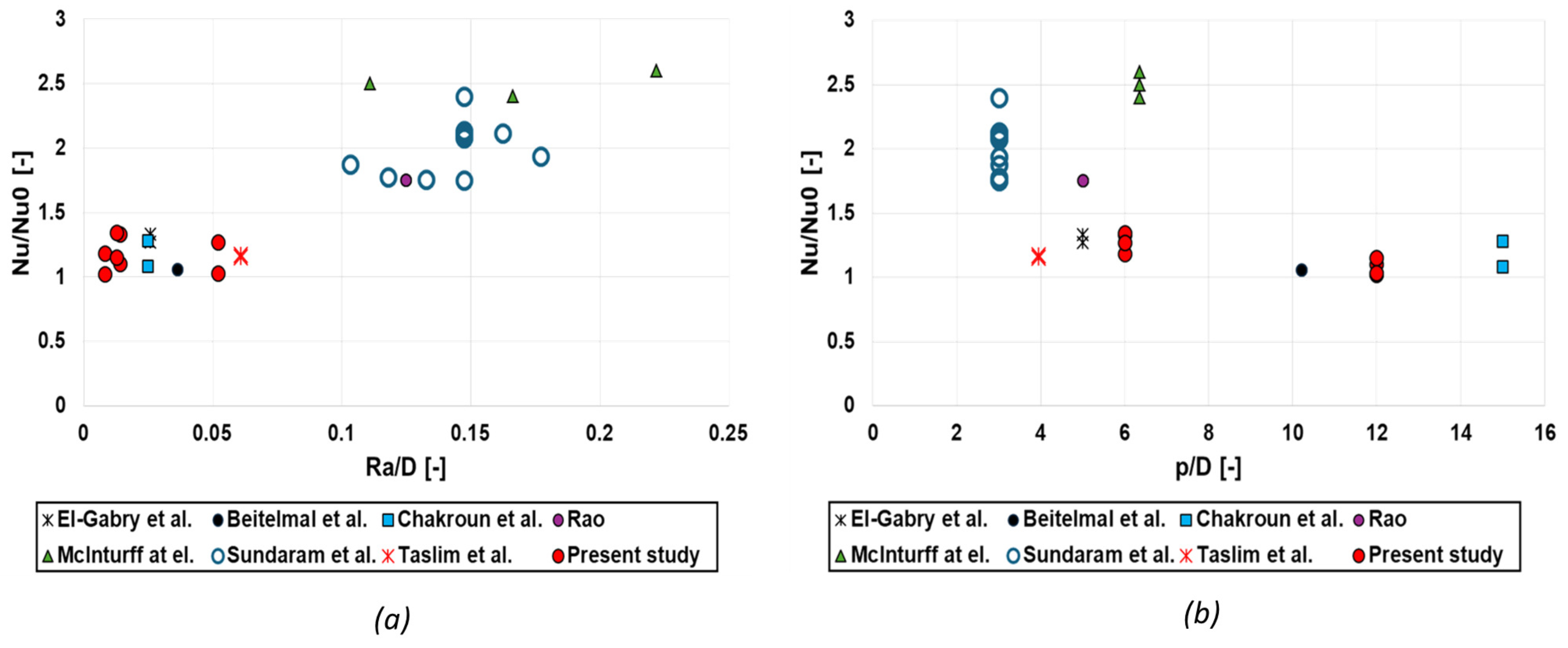
5.2. Heat Transfer

Once the frictional characteristics have been discussed, it is possible to move to the main focus of the paper, which is the impact of the target roughness on the heat transfer. As anticipated, this is evaluated in terms of average Nusselt number enforced by the impingement system on the target plates. The measured Nusselt numbers, for each target plate and hole spacing, are reported in Figure 8a, while Figure 8b shows the Nusselt enhancement over the smooth surface ($Nu/N{u}_0$) at the same Reynolds number.

Figure 8a shows a somewhat similar qualitative behavior to what was evidenced for the required pumping power in Figure 6, with rough surfaces leading to an increase in the heat transfer, with respect to the smooth one, and higher Nusselt numbers for the case with $p/D=6$ due to the higher number of impingement jets. The impact of roughness can be better appreciated from the enhancement factor shown in Figure 8b; again, Target-0 shows the minimum increase in heat transfer, while significant values can be achieved moving to Target-45 and 90. On the other hand, for Target-135, the values of $Nu/N{u}_0$ do not show a further increase, despite the significant roughness, while falling back towards values close to the horizontal upskin surface. The trend of $Nu/N{u}_0$ is generally constant with Reynolds number for p/D = 12, while it shows a slightly decreasing trend for $p/D=6$.

At first, this result could be expected to be generated by the different impact of crossflow on the two configurations. In general, it is well known that crossflow can significantly reduce the heat transfer promoted by an impingement array due to both entrainment of spent air and alteration of the jet behavior, leading to thicker thermal boundary layer [33,34]; this would reduce the roughness-induced marginal heat transfer enhancement, as roughness elements stay in a region with relatively hot fluid. Florshuetz and Metzger [33] found negligible effects of crossflow as the ratio $\rho V_{cr}/\rho V_j$ stays below 0.2; on the other hand, significant impact was evidenced once this value moved between 0.2 and 0.4. Since the flow conditions for $p/D=12$ of the present investigation fall in the former range of values, while the opposite can be said for $p/D=6$ (see the Operating Conditions section), a different weight of crossflow effects on the overall heat transfer must be expected between the two configurations. Nevertheless, this would not justify the decreasing $Nu/N{u}_0$ trend highlighted for $p/D=6$, since, once the spacing is fixed, the term $\rho V_{cr}/\rho V_j$ is approximately constant with increasing Reynolds number. The actual expected reason for it is discussed in the following.

The average $Nu/N{u}_0$ over the tested Reynolds range is reported in Figure 9. As it was also possible to see in the previous results, the Nusselt number increase due to roughness is higher for the configuration with reduced hole spacing; again, the higher number of impingement jets, and therefore of stagnation areas, produces an overall thinner thermal boundary layer, thus increasing the impact of roughness. For $p/D=6$, the maximum increase in Nu stays around 33%, a far from negligible increase, for Target-45 and Target-90, which share similar surface roughness, albeit very different $Rsk$ and $Rku$, and similar thermal performance; for $p/D=12$ the enhancement factor falls to about 10–15% for the same configurations. The minimum $Nu/N{u}_0$ is measured for Target-0, between 1 and 1.15, for $p/D=12$ and $p/D=6$ respectively. As already pointed out, Target-135 shows results that stay in between the minimal increase of the horizontal surface and the maximum one of the vertical surface, despite the highest roughness height. While this result could seem unexpected, the reason should stay in the highly packed roughness that characterize this downskin surface; as also reported in the introduction, Sundaram et al. [16] showed that if roughness elements are assembled too close to each other, they can prevent the impingement jets to effectively penetrate between them, thus significantly reducing the actual heat transfer coefficient and, therefore, the overall cooling of the target surface, despite a significant increase in the wetted surface. Roughness shape morphology, in the form of $Rsk$ and $Rku$, does not seem to be a primary driver for this specific behavior, since Target-135 and Target-45 share similar characteristics but different thermal performance.

This behavior can be also expected to be the reason for the decreasing $Nu/N{u}_0$ shown in Figure 8 for p/D = 6. The increase in Reynolds number leads to higher flow velocity, and momentum, inside the crossflow cavity, thus reducing the cooling flow capability to penetrate between rough structures and reducing the heat transfer increase due to roughness; noteworthy, Target-135 is the configuration with the more decreasing trend, presenting the highest and more packed roughness, thus suffering the most from the increased flow momentum. As far as p/D = 12 is concerned, velocity is much lower, and so is the impact of increased Re.

In order to compare the measured heat transfer enhancement to the ones reported in literature, for surfaces with variable roughness, the present results are added to the ones of Figure 1, to produce Figure 10.

The results clearly show that as far as the AM surface roughness is limited (i.e., Target-0, -45 and -90), the heat transfer enhancement shows similar values to other literature investigations, both considering distributed roughness and micro-elements. Moving to downskin surfaces (Target-135) the surface roughness, while significantly increased, still does not reach the highest values tested in literature through the design of specific roughness features; on the other hand, this would not seem to be useful, as the increase in roughness achieved by AM comes with a “more packed” configurations which is, in turn, detrimental to heat transfer. If the comparison is limited to configurations with distributed roughness, present results appear in line with literature ones and suggest slightly higher heat transfer enhancement than the sandpaper roughness tested by Taslim et al. [22] (e.g., see the $Nu/N{u}_0$ trend with $p/D$ in Figure 10b).

6. Conclusions

The impact of AM surface roughness on the performance of impingement systems was experimentally investigated in the present study. Target surfaces manufactured with different building direction were coupled with base parts featuring a plenum chamber and impingement plates with two different hole spacing configurations equal to $p/D=6$ and $p/D=12$. A lumped approach was adopted to retrieve an average heat transfer coefficient over the target surface and results were compared to the ones obtained with a smooth plate made by CNC. The novelty and contribution of the reported results stay a precise assessment of the impingement heat loads alteration due to specific AM roughness of the target surface, which was lacking in the impingement literature, despite the large number of studies related to impingement performance enhancement through surface roughening.

The outcome of the study can be summarized as follows:

• The as-built surface roughness on the target surfaces, as expected, increases moving from upskin configurations, to vertical, to downskin ones; nevertheless, a significant reduction in the average distance between roughness peaks ($Rsm$) occurs at the same time.
• The increase in surface roughness results in an increase in pressure losses or required pumping power. If a fixed pumping power is considered, a limited, but not completely negligible reduction in the mass flow rate is enforced, mostly around 10%.
• A heat transfer enhancement is also achieved, as expected. This is higher for reduced jet spacing, since a thinner thermal boundary layer is achieved, thus maximizing the effect of roughness. The maximum enhancement is achieved for the vertical plate configuration.
• Downskin surfaces with significantly higher roughness, do not achieve higher heat transfer enhancement. By comparing the measured roughness parameters, the reason seems to stay in the fact that the increase in $Ra$ comes with a relevant reduction in $Rsm$, which compromises the actual heat transfer coefficient, as also suggested by other studies. The impact of the roughness shape (skewness, kurtosis) does not seem to be responsible for this specific behavior.
• The trend of $HTC$ with a maximum between 45 and 90° is not described by any single standard parameter used to characterize the roughness. This highlights the difficulty in scaling the heat transfer enhancement with respect to the roughness geometry, demanding for further experimental investigations and, in general, complex relations considering multiple roughness parameters.
• AM roughness impact on heat transfer is in line with literature results with distributed roughness achieved with dedicated processes. On the other hand, it is not able to reach the very high enhancements achieved with specifically designed features with higher equivalent $Ra$. Additional AM configurations could be evaluated, with the aim of increasing $Ra$ without significantly compromising $Rsm$ (e.g., increased laser hatching).
• Despite the fact that the measured heat transfer enhancement does not reach the highest values reported in literature, non-negligible increases up to more than 30% has been highlighted. This, together with the fact that this value significantly changes with building direction, suggests that the heat transfer enhancement due to surface roughness must be accurately considered, in the view of designing an AM cooled component, not to incur in efficiency detrimental over-cooled surfaces or dangerous underestimation of the component’s operating temperature.