Research on the Criteria for Determining the Starting Performance of an Inward-Turning Inlet by Integrating the Concept of the Equivalent Contraction Ratio
Abstract
:1. Introduction
2. Design and Calculation Method of the Inward-Turning Inlet
2.1. Design of the Inward-Turning Inlet
2.2. Numerical Calculation Method
2.2.1. Numerical Details
2.2.2. Validation of Turbulence Models
2.2.3. Grid Independence Research
3. Results
3.1. Prediction Method for Starting Performance of the Inward-Turning Inlet
3.1.1. Analysis of the Start Boundary for the Inward-Turning Inlet
3.1.2. Definition of the Equivalent Contraction Ratio
3.2. Performance Analysis of Inward-Turning Inlet
3.2.1. Inlet Performance with Different Geometric Contraction Ratios
3.2.2. Inlet Performance with Different Angles of Attack
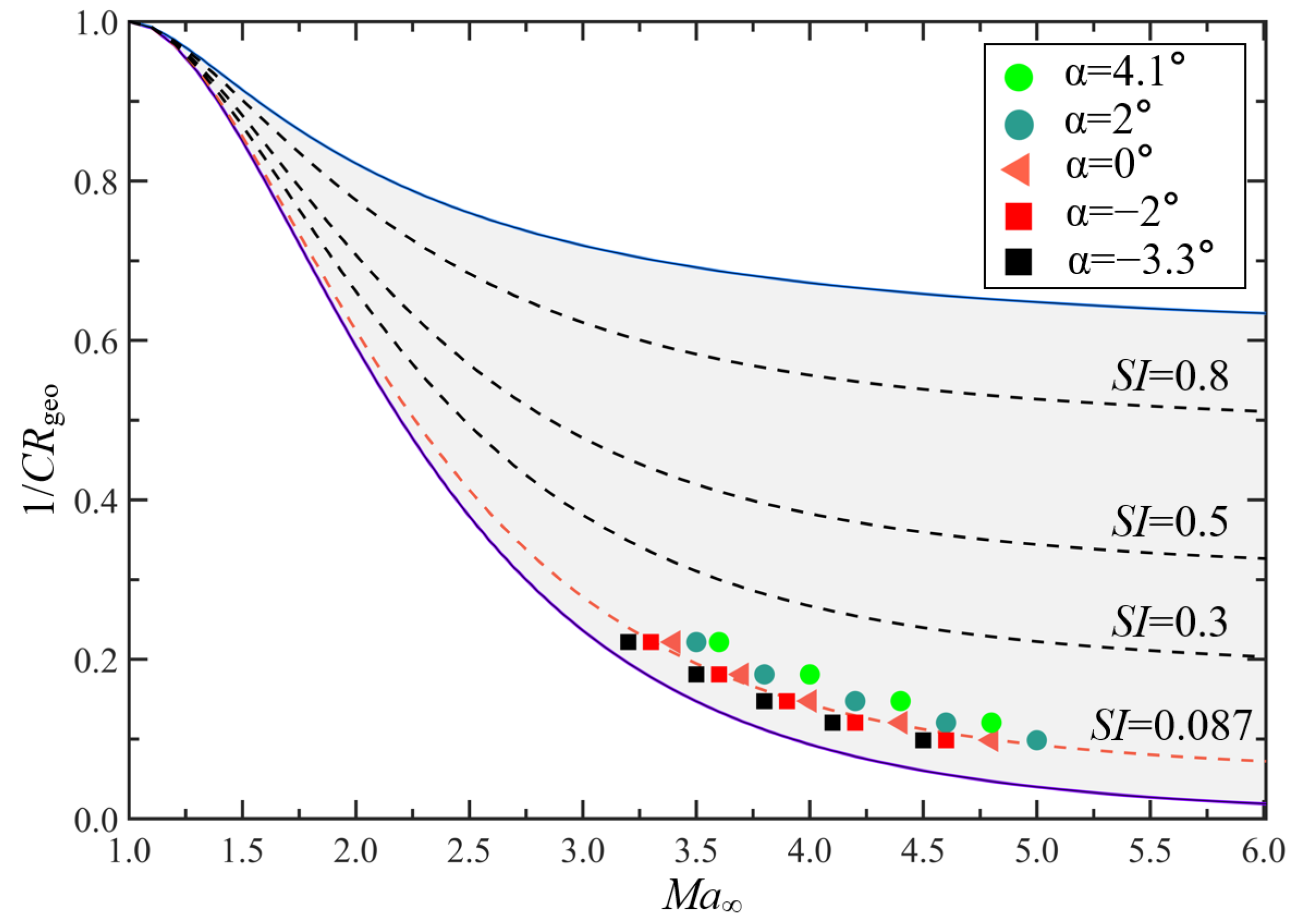
3.2.3. Inlet Performance Under the Same Equivalent Contraction Ratio
4. Conclusions
- (1)
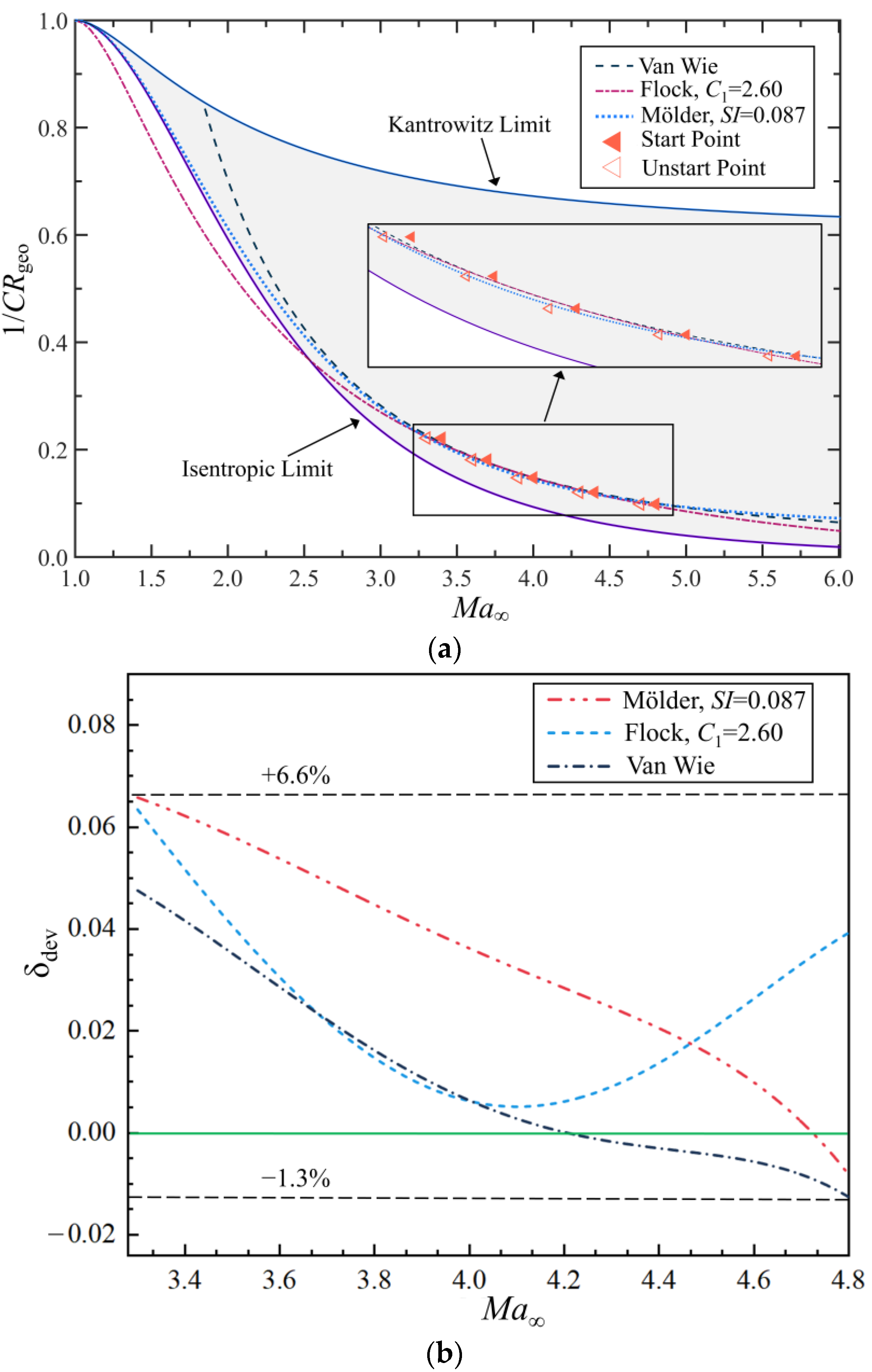
- The start boundary of the inward-turning inlet in the design state can be predicted using the startability index (SI = 0.087) proposed by Mölder, with a maximum error of approximately 6.6%, which is consistent with the maximum geometric contraction ratio boundary summarized by Van.
- (2)
- By incorporating the angle of attack into the geometric contraction ratio, the concept of the equivalent contraction ratio is introduced and compared with the startability index. Predictions under positive angle-of-attack conditions are relatively accurate, with an error not exceeding 4.0%; however, under negative angle-of-attack conditions, the deviation is larger at 13.3%. After applying a fitting function correction, the deviation can be reduced to within 2.0%. This theory allows for the rapid and straightforward determination of the accurate inlet start boundaries at different angles of attack, making it suitable for engineering estimates and saving computational resources.
- (3)
- The effects of the Mach number, angle of attack, and geometric contraction ratio on the performance of the inlet are analyzed. A decrease in the Mach number leads to an expanding separation zone, ultimately resulting in the inlet failing to start. An increase in the angle of attack enhances the strength of the oblique shock at the inlet’s leading edge. Increasing the geometric contraction ratio strengthens the compressibility of the internal compression region. The combined effects of the angle of attack and geometric contraction ratio ultimately unify into the inlet’s compression strength. The differences in prediction accuracy between positive and negative angle of attack conditions are attributed to the internal pressure of the inlet at negative angles being significantly higher than that at positive angles and the design state, resulting in a poorer starting performance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, X.; Yang, H. Development of hypersonic inlet. Aerosp. Technol. 2022, 3, 62–70. [Google Scholar]
- Smart, M.K. How much compression should a scramjet inlet do? AIAA J. 2012, 50, 610–619. [Google Scholar] [CrossRef]
- Bai, Y.; Bai, Y. Failure Analysis of the X-51A Aircraft Flight Test. Aeronaut. Missile J. 2012, 3, 27–30+46. [Google Scholar]
- Liang, D.; Yuan, H.; Zhang, X. Research on the Effects of Start Ability of Hypersonic Inlet. J. Astronaut. 2006, 4, 714–719. [Google Scholar]
- Guo, S.; Li, Z.; Gao, W.; Yang, J. Analogy Between Effects of Attack Angle and Mach Number on Inlet Starting. J. Propul. Technol. 2017, 38, 983–991. [Google Scholar]
- Xu, S.; Wang, Y.; Wang, Z.; Fan, X.; Xiong, B. Unsteady behavior of hypersonic inlet unstart caused by high angle of attack. Aerosp. Sci. Technol. 2022, 130, 107884. [Google Scholar] [CrossRef]
- Hillier, R. Shock-wave/expansion-wave interactions and the transition between regular and mach reflection. J. Fluid Mech. 2007, 575, 399–424. [Google Scholar] [CrossRef]
- Devaraj, M.K.K.; Jutur, P.; Rao, S.M.; Jagadeesh, G.; Anavardham, G.T. Investigation of local unstart in a hypersonic scramjet intake at a mach number of 6. Aerosp. Sci. Technol. 2021, 115, 106789. [Google Scholar] [CrossRef]
- Chen, H.; Tan, H.J. Buzz flow diversity in a supersonic inlet ingesting strong shear layers. Aerosp. Sci. Technol. 2019, 95, 105471. [Google Scholar] [CrossRef]
- Chang, J.; Li, N.; Xu, K.; Bao, W.; Yu, D. Recent research progress on unstart mechanism, detection and control of hypersonic inlet. Prog. Aerosp. Sci. 2017, 89, 1–22. [Google Scholar] [CrossRef]
- Saravanan, R.; Desikan, S.; Francise, K.; Kalimuthu, R. Experimental investigation of start/unstart process during hypersonic intake at mach 6 and its control. Aerosp. Sci. Technol. 2021, 113, 106688. [Google Scholar] [CrossRef]
- Tang, X.; Xiong, B.; Fan, X.; Liu, J.; Zhao, J. Experimental research on the flow mechanism of dual-separation unstart phenomenon in hypersonic inlet. Aerosp. Sci. Technol. 2024, 150, 109189. [Google Scholar] [CrossRef]
- Kantrowitz, A.; Donaldson, C. Preliminary Investigation of Supersonic Diffusers; National Advisory Committee for Aeronautics: Washington, DC, USA, 1945; p. 336. [Google Scholar]
- Van Wie, D.; Kwok, F.; Walsh, R. Starting characteristics of supersonic inlets. In Proceedings of the 32nd Joint Propulsion Conference and Exhibit, Lake Buena Vista, FL, USA, 1–3 July 1996. [Google Scholar]
- Molder, S.; Timofeev, E.; Tahir, R. Flow starting in high compression hypersonic air inlets by mass spillage. In Proceedings of the 40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Fort Lauderdale, FL, USA, 11–14 July 2004. [Google Scholar]
- Flock, A.K.; Gülhan, A. Experimental investigation of the starting behavior of a three-dimensional scramjet intake. AIAA J. 2015, 53, 2686–2693. [Google Scholar] [CrossRef]
- Flock, A.K.; Guelhan, A. Modified kantrowitz starting criteria for mixed compression supersonic intakes. AIAA J. 2019, 57, 2011–2016. [Google Scholar] [CrossRef]
- Sun, B.; Zhang, K.Y. Empirical equation for self-starting limit of supersonic inlets. J. Propul. Power 2010, 26, 874–875. [Google Scholar] [CrossRef]
- Xie, W.Z.; Ma, G.F.; Guo, R.W.; Chen, H.; Wen, Y.F.; Guo, S.M. Flow-based prediction for self-starting limit of two-dimensional hypersonic inlets. J. Propul. Power 2016, 32, 463–471. [Google Scholar] [CrossRef]
- Pan, J.; Shi, C.; Li, Y.; You, Y.; Chen, R. A New Understanding of Hypersonic Inlets’ Startability Criterion. J. Propul. Technol. 2016, 37, 2039–2047. [Google Scholar]
- Tong, X.T.; Yue, L.J.; Chen, H.; Zhang, Q.F.; He, C.M. Similarity analysis on two-dimensional hypersonic inlets unstart. AIAA J. 2023, 61, 555–572. [Google Scholar] [CrossRef]
- You, Y.C. An overview of the advantages and concerns of hypersonic inward turning inlets. In Proceedings of the 17th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, San Francisco, CA, USA, 11–14 April 2011. [Google Scholar]
- Nan, X.; Zhang, K.; Jin, Z.; Sun, B. Numerical and experimental investigation of hypersonic inward turning inlets with rectangular to circular shape transition. Acta Aeronaut. Astronaut. Sin. 2011, 32, 988–996. [Google Scholar]
- Huang, H.; Huang, G.; Yu, Z.; Qiao, W. The design of internal waverider hypersonic inlet with high ratio of external compression. J. Eng. Thermophys. 2015, 36, 1233–1237. [Google Scholar]
- Guo, J.; Huang, G.; You, Y.; Liang, D. Study of internal compression flow field for improving the outflow uniformity of internal waverider inlet. J. Astronaut. 2009, 30, 1934–1940+1952. [Google Scholar]
- Wang, Y. Investigation on the Starting Characteristics of Hypersonic Inlet. Doctor’s Thesis, National University of Defense Technology, Changsha, China, 2008. [Google Scholar]
- Musa, O.; Huang, G.; Yu, Z. Evaluation of the pressure-corrected osculating axisymmetric flows method for designing hypersonic wavecatcher intakes with shape transition. J. Aerosp. Eng. 2024, 37, 04024023. [Google Scholar] [CrossRef]
- Hao, C.; Luo, W.; Yu, Z.; Zhu, J.; You, Y. Novel design method for inward-turning inlets with non-uniform inflow. Aerosp. Sci. Technol. 2024, 148, 109098. [Google Scholar] [CrossRef]
- Yuan, H.; Li, Z.; Zhang, J.; Wang, X. Experimental and numerical research on a three-dimensional inward-turning inlet. J. Aerosp. Eng. 2023, 36, 04023008. [Google Scholar] [CrossRef]
- Panchal, S.; Gudlanarva, K.; Tran, M.-K.; Herdem, M.S.; Panchal, K.; Fraser, R.; Fowler, M. Numerical simulation of cooling plate using k-epsilon turbulence model to cool down large-sized graphite/lifepo4 battery at high c-rates. World Electr. Veh. J. 2022, 13, 138. [Google Scholar] [CrossRef]
- Liu, J.; Wang, D.; Huang, X. Investigation of turbulence models for aerodynamic analysis of a high-pressure-ratio centrifugal compressor. Phys. Fluids 2023, 35, 106108. [Google Scholar] [CrossRef]
- Hua, Z.; Yuan, H.; Wang, J.; Chen, W. Effects of swept lip on starting characteristies of 2-D hypersonic inlet. J. Propul. Technol. 2017, 38, 241–248. [Google Scholar]
- De Vanna, F.; Bof, D.; Benini, E. Multi-objective rans aerodynamic optimization of a hypersonic intake ramp at mach 5. Energies 2022, 15, 2811. [Google Scholar] [CrossRef]
- Li, Y.; Shi, C.; Zhu, C.; You, Y. Aerodynamic combination design concept for hypersonic waverider forebody and inward turning inlet. J. Propul. Technol. 2018, 39, 2320–2328. [Google Scholar]
- Hao, C.; Huang, G.; Yu, Z. Numerical study on effects of typical characteristic parameters on flight performance for rapid turning APU inlet. J. Propul. Technol. 2022, 43, 151–162. [Google Scholar]
- Lockman, W.K.; Lawrence, S.L.; Cleary, J.W. Flow over an all-body hypersonic aircraft-experiment and computation. J. Spacecr. Rockets. 1992, 29, 7–15. [Google Scholar] [CrossRef]


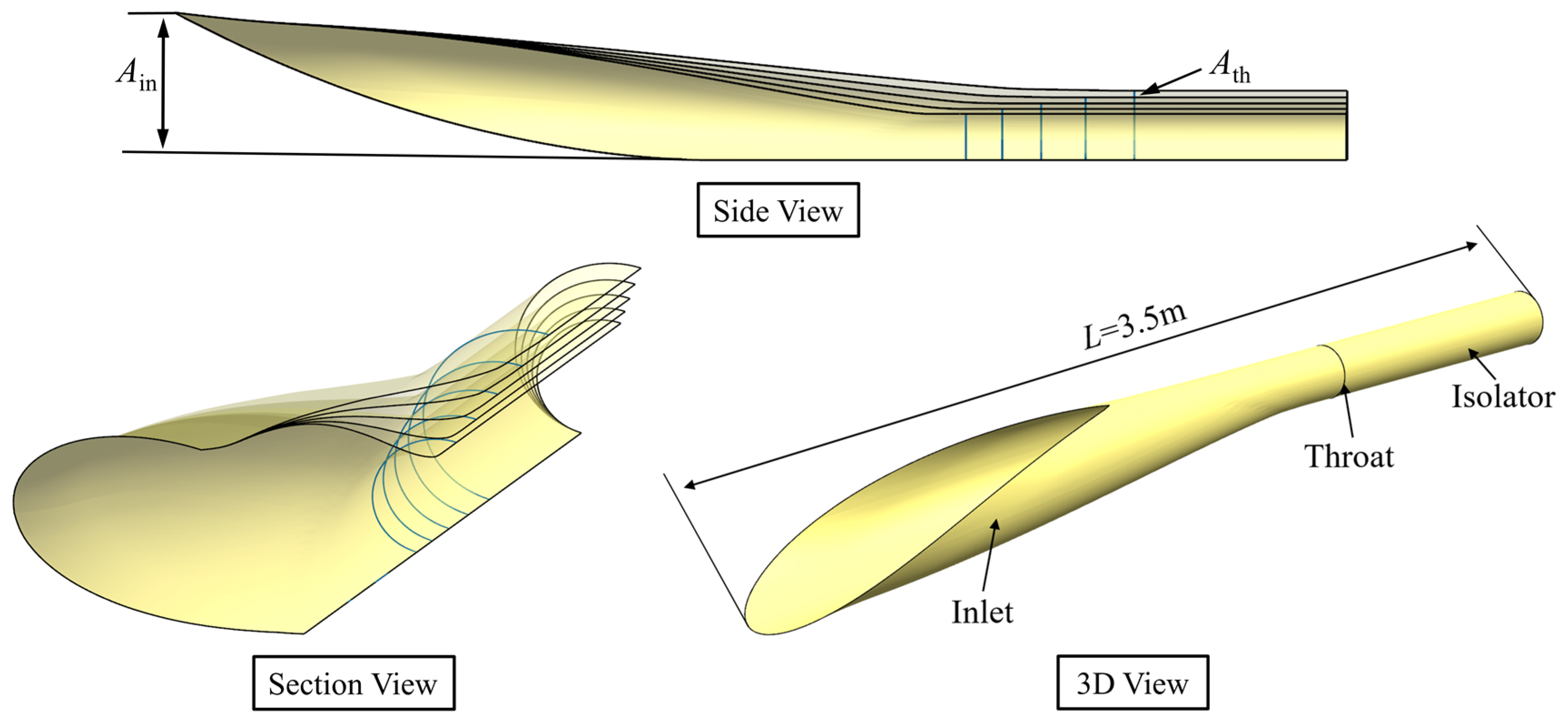














| CRgeo | Ain (m2) | Ath (m2) | Lth (m) |
|---|---|---|---|
| 4.51 | 0.1529 | 0.03384 | 2.864 |
| 5.53 | 0.1529 | 0.02761 | 2.719 |
| 6.77 | 0.1529 | 0.02256 | 2.587 |
| 8.29 | 0.1529 | 0.01845 | 2.471 |
| 10.14 | 0.1529 | 0.01508 | 2.363 |
| Parameters | Nodes (million) | Math | πth | σth | φ | η |
|---|---|---|---|---|---|---|
| Coarse | 2.13 | 3.055 | 24.338 | 0.709 | 99.50% | 0.986 |
| Medium | 5.68 | 3.051 | 24.486 | 0.705 | 99.59% | 0.985 |
| Fine | 8.25 | 3.053 | 24.513 | 0.706 | 99.61% | 0.985 |
| CRgeo | α (°) | ||||
|---|---|---|---|---|---|
| 4.1 | 2 | 0 | −2 | −3.3 | |
| 4.51 | Ma 3.6 | Ma3.5 | Ma 3.4 | Ma 3.3 | Ma 3.2 |
| 5.53 | Ma 4.0 | Ma 3.8 | Ma 3.7 | Ma 3.6 | Ma 3.5 |
| 6.77 | Ma 4.4 | Ma 4.2 | Ma 4.0 | Ma 3.9 | Ma 3.8 |
| 8.29 | Ma 4.8 | Ma 4.6 | Ma 4.4 | Ma 4.2 | Ma 4.1 |
| 10.14 | Ma 5.0 | Ma 4.8 | Ma 4.6 | Ma 4.5 | |
| Ma∞ | α (°) | CRgeo | Math | πth | σth | Mao | πo | σo | m (kg/s) | φ |
|---|---|---|---|---|---|---|---|---|---|---|
| 6.0 | 0 | 4.51 | 3.478 | 13.061 | 0.714 | 3.371 | 13.759 | 0.664 | 8.016 | 99.54% |
| 6.0 | 0 | 5.53 | 3.260 | 17.813 | 0.708 | 3.120 | 19.065 | 0.639 | 8.021 | 99.60% |
| 6.0 | 0 | 6.77 | 3.051 | 24.489 | 0.705 | 2.854 | 27.940 | 0.617 | 8.020 | 99.59% |
| 6.0 | 0 | 8.29 | 2.831 | 34.264 | 0.699 | 2.639 | 37.547 | 0.592 | 8.015 | 99.53% |
| 6.0 | 0 | 10.14 | 2.604 | 48.893 | 0.693 | 2.351 | 56.059 | 0.557 | 8.016 | 99.54% |
| α (°) | CRgeo | Ma∞ | Math | πth | σth | Mao | πo | σo | m (kg/s) | φ |
|---|---|---|---|---|---|---|---|---|---|---|
| 4.1 | 6.77 | 6.0 | 2.687 | 37.731 | 0.597 | 2.525 | 39.853 | 0.519 | 9.844 | 99.93% |
| 2 | 6.77 | 6.0 | 2.894 | 29.827 | 0.666 | 2.710 | 33.364 | 0.583 | 8.929 | 99.92% |
| 0 | 6.77 | 6.0 | 3.052 | 24.516 | 0.706 | 2.858 | 27.875 | 0.619 | 8.016 | 99.51% |
| −2 | 6.77 | 6.0 | 3.221 | 19.757 | 0.740 | 3.012 | 22.432 | 0.644 | 7.008 | 97.87% |
| −3.3 | 6.77 | 6.0 | 3.326 | 17.235 | 0.756 | 3.104 | 19.443 | 0.651 | 6.363 | 96.76% |
| Ma∞ | α (°) | CRgeo | Math | πth | σth | Mao | πo | σo | m (kg/s) | φ |
|---|---|---|---|---|---|---|---|---|---|---|
| 4.1 | 4.1 | 5.53 | 1.555 | 28.700 | 0.706 | 1.452 | 31.153 | 0.629 | 5.994 | 89.14% |
| 4.1 | 0 | 6.77 | 1.597 | 27.756 | 0.737 | 1.447 | 31.366 | 0.664 | 4.883 | 88.78% |
| 4.1 | −3.3 | 8.29 | 1.493 | 31.393 | 0.729 | 1.319 | 35.675 | 0.629 | 4.020 | 89.40% |
| 6.0 | 4.1 | 5.53 | 2.954 | 25.271 | 0.621 | 2.790 | 27.872 | 0.552 | 9.842 | 99.91% |
| 6.0 | 0 | 6.77 | 3.052 | 24.516 | 0.706 | 2.858 | 27.875 | 0.619 | 8.016 | 99.51% |
| 6.0 | −3.3 | 8.29 | 3.075 | 24.113 | 0.732 | 2.878 | 25.971 | 0.621 | 6.366 | 96.80% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, F.; Jin, B.; He, X.; Chen, Z.; Yan, W.; Zhao, Z.; Yu, Z. Research on the Criteria for Determining the Starting Performance of an Inward-Turning Inlet by Integrating the Concept of the Equivalent Contraction Ratio. Aerospace 2024, 11, 941. https://doi.org/10.3390/aerospace11110941
Meng F, Jin B, He X, Chen Z, Yan W, Zhao Z, Yu Z. Research on the Criteria for Determining the Starting Performance of an Inward-Turning Inlet by Integrating the Concept of the Equivalent Contraction Ratio. Aerospace. 2024; 11(11):941. https://doi.org/10.3390/aerospace11110941
Chicago/Turabian StyleMeng, Fanshuo, Bo Jin, Xiaolong He, Zheng Chen, Wenhui Yan, Zhenjun Zhao, and Zonghan Yu. 2024. "Research on the Criteria for Determining the Starting Performance of an Inward-Turning Inlet by Integrating the Concept of the Equivalent Contraction Ratio" Aerospace 11, no. 11: 941. https://doi.org/10.3390/aerospace11110941
APA StyleMeng, F., Jin, B., He, X., Chen, Z., Yan, W., Zhao, Z., & Yu, Z. (2024). Research on the Criteria for Determining the Starting Performance of an Inward-Turning Inlet by Integrating the Concept of the Equivalent Contraction Ratio. Aerospace, 11(11), 941. https://doi.org/10.3390/aerospace11110941







