Position Normalization of Propellant Grain Point Clouds

Abstract

Point cloud data obtained from scanning propellant grains with 3D scanning equipment exhibit positional uncertainty in space, posing significant challenges for calculating the relevant parameters of the propellant grains. Therefore, it is essential to normalize the position of each propellant grain’s point cloud. This paper proposes a normalization algorithm for propellant grain point clouds, consisting of two stages, coarse normalization and fine normalization, to achieve high-precision transformations of the point clouds. In the coarse normalization stage, a layer-by-layer feature points detection scheme based on k-dimensional trees (KD-tree) and k-means clustering (k-means) is designed to extract feature points from the propellant grain point cloud. In the fine normalization stage, a rotation angle compensation scheme is proposed to align the fitted symmetry axis of the propellant grain point cloud with the coordinate axes. Finally, comparative experiments with iterative closest point (ICP) and random sample consensus (RANSAC) validate the efficiency of the proposed normalization algorithm.

1. Introduction

For solid missiles and space launch rockets, solid rocket motors remain the primary propulsion devices [1,2,3]. A typical solid rocket motor consists of a combustion chamber casing, propellant grain, a nozzle, and an igniter. Additionally, between the propellant grain and the casing, there is an overcoat structure [4], primarily composed of an adhesive that bonds the propellant grain to the inner wall of the casing, along with insulation and a liner. This structure ensures the integrity of the propellant grain and plays a crucial role in the reliability and safety of the solid rocket motor. Propellant grain are composite materials containing various chemical components [5]. The common composition of the propellant grain mainly includes oxidizers, nano-scale metal oxides [6], and adhesives mixed in specific proportions, forming a structurally heterogeneous composite material [7,8,9]. For a typical propellant grain, the surface is rough and granular, with the oxidizer content comprising 60–80 wt%. The performance of the propellant grain is primarily constrained by the inherent properties of the oxidizer [10]. Based on the formulation of the propellant, the grain exhibits nonlinear viscoelastic properties [11]. Due to the mechanical properties of the propellant, it undergoes physical and chemical adsorption, resulting in wetting and surface separation under load [12]. This damage leads to a decline in the mechanical properties of the propellant, thereby affecting the integrity of the propellant grain structure.

The overcoat structure and the solid propellant are two critical weak points in the structural integrity of solid rocket motors [13,14], and the compromise of propellant grain integrity is one of the primary causes of solid rocket motor failure [15]. Ensuring the uniformity of the overcoat structure and the mechanical properties of the propellant grain presents significant challenges in the loading of the propellant. Currently, most solid propellant assemblies utilize the wall pouring method [16]. The wall pouring method involves directly pouring the solid propellant slurry into the combustion chamber shell, which has already been lined. After the propellant cures, it forms an inseparable unit with the combustion chamber shell. However, this method makes replacement difficult and renders the structure irreparable [17]. Due to the lower reliability of the wall pouring assembly method, a free assembly method is adopted. Figure 1 illustrates the free assembly method and the wall pouring method. In the free assembly method, the propellant grain is formed in a specialized mold. Once cured, the propellant grain is assembled with the insulated combustion chamber shell to complete the manufacturing of the solid rocket motor. The propellant grain and the combustion chamber shell are detachable.

In free assembly mode, the propellant is composed of several propellant grains, and assembly is completed by loading each grain individually. Unlike the wall pouring assembly method, the free assembly method does not use pouring for assembly. Instead, the propellant grains are assembled into the casing one by one. Due to production constraints, each propellant grain has a different geometric shape. Before being loaded into the casing, the overall assembly sequence and the assembly position of each propellant grain can be determined in advance based on the geometric characteristics of each grain. During the assembly process, the assembly scheme is dynamically adjusted based on the progress of the assembly and the assessment results of the integrity of the propellant column within the casing. After the free assembly method is completed, all propellant grains are arranged neatly and uniformly inside the casing, with uniform gaps between the grains and stabilized pressure within the gaps, ensuring the integrity of the propellant column structure [18,19]. Therefore, this method allows for dynamic adjustment of the loading process, ensuring the uniformity of the overcoat structure and the integrity of the propellant grain. However, this assembly method also faces certain challenges: On one hand, during the assembly of propellant grains, the assembly space may undergo changes. The assembly sequence of the propellant grains might need to be adjusted due to this deformation. On the other hand, because the propellant grains have different sizes and possess a certain degree of elasticity, the geometric shapes of the propellant grains are not regular, and each grain has unique geometric characteristics. In the traditional free assembly model, The geometric properties of the propellant grain were measured using a manual contact-based method. Due to the size of the propellant grain and its nonlinear viscoelastic properties, the measurement results were highly inaccurate, with significant errors, making it difficult to plan an assembly strategy. In assembly attempts, these inaccuracies may lead to failures.

To address these challenges, this paper introduces point cloud for the free assembly method. Three-dimensional laser scanning is a non-contact measurement method that maximizes the preservation of the geometric properties of the propellant grain, preventing damage from human interference or compression. Using 3D laser scanning, the entire propellant grain is accurately represented by a high-precision point cloud. These data are then used to predict the variation of assembly space and match the geometric characteristics between the casing and the propellant grains. Pre-assembly of the propellant grains is conducted in virtual space, and this virtual assembly is mapped to the real world to achieve actual free assembly. Due to the physical nature of the scanning mechanism, the top and bottom surfaces of the propellant grain point clouds are parallel to the XOZ plane, but their overall positions are arbitrarily distributed in space. Therefore, the prerequisite for this improved free assembly method is that the point cloud data of all propellant grains must be normalized to the same position in the coordinate system. Without this normalization, the rotation and translation of the propellant grains in virtual space would lack a reference point, making the entire assembly process unfeasible, as illustrated in Figure 2.

This study proposes a point cloud position normalization algorithm to address the issue of inconsistent positions of propellant grain point clouds. Additionally, normalizing the position of the propellant point cloud involves shifting the center of the curved surface of the propellant grain point cloud to the calibrated position in virtual space and aligning the overall axis of the point cloud. Point cloud position normalization is similar to point cloud registration in that both involve transforming the point cloud to a specific position. The propellant grain point cloud normalization algorithm proposed in this study establishes the prerequisites for the free assembly of propellants in a virtual space.

Based on the aforementioned research context, this paper proposes a position normalization algorithm for the point clouds of propellant grains:

(1)

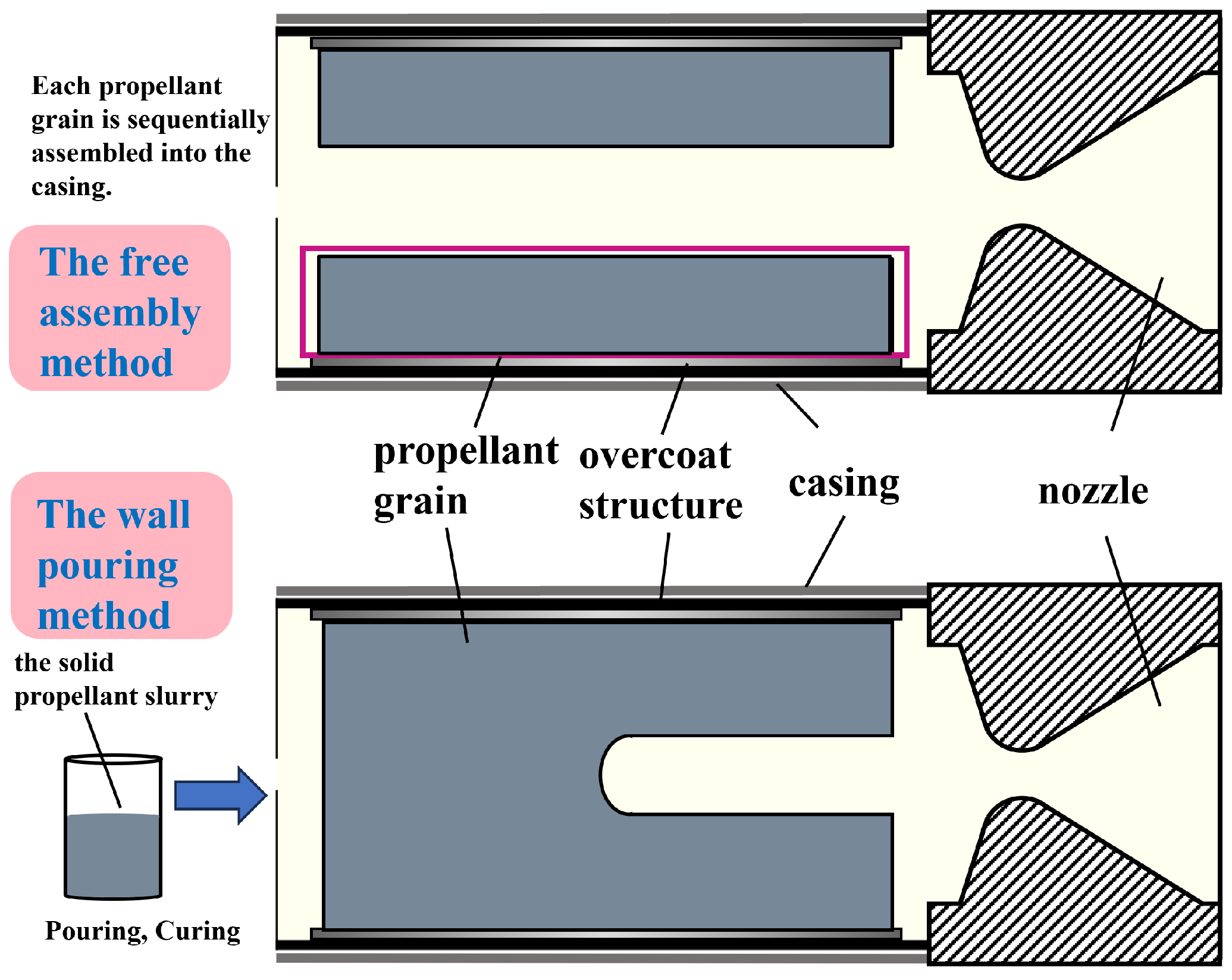
The algorithm first performs down-sampling on the point cloud. The 3D laser scanning generates a large volume of point cloud data for the propellant grain. Without appropriate down-sampling, the subsequent processing would consume a significant amount of computational resources.

(2)

The proposed algorithm consists of two stages: coarse normalization and fine normalization. In the coarse normalization stage, the algorithm extracts the feature points of the point cloud based on clustering segmentation. In the fine normalization stage, firstly, reduce angular errors through multiple symmetry axis fittings. Finally, it compensates for the axial offset through point correspondence to complete the position normalization of the point cloud.

(3)

In the experimental section, the accuracy of this algorithm is evaluated by comparing it with the most representative algorithms in point cloud registration: RANSAC and ICP.

The structure of this paper is as follows. Section 2 presents a review of relevant literature pertaining to this problem. Section 3 outlines the algorithms utilized in this research. Section 4 presents comparative experiments with algorithms composed of RANSAC and ICP. Finally, Section 5 concludes with remarks and future prospects.

2. Related Work

2.1. Point Cloud Registration

Point cloud registration, as a prerequisite for various tasks in computer vision such as 3D reconstruction [20,21,22], 3D segmentation [23,24], and pose estimation [25], primarily addresses the challenge of merging and transforming point cloud data obtained from different perspectives, scenes, and time instances into a reference coordinate system. Point cloud registration problems can be classified into rigid registration [26,27] and non-rigid registration [28,29]. Rigid registration pertains to problems involving only translation and rotation transformations, while non-rigid registration involves transformations such as scaling, deformation, and affine transformations. The registration problem for propellant grain point clouds falls under the category of rigid registration.

Existing point cloud registration methods can be broadly categorized into two types. The first type involves registration achieved through learning-based models. Leveraging the robustness of deep learning in handling large quantities of noisy point cloud data [30], various research efforts have proposed deep learning models to extract point cloud features. These models utilize techniques such as singular value decomposition to obtain transformation matrices for registration. Examples of such models include PointNet [31], PointNet++ [32], and others. However, learning-based algorithms are not only complex but also relatively lacking in interpretability, and they require substantial computational resources during the training phase. Moreover, learning-based registration models, being trained models, inherently have accuracy issues, which is especially critical for propellant assembly where safety requirements are extremely high.

The second category of algorithms consists of traditional non-learning-based methods based on feature matching, such as ICP and RANSAC. For rigid registration problems, extracting feature points that reflect the overall geometric properties of the entire point cloud from vast point cloud data obtained from 3D laser scanning, especially in the presence of a large number of outliers and missing points, poses a significant challenge. Point cloud features mainly include edge and corner points, normal vectors, creases, and boundary points [33]. By matching these features, a transformation matrix can be derived to achieve point cloud registration. However, unlike feature point extraction in 2D images, which benefits from the connectivity information, algorithms for extracting feature points from point clouds are not yet mature [34]. Existing feature-based registration algorithms often start with the extraction of point cloud features from neighboring point features and clustering segmentation [35,36]. For neighboring point features, common methods include multi-scale covariance matrices of local point neighborhoods, differences between normal vectors, and eigenvalue decomposition [37,38,39]. As for clustering segmentation, it involves clustering based on certain features of point clouds, such as the angles between neighboring point normal vectors [36], to narrow down the search range for feature point extraction. Regarding the acquisition of the transformation matrix needed for registration, the majority of feature point-based registration algorithms require the transformation matrix to be computed via singular value decomposition (SVD), with the registration accuracy constrained by the quality of the feature point set. Additionally, besides directly extracting features from point cloud data, some research transforms point clouds into 2D images for feature extraction, leveraging the powerful feature extraction capabilities in the field of computer vision for 2D images. Lu et al. [40], for example, projected segmented point clouds onto a 2D plane to form images and then processed these images for feature extraction. However, despite the abundance of points in the three-dimensional space, point distribution is relatively sparse, leading to the discreteness of pixels in 2D images and posing challenges for feature extraction.

Currently, most non-learning-based registration algorithms are based on improvements to algorithms such as iterative closest point (ICP) and random sample consensus (RANSAC). Therefore, for the comparison of algorithms applied to the point clouds of propellant grains, this paper compares the proposed method with the most representative algorithms: RANSAC and ICP.

2.1.1. RANSAC

Random ample consensus (RANSAC) is an iterative algorithm used to estimate mathematical model parameters, such as fitting lines and planes [41]. When applied to the field of point cloud registration, the basic idea is to exhaustively search points in the source point cloud, match them with corresponding points in the target point cloud based on geometric features, and calculate the transformation matrix. The transformation matrix is evaluated and iterated upon.

For extracting geometric features between corresponding points, the fast point feature histograms (FPFH) algorithm [42] is commonly used. Based on this theory, several registration algorithms have been developed. For instance, Tsai et al. [43] proposed a RANSAC RGB-D mapping algorithm, which utilizes the RANSAC outlier removal algorithm to eliminate correspondences causing significant errors. Subsequently, the RGB-D mapping algorithm finds the optimal transformation matrix for registration, thereby improving registration accuracy and efficiency. Dou et al. [44] first use the RANSAC algorithm for coarse registration and then employ local structural descriptors and Gaussian mixture models to achieve non-rigid point cloud registration. Peng et al. [45] introduced a point cloud registration strategy combining k-means with RANSAC ICP, where the point cloud after k-means clustering is registered using both RANSAC and ICP.

While RANSAC is widely used in point cloud registration, it has its limitations: it lacks a clear limit on the number of iterations, the determination of relevant thresholds can be challenging, and it can only find one model for problems with multiple possible model fits.

2.1.2. ICP

The most widely used algorithm in point cloud registration is the iterative closest point (ICP) algorithm [46]. ICP has had a groundbreaking impact on rigid registration, with many registration algorithms evolving from it. ICP is an iterative algorithm that minimizes the Euclidean distance function between corresponding points in the source and target point clouds. However, this algorithm is sensitive to noise, and as the size of the point cloud data increases, solving the distance function slows down and may even lead to convergence to local optima.

Several variants of the ICP algorithm have been developed. For example, Yu et al. [47] improved the ICP algorithm by introducing second-order filtering based on matched point pairs, which enhances registration accuracy and reduces registration time. Chen et al. [48] first used the Super 4PCS algorithm for coarse registration to achieve initial alignment of point clouds. Then, they improved the ICP algorithm by adaptively removing boundary points in overlapping regions, addressing registration problems involving overlapping areas.

However, ICP requires a relatively strict relationship between the target point cloud and the original point cloud, meaning that there should not be significant deviations in the initial positions of the target and original point clouds.

3. Method

3.1. Geometric Features

Since the algorithm proposed in this paper is closely related to the geometric features of the propellant grain, a dedicated subsection has been included to introduce its geometric properties.

To accurately replicate the geometric shape of the propellant, the propellant grain is mapped into virtual space in the form of a point cloud. Depending on the cross-sectional dimensions of assembly space, each layer of the propellant is divided into several propellant grains. Each propellant grain has a columnar shape, with a fan-shaped cross-section.

The propellant grain point cloud is generally shaped like a sector cylinder, with the back surface (curved surface) typically referred to as a cylindrical or arc surface. On the arc surface, densely arrayed convex points are present, with adhesive material filling the gaps between each convex point for bonding with the casing. There are many corner points on the propellant grain point cloud, some of which are on the arc surface, while others are not. In the following text, only the corner points on the arc surface are the ones we aim to extract. The main reason for using arc corner points as features is the distinct distribution difference between the neighborhood of corner points and non-arc corner points. As shown in Figure 3.

3.2. Method Overview

The overall algorithm consists of two stages: coarse normalization and fine normalization as shown in Figure 4. In the coarse normalization stage: The original point cloud undergoes downsampling. It is then projected layer by layer and processed using techniques such as KD-tree and multiple k-means to extract arc corner points. Based on these arc corner points, the transformation matrix is computed. In the fine normalization stage: Fine normalization is performed by fitting a symmetric axis to refine the transformation matrix.

3.3. Problem Setting

Let the original point cloud obtained from the 3D laser scanner, which has its upper and lower surfaces parallel to the $XOZ$ plane but randomly distributed in position, be denoted as P. After point cloud downsampling, P is represented as $P_S$. After undergoing both coarse and fine normalization stages, $P_S$ is transformed into $P_S^{\prime }$ and $P_S^{″}$, respectively. We refer to Appendix A for the meaning of the mathematical symbols used in this paper.

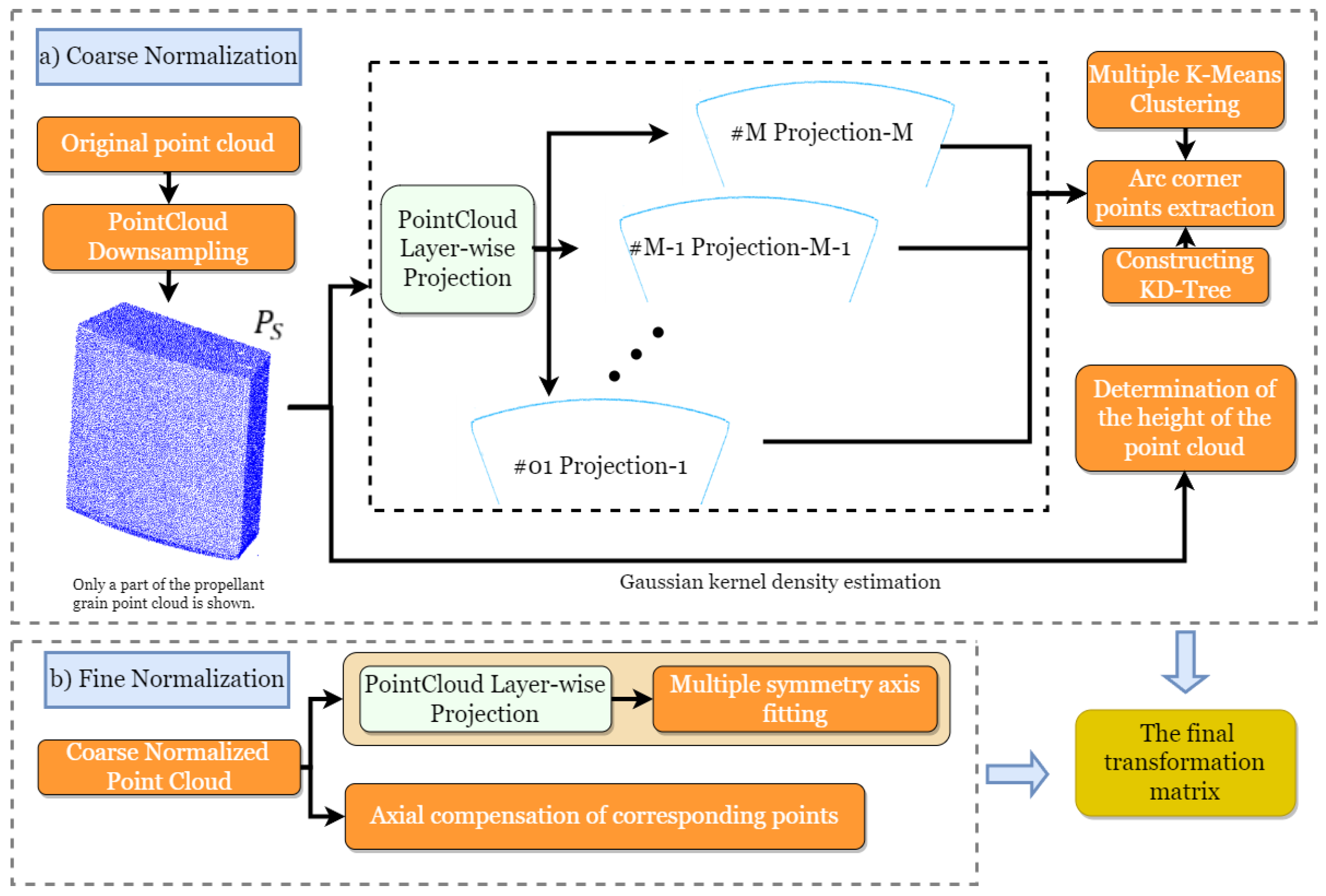
3.4. Coarse Position Normalization

3.4.1. Point Cloud Downsampling

Based on the characteristics of the original point cloud data, Poisson disk sampling is employed to downsample the original point cloud data to ensure uniform point cloud density as much as possible, given that the original point cloud dataset may contain hundreds of thousands of points.

Let $P=\{p_i;i=1,2,\cdots ,N\}$ be the original point cloud dataset with N points $p_i$. The sampling conditions for Poisson disk sampling are as follows:

$$\forall {\mathbf{p}}_i,{\mathbf{p}}_j\in P:\parallel {\mathbf{p}}_i-{\mathbf{p}}_j\parallel \ge 2r,i\ne j$$

(1)

where r denotes the distribution radius.

After applying Poisson disk downsampling to the original point cloud P, we obtain the point cloud $P_S$ with $N^{\prime }$ points. In point cloud $P_S$, the distance between any two points is greater than twice the value of r, ensuring that the density of each face in the point cloud $P_S$ tends to be balanced, while preserving its geometric properties. Compared to other downsampling methods, Poisson disk downsampling offers certain advantages in avoiding interference caused by excessively dense local point clouds when selecting feature points.

3.4.2. Point Cloud Layer-Wise Projection

After downsampling the original point cloud to obtain $P_S$, to reduce the influence of vertical tilt and convex points on arc corner extraction, the point cloud is projected layer by layer. Based on the characteristics of the point cloud $P_S$, the upper and lower surfaces of the point cloud are parallel to the $XOZ$ plane, and there are convex points arranged in arrays on the arc surface. The point cloud $P_S$ is divided into M layers, corresponding to M intervals in the y-direction. The i-th layer contains the point cloud denoted as $P_i=\{p_{ij}(x_{ij},y_{ij},z_{ij})\in P_i,j=1,2,3,\dots ,l_i\}$, where $l_i$ is the number of points within this layer of the point cloud.

$$\left\{\begin{array}{c}{P}_S=\sum _i^M{P}_i\hfill \\ H=\sum _i^M\Delta h_i\hfill \end{array}\right.i=1,\cdots ,M$$

(2)

where H is the total height of the point cloud $P_S$, and $\Delta h_{\mathrm{i}}$ be the height of each layer. Suppose the scattered point set after projecting the point cloud $P_i$ onto the XOZ plane is denoted as $P_i^{\prime }=\{p_{ij}^{\prime }\left(x_{ij}^{\prime },y_{ij}^{\prime },z_{ij}^{\prime }\right)\in P_i^{\prime },j=1,2,3,\dots ,l_i\}$. Because $P_i^{\prime }$ is in the $XOZ$ plane, the relationship between the point cloud before and after projection is as follows:

$$\left\{\begin{array}{c}{x}_{ij}^{\prime }=x_{ij}\hfill \\ y_{ij}^{\prime }=0\hfill \\ z_{ij}^{\prime }=z_{ij}\hfill \end{array}\right.$$

(3)

The y-coordinate of points in $P_i^{\prime }$ is equal to 0. To simplify computation, $y_{ij}^{\prime }$ can be omitted in the subsequent steps.

The selections of the height for each layer of projection and the position of each layer during the layer-by-layer projection process are crucial, as shown in Figure 5b. From Figure 5a, it can be observed that some of the propellant grains are tilted when viewed from the side. However, their upper and lower surfaces remain parallel to the XOZ plane. By projecting the point cloud of each propellant grain layer by layer, the subsequent algorithm can average the calculated results of each layer. This process compensates for the tilt of the propellant grains and eliminates the need to determine the tilt angle. However, the height selection for each layer in the layer-by-layer projection method must meet certain conditions: If the length of interval is too small, it may lead to missing corner points, while if it is too large, it may be difficult to offset the overall tilt effect during corner point detection. If the y-intervals selected for the layers do not avoid the convex points on the arc surface, the projection of the convex points on the projection surface will generate a large number of non-arc corner points, causing interference in the subsequent specific recognition of arc corner points. As shown in Figure 5c,d.

3.4.3. Arc Corner Points Extraction

A KD-tree is constructed and utilized to search for the nearest neighbor point set $S_{ij}$ of each point $p_{ij}^{\prime }$ in $P_i^{\prime }$ using Euclidean distance as the metric, with n being the number of neighboring points. After obtaining the nearest neighbor point set $S_{ij}$ of point $p_{ij}^{\prime }$ in the scattered point set $P_i^{\prime }$, k-means clustering (k-means) is applied to cluster $S_{ij}$ into two clusters $\{C_1,C_2\}$ (the number of clusters is set to 2), representing the left and right neighborhoods of point $p_{ij}^{\prime }$, respectively, as shown in Figure 6. For details regarding the KD-tree and k-means, refer to the Appendix B.

With the method described above, for any point in the scattered point set $P_i^{\prime }$ on the projection plane, it is possible to obtain the n nearest points around that point. These points can then be divided into two subset $C_1$ and $C_2$, defined as follows: $C_1=\{p_{ij}^{\prime }\left(x_{ij}^{\prime },z_{ij}^{\prime }\right)\in C_1,j=1,2,3,\dots ,n_{c_1}\}$ and $C_2=\{p_{ij}^{\prime }\left(x_{ij}^{\prime },z_{ij}^{\prime }\right)\in C_2,j=1,2,3,\cdots ,n_{c_2}\}$. These two subsets are located at both ends of the point. Then, a least squares line fitting is performed on these two subsets:

$$\left\{\begin{array}{c}n=n_{c_2}+n_{c_1}\hfill \\ \begin{array}{cc}\hfill k_m& ={\displaystyle \frac{{\sum }_{n_{c_m}}{z}_{ij}^{\prime }{x}_{ij}^{\prime }-n_{c_m}\overline{z_{ij}^{\prime }}·\overline{x_{ij}^{\prime }}}{{\sum }_{n_{c_m}}{\left(x_{ij}^{\prime }\right)}^2-n_{c_m}·{\overline{x_{ij}^{\prime }}}^2}},m=1,2,j=1,2,\cdots ,n_{c_m}\hfill \end{array}\hfill \end{array}\right.$$

(4)

where $k_m$ represents the slope of the fitted line.

Given the fitted line equations for the two subsets as obtained from the above equations, the angle $\theta$ between the two lines can be calculated as follows:

$$\theta ={\displaystyle \frac{{180}^{\circ }}{\pi }}\times arctan\left({\displaystyle \frac{|k_1-k_2|}{1+k_1·k_2}}\right)$$

(5)

(a)

if $\left|\theta \right|\le |{\theta }_{thr}|$, the angle change on both sides of the point is gradual, so the point is discarded.

(b)

if $\left|\theta \right|>|{\theta }_{thr}|$, the angle change on both sides of the point is significant, so the point is stored in the corner point set.

where ${\theta }_{thr}$ is the angle threshold.

Repeat the above steps iteratively until all points in the projected point set $P_i^{\prime }$ are traversed, thereby obtaining all corner points in that plane as shown in Figure 6. All obtained corner points form a set: the corner point set. Additionally, due to the large angle between the fitted lines on both sides of some noise points, a small number of noise points will also be stored in the corner point set.

Since $P_i^{\prime }$ is obtained by projecting $P_i$, each corner point of $P_i$ is mapped to the $XOZ$ plane. In $P_i^{\prime }$, all corner points form a clustered structure within the $XOZ$ plane. Based on the actual shape of the point cloud, the number of clusters is set to t. Through secondary clustering, as described in Equations (A2)–(A5) in Appendix B, the corner point set is clustered by using k-means clustering. The cluster centroids of each cluster are obtained, resulting in a set of cluster centers $P_{ClusterCenter}=\{(x_1,z_1),\dots ,(x_t,z_t)\}$. In this process, noise points have been automatically clustered into the corner point cluster (due to the performance of the scanning equipment, the distance between noise points and corner points is relatively small).

The presence of some unnecessary corner points in $P_{ClusterCenter}$ (those on non-arc surfaces of the propellant grain), significant interference occurs in the extraction of corner points on the arc surface. To address this issue, we define the distance matrix $D_C$ between any pair of cluster centroids as follows:

$$D_C={\left[\begin{array}{ccccc}0& d_{1,2}& \cdots & d_{1,t-1}& d_{1,t}\\ & 0& d_{2,3}& \cdots & d_{2,t}\\ & & \ddots & \ddots & ⋮\\ & & & \ddots & d_{t-1,t}\\ & & & & 0\end{array}\right]}_{t\times t}$$

(6)

where $d_{i,j}$ represents the distance between any two points:

$$d_{i,j}=\sqrt{{(x_i-x_j)}^2+{(z_i-z_j)}^2}$$

(7)

The i-th row of matrix $D_C$ represents the distance from the i-th point in $P_{ClusterCenter}$ to all other points.

To avoid the interference mentioned above from affecting the corner point extraction, $P_{ClusterCenter}$ must be further refined. Corner points in same location may be classified into two or more clusters after the previous clustering, leading to multiple cluster centroids. Therefore, the next step is to merge multiple nearby centroids into one (this is related to the setting of parameter t; if t is set too small, the desired corner points may be clustered into other clusters; if t is set larger, this situation will occur more frequently. To extract the desired corner points, t should be set slightly larger). For this, $d_{thr}$ is defined as a metric to filter points that are too close. The process is defined as follows:

$$\left\{\begin{array}{c}{P}_{ClusterCenter}^{\prime }=\left\{(x_i^{\prime },z_i^{\prime })={\displaystyle \frac{1}{2}}\left(x_i+x_j,z_i+z_j\right)|[i,j|D_C(i,j)\le d_{thr}]\right\}\hfill \\ P_{ClusterCenter}=P_{ClusterCenter}\setminus \left\{\left(x_j,z_j\right)\right\}\hfill \end{array}\right.$$

(8)

Repeat the above process in a loop, updating $P_{ClusterCenter}$, $D_C$, and the values of $P_{ClusterCenter}^{\prime }$ each time, and iterating step by step until all elements in $D_C$ are greater than $d_{thr}$. At this point, the final $P_{ClusterCenter}^{\prime }$ is obtained, and its distance matrix is denoted as $D_C^{\prime }$.

To extract the final two corner points of $P_i^{\prime }$, $P_{ClusterCenter}^{\prime }$ must be further refined. Due to the unique geometric properties of the propellant grain, the two corner points to be extracted are significantly farther from the other corner points, while the corner points not to be extracted have several smaller distances between them. Additionally, based on the 3D laser scan results, noise points are mostly concentrated near the corner points. Using these two characteristics, the following equation is applied:

$$\left\{\begin{array}{c}{P}_{ClusterCenter}^{″}=\{(x_i,z_i)\in P_{ClusterCenter}^{\prime }|\forall i,j=1,\cdots ,t^{\prime },D_C^{\prime }(i,j)\ge d_{thr}^{\prime }\}\hfill \\ P_{ClusterCenter}^{\prime }=P_{ClusterCenter}^{\prime }\setminus \left\{(x_i,z_i)\right\}\hfill \end{array}\right.$$

(9)

By iterating the above equation twice, the corner point set $P_{ClusterCenter}^{″}$ containing only the two required corner points can be obtained. The expression for $P_{ClusterCenter}^{″}$ is $P_{ClusterCenter}^{″}=\{(x_{\alpha },z_{\alpha }),(x_{\beta },z_{\beta })\}$. Finally, through

$$\left\{\begin{array}{c}{\theta }_i={\displaystyle \frac{180°}{\pi }}\times arctan\left({\displaystyle \frac{z_{\beta }-z_{\alpha }}{x_{\beta }-x_{\alpha }}}\right)\hfill \\ \Delta x_i=mean(x_{\alpha },x_{\beta })\hfill \\ \Delta z_i=mean(z_{\alpha },z_{\beta })\hfill \end{array}\right.$$

(10)

Calculate the rotation angle and translation amount for each layer of point cloud $P_S$, and for the entire point cloud, obtain the vector R:

$$R=\left[\begin{array}{c}{r}_{\theta }\\ t_x\\ t_z\end{array}\right]=mean\left[\begin{array}{ccc}{\theta }_1& \cdots & {\theta }_M\\ \Delta x_1& \cdots & \Delta x_M\\ \Delta z_1& \cdots & \Delta z_M\end{array}\right]$$

(11)

3.4.4. Determination of the Height of the Point Cloud

Although the upper and lower surfaces of the propellant grain point cloud are parallel to the $XOZ$ plane, the actual scanning results from the 3D laser scanner show that the height of each propellant grain point cloud in the y-direction is inconsistent. To achieve coarse position normalization, the point cloud needs to be transformed to a uniform height. Obviously, using the extreme values directly as the coordinates of the top and bottom surfaces is not feasible due to the presence of noise. Therefore, projecting $P_S$ as a whole onto the $XOY$ plane to obtain $P_{xoy}$, where the points in $P_{xoy}$ can be expressed as $p_{xoy}^1,\dots ,p_{xoy}^m$, with $p_{xoy}^i\in P_{xoy}$ and m being the number of points on the projection plane. Additionally, the y-coordinate of $p_{xoy}^i$ is given by $y_{xoy}^i$. Then, the Gaussian kernel density estimation function can be expressed as follows:

$$f_h\left(y_{xoy}\right)={\displaystyle \frac{1}{m{h}^2}}\sum _{i=1}^m\kappa \left({\displaystyle \frac{y_{xoy}-y_{xoy}^i}{h}}\right)$$

(12)

where h is the bandwidth and $K(·)$ is the kernel function. $f_h\left(y_{xoy}\right)$ represents the density distribution of all points in $P_{xoy}$ along the y-direction. The selected kernel function is:

$$K\left(u\right)={\displaystyle \frac{1}{\sqrt{2\pi }}}{e}^{-{\displaystyle \frac{u^2}{2}}}$$

(13)

Based on Gaussian kernel density estimation, the position of maximum density corresponds to the upper and lower surfaces of the propellant grain. Thus, the mean of the y-coordinate of the points in the point cloud at this position is taken as the height corresponding to these surfaces. Finally, by averaging the heights of the upper and lower surfaces, we obtain the height $t_y$ of the cross-section located between the upper and lower surfaces of the propellant grain point cloud $P_S$.

3.4.5. Coarse Normalization Transformation Matrix

Finally, the coarse position normalization of the point cloud is achieved using the transformation matrix $T_C$, resulting in the coarse registered point cloud $P_S^{\prime }$:

$$T_C=\left[\begin{array}{cccc}cos\left(r_{\theta }\right)& 0& sin\left(r_{\theta }\right)& t_x\\ 0& 1& 0& t_y\\ -sin\left(r_{\theta }\right)& 0& cos\left(r_{\theta }\right)& t_z\\ 0& 0& 0& 1\end{array}\right]$$

(14)

3.5. Fine Position Normalization

After coarse position normalization, the point cloud $P_S^{\prime }$ has been accurately transformed to the reference coordinate system. However, there is still a certain discrepancy from the calibration position of the reference coordinate system. Through fine position normalization, we further narrow down this difference. The specific manifestation of this small difference is that there is a small angular difference between the axis of symmetry of the propellant grain point cloud and the coordinate axes, along with a certain offset from the calibrated position in the reference coordinate system.

To determine the symmetry axis of the propellant grain point cloud, two edges of the point cloud need to be fitted. The symmetry axis is then defined by these two edges to complete the fine normalization of the position.

3.5.1. Partitioning of Intervals

Firstly, following the layer-wise projection approach described earlier, we obtain scatter point sets $W_i,i=1,2,\dots ,M$, where the points within each scatter set are denoted as $w_j^i,j=1,2,\dots ,N$. After coarse position normalization, $W_i$ is approximately symmetrical with respect to the x-axis. Thus, selecting two intervals $D_1^i,D_2^i\in [a_i,b_i]$ along the x-axis corresponds to the upper and lower sides of the two-dimensional shape(i represents the i-th layer). However, since the data are in the form of scatter points, further discretization of these intervals is necessary. Let $m_i$ denote the number of subdivisions for each interval. The centroid of each discretized interval is considered as the point for linear fitting within that interval.

Due to the specific scanning frequency of the 3D laser scanner and the large size of the propellant grain, during the scanning process around the grain, the point cloud is generated only when the laser reflects back from the grain. Since the scanning mechanism is rotational, the points on the side edges of the resulting propellant grain point cloud exhibit a periodic density distribution. As shown in Figure 7, the points on the edges of $W_i$ exhibit a periodic density distribution in the two-dimensional plane. To ensure that each interval contains a higher density of point clouds as much as possible, the values of $m_i$ should satisfy the following condition according to the sampling theorem:

$$\Delta D_n^i={\displaystyle \frac{b_i-a_i}{m_i}}\ge 2\eta {\displaystyle \frac{\omega }{\sigma f}},n=1,2i=1,\cdots ,M$$

(15)

where f represents the scanning frequency of the 3D laser scanner; $\omega$ denotes the scanning linear velocity; $\sigma$ is the downsampling factor, defined as the ratio of points in the downsampled point cloud to the original point cloud; $\eta$ is the magnification factor, calculated as follows:

$$\eta ={\displaystyle \frac{1}{cos\left({\theta }_{max}\right)}}$$

(16)

where the parameter ${\theta }_{max}$ represents the maximum inclination angle of the two sides of the standard propellant grain.

3.5.2. Multiple Symmetry Axis Fitting

After coarse position normalization, $W_i$ is divided into two parts by the x-axis. Therefore, once the length of the subinterval is determined, the set of points in the k-th subinterval of $D_n^i,n=1,2$ can be represented as $d_{nk}^i$: $d_{1k}^i=\{w_j^i(x_j,z_j)\in W_i|a_i+(k-1)\Delta D_1^i\le x_j\le a_i+k\Delta D_1^i,z_j>0,k=1,\cdots ,m_i\}$ and $d_{2k}^i=\{w_j^i(x_j,z_j)\in W_i|a_i+(k-1)\Delta D_2^i\le x_j\le a_i+k\Delta D_2^i,z_j<0,k=1,\cdots ,m_i\}$. The centroids of $d_{1k}^i$ and $d_{2k}^i$ are as follows:

$$\left\{\begin{array}{c}centroi{d}_{x-nk}^i={\displaystyle \frac{{\sum }_{w_j^i\in d_{nk}^i}{x}_j}{N_{nk}^i}}\hfill \\ centroi{d}_{z-nk}^i={\displaystyle \frac{{\sum }_{w_j^i\in d_{nk}^i}{z}_j}{N_{nk}^i}}\hfill \end{array}\right.n=1,2j=1,\cdots ,N_{nk}^i$$

(17)

where $N_{nk}^i$ is the number of points contained in $d_{nk}^i$.

Based on the scanning mechanism, only the surface of the propellant grain can be scanned as points in the point cloud. Therefore, finding the centroids of $d_{1k}^i$ and $d_{2k}^i$ represents the line fitting points for the boundary in that region. Next, the midpoint between the corresponding centroids is taken as the fitting point for the symmetry axis. This process is repeated for all small intervals to obtain all centroids and fitting points for the symmetry axis. Line fitting is then performed based on Equation (4) to obtain the axis line $l_c^i$ and boundary lines $l_1^i$ and $l_2^i$ for $W_i$, with their line parameters represented as $\left(k_c^i,b_c^i\right)$,$\left(\begin{array}{c}{k}_1^i,b_1^i\end{array}\right)$ and $\left(k_2^i,b_2^i\right)$, respectively. The slopes $k_c^i$, $k_1^i$, and $k_2^i$ correspond to the angles of inclination ${\theta }_c^i$, ${\theta }_1^i$, and ${\theta }_2^i$.

As shown in Figure 8, two adjacent small intervals of $W_i$ are randomly selected, with fitting points on the boundary denoted as $A_1$, $A_2$, $B_1$ and $B_2$, and corresponding points on the axis denoted as $A_C$ and $B_C$ (to facilitate presentation, the subintervals in the figure appear non-adjacent, but the selected subintervals are actually adjacent).

Due to the existence of a slight inclination, $A_1$ and $A_2$ and $B_1$ and $B_2$ are not symmetric points geometrically. Let $A_2^{\prime }$ and $B_2^{\prime }$ be the symmetric points of $A_1$ and $B_1$, respectively. The axis line fitting points between the symmetric points are denoted as $A_C^{\prime }$ and $B_C^{\prime }$.

According to the triangle median line theorem, $A_C{A}_C^{\prime }\Vert A_2{A}_2^{\prime }$ and $|A_C{A}_C^{\prime }|=0.5|A_2{A}_2^{\prime }|$. Similarly, we have $B_C{B}_C^{\prime }\Vert B_2{B}_2^{\prime }$ and $|B_C{B}_C^{\prime }|=0.5|B_2{B}_2^{\prime }|$. Since $A_2$, $A_2^{\prime }$, $B_2$, and $B_2^{\prime }$ lie on the same fitted line, $A_C{A}_C^{\prime }\Vert B_C{B}_C^{\prime }$. Due to symmetry, $|A_1{B}_1^{\prime }|=|A_2^{\prime }{B}_2^{\prime }|={\displaystyle \frac{\Delta D_n^i}{cos{\theta }_1^i}}$, and because $|A_2{B}_2|={\displaystyle \frac{\Delta D_n^i}{cos{\theta }_2^i}}$, we finally obtain the following:

$$|A_C{A}_C^{\prime }|-|B_C{B}_C^{\prime }|=2(|A_2{A}_2^{\prime }|-|B_2{B}_2^{\prime }\left|\right)=2\Delta D_n^i({\displaystyle \frac{1}{cos{\theta }_2^i}}-{\displaystyle \frac{1}{cos{\theta }_1^i}})$$

(18)

Due to the coarse normalization, $W_i$ is already highly symmetrical about the x-axis, ${\theta }_1^i$ and ${\theta }_2^i$ are very close, and $\Delta D_n^i$ is very small, it can be assumed that $|A_C{A}_C^{\prime }|=|B_C{B}_C^{\prime }|$, and $A_C{A}_C^{\prime }{B}_C^{\prime }{B}_C$ can almost be regarded as a parallelogram. Therefore, $A_C^{\prime }{B}_C^{\prime }\Vert A_C{B}_C$, indicating that the angle of the fitting axis line equals the actual axis angle. Thus, adjusting the angle using the fitting axis line angle is reliable.

Then, the inclination angle of $P_S^{\prime }$ is as follows:

$${\theta }_d=\sum _i^M{\displaystyle \frac{{\theta }_c^i}{M}}$$

(19)

Repeat Equation (15)–(17) and (19) until $abs\left({\theta }_d\right)\le m_{\theta }$, where $m_{\theta }$ is a given threshold and M refers to the number of projection layers mentioned above. The entire process is shown in Figure 9.

3.5.3. Axial Compensation of Corresponding Points

Then, set $t_x=t_y=t_z=0$ and $r_{\theta }={\theta }_d$, substitute $r_{\theta }$ into Equation (14) to transform the point cloud $P_S^{\prime }$ to obtain $P_{{\theta }_d}^{\prime }$. At this point, $P_{{\theta }_d}^{\prime }$ is approximately symmetrical with the coordinate axes of the reference coordinate system, but there are still minor deviations along the x and z axes. To achieve fine normalization, axial compensation is performed by averaging the sum of the intersection coordinates of lines $l_1^i$ and $l_2^i$ for each layer $W_i$. This part of the process can be described as:

$$\left\{\begin{array}{c}{t}_x={\displaystyle \frac{1}{M}}\sum _i^M{\displaystyle \frac{b_1^i-b_2^i}{k_2^i-k_1^i}}\hfill \\ t_z={\displaystyle \frac{t_x}{M}}\sum _i^M{k}_2^i+{\displaystyle \frac{1}{M}}\sum _i^M{b}_2^i\hfill \end{array}\right.i=1,\cdots ,M$$

(20)

In the above expression, $\left(\begin{array}{c}{k}_1^i,b_1^i\end{array}\right)$ and $\left(k_2^i,b_2^i\right)$ represent the slopes and intercepts of lines $l_1^i$ and $l_2^i$, respectively. By substituting $t_x$ and $t_z$ into Equation (14) and setting $r_{\theta }$ and $t_y$ to 0, a new transformation matrix is obtained. This matrix is then used to transform $P_{{\theta }_d}^{\prime }$ into $P_S^{″}$, completing the fine normalization.

If there exists a point cloud $P_C$ at the calibrated position of the reference coordinate system that is identical to the point cloud $P_S$, and the values of $t_x$, $t_y$, and $t_z$ can be further optimized:

$$(t_x,t_y,t_z)={\displaystyle \frac{1}{N^{\prime }}}\sum _i^{N^{\prime }}(p_{si}^{″}-p_{ci})$$

(21)

where $p_{si}^{″}$ and $p_{ci}$ represent the points in $P_S^{″}$ and $P_C$, respectively, and $N^{\prime }$ represents the number of points in the point cloud.

Finally, substitute $t_x,t_y$ and $t_z$ into Equation (14) again to obtain the final transformation matrix of our method.

4. Experiments

This section first introduces several propellant grain point clouds used in the experiments, followed by a description of the evaluation criterion employed. The point cloud down-sampling experiment has subsequently been completed. Two experimental groups were then established, each comparing the proposed algorithm with the RANSAC and ICP algorithms, followed by an analysis of the results.

4.1. Experimental Setup

4.1.1. Propellant Grain Point Clouds and Experimental Environment

To validate the effectiveness of the position normalization algorithm, different experiments were designed and conducted. All experiments were performed on hardware including an Intel(R) Core(TM) i5-12490F CPU and an NVIDIA RTX 4060 Ti GPU.

Four different propellant grain point clouds (FP-1, FP-2, FP-3, FP-4) were used as the original point clouds for the experiments. Due to the manufacturing process of the propellant grains, the surface of each grain has varying degrees of indentations and protrusions and slight differences in size between grains. After scanning these grains into point clouds, these differences are reflected in the point cloud of each propellant grain, as shown in Figure 10.

4.1.2. Definition of the Target Point Cloud

Based on the symmetry and geometric properties of propellant grains, the propellant grain point clouds (FP-1, FP-2, FP-3, FP-4) were manually transformed to the calibrated position in the reference coordinate system the point cloud mentioned above has already undergone down-sampling processing), resulting in $P_T^1,P_T^2,P_T^3$, and $P_T^4$, which will be replaced by $P_T^i$ in the following text, where $i=1,\dots ,4$. For $P_T^i$, there are a total of $N_i^{\prime }$ points, with each point denoted as $p_T^i$. These four point clouds are referred to as the target point clouds. The target point cloud serves as a benchmark, providing a basis for verifying whether the post-experimental point clouds have been transformed to the calibrated position.

Once a propellant grain point cloud is manually transformed to the calibrated position, the processes of position normalization and point cloud registration become identical. Therefore, algorithms from the field of point cloud registration can be employed to verify the accuracy of the proposed position normalization algorithm.

4.1.3. Parameter Settings

By applying some perturbations to the position of $P_T^i$, we transform $P_T^i$ to a specified location, resulting in the original point cloud $P_O^i$. Then, we apply the proposed algorithm and the RANSAC + ICP algorithm to perform the corresponding transformation on $P_O^i$:

$$\left\{\begin{array}{c}{P}_O^i\stackrel{coarsenormalization}{\to }{P}_{ours-c}^i\stackrel{finenormalization}{\to }{P}_{ours-f}^i\hfill \\ P_O^i\stackrel{RANSAC}{\to }{P}_{RANSAC}^i\stackrel{ICP}{\to }{P}_{ICP}^i\hfill \end{array}\right.$$

(22)

The definition of perturbation is as follows: In practical situations, the position of the point cloud obtained from the three-dimensional laser scanner exhibits four degrees of freedom relative to the calibrated spatial position. These degrees of freedom include the rotation angle relative to the y-axis and the offsets along the x-, y-, and z-axes. These rotation and translation parameters are encoded in a vector as $V_p=[{\theta }_y,\Delta x,\Delta y,\Delta z]$.

For single-variable experiments: Based on the statistical analysis of the offset of the propellant grain point cloud relative to the calibrated position, the parameter ranges are defined as follows: ${\theta }_y\in [-{30}^{\circ },{30}^{\circ }]$, $\Delta x\in [-500\mathrm{mm},500\mathrm{mm}]$, $\Delta y\in [-500\mathrm{mm},0]$, and $\Delta z\in [-500\mathrm{mm},500\mathrm{mm}]$. For each experiment, one of ${\theta }_y,\Delta x,\Delta y$, or $\Delta z$ is set to a specific value within the corresponding range as the perturbation, transforming $P_T^i$ into $P_O^i$. For example, when the ${\theta }_y$ between $P_O^i$ and $P_T^i$ is set to a certain value, the values of $\Delta x$, $\Delta y$, and $\Delta z$ are all set to zero.

For multivariable experiments: For each experiment, all elements of ${\theta }_y,\Delta x,\Delta y$, and $\Delta z$ are simultaneously assigned random values to as the perturbation, transforming $P_T^i$ into $P_O^i$.

4.1.4. Evaluation Criterion

Since $P_{ours-c}^i,P_{ours-f},P_{RANSAC}^i,P_{ICP}^i$ are all derived from the transformation of $P_O^i$, which in turn is transformed from $P_T^i$, the difference between these point clouds lies in their positions, while the number of points in each point cloud is the same. This section describes the evaluation criteria. For the sake of readability, any one of the point clouds from $P_{ours-c}^i,P_{ours-f},P_{RANSAC}^i,P_{ICP}^i$ will be uniformly represented as ${P_T^i}^{\prime }$.

The degree of position normalization for the point cloud is evaluated using two metrics: root mean square error (RMSE) and transformation matrix error. The computation formula for RMSE is as follows:

$$\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{N_i^{\prime }}}{\sum }_{j=1}^{N_i^{\prime }}{\parallel {p_{Tj}^i}^{\prime }-p_{Tj}^i\parallel }^2}j=1,\cdots ,N_i^{\prime }i=1,\cdots ,4$$

(23)

where ${p_{Tj}^i}^{\prime }$ and $p_{Tj}^i$ represent the points in ${P_T^i}^{\prime }$ and $P_T^i$, respectively.

This formula represents the square root of the average squared distance between corresponding points ${P_T^i}^{\prime }$ and $P_T^i$ reflecting the overall disparity between these two point clouds. A smaller RMSE value indicates that the processed point cloud ${P_T^i}^{\prime }$ deviates less from $P_T^i$ at the calibrated position, as shown in Figure 11.

The definition of the transformation matrix is as follows:

$$\mathbf{T}=\left(\begin{array}{cccc}{R}_{11}& R_{12}& R_{13}& t_x\\ R_{21}& R_{22}& R_{23}& t_y\\ R_{31}& R_{32}& R_{33}& t_z\\ 0& 0& 0& 1\end{array}\right)$$

(24)

where R is a $3\times 3$ rotation matrix used to describe rotation, defined as follows:

$$\mathbf{R}=\left(\begin{array}{ccc}{R}_{11}& R_{12}& R_{13}\\ R_{21}& R_{22}& R_{23}\\ R_{31}& R_{32}& R_{33}\end{array}\right)=\left(\begin{array}{ccc}cos\left(r_{\theta }\right)& 0& sin\left(r_{\theta }\right)\\ 0& 1& 0\\ -sin\left(r_{\theta }\right)& 0& cos\left(r_{\theta }\right)\end{array}\right)$$

(25)

t is a $1\times 3$ translation vector used to describe translation, defined as follows:

$$\mathbf{t}=\left(\begin{array}{c}{t}_x\\ t_y\\ t_z\end{array}\right)$$

(26)

The error of the transformation matrix is defined as follows:

$$\left\{\begin{array}{c}\hfill {\delta }_{\theta }={\displaystyle \frac{1}{4}}sqrt[{(R_{11}^{i^{\prime }}-R_{11}^i)}^2+{(R_{13}^{i^{\prime }}-R_{13}^i)}^2+\\ \hfill {(R_{31}^{i^{\prime }}-R_{31}^i)}^2+{(R_{33}^{i^{\prime }}-R_{33}^i)}^2]\\ \hfill \left[{\delta }_x,{\delta }_y,{\delta }_z\right]=|t_T^{i^{\prime }}-t_T^i|\end{array}\right.$$

(27)

where $R_{11}^i,R_{13}^i,R_{31}^i$ and $R_{33}^i$ and $t_T^i$ represent the elements of rotation matrix and translation vector from $P_O^i$ to $P_T^i$, and $R_{11}^{i^{\prime }},R_{13}^{i^{\prime }},R_{31}^{i^{\prime }}$ and $R_{33}^{i^{\prime }}$ and ${t_T^i}^{\prime }$ represent the elements of rotation matrix and translation vector from $P_O^i$ to ${P_T^i}^{\prime }$, respectively. $sqrt(·)$ represents the square root operation.

Using Equations (25) and (27), ${\delta }_{\theta }$ can be further simplified:

$${\delta }_{\theta }={\displaystyle \frac{1}{2}}sqrt\left[1-cos\left(r_{\theta }^{i^{\prime }}-r_{\theta }^i\right)\right]$$

(28)

where $r_{\theta }^{i^{\prime }}$ represents the transformation angle from $P_O^i$ to ${P_T^i}^{\prime }$ and $r_{\theta }^i$ represents the transformation angle from $P_O^i$ to $P_T^i$.

${\delta }_{\theta }$ represents the difference between the rotation matrix from $P_O^i$ to ${P_T^i}^{\prime }$ and the rotation matrix from $P_O^i$ to $P_T^i$. A smaller value indicates that the angular difference between ${P_T^i}^{\prime }$ and $P_T^i$ is smaller.

${\delta }_x,{\delta }_y,{\delta }_z$ represent the differences between the translation vectors from $P_O^i$ to ${P_T^i}^{\prime }$ and from $P_O^i$ to $P_T^i$, respectively. Smaller values indicate smaller positional differences between ${P_T^i}^{\prime }$ and $P_T^i$ along the x-, y-, and z-axes.

4.2. Downsampling Experiments

Before starting the experiments, it is necessary to determine an appropriate number of downsampled point cloud points. Based on the three-dimensional laser scanning mechanism, the propellant grain point cloud consists of five faces. Considering the area of each face and the downsampling distribution radius of 0.1 mm, the minimum number of points per face is 10,000, which means the minimum number of points after downsampling the propellant point cloud is 50,000. Based on this minimum number of points, each experiment incrementally increases the number of downsampled points and measures the processing time of our method. The experimental results are shown in

Table 1. Downsampled number of points experiment.

Number of Downsampled Points:	140,000	130,000	120,000	110,000	100,000	90,000	80,000	70,000	600,000	500,000
Processing Time (s):	484.13	457.39	428.39	396.12	352.46	321.16	277.90	254.07	215.04	174.95

. From the results in the table, it can be observed that the number of points in the point cloud is positively correlated with the algorithm’s processing time. Therefore, based on the algorithm’s processing time, the number of downsampled points for the propellant grain point cloud is set to 50,000, as shown in

Table 2. Number of Points.

Point Cloud	Number of Points	After Down Sampling
FP-1	13,333,095	49,987
FP-2	20,128,476	50,728
FP-3	15,943,085	51,301
FP-4	17,933,175	48,375

.

4.3. Single-Variable Experiments

In the single-variable experiments, for each $P_T^i,i=1\cdots 4$, 12 experiments are conducted with different ${\theta }_y$ values while keeping the other parameters constant. Similarly, 10 experiments are conducted for different $\Delta x$ values, 5 experiments for different $\Delta y$ values, and 10 experiments for different $\Delta z$ values, while keeping the other parameters constant. In total, 37 × 4 experiments are performed.

For the 12 experiments with varying ${\theta }_y$, the mean RMSE and the mean transformation matrix error across the 12 experiments are recorded as $\overline{\mathrm{RMSE}}\left({\theta }_y\right)$ and $\overline{{\delta }_{\theta }}$, respectively. In each of the 12 experiments, only the angle is changed, and ${\delta }_x,{\delta }_y,{\delta }_z$ in the transformation matrix errors are all 0. Therefore, ${\delta }_{\theta }$ can be used directly to represent the transformation matrix error. The same applies below. For the 10 experiments with varying $\Delta x$, the mean RMSE and mean transformation matrix error are recorded as $\overline{\mathrm{RMSE}}(\Delta x)$ and $\overline{{\delta }_x}$. Similarly, for the 5 experiments with varying $\Delta y$, the mean RMSE and mean transformation matrix error are recorded as $\overline{\mathrm{RMSE}}(\Delta y)$ and $\overline{{\delta }_y}$, and for the 10 experiments with varying $\Delta z$, these values are recorded as $\overline{\mathrm{RMSE}}(\Delta z)$ and $\overline{{\delta }_z}$. The experimental results are shown in

Table 3. Results of single-variable normalization experiment.

Point Cloud	Algorithm Model		$[\overline{{\mathsf{\delta }}_{\mathsf{\theta }}},\overline{{\mathsf{\delta }}_{\mathit{x}}},\overline{{\mathsf{\delta }}_{\mathit{y}}},\overline{{\mathsf{\delta }}_{\mathit{z}}}]$				$[\overline{\mathbf{RMSE}}\left({\mathsf{\theta }}_{\mathit{y}}\right),\overline{\mathbf{RMSE}}(\mathit{\Delta }\mathit{x}),\overline{\mathbf{RMSE}}(\mathit{\Delta }\mathit{y}),\overline{\mathbf{RMSE}}(\mathit{\Delta }\mathit{z})]$
FP-1	RANSAC		[2.7519	$7.72\times {10}^{-8}$	71.3267	$1.6005\times {10}^{-7}]$	[45.6162	$2.1546\times {10}^{-5}$	308.2656	$2.1381\times {10}^{-5}$
	ICP						[9.4203	$2.1082\times {10}^{-5}$	246.8501	$2.1093\times {10}^{-5}$
	Ours	Coarse normalization	$[6.2778\times {10}^{-3}$	$4.6826\times {10}^{-3}$	$6.4697\times {10}^{-5}$	$4.9118\times {10}^{-3}$	[2.7828	1.4542	$6.6201\times {10}^{-5}$	4.2702]
		Fine normalization					$[1.927\times {10}^{-2}$	$1.7841\times {10}^{-2}$	−	$1.8759\times {10}^{-2}$
FP-2	RANSAC		[1.7348	$1.3558\times {10}^{-4}$	67.2147	$1.4084\times {10}^{-7}$	[36.8562	$2.1464\times {10}^{-5}$	359.3677	$3.5136\times {10}^{-5}$
	ICP						[6.3411	$4.6483\times {10}^{-4}$	315.9922	$2.0999\times {10}^{-5}$
	Ours	Coarse normalization	$[3.7423\times {10}^{-3}$	$9.7675\times {10}^{-4}$	$3.3594\times {10}^{-5}$	$2.2935\times {10}^{-3}$	[2.959	3.9315	$3.5526\times {10}^{-5}$	28.1718]
		Fine normalization					$[9.2156\times {10}^{-3}$	$3.5941\times {10}^{-3}$	−	$8.6835\times {10}^{-3}$
FP-3	RANSAC		[2.593	$7.72\times {10}^{-8}$	117.2881	$1.6005\times {10}^{-7}$	[45.2615	$2.1247\times {10}^{-5}$	793.146	$2.124\times {10}^{-5}$
	ICP						[8.6269	$2.1082\times {10}^{-5}$	650.5938	$2.1093\times {10}^{-5}$
	Ours	Coarse normalization	$[5.6036\times {10}^{-3}$	$3.8561\times {10}^{-2}$	$6.9092\times {10}^{-5}$	$2.6747\times {10}^{-3}$	[6.5244	2.4333	$6.9969\times {10}^{-5}$	2.9202]
		Fine normalization					$[1.049\times {10}^{-2}$	$1.516\times {10}^{-1}$	−	$1.0468\times {10}^{-2}$
FP-4	RANSAC		[1.4392	$7.72\times {10}^{-8}$	105.2849	$1.6005\times {10}^{-7}$	[42.2502	$2.142\times {10}^{-5}$	517.5345	$2.1223\times {10}^{-5}$
	ICP						[4.7415	$2.1082\times {10}^{-5}$	409.91	$2.1093\times {10}^{-5}$
	Ours	Coarse normalization	$[3.7006\times {10}^{-3}$	$1.2487\times {10}^{-2}$	$3.5645\times {10}^{-5}$	$1.4475\times {10}^{-2}$	[2.7779	$7.7289\times {10}^{-1}$	$3.9265\times {10}^{-5}$	$7.7043\times {10}^{-1}$
		Fine normalization					$[9.6007\times {10}^{-3}$	$4.7459\times {10}^{-2}$	−	$4.5678\times {10}^{-2}$

.

As for the specific details of each of the 37 experiments on $P_T^i$, they are shown in Figure 12 and Figure 13.

Single-Variable Experiments Results Analysis

The experimental results indicate that when there is an angular deviation between the original point cloud and the target point cloud, The normalization accuracy of our method is 1 to 2 orders of magnitude higher than that of the RANSAC + ICP method. Therefore, compared to RANSAC + ICP, our method has a significant advantage in cases where there is an angular difference between the target and source point clouds, with a much higher accuracy. For cases where only translational differences exist between the original and target point clouds, RANSAC + ICP performs better due to its point-to-point registration principle, making it easier to obtain corresponding point differences in the axial direction. However, as observed in the graphs, when aligning original point clouds with changes only in the y-direction, the performance of RANSAC + ICP is unstable, exhibiting significant fluctuations due to the algorithm getting trapped in local optima. Nevertheless, the normalization accuracy of our method also meets the standard requirements.

4.4. Multivariable Experiments

It is evident that cases where there is only translational difference between the point cloud obtained by the 3D laser scanner and the target point cloud are rare. In the majority of cases, there are angular differences. Therefore, FP-1 is selected as the target point cloud ($P_T^1$), and $P_T^1$ is randomly transformed across four degrees of freedom (${\theta }_y,\Delta x,\Delta y$, and $\Delta z$). Each transformation results in an original point cloud $P_O^1$. A total of 10 transformations are performed, resulting in 10 experiments.

The RMSE between the normalized point cloud and the target point cloud was calculated as evaluation metrics. The results of all 10 experiments are shown in Figure 14.

Multivariable Experiments Results Analysis

The result of one of the aforementioned ten sets of propellant grain point cloud position normalization experiments is shown in Figure 15. After position normalization using our method, the point cloud tends to overlap with the target point cloud, while with RANSAC + ICP, there are still some distances between corresponding points. The position normalization experiments on 10 randomly transformed original point clouds indicate that the $\mathrm{RMSE}$ is smaller with our method compared to RANSAC + ICP. In the RANSAC + ICP algorithm, RANSAC is merely a fitting method for a mathematical model, and its fitting result may not necessarily be optimal. Moreover, if RANSAC does not provide a good initial transformation for the original point cloud, it directly affects the accuracy of the ICP algorithm, ultimately resulting in a lower overall normalization accuracy. Additionally, based on the experimental results in Figure 12 and Figure 13, it can be observed that the ICP algorithm tends to become trapped in local optima. RANSAC + ICP only focuses on the correspondence between points, while our method utilizes both the correspondence between points and the structural information of the point cloud. The final results demonstrate that in practical applications, when dealing with scanned propellant grain point clouds, our method achieves higher accuracy.

5. Conclusions

To solve the problem of transforming the unordered propellant grain point cloud position to the calibrated position for planning the free assembly scheme in virtual space, this paper proposes a position normalization method that combines coarse and fine position normalization stages. In the coarse position normalization stage, arc corner points are extracted using KD-tree nearest neighbor search and k-means clustering, while in the fine position normalization stage, angle adjustments are made using axis fitting. Both stages employ a layer-by-layer projection method to avoid interference, thus eliminating the need for other complex denoising strategies.

RANSAC + ICP is prone to local optima. Our algorithm, designed based on the geometric properties of the propellant grain point cloud, shows an average accuracy improvement of two orders of magnitude over RANSAC + ICP according to experimental results. This meets the prerequisites for the subsequent task of free assembly of propellant grains in a virtual space.

Although designed for propellant grain point cloud position normalization, our method provides a universal handling idea for normalizing point clouds of arbitrarily shaped objects obtained by rotating three-dimensional laser scanners. Finally, the position normalization of point clouds involves complex and variable scenarios, necessitating an improvement in the algorithm’s generalization ability across different contexts.