Shock Wave and Aeroelastic Coupling in Overexpanded Nozzle
Abstract
1. Introduction
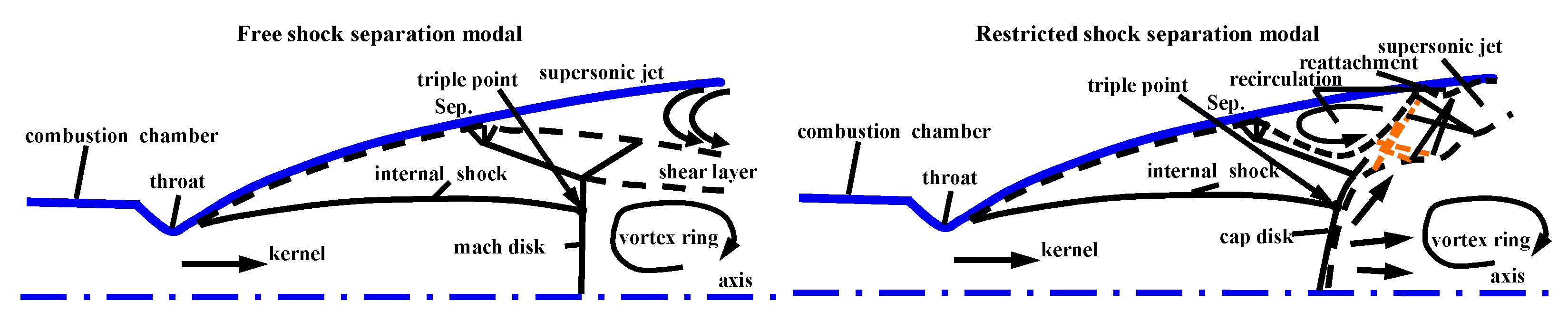
2. Flow Separation Analysis
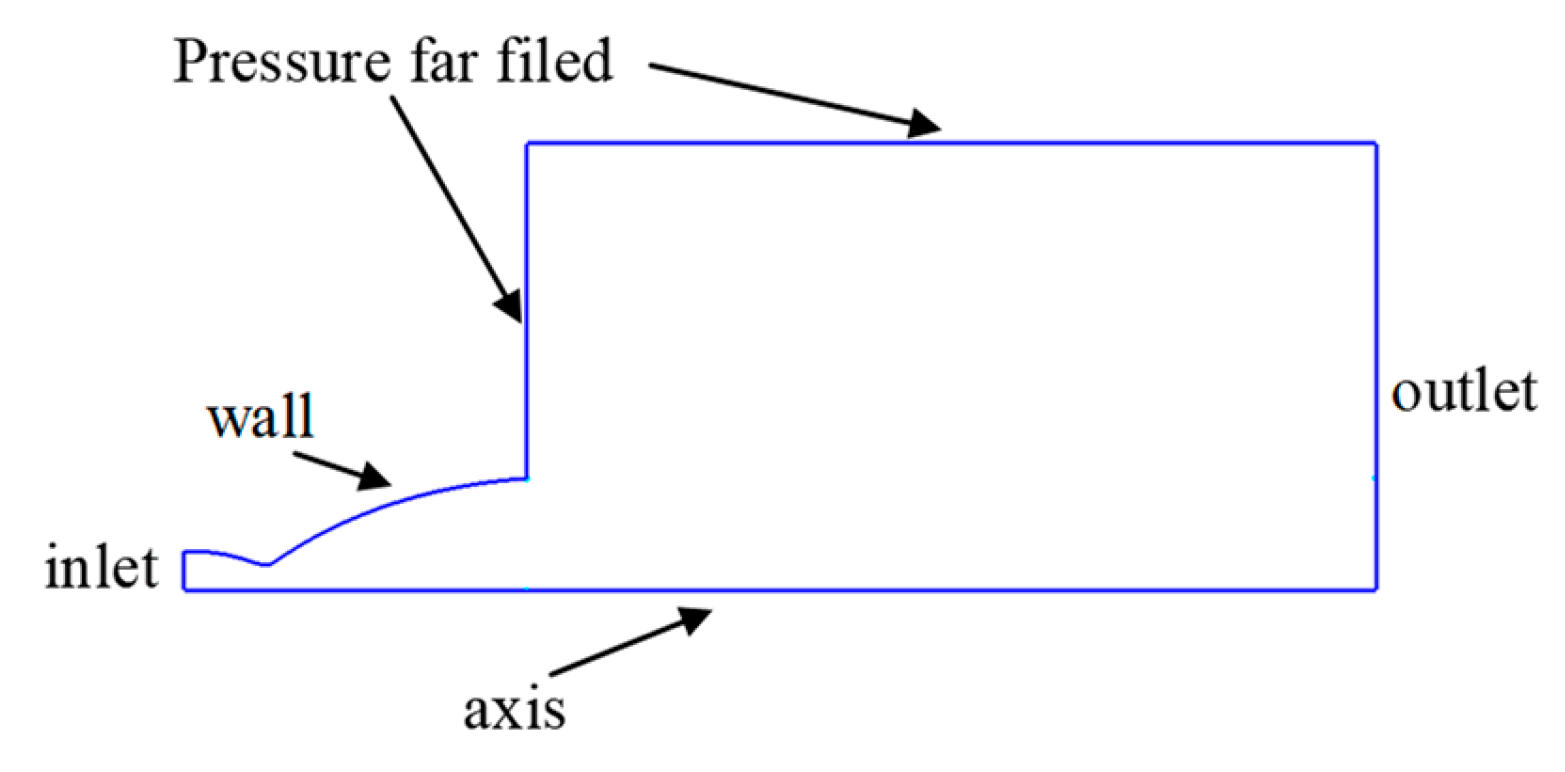
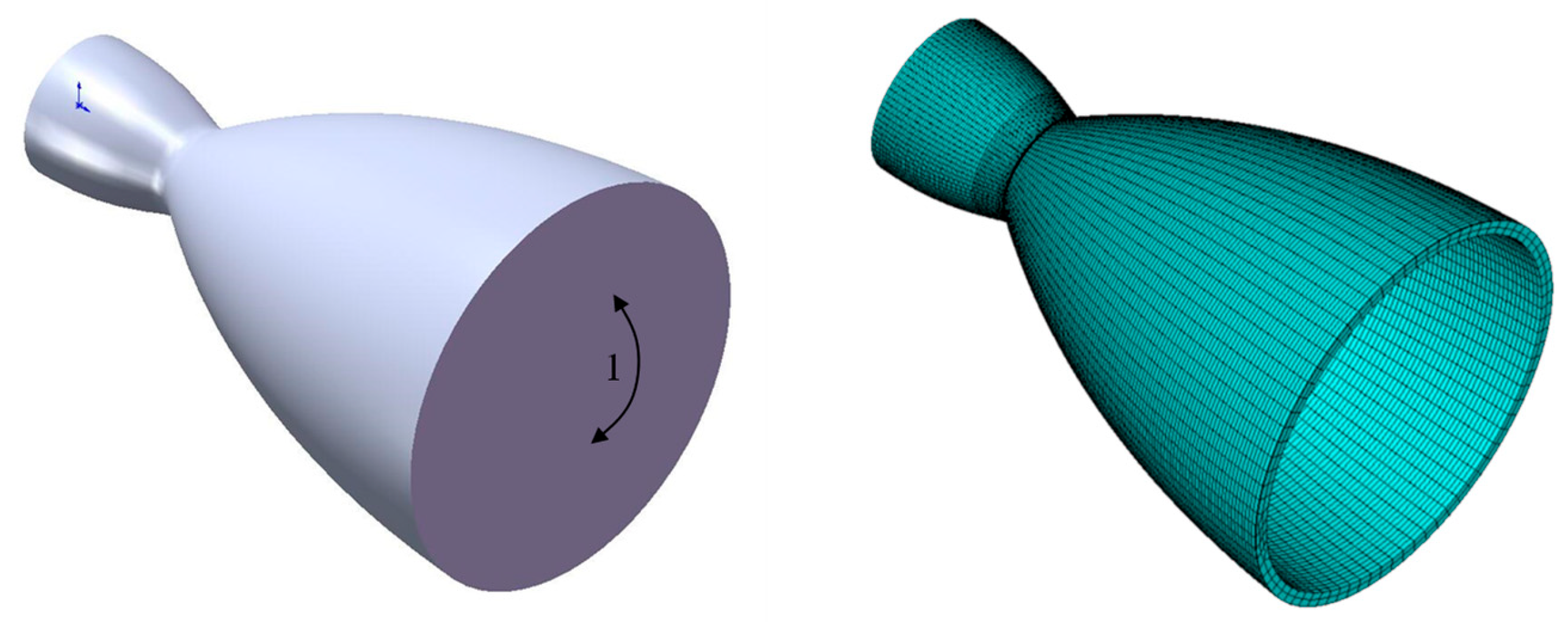
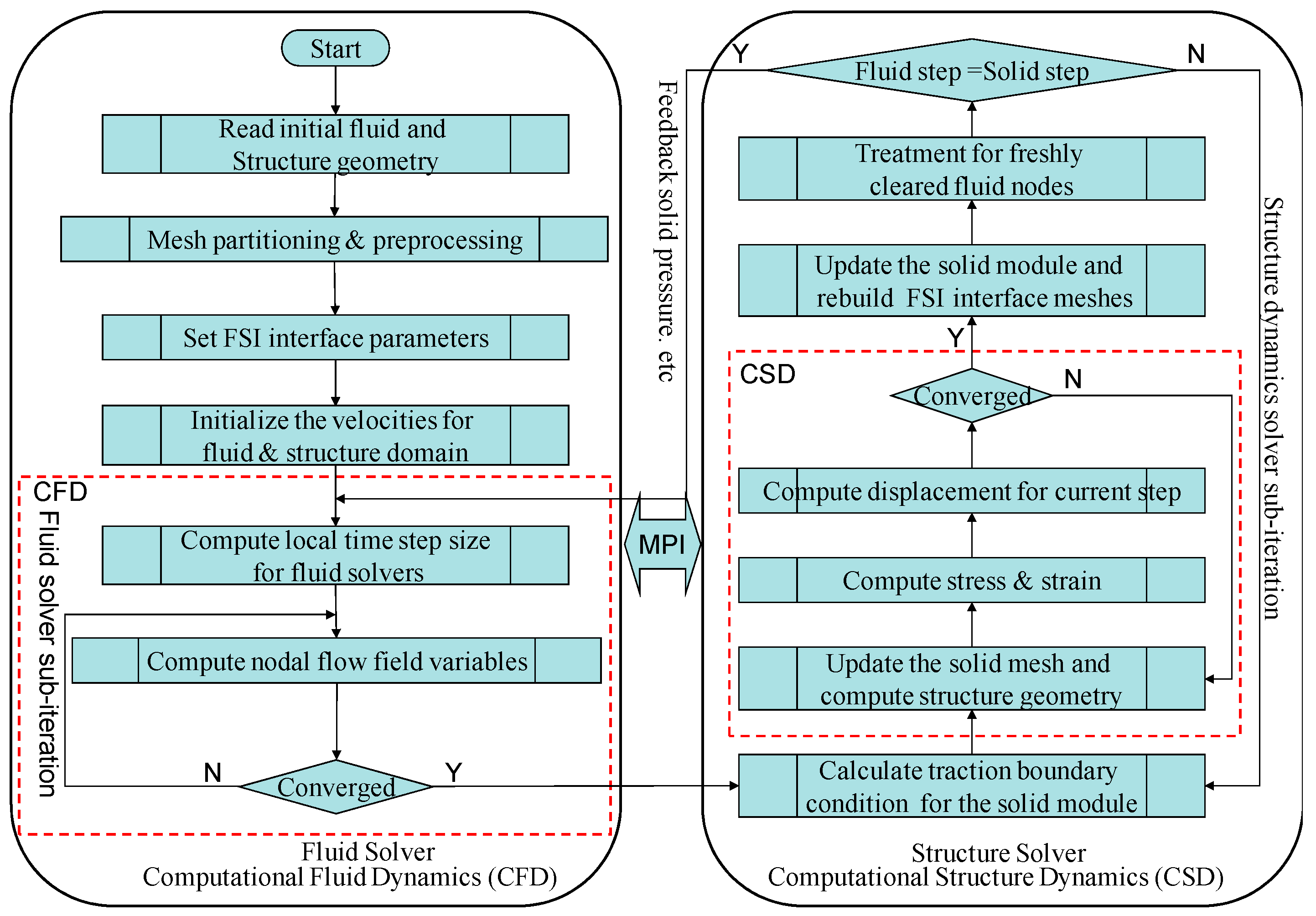
2.1. Numerical Methodology (CFD)
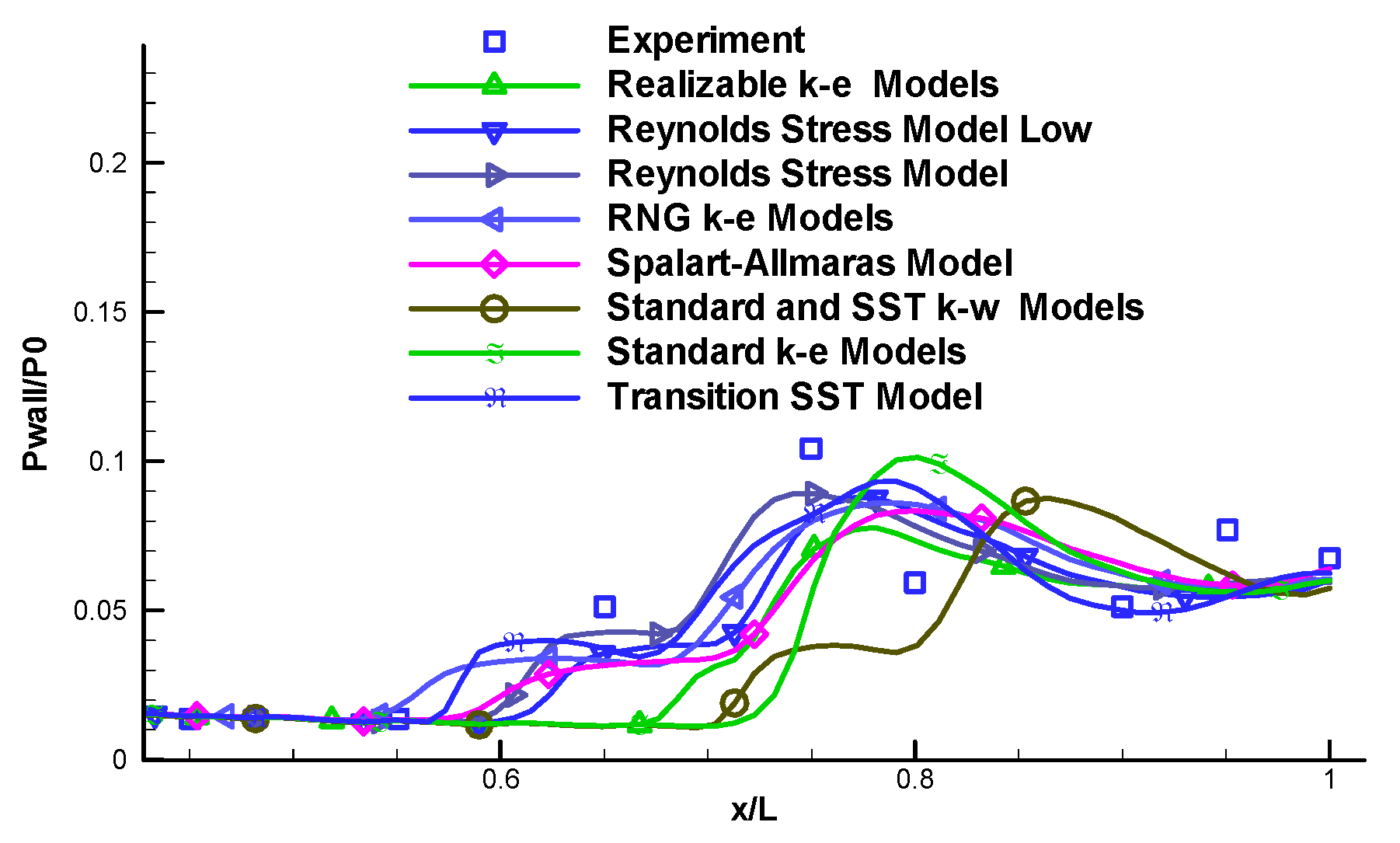
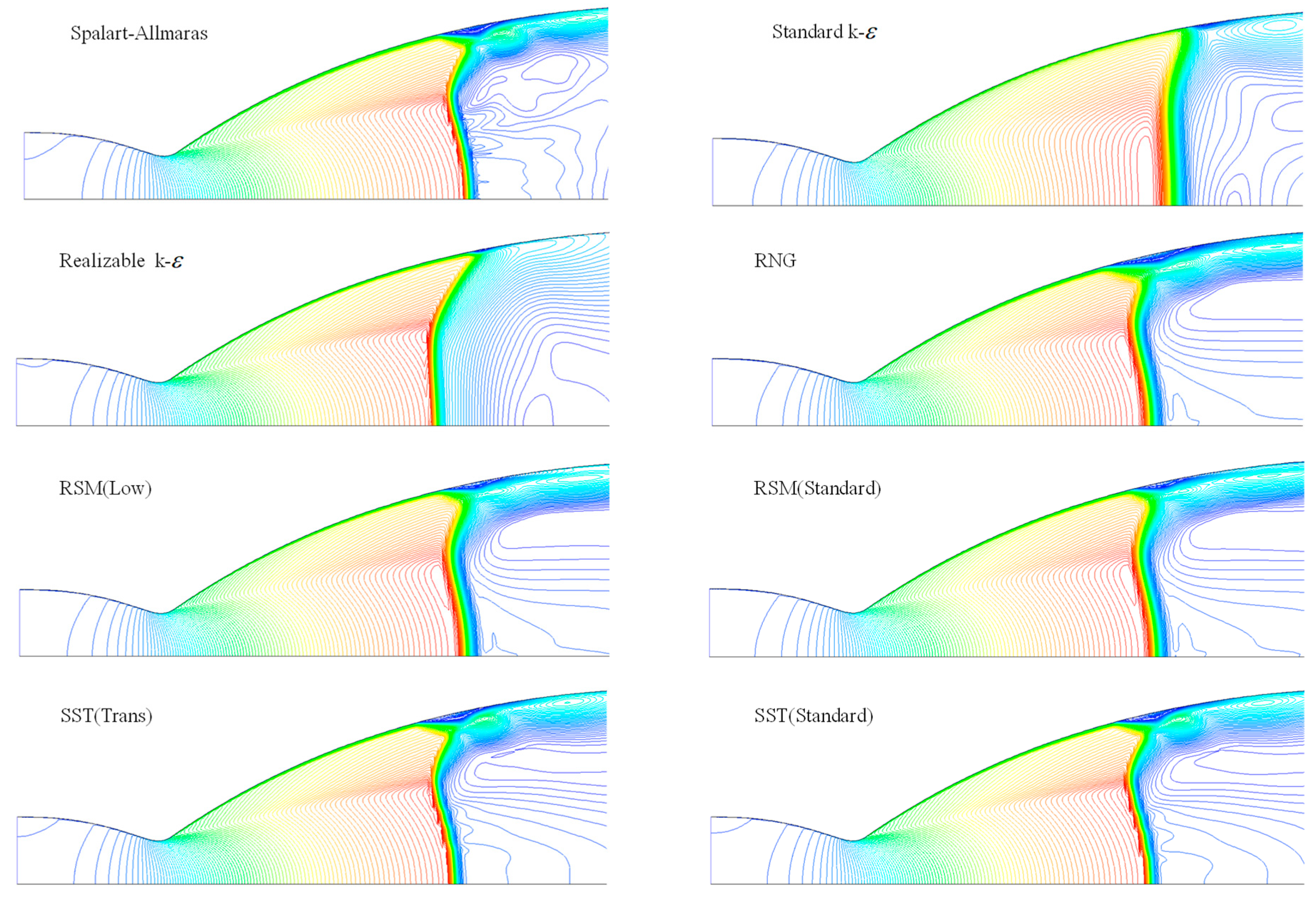
2.2. Turbulence Model
2.3. Case Test
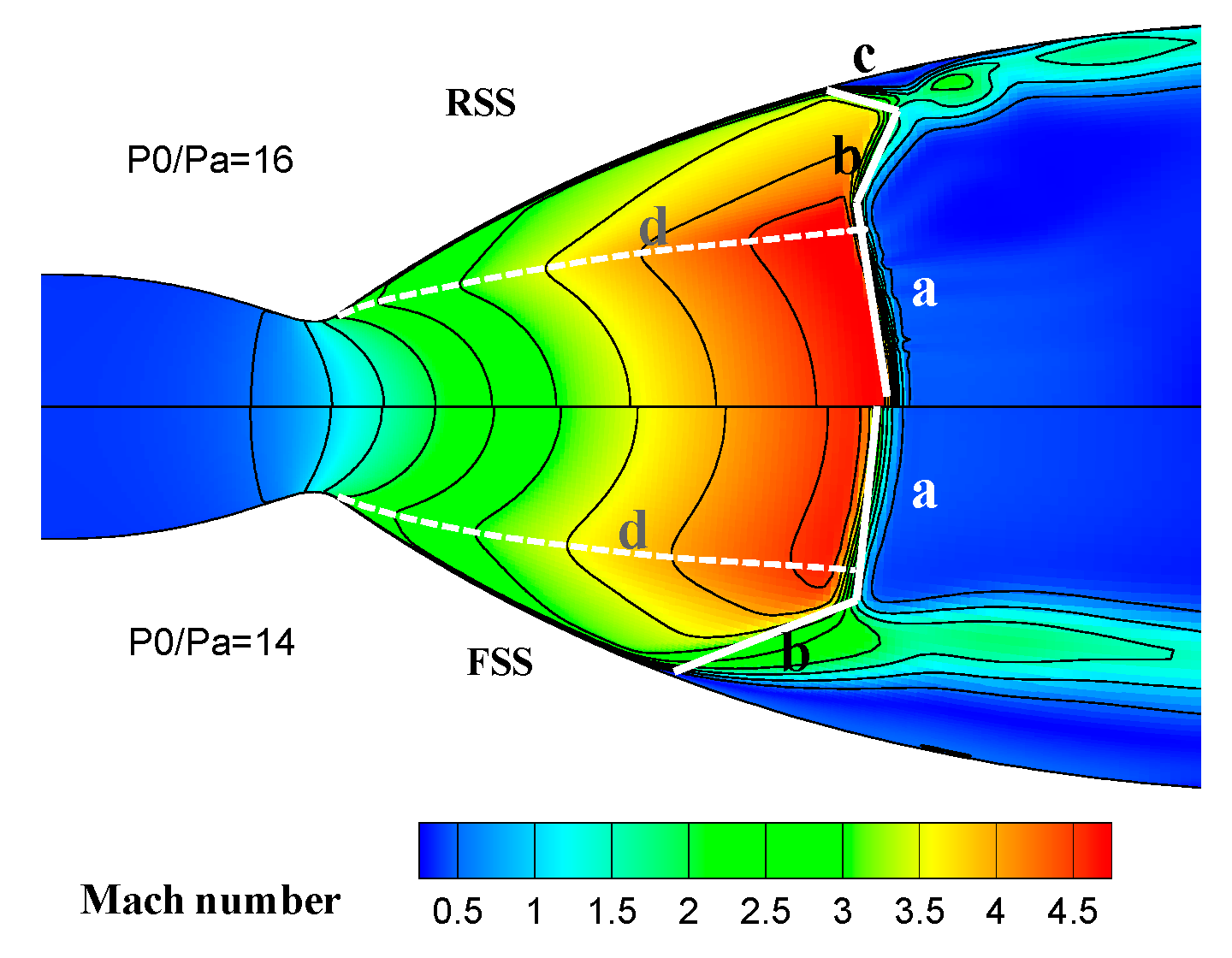
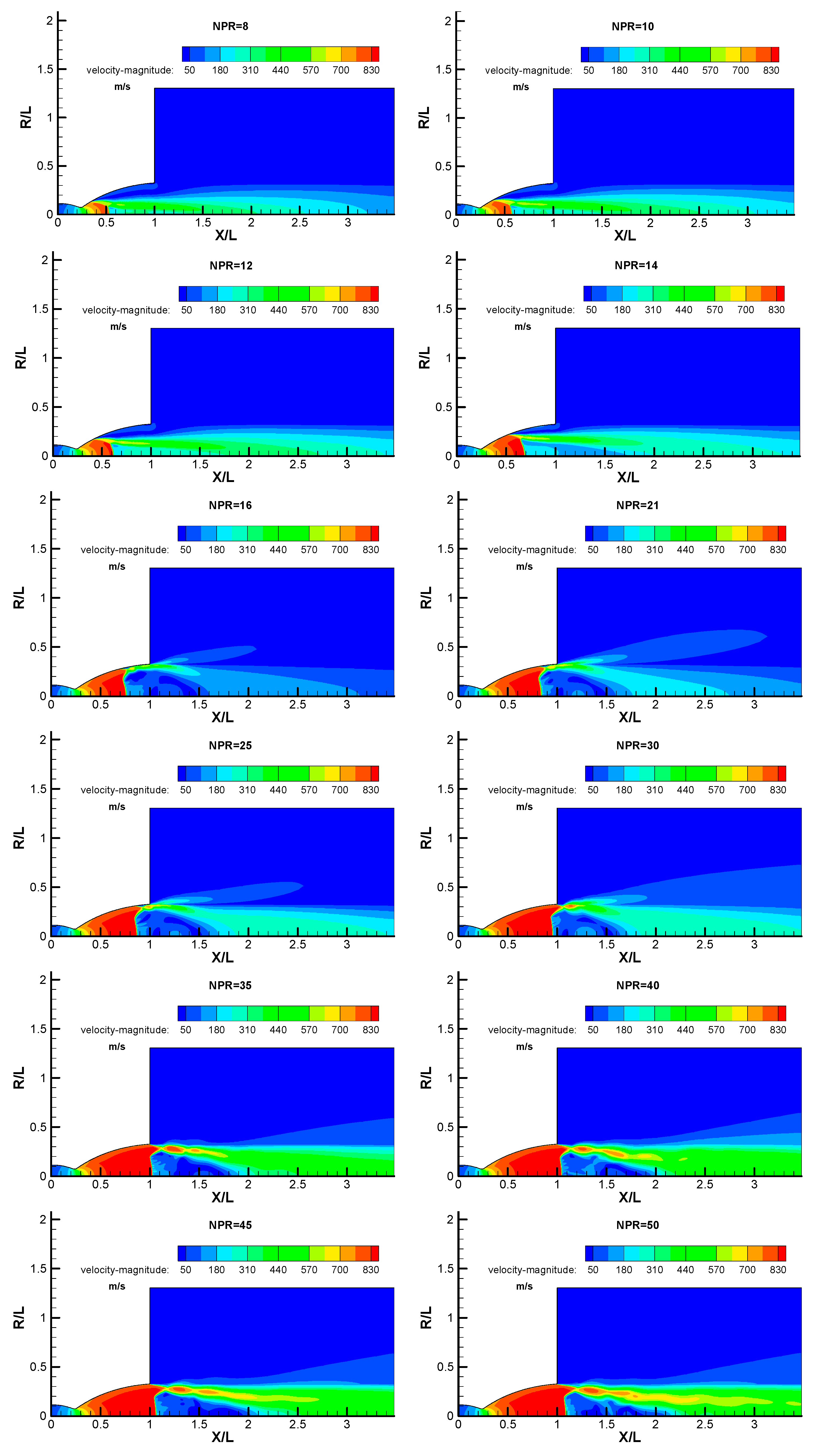
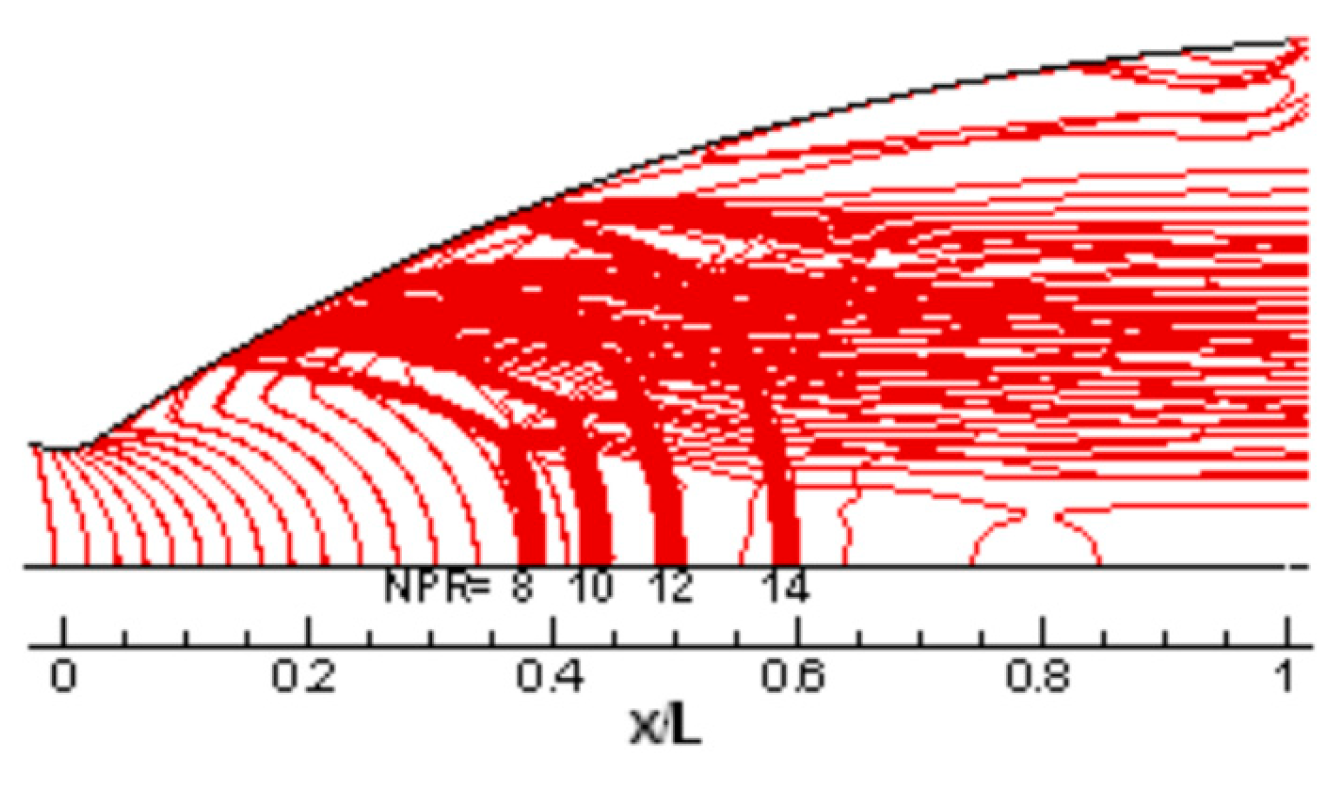
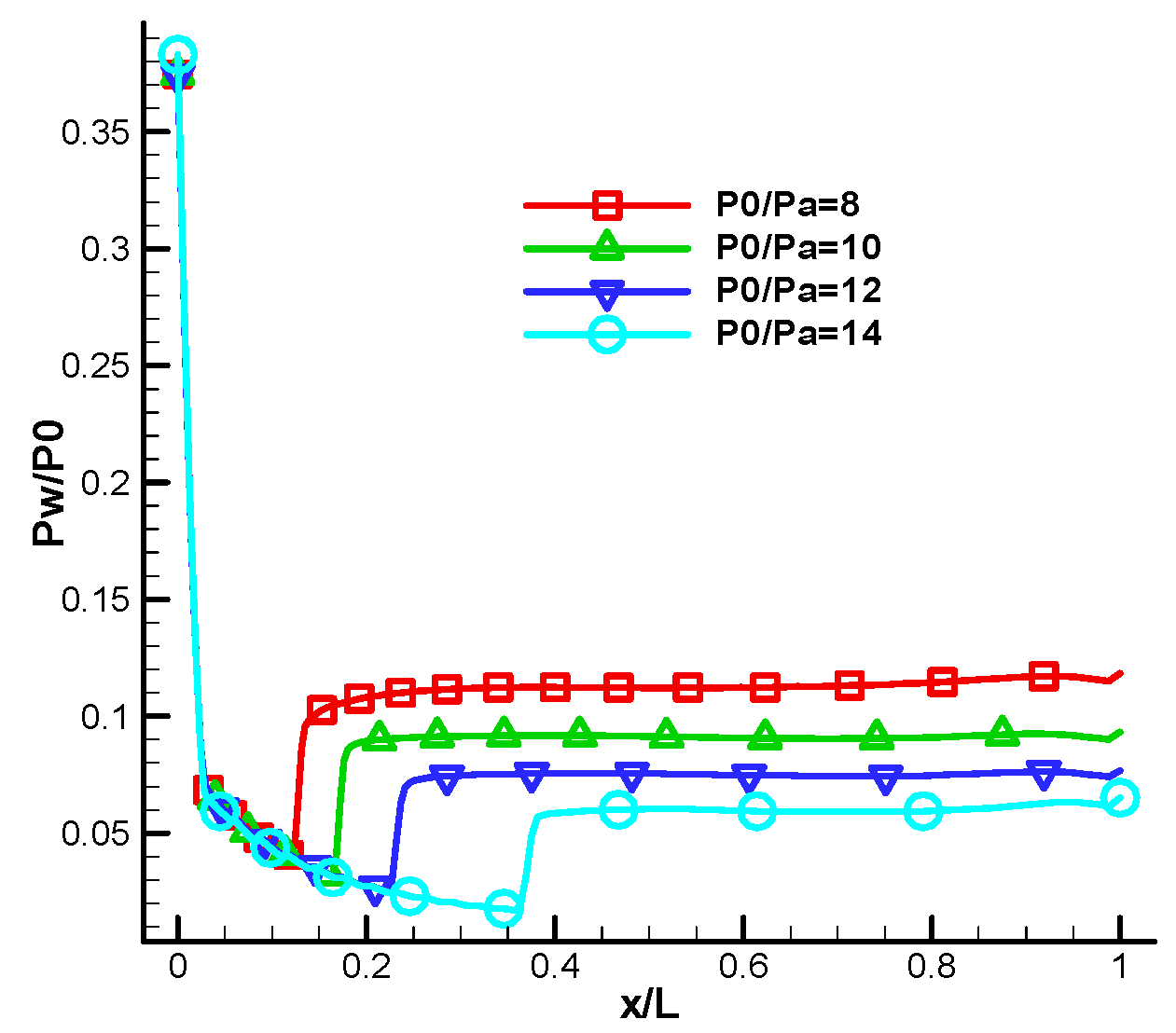
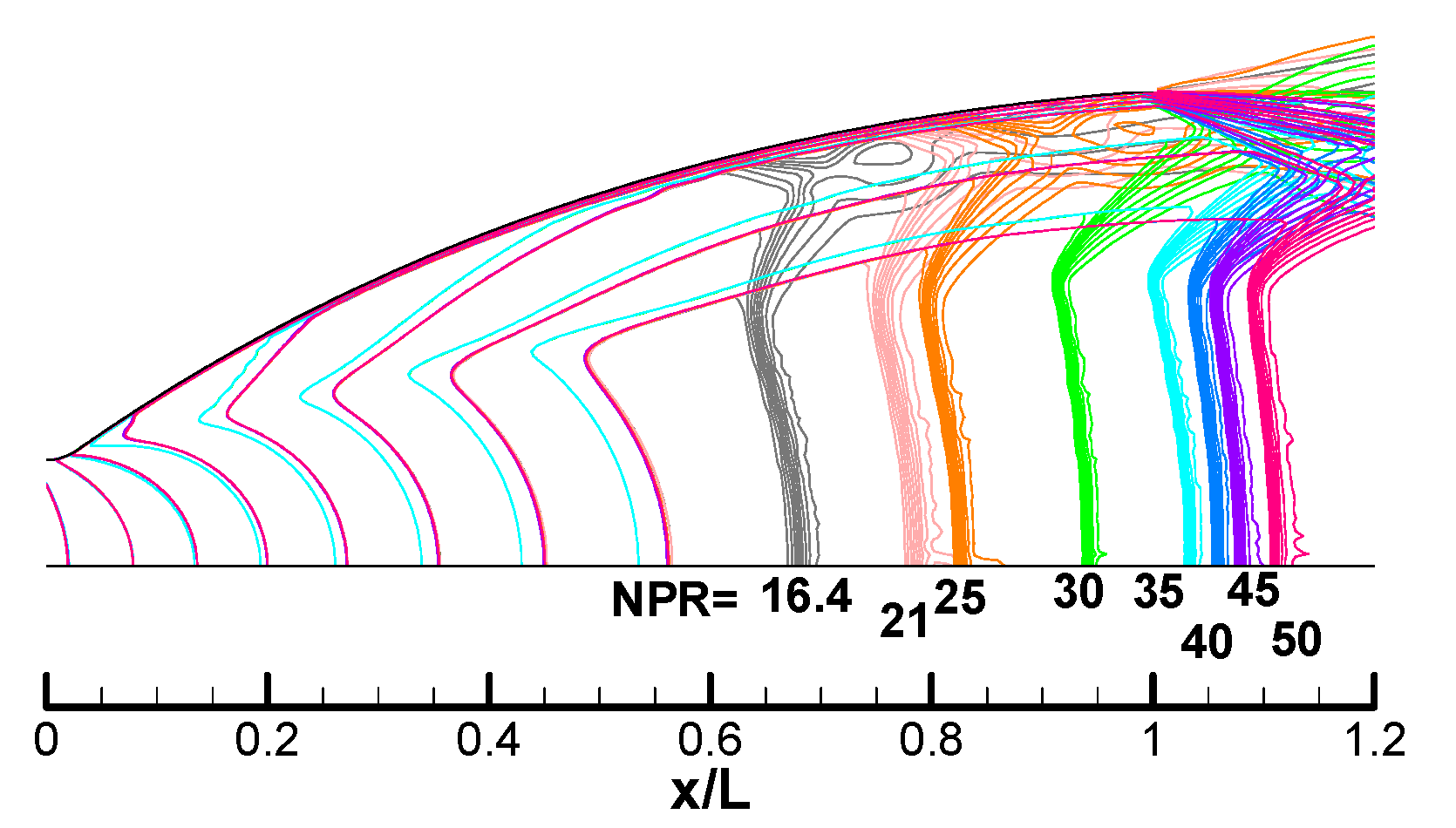
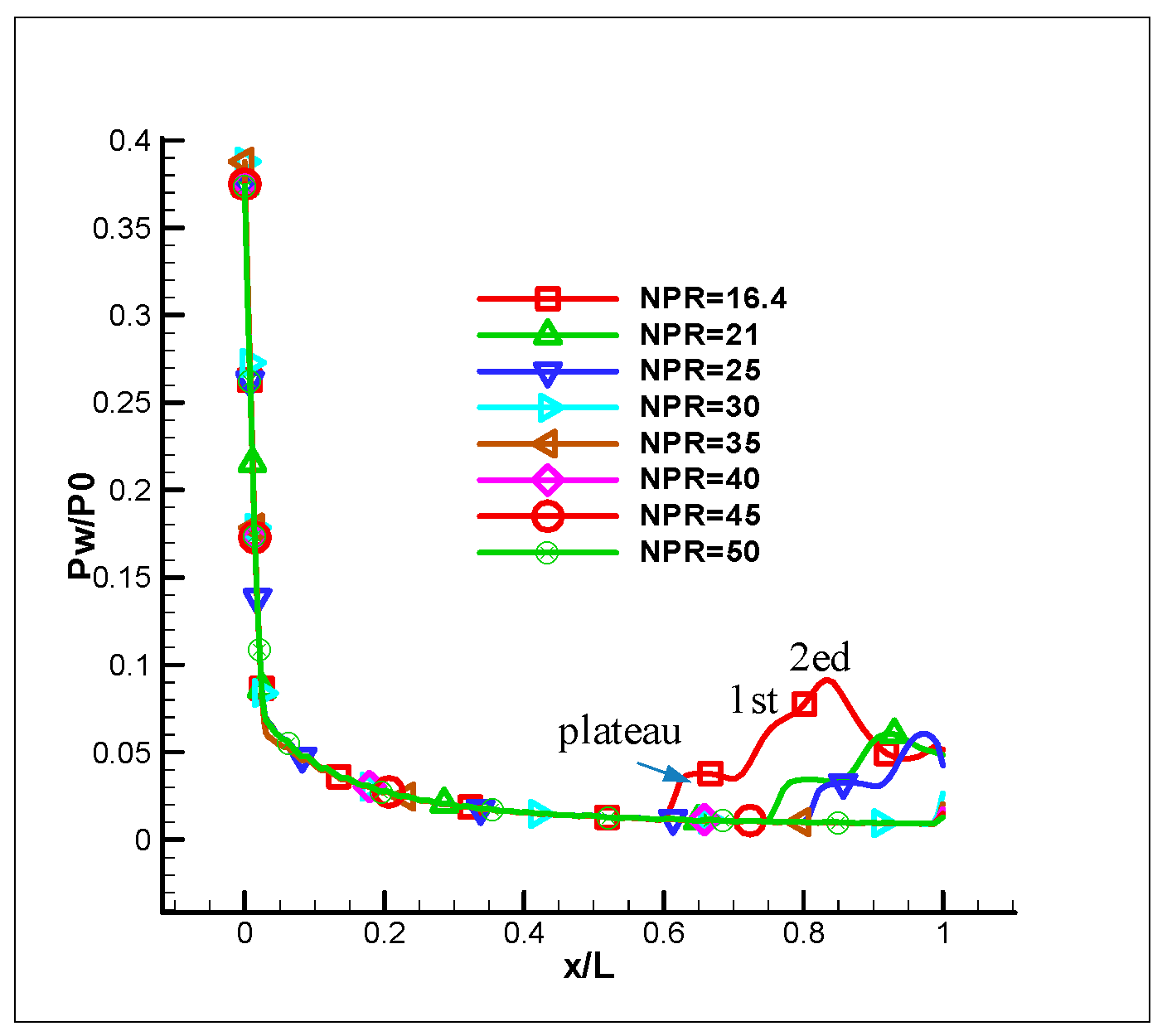
2.4. Ressult
3. Static Structure Analysis
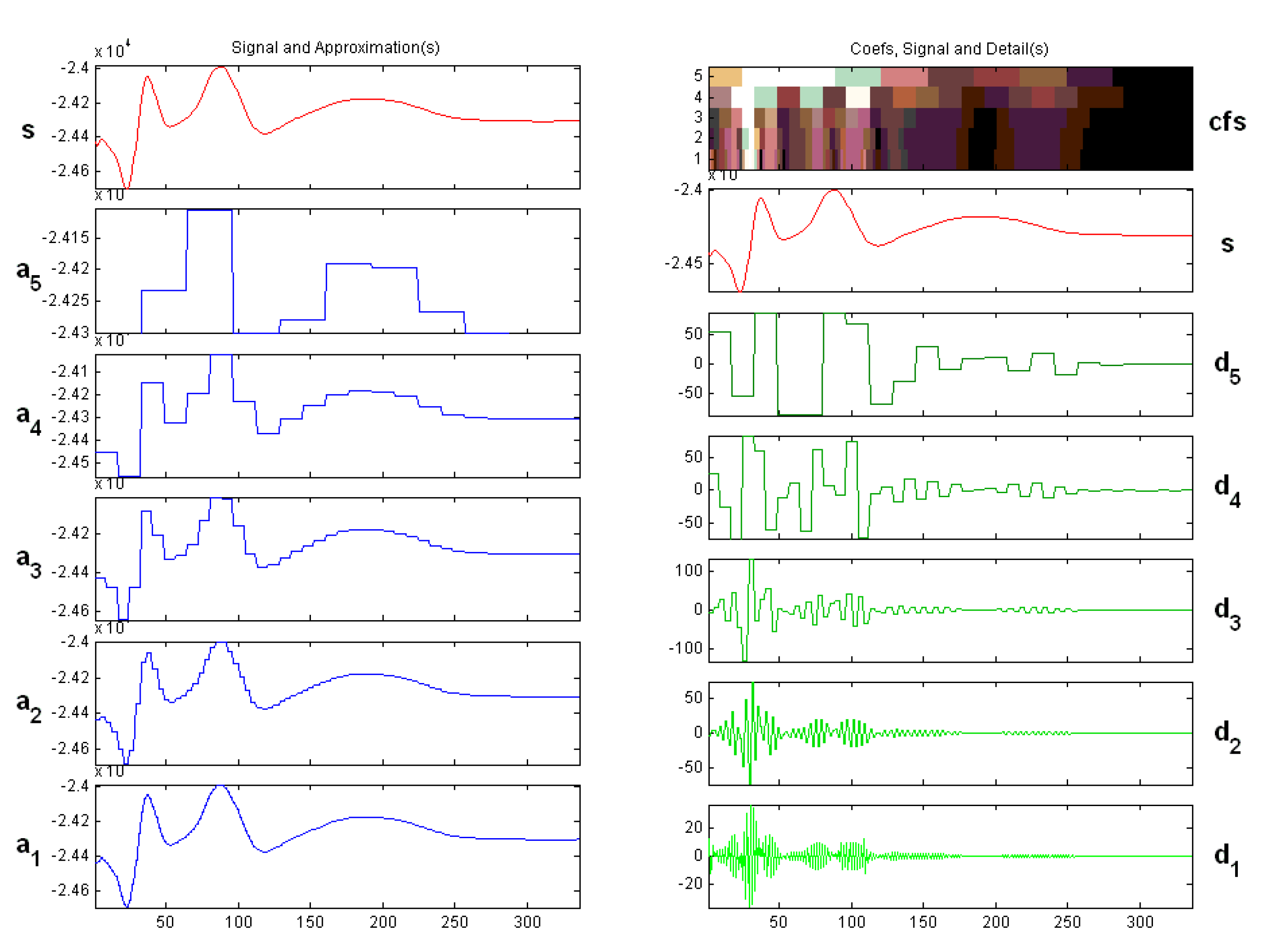
3.1. Wavelet Transfer Method
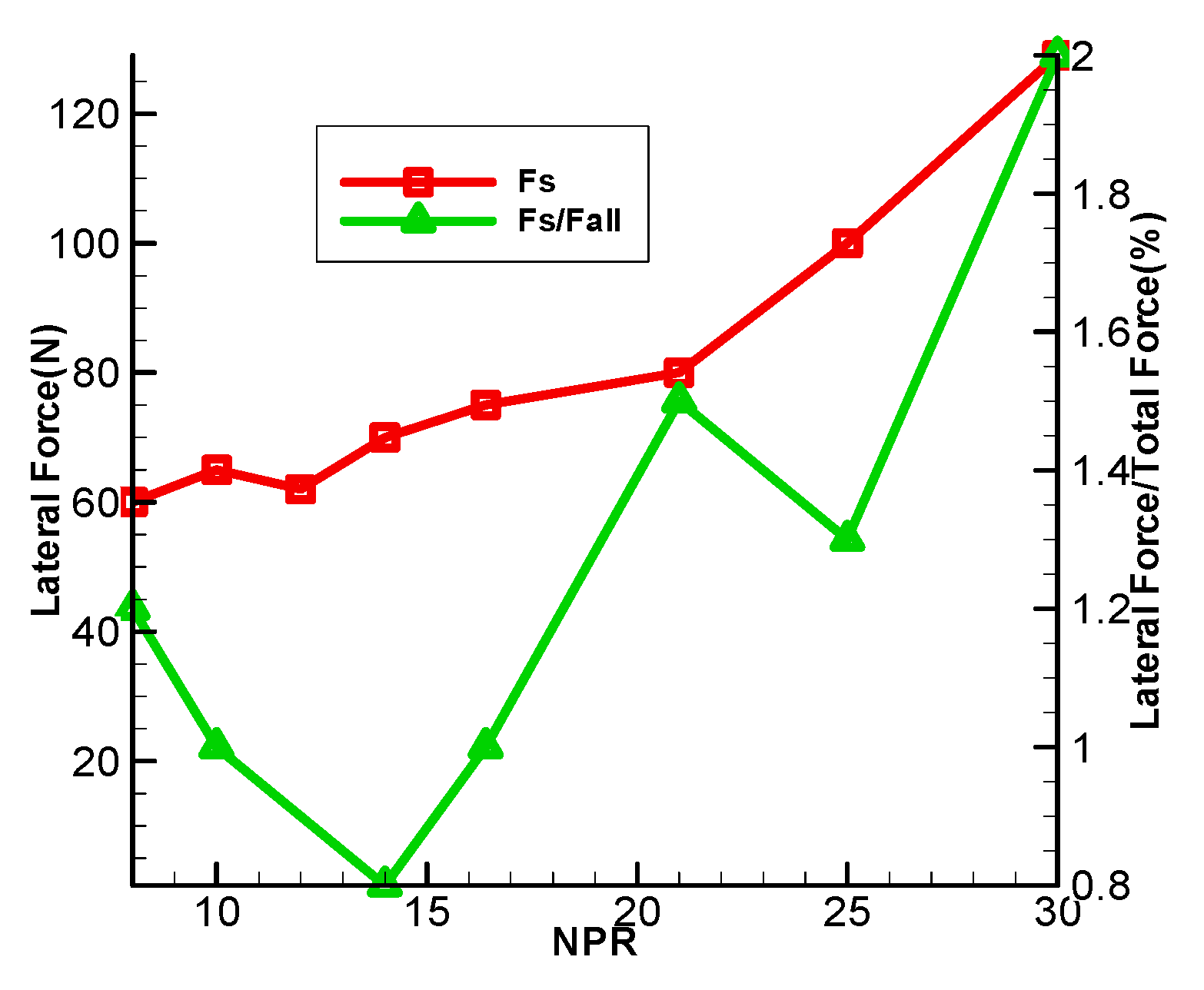
3.2. Analysis of the Lateral Side-Load Force
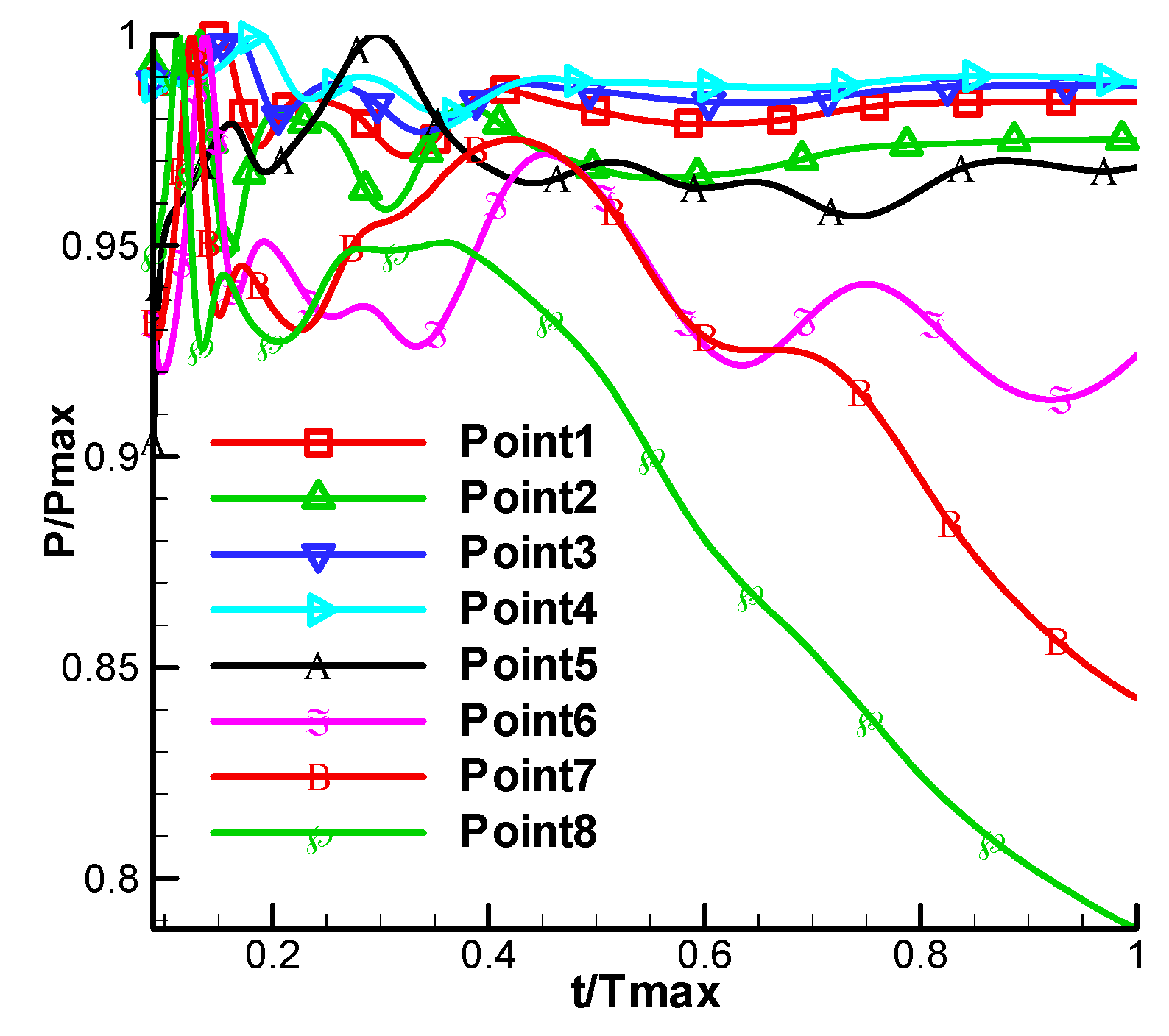
3.3. Frequency Result Discuss
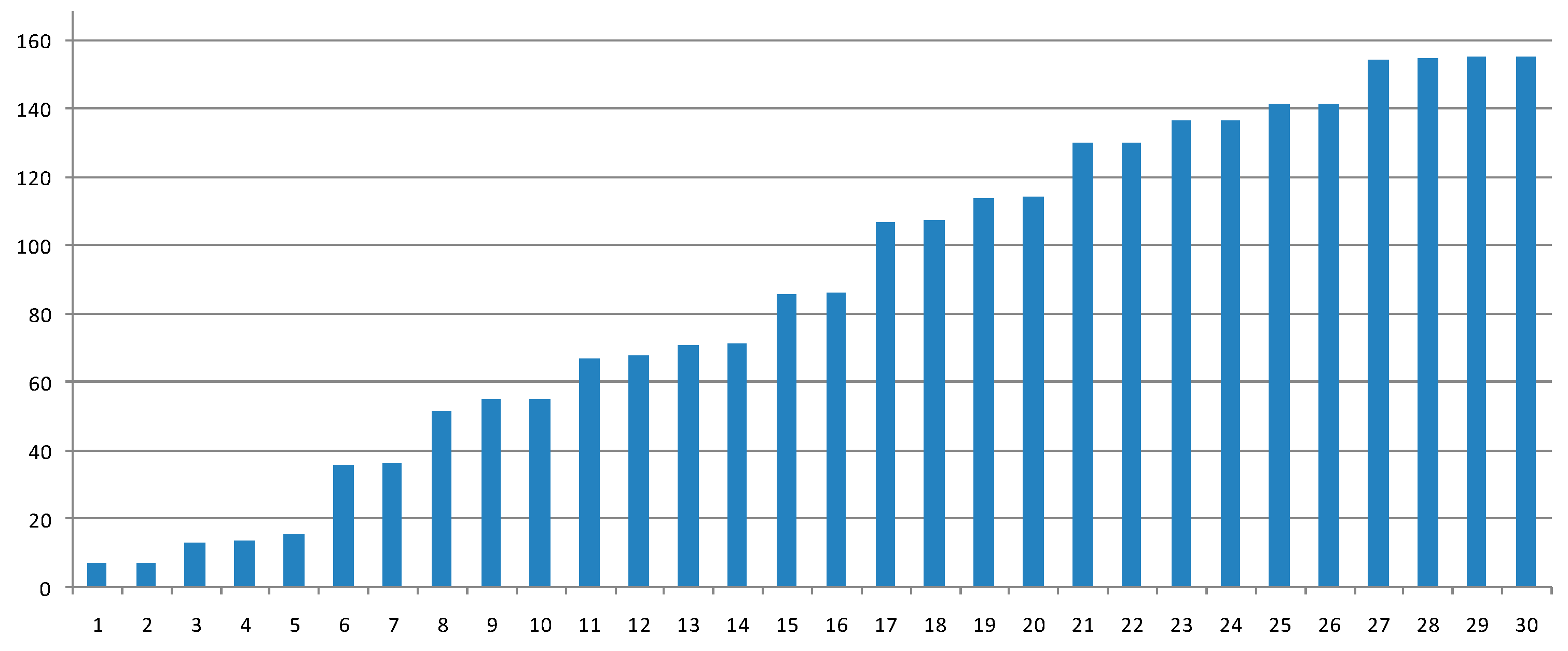
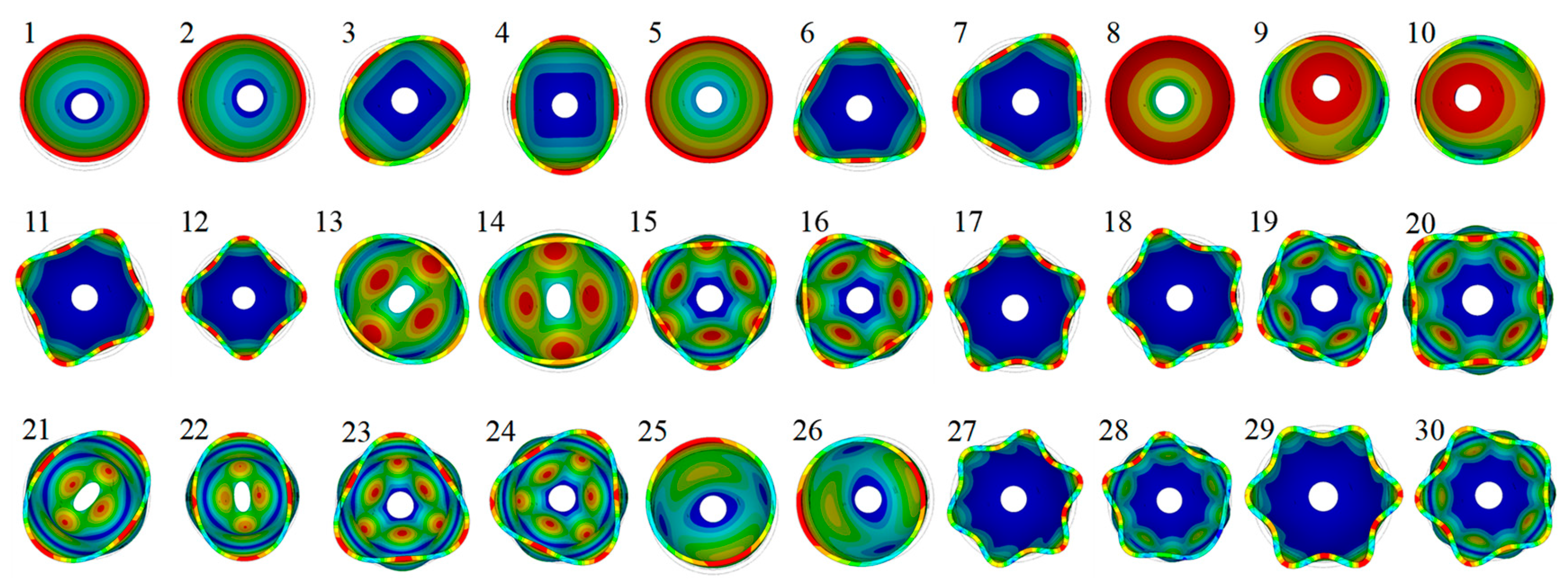
3.4. Modal Analysis
4. Aeroelastic Coupling
4.1. Numerical Methodology (CSD)
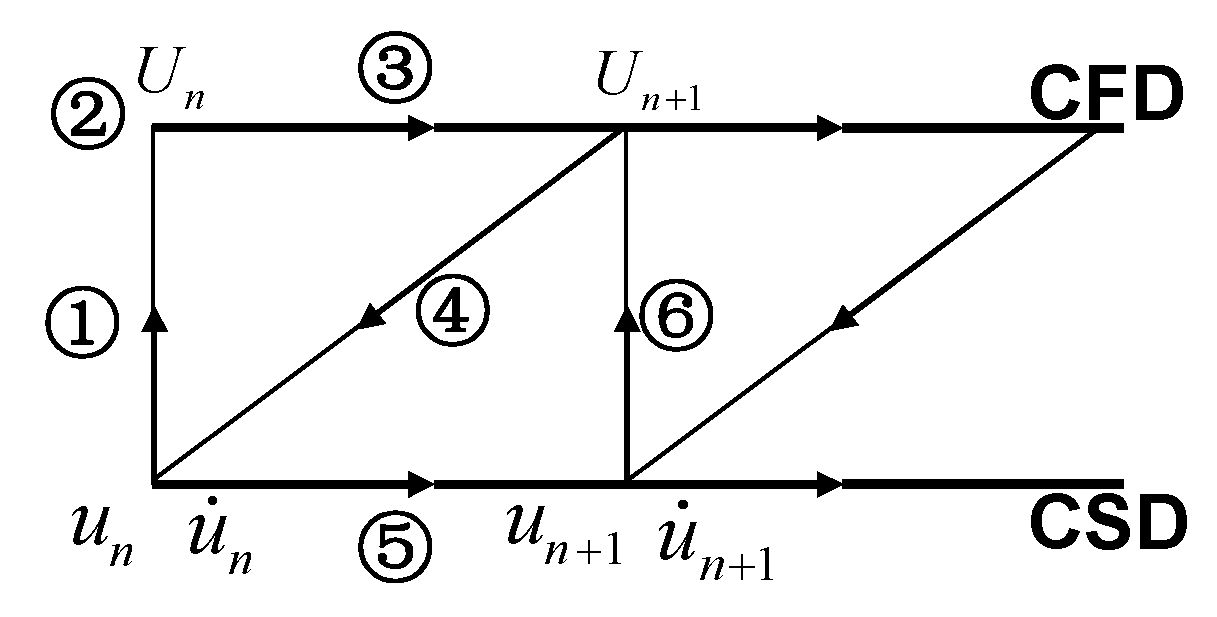
4.2. Fluid/Structure Coupling
- (i)
- The structural deformation resulting from the transition of the solid domain to the fluid domain is calculated.
- (ii)
- The fluid domain mesh grid is reconfigured, and the variables of the FSI boundary are updated.
- (iii)
- The fluid system is updated, and the flow field is simulated.
- (iv)
- The new fluid pressure of the FSI boundary (and stress field) is updated into a structural load.
- (v)
- the structural system under the given pressure loads is advanced.
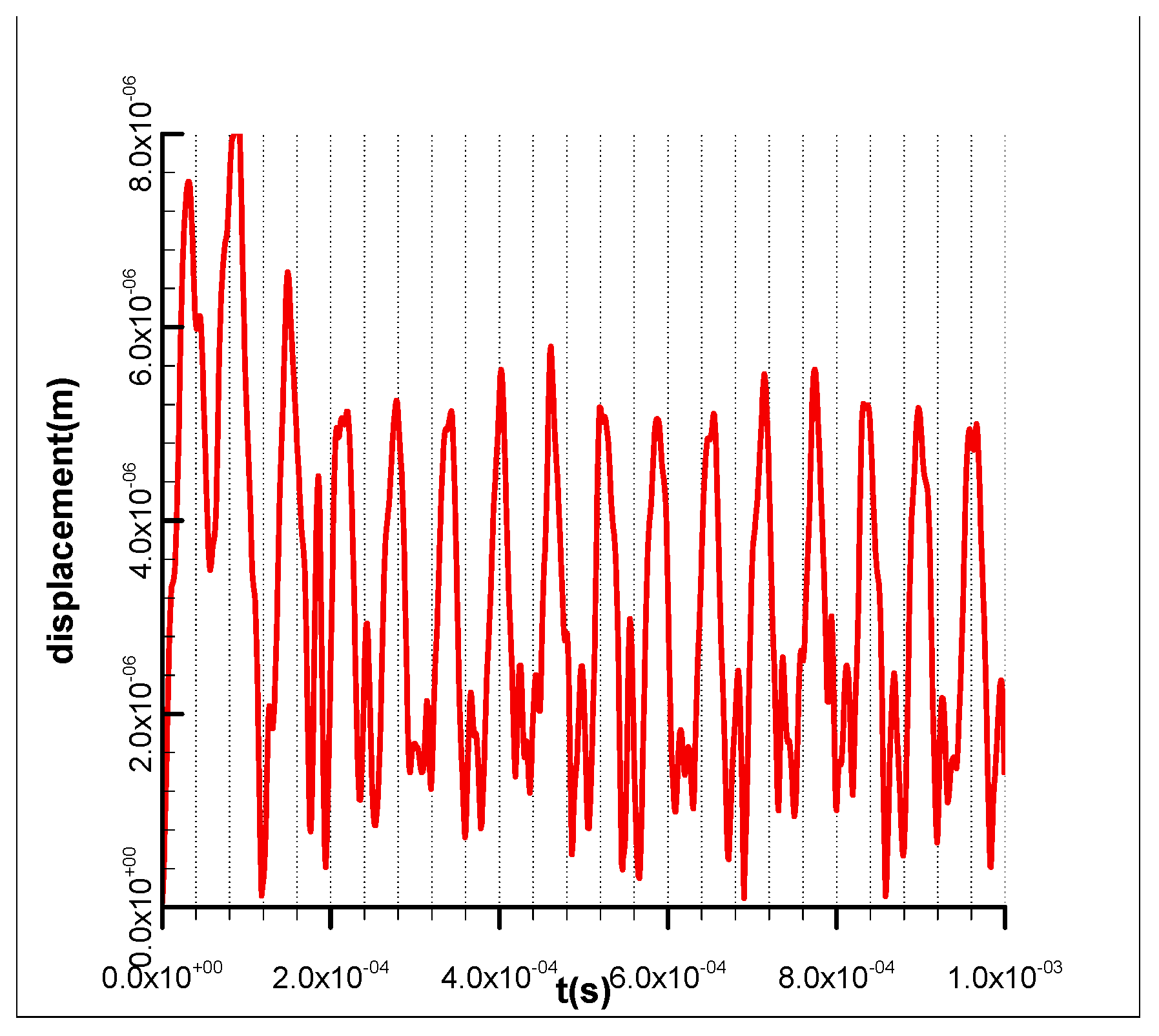
4.3. Result Disscuss
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cowles, F.B.; Foster, C.R. Experimental Study of Gas-Flow Separation in Overexpanded Exhaust Nozzles for Rocket Motors; No. JPL-PR-4-103; Jet Propulsion Laboratory: Pasadena, CA, USA, 1949. [Google Scholar]
- Keanini, R.G.; Brown, A.M. Scale analysis and experimental observations of shock-induced turbulent boundary layer separation in nozzles. Eur. J. Mech. B Fluids 2007, 26, 494–510. [Google Scholar] [CrossRef]
- Nave, L.H.; Coffey, G.A. Sea Levels Side Loads in High Area-Ratio Rocket Engines. In Proceedings of the 9th Propulsion Conference, Las Vegas, NV, USA, 5–7 November; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1973. AIAA Paper 1973-1284. [Google Scholar]
- Frey, M.; Hagemann, G. Status of flow separation prediction in rocket nozzles. In Proceedings of the 34th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Cleveland, OH, USA, 13–15 July 1998. [Google Scholar] [CrossRef]
- Stark, R. Flow separation in rocket nozzles, a simple criteria. In Proceedings of the 41st AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Tucson, AZ, USA, 10–13 July 2005. AIAA Paper 2005-3940. [Google Scholar] [CrossRef]
- Östlund, J. Flow Processes in Rocket Engine Nozzles with Focus on Flow Separation and Side-Loads; TRITA-MEK Technical Report 2002:09; Royal Institute of Technology Department of Mechanics S-100 44: Stockholm, Sweden, 2002; ISSN 0348-467X. ISRN KTH/MEK/TR–02/09-SE. [Google Scholar]
- Takahashi, M.; Ueda, S.; Tomita, T.; Takahashi, M.; Tamura, H.; Aoki, K. Transient flow simulation of a compressed truncated perfect nozzle. In Proceedings of the 37th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Salt Lake City, UT, USA, 8–11 July 2001. [Google Scholar]
- Verma, S.B.; Haidn, O. Unsteady Side-Load Evolution in a Liquid Rocket Engine Nozzle. J. Spacecr. Rocket. 2020, 57, 391–397. [Google Scholar] [CrossRef]
- Perigo, D.; Schwane, R.; Wong, H. A numerical comparison of the flow in conventional and dual-bell nozzles in the presence of an unsteady external pressure environment. In Proceedings of the 39th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, 20–23 July 2003; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2003. AIAA Paper 2003-4771. [Google Scholar]
- Wang, T.-S. Transient Three-Dimensional Analysis of Side Load in Liquid Rocket Engine Nozzles. In Proceedings of the 40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Fort Lauderdale, FL, USA, 11–14 July 2004; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2004. AIAA Paper 2004-3681. [Google Scholar]
- Wang, T.-S. Transient Three-Dimensional Analysis of Nozzle Side Load in Regeneratively Cooled Engines. In Proceedings of the 41st AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Tucson, AZ, USA, 10–13 July 2005; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2005. AIAA Paper 2005-3942. [Google Scholar]
- Verma, S.B.; Stark, R.; Haidn, O. Relation between shock unsteadiness and the origin of side-loads inside a thrust optimized parabolic rocket nozzle. Aerosp. Sci. Technol. 2006, 10, 474–483. [Google Scholar] [CrossRef]
- Zebiri, B.; Piquet, A.; Hadjadj, A. Analysis of shock-wave unsteadiness in conical supersonic nozzles. Aerosp. Sci. Technol. 2020, 105, 106060. [Google Scholar] [CrossRef]
- Khan, M.S.; Minhaj, S.A. Numerical Analysis of de Laval Nozzle Under Surrounding Zone and Compressed Flow. Int. J. Res. Appl. Sci. Eng. Technol. 2021, 9, 98–105. [Google Scholar] [CrossRef]
- Martelli, E.; Nasuti, F.; Onofri, M. Numerical calculation of FSS/RSS transition in highly overexpanded rocket nozzle flows. Shock Waves 2010, 20, 139–146. [Google Scholar] [CrossRef]
- Hadjadj, A.; Onofri, M. Nozzle flow separation. Shock Waves 2009, 19, 163–169. [Google Scholar] [CrossRef]
- Lijo, V.; Kim, H.D.; Setoguchi, T.; Matsuo, S. Numerical simulation of transient flows in a rocket propulsion nozzle. Int. J. Heat Fluid Flow 2010, 31, 409–417. [Google Scholar] [CrossRef]
- Bekka, N.; Sellam, M.; Chpoun, A. Aeroelastic Stability Analysis of Flexible Overexpanded Rocket Nozzle. Shock Waves 2016, 26, 513–527. [Google Scholar] [CrossRef]
- Garelli, L.; Paz, R.R.; Storti, M.A. Fluid–structureinteractionstudyofthestart-upofarocketenginenozzle. Comput. Fluids 2010, 39, 1208–1218. [Google Scholar] [CrossRef]
- Ansys Fluent Theory Guide. Available online: https://www.ansys.com/ (accessed on 16 January 2024).



| Model | Description |
|---|---|
| Spalart– Allmaras | A single transport equation model that directly solves for modified turbulent viscosity. This device has been designed specifically for aerospace applications involving wall-bounded flows on a fine near-wall mesh. SA is a low-cost RANS model that is mainly intended for aerodynamic applications with mild separation, such as supersonic/transonic flows over airfoils and boundary-layer flows. |
| Standard k–ε | The baseline two-transport-equation model for solving k and ε. This model is the default k–ε model. Coefficients are empirically derived and are valid for fully turbulent flows. This model can account for viscous heating, buoyancy, and compressibility, which can be calculated with other k–ε models. |
| RNG k–ε | A variant of the standard k–ε model. The equations and coefficients are analytically derived. Significant changes in the ε equation improve the ability to model highly strained flows. Additional options aid in predicting swirling and low Reynolds number flows. |
| Realizable k–ε | A variant of the standard k–ε model. The realizability of this model stems from changes that allow for the application of certain mathematical constraints, which ultimately improves the performance of this model. |
| Standard k–ω | A two-transport-equation model for solving for k and ω. The specific dissipation rate (ε/k) is based on Wilcox (1998), and it is the default k–ω model. This model performs very well for wall-bounded and low-Reynolds-number flows. This approach has potential for use in predicting transitions. This model accounts for transitional, free shear, and compressible flows. |
| SST k–ω | a variant of the standard k–ω model. The original Wilcox model for use near walls and the standard k–ε model for use away from walls are combined using a blending function. Additionally, the turbulent viscosity is limited to guarantee that τT~k. The transition and shearing options are borrowed from standard k–ω. Compressibility is not included in this model. |
| Reynolds Stress | The Reynolds stresses are directly solved using transport equations, avoiding the isotropic viscosity assumption of other models. This model can be used for highly swirling flows. The quadratic pressure–strain model improves the performance for many basic shear flows. |
| NPR | Case | x/mm | y/mm | Total Nodes |
|---|---|---|---|---|
| 14 | A | 200 | 90 | 50,538 |
| B | 300 | 150 | 54,818 | |
| 16 | A | 270 | 120 | 52,680 |
| B | 370 | 180 | 67,658 |
| Location | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Nodes | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| X (mm) | 210 | 250 | 280 | 320 | 360 | 400 | 420 | 440 | 460 | |
| Y (mm) | 88 | 105 | 116 | 128 | 137 | 144 | 146 | 148 | 150 | |
| Z (mm) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Young’s Modulus (N m−2) | Poisson’s Ratio | Mass Density (kg m−3) | Thickness (mm) |
| 7 × 1010 | 0.34 | 2890 | 11.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, H.; Gao, X.; Gao, Y.; Yang, J. Shock Wave and Aeroelastic Coupling in Overexpanded Nozzle. Aerospace 2024, 11, 818. https://doi.org/10.3390/aerospace11100818
Hu H, Gao X, Gao Y, Yang J. Shock Wave and Aeroelastic Coupling in Overexpanded Nozzle. Aerospace. 2024; 11(10):818. https://doi.org/10.3390/aerospace11100818
Chicago/Turabian StyleHu, Haifeng, Xinni Gao, Yushan Gao, and Jianwen Yang. 2024. "Shock Wave and Aeroelastic Coupling in Overexpanded Nozzle" Aerospace 11, no. 10: 818. https://doi.org/10.3390/aerospace11100818
APA StyleHu, H., Gao, X., Gao, Y., & Yang, J. (2024). Shock Wave and Aeroelastic Coupling in Overexpanded Nozzle. Aerospace, 11(10), 818. https://doi.org/10.3390/aerospace11100818





