Energy Absorption Properties of 3D-Printed Polymeric Gyroid Structures for an Aircraft Wing Leading Edge
Abstract
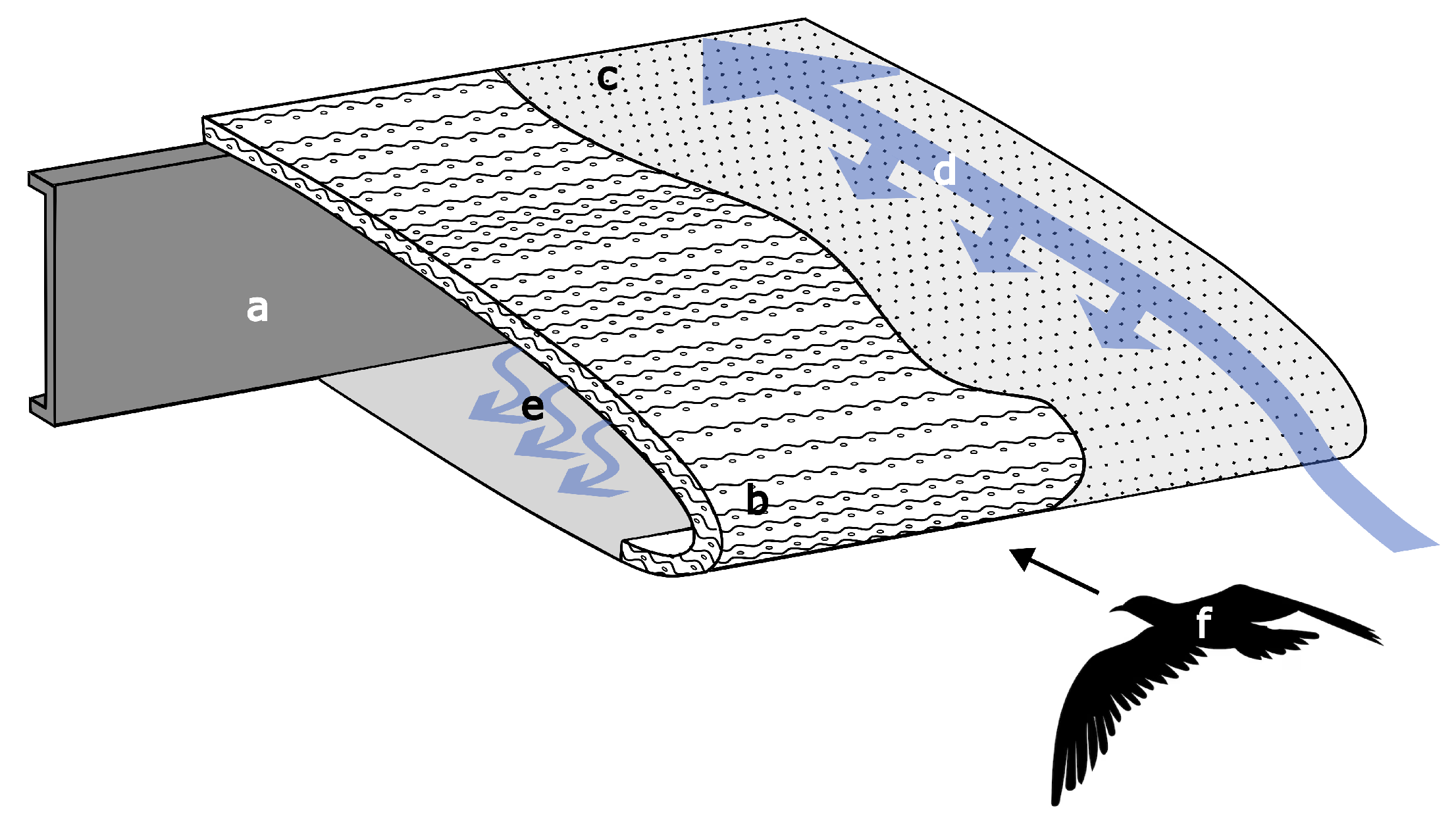
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Gyroid Configuration
2.3. Methods
2.3.1. Manufacturing of Specimens
2.3.2. Testing
Quasi-Static Compression
Dynamic Crushing
3. Results and Discussion
3.1. Manufacturing of Specimens
3.2. Standard Resin
3.3. Polyurethane Rigid 650
3.4. Nylon 11
3.5. Comparison of Materials
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AM | Additive manufacturing |
| FDM | Fused deposition modelling |
| LFC | Laminar flow control |
| HLFC | Hybrid laminar flow control |
| NLF | Natural laminar flow |
| SLA | Stereolithography |
| SLS | Selective laser sintering |
| TPMS | Triply periodic minimal surface |
| xHLFC | Extended hybrid laminar flow control |
References
- Beck, N.; Landa, T.; Seitz, A.; Boermans, L.; Liu, Y.; Radespiel, R. Drag reduction by laminar flow control. Energies 2018, 11, 252. [Google Scholar] [CrossRef]
- Salmasi, A.; Shadaram, A.; Taleghani, A.S. Effect of plasma actuator placement on the airfoil efficiency at poststall angles of attack. IEEE Trans. Plasma Sci. 2013, 41, 3079–3085. [Google Scholar] [CrossRef]
- Krishnan, K.; Bertram, O.; Seibel, O. Review of hybrid laminar flow control systems. Prog. Aerosp. Sci. 2017, 93, 24–52. [Google Scholar] [CrossRef]
- Lobitz, L.; Traub, H.; Overbeck, M.; Bień, M.; Heimbs, S.; Hühne, C.; Friedrichs, J.; Horst, P. Aircraft wing design for extended hybrid laminar flow control. Aerospace 2023, 10, 938. [Google Scholar] [CrossRef]
- Wiedemann, M.; Badrya, C.; Prasannakumar, A.; Lobitz, L.; Traub, H.; Heimbs, S.; Hühne, C.; Saemann, P.; Buelow, C.; Scheffler, S.; et al. The suction panel—xHLFC and structural solution for energy efficient aviation. In Proceedings of the AIAA Scitech 2022 Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar] [CrossRef]
- Horn, M.; Seitz, A.; Schneider, M. Novel tailored skin single duct concept for HLFC fin application. In Proceedings of the 7th European Conference for Aeronautics and Space Sciences (EUCASS), Milan, Italy, 3–6 July 2017. [Google Scholar] [CrossRef]
- Schrauf, G.H.; von Geyr, H. Simplified hybrid laminar flow control for the A320 fin—Aerodynamic and system design, first results. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar] [CrossRef]
- Wicke, K.; Kruse, M.; Linke, F.; Gollnick, V. Impact of insect contamination on operational and economic effectiveness of aircraft with natural laminar flow technology. In Proceedings of the 29th Congress of the International Council of the Aeronautical Sciences, St. Petersburg, Russia, 7–12 September 2014. [Google Scholar]
- Lohner, H.; Kröger-Kallies, B.; Rives, B.; Fangmeier, A. Aircraft surface protection—Principles, application, future trends. In Proceedings of the Deutscher Luft- und Raumfahrtkongress 2011, Bremen, Germany, 27–29 September 2011. [Google Scholar]
- Joslin, R.D. Aircraft laminar flow control. In Annual Review of Fluid Mechanics; NASA Langley Research Center: Hampton, VA, USA, 1998. [Google Scholar]
- Heimbs, S. Computational methods for bird strike simulations: A review. Comput. Struct. 2011, 89, 2093–2112. [Google Scholar] [CrossRef]
- Cihan Tezel, M.; Yamaner, Y.; Aziz Çoğuz, B.; Acar, E. Exploring design options for wing leading edge against bird strike. J. Aircr. 2023, 60, 66–80. [Google Scholar] [CrossRef]
- Schoen, A.H. Infinite Periodic Minimal Surfaces without Self-Intersections; Technical Note NASA TN D-5541; National Aeronautics and Space Administration: Washington, DC, USA, 1970.
- Schwarz, H.A. Gesammelte Mathematische Abhandlungen; Springer: Berlin/Heidelberg, Germany, 1890. [Google Scholar] [CrossRef]
- Buratti, G. Computational process and code-form definition in design. In Faces of Geometry. From Agnesi to Mirzakhani; Magnaghi-Delfino, P., Mele, G., Norando, T., Eds.; Lecture Notes in Networks and Systems; Springer International Publishing: Cham, Switzerland, 2020; Volume 88, pp. 31–40. [Google Scholar] [CrossRef]
- Han, L.; Che, S. An overview of materials with triply periodic minimal surfaces and related geometry: From biological structures to self-assembled systems. Adv. Mater. 2018, 30, 201705708. [Google Scholar] [CrossRef] [PubMed]
- Al-Ketan, O.; Abu Al-Rub, R.K. Multifunctional mechanical metamaterials based on triply periodic minimal surface lattices. Adv. Eng. Mater. 2019, 21, 201900524. [Google Scholar] [CrossRef]
- Li, D.; Liao, W.; Dai, N.; Xie, Y.M. Comparison of mechanical properties and energy absorption of sheet-based and strut-based gyroid cellular structures with graded densities. Materials 2019, 12, 2183. [Google Scholar] [CrossRef] [PubMed]
- Ashby, M.F.; Medalist, R.F.M. The mechanical properties of cellular solids. Metall. Trans. A 1983, 14, 1755–1769. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Lee, D.W.; Rowshan, R.; Abu Al-Rub, R.K. Functionally graded and multi-morphology sheet TPMS lattices: Design, manufacturing, and mechanical properties. J. Mech. Behav. Biomed. Mater. 2020, 102, 103520. [Google Scholar] [CrossRef] [PubMed]
- Abueidda, D.W.; Elhebeary, M.; Shiang, C.S.; Pang, S.; Abu Al-Rub, R.K.; Jasiuk, I.M. Mechanical properties of 3D printed polymeric gyroid cellular structures: Experimental and finite element study. Mater. Des. 2019, 165, 107597. [Google Scholar] [CrossRef]
- Wallat, L.; Selzer, M.; Wasmuth, U.; Poehler, F.; Nestler, B. Energy absorption capability of graded and non-graded sheet-based gyroid structures fabricated by microcast processing. J. Mater. Res. Technol. 2022, 21, 1798–1810. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge Solid State Science Series; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Maskery, I.; Aboulkhair, N.T.; Aremu, A.O.; Tuck, C.J.; Ashcroft, I.A. Compressive failure modes and energy absorption in additively manufactured double gyroid lattices. Addit. Manuf. 2017, 16, 24–29. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, T.; Chen, H.; Li, Z.; Li, S.; Wang, D.; Wang, Y.; Kosiba, K. Impact behaviors of additively manufactured metals and structures: A review. Int. J. Impact Eng. 2024, 191, 104992. [Google Scholar] [CrossRef]
- Li, X.; Xiao, L.; Song, W. Compressive behavior of selective laser melting printed gyroid structures under dynamic loading. Addit. Manuf. 2021, 46, 102054. [Google Scholar] [CrossRef]
- Lu, C.; Zhang, Y.; Aziz, M.; Wen, P.; Zhang, C.; Shen, Q.; Chen, F. Mechanical behaviors of multidimensional gradient gyroid structures under static and dynamic loading: A numerical and experimental study. Addit. Manuf. 2022, 59, 103187. [Google Scholar] [CrossRef]
- Ramos, H.; Santiago, R.; Soe, S.; Theobald, P.; Alves, M. Response of gyroid lattice structures to impact loads. Int. J. Impact Eng. 2022, 164, 104202. [Google Scholar] [CrossRef]
- Formlabs. Standard: Materials for High-Resolution Rapid Prototyping; Formlabs: Somerville, MA, USA, 2016. [Google Scholar]
- Formlabs. PU Rigid 650: For Impact Resistant and Semi-Stiff Polyurethane Parts; Formlabs: Somerville, MA, USA, 2022. [Google Scholar]
- Formlabs. Nylon 11: Nylon 11 Powder for High Performance, High Impact; Formlabs: Somerville, MA, USA, 2021. [Google Scholar]
- Ramírez, E.A.; Béraud, N.; Pourroy, F.; Villeneuve, F.; Museau, M. Design parameters effects on relative density of triply periodic minimal surfaces for additive manufacturing. Procedia CIRP 2021, 100, 13–18. [Google Scholar] [CrossRef]
- 3M Company. 3M™ Scotch-Weld™ Structural Epoxy Adhesive EC-9323 B/A: Technical Data Sheet; 3M Company: Saint Paul, MN, USA, 2022. [Google Scholar]
- Bergmann, T. Beitrag zur Charakterisierung und Auslegung Zugbelasteter Energieabsorptionskonzepte Mittels Experimenteller, Analytischer und Numerischer Methoden. Ph.D. Thesis, Technische Universität Kaiserslautern, Kaiserslautern, Germany, 2016. [Google Scholar]
- DIN Deutsches Institut für Normung e.V. Testing of metallic materials—Compression test of metallic cellular materials. In Deutsche Norm—DIN 50134; Beuth Verlag GmbH: Berlin, Germany, 2008. [Google Scholar]













| Material | ||||
|---|---|---|---|---|
| Property | Unit | Formlabs Standard Resin [29] | Formlabs PU Rigid 650 [30] | Formlabs Nylon 11 [31] |
| Young’s modulus | ± | |||
| Ultimate tensile strength | 65 | 34 ± | 49 | |
| Elongation at break | % | 170 ± 17 | 40 | |
| Density | g cm−3 | |||
| Notched Izod | J m−1 | 25 | 375 | 71 |
| Wall Thickness/mm | Unit Cell Size/mm | ||||
|---|---|---|---|---|---|
| 7 | 10 | 14 | 20 | ||
| Relative density/% | 7 | 0.179 | 0.252 | 0.349 | 0.492 |
| 12 | 0.306 | 0.432 | 0.598 | 0.844 | |
| 17 | 0.434 | 0.612 | 0.847 | 1.196 | |
| 23 | 0.587 | 0.828 | 1.146 | 1.618 | |
| Standard Resin | ||||||
|---|---|---|---|---|---|---|
| SEA at 50% Compaction// | Unit Cell Size/mm | |||||
| 7 | 10 | 14 | 20 | |||
| Relative density/% | 7 | QS | 1.75 ± 0.16 | 1.54 ± 0.47 | 1.18 ± 0.21 | |
| 12 | QS | 2.24 ± 0.43 | 1.68 ± 0.17 | 1.05 ± 0.38 | ||
| 17 | QS | 3.43 ± 0.35 | 3.40 ± 0.16 | 2.35 ± 0.54 | 1.42 ± 0.29 | |
| 23 | QS | 3.66 ± 0.36 | 4.40 ± 0.32 | 2.72 ± 0.42 | ||
| 12 | Dyn | 1.41 ± 0.52 | 0.75 ± 0.42 | 0.73 ± 0.21 | 0.38 ± 0.27 | |
| 17 | Dyn | 2.50 ± 0.41 | 1.53 ± 0.51 | 0.89 ± 0.33 | 0.45 ± 0.38 | |
| 23 | Dyn | 1.84 ± 0.83 | 0.93 ± 0.50 | 0.44 ± 0.26 | 0.40 ± 0.20 | |
| Polyurethane Rigid 650 | ||||||
|---|---|---|---|---|---|---|
| SEA at 50% Compaction// | Unit Cell Size/mm | |||||
| 7 | 10 | 14 | 20 | |||
| Relative density/% | 23 | QS | 1.34 | 2.00 | 3.15 | 2.85 |
| 23 | Dyn | 2.15 | 3.06 | 4.57 | 4.27 | |
| Nylon 11 | ||||
|---|---|---|---|---|
| SEA at 50% Compaction// | Unit Cell Size/mm | |||
| 14 | 20 | |||
| Relative density/% | 7 | QS | 1.48 | |
| 12 | QS | 3.40 | 4.17 | |
| 17 | QS | 5.57 | 5.96 | |
| 23 | QS | 7.03 | 7.96 | |
| 7 | Dyn | 0.67 | ||
| 12 | Dyn | 1.24 | 1.07 | |
| 17 | Dyn | 2.44 | 1.53 | |
| 23 | Dyn | 2.40 | 1.66 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Overbeck, M.; Heimbs, S.; Kube, J.; Hühne, C. Energy Absorption Properties of 3D-Printed Polymeric Gyroid Structures for an Aircraft Wing Leading Edge. Aerospace 2024, 11, 801. https://doi.org/10.3390/aerospace11100801
Overbeck M, Heimbs S, Kube J, Hühne C. Energy Absorption Properties of 3D-Printed Polymeric Gyroid Structures for an Aircraft Wing Leading Edge. Aerospace. 2024; 11(10):801. https://doi.org/10.3390/aerospace11100801
Chicago/Turabian StyleOverbeck, Mats, Sebastian Heimbs, Jan Kube, and Christian Hühne. 2024. "Energy Absorption Properties of 3D-Printed Polymeric Gyroid Structures for an Aircraft Wing Leading Edge" Aerospace 11, no. 10: 801. https://doi.org/10.3390/aerospace11100801
APA StyleOverbeck, M., Heimbs, S., Kube, J., & Hühne, C. (2024). Energy Absorption Properties of 3D-Printed Polymeric Gyroid Structures for an Aircraft Wing Leading Edge. Aerospace, 11(10), 801. https://doi.org/10.3390/aerospace11100801







