Numerical Simulation of Spectral Radiation for Hypersonic Vehicles

Abstract

The spectral radiation of hypersonic vehicles and surrounding flow fields is crucial for optical target detection. A novel approach combines Low-Discrepancy Sequences with the Reverse Monte Carlo Method to simulate the spectral radiation of hypersonic missiles. The effects of chemical non-equilibrium reactions and high-emissivity coating failures on the spectral radiation of a typical biconical hypersonic missile were investigated. Significant differences were found among chemical equilibrium, non-equilibrium, non-reactive, and catalytic wall models. High-emissivity coating failures occur mainly in the high-temperature regions of the nose cone and fins. The non-equilibrium model shows a transition peak distribution of NO in the head shock layer within the ultraviolet gamma band, with integrated ultraviolet radiation (200–300 nm) three times higher than the equilibrium model. In the 1–3 μm band, the non-equilibrium model’s radiation intensity at a 120° horizontal detection angle is about 1.46 times that of the equilibrium model. Using real coating emissivity, the 3–5 μm band radiation intensity is about 5% higher, and the 8–14 μm band is about 8.51% lower than the uniform emissivity model. When high-emissivity coating emissivity fails by 40%, the 3–5 μm band intensity decreases by about 15.38%, and the 8–14 μm band intensity decreases by about 12.67%.

1. Introduction

Hypersonic glide vehicles (HGVs) are pivotal in contemporary warfare due to their remarkable maneuverability and ability to penetrate defenses. Examples include Russia’s Dagger [1] missile, the United States’ Hypersonic Technology Vehicle (HTV-2) [2], and Iran’s Fattah [3] missile. During the gliding reentry phase, these missiles encounter complex physical phenomena, such as intricate dissociation and ionization reactions within the shock layer gas at the missile’s nose and in the separation and expansion region at the tail. These non-equilibrium processes cause the high-temperature gas components in the missile’s flow field to emit ultraviolet and infrared spectrum radiation. These radiation signals are critical for early warning systems (EWSs), target identification and tracking, and mitigating radiation noise in optical windows.

Understanding the spectral radiation characteristics of hypersonic missiles requires a comprehensive grasp of the principles and mechanisms governing radiation sources. Kumar and Bansal [4] introduced a novel spectral model based on the k-distribution, which they integrated with a hypersonic flow solver in OpenFOAM-v1706 to simulate heat transfer over a Martian entry vehicle. They modeled the non-gray radiative properties of shock layer gases using the Emission-weighted Full Spectrum k-distribution (EFSK) method, highlighting that radiative heat flux dominates over convective heat at high Mach numbers. Kozlov et al. [5,6] utilized the detonation-driven shock tube DDST-M to measure the radiation properties of high-temperature gases at a pressure of 0.25 Torr ahead of the shock wave, covering shock wave velocities from 7.7 to 11.4 km/s. They proposed a new spectral model for the line-by-line (LBL) calculation of atomic and molecular emission and absorption spectra. Binauld et al. [7,8] proposed a numerical simulation approach for computing infrared radiation from exhaust plumes and multiphase flows of alumina particles using a two-dimensional model of the Antares II rocket. They created a CO₂ non-equilibrium infrared radiation model and examined the changes in infrared radiation under varying engine intake conditions that included alumina particles. Niu et al. [9] performed simulations of ultraviolet spectral radiation in the shock layer at the nose of a bow shock ultraviolet (BSUV) aircraft within the 200–400 nm wavelength range. They compared shock waves at altitudes of 38 km, 53.5 km, and 71 km, discovering that the ultraviolet radiation intensity at the nose was notably higher at an altitude of 38 km than under other conditions. Fu et al. [10,11] employed an equilibrium temperature model to study aerodynamic heat and infrared radiation characteristics of hypersonic aircraft during the operation of the reaction control system.

In existing research, the LBL model achieves high accuracy in calculating gas radiation. However, the time consumption in practical calculations is unacceptable. There are few reports in the literature on the statistical narrow-band (SNB) model for non-equilibrium gas radiation. The accuracy of the existing Reverse Monte Carlo Method (RMCM) also requires improvement. Since the radiation intensity of real and scaled models does not satisfy the similarity assumption, the conclusions about the radiation characteristics of scaled models in existing studies are not applicable to full-scale models. To thoroughly understand the spectral radiation characteristics of hypersonic targets, this study addresses the limitations of existing research. It focuses on a three-dimensional, full-scale hypersonic missile as the subject of investigation. The research integrates the line-of-sight (LOS) method using LBL calculation and an enhanced RMCM employing SNB calculation techniques. The objective is to explore various models, including chemical equilibrium and non-equilibrium, both with and without chemical reactions, catalytic and non-catalytic wall treatments, and failure models of high-emissivity coatings. These factors significantly influence the radiation characteristics of hypersonic missiles. This approach aims to provide a comprehensive analysis of spectral radiation properties, moving beyond simplistic two-dimensional models and localized spectral analysis commonly found in the current literature.

2. Numerical Methodology

2.1. Flow Field Computational Approach

In the numerical simulation of hypersonic flow fields, the Navier–Stokes (N-S) [12] equations incorporating chemical reaction source terms are utilized. These equations can be expressed in a dimensionless form as follows:

$${\displaystyle \frac{\partial Q}{\partial t}}+{\displaystyle \frac{\partial F}{\partial x}}+{\displaystyle \frac{\partial G}{\partial y}}+{\displaystyle \frac{\partial H}{\partial z}}=\left({\displaystyle \frac{\partial F_{\mathrm{v}}}{\partial x}}+{\displaystyle \frac{\partial G_{\mathrm{v}}}{\partial y}}+{\displaystyle \frac{\partial H_{\mathrm{v}}}{\partial z}}\right)+W$$

(1)

where $Q$ denotes the vector of conserved quantities, $Q={\left[\rho ,{\rho }_{\mathrm{s}},\rho u,\rho v,\rho w,E_{\mathrm{ve},\mathrm{m}},E\right]}^{\mathrm{T}}$, $\rho$ represents the mass density of the fluid, ${\rho }_{\mathrm{s}}$ stands for the partial density of species $\mathrm{s}$, $E_{ve,m}$ represents the vibrational electron energy of the mixture, and $E$ denotes the total energy of the mixture; $F$, $G$, $H$ and $F_{\mathrm{v}}$, $G_{\mathrm{v}}$, ${\mathit{H}}_{\mathit{v}}$ represent the inviscid flux vectors in the x, y, and z directions, respectively; $W$ denotes the vector of non-equilibrium source terms for chemical reactions, $W={\left[0,{\omega }_{\mathrm{s}},0,0,0,{\omega }_{\mathrm{v},\mathrm{m}},0\right]}^{\mathrm{T}}$, ${\omega }_{\mathrm{s}}$ is the rate of net mass production for species $\mathrm{s}$, and ${\omega }_{\mathrm{v},\mathrm{m}}$ is the term representing vibrational energy sources.

A fully catalyzed wall does not account for the mass fraction of components present at the wall. In contrast, a non-catalyzed wall considers the mass fraction near the wall as an equilibrium value under local wall pressure and temperature. Hypersonic missile bodies typically use high-emissivity coating materials and thermal insulation interlayers on the wall surface. The surface temperature is established through thermal radiation equilibrium:

$$q_{\mathrm{w}}=\epsilon \sigma T_{\mathrm{w}}^4$$

(2)

where $q_{\mathrm{w}}$ represents the surface heat flux; $\epsilon$ is the radiative emissivity of the surface material; $\sigma$ is the Stefan–Boltzmann constant; $T_{\mathrm{w}}$ denotes the wall temperature.

The cell-centered finite volume method is used for the implicit solution of the Navier–Stokes equations on structured grids. The Advection Upstream Splitting Method (AUSM) is utilized to discretize the convective flux term, while a second-order upwind scheme is employed for the discretization of the viscous flux term. For the prediction of hypersonic flow, the Menter Shear Stress Transport (SST) [13] two-equation model, a widely accepted turbulence model, is adopted. Eucken’s [14] relationship is used to determine the thermal conductivities of species, and Blottner’s [15] curve fits are employed to set the dynamic viscosities of species. The transport coefficients of the mixed gas are determined using Wilke’s [16] semi-empirical formula. The forward and reverse reaction rates are calculated using the Arrhenius [17,18] relationship. The analysis encompasses seven components of partially ionized air (N₂, O₂, NO, N, O, NO⁺, e⁻) and six chemical reactions without considering ablation effects. Parameters for the detailed chemical reaction rate calculations are derived from Surzhikov’s [19] research.

2.2. Gas Radiation Properties Computation Methods

According to established research findings, particles in high-energy and low-energy states at the equilibrium temperature $T$ follow the Boltzmann distribution. Parameters required for calculating line intensities at the equilibrium temperature $T$ can be found in the high-temperature molecular spectroscopic database (HITEMP2010) [20]. The specific equation [21] is as follows:

$$S_{\nu }(T)=S_{\nu }\left(T_{\mathrm{ref}}\right)·{\displaystyle \frac{Q_{\mathrm{tot}}\left(T_{\mathrm{ref}}\right)}{Q_{\mathrm{tot}}(T)}}·{\displaystyle \frac{\exp (-c_2{E}^{″}/T)}{\exp (-c_2{E}^{″}/T_{\mathrm{ref}})}}·{\displaystyle \frac{1-\exp \left(-c_2{\nu }_0/T\right)}{1-\exp \left(-c_2{\nu }_0/T_{\mathrm{ref}}\right)}}$$

(3)

where $S_{\nu }\left(T_{\mathrm{ref}}\right)$ is the line intensity at 296 K in the database, $E^{″}$ denotes the lower state energy, ${\nu }_0$ denotes the center wave number of the line, $Q_{\mathrm{tot}}(T)$ represents the total internal partition sums at temperature $T$, and $c_2$ denotes the second radiation constant.

Under non-equilibrium conditions, neglecting the coupling between molecular rotational and vibrational states, the total internal partition function [22] of a molecule can be expressed as the product of the vibrational partition function $Q_{\mathrm{v}}$ and the rotational partition function $Q_{\mathrm{r}}$:

$$Q_{\mathrm{tot}}(T)=Q_{\mathrm{v}}\left(T_{\mathrm{v}}\right)·Q_{\mathrm{r}}(T)=({\displaystyle \sum _v{g}_v{e}^{-\frac{E_{\mathrm{vib}}(v)}{k{T}_{\mathrm{vib}}}}})·({\displaystyle \sum _J{g}_s{g}_i{g}_J{e}^{-\frac{E_{\mathrm{rot}}(J)}{k{T}_{\mathrm{rot}}}}})$$

(4)

where $g_s$ is the state-dependent weight, $g_i$ is the state-independent weight, $g_v$ is the degeneracy of the vibrational levels, $g_J$ is the degeneracy of the rotational levels. $E_{\mathrm{vib}}(v)$, $E_{\mathrm{rot}}(J)$ are the vibrational energy and rotational energy of molecules, respectively. The rovibrational energy levels of molecules are calculated with a coupled rotating vibrator model using Dunham [23] expansions.

The absorption coefficient of each gas at a specific wavenumber $\nu$ is influenced by all spectral lines at that wavenumber. Therefore, the total absorption coefficient [21] can be calculated by summing the contributions of each individual absorption coefficient:

$${\kappa }_{\nu }=\sum _i{\kappa }_{\nu ,i}=\sum _i{S}_{i}F\left(\nu -{\nu }_{0,i}\right)N_{\mathrm{d}}$$

(5)

where ${\kappa }_{\nu ,i}$ is the absorption coefficient of $\nu$, ${\nu }_{0,i}$ is the center wave number of the $i$ spectral line, $S_i$ is the integrated line intensity of one molecule, $F\left(\nu -{\nu }_{0,i}\right)$ is the line shape function, and $N_{\mathrm{d}}$ is the number density.

Molecular radiation theory asserts that each transition produces a discrete line, representing vibrational, rotational, or electronic transitions within the molecule. The radiation in the ultraviolet band results from electronic excitation transitions. Consequently, the line absorption coefficient [24] is expressed as follows:

$${\kappa }_v={\displaystyle \frac{8{\pi }^3{v}_0}{3hc}}·{\displaystyle \frac{N_d{\left|{\mathit{R}}_{\mathrm{e}}\left({\mathit{r}}_{v^{\prime },v^{″}}\right)\right|}^{2}q\left(v^{\prime },v^{″}\right)S_{J^{″}{\mathsf{\Lambda }}^{″}}^{J^{\prime }{\mathsf{\Lambda }}^{\prime }}}{2J^{″}+1}}·F\left(\nu -{\nu }_{0,i}\right)$$

(6)

where the single and the double prime represent the upper energy level and the lower energy level, respectively. ${\left|{\mathit{R}}_{\mathrm{e}}\left({\mathit{r}}_{v^{\prime },v^{″}}\right)\right|}^2$ denotes the square of the electronic transition moment, $q\left(v^{\prime },v^{″}\right)$ is the Franck–Condon factor, $S_{J^{″}{\mathsf{\Lambda }}^{″}}^{J^{\prime }{\mathsf{\Lambda }}^{\prime }}$ is the Hönl–London factor with rotational degeneracy in the high-energy state.

2.3. Solving Method of Radiative Transfer Equation

The Reverse Monte Carlo Method (RMCM) is a rapid approach to solving the spectral radiative transfer equation. Its logic involves approximating the target as a radiating point source when the characteristic length of the target is much smaller than the distance to the detector. Thus, the radiation intensity [25] of the target can be expressed as follows:

$$I={\int }_{{\lambda }_1}^{{\lambda }_2}{I}_{\lambda }\mathrm{d}\lambda ={\int }_{{\lambda }_1}^{{\lambda }_2}{H}_{\lambda }·R^2\mathrm{d}\lambda$$

(7)

where $H_{\lambda }$ represents radiation illumination on the detector surface $R$ denotes the distance to the detector, and ${\lambda }_1$, ${\lambda }_2$ are the lower and upper limit, respectively.

The Reverse Monte Carlo Method replaces discrete solid angles with uniformly emitted $N$ rays within the spatial solid angle. These rays are then tracked for absorption probabilities using a probability density function, resulting in statistically significant radiation calculations. Therefore, the radiation illumination $H_{\lambda }$ can be expressed as follows:

$$H_{\lambda }=\sum _{i=1}^N\left(L_{\mathrm{b}\lambda }(i)\cos {\theta }_i/N\right)·{\Omega }_{\mathrm{d}}$$

(8)

where $L_{\mathrm{b}\lambda }(i)$ represents the blackbody spectral radiance calculated from the local temperature at the point where a random ray is absorbed, ${\theta }_i$ is the angle between the random ray and the normal of the detection surface, $N$ denotes the ray number, and ${\Omega }_{\mathrm{d}}$ is the solid angle. Due to the significant distance between the detection point and the target, $\cos {\theta }_i\approx 1,{\Omega }_{\mathrm{d}}=A_{\mathrm{d}}/R^2$. where $A_{\mathrm{d}}$ is the area of the target as seen when projected onto the plane perpendicular to the detection direction. Therefore, Equation (7) can be further written as follows:

$$I={\int }_{{\lambda }_1}^{{\lambda }_2}{A}_{\mathrm{d}}\sum _{i=1}^N{L}_{\mathrm{b}\lambda }(i)/N\mathrm{d}\lambda$$

(9)

The LBL method is known for its precise computation of gas radiation intensity, but its computational efficiency is low, especially for targets with numerous complex grids, making the required computational time unacceptable. Consequently, the SNB model [26] is commonly employed as an alternative to LBL. The equation for calculating radiation intensity in the narrow-band model is given as follows:

$$I=A_{\mathrm{d}}·\mathsf{\Delta }\lambda ·\sum _{j=1}^M\sum _{i=1}^N{L}_{\mathrm{b}\lambda }\left(i,{\lambda }_j\right)/N$$

(10)

where $\mathsf{\Delta }\lambda$ represents the computed spectral bandwidth, and $M$ represents the number of discrete points within the spectral bandwidth.

2.4. Enhancements in Ray Tracing Methods in RMCM

Figure 1 is a schematic diagram of the RMCM program’s computational process. The grid discretization of the computational domain supports tetrahedral, hexahedral, and polyhedral meshes. At the start of the calculation, it is assumed that rays are emitted from the detector and pass through the grid domain where the target is located. During ray tracing, each ray is calculated based on the absorption and reflection coefficients of gases, solids, and particles. Rays may be absorbed, reflected, or exit the computational domain. Finally, according to the reciprocity principle of radiation transmission, the absorption points of the rays are treated as radiation sources, and the radiation contributions along the ray paths are calculated. This results in the determination of the target’s radiation intensity. Figure 2 shows the distribution of horizontal and pitch detection angles.

Due to the large number of rays required for computation in the RMCM method, Chen [27] and Gao [28] introduced ray tracing techniques into the RMCM program to enhance computational efficiency. However, this method’s algorithm for generating detection points uses a pseudo-random number generator, which results in a correlation between the computational accuracy of the RMCM program and the unbiased distribution (uniformity) of pixel detection points. Pseudo-random numbers have the drawback of clustering within specific subintervals, reducing the uniformity of detection points and affecting the computational accuracy of the RMCM program.

To address the shortcomings in the generation of detection points in the RMCM program, this paper proposes a method using Low-Discrepancy Sequence [29] (LDS) to generate pixel detection points. Since LDS have better unbiased distribution characteristics compared to pseudo-random numbers, they can achieve higher spectral radiation calculation accuracy under the same number of detection points. Figure 3 compares the generation of 20, 50, and 100 seeds in a two-dimensional random number interval using both methods. It is evident that the LDS method exhibits significantly higher uniformity compared to the PRNG method.

The uniformity of the two methods can be measured by calculating the numerical integration error:

$$s_n=\left|A-A_n\right|$$

(11)

where $A={\int }_0^{1}f(x)\mathrm{d}x$, $A_n={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n}f\left(x_i\right),x_i\in [0,1]$, $f(x)=\exp \left(-x^2/2\right),x\in [0,1]$.

From the comparative error regression analysis of the two methods in Figure 4, it is evident that the integration error of the PRNG algorithm fluctuates significantly and lacks consistency, whereas the LDS method demonstrates better consistency in its error. This proves that LDS maintains good uniformity across different seed magnitudes.

LDS has been incorporated into the RMCM computational program (NPUIR-v1.0) to compute the backward infrared radiation of a typical aerospace engine nozzle mixer, as depicted in Figure 5. The figure contrasts the infrared radiation images computed by both methods. It is apparent that the LDS method yields sharper edge contours, particularly in imaging high-temperature components. Using a high-density infrared radiation intensity image (1204 × 1768 pixels) as the reference, the root mean square error (RMSE) [30] between the infrared radiation images of the two models and the reference image is compared to quantify the errors of both methods. A smaller RMSE for the same pixel condition indicates higher computational accuracy. As shown in Figure 5, the RMSE of the LDS model is lower than that of the PRNG model at different pixel densities, indicating that the LDS model has higher computational accuracy. Additionally, the graph illustrates the computational time required by both methods for pixel discretization, with LDS demonstrating lower time requirements compared to PRNG, especially at higher pixel densities. This underscores the superior computational efficiency of the LDS method over PRNG.

Based on the above computational theories, this research developed a gas radiation calculation program and a target radiation transfer calculation program. Both programs were written in C++ using the Visual Studio 2017 development platform.

3. Model Validation

3.1. Validity of Hypersonic Flow Field Parameters

The reliability verification of the flow field parameter solver is conducted for the hypersonic aircraft ELECTRE [31], based in Noordwijk, Holland. The flight test occurred at approximately 53.3 km altitude and Mach 13 speed at time 293 s. The chemical reaction equations were modeled using the well-known Park 5 air species reaction model [17]. The wall temperature, based on measurements, was set at a constant 343 K, with wall catalysis modeled under both non-catalytic and fully catalytic conditions. When the boundary condition of the wall adopts the fully catalytic wall model, O and N produced by the dissociation of air near the wall will undergo recombination reactions to form O₂ and N₂. In contrast, with the non-catalytic wall model, no reactions occur among the gas components near the wall.

Figure 6a shows a comparison between the computed missile wall heat flux in this paper and the flight test data. The heat flux density on the fully catalytic wall is higher than on the non-catalytic wall. The measured parameters at the nose cone align well with the results from the non-catalytic wall, whereas those at the rear wall correlate better with the fully catalytic wall results. The heat flux at the stagnation point of the fully catalytic wall model and the non-catalytic wall model are approximately 949.79 kW/m² and 814.31 kW/m², respectively. Figure 6b compares the computed trans-rotational temperature (T_tr) and vibro-electronic temperature (T_ve) in the missile shock layer with the numerical results from the literature. The computed data show good agreement with the reference data. Overall, this validates the high accuracy of the flow field parameter solver utilized in this study.

3.2. Reliability of Radiative Physical Data

The primary source of ultraviolet radiation in the hypersonic shock layer comes from the excited state transitions γ (${\mathrm{A}}^2{\mathsf{\Sigma }}^{+}\to {\mathrm{X}}^2{\mathsf{\Pi }}_r$) and β (${\mathrm{A}}^2{\mathsf{\Sigma }}^{+}\to {\mathrm{X}}^2{\mathsf{\Pi }}_r$) of NO molecules. The BSUV-II [32] flight test, conducted at an altitude of 38 km and a speed of Mach 11, provides measurements of ultraviolet radiation intensity. This intensity, measured by a spectrometer directed toward the head bow shock wave along the stagnation line, serves to validate the accuracy of the computational program discussed in this article. Figure 7a compares the spectral radiation intensity between calculated and measured values in the 200–400 nm band. The figure shows variations in peak positions, trough positions, and spectral radiation intensity values between the program’s calculations and measurements. These variations can be attributed to simplifications in the modeling of the hypersonic flow field and uncertainties in incoming flow conditions. Despite these variations, the computational program demonstrates accuracy in predicting ultraviolet radiation within this spectral band.

Laux et al. [33] conducted measurements of the infrared radiation spectrum emitted by high-temperature plasma NO gas in the 4.9–5.6 μm band. The plasma operated at 1 atm pressure with a maximum temperature of 3400 K. Spectrometer measurements accounted for H₂O gas absorption along the measurement path. Figure 7b compares the spectral radiation intensity between the program’s calculated values and the measured values in the 4.9–5.6 μm band. The spectral intensity values show a relatively consistent agreement. Errors occur at certain wavenumber positions in the spectrum due to the absence of consideration for H₂O molecule absorption along the measurement path in the calculations. According to the literature findings [33], the blue markers in the figure indicate all absorption peaks of H₂O. Given that this article does not account for gas path absorption, the radiation intensity calculated by the program remains credible.

The program for solving the radiative transfer equation is validated using spectral radiation measurements of the exhaust plume from a small solid rocket motor (BEM-2) [34]. The plume of the solid rocket motor contains gases such as CO₂, CO, H₂O, and HCl. The experiment considers a detector–target distance of 0.8 m, accounting for the effects of radiation absorption along this path. The comparison between the calculated results and the measured values is depicted in Figure 8. It is evident that within the 1.5–5.5 μm wavelength range used by the radiometer, the calculated values closely match the measured radiation peaks near 2.7 μm and 4.3 μm. Additionally, the integrated radiation error within this wavelength band is approximately 3.63%, demonstrating the high computational accuracy of the program.

4. Results and Discussion

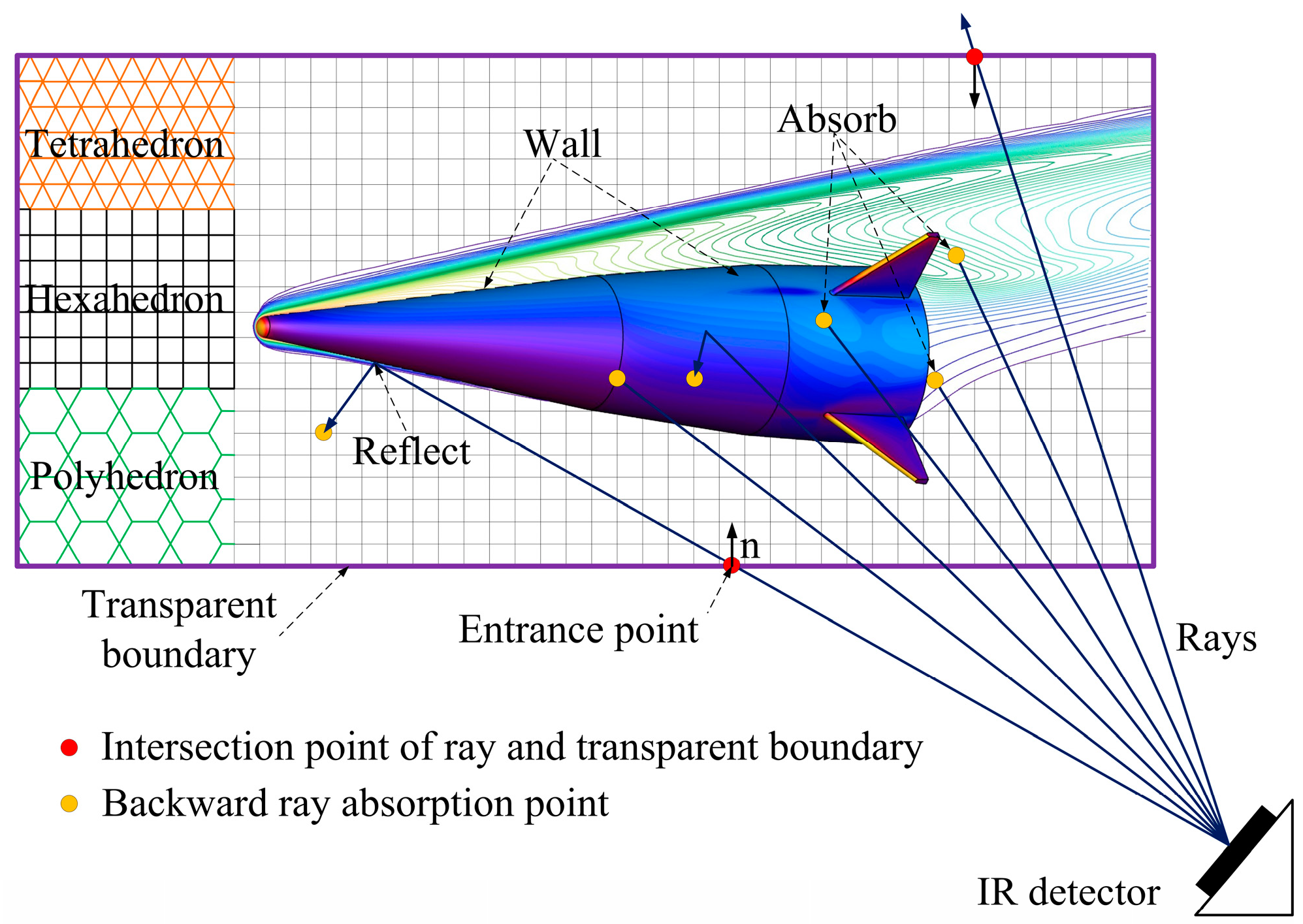
4.1. Mesh and Boundary

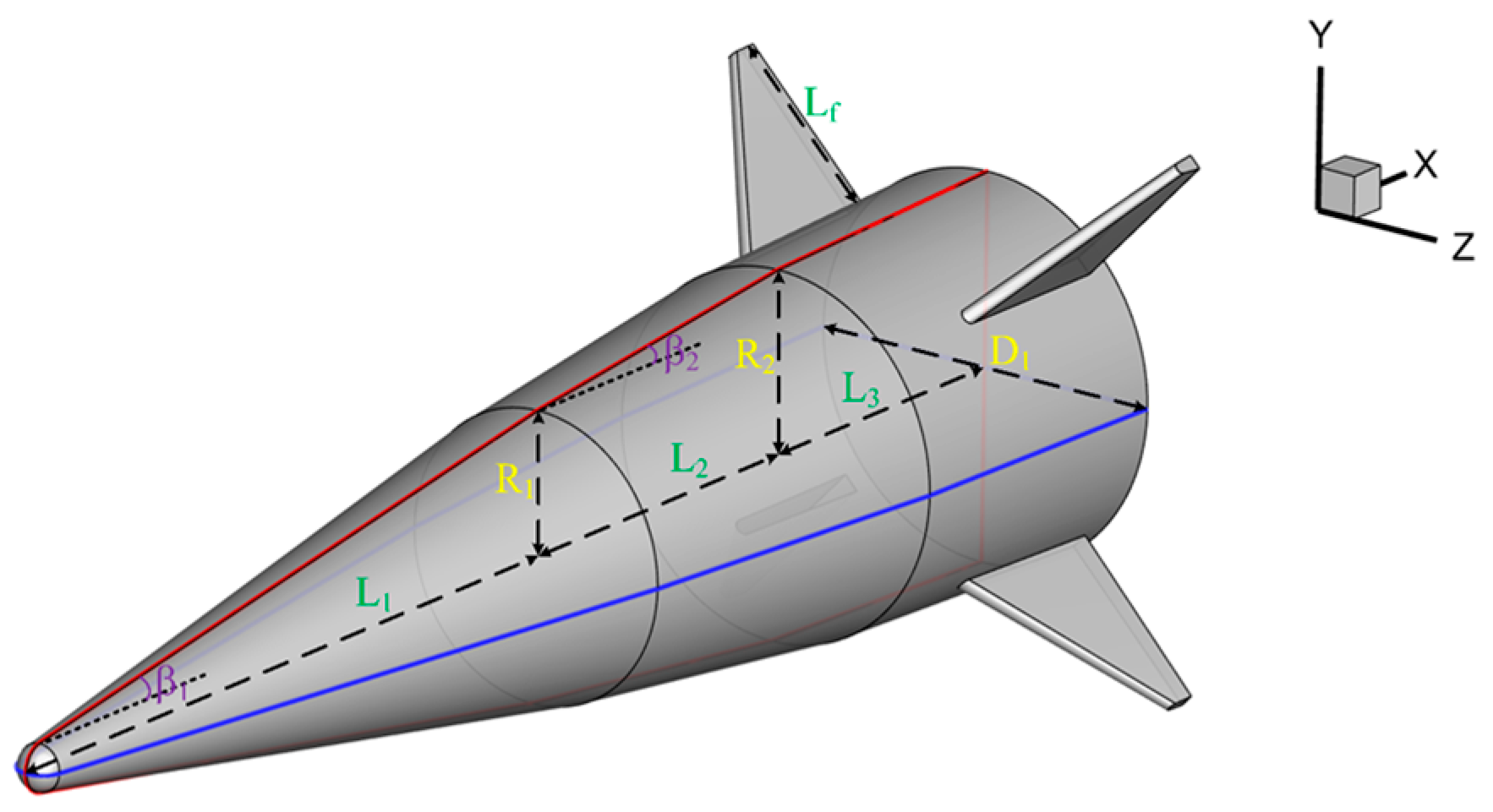
The study concerns a physically simplified model of the typical conical missile “Fattah” [3]. Figure 9. depicts the geometric structure of the simplified missile model, with specific dimensional parameters detailed in

Table 1. Dimensions of the Fattah missile model.

Parameter	Value
Total missile length (m)	3.4
Front cone length L1 (m)	1.72
Rear cone length L2 (m)	0.78
Cylinder length L3 (m)	0.7
Front cone radius R1 (m)	0.3
Rear cone radius R2 (m)	0.4
Cylinder diameter D1 (m)	0.8
Fin height Lf (m)	0.38

. This research aims to explore intrinsic radiation and flow field radiation of hypersonic vehicles, excluding the propulsion solid rocket motor from all physical models.

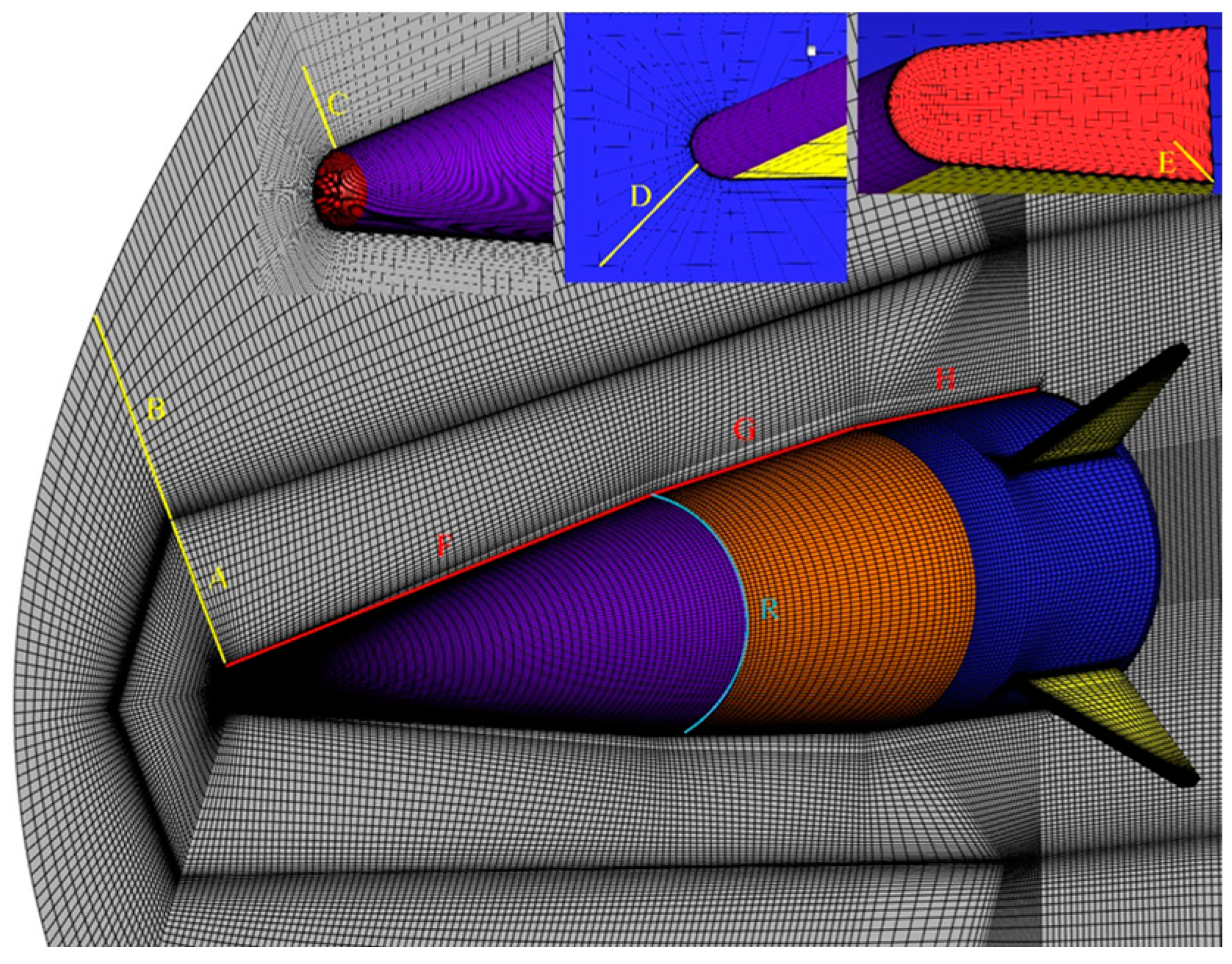
In the finite volume method, hexahedral grids are advantageous for achieving convergence in flow field calculations. As shown in Figure 10, the computational domain is divided into multiple topological blocks to discretize space effectively. “Y”-shaped grid areas were utilized near the missile body and fin to segment the ring wall. The far-field region of the missile is segmented using a “C”-type grid, while an “O”-type grid discretizes the boundary layer near the missile’s surface. The hyperbolic tangent spacing function controlled the distribution of grid points along all block grid connection lines, ensuring a growth rate of less than 1.2 between grid points. Control line locations between coarse, medium, and dense grids are marked in Figure 10 and are further illustrated in Figure 11.

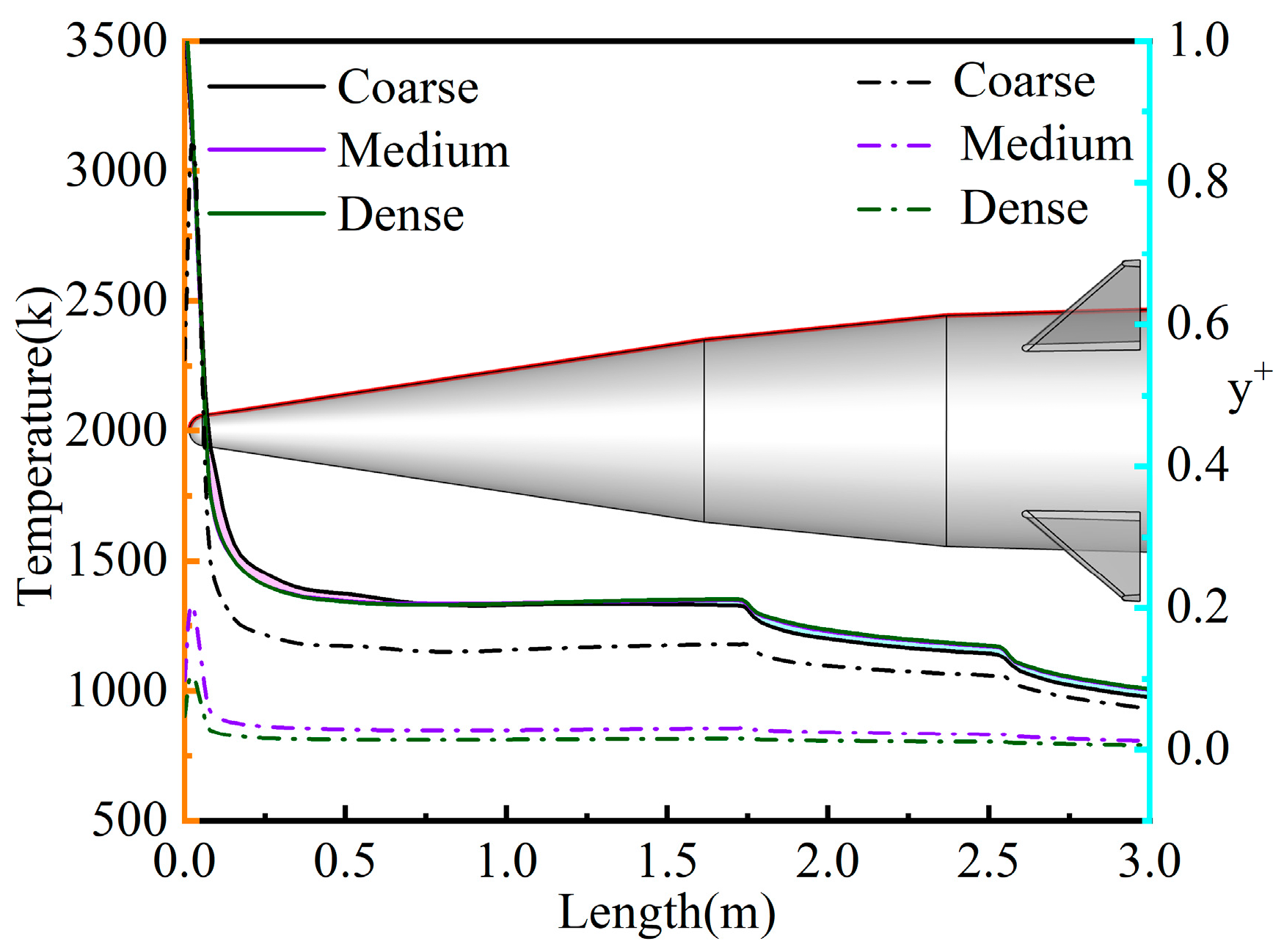
Based on the discretization of grid control points shown in Figure 10, the entire flow domain of the missile is segmented into three mesh configurations for subsequent independent mesh convergence testing: a coarse mesh (2.5 million cells), a medium mesh (3.8 million cells), and a dense mesh (5.5 million cells). Analysis of the missile’s surface wall temperature revealed that the coarse grid model overestimated the temperature in the 0–1 m range and underestimated it in the 1–3 m range. Additionally, the coarse grid model exhibited significantly higher wall y⁺ values compared to the medium and dense grid models. However, differences in wall temperature and wall y⁺ values between the dense and medium mesh models were minimal. Based on the above comparison, while considering the accuracy of flow field parameter calculations, it is advisable to select a medium mesh for discretizing the missile flow field domain, aiming to improve computational efficiency from the perspective of computing resources.

In the analysis of a hypersonic missile’s trajectory [3], the operating conditions are set with a flight speed of 15 Mach and a flight altitude of 50 km. Due to the limited scope of this study, the effects of changes in the angle of attack are temporarily disregarded, assuming a constant angle of attack of 0°. Four calculation models are taken into account: Non-equ, Equ, No-reac, and Cat-W models. The parameters of the far-field free flow and calculation models are detailed in

Table 2. Freestream conditions and calculation models for hypersonic missile.

Item	Value
Altitude (km)	50
Velocity (m/s)	4947
Mach number	15
Pressure (Pa)	79.779
Temperature (K)	270.7
Non-equ	Non-equilibrium temperature + Reaction
Equ	Equilibrium temperature + Reaction
No-reac	Non-equilibrium temperature
Cat-W	Non-equilibrium temperature + Reaction + Catalytic wall

.

4.2. Aerodynamic Analysis of Different Calculation Models

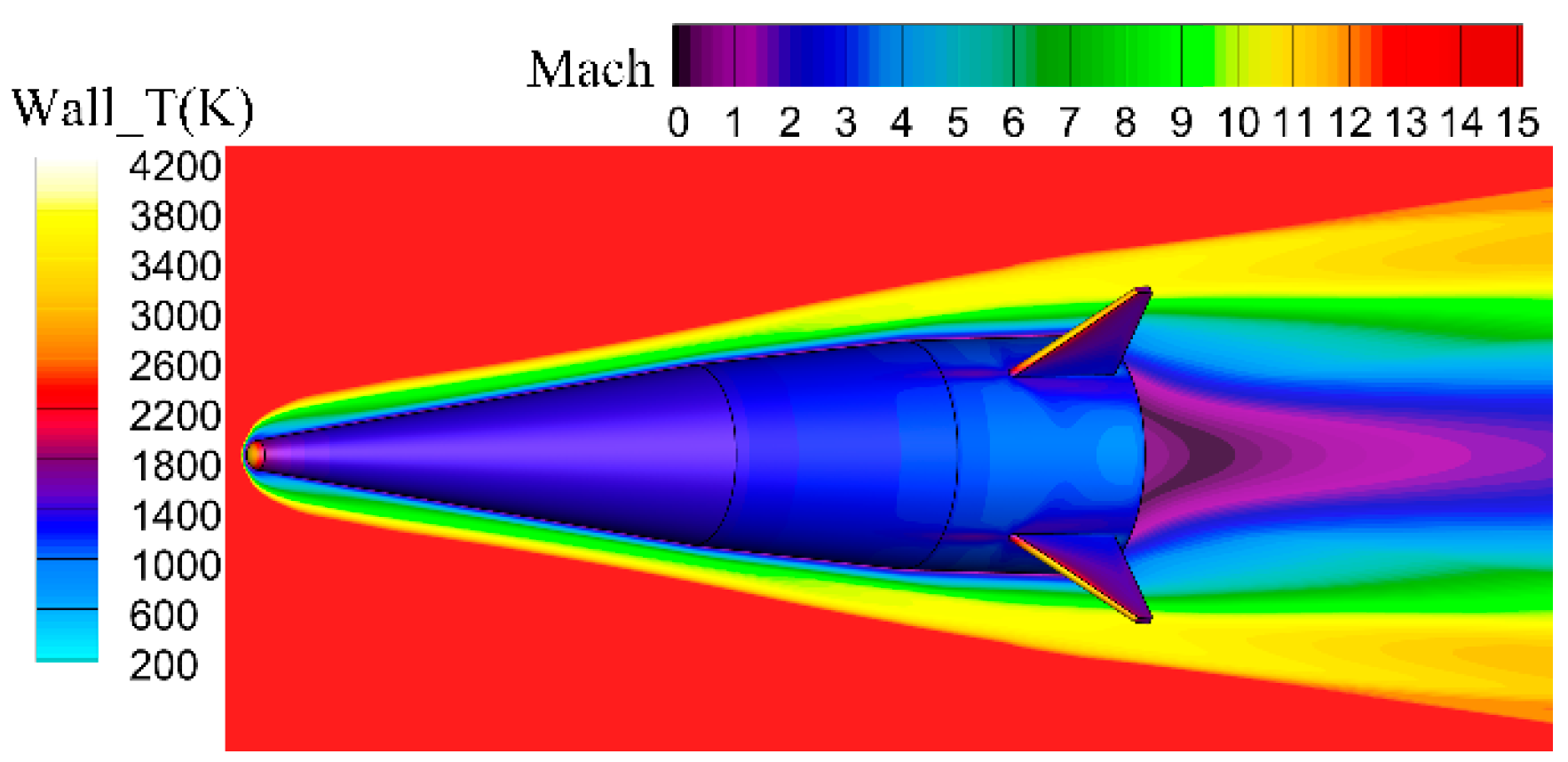
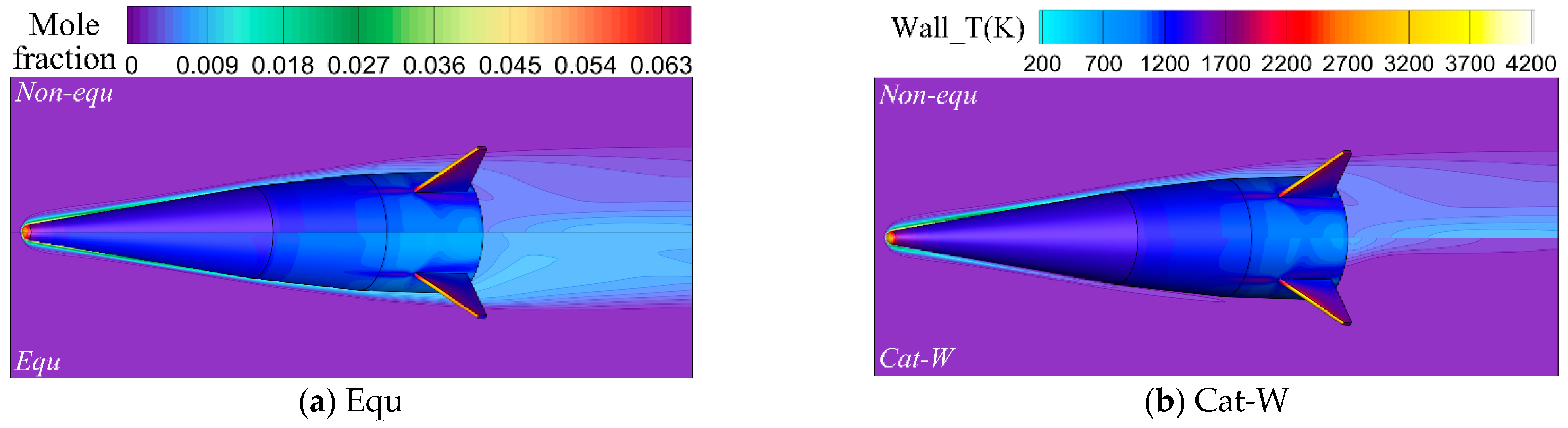
Figure 12 presents the Mach number and wall temperature distribution for the Non-equ model. Figure 12 reveals high-temperature areas on the nose cone head and the windward head wall of the fin, resulting from the aerodynamic heating of the high-temperature airflow in the missile head’s strong shock wave layer. The nose cone head’s wall surface reaches a maximum temperature exceeding 4000 K. High-emissivity coatings and thermal insulation materials at these locations induce an ablation effect, reducing the head wall surface temperature and providing missile protection. The front cone’s wall temperature ranges between 1500 and 2000 K, while the rear cone’s wall temperature lies between 1000 and 1500 K. Most of the cylinder’s wall surface maintains a temperature below 1000 K, with a temperature around 1500 K appearing near the fin’s root. The missile’s wall temperature distribution satisfies the endurance limit temperature requirements of existing thermal protection materials [35].

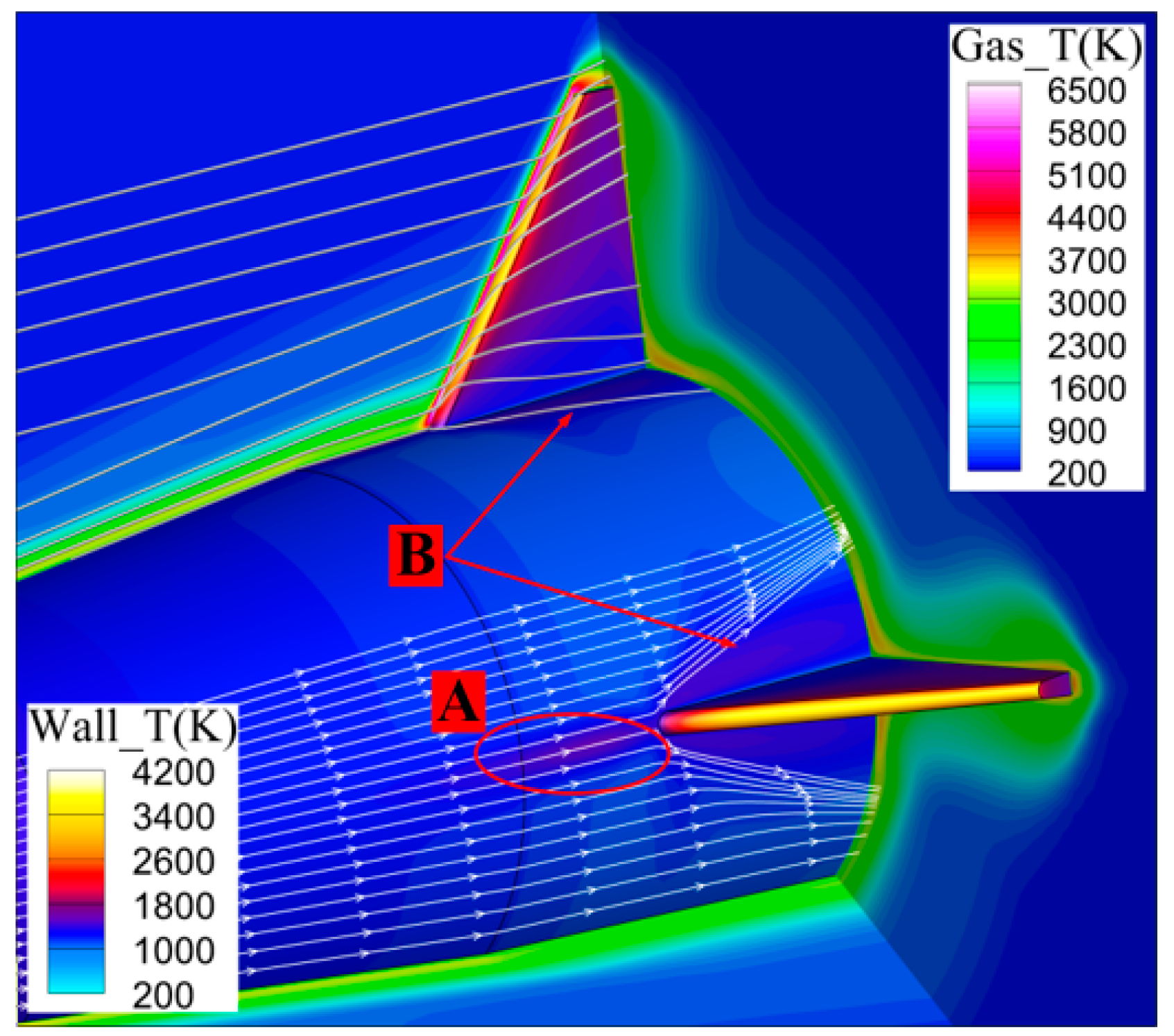
Figure 13 illustrates the flow field structure near the missile tail for the Non-equ model. A strong shock layer exists at the windward head of the fin, leading to a high-temperature area due to the radiative heating of the fin’s wall surface by the high-temperature shock layer. The high-temperature wall surface of the fin also radiates heat to the surrounding space airflow and solid wall. Position A, marked in the figure, exhibits a high-temperature wall zone due to the combined effect of the fin head’s strong shock wave aerodynamic heating and high-temperature wall radiation heating. The distribution of space and wall streamlines indicates hypersonic airflow separation on both sides of the fin wall. This separation leads to a decrease in hypersonic airflow speed and an increase in temperature, aerodynamically heating the solid wall near the separation area, marked as position B in the figure.

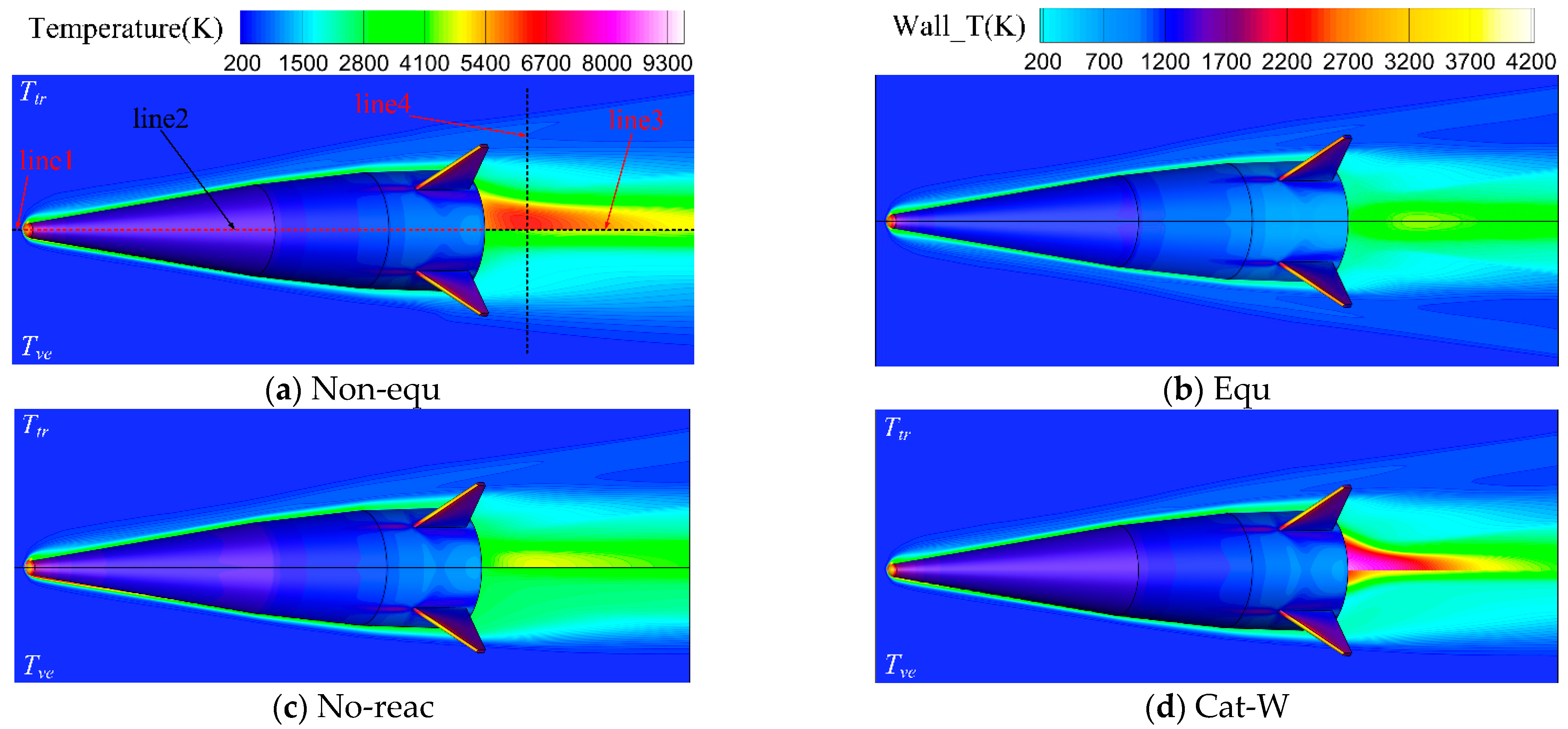
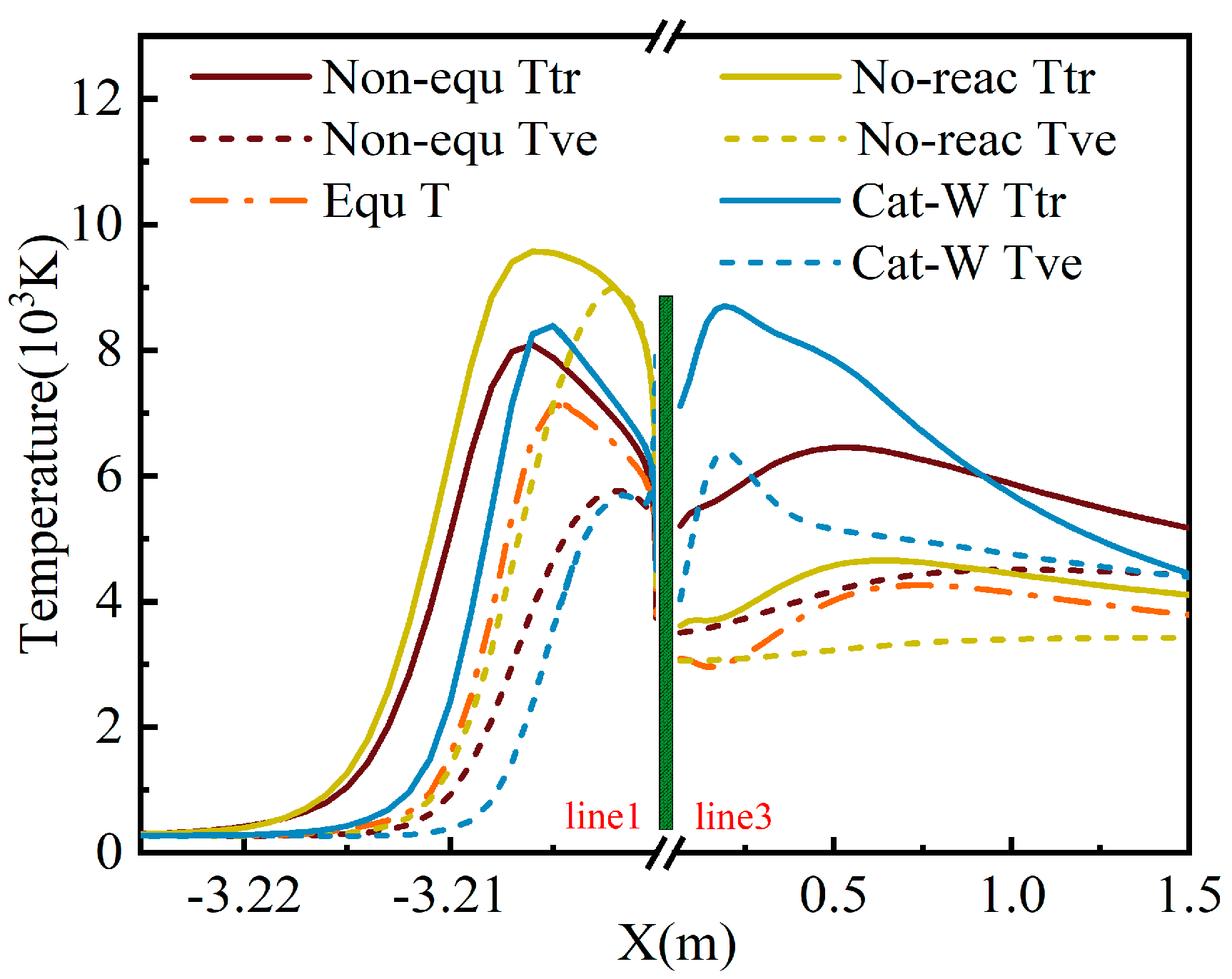
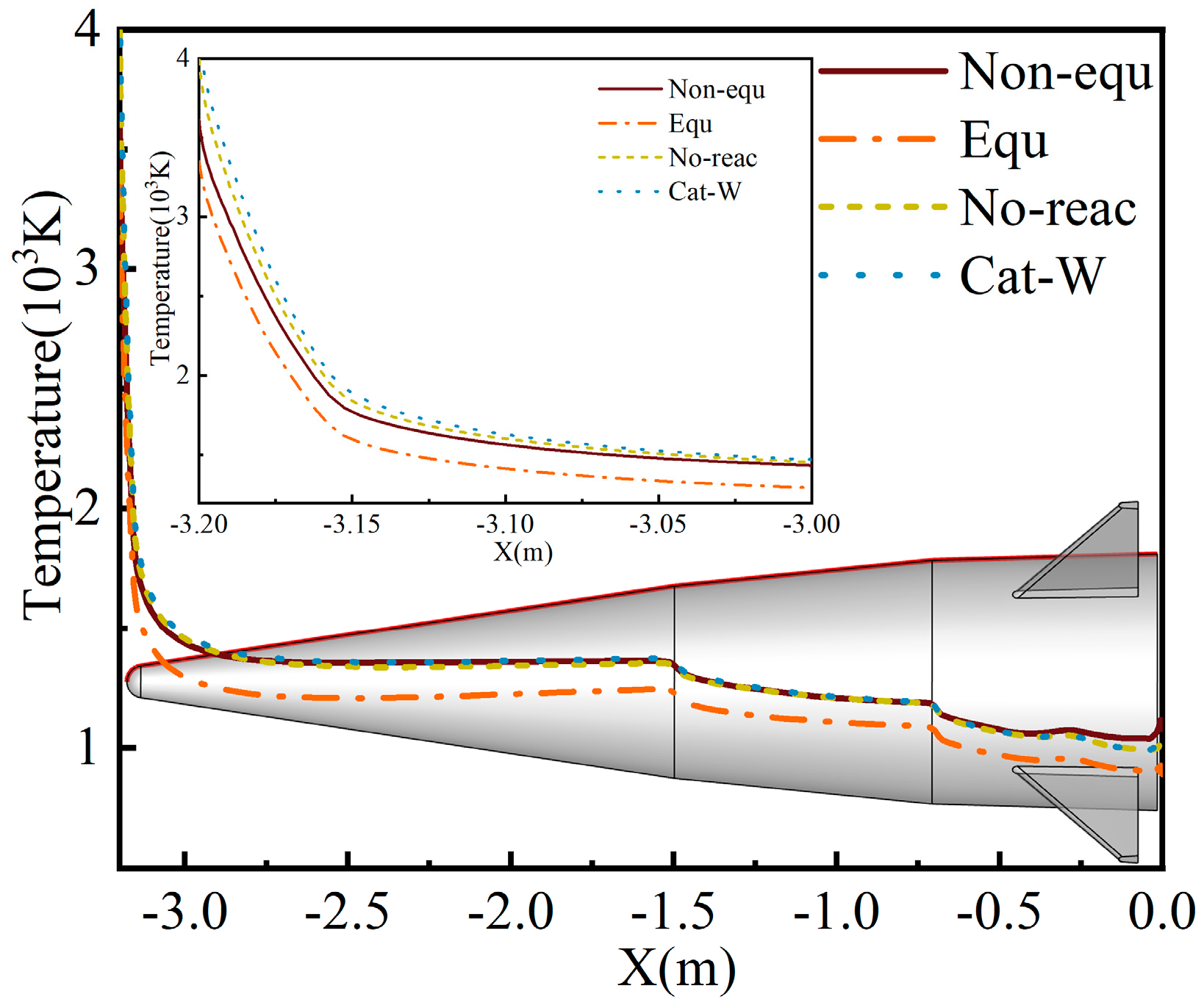
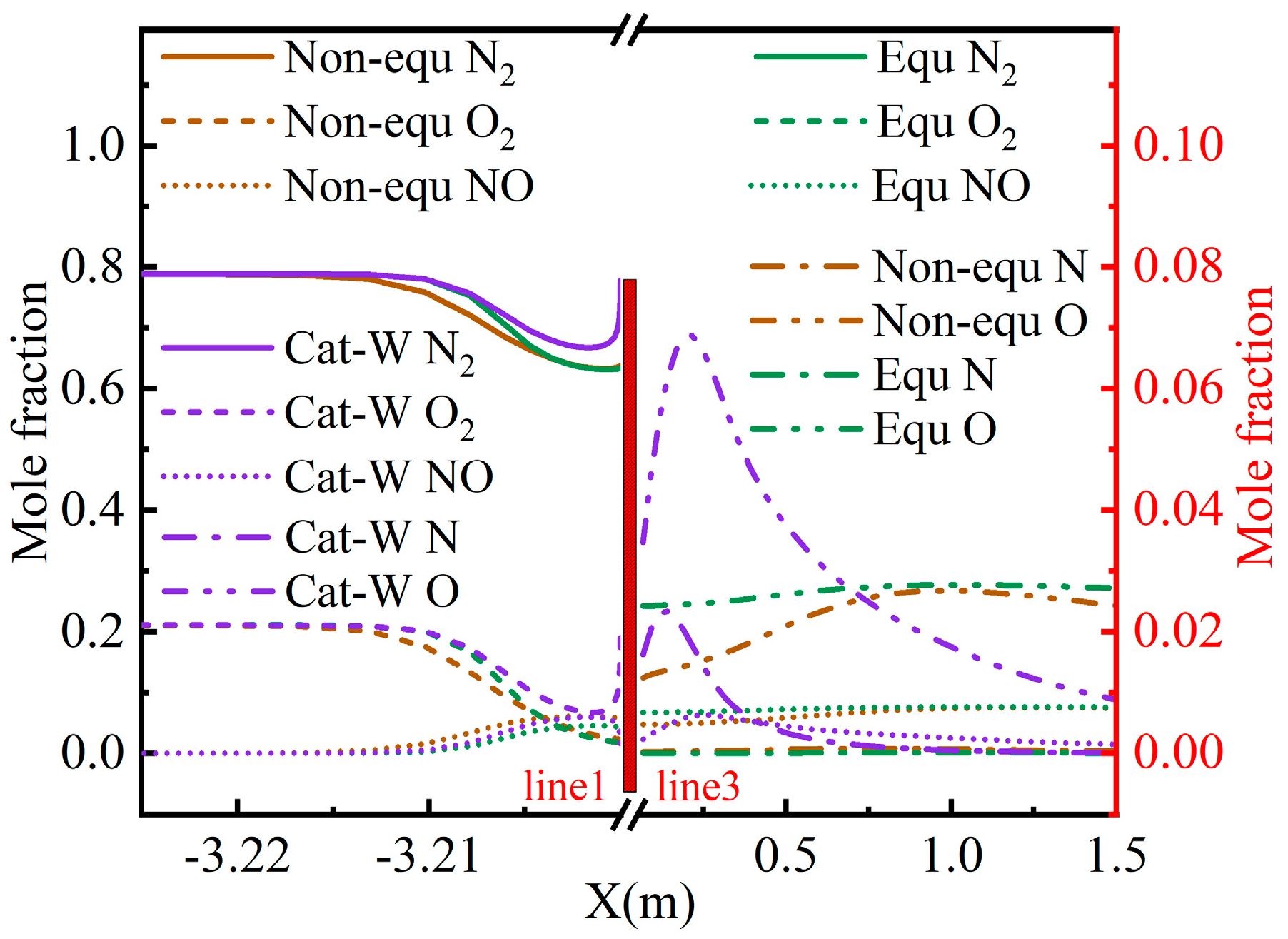
Figure 14 illustrates the flow field and wall temperature distribution of four calculation models. In the figure, line 1 represents the stagnation line along the X-axis at the model’s head, starting from the stagnation point (−3.2, 0.0, 0.0) and ending at (−3.225, 0.0, 0.0). All coordinates in this paper are in meters. Line 2 is the intersection between the model’s surface and the symmetry plane of the computational domain, starting from the stagnation point (−3.2, 0.0, 0.0) and ending at the junction of the cylinder and aft body (0.0, 0.4, 0.0). Line 3 is the characteristic line along the X-axis in the missile separation region, starting at (0.0, 0.0, 0.0) and ending at (1.5, 0.0, 0.0). Line 4 is the characteristic line along the Y-axis in the missile separation region, starting at (0.52, −2.0, 0.0) and ending at (0.52, 2.0, 0.0). Temperature data for line 1 and line 3, marked in Figure 14a, are provided in Figure 15, while the wall temperature distribution for line 2 is presented in Figure 16.

Given the large mean free path of the atmosphere at an altitude of 50 km, the airflow in the missile head’s shock layer and the tail’s separation and expansion zone under a 15 Ma flight condition exhibit significant non-equilibrium effects. In Figure 14a, the maximum T_tr of the gas in the Non-equ model missile head’s shock layer exceeds 8000 K, with a maximum T_ve of approximately 5500 K. The maximum T_tr near the tail’s separation expansion zone is about 6500 K, with T_ve reaching about 4500 K. Comparing Figure 14a,b, the Equ model’s calculated gas temperatures in the flow field are significantly lower than the Non-equ model’s T_tr in both the head and tail regions, and slightly higher than its T_ve. According to the radiant heat balance wall boundary condition, the Non-equ model’s wall temperature will also be higher than that of the Equ model. The difference in wall temperature data distribution between the two is evident in Figure 16.

The dissociation reaction of high-temperature gas in the missile head’s shock layer necessitates energy absorption to break the chemical bonds between molecules. In Figure 14c, the high-temperature shock layer of the No-reac model does not undergo a gas dissociation reaction. Consequently, the T_tr and T_ve on the head stagnation line 1 of the No-reac model are higher than those of the Non-equ model. Conversely, in the missile tail’s separation expansion zone, the NO generation reaction is overall exothermic. Thus, on the separation expansion zone line 3 in Figure 15, the No-reac model’s T_tr and T_ve are lower than those of the Non-equ model. Influenced by the increased temperature of the flow field around the head, the wall temperature data distribution of the No-reac model’s nose cone in Figure 14c andFigure 16 is slightly higher than that of the Equ model.

Compared to the Non-equ model in Figure 14a, the Cat-W model in Figure 14d incorporates a complete catalytic wall model based on the non-equilibrium temperature model. The molecules dissociated in the flow around the wall undergo a polymerization reaction, releasing energy. Consequently, the wall temperature data distribution of the Cat-W model in Figure 14d and Figure 16 is higher than that of the Equ model. According to the radiant heat balance wall boundary condition, the wall heats the surrounding gas through thermal radiation, leading to an increase in the temperature of the gas in the surrounding flow field. Upon reaching radiation heat balance, the temperature of the Cat-W model line 1 in Figure 15 significantly increases near the wall, and the T_tr and T_ve on the tail separation zone line 3 are also significantly higher than the Non-equ model.

As the No-reac model does not generate NO, Figure 17 displays the NO mole fraction distribution for the remaining three models. Figure 18 provides the NO mole fraction distribution for these models at line 1 and line 3 positions. Figure 17a reveals minimal difference in the NO mole fraction in the nose cone between the Non-equ and Equ models. However, the Equ model exhibits an increased NO mole fraction in the flow around the missile. Due to the combined effects of NO transport in the front flow field and NO generation in the tail, the NO mole fraction in the Equ model’s tail separation expansion zone is significantly higher than that of the Non-equ model. In Figure 18, the NO mole fraction on line 1 of the Equ model’s head stagnation line is smaller than that of the Non-equ model. The mole fractions of N₂ and O₂ show little variation, but the O mole fraction on line 3 of the Equ model is significantly larger than that of the Non-equ model. As NO is primarily generated by neutral exchange reactions, the NO mole fraction of the Equ model on line 3 is also significantly higher than that of the Non-equ model. By combining the data in Figure 17a and Figure 18, it can be inferred that the amount of O₂ dissociation in the Equ model’s flow field is higher than that of the Non-equ model. Consequently, more O atoms participate in the neutral exchange reaction, leading to an increase in NO production.

Under the complete wall catalytic boundary condition of the Cat-W model, the dissociated components undergo polymerization reactions near the wall, resulting in a decrease in the NO mole fraction. Therefore, the NO mole fraction in the flow around the Cat-W model missile in Figure 17b is significantly less than that of the Non-equ model. The mole fractions of N atoms and O atoms on line 3 of the Cat-W model in Figure 18 are higher than those of the Non-equ model due to the higher temperature causing increased dissociation of N₂ and O₂ in the extremely small separation core area. This is substantiated by the data in Figure 14d and Figure 15. Generally, the N and O mole fractions in the tail separation expansion zone of the Cat-W model are reduced compared to the Non-equ model, resulting in the NO mole fraction in the tail separation expansion zone of the Cat-W model being noticeably lower than that of the Non-equ model in Figure 17b.

4.3. Radiation Characteristics of Hypersonic Missiles under Different Calculation Models

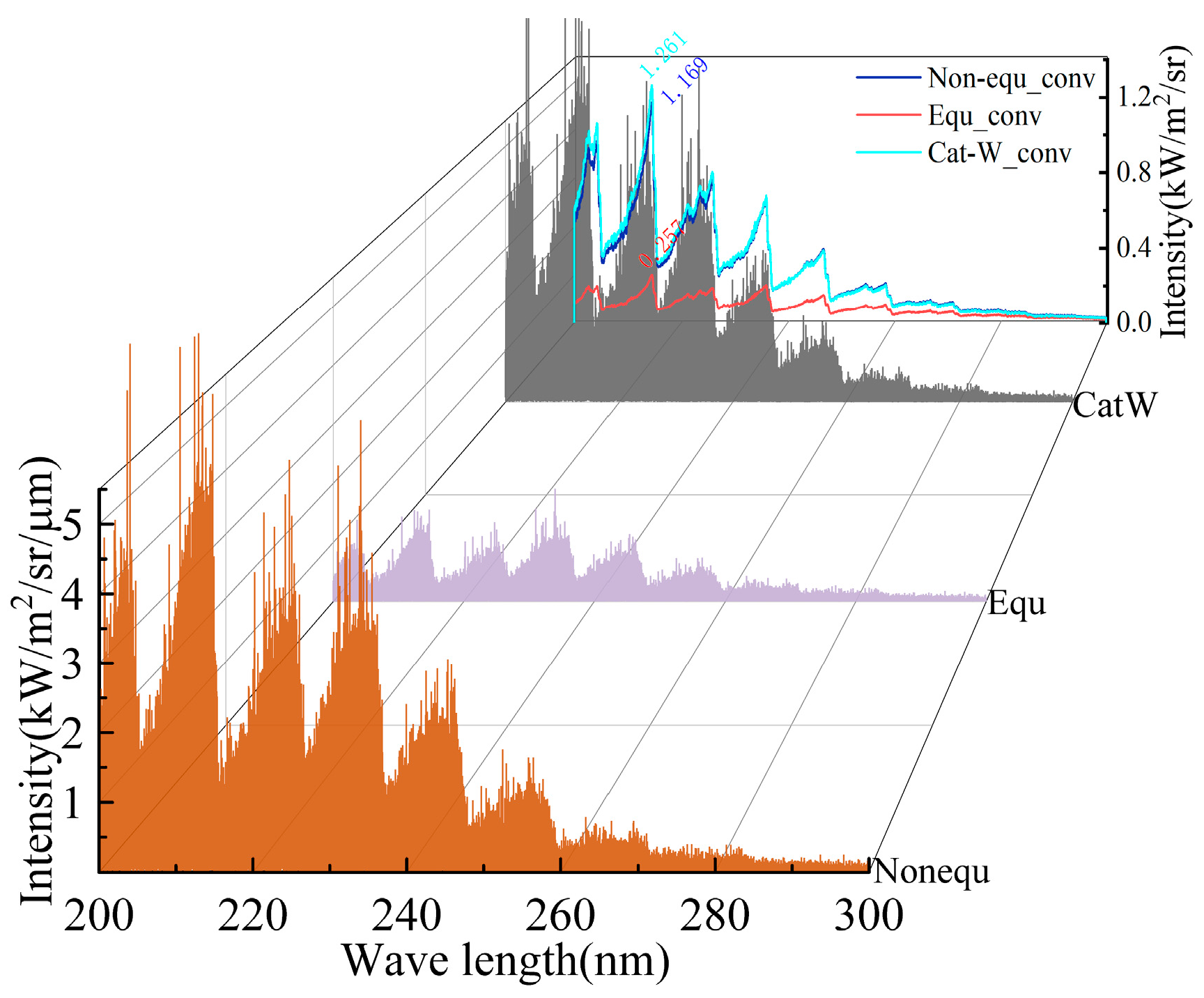
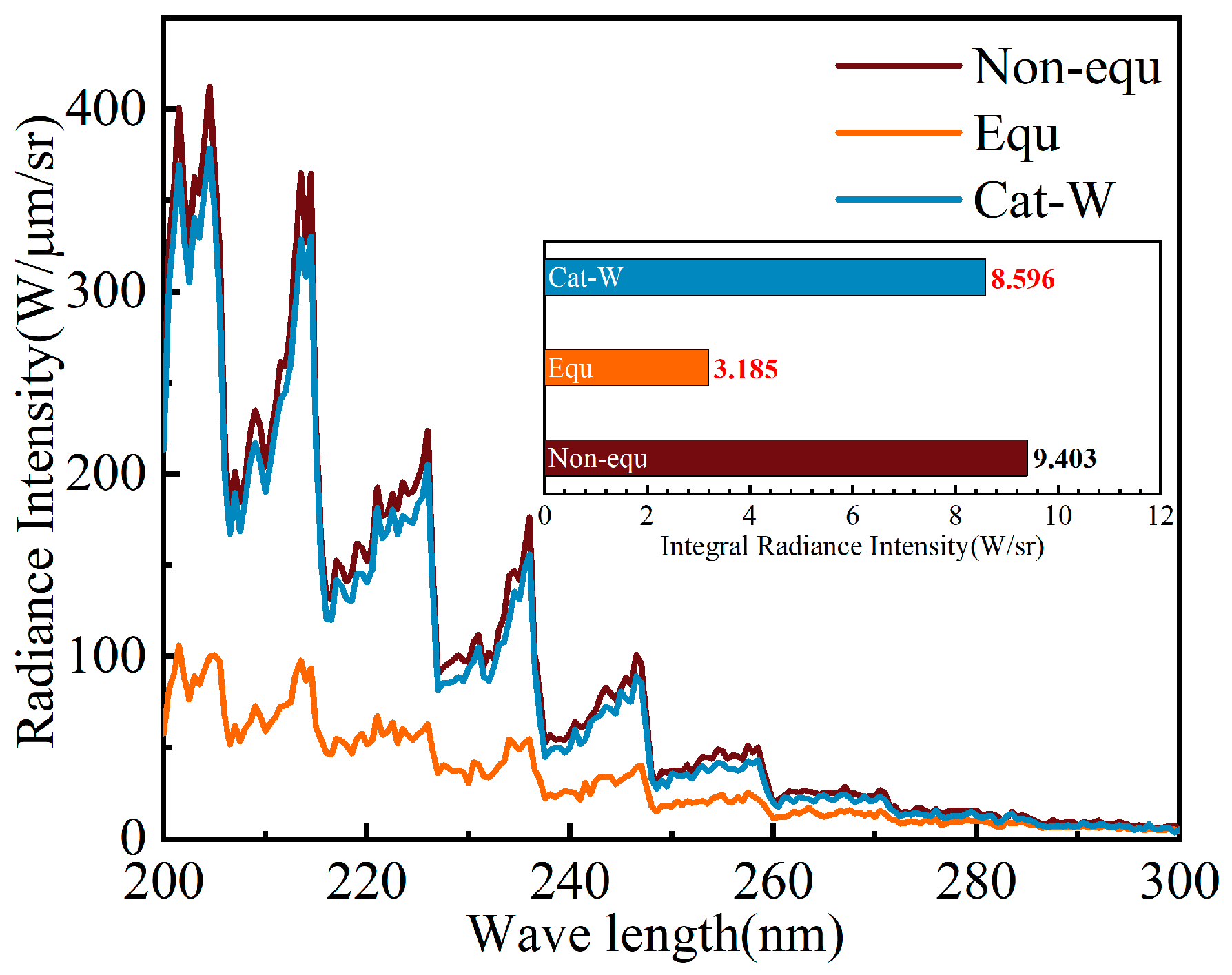
NO generated in the flow field around the hypersonic missile undergoes excitation and emits radiation in the ultraviolet band. Figure 19 presents the line-by-line calculation results of the ultraviolet spectral radiation intensity on the missile head’s stagnation line 1, within the wavelength range of 200–300 nm. The upper right of the figure shows the radiation intensity after convolution with the slit function (Full Width at Half Maximum, FWHM = 0.2 nm). The calculation results from all three models display distinct excited state transition peaks at γ (1, 0), γ (0, 0), γ (0, 1), γ (0, 2), γ (0, 3), and γ (0, 4). The maximum transition radiation intensity peak occurs at the γ (1, 0) position, with the radiation intensity peak decreasing as the wavelength increases.

Based on the data analysis results from Figure 15 and Figure 18, the NO mole fraction generated on the head’s stagnation line 1 of the Equ model is smaller than that of the Non-equ model. Its equilibrium temperature is also lower than the T_tr of the Non-equ model. Consequently, the radiation intensity values calculated by the Equ model in Figure 19 are significantly lower than those of the Non-equ model in the 200–300 nm range. The convolution peak values of the maximum transition radiation intensity for the Non-equ model and the Equ model are approximately 1169 W/m²/sr and 257 W/m²/sr, respectively. The NO mole fraction generated on the head’s stagnation line 1 of the Cat-W model is not significantly different from that of the Non-equ model. However, its maximum T_tr is slightly higher than that of the Non-equ model. Therefore, the radiation intensity value calculated by the Cat-W model in Figure 19 is slightly higher than that of the Non-equ model in the 200–230 nm range.

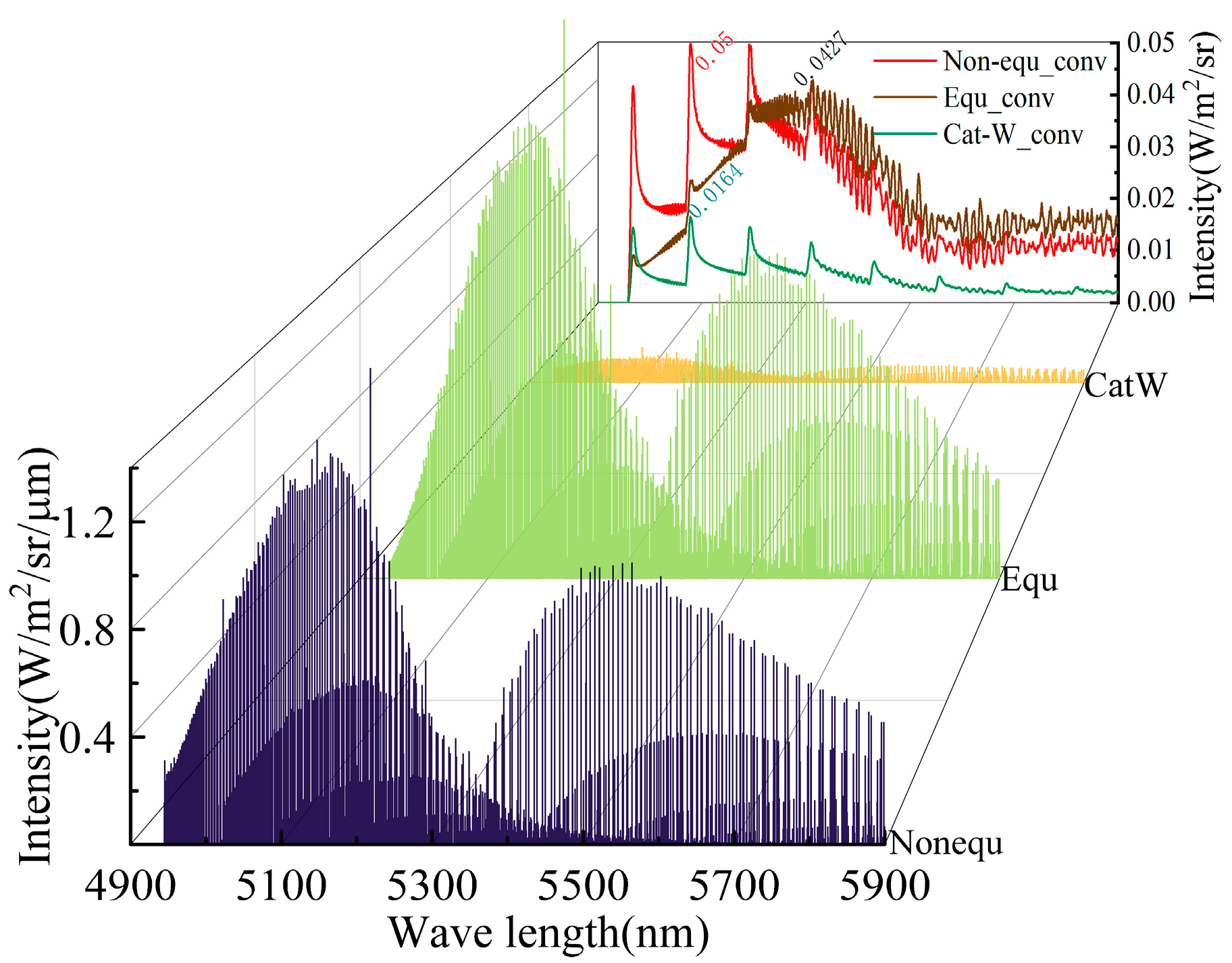
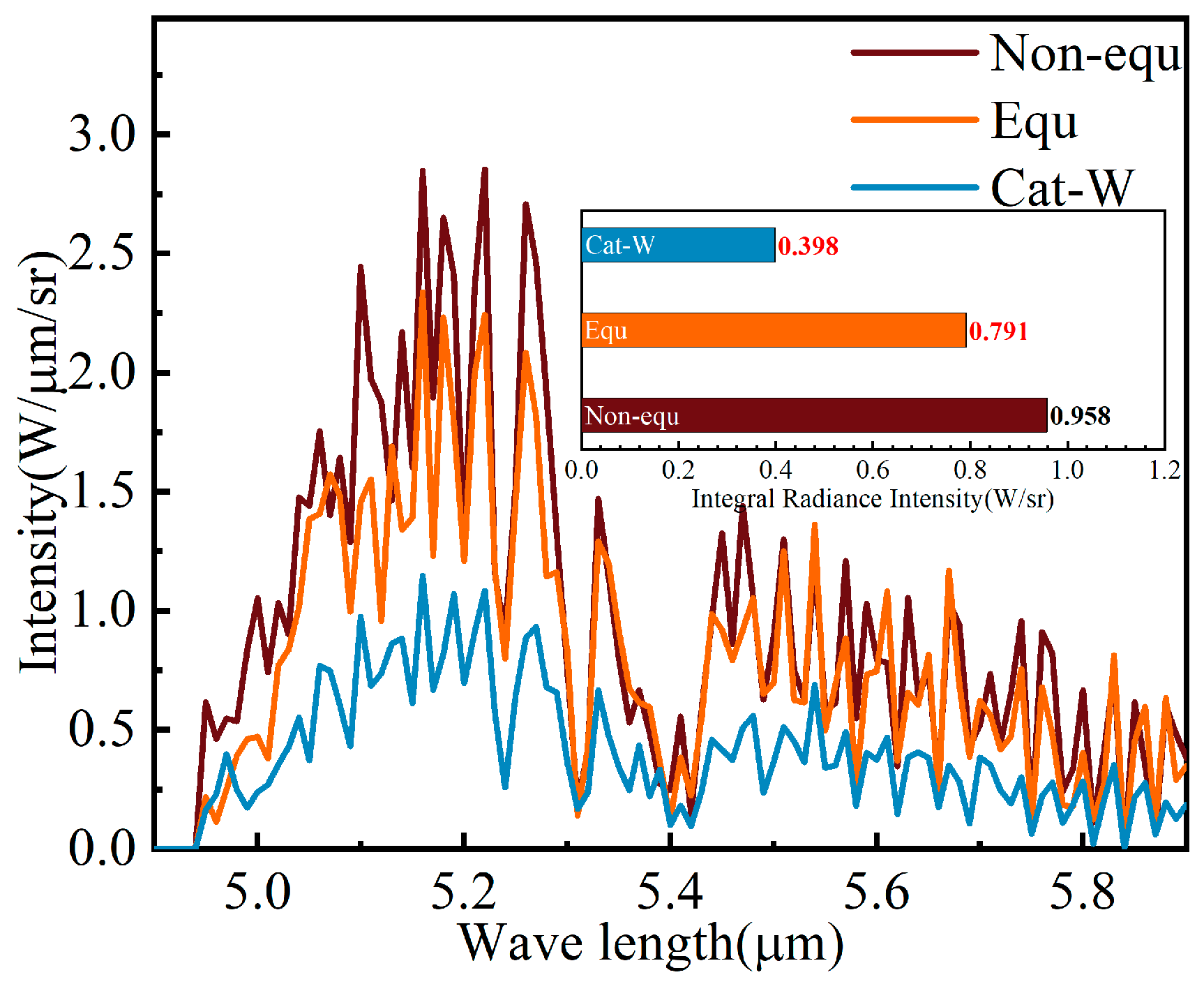
Figure 20 presents the line-by-line calculation results of the infrared spectral radiation intensity within the wavelength range of 4900–5900 nm. These results are for the missile tail separation expansion zone line 4. The upper right of the figure displays the radiation intensity after convolution with the slit function (FWHM = 5 nm). The three models’ calculation results all exhibit distinct fundamental frequency band ($\mathsf{\Delta }v=1$) transition peaks. The Non-equ model’s maximum transition radiation intensity convolution peak appears at the (2, 1) position, approximately 0.05 W/m²/sr. The Equ model’s peak appears at the (4, 3) position, approximately 0.0427 W/m²/sr. The Cat-W model’s peak appears at the (2, 1) position, approximately 0.0164 W/m²/sr.

According to the data analysis results from Figure 15 and Figure 18, the Equ model’s equilibrium temperature in the tail’s separation expansion core region is lower than the Non-equ model’s T_tr and T_ve. However, the Equ model generates a larger NO mole fraction. Comparing the convolved radiation intensities, it is evident that in the 4900–5300 nm range, the fundamental frequency transition peaks at (1, 0), (2, 1), and (3, 2) positions are influenced by the increase in T_tr and T_ve. The Non-equ model’s radiation intensity at these positions is greater than that of the Equ model. Within the 5300–5900 nm range, the fundamental frequency transitions at the (4, 3) and (5, 4) positions are primarily affected by the NO mole fraction. The spectral radiation intensity distributions of the Non-equ model and the Equ model are relatively similar, but the Equ model’s radiation intensity at each wavelength position is greater than that of the Non-equ model.

The Cat-W model generates a much smaller NO mole fraction in the tail separation expansion zone than the Non-equ model. Therefore, the spectral radiation intensity value calculated by the Cat-W model in Figure 19 is also much smaller than that of the Non-equ model in the 4900–5900 nm range.

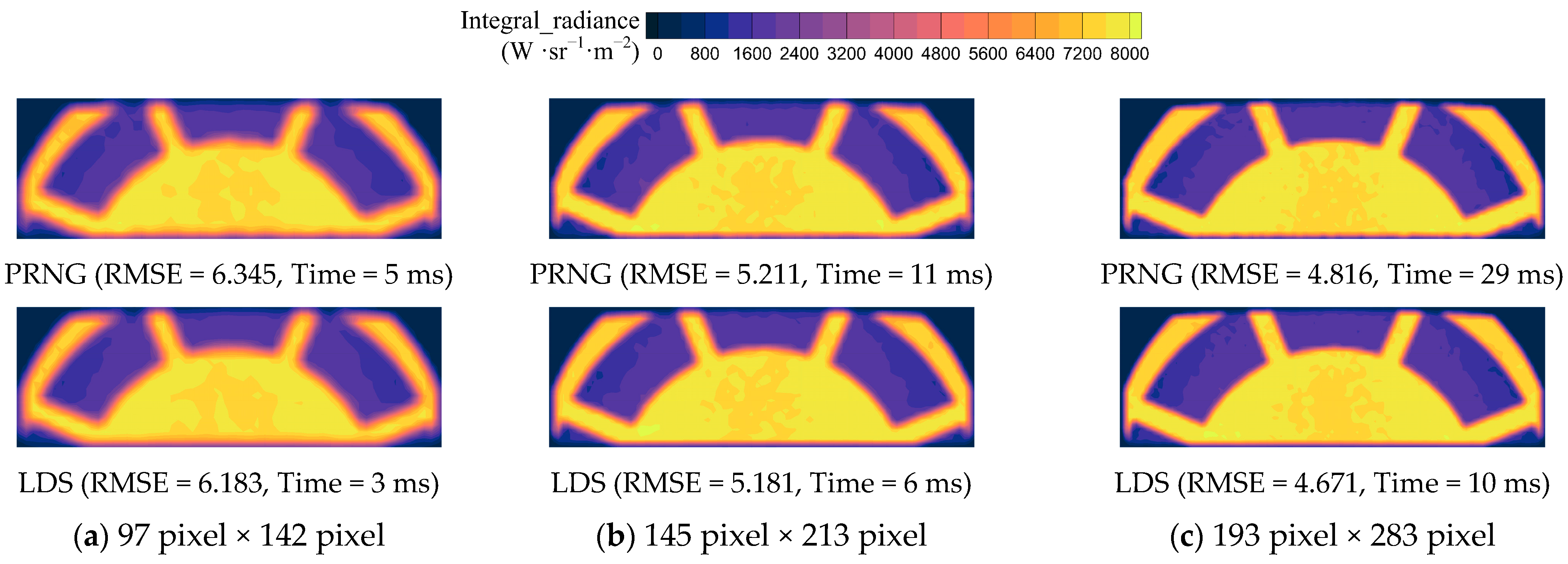
Due to the computational speed limitations of the line-by-line method, the SNB + RMCM method is employed to calculate the spectral radiation intensity within the detection angle range, as shown in Figure 21. Figure 21 illustrates the intensity of ultraviolet radiation within the 200–300 nm band for the head shock layer across three models. The calculation results from all three models, similar to the LBL results for the head stagnation line 1 in Figure 19, exhibit distinct excited state transition peaks. The maximum transition peak occurs at the δ (0, 2) position, with the radiation intensity peak decreasing as the wavelength increases. The radiation peaks for the Non-equ, Equ, and Cat-W models are approximately 400 W/μm/sr, 100 W/μm/sr, and 370 W/μm/sr, respectively. Overall, the band distribution and intensity of the ultraviolet spectral radiation of the shock layer in the Non-equ model and the Cat-W model are quite similar.

Figure 21 also displays the integrated radiation intensity of the three models in the 200–300 nm band. The integrated radiation intensities for the Non-equ, Equ, and Cat-W models are approximately 9.403 W/sr, 3.185 W/sr, and 8.596 W/sr, respectively. Notably, the integrated radiation intensity of the Non-equ model is about three times that of the Equ model.

Figure 22 presents the SNB + RMCM calculation results of the infrared radiation intensity in the 4.9–5.9 μm band for three flow field models at a 90° horizontal detection angle. Despite the limitations imposed by the selected wavelength range, which obscure the transition peak of the spectral distribution, the radiation intensity peak for all three models still appears near 5.2 μm. The Non-equ model exhibits a radiation peak of approximately 2.75 W/μm/sr and an integrated radiation intensity of about 0.958 W/sr. The Equ model shows a radiation peak of about 2.3 W/μm/sr and an integrated radiation intensity of approximately 0.791 W/sr. The Cat-W model has a radiation peak of about 1.1 W/μm/sr and an integrated radiation intensity of approximately 0.398 W/sr.

The combined effects of gas temperature and the generated NO mole fraction result in the Equ model’s radiation intensity being slightly smaller than that of the Non-equ model. Although the Cat-W model has the smallest NO mole fraction in the surrounding flow field and a higher temperature, its calculated infrared radiation intensity is smaller than those of the Non-equ and Cat-W models.

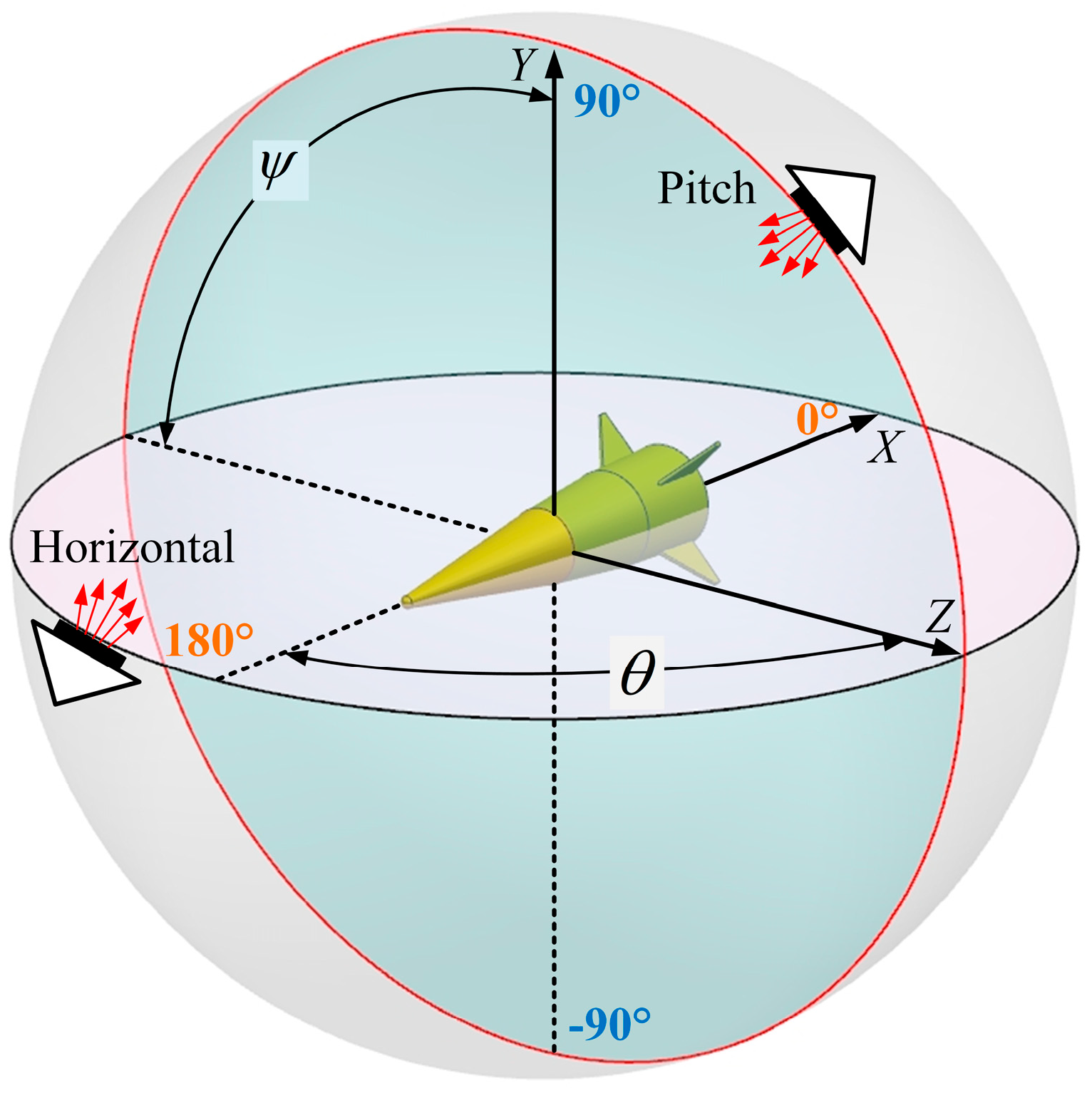
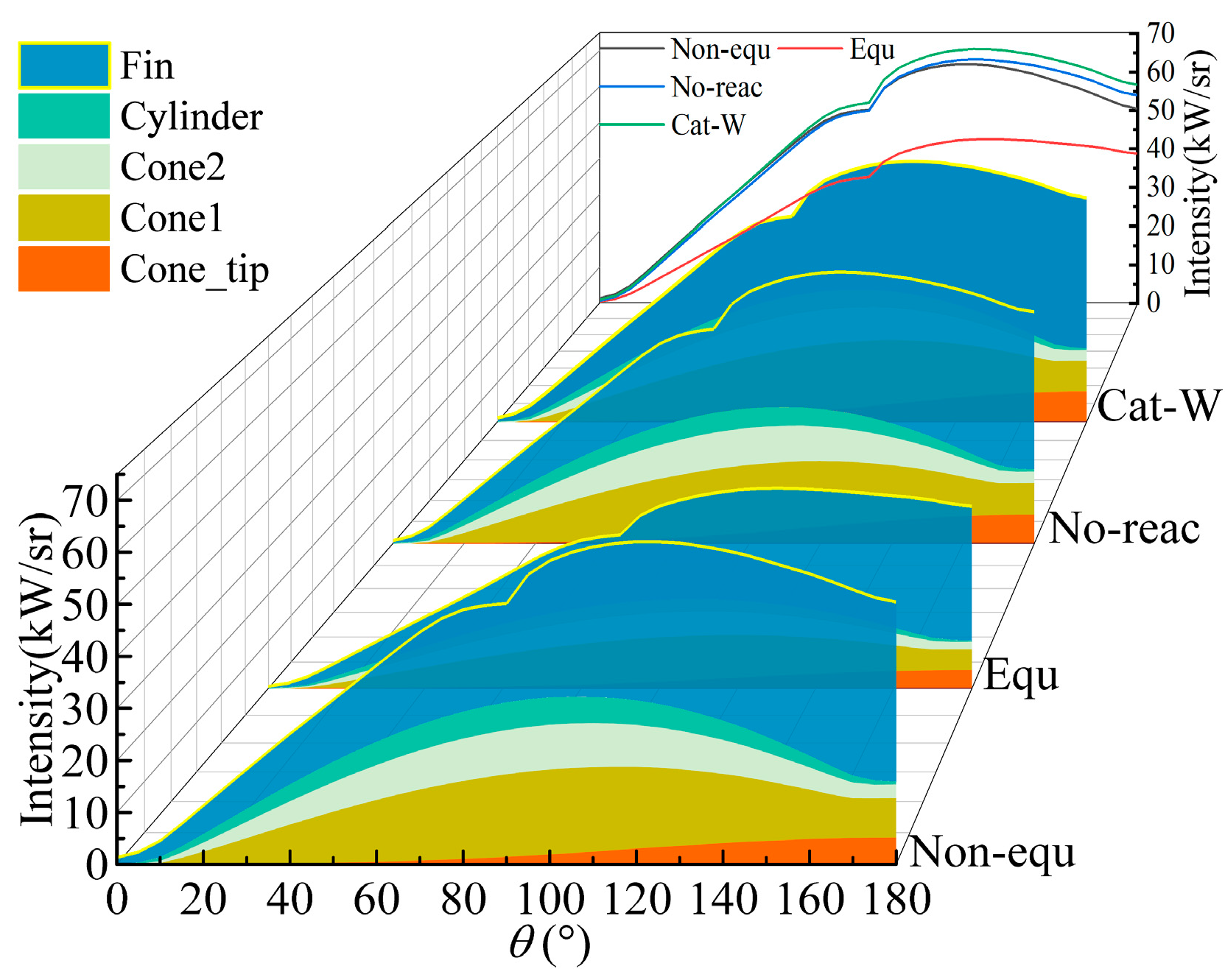
Figure 23 presents the integrated radiation intensity contributions of each missile component within the 1–3 μm band for four models across a horizontal detection plane of 0–180°. The upper right corner displays the total integrated infrared radiation intensity for each model. For all four models, as the horizontal detection angle expands from 0 to 90°, the visible area of the missile’s high-temperature wall enlarges, leading to an increase in the calculated infrared radiation intensity. This increase is consistent with Planck’s law, which states that the calculated value of infrared radiation intensity on the wall is a function of temperature and wavelength.

Interestingly, as the horizontal detection angle further increases from 90 to 180°, the infrared radiation intensity of the missile does not consistently rise. Instead, it peaks near 127°, after which the infrared radiation intensity decreases with the increasing detection angle. This pattern results from the combined effect of the shrinking visible area of the missile’s high-temperature wall and the rising average temperature of the visible missile wall.

In the 0–90° range, the Cat-W model’s radiation intensity is marginally higher than that of the Non-equ and No-reac models, but the overall difference is minimal. The Equ model exhibits the lowest calculated radiation intensity. In the 90–180° range, the differences between the Cat-W, Non-equ, and No-reac models become more pronounced. This divergence is primarily due to the increasing difference in the infrared radiation intensity of the nose cones of the three models as the detection angle widens. The total radiation intensity decreases in the order of Cat-W, No-reac, and Non-equ models, with the Equ model still showing the lowest calculated radiation intensity. In general, the fin and the first cone are the main contributors to the missile’s infrared radiation intensity.

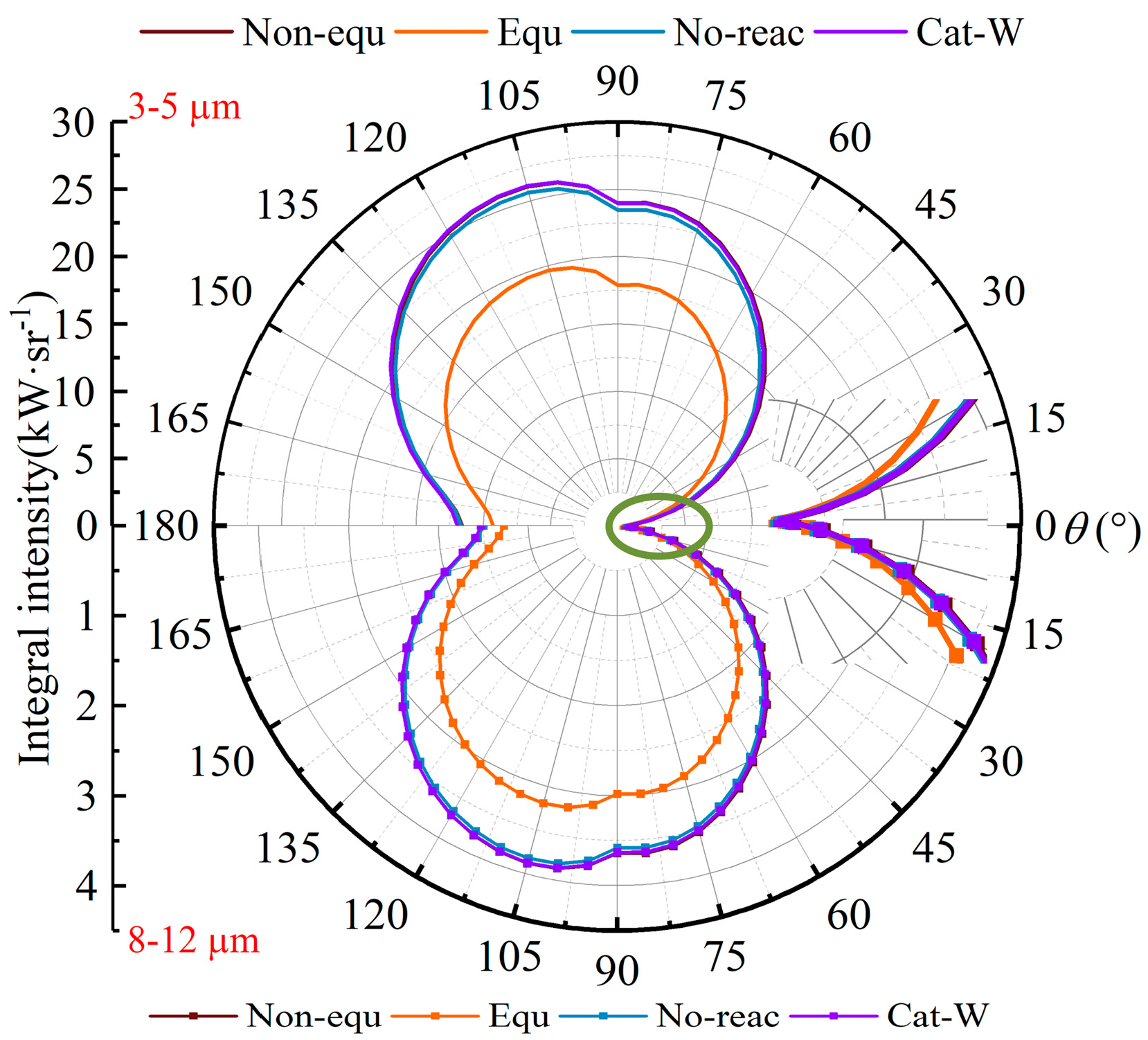
Figure 24 illustrates the integrated infrared radiation intensity of four missile models within the 3–5 μm and 8–12 μm bands across a horizontal detection plane of 0–180°. For all models, as the horizontal detection angle widens from 0 to 90°, the visible area of the missile’s high-temperature wall expands, leading to an increase in the calculated infrared radiation intensity in both bands.

As the detection angle further increases from 90 to 180°, the infrared radiation intensity of the missile in both bands peaks near 105°. Beyond this point, the infrared radiation intensity decreases with the increasing detection angle. This trend is a result of the combined effect of the decreasing visible area of the missile’s high-temperature wall and the increasing average temperature of the visible missile wall.

Referring to Figure 23, the radiation intensity of the 3–5 μm band is typically about 40% of that of the 1–3 μm band, while the radiation intensity of the 8–12 μm band is generally about 6% of that of the 1–3 μm band. Moreover, the ratio of each model’s radiation intensity to the maximum value at the 180° detection angle diminishes as the wavelength increases. The difference ratio between the four models also decreases with increasing wavelength. This is in line with Planck’s law, which states that the calculated value of infrared radiation intensity on the wall is a function of temperature and wavelength. As the wavelength lengthens, the relative influence of temperature on the radiation intensity value lessens. The total radiation intensity of the Cat-W, No-reac, and Non-equ models shows little variation, with the Equ model consistently exhibiting the lowest calculated radiation intensity.

4.4. The Effect of High-Emissivity Coating Failure on Missile Radiation Characteristics

High-emissivity missile coatings can exhibit failure behaviors such as cracking, ablation, and peeling under extreme thermal conditions of high temperature and velocity. To analyze the impact of these failures on the infrared radiation characteristics of solid missiles, a new high-emissivity coating material referenced in Reference [36] was selected.

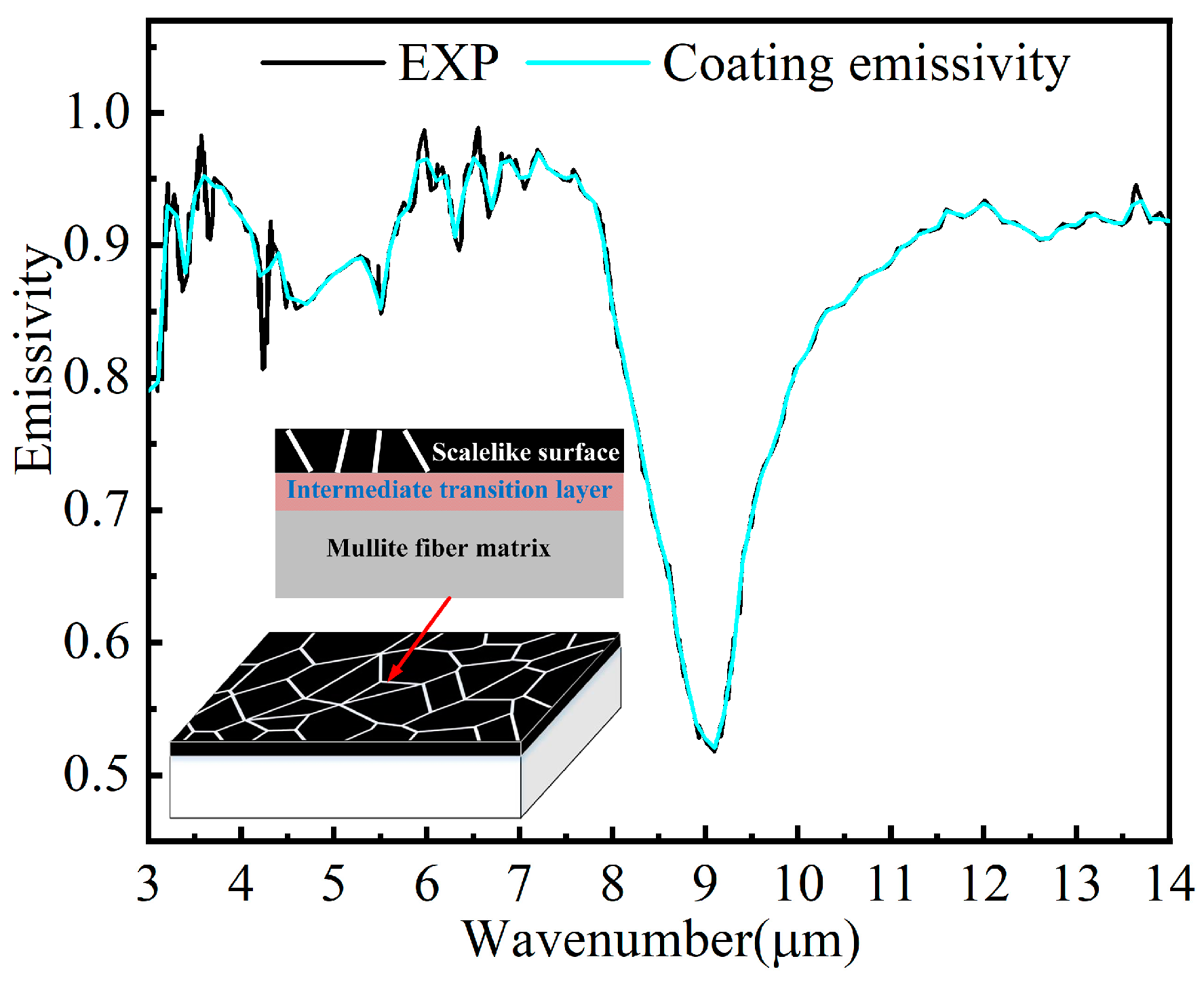
Figure 25 provides a schematic diagram of this coating material and its emissivity within the 3–14 μm band. The coating comprises a scale-like surface layer, an intermediate transition layer, and a mullite fiber matrix. The total hemispheric emissivity of the coating is approximately 0.85, with a notable infrared absorption peak at 8–10 μm. This peak primarily results from the asymmetric Si-O stretching vibration absorption of SiO₄ tetrahedra [37], a common occurrence in many silicate glasses. An additional absorption peak at 4–6 μm is attributed to the Bo and Si-O bonds in borosilicate glass [38]. The experimentally measured coating emissivity, fitted with a wavelength interval of 0.1 μm in the 3–14 μm band, was used as the calculated wavelength of the SNB + RMCM program.

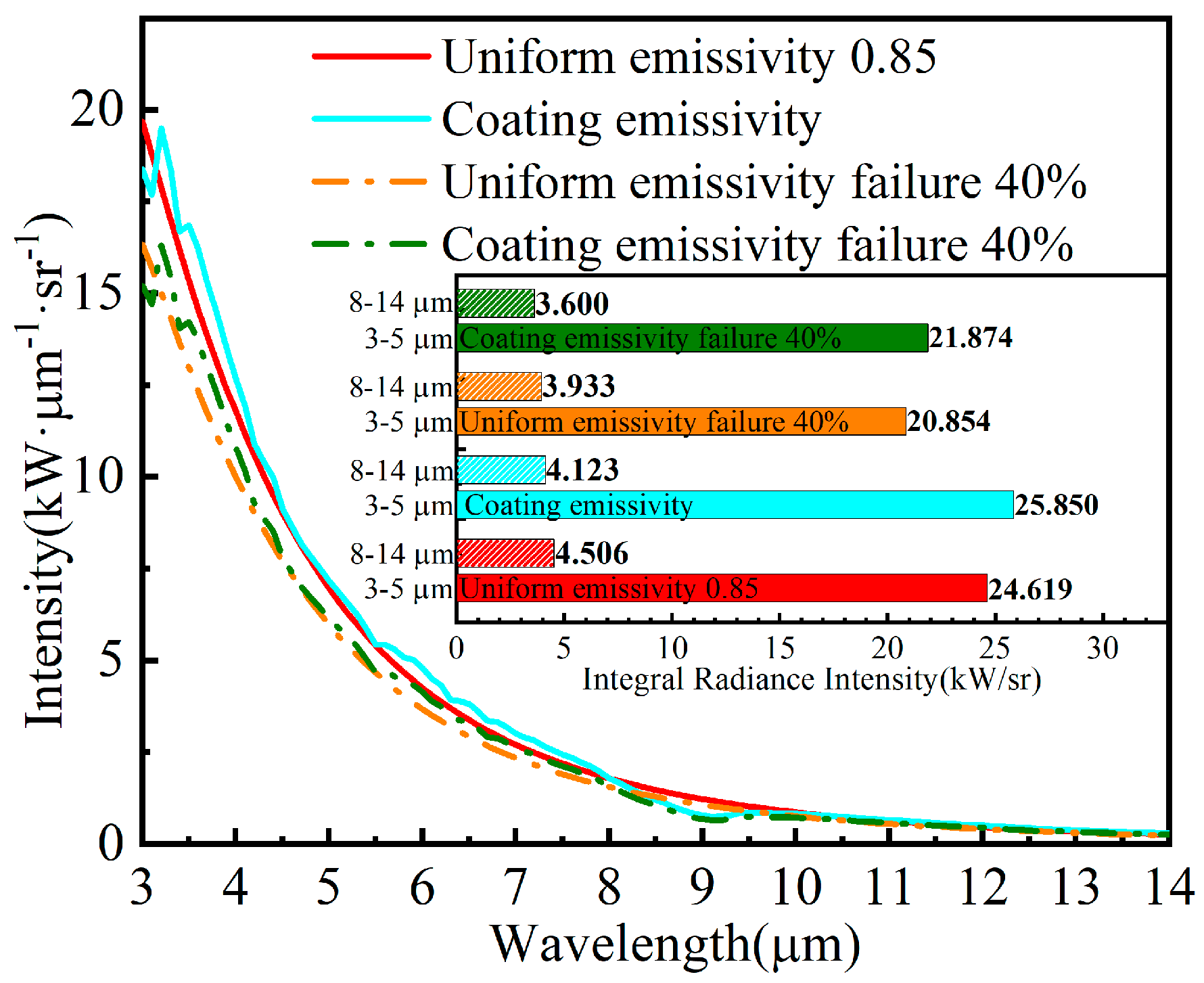
Figure 26 compares the spectral radiation intensity of two solid missile wall models: one using a uniform emissivity of 0.85 and the other using the experimentally measured coating emissivity. The figure reveals that the infrared radiation intensity of the real coating emissivity solid wall exceeds that of the uniform emissivity model in the 3–8 μm and 10–14 μm bands but falls short in the 8–10 μm band. This discrepancy is due to the Si-O absorption peak depicted in Figure 25.

Moreover, the integrated radiation intensity of the real coating emissivity solid wall in the 3–5 μm band is roughly 5% higher than that of the uniform emissivity model, while the integrated radiation intensity in the 8–14 μm band is about 8.51% lower. However, according to Wien’s displacement law, the wavelength corresponding to the maximum blackbody light radiation emission is inversely proportional to the absolute temperature of the blackbody. As the temperature rises, a greater proportion of radiation occurs in the short wavelength range. Given that the radiant energy of high-emissivity, high-temperature-resistant coatings in the short wavelength range accounts for over 90% of the radiated energy in the full wavelength range, the thermal radiation performance of the real coating emissivity solid wall is superior in the overall band.

Coating failure is an extremely complex process in real-world scenarios. This article uses the thermal shock characteristic test results from Reference [36] as a reference and calculates the thermal stress of the high-emissivity coating according to the Tsui and Stoney formula [39]. Simplifying the coating failure mechanism, it is assumed that the high-emissivity coating will fail if the thermal stress exceeds 40 MPa.

Figure 26 displays the spectral radiation intensity of the two models—uniform emissivity and real coating emissivity—after a 40% failure in coating emissivity. Following partial coating failure, the integrated radiation intensity of the real coating emissivity solid wall in the 3–5 μm band decreases by about 15.38%, and the integrated radiation intensity in the 8–14 μm band decreases by about 12.67%. The uniform emissivity solid wall sees a decrease in the integrated radiation intensity in the 3–5 μm band by approximately 15.29% and a decrease in the integrated radiation intensity in the 8–14 μm band by approximately 12.72%.

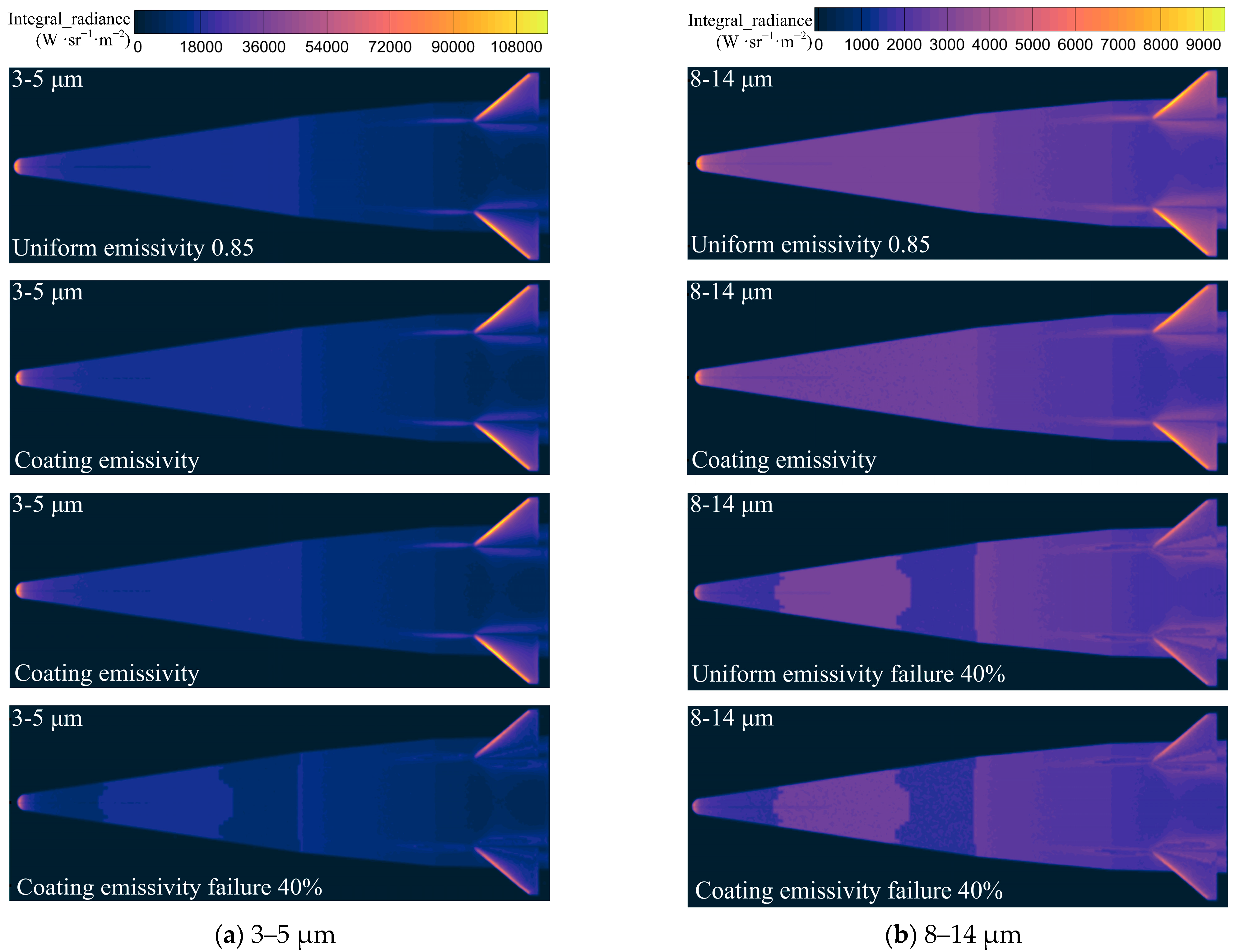
Figure 27 depicts the integrated radiance of the missile’s solid wall surface at a 90° horizontal detection angle. In the 3–5 μm detection band, the difference in infrared integrated radiance caused by the temperature variation of the wall is more pronounced than in the 8–14 μm band. A comparison between Figure 27a,b reveals that the 3–5 μm integrated radiance of the real coating emissivity model at the missile head and fin positions slightly exceeds that of the uniform emissivity model. Conversely, in the 8–14 μm band, the situation is reversed, consistent with the analysis presented in Figure 26. Upon comparing the integrated radiance of the four models in Figure 27, it becomes evident that, under the coating failure assumption, the primary failure locations are the missile head and fin. After a 40% failure in emissivity, both the uniform emissivity and the integrated radiation intensity of the real coating emissivity model significantly decrease at the missile head and fin positions.

5. Conclusions

In this study, an application based on an enhanced Reverse Monte Carlo Method significantly improves the accuracy of calculating target infrared radiation characteristics. This program evaluates the chemical non-equilibrium flow field around a hypersonic missile and the missile body’s radiation characteristics, considering different calculation models and coating failure effects.

At a flight altitude of 50 km and a speed of 15 Ma, severe non-equilibrium effects occur at the missile’s head and tail flow fields. In the fully catalyzed wall model, exothermic reactions near the missile increase the wall and surrounding flow field temperatures, decreasing the mole fraction of NO. Compared to the equilibrium model, the non-equilibrium model alters the transition peak distribution of NO in the head shock layer within the ultraviolet radiation gamma band system. The integrated ultraviolet radiation intensity in the 200–300 nm band is three times that of the equilibrium model. The fundamental frequency transition of NO in the flow field around the missile tail at (1, 0), (2, 1), and (3, 2) is significantly influenced by the trans-rotational temperature and vibro-electronic temperature. At a 90° horizontal detection angle, the integrated infrared radiation intensity of the non-equilibrium model in the 4.9–5.9 μm band is 2.4 times that of the catalytic wall model and 1.2 times that of the equilibrium model.

In the 1–3 μm, 3–5 μm, and 8–14 μm bands, the integrated radiation intensity of the missile reaches a maximum value within a 0–180° horizontal detection plane. The radiation intensity of each model in the 3–5 μm band is generally about 40% of that in the 1–3 μm band, and the radiation intensity of the 8–12 μm band is about 6% of that in the 1–3 μm band. Using real coating emissivity, the integrated radiation intensity of the solid wall in the 3–5 μm band is approximately 5% higher than that of the uniform emissivity model, and the integrated radiation intensity in the 8–14 μm band is approximately 8.51% lower. When the high-emissivity coating’s emissivity fails by 40%, the integrated radiation intensity of the real coating emissivity solid wall in the 3–5 μm band decreases by about 15.38%, and the integrated radiation intensity in the 8–14 μm band decreases by about 12.67%.