Contribution of Different Parameters on Film Cooling Efficiency Based on the Improved Orthogonal Experiment Method
Abstract
1. Introduction
2. Physical Model and Calculation Method
2.1. Flow Field Domain and Grid
2.2. Governing Equation and Turbulence Model
2.3. Parameter Definition
2.4. Boundary Condition
2.5. Accuracy Verification
2.6. Modified Orthogonal Design of Experiments Method
- Controllable influence parameters, as well as output characteristic values, are determined;
- The table of levels of the parameters and the orthogonal table of the parameter design are determined;
- By numerical simulation, the average film cooling efficiency is calculated for each operating condition;
- The average of each level of each parameter is analyzed, denoted as Kij.
- The extreme difference of each parameter, denoted as Rj, is calculated by Equation (6). The contribution rate CRj is calculated by Equation (7);
- The optimal combination is determined (noted as optim-case): the three parameters determined by the three Kj,max is selected to form the optim-case.
3. Results and Discussion
3.1. Design of Numerical Simulation Parameter
3.1.1. Flat Plate Film Cooling
- BR, α, and S/D were identified as controllable influencing parameters with output characteristic values of ;
- The for each case was calculated by numerical simulation according to the parameter design table;
- The K value for each level of each parameter, the R-value for each parameter, and the CRj were calculated separately;
- The optimal combination is determined (optim-case).
3.1.2. Transverse Groove Film Cooling
3.2. Flat Plate Film Cooling
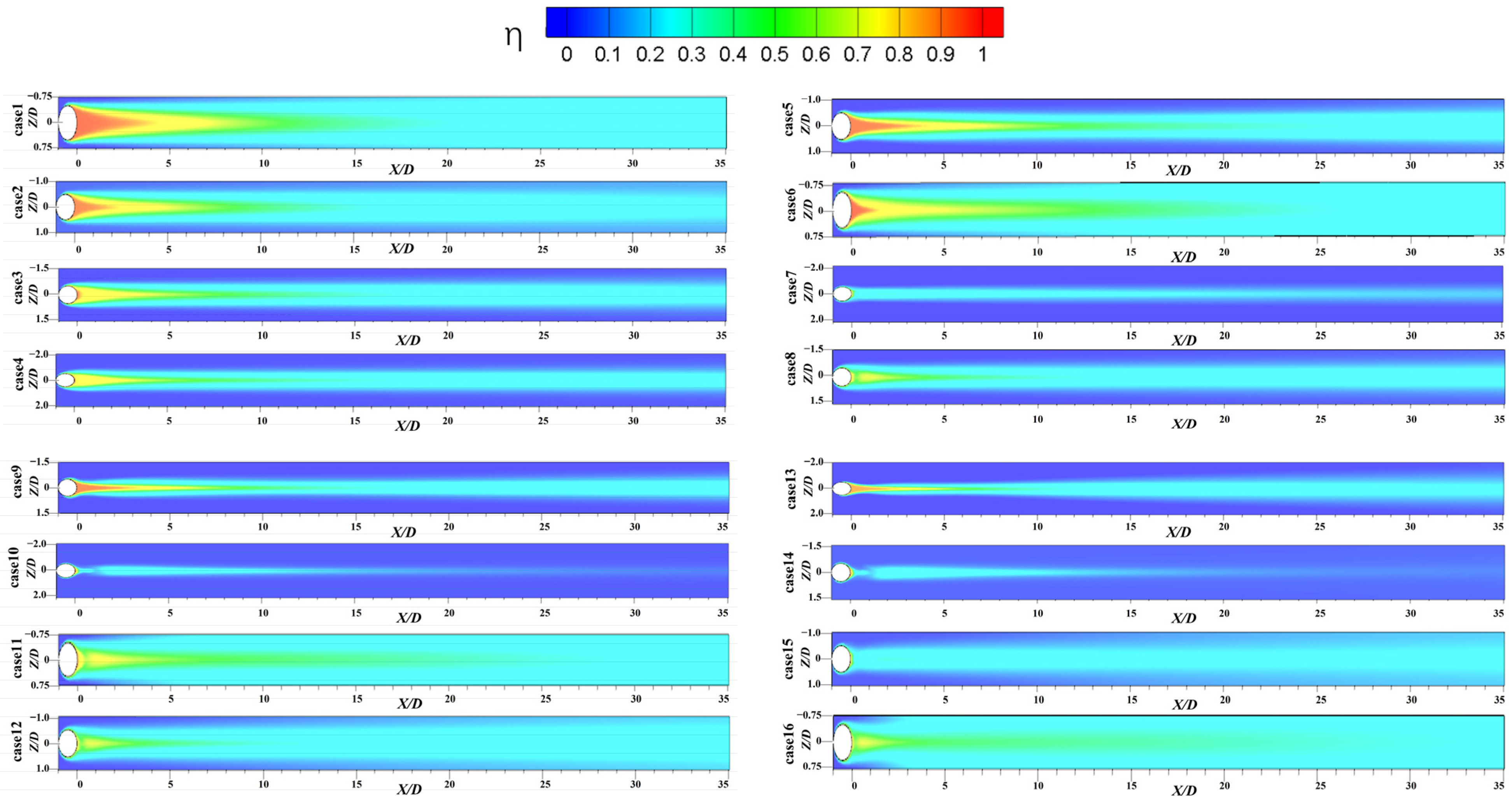
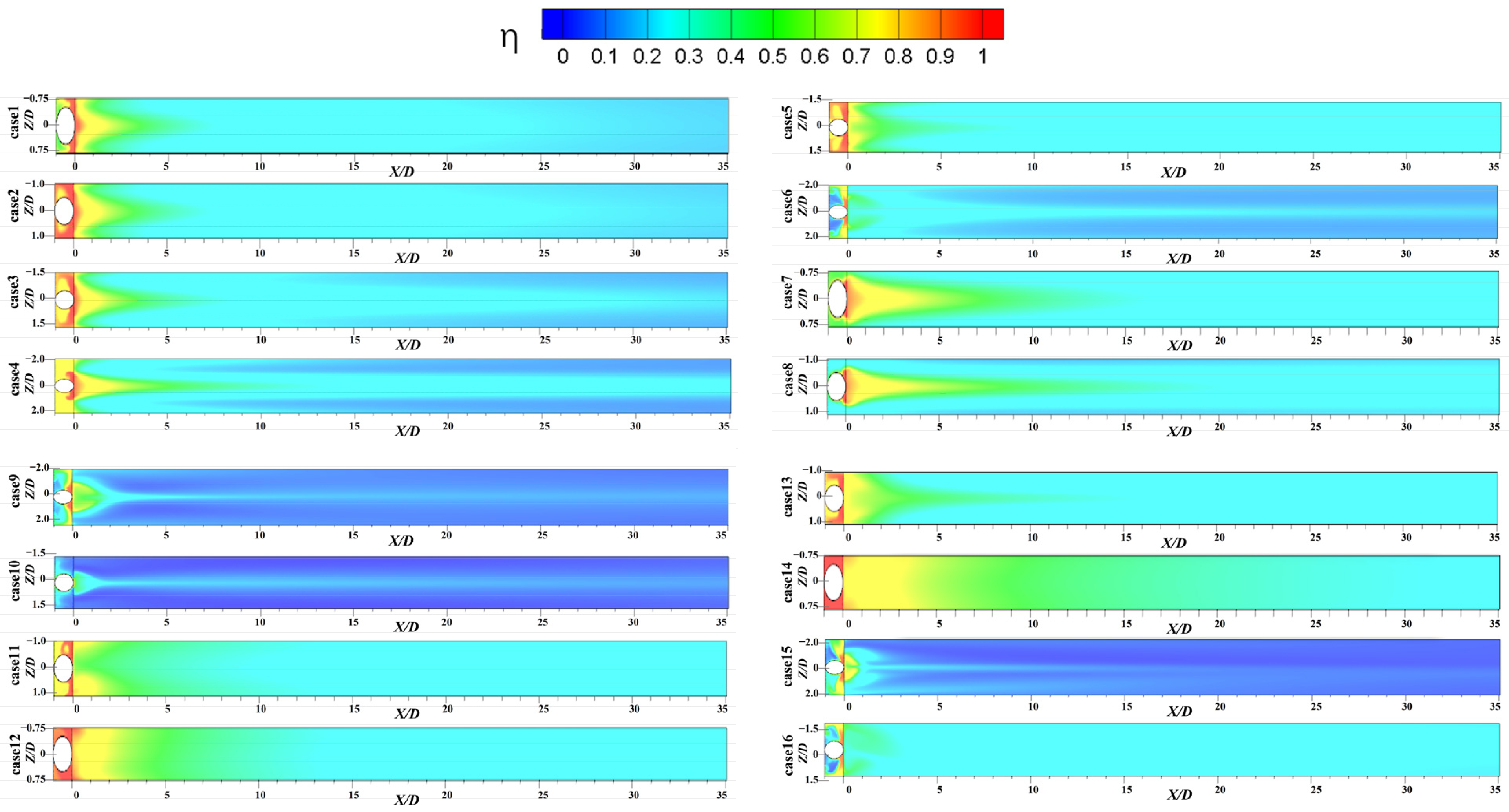
3.2.1. Display of Film Cooling Efficiency Results
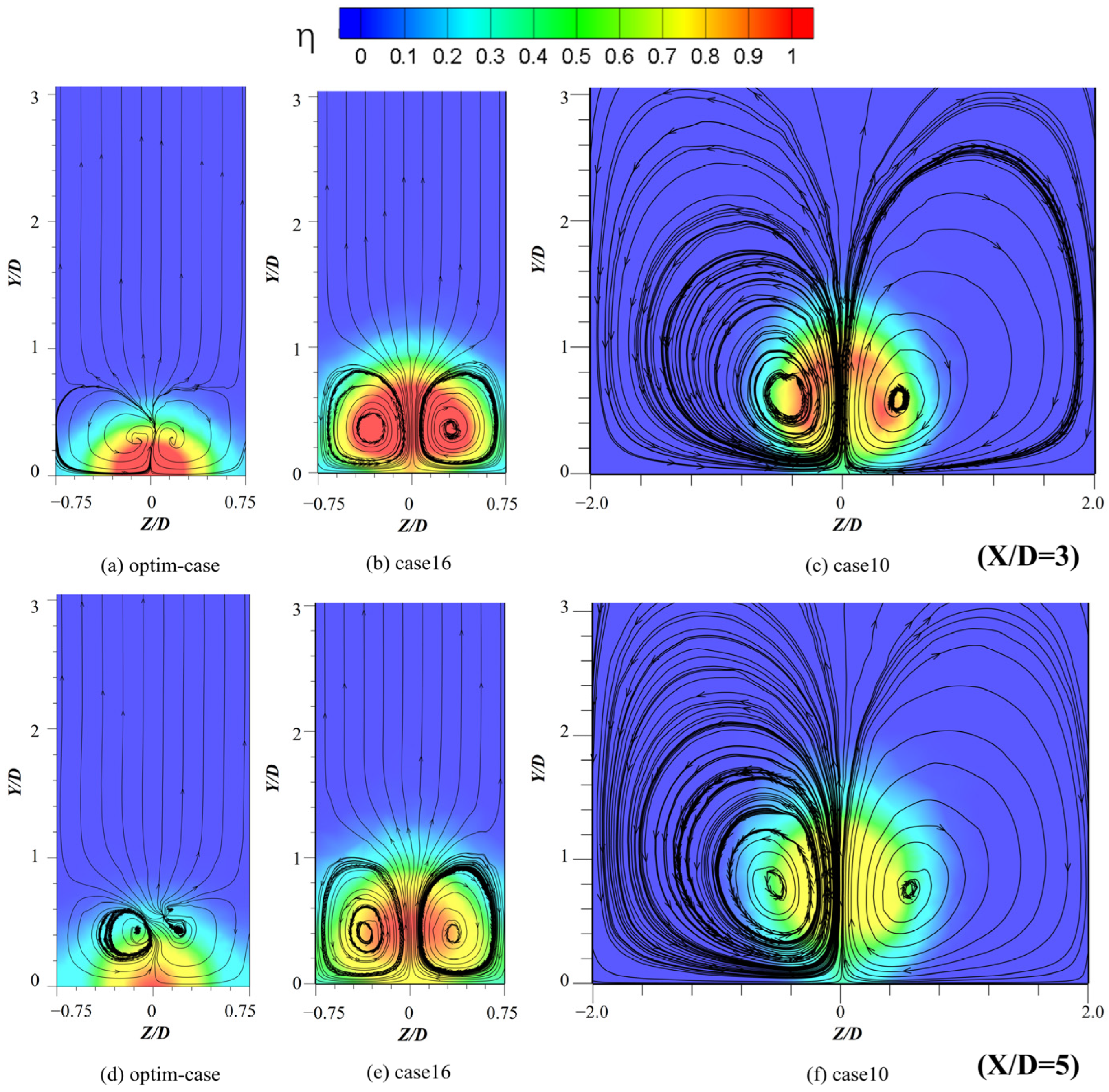
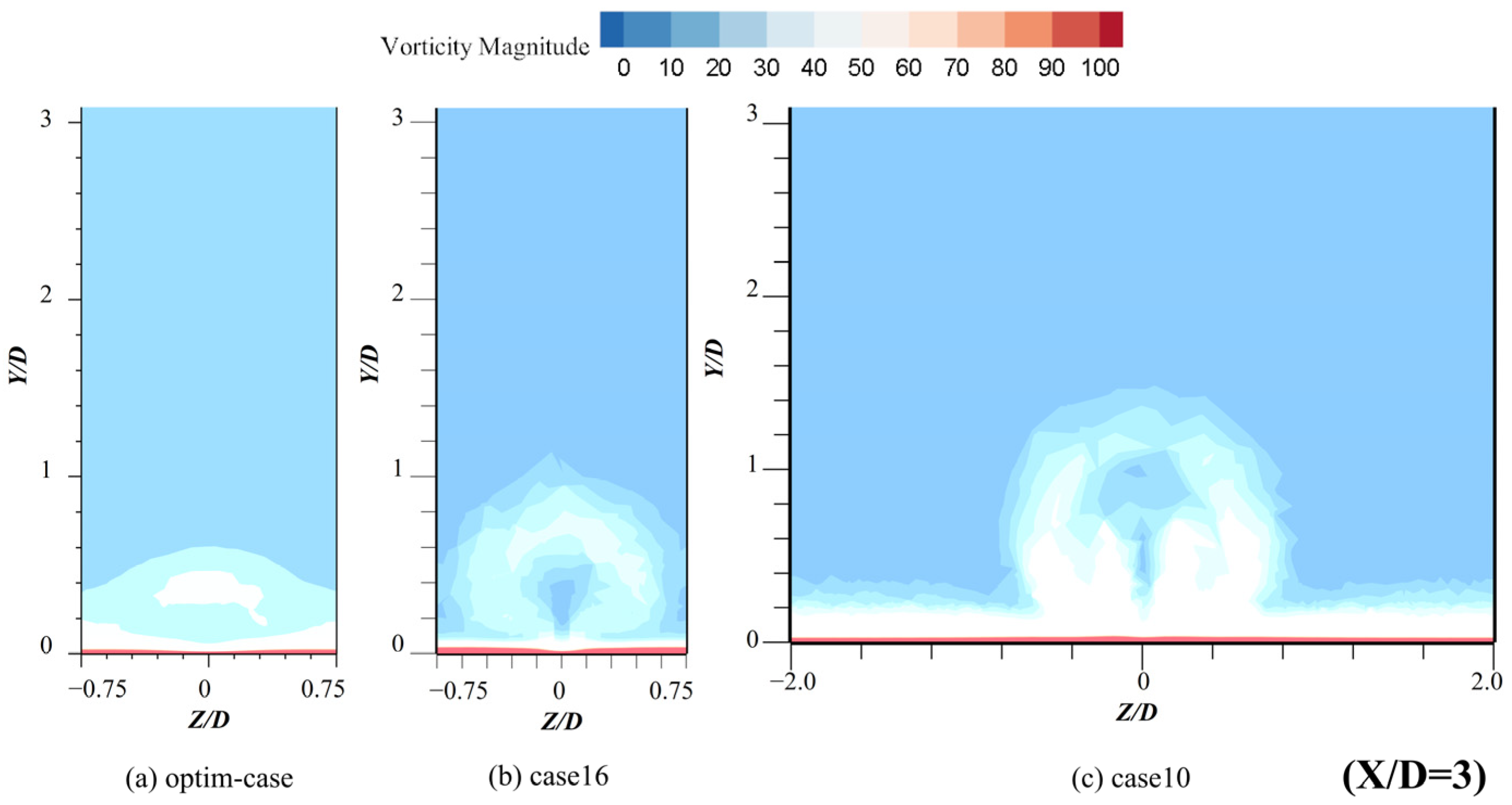
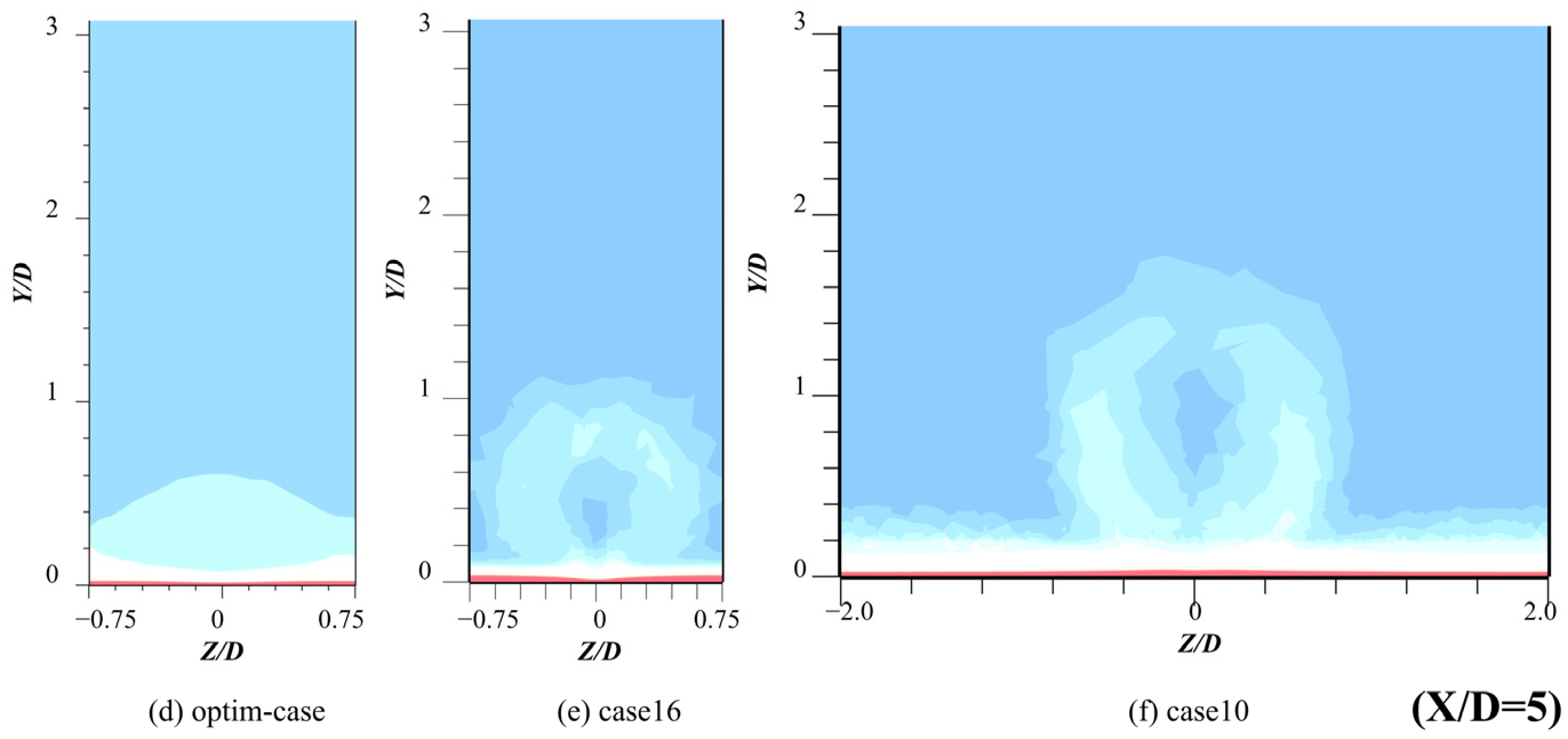
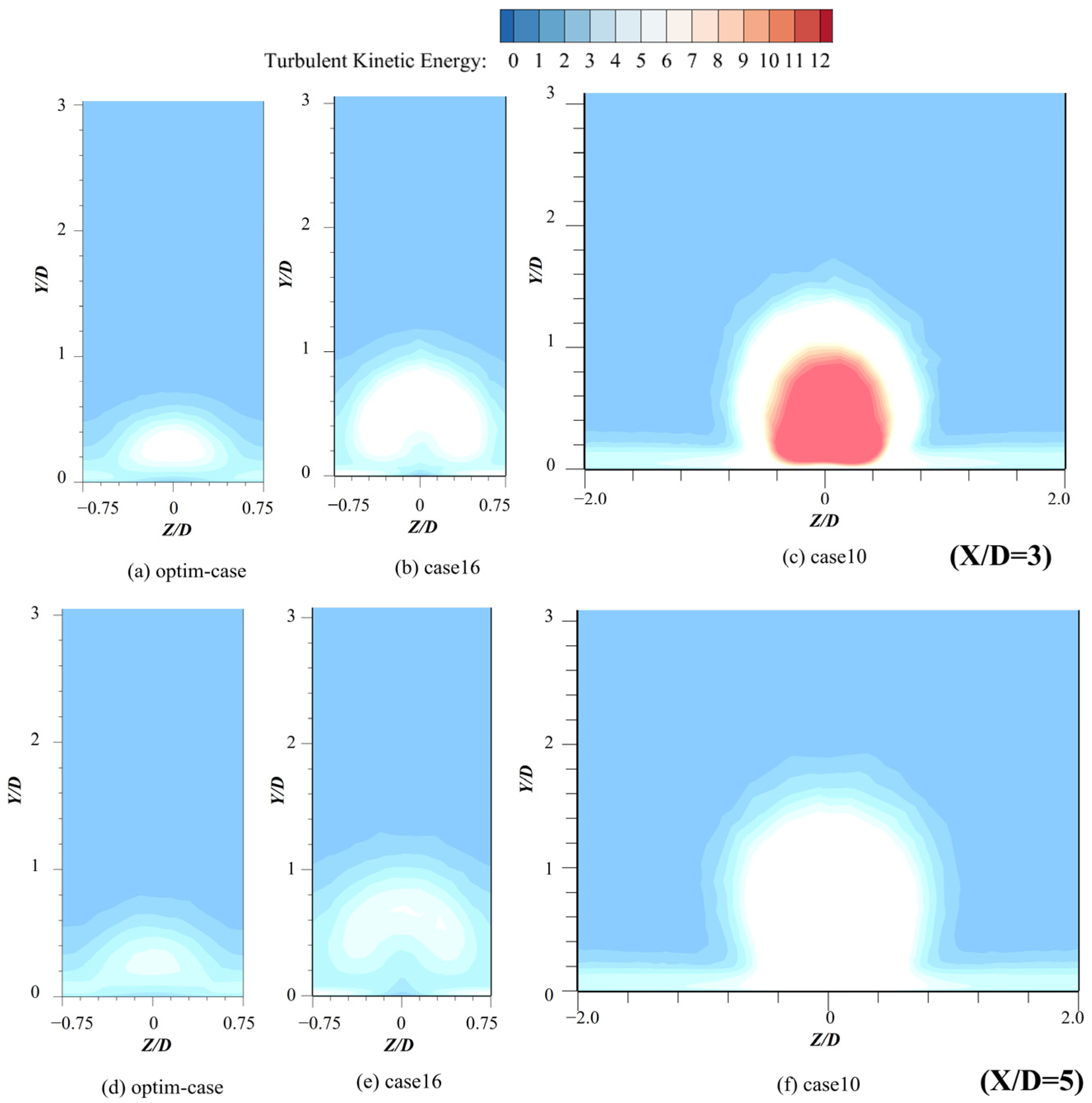
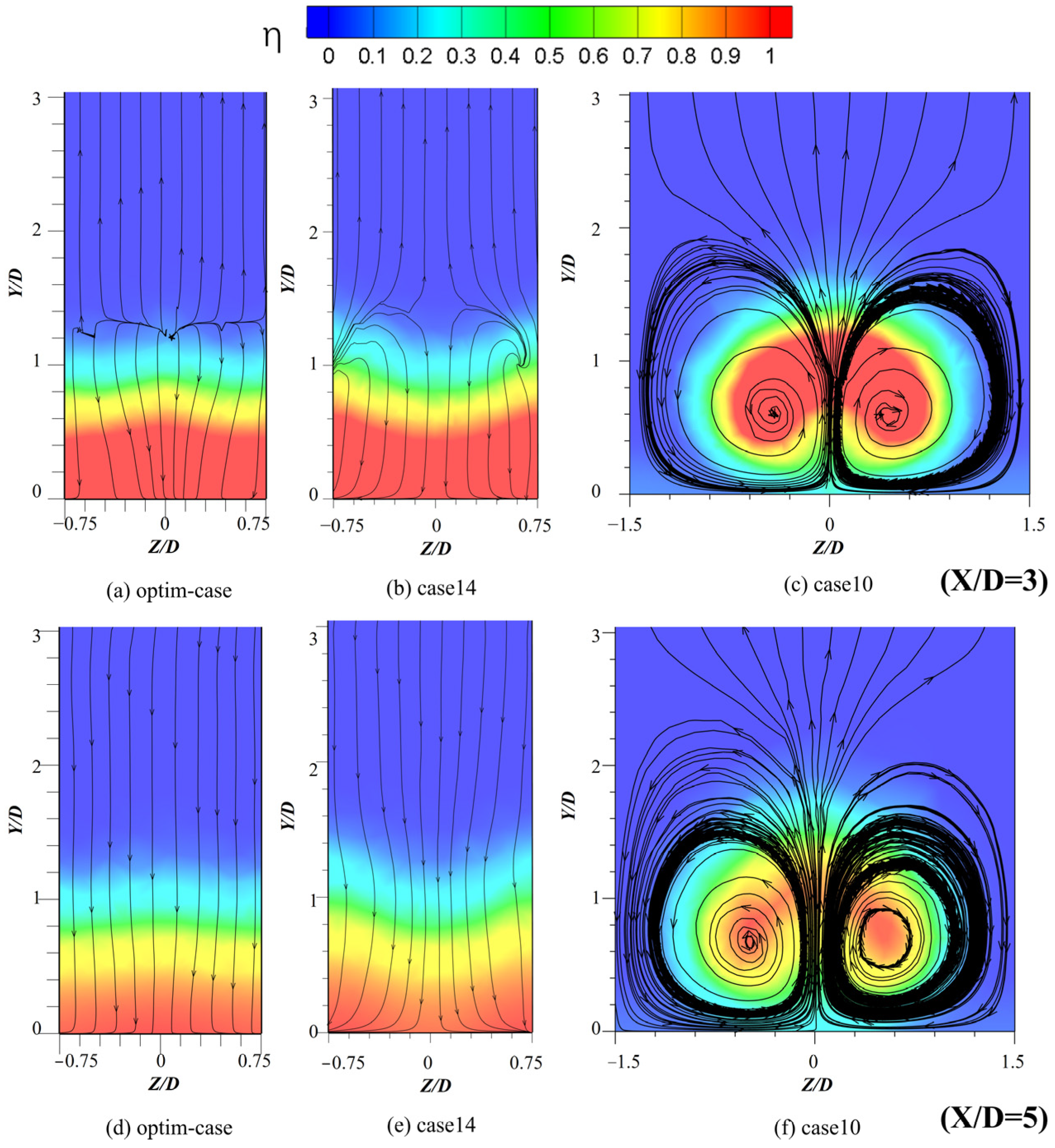
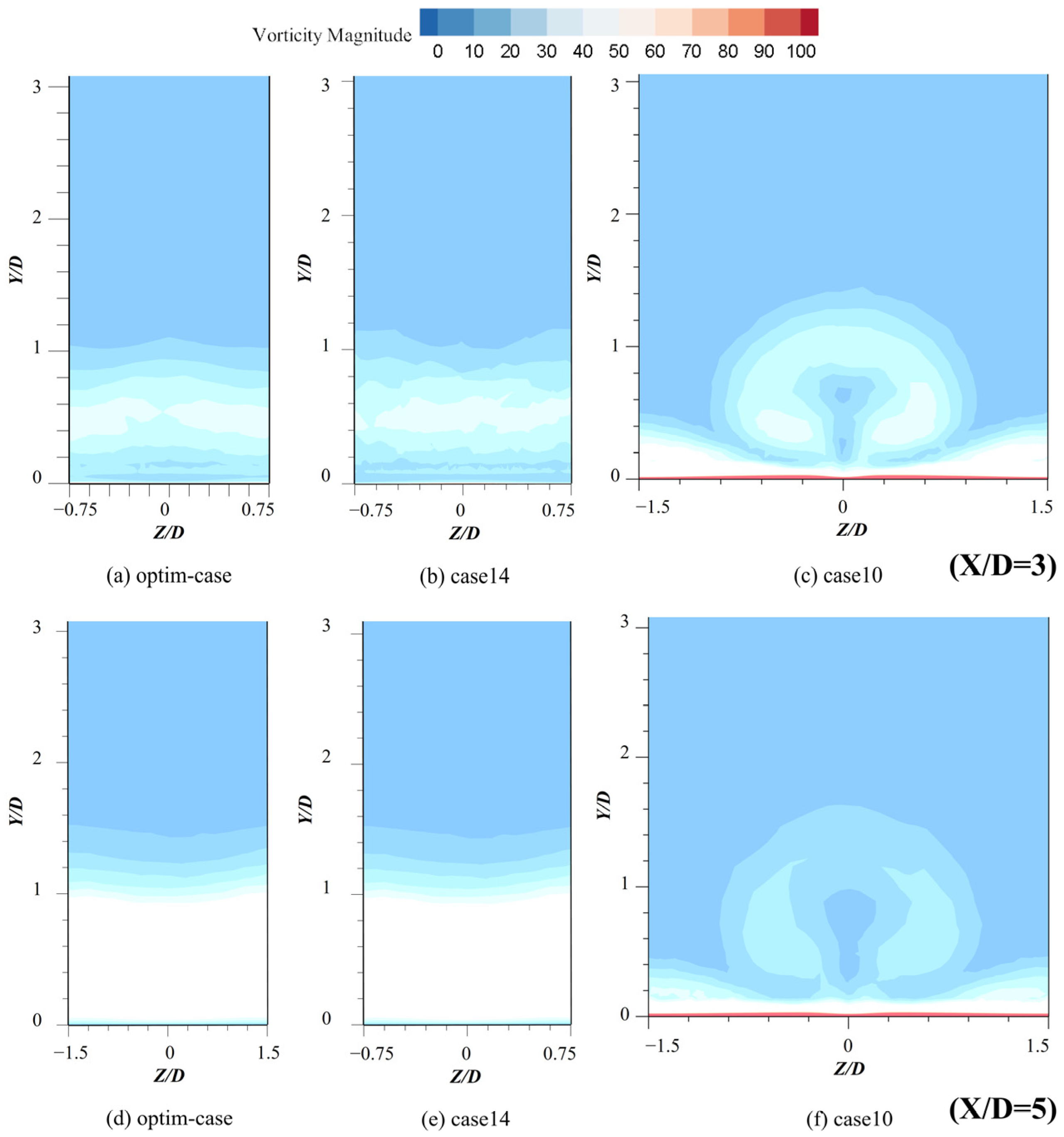
3.2.2. Flow Field Structure Analysis
3.3. Transverse Groove Film Cooling
3.3.1. Display of Film Cooling Efficiency Results
3.3.2. Flow Field Structure Analysis
4. Conclusions
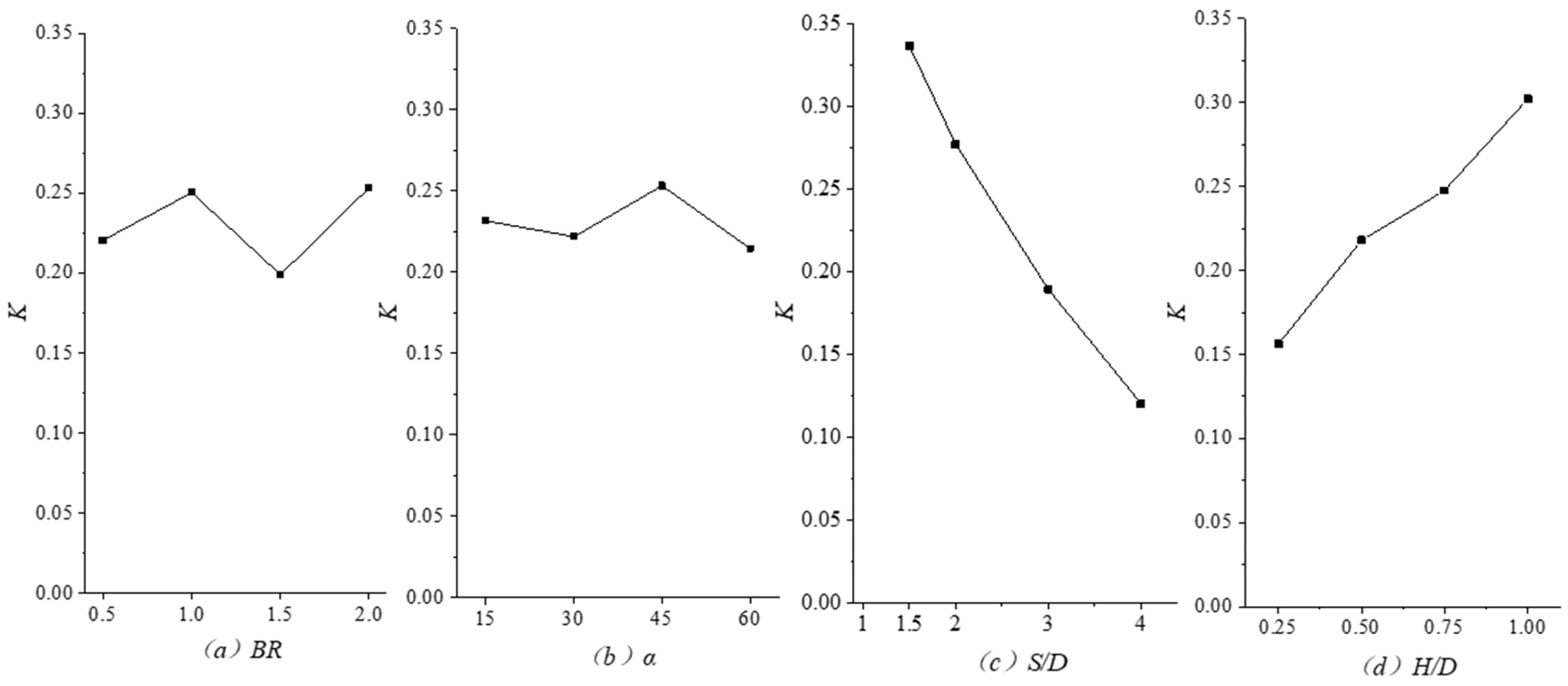
- By comparing the K, R, and CR of each parameter, it is concluded that in flat plate film cooling, the magnitude of the contribution of three parameters to the efficiency of flat plate film cooling is ranked as S/D > α > BR. At transverse groove film cooling, the magnitude of the contribution of four parameters to the efficiency of gas film cooling is ranked as S/D > H/D > BR > α;
- When flat plate film cooling is adopted, and the wall hole spacing is S/D > 2.0, a strip of film will be formed on the wall, which will cause the metal wall surface to overheat. When using transverse groove film cooling for larger S/D, the cooling jet can still expand in the Z-direction when the BR is small, and a less efficient film is formed on both sides. When the BR is large, both sides of the wall are basically unprotected;
- Comparing the film cooling efficiency contours of the two structures, it can be found that a more complete film in most cases in the transverse groove film cooling is generated, which is better than the flat plate film cooling;
- By analyzing and comparing the Streamline diagrams and Vorticity diagrams of the YZ cross-section, it can be obtained that CRVP is the most important factor affecting the film cooling efficiency. Without CRVP, in the case where the influence range of the vortex in the normal direction is larger, the cooling flow will be more likely to break away from the wall, resulting in a lower film cooling efficiency.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| AFCE | Average Film Cooling Efficiency |
| BR | Blowing ratio |
| CR | Contribution rate |
| CRVP | Counter-rotating vortex pair |
| D | Hole diameter |
| DR | Density ratio |
| FCE | Film Cooling efficiency |
| H/D | Transverse groove depth |
| K | The average of each level of each parameter |
| L/D | Film hole length |
| R | The extreme difference of each parameter |
| S/D | Film hole spacing |
| T | Temperature |
| u | Flow velocity |
| VOF | Volume of Fluid |
| W/D | Transverse groove width |
| X | Positive direction of flow |
| Y | Normal flow direction |
| Z | Lateral flow direction |
| α | Angle of incidence |
| Fluid density | |
| The area-averaged film cooling efficiency |
References
- Fry, R.S. A Century of Ramjet Propulsion Technology Evolution. J. Propuls. Power 2004, 20, 27–58. [Google Scholar] [CrossRef]
- Hewitt, P. Status of Ramjet Programs in the United States. In Proceedings of the 44th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Hartford, CT, USA, 21–23 July 2008; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2008. [Google Scholar]
- Ma, W.; Yin, Z.; Pan, C.; Li, B.; Zhang, H. Thermodynamics Cycle Analysis of a One-Dimensional Scramjet Model in Different Combustion Modes. In Proceedings of the 21st AIAA International Space Planes and Hypersonics Technologies Conference; American Institute of Aeronautics and Astronautics, Xiamen, China, 6 March 2017; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2017. [Google Scholar]
- Roux, J.; Tiruveedula, L. Constant Velocity Combustion Scramjet Cycle Analysis for Non-Ideal Mass Flow Rate. Therm. Sci. Eng. Prog. 2017, 2, 8–14. [Google Scholar] [CrossRef]
- Wang, J.; Wen, Y.; Zha, B.; Xu, Z.; Zhang, T. Effects of the Air Inlet Angle on the Combustion and Ablation Environment of a Hybrid Powder-Solid Ramjet. Int. J. Aerosp. Eng. 2022, 2022, 8091927. [Google Scholar] [CrossRef]
- Jing, T.; Xu, Z.; Xu, J.; Qin, F.; He, G.; Liu, B. Characteristics of Gaseous Film Cooling with Hydrocarbon Fuel in Supersonic Combustion Chamber. Acta Astronaut. 2022, 190, 74–82. [Google Scholar] [CrossRef]
- Kanda, T.; Masuya, G.; Ono, F.; Wakamatsu, Y. Effect of Film Cooling/Regenerative Cooling on Scramjet Engine Performances. J. Propuls. Power 1994, 10, 618–624. [Google Scholar] [CrossRef]
- Park, K.H.; Yang, K.M.; Lee, K.W.; Cho, H.H.; Ham, H.C.; Hwang, K.Y. Effects of Injection Type on Slot Film Cooling for a Ramjet Combustor. J. Mech. Sci. Technol. 2009, 23, 1852–1857. [Google Scholar] [CrossRef]
- Zhang, T.; Zhao, H.; He, L.; Wang, T. Study on the Combustion Process of the Ramjet Combustion Chamber. J. Phys. Conf. Ser. 2023, 2489, 012010. [Google Scholar] [CrossRef]
- Mahoney, J. Inlets for Supersonic Missiles; AIAA Education Series; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1990. [Google Scholar]
- Oh, J.Y.; Ma, F.; Hsieh, S.-Y.; Yang, V. Interactions between Shock and Acoustic Waves in a Supersonic Inlet Diffuser. J. Propuls. Power 2005, 21, 3. [Google Scholar] [CrossRef]
- Chang, J.; Duan, X.; Du, Y.; Guo, B.; Pan, Y. Investigations on the Effect of Different Influencing Factors on Film Cooling Effectiveness under the Injection of Synthetic Coolant. Sci. Rep. 2021, 11, 3408. [Google Scholar] [CrossRef]
- Bontempo, R.; Manna, M. Work and Efficiency Optimization of Advanced Gas Turbine Cycles. Energy Convers. Manag. 2019, 195, 1255–1279. [Google Scholar] [CrossRef]
- Masci, R.; Sciubba, E. A Lumped Thermodynamic Model of Gas Turbine Blade Cooling: Prediction of First-Stage Blades Temperature and Cooling Flow Rates. J. Energy Resour. Technol. 2018, 140, 020901. [Google Scholar] [CrossRef]
- Khalatov, A.; Shi-Ju, E.; Wang, D.; Borisov, I. Film Cooling Evaluation of a Single Array of Triangular Craters. Int. J. Heat Mass Transf. 2020, 159, 120055. [Google Scholar] [CrossRef]
- Hou, R.; Wen, F.; Luo, Y.; Tang, X.; Wang, S. Large Eddy Simulation of Film Cooling Flow from Round and Trenched Holes. Int. J. Heat Mass Transf. 2019, 144, 118631. [Google Scholar] [CrossRef]
- Chang, J.; Du, Y.; Zheng, S.; Duan, X.; Liu, Y. Performance Analysis of Different Influencing Factors on Film Cooling and the Internal Relations with Vortex Structures. AIP Adv. 2019, 9, 070701. [Google Scholar] [CrossRef]
- Bunker, R.S.; Bailey, J.C.; Lee, C.; Abuaf, N. Method for Improving the Cooling Effectiveness of a Gaseous Coolant Stream, and Related Articles of Manufacture. U.S. Patent 6234755 B1, 22 May 2001. [Google Scholar]
- Wei, J.; Zhu, H.; Liu, C.; Song, H.; Liu, C.; Meng, T. Experimental Study on the Film Cooling Characteristics of the Cylindrical Holes Embedded in Sine-Wave Shaped Trench. J. Eng. Gas Turbines Power 2016. [Google Scholar] [CrossRef]
- Waye, S.; Bogard, D. High-Resolution Film Cooling Effectiveness Measurements of Axial Holes Embedded in a Transverse Trench With Various Trench Configurations. J. Turbomach.-Trans. ASME 2007, 129, 294–302. [Google Scholar] [CrossRef]
- Li, J.; Ren, J.; Jiang, H. Film Cooling Performance of the Embedded Holes in Trenches with Compound Angles. In Proceedings of the Volume 4: Heat Transfer, Parts A and B, Glasgow, UK, 10 October 2010; pp. 1415–1424. [Google Scholar]
- Lu, Y.; Nasir, H.; Ekkad, S.V. Film Cooling From a Row of Holes Embedded in Transverse Slots. In Proceedings of the Volume 3: Turbo Expo 2005, Parts A and B, Reno, NV, USA, 1 January 2005; pp. 585–592. [Google Scholar]
- Bunker, R.S. Film Cooling Effectiveness Due to Discrete Holes Within a Transverse Surface Slot. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers Digital Collection: Amsterdam, The Netherlands, 2009; pp. 129–138. [Google Scholar]
- Lee, K.-D.; Kim, K.-Y. Surrogate Based Optimization of a Laidback Fan-Shaped Hole for Film-Cooling. Int. J. Heat Fluid Flow 2011, 32, 226–238. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, J.; Zhou, J. Optimization of a Fan-Shaped Hole to Improve Film Cooling Performance by RBF Neural Network and Genetic Algorithm. Aerosp. Sci. Technol. 2016, 58, 18–25. [Google Scholar] [CrossRef]
- Yang, X.; Liu, Z.; Feng, Z. Numerical Evaluation of Novel Shaped Holes for Enhancing Film Cooling Performance. J. Heat Transf. 2015, 137, 071701. [Google Scholar] [CrossRef]
- Wei, H.; Zu, Y.Q.; Ai, J.L.; Ding, L. Experimental Study on the Full-Coverage Film Cooling of Fan-Shaped Holes with a Constant Exit Width. Int. J. Heat Mass Transf. 2019, 140, 379–398. [Google Scholar] [CrossRef]
- Lu, Y.; Dhungel, A.; Ekkad, S.; Bunker, R. Film Cooling Measurements for Cratered Cylindrical Inclined Holes. J. Turbomach.-Trans. ASME 2009, 131, 011005. [Google Scholar] [CrossRef]
- Cao, N.; Li, X.; Wu, Z.; Luo, X. Effect of Film Hole Geometry and Blowing Ratio on Film Cooling Performance. Appl. Therm. Eng. 2020, 165, 114578. [Google Scholar] [CrossRef]
- Maiteh, B.Y.; Jubran, B.A. Effects of Pressure Gradient on Film Cooling Effectiveness from Two Rows of Simple and Compound Angle Holes in Combination. Energy Convers. Manag. 2004, 45, 1457–1469. [Google Scholar] [CrossRef]
- Ahn, J.; Sung Jung, I.; Lee, J.S. Film Cooling from Two Rows of Holes with Opposite Orientation Angles: Injectant Behavior and Adiabatic Film Cooling Effectiveness. Int. J. Heat Fluid Flow 2003, 24, 91–99. [Google Scholar] [CrossRef]
- Bashir, M.H.; Shiau, C.-C.; Han, J.-C. Film Cooling Effectiveness for Three-Row Compound Angle Hole Design on Flat Plate Using PSP Technique. Int. J. Heat Mass Transf. 2017, 115, 918–929. [Google Scholar] [CrossRef]
- Bunker, R.S. A Review of Shaped Hole Turbine Film-Cooling Technology. J. Heat Transf. 2005, 127, 441–453. [Google Scholar] [CrossRef]
- Fan, X.; Du, C.; Li, L.; Li, S. Numerical Simulation on Effects of Film Hole Geometry and Mass Flow on Vortex Cooling Behavior for Gas Turbine Blade Leading Edge. Appl. Therm. Eng. 2017, 112, 472–483. [Google Scholar] [CrossRef]
- Oliver, T.A.; Bogard, D.G.; Moser, R.D. Large Eddy Simulation of Compressible, Shaped-Hole Film Cooling. Int. J. Heat Mass Transf. 2019, 140, 498–517. [Google Scholar] [CrossRef]
- Zuo, W.; Jiaqiang, E.; Liu, X.; Peng, Q.; Deng, Y.; Zhu, H. Orthogonal Experimental Design and Fuzzy Grey Relational Analysis for Emitter Efficiency of the Micro-Cylindrical Combustor with a Step. Appl. Therm. Eng. 2016, 103, 945–951. [Google Scholar] [CrossRef]
- Jiaqiang, E.; Han, D.; Qiu, A.; Zhu, H.; Deng, Y.; Chen, J.; Zhao, X.; Zuo, W.; Wang, H.; Chen, J.; et al. Orthogonal Experimental Design of Liquid-Cooling Structure on the Cooling Effect of a Liquid-Cooled Battery Thermal Management System. Appl. Therm. Eng. 2018, 132, 508–520. [Google Scholar] [CrossRef]
- Su, L.; Zhang, J.; Wang, C.; Zhang, Y.; Li, Z.; Song, Y.; Jin, T.; Ma, Z. Identifying Main Factors of Capacity Fading in Lithium Ion Cells Using Orthogonal Design of Experiments. Appl. Energy 2016, 163, 201–210. [Google Scholar] [CrossRef]
- Ji, L.; Si, Y.; Liu, H.; Song, X.; Zhu, W.; Zhu, A. Application of Orthogonal Experimental Design in Synthesis of Mesoporous Bioactive Glass. Microporous Mesoporous Mater. 2014, 184, 122–126. [Google Scholar] [CrossRef]
- Shan, W.; Wu, L.; Tao, N.; Chen, Y.; Guo, D. Optimization Method for Green SrAl2O4: Eu2+, Dy3+ Phosphors Synthesized via Co-Precipitation Route Assisted by Microwave Irradiation Using Orthogonal Experimental Design. Ceram. Int. 2015, 41, 15034–15040. [Google Scholar] [CrossRef]
- Yang, P.; Tan, X.; Sun, H.; Chen, D.; Li, C. Fire Accident Reconstruction Based on LES Field Model by Using Orthogonal Experimental Design Method. Adv. Eng. Softw. 2011, 42, 954–962. [Google Scholar] [CrossRef]
- Zhang, R.; Zhou, L.; Xing, J.; Luo, C.; Du, X. Numerical Evaluation of Film Cooling Performance of Transverse Trenched Holes with Shaped Lips. Int. Commun. Heat Mass Transf. 2021, 125, 105326. [Google Scholar] [CrossRef]
- Wang, J.; Liu, C.; Zhao, Z.; Baleta, J.; Sundén, B. Effect and Optimization of Backward Hole Parameters on Film Cooling Performance by Taguchi Method. Energy Convers. Manag. 2020, 214, 112809. [Google Scholar] [CrossRef]
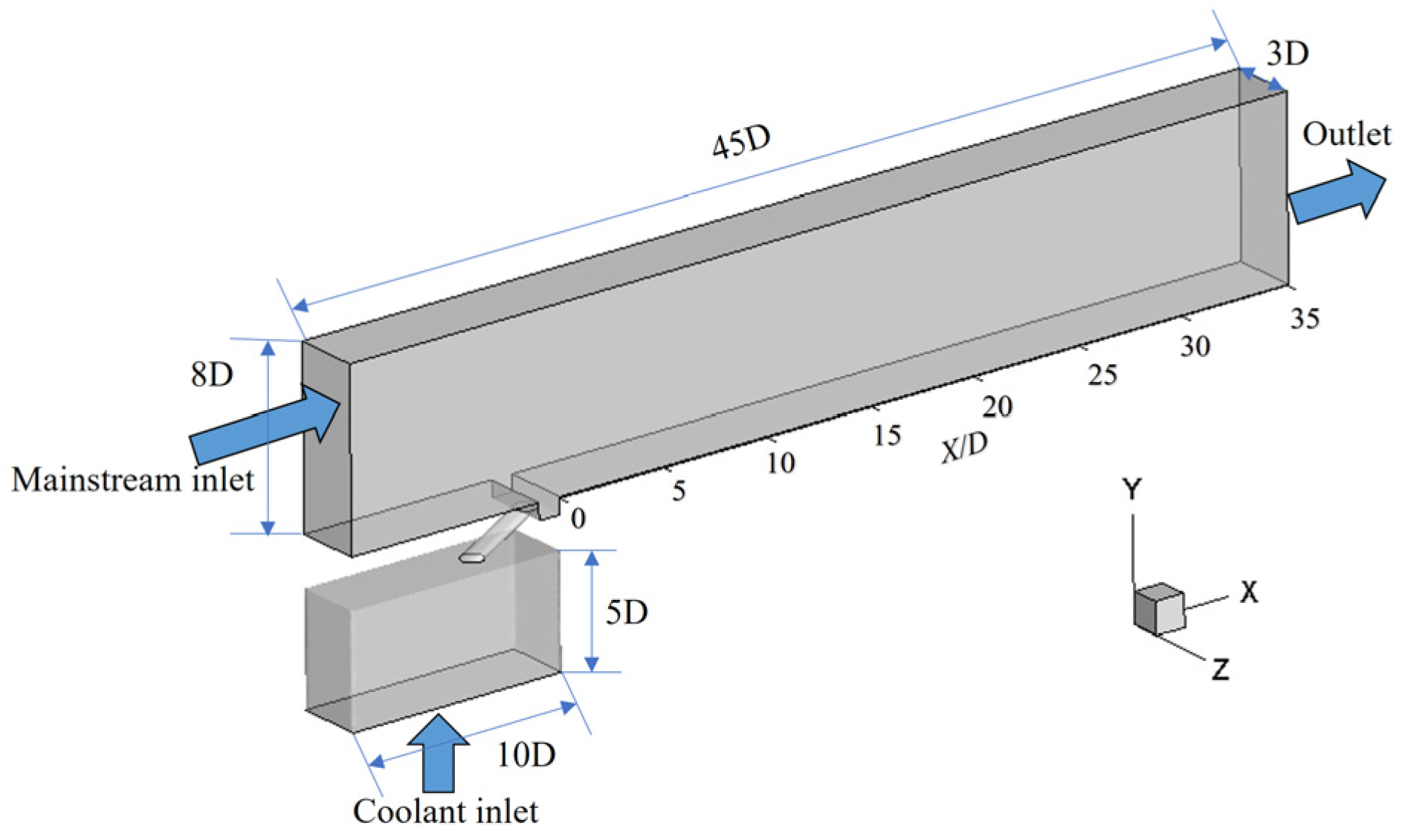


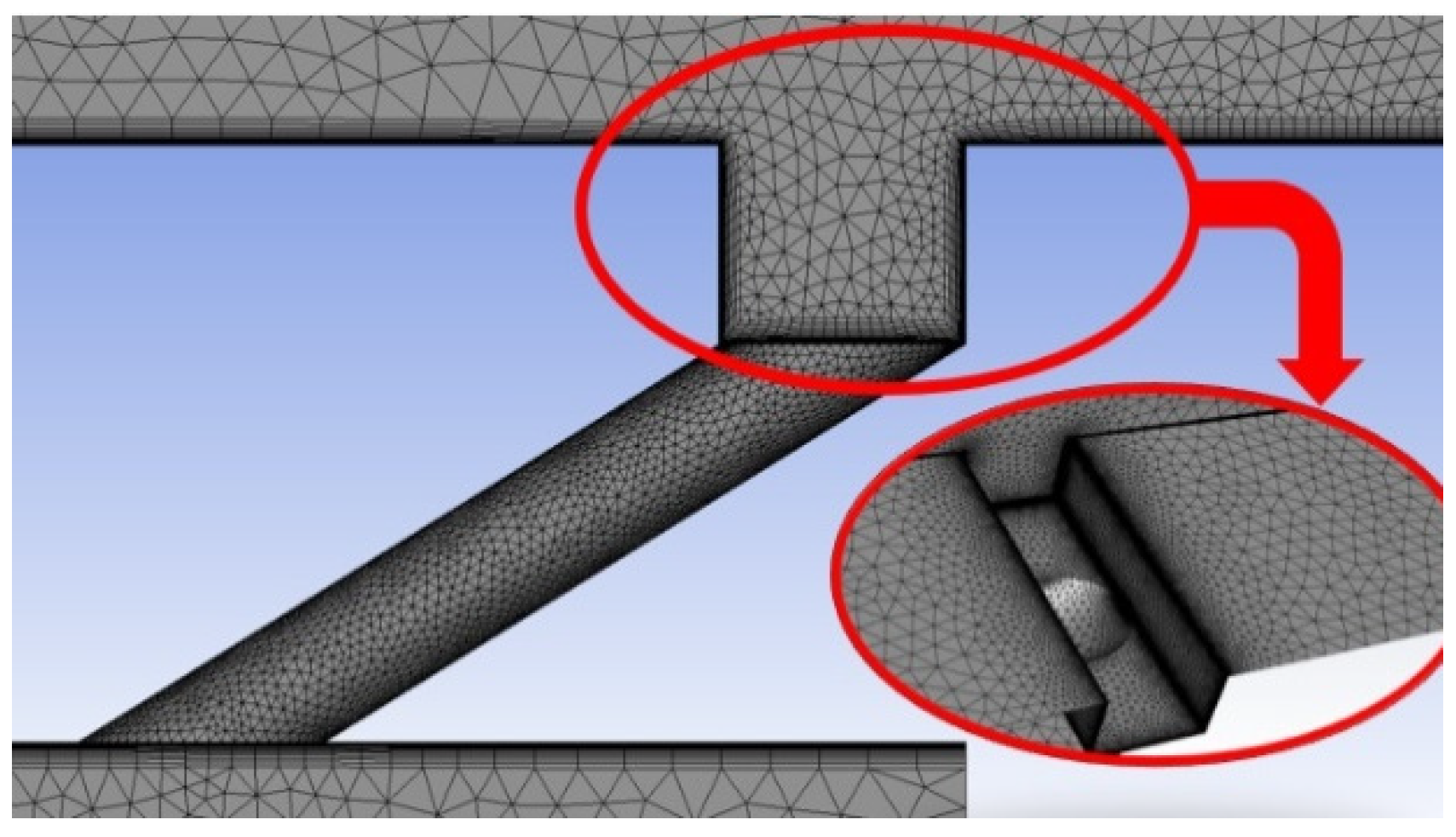



| Boundary Conditions | Parameter | |
|---|---|---|
| Mainstream inlet temperature | Tm | 321 K |
| Mainstream inlet velocity | Um | 13.8 m/s |
| Density ratio | DR | 1.08 |
| Coolant inlet temperature | Tc | 296 K |
| Zhang [42] | This Study | |
|---|---|---|
| BR | 1.0 | 1.0 |
| H/D | 0.75 | 0.75 |
| S/D | 3 | 3 |
| Tm | 321 K | 321 K |
| Um | 13.8 m/s | 13.8 m/s |
| Tc | 296 K | 296 K |
| BR | α | S/D | |
|---|---|---|---|
| 1 | 0.5 | 15 | 1.5 |
| 2 | 1.0 | 30 | 2 |
| 3 | 1.5 | 45 | 3 |
| 4 | 2.0 | 60 | 4 |
| BR | α | S/D | ||
|---|---|---|---|---|
| case1 | 0.5 | 15 | 1.5 | 0.2469927 |
| case2 | 0.5 | 30 | 2 | 0.1904861 |
| case3 | 0.5 | 45 | 3 | 0.1358421 |
| case4 | 0.5 | 60 | 4 | 0.1043346 |
| case5 | 1.0 | 15 | 2 | 0.1672836 |
| case6 | 1.0 | 30 | 1.5 | 0.2941980 |
| case7 | 1.0 | 45 | 4 | 0.0433108 |
| case8 | 1.0 | 60 | 3 | 0.1199711 |
| case9 | 1.5 | 15 | 3 | 0.0877685 |
| case10 | 1.5 | 30 | 4 | 0.0157799 |
| case11 | 1.5 | 45 | 1.5 | 0.3111021 |
| case12 | 1.5 | 60 | 2 | 0.1921019 |
| case13 | 2.0 | 15 | 4 | 0.0764805 |
| case14 | 2.0 | 30 | 3 | 0.0210804 |
| case15 | 2.0 | 45 | 2 | 0.1297517 |
| case16 | 2.0 | 60 | 1.5 | 0.3421512 |
| K1 | 0.1694139 | 0.1446313 | 0.2986111 | |
| K2 | 0.1561909 | 0.1303861 | 0.1699058 | |
| K3 | 0.1516881 | 0.1550017 | 0.0911655 | |
| K4 | 0.142366 | 0.1896397 | 0.0599765 | |
| R | 0.0270479 | 0.0592536 | 0.2386346 | |
| CR | 0.0832407 | 0.1823546 | 0.7344047 |
| BR | α | S/D | H/D | |
|---|---|---|---|---|
| 1 | 0.5 | 15 | 1.5 | 0.25 |
| 2 | 1.0 | 30 | 2 | 0.5 |
| 3 | 1.5 | 45 | 3 | 0.75 |
| 4 | 2.0 | 60 | 4 | 1.0 |
| BR | α | S/D | H/D | ||
|---|---|---|---|---|---|
| case1 | 0.5 | 15 | 1.5 | 0.25 | 0.2405908 |
| case2 | 0.5 | 30 | 2 | 0.5 | 0.2300447 |
| case3 | 0.5 | 45 | 3 | 0.75 | 0.2156554 |
| case4 | 0.5 | 60 | 4 | 1.0 | 0.1959852 |
| case5 | 1.0 | 30 | 3 | 1.0 | 0.2570157 |
| case6 | 1.0 | 15 | 4 | 0.75 | 0.1447769 |
| case7 | 1.0 | 60 | 1.5 | 0.5 | 0.3247846 |
| case8 | 1.0 | 45 | 2 | 0.25 | 0.2755169 |
| case9 | 1.5 | 45 | 4 | 0.5 | 0.0834556 |
| case10 | 1.5 | 60 | 3 | 0.25 | 0.0515732 |
| case11 | 1.5 | 15 | 2 | 1.0 | 0.3176071 |
| case12 | 1.5 | 30 | 1.5 | 0.75 | 0.3435283 |
| case13 | 2.0 | 60 | 2 | 0.75 | 0.2861350 |
| case14 | 2.0 | 45 | 1.5 | 1.0 | 0.4383596 |
| case15 | 2.0 | 30 | 4 | 0.25 | 0.0565686 |
| case16 | 2.0 | 15 | 3 | 0.5 | 0.2332421 |
| K1 | 0.220569025 | 0.231601245 | 0.3368158 | 0.1560624 | |
| K2 | 0.250523525 | 0.221789325 | 0.2773259 | 0.2178818 | |
| K3 | 0.19904105 | 0.253246875 | 0.1893716 | 0.2475239 | |
| K4 | 0.253576325 | 0.2146195 | 0.1201966 | 0.3022419 | |
| R | 0.054535275 | 0.038627375 | 0.2166193 | 0.1461795 | |
| CR | 0.119605013 | 0.084716318 | 0.475082488 | 0.320596182 |
| Optim-Case | Case16 | Case10 | |
|---|---|---|---|
| 0.2104689 | 0.3421512 | 0.0157799 |
| Optim-Case | Case14 | Case10 | |
|---|---|---|---|
| 0.4747241 | 0.4383596 | 0.05157319 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, X.; Chang, J.; Chen, G.; Liu, T.; Ma, H. Contribution of Different Parameters on Film Cooling Efficiency Based on the Improved Orthogonal Experiment Method. Aerospace 2024, 11, 67. https://doi.org/10.3390/aerospace11010067
Duan X, Chang J, Chen G, Liu T, Ma H. Contribution of Different Parameters on Film Cooling Efficiency Based on the Improved Orthogonal Experiment Method. Aerospace. 2024; 11(1):67. https://doi.org/10.3390/aerospace11010067
Chicago/Turabian StyleDuan, Xinlei, Jianlong Chang, Guangsong Chen, Taisu Liu, and He Ma. 2024. "Contribution of Different Parameters on Film Cooling Efficiency Based on the Improved Orthogonal Experiment Method" Aerospace 11, no. 1: 67. https://doi.org/10.3390/aerospace11010067
APA StyleDuan, X., Chang, J., Chen, G., Liu, T., & Ma, H. (2024). Contribution of Different Parameters on Film Cooling Efficiency Based on the Improved Orthogonal Experiment Method. Aerospace, 11(1), 67. https://doi.org/10.3390/aerospace11010067







