Research on the Motion and Dynamic Characteristics of the Hose-and-Drogue System under Bow Wave
Abstract
:1. Introduction
2. Modeling
2.1. The Hose-and-Drogue System
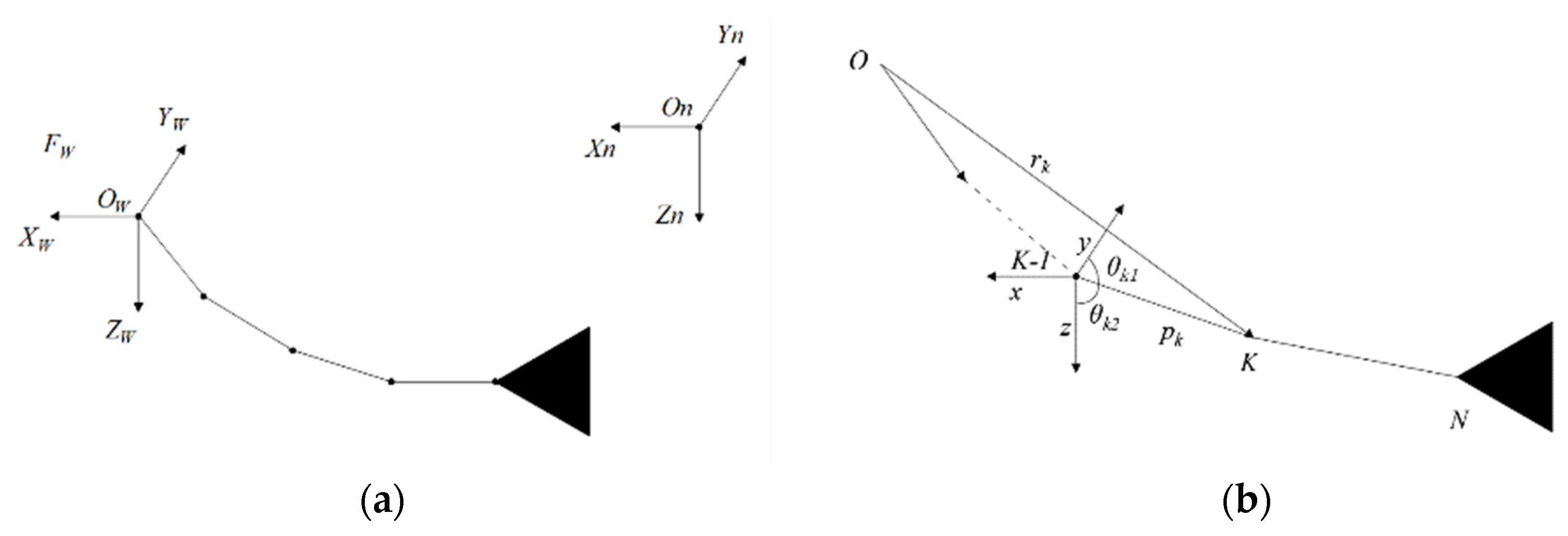
2.1.1. Kinematic Analysis
2.1.2. Dynamic Analysis
2.1.3. External Force Analysis
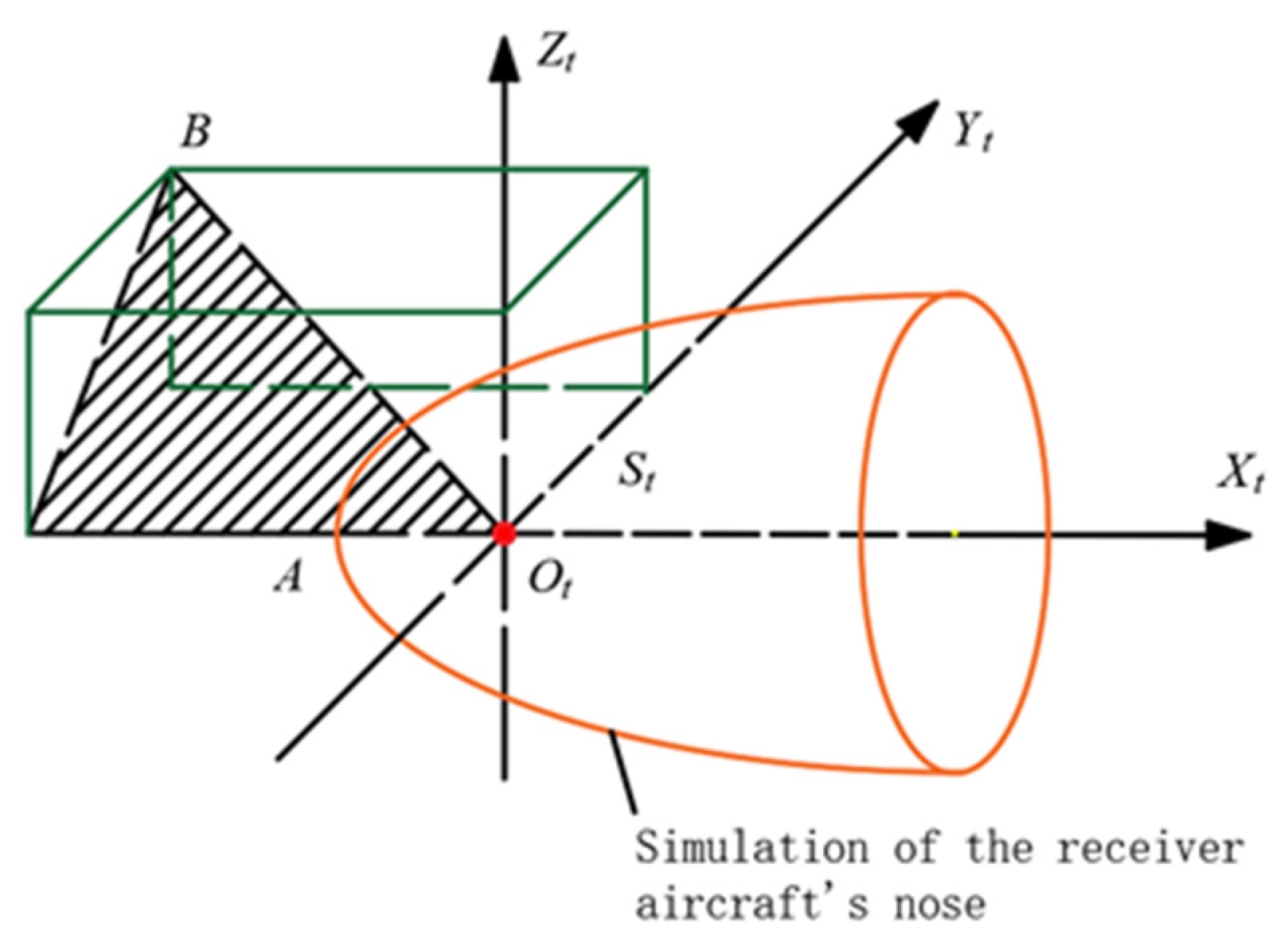
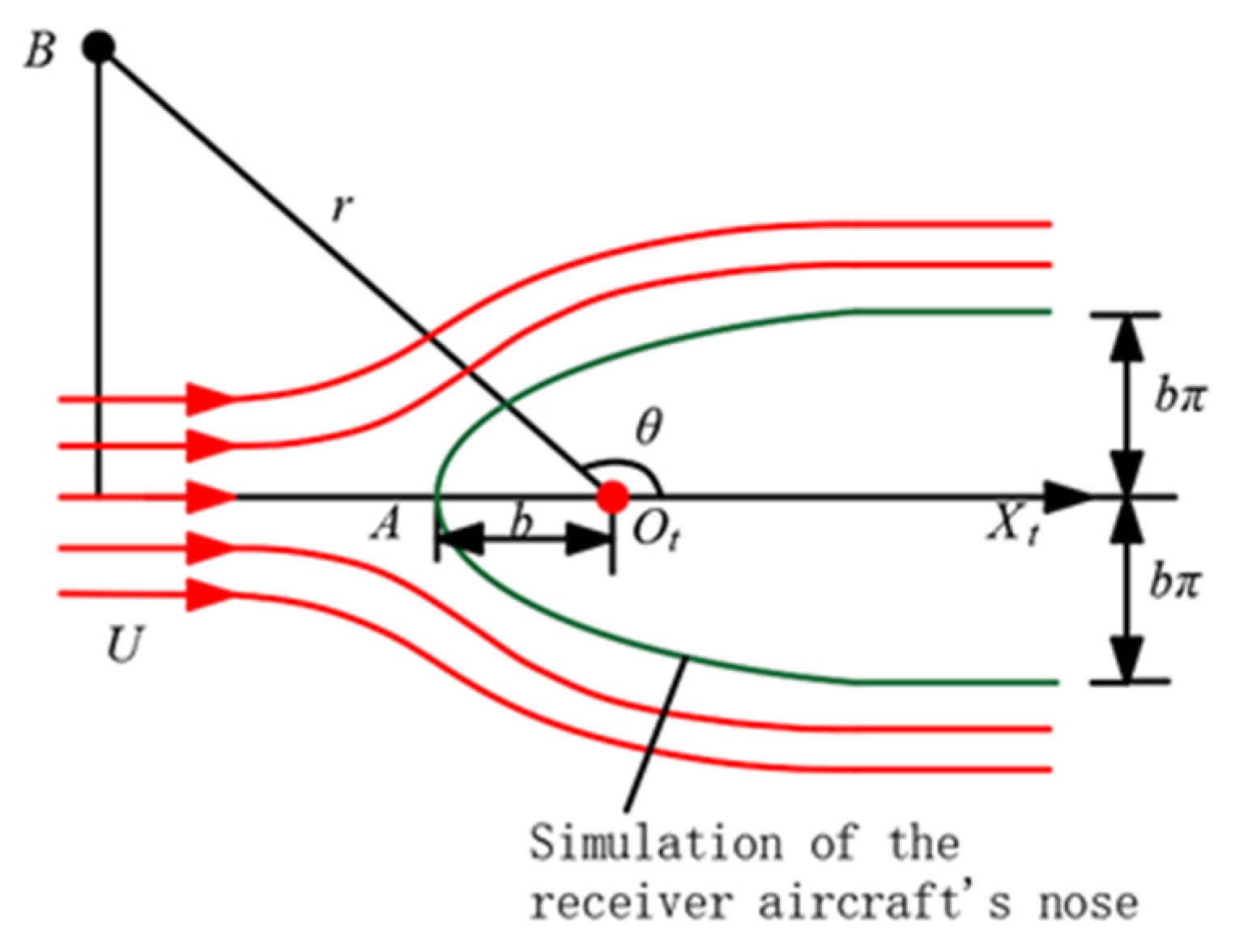
2.2. Bow Wave
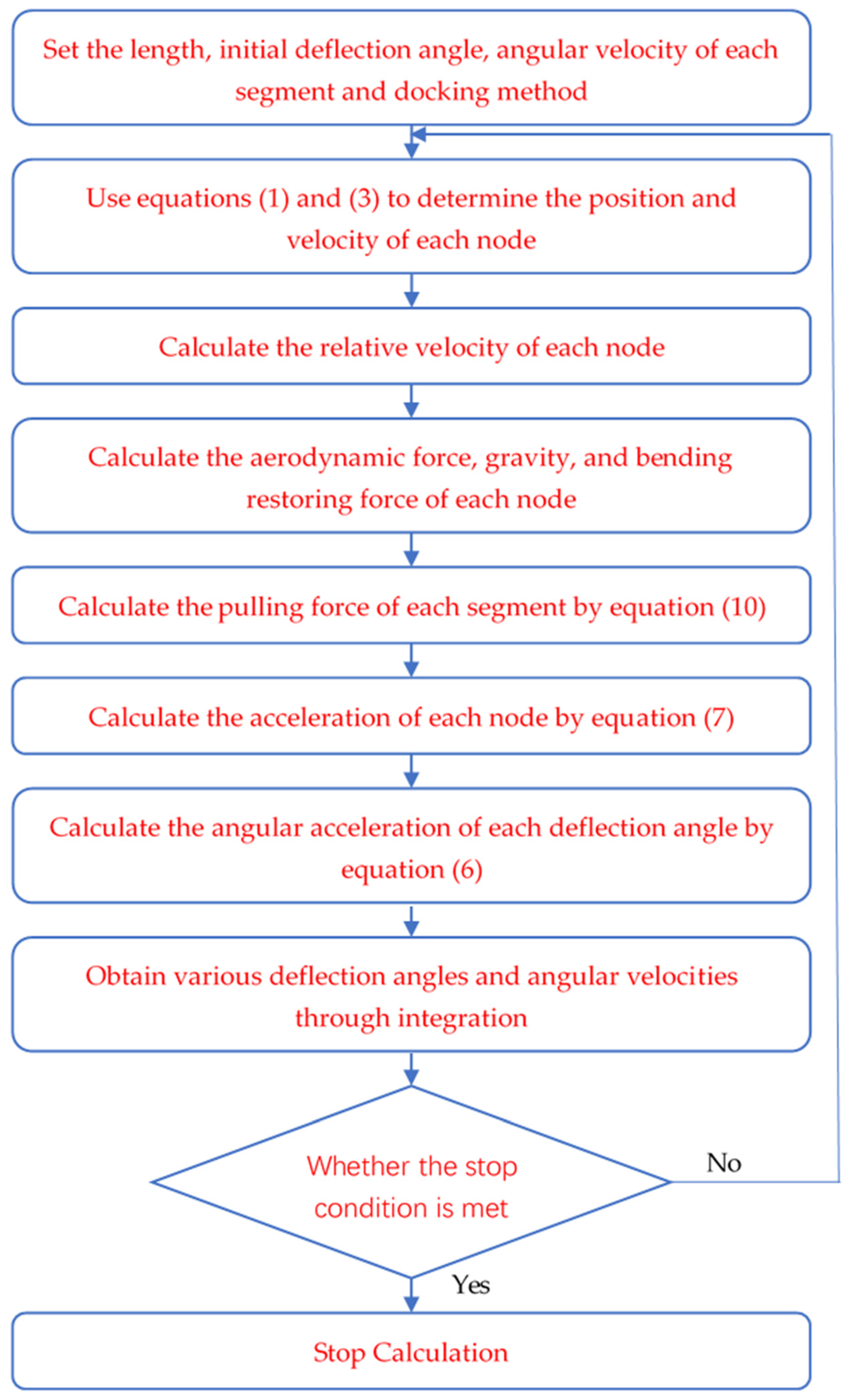
3. Numerical Simulation and Analysis
3.1. Model Accuracy Verification
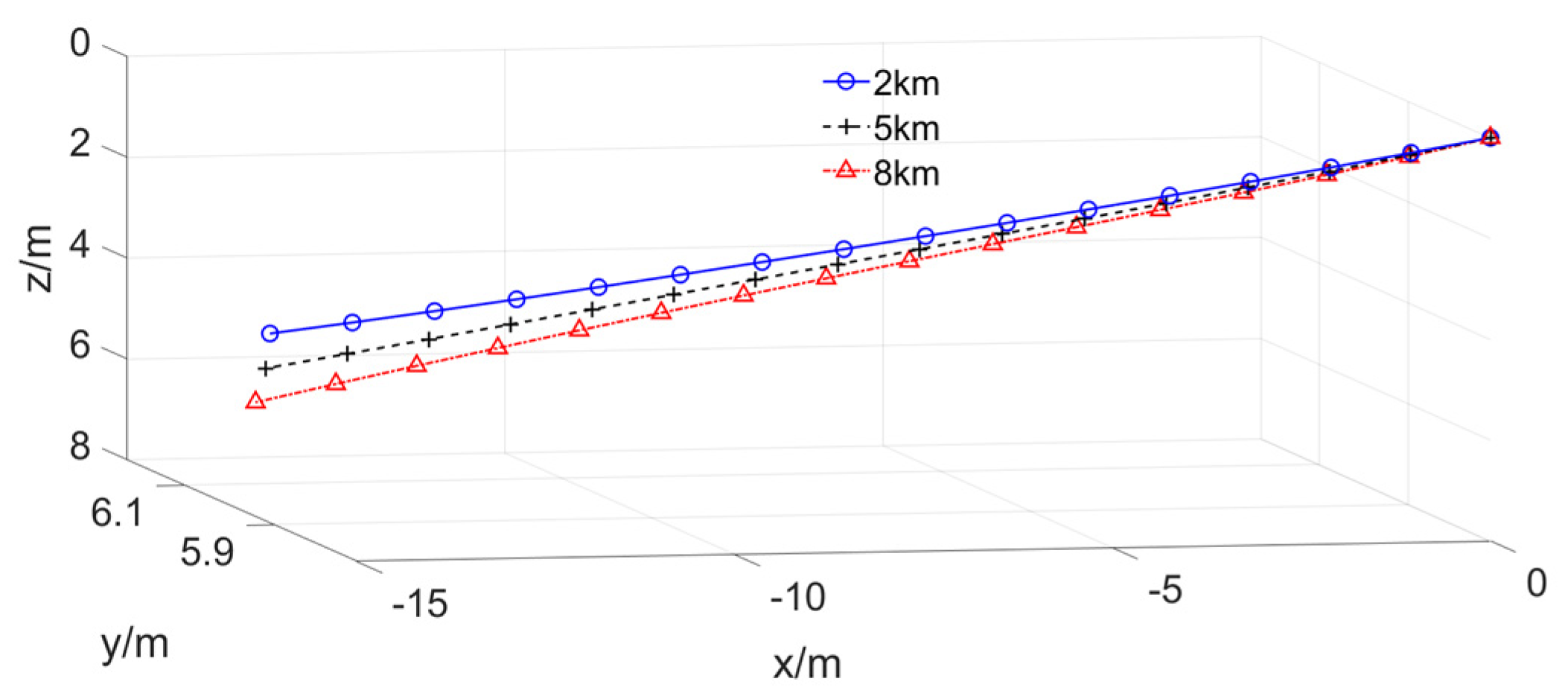
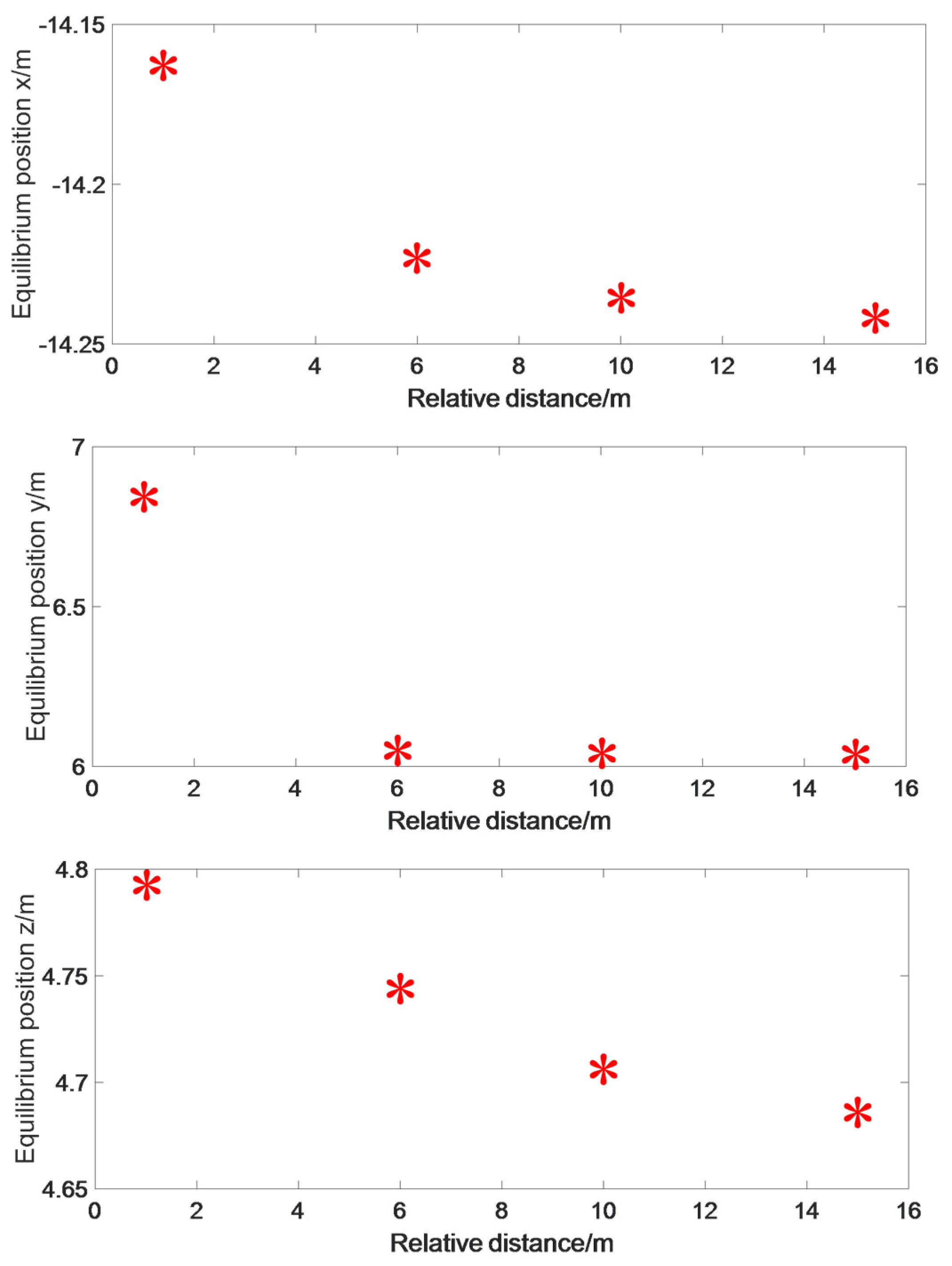
3.2. The Equilibrium Position of the Drogue under the Bow Wave
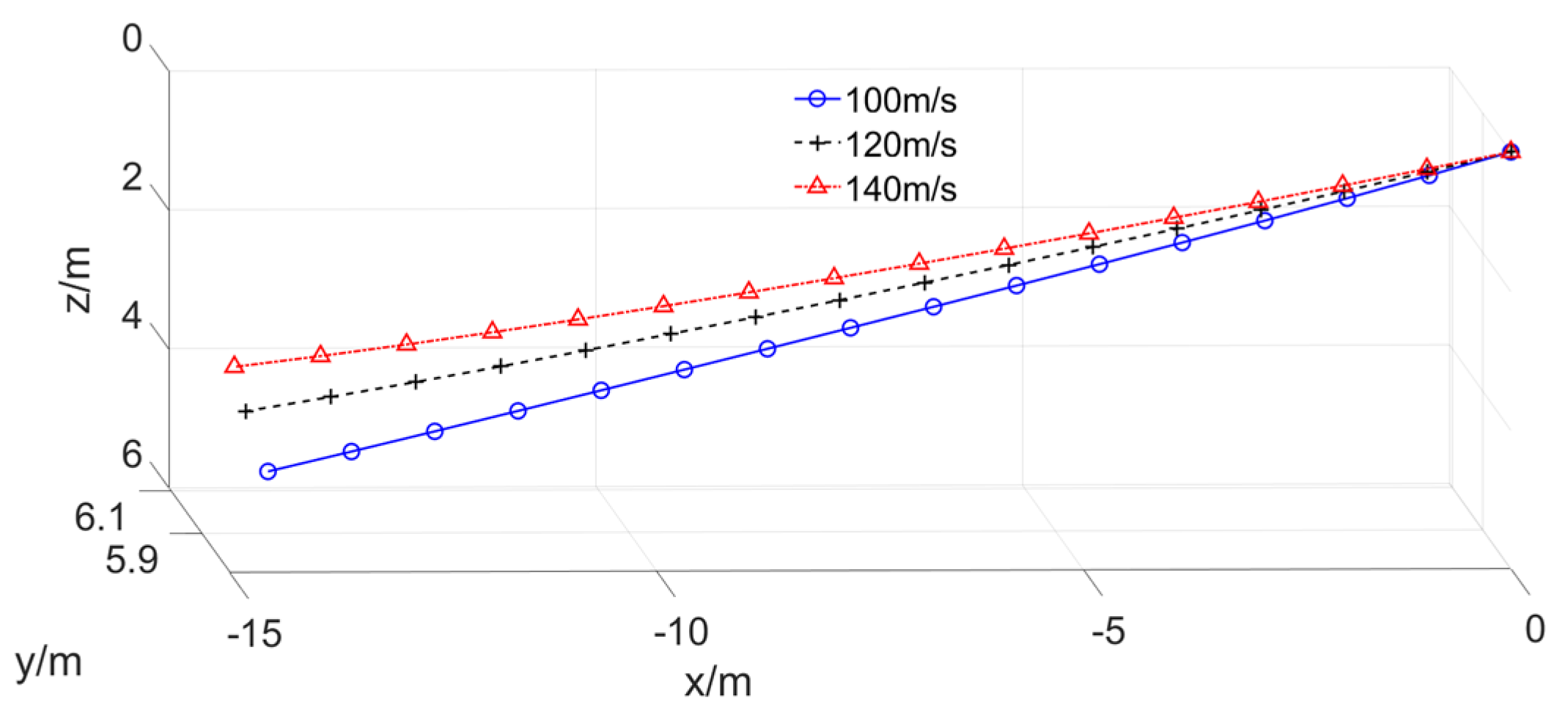
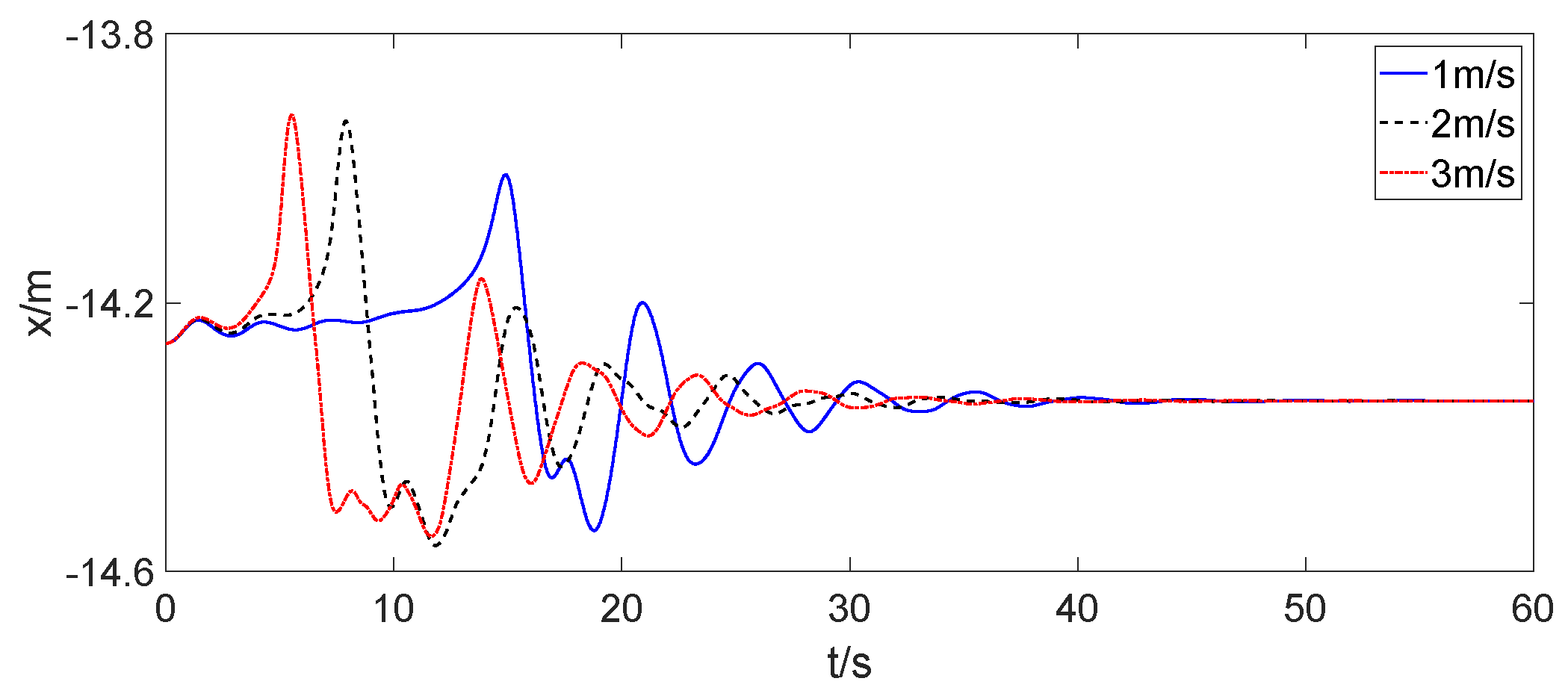
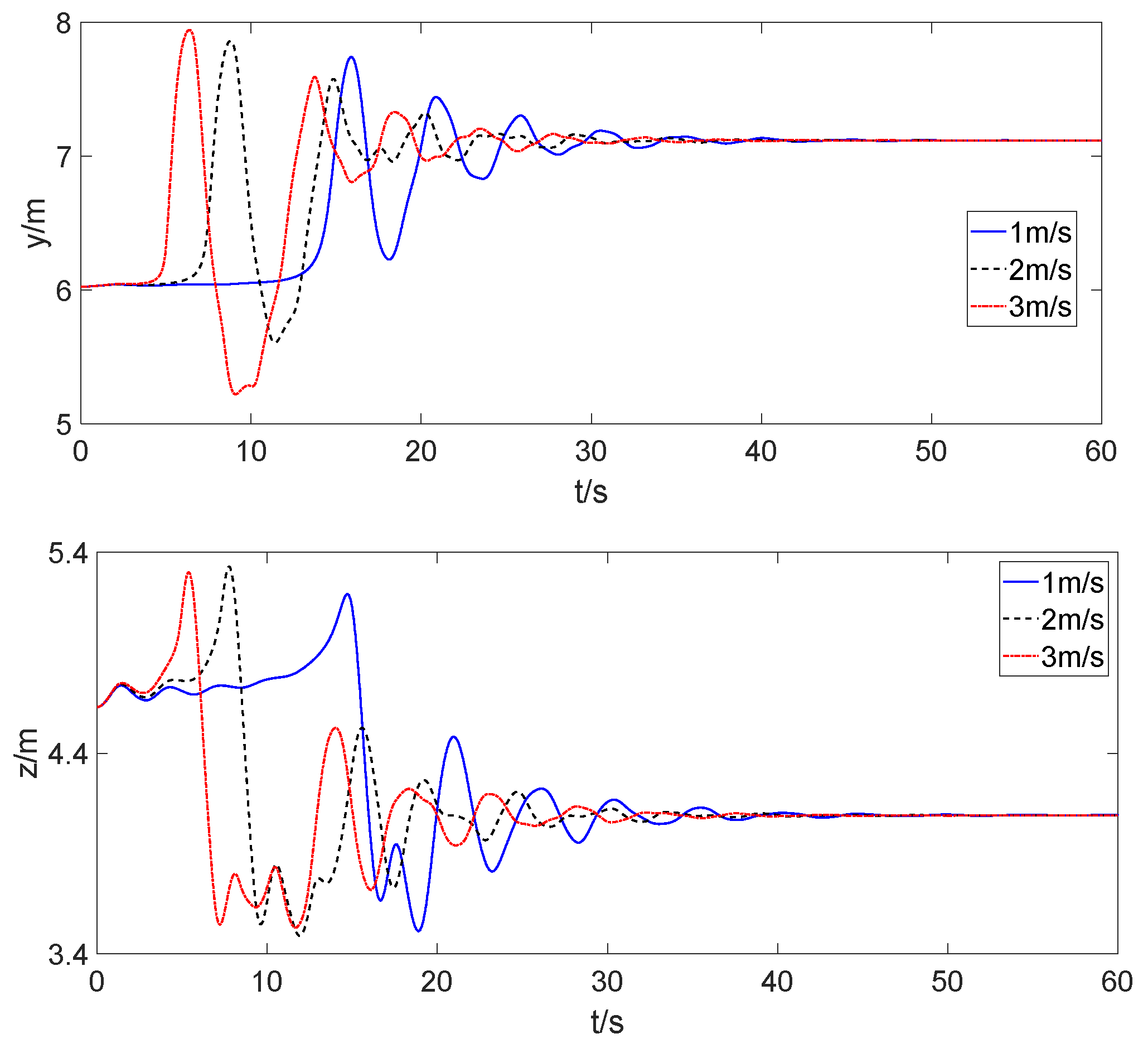
3.3. Change of the Drogue When the Receiver Aircraft Approached at a Constant Speed
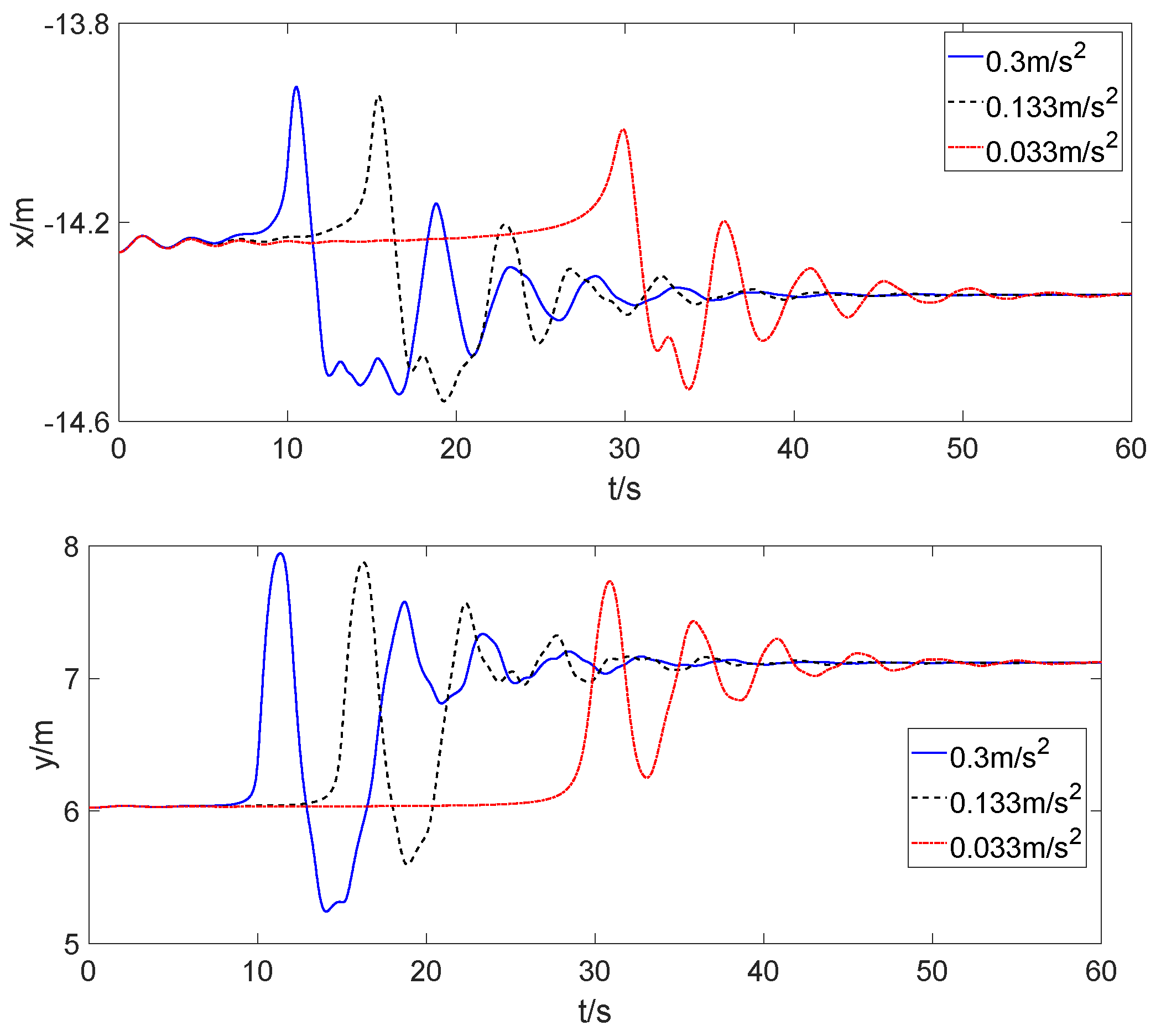
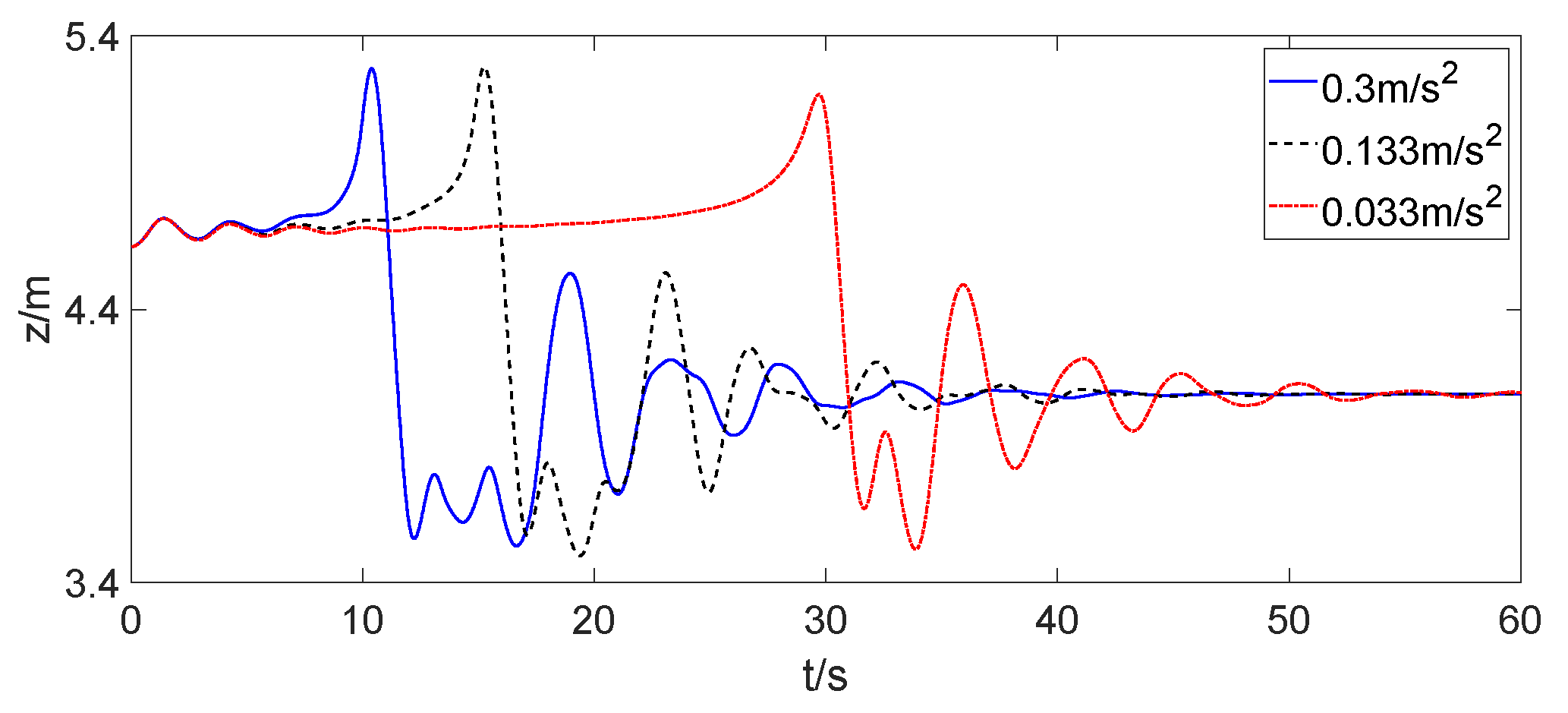
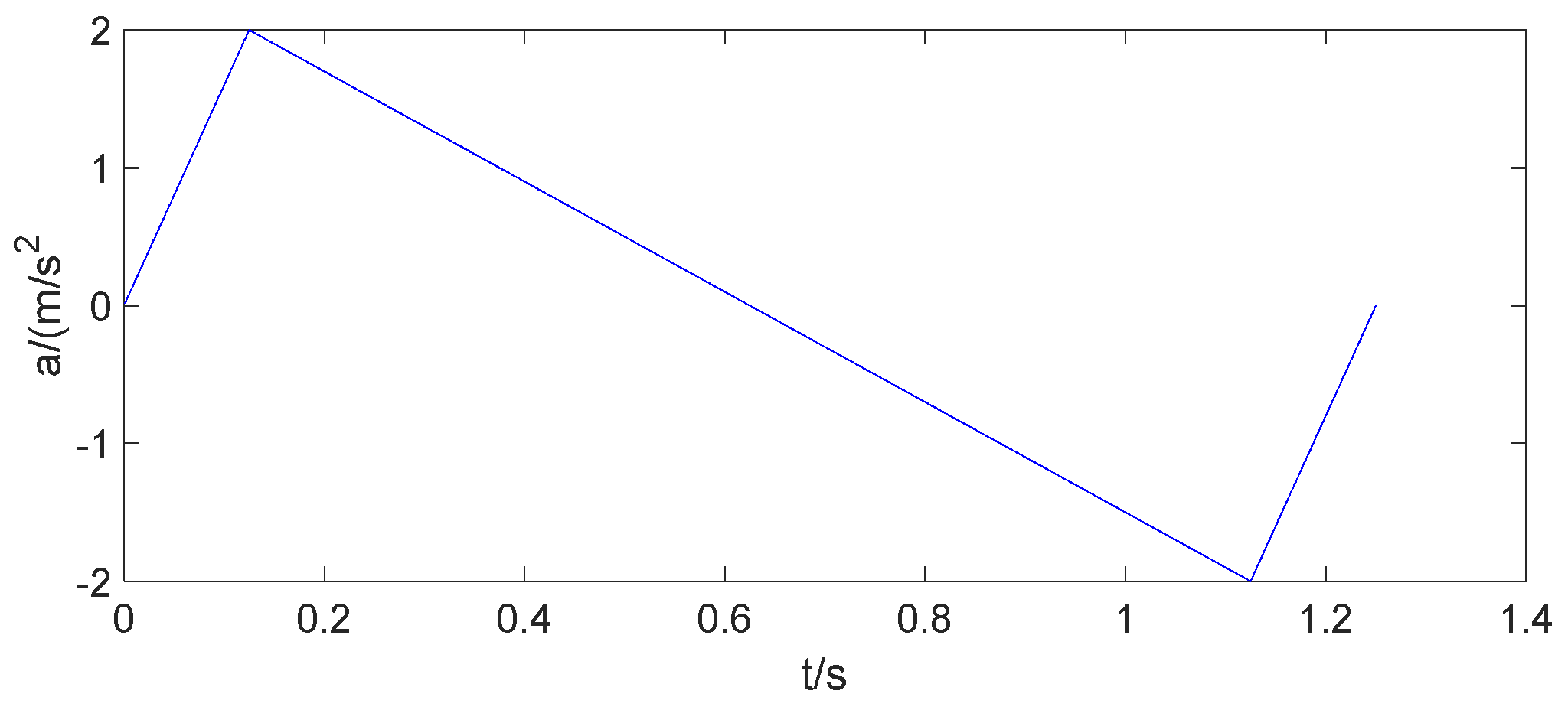
3.4. Change of the Drogue When the Receiver Aircraft Approached at a Uniform Acceleration
3.5. Dynamic Analysis after Docking
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lu, Y.P.; Yang, C.X.; Liu, Y.Y. A survey of modeling and control technologies for aerial refueling system. Acta Aeronaut. Astronaut. Sin. 2014, 35, 2375–2389. [Google Scholar]
- Zhong, D.X.; Li, Y.Q.; Li, Y.R. State-of-the-art and Tendency of Autonomous Aerial Refueling Technologies for Unmanned Aerial Vehicles. Aeronaut. Sci. Technol. 2014, 25, 1–6. [Google Scholar]
- Lofthouse, A.J.; Nathan, B. CFD modeling of B-52 and KC-135 in air refueling formation. In Proceedings of the 35th AIAA Applied Aerodynamics Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar]
- Chen, L.L.; Liu, X.Q. Numerical Analysis of Refueling Drogue Oscillation During Refueling Docking. Trans. Nanjing Univ. Aeronaut. Astronaut. 2016, 33, 173–179. [Google Scholar]
- Li, M.Z.; Wang, Z.; Zhao, Y.T.; Zhang, K.Y.; Shi, Y.Q. Dynamic response analysis of aerial refueling hose-drogue under complex flow field. Flight Dyn. 2020, 38, 32–36. [Google Scholar]
- Zhang, X.M.; Shao, Z.; Shi, J.Y. Dynamic modeling and simulation of aerial refueling hose-drogue. Technol. Innov. Appl. 2020, 1, 19–21. [Google Scholar]
- Xu, F.R. Calculation of the towing position of aerial refueling hose. Chin. Q. Mech. 1985, 3, 57–63. [Google Scholar]
- Ribbens, W.; Saggio, F.; Wierenga, R.; Feldmann, M. Dynamic modeling of an aerial refueling hose & drogue system. In Proceedings of the 25th AIAA Applied Aerodynamics Conference, Miami, FL, USA, 25–28 June 2007. [Google Scholar]
- Erickson, A.J.; Richards, P.W.; Chaturvedi, A.N. Aeroelastic Modeling of Hose and Drogue Aerial Refueling Systems Including a Hose Reeling Mechanism. In Proceedings of the AIAA SciTech Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar]
- Zhu, Z.H.; Meguid, S.A. Elastodynamic analysis of aerial refueling hose using curved beam element. AIAA J. 2006, 44, 1317–1324. [Google Scholar] [CrossRef]
- Ro, K.; Kamman, J.W. Modeling and Simulation of Hose-Paradrogue Aerial Refueling Systems. J. Guid. Control Dyn. 2010, 33, 53–63. [Google Scholar] [CrossRef]
- Zhang, J.; Yuan, S.Z.; Gong, Q.Q. Modeling and Control of Shaking Motion of Aerial Refueling Hose-Drogue. J. Syst. Simul. 2016, 28, 388–395. [Google Scholar]
- Cheng, J.F.; Ji, K. Dynamic modeling and simulation of variable-length hose–drogue aerial refueling systems. AIP Adv. 2022, 12, 015104. [Google Scholar] [CrossRef]
- Cheng, J.F.; Deng, F.; Liu, X.Q.; Ji, K. Active Control of Aerial Refueling Hose-Drogue Dynamics with the Improved Reel Take-Up System. Int. J. Aerosp. Eng. 2022, 2022, 4696037. [Google Scholar] [CrossRef]
- Cai, Y.P.; Wang, Y.X.; Wang, D.Y.; Ren, B.; Wang, H.L. Study on dynamic characteristics of refueling hose during release. Tactical Missile Technol. 2022, 6, 54–62. [Google Scholar]
- Min, Q. Dynamic modeling and load calculation of hose whipping phenomenon of aerial refueling hose-drogue assembly. J. Sichuan Univ. Sci. Eng. (Nat. Sci. Ed.) 2020, 33, 76–82. [Google Scholar]
- Wang, H.T.; Dong, X.M.; Dou, H.F. Dynamic modeling and characteristics analysis of hose-paradrogue aerial refueling system. J. Beijing Univ. Aeronaut. Astronaut. 2014, 40, 92–98. [Google Scholar]
- Wang, H.T.; Dong, X.M.; Xue, J.P.; Liu, J.L. Dynamic modeling of a hose-drogue aerial refueling system and integral sliding mode backstepping control for the hose whipping phenomenon. Chin. J. Aeronaut. 2014, 27, 930–946. [Google Scholar] [CrossRef]
- Wang, H.T.; Dong, X.M. Dynamics and Control of Aerial Refueling, 1st ed.; National Defense Industry Press: Beijing, China, 2016; pp. 202–207. [Google Scholar]
- Styuart, A.; Yamashiro, H.; Stirling, R.; Mor, M. Numerical simulation of hose whip phenomenon in aerial refueling. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Portland, OR, USA, 8–11 August 2011. [Google Scholar]
- Zhang, X.F.; Hu, M.Q.; Tian, P.Y. Analysis of impact on bending moment of the hose in dynamic modeling of aerial refueling hose-drogue system. Flight Dyn. 2018, 36, 92–96. [Google Scholar]
- Wang, W.; Liu, X.Z.; Wang, P. Dynamics of hose-drogue refueling systems during coupling. Flight Dyn. 2013, 31, 180–183. [Google Scholar]
- Bhandari, U.; Thomas, P.R.; Bullock, S.; Richardson, T.S. Bow Wave Effect in Probe and Drogue Aerial Refueling. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Boston, MA, USA, 19–22 August 2013. [Google Scholar]
- Zhou, R.X.; Yang, S.J.; Lin, Y.J. Design and research of the hose-drogue aerial refueling hardware-in-the-loop simulation system. J. Graph. 2021, 42, 478–484. [Google Scholar]
- Zhang, X.F.; Hu, M.Q.; Zhang, D.; Tian, P.Y.; Wang, N. Influence of the receiver aircraft’s bow wave on the motion characteristics of the drogue in hose-drogue refueling system. In Journal of Physics: Conference Series, Proceedings of the 2st International Conference on Fluid Mechanics and Industrial Applications, Guilin, China, 12–14 July 2018; IOP Publishing: Bristol, UK, 2018. [Google Scholar]
- Dai, X.H.; Wei, Z.B.; Quan, Q. Modeling and simulation of bow wave effect in probe and drogue aerial refueling. Chin. J. Aeronaut. 2016, 29, 448–461. [Google Scholar] [CrossRef]
- Wang, J.; Dong, X.M.; Xu, Y.J.; Wang, H.T.; Liu, J.L.; Shi, C. Simulation and analysis of the bow wave effect of the receiver in hose-drogue aerial refueling. Flight Dyn. 2016, 34, 54–58. [Google Scholar]
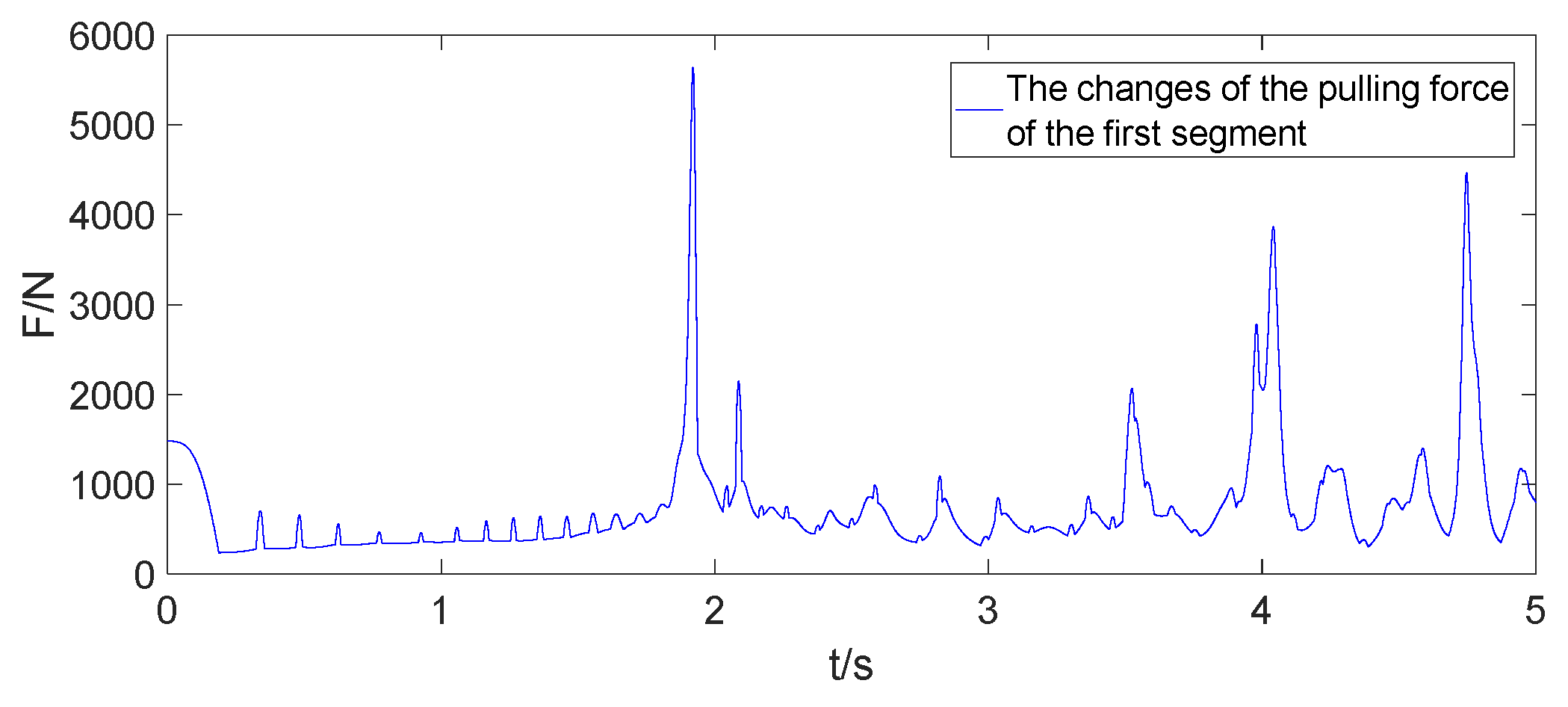

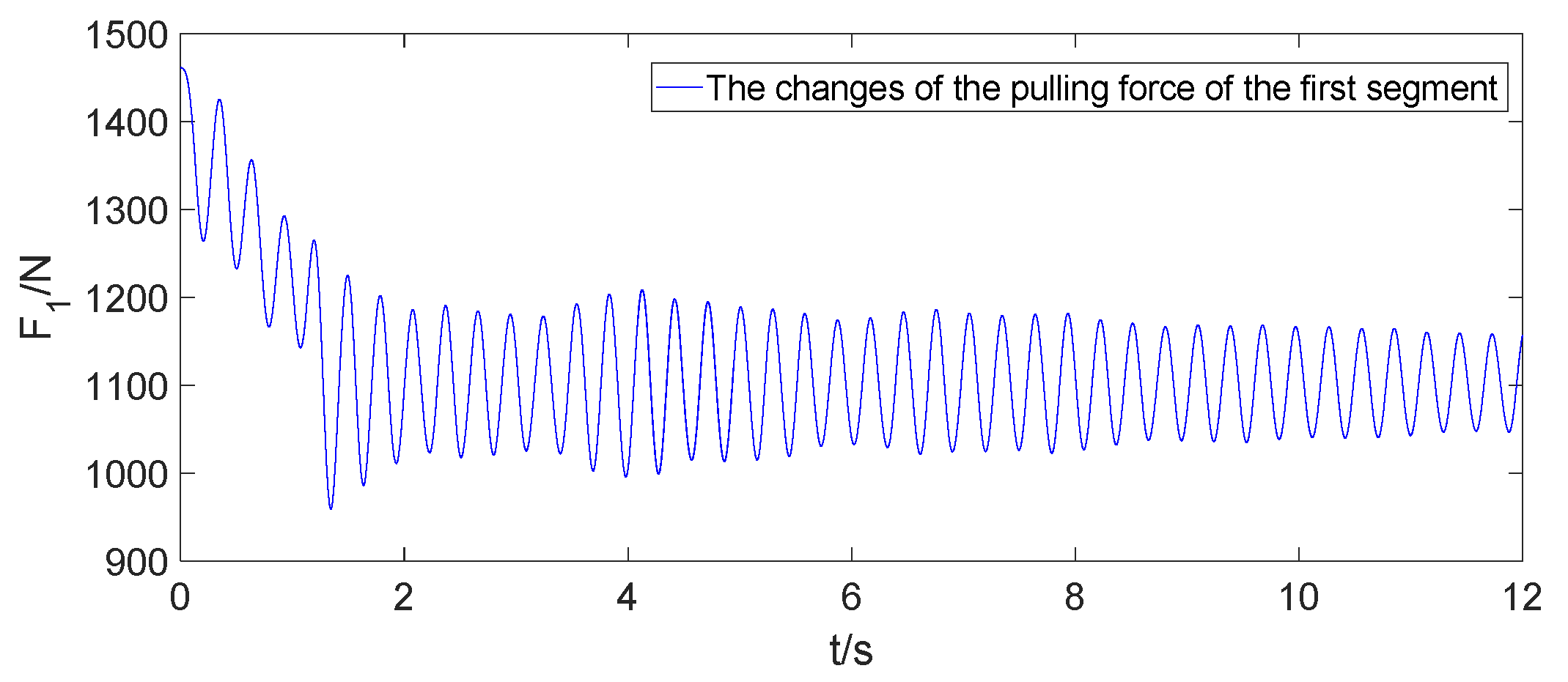
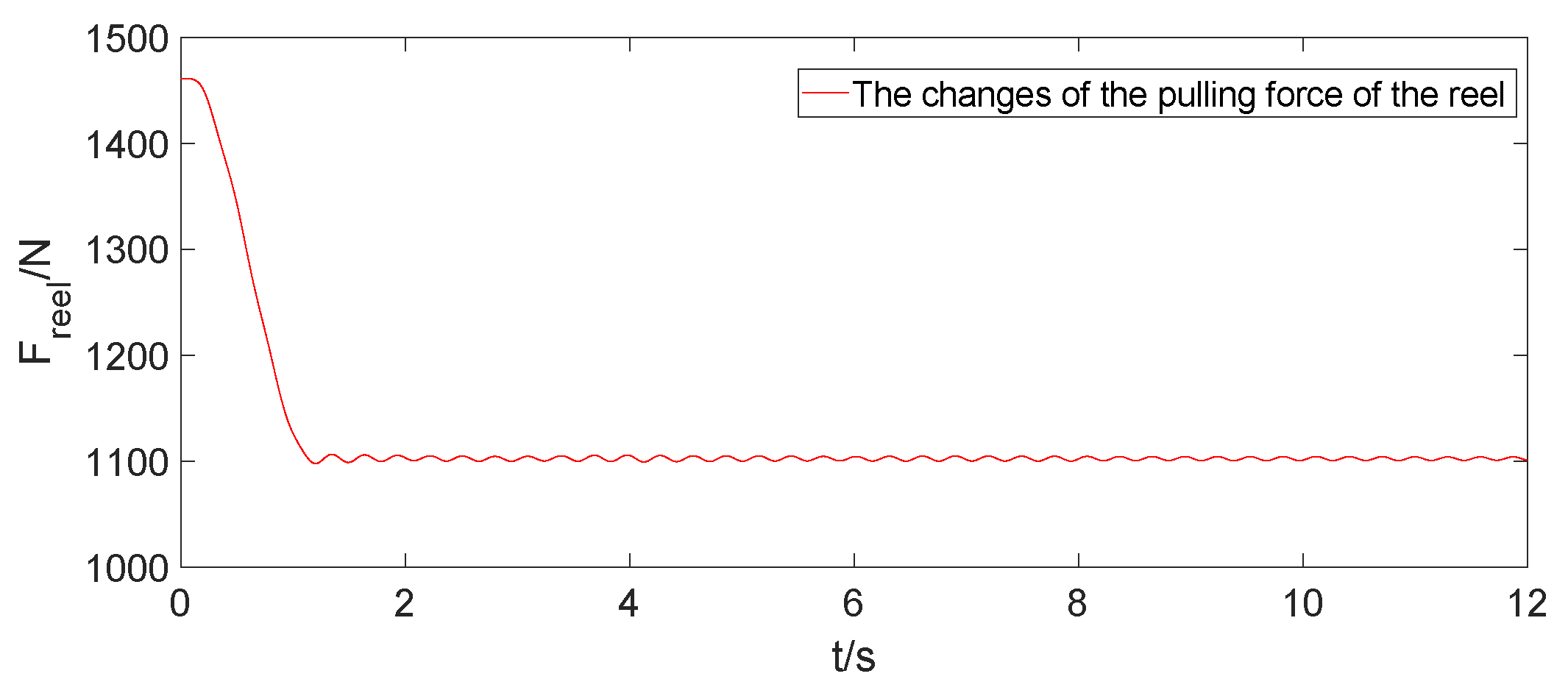
| Parameter/Unit | Symbol | Value |
|---|---|---|
| Hose length/m | L | 15 |
| Mass per unit length hose/(kg/m) | μ | 4 |
| Hose outer diameter/m | do | 0.066 |
| Hose inner diameter/m | di | 0.051 |
| Drogue mass/kg | mdrogue | 30 |
| Drogue diameter/m | ddrogue | 0.61 |
| Hose elastic modulus/MPa | E | 13.78 |
| Hose polar moment of inertia/m4 | I | 5.993 × 10−7 |
| Drogue drag coefficient | cdrogue | 0.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, C.; Wang, H.; Hu, L.; Cai, Y. Research on the Motion and Dynamic Characteristics of the Hose-and-Drogue System under Bow Wave. Aerospace 2024, 11, 13. https://doi.org/10.3390/aerospace11010013
Zheng C, Wang H, Hu L, Cai Y. Research on the Motion and Dynamic Characteristics of the Hose-and-Drogue System under Bow Wave. Aerospace. 2024; 11(1):13. https://doi.org/10.3390/aerospace11010013
Chicago/Turabian StyleZheng, Chunjie, Haitao Wang, Lanxiang Hu, and Yuanli Cai. 2024. "Research on the Motion and Dynamic Characteristics of the Hose-and-Drogue System under Bow Wave" Aerospace 11, no. 1: 13. https://doi.org/10.3390/aerospace11010013
APA StyleZheng, C., Wang, H., Hu, L., & Cai, Y. (2024). Research on the Motion and Dynamic Characteristics of the Hose-and-Drogue System under Bow Wave. Aerospace, 11(1), 13. https://doi.org/10.3390/aerospace11010013







