Delay in the Air or Detour on the Ground?—A Case Study in Guangzhou Baiyun International Airport
Abstract
:1. Introduction
2. Model Formulation
2.1. Formulation of the Runway Assignment Model
- The initial EF time , initial pushback time , and initial speed are known based on the historical data;
- Aircraft follows the STAR route and taxi route precisely;
- Final speed landing on the runway is a constant according to Charts;
- Arrivals are to approach with a constant deceleration ;
- Taxi speeds are a constant for arrivals and departures;
- TMA and taxi route networks are treated as a graph containing nodes and links.
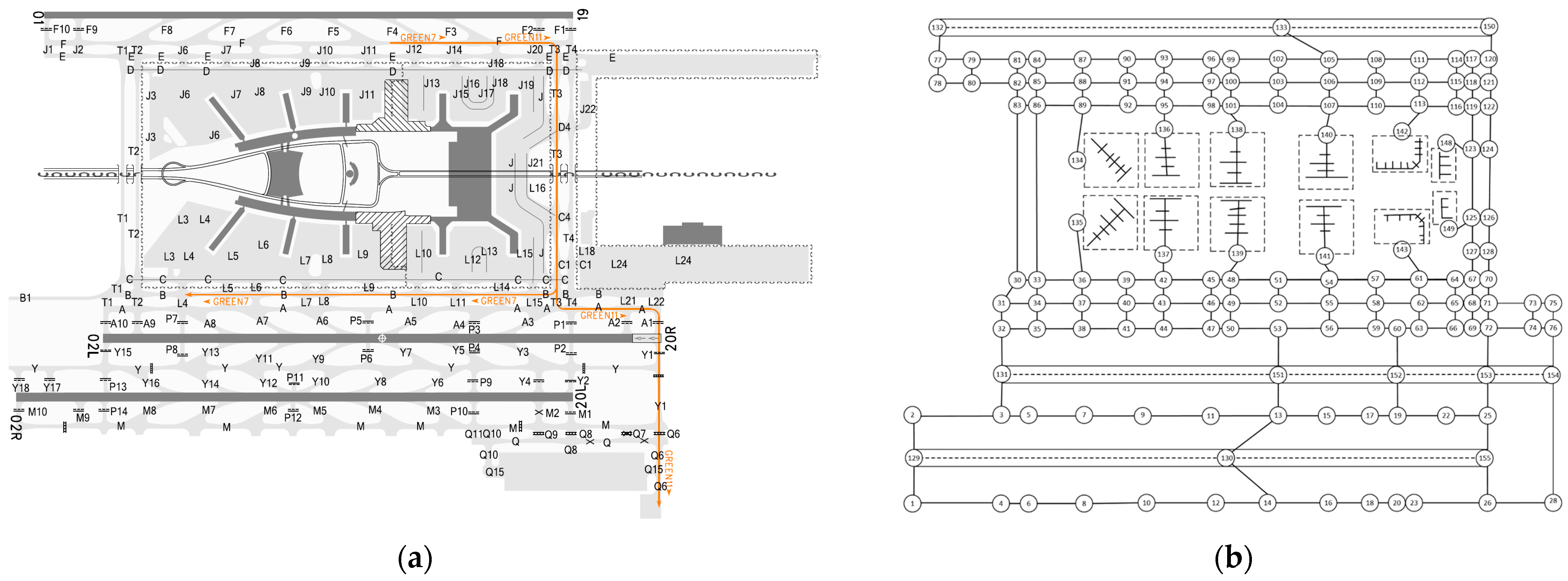
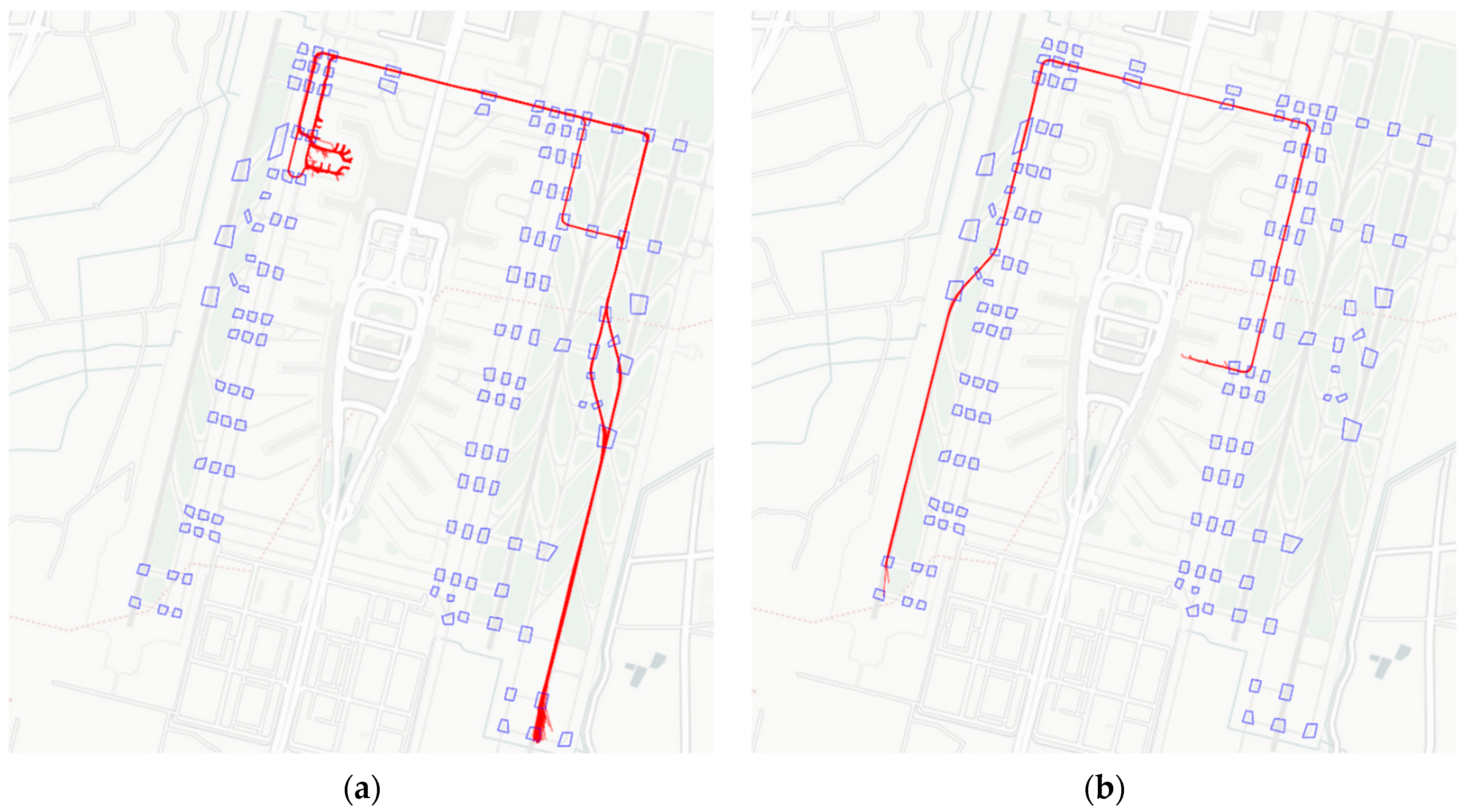
2.2. Taxi Route Recognition based on Historical Trajectories
| Algorithm 1. Taxi routes recognition |
 |
3. Solution Algorithm
| Algorithm 2. Simulated annealing |
 |
 |
| Algorithm 3. Adaptive initial temperature |
 |
| Algorithm 4. Neighborhood function |
 |
 |
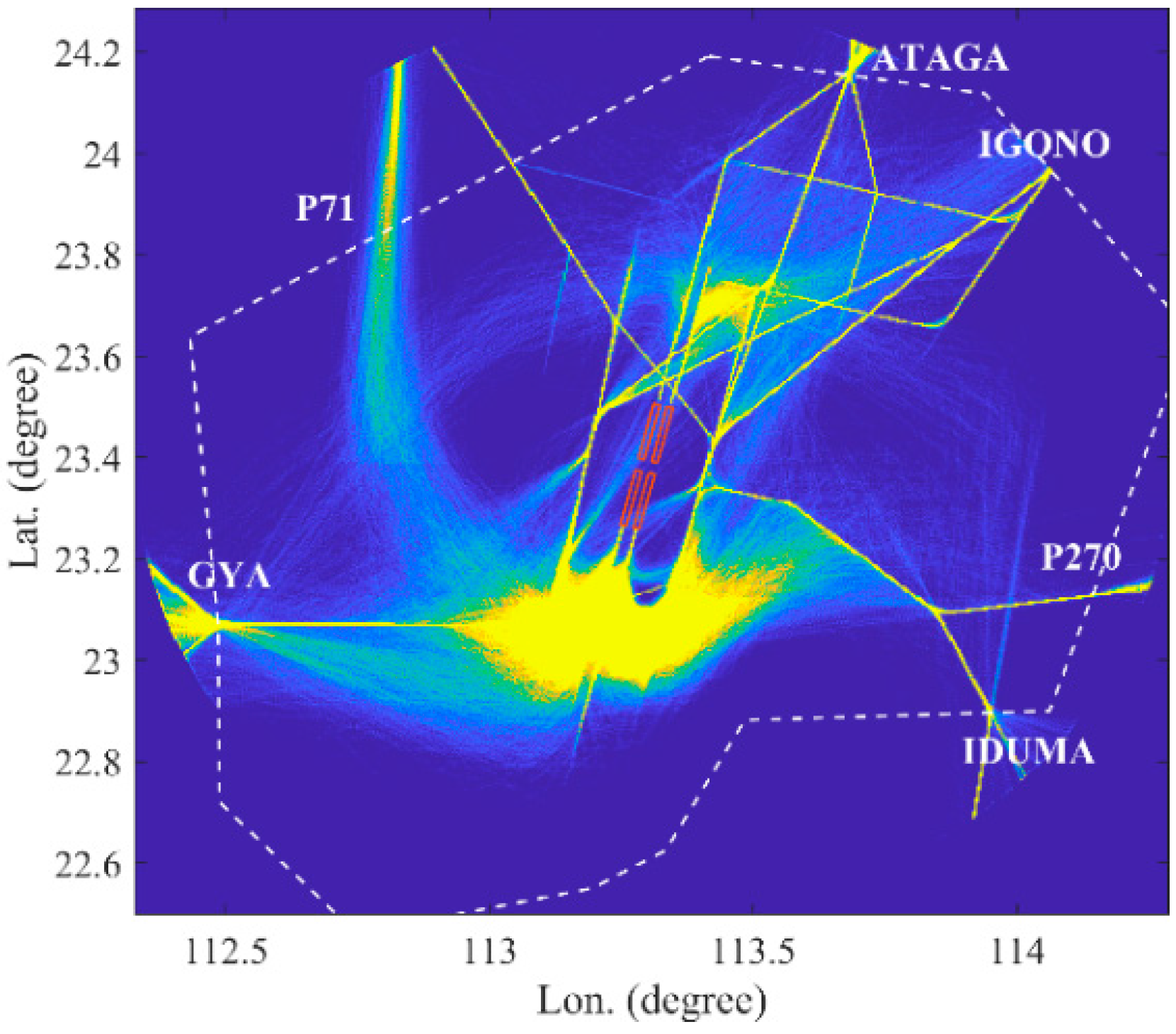
4. Case Study
5. Results
5.1. Experimental Settings
5.2. Results Analysis
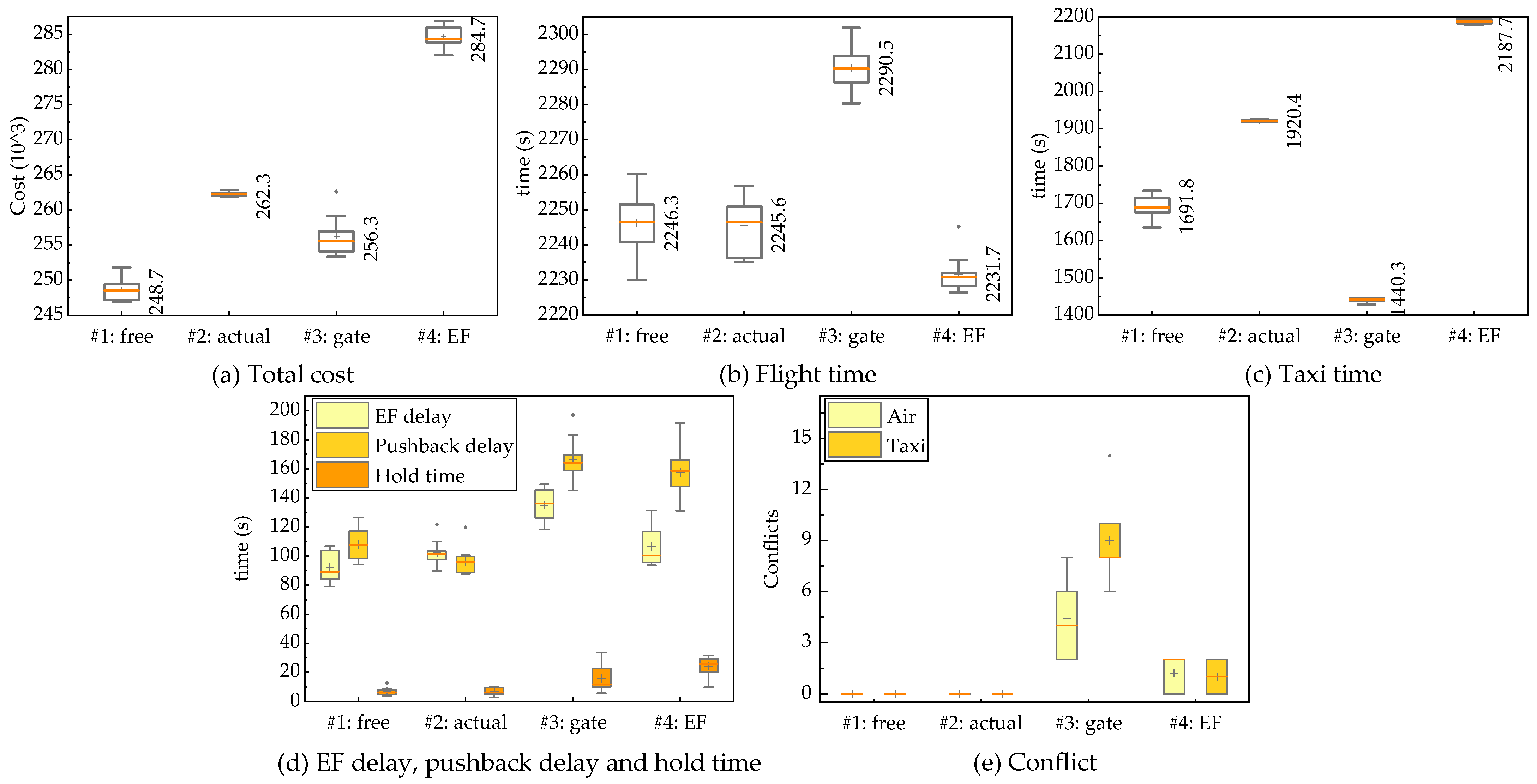
5.2.1. Cost Function
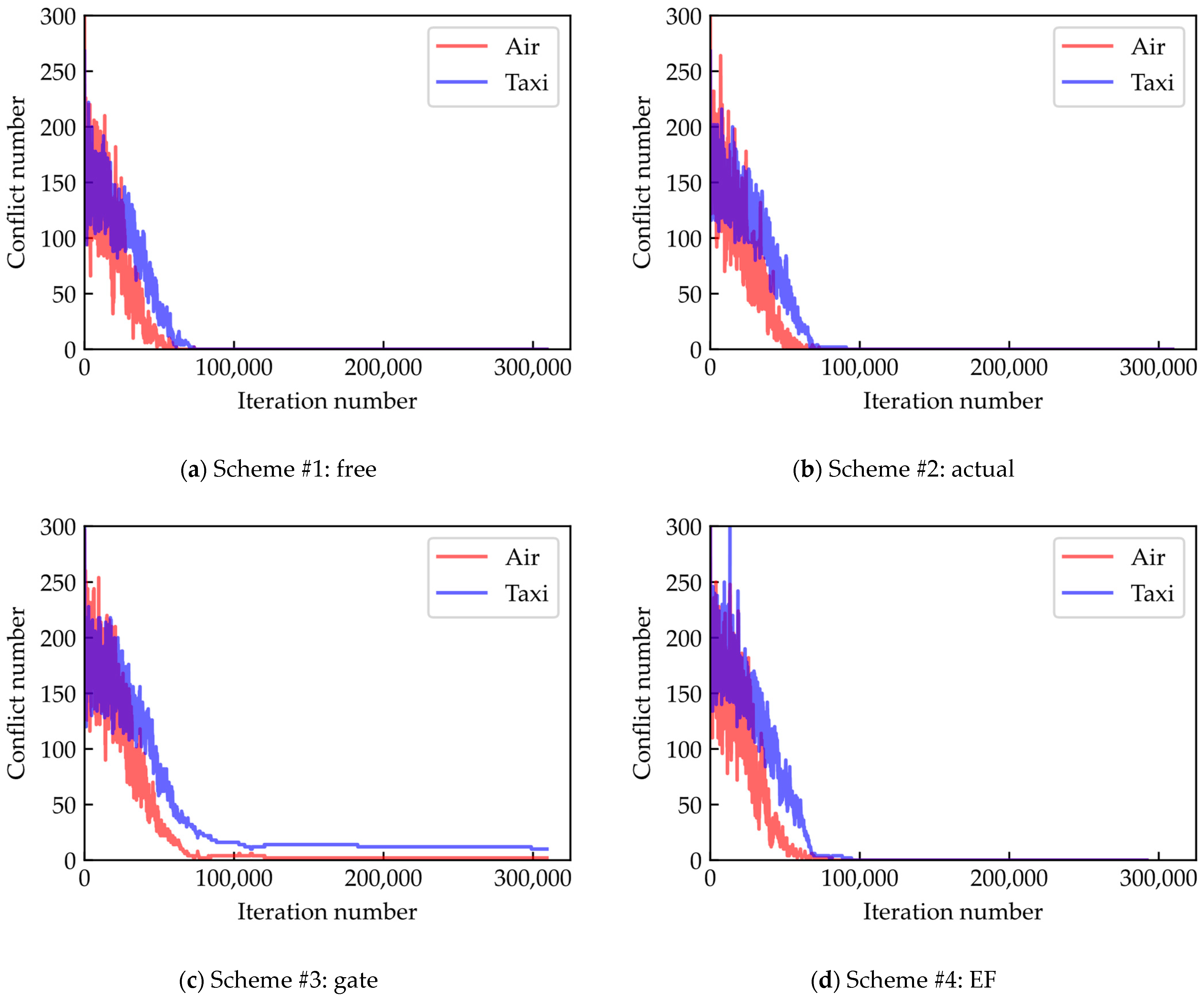
5.2.2. Conflict
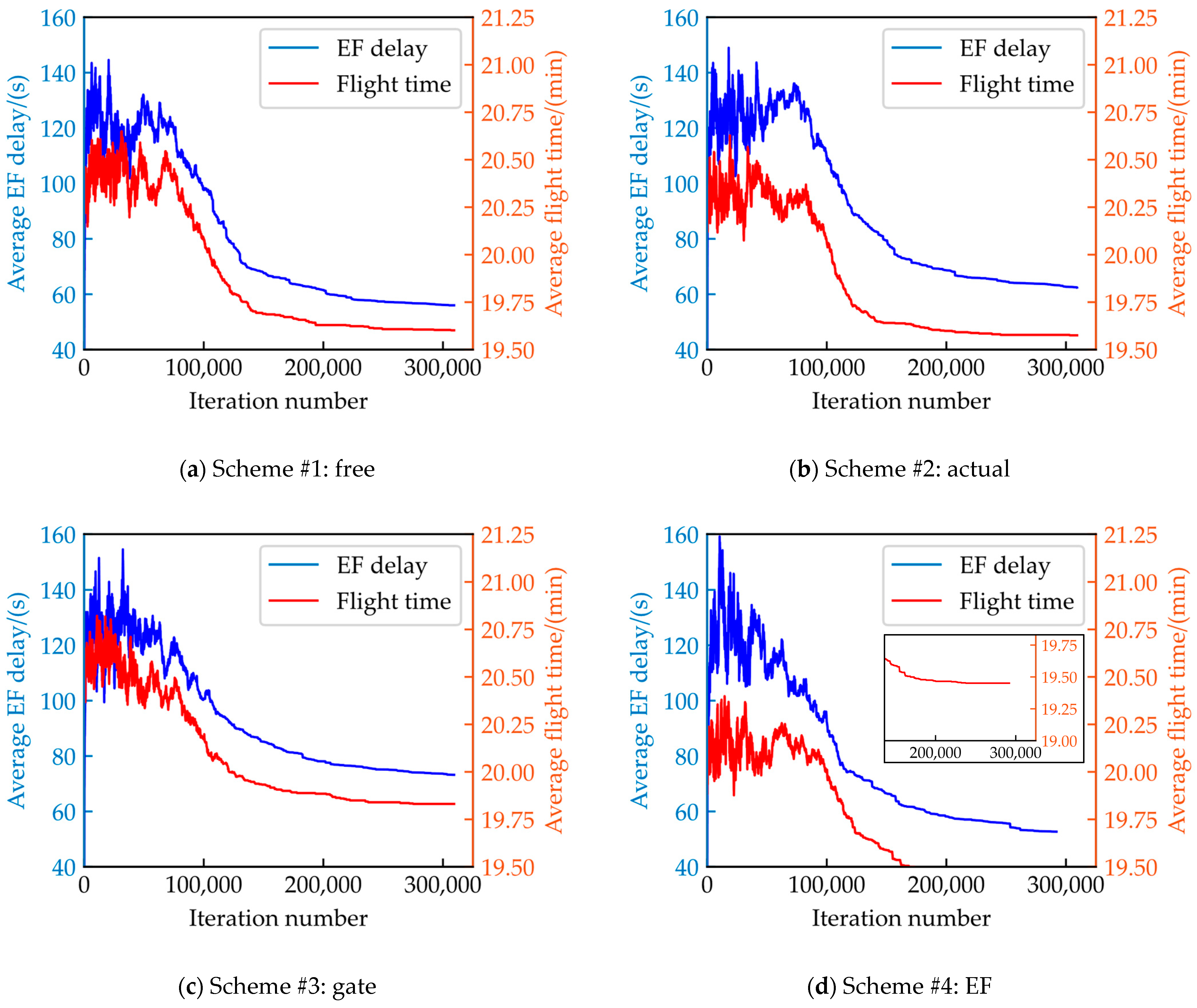
5.2.3. Flight Time and Delay
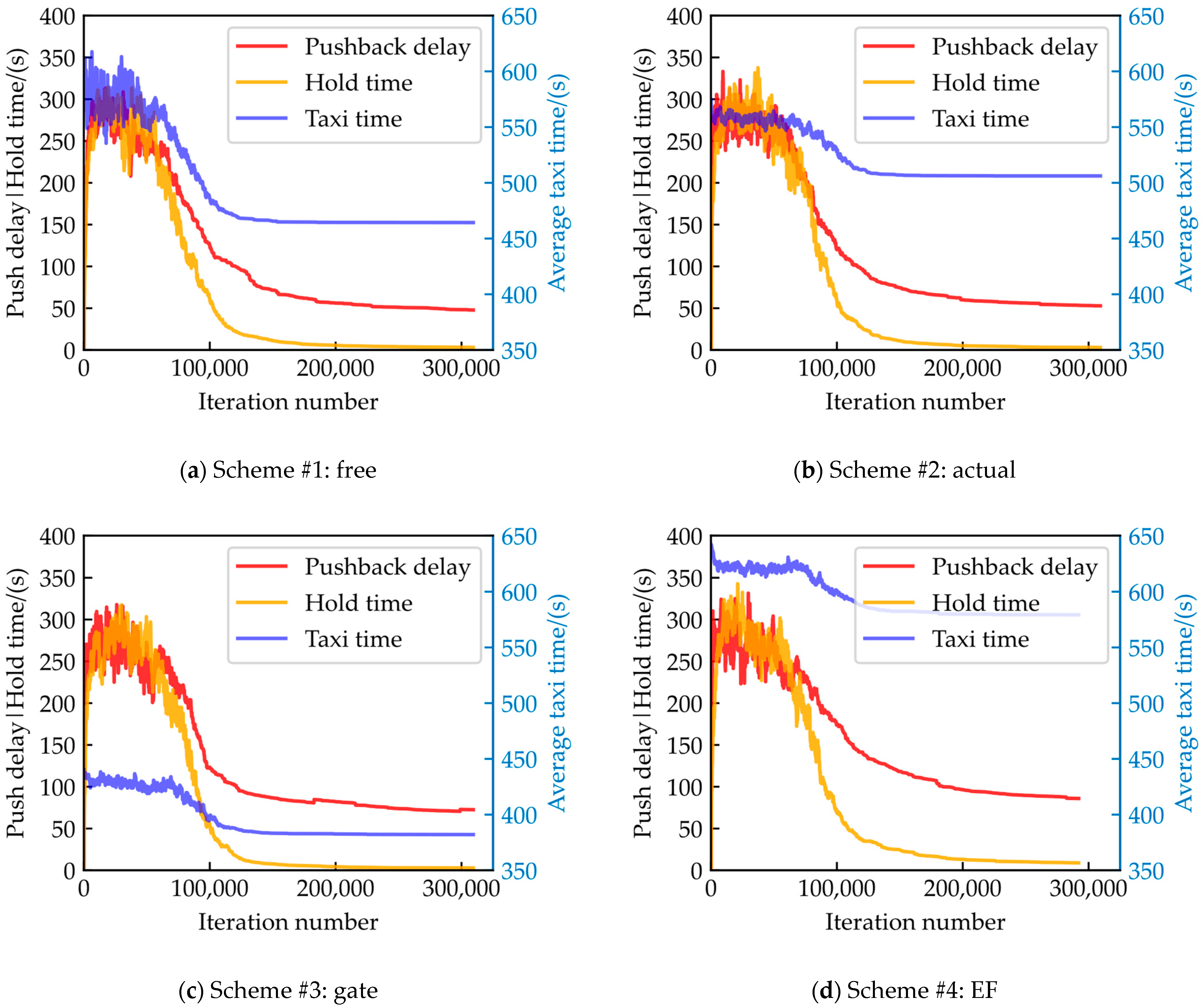
5.2.4. Taxi Time, Hold Time and Pushback Delay
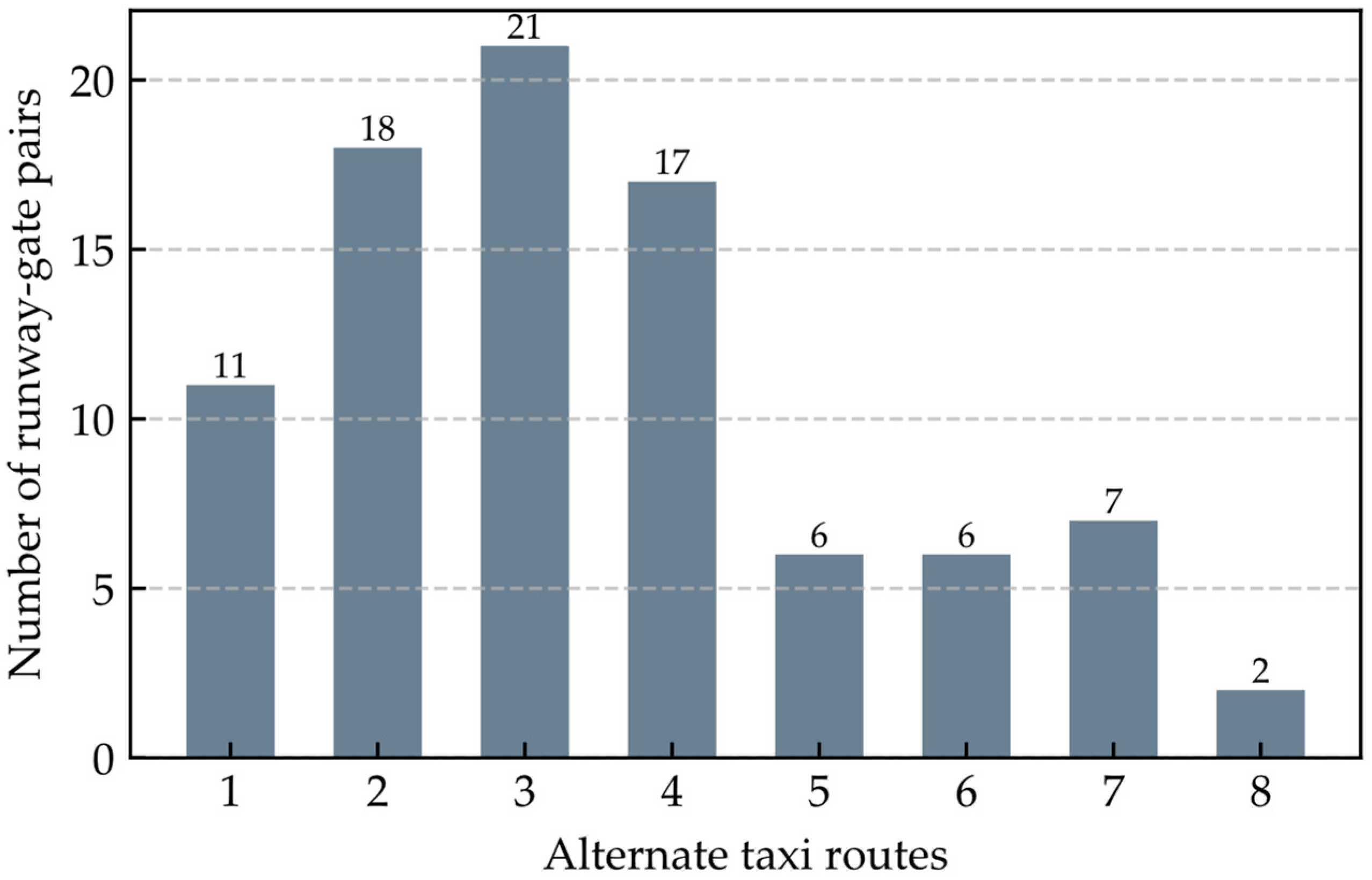
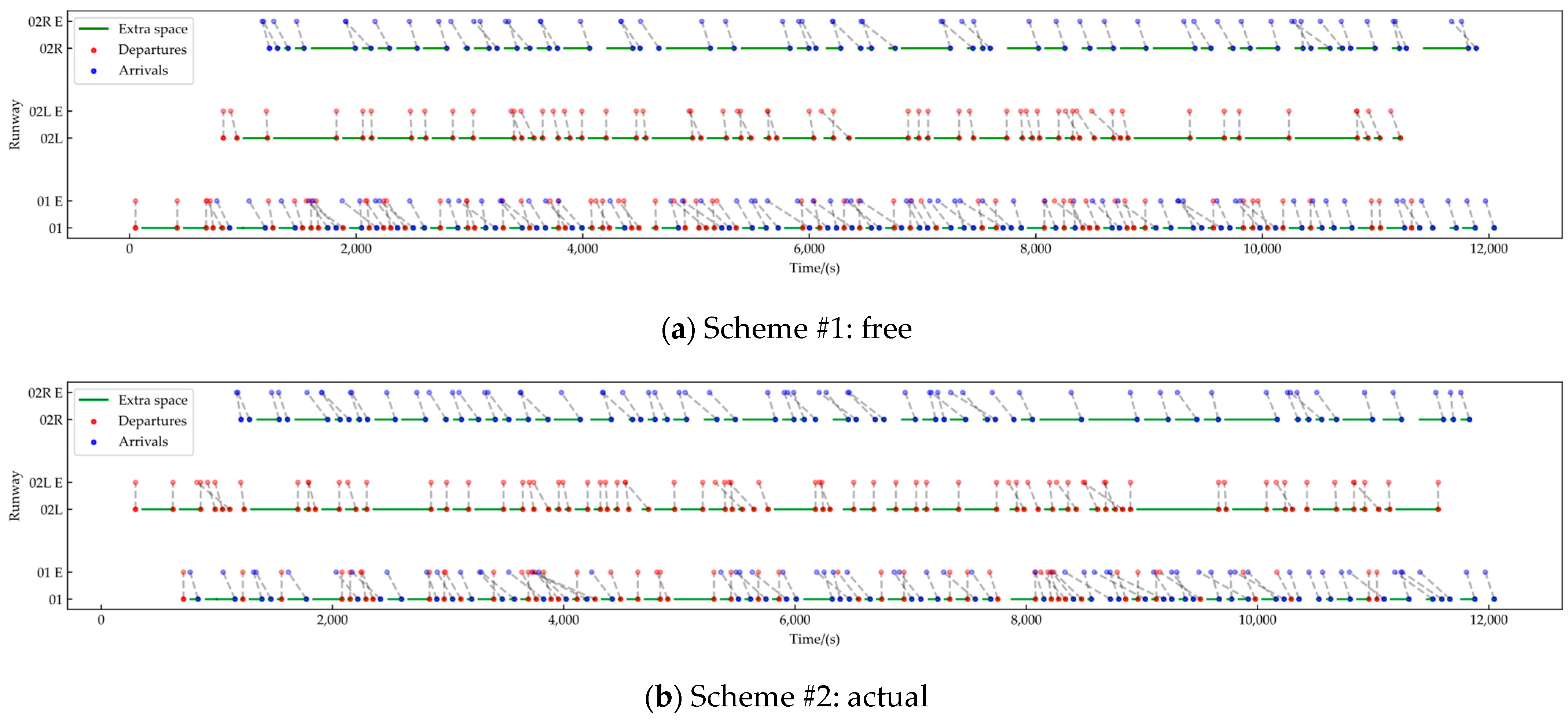
5.2.5. Runway Usage
6. Discussion
6.1. Analysis of Ten Days’ Peak Hours
6.2. Solution Validation
6.3. Insights on Operational Feasibility of Free Assignment Schemes
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Adacher, L.; Flamini, M.; Romano, E. Airport Ground Movement Problem: Minimization of Delay and Pollution Emission. IEEE Trans. Intell. Transp. Syst. 2018, 19, 3830–3839. [Google Scholar] [CrossRef]
- Liu, Y.; Hansen, M. Incorporating Predictability Into Cost Optimization for Ground Delay Programs. Transp. Sci. 2016, 50, 132–149. [Google Scholar] [CrossRef]
- Jiang, Y.; Liu, Z.; Hu, Z.; Zhang, H. A Priority-Based Conflict Resolution Strategy for Airport Surface Traffic Considering Suboptimal Alternative Paths. IEEE Access 2021, 9, 606–617. [Google Scholar] [CrossRef]
- Bosson, C.S.; Sun, D. Optimization of Airport Surface Operations Under Uncertainty. J. Air Transp. 2016, 24, 84–92. [Google Scholar] [CrossRef]
- Ma, J.; Delahaye, D.; Sbihi, M.; Scala, P.M.; Mota, M.M. A Study of Tradeoffs in Airport Coordinated Surface Operations. In Proceedings of the 5th ENRI International Workshop on ATM/CNS: Drafting Future Skies, Tokyo, Japan, 14–16 November 2017. [Google Scholar]
- Weiszer, M.; Burke, E.K.; Chen, J. Multi-Objective Routing and Scheduling for Airport Ground Movement. Transp. Res. Part C Emerg. Technol. 2020, 119, 102734. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, Y.; Liu, M.; Xue, Q.; Zhang, H.; Zhang, H. Bilevel Spatial–Temporal Aircraft Taxiing Optimization Considering Carbon Emissions. Sustain. Energy Technol. Assess. 2023, 58, 103358. [Google Scholar] [CrossRef]
- Murça, M.C.R. A Robust Optimization Approach for Airport Departure Metering under Uncertain Taxi-out Time Predictions. Aerosp. Sci. Technol. 2017, 68, 269–277. [Google Scholar] [CrossRef]
- Ma, J.; Zhou, J.; Liang, M.; Delahaye, D. Data-Driven Trajectory-Based Analysis and Optimization of Airport Surface Movement. Transp. Res. Part C Emerg. Technol. 2022, 145, 103902. [Google Scholar] [CrossRef]
- Badrinath, S.; Balakrishnan, H.; Ma, J.; Delahaye, D. Comparative Analysis of Departure Metering at United States and European Airports. J. Air Transp. 2020, 28, 93–104. [Google Scholar] [CrossRef]
- Khadilkar, H.; Balakrishnan, H. Network Congestion Control of Airport Surface Operations. J. Guid. Control Dyn. 2014, 37, 933–940. [Google Scholar] [CrossRef]
- Ma, J.; Delahaye, D.; Sbihi, M.; Scala, P.; Mujica Mota, M.A. Integrated Optimization of Terminal Maneuvering Area and Airport at the Macroscopic Level. Transp. Res. Part C Emerg. Technol. 2019, 98, 338–357. [Google Scholar] [CrossRef]
- Khadilkar, H.; Balakrishnan, H. Integrated Control of Airport and Terminal Airspace Operations. IEEE Trans. Control Syst. Technol. 2016, 24, 216–225. [Google Scholar] [CrossRef]
- Bosson, C.; Xue, M.; Zelinski, S.; Field, M. Optimizing Integrated Arrival, Departure and Surface Operations Under Uncertainty. In Proceedings of the 10th USA/Europe Air Traffic Management Research and Development Seminar (ATM2015), Lisbon, Portugal, 23 June 2015. [Google Scholar]
- Chandrasekar, S.; Hwang, I. Algorithm for Optimal Arrival and Departure Sequencing and Runway Assignment. J. Guid. Control Dyn. 2015, 38, 601–613. [Google Scholar] [CrossRef]
- Kim, B.; Li, L.; Clarke, J.-P. Runway Assignments That Minimize Terminal Airspace and Airport Surface Emissions. J. Guid. Control Dyn. 2014, 37, 789–798. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, P.; Zhang, Y.; Dai, X.; Sui, D. Criteria Selection and Multi-Objective Optimization of Aircraft Landing Problem. J. Air Transp. Manag. 2020, 82, 101734. [Google Scholar] [CrossRef]
- Solveling, G.; Solak, S.; Clarke, J.-P.; Johnson, E. Runway Operations Optimization in the Presence of Uncertainties. J. Guid. Control Dyn. 2011, 34, 1373–1382. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, P. A New Meta Heuristic Approach for Aircraft Landing Problem. Trans. Nanjing Univ. Aeronaut. Astronaut. 2020, 37, 197–208. [Google Scholar]
- Zhang, J.; Liu, J.; Hu, R.; Zhu, H. Online Four Dimensional Trajectory Prediction Method Based on Aircraft Intent Updating. Aerosp. Sci. Technol. 2018, 77, 774–787. [Google Scholar] [CrossRef]
- Zhang, J.; Peng, Z.; Yang, C.; Wang, B. Data-Driven Flight Time Prediction for Arrival Aircraft within the Terminal Area. IET Intell. Transp. Syst. 2022, 16, 263–275. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, J.; Peng, Z.; Bao, J.; Wang, B. Data-Driven Departure Flight Time Prediction Based on Feature Construction and Ensemble Learning. J. Aerosp. Inf. Syst. 2023, 20, 1–14. [Google Scholar] [CrossRef]
- Khassiba, A.; Bastin, F.; Cafieri, S.; Gendron, B.; Mongeau, M. Two-Stage Stochastic Mixed-Integer Programming with Chance Constraints for Extended Aircraft Arrival Management. Transp. Sci. 2020, 54, 897–919. [Google Scholar] [CrossRef]
- Khassiba, A.; Cafieri, S.; Bastin, F.; Mongeau, M.; Gendron, B. Two-Stage Stochastic Programming Models for the Extended Aircraft Arrival Management Problem with Multiple Pre-Scheduling Points. Transp. Res. Part C Emerg. Technol. 2022, 142, 103769. [Google Scholar] [CrossRef]
- Khassiba, A.; Bastin, F.; Gendron, B.; Cafieri, S.; Mongeau, M. Extended Aircraft Arrival Management Under Uncertainty: A Computational Study. J. Air Transp. 2019, 27, 131–143. [Google Scholar] [CrossRef]
- Sáez, R.; Prats, X.; Polishchuk, T.; Polishchuk, V. Traffic Synchronization in Terminal Airspace to Enable Continuous Descent Operations in Trombone Sequencing and Merging Procedures: An Implementation Study for Frankfurt Airport. Transp. Res. Part C Emerg. Technol. 2020, 121, 102875. [Google Scholar] [CrossRef]
- Kamo, S.; Rosenow, J.; Fricke, H.; Soler, M. Robust Optimization Integrating Aircraft Trajectory and Sequence under Weather Forecast Uncertainty. Transp. Res. Part C Emerg. Technol. 2023, 152, 104187. [Google Scholar] [CrossRef]
- Gui, D.; Le, M.; Huang, Z.; Zhang, J.; D’Ariano, A. Optimal Aircraft Arrival Scheduling with Continuous Descent Operations in Busy Terminal Maneuvering Areas. J. Air Transp. Manag. 2023, 107, 102344. [Google Scholar] [CrossRef]
- Gui, X.; Zhang, J.; Tang, X.; Bao, J.; Wang, B. A Data-Driven Trajectory Optimization Framework for Terminal Maneuvering Area Operations. Aerosp. Sci. Technol. 2022, 131, 108010. [Google Scholar] [CrossRef]
- Badrinath, S.; Li, M.Z.; Balakrishnan, H. Integrated Surface-Airspace Model of Airport Departures. J. Guid. Control Dyn. 2019, 42, 1049–1063. [Google Scholar] [CrossRef]
- Ma, J.; Delahaye, D.; Sbihi, M.; Scala, P.M. Integrated Optimization of Arrival, Departure, and Surface Operations. In Proceedings of the 8th International Conference for Research in Air Transportation (ICRAT2018), Catalonia, Spain, 26–29 June 2018. [Google Scholar]
- Deau, R.; Gotteland, J.-B.; Durand, N. Airport Surface Management and Runways Scheduling. In Proceedings of the 8th USA/Europe Air Traffic Management Research and Development Seminar (ATM2009), Napa, CA, USA, 29 June–2 July 2009. [Google Scholar]
- Beasley, J.E.; Krishnamoorthy, M.; Sharaiha, Y.M.; Abramson, D. Scheduling Aircraft Landings—The Static Case. Transp. Sci. 2000, 34, 180–197. [Google Scholar] [CrossRef]
- Evertse, C.; Visser, H.G. Real-Time Airport Surface Movement Planning: Minimizing Aircraft Emissions. Transp. Res. Part C Emerg. Technol. 2017, 79, 224–241. [Google Scholar] [CrossRef]
- Franzin, A.; Stützle, T. Revisiting Simulated Annealing: A Component-Based Analysis. Comput. Oper. Res. 2019, 104, 191–206. [Google Scholar] [CrossRef]
- Khassiba, A.; Delahaye, D. Simulated-Annealing Hyper-Heuristic for Demand-Capacity Balancing in Air Traffic Flow Management. In Proceedings of the 12th SESAR Innovation Days, Budapest, Hungary, 5–8 December 2022. [Google Scholar]
- Peng, Z.; Zhang, J.; Xiang, T.; Wang, B.; Guo, H. Benefits Derived from Arrival Management and Wake Turbulence Re-Categorization in China. Transp. Res. Rec. 2021, 2675, 373–383. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, Y.; Hu, Z.; Xue, Q.; Yu, B. Airport Gate Assignment Problem with Harbor Constraints Based on Branch-and-Price Algorithm. Transp. Res. Part E Logist. Transp. Rev. 2023, 176, 103192. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, C.; Wang, H.; Duong, V. Slot Allocation for a Multiple-Airport System Considering Airspace Capacity and Flying Time Uncertainty. Transp. Res. Part C Emerg. Technol. 2023, 153, 104185. [Google Scholar] [CrossRef]
- Xu, Y.; Wandelt, S.; Sun, X. A Distributionally Robust Optimization Approach for Airline Integrated Recovery under In-Flight Pandemic Transmission Risks. Transp. Res. Part C Emerg. Technol. 2023, 152, 104188. [Google Scholar] [CrossRef] [PubMed]
- Huo, Y.; Delahaye, D.; Sbihi, M. A Probabilistic Model Based Optimization for Aircraft Scheduling in Terminal Area under Uncertainty. Transp. Res. Part C Emerg. Technol. 2021, 132, 103374. [Google Scholar] [CrossRef]
- Jacquillat, A. Predictive and Prescriptive Analytics Toward Passenger-Centric Ground Delay Programs. Transp. Sci. 2022, 56, 265–298. [Google Scholar] [CrossRef]




| Notation | Description |
|---|---|
| Sets | |
| Set of aircraft in the time horizon, | |
| Subset of , set of arrival aircraft | |
| Subset of , set of departure aircraft | |
| Set of gates, | |
| Set of runways, | |
| Set of entry fixes, | |
| Set of taxi routes from runway to gate , | |
| Subset of , set of intersections of taxi route of , intersection | |
| Set of waypoints from an entry fix to runway , | |
| Parameters | |
| , | Radar separation when aircraft precedes , |
| , | Runway and taxi separation when aircraft precedes , |
| Pre-allocated gate for aircraft | |
| Constant deceleration for aircraft | |
| Constant taxi speed | |
| Initial entry time over a predefined EF for aircraft | |
| Initial pushback time for aircraft | |
| , | Lower and upper bound time difference for entry time |
| , | Lower and upper bound coefficient for pushback time |
| , | Lower and upper bound coefficient for entry speed |
| , | Lower and upper bound time difference for hold time |
| Distance from EF to waypoint for aircraft | |
| Distance from runway to gate for aircraft | |
| Decision variables | |
| Speed at EF for aircraft | |
| Entry time at EF for aircraft | |
| Taxiway entrance hold time for aircraft | |
| Pushback time for aircraft | |
| Assigned runway for aircraft | |
| Assigned taxi route of for aircraft | |
| Auxiliary decision variables | |
| Binary decision variables for sequencing in the air when aircraft precedes , | |
| , | Binary decision variables for sequencing on the runway and taxiway when aircraft precedes , |
| Indirect decision variables | |
| , | Speed and time at waypoint for aircraft |
| Average speed for aircraft | |
| Time at intersection for aircraft | |
| Landing or take off time for aircraft | |
| Taxi time for aircraft | |
| Objective | |
| Total delay at entry fix for aircraft | |
| Total flight time for aircraft | |
| Total hold time for aircraft | |
| Total pushback delay for aircraft | |
| Total taxi time for aircraft |
| Runway Assigned | Arrivals | Departures | ||
|---|---|---|---|---|
| Number | Percentage | Number | Percentage | |
| Close to gate | 12,202 | 77.16% | 6594 | 42.26% |
| Close to EF | 9365 | 59.22% | 12,250 | 78.52% |
| Close to both gate and EF | 6899 | 43.62% | 5428 | 34.79% |
| Far from both gate and EF | 1145 | 7.24% | 2184 | 14.00% |
| Total number | 15,813 | 100% | 15,600 | 100% |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| SA terminal time | 1000 s | Conflict penalty coefficient | 1000 |
| SA terminal temperature | Taxi speed | 5 m/s | |
| SA cooling coefficient | 0.99 | Initial pushback time | History data |
| SA iterations at temperature | 100 | Initial entry time and speed , | |
| bound of pushback time window , | [0, 600] | Bound of entry time window , | [−60, 300] |
| bound of hold time window , | [0, 300] | Bound of entry speed window , | 0.9, 1.1 |
| Date and Scheme (No. of Dep. and Arr.) | Conflicts | Performance in Difference | Numbers in Runway | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Air | Taxi | Total Cost | EF Delay | Pushback Delay | Hold Time | Flight Time | Taxi Time | 01 | 02L | 02R | ||
| /(min) | /(min) | /(min) | /(min) | /(min) | ||||||||
| 3 | #2: actual | 0 | 0 | 263,414.2 | 119.7 | 98.7 | 5.8 | 2251.2 | 1915 | 101 | 68 | 58 |
| 112 | #1: free | 0 | 0 | −10,596.1 | −12.4 | −9.5 | 0.3 | 3 | −158.2 | 120 | 54 | 53 |
| 115 | #3: gate | 2 | 10 | −10,975 | 20.6 | 36.7 | −0.3 | 29.4 | −469.5 | 150 | 40 | 37 |
| #4: EF | 0 | 0 | 18,993.6 | −18.7 | 61.7 | 11.2 | −14.3 | 276.5 | 53 | 96 | 78 | |
| 4 | #2: actual | 2 | 0 | 257,931.6 | 138.9 | 68.2 | 20.7 | 2220.8 | 1816.9 | 100 | 66 | 50 |
| 104 | #1: free | 0 | 0 | −14,663.7 | −20.4 | 12.2 | −18.2 | −4.2 | −180.4 | 117 | 51 | 48 |
| 112 | #3: gate | 10 | 6 | −4879.8 | −8.1 | 73.2 | 24.1 | 34.7 | −438.6 | 144 | 36 | 36 |
| #4: EF | 4 | 0 | 19,673.6 | −8.3 | −4.5 | 5.3 | −41.7 | 343.8 | 61 | 77 | 78 | |
| 5 | #2: actual | 2 | 0 | 268,514.9 | 122.9 | 127.3 | 8.7 | 2387.7 | 1795.3 | 115 | 69 | 41 |
| 111 | #1: free | 0 | 0 | −9631 | −21.7 | −41 | −1.8 | −37.8 | −24.9 | 117 | 56 | 52 |
| 114 | #3: gate | 4 | 18 | 1697.9 | 14.1 | 28.7 | 6.7 | 2.1 | −356.6 | 152 | 35 | 38 |
| #4: EF | 0 | 0 | 22,656 | 37.6 | −22.9 | 12 | −52.4 | 436.6 | 65 | 78 | 82 | |
| 6 | #2: actual | 4 | 0 | 258,110.3 | 140.8 | 92.9 | 26.6 | 2136.3 | 1838.6 | 111 | 69 | 46 |
| 114 | #1: free | 2 | 0 | −10,811.9 | −21.6 | 21.2 | −21 | 3.9 | −129.3 | 119 | 57 | 50 |
| 112 | #3: gate | 12 | 10 | 705.7 | −2.3 | 53.9 | 0.6 | 40.2 | −380.6 | 149 | 39 | 38 |
| #4: EF | 0 | 0 | 14,411.5 | −11.7 | 7.1 | −17.3 | −18.4 | 347.1 | 70 | 80 | 76 | |
| 7 | #2: actual | 0 | 2 | 255,654.9 | 120.5 | 124.6 | 5.6 | 2147.3 | 1829.6 | 108 | 68 | 49 |
| 112 | #1: free | 0 | 0 | −11,287.3 | −11.7 | −3.4 | 2.6 | −1.3 | −141.1 | 118 | 57 | 50 |
| 113 | #3: gate | 6 | 18 | 1258.6 | 10.1 | 33.4 | 6.4 | 25 | −420.6 | 147 | 40 | 38 |
| #4: EF | 6 | 0 | 25,900.5 | 25 | −19.6 | 22.6 | −32.1 | 369.1 | 67 | 79 | 79 | |
| 8 | #2: actual | 0 | 0 | 259,398 | 141.2 | 84.3 | 8.2 | 2268.6 | 1820.9 | 111 | 68 | 50 |
| 110 | #1: free | 0 | 0 | 198.9 | −31.6 | 23.4 | 1 | 17.4 | −6.7 | 120 | 52 | 57 |
| 119 | #3: gate | 2 | 4 | −9111.9 | 5.6 | 60.1 | −2.2 | 32 | −347.2 | 150 | 37 | 42 |
| #4: EF | 0 | 0 | 11,955.6 | −37.1 | 18.6 | 11 | −20.5 | 227.3 | 89 | 77 | 63 | |
| 9 | #2: actual | 0 | 0 | 252,097.1 | 117.9 | 83.8 | 9.4 | 2204 | 1786.5 | 111 | 64 | 49 |
| 111 | #1: free | 0 | 0 | −5681.5 | 2.5 | 12 | −1.2 | 7.3 | −115.3 | 123 | 50 | 51 |
| 113 | #3: gate | 4 | 10 | 1096 | 44.7 | 55 | 10.3 | 42.9 | −367.9 | 148 | 36 | 40 |
| #4: EF | 0 | 0 | 9989.2 | −26.2 | 15.2 | 4 | −34.6 | 208.1 | 85 | 77 | 62 | |
| 10 | #2: actual | 2 | 0 | 248,500.6 | 119.6 | 76.2 | 11.9 | 2219.1 | 1681.6 | 107 | 61 | 47 |
| 103 | #1: free | 0 | 0 | −16,950.0 | −43 | 35 | −8.7 | −7.7 | −224.8 | 112 | 55 | 48 |
| 112 | #3: gate | 2 | 4 | −10,876.8 | −1.2 | 79.2 | −6.1 | 24.6 | −344.6 | 138 | 38 | 39 |
| #4: EF | 2 | 0 | 25,408.8 | 25.9 | 10.9 | 1.9 | −22.2 | 406.9 | 63 | 72 | 80 | |
| 11 | #2: actual | 6 | 0 | 257,852.5 | 125.1 | 94.8 | 15.8 | 2244.2 | 1717.6 | 107 | 68 | 44 |
| 107 | #1: free | 0 | 0 | −13,779 | −42.3 | 8.3 | −11 | −22.7 | −61.9 | 116 | 50 | 53 |
| 112 | #3: gate | 10 | 18 | 4204.3 | 15.1 | 15 | −0.7 | 11 | −337 | 146 | 34 | 39 |
| #4: EF | 6 | 0 | 25813 | 10.7 | −2 | 18.6 | −31.1 | 434 | 64 | 75 | 80 | |
| 12 | #2: actual | 0 | 0 | 248,336.2 | 116.7 | 92.8 | 7.8 | 2201.7 | 1720 | 103 | 61 | 50 |
| 101 | #1: free | 0 | 0 | −2644 | −8.8 | 3.2 | −0.1 | 20.4 | −58.8 | 112 | 50 | 52 |
| 113 | #3: gate | 10 | 12 | 11,320.7 | 14 | 81.4 | 17.7 | 54.6 | −345.6 | 145 | 33 | 36 |
| #4: EF | 0 | 0 | 21,179.8 | 24.7 | −4.2 | 5.3 | −13.4 | 340.6 | 64 | 73 | 77 | |
| Date | History Percentage | Scheme Free | Scheme Gate | ||||
|---|---|---|---|---|---|---|---|
| Gate | EF | Both | Gate | EF | Both | Gate | |
| 3 | 58.15% | 76.21% | 41.85% | 78.63% | 66.04% | 47.00% | 93.83% |
| 4 | 56.94% | 79.63% | 40.74% | 78.80% | 60.65% | 42.18% | 94.44% |
| 5 | 61.78% | 71.11% | 39.11% | 77.73% | 59.69% | 41.38% | 94.67% |
| 6 | 59.73% | 76.99% | 42.04% | 77.43% | 63.63% | 44.20% | 93.81% |
| 7 | 60.44% | 77.33% | 43.11% | 78.67% | 64.62% | 45.87% | 94.67% |
| 8 | 63.76% | 81.22% | 49.78% | 77.60% | 64.85% | 48.52% | 94.32% |
| 9 | 64.73% | 81.25% | 49.55% | 76.43% | 65.71% | 47.63% | 94.64% |
| 10 | 63.26% | 73.49% | 41.86% | 79.12% | 61.72% | 43.91% | 93.02% |
| 11 | 62.10% | 75.80% | 42.47% | 76.30% | 62.69% | 43.01% | 94.52% |
| 12 | 64.49% | 77.10% | 44.39% | 75.75% | 66.40% | 44.67% | 92.52% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, Z.; Zhang, J.; Ma, Z.; Xu, J. Delay in the Air or Detour on the Ground?—A Case Study in Guangzhou Baiyun International Airport. Aerospace 2024, 11, 10. https://doi.org/10.3390/aerospace11010010
Du Z, Zhang J, Ma Z, Xu J. Delay in the Air or Detour on the Ground?—A Case Study in Guangzhou Baiyun International Airport. Aerospace. 2024; 11(1):10. https://doi.org/10.3390/aerospace11010010
Chicago/Turabian StyleDu, Zhuoming, Junfeng Zhang, Zhao Ma, and Jiaxin Xu. 2024. "Delay in the Air or Detour on the Ground?—A Case Study in Guangzhou Baiyun International Airport" Aerospace 11, no. 1: 10. https://doi.org/10.3390/aerospace11010010
APA StyleDu, Z., Zhang, J., Ma, Z., & Xu, J. (2024). Delay in the Air or Detour on the Ground?—A Case Study in Guangzhou Baiyun International Airport. Aerospace, 11(1), 10. https://doi.org/10.3390/aerospace11010010







