Very High Cycle Fatigue Life Prediction of SLM AlSi10Mg Based on CDM and SVR Models
Abstract
:1. Introduction
2. CDM-Based Theoretical Damage Model
2.1. Damage-Coupled Constitutive Model
2.2. Fatigue Damage Model
2.3. The VHCF Fatigue Model Considering the Effect of Defect Size and AM Building Direction
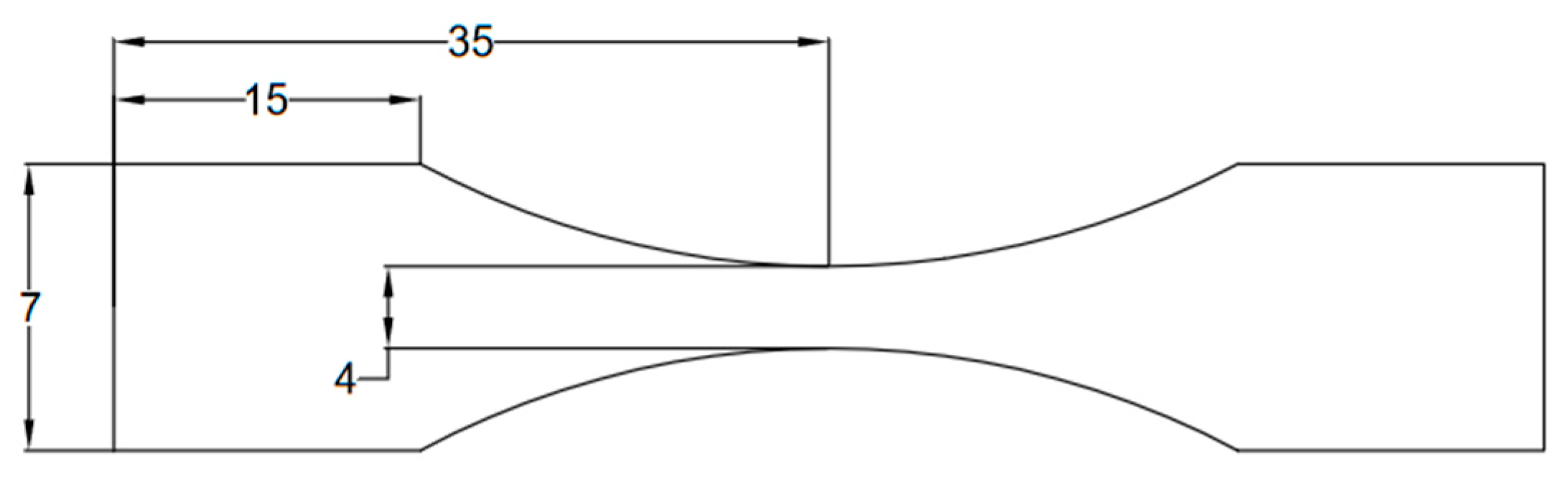
3. Numerical Calculation and Validation
3.1. Material Parameter Calibration
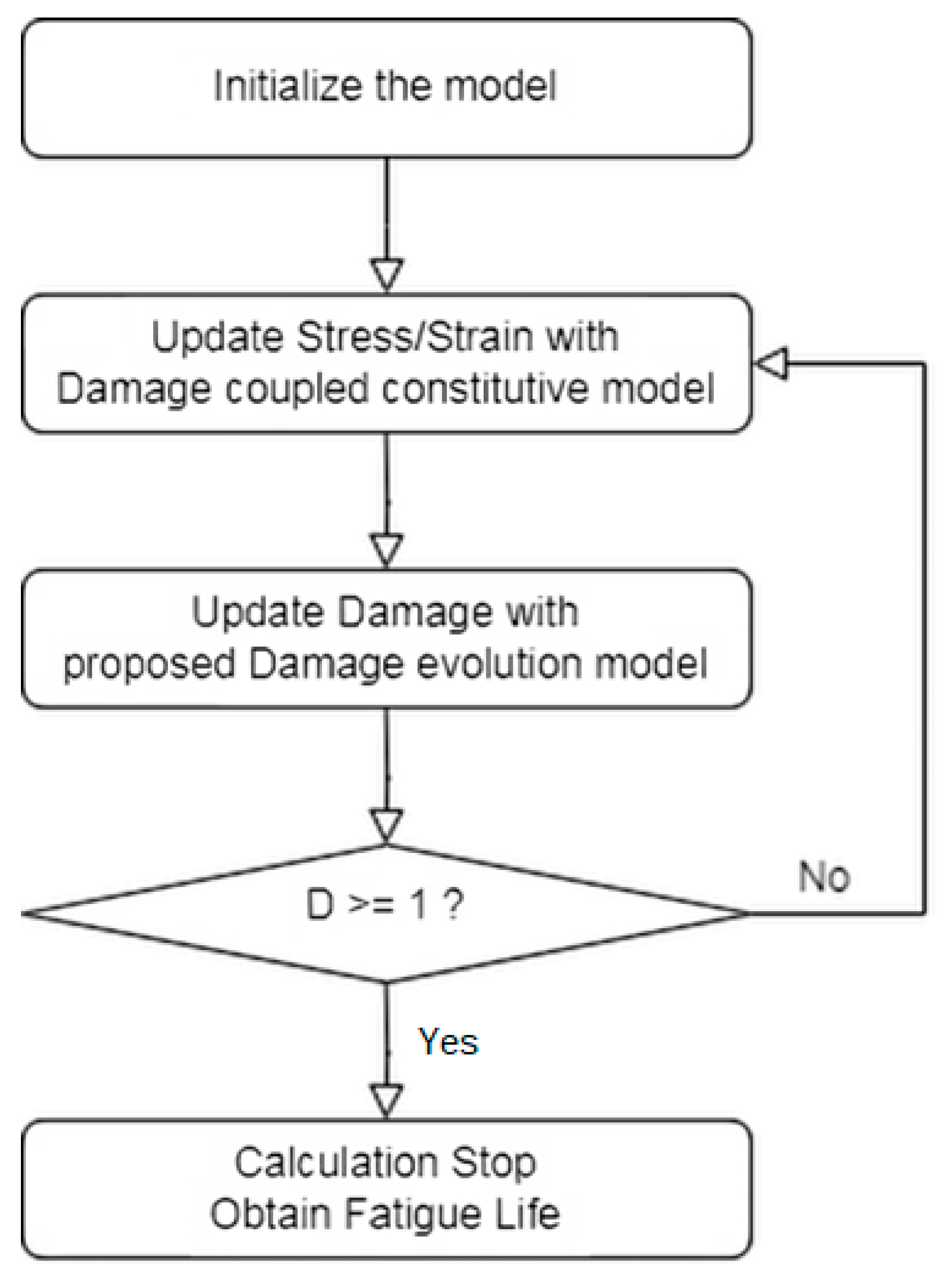
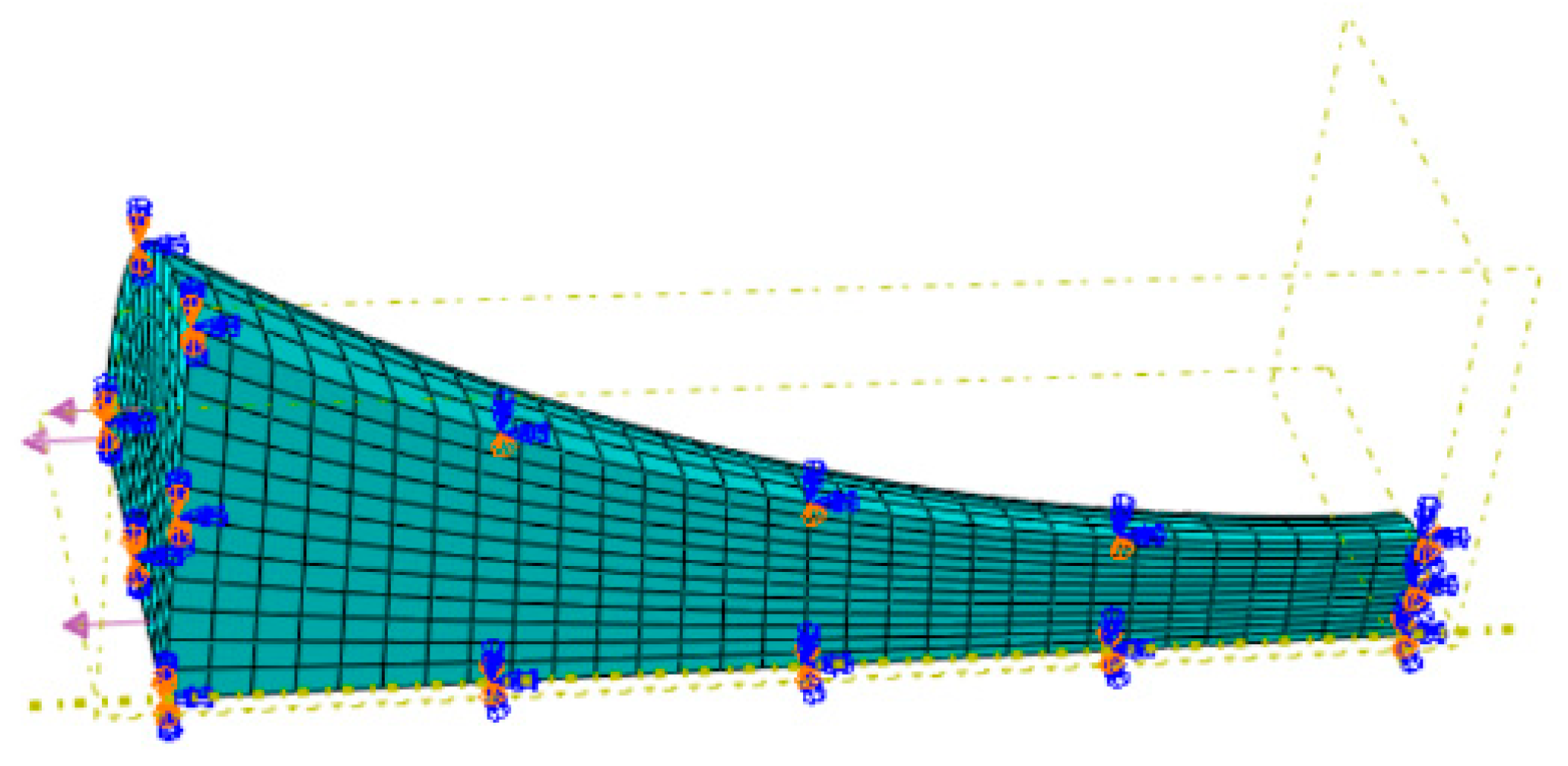
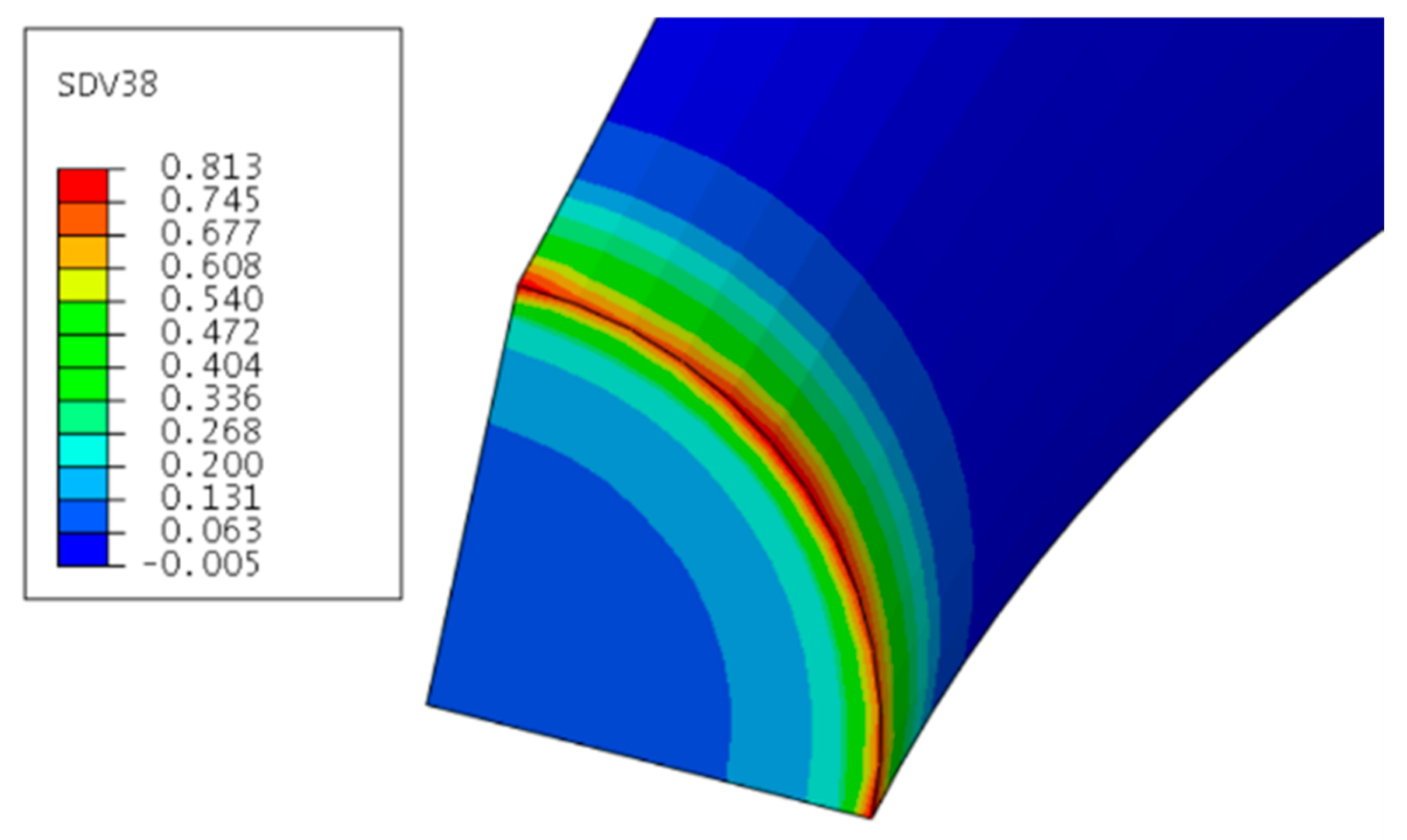
3.2. Finite Element Implementation of Theoretical Model
- 1.
- Initialize the model and variables, such as damage variable and fatigue life ;
- 2.
- Apply cyclic loading and update the elastic modulus based on the accumulated fatigue damage;
- 3.
- Calculate the stress–strain distribution at each integration point of the FE model with the damage-coupled constitutive model;
- 4.
- Calculate and update the damage rate at each integration point according to the proposed damage model. To save computational time, assume that the damage accumulation is linear in cycles. The damage increment will be , and is updated at each integration point;
- 5.
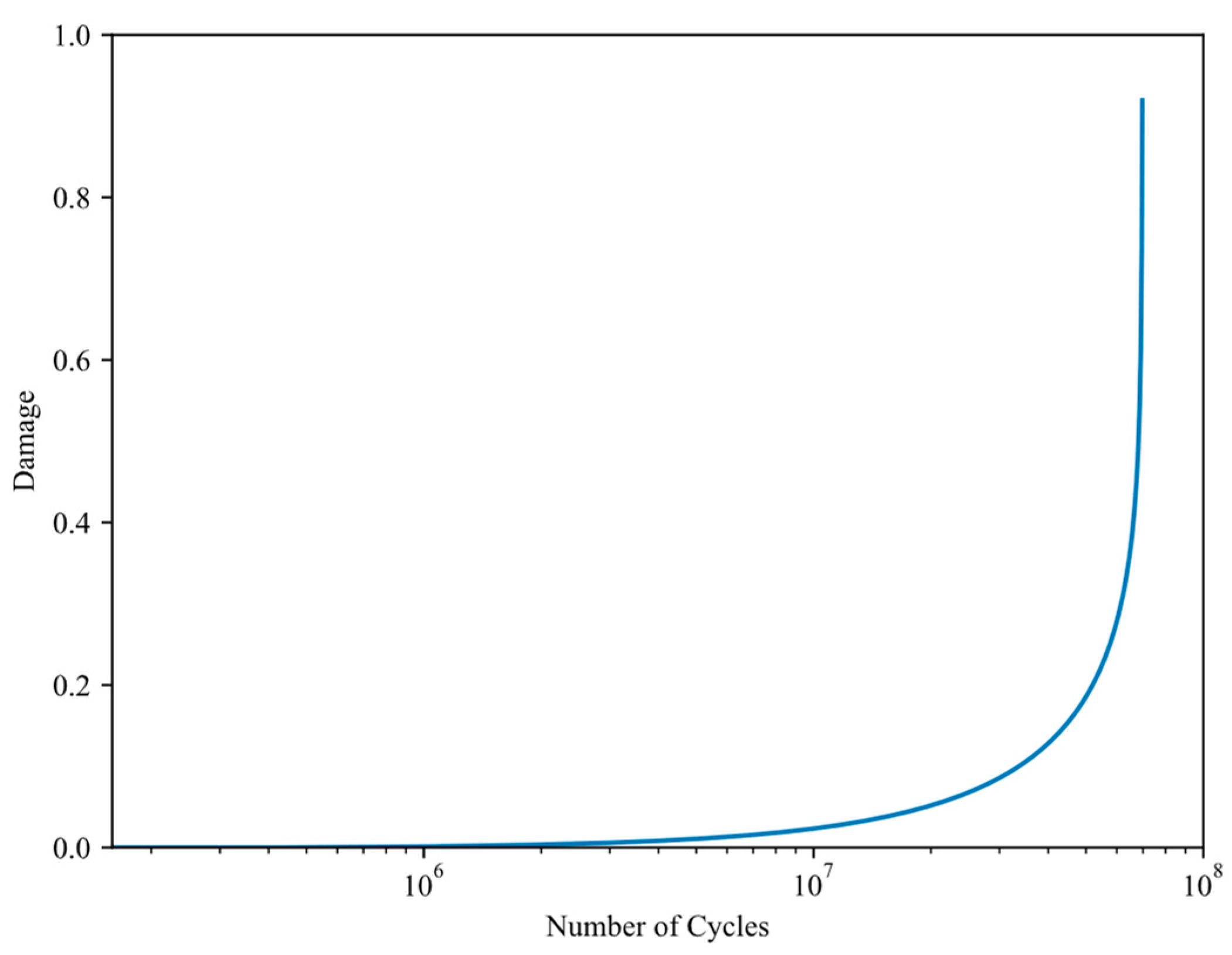
- Check if damage at any integration point exceeds 1. If so, terminate the calculation and output the fatigue life. Otherwise, return to step 2 and repeat. It is clear from Equation (3) that the elastic modulus of the material will drop to 0 once the damage exceeds 1, and this is considered crack initiation.
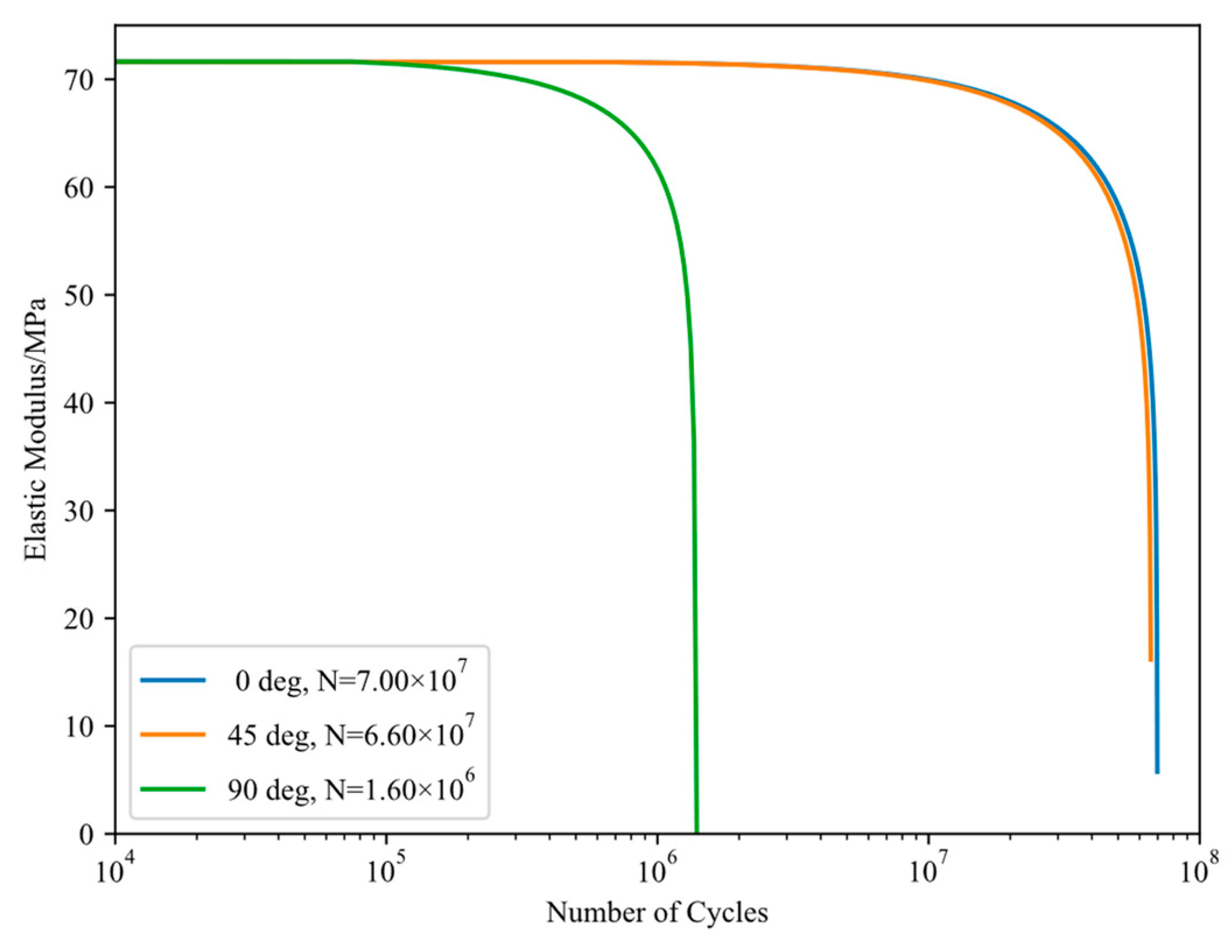
3.3. CDM-Based Numerical Results
4. A Machine Learning Approach for SLM AlSi10Mg VHCF Life Prediction
- 1.
- Data Cleaning: This step removes inconsistencies from the original data, such as missing values and duplicate records. These inconsistencies can prevent the model from accurately reading the data. Typically, the entries with missing values are removed from the dataset.
- 2.
- Data Transformation: This step converts the data into a format that is convenient for programming and models to understand. This process often includes dimension reduction.
- 3.
- Data Splitting: This step splits the data into two or more sets, each set with a different purpose. Typically, data are split into two parts, a training set and a test set. The model is trained on the training set and tested on the test set. This helps avoid overfitting and tests the ability of the model to process unseen data.
- 4.
- Data Normalization: This step normalizes the data to a certain range. This helps speed up the learning process. Typically, data are normalized to have a mean of zero and a deviation of one.
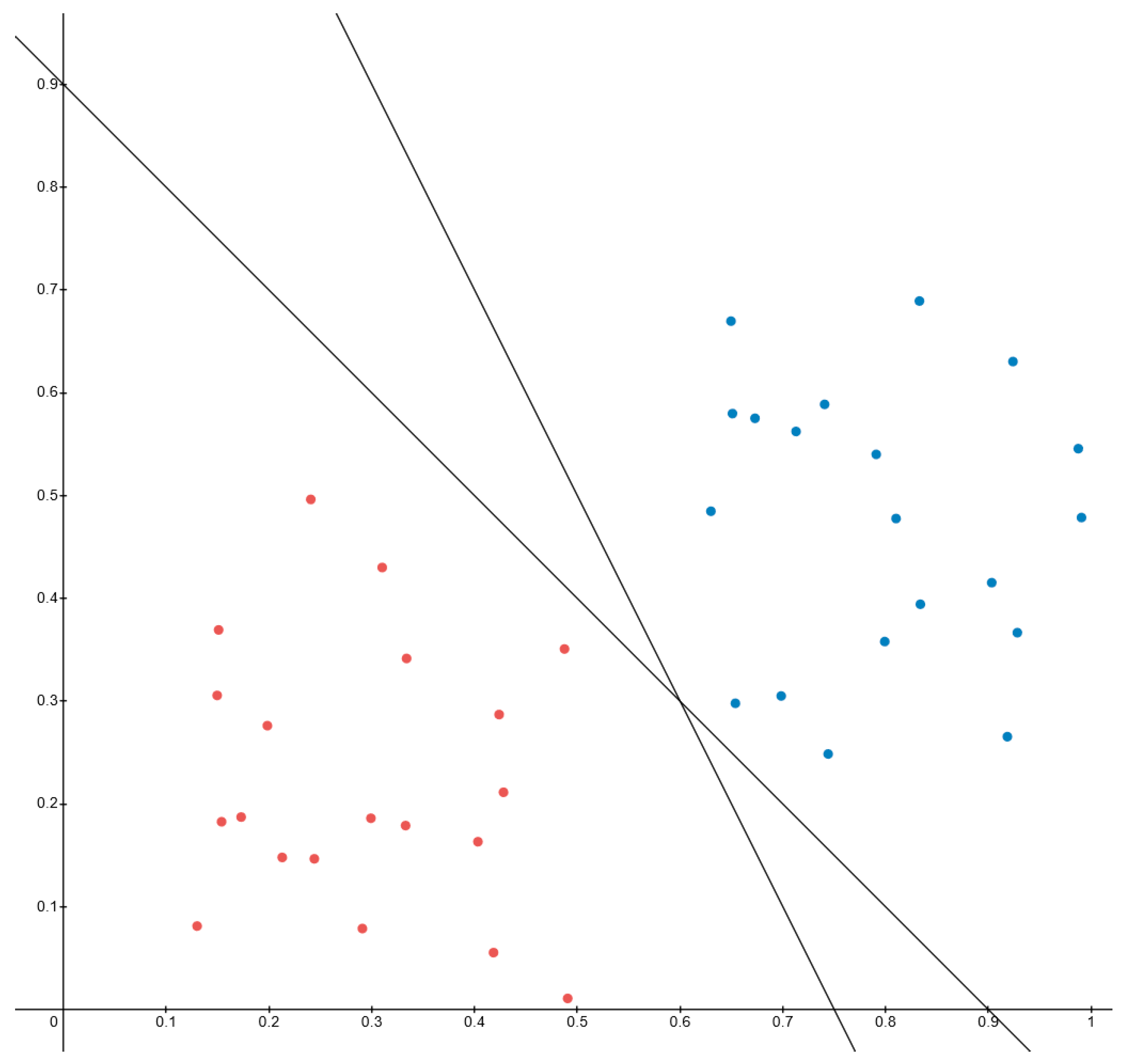
4.1. Support Vector Machine and Support Vector Regression
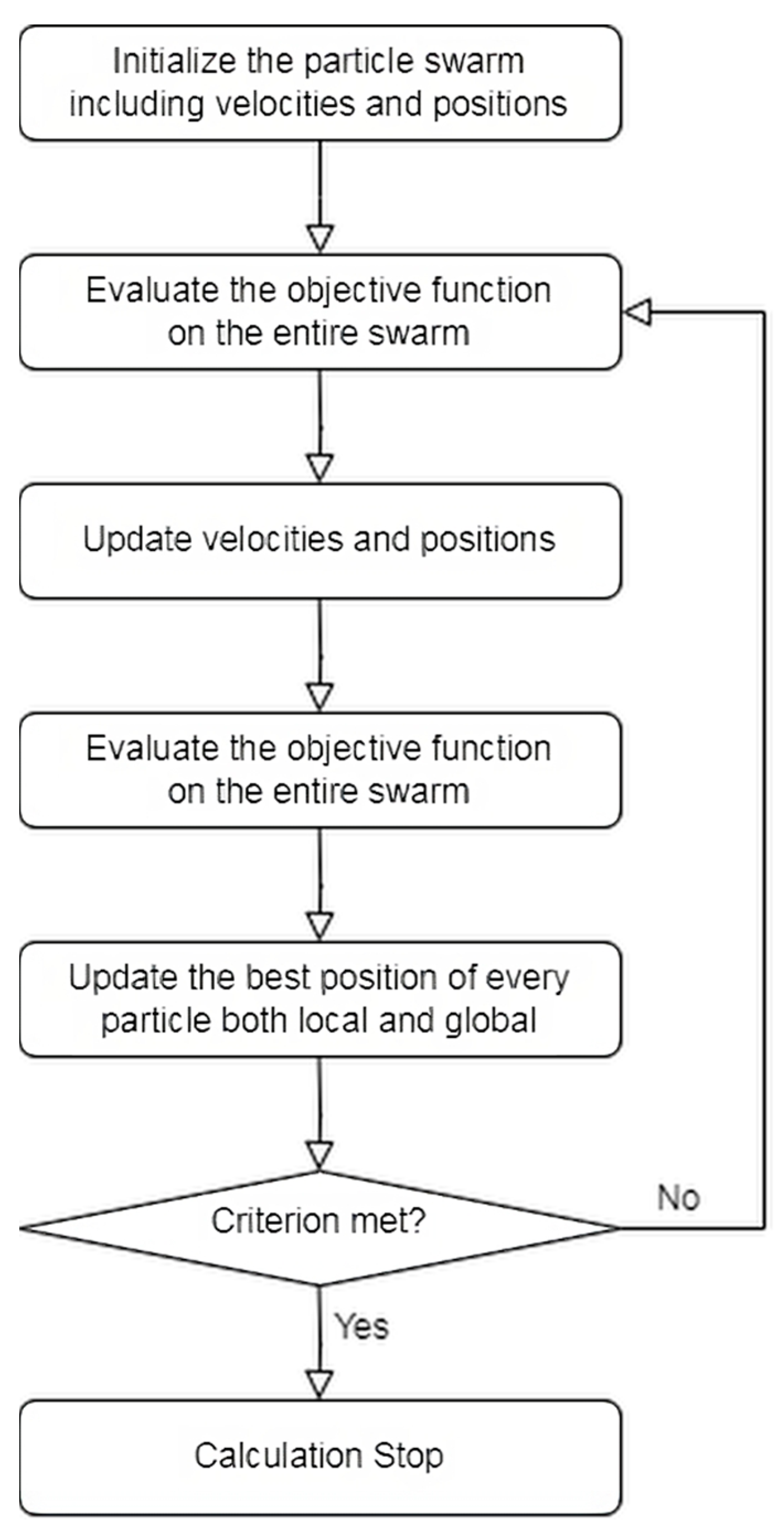
4.2. SVR Parameter Calibration with PSO and Training
- 1.
- Initialize the search space with particles randomly distributed through the search space;
- 2.
- Evaluate the objective function for each particle;
- 3.
- Update the velocity of particles based on the evaluation results of itself and its neighbors for each particle;
- 4.
- Reevaluate the objective function for each particle;
- 5.
- Compare the evaluation results in step 4 to the best-known positions of each particle and update if necessary;
- 6.
- Determine the best particle based on the evaluation results in step 4;
- 7.
- Repeat steps 3–6 until the criterion is met or the global optimum is found.
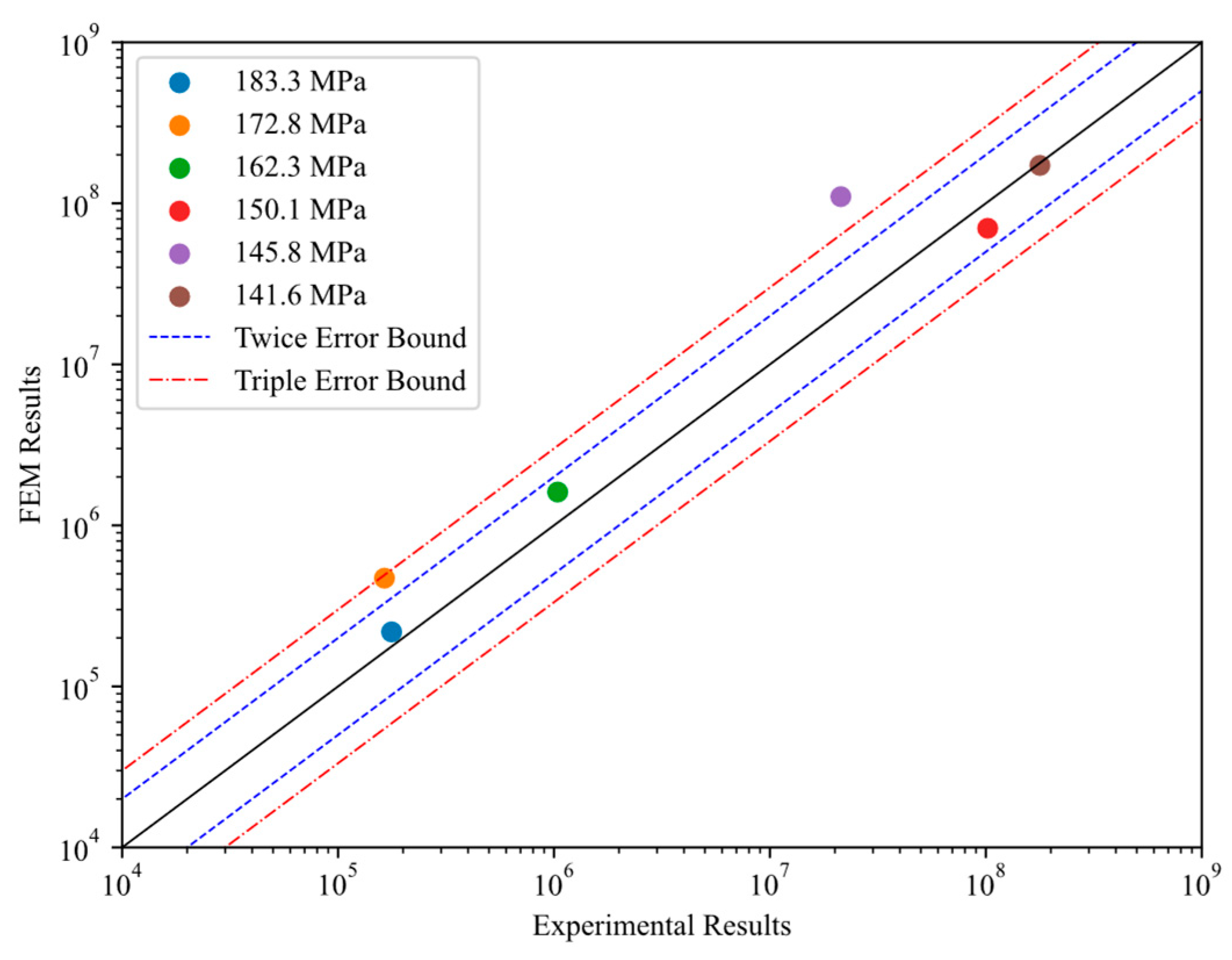
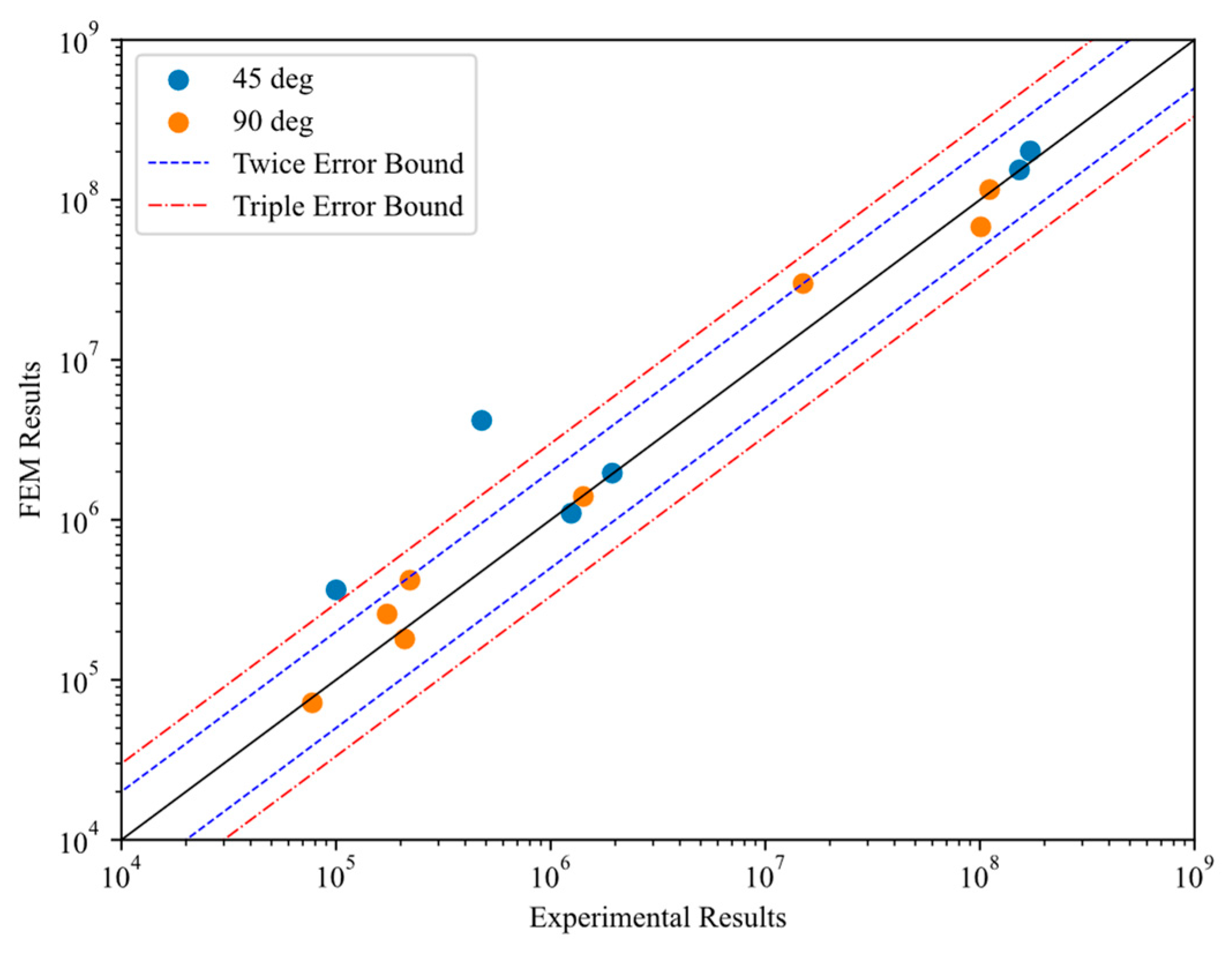
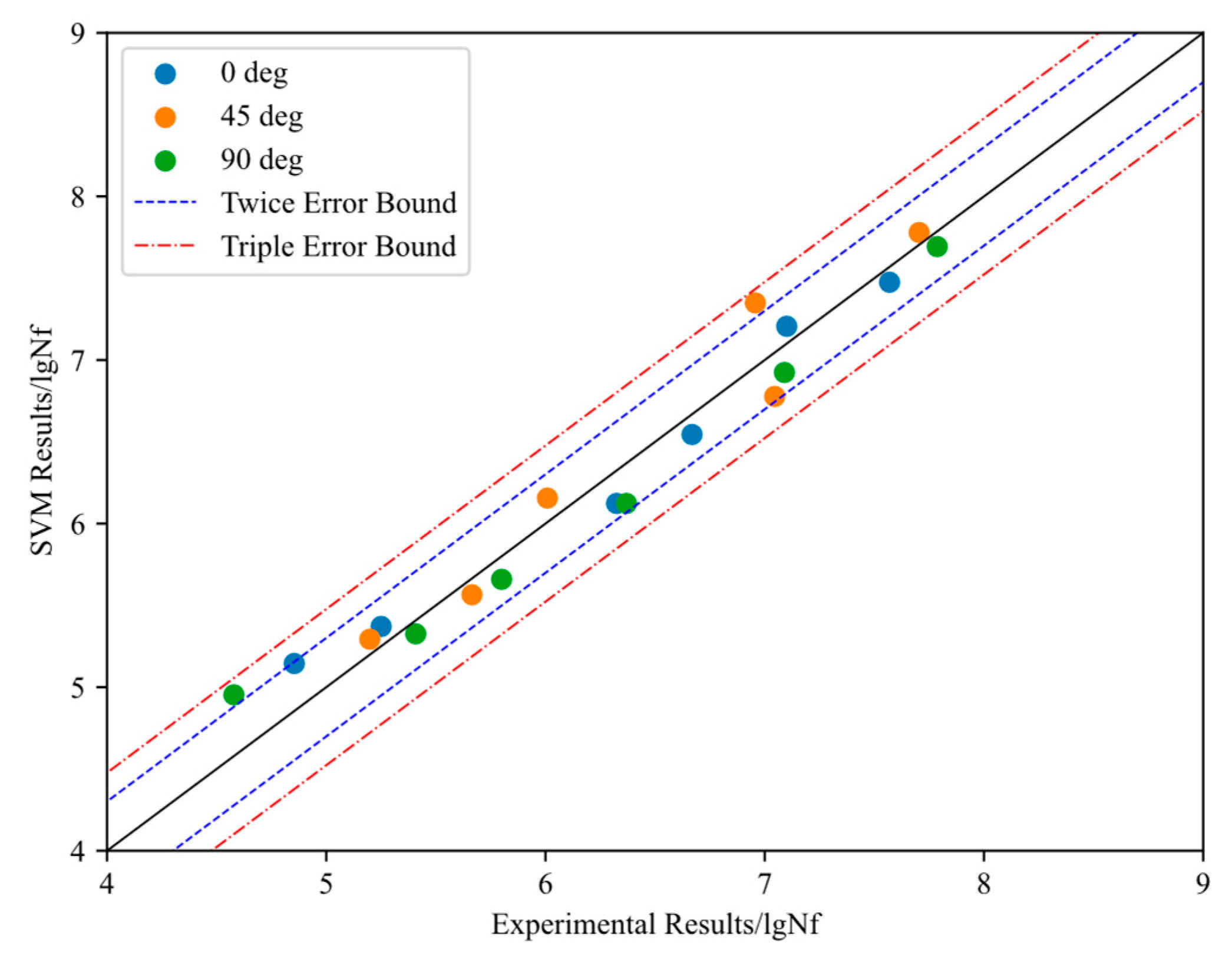
4.3. SVR-CDM Based Predictions
5. Discussion
5.1. Influence of Building Direction on the Fatigue Life
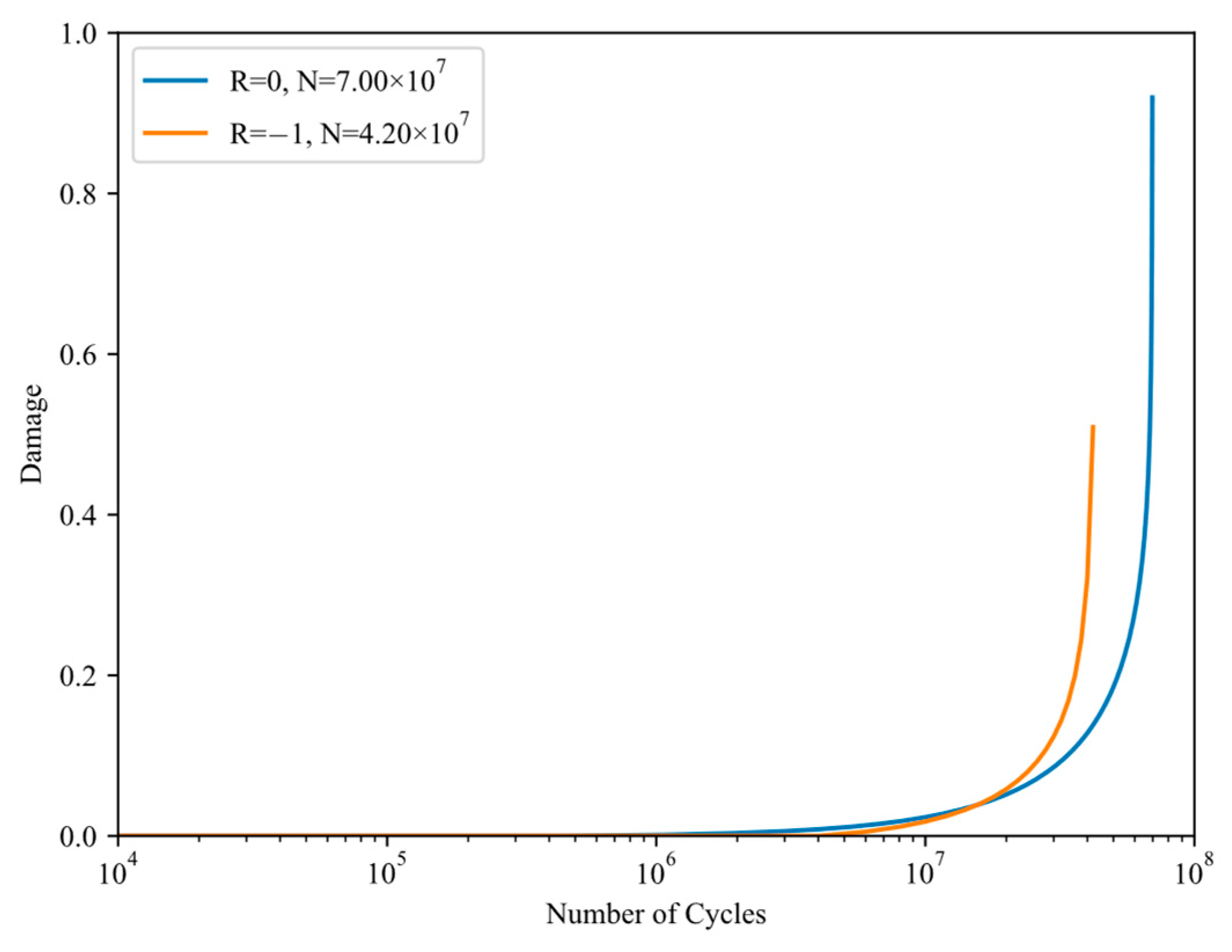
5.2. Influence of Stress Ratio and Stress Level on the Damage Accumulation and Evolution Rate
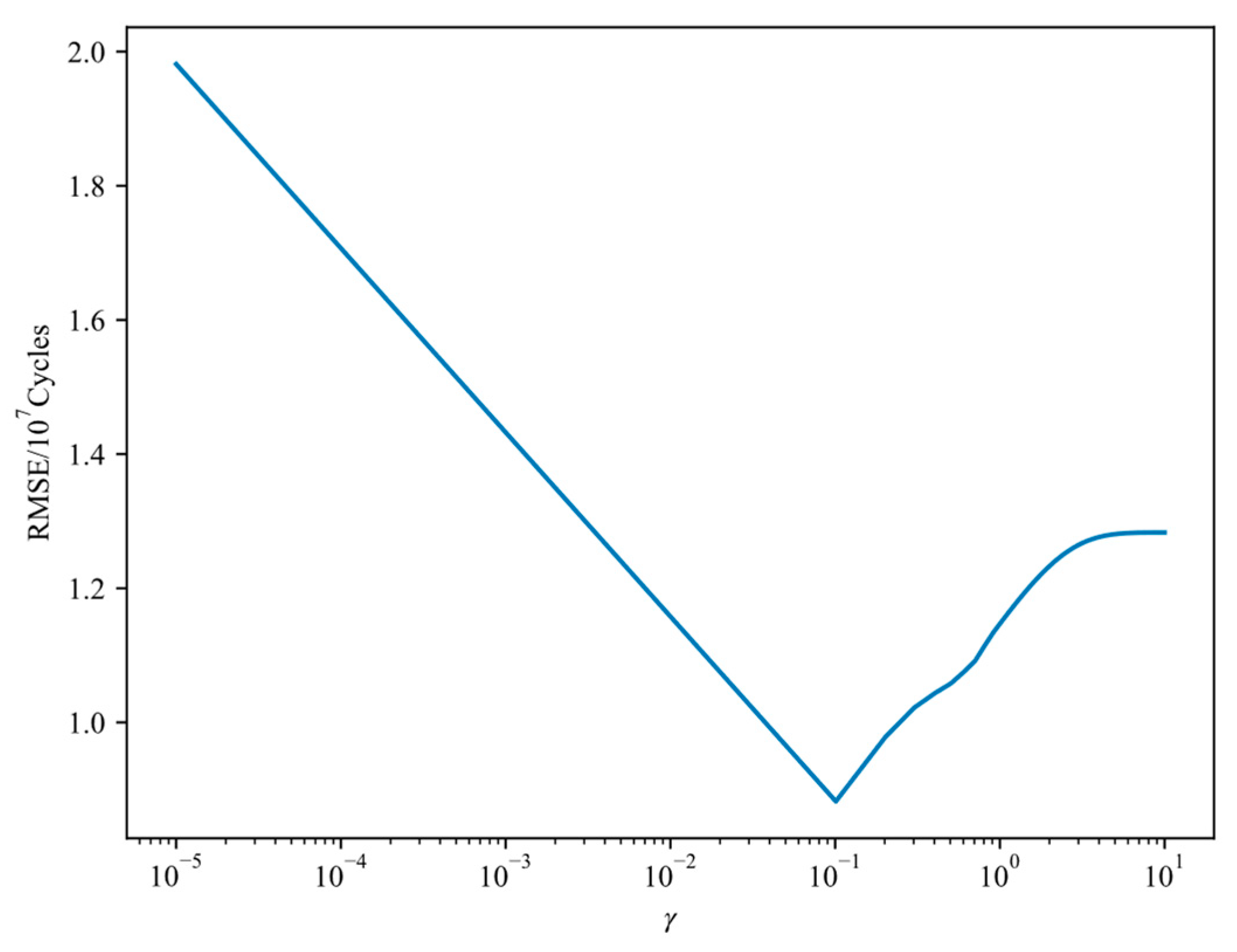
5.3. Influence of SVR Parameters on the Prediction Accuracy
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| damage variable | |
| Young’s modulus | |
| total strain | |
| elastic strain | |
| plastic strain | |
| stress component | |
| triaxial stress function | |
| Poisson’s ratio | |
| Kronecker delta | |
| damage strain energy density release rate | |
| Helmholtz free energy | |
| von Mises equivalent stress | |
| material parameters of constitutive model | |
| amplitude of a loading cycle | |
| mean stress of a loading cycle | |
| material parameters of damage evolution model | |
| octahedral shear stress amplitude | |
| mean hydrostatic stress | |
| maximum of von Mises equivalent stress | |
| yield stress | |
| fatigue limit | |
| maximum and minimum of the deviatoric stress tensor in a loading cycle | |
| initiation life | |
| stress ratio | |
| input data | |
| experimental data | |
| predicted data | |
| AM | additive manufacturing |
| SLM | selective laser melting |
| CDM | continuum damage mechanics |
| SVM | support vector machine |
| SVR | support vector regression |
| FE | finite element |
| PSO | particle swarm optimization |
References
- Wang, H.M. Materials’ fundamental issues of laser additive manufacturing for high-performance large metallic components. Acta Aeronaut. Astronaut. Sin. 2014, 35, 2690–2698. [Google Scholar]
- Liu, Q.; Lu, B.H. Review on Quality Control and Relevant Hybrid Technology in Additive Manufacturing of Metallic Materials. Mater. Rep. 2024, 1–15. Available online: http://kns.cnki.net/kcms/detail/50.1078.TB.20230410.1937.051.html (accessed on 19 April 2023).
- Sola, A.; Nouri, A. Microstructural porosity in additive manufacturing: The formation and detection of pores in metal parts fabricated by powder bed fusion. J. Adv. Manuf. Process. 2019, 1, e10021. [Google Scholar] [CrossRef]
- Lu, H.F.; Lv, J.M.; Luo, K.Y.; Lu, J. Microstructure and Mechanical Properties of Ti6Al4V Alloy by Laser Integrated Additive Manufacturing with Alternately Thermal/Mechanical Effects. Acta Metall. Sin. 2023, 59, 125–135. [Google Scholar]
- Zhang, W.Q.; Zhu, H.H.; Hu, Z.H.; Zeng, X. Study on the selective laser melting of AlSi10Mg. Acta Metall. Sin. 2017, 53, 918–926. [Google Scholar]
- Zhang, X.; Liu, S. Aerocraft aluminum alloys and their materials processing. Mater. China 2013, 32, 39–55. [Google Scholar]
- Li, S.; Fu, G.; Li, H.; Peng, Q.; Xiao, H.; Zhang, J.; Zhang, Z. Research Progress on Absorptivity of Selective Laser Melting Additive Manufacturing. Mater. Rep. 2023, 1–24. Available online: http://kns.cnki.net/kcms/detail/50.1078.tb.20230206.1618.001.html (accessed on 19 April 2023).
- Tan, Y.; Zhang, Y.; Lu, B.; Yan, X.; Li, Y.; Dai, M.; Liu, M. High Temperature Hardness and Oxidation Behavior of TiAl Alloy Fabricated by Electron Beam Selective Melting Additive. Rare Met. Mater. Eng. 2023, 52, 222–229. [Google Scholar]
- Zhang, Z.; Zeng, Q.; Liu, L.; Sun, C. Forming regularity of aluminum alloy formed by laser induced MIG arc additive manufacturing. Trans. China Weld. Inst. 2019, 40, 7–12. [Google Scholar]
- Zhang, G.; Zhang, P.; Gao, J.; Yu, H.; Yuan, H.; Ding, Y.; Xiong, H. Microstructure and Mechanical Properties of TC11 Titanium Alloy Fabricated by Wire-feed Electron Beam Additive Manufacturing. J. Mech. Eng. 2023, 1–8. Available online: http://kns.cnki.net/kcms/detail/11.2187.TH.20230202.1604.011.html (accessed on 19 April 2023).
- Ying, W.; Han, F. Oxidation Behavior and Control of Rene 104 Superalloy Produced by Laser Solid Forming. Electromach. Mould. 2018, 31, 39–44. [Google Scholar] [CrossRef]
- Ao, N.; He, Z.; Wu, S.; Peng, X.; Wu, Z.; Zhang, Z.; Zhu, H. Recent progress on the mechanical properties of laser additive manufacturing AlSi10Mg alloy. Trans. China Weld. Inst. 2022, 43, 1–19+113. [Google Scholar]
- Wang, K.; Jiao, X.; Zhu, J.; Li, J.; Du, S. Effect of laser power density on wear resistance of TC4 alloy manufactured by SLM. Trans. China Weld. Inst. 2020, 41, 61–64. [Google Scholar]
- Fiegl, T.; Franke, M.; Koerner, C. Impact of build envelope on the properties of additive manufactured parts from AlSi10Mg. Opt. Laser Technol. 2019, 111, 51–57. [Google Scholar] [CrossRef]
- Aboulkhair, N.T.; Everitt, N.M.; Ashcroft, I.; Tuck, C. Reducing porosity in AlSi10Mg parts processed by selective laser melting. Addit. Manuf. 2014, 1, 77–86. [Google Scholar] [CrossRef]
- Thijs, L.; Kempen, K.; Kruth, J.P.; Van Humbeeck, J. Fine-structured aluminium products with controllable texture by selective laser melting of pre-alloyed AlSi10Mg powder. Acta Mater. 2013, 61, 1809–1819. [Google Scholar] [CrossRef]
- Wu, H.H.; Li, J.F.; Wei, Z.Y.; Wei, P. Effect of processing parameters on forming defects during selective laser melting of AlSi10Mg powder. Rapid Prototyp. J. 2020, 26, 871–879. [Google Scholar] [CrossRef]
- Cai, X.; Dong, B.; Yin, X.; Lin, S.; Fan, C. Influences of pre-heating temperatures on the microstructures and mechanical properties of GTA additive manufactured TiAl based alloy. Trans. China Weld. Inst. 2021, 42, 14–21. [Google Scholar]
- Jian, Z.M.; Qian, G.A.; Paolino, D.S.; Tridello, A.; Berto, F.; Hong, Y.S. Crack initiation behavior and fatigue performance up to very-high-cycle regime of AlSi10Mg fabricated by selective laser melting with two powder sizes. Int. J. Fatigue 2021, 143, 106013. [Google Scholar] [CrossRef]
- Larrosa, N.O.; Wang, W.; Read, N.; Loretto, M.H.; Evans, C.; Carr, J.; Tradowsky, U.; Attallah, M.M.; Withers, P.J. Linking microstructure and processing defects to mechanical properties of selectively laser melted AlSi10Mg alloy. Theor. Appl. Fract. Mech. 2018, 98, 123–133. [Google Scholar] [CrossRef]
- Wu, Z. Evaluation of Anisotropic Fatigue Performance of Additively Manufactured Aluminum Alloy Based on 3D X-ray Computed Tomography of Defects. Ph.D. Thesis, Southwest Jiao-Tong University, Chengdu, China, 2020. [Google Scholar]
- Xu, Z.W.; Liu, A.; Wang, X.S. Fatigue performance and crack propagation behavior of selective laser melted AlSi10Mg in 0°, 15°, 45° and 90° building directions. Mater. Sci. Eng. A 2021, 812, 141141. [Google Scholar] [CrossRef]
- Zhao, X.; Lu, G.; Peng, X.; Zhang, N.; Qin, J. Fatigue life prediction of complex aeronautical components based on damage mechanics. Chin. J. Appl. Mech. 2020, 37, 1007–1012+1386–1387. [Google Scholar]
- Wu, L.; Wang, R.; Liu, F.; Qin, Q.; Chang, Y.; Wang, Z. Fatigue life prediction of resistance spot welded joints of AZ31B/TA15 dissimilar materials. Trans. Mater. Heat Treat. 2022, 43, 168–176. [Google Scholar]
- Zhang, S.; Wu, H. Life Evaluation of Multiaxial Variable Amplitude Low-Cycle Fatigue Based on Sequential Rain flow Method and Critical Plane Method. Chin. Q. Mech. 2020, 41, 465–476. [Google Scholar] [CrossRef]
- Zhang, D. Fatigue Life Prediction of High Strength Steel Welds under Prestrain Based on Energy Method and Its Application. Ph.D. Thesis, Hunan University of Technology, Hunan, China, 2022. [Google Scholar] [CrossRef]
- Shao, Q. Numerical Simulation of Fatigue Crack Propagation of Brittle Fracture Based on Phase Field Method. Ph.D. Thesis, Southwest Jiaotong University, Chengdu, China, 2019. [Google Scholar] [CrossRef]
- Gao, T.; Tong, Y.; Zhan, Z.; Mei, W.; Hu, W.; Meng, Q. Development of a non-local approach for life prediction of notched specimen considering stress/strain gradient and elastic-plastic fatigue damage. Int. J. Damage Mech. 2022, 31, 1057–1081. [Google Scholar] [CrossRef]
- Zhan, Z.; Hu, W.; Meng, Q. Data-driven fatigue life prediction in additive manufactured titanium alloy: A damage mechanics based machine learning framework. Eng. Fract. Mech. 2021, 252, 107850. [Google Scholar] [CrossRef]
- Zhan, Z. Fatigue life calculation for TC4-TC11 titanium alloy specimens fabricated by laser melting deposition. Theor. Appl. Fract. Mech. 2018, 96, 114–122. [Google Scholar] [CrossRef]
- Chen, P. Fatigue Reliability Analysis of Bogie Frame Based on Active Learning Neural Network. Chin. J. Comput. Mech. 2022, 1–9. Available online: http://kns.cnki.net/kcms/detail/21.1373.O3.20220728.1108.002.html (accessed on 3 April 2023).
- Raja, A.; Chukka, S.T.; Jayaganthan, R. Prediction of fatigue crack growth behaviour in ultrafine grained al 2014 alloy using machine learning. Metals 2020, 10, 1349. [Google Scholar] [CrossRef]
- Liu, S.; Shi, W.; Zhan, Z.; Hu, W.; Meng, Q. On the development of error-trained BP-ANN technique with CDM model for the HCF life prediction of aluminum alloy. Int. J. Fatigue 2022, 160, 106836. [Google Scholar] [CrossRef]
- Gao, T.; Ji, C.; Zhan, Z.; Huang, Y.; Liu, C.; Hu, W.; Meng, Q. A novel defect-based fatigue damage model coupled with an optimized neural network for high-cycle fatigue analysis of casting alloys with surface defect. Int. J. Fatigue 2023, 170, 107538. [Google Scholar] [CrossRef]
- Kaveh, A.; Dadras Eslamlou, A.; Javadi, S.M.; Geran Malek, N. Machine learning regression approaches for predicting the ultimate buckling load of variable-stiffness composite cylinders. Acta Mech. 2021, 232, 921–931. [Google Scholar]
- Horňas, J.; Běhal, J.; Homola, P.; Senck, S.; Holzleitner, M.; Godja, N.; Pásztor, Z.; Hegedüs, B.; Doubrava, R.; Růžek, R.; et al. Modelling fatigue life prediction of additively manufactured Ti-6Al-4V samples using machine learning approach. Int. J. Fatigue 2023, 169, 107483. [Google Scholar] [CrossRef]
- Li, X.Q.; Song, L.K.; Choy, Y.S.; Bai, G.C. Multivariate ensembles-based hierarchical linkage strategy for system reliability evaluation of aeroengine cooling blades. Aerosp. Sci. Technol. 2023, 138, 108325. [Google Scholar] [CrossRef]
- Li, X.Q.; Song, L.K.; Bai, G.C.; Li, D.G. Physics-informed distributed modeling for CCF reliability evaluation of aeroengine rotor systems. Int. J. Fatigue 2023, 167, 107342. [Google Scholar]
- Li, X.Q.; Song, L.K.; Bai, G.C. Deep learning regression-based stratified probabilistic combined cycle fatigue damage evaluation for turbine bladed disks. Int. J. Fatigue 2022, 159, 106812. [Google Scholar] [CrossRef]
- Lemaitre, J.; Desmorat, R. Engineering Damage Mechanics: Ductile, Creep, Fatigue and Brittle Failures; Springer Science & Business Media: New York, NY, USA, 2006. [Google Scholar]
- Chaboche, J.L.; Lesne, P.M.A. A non-linear continuous fatigue damage model. Fatigue Fract. Eng. Mater. Struct. 1988, 11, 1–17. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, X.; Yuan, S.; Sun, R.; Sakai, T.; Lashari, M.I.; Hamid, U.; Li, W. High-cycle-fatigue properties of selective-laser-melted AlSi10Mg with multiple building directions. Int. J. Mech. Sci. 2022, 224, 107336. [Google Scholar] [CrossRef]

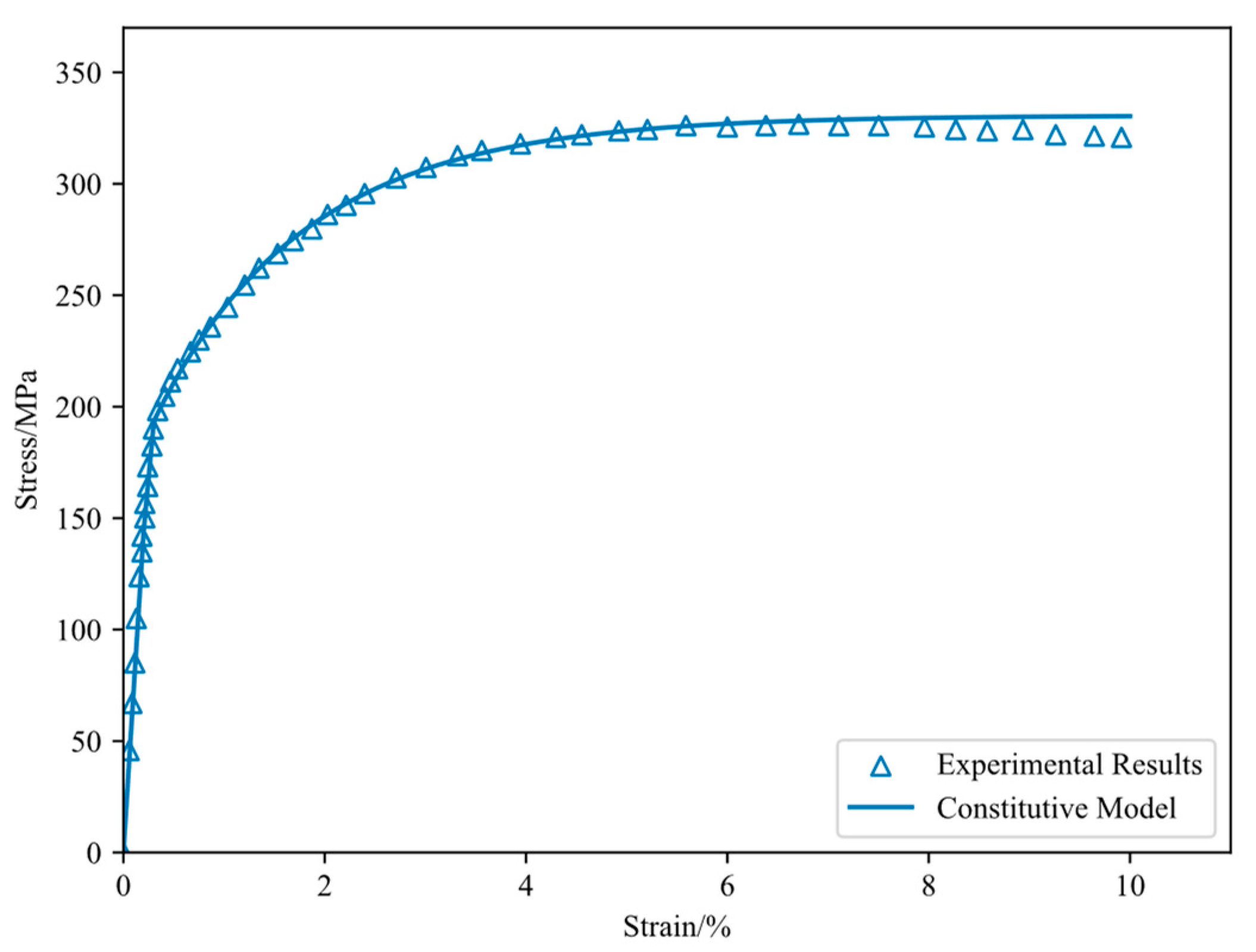




| C1 | C2 | C3 | γ1 | γ2 | γ3 | ||
|---|---|---|---|---|---|---|---|
| 7601.7 | 500.01 | 1527.63 | 62.10 | 62.10 | 150.0 | 71.632 | 190.0 |
| Direction | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0 | 9.16 | 175.0 | 1296.3 | 0.00001 | 0.006 | 70 | 1 | 44.63 |
| 45 | 0.0014 | 0.0042 | −196.9 | 49.43 | ||||
| 90 | 0.0053 | 0.00001 | −46.4 | 55.79 |
| Element Counts | 3240 | 9720 | 25,920 |
|---|---|---|---|
| von Mises stress/MPa | 138.97 | 139.13 | 139.23 |
| Models | RMSE | MAE | |
|---|---|---|---|
| CDM-FE | 2.37 × 107 | 1.1 × 107 | 0.87 |
| SVR | 5.36 × 106 | 3.2 × 106 | 0.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Y.; Sun, L.; Bian, Z.; Wang, X.; Zhang, Z.; Song, C.; Hu, W.; Chen, X. Very High Cycle Fatigue Life Prediction of SLM AlSi10Mg Based on CDM and SVR Models. Aerospace 2023, 10, 823. https://doi.org/10.3390/aerospace10090823
Yu Y, Sun L, Bian Z, Wang X, Zhang Z, Song C, Hu W, Chen X. Very High Cycle Fatigue Life Prediction of SLM AlSi10Mg Based on CDM and SVR Models. Aerospace. 2023; 10(9):823. https://doi.org/10.3390/aerospace10090823
Chicago/Turabian StyleYu, Yibing, Linlin Sun, Zhi Bian, Xiaojia Wang, Zhe Zhang, Chao Song, Weiping Hu, and Xiao Chen. 2023. "Very High Cycle Fatigue Life Prediction of SLM AlSi10Mg Based on CDM and SVR Models" Aerospace 10, no. 9: 823. https://doi.org/10.3390/aerospace10090823
APA StyleYu, Y., Sun, L., Bian, Z., Wang, X., Zhang, Z., Song, C., Hu, W., & Chen, X. (2023). Very High Cycle Fatigue Life Prediction of SLM AlSi10Mg Based on CDM and SVR Models. Aerospace, 10(9), 823. https://doi.org/10.3390/aerospace10090823






