Trend Analysis of Civil Aviation Incidents Based on Causal Inference and Statistical Inference

Abstract

The efficient management of aviation safety requires the precise analysis of trends in incidents. While classical statistical models often rely on the autocorrelation of indicator sequences for trend fitting, significant room remains for performance improvement. To enhance the accuracy and interpretability of trend analyses for aviation incidents, we propose the Causal-ARIMA model, which is grounded in causal inference theory, and we employ four distinct modeling strategies to fit the trend of incidents in China’s civil aviation sector between 1994 and 2020. The objective is to validate the performance of the Causal-ARIMA model and identify optimal trend analysis strategies. The four modeling strategies account for causation factors, stationarity, and causality with operational volume, incorporating models like AR, ARMA, ARIMA, and Causal-ARIMA. Our findings reveal that ensemble techniques incorporating the Causal-ARIMA model (Strategy 2 and 3) outperform classical trend analysis methods (Strategy 1) in terms of model fit. Specifically, the causality-based binary fitting technique (Strategy 3) achieves the most uniformly dispersed fitting performance. When the premises for using the Causal-ARIMA model are relaxed, applying it to variables without Granger causal relationships results in uneven model performance (Strategy 4). According to our study, the Causal-ARIMA model can serve as a potent tool for the analysis of trends in the domain of aviation safety. Modeling strategies based on the Causal-ARIMA model provide valuable insights for aviation safety management.

1. Introduction

In civil aviation, the occurrence of zero accidents remains the ultimate objective. According to Heinrich [1], a significant number of non-injurious incidents must be under control and reduced to prevent fatalities and serious injuries because they frequently precede accidents. Incidents are commonly viewed as precursors to accidents [2], making incidents crucial steps toward improving safety. The aviation sector makes enormous investments in gathering and analyzing data on incidents and safety occurrences to prevent aircraft tragedies. Every year, thorough statistics on global civil aviation aircraft accidents, incidents, and other safety occurrences are compiled by the International Civil Aviation Organization (ICAO) [3], Boeing [4], and Airbus [5]. They illustrate the present and potential safety conditions of the global aviation sector using descriptive statistics and straightforward linear extrapolation methods, serving as a resource for management choices in the aviation business.

Scholars have devoted a significant amount of attention to aviation accidents and incidents at the global [6], national [7,8,9,10,11,12], and operational [13,14,15] levels. Recommendations for managing aviation safety might be provided by analyzing trends or statistical patterns of events. To predict future aviation accidents and casualty figures, Li [6] studied varying trends in worldwide civil aviation accidents and casualty figures from 1942 to 2016. He then developed an Autoregressive Integrated Moving Average (ARIMA) time series analysis model. Duanmu and others [12] established the ARIMA-SVM model to predict the 10,000-h rate of damaged aircraft for the United States Air Force, which can provide an opportunity to grasp the overall trend in flight safety. Bartulovic and Steiner [15] implemented a predictive analysis of Split Airport safety performance and used causal modeling methods to identify potential and possible hazards in the future.

Methods like neural networks [16,17] and support vector machines [18,19], which are part of a series of big data analysis approaches, are increasingly employed in aviation safety research as a result of the quick development of machine learning and artificial intelligence algorithms. These techniques primarily predict occurrence counts or operational risks for the following time point, paying little regard to or providing an explanation for incident trends. Furthermore, the use of big data analysis is still limited [20] because the volume of data on aviation incidents is generally small and sampling intervals are frequently measured in years and months. Time series analysis techniques based on statistical inferences, such as Autoregressive (AR), Autoregressive Moving Average (ARMA), and ARIMA, are currently popular in the study of aviation incident trends. However, these models mostly ignore causal relationships and instead concentrate on the incident series’ stationarity and correlations with exogenous variables, suggesting room for improvement [21].

In recent years, theories relating to causal inference have gained widespread attention in both academia and industry. Compared to statistical inference models, models based on causal relationships offer superior accuracy and interpretability. Therefore, this study builds upon the theory of causal inference to improve the ARIMA model, culminating in the introduction of the Causal-ARIMA model for trend analysis. The research questions addressed are as follows:

(1)

Can the Causal-ARIMA model provide better fitting performance in trend analysis?

(2)

What is the applicability of the Causal-ARIMA model? Specifically, if the requirement for causal relationships in using the Causal-ARIMA model is relaxed, can it still offer superior fitting performance?

To address these research questions, we gathered data on civil aviation incidents and operational volumes in China from 1994 to 2020. We developed four integrated modeling strategies using the AR, ARMA, ARIMA, and Causal-ARIMA models based on incident causation, stationarity, and causality with operational volume. We employed in-sample forecasts to compare the trend-fitting performances of various techniques. This allowed us to validate the advantages of the Causal-ARIMA model, providing valuable references for the safety management and trend analysis of aviation incidents.

2. Data and Methods

2.1. Data

This study gathered a total of 6357 incident (INC) data entries and flight hour (FH) data that represent the operational volume of China’s civil aviation from 1994 to 2020. This was achieved by using data from the Chinese Civil Aviation Safety Information Statistical Analysis Report and the Civil Aviation Industry Development Statistical Bulletin. An “incident” is defined as an event involving an aircraft that takes place during the operational phase of the aircraft or within the airport activity area and does not constitute an accident but affects or may potentially affect safety, according to Annex 13 to the Convention on International Civil Aviation—Aircraft Accident and Incident Investigation [22]. Chinese civil aviation divides these incidents into seven categories depending on their primary causes: a flight crew (FC), air traffic control (ATC), maintenance (MT), machinery (MACH), ground support (GS), weather anomalies (WEA), and other circumstances (OTH). The unit for FH in

Table 1. Descriptive statistics of variables.

Variable	Min	Max	Mean	Median	Sum	Standard Deviation
FH	69.51	1231	467.11	368.9	12,612	362.2
INC	93	599	235.44	133	6357	171.8
WEA	15	493	149.33	58	4032	161.6
MACH	11	50	28.93	28	781	9.302
FC	16	55	27.11	23	732	10.38
GS	3	33	11.33	9	306	9.004
OTH	0	35	11.00	4	297	12.07
MT	0	10	4.15	4	112	3.097
ATC	0	12	3.59	2	97	2.925

is 10⁴ h, and the table includes descriptive statistics for incidents and flight hours. Table 1 indicates that WEA account for the bulk of incidents, with 4032 in total or around 63.4% of INCs. Following this are MACH and FC, which account for 12.3% and 11.5%, respectively. Finally, GS, OTH, MT, and ATC are listed in decreasing order.

In this study, FH is incorporated as an exogenous variable, and the causal relationships between different causative incidents and this exogenous variable are considered in the construction of our trend analysis strategies. Admittedly, treating FH solely as an exogenous variable is a simplification. This is because the aviation system, as a complex socio-technical system, has safety outcomes, namely, incidents, that are influenced by a myriad of contributing factors. These could include changes in aircraft technologies and successive aircraft generation configurations, alterations in air traffic controllers’ operational practices, maintenance issues, and changes in pilot skills and training requirements. However, given the extensive time span of the incidents under study, not all investigation reports provide detailed information on these variables. As a result, this study focuses only on FH as the exogenous variable in trend analysis modeling. The stationarity of various causative incidents and their causal links with FH were thoroughly explored and discussed in our earlier research [9]. The findings are summarized in

Table 2. Stationarity of incidents and their causal relationships with FH.

Variable	Stationarity (ADF Test)	Stationarity of First-Order Difference	Causal Relationship with FH (Toda and Yamamoto Causality Test)
FH	Non-stationary	Stationary	/
INC	Non-stationary	Stationary	FH is not the Granger cause of INC
WEA	Non-stationary	Stationary	FH is the Granger cause of WEA
MACH	Non-stationary	Stationary	FH is not the Granger cause of MACH
FC	Non-stationary	Stationary	FH is not the Granger cause of FC
GS	Non-stationary	Stationary	FH is the Granger cause of GS
OTH	Non-stationary	Stationary	FH is not the Granger cause of OTH
MT	Stationary	Stationary	FH is not the Granger cause of MT
ATC	Non-stationary	Stationary	FH is not the Granger cause of ATC

.

2.2. Model

2.2.1. AR Model

The simplest time-series-fitting model is the AR model. By running a linear regression on the prior historical values of a variable, the present value is predicted. The AR (p) model is shown in Equation (1):

$$Y_t=\alpha +{\beta }_1{Y}_{t-1}+{\beta }_2{Y}_{t-2}{+\dots +{\beta }_p{Y}_{t-p}+\epsilon }_t$$

(1)

It is possible to prevent contradictory estimates brought on by a residual autocorrelation by correctly identifying the model order p. Sequential rule and minimal information criteria are two strategies that are frequently used to establish the order p. These standards include the Schwarz criterion (SC), Hannan–Quinn criterion (HQ), and Akaike information criterion (AIC). Information criteria consist of two components: the first rewards a model’s fitting accuracy, and the second penalizes an over-abundance of model parameters.

2.2.2. ARMA Model

For fitting a stationary time series, the ARMA model—a fusion of the AR and Moving Average (MA) models—is used. This model incorporates two orders, p and q, and the ARMA (p,q) formulation is presented in Equation (2):

$$Y_t=\alpha +{\beta }_1{Y}_{t-1}+{\beta }_2{Y}_{t-2}{+\dots +{\beta }_p{Y}_{t-p}+\epsilon }_t+{\theta }_1{\epsilon }_{t-1}+\dots +{\theta }_q{\epsilon }_{t-q}$$

(2)

ARMA is preferred as a single-variable stationary-time-series-fitting technique because of its broad applicability and lower rates of fit errors. To generate an initial estimate of the model orders p and q, one often uses the trailing or truncation aspects of the autocorrelation function (ACF) and partial autocorrelation function (PACF). The subsequent refinement of these orders is often achieved using information criteria.

2.2.3. ARIMA Model

Non-stationary time series can be modeled using the ARIMA model. ARIMA transforms non-stationary time series into stationary time series by differencing its d times and then analyzes the differentiated series based on the ARMA model. Taking d as 1, for instance, the first-order differenced series is shown in Equation (3), and the ARIMA (p,1,q) model is expressed in Equation (4):

$$∆Y_t=Y_t{-Y}_{t-1}$$

(3)

$${∆Y}_t=\alpha +{\beta }_1∆Y_{t-1}+{\beta }_2{∆Y}_{t-2}+\dots +{\beta }_p{∆Y}_{t-p}+{\theta }_1{\epsilon }_{t-1}+\dots +{\theta }_q{\epsilon }_{t-q}$$

(4)

The same procedures used for finding the orders p and q in the ARMA model are used to determine the differencing order d in the ARIMA model.

2.2.4. Causal-ARIMA Model

It can be assumed that the information used by the aforementioned time-series-modeling techniques is still limited since they are intended for single-variable series. It is likely that including causally related exogenous variables in the ARIMA model could improve both its fitting effectiveness and interpretability because some incident series show a relationship of Granger causality with operational volume. To fit and predict the Y series, this paper presents the Causal-ARIMA model, which includes an exogenous causal variable X. If X is a Granger cause of Y, taking d as 1 for instance, the Casual-ARIMA (p,1,q,n) model is as shown in Equation (5):

$${∆Y}_t=\alpha +{\beta }_1∆Y_{t-1}+{\beta }_2{∆Y}_{t-2}+\dots +{\beta }_p{∆Y}_{t-p}+{\delta }_1∆X_t+..+{\delta }_n∆X_{t-n+1}+{\theta }_1{\epsilon }_{t-1}+\dots +{\theta }_q{\epsilon }_{t-q}$$

(5)

The exogenous variable X and its order n can take the form of vectors. Identifying n requires that the information criteria are minimized and the model residuals are ensured to be uncorrelated.

The ARIMAX model (also known as the extended ARIMA) and the Causal-ARIMA model have very similar shapes. However, the exogenous variable X merely has to be connected to the prediction variable Y in the ARIMAX model; a statistical causal relationship between X and Y is not necessary. As a result, Causal-ARIMA can be seen as an advancement/extension of the ARIMAX model.

2.3. Trend Analysis Strategies

This study suggests the following four analysis strategies to precisely match and estimate the trend in INC in China’s civil aviation based on the modeling approaches covered in Section 2.2.

Strategy 1: To directly simulate the INC series, the ARIMA model is required because INC exhibits non-stationary properties.

Strategy 2: Considering that the seven causative incidents have varying degrees of stationarity and have varied causal correlations with operational volume, the AR or ARMA model is applied to the stationary series. The ARIMA or Causal-ARIMA model is used for non-stationary series, depending on the causal relationship between the series and capacity. To acquire the results of the INC series fitting, the models of various causative incident series are finally integrated.

Strategy 3: The seven causative incidents are split into two main categories when only the causal relationships between the incidents and operational volume are taken into account; AR/ARMA/ARIMA can be used to model one class of situations without regard to operational volume. Using Causal-ARIMA, another category of incidents with causal connections to operational volume are modeled. Lastly, the two types of models are integrated to obtain the fitting results for the INC series.

Strategy 4: Even though there is no causal relationship between INC and FH, FH is nonetheless employed as an exogenous causal variable because of their substantial association. The Causal-ARIMA model is applied to INC for modeling and analysis.

Among the four methods outline above, the most classical statistical inference technique currently employed in trend research is Strategy 1. The fitting performance of Strategy 1 serves as a baseline for evaluating the performance of other analytical techniques. The analytical methods in Strategies 2 and 3 combine causal reasoning with statistical inference, reflecting improvements over classical statistical inference techniques. To ascertain the impact of the causality premise on the fitting performance of the Causal-ARIMA model, Strategy 4 applies the Causal-ARIMA model to two variables that lack a Granger causal relationship.

3. Results

3.1. Fitting Models under Different Analysis Strategies

3.1.1. Strategy 1

The ARIMA (p,d,q) model was employed to model INC. As shown in Table 2, the ARIMA model’s differencing order d is set to 1 because INC is non-stationary and its first-order differenced series is stationary. Based on the ACF and PACF of the differenced series, the ranges of p and q were determined to be between 0 and 1. Consequently, three fitting models were established: ARIMA (1,1,1), ARIMA (1,1,0), and ARIMA (0,1,1). These three models’ residuals all showed no autocorrelation, which met the white noise requirement. According to

Table 3. Fitting models for Strategy 1.

Variable	Fitting Model	Model Expressions	AIC	SC	HQ
INC	ARIMA (1,1,1)	$\Delta IN{C}_t=0.564\Delta IN{C}_{t-1}+0.024{\epsilon }_{t-1}$	10.462	10.607	10.504
	ARIMA (1,1,0)	$\Delta IN{C}_t=0.580\Delta IN{C}_{t-1}$	10.385	10.482	10.413
	ARIMA (1,1,0)	$\Delta IN{C}_t=0.456{\epsilon }_{t-1}$	10.473	10.569	10.500

, the ARIMA (1,1,0) model fits the data the best under Strategy 1 based on the model’s AIC, SC, and HQ values.

3.1.2. Strategy 2

The seven causative incident series were divided into four groups based on stationarity and their causal linkages with operation volume (see Table 2).

HF represents incidents related to human factors, encompassing FC, ATC, and MT. Since MT is stationary but FC, ATC, and HF are non-stationary, it follows that HF is also non-stationary. Furthermore, HF has no causal association with FH because FC, ATC, and MT do not have any causal relationships with FH.

MACH relates to incidents brought on by machinery issues. These incidents are categorized separately because they have an inherent connection to hardware problems. MACH is non-stationary and has no causal relationship with FH.

GW indicates incidents brought on by both unexpected weather and ground support (GS/WEA). These two incidents are associated with how the environment affects flight operations. They both display non-stationary properties and are causally related to FH according to Granger’s theory.

OTH represents incidents brought about by other causes. These incidents’ complicated underlying causes are taken into account independently. OTH is non-stationary and has no causal relationship with FH.

The ADF test was used to examine the stationarity of the aforementioned four occurrence groups. All the incident series were determined to be non-stationary by the results, although their first-order differenced series were found to be stationary. To fit HF, MACH, and OTH, the ARIMA (p,1,q) model was used, with the best orders p and q being determined by minimizing the three information criteria. While OTH’s best model had p and q values of 0, simplifying to an AR (1) model, the best forecast models for HF and MACH were ARIMA (1,1,0) and ARIMA (1,1,1), respectively. With FH acting as the causal variable, GW was fitted using Causal-ARIMA (p,1,d,n). The model achieved the best fit when the differencing order n was set to 1. The fitting models for these four categories of incidents are detailed in

Table 4. Fitting models for Strategy 2.

Variable	Fitting Model	Model Expressions
HF	ARIMA (1,1,0)	$\Delta H{F}_t=-0.487\Delta H{F}_{t-1}$
MACH	ARIMA (1,1,1)	$\Delta MAC{H}_t=0.995\Delta MAC{H}_{t-1}-0.593{\epsilon }_{t-1}$
GW	Causal-ARIMA (1,1,0,1)	$\Delta G{W}_t=0.308\Delta G{W}_{t-1}-0.252\Delta F{H}_t$
OTH	AR (1)	$OT{H}_t=0.878OT{H}_{t-1}+{\epsilon }_t$

.

3.1.3. Strategy 3

The incident series can be separated into two groups based on the causal connection with FH. GS and WEA are included in the first category. As GS and WEA are related to the FH via a Granger causal relationship, they are nonetheless grouped into a single category designated GW. The remaining five series are categorized under a different heading called NGW. An ADF test was run on NGW’s stationarity because the stationarity characteristic of GW was already examined in Strategy 2. According to the findings, NGW is stationary.

Therefore, in Strategy 3, Causal-ARIMA (1,1,0,1) continues to be the optimal fitting model for GW, while the AR (1) model is the optimal fitting model for NGW, as shown in

Table 5. Fitting models for Strategy 3.

Variable	Fitting Model	Model Expressions
GW	Causal-ARIMA (1,1,0,1)	$\Delta G{W}_t=0.308\Delta G{W}_{t-1}-0.252\Delta F{H}_t$
NGW	AR (1)	$NG{W}_t=0.987NG{W}_{t-1}+{\epsilon }_t$

.

3.1.4. Strategy 4

According to findings from earlier studies, there is a significant positive correlation between INC and the operational volume FH. Correlated variables are frequently used in fitting models in existing statistical inference studies to improve model accuracy. FH is still treated as an exogenous variable in Strategy 4 even though there is no causal relationship between INC and FH, fitting INC through the Causal-ARIMA model.

To fit INC, the Causal-ARIMA model was used. The order d was set to 1. A thorough analysis of the information criteria minimization and model residual uncorrelation was necessary to determine the orders p, q, and n. As shown in

Table 6. Fitting models for Strategy 4.

Variable	Fitting Model	Model Expressions
INC	Causal-ARIMA (1,1,0,1)	$\Delta IN{C}_t=0.267\Delta IN{C}_{t-1}+0.349\Delta F{H}_t$

, Causal-ARIMA (1,1,0,1) is the optimal fitting model.

3.2. Fitting Performance Comparison

We conducted an in-sample forecast method to project the INC values from 1994 to 2020, using models from the four strategies. The goal was to assess how well the models fit the data by comparing the discrepancies between the fitted values and the actual observed values. The Mean Absolute Error (MAE), Mean Absolute Percentage Error (MAPE), and Root Mean Square Error (RMSE) are the performance metrics used.

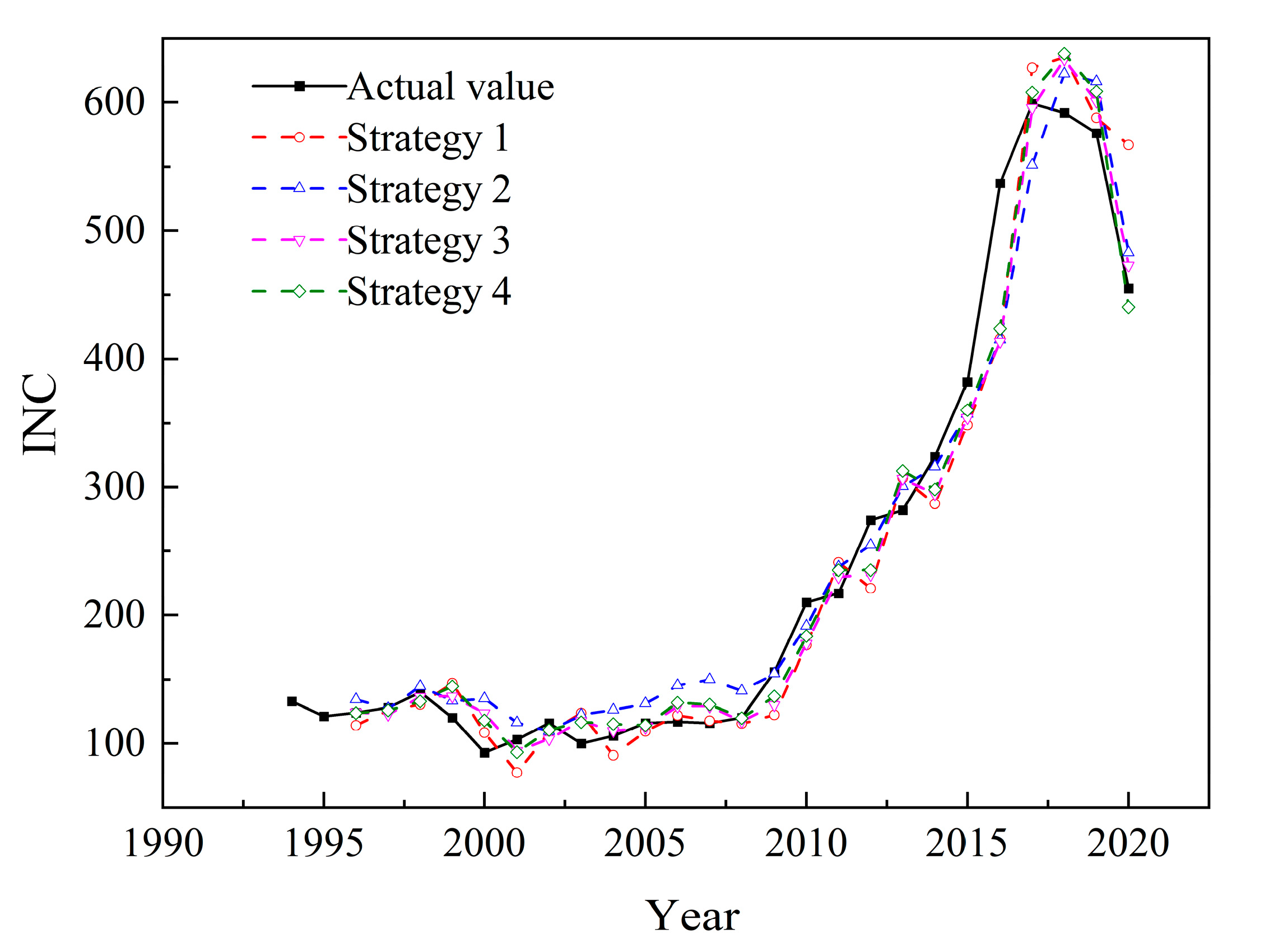
The fitted INC values compared to the actual INC values for each of the four strategies are illustrated in Figure 1. It is evident that the fitting models for all four strategies reliably represent the INC trend. However, the fitting curve for Strategy 1 diverges significantly from the actual values, especially at the time point of 2020. This suggests that using the ARIMA model alone to fit incident trends may not always yield optimal results, particularly when there are significant changes in FH as the ARIMA model does not take into account exogenous variables. It is challenging to determine any obvious superiority in the fitting performance for Strategies 2 to 4 based solely on the curves; more detailed performance metrics are required to evaluate their fitting performances.

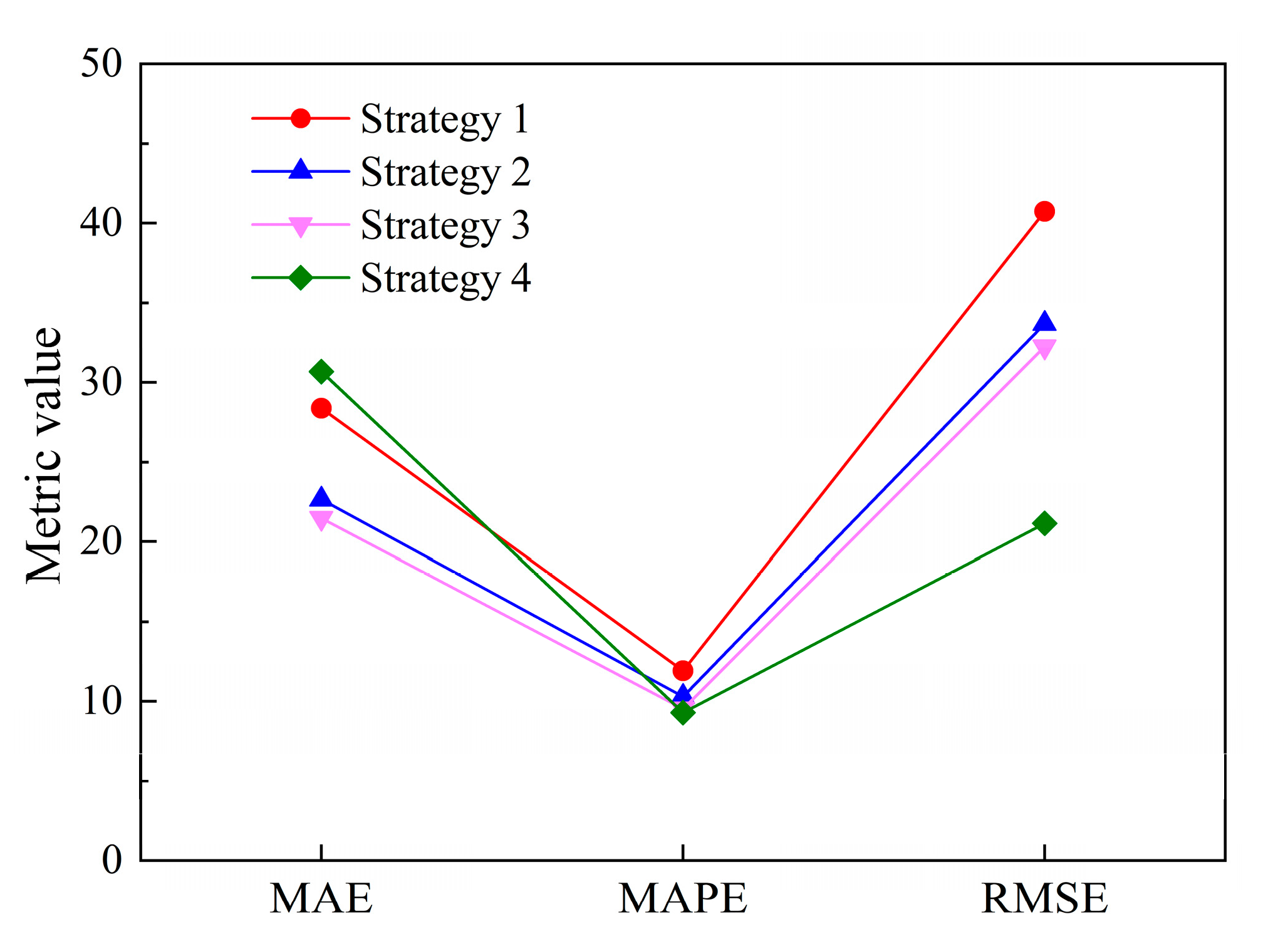
Based on performance metrics such as MAE, MAPE, and RMSE, we evaluated fitting performance across several strategies, as shown in Figure 2.

The lower the values for MAE, MAPE, and RMSE, the better the model’s performance in trend fitting. Given that Strategy 1 is the most traditional and commonly used method in current trend analyses, its performance metrics serve as the baseline for the evaluation. The MAE, MAPE, and RMSE values for Strategy 2 and Strategy 3 are significantly lower than those for Strategy 1 in each of these categories. Compared to the use of only traditional statistical inference models, the integrated use of the Causal-ARIMA model and traditional statistical models leads to a better trend-fitting performance. Moreover, Strategy 3’s three performance metrics marginally outperform those of Strategy 2. This suggests that fitting strategies distinguished by both causality and stationarity are less effective than those based solely on causality. The accumulation of fitting errors due to more categories could be the reason for Strategy 2’s inferior fitting performance.

For Strategy 4, the Causal-ARIMA model is employed to project variables that are highly correlated but have no apparent causal relationship. Although this strategy’s MAPE and RMSE values are lower than those of the other strategies, it falls short of the baseline model (Strategy 1) in terms of its MAE. Therefore, fits made within a narrow range may suffer due to a higher MAE. This indicates that using the Causal-ARIMA model for variables that are purely correlated without distinguishing for causality can result in unbalanced performance. Consequently, caution is needed when using the Causal-ARIMA model as it does not offer a comprehensive advantage in fitting variables that are merely correlated.

The most balanced and effective fitting results are provided by the binary fitting strategy (Strategy 3), which integrates statistical and causal reasoning. Therefore, we advise using Strategy 3 for trend analysis when creating regulations for aviation operational units or civil aviation authorities based on trends om incidents. The Causal-ARIMA causal inference model and the suitable statistical inference model based on the causality between incidents and exogenous variables are used in this method.

4. Conclusions

Enhancing safety requires a thorough understanding of incidents. Operational units and policymakers can apply more focused safety management measures through modeling and conducting trend analyses of incident data. This study, based on causal inference theory, extends the classic ARIMA model for trend analysis by introducing the Causal-ARIMA model. To validate the advantages and applicability of the Causal-ARIMA model in trend analysis, this study collected incident and operational volume data from China’s civil aviation sector from 1994 to 2020 and established four trend analysis strategies. The results show that Strategies 2 and 3, which include the Causal-ARIMA model, outperform the traditional trend analysis techniques (Strategy 1). Specifically, Strategy 3, which employs a two-category modeling approach based on causal inference, achieves the best fitting results. This suggests that the Causal-ARIMA model positively contributes to trend analysis, and combining causal inference models with statistical inference models can optimize existing trend analysis methodologies. Strategy 4 investigates the applicability of the Causal-ARIMA model when relaxed assumptions about the existence of “causal relationships” are used, and we find that the model’s performance metrics are highly unbalanced. Thus, it is important to be cautious about the premises when applying the Causal-ARIMA model.

The innovation of this study lies in the incorporation of the increasingly popular concept of causal inference into the analysis of aviation safety trends. It introduces the Causal-ARIMA model and establishes a trend analysis technique that synergizes causal inference with statistical inference. However, the study has its limitations, particularly in the selection of exogenous variables. In applying the Causal-ARIMA model, we only considered operational volume as the exogenous variable. In reality, trends in incidents are the outcomes of complex interactions involving a multitude of variables both internal and external to the system, such as different aircraft generation configurations, changes in air traffic controllers’ operational practices, and pilot training requirements. Given that this study relies on long-term, national-level incident data, not all incident investigations provide an equally detailed account of these factors. This restricts the range of exogenous variables that can be used in the trend analysis. However, it is certain that if the quality of input data could be enhanced, particularly by including more variables from the operational and design phases of aircraft, the trend analysis techniques proposed in this study would offer even greater value in understanding the mechanisms and trends of incidents. Therefore, future research should focus on deeply analyzing the relationships between incidents and various exogenous variables, continually improving the quality of data used in trend analysis, so that the analytical techniques proposed in this study can provide deeper insights into the underlying trends and frequencies of failure mechanisms.