Using the Impulse Method to Determine High-Pressure Dynamic Burning Rate of Solid Propellants
Abstract
:1. Introduction
2. Measurement Principle and Experiment
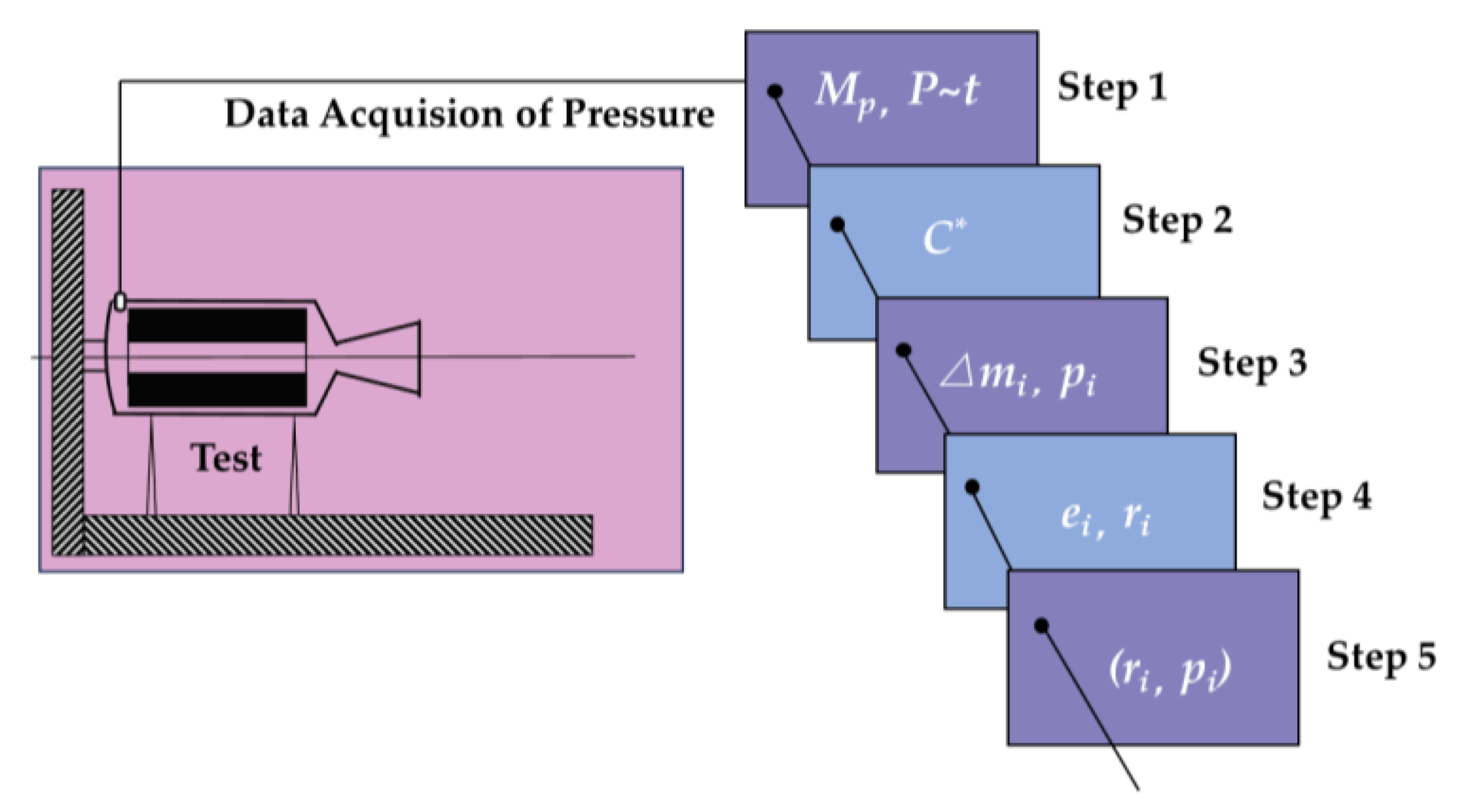
2.1. Test System
2.2. Principles
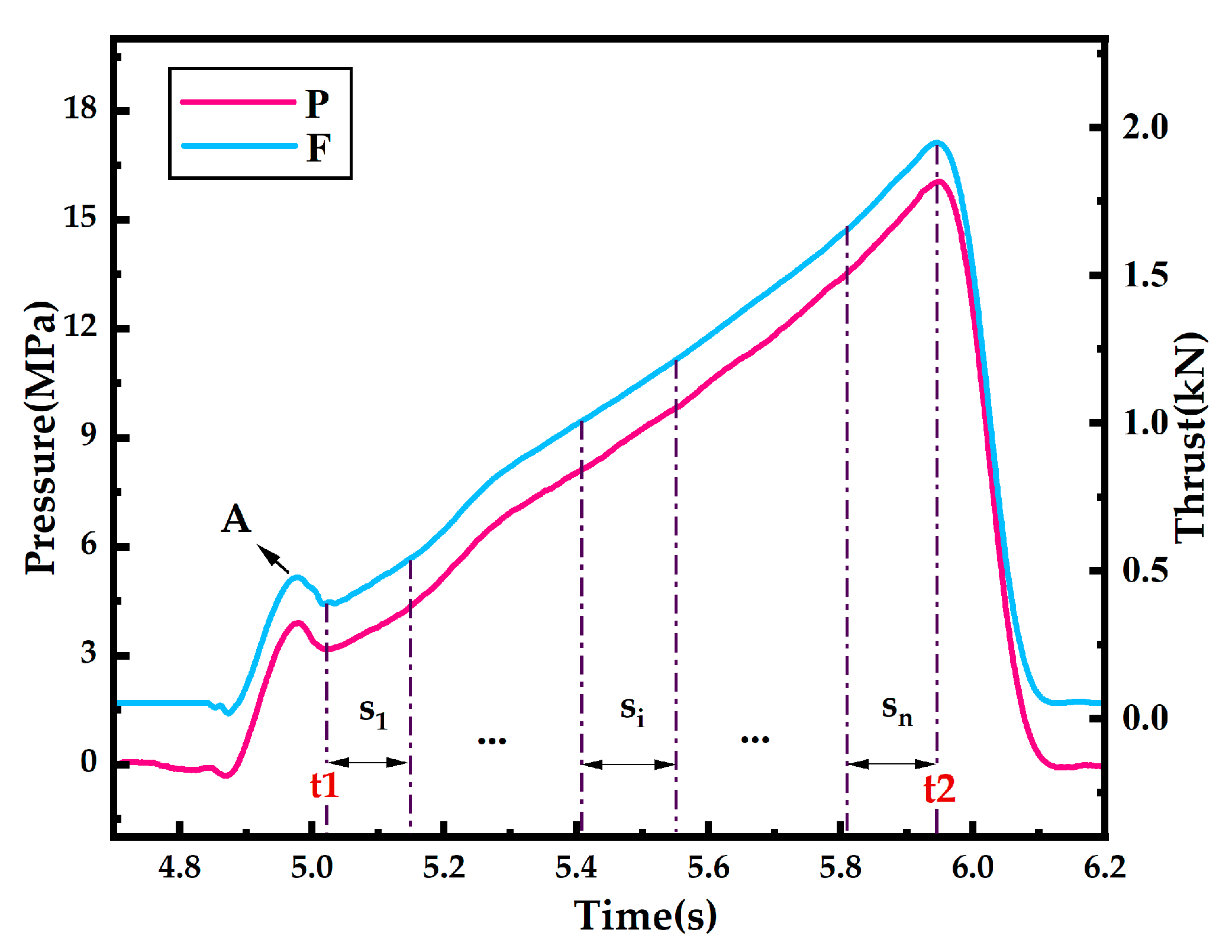
2.2.1. Data Processing
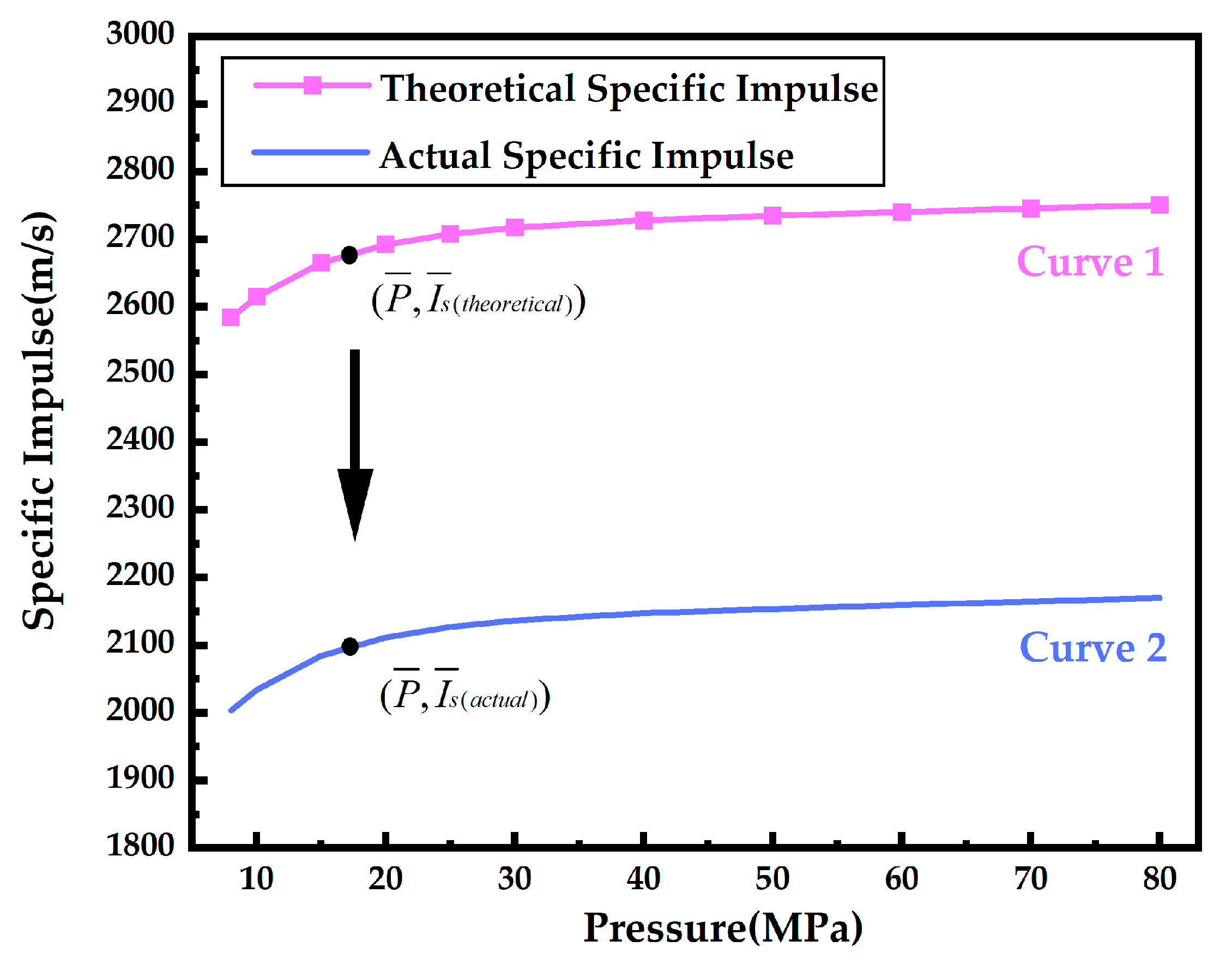
2.2.2. Actual Specific Impulse
- (1)
- Use the chemical thermodynamic calculations based on the tested propellant’s composition to obtain the theoretical specific impulse values at a series of different pressures.
- (2)
- Fit the pressures and corresponding theoretical specific impulse values using an appropriate mathematical function, which will result in a function depicting the variation of the theoretical specific impulse with the pressure (Is(theoretical)P), as shown by curve 1 in Figure 4.
- (3)
- Use Equations (2) and (3) to calculate the average specific impulse and the average pressure values, respectively. Locate the corresponding point () in Figure 4.
- (4)
- Since the actual specific impulse should be lower than the theoretical specific impulse, shift curve 1 in Figure 4 downward in parallel until it passes through the point (). This adjustment will produce curve 2, representing the relationship between the actual specific impulse and the pressure (Is(actual)P).
3. Experimental Results and Analysis
3.1. Experimental Samples
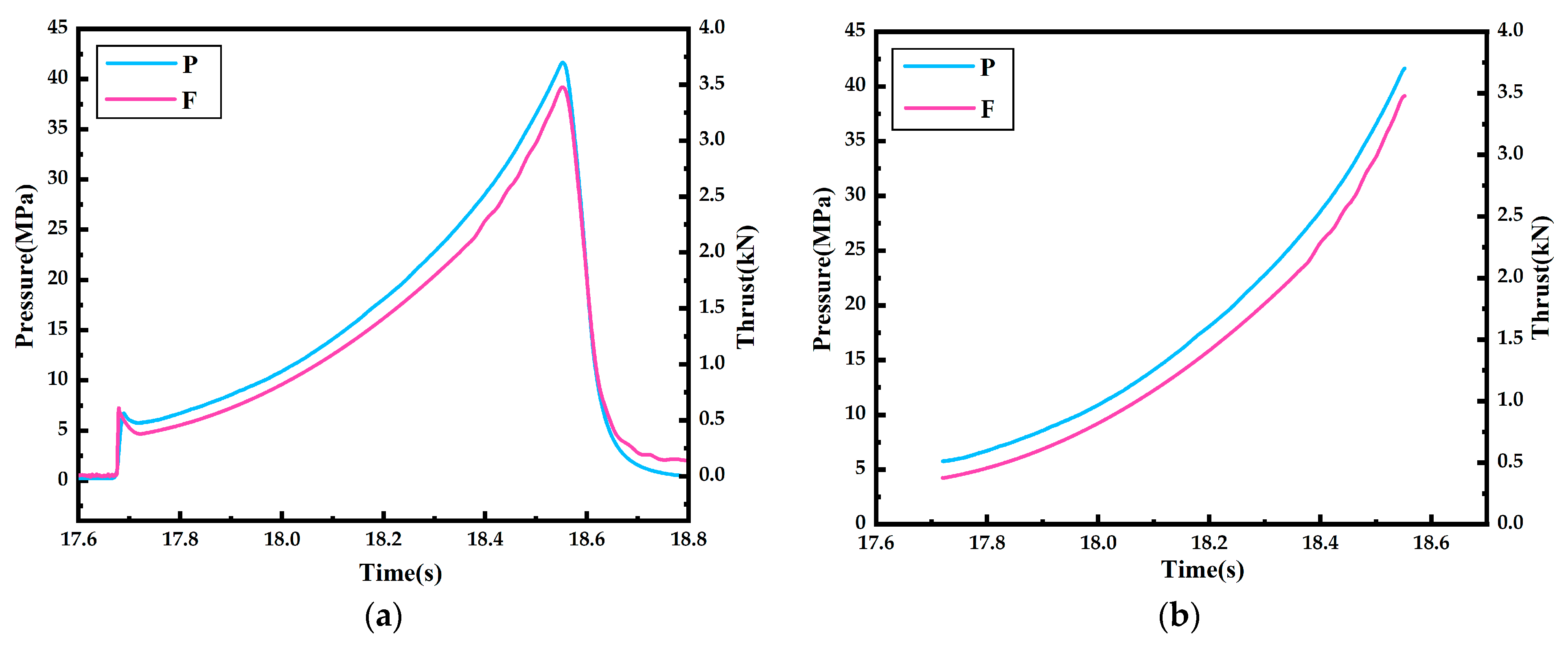
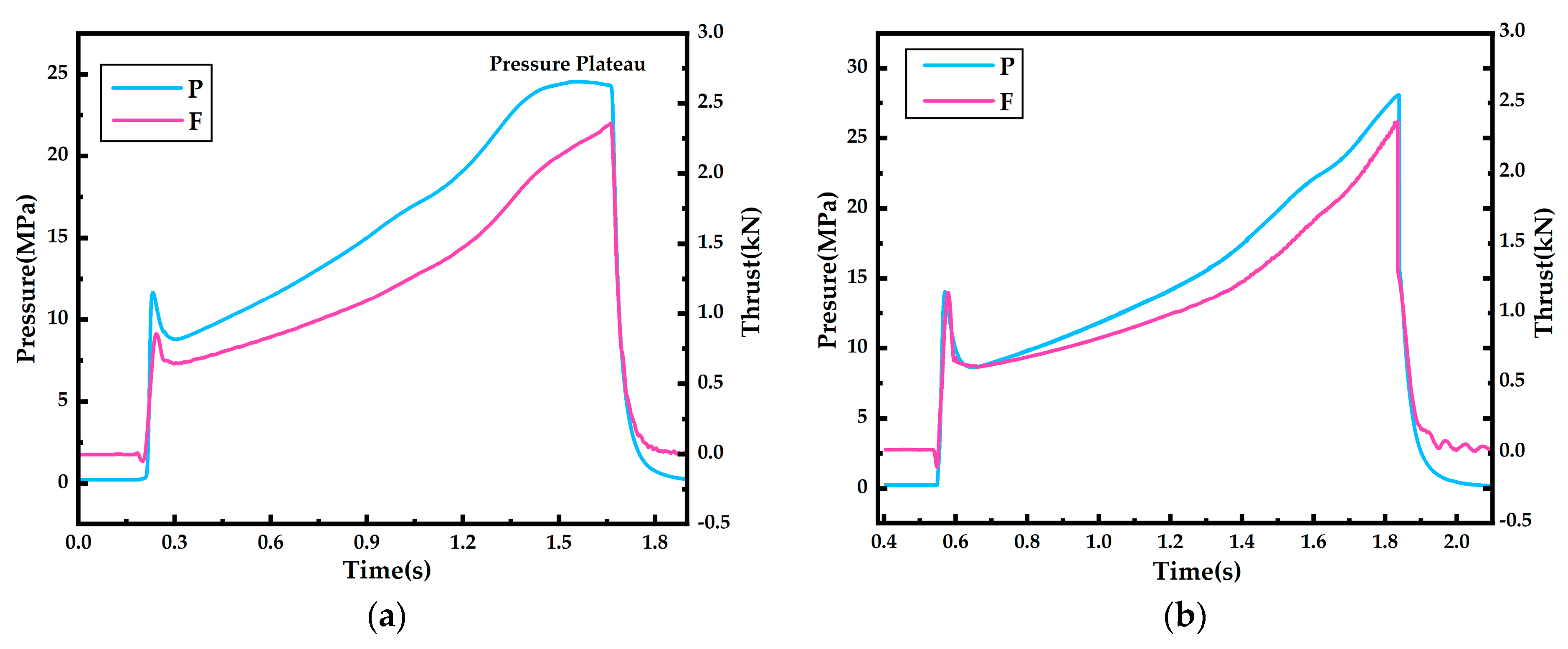
3.2. Processing of Test Data for GAP-1
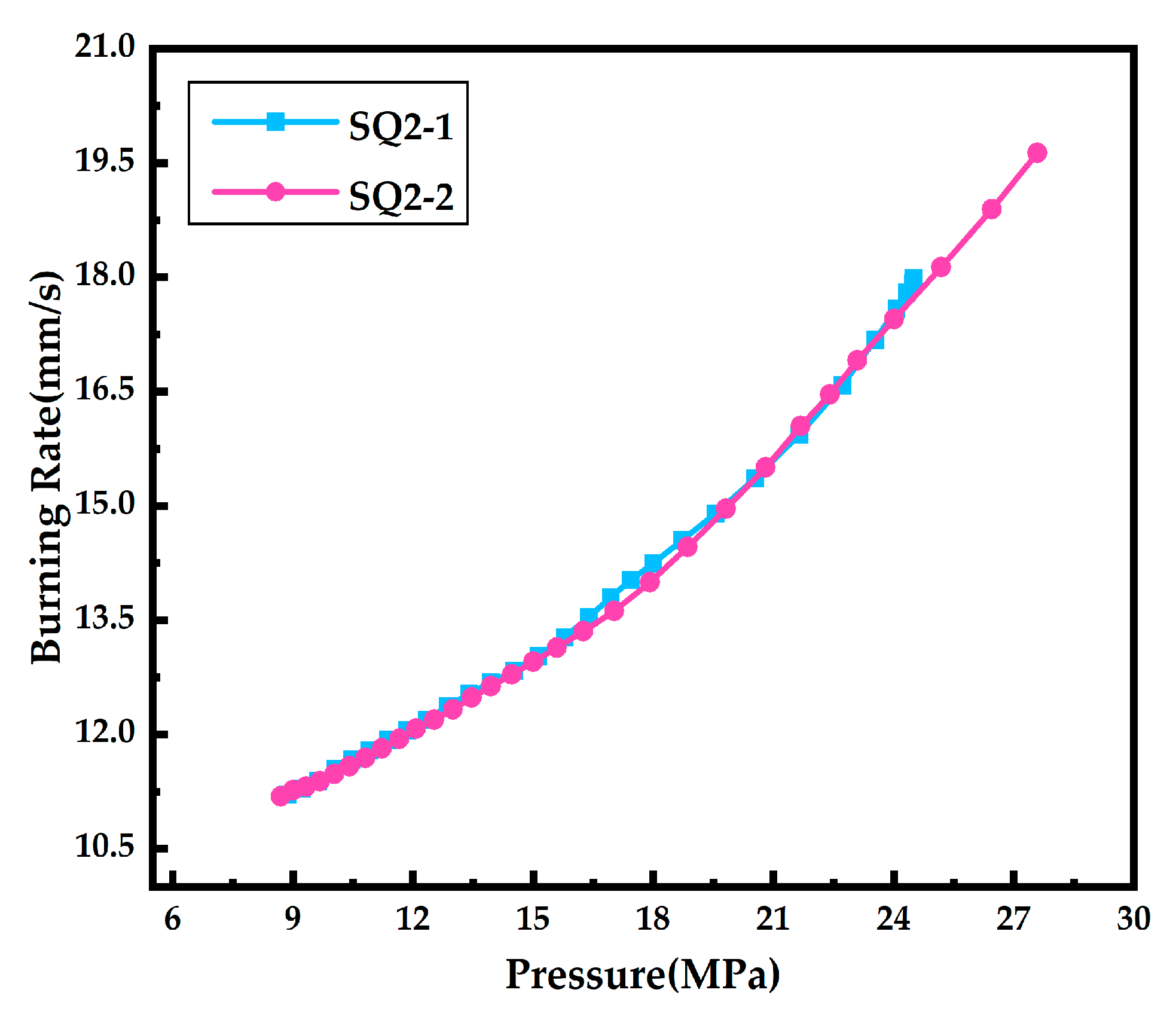
3.3. Burning Rate Test Results and Analysis
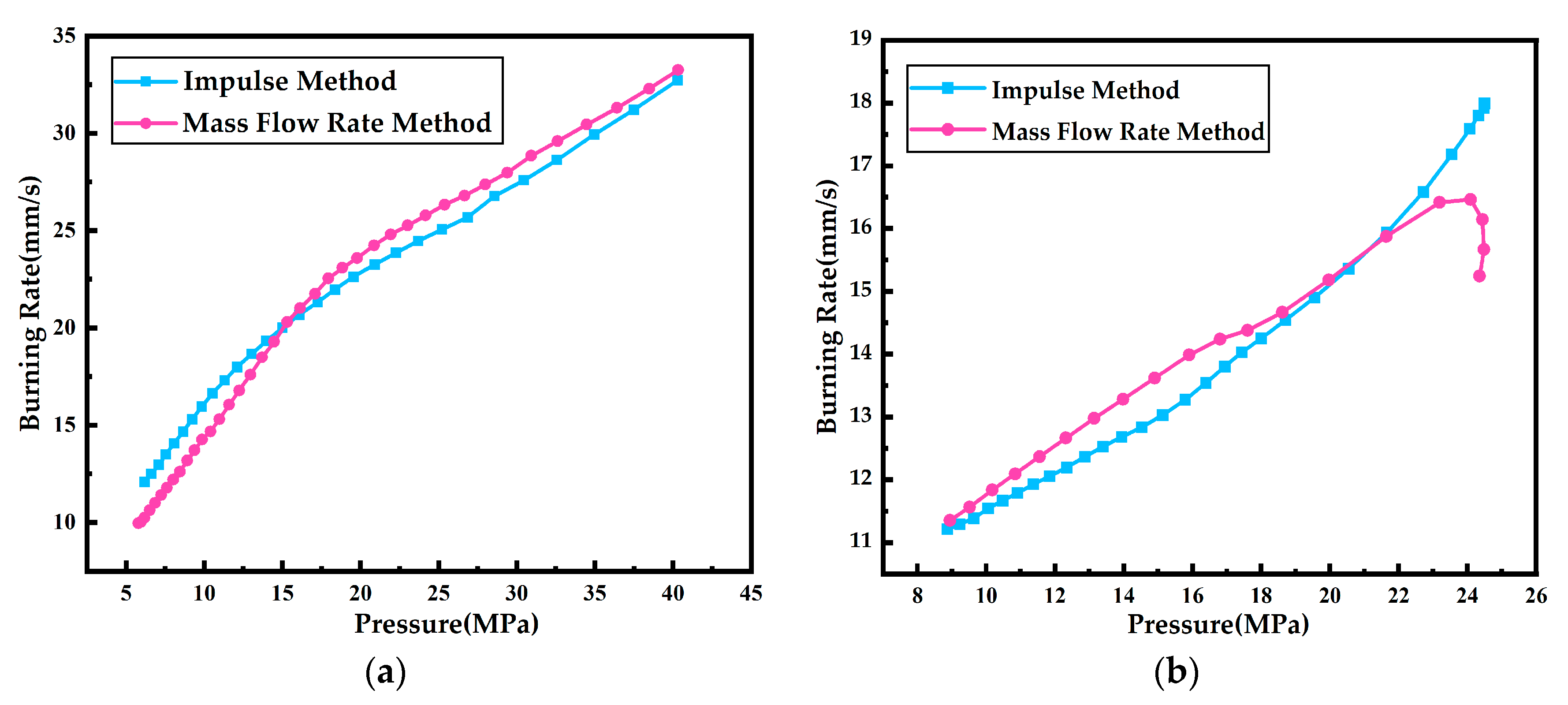
3.4. Rationality of the Method for Determining Is(actual)
4. Conclusions
- (1)
- Two types of propellants were subjected to burning rate tests using the Impulse Method. The burning rates were nearly equal for propellants of the same type at the corresponding pressures, demonstrating the feasibility of the method.
- (2)
- The Impulse Method is efficient for testing the burning rate of a solid propellant. It allows one to obtain the burning rate of a solid propellant at any pressure within an increased pressure range through a single test. The burning rates obtained using the Impulse Method and the Standard Motor Method at the same pressure were consistent, indicating the comparability between the Impulse Method and the Standard Motor Method. Furthermore, the Impulse Method eliminates the need to consider errors introduced by nozzle erosion.
- (3)
- A comparative analysis was conducted on the burning rates obtained through the Mass Flow Rate Method and the Impulse Method. The results provide evidence supporting the rationality of the approach in determining the actual specific impulse.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| D | outer diameter of propellant grain |
| D | inner diameter of propellant grain |
| L | length of propellant grain |
| P~t | pressure versus time trace |
| F~t | thrust versus time trace |
| I0 | total impulse of the propellant |
| t1 | initial moment of propellant burning |
| t2 | final moment of propellant burning |
| average specific impulse of propellant | |
| average pressure of during the whole burning process of propellant | |
| si | time segment of propellant burning time |
| ti | duration of si |
| mi | mass of the propellant burned off si |
| average pressure of si | |
| Is | specific impulse at the corresponding |
| I0i | total impulse of the si |
| ei | web thickness of propellant burned off during ti |
| density of the propellant grain | |
| ri | burning rate of propellant corresponding to |
| Is(actual) | actual specific impulse |
| Is(theoretical) | theoretical specific impulse |
| Is(theoretical)~P | theoretical specific impulse versus pressure trace |
| Is(actual)~P | actual specific impulse versus pressure trace |
| At | cross-sectional area of the nozzle throat |
| dt1 | initial throat diameter of the nozzle |
| dt2 | final throat diameter of the nozzle |
| CF | thrust coefficient |
| P | chamber pressure |
| C* | characteristic velocity |
| ravg | the average burning rate throughout the combustion process |
| ea | the total web thickness of propellant grain |
| ta | the total burning time of propellant grain |
References
- Liu, J.H. Physical and Chemical Properties of Gunpowder, 1st ed.; Beijing Institute of Technology Press: Beijing, China, 1997; p. 160. [Google Scholar]
- Yue, S.; Liu, L.; Liu, H.; Jiang, Y.; Liu, P.; Pang, A.; Zhang, G.; Ao, W. Agglomerate Size Evolution in Solid Propellant Combustion under High Pressure. Aerospace 2023, 10, 515. [Google Scholar] [CrossRef]
- Sun, D.; Li, Y.; Liu, P.; Chen, B.; Fan, W. Numerical Investigation on the Effect of Ammonium Perchlorate Content and Position on the Combustion Characteristics of an Ammonium Perchlorate/Hydroxyl-Terminated Polybutadiene Propellant. Aerospace 2023, 10, 692. [Google Scholar] [CrossRef]
- Wang, B.X.; Feng, Z.G.; Yang, R.J. Theory of Gunpowder Combustion, 1st ed.; Beijing Institute of Technology Press: Beijing, China, 1997; p. 123. [Google Scholar]
- Liu, K.X.; Zhao, L.; Li, B. Testing Method for Dynamic Burning Rate of Closed Chamber Pressurized Solid Propellant. J. Explos. Propellants 2014, 37, 78–81. [Google Scholar]
- Pei, Q. Research on the Method and Testing System for Quasi-Dynamic Burning Rate Testing of Solid Propellants with Multiple Strain Gauges. Master Thesis, Xidian University, Xi’an, China, 2013. [Google Scholar]
- Yilmaz, N.; Donaldson, B.; Gill, W.; Erikson, W. Solid propellant burning rate from strand burner pressure measurement. Propellants Explos. Pyrotech. 2008, 33, 109–117. [Google Scholar] [CrossRef]
- Pei, Q.; Zhao, F.Q.; Luo, Y. Research Progress on Burning Rate Testing Techniques of Solid Propellants. J. Explos. Propellants 2015, 38, 9–14+21. [Google Scholar]
- Hu, S.Q.; Li, B.X.; Li, F.C. Research on Burning Rate of Propellants Under High Pressure Using Closed Vessel Combustion Method. Chin. J. Energ. Mater. 2005, 13, 189–191. [Google Scholar]
- Celminš, A. Solid propellant burning rate measurement in a closed bomb. Combust. Flame 1974, 23, 381–397. [Google Scholar] [CrossRef]
- Liu, H.Q.; Li, B.X.; Wang, Y. Closed Vessel Combustion Method for Solid Propellant Burning Rate Testing System. J. Solid Rocket Technol. 2000, 23, 75–78. [Google Scholar]
- Wang, J.Y.; Sang, B.C. Measurement of Transient Burning Rate and Delayed Response of Burning Rate to Pressure Variation in Solid Propellants. Chin. J. Aeronaut. 1997, 1, 93–96. [Google Scholar]
- Zarko, V.E.; Vdovin, D.V.; Perov, V.V. Methodical problems of solid-propellant burning-rate measurements using microwaves. Combust. Explos. Shock Waves 2000, 36, 62–71. [Google Scholar] [CrossRef]
- Vladica, S.; Bozi, D.J. Measurement System for Determining Solid Rocket Propellant Burning Rate Using Reflection Microwave Interferometry. J. Propuls. Power 1997, 13, 457–462. [Google Scholar]
- Vladica, S.; Bozi, D.J. Measurement System for Determining Solid Propellant Burning Rate Using Transmission Microwave Interferometry. J. Propuls. Power 1998, 14, 421–428. [Google Scholar]
- Qu, C.J. A New Microwave Method for Measuring Transient Burning Rate of Solid Propellants. J. Propuls. Technol. 1993, 1, 70–77. [Google Scholar]
- Zhang, J.M.; Yuan, H.; Zhang, J. Ultrasonic Method for Testing Burning Rate of Solid Propellant. J. Explos. Propellants 2008, 31, 64–66. [Google Scholar]
- Song, S.J.; Jeon, J.H.; Kim, H.J.; Kim, I.C.; Yoo, J.C.; Jung, J.Y. Burning rate measurement of solid propellant using ultrasound—Approach and initial experiments. AIP Conf. Proc. 2006, 820, 1229–1236. [Google Scholar]
- Jeon, S.K.; Song, S.J.; Kim, H.J.; Ko, S.F.; Oh, H.T.; Kim, I.C.; Yoo, J.C.; Jung, J.Y. Ultrasonic Signal Denoising for Robust Measurement of Solid-Propellant Burning Rates. J. Propuls. Power 2010, 26, 473–478. [Google Scholar] [CrossRef]
- Song, S.J.; Kim, H.J.; Ko, S.F.; Oh, H.T.; Kim, I.C.; Yoo, J.C.; Jung, J.Y. Measurement of solid propellant burning rates by analysis of ultrasonic full waveforms. J. Mech. Sci. Technol. 2009, 23, 1112–1117. [Google Scholar] [CrossRef]
- Zhang, J.M.; Wang, Z.Q.; Yuan, H. Application of Ultrasonic Burning Rate Testing Technique in Solid Propellant Development. J. Explos. Propellants 2006, 29, 9–12. [Google Scholar]
- Hasegawa, K.; Hori, K. Novel burning rate measurement technique for solid propellant by means of ultrasonics. Combust. Explos. Shock Waves 2010, 46, 188–195. [Google Scholar] [CrossRef]
- Traineau, J.C.; Kuentzman, P. Ultrasonic measurements of solid propellant burning rates in nozzleless rocket motors. J. Propuls. Power 1986, 2, 215–222. [Google Scholar] [CrossRef]
- Brewster, M.Q.; Hites, M.H.; Son, S.F. Dynamic burning rate measurements of metalized composite propellants using the laser-recoil technique. Combust. Flame 1993, 94, 178–190. [Google Scholar] [CrossRef]
- Osborn, J.R.; Murphy, J.M.; Kershner, S.D. Photographic measurement of burning rates in solid propellant rocket motors. Rev. Sci. Instrum. 1963, 34, 305–306. [Google Scholar] [CrossRef]
- Rajak, R.; Chakravarthy, S.R.; Ganesan, S. Measurement of admittance and acoustic augmentation of burning rate of composite solid propellants using Laser Doppler Velocimetry. Proc. Combust. Inst. 2021, 38, 4391–4399. [Google Scholar] [CrossRef]
- Wang, J.; Gao, Z.; Sang, B. Laser technology for measurement of solid propellant transient burning rates during rapid depressurization. Fuel 2001, 80, 263–271. [Google Scholar] [CrossRef]
- Wang, Y.H.; Zhu, Q.L.; Zhang, H. Research on Burning Rate Testing Method Based on Mass Flow Rate and Working Principle of Solid Rocket Engines. J. Explos. Propellants 2020, 43, 428–4321. [Google Scholar]
- Marko, V.M.; Viladica, S.B. Small motor measurement method for determining burning rate of solid rocket propellants. In Proceedings of the 34th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Cleveland, OH, USA, 13–15 July 1998; p. 3390. [Google Scholar]

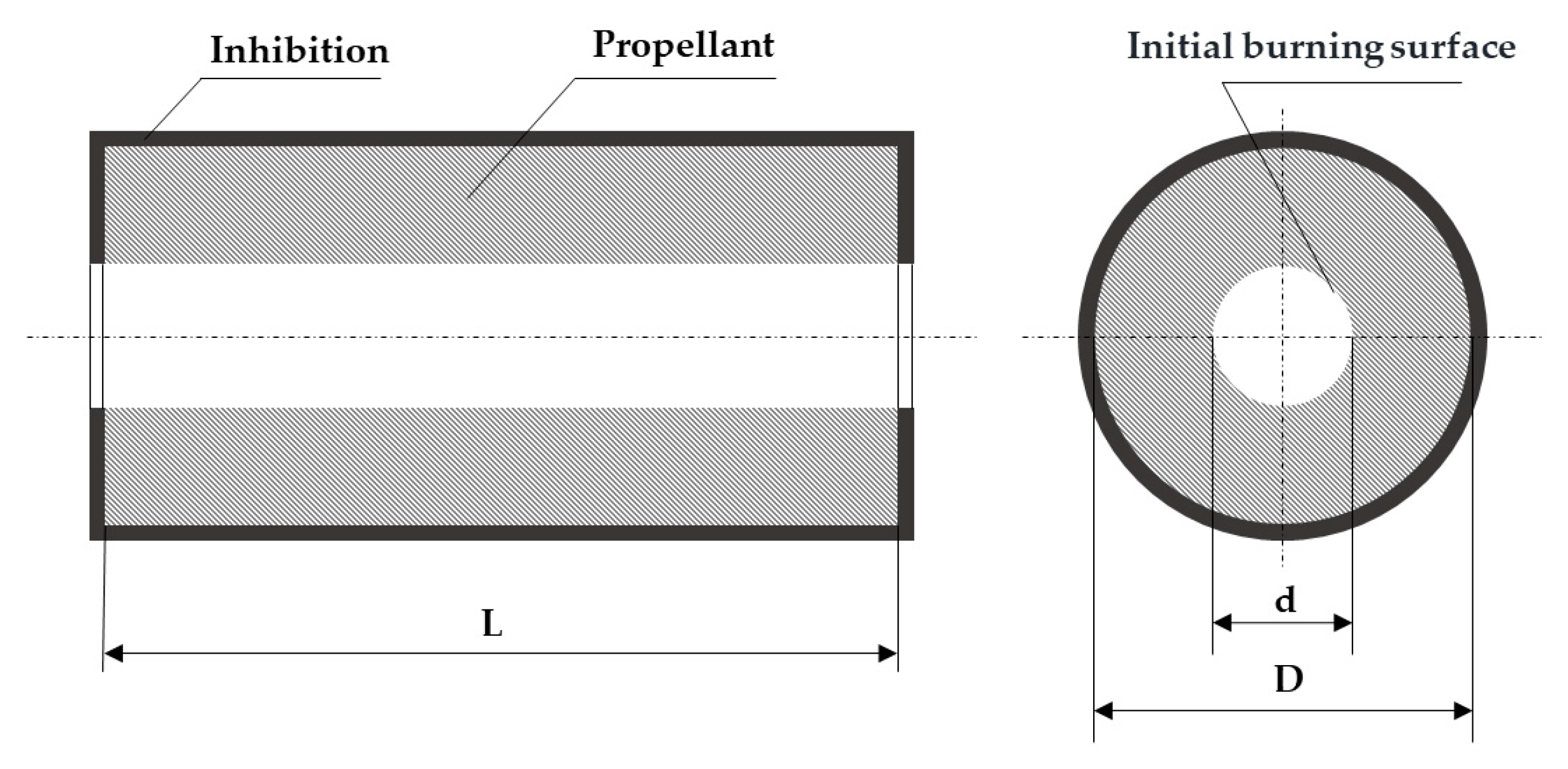

| Types of Propellants | Densities (g·cm3) | Experiment No. | d (mm) | D (mm) | L (mm) | dt1 (mm) | dt2 (mm) |
|---|---|---|---|---|---|---|---|
| GAP composite propellant | 1.735 | GAP-1 | 20.0 | 54.0 | 170.0 | 7.80 | 8.10 |
| GAP-2 | 20.0 | 54.0 | 184.0 | 8.40 | 8.90 | ||
| SQ2 double-base propellant | 1.610 | SQ2-1 | 35.0 | 73.3 | 180.0 | 8.00 | 9.42 |
| SQ2-2 | 30.0 | 63.0 | 200.0 | 8.00 | 8.55 |
| Pressure (MPa) | Theoretical Impulse (m/s) |
|---|---|
| 8 | 2582 |
| 10 | 2617 |
| 15 | 2666 |
| 20 | 2691 |
| 25 | 2706 |
| 30 | 2716 |
| 40 | 2728 |
| 50 | 2737 |
| 60 | 2742 |
| 70 | 2746 |
| 80 | 2749 |
| Pressure (MPa) | Burning Rate (mm/s) | Burned Mass (g) | Pressure (MPa) | Burning Rate (mm/s) | Burned Mass (g) |
|---|---|---|---|---|---|
| 5.82 | 11.70 | 5.88 | 16.00 | 20.73 | 17.57 |
| 6.12 | 12.06 | 6.27 | 17.18 | 21.39 | 18.78 |
| 6.53 | 12.58 | 6.77 | 18.29 | 21.90 | 19.91 |
| 6.99 | 13.16 | 7.32 | 19.48 | 22.50 | 21.16 |
| 7.46 | 13.81 | 7.96 | 20.84 | 23.23 | 22.61 |
| 7.98 | 14.47 | 8.63 | 22.22 | 23.86 | 24.03 |
| 8.54 | 15.10 | 9.33 | 23.64 | 24.55 | 25.58 |
| 9.15 | 15.73 | 10.07 | 25.18 | 25.35 | 27.31 |
| 9.76 | 16.34 | 10.84 | 26.82 | 26.13 | 29.13 |
| 10.44 | 16.97 | 11.66 | 28.55 | 26.99 | 31.11 |
| 11.20 | 17.68 | 12.59 | 30.45 | 28.01 | 33.39 |
| 12.01 | 18.33 | 13.53 | 32.58 | 29.14 | 35.93 |
| 12.93 | 18.97 | 14.51 | 34.99 | 30.45 | 38.84 |
| 13.89 | 19.61 | 15.49 | 37.55 | 32.01 | 42.26 |
| 14.91 | 20.19 | 16.53 | 40.36 | 33.42 | 45.68 |
| GAP-1 | GAP-2 | SQ2-1 | SQ2-2 | ||||
|---|---|---|---|---|---|---|---|
| Pressure /MPa | Burning Rate/mm/s | Pressure /MPa | Burning Rate/mm/s | Pressure /MPa | Burning Rate/mm/s | Pressure /MPa | Burning Rate/mm/s |
| 5.87 | 11.71 | 5.31 | 12.40 | 8.87 | 11.16 | 9.00 | 11.15 |
| 6.62 | 12.49 | 6.05 | 12.59 | 9.64 | 11.35 | 9.68 | 11.28 |
| 7.55 | 13.49 | 6.87 | 13.09 | 10.48 | 11.63 | 10.42 | 11.49 |
| 8.64 | 14.67 | 7.78 | 13.86 | 11.37 | 11.90 | 11.23 | 11.73 |
| 9.85 | 15.96 | 8.83 | 14.80 | 12.34 | 12.18 | 12.08 | 12.00 |
| 11.30 | 17.31 | 10.05 | 15.86 | 13.39 | 12.52 | 13.00 | 12.27 |
| 13.02 | 18.66 | 11.45 | 16.98 | 14.15 | 12.70 | 13.95 | 12.58 |
| 13.98 | 19.34 | 12.23 | 17.56 | 15.78 | 13.27 | 15.59 | 13.09 |
| 16.08 | 20.67 | 13.95 | 18.73 | 16.94 | 13.81 | 16.25 | 13.32 |
| 18.36 | 21.98 | 15.89 | 19.90 | 18.00 | 14.25 | 17.92 | 13.96 |
| 20.00 | 22.70 | 18.09 | 21.08 | 19.55 | 14.91 | 20.81 | 15.48 |
| 22.27 | 23.87 | 20.00 | 22.20 | 21.65 | 15.95 | 21.69 | 16.08 |
| 25.21 | 25.06 | 21.77 | 22.91 | 22.71 | 16.59 | 22.41 | 16.63 |
| 26.85 | 25.68 | 23.10 | 23.57 | 23.54 | 17.19 | 23.09 | 17.07 |
| 28.57 | 26.77 | 24.44 | 24.18 | 24.07 | 17.59 | 24.01 | 17.50 |
| 30.45 | 27.58 | 25.83 | 24.83 | 24.32 | 17.81 | 24.50 | 17.98 |
| 32.56 | 28.63 | 27.40 | 25.60 | 24.49 | 17.99 | 25.19 | 18.10 |
| 34.96 | 29.94 | 29.14 | 26.46 | 24.50 | 18.00 | 26.45 | 18.85 |
| 40.28 | 32.72 | 30.97 | 27.32 | 24.41 | 18.04 | 27.59 | 19.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Wang, Y.; Li, X.; Cong, J. Using the Impulse Method to Determine High-Pressure Dynamic Burning Rate of Solid Propellants. Aerospace 2023, 10, 818. https://doi.org/10.3390/aerospace10090818
Liu J, Wang Y, Li X, Cong J. Using the Impulse Method to Determine High-Pressure Dynamic Burning Rate of Solid Propellants. Aerospace. 2023; 10(9):818. https://doi.org/10.3390/aerospace10090818
Chicago/Turabian StyleLiu, Jiahao, Yinghong Wang, Xinyang Li, and Junhao Cong. 2023. "Using the Impulse Method to Determine High-Pressure Dynamic Burning Rate of Solid Propellants" Aerospace 10, no. 9: 818. https://doi.org/10.3390/aerospace10090818
APA StyleLiu, J., Wang, Y., Li, X., & Cong, J. (2023). Using the Impulse Method to Determine High-Pressure Dynamic Burning Rate of Solid Propellants. Aerospace, 10(9), 818. https://doi.org/10.3390/aerospace10090818






