Intelligent Maneuver Strategy for a Hypersonic Pursuit-Evasion Game Based on Deep Reinforcement Learning

Abstract

In order to improve the problem of overly relying on situational information, high computational power requirements, and weak adaptability of traditional maneuver methods used by hypersonic vehicles (HV), an intelligent maneuver strategy combining deep reinforcement learning (DRL) and deep neural network (DNN) is proposed to solve the hypersonic pursuit–evasion (PE) game problem under tough head-on situations. The twin delayed deep deterministic (TD3) gradient strategy algorithm is utilized to explore potential maneuver instructions, the DNN is used to fit to broaden application scenarios, and the intelligent maneuver strategy is generated with the initial situation of both the pursuit and evasion sides as the input and the maneuver game overload of the HV as the output. In addition, the experience pool classification strategy is proposed to improve the training convergence and rate of the TD3 algorithm. A set of reward functions is designed to achieve adaptive adjustment of evasion miss distance and energy consumption under different initial situations. The simulation results verify the feasibility and effectiveness of the above intelligent maneuver strategy in dealing with the PE game problem of HV under difficult situations, and the proposed improvement strategies are validated as well.

1. Introduction

A hypersonic vehicle (HV) refers to a vehicle that flies through the atmosphere between 20 km and 100 km at a speed above Mach 5, which possesses the characteristics of special flight airspace and high flight speed [1]. In recent years, with the continuous development of anti-hypersonic technology, it has become necessary for the HV to solve the pursuit–evasion (PE) problem [2,3,4] between itself and the interceptor.

The PE problem of HV is capable of describing a scenario where the interceptor called pursuer aims at capturing the HV called evader, while the evader struggles to avoid getting caught [2].

In the past, hypersonic aircraft mainly used traditional solutions, including unilateral trajectory planning [5,6,7,8,9,10,11] and bilateral game maneuvering [12,13,14,15,16,17,18,19], to deal with the PE problem.

Unilateral trajectory planning is achieved by pre-planning a trajectory and optimizing it to bypass the interceptor using optimal control [5,6,7,8] or other algorithms [9,10,11]. In the trajectory optimization strategy mentioned above, the literature [5] considers the optimization of hypersonic glide vehicle (HGV) evasion trajectory as a nonconvex optimal control problem and solves the second-order cone programming (SOCP) problem by state-of-the-art interior-point methods. In the study [9], the improved pigeon-inspired optimization algorithm (PIO) is proposed to adjust the anticipated control parameters and to achieve the ideal trajectory for hypersonic vehicles.

Contrary to the unilateral design, game maneuvering considering the capabilities of both offensive and defensive sides generates maneuvering instructions by differential games [12,13,14], game theory [15,16,17], or other methods [18,19] to evade interceptors and implement target strikes. Among them, the most representative ones are the reference [13,15]. According to the article [13], PE problems for the spacecraft in an uncompleted environment can be solved by switching methods based on differential game theory. Another study [15] used game theory and the speed advantage of hypersonic aircraft for capability gaming to design a broad evasion strategy for the cruise phase of the air-breathing hypersonic vehicle (AHV). The references [18,19] all utilize an adaptive dynamic program (ADP), which is a unique solution method belonging to the differential game to solve the hypersonic PE game and keep track of the control system. The above methods each have their own advantages; the requirements, however, of the detection of current excessive situation information of both the pursuer and the evader as well as of computing power of missile-borne computers, make the traditional solutions unsuitable for practical engineering applications.

Nowadays, with the increasing artificial intelligence technology, the development direction of the solutions of the HV’s PE problem is shifting from traditional maneuver solutions to intelligent game maneuver strategies [20]. That is, obtaining interceptor motion information through external data links or self-detectors, and generating corresponding game maneuvers by intelligent algorithms at the intersection critical point based on the guidance method characteristics. The intelligent game maneuver adopts a closed-loop maneuver scheme of “interceptor movement-situational awareness-maneuver strategy generation-maneuver control implementation” that realizes timely maneuvering to increase miss distance and increase evasion probability. The key to intelligent game maneuver lies in the selection of intelligent algorithms

Among the intelligent algorithms associated with hypersonic aircraft, deep learning (DL)and reinforcement learning (RL) are the first to bear the brunt [21,22,23,24,25,26,27,28,29,30,31,32]. Due to its strong nonlinear fitting ability, the deep neural network (DNN) in DL has been widely used in the PE problems of hypersonic aircraft [21,22,23]. Among these, the most prevalent study [21] resolves the tension between the accuracy and speed of the IPP by building an IPP neural network model after using the ballistic model to create training data. And the algorithms of reinforcement learning, especially deep reinforcement learning (DRL), provide a new approach to the design of HVs’ evasion strategies [24,25,26,27,28,29,30,31,32]. As an unsupervised heuristic algorithm without an accurate model, RL and DRL can generate actions based on the interaction with the environment, that is, conduct intelligent maneuvering games based on both attack and defense sides. It was suggested in references [24,25] to create a new guidance law based on proximal policy optimization (PPO) and meta-learning for an exo-atmospheric interception because interceptors using IR seekers can only gather angle information. The study [26], based on DRL, created a maneuver evasion guidance method considering both guidance accuracy and evasion capabilities with a focus on the terminal evasion scenario. Another study [27] transformed the problem into a Markov decision process (MDP) and proposed the anti-interception guidance law utilizing a DRL algorithm consisting of an actor–critic framework to solve it. The research [28] improved the reinforcement learning algorithm to a certain extent to achieve the interception of the maneuvering target. In the study [29], the RL was used to solve the optimal attitude-tracking problem for hypersonic vehicles in the reentry phase. Another study [30] based on the RL algorithm and deep neural network (DNN), generated the HV’s three-dimensional (3D) trajectory in the glide phase. One paper [31] designs the HV’s autonomous optimal trajectory planning method based on the deep deterministic policy gradient (DDPG) algorithm, where the trajectory terminal position errors with satisfying hard constraints are minimized by the design of the reward function. It is worth noting that the reference [32] carefully designed offensive and defensive adversarial scenario, namely the standard head-on scenario, where the speed advantage of HV was offset, and directly applied the twin delayed deep deterministic (TD3) gradient strategy to solve the hypersonic PE problem under the standard head-on scenario but ignoring the shortcomings of the algorithm itself, such as the weak generalization and slow training speed.

In addition to reference [32], references [5] and [33] also believe that the PE game problem of HV should be considered and solved in head-on situations, and reference [5] distinguishes the head-on situations from other situations in detail through illustrations. Among various offensive and defensive confrontation situations, the head-on situation is the toughest challenge for the HV to deal with, because the interceptor can intercept HV in the head-on situation easily and successfully. On the one hand, under the head-on situation, the speed difference between HV and interceptor is greatly eliminated, which is significantly beneficial for the low-speed interceptor. On the other hand, the interceptor’s seeker can stably track the target from the front until successful interception is achieved. In other words, considering existing interception technologies, the pursuer is most likely to adopt the head-on impact strategy [28,34] to achieve a successful intercept.

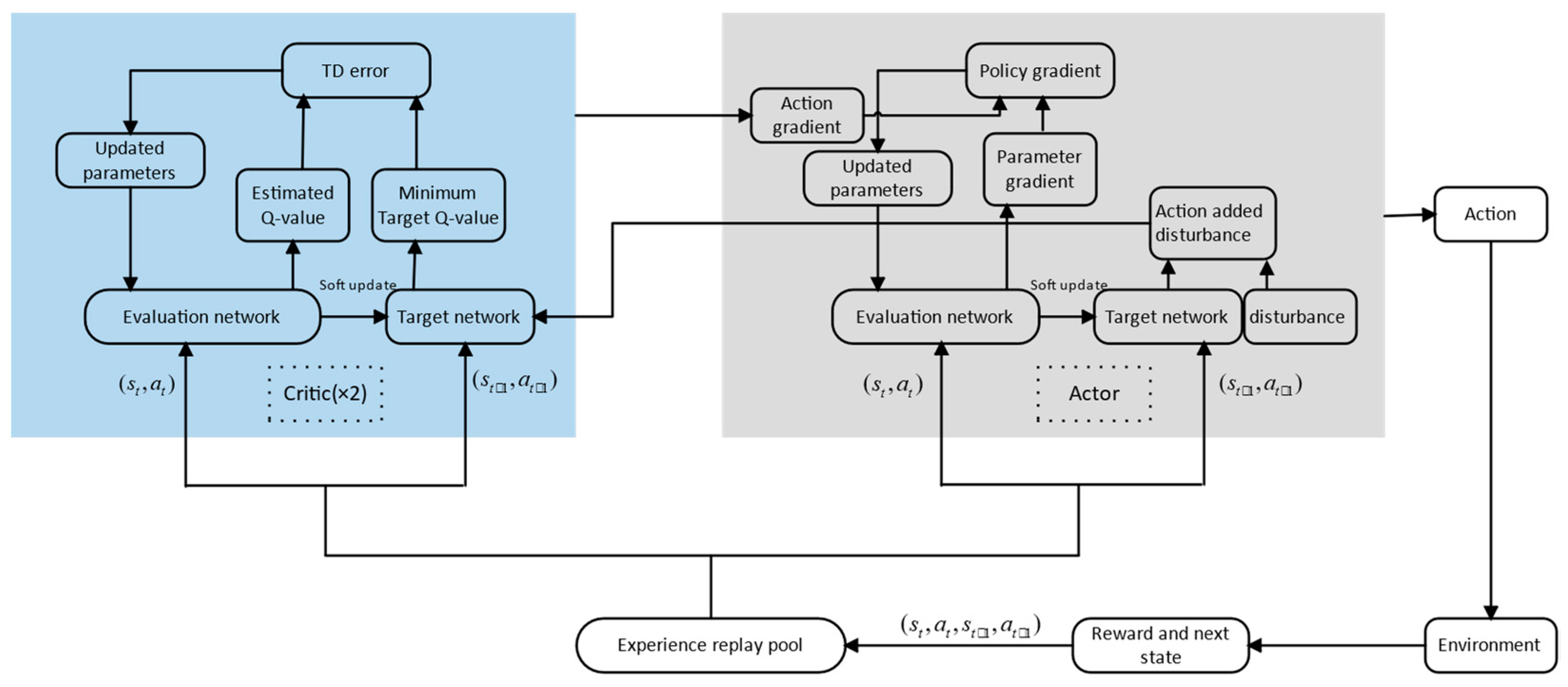
Motivated by the above research status and research difficulties, an intelligent maneuver strategy combining TD3 and DNN algorithms is studied to solve the hypersonic PE game problem. The attack and defense confrontation scenarios expand from the standard head-on situation in reference [32] to approximate head-on situations. The twin delayed deep deterministic (TD3) gradient strategy algorithm is used to explore potential maneuver instructions, the DNN is used to fit to broaden application scenarios, and an intelligent maneuver strategy is generated with the initial situation of both the pursuit and evasion sides as the input and the maneuver game overload of the HV as the output. In order to increase the training convergence, the study proposes the experience pool classification strategy to improve the TD3 algorithm. The study designs a set of reward functions to achieve adaptive adjustment of evasion miss distance and energy consumption under different initial situations. The numerical simulation results show the effectiveness of the proposed method.

Compared with the existing literature, the benefits of the proposed method are as follows: The proposed intelligent maneuver is based on DRL, which is generated through continuous interaction between the pursuer and evader, two parties in the game of confrontation and is more suitable than the unilateral penetration trajectory optimization [5] under the highly dynamic adversarial situation. And the intelligent method proposed does not occupy awful onboard computer resources and does not require intercepting information from the pursuer at all times in the PE procedure compared with the differential game method [12]. In addition, compared with the DDPG algorithm used in the study [27], the TD3 algorithm owns better performance by improving the shortcoming of overestimation of DDPG. And the proposed method further improves the TD3 algorithm in the training stage. In addition to the above algorithm improvement, the biggest difference from reference [32] is that the TD3 algorithm in the proposed method does not directly output overload instructions but serves as the data generator; using DNN instead of the actor network to merge and output overload instructions. The computational complexity has been further reduced and the generalization has been improved.

Accordingly, the main novelties of this study are as follows:

• The study constructs the adversarial model of both pursuer and evader under the most difficult head-on scenarios and proposes the maneuver strategy based on improved TD3 and DNN to achieve intelligent game maneuvers under the above model.
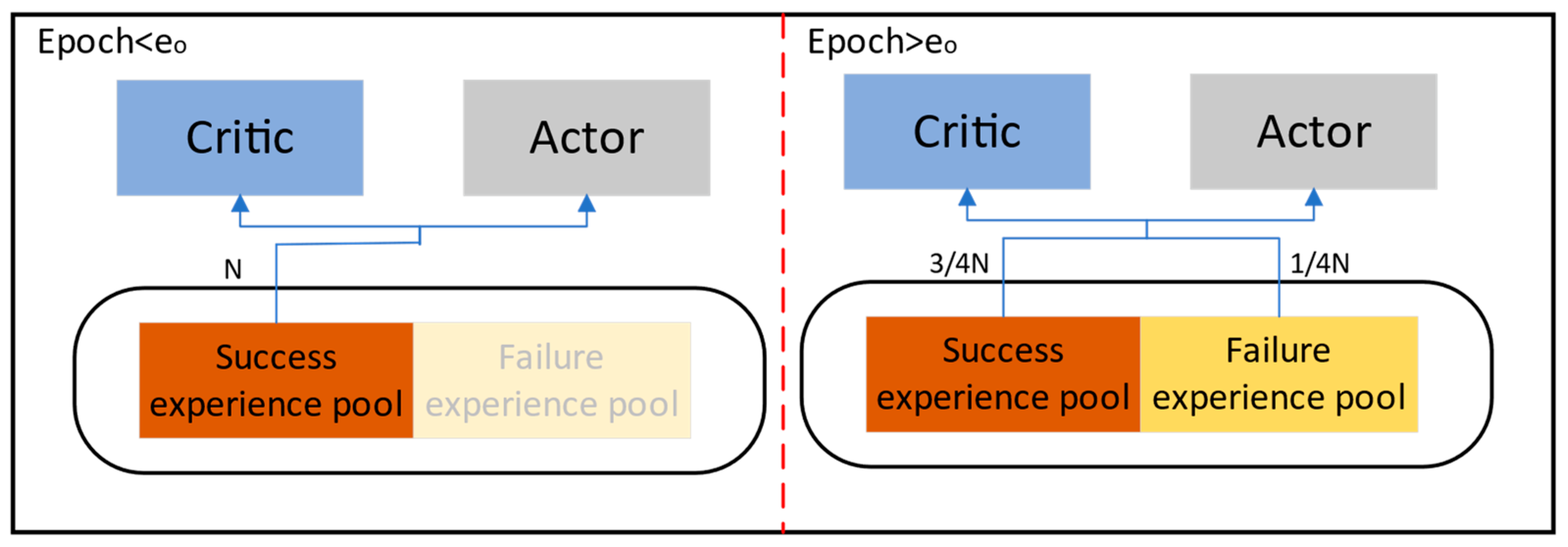
• In order to improve the rate and stability of convergence of the TD3 algorithm, the study proposes the experience pool classification strategy, which classifies and stores samples in different experience pools and adaptively adjusts the number of samples taken in training.
• The study designs a set of reward functions considering both successful evasion and energy consumption and introduces NN to improve the generalization of the algorithm. The intelligent maneuver strategy can achieve successful evasion and maneuver overload adaptively adjustment under different scenarios.

The research arrangement is as follows: Section 2 provides a model for the PE problem of the HV and the interceptor under the head-on situation. In Section 3, the intelligent maneuver strategy based on the “offline training + online application” framework is designed. In Section 4, simulations are conducted to validate the algorithms and methods derived from the intelligent maneuver strategy. The conclusion is drawn in Section 5.

2. PE Problem Modeling

2.1. The HV and the Interceptor Modeling

The centroid kinetic and centroid kinematic models of HV and pursuer are created through a coordinate transformation in accordance with the flight dynamic features of HV.

$$\{\begin{array}{l}\frac{\mathrm{d}{V}_i}{\mathrm{d}t}=g(n_{xi}-\sin {\theta }_i)\\ \frac{\mathrm{d}{\theta }_i}{\mathrm{d}t}=\frac{g}{V_i}(n_{yi}-\cos {\theta }_i)\\ \frac{\mathrm{d}{\psi }_{vi}}{\mathrm{d}t}=-\frac{g}{V_i\cos {\theta }_i}{n}_{zi}\end{array}$$

(1)

$$\{\begin{array}{l}\frac{\mathrm{d}{x}_i}{\mathrm{d}t}=V_i\cos {\theta }_i\cos {\psi }_{vi}\\ \frac{\mathrm{d}{y}_i}{\mathrm{d}t}=V_i\sin {\theta }_i\\ \frac{\mathrm{d}{z}_i}{\mathrm{d}t}=-V_i\cos {\theta }_i\sin {\psi }_{vi}\end{array}$$

(2)

where $i=H,I$ and the letters $H$ and $I$ stand for the HV and interceptor, respectively; $V$ stands for velocity; $\theta$ and ${\psi }_v$ stand for the ballistic inclination and deflection angles, respectively, in the ballistic coordinate system. In the same system, the aircraft’s three axes overload are indicated by $n_x, n_y$ and $n_z$, respectively, while the distance traveled by HV flying in three directions is represented by $x, y$, and $z$ respectively, according to the geographic coordinate system.

In addition, the study incorporates an autopilot into the control loop and designed it as a first-order inertial loop. The relationship between the actual overload of HV and the overload command can be expressed as:

$$\frac{n_H(s)}{n_{H\_order}(s)}=\frac{1}{1+Ts}$$

(3)

where $n_{H\_order}$ is the overload command, $n_H$ is the actual overload for the HV, and $T$ is the first-order inertial link’s response time constant.

2.2. The Confrontation Situation Description

In the study, the pursuit–evasion confrontation model is built up based on the standard head-on situation [32], known as the strict head-on scenario as well, and further expands to approximate head-on situations.

According to Assumption 1, the relative motion diagram of HV and interceptor on the two-dimensional plane in the PE problem is shown in Figure 1:

In Figure 1, $r_{HI}$ is the relative distance between the HV and interceptor, $q$ is the line-of-sight angle between the HV and the interceptor, $\phi$ is the missile ballistic angle, which is the angle between the velocity vector and the horizontal line. And the missile ballistic angle is equal to the ballistic deflection angle under Assumption 1, namely $\phi ={\psi }_v$.

According to the reference [32], when the velocity vectors of HV and interceptor coincide with the line connecting their positions and have opposite directions, it is the strict head-on scenario between HV and interceptor and the differences between their missile ballistic angle and line-of-sight angle are equal to 0. In practical engineering applications, however, it is difficult to strictly equal the above angle to 0. Accordingly, by analogy with the strict head-on scenario, the study believes that the approximate head-on situations are constituted between the two sides when the above angles exist but are small, and the angles’ range in this study is chosen less than 2°.

The relationship between the above variables can be represented by the following equation:

$$\{\begin{array}{l}{r}_{HI}=\sqrt{x_{HI}^2+z_{HI}^2}\\ {\stackrel{.}{r}}_{HI}=\frac{{\stackrel{.}{x}}_{HI}{x}_{HI}+{\stackrel{.}{z}}_{HI}{z}_{HI}}{\sqrt{x_{HI}^2+z_{HI}^2}}\\ q=-\arctan (\frac{z_{HI}}{x_{HI}})\\ \stackrel{.}{q}=\frac{z_{HI}{\stackrel{.}{x}}_{HI}-x_{HI}{\stackrel{.}{z}}_{HI}}{x_{HI}^2+z_{HI}^2}\end{array}$$

(4)

where $x_{HI}$ represents the projection of the relative distance between the pursuit and evasion parties in the x-axis direction, and $z_{HI}$ represents the relative distance on the z-axis. Considering the small-angle hypothesis, the linear equation of the state variable $x_{HI}={[z_{HI},z_{HI},n_H,n_I]}^T$ in the PE game can be expressed as follows:

$${\dot{x}}_{HI}=A{x}_{HI}+B_H{n}_H+B_I{n}_I$$

(5)

$$A=\left[\begin{array}{l}0 1 0 0\\ 0 0 \mathrm{gcos}{\phi }_{H0} \mathrm{gcos}{\phi }_{I0}\\ 0 0 -1/T_H 0\\ 0 0 0 -1/T_I\end{array}\right],B_H=\left[\begin{array}{l}0\\ 0\\ 1/T_H\\ 0\end{array}\right],B_I=\left[\begin{array}{l}0\\ 0\\ 0\\ 1/T_I\end{array}\right]$$

(6)

In order to ensure the tracking ability of the interceptor, the study selects the augmented proportional navigation (APN) guidance whose tracking effect is better than the basic proportional guidance (PN) guidance, which can be divided into longitudinal and lateral overload commands as follows:

$$\{\begin{array}{l}{n}_{zI}=-\frac{N{V}_c\stackrel{.}{q_z}\cos {\theta }_I}{g}+\frac{1}{2}{n}_{zH}\\ n_{yI}=\frac{N{V}_C\stackrel{.}{q_y}}{g}+\cos {\theta }_I\end{array}$$

(7)

where $N$ is the navigation coefficient chosen between 3 and 5 in general, and $V_c$ is the speed difference of the pursuer and evader. As the pursuit confrontation scenario has been reduced to a two-dimensional plane, the confrontation process in this scenario will only use a horizontal overload expression.

2.3. The Design Goal

As a prerequisite for researching the PE problem of HV, it is necessary to define the concept of successful evasion of HV and propose reasonable assumptions and constraints based on the HV’s inherent characteristics. In the study, the definition of successful evasion, according to the literature [33], is that the minimum relative distance between the evader and the pursuer is greater than the prescribed minimum off-target amount, namely:

$$r(t_f)>\delta$$

(8)

where $\delta$ is the lowest boundary value of the prescribed off-target amount.

The study considers the satisfaction of the off-target distance as a terminal constraint. Furthermore, we also need to think of process constraint, and in HV’s relevant studies, we usually regard the constraint on overload as process constraint, namely:

$$|u(t)|\le u_{H\max }$$

(9)

Meanwhile, considering practical engineering applications, we should consider the energy consumed during the entire evasion process as well based on the availability of HV’s overload and the successful evasion, that is:

$${\displaystyle \underset{t_0}{\overset{t_f}{\int }}{u}^2\mathrm{d}t}$$

(10)

To conclude, the designed goal can be expressed as Problem 1:

Problem 1.

Considering the PE game model given by Equation (6), the intelligent maneuver strategy should be derived to minimize the energy consumption given by Equation (10), while the miss distance subject to Equation (8) and the control constraint subject to Equation (9).

Assumption 1.

Under the head-on situations, the offensive and defensive confrontation model is reduced to a two-dimensional plane.

Remark 1.

Assumption 1 is reasonable. Affected by the inherent characteristics of the HV’s engine, the HV tends to complete evasion through lateral maneuvering in the horizontal plane. Therefore, it can be assumed that the pursuer and hypersonic aircraft engage in a PE game confrontation at the same altitude, which simplifies the confrontation scenario to a two-dimensional plane.

Assumption 2.

During the procedure of the PE game, the velocity of HV and interceptor are considered as the constant values, respectively.

Remark 2.

Due to the negligible longitudinal overload $n_x$ compared to hypersonic speeds, the hypersonic lateral maneuver overload $n_z$ perpendicular to the speed direction is the main force to evade the interceptor in the X–Z two-dimension plane, only changing the speed direction without changing the speed magnitude.

Remark 3.

The speed of HV is much higher than that of interceptors, but the overload usually does not reach half of that of interceptors. According to reference [33], in non-head-on situations, the HV can easily escape interception by interceptors due to their significant speed disadvantage. In head-on situations, the speed difference is offset, and the interceptor will utilize the large overload relative to HV to achieve successful interception. Therefore, when studying the PE problem of HV, we should build up the difficult adversarial model based on the head-on situation and conduct research on maneuver strategy based on it.

3. Method

3.1. Intelligent Maneuver Strategy Framework

Drawing on the mode of “offline training + online application”, the study proposes an intelligent maneuver strategy based on DRL and DNN. The framework of the strategy is shown in Figure 2.

In the process of “offline training”, the strict head-on scenario is selected as the feature point for the RL agent training using the improved TD3 (ITD3) algorithm. After obtaining the trained agent, Monte Carlo simulations are performed on different initial parameters under the approximate head-on scenarios and using the neural network for fitting to generate the intelligent maneuver model.

In actual offensive and defensive confrontation scenarios, through the “online application” method, we can use the intelligent maneuver model to quickly generate maneuver commands through the initial situation under the approximate head-on scenarios.

The intelligent maneuver strategy ensures the success of evasion and the generalization and reliability, meanwhile, are certainly improved and guaranteed.

The rest of Section 3 describes the intelligent algorithms and related methods included in the intelligent maneuver strategy.

3.2. TD3 Algorithm

The twin delayed deep deterministic policy gradient (TD3) algorithm is a deep reinforcement learning algorithm used to solve continuous control problems improved based on the deep deterministic policy gradient (DDPG) algorithm. In essence, the TD3 algorithm is designed to solve the overestimation problem of the DDPG algorithm by incorporating the ideas of the DDQN algorithm. The TD3 algorithm, like the DDPG algorithm, is based on the actor–critic (AC) framework, learning two networks simultaneously: the actor network ${\pi }_{\phi }(s)$ and the critic network $Q_{\theta }(s,a)$. In addition, there are the target networks corresponding to the actor network and critic network respectively. Input the state and action into the critic network to obtain the corresponding Q value. The relevant action of the state can be obtained through the actor network as well as the target network is to calculate the loss function. Accordingly, the algorithm possesses many advantages compared with other algorithms. The TD3 algorithm with the AC framework is illustrated in Figure 3:

Based on the DDPG algorithm, the TD3 algorithm solves the overestimation problem and proposes three key improved technologies: double network, target policy smoothing regulation, and delayed update.

Double network, which originated from DDQN, adopts two sets of critic networks, $Q_{\theta 1}$ and $Q_{\theta 2}$. And the difference between TD3 and DDQN is that when calculating the target value, the TD3 algorithm takes the smaller value of two critic networks to suppress the network overestimation problem; that is:

$$y\leftarrow r+\gamma {\min }_{i=1,2}{Q}_{{\theta }_i^{’}}(s^{’},\tilde{a})$$

(11)

where $y$ is the target value of temporal difference, $r$ is the reward value, $\gamma$ is the discount factor, $Q_{{\theta }_i^{’}}(s,a)$ is the target critic network, $\tilde{a}$ is the action related to the next state adding disturbance, which would be introduced in the second improved technology. The TD3 algorithm is composed of six deep neural networks: one actor network, two critic networks, and their corresponding target networks

Target policy smoothing regulation adds perturbations to the next state actions, making the value evaluation more accurate when calculating the target value, is:

$$\tilde{a}\leftarrow {\pi }_{{\phi }^{’}}(s^{’})+\epsilon ,\epsilon ~clip({\rm N}(0,\tilde{\sigma }),-c,c)$$

(12)

where ${\pi }_{{\phi }^{’}}(s^{’})$ is the target actor network, $\epsilon$ is the small amount of random noise adding to the target action. To maintain the target action close to the original action, the additional noise is subject to normal distribution. It is advantageous to smooth the estimated value and make the critic update less aggressive by using the area surrounding the target action in Equation (12) to determine the target value.

The delayed update refers to updating the actor network after updating the critic network multiple times to ensure a more stable training of the actor network. As the updates of the actor network require the critic networks to evaluate. If the critic network is quite unstable, the actor network will naturally experience oscillations. It is conceivable to increase the update frequency of the critic network over the actor network, i.e., wait till the critic network has achieved more stability before assisting the actor network in updating. Firstly, this is to update the critic:

$${\theta }_i\leftarrow \arg {\min }_{{\theta }_i}{N}^{-1}{\displaystyle \sum {(y-Q_{{\theta }_i}(s,a))}^2}$$

(13)

Using the mini-batch processing method to update data, the computing complexity decreases and efficiency increases. For training, the algorithm separates $N$ groups from the data gathered from previous interactions with the environment. After that, make updates to the policy and target network at a relatively low frequency, as follows:

$${\nabla }_{\phi }J(\phi )\approx N^{-1}{\displaystyle \sum _i{\nabla }_a{Q}_{{\theta }_i}(s,a){|}_{a={\pi }_{\phi }(s)}{\nabla }_{\phi }{\pi }_{\phi }(s)}$$

(14)

$${\theta }_i^{’}\leftarrow \tau {\theta }_i+(1-\tau ){\theta }_i^{’}$$

(15)

$${\phi }^{’}\leftarrow \tau \phi +(1-\tau ){\phi }^{’}$$

(16)

The update of the actor also involves the critic. The first gradient in Equation (14) is obtained from the critic, and the second gradient is obtained from the actor. The combination of two gradients reveals that the improvement of the actor parameter is to obtain a larger Q value.

3.3. Algorithm Improvement Strategy

The experience reply pool is an important part of the whole TD3 algorithm. After the training epochs reach the line, the experience pool stores each sample $(s_t,a_t,r_t,s_{t+1})$ and provides small batches of samples in subsequent parameter updates. Experience pool plays a unique role in the training of the agent. In order to improve the rate and steady convergence in the training process of the TD3 algorithm, the study proposes the experience pool classification strategy.

According to Section 2.3, it is easy to judge the agent’s success during the HV’s PE game. Thus, the samples $(s_t,a_t,r_t,s_{t+1})$ are classified and stored in the success experience pool or failure experience pool based on whether the interaction was successful or not during training. Afterward, according to Equation (17), collect small sample sets $N_{batch}$ from two experience pools to update the network. Equation (17) indicates that in the early stage of training, high-quality samples need to be extracted to accelerate the learning speed of the intelligent agent as well as in the later stage of training, to avoid overfitting in the algorithm, it is necessary to simultaneously extract samples from two experience pools, namely sampling $N_{batch}$ training samples from $N_{success}$ and $N_{failure}$. The method of “classified experience pool +adaptive sampling” can improve the rate and steady convergence of the TD3 algorithm effectively.

$$\{\begin{array}{l}{N}_{batch}=N_{success}, epoch<e_0\\ N_{batch}=\lambda N_{failure}+(1-\lambda )N_{success}/3, epoch\ge e_0\end{array}$$

(17)

where the $\lambda \in (0,1)$ and when the $epoch\ge e_0$, $N_{failure}=N_{batch}$ and $N_{success}=3N_{batch}$. And the schematic diagram of experience pool classification strategy is shown in Figure 4.

3.4. The Design Related to the Algorithm

3.4.1. State Space and Action Space Design

The input to the actor network in the DRL algorithm should be observable state vectors. In the HV maneuver scenarios, the state space should select the states of the HV and the pursuer, namely:

$$x_{state}=[r_{HI}/r_{HI0},q,\sigma \stackrel{.}{q},V_H/V_I]$$

(18)

We should select easily accessible state variables in the scenario environment and standardize them to achieve better interaction between the agent and the environment.

In the HV’s PE game problem, the output from the actor network should be a lateral overload $n_{zH}$ of HV within the two-dimensional horizontal plane, namely:

$$n_{zH}\in [-n_{zH\_\max },n_{zH\_\max }]$$

(19)

where $n_{zH\_\max }$ is the maximum available lateral overload value of HV.

3.4.2. Termination Function and Reward Function Design

In solving the PE game problem, when the simulation and single training are over is determined by the setting of the termination function, and the learning effectiveness and convergence are directly impacted by the setting of the reward function. The termination function needs to conform to the PE problem in specific scenarios, and the reward function design is the point and difficulty of RL. Therefore, both functions have a great effect on the simulation.

When setting the termination function of RL, it is necessary to consider the termination of both successful and failed evasion. According to the experience and actual trend, the study considers a failed evasion is that the relative distance is less than the minimum avoidance distance, namely:

$$r(t_f)\le \delta \to end$$

(20)

On the contrary, when the relative distance between the HV and the pursuer is always greater than the minimum avoidance distance and the relative distance begins to increase, it can be determined that the HV has successfully evaded and the PE game process has ended, that is:

$$r(t_f)>\delta \cap \frac{\mathrm{d}r}{\mathrm{d}t}>0\to end$$

(21)

Terminal reward and process reward are both included in the reward function design. The terminal reward has a direct bearing on the training success and the process rewards direct the train in the progress. An appropriate reward function is helpful to accelerate the convergence of the model.

For the offensive side, there are two main purposes: (1) to evade the interception of interceptors; (2) based on purpose (1) to reduce the loss of mechanical energy from the maneuver. The reward function is set as follows:

$$R=r1+r2+r3+r4$$

(22)

$$\{\begin{array}{l}r1=-c_1{e}^{-\stackrel{.}{q}}+1\\ r2=-c_2\Delta E\\ r3=c_3{\log }_2(R_f-4)\\ r4=\{\begin{array}{l}-10, bad\_end\\ 10, good\_end\end{array}\end{array}$$

(23)

where $r1$ is a reward function related to relative angle and $r1$ introduces punishment based on the angle information between HV and pursuer, guiding HV to break away from the head-on situation. $r2$ represents the overload consumption of the HV and the mechanical energy loss of the aircraft during the decision-making period and should be dealt with standardization processing. $r3$ indicates that introducing a final distance reward is to guide the training of intelligent agents to appropriately pursue larger miss distance. $r4$ is defined as the termination reward function and corresponding rewards or punishments are given based on whether they successfully escape each time.

Among them, $r1$ and $r2$ belong to process rewards, while $r3$ and $r4$ belong to terminal rewards. In addition, there is a contradiction between pursuing greater miss distance and reducing energy consumption. Therefore, it is necessary to balance the two by setting $c2$ and $c3$, adjusting, and choosing more suitable parameters based on specific scenarios and needs.

3.5. DNN Fitting Strategy

The agent trained by the improved TD3 method can achieve HV evasion at the training point. However, considering the high dynamic characteristics of HV itself, it is necessary to achieve successful evasion in different initial situations. Therefore, the study introduces the neural network and utilizes its strong fitting ability to increase the generalization of HV in PE games.

The trained agent is used to conduct a large number of Monte Carlo simulations and collect the eligible evasion dataset under different initial situations in the approximate head-on scenarios. The corresponding initial situation and evasion overload are inputted into the neural network for training as Figure 5:

To facilitate the training of neural networks, the form of maneuvering overload should be handled first before fitting. And the output overload can be approximately equal to a polynomial of degree 4, that is:

$$n_{zH}=p1\times t^4+p2\times t^3+p3\times t^2+p4\times t+p5$$

(24)

According to the above form, the corresponding overload can be obtained by determining the values of p1~p5 and the independent variable t. The initial situation and corresponding 5 parameters, accordingly, can be classified, respectively, as input and label using deep neural networks for training.

Through the trained model and the initial situations, the corresponding maneuverable evasion overload can be obtained online; that is:

$$\{\begin{array}{l}(p1,p2,p3,p4,p5)=f(x,z,q,\phi ,v)\\ n_{zH}=p1\times t^4+p2\times t^3+p3\times t^2+p4\times t+p5\end{array}$$

(25)

Remark 4.

The design of the reward function in the improved TD3 algorithm aiming at the head-on situation is an innovative point in the study. When designing reinforcement learning reward functions, nearly all studies on using reinforcement learning to achieve HV evasion pay too much attention to how to successfully evade while neglecting the energy consumption during the evasion process. As a high-speed aircraft, blindly using full overload for evasion without considering specific scenarios will consume unnecessary energy and have a negative impact on subsequent target strikes. By introducing Equation (23), perform different maneuvers based on different initial situations. It can achieve successful evasion while further saving energy.

Remark 5.

The intelligent maneuver strategy is based on “offline training + online application”. Among them, the TD3 algorithm is used to explore possible maneuvering strategies as the dataset generator, while the introduced DNN is used as a regression fitting tool and output instruction generator. Compared with directly using TD3 to generate instructions, the combined strategy not only improves generalization but also simplifies the neural network structure. The introduced DNN, regardless of the number of layers or neurons, is much smaller than the deep neural network in TD3. Simplifying the network structure can effectively reduce computing speed, which is more suitable for high-speed scenarios, and reduce the amount of onboard computer resources occupied, which is more available for practical engineering applications. The reason why it can be simplified is that the input and output of the maneuvering strategy are all simple vectors, without the need for complex calculation. Only vector fitting needs to be achieved. Therefore, the DNN fitting strategy can greatly improve computational complexity while improving generalization.

4. Discussion

To solve the PE game successfully, using the intelligent maneuver strategy requires the following operations: firstly, training the DRL agent under the feature point, then making the Monte Carlo simulation biasing initial parameters, and finally training the DNN to obtain the intelligent maneuver model. The simulation software selected is MATLAB 2021a in the study, and the hardware information is Intel (R) Core (TM) i5-10300H CPU @ 2.50 GHz, RTX 2060 14 GB, DDR4 16 GB, 512 GB SSG. Considering the need for the application of deep reinforcement learning and deep neural networks, it is recommended to use software and hardware not lower than the above specifications.

Table 1. Simulation, TD3, and DNN training conditions.

Simulation Condition	Value	TD3 Parameter	Value	DNN Parameter	Value
HV velocity	6 Ma	Actor network learning rate	0.005	The type of NN	Bp
Interceptor velocity	3 Ma	Critic network learning rate	0.005	Training epoch	1000
HV overload	3	Discount factor	0.9	The goal of minimum error	0.0001
Interceptor overload	6	Inertial factor	0.99	Learning rate	0.01
HV initial position	(0, 0)	Soft update rate	0.001	Minimum performance gradient	10−6
Interceptor initial position	(10,000, 0)	Experience playback pool capacity	4000	Damping factor	108
The lowest boundary value of miss distance	5	Sampling time	0.1	Number of failed confirmations	20
Navigation coefficient	4	The mean of reward window length	100	Number of hidden neurons	10
The initial line-of-sight angle	0	Attenuation Noise standard deviation	0.4	Training sample proportion	70%
HV initial deflection angle	0	Attenuation noise standard deviation rate	10−5	Testing sample proportion	15%
Interceptor initial deflection angle	−π	Small batch sample size	128	Validation sample proportion	15%

shows the parameters used in the entire simulation process. Figure 6 shows the training curve of the reinforcement learning agent. Figure 7 shows the simulation verification of the trained agent under the selected feature point. Figure 8 shows Monte Carlo simulation and Figure 9 shows neural network training. Figure 10 shows the simulation verification of the obtained intelligent maneuvering strategy under several typical situations.

The initial relative positions and pertinent angles determine the strict head-on scenario between HV and interceptor. Among these, the HV’s initial position is set to (0, 0), and the pursuer’s initial position is set to (10,000, 0). Set the pursuer’s initial line-of-sight angle to 0 between the HV. The HV’s initial ballistic deflection angle is set to 0, and the pursuer’s initial ballistic deflection angle is set to −π.

In real engineering practice, due to the limitations of its own characteristics, HV usually has more speed and less overload during PE games compared to the interceptor. Therefore, we set the speed of the pursuer to 3 Ma and the speed of the HV to 6 Ma. At the same time, the overload capacity of HV is set to 3, and the overload capacity of the pursuer is set to 6. Accordingly, we need to take advantage of the HV’s high speed and seize the opportunity and time of maneuvering to achieve successful evasion within limited overload. And the lowest boundary value of miss distance is set to 5 m.

Set the maximum number of training rounds to 600. To ensure the effectiveness of training, some initial parameters will be randomly skewed during each training process.

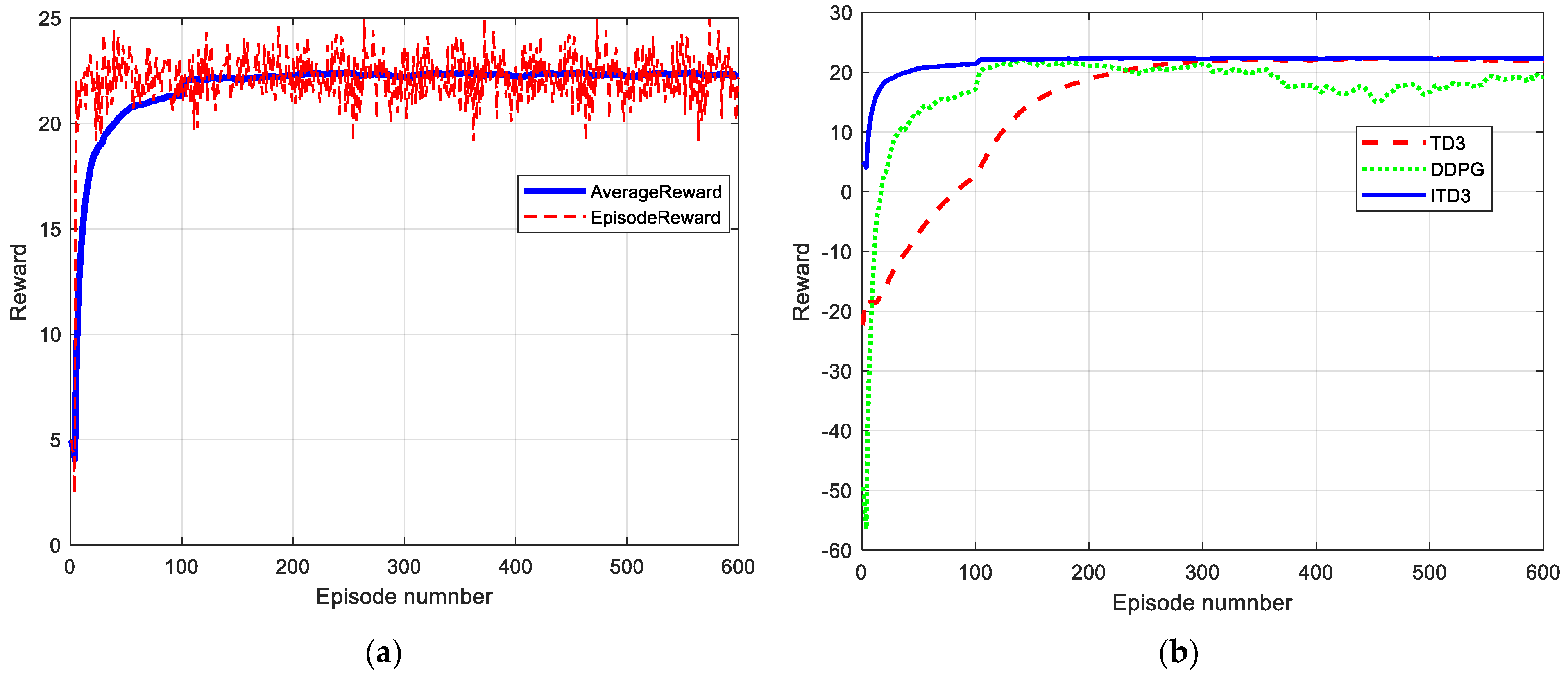
Figure 6a shows that as the number of training updates grows, the average reward and episode reward gradually rise. The agent continuously engages with the environment during the iterative training process to modify its approach to maximize reward values. As training rounds increase, the agent gradually finds the optimal maneuvering strategy. It can be seen that after nearly 100 rounds of training, the reward value curve converges to the highest point, which means that the agent ultimately gets the best solution to the HV’s PE game problem through continuous interaction with the environment. This indicates that the entire training process of the DRL algorithm designed in this study is stable and successful with good convergence.

Figure 6b shows that in contrast to the still fluctuating training process of the DDPG algorithm after 300 rounds, the TD3 and ITD3 algorithms, which have better performances, gradually approach a stable optimal solution through training and interaction. In the comparison between TD3 and ITD3 algorithms, due to the classified experience pool strategy, the convergence speed of ITD3 is better than the basic TD3′s speed that basic TD3 algorithm requires 300 rounds to converge to the stable state. In addition, the small batch sampling during the training process is adaptively adjusted according to the training rounds, which ensures that the ITD3 algorithm not only has good training speed, but also has good convergence stability, and the two curves nearly coincide after 300 rounds in Figure 6b. Through comparison, it is verified that the experience pool classification strategy proposed in the study can effectively improve the speed of algorithm training and ensure training convergence.

After completing the agent training, we selected a strict head-on scenario for aircraft pursuit and evasion confrontation and conducted agent scenario testing. The simulation results are shown in Figure 7:

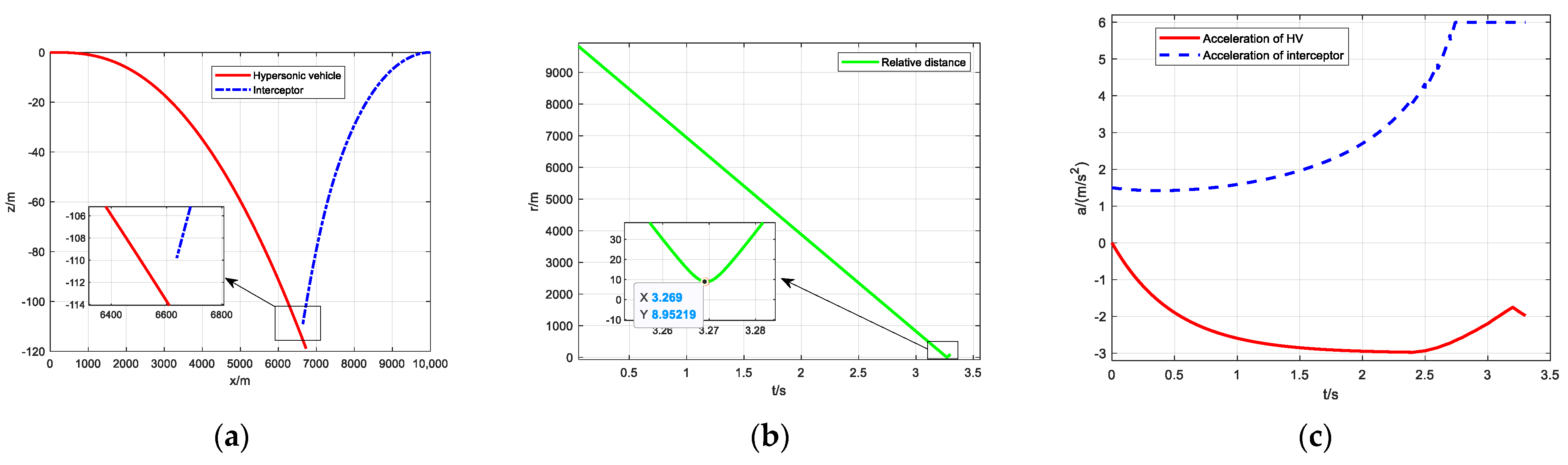
Figure 7. Simulation results of DRL verifying: (a) two–dimensional planar trajectory map; (b) relative distance curve; (c) overload change curve.

Figure 7. Simulation results of DRL verifying: (a) two–dimensional planar trajectory map; (b) relative distance curve; (c) overload change curve.

Figure 7a shows the motion trajectories of the attacking and defending sides in a horizontal two-dimensional plane, and Figure 7b shows the variation of their relative distance over time. Combining the two figures, it can be seen that both the attack and defense sides are initially in the strict head-on scenario. The interceptor is guided by the APN guidance law, and the HV uses an intelligent maneuver strategy obtained through reinforcement learning training to start game maneuvering. The minimum relative distance during the entire evasion process is 8.95219, which met the minimum miss distance requirement for evasion. It is judged that the HV successfully evaded in this scenario. Figure 7c shows the overload changes between HV and interceptor. It can be seen that the interceptor, based on its guidance law, exerts the advantage of large maneuvers within the overload capacity range to intercept as much as possible, while HV also successfully achieves maneuver avoidance based on intelligent games within the overload capacity range. This indicates that the selected state space, action space, and designed reward and termination functions are all reasonable. In addition, HV’s overload does not always maintain full overload but decreases after 2.5 s, indicating that the intelligent agent is pursuing greater miss distance while also minimizing energy consumption, proving that the initial goal can be achieved through the designed reward function.

The agent trained through DRL can already achieve maneuvering evasion in the strict head-on scenario. However, to apply the strategy in more scenarios, we pull off the initial parameters under the premise of the approximate head-on scenarios, and select different initial parameters within the range of the initial line-of-sight angle [0°, 1.8°] and initial relative distance [8500, 10,000] for Monte Carlo simulations to collect the dataset full of successful samples. The available simulation results obtained are as follows:

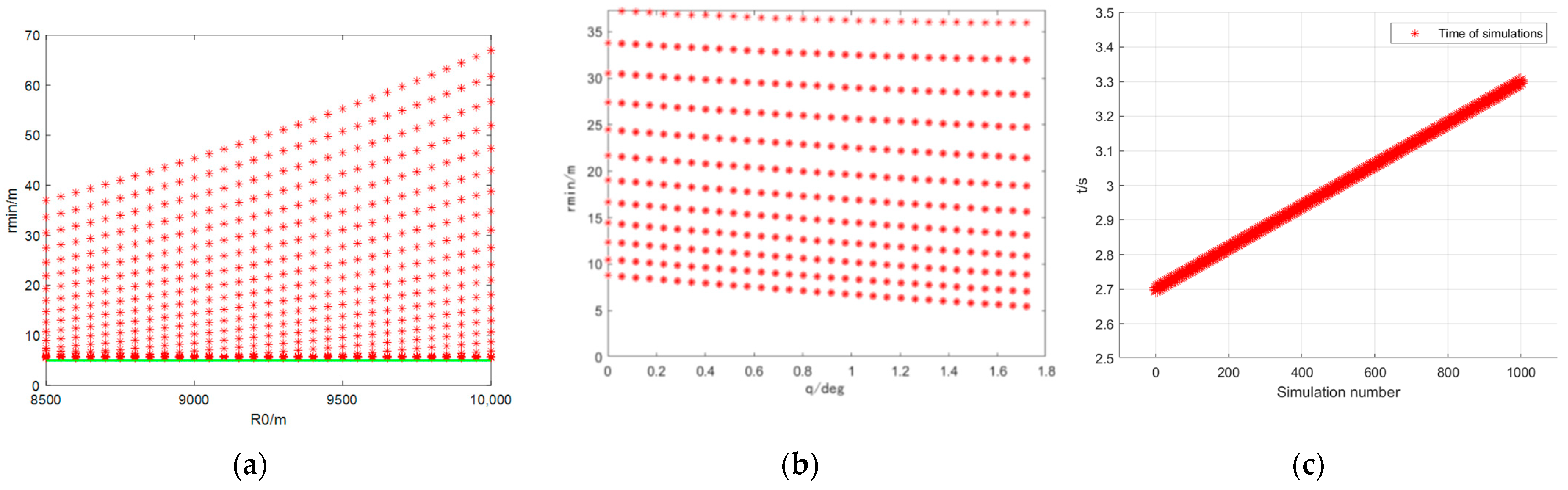
Figure 8. Monte Carlo simulation biasing initial parameters: (a) miss distances at different initial distances; (b) miss distances at different initial line-of-sight angles; (c) time spent at different initial parameters.

Figure 8. Monte Carlo simulation biasing initial parameters: (a) miss distances at different initial distances; (b) miss distances at different initial line-of-sight angles; (c) time spent at different initial parameters.

By the way, from Figure 8c, it can be found that the reinforcement learning agent generates maneuver commands while interacting with the environment taking time between 2.7 s and 3.3 s. If applied to the airborne computer, the ability to generate evasion commands in real time is questionable. That also indicates that we need the intelligent evasion strategy can generate evasion commands only from the initial situation.

After the Monte Carlo simulation, input the selected maneuver data into DNNs for training to generate the intelligent evasion model. The training outcomes of the neural network are as follows:

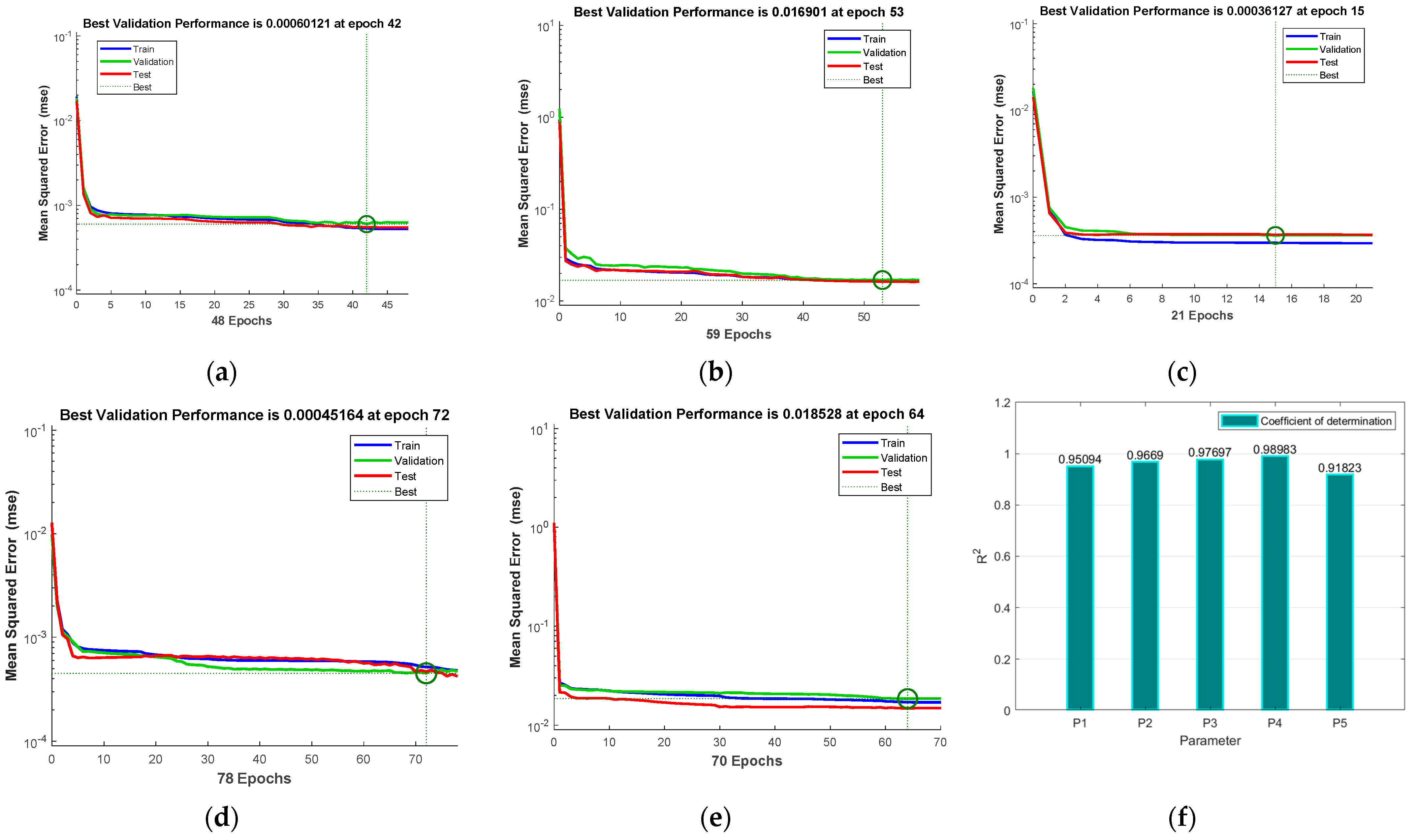
Figure 9. Performance indicators of neural networks: (a–e) DNNs’ MSE values in different datasets; (f) DNNs’ determination coefficient values.

Figure 9. Performance indicators of neural networks: (a–e) DNNs’ MSE values in different datasets; (f) DNNs’ determination coefficient values.

As the standard for evaluating network performance, the smaller the mean square error (MSE) value and the closer the determination coefficient (R²) to 1, the better the accuracy of the sample data described by the prediction model. Figure 9a–e show that the MSE values of the training set, validation set, and test set ultimately converge to minimum values close to 0. Figure 9f shows the determination coefficient of the model, and the r-squared values of the five coefficients fitted by the model are all greater than 0.9. These two evaluation criteria demonstrate that the model has a good fitting performance.

To verify the generalization of intelligent evasion strategies, three extreme scenarios were selected for verification: strict head-on scenario, maximum initial line-of-sight angle situation, and minimum initial relative distance situation.

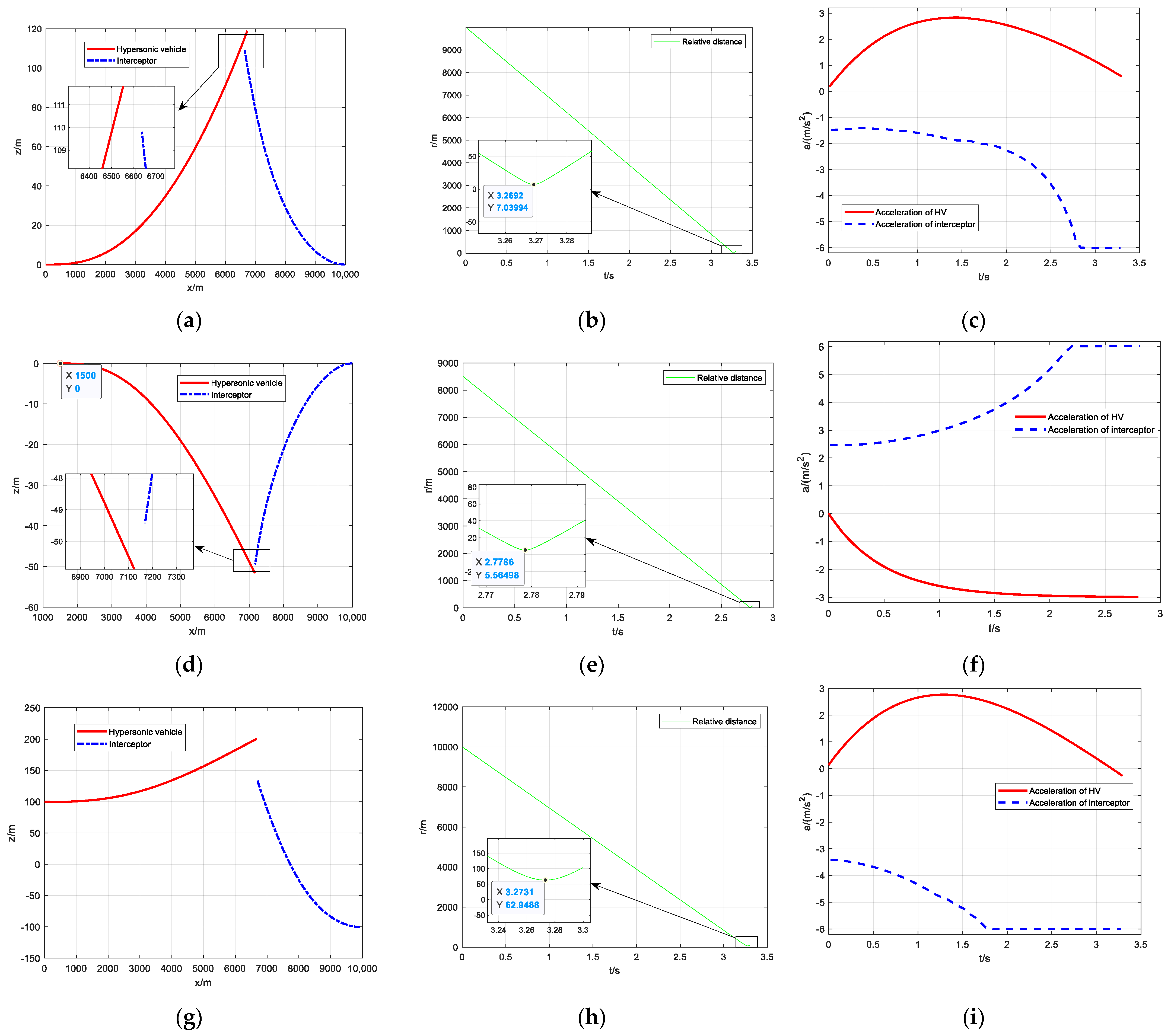
Figure 10. Simulation results of intelligent maneuver strategy under three typical situations: (a,d,g) two−dimensional planar trajectory map; (b,e,h) relative distance curve; (c,f,i) overload change curve.

Figure 10. Simulation results of intelligent maneuver strategy under three typical situations: (a,d,g) two−dimensional planar trajectory map; (b,e,h) relative distance curve; (c,f,i) overload change curve.

Figure 10a–c show the application of intelligent maneuver strategy for HV to achieve evasion under the strict head-on scenario. Compared with the previous reinforcement learning maneuvers, both of them can successfully evade, but as the price for improving reliability and generalization, the minimum relative distance under the intelligent maneuver strategy has been reduced by 1 m, which is caused by the relevant deviation in the parameter fitting process. In Figure 10c, the overload curve of HV still takes into account both successful evasion and energy consumption. Therefore, the study believes that the performance of the intelligent evasion strategy is acceptable.

Figure 10d–f shows the evasion strategy at the minimum relative distance, which is also the most difficult initial situation considering the initial position of HV (1500, 0). From Figure 10e, although HV has successfully evaded, the minimum relative distance is only 5.56498, which is just enough to meet the minimum miss distance. To successfully evade, HV directly chooses to fully inflate the overload, as shown in Figure 10f.

Figure 10g–i shows the evasion strategy at the maximum initial line-of-sight angle under the approximate head-on situations we have determined. Due to deviating from the strict head-on scenario, HV can use speed advantage to achieve relatively easy evasion. From Figure 10i, HV can significantly reduce overload and energy consumption.

Through the analysis of three typical characteristic scenarios, the study believes that the proposed intelligent maneuver strategy can generate maneuver overload with the effect of solving the PE game of HV in the head-on situation.

To further verify the improvement in terms of generalization, the combined dispersion and Monte Carlo simulation are conducted, respectively, on the proposed method based on ITD3 and DNN and the TD3 method under approximate head-on situations, with specific parameter ranges as above. And the simulation results are shown in the following Figure 11.

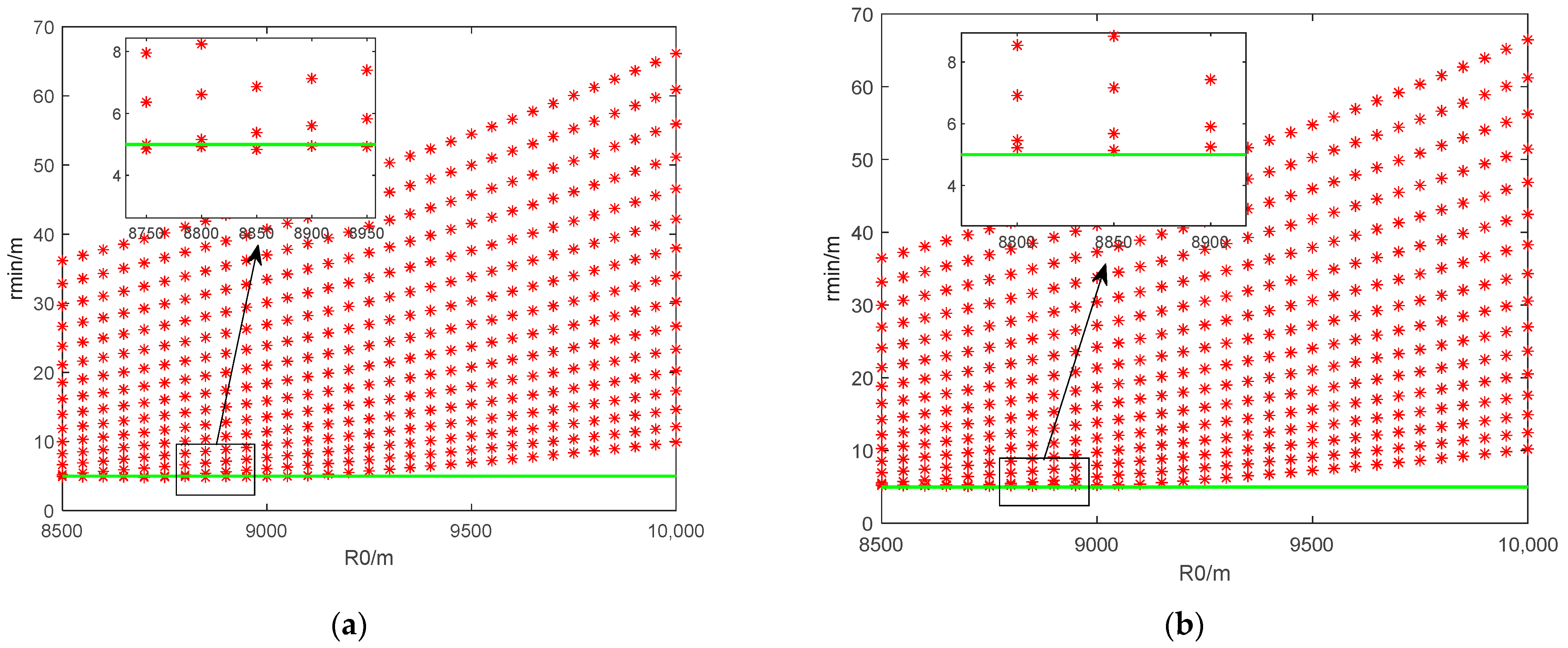
As the initial situation changes, using the TD3 algorithm solely to evade under certain harsh initial situations may result in evasion failure, where the minimum relative distance is less than 5, as shown in Figure 11a. Correspondingly, the proposed method by combining ITD3 and DNN algorithms utilizes successful sample fitting to replace failed cases, which can achieve successful evasion against interceptors in different initial situations under all difficult approximate head-on situations shown in Figure 11b, greatly improving the generalization of maneuvering strategies. Through comparison, it is verified that the proposed method can handle more difficult situations, and the application scenarios of the intelligent maneuver strategy are further expanded.

In addition, the average time consumption would not exceed 1 ms after testing, and the DNN used during “online application” only occupies approximately 10 kB of storage space. The above analysis indicates that the intelligent maneuver strategy proposed in this study has less computational burden and can be executed on modern-borne computers.

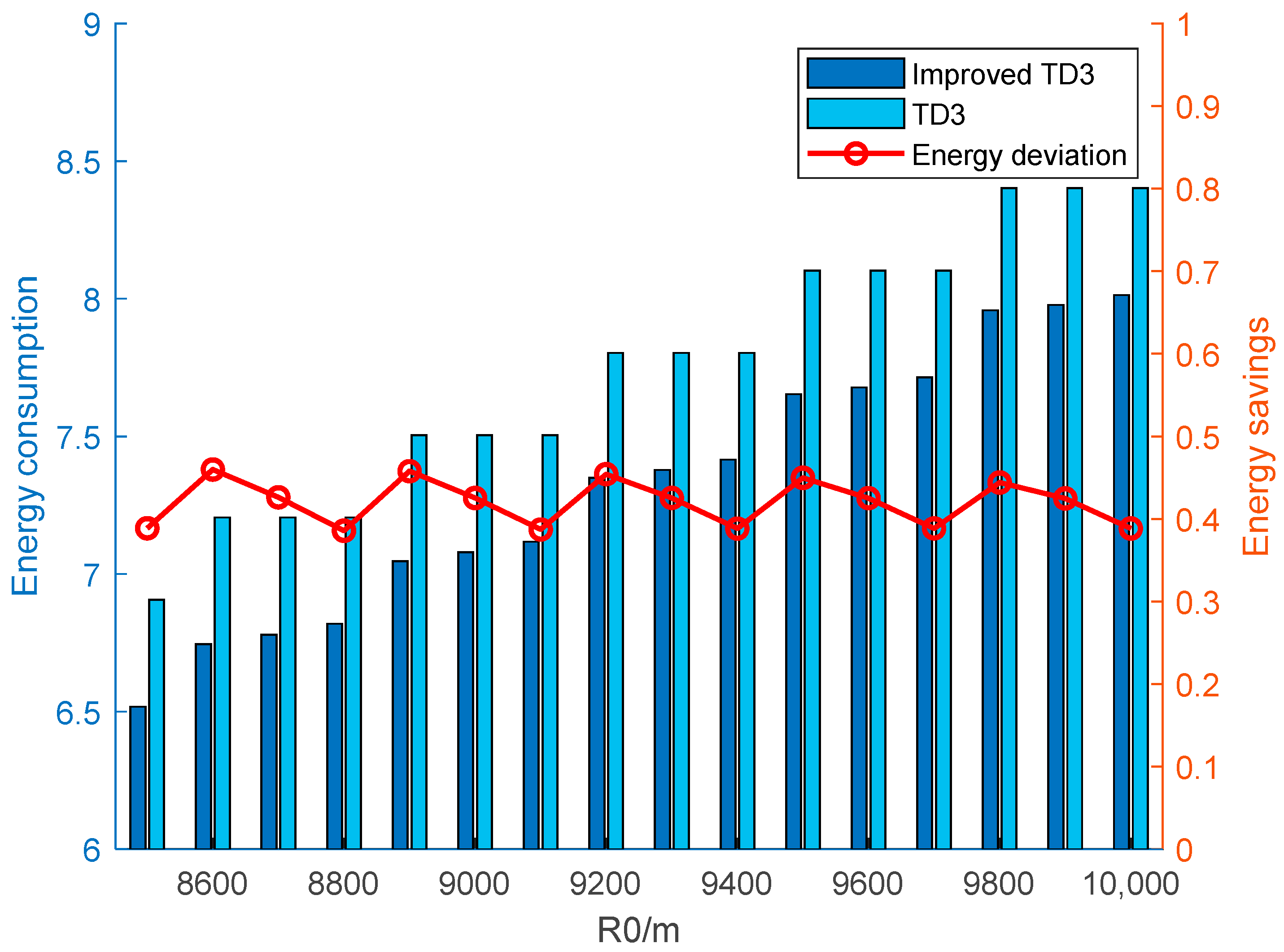
Finally, numerical simulations are conducted on the energy consumption issue. In the study, the accumulation of overload over time is utilized to represent the energy consumed, namely $E={\displaystyle \underset{t_0}{\overset{t_f}{\int }}{u}_H(t)\mathrm{d}t}$. The energy consumptions of the proposed ITD3 method and the TD3 method in the maneuver evasion process are calculated for different initial relative distances. From Figure 12, as the relative distance increases, the energy consumption of both methods increases, which is due to the longer maneuvering time. Regardless of the initial state, the energy consumption of the proposed ITD3 method is lower than that of the TD3 method, and the energy consumption difference between the two methods fluctuates between 0.4 and 0.5 g. That proves that the proposed method’s energy-saving design is effective, and the intelligent maneuvering strategy can effectively balance energy consumption and evasion miss distance, and adaptively adjust according to the initial states.

5. Conclusions

With the development of interception technology, traditional maneuvering strategies cannot effectively cope with the interception of chasers in unfavorable situations of short distances and high dynamics. Therefore, it is necessary to propose more intelligent maneuver strategies based on DRL. Under the framework of “offline training + online application”, this article is based on the improved TD3 algorithm and DNN to generate maneuver evasion instructions. The effectiveness of the combined strategy was verified through simulations under different initial situations. The experience pool classification strategy has been proposed to improve the training convergence rate and speed of the TD3 algorithm, which can be successfully trained in about 100 rounds to achieve convergence. In addition, a well-designed reward function can achieve adaptive adjustment of miss distance and energy consumption, rather than blindly pursuing the maximum miss distance. The combination of an improved TD3 algorithm and DNN simplifies the network structure, reduces computational time and space consumption, and is more in line with practical missile-borne computers. In the process of online application, the proposed method only needs to chase and escape the initial situation of both parties to generate maneuver instructions. Therefore, the proposed maneuver strategy is beneficial for the practice and application of engineering design. The simulation results show that the minimum distance between the pursuers and evaders in several typical situations is less than the specified critical miss distance of 5 m, which can achieve successful evasion. And the feasibility and effectiveness of the intelligent maneuver strategy are verified when facing a pursuer in head-on situations.

The reason why an intelligent algorithm can effectively solve hypersonic PE game problems is that it can grasp the appropriate maneuvering opportunities under high dynamics and provide the optimal solution.

Next, we will study the three-player PE game problem of one evader to two pursuers or two evaders to one pursuer, further enriching the pursuit scenarios and maneuvering strategies.