Parametric Analysis of the Toothed Electromagnetic Spring Based on the Finite Element Model
Abstract
:1. Introduction
2. Finite Element Simulation
2.1. Structure of the TES
2.2. Finite Element Simulation
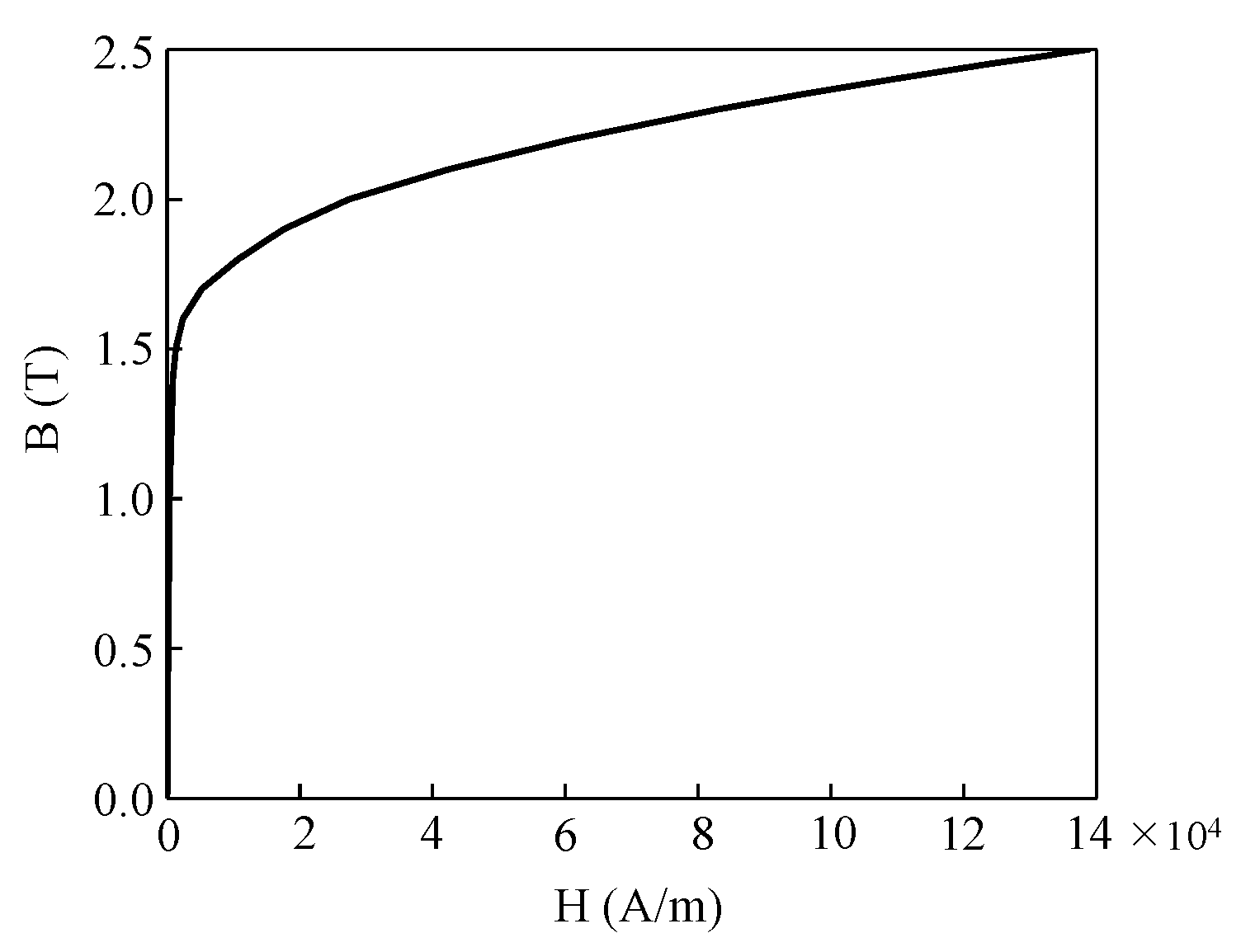
2.2.1. Finite Element Model
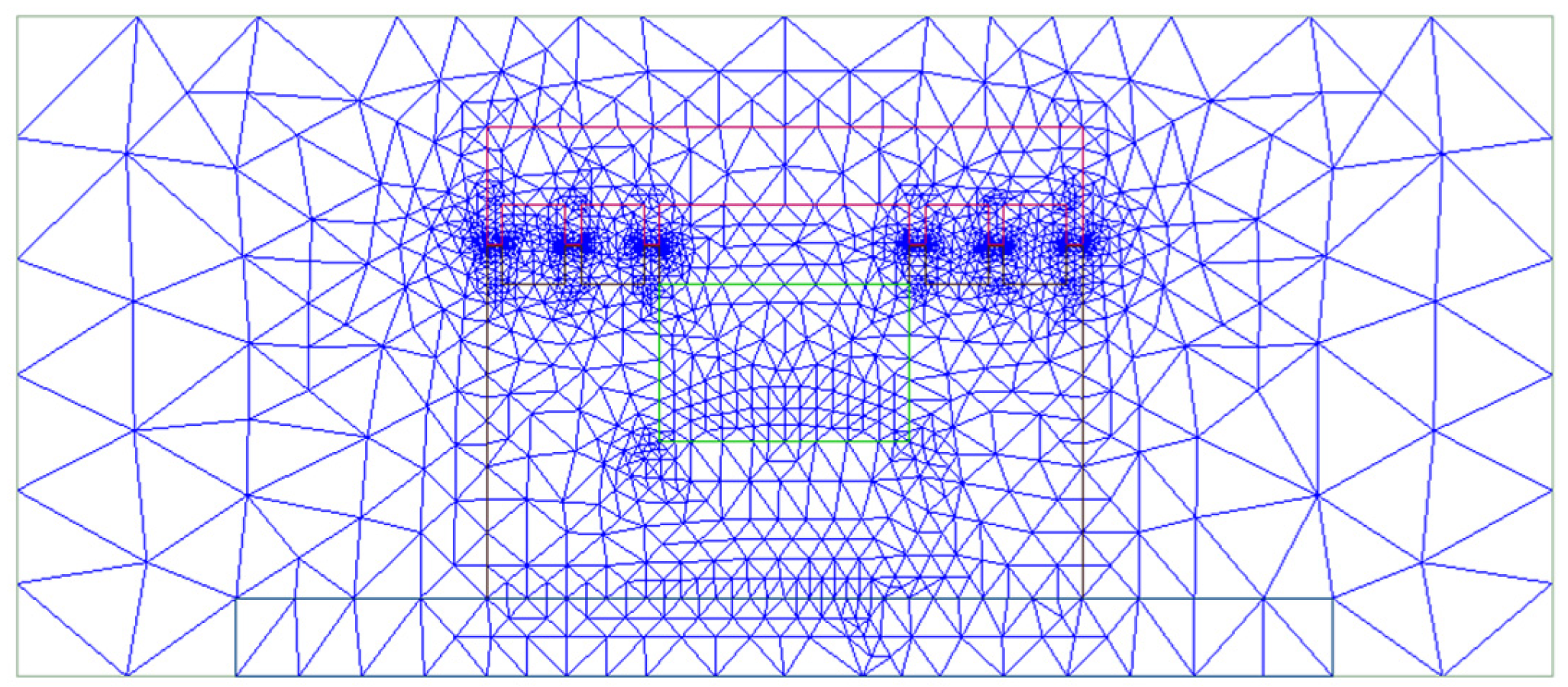
2.2.2. Grid Demarcation
2.2.3. Application of Constraints
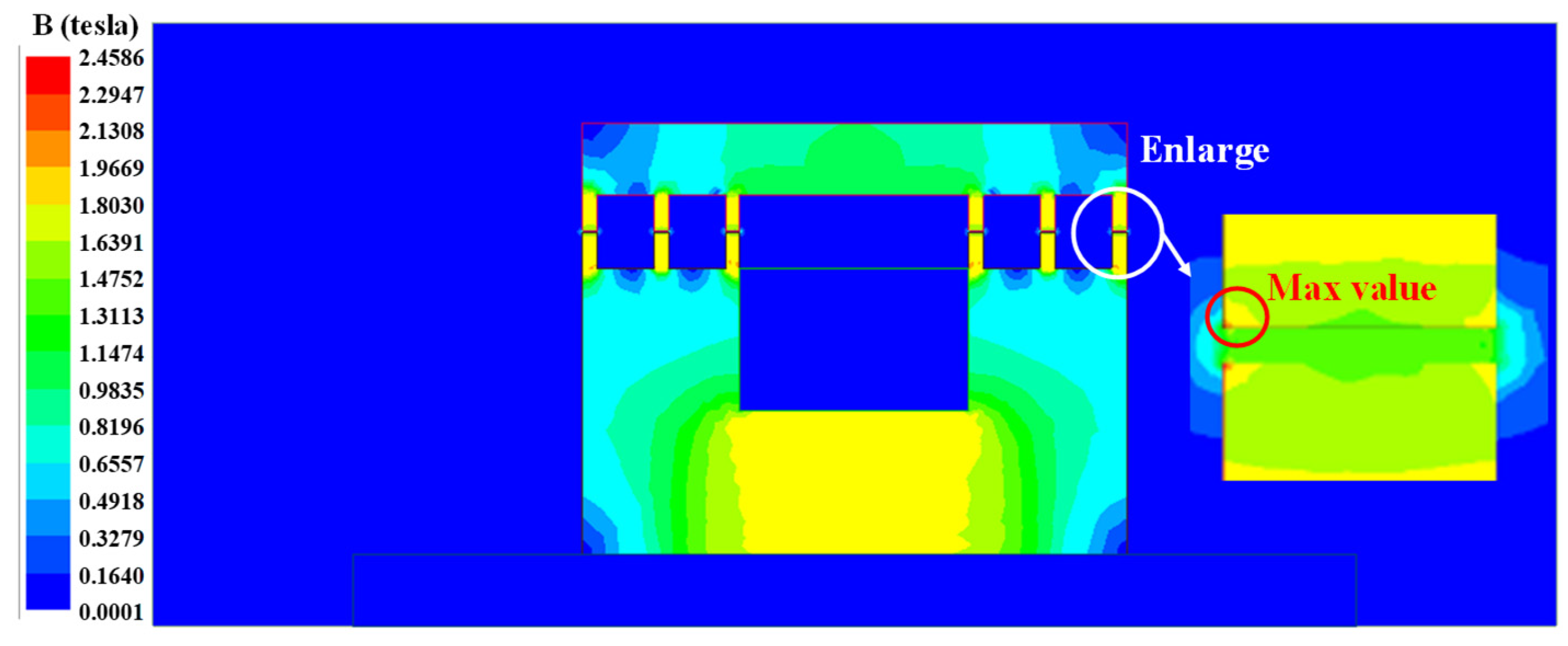
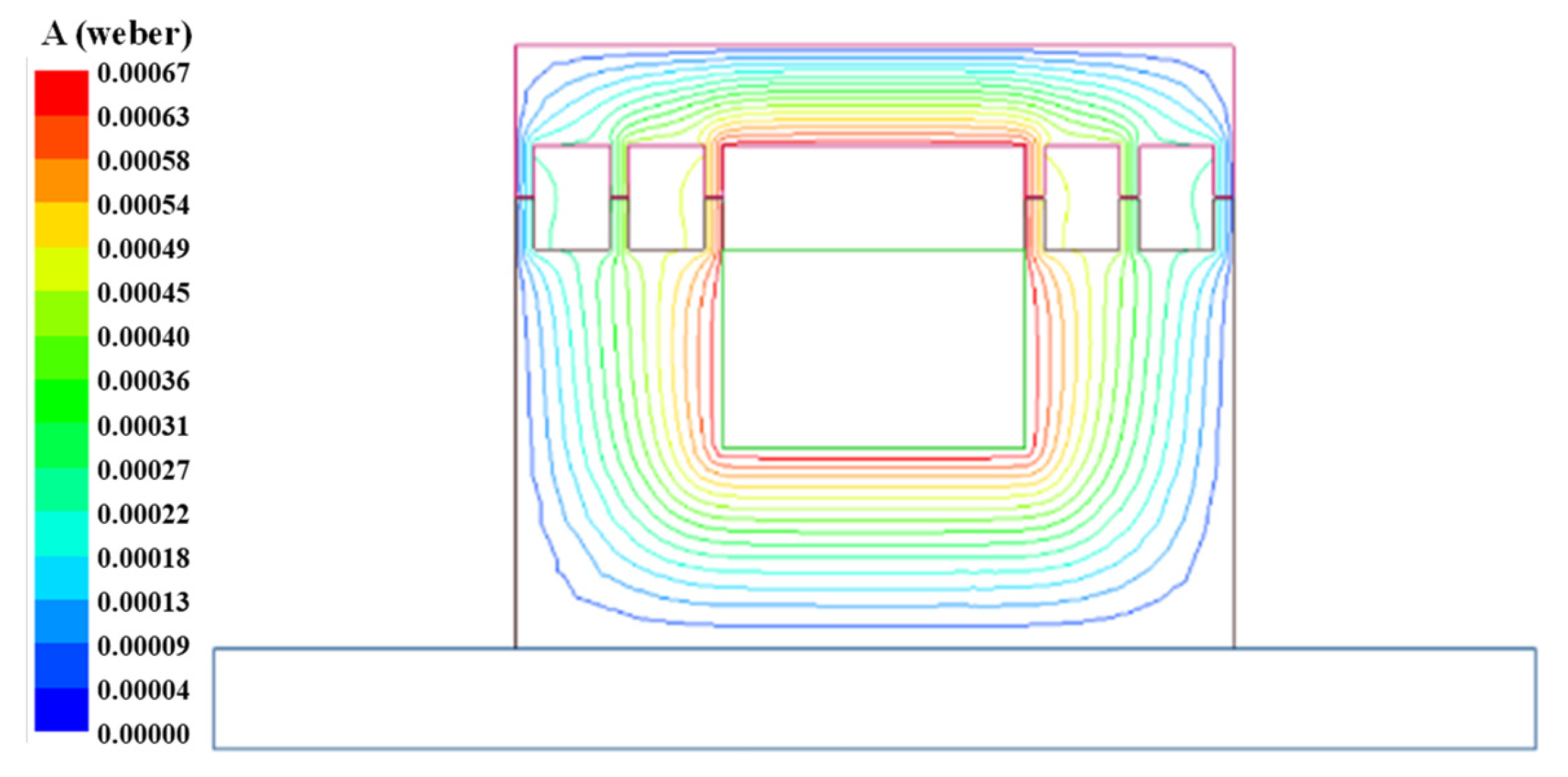
2.2.4. Results
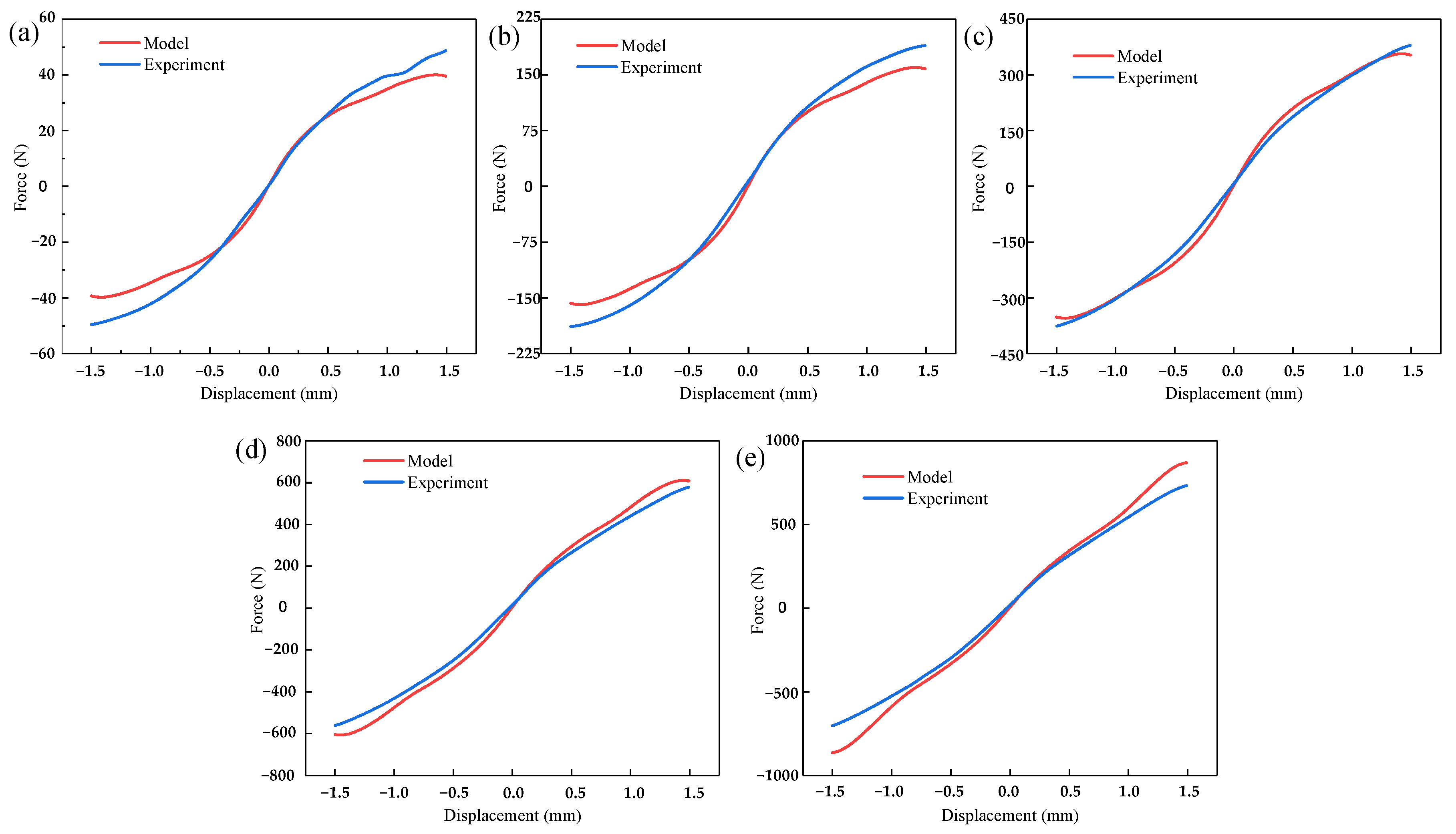
3. Model Verification
4. Parametric Analysis
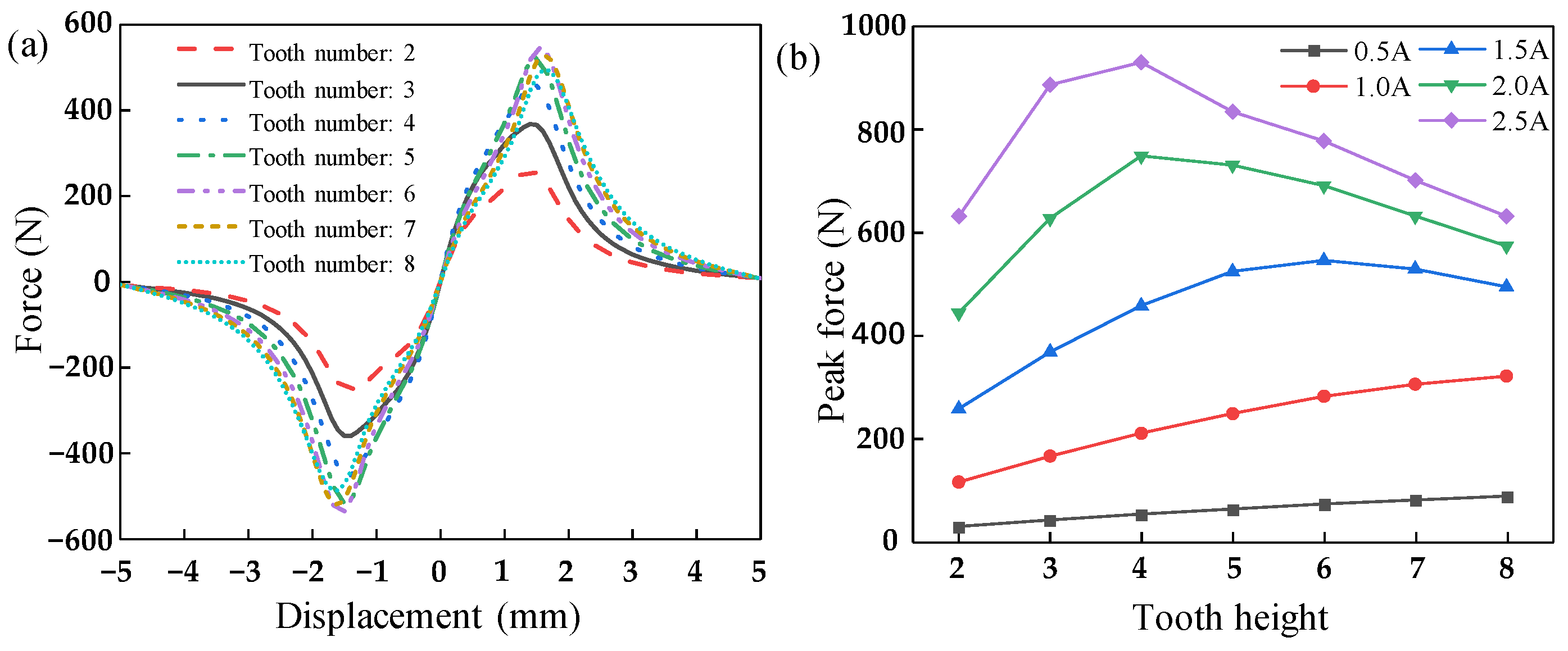
4.1. Influence of the Number of Teeth
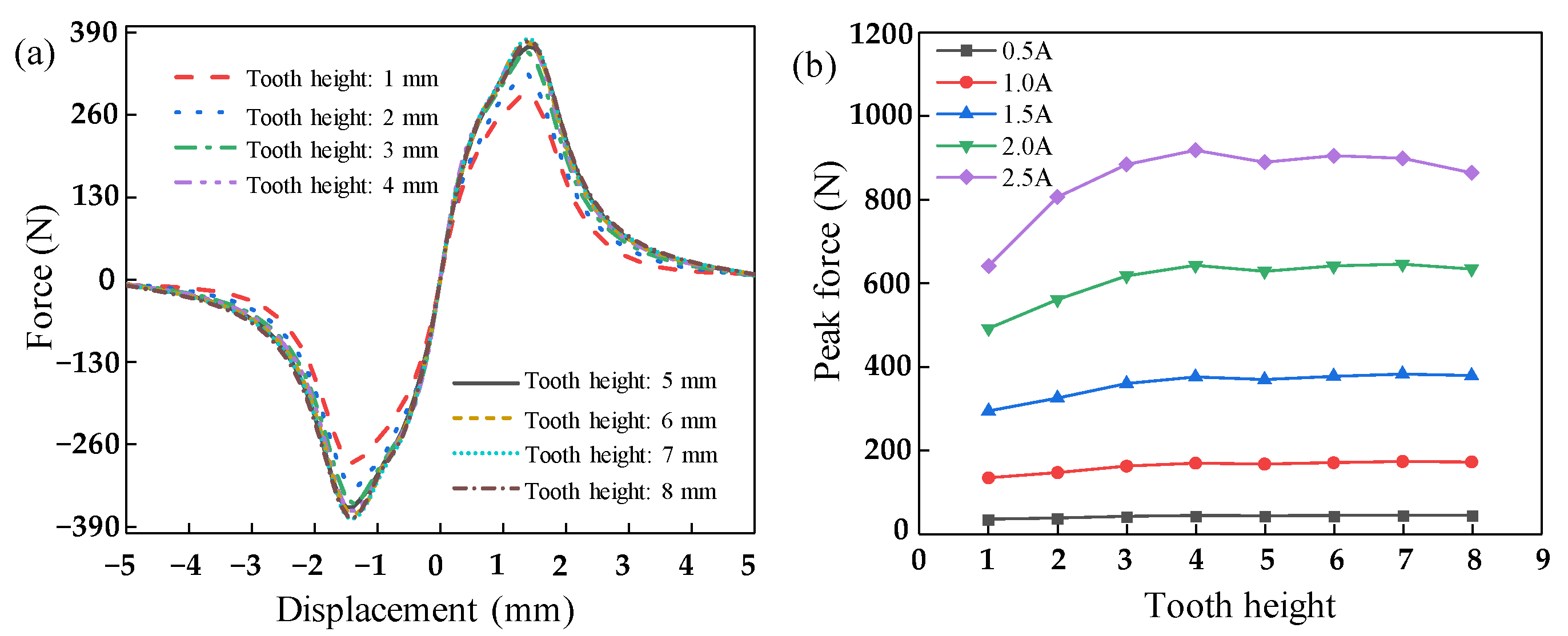
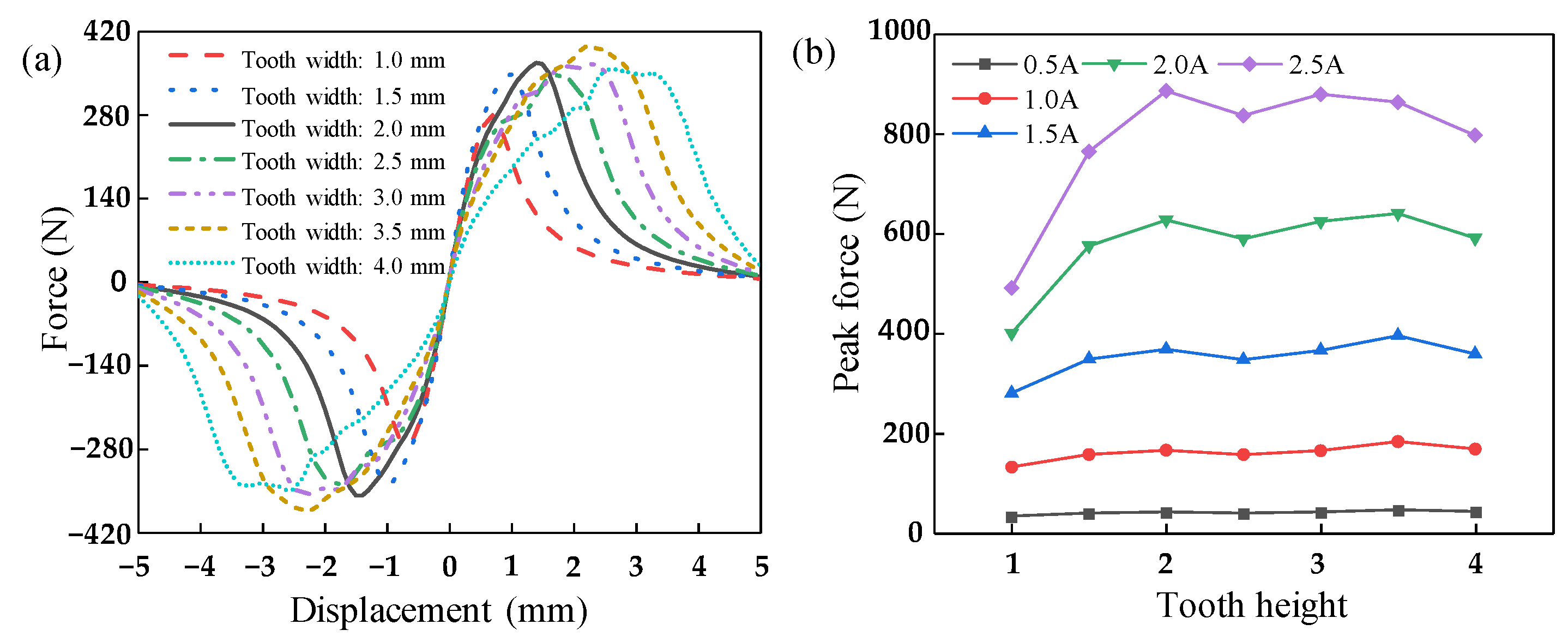
4.2. Influence of Tooth Height
4.3. Influence of Tooth Width
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.; Fu, Y.; He, W.; Hui, Q. Modeling and observer-based vibration control of a flexible spacecraft with external disturbances. IEEE Trans. Ind. Electron. 2019, 66, 8648–8658. [Google Scholar] [CrossRef]
- Li, J.Y.; Jing, X.J.; Li, Z.C.; Huang, X.L. Fuzzy adaptive control for nonlinear suspension systems based on a bioinspired reference model with deliberately designed nonlinear damping. IEEE Trans. Ind. Electron. 2019, 66, 8713–8723. [Google Scholar] [CrossRef]
- McNeil, S.; Meylan, M.H. Time-dependent modelling of the wave-induced vibration of ice shelves. Mar. Sci. Eng. 2023, 11, 11061191. [Google Scholar] [CrossRef]
- Wei, J.; Liu, W.; Gao, P.X.; Ding, Y.J. An analytical dynamic model for vibration suppression of a multi-span continuous bridge by tuned mass dampers. Mar. Sci. Eng. 2023, 11, 11051017. [Google Scholar] [CrossRef]
- Carrella, A.; Brennan, M.J.; Kovacic, I.; Waters, T.P. On the force transmissibility of a vibration isolator with quasi-zero-stiffness. J. Sound Vib. 2009, 322, 707–717. [Google Scholar] [CrossRef]
- Carrella, A.; Brennan, M.J.; Waters, T.P.; Lopes, V. Force and displacement transmissibility of a nonlinear isolator with high-static-low-dynamic-stiffness. Int. J. Mech. Sci. 2012, 55, 22–29. [Google Scholar] [CrossRef]
- Zheng, X.Y.; Wu, Y.W.; Zheng, C.; Bai, H.B.; Liu, R. Quasistatic and low-velocity impact properties of entangled metallic wire material–silicone rubber composite. J. Mater. Res. Technol. 2023, 23, 143–152. [Google Scholar] [CrossRef]
- Zheng, X.Y.; Ren, Z.Y.; Bai, H.B.; Wu, Z.B.; Guo, Y.S. Mechanical behavior of entangled metallic wire materials-polyurethane interpenetrating composites. Def. Technol. 2023, 20, 120–136. [Google Scholar] [CrossRef]
- Wu, J.L.; Zeng, L.Z.; Han, B.; Zhou, Y.F.; Luo, X.; Li, X.Q.; Chen, X.D.; Jiang, W. Analysis and design of a novel arrayed magnetic spring with high negative stiffness for low-frequency vibration isolation. Int. J. Mech. Sci. 2021, 15, 106980. [Google Scholar] [CrossRef]
- Wang, Y.; Li, S.M.; Cheng, C.; Su, Y.Q. Adaptive control of a vehicle-seat-human coupled model using quasi-zero-stiffness vibration isolator as seat suspension. J. Mech. Sci. Technol. 2018, 32, 2973–2985. [Google Scholar] [CrossRef]
- Wang, K.; Zhou, J.X.; Chang, Y.P.; Ouyang, H.J.; Xu, D.L.; Yang, Y. A nonlinear ultra-low-frequency vibration isolator with dual quasi-zero-stiffness mechanism. Nonlinear Dyn. 2020, 101, 755–773. [Google Scholar] [CrossRef]
- Wu, M.K.; Wu, J.L.; Che, J.X.; Gao, R.Q.; Chen, X.D.; Li, X.Q.; Zeng, L.Z.; Jiang, W. Analysis and experiment of a novel compact magnetic spring with high linear negative stiffness. Mech. Syst. Signal. Process. 2023, 198, 110398. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, Q.; Yan, B.; Luo, Y.; Zhang, X. A Stewart isolator with high-static-low-dynamic stiffness struts based on negative stiffness magnetic springs. J. Sound. Vib. 2018, 422, 390–408. [Google Scholar] [CrossRef]
- Liu, Y.Q.; Matsuhisa, H.; Utsuno, H. Semi-active vibration isolation system with variable stiffness and damping control. J. Sound Vib. 2008, 313, 16–28. [Google Scholar] [CrossRef]
- Pu, H.Y.; Yuan, S.J.; Peng, Y.; Meng, K.; Zhao, J.L.; Xie, R.Q.; Huang, Y.N.; Sun, Y. Multi-layer electromagnetic spring with tunable negative stiffness for semi-active vibration isolation. Mech. Syst. Signal Process. 2019, 121, 942–960. [Google Scholar] [CrossRef]
- Carrella, A.; Brennan, M.J.; Waters, T.P.; Shin, K. On the design of a high-static–low-dynamic stiffness isolator using linear mechanical springs and magnets. J. Sound Vib. 2008, 315, 712–720. [Google Scholar] [CrossRef]
- Dong, G.; Zhang, X.; Xie, S.; Yan, B.; Luo, Y. Simulated and experimental studies on a high-static-low-dynamic stiffness isolator using magnetic negative stiffness spring. Mech. Syst. Signal Process. 2017, 86, 188–203. [Google Scholar] [CrossRef]
- Wu, W.; Chen, X.; Shan, Y. Analysis and experiment of a vibration isolator using a novel magnetic spring with negative stiffness. J. Sound Vib. 2014, 333, 2958–2970. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, X.; Luo, Y.; Zhang, Y.; Xie, S. Analytical study of a quasi-zero stiffness coupling using a torsion magnetic spring with negative stiffness. Mech. Syst. Signal Process. 2018, 100, 135–151. [Google Scholar] [CrossRef]
- Yu, J.; Li, D.; Li, S.; Xiang, Z.; He, Z.; Shang, J.; Wu, Y.; Liu, Y.; Li, R.-W. Electromagnetic vibration energy harvester using magnetic fluid as lubricant and liquid spring. Energy Convers. Manag. 2023, 286, 117030. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, X.; Ding, S.; Zhang, R.; McNabb, L. A new concept of speed amplified nonlinear electromagnetic vibration energy harvester through fixed pulley wheel mechanisms and magnetic springs. Mech. Syst. Signal Process. 2019, 126, 305–325. [Google Scholar] [CrossRef]
- Zhou, R.; Gao, W.; Liu, W.; Xu, J. Effects of Open-Hole and Reinforcement on the Bearing Performance of the Plain-Woven Fabric Composite I-Section Beams under Shear Load. Aerospace 2022, 9, 537. [Google Scholar] [CrossRef]
- Yuan, S.; Sun, Y.; Zhao, J.; Meng, K.; Wang, M.; Pu, H.; Peng, Y.; Luo, J.; Xie, S. A tunable quasi-zero stiffness isolator based on a linear electromagnetic spring. J. Sound Vib. 2020, 482, 115449. [Google Scholar] [CrossRef]
- Kallenbach, E.; Kube, H.; Zöppig, V.; Feindt, K.; Hermann, R.; Beyer, F. New polarized electromagnetic actuators as integrated mechatronic components-design and application. Mechatronics 1999, 9, 769–784. [Google Scholar] [CrossRef]
- Kim, J. A study on the optimal design and the performance evaluation of electromagnetic energy harvesting device for the rolling stock application. J. Intell. Mater. Syst. Struct. 2020, 31, 2362–2377. [Google Scholar] [CrossRef]
- Mahdi, S.M.; Bardaweel, H. Theoretical study and experimental identification of elastic-magnetic vibration isolation system. J. Intell. Mater. Syst. Struct. 2018, 29, 1045389. [Google Scholar]
- Olaru, R.; Petrescu, C.; Arcire, A. Design of a magnetic spring for variable stiffness actuators. Proc. Rom. Acad. Sci. Ser. A Math. Phys. Tech. Sci. Inf. Sci. 2021, 2, 235–243. [Google Scholar]
- Liu, X.G.; Feng, X.X.; Shi, Y.; Wang, Y.; Shuai, Z.J. Development of a Semi-Active Electromagnetic Vibration Absorber and Its Experimental Study. J. Vib. Acoust. 2013, 135, 151–159. [Google Scholar] [CrossRef]

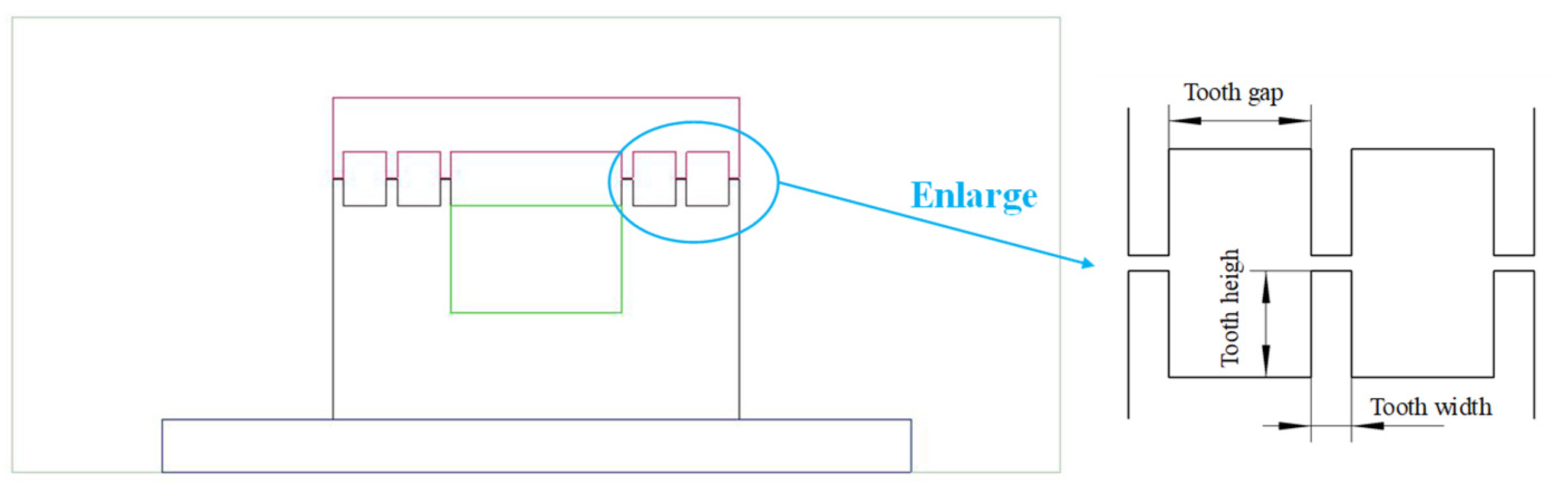


| Parameters | Coil Height (mm) | Coil Width (mm) | Air Gap (mm) | Tooth Number | Tooth Pitch (mm) |
| Value | 32 | 20 | 0.25 | 3 | 10 |
| Parameters (mm) | Tooth Height | Tooth Width | Stator Shell Thickness | Armature Diameter | Shaft Diameter |
| Value | 5 | 2 | 10 | 100 | 20 |
| Region | Shaft | Stator | Armature | Coil | Solution Domain |
|---|---|---|---|---|---|
| Maximum length (mm) | 10 | 5 | 5 | 2 | 15 |
| Equipment | Model | Parameters | Manufacture |
|---|---|---|---|
| Force sensor | AR-DN23 | Range: 0–5 kN Accuracy: 0.015% F.S | Ailixun, Chian |
| Displacement sensor | ML33-12.5-A | Range: 0–12.5 mm Accuracy: 0.1% F.S | Miran, China |
| Servo electric | ECMA-C200807SS | Output: 3000 rpm | Delta, China |
| Power supply | DC-3010D | Range: 0–10 A, 0–30 V | Yihua, China |
| Current (A) | RSS | TSS | R2 |
|---|---|---|---|
| 0.5 | 3.9947 × 104 | 1.8890 × 106 | 0.9788 |
| 1.0 | 4.8120 × 105 | 2.9294 × 107 | 0.9835 |
| 1.5 | 4.6403 × 105 | 1.0754 × 108 | 0.9956 |
| 2.0 | 3.5733 × 106 | 3.2686 × 108 | 0.9890 |
| 2.5 | 1.0330 × 107 | 4.5877 × 108 | 0.9774 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, X.; Zhang, C.; Lou, Y.; Xue, G.; Bai, H. Parametric Analysis of the Toothed Electromagnetic Spring Based on the Finite Element Model. Aerospace 2023, 10, 750. https://doi.org/10.3390/aerospace10090750
Zheng X, Zhang C, Lou Y, Xue G, Bai H. Parametric Analysis of the Toothed Electromagnetic Spring Based on the Finite Element Model. Aerospace. 2023; 10(9):750. https://doi.org/10.3390/aerospace10090750
Chicago/Turabian StyleZheng, Xiaoyuan, Cheng Zhang, Yifang Lou, Guangming Xue, and Hongbai Bai. 2023. "Parametric Analysis of the Toothed Electromagnetic Spring Based on the Finite Element Model" Aerospace 10, no. 9: 750. https://doi.org/10.3390/aerospace10090750
APA StyleZheng, X., Zhang, C., Lou, Y., Xue, G., & Bai, H. (2023). Parametric Analysis of the Toothed Electromagnetic Spring Based on the Finite Element Model. Aerospace, 10(9), 750. https://doi.org/10.3390/aerospace10090750






