Aerodynamic Characteristics of a Z-Shaped Folding Wing
Abstract
:1. Introduction
2. Materials and Methods
2.1. Model and Numerical Method
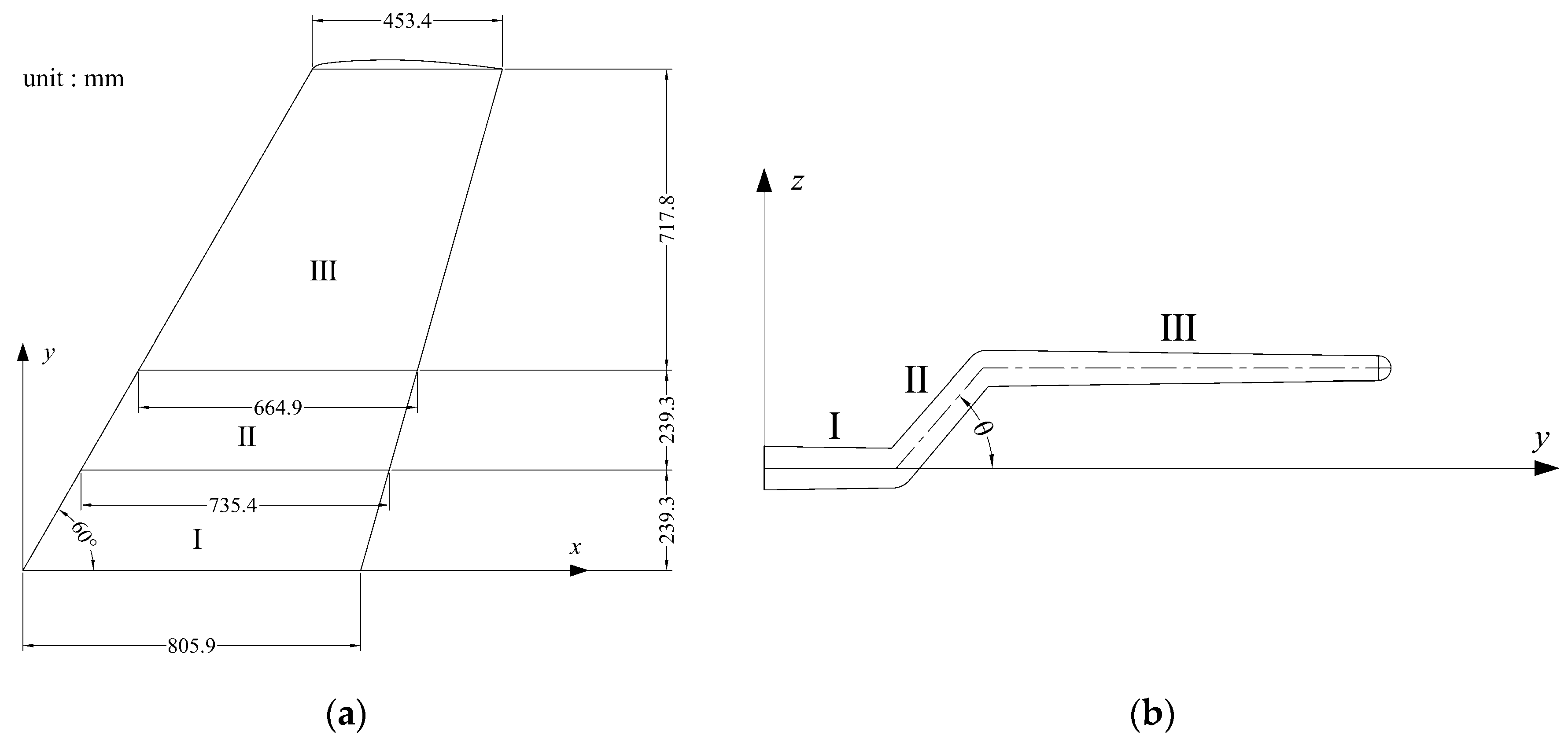
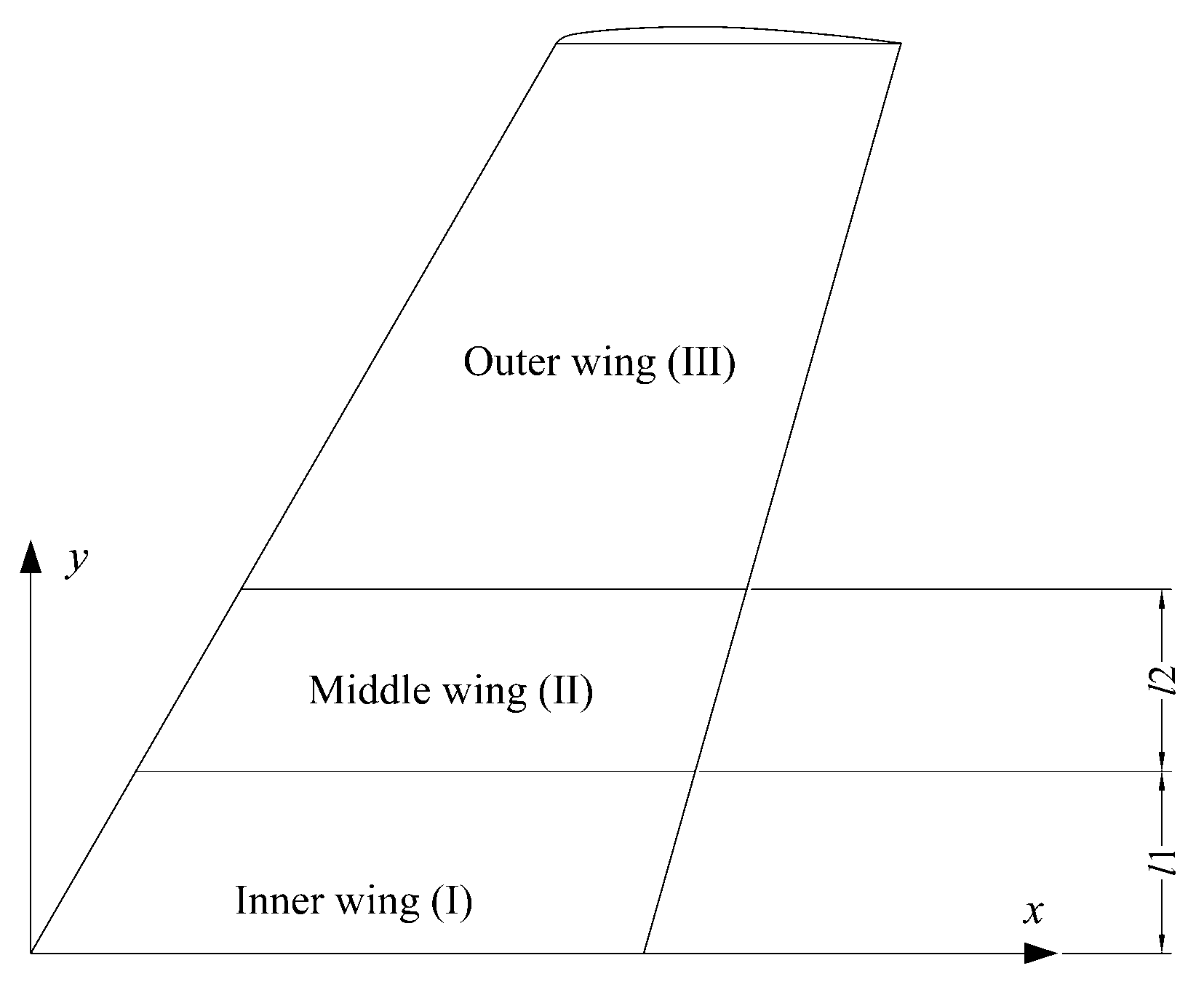
2.1.1. Model of Folding Wing Aircraft
2.1.2. Definition of the Folding Motion
2.1.3. Numerical Simulation Method
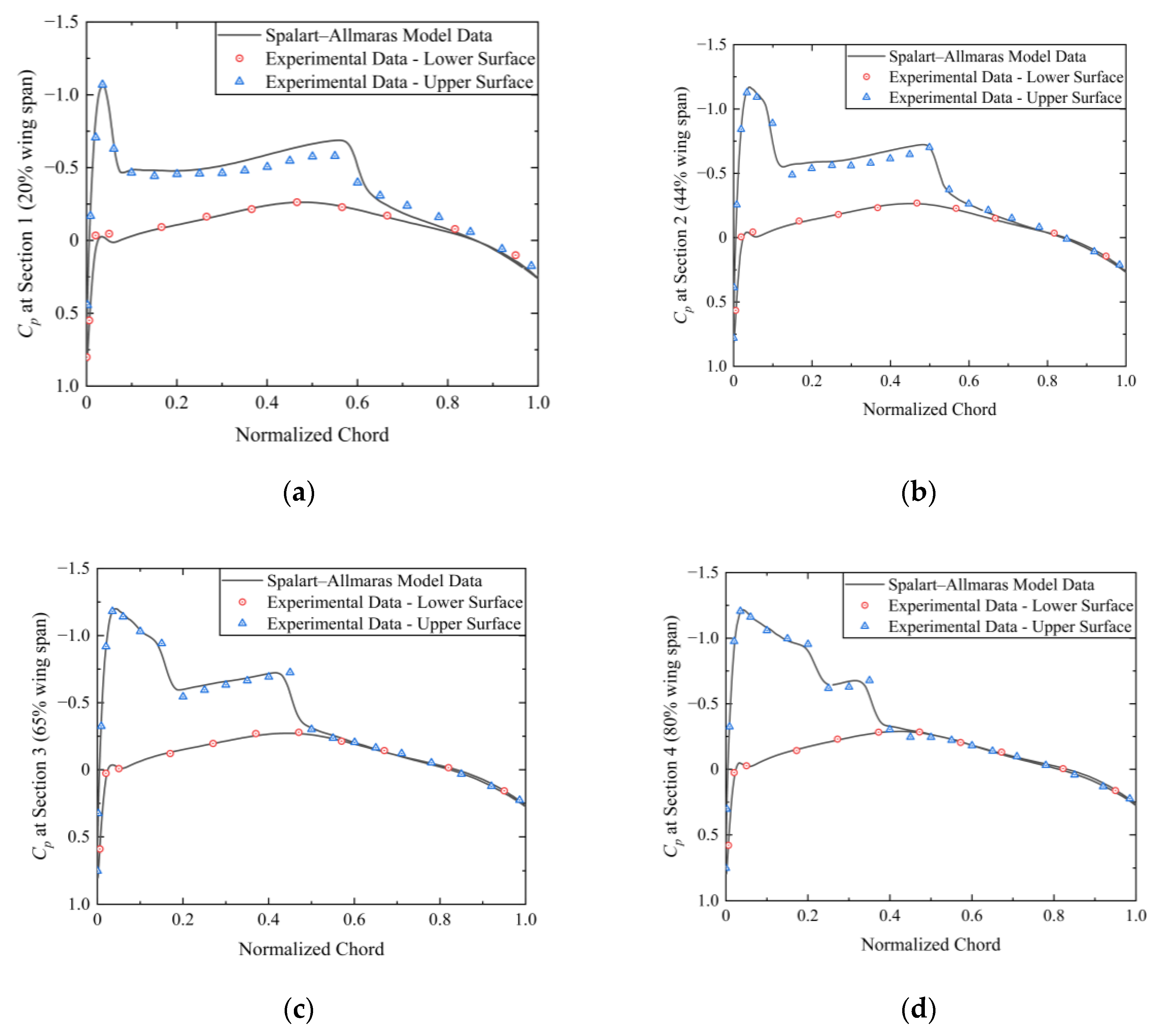
2.2. Validation of the Model in Steady State
3. Results and Discussion
3.1. The Steady Aerodynamic Characteristics of Folding Wing
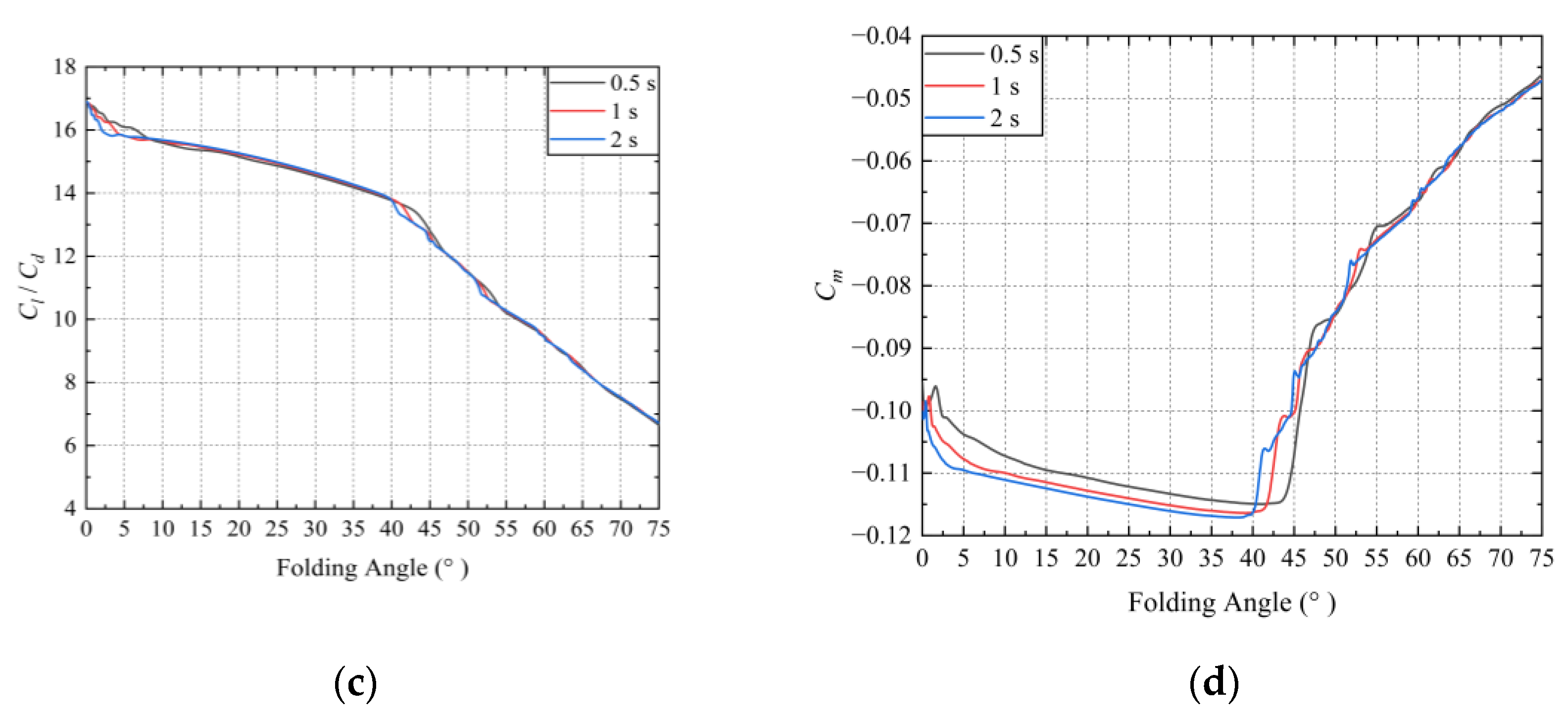
3.2. The Unsteady Aerodynamic Characteristics of Folding Wing
4. Conclusions
- (1)
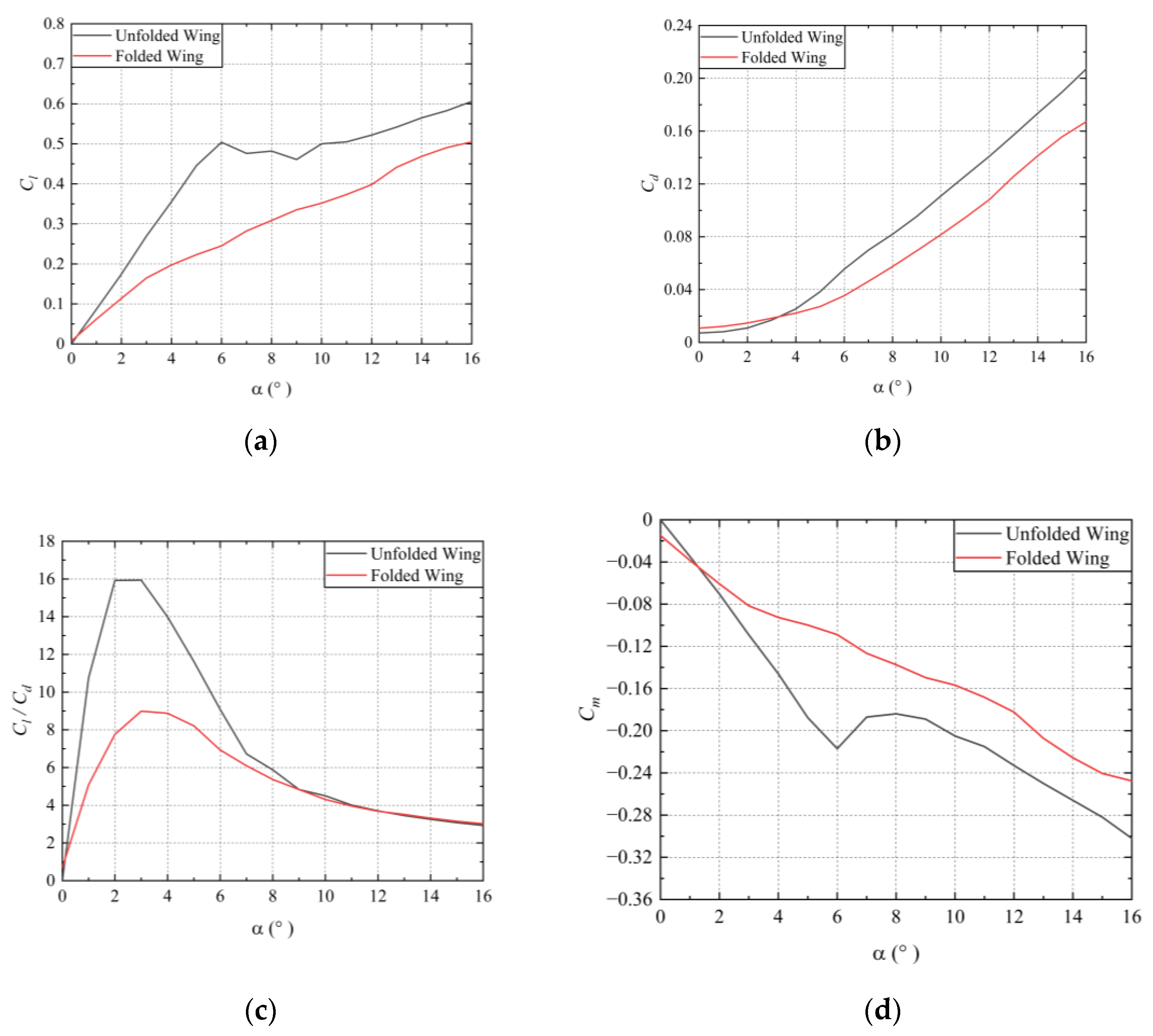
- For the steady aerodynamic characteristics, when the wing is folded at an angle of 75°, the lift coefficient of the folded wing is smaller than that of the unfolded wing at various angle of attacks. Conversely, the drag coefficient of the folded wing is slightly larger than that of the unfolded wing at low angles of attack, but it gradually becomes smaller as the angle of attack increases. Moreover, the folded wing exhibits a smaller lift-to-drag ratio compared to the unfolded wing at different angles of attack. Regarding the pitching moment coefficient, the folded wing experiences a smaller nose-down pitching moment in comparison to the unfolded wing as the angle of attack increases.
- (2)
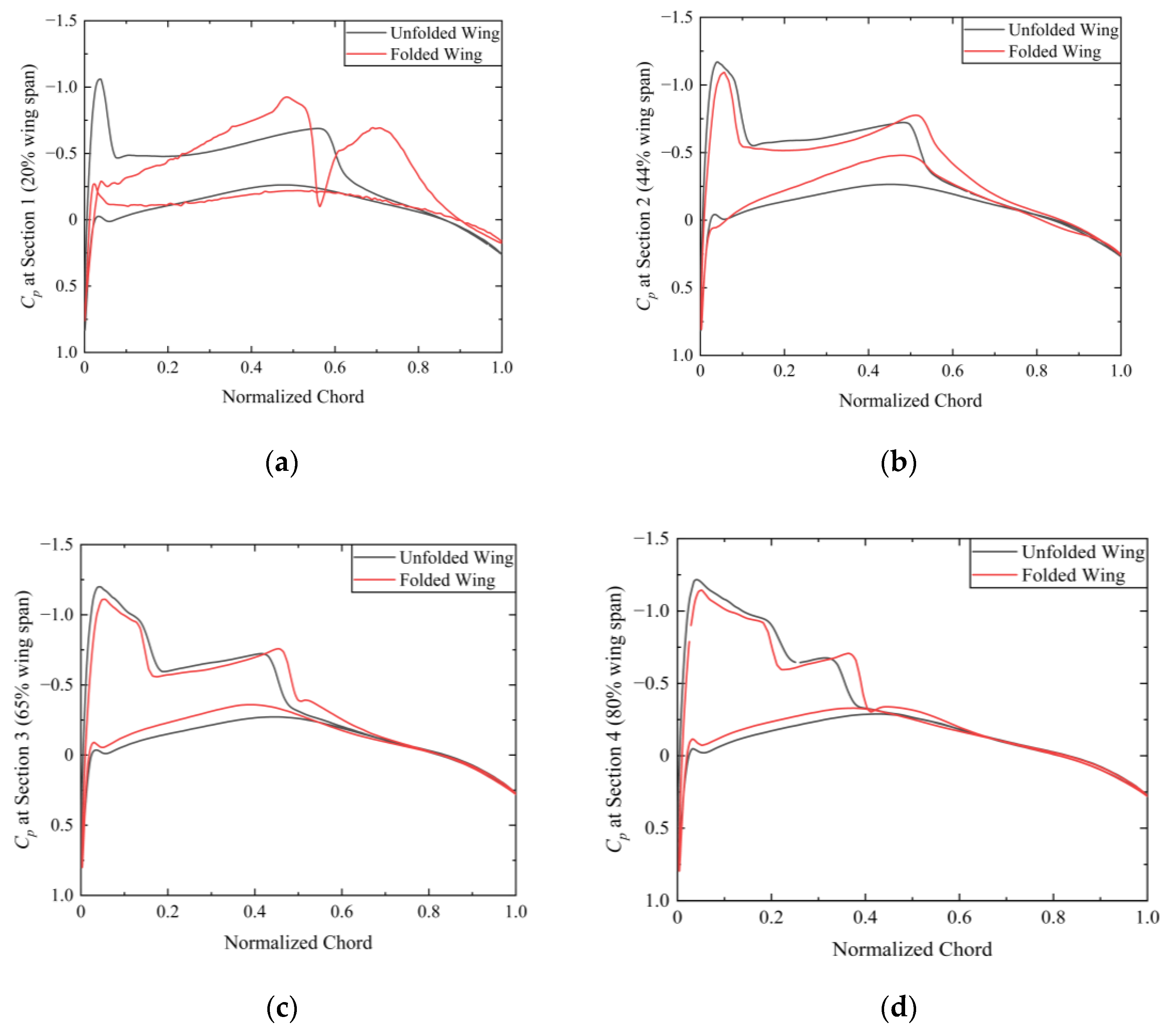
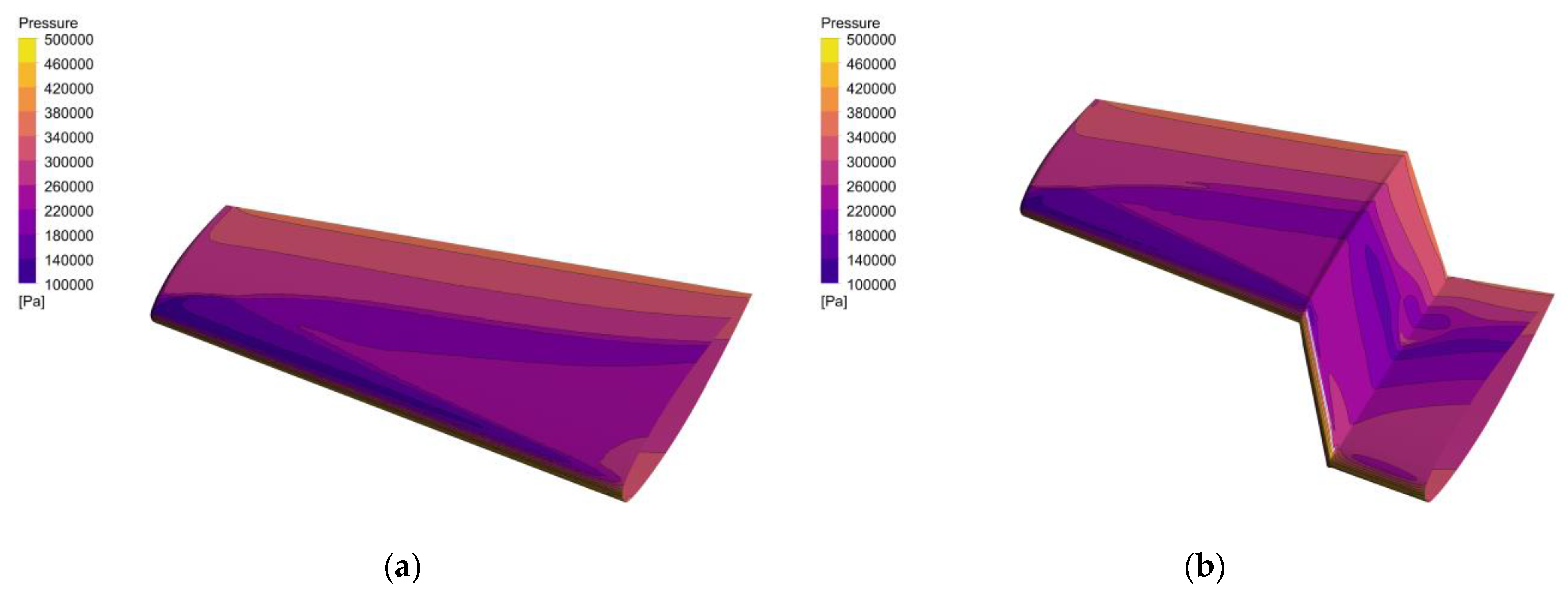
- Regarding the steady aerodynamic characteristics, the difference between the pressure coefficients of the folded wing and the unfolded wing is primarily focused on the wing’s folding position. Specifically, under high subsonic flight conditions, local supersonic regions are generated. In addition to the λ-shock generated by an unfolded wing under the same conditions, a folded wing also generates additional shock waves. The flow separation coalesces to form two vortices at the folded position, which may contribute to the lower lift-to-drag ratio of the folded wing, in addition to the reduced lift area.
- (3)
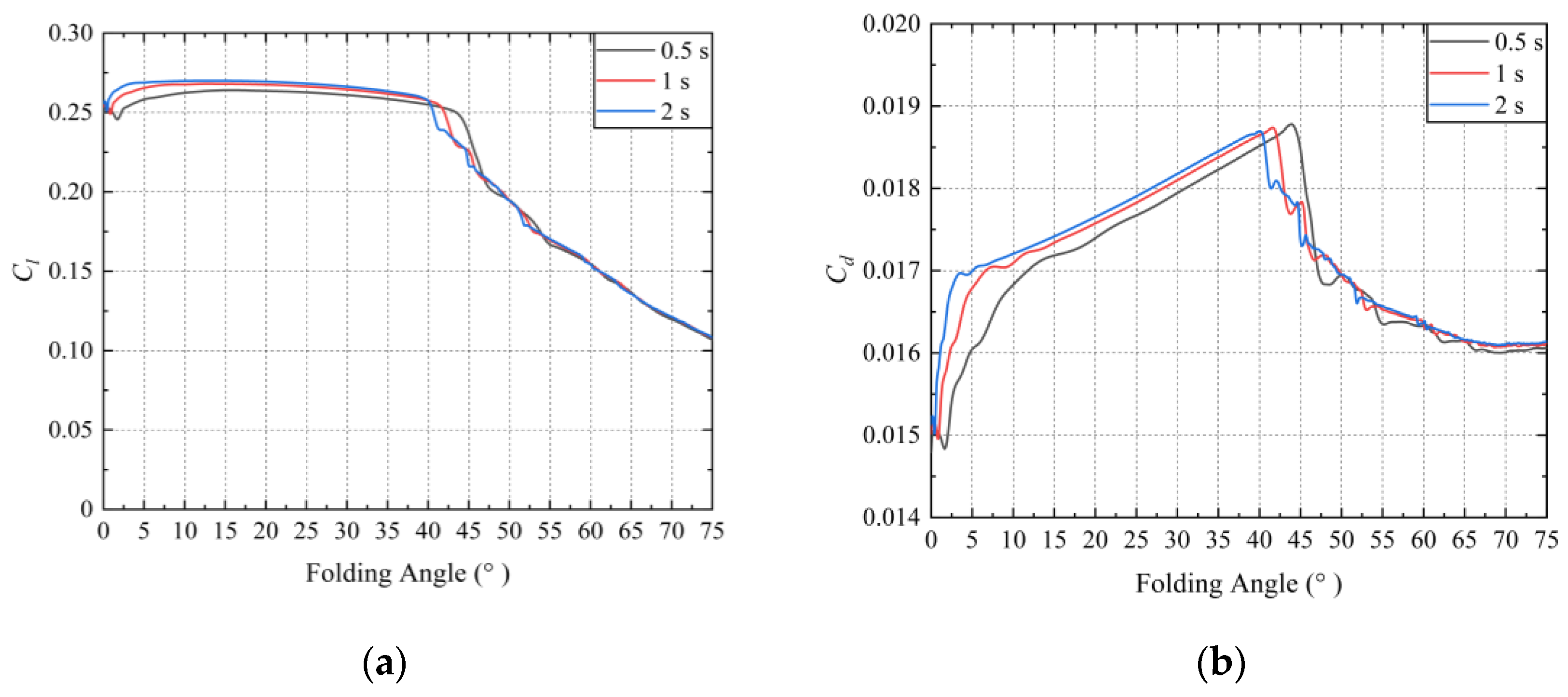
- Concerning the unsteady aerodynamic characteristics, the aerodynamic coefficients of the wing are compared at three different folding speeds. It is observed that during the folding process, the aerodynamic coefficients do not vary significantly with an increasing folding speed, and their changes remain consistent. However, at approximately 40° to 45°, the trends in the aerodynamic coefficients undergo a significant shift, and this shift is advanced as the folding speed decreases. Eventually, the aerodynamic coefficients at the three different folding speeds converge to the same value. Generally, as the wing folds, the folding wing compromises its lift-to-drag ratio characteristics to achieve a smaller nose-down pitching moment, thereby enhancing maneuverability.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kan, Z.; Li, D.; Shen, T.; Xiang, J.; Zhang, L. Aerodynamic characteristics of morphing wing with flexible leading-edge. Chin. J. Aeronaut. 2020, 33, 2610–2619. [Google Scholar] [CrossRef]
- Abdessemed, C.; Bouferrouk, A.; Yao, Y. Effects of an unsteady morphing wing with seamless side-edge transition on aerodynamic performance. Energies 2022, 15, 1093. [Google Scholar] [CrossRef]
- Courchesne, S.; Popov, A.; Botez, R. New Aeroelastic Studies for a Morphing Wing. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, USA, 4–7 January 2010. [Google Scholar]
- Coutu, D.; Brailovski, V.; Terriault, P.; Mamou, M.; Mebarki, Y. Aerostructural Model for Morphing Laminar Wing Optimization in a Wind Tunnel. J. Aircr. 2011, 48, 66–76. [Google Scholar] [CrossRef]
- Prabhakar, N.; Prazenica, R.J.; Gudmundsson, S.; Balas, M.J. Transient dynamic analysis and control of a morphing UAV. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, San Diego, CA, USA, 4–8 January 2016; p. 893. [Google Scholar]
- Santos, P.; Sousa, J.; Gamboa, P. Variable-span wing development for improved flight performance. J. Intell. Mater. Syst. Struct. 2017, 28, 961–978. [Google Scholar] [CrossRef]
- Raither, W.; Heymanns, M.; Bergamini, A.; Ermanni, P. Morphing wing structure with controllable twist based on adaptive bending–twist coupling. Smart Mater. Struct. 2013, 22, 065017. [Google Scholar] [CrossRef]
- Bishay, P.L.; Aguilar, C. Parametric Study of a Composite Skin for a Twist-Morphing Wing. Aerospace 2021, 8, 259. [Google Scholar] [CrossRef]
- Ivanco, T.; Scott, R.; Love, M.; Zink, S.; Weisshaar, T. Validation of the Lockheed Martin Morphing Concept with Wind Tunnel Testing. In Proceedings of the 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Honolulu, HI, USA, 23–26 April 2007. [Google Scholar]
- Ortiz, P.; Alley, N. Spanwise Adaptive Wing-PTERA Flight Test. In Proceedings of the AIAA Aviation Forum, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar]
- Hassanalian, M.; Abdelkefi, A.; Wei, M.; Ziaei-Rad, S. A novel methodology for wing sizing of bio-inspired flapping wing micro air vehicles: Theory and prototype. Acta Mech. 2017, 228, 1097–1113. [Google Scholar] [CrossRef]
- Healy, F.; Cheung, R.; Neofet, T.; Lowenberg, M.; Rezgui, D.; Cooper, J.; Castrichini, A.; Wilson, T. Folding Wingtips for Improved Roll Performance. J. Aircr. 2022, 59, 15–28. [Google Scholar] [CrossRef]
- Xu, H.; Han, J.; Xi, Y.; Chen, G.; Cao, P. Comparative Study of Lifting Surface and CFD Methods in the Simulation of Morphing Process of Folding Wing. Int. J. Aerosp. Eng. 2022, 2022, 2476196. [Google Scholar] [CrossRef]
- Zhou, Z.; Huang, J. Z-folding aircraft electromagnetic scattering analysis based on hybrid grid matrix transformation. Sci. Rep. 2022, 12, 4452. [Google Scholar] [CrossRef] [PubMed]
- Guo, X.; Zhang, Y.; Zhang, W.; Sun, L. Theoretical and experimental investigation on the nonlinear vibration behavior of Z-shaped folded plates with inner resonance. Eng. Struct. 2019, 182, 123–140. [Google Scholar] [CrossRef]
- Zhao, J.; Zeng, L.; Shao, X. A novel prediction method for unsteady aerodynamic force on three-dimensional folding wing aircraft. Aerosp. Sci. Technol. 2023, 137, 108287. [Google Scholar] [CrossRef]
- Gao, L.; Zhu, Y.; Liu, Y.; Zhang, J.; Liu, B.; Zhao, J. Analysis and Control for the Mode Transition of Tandem-Wing Aircraft with Variable Sweep. Aerospace 2022, 9, 463. [Google Scholar] [CrossRef]
- Xu, H.; Han, J.; Yun, H.; Chen, X. Calculation of the Hinge Moments of a Folding Wing Aircraft during the Flight-Folding Process. Int. J. Aerosp. Eng. 2019, 2019, 9362629. [Google Scholar] [CrossRef]
- Changchuan, X.; Zhiying, C.; Chao, A. Aeroelastic Response of a Z-Shaped Folding Wing During the Morphing Process. AIAA J. 2022, 60, 3166–3179. [Google Scholar] [CrossRef]
- Abdessemed, C.; Yao, Y.; Abdessalem, B.; Narayan, P. Morphing airfoils analysis using dynamic meshing. Int. J. Numer. Methods Heat Fluid Flow 2018, 5, 1117–1133. [Google Scholar] [CrossRef]
- Schmitt, V.; Charpin, F. Pressure Distributions on the ONERA M6 Wing at Transonic Mach Numbers. Experimental Data Base for Computer Program Assessment: Report of the Fluid Dynamics Panel Working Group 04; No.: AR-138 Report; NATO Research and Technology Organisation AGARD: Brussels, Belgium, 1979. [Google Scholar]
- Balan, A.; Park, M.A.; Anderson, W.K.; Kamenetskiy, D.S.; Krakos, J.A.; Michal, T.; Alauzet, F. Verification of anisotropic mesh adaptation for turbulent simulations over ONERA M6 wing. AIAA J. 2020, 58, 1550–1565. [Google Scholar] [CrossRef]
- Munshi, A.; Sulaeman, E.; Omar, N.; Ali, M.Y. CFD analysis on the effect of winglet cant angle on aerodynamics of ONERA M6 wing. J. Adv. Res. Fluid Mech. Therm. Sci. 2018, 45, 44–54. [Google Scholar]
- Kuzmin, A. On the lambda-shock formation on ONERA M6 wing. Int. J. Appl. Eng. Res. 2014, 9, 7029–7038. [Google Scholar]
- Chainok, S.; Rungroch, T.; Chairach, P.; Prapamonthon, P.; Yooyen, S.; Yin, B.; Yang, G.; Ju, S. Parametric Study on Wing-Lambda-Shock Formation. In Proceedings of the ASME 2021 Fluids Engineering Division Summer Meeting, Virtual, 10–12 August 2021. [Google Scholar]




| Mach | Reynolds Number | Angle of Attack (deg) | Angle of Sideslip (deg) | Temperature (R) | Pressure (psia) |
|---|---|---|---|---|---|
| 0.8395 | 11.72 × 106 | 3.06 | 0 | 460 | 45.82899 |
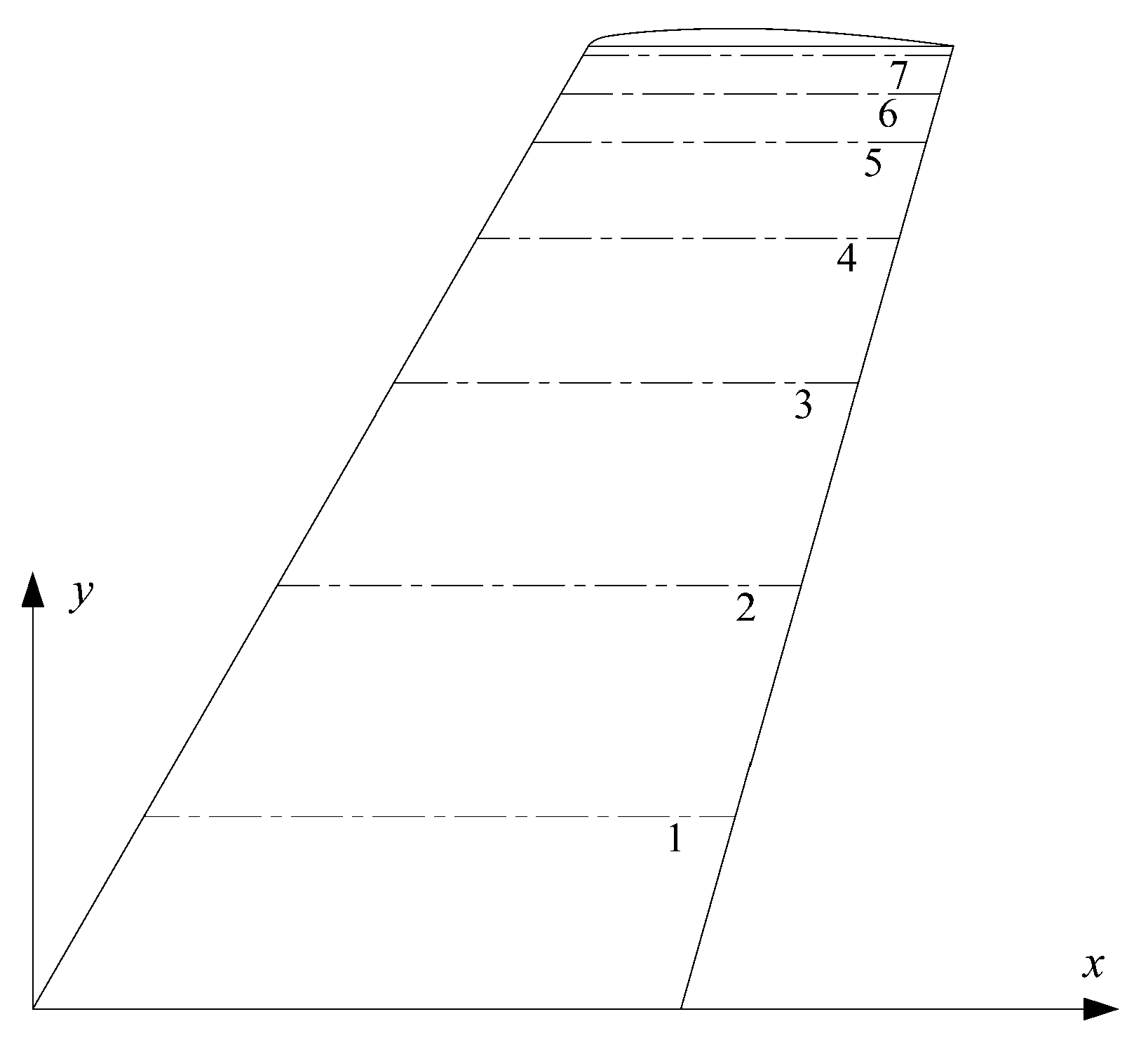
| Section | y/b | y (mm) |
|---|---|---|
| 1 | 0.2 | 239.26 |
| 2 | 0.44 | 526.372 |
| 3 | 0.65 | 777.595 |
| 4 | 0.8 | 957.04 |
| 5 | 0.9 | 1076.67 |
| 6 | 0.95 | 1136.485 |
| 7 | 0.99 | 1184.337 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Guo, X.; Cao, D. Aerodynamic Characteristics of a Z-Shaped Folding Wing. Aerospace 2023, 10, 749. https://doi.org/10.3390/aerospace10090749
Huang Y, Guo X, Cao D. Aerodynamic Characteristics of a Z-Shaped Folding Wing. Aerospace. 2023; 10(9):749. https://doi.org/10.3390/aerospace10090749
Chicago/Turabian StyleHuang, Yongchang, Xiangying Guo, and Dongxing Cao. 2023. "Aerodynamic Characteristics of a Z-Shaped Folding Wing" Aerospace 10, no. 9: 749. https://doi.org/10.3390/aerospace10090749
APA StyleHuang, Y., Guo, X., & Cao, D. (2023). Aerodynamic Characteristics of a Z-Shaped Folding Wing. Aerospace, 10(9), 749. https://doi.org/10.3390/aerospace10090749






