Adaptive IMM-UKF for Airborne Tracking
Abstract
1. Introduction
2. Tracking Logic
- A Cartesian tracker to estimate the horizontal coordinates and velocity of an aircraft relative to the ownship by means of an augmented UKF;
- A range tracker to estimate the horizontal range and the relative horizontal speed by means of a UKF as well;
- A vertical tracker to estimate the vertical position and velocity of an othership aircraft using a Kalman filter.
- Mode 1 or non-maneuvering mode: in uniform linear motion, this mode is modeled with the same equations previously described.
3. Monte Carlo Method
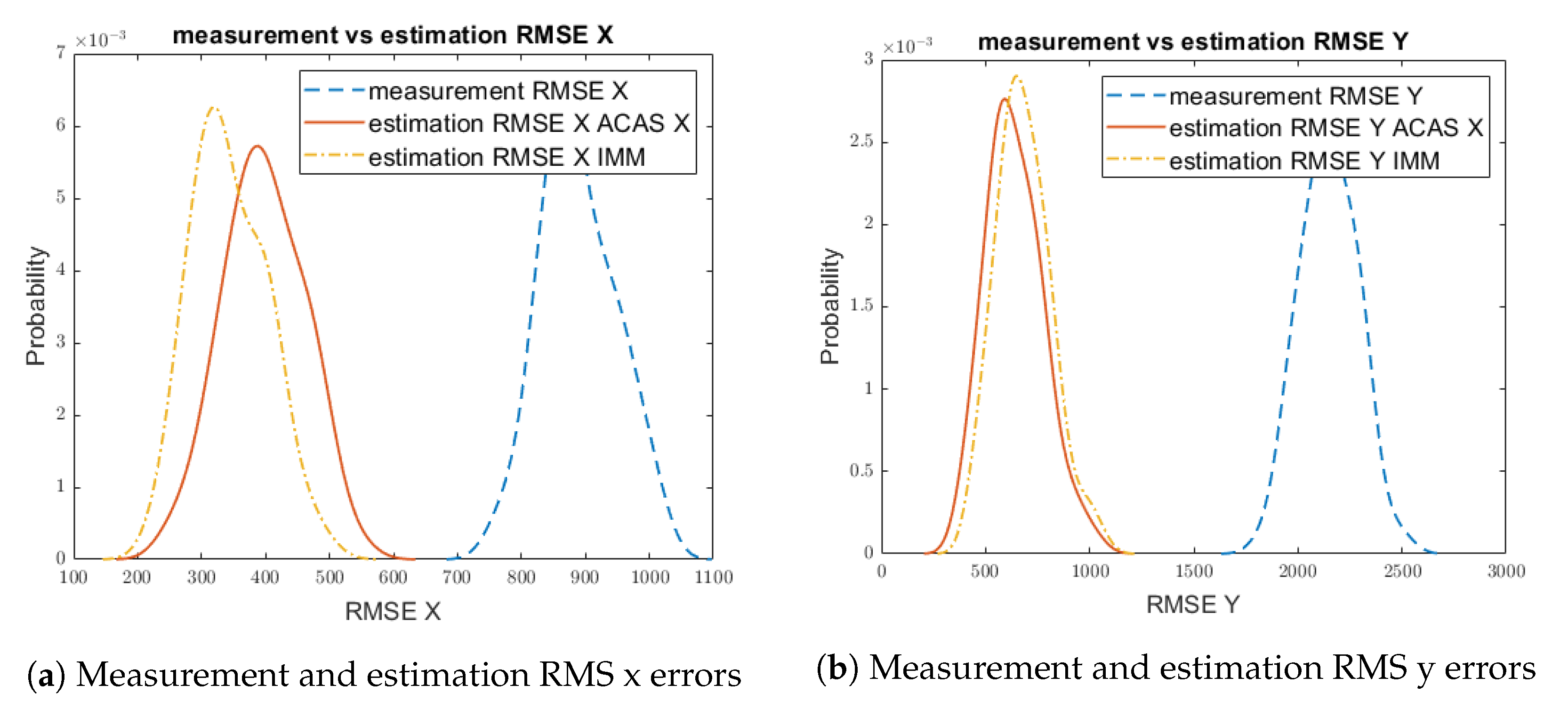
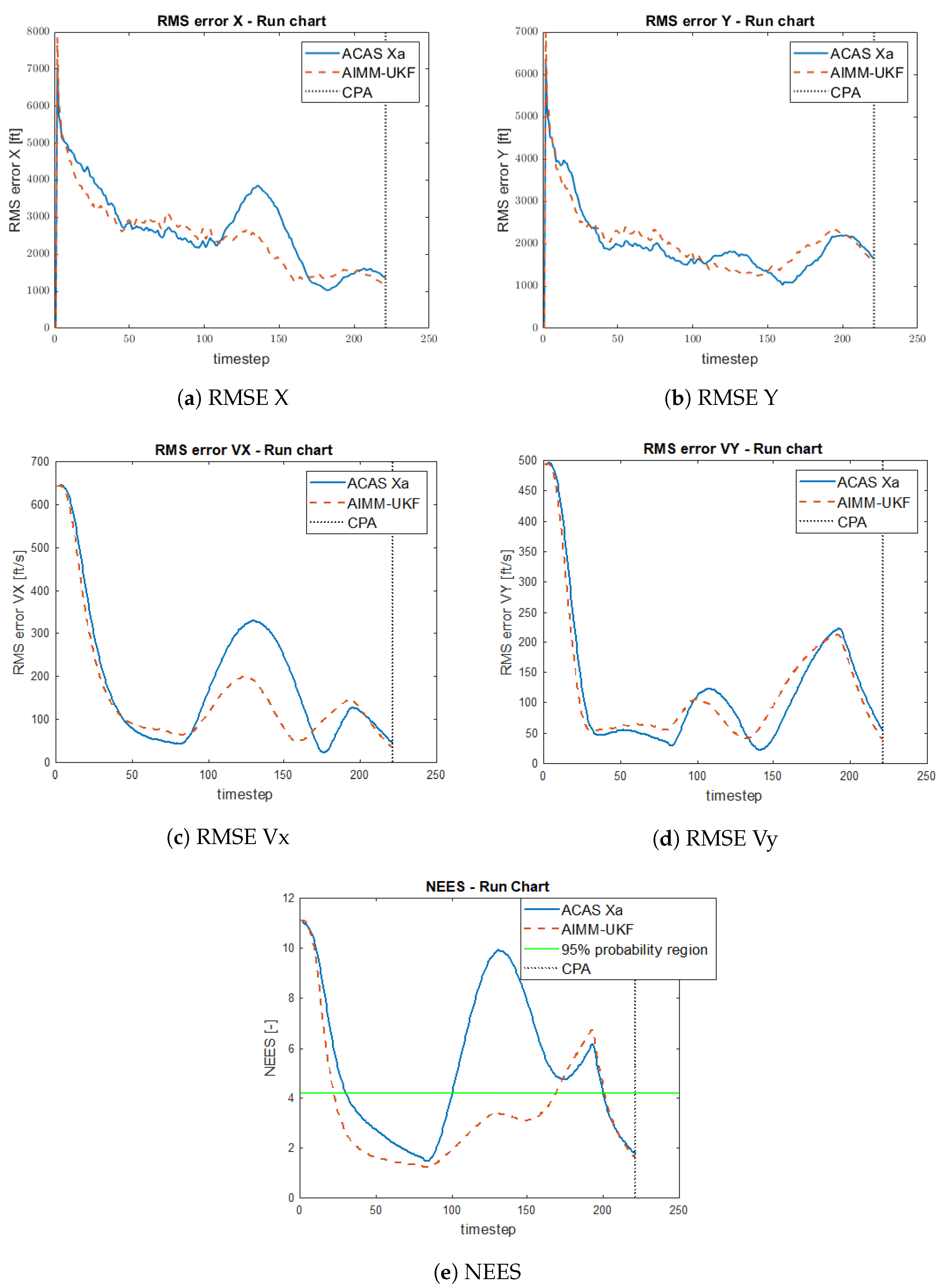
- The RMS errors in each of the state variables (x, y, , ). This is the most popular type of error in tracking for measuring accuracy because it is sensitive to outliers (i.e., it penalizes large estimation errors more heavily due to the squared differences).
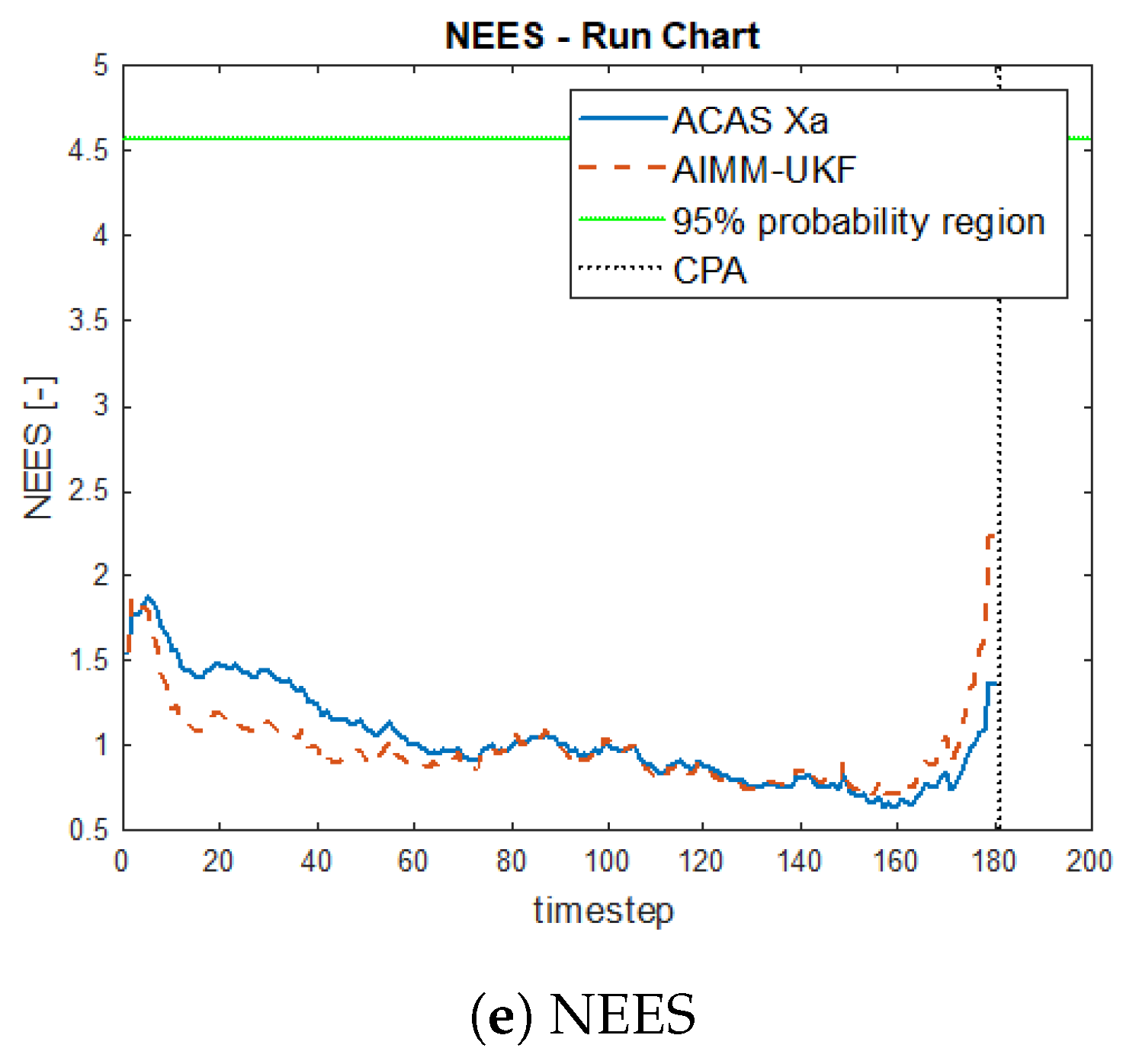
- The normalized estimation error squared (NEES) error and its 95% probability region for checking the consistency of the filter, as stated in [21]. The consistency analysis studies whether the output covariance matrix corresponds or not to the provided state. If the estimation error is much greater than its corresponding covariance, then the filter is overconfident; otherwise, it is underconfident. This is the preferred metric when the ground truth is available due to its easy interpretation and normalization.
- The settling time against velocity changes to measure the tracker’s lag. This is useful for assessing the velocity of adaptation in dynamic systems during transient periods.
- The noise reduction factor provided by the tracker. This is accomplished by assessing the difference between the measurement error (tracker´s input) and the estimation error (tracker´s output), and it shows how much noise is filtered out by the tracking logic.
4. Experiments and Results
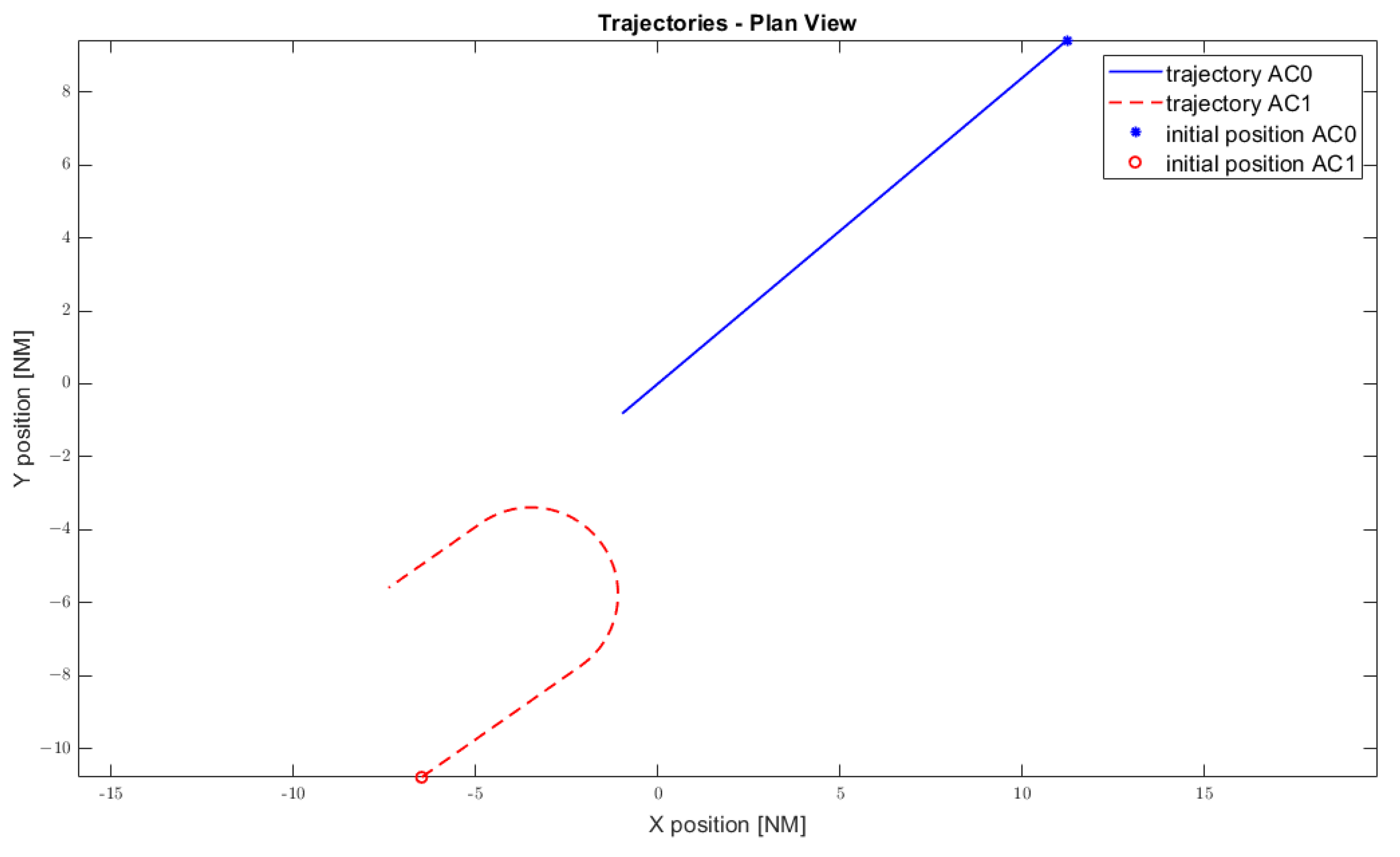
- Uniform linear motion applied for both aircraft;
- The ownship aircraft behaved in uniform linear motion, while the othership aircraft made a turn;
- This encounter simulates a relative trajectory with a step function as the velocity.
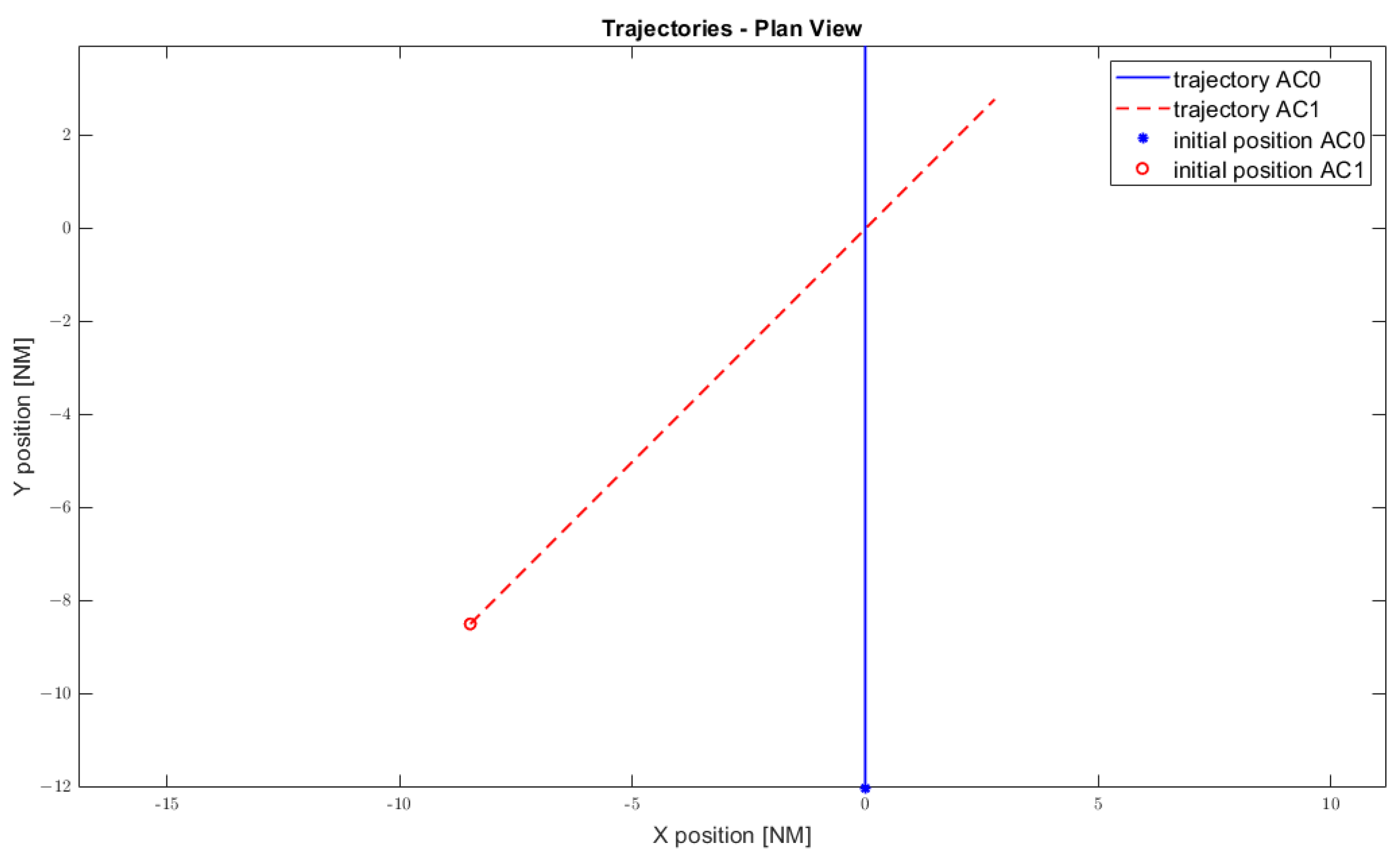
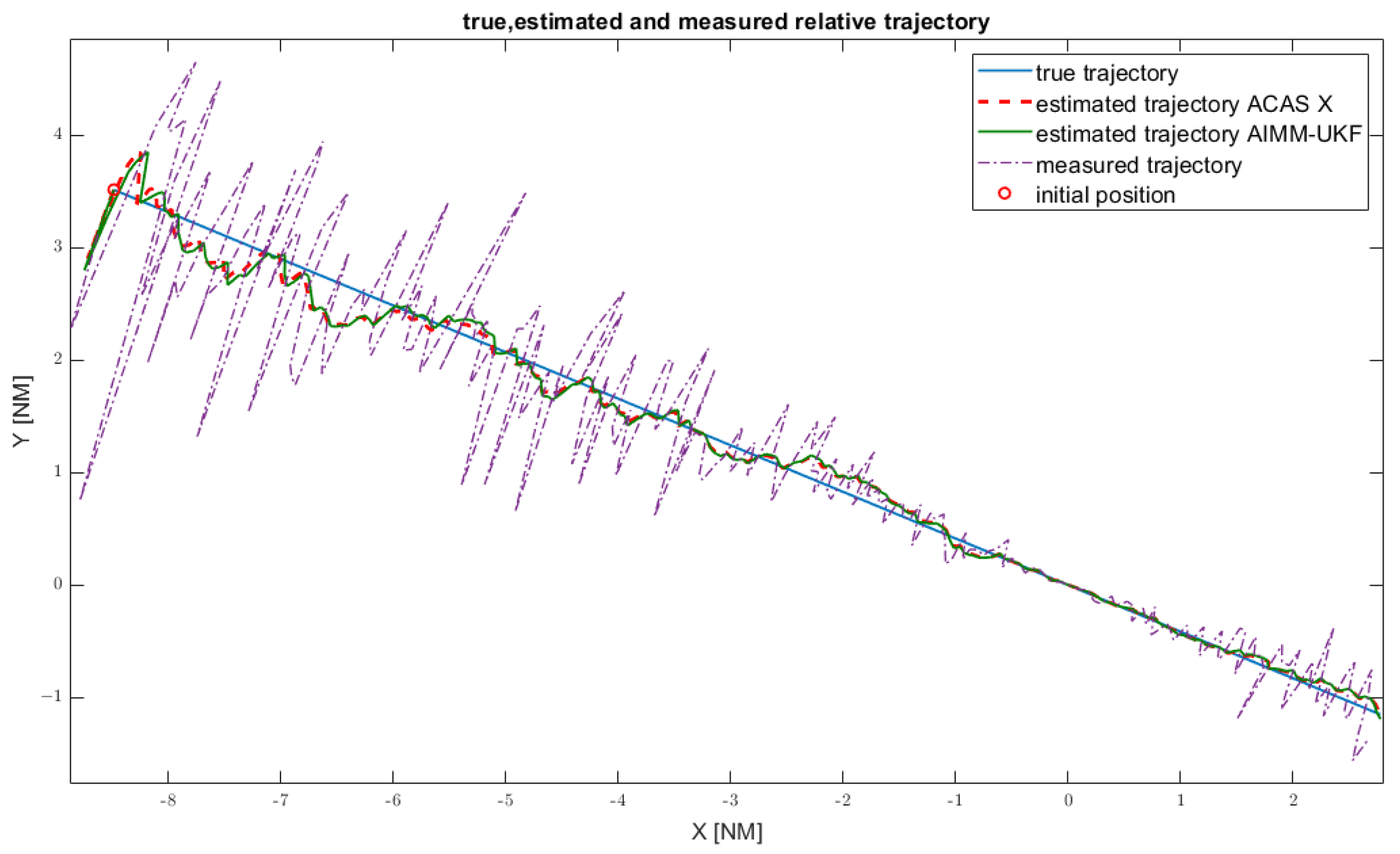
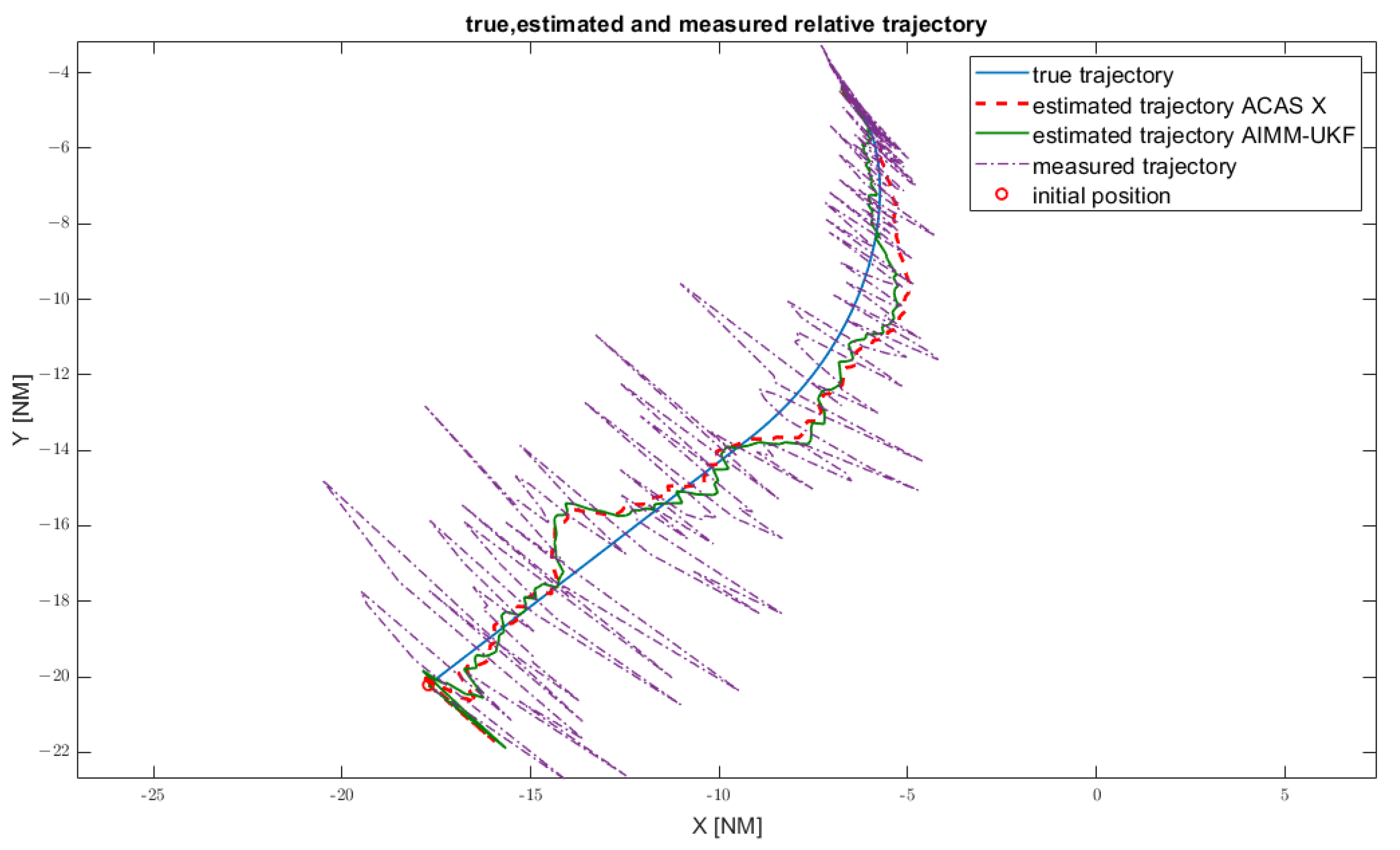
4.1. Encounter 1
4.2. Encounter 2
4.3. Encounter 3
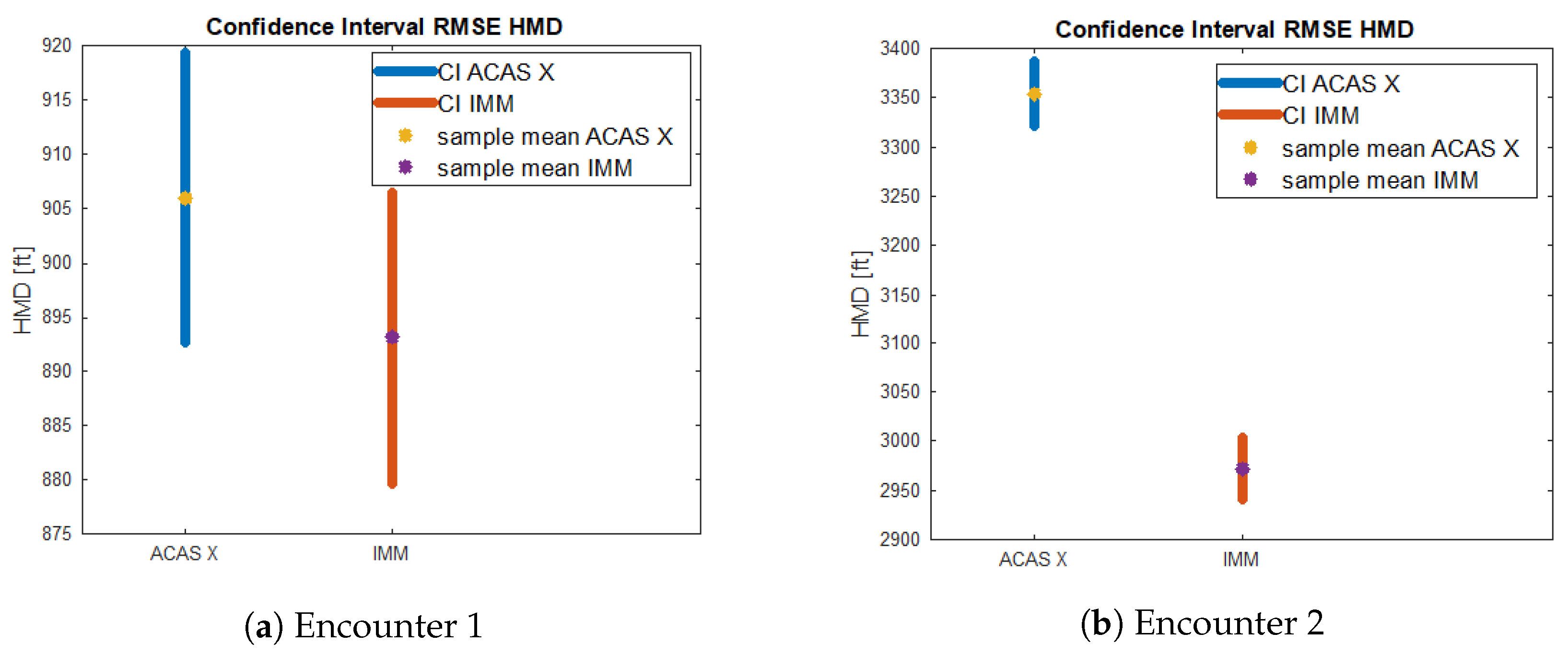
4.4. Estimation Error Analysis
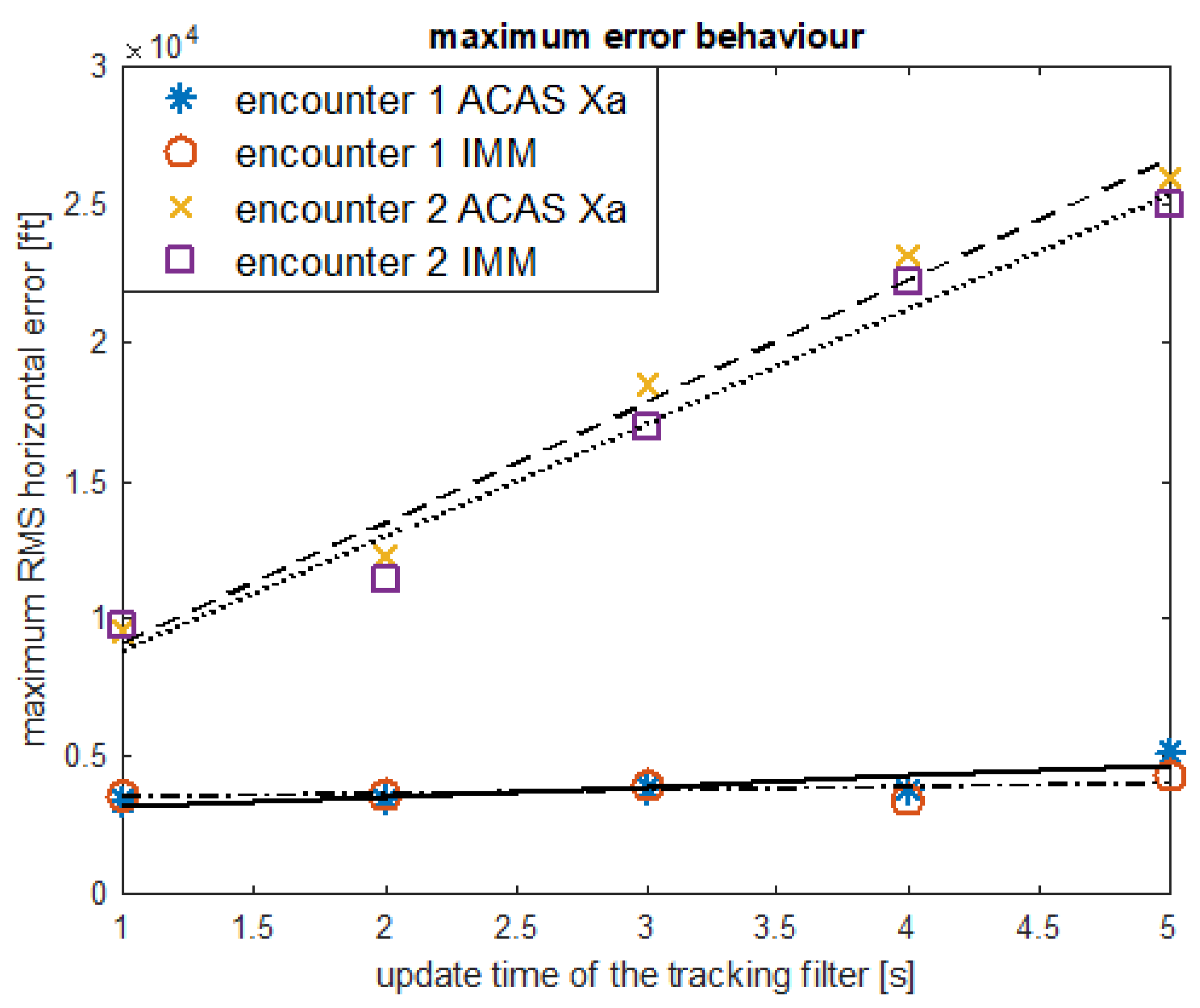
4.5. Robustness of the Prediction
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Li, X.R.; Jilkov, V.P. Survey of Maneuvering Target Tracking. Part I. Dynamic Models. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1333–1364. [Google Scholar] [CrossRef]
- Mahapatra, P.R.; Mehrotra, K. Mixed Coordinate Tracking of Generalized Maneuvering Targets using acceleration and Jerk Models. IEEE Trans. Aerosp. Electron. Syst. 2000, 36, 992–1000. [Google Scholar] [CrossRef]
- Li, X.R.; Jilkov, V.P. A Survey of Maneuvering Target Tracking: Decision-Based Methods. Proc. SPIE Conf. Signal Data Process. Small Targets 2002, 4728, 511–534. [Google Scholar] [CrossRef]
- Li, X.R.; Jilkov, V.P. Survey of Maneuvering Target Tracking. Part V. Multiple-Model Methods. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 1255–1321. [Google Scholar] [CrossRef]
- Li, L.-Q.; Xie, W.-X.; Huang, J.-X.; Huang, J.-J. Multiple Model Rao-Blackwellized Particle Filter for Manoeuvring Target Tracking. Def. Sci. J. 2009, 59, 197–204. [Google Scholar] [CrossRef]
- Foo, P.H.; Ng, G.W. Combining the Interacting Multiple Model Method with Particle Filters for Manoeuvring Target Tracking. IET Radar Sonar Navig. 2011, 5, 234–255. [Google Scholar] [CrossRef]
- Osipov, Y.S.; Maksimov, V.I. Tracking the Solution to a Nonlinear Distributed Differential Equation by Feedback Laws. Numer. Anal. Appl. 2018, 11, 158–169. [Google Scholar] [CrossRef]
- Liu, H.; Wu, W. Interacting Multiple Model (IMM) Fifth-Degree Spherical Simplex-Radial Cubature Kalman Filter for Maneuvering Target Tracking. Sensors 2017, 17, 1374. [Google Scholar] [CrossRef] [PubMed]
- Han, B.; Huang, H.; Lei, L.; Huang, C.; Zhang, Z. An improved IMM algorithm Based on STSRCKF for Maneuvering Target Tracking. IEEE Access 2019, 7, 57795–57804. [Google Scholar] [CrossRef]
- Ghosh, S.; Mukhopadhyay, S. Tracking Reentry Ballistic Targets using Acceleration and Jerk Models. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 666–683. [Google Scholar] [CrossRef]
- Xu, Q.; Li, X.; Chan, C.Y. A Cost-Effective Vehicle Localization Solution Using and Interacting Multiple Model Unscented Kalman Filters (IMM-UKF) Algorithm and Grey Neural Network. Sensors 2017, 17, 1431. [Google Scholar] [CrossRef]
- Zhiwen, H.; Fanliang, B. A small UAV tracking algorithm based on AIMM-UKF. Aircr. Eng. Aerosp. Technol. 2021, 93, 579–592. [Google Scholar]
- Ding, Z.; Liu, Y.; Liu, J.; Yu, K.; You, Y.; Jing, P.; He, Y. Adaptive Interacting Multiple Model Algorithm Based on Information-Weighted Consensus for Maneuvering Target Tracking. Sensors 2018, 18, 2012. [Google Scholar] [CrossRef] [PubMed]
- Guo, Q.; Teng, L. Maneuvering Target Tracking with Multi-Model Based on the Adaptive Structure. IEEJ Trans. Electr. Electron. Eng. 2022, 17, 865–871. [Google Scholar] [CrossRef]
- Puranik, S.P.; Tugnait, J.K. On Adaptive sampling for Multisensor Tracking of a Maneuvering Target using IMM/PDA filtering. In Proceedings of the 2005 American Control Conference, Portland, OR, USA, 8–10 June 2005. [Google Scholar] [CrossRef]
- Kim, W.C.; Musicki, D.; Song, T.L. Adaptive Mode Transition Matrix for Variable Sampling Time, In Proceedings of the 17th International Conference on Information Fusion, Salamanca, Spain, 7–10 July 2014; IEEE: Piscataway, NJ, USA, 2014.
- Revach, G.; Shlezinger, N.; Ni, X.; Lopez, A.; van Sloun, R.J.G.; Eldar, Y.C. KalmanNet: Neural Network Aided Kalman Filtering for Partially Known Dynamics. IEEE Trans. Signal Process. 2022, 70, 1532–1547. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Z.; Xu, M. DeepMTT: A Deep Learning Maneuvering Target Tracking Algorithm Based on Bidirectional LSTM network. Inf. Fusion 2020, 53, 289–304. [Google Scholar] [CrossRef]
- Zao, G.; Wang, Z.; Huang, Y.; Zhang, H.; Ma, X. Transformer-Based Maneuvering Target Tracking. Sensors 2022, 22, 8482. [Google Scholar] [CrossRef]
- Tian, W.; Fang, L.; Li, W.; Ni, N.; Wang, R.; Hu, C.; Liu, H.; Luo, W. Deep-Learning-Based Multiple Model Tracking Method for Targets with Complex Maneuvering Motion. Remote Sens. 2022, 14, 3276. [Google Scholar] [CrossRef]
- Bar Shalom, Y.; Li, X.R.; Kirubarajan, T. Estimation with Applications to Tracking and Navigation; Wiley: Hoboken, NJ, USA, 2001. [Google Scholar]
- Schubert, R.; Richter, E.; Wanielik, G. Comparison and Evaluation of Advanced Motion Models for Vehicle Tracking. In Proceedings of the 11th International Conference on Information Fusion IEEE, Cologne, Germany, 30 June–3 July 2008; pp. 1–6. [Google Scholar]
- Li, L.Q.; Xie, W.X. Bearings-only maneuvering target tracking based on fuzzy clustering in a cluttered environment. Int. J. Electron. Commun. 2014, 68, 130–137. [Google Scholar]
- Farina, A.; Ristic, B.; Benvenutti, D. Tracking a Ballistic Target: Comparison of several non linear filters. Trans. Aerosp. Electron. Syst. 2002, 38, 854–867. [Google Scholar] [CrossRef]
- RTCA. Minimum Operational Performance Standards for Airborne Collision Avoidance System X (ACAS X); RTCA: Washington, CA, USA, 2019. [Google Scholar]
- EUROCAE. MOPS for ACAS Xa with ACAS Xo Functionality, Volume II; EUROCAE: Saint-Denis, France, 2018. [Google Scholar]
- Blom, H.A.P.; Bar-Shalom, Y. The Interacting Multiple Model Algorithm For Systems with Markovian Switching Coefficents. IEEE Trans. Autom. Control 1988, 33, 780–783. [Google Scholar] [CrossRef]
- Blom, H.A.P. An Efficient Decision-Making-Free Filter For Processes With Abrupt Changes. IFAC Proc. Vol. 1985, 18, 631–636. [Google Scholar] [CrossRef]
- Blom, H.A.P. Overlooked Potential of Systems with Markovian Coefficients. In Proceedings of the IEEE Conference on Decision and Control, Athens, Greece, 10–12 December 1986; pp. 1758–1764. [Google Scholar]
- Bar-Shalom, Y.; Challa, S.; Blom, H.A.P. IMM Estimator versus Optimal Estimator for Hybrid Systems. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 986–991. [Google Scholar] [CrossRef]
- Blackman, S.S.; Popoli, R.F. Design and Analysis of Modern Tracking Systems; Artech House: Norwood, MA, USA, 1999; p. 1232. [Google Scholar]
- Stroeve, S.; Blom, H.; Hernandez Medel, C.; Garcia Daroca, C.; Arroyo Cebeira, A.; Drozdowski, S. Development of a Collision Avoidance Validation and Evaluation Tool (CAVEAT): Adressing the intrinsic uncertainty in TCAS II and ACAS X. In Proceedings of the 13th USA/Europe Air Traffic Management Research and Development Seminar, Vienna, Austria, 17–21 June 2019. [Google Scholar]
- Stroeve, S.; Blom, H.A.; Canizares, C.V.; Ba, G.J. CAVEAT Phase 2 Models and Algorithms, Development of a Collision Avoidance Validation and Evaluation Tool, Report NLR-CR-2018-429; NLR: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Stroeve, S.; Blom, H.A.; Hernandez Medel, C.; Garcia Daroca, C.; Arroyo Cebeira, A.; Drozdowski, S. Modeling and Simulation of Intrinsic Uncertainties in Validation of Collision Avoidance Systems. J. Air Transp. AIAA 2020, 28, 173–183. [Google Scholar] [CrossRef]
- Chryssanthacopolos, P.; Kochenderfer, M.J. Accounting for State Uncertainty in Collision Avoidance. J. Guid. Control Dyn. 2011, 34, 951–960. [Google Scholar] [CrossRef]
- Panken, A.D.; Kochenderfer, M.J. Error Model Estimation for Airborne Beacon-based. IET Radar Sonar Navig. 2014, 8, 667–675. [Google Scholar] [CrossRef]
- Hayya, J.; Armstrong, D.; Gressis, N. A Note on the Ratio of Two Normally Distributed Variables. Manag. Sci. 1975, 56, 635–639. [Google Scholar] [CrossRef]
- Eurocontrol. SESAR PJ.13-Solution 111 Description of Collision Avoidance Fast-Time Evaluator (CAFE) Revised Encounter Model for Europe (CREME) (Report No. D2.1.090). Available online: https://skybrary.aero/sites/default/files/bookshelf/33312.pdf (accessed on 20 June 2023).




| Variable | Mean | Median | Std Dev | 75th Percentile | 25th Percentile |
|---|---|---|---|---|---|
| ACAS Xa-RMSE x (ft) | 426 | 281.3 | 457 | 573.7 | 121 |
| ACAS Xa-RMSE y (ft) | 724.1 | 464.6 | 853.4 | 973.7 | 180.8 |
| ACAS Xa-RMSE (ft/s) | 33.17 | 13.1 | 61.3 | 25.8 | 5.9 |
| ACAS Xa-RMSE (ft/s) | 35.7 | 25 | 34.4 | 47.3 | 11.4 |
| IMM-RMSE x (ft) | 390.9 | 265.5 | 417.3 | 528 | 115.9 |
| IMM-RMSE y (ft) | 749.4 | 490.2 | 862.5 | 1021.4 | 189.9 |
| IMM-RMSE (ft/s) | 33.5 | 16 | 56.9 | 30.2 | 14.1 |
| IMM-RMSE (ft/s) | 41.5 | 31.2 | 36.5 | 57.8 | 14.2 |
| Measured RMSE x (ft) | 906.2 | 904.2 | 63.6 | 949 | 860.1 |
| Measured RMSE y (ft) | 2145.5 | 2137.8 | 143 | 2241.7 | 2051 |
| Variable | Mean | Median | Std Dev | 75th Percentile | 25th Percentile |
|---|---|---|---|---|---|
| ACAS Xa-RMSE x (ft) | 2515 | 2001 | 2195 | 3407 | 1017 |
| ACAS Xa-RMSE y (ft) | 1783 | 1470 | 1655 | 2362 | 736 |
| ACAS Xa-RMSE (ft/s) | 187.6 | 135.8 | 159.2 | 279.6 | 66.3 |
| ACAS Xa-RMSE (ft/s) | 121.5 | 92.9 | 112 | 157 | 44 |
| IMM-RMSE x (ft) | 2182 | 1700 | 2049 | 2817 | 866.8 |
| IMM-RMSE y (ft) | 1698 | 1390 | 1600 | 2277 | 677.7 |
| IMM-RMSE (ft/s) | 153.7 | 113.5 | 146.4 | 186.1 | 58.7 |
| IMM-RMSE (ft/s) | 122.2 | 83.4 | 107.6 | 166 | 46 |
| Measured RMSE x (ft) | 5628 | 5618 | 321 | 5837 | 5415 |
| Measured RMSE y (ft) | 4568 | 4561 | 262 | 4741 | 4380 |
| Encounter | Hypothesis Test | p-Value | Outcome |
|---|---|---|---|
| Encounter 1 | Two-sample t-test | 0.18 | Not rejected |
| Encounter 2 | Two-sample t-test | 6.8 × 10−60 | Rejected |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arroyo Cebeira, A.; Asensio Vicente, M. Adaptive IMM-UKF for Airborne Tracking. Aerospace 2023, 10, 698. https://doi.org/10.3390/aerospace10080698
Arroyo Cebeira A, Asensio Vicente M. Adaptive IMM-UKF for Airborne Tracking. Aerospace. 2023; 10(8):698. https://doi.org/10.3390/aerospace10080698
Chicago/Turabian StyleArroyo Cebeira, Alvaro, and Mariano Asensio Vicente. 2023. "Adaptive IMM-UKF for Airborne Tracking" Aerospace 10, no. 8: 698. https://doi.org/10.3390/aerospace10080698
APA StyleArroyo Cebeira, A., & Asensio Vicente, M. (2023). Adaptive IMM-UKF for Airborne Tracking. Aerospace, 10(8), 698. https://doi.org/10.3390/aerospace10080698






