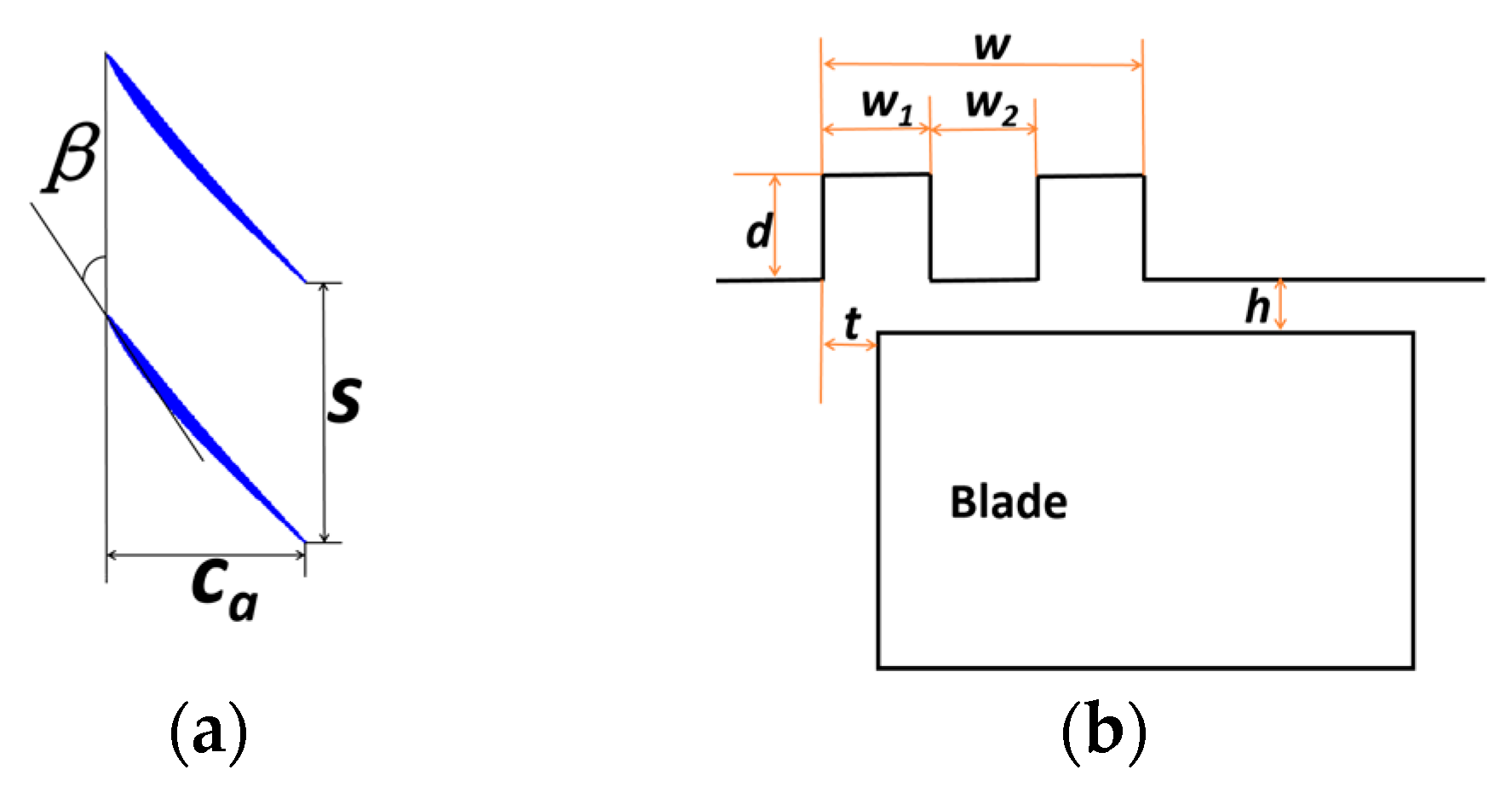
3.2. Casing Treatment
This article focuses on the tip clearance leakage and how the casing treatment improves flow at the tip of the blade. Therefore, in order to examine how to improve the tip clearance leakage, the total pressure loss coefficient is calculated at 10% of the span height of the blade tip, as shown in
Figure 10. Five groups of modified cascades with maximum and minimum total pressure losses were selected for comparative analysis. It was determined how the casing treatment’s flow mechanism improved the aerodynamic performance of the cascade.
Table 5 focuses on the leakage per unit tip clearance height. Although models 51 and 92 increase the total pressure loss, they decrease the leakage per unit tip clearance height. In contrast, models 14 and 23 decrease the total pressure loss but increase the leakage per unit tip clearance height, which shows that the casing treatment has the effect of deterioration and gain on the tip leakage simultaneously. In order to explore the effect and mechanism of improving the tip clearance leakage, we selected four models for detailed analysis. The specific parameters and geometric shapes of the models are shown in
Table 6 and
Figure 11. The tip clearance height and groove depth of models 14 and 23 are small, and the tip clearance height and groove depth of models 51 and 92 are large.
Figure 12 shows the total pressure loss and Mach number distribution of the outlet section. In the range of 94% of the span height of the tip, the total pressure loss of model 14 is lower than that of the smooth casing. Although the total pressure loss of model 23 at 97% of the span height of the tip is higher than that of the smooth casing, the total pressure loss at 88–97% of the span height is lower. The total pressure loss of models 51 and 92 at 92% of the span height of the blade tip is higher than that of the smooth casing. The Mach number of model 14 at 99% of the span height of the blade tip is lower than that of the smooth casing, while the Mach number of the 86–99% of the span height is higher than that of the smooth casing. The Mach number distribution of model 23 is the same as that of model 14, but its turning point is at 97% of the span height, indicating that the blockage at the tip clearance is slightly greater than that of the smooth casing but below the clearance, it is more clogged than that of the smooth casing. The Mach number of models 51 and 92 with large clearance height and groove depth is much lower than that of the smooth casing, indicating that the blockage is considerable and that the total pressure loss is also high.
In order to analyze the total pressure loss in the passage,
Figure 13 shows the total pressure loss distribution at 10% of the span height of the tip along the flow direction. The horizontal coordinate is normalized from the leading edge of the blade to the outlet. The total pressure loss gradually increases along the flow direction, and the increase is greater at the position of the cascade passage (0–0.45x). The increase in total pressure loss of models 14 and 23 with small clearance height and groove depth is lower than that of the smooth casing, so the total pressure loss in the downstream section of the passage is lower than that of the smooth casing; The total pressure loss and increase level of models 51 and 92 with large clearance height and groove depth are significantly greater than those of the smooth casing from the inlet section to the outlet section of the cascade passage.
The total pressure loss in the blade tip passage is mainly caused by the blockage of the leakage vortex, so the aerodynamic blockage coefficient is defined to analyze the blockage in the passage:
where
ρe and
Ve are the density and velocity of the fluid in the mainstream region,
ρ and
V are the density and velocity of the fluid in the blockage region,
A is the section area,
is the mass flow.
The section position is shown in
Figure 14, and the horizontal coordinate is normalized by the length of the section passage.
Figure 14 shows that the airflow stagnates at the leading edge of the blade, resulting in an increase in the blockage coefficient at the leading edge. At the inlet of the blade passage, the blockage coefficient first decreases, and then, due to the development of the leakage vortex in the passage, the aerodynamic blockage coefficient significantly increases. When the airflow flows out of the blade passage, the actual circulation area increases due to the lack of blade limit; the blockage coefficient decreases and then begins to increase due to the influence of the wake in the wake region.
The blockage of models 14 and 23 is similar to that of the smooth casing. At the leading edge of the cascade passage, the leakage increases due to the grooves, so the aerodynamic blockage is high. Due to the influence of the leakage vortex in the passage downstream of the cascade passage, the blockage coefficient tends to increase slightly; the blockage coefficient is smaller than that of the smooth casing. The leakage and the blockage of models 51 and 92 decrease near the leading edge. However, downstream of the blade passage, the blockage increases sharply and continues to the trailing edge, becoming greater than the smooth casing downstream the trailing edge of the blade.
The design schemes with small clearance height and groove depth have a lower aerodynamic blockage, resulting in smaller total pressure loss and better flow field. However, the design schemes with large clearance height and groove depth are the opposite.
By comparing the Mach number and the flow angle, an analysis of the flow field at 10% of the span height of the tip is carried out, as shown in
Table 7. The inlet Mach number and outlet Mach number of models 51 and 92 with large clearance height and groove depth both decrease, indicating that the passage blockage of these two models is greater than that of the smooth casing. The inlet flow angle of the modifications is the same as that of the smooth casing. The outlet flow angle and the backward angle of models 14 and 23, with small clearance height and groove depth, are smaller than that of the smooth casing, and the turning angle is larger. The outlet flow angle of models 51 and 92 is larger than that of the smooth casing. A small turning angle indicates that the passage is seriously blocked and the blade turning ability is weakened. The flow angle at the leading edge of the blade and the smooth casing are basically the same as those of models 14 and 23. The increase in the flow angles of the leading edges of models 51 and 92 indicates a serious blockage in the passage, resulting in poor air intake at the leading edge and a degree of lateral airflow.
Figure 15 shows the leakage streamline and vorticity distribution. The leading edge leakage flow interacts with the mainstream, and a leakage vortex is formed at the leading edge of the blade, developing downstream along the blade height direction and gradually moving away from the blade. The vortex core cannot be confined, and the vortex structure gradually expands. The vortex structure eventually grows as the vortex core cannot be confined. The vorticity of models 14 and 23 in region A is closer to the shroud and concentrated in the tip region than that of the smooth casing, and the leakage vortex area in region B is smaller than that of the smooth casing. The vortex core is more concentrated than that of the smooth casing, minimizing the region where the leaking vortex is obstructed in the span direction and lowering the total pressure loss. In models 51 and 92, because part of the airflow is sucked into the grooves, the development of the leakage vortex is restricted. At the leading edge C, the airflow is close to the suction surface of the blade and develops downward along the blade without spreading to the passage. Behind the grooves, due to the interaction between the grooves and the shroud, the leakage vortex is broken. The broken low-energy fluid gathers in the passage, resulting in a large vortex and passage blockage. The conclusions of aerodynamic blockage are consistent (as shown in
Figure 16), resulting in a decrease in flow rate, which intensifies the total pressure loss.
The design schemes with small clearance height and groove depth keep the leakage vortex core in a concentrated form. However, the leakage vortex is broken in the design schemes with large clearance height and groove depth. In order to better explore the effect of casing treatment on the leakage at the tip clearance, a flow analysis was conducted.
Figure 16, normalized according to the length of the blade, shows the ratio of leakage at different positions to the total leakage. From the leading edge to the trailing edge of the smooth casing and the casing treatment, the tip clearance leakage first increases and then decreases. The leakage of models 14 and 23 occurs mainly in the front half of the cascade passage, and the overall leakage is less than that of the smooth casing. The leakage at the tip clearance of models 51 and 92 is mainly concentrated in the middle of the blade. The mass flow at the leading edge is less than that of the smooth casing, and at the rear of the middle, the leakage increases significantly, reaching a peak the leakage near the trailing edge is greater than that of the smooth casing. The analysis shows that the passage area of the casing treatment for the grooves increases, so the leakage increases and reaches a peak here.
Figure 17 compares the velocity vectors at the tip clearance. There is a strong secondary flow in the tip clearance of the smooth casing. The smooth casing’s tip clearance has a high secondary flow. To some extent, lateral secondary flow occurs from the leading edge and spirals upward, eventually weakening along the blades. The flow of the casing treatment is more complicated. Because of the grooves, the airflow curves in the direction of the grooves, preventing the development of lateral secondary flow. This curling in a groove is restricted to the groove’s shoulder, and the process is repeated until there is no groove, and the curl gradually begins to weaken. Due to the interaction between the lateral secondary flow and the curled fluid in the suction grooves, their development of them is restricted, and the leakage at the tip clearance is weakened. The transverse velocity vector of models 14 and 23 at the leading edge is slightly weakened, and the transverse flow at the rear of the grooves also decreases. Models 51 and 92 clearly suppress the lateral velocity vector at the leading edge and weaken the lateral secondary flow and the leakage flow here. The airflow curls into the grooves, but the lateral velocity vector at the trailing edge increases, resulting in increased leakage, increasing the blockage in the passage.
The tip clearance leakage movement is mainly driven by the pressure difference between the suction surface and the pressure surface. The leakage flow interacts with the mainstream to generate a leakage vortex, which causes passage blockage. Therefore, the static pressure coefficient distribution at 98% of the span height of the blade is analyzed.
Define the pressure coefficient:
where
p is the pressure and
p* is the total pressure.
Figure 18 shows that near the leading edge, the pressure of the casing treatment varies considerably, but the overall pressure has been improved. Models 14 and 23 are similar to the smooth casing. The pressure difference at the leading edge increases slightly, the distribution at the trailing edge remains roughly constant, and the pressure of the casing treatment on the suction surface decreases. The pressure on the pressure surface of models 51 and 92 decreases, and the pressure difference significantly decreases, which reduces the driving force of the tip clearance leakage—this is the reason why the two types of modifications have reduced leakage at the leading edge. The area of the low Mach number decreases, but the pressure difference between the two modifications at the trailing edge increase—this corresponds to an increase in the lateral secondary flow at the trailing edge and an increase in leakage.
The design schemes with large clearance height and groove depth effectively decrease the pressure difference at the leading edge of the cascade and weaken the leakage at the tip clearance. The design schemes with small clearance height and groove depth are similar to the smooth casing.