Quadrotor Robust Fractional-Order Sliding Mode Control in Unmanned Aerial Vehicles for Eliminating External Disturbances
Abstract
1. Introduction
2. Literature Review
3. Dynamics of Slung Load
Load Angles
4. Load Coupling Dynamics
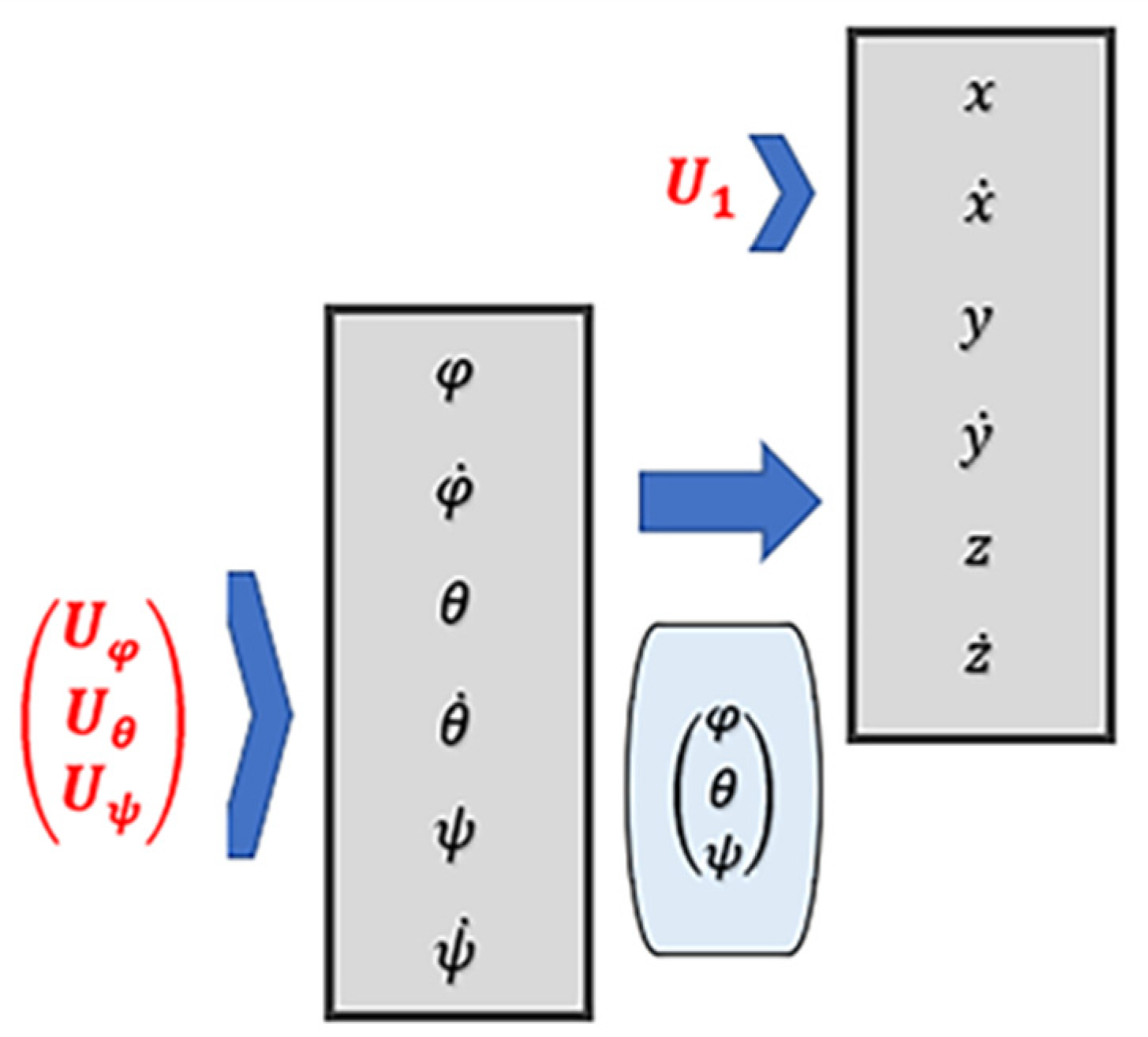
5. Control Design
6. Designing Robust FOSMC in the Presence of External Disturbances
6.1. Altitude Control Design
Stability Analysis
6.2. Attitude Control Design
Stability Analysis
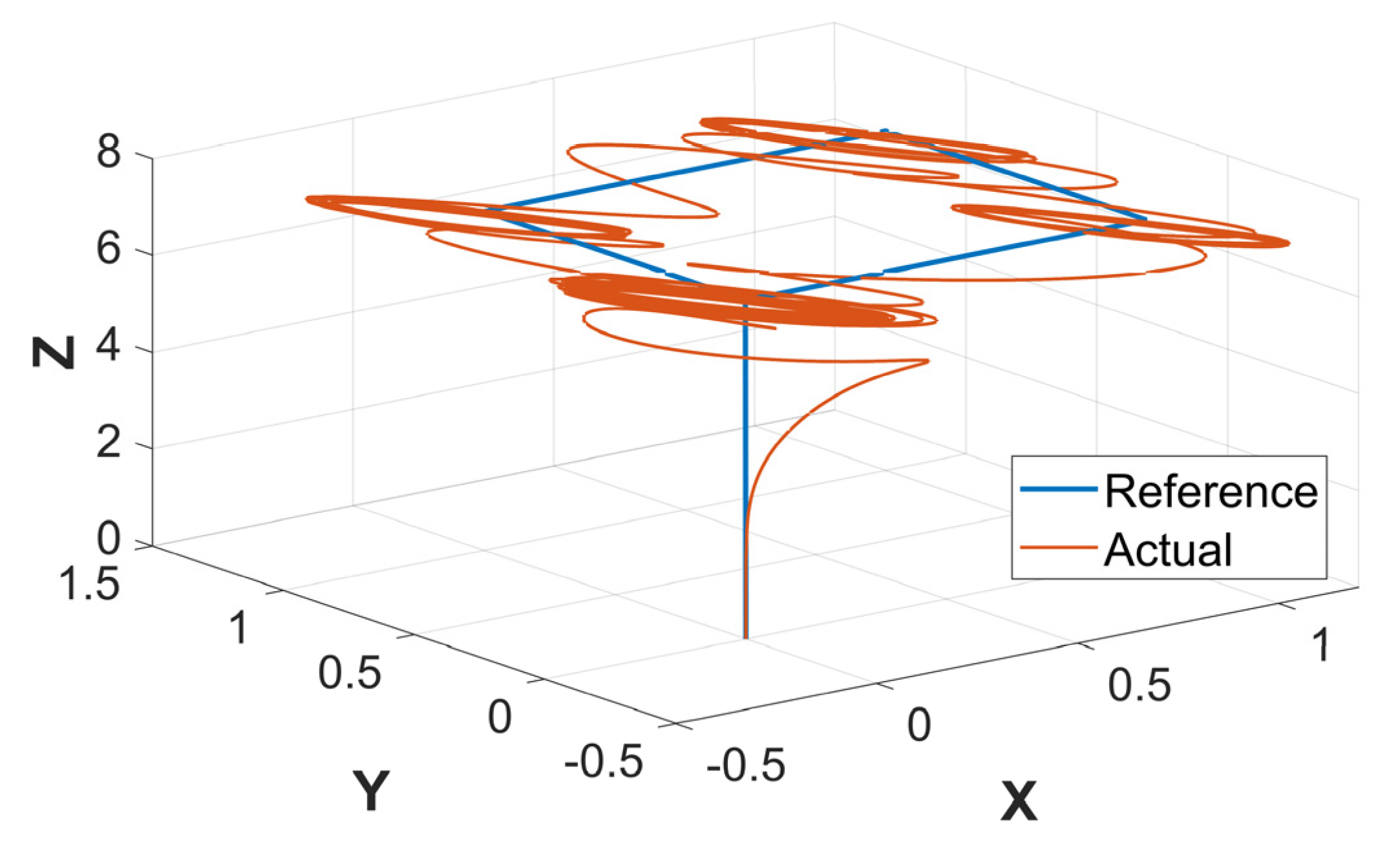
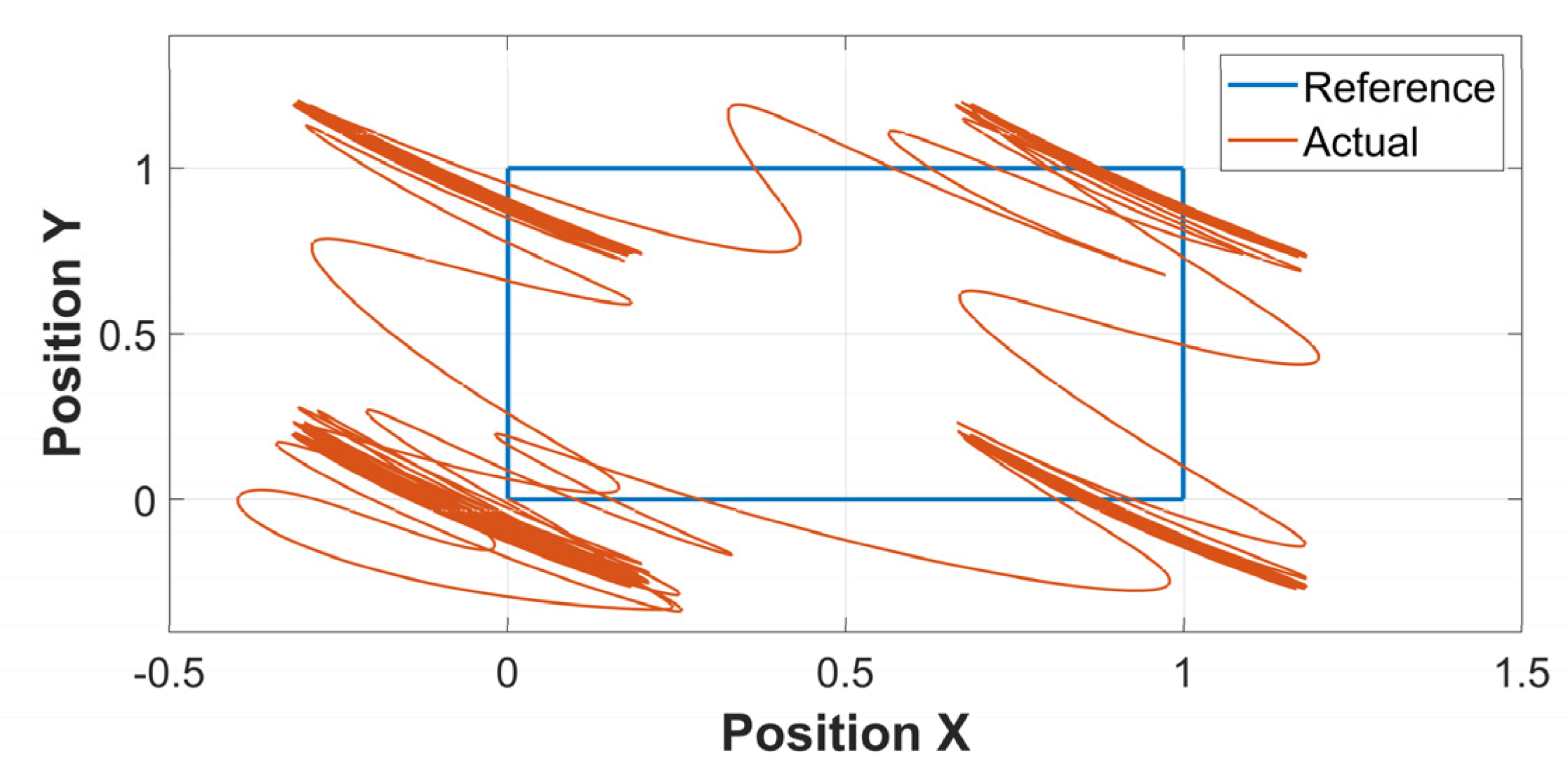
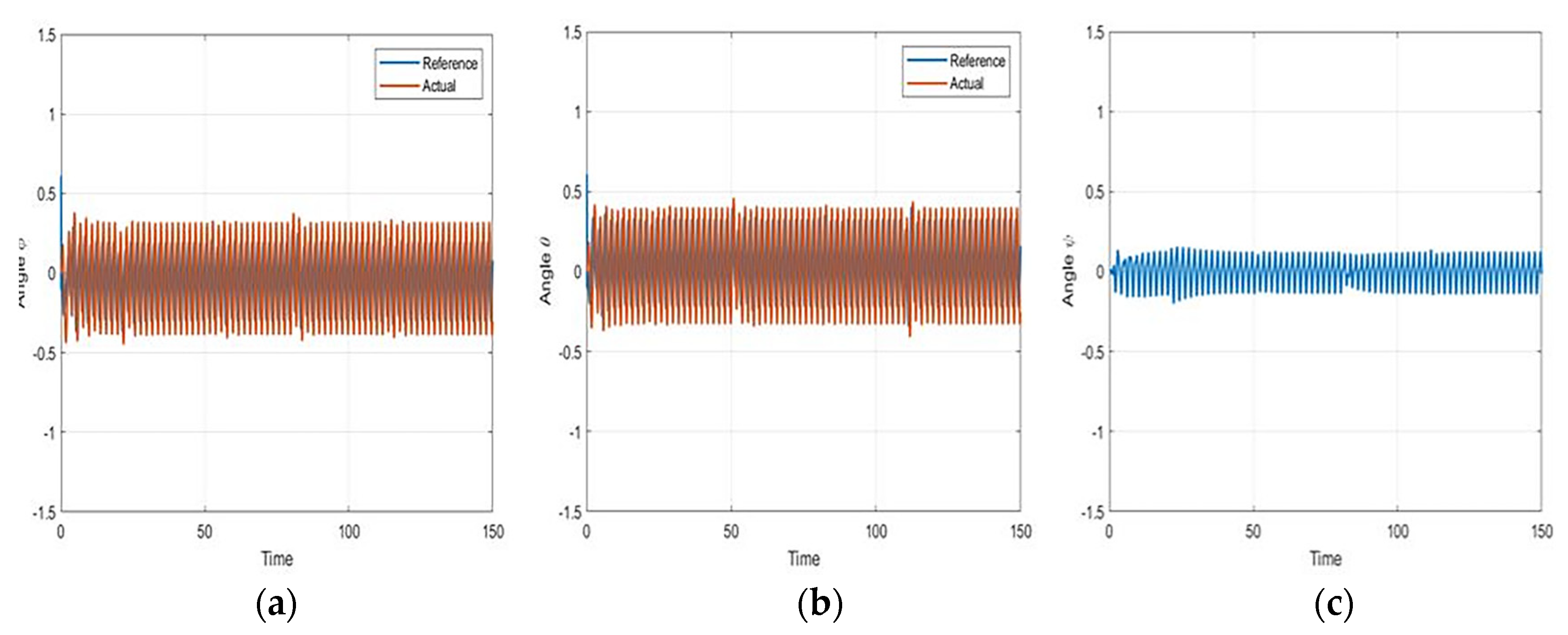
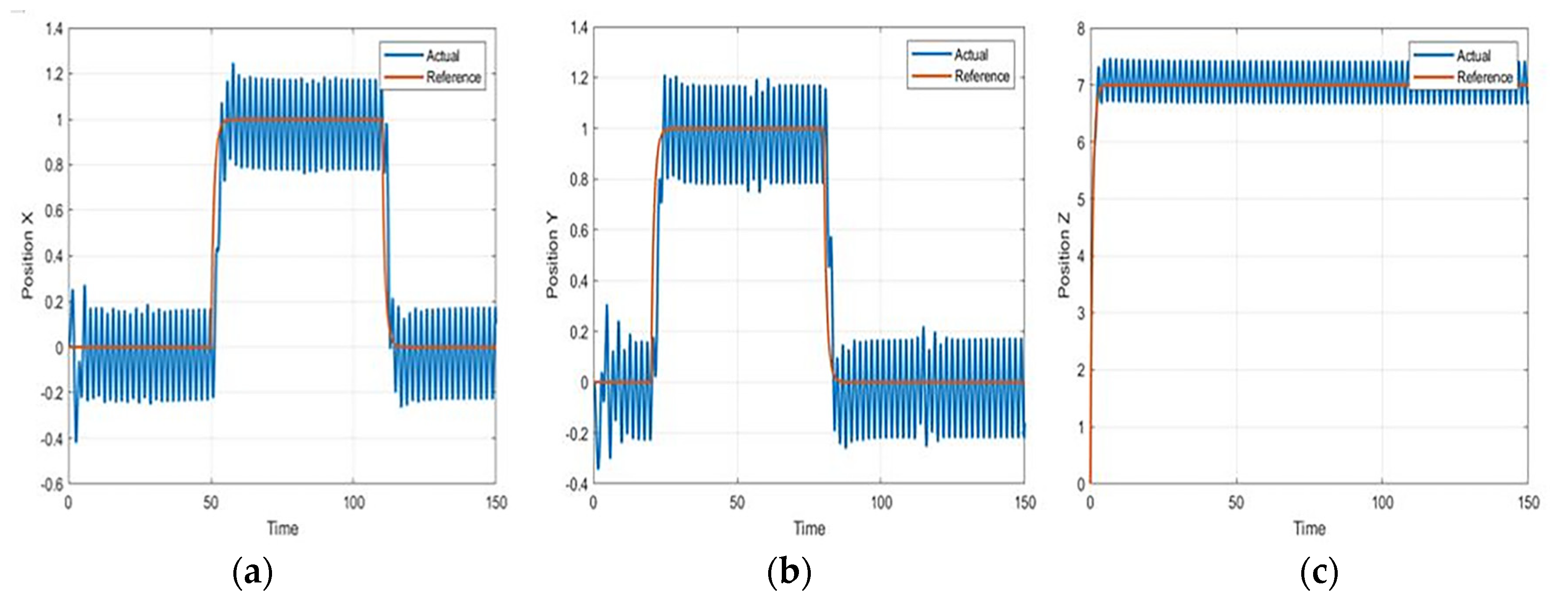
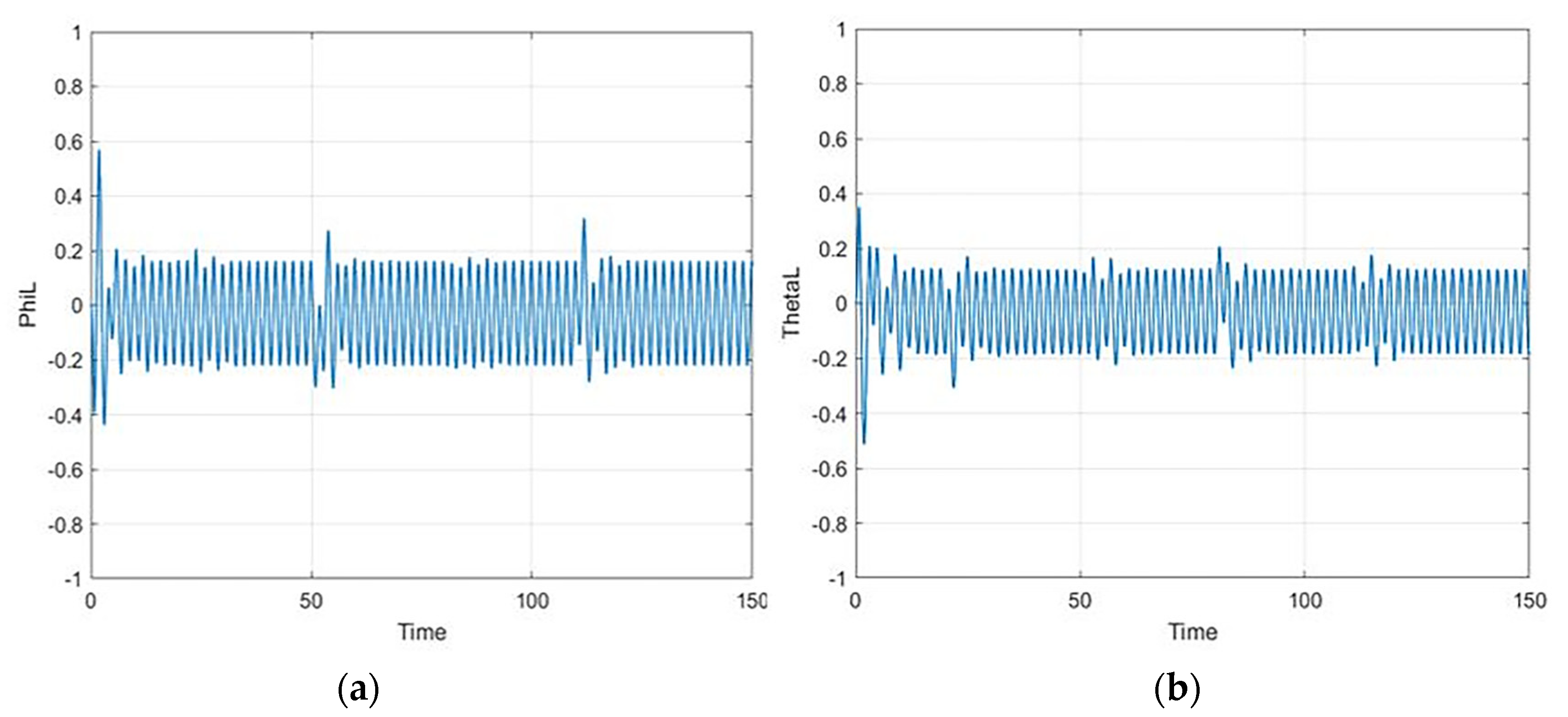
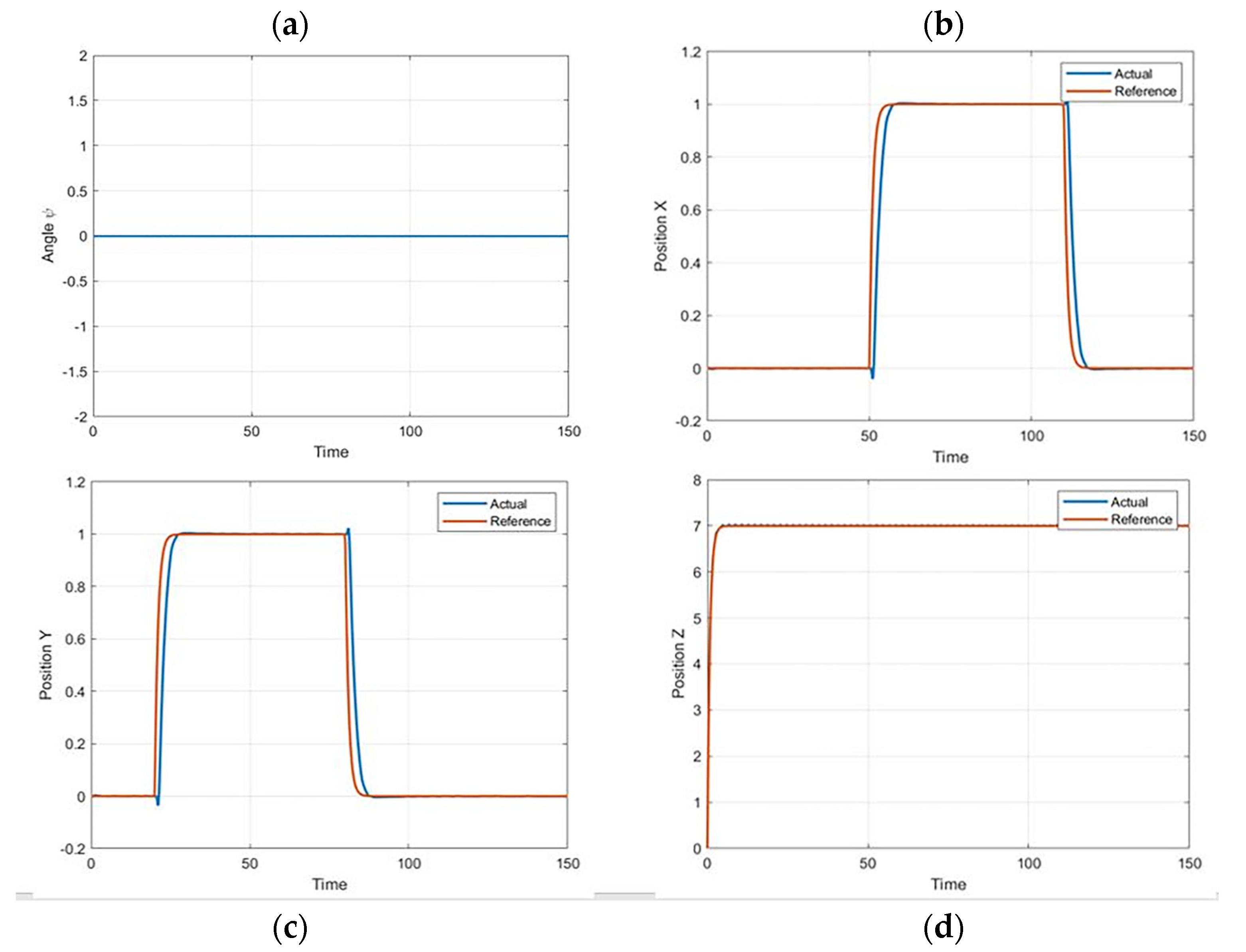
7. Results
8. Conclusions
9. Implications
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dougherty, M.J. Drones: An Illustrated Guide to the Unmanned Aircraft That Are Filling Our Skies; Amber Books Ltd.: London, UK, 2015. [Google Scholar]
- Hassanalian, M.; Abdelke, A. Classifications applications and design challenges of drones: A review. Prog. Aerosp. Sci. 2017, 91, 99–131. [Google Scholar] [CrossRef]
- Ansari, U.; Bajodah, A.H.; Kada, B. Development and experimental investigation of a Quadrotor’s robust generalized dynamic inversion control system. Nonlinear Dyn. 2019, 96, 1541–1557. [Google Scholar] [CrossRef]
- Ansari, U.; Bajodah, A.H.; Hamayun, M.T. Quadrotor control via robust generalized dynamic inversion and adaptive non-singular terminal sliding mode. Asian J. Control. 2019, 21, 1237–1249. [Google Scholar] [CrossRef]
- Rosaldo-Serrano, M.A.; Aranda-Bricaire, E. Trajectory tracking for a commercial quadrotor via time-varying backstepping. IFAC-Pap. 2018, 51, 532–536. [Google Scholar] [CrossRef]
- Labbadi, M.; Cherkaoui, M. Robust adaptive backstepping fast terminal sliding mode controller for uncertain quadrotor UAV. Aerosp. Sci. Technol. 2019, 93, 105306. [Google Scholar] [CrossRef]
- Castaldi, P.; Mimmo, N.; Naldi, R.; Marconi, L. Robust trajectory tracking for underactuated VTOL aerial vehicles: Extended for adaptive disturbance compensation. IFAC Proc. Vol. 2014, 47, 3184–3189. [Google Scholar] [CrossRef]
- Tamayo, A.J.M.; Ríos, C.A.V.J.; Zannatha, M.I.; Soto, S.M.O. Quadrotor input-output linearization and cascade control. IFAC-Pap. 2018, 51, 437–442. [Google Scholar] [CrossRef]
- van de Wiel, T.T.; Tóth, R.; Kiriouchine, V.I. Comparison of parameter-varying decoupling-based control schemes for a quadrotor. IFAC-Pap. 2018, 51, 55–61. [Google Scholar] [CrossRef]
- Wang, N.; Deng, Q.; Xie, G.; Pan, X. Hybrid finite-time trajectory tracking control of a quadrotor. ISA Trans. 2019, 2019, 278–286. [Google Scholar] [CrossRef]
- Ansari, U.; Bajodah, A.H. Robust generalized dynamic inversion quadrotor control. IFAC-Pap. 2017, 50, 8181–8188. [Google Scholar] [CrossRef]
- Golestani, M.; Mobayen, S.; Tchier, F. Adaptive finite-time tracking control of uncertain non-linear n-order systems with unmatched uncertainties. IET Control. Theory Appl. 2016, 10, 1675–1683. [Google Scholar] [CrossRef]
- Yin, C.; Chen, Y.; Zhong, S.M. Fractional-order sliding mode-based extremum seeking control of a class of nonlinear systems. Automatica 2014, 50, 3173–3181. [Google Scholar] [CrossRef]
- Vahdanipour, M.; Khodabandeh, M. Adaptive fractional order sliding mode control for a quadrotor with a varying load. Aerosp. Sci. Technol. 2019, 86, 737–747. [Google Scholar] [CrossRef]
- Alexis, K.; Nikolakopoulos, G.; Tzes, A. Model predictive quadrotor control: Attitude, altitude, and position experimental studies. IET Control. Theory Appl. 2012, 6, 1812–1827. [Google Scholar] [CrossRef]
- Shi, X.; Cheng, Y.; Yin, C.; Dadras, S.; Huang, X. Design of fractional-order backstepping sliding mode control for quadrotor UAV. Asian J. Control. 2019, 21, 156–171. [Google Scholar] [CrossRef]
- Eliker, K.; Zhang, W. Finite-time adaptive integral backstepping fast terminal sliding mode control application on quadrotor UAV. Int. J. Control. Autom. Syst. 2020, 18, 415–430. [Google Scholar] [CrossRef]
- Islam, S.; Liu, P.X.; El Saddik, A. Robust control of four-rotor unmanned aerial vehicle with disturbance uncertainty. IEEE Trans. Ind. Electron. 2014, 62, 1563–1571. [Google Scholar] [CrossRef]
- Roy, P.; Roy, B.K. Sliding Mode Control Versus Fractional-Order Sliding Mode Control: Applied to a Magnetic Levitation System. J. Control. Autom. Electr. Syst. 2020, 31, 597–606.–606. [Google Scholar] [CrossRef]
- Zhu, P.; Chen, Y.; Li, M.; Zhang, P.; Wan, Z. Fractional order sliding mode position tracking control for servo system with disturbance. ISA Trans. 2020, 105, 269–277.–277. [Google Scholar] [CrossRef]
- Liu, K.; Wang, Y.; Ji, H.; Wang, S. Adaptive saturated tracking control for spacecraft proximity operations via integral terminal sliding mode technique. Int. J. Robust Nonlinear Control 2021, 31, 9372–9396. [Google Scholar] [CrossRef]
- Bolandi, H.; Rezaei, M.; Mohsenipour, R.; Nemati, H.; Smailzadeh, S.M. Attitude Control of a Quadrotor with Optimized PID Controller. 2013. Available online: http://www.scirp.org/journal/PaperInformation.aspx?PaperID=35654 (accessed on 1 June 2023).
- Lee, D.; Jin Kim, H.; Sastry, S. Feedback linearization vs. adaptive sliding mode control for a quadrotor helicopter. Int. J. Control. Autom. Syst. 2009, 7, 419–428.–428. [Google Scholar] [CrossRef]
- Ghandour, J.; Aberkane, S.; Ponsart, J.-C. Feedback Linearization approach for Standard and Fault Tolerant control: Application to a Quadrotor UAV Testbed. J. Physics Conf. Ser. 2014, 570, 082003. [Google Scholar] [CrossRef]
- Dolatabadi, S.H.; Yazdanpanah, M.J. IMO sliding mode and backstepping control for a quadrotor UAV. In Proceedings of the 2015 23rd Iranian Conference on Electrical Engineering, New York, NY, USA, 10–14 May 2015; pp. 994–999. [Google Scholar] [CrossRef]
- Xu, R.; Özgüner, Ü. Sliding mode control of a class of underactuated systems. Automatica 2008, 2008, 233–241. [Google Scholar] [CrossRef]
- Zheng, E.H.; Xiong, J.J.; Luo, J.L. Second-order sliding mode control for a quadrotor UAV. ISA Trans. 2014, 53, 1350–1356. [Google Scholar] [CrossRef]
- Omar, H.M. Anti-swing controller based on time-delayed feedback for helicopter-slung load system near hover. J. Aerosp. 2012, 4, 297–305. [Google Scholar] [CrossRef]
- El Ferik, S.; Ahmed, G.; Omar, H.M. Load swing control for an Unmanned Aerial Vehicle with a slung load. In Proceedings of the 2014 IEEE 11th International Multi-Conference on Systems, Signals, and Devices (SSD14), New York, NY, USA, 11–14 February 2014; pp. 1–9. [Google Scholar] [CrossRef]
- Guglieri, G.; Marguerettaz, P. Dynamic Stability of a Helicopter with an External Suspended Load. J. Am. Helicopter Soc. 2014, 59, 1–12. [Google Scholar] [CrossRef]
- Klausen, K.T.; Fossen, I.; Johansen, T.A. Nonlinear control with swing damping of a multirotor UAV with a suspended load. JINT 2017, 88, 379–394. [Google Scholar] [CrossRef]
- Bonna, R.; Camino, J.F. Trajectory tracking control of a quadrotor using feedback linearization. In Proceedings of the International Symposium on Dynamic Problems of Mechanics, Sao Paulo, Brazil, 22-27 February 2015. [Google Scholar]
- Mo, H.; Farid, G. Nonlinear and adaptive intelligent control techniques for quadrotor uav–A survey. Asian J. Control 2019, 21, 989–1008. [Google Scholar] [CrossRef]
- Slotine, J.J.E.; Li, W. Applied Nonlinear Control, Englewood Cliffs; Prentice Hall: Hoboken, NJ, USA, 1991; Volume 705. [Google Scholar]
- Eray, O.; Tokat, S. The design of a fractional-order sliding mode controller with a time-varying sliding surface. Trans. Inst. Meas. 2020, 42, 3196–3321. [Google Scholar] [CrossRef]
- Liu, K.; Gao, H.; Ji, H.; Hao, Z. Adaptive sliding mode based disturbance attenuation tracking control for wheeled mobile robots. Int. J. Control Autom. Syst. 2020, 18, 1288–1298. [Google Scholar] [CrossRef]


| Parameter Name | Symbol | Value |
|---|---|---|
| Mass of the load | 1 kg | |
| Cable length | 2 m | |
| Air density | 1.2 kg/m−3 | |
| Load flat plate area | 0.9 m2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Dhaifallah, M.; Al-Qahtani, F.M.; Elferik, S.; Saif, A.-W.A. Quadrotor Robust Fractional-Order Sliding Mode Control in Unmanned Aerial Vehicles for Eliminating External Disturbances. Aerospace 2023, 10, 665. https://doi.org/10.3390/aerospace10080665
Al-Dhaifallah M, Al-Qahtani FM, Elferik S, Saif A-WA. Quadrotor Robust Fractional-Order Sliding Mode Control in Unmanned Aerial Vehicles for Eliminating External Disturbances. Aerospace. 2023; 10(8):665. https://doi.org/10.3390/aerospace10080665
Chicago/Turabian StyleAl-Dhaifallah, Mujahed, Fahad M. Al-Qahtani, Sami Elferik, and Abdul-Wahid A. Saif. 2023. "Quadrotor Robust Fractional-Order Sliding Mode Control in Unmanned Aerial Vehicles for Eliminating External Disturbances" Aerospace 10, no. 8: 665. https://doi.org/10.3390/aerospace10080665
APA StyleAl-Dhaifallah, M., Al-Qahtani, F. M., Elferik, S., & Saif, A.-W. A. (2023). Quadrotor Robust Fractional-Order Sliding Mode Control in Unmanned Aerial Vehicles for Eliminating External Disturbances. Aerospace, 10(8), 665. https://doi.org/10.3390/aerospace10080665







