Abstract
This paper provides an overview of modern research on magnetoplasma methods of influencing gas-dynamic and plasma flows. The main physical mechanisms that control the interaction of plasma discharges with gaseous moving media are indicated. The ways of organizing pulsed energy input, characteristic of plasma aerodynamics, are briefly described: linearly stabilized discharge, magnetoplasma compressor, capillary discharge, laser-microwave action, electron beam action, nanosecond surface barrier discharges, pulsed spark discharges, and nanosecond optical discharges. A description of the physical mechanism of heating the gas-plasma flow at high values of electric fields, which are realized in high-current and nanosecond (ultrafast heating) electric discharges, is performed. Methods for magnetoplasma control of the configuration and gas-dynamic characteristics of shock waves arising in front of promising and advanced aircraft (AA) are described. Approaches to the control of quasi-stationary separated flows, laminar–turbulent transitions, and static and dynamic separation of the boundary layer (for large PA angles of attack) are presented.
1. Introduction
The application of plasma technologies in aerodynamics contributes to a permanent interest, which is mainly related to the potential impact on the integral and local flow characteristics of bodies: modification of the shape and the intensity of densification jumps, control of boundary layers and flow separation areas, and the impact on vortex structure in a flow, a cavern, and others. For instance, several new methods of control and modification of a gas flow near AA were proposed in the article [1]. These methods were applied in plasma generation, magnetoplasma control of a flow and generation of the energy in it by the counterflow of a hot gas and other thermal effects.
The attractiveness of MagnetoPlasma Aerodynamics (MPA) is associated with the reliability and absence of control elements in the gas-plasma flow, the flexibility of controlling the spatio-temporal impact, the smallness of the inertia of the impact [2,3,4,5,6,7,8,9,10,11,12,13], the weight and energy consumption, the geometric dimensions of the plasma actuators, as well as the possibility of changing the plasma-dynamic characteristics of the flow using electric and magnetic fields, broadband radiation and external thermal effects. At the same time, the relatively low power consumption of plasma actuators makes it possible to create fundamentally new systems for controlling the trajectory of Advanced Aircraft (AA).
Thus, an important practical advantage of the effect of plasma on a gas-dynamic flow is its speed. At the same time, this kind of influence can be effective in a wide range of frequencies and gas-dynamic flows, ranging from stationary flows to separated and turbulent flows. Electric discharge technologies based on the creation of plasma formations using electric discharges, laser or microwave plasma can be effective ways to reduce the ignition time and control supersonic gas flows in the propulsion systems of advanced aircraft. The idea of using plasma methods for fuel ignition is based on the non-equilibrium generation of chemically active particles or clusters that accelerate the combustion process. As a rule, it is assumed that a possible gain in the energy expended to accelerate combustion in plasma methods is achieved by creating a non-equilibrium state of the plasma in the discharge.
Long studies of complicated physical processes occurring at high altitudes (about 20–30 km) and flight speeds of advanced aircraft (Mach number 6) have led to the emergence of a new scientific direction, which is physical gas dynamics (the subject of study is high-speed and high-temperature gas flows normally accompanied by a great amount of non-linear physical processes). One of the most exciting scientific directions (in physical gas dynamics), which is related to recently discovered methods of AA control, is based on MPA. Magnetoplasma aerodynamics studies the phenomena and processes of interaction between a high-temperature gas flow and electric and magnetic fields. The main advantages of MPA (over gas-jet and mechanical actuators) in the methods of controlling high-speed flows are illustrated in articles [14,15] and the review [11]. As a reminder, a technical device employed in controlling gas-dynamic flows by plasma is a plasma actuator.
The term “plasma dynamics” used in the review implies a branch of physics that includes a mathematical description (as a continuum) of plasma dynamics (considering the electromagnetic fields and the currents), radiative transfer processes in plasma (in a wide wavelength range), and its interaction with solids (electrodes, vessel walls, etc.).
In general, technical devices for controlling a gas-plasma flow can be roughly divided into the following main classes: acoustic; mechanical; electric; thermal; plasma–chemical. This review only considers the mechanical class of device (plasma actuators), which controls a gas’s dynamic flow by plasma. As of now, the following main devices can be categorized as the main types of plasma actuators: pulsed surface discharges with a solid insulator; pulsed electric discharge jet actuators (magnetoplasma compressors, capillary discharge, etc.); stationary arcing; microwave discharge; laser discharge; actuators based on combined thermal and MagnetoHydroDynamics (MHD) effects.
The research areas mentioned above correspond to a class of currents related to the external flow stream of an AA construction surface. Nowadays, methods and technologies aimed at intensifying the processes of mixing fuel components, reducing induction time, stabilizing combustion, and increasing the fuel burnout rate in modern and advanced propulsion systems are intensively researched.
It is worth mentioning that the possibilities for experimental research on these sorts of flows near the surface and inside the construction of AA involve a lot of technical difficulties and require large financial investments. Therefore, the study of the possibilities of controlling a flow by magnetoplasma (with AA aerodynamics) requires the development of physical and mathematical models and computational models appropriate for the analysis of magnetohydrodynamic flows in high-speed, radiating, non-equilibrium gas and plasma streams in a highly heterogeneous environment. However, in this case, high accuracy of calculations is necessary (particularly in the calculations of temperature and heat flux distributions), and strict requirements are imposed on the software package and numerical methods for modelling high-speed gas-plasma flows near bodies with complex geometric shapes. It is also important to note that the mathematical modelling of a gas flow reacting in an AA engine includes the choice of a chemical kinetics scheme.
There is a need to explore new methods of controlling the motion of advanced aircraft and high-speed gas and plasma flows under the conditions considered here. Consequently, there is a need for the review, which analyses experimental and mathematical modelling [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15], currently playing an enormous part in the development of AA:
- Controlling the flow and surface flow of the AA with volumetric ponderomotive forces. It is worth noting that controlling the flow near AA with the magnetoplasma effect is based on controlling the main flow as well as the boundary layer;
- Controlling plasma-stimulated combustion in high-speed gas and plasma flows.
The initial effect may be accompanied by flow resistance reduction, modification of the boundary layer (e.g., by controlling laminar–turbulent transition), and emergence of controlling forces and momentum on aerodynamic surfaces, may lead to the changing of the Shock Wave (SW) structure of the stream in a high-speed motor circuit, may also be accompanied by reducing thermal stress on the surface of AA and separate components of its structure, reducing wave impedance and frictional resistance by generating or suppressing flow separation area, and may lead to the suppression of the unstable flow pattern of AA.
Plasma-stimulated effects may result in plasma activation of the fuel and an oxidant, initiation of chemical reactions provided that the flow has a high speed, stabilization of the flame front, plasma–chemical fuel conversion, and the kinetic effect on the reacting flow.
2. Methods for Controlling the Flow around the External and Internal Surfaces of AA
2.1. Methods Description
As it has already been mentioned, the primary focus these days is on active methods of influencing the flowing process of AA that not only stabilize the boundary layer but also generate a desired flow regime in a selected area on the AA surface. Magnetoplasma aerodynamics provides a rather large set of tools to accomplish these goals. There are two ways of affecting gas-plasma flow that are most commonly used in practice:
- Dynamic influence based on Lorentz force and electrostatic force (in the presence of uncompensated charges in the environment);
- Thermal influence.
The characteristic length and time scales of a high-speed gas-plasma stream are the maximum geometrical dimensions of AA and the time a stream particle spent near a plasma actuator (or AA). In the meantime, a considerable number of characteristic times that have a value of the order of 10−10 to 10−2 s occur in a plasma flow with chemical reactions and electric charge relaxation as well as translational, rotary, and oscillating relaxations. Minimum time scale is determined by the establishment of electroneutrality in a plasma flux and has a value of the order 10−11 to 10−9 s. Maximum characteristic time varying from 10−3 to 10−1 corresponds to the time spent in a gas-plasma environment near (or within) AA.
In this case, the main physical mechanisms of influence on the characteristics and structure of the flow close to the surface and inside AA are a change in the thermodynamic properties of the gas (thermal influence), modification of structural elements of the flow field, generation or stabilization of the local flow separation areas, a change in boundary layer characteristics (dynamic or thermal influence), and others. Such effects in the magnetoplasma aerodynamics of AA may be realised by generating microwave plasma, plasma in electric discharges of direct and alternating current, mixing the initial flow with high-enthalpy plasma jets containing active radicals, etc. Surface discharge, a laser torch, as well as a beam of electrons (to initiate “emergency” ignition of the fuel mixture in the working channel of AA) can be used for the purpose previously mentioned.
Volume gas discharges are employed in controlling flowing regimes around bodies of various shapes; surface discharges make it possible to impact boundary (dynamic, thermal) layers near the streamlined AA surfaces. The definition of physical mechanisms causing the change of modes of discharge development in a gas flow, optimization of energy input into the flow, analysis of physical and chemical kinetic processes in discharge plasma, research of discharge effects on the value of surface friction, heat exchange, and the local structure of a flow (flow separation areas, compaction jumps) remain relevant in this kind of research.
The beginning of the paragraph is devoted to different types of surface discharges (volume discharges are described below) and the physical mechanisms of their impact on the gas-plasma stream. The first significant feature of a surface discharge is that a solid wall largely defines the energy input mode and the plasma parameters of the discharge, limiting the current channel and stabilizing its position in space (a solid wall essentially limits the spectrum of possible oscillations in plasma). The next distinctive feature is that the Dielectric Inter-Electrode (DIE) (placed in a homogeneous electric field) disturbs its uniformity. In this situation, plasma surface discharge always occurs along the DIE surface. And the voltage at the inter-electrode gap is lower (compared to an air gap without a DIE), provided there is a DIE.
The whole range of surface discharges (see Figure 1) with a solid dielectric can be described by two typical cases.
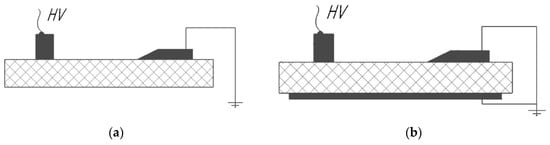
Figure 1.
A system of electrodes with a predominant tangential (a) and normal (b) component of the electric field.
First typical case. In this situation, the inhomogeneous electric field is mainly determined by the tangential (to the surface of a DIE) component of the electric field strength at all points of the dielectric surface (Figure 1a).
Second typical case. The inhomogeneous electric field is characterized by the predominance of the normal (to the surface of a DIE) component of the electric field strength (Figure 1b).
These and intermediate options for surface discharges with a solid insulator can be explained with a simple circuit diagram. If the capacitance is high, a “sliding” discharge with capacitive feeding is realised, if the electrical resistance is high, the discharge develops as a “barrier” discharge due to surface conductivity. Capacitance depends on the dielectric constant of the insulator . The resistance depends on surface conductivity that is related to the conductivity of the insulator and to its surface state.
Further in the review, we consider various options for the use of pulsed plasma-dynamic and non-equilibrium discharges (see, e.g. Figure 2).
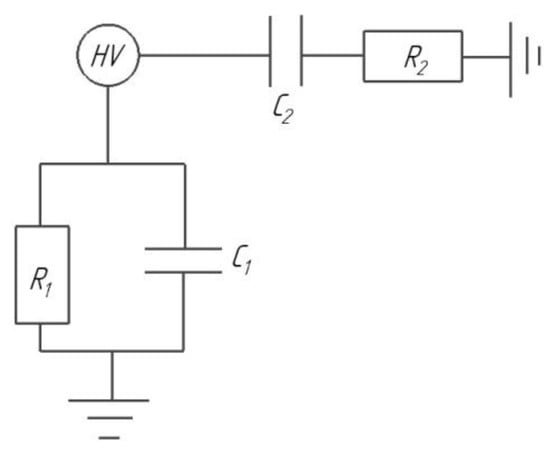
Figure 2.
Conventional scheme of a nanosecond “sliding” or “barrier” surface discharge: are the resistance and capacitance of a solid dielectric; R2, C2 are the resistance and capacitance of solid air in the interelectrode gap.
2.2. Pulsed Plasma Dynamic Surface Discharges
The circuit (1st typical case) of a Line-Stabilised Surface Discharge (LSSD) and general structure of the plasma discharge in the cross-section consist of 1—dielectric inter-electrode; 2—power electrodes; 3—initiating electrodes; 4—discharger; 5—light-erosion vapour area; 6—contact boundary; 7—plasma-gas area; 8—the front of the outer discharge boundary with surrounding gas; —capacitance of the capacitor bank; —inductance of an LSSD switching system; —energy stored in the capacitor bank.
These are the characteristic electrical parameters: inter-electrode element made from with the length varying between L = (25–100) cm; the characteristics of the electric circuit of a discharge varying in the ranges = 3F, = 0.01 Ω, = (25–100) kV, kJ, = 0.5 H.
As a reminder, LSSD is one of the forms of pulsed high-current discharge in gas occurring during a pulsed discharge of a capacitor bank into an inter-electrode gap above the special insulating element. A discharge of this type can be carried out both in an inert gas environment and in the air [16].
Given the characteristic electrical parameters of the discharge circuit, the current pulse of an LSSD is a damped sinusoidal signal with a first current half-period duration of , which contains approximately four half-periods, and the duration of the first discharge half-period is longer than the other. The characteristic scale of the discharge current amplitude ranges from a few tens to hundreds of kiloamperes (with almost no influence of the gas type on the current characteristics of the discharge). It also should be noted that a sufficiently large value of current during the second and third half-periods leads to a considerable influence of electromagnetic forces on the characteristics of the discharge plasma of an LSSD.
The possible range of LSSD operating in the air (at pressure 1 atm, discharge channel length L < 1 m) corresponds to variations in the capacitance of the capacitor bank F and an initial voltage = (25–200) kV. LSSD is characterized by a strong decay of the discharge current with a maximum joule energy release into the plasma in the first half-period () of the discharge current .
The most important complex parameter (average specific electric power) that determines nearly all LSSD characteristics may be suggested as (in the formula, —energy supplied to the LSSD plasma at the end of the first half-period of current) and its variation range is for the discharge circuit parameters mentioned above. The energy release dynamics depend on the efficiency of the transformation of the primary energy source W0 (capacitor bank) into the energy of discharge plasma , which can be defined as the transformation efficiency factor for arbitrary time .
Furthermore, the kinetic energy of the LSSD plasma is significantly lower than the internal energy of the plasma during discharge. In the calculations, , , , and , where —velocity vector; —LSSD plasma density; —specific internal energy of the LSSD plasma.
According to the calculations in the article [16], two different modes of LSSD are possible for this range: “explosive” and “magnetogasdynamic”. Physical processes (W0®QJ®Eint + Ekin + Epl) occurring in these modes are further considered with two energy-power options of LSSD: “explosive” mode— ( = 50 kV, L = 50 cm), “magnetogasdynamic” mode— ( = 100 kV, L = 25 cm). Based on the results presented in the article [16], during the first half-period of discharge current, lateral expansion of an LSSD discharge channel has an approximately constant velocity (, ,). If , the spatial size of a LSSD discharge channel along the Z-axis is larger than along the Y-axis. There is radiation and magnetogasdynamic change of the parameters in the rupture area; the outer boundary of the discharge is a GD-rupture with parameters different from the parameters of a strong UW (e.g., ). This effect is most prominent in the direction of the Y-axis due to a “stiff” non-deformable limiter in the form of DIE along the Z-axis and its absence in the direction of the Y-axis.
The main characteristic of LSSD broadband radiation is the brightness temperature.. The dynamics of the brightness temperature change in the corresponding spectral interval are investigated in the works [17,18]. These results show:
- -
- In the initial and final stages of discharge, the distribution of electro-discharge plasma radiation is close to the spectrum of black body radiation—the bright temperatures in all studied spectral intervals are almost identical [17,18];
- -
- LSSD Brightness temperatures reach maximum in moments of time close to maximum energy input power (maximum current) (at ≈ 10 MW/cm—Tbr2,3 ~ 30 kK; for ≈ 100 MW/cm—Tbr,2 ~ 30 kK, in argon Tbr,3 ~ 40 kK and in the air Tbr,2,3 ~ 40 kK) and significantly fall for the second and third spectral intervals in the second (16 kK—MW/cm; 25 kK— ≈ 100 MW/cm) and the third half-periods of full current (13 kK— ≈ 10 MW/cm; 20 kK— ≈ 100 MW/cm) [17,18];
- -
- The distribution of the radiation intensity by spectrum (and therefore Tbr,i), at moments close to the maximum discharge current, is markedly different from the energy distribution of the completely black body, both in air and argon, only for the variant with ≈ 100 MW/cm [17,18].
As a rule, the aerodynamic performance of the AA is improved by optimizing the shape (mainly resulting in reduced wave resistance) of the structure’s surface. For example, a method for controlling the aerodynamic characteristics of the airfoil AA by modifying the configuration of the bearing surface by means of a magnetoplasma impact is proposed in the work [16]. Following the work of [16], the main mechanisms for influencing (in terms of practical use) linear surface discharge (LSSD) gas flow near AA can be attributed to the LSSD plasma channel system, which creates an obstacle (approximately as a «solid» barrier) for an incident flow. As a result, not only the curvature of the AA profile changes but also the aerodynamic characteristics of the profile.
The studies carried out in the works [19,20,21,22] showed that it is possible to control the burning mode in the combustion channel of a hypersonic scramjet engine-type power plant using a pulse-periodic transverse air injection upstream and downstream of the ignition area of the fuel components (see Figure 3, for example). Here we shall notice that the LSSD-type surface discharge can be used for the same purpose.
Figure 3.
The scheme of the propulsion system of the experiment HIFiRE-2 [4,6]: 1—first injector, 2—second injector.
The method of initiation of long radiating discharges in dense gas environments, based on the use of the so-called «sliding» discharge technique, was widely used for improving the aerodynamic characteristics of AA. The essence of the method consists of the preionization of a gas in an interelectrode gap by charging currents of the distributed surface capacity of a dielectric. Another possible way to initiate high-current surface discharges is through the use of the so-called «barrier» discharge. Barrier discharge is a type of sliding discharge and therefore inherits its main disadvantages.
2.3. Pulsed Nanosecond Surface Discharges
Consider in more detail the second typical case of surface discharges with solid dielectric: the interaction of streamers and spark discharges with the surface of the interelectrode dielectric insert. The main physical mechanisms of nanosecond discharge interaction with the insert surface are shown in Figure 4. It follows from Figure 4 that the spread along the surface of discharge streamers is accompanied by photoemission (a photoeffect caused by UV radiation) of electrons and charge accumulation (adsorption) on the surface of the interelectrode insert. As seen in Figure 4, the interaction of streamers and spark discharge with the surface of the insert is of different character (Figure 5) [23].
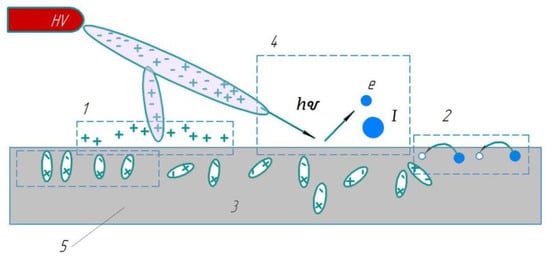
Figure 4.
Interaction of streamers with the surface, various mechanisms: 1—through a dustable surface charge, 2—through surface conductivity, 3—through dielectric polarization, 4—through photoemission and thermoemission (in the case of a spark), 5—dielectric.
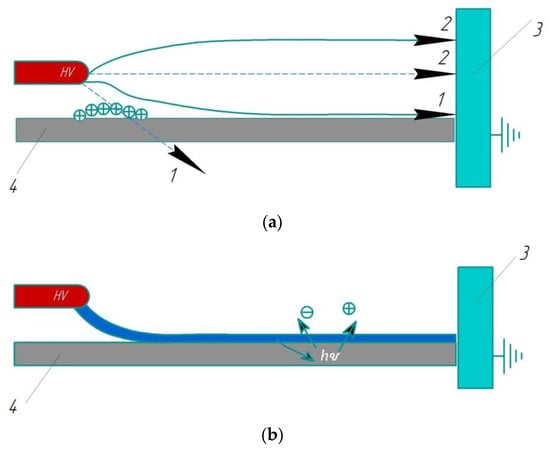
Figure 5.
The difference between the streamer and sparks on the surface with electric field lines (a) and without (b): 1—initial electric field lines, 2—electric field lines perturbed by surface charge, 3—metal, and 4—dielectric.
Figure 5 shows two types of streamers (recorded in experimental studies [24]) that can be formed in a nanosecond surface discharge: the first type is associated with an increase (due to the accumulation of bulk spatial charge) in electric field intensity along the insert surface; the second type is associated with distortion (due to the accumulation of photoemission electrons on the insert surface) of the shortest electric field power lines.
Experimental studies [23,24] investigated the influence of the geometric parameters of dielectrics (thickness, length) as well as the physical properties (conductivity, dielectric permeability) of various dielectrics and semiconductors. Studies have concluded that dielectric permeability is weak (works [23,24] used BK7 optical glass with dielectric permeability 2.3–4.5 as well as aluminum oxide) in the process of forming a pulsed nanosecond surface discharge. In these studies, it was also noted that specific surface conductivity influences physical processes in the discharge, apart from dielectric permeability. This conductivity in air experiments may depend on the humidity and properties of the Earth’s atmosphere.
The necessary conditions for the breakdown of the «sliding» or «barrier» surface discharges are the achievement of a sufficiently large charging current of the distributed capacitance of the interelectrode dielectric insert: , where the is the distributed dielectric capacitance; is the voltage; are the dielectric permeability of the vacuum and interelectrode dielectric insert material; are the width and thickness of the interelectrode dielectric insert; and is the current coordinate of the ionization wave (current front). The specific current required depends on a number of factors (length of discharge interval, gas type, etc.).
At the same time, it is obvious that to organize (in this way) a reliable breakdown of the discharge gap, it is necessary to use dielectrics with low thickness and with special electrical properties (high values of dielectric permeability and electrical strength); apply a high operating voltage and the rise rate . The need to use dielectrics with special properties greatly limits the choice of construction materials and complicates the technology of this kind of plasma actuator. Note that the linear-stabilized surface discharge is largely free from the noted shortcomings of the «sliding» and «barrier» surface discharges.
Pulse-distributed surface «sliding» discharge (surface discharge with solid dielectric) of nanosecond duration (plasma sheet) can be used as a plasma actuator to affect flow [25,26,27,28,29]. It consists of surface-sliding dielectric channels (streamers, Figure 5), forming a plasma layer comparable in thickness to the boundary layer of supersonic flow (~0.5 mm). With the help of such discharges, it is possible to transfer energy and ultraviolet radiation into the near-surface (subsonic, transsonic or supersonic) gas flow area.
In the works [30,31,32], it is shown that by acting (by means of ejection Joule heat) on the gas-plasma medium with the aid of a surface sliding discharge, it is possible to reduce (more than twice) the wave resistance of the streaming wing in the transsonic flow.
Figure 6 shows a system of electrodes (two typical cases) used to create a pulsed sliding nanosecond surface discharge. When a high-voltage voltage pulse is applied to electrode 4, the dielectric surface 3 exhibits an offset current, which is determined by the voltage value, the steepness of its growth, and the variable capacity between the surface discharge plasma and electrode 2, covering the opposite side of the dielectric. In this case, the sliding surface discharge acts as an ionizer around the first electrode 1, wherein the constant voltage component creates a sliding corona discharge between electrodes 1 and 4.
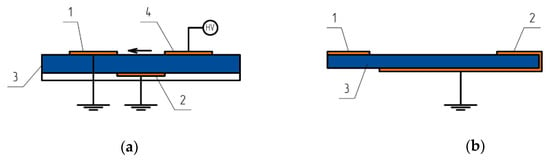
Figure 6.
Configuration of electrodes for sliding surface discharge: 1—anode; 2—cathode; 3—interelectrode dielectric insert; 4—additional electrode.
The two main advantages of such a discharge Figure 6a shows that a large area of plasma can be created (this requires at least 7 kV per centimeter between electrode 1 and electrode 2). In addition, this discharge is resistant to the transition from a smoldering discharge to an arc discharge. In the work [33], studies have been carried out on the management of flow separation at the flow of the profile NACA0015. Studies have shown that irregular (impulse) action with a surface sliding discharge is more likely to delay the flow, requiring less plasma actuator power. Experimental studies on changing the structure of the current near the AA with a sliding discharge are presented in the papers [34,35].
Interesting experiments (for attack angles up to 20 degrees and a flow rate of 110 m/s) were performed by a scientific group from Russia [36,37,38,39]. The influence of air humidity on the sliding surface discharge while controlling the flow is described in [40,41].
In all the above experimental cases [30,31,32] and [33,34,35,36,37,38,39,40,41], perturbations (from «thermal» and «plasma» effects) are determined by parameters of thermal and plasma sources (actuators), geometry of the arrester, component composition of the environment, etc. In order to study the physical basis of the change in the current structure near the AA, we will obtain an expression for vorticity = rot(). To do this, the rotor operation is applicable rot() to the Navier–Stokes equation (including kinematic viscosity = const), which additionally takes into account the influence of electrical and magnetic fields:
wherein = rot()—vortex vector; ρ, V, —density, velocity vector, flow pressure; , , —vector of electric, magnetic and current density strength, —space charge, —kinematic viscosity, —acceleration of gravity. Here we note that the part also the part may be neglected. Then the equation for vorticity = rot() will take a simpler look:
This equation implies that a vortex movement may occur when ; the condition of vortex formation (vortex is not formed if ) with an external magnetic field .
Note that for a gas-plasma flow moving at some speed along a heated surface, see Figure 7a. The pressure gradient is directed against the flow, but the temperature gradient —directed toward the interelectrode insert surface. As follows from the equation for vorticity in the case of «thermal action» the circulation of the vortex is determined by the form (a consequence of the non-collinearity of pressure and temperature gradients). Thus, the «thermal effect» twists the flow counterclockwise [42,43].
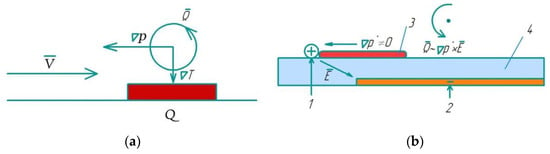
Figure 7.
Thermal and plasma formation of vortices: 1—open electrode; 2—closed electrode; 3—plasma; 4—dielectric.
For the gas flow at the surface from the surface «barrier» surface discharge (Figure 7b), on one half-period of the discharge current, when the open (gas flow) electrode has a positive potential relative to the closed (located under insert) electrode, electrons drift to the edge of the open electrode. Since electrons are much more mobile than ions, when they move in the plasma, a gradient of volumetric charge is created, directed to a positive electrode, and an electric field is directed to the lower electrode. In this situation (according to the vortex equation), the circulation of the vortex is determined by a part (the consequence of the non-collinearity of the volumetric charge gradient and electric field intensity), which in this case twists the incoming flow counterclockwise [42,43] to create a vortex interacting with the outer flow.
The basic idea of the given approach is the viscous–non-viscous interaction of the formed vortex and gas-plasma flow. For energy reasons, it is clear that there will be a capacity limit on the actuator, above which the use of «thermal» or «plasma» impact is not effective. So, the question arises as to the shape of the pulse and the location of the actuator for a more effective impact on the flow.
In the work, Ref. [44] experimentally investigated the characteristics of a distributed sliding discharge surface length of 300 ns (plasma sheet) in heterogeneous supersonic air flow with a vortex zone behind a thin wedge (Figure 8) in an impact tube channel. The spatial distribution of the discharge radiation, the spectral composition of the radiation, and the discharge current in the fluxes behind the flat shock waves with Mach numbers 2.4–3.5 (Mach numbers 1.16–1.47, the density 0.02–0.20 kg/m3) have been analyzed in the work [44]. It is shown that in flow with vortex zones, «sliding» surface discharge develops in the form of a channel width of 1–3 mm, located in the area of reduced density at a distance (5.5–9.0) ± 2 mm from the bottom of the wedge. The electron concentration in the discharge channel, which is significantly (10–20 times) higher than the electron concentration at discharge initiation in a homogeneous medium, has been found.
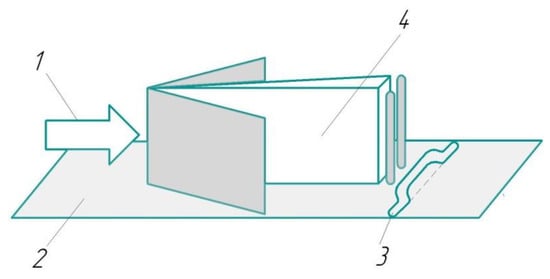
Figure 8.
Schematic representation of gas flow near the wedge and distributed sliding surface discharge: 1—flow; 2—discharge area; 3—discharge channel; 4—wedge.
The research [45,46,47] elaborates further on the paper [44]. In this case, gas flows with Mach numbers 1.30–1.60 were created behind flat shock waves with Mach numbers 2.8–4.2 in the shock tube (Figure 9). On the lower wall of the shock tube (Figure 9) was placed a small obstacle of dielectric in the form of a 48.0 × 6.2 × 1.9 mm3 rectangular block. The long part of the obstacle was perpendicular to the glass (walls) of the shock tube. Quasi-static current field (installed for ~200 μs) contained an angled shock wave that interacted with the boundary layer on the top wall of the shock tube.
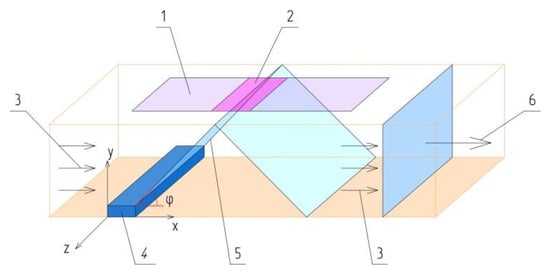
Figure 9.
Structure of the plasma gas flow in the discharge chamber with a barrier on the bottom wall: 1—discharge area; 2—research area; 3—flow; 4—obstacle; 5—oblique shock wave; 6—shock wave.
Schemes of two types of interaction that are realized when an oblique shock “falls” onto the boundary layer are shown in Figure 10. In the case of a laminar boundary layer, the interaction with the boundary layer can be continuous but contain a region of reduced density (Figure 10a); in the other case, interaction occurs with the formation of flow separation (Figure 10b). A pulsed surface “sliding” discharge was initiated on the upper wall of the shock tube in the time range of 70–1200 μs after the shock wave passed through the obstacle. Synchronization of the discharge started with the passage of the shock wave front and was carried out from the signals of pressure piezo sensors in the shock tube channel.
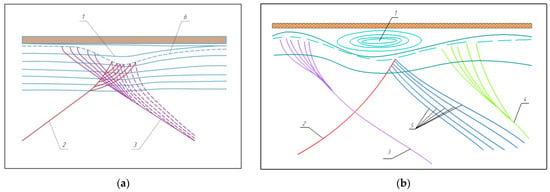
Figure 10.
Schemes of interaction of the oblique shock of the seal with the boundary layer: (a) continuous interaction; (b) interaction with the formation of flow separation: 1—subsonic layer (a) or separation area (b); 2—incident shock wave; 3—reflected shock wave; 4—compression waves; 5—rarefaction waves; 6—sound line.
The discharge was triggered at a specified time after the shock wave passed the test area in the discharge chamber, including the stage of quasi-static flow around the obstacle by the supersonic flow. In the experiments, the discharge current, emission spectra, spatial characteristics of radiation at the initiation of discharge at different stages of non-stationary supersonic flow, and different parameters of flows behind shock waves are recorded and analyzed.
Based on the analysis of the dynamics of shock waves from the discharge region, it is shown that this type of discharge provides a high energy impact on both the laminar and turbulent boundary layers. By comparing the experimental and computational dynamics of the flow in the shock tube channel, it was established [45,46,47] that the fraction of discharge energy converted to heat during energy conversion to heat during energy supply (~200 ns) increases from 15% to 65% with an increase in medium density from 0.05 to 0.45 kg/m3. The temperature of the near-surface layer of the gas increases by 600–1000 K. It has also been established that the initiation of a «sliding» surface discharge leads to an increase in the mean pressure at the channel wall in the flow behind the shock wave by 6–18% (at flow Mach numbers 1.1–1.6 and densities 0.06–0.20 kg/m3).
In the work [36], it was proposed to use a pulsed nanosecond «sliding» surface discharge in the plasma actuator. The values E/n (n is the concentration of neutral particles and E is the intensity of the electric field) in discharges of this type may exceed the threshold of breakdown several times. The high values of the reduced electric field seem to be the obvious advantage of this discharge. The first experiments [36] showed that with nanosecond pulse discharge, it is possible to reliably manage the separation of the boundary layer at speeds of up to 75 m/s with a linear power consumption of less than 1 W/cm. Later, the effect of the pulse sliding discharge on the flow separation was experimentally investigated in [38]. Here, the high efficiency of pulse discharge was demonstrated up to 110 m/s. It was concluded that the main mechanism of plasma impact was perturbation introduced into the boundary layer, not gas acceleration. It has been shown that changing the pulse rate in a plasma actuator optimizes its impact on resistance force, lift force and flow connection. The optimum frequency turned out to be ~U∞/L, where U∞ is the speed of the main flow and L is the typical distance along the surface to the separation zone. This result was later confirmed in an experiment [48] for Reynolds numbers up to 106 and a maximum free flow rate of 60 m/s.
2.4. Pulse Nanosecond «Barrier» Surface Discharges
Figure 11 provides a typical diagram of nanosecond surface dielectric «barrier» discharge (Surface Dielectric Barrier Discharge (ns-SDBD)) [49,50,51,52]: Two flat electrodes (a high-voltage electrode (1) are shown above and a low-voltage (grounded) electrode (2) at the bottom in Figure 11) are separated by an interelectrode dielectric insert.
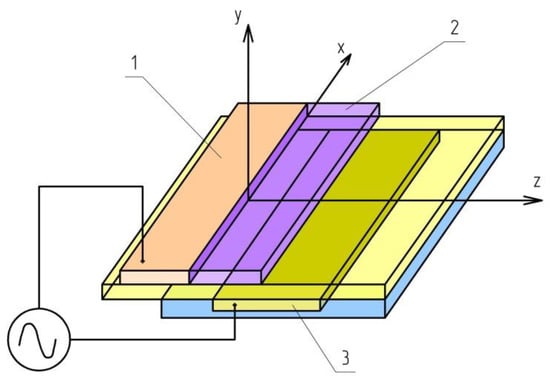
Figure 11.
SDBD bit gap diagram: 1—high-voltage electrode; 2—low-voltage (grounded) electrode; 3—plasma layer.
The plasma channel of the SDBD discharge at the beginning of the puncture process occurs on the edge of the high-voltage electrode after the high-voltage pulse is applied to it.
Development of SDBD-discharge in air at atmospheric pressure under the action of 28 kV high-voltage pulses on high-voltage electrodes is demonstrated in works [50,51,53,54]. The half-width of the pulse was 23 ns, and the rise time and the drop time of the pulse were 8 ns and 15 ns, respectively. The frequency of repetition of high-voltage pulses was 1 kHz. The low-voltage electrode was covered with a 0.4-mm-thick PVC film. The dielectric permeability of the film was ε ≈ 2.7.
The distribution of a cathode-directed (positive) SDBD-discharge can be conditionally described by means of four stages.
In the first stage, the discharge grew over the grounded electrode (1 ns, 3 ns and 4 ns). The discharge propagation rate at this stage was approximately 1 mm/ns. At the same time, you can see the broadband radiation of the entire streamer channel, not only the wavefront of the ionization wave.
The second stage took 5 ns (6 and 10 ns) and was observed when the length of the streamers exceeded the length of the lower electrode (the speed of the streamer propagation < 0.3 mm/ns).
The third stage (the «dark» phase of SDBD-discharge) came when the radiation discharge was not observed (from 13 ns to 20 ns). In the third stage, during the time of the distribution of streamers, the surface of the interelectrode dielectric insert was charged. Thus, when the ionization wave reached the electrode surface, the potential of the electrode became smaller than the potential of the interelectrode dielectric insert surface.
This led to the start of a reverse-discharge wave (fourth stage), which contributed to the removal of the charge (second burst of radiation) from the dielectric surface of the SDBD discharge (22 and 37 ns). Anode-directed (negative) discharge developed almost as well as cathode-directed discharge [52]. Thus, an SDBD discharge (any polarity) radiates not only a front of ionization but also plasma channels. This circumstance indirectly indicates the presence of a high intensity of electric field in a sufficiently large area behind the front of the ionization wave.
The possibility of a significant effect of SDBD on the gas-plasma flow is mainly determined by rapid heating, which is related to characteristics such as discharge energy, efficiency and energy transmission speed from electric current carriers (electrons) into the internal energy of the gas-plasma medium. The dynamics and physicochemical kinetics of heating gas-plasma medium by SDBD discharge are determined by the degree of freedom of molecules (translational, rotational, oscillating or internal) and the transfer of energy as a result of interaction with electrons generated by the discharge. This heating process in weakly ionized non-equilibrium plasma is determined by the [55] reduced electric field E/n (n—concentration of neutral particles), on which the average energy of electrons in the discharge and all other electronic characteristics depend. Another important characteristic of rapid gas heating in ns-SDBD is the dynamics of gas temperature change. The dependence of the positive temperature of the molecules in ns-SDBD on the voltage during the discharge phase and 1 μs after it for different polarity discharges shows that with an increase in voltage, the temperature increased in both polarities of the discharge. From the data obtained, it appears that air at atmospheric pressure can be noticeably heated (by 150 K) during the discharge stage at times of the order of 10 ns and that this heating is significantly increased and reaches hundreds of degrees after 1 μs after the pulse. Systematic measurements of ns-SDBD characteristics, including the limit length and rate of ionization wave propagation, as well as the plasma layer thickness, were made in the air [51] at different pressures and voltage pulses.
The discharge propagation length was reduced from 50 to 5 mm with an increase in pressure from 0.1 to 1 atm. The plasma layer thickness decreased from 1.5 to 0.2 mm. Thus, the increase in air pressure leads to a proportional reduction in plasma layer size.
In [56,57], the share of energy quickly transferred to heat in SDBD discharge was determined. After 50 ns, the discharge was 25% at E/n = 164 Td and increased to 75% at 270 Td. The initial pressure was atmospheric, and the initial gas temperature was between 300 and 1000 K. Thus, numerous experiments show that the efficiency of rapid (on times less than 1 μs at 1 atm) heating of air in the discharge plasma increases with the growth of the led electric field E/n and gas pressure. At high (>400 Td) electric fields, the energy quickly transfers to heat in the air plasma of the same order as the energy invested in the discharge. Thus, available experimental research shows a high efficiency of rapid heating in SDBD discharge in air at high (up to ~1000 Td) electric fields and pressures.
Thus, the results of these works [58,59,60,61,62,63,64,65] clearly demonstrate the thermal nature of impact wave interaction with non-equilibrium plasma. The effect of plasma ns-SDBD actuators on turbulent shear layers (both in the case of a normal mixing layer and the flow near the wall with the reverse step) has been experimentally investigated in the cycle of the work.
The result of the interaction between the nanosecond SDBD discharge and the ejected shock wave in front of the cylinder in a flow at M = 5 is represented in ref. [65]. The gas temperature in the plasma layer was only a few tens of degrees above the flow braking temperature (T = 340 ± 30 K). The interaction between the compression wave created by the expanding gas from the discharge area and the head of the deflected shock wave causes it to shift upwards in the flow direction, thereby increasing the wavelength departure distance from the body surface by 25%.
Scaling of the Nanosecond Pulse Plasma Actuator was Investigated in [66,67,68]. Flow separation control experiments were performed on a rectangular wing (size 0.5 × 1 m2) using DBD discharge in subsonic flow with Reynolds numbers Re = (0.35–0.875) × 106 by chord. Surface pressure measurements and flow visualization showed that plasma actuators can significantly reduce or eliminate the flow separation from the wing, which results in a reduction of the negative pressure peak near the front edge on the top surface of the profile. Data were obtained from a wide range of attack angles, flow velocities, plasma excitation frequencies and input power. In works [67,68,69], the possibility of using different voltage pulses was also discussed, including microsecond and nanosecond pulses. As in [66], it has been shown that the efficiency of the actuator is highly dependent on the discharge frequency.
2.5. Surface Glow DC Discharge between Sectioned Electrodes
Calculations and experimental studies on the spatial structure of the high-speed gas flow in a flat channel with a glow surface discharge are given in works [69,70,71]. Note that in all of the listed works [69,70,71], the flow of high-speed gas near the flat surface (actually a plate) was considered. Thus, recall, the classic theory [72] of viscous–non-viscous interaction near a flat surface crossed by a flow of gas at high speed.
In this theory, the pressure distribution along the surface of the streamlined plate is related to the thickness of the growing boundary layer and is calculated using the viscous interaction parameter: , where , , , , —density and dynamic viscosity coefficient, , —speed of an oncoming flow and speed of sound in it, —distance along the surface of the plate from its front edge, and indexes and specify the properties on the outer limit of the boundary layer and in the incoming gas flow.
In the asymptotic theory of weak Lisa–Probstein interaction shown (for a flat plate with adiabatic index and the number of Prandtl , , —constant pressure specific heat capacity and thermal conductivity of the oncoming gas flow), the distribution of the pressure induced by the viscous interaction of the incident flow with the boundary layer is determined by the following dependence (with second-order accuracy of this theory): . The work [72] contains experimental data on the pressure distribution on the heat-insulated plate located at the zero angle of attack to the oncoming flow. This data is well described by the specified asymptotic theory of viscous interaction parameter values . The asymptotic theory of strong interactions gives good results when . With the first order of accuracy by obtained [72]: . A comparison of Bertram’s experimental data for heat-insulated plates with the dependency presented in [72] also indicates a good match. In the case of a glow DC surface discharge near a flat surface, the following aerodynamic coefficients are of interest. Pressure coefficient and the coefficient of friction, and the coefficient of heat exchange , where , —frictional stress and density of convective heat flow on the flat surface. These ratios suggest that for (for example: ) and coefficients and . That is, to reduce the motion resistance of the high-speed gas flow in the flat channel, it is necessary to increase the temperature (and thus the speed of the sound. Another modification of the action of high-speed flow on the surface of the plate can be organized by means of a surface DC glow discharge, either by heating the gas near the electrodes or by the action of volume forces having a Lorentz character. In this case (at a sufficiently high temperature near the surface of the discharge electrodes), the coefficient of friction may be negative with the occurrence of a reversible (negative speed) current.
First, we show the influence on the aerodynamics of the flow of the plate and on the viscous interaction characteristics of the local heating of two areas on the surface of the plate (), heat-imitating electrodes built into the streamlined surface. The temperature of the local surface heating varied between 300 and 800 K, corresponding to the surface temperature measurements of the electrodes in experiments [73,74].
The next range of determining gas dynamic parameters [75] was selected for the study of the interaction of the abnormal glowing discharge with the supersonic gas flow at the plate surface: pressure = 0.635 tor, speed = 5–8, temperature = 41–290 K. The surface temperature is assumed to be constant and equal = 290 K.
The scheme of the solved problem is shown in Figure 12. Supersonic gas flow with parameters , , , (respectively: pressure, density, temperature and speed) is applied to the sharp plate, resulting in a classical flow configuration above its surface in the compressed layer between the shock front and the surface and in the boundary layer at the surface. Two electrodes located across the direction of the gas flow are arranged on the same level as the plate surface, as shown in Figure 12.
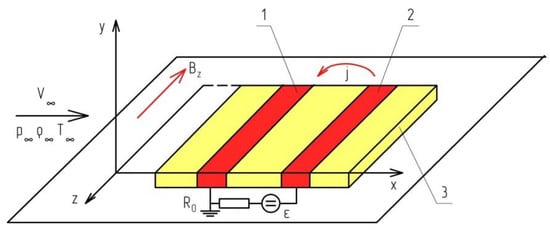
Figure 12.
Scheme of the problem of flow around a sharp plate by a supersonic flow of compressible gas, on the surface of which a DC glow discharge burns in an external magnetic field: 1—cathode; 2—anode; 3—dielectric.
The feature of the combined problem to be solved is the joint solution of a full system of two-dimensional Navier–Stokes equations to determine the properties of the compressed impact layer as well as the boundary layer between the shock wave front and the plate surface, and systems of DC glow discharge equations describing the electrodynamic structure of the current pole. To solve the equations of the glow discharge, an ambipolar model is used [75].
A comparison of the surface pressure profiles for these three series shows that, firstly, with the increase in the electrode temperature, there is a natural electrode pressure increase, which indicates the formation of shock waves departing from the areas of local surface heating. This can also be seen on pressure lines. Secondly, as the temperature increases, the disturbed pressure profile is visibly bruised, which indicates the transmission of perturbation not only by the flow but also against the flow, which can be attributed to the free interaction effect [74]. Let us note another important effect. At high temperatures in the electrodes, there is a flow separation, as evidenced by the fact .
Below are the results of the studies of the flow of the plate with heated electrodes and DC surface glow discharge switched on (Transverse magnetic field influence is taken into account). Area discharge parameters and transverse magnetic field induction correspond to experimental data [73].
A glowing DC discharge is ignited between the electrodes using an electrical circuit, powered by an electromotive power supply (EMF, ) and Ohmic Resistance . An external magnetic field may be superimposed across the flow. The external magnetic field is applied so that its induction vector is oriented either along or against the axis Z. Low-current glowing discharge with typical current I ~ 1 mA is considered with a voltage between electrodes 100–1000 volt; therefore, its own magnetic field is not considered. The characteristic value of the external magnetic induction module is selected in the range 0.01–0.5 T.
An increase in the absolute value of induction of the magnetic field to level 0.5 T leads to a natural increase in the influence of magnetic force on the flow of the plate with discharge. With parameters = 800 K, E = 1.2 kV, Ro = 12 kΩ, and B = +0.5 T, the magnetic field influence is already very strong (the pressure between the electrodes increases about twice, and near the anode it triples). The return current area in front of the anode is significantly increased (see the area ).
2.6. Pulse-Periodic Nanosecond (Volumetric) Discharge
During the pulse breakdown of a gas medium in the nanosecond and subnanosecond time domains, the development time of the electrical discharge becomes comparable to the timescales of elementary processes. For example, the time it takes for an electron avalanche to reach a critical size in such an electrical discharge is comparable to or less than the average lifetime of excited gas molecules. An important feature of this type of discharge is that the critical number of electrons and the corresponding number of excited molecules in the avalanche decrease with increasing externally applied electric field intensity. This leads to a noticeable decrease in the photon output from the electron avalanche, causing the discharge to stop being streamer-like. That is, the electron avalanche initiated by one or more electrons does not lead to the formation of a streamer and its transition into a spark (channel) discharge form. However, the formation of a large number of electron avalanches due to photoelectrons from the cathode is necessary to complete the discharge. This volume of electrical discharge is observed in air, nitrogen, and other gases under pressures ranging from a few atmospheres to several tens of nanoseconds. When a large current is reached in the discharge gap, not one but many spark channels are formed within it [76].
A particular interest is the nanosecond electrical discharge initiated by a beam of fast electrons. In this case, a pulsed-periodic nanosecond (volume) discharge can be obtained even at pressures of tens of atmospheres and with an interelectrode voltage below the static breakdown voltage [76].
Currently, technical methods for non-equilibrium plasma-stimulated ignition of fuel mixtures using pulsed-periodic nanosecond (volume) discharges are actively being discussed. Such additional non-equilibrium excitation (in addition to heating) created by the nanosecond (volume) discharge can lead to a reduction in the induction period of ignition of the fuel mixture and a decrease in the temperature limit of ignition. In this case, the impact of the gas discharge plasma on the process of igniting fuel mixtures is reduced to accumulating chemically active particles in the discharges, which participate in chain chemical reactions and lead to the ignition of the mixture. Depending on the magnitude of the reduced field strength E/N, which is realized in the discharges used, either atomic particles or electronically excited O2(a1Δg), O2(b1Σg), and vibrationally excited molecules are preferentially accumulated. The presence of electronically and vibrationally excited molecules significantly increases the rate of chain reactions involving them and allows for the possibility of igniting fuel mixtures at relatively low initial temperatures. This is significant for increasing the completeness of fuel combustion in gas streams with sharply non-homogeneous temperature profiles (when there are regions of relatively cold gas), analyzing the possibility of using lean fuel mixtures, etc.
An important characteristic of plasma-stimulated ignition of fuel mixtures is the rate of heating of the mixture in the discharge zone. Experimental studies show significantly faster gas heating (compared to vibrational relaxation times) in discharges, which is associated with the quenching of electronic excitation of atoms and molecules. “Fast” heating will be referred to as heating that occurs on timescales significantly smaller than vibrational relaxation times (VT, VV, and VV′ exchange times). In a number of experiments (see, for example, [77,78], and others), anomalously high (compared to vibrational relaxation rates) gas heating rates at the initial stage of discharge combustion were observed at E/N > (80–100) Td fields. Additionally, up to 10–15% of the discharge energy was delivered to heating the gas, with noticeable dissociation of oxygen molecules (the degree of dissociation reaches 50%).
This study [79] is devoted to investigating the conditions of ignition and subsequent formation of a combustion wave in an acetylene–air stoichiometric mixture near a high-voltage electrode of the surface barrier discharge. In this experiment [79], ignition and spreading of the combustion wave in the air and C2H2 mixture were observed at P = 1 atm and T0 = 300 K. Based on the 2D discharge calculations and estimates of ignition in [79], it was concluded that it is possible to ignite the fuel mixture in the cathode region of this discharge with a single nanosecond pulse.
Experimental studies on the use of several plasma actuators have been carried out simultaneously in [80]. In this study [80,81], the problem was formulated as follows: Near a metal wall simulating the surface of an electrode, a hot layer of thickness 0.01 mm was created using a heat source for 40 ns. The power of the source was chosen such that by the end of its action, the maximum temperature in the layer was approximately T0 ~ 1500 K, according to calculations [79]. The initial concentration of O atoms in the layer, [O]0 = 1.5 × 1018 cm−3, was taken from [79] in the hot zone near the edge of the electrode. The goal of the modeling was to determine the conditions under which the mixture ignites and a combustion wave forms before the layer cools due to heat transfer to the metal electrode. One-dimensional numerical modeling is based on solving the Navier–Stokes equation together with mass conservation equations for each component [80]. A kinetic equation system was written for 103 components and 700 reactions. The results of testing the system and the main reactions are presented in [81]. The calculations show that even during the discharge stage (40 ns), fuel conversion begins in the mixture, resulting in the formation of CO and H2. The hot region with partially converted fuel expands, and ignition begins at 4 microseconds. The temperature increases, including due to the combustion of CO and H2. At first, the flame front moves towards the electrode, then the temperature drops due to cooling, the flame front changes direction, and then it all repeats; overall, the region expands. Ignition occurs only in the hot layer (T = 1500–2100 K), without taking into account oxygen atoms accumulated during the discharge. Overall, work [81] has shown that thanks to nanosecond discharge actions, a decrease in the initial ignition temperature by 250° and the induction time by 100 times can be achieved.
2.7. Magnetoplasmic Control in High-Speed Gas and Plasma Flows
Let us consider the possibility of magnetoplasmic control in high-speed gas flows using the example of the concept of accelerated deceleration and electromagnetic thermal protection [82] of the surface of a spacecraft (the returning capsule of the Stardust spacecraft). In this case, the high speeds of the spacecraft (8–12) km/s and large transverse geometric dimensions ( m) lead (in the region of flow deceleration, i.e., the front critical point) to high temperatures (10–12) K and degrees of ionization (which can reach values of 10–20%) of the gas-plasma flow. In this case, the thermodynamic state of the plasma is close to equilibrium. The idea of accelerated deceleration of the spacecraft in the upper atmosphere—the MHD parachute—is to prevent high thermal loads on the surface, rather than protect it, by providing MHD braking at altitudes where thermal fluxes are still low. Effective braking can be achieved in plasma volumes much larger than the nose of the spacecraft. Additionally, organizing MHD interaction at such scales potentially does not require the creation of high magnetic field values. Under the conditions considered, it can be expected: (a) a very intense MHD interaction (MHD interaction parameter estimation 1–50) with a significant reduction in the influence of the Hall effect; (b) the possibility of a noticeable influence of the self-induced magnetic field generated by currents in the plasma (Reynolds magnetic number estimation (2–15). The magnetohydrodynamic (MHD) interaction parameter (Stewart parameter) represents the ratio of the mean integrated ponderomotive force to the total momentum flux . The sign “< >“ represents the mean integral over the volume of the function . The magnetic Reynolds number is defined as: , where —the magnetic permeability of vacuum; —the mean integrated conductivity of the spatial domain estimated from flow parameters with zero magnetic field, —the maximum transverse size of the spacecraft, and —the gas dynamic parameters of the inflow to the spacecraft.
In works [82,83,84,85,86,87,88,89], the magnetic field created by a magnetic coil (see Figure 13) with an inner radius of Rm = 0.14 m (Magnetic System (MS) 1 magnet) located in the nose of the spacecraft and a coil with an inner radius of Rm = 0.28 m (MS 2 magnet) located near the maximum cross-section were considered. The magnetic coil consists of a current-carrying loop, so the magnetic field in the flow region closely resembles a dipole field. The results obtained were typical for all studied modes at six points of the spacecraft trajectory (ranging in altitude from H = (81–51) km and corresponding velocities V = (12385–7936) m/s).
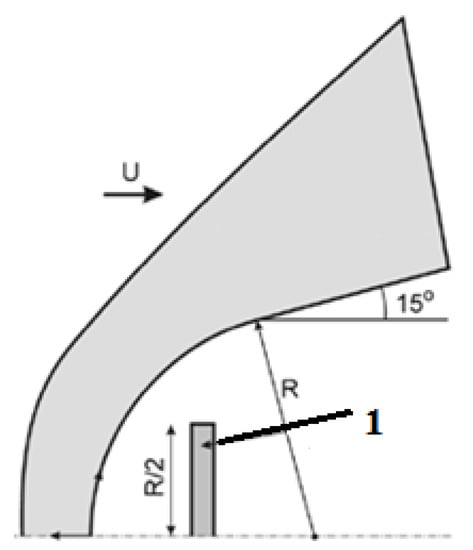
Figure 13.
Geometry of the spatial region in the case of magnetoplasma control of the motion of the descent spacecraft. 1—magnetic field source (electromagnetic coil).
It should be noted that there is a significant decrease in the heat flux density at the spacecraft surface for magnetic field amplitudes of B = 0.1–0.2 T. Additionally, the larger magnetic system (MS 2) contributes to a greater reduction in the heat flux at the surface of the heat shield compared to the MS 1 magnetic system. However, there is an increase in the heat flux in the aft section of the spacecraft. When using the smaller MS 1 magnetic system, a recirculation zone is formed downstream of the magnetic system, causing a dip in the heat flux distribution. This dip becomes deeper the lower the role of viscous effects, i.e., at lower altitudes. Nevertheless, the decrease in the heat flux in the nose (spherical) part of the spacecraft is less than in the case of MS 2, and there is a rise in the heat flux in the mid-section.
An important distinguishing characteristic of all modes considered is the saturation effect of heat flux. The decrease in heat flux occurs until a certain magnetic induction value (specific to each mode) is reached. Upon exceeding this value, the heat flux distribution either changes slightly or even rises. The saturation of the heat flux weakly correlates with increasing shock wave distance from the surface of the body and an increase in magnetic induction.
Therefore, the commonly accepted viewpoint that the decrease in heat flux is due to the decrease in the mean temperature gradient in the shock layer as a result of the shock wave’s distance from the body’s surface is not entirely accurate in this case. The impact of the magnetic field on heat flux is only effective in areas with high temperature and concentration gradients, i.e., near the wall. With an increasing shock layer thickness, the temperature in most of the layer tends to an equilibrium value, and the temperature gradient, which determines the heat flux to the wall, stabilizes.
The concept of accelerated deceleration of the spacecraft in the upper layers of the atmosphere, the MHD parachute, proposed in works [83,84], is based on the generation of current interaction in the plasma of the shock layer with the magnetic field created by the onboard magnetic system. The estimates conducted for the conditions of the experimental installation show the possibility of increasing the hydrodynamic drag tenfold. Estimates of the effect for real atmospheric conditions indicate that significant interaction can only occur near the critical point of the body, where the high temperature in the shock layer may provide a degree of ionization of the air sufficient to create intensive MHD interaction. Downstream from the surface of an elongated object, the degree of ionization at a level of 10−4 and below is clearly insufficient to provide an acceptable level of electrical conductivity of about 103 Siemen/m. At the same time, attention was drawn to the fact that the value of the induced electric field can reach hundreds of Townsend in the area of interest for the MHD parachute and/or onboard generator.
Now consider the possibility of ionization in a strong, induced electric field. Initial estimates of the effect of non-equilibrium “field” ionization for the “MHD parachute” configuration [85,86] demonstrated a significant effect: the degree of ionization of the air plasma reached several percent at very moderate values of magnetic induction. As for the MHD effect of field ionization, calculations have shown a three-fold increase in resistance.
Next, the effects of non-equilibrium ionization in hypersonic nitrogen flow generated by a magnetic field (MHD parachute/generator configuration) are considered. It is assumed that the traditional (thermal) chemical kinetics are valid for the N2, N, N2+, N+, and electron mixtures. In addition to this, the kinetic scheme contains ionization reactions of N2 and N by electron impact, dissociation reactions of N2 by electron impact, and corresponding reverse reactions of recombination and association. It is assumed that the rates of forward reactions are determined by the value of the reduced electric field, E/N0 (E—the magnitude of the field intensity, N0—gas number density). The rate constants of the reverse reactions are considered to be functions of the electron temperature. When calculating the transport properties of the mixture, it is assumed that the collision frequencies of processes involving electrons are determined by the electron temperature. The electron temperature is found through the solution of the electron energy transport equation, taking into account the tensor nature of electron thermal conductivity, the inflow of energy from the electromagnetic field, and elastic and inelastic losses. The latter includes losses due to ionization and dissociation in electron impact reactions, as well as losses from the excitation of vibrational and electronic states of neutral components. The field kinetics model and inelastic loss model were developed based on works [86,87,88,89].
2.8. The Possibility of Controlling the High-Speed Flow of Gas and Plasma Using Pulsed Optical Discharge or Microwave Discharge
Optical breakdown by coherent laser (or broadband) radiation in a gas medium can be described based on the following sequence of stages: the appearance of initial electrons as a result of multi-photon ionization, avalanche ionization of the gas in the focal region of laser radiation, absorption of laser energy by the gas-plasma medium, and intense expansion of plasma into the surrounding space with the formation of a shock wave [90,91,92]. It should be noted that optical breakdown is usually defined as a fast, irreversible process of transforming (a condensed or gaseous) medium from a transparent to a strongly absorbing medium (with the destruction of its internal structure) under the influence of intense radiation.
There are two main physical mechanisms for electron multiplication in gas under the influence of radiation.
The first mechanism is multi-photon ionization (in this case, the electron density increases linearly with time), in which a neutral particle simultaneously absorbs a sufficient number of photons for ionization. In the process of ionization, the energy of photons absorbed by the elementary particles of the medium must exceed the ionization potential I (in air eV): hν > I. As the energy of radiation quanta in the visible and near-IR ranges of the spectrum is usually about 1 eV, the ionization of air molecules by a laser must be multi-photon.
The second ionization mechanism is based on the absorption of laser radiation by free electrons in processes of inverse bremsstrahlung. This physical process causes avalanche ionization, in which the electron density increases exponentially with time. As avalanche ionization develops further, the resulting plasma begins to efficiently absorb the energy supplied by laser radiation. In addition to thermal radiation from the plasma, there are other physical mechanisms that lead to gas ionization, including molecular, atomic, electronic heat conduction, and gas heating behind the shock wave front.
The spatial region of high-frequency discharges (a type of gas discharge that occurs in the presence of high-frequency electromagnetic fields) is determined by the processes of shock ionization of gas molecules and atoms by electrons accelerated in a high-frequency electromagnetic field. The development of these physical processes is limited by the process of electron diffusion from the localized region in space where the amplitude of the high-frequency (HF) electromagnetic field is maximal, as well as by processes of their recombination with ions, or “adhesion,” to neutral molecules and atoms [55]. The amplitude of the HF field required for the breakdown and development of high-frequency discharge increases with increasing gas pressure P and frequency of the field f [55].
One advantage of optical or microwave discharges (compared to other types of discharges) is the ability to heat the gas-plasma medium at a significant distance from the source of electromagnetic radiation. It should also be noted that the experimental results in works [93,94] indicate the possibility of reducing the breakdown threshold (by using laser initiation) in a supersonic flow for microwave discharge. These works [93,94] revealed that by choosing parameters (geometry of laser and microwave focusing systems, temporal and energy parameters of microwave and laser radiation pulses), it is possible to position the microwave discharge in the thermal trace of the laser breakdown area and also to control its shape (length).
Several works [60,61,95,96] (microwave radiation, lasers) related to the creation of plasma formation in the atmospheric conditions in front of a body moving in a high-speed gas flow will be considered. The work [97] presents the results of controlling the structure of the head shock wave with a microwave discharge. A spatial region with a temperature of 2800 K (at a heating rate of ~2000–3000 K/μs) was formed within 1–2 ns and had a transverse dimension of no more than 3 × 10−3 cm at a specific energy contribution of about 7 eV per particle with a peak electron density Ne ≅ 5 × 1016 cm−3. The work [97] showed that the energy efficiency of the microwave method of reducing stagnation pressure at the leading critical point is directly proportional to the ratio D/d, where D and d are the diameters of the blunt body and the heated region, respectively. The universality of this relationship was confirmed in works [98,99] (for model diameters from 8 to 30 mm). These same results confirm the important conclusion about the increase in efficiency (reduction of aerodynamic drag with a decrease in the thickness of the heated layer) when the microwave discharge interacts with the boundary layer.
The work [100] presents an experimental and theoretical analysis of controlling the trajectory of fast-rotating supersonic objects using a laser spark. Based on the obtained experimental and theoretical data [100,101], it was concluded that controlling the trajectory of rotating objects with laser discharges is highly effective.
The first series of experiments in works [100,101] demonstrated the destabilization of the rotating object with a single laser spark. In the second and third series of experiments, the dynamics of the angle of attack change of the object were analyzed using three consecutive laser sparks, following each other with intervals of 50 to 100 μs. In all three cases, the possibility of destabilizing the trajectory of a rotating object was demonstrated. The duration (~50 ms) of the disturbance of the object’s axis corresponds to the time of propagation of the hot spot along its surface. The gas region of low density in front of a fast-spinning supersonic object causes a redistribution of pressure and maintains the development of the trajectory disturbance. However, a non-central impact on the fast-flying object can lead to a disruption of symmetry in the distribution of forces and significantly alter its trajectory. After the hot spot formed by the laser spark leaves the interaction region, the disturbance of the object’s rotation axis decreases. An increase in the number of consecutive pulses increases the duration of the unstable motion of the object. Thus, the ability to control the trajectory of a spinning object depends heavily on the duration of the interaction, which is limited by the length of the laser spark in the direction of the object’s motion.
Note that the main mechanism of interaction of laser plasma with a stream (regardless of the duration of the laser pulse) is the heating of gas due to plasma breakdown. On the other hand, the reduction in resistance obtained in such experiments and calculations usually becomes significant only for blunt bodies. If the object has high aerodynamic qualities, obtaining a significant reduction in the drag coefficient is usually difficult [101].
3. Methods for Controlling Plasma-Stimulated Combustion in High-Speed Gas and Plasma Flows
3.1. The Fuel and Air Components
It is known that in the engine of a promising aircraft (in the combustion chamber), the main part of the fuel and air components has a supersonic speed. In this situation, special requirements must be met by the fuel and combustion chamber geometry. With a relatively short residence time ( s) of the combustible mixture in the engine of a promising aircraft, the problem of organizing effective () mixing of fuel and oxidizer, ignition and combustion stabilization is particularly acute.
Thus, the most important problems facing developers of plasma thrusters are the stimulation of fuel and air mixing, acceleration (up to supersonic speeds) of the combustion wave, and preferably, volumetric ignition of the fuel mixture. Usually, in fuel–air mixtures, the combustion wave is mainly determined by heat transfer processes. However, if the energy released in the area of the combustion wave is somehow directed by non-chemical means, the propagation speed of the “heat conductivity wave” will sharply increase. Even with significant turbulence in the combustion area, heat transfer processes alone may not provide sufficient combustion wave propagation speed. Electrical discharge technologies, based on creating plasma formations using electric discharges, laser or microwave plasma, can be effective ways to reduce ignition time [102] and control supersonic gas flows in the power plants of advanced aircraft. The idea of using plasma fuel ignition methods is based on the non-equilibrium generation of chemically active particles or clusters that accelerate the combustion process. It is assumed that the possible gain in energy expended for accelerating combustion in plasma methods is achieved by creating a non-equilibrium state of the plasma during the discharge. This plasma state allows for the creation of a “quasi-equilibrium” (preferably volumetric) concentration of radicals directly in the flow or to introduce them (from the point of generation) into the flow from the outside. Obviously, the magnitude of the combustion acceleration effect depends heavily on initial temperature, pressure, fuel mixture composition, and methods of plasma generation.
3.2. Initiation of Combustion of the Fuel-Air Mixture by an Electron Beam
In [103], experimental and theoretical studies on the initiation of combustion in an oxygen–hydrogen mixture (the initial pressure of the mixture is 500 Pa) using an electron beam with an energy of keV and an average transverse size of the beam of cm. The progress of the reaction was observed by registering the temporal dependence of the intensity of the glow in the lines of molecular (λ = 310 nm) and atomic hydrogen and the sodium doublet (λ = 589 nm). Experiments and calculations carried out in [103] showed that the generation of radicals in the oxygen–hydrogen mixture accelerates ignition by significantly reducing the time taken by the so-called induction stage. Thus, with the use of high-current, low-energy electron beams, the combustion reaction of hydrogen in oxygen can be initiated at different concentrations of the mixture. It is also worth noting that electron beams can be used in conjunction with ignition devices, such as pulsed high-temperature laser jet devices.
3.3. Initiation of a Detonation Wave by Laser Radiation
Let us consider the possibility of initiating a detonation wave with laser radiation in a supersonic flow of hydrogen–oxygen mixture [104]. The implementation of detonation combustion of the mixture in a supersonic flow makes it possible to significantly reduce the length of the energy release zone compared to conventional homogeneous or diffusion combustion modes, as well as to obtain higher values of gas temperature (and therefore efficiency) and pressure [105]. A significant number of studies [106,107,108,109,110] have been devoted to analyzing the possibility of implementing detonation combustion in combustible mixtures moving at supersonic speeds. The main tasks when implementing detonation combustion are the stabilization of the detonation wave in the supersonic flow and the initiation of mixture ignition at low gas temperature values.
The simplest flow scheme in which stabilization of the detonation wave is achieved is the flow around a wedge or cone by a supersonic flow of the combustible mixture. Ignition occurs ahead of the inclined shock wave front, centered in the sharp part of the wedge. In this case, the detonation wave is formed at a certain distance from the surface of the wedge as a result of the interaction of the compression wave, arising in the combustion zone (heat release), with the inclined shock wave front [106]. At small wedge opening angles ( = 8–10°), the distance at which the detonation wave is formed in the practically interesting range of flow parameters (pressure = 103–104 Pa. temperature 400–700 K, and Mach number 4–6) is too large (10 m) even for the hydrogen–oxygen mixture [111]. Therefore, the search for methods to intensify the processes of detonation wave formation in such geometry is an extremely important task.
Research conducted in works [112,113] has shown that a significant reduction in the length of ignition zones and heat release (and the distance at which a detonation wave is formed in supersonic flows of H2/O2 (air) and CH4/O2 (air) mixtures behind an inclined shock-wave front can be achieved by exciting O2 molecules to an electronic state . For example, this can be performed by laser radiation with a wavelength = 762 nm generated by a diode laser, even at low values of energy irradiated to the gas ( J/cm3).
In [114] (based on numerical experiments), an initial assessment was given of the possibility of intensifying ignition of an oxygen–hydrogen mixture in an LPP channel by laser plasma generated near a condensed barrier. The numerical analysis of the formation, expansion, and ignition of the fuel mixture, taking into account the effect of the external gas flow on the laser beam, shows that the pressure increases four-fold and the molar concentration of H2O increases by approximately 20 times (compared to the stagnant gas medium) in the interaction region. Overall, the following parameters of laser radiation are required to create laser plasma in LPP channels: laser beam intensity <1.5 × 109 W/cm2, pulse energy of several mJ, duration of laser radiation of hundreds of ns, and a pulse spacing of >5 Hz.
In [104], the flow around a wedge-shaped body with a semi-open angle in a supersonic flow of H2/O2 was considered. Laser radiation with a wavelength = 762 nm and uniform intensity throughout the affected area, is applied to the flow in a certain region before the wedge nose, with a length along the flow of and a height of . The frequency of this radiation, v, is resonant with the frequency of the bound-electron electronic transition, of the molecule , where and — vibrational, and and —rotational quantum numbers in the states and -e, respectively. Given and the absorption coefficient for the considered electronic–vibrational transition is maximal at a gas temperature of T = 300 K. Parameters of the supersonic flow ahead of the affected area: = 104 Pa, = 500–600 K, = 6.
As a result of the calculations presented in work [104], it has been shown that exciting molecular oxygen to the electronic state with resonant laser radiation at a wavelength of 762 nm (transition , , ) enables the realization of detonation combustion during the supersonic flow of hydrogen–oxygen mixture around a wedge at distances no greater than 1.5 m from its nose, even at low irradiation energy to the gas of and a gas temperature of T = 500–600 K. In the absence of irradiation at such flow parameters, it is not possible to stabilize the detonation wave at distances less than 5.5 m from the wedge nose.
The effects of reducing the length of the ignition zone and the zone of detonation wave formation (Figure 14) are due to the intensification of chain reactions resulting from the presence of electronically excited molecules , and in the reacting mixture and the formation of new channels for the formation of active atoms O, H, and OH radicals in the reactions involving these molecules. It has been found that to stabilize a detonation wave in a supersonic flow over a wedge at small distances from the affected area ( < 1.5 m), it is sufficient to irradiate a narrow axial region of the flow with a transverse size of = 0.5–1 cm directly in front of the wedge nose. Laser-induced excitation of molecules is much (several times) more effective than simple heating of the medium by laser radiation for initiating detonation combustion in a supersonic flow of the fuel mixture. This method of energy transfer from laser radiation to the flow allows even a small volume of gas to be irradiated with a sufficiently weak source to stabilize a detonation wave in a supersonic flow at distances acceptable for realizing a detonation combustion mode.
Figure 14.
Scheme of flow and laser exposure.
3.4. Ignition of a Combustible Mixture by a Laser Torch Formed near a Condensed Barrier
It should be noted that there are two types of breakdowns: breakdown of the vapor of the condensed material and breakdown of the surrounding gas medium target [115,116]. In the case of laser irradiation of a condensed obstacle, the laser beam, propagating into the combustible mixture at supersonic speed, is both the source of radicals and the region of thermal exposure. It is known [115,116] that in an unbounded gas medium (in this case, air), the required laser irradiation flux density for a CO2—laser is 109 W/cm2, and for Nd—laser is 1011 W/cm2. However, the presence of a metallic barrier significantly reduces (by several orders of magnitude compared to an unbounded gas medium) the required density of the radiation flux for gas breakdown . This phenomenon is explained by the high-temperature ionized layer (usually consisting of easily ionizable vapor of the obstacle) that forms on the surface of the target under certain critical conditions and which intensely absorbs the incident laser irradiation. The breakdown occurs in the focus region of the laser beam, where there are strong spatial-temporal inhomogeneities of the electric field. The breakdown is possible if so-called seed electrons (for example, by the thermoelectron emission mechanism) enter the breakdown region and if the probability of electrons escaping from the focal spot volume is low (the probability of this process is determined by the electron diffusion coefficient).
To obtain the breakdown criterion, the following relationship is used to estimate the rate of generation of “seed” electrons (at a distance of the radius of focus ) due to ionization : , where —the concentration of vapor atoms; —is the concentration of electrons; —the ionization coefficient of the obstacle vapor, , —the statistical sum of the residual ion and the statistical weight of the ground state of the atom, and —the ionization potential and is the electron temperature in eV. Comparison of the electron diffusion rate (—the diffusion coefficient) and the convection rate (—the velocity of vapor motion) indicates that electron losses will be determined by convective transport. Thus, the breakdown criterion (due to its exponential dependence ) takes the form [117]: or (for example, for titanium obstacle breakdown, the laser irradiation flux density is about MW/cm2).
3.5. Photoplasmodynamic Method of Combustion Initiation
Solving a complex problem like combustion in high-speed gas flows () requires new methods to intensify the physical and chemical processes of mixing and combustion of mixtures. To address this type of problem, the photoplasmodynamic method has been proposed and experimentally studied, in which powerful electric discharges (MPC, capillary discharge, LSSD, etc.) are carried out directly in the combustible medium. As a result, the fuel mixture undergoes a combined (and volumetric) effect of UV radiation, plasma, and UV that initiates complex photochemical, plasmachemical, and thermobaric reactions in the medium. As a technical device that implements this approach, the end-type MPC electrode assembly can be provided. This electrode assembly (see Figure 15) is a system of separated interelectrode dielectric inserts between coaxial electrodes.
Figure 15.
Plasma-dynamic discharge (magnetoplasma compressor-MPC) of an erosive type in a gaseous medium: 1—discharge electrodes; 2—plasma of gas and (or) erosion products of the structural elements of the electrode system; 3—interelectrode dielectric insert (MID); 4—shock-compressed gas region; 5—undisturbed gas medium; 6—external radiative magnetogasdynamic discontinuity.
The physical processes occurring in a magnetoplasma compressor can be described as follows. After this, the capacitive accumulator begins to discharge into the interelectrode gap, and the main high-current stage of the discharge occurs. From this moment on, the composition of the electrodischarge plasma is determined by the erosion products of the MHD accelerator electrodes, which are mainly formed under the influence of radiation fluxes from the plasma. The accelerated magnetohydrodynamic force of light-erosion plasma is decelerated by the surrounding gas. In the radially non-uniform plasma flow impinging on the gas barrier, a complex flow structure with a system of shock waves and contact boundaries arises (see Figure 16).
Figure 16.
Gas-dynamic structure of the region of shock deceleration of the plasma flow of the MPC-discharge on a dense gaseous medium.
Thus, in the case under consideration, the interest lies in the MHD discharge created in the deformed (due to deceleration on the “dense” gas medium of the erosion plasma flow of the MHD compressor) gas medium. In the one-dimensional approximation, the gas-dynamic structure of the deceleration zone (the configuration of the shock wave decay) consists of two shock waves (in the plasma flow SWII and in the undisturbed gas SWI) and a Contact Boundary (CB) separating the regions of shock-compressed gas and plasma. Let us present the relationships that connect the parameters of the shock-compressed gas-plasma medium in the deceleration zone. The velocity of the contact boundary , is determined by the velocity of the plasma flow and the ratio of the initial densities of the plasma and the undisturbed gas medium . We will consider the contact boundary as a piston moving at a velocity in a “stationary” (relative to the piston) plasma with a density . Then, the density , pressure and temperature of the shock-compressed plasma behind the SWII front will be equal to: , , , where —the adiabatic index, average molecular weight, and average ion charge of the shock-compressed plasma (SWII).
The expressions for the expansion velocity of the shock-compressed plasma region and the velocity (shock wave SWII in the laboratory coordinate system) are: , . From these relationships, it follows that depending on the initial parameters, two characteristic modes can be distinguished in the region of shock deceleration of the MHD discharge plasma flow: shock wave acceleration mode and deceleration mode [118].
The shock wave acceleration mode is implemented when the density of the driving plasma flow is of the order of or exceeds the initial density of the gas medium and is most effective when . In this case, the efficiency of transferring the kinetic energy of the high-speed flow to shock-compressed gas energy is at its maximum, reaching 50%.
The braking mode is realized when the density of the plasma flow is significantly higher than the density of undisturbed gas . In this case, about 70–90% of the kinetic energy of the plasma flow is converted into the internal energy of the shock-compressed plasma.
However, it should be remembered that the MPC discharge in practice has a spatial 3D gas-dynamic structure. This structure approximately (there is a difference: there is a cumulation zone near the central electrode) corresponds to the flow structure in an underexpanded gas jet [119,120] flowing into a flooded space. For example, in a radially inhomogeneous plasma flow incident on a gas barrier, not a straight line arises, as was considered above (in the 1D approximation), but a conical magnetogasdynamic shock wave, in front of which the velocity component normal to the boundary with the gas is triggered and the pressure and plasma temperature increase.
To clarify this flow structure, a 2D physical and mathematical model was formulated in [119,120], and a numerical study of MPC discharges in gases was carried out for a wide range of changes in the main electrical parameters and characteristics of the surrounding gaseous medium. The features of radiation-plasmadynamic structures were revealed, and the behavior of the main parameters of the MPC-discharge plasma was described [119,120].
In [121,122,123], the results of experimental studies on the possibility of using a small-sized MPC operating in the frequency mode for the combustion of an air–propane mixture in a high-speed flow are presented. In these works [121,122,123], a series of control experiments were carried out to determine the performance of this design of a small-sized MPC and the possibility of using it to initiate the volumetric ignition mode and combustion of the fuel mixture in a supersonic flow. The results of the experiments performed almost completely coincided with the data given in [124,125] for a classical high-power MPC, namely: a sharp pressure jump was observed when a discharge was triggered in an air–propane mixture, and a pressure wave propagating towards the flow was recorded. The average propagation velocity of this wave was ~200 m/s, which also agrees with the data in [124,125]. Similar to [124,125], a decrease in the duration and an increase in the leading edge of the signal were recorded when the combustion wave entered the ballast chamber.
The totality of the established facts [121,122,123,124,125] allows us to state that in the control experiments carried out, the regime of volumetric ignition and combustion of an air–propane mixture initiated by plasma created by a small-sized MPC is realized. From the experimental results in [121,122,123], the following initial conclusion can be drawn: it is possible to implement volumetric ignition in the frequency mode of operation for this MPC design. The maximum operating frequency of the installation is approximately f = 25 Hz. A further increase in frequency is possible either with an increase in the initial voltage on the storage capacitor or with a decrease in the resistance in the electrical circuit of its charge, i.e., in any case, with an increase in the charging current of the capacitor bank used to store energy in the MPC discharge. It was also shown in [121,122,123] that by changing the magnitude and orientation of the induction vector of the external magnetic field relative to the direction of the discharge current, it is possible to influence the processes of plasma-assisted ignition of an air–propane mixture in a supersonic flow.
3.6. Capillary Discharge and Ignition of the Combustible Mixture
The erosive plasma characteristic of a pulsed plasmodynamic capillary discharge can also be used to initiate the ignition and combustion of supersonic fuel mixtures [126,127,128,129].
Figure 17 shows a schematic representation of a capillary plasma torch. It consists of two electrodes placed in a cone-shaped housing made of dielectric (4) at a distance of 5 mm from each other. Between the electrodes, there is a washer made of plexiglass with a channel 1–2 mm in diameter (2). The inner electrode (3) is made of graphite and is a washer 10 mm in diameter and 5 mm thick. A hole with a diameter of 3 mm was made in the copper outer electrode (1), which is cone-shaped.
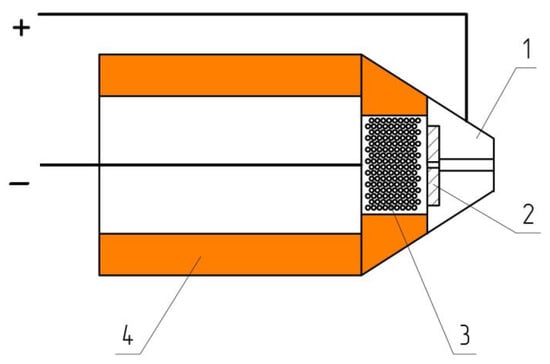
Figure 17.
Capillary plasmatron structure. 1—anode, 2—puck of organic glass, 3—cathode, 4—body of insulation material.
In works [126,127,128,129], the process of interaction of a capillary discharge with a supersonic air flow was studied experimentally as well as by the theoretical method [130,131,132,133,134,135,136,137,138,139,140]. It is shown that, depending on the initial conditions (the power released in the discharge, the speed of the incoming air flow, the initial pressure in the channel, etc.), the plasma jet created by the capillary discharge can either penetrate into the flow at insignificant distances (cm) or propagate along its outer borders. At low values of current (100 A) and stored electrical energy (200–400 J), a subsonic plasma jet is formed, which penetrates into a dense gas at distances significantly exceeding the characteristic dimensions of the electrode system.
The maximum velocity of the plasma jet propagation along its axis is 300 m/s (at a pressure of 80 Torr in the chamber) and 450 m/s (at a pressure of 20 Torr). Thus, the jet velocity depends on the pressure of the gas mixture. At low pressures, when the plasma velocity is comparable to the flow velocity, the jet deflection angle in the flow is close to zero, while at high pressures (at low plasma velocities), the jet practically propagates along the flow and the deflection angle approaches zero. The results of [126,127,128,129,130,131] show that the main parameter that determines the nature of the interaction of plasma jets with supersonic air flows is the power released in the discharge. When the power decreases to values ≤ 0.8 mW (capillary discharge), the plasma propagation velocity decreases, and it practically does not penetrate into the flow.
4. Discussion and Conclusions
The purpose of this review, «Computational and experimental modeling in magnetoplasma aerodynamics and high-speed gas and plasma flows» is an analysis of the current state of the methods of non-contact management of aerodynamic quality and/or other characteristics of aerodynamic bodies, methods for establishing the AA command and control forces, and magnetoplasma methods of control of combustion and combustion processes in flow combustion chambers.
The first factor determining the efficiency of high-speed gas and plasma flow control using plasma actuators is their location in key (down points of the shock wave, as well as braking, separation and mixing of the flow) areas of the surface of the AA facility and flow. The second important factor in magnetoplastic gas plasma flow control near AA is the energy actuated in a single pulse as well as the frequency of the plasma actuator. Various experiments have been shown to have an effective impact on the configuration of shock waves and ripple currents. The Struchal number range should be close to one. Thus, the effective application of plasma actuators is determined by their ability to control the speed, position, frequency and intensity of energy output in the gas-plasma flow.
The most famous plasma actuators are based on plasma dynamic discharges. In this case, the flowing pulse current is very large (from 10 kA to 1 MA), and the energy in the pulse is about kilojoules and above. The review provides a brief description of experimental and computational theoretical studies of such plasma actuators. These include magnetoplastic compressors, capillary plasmotrons, longitudinal transverse electrode discharges, linear-stabilized discharges. The results described above show that gas discharges and plasma jets from these plasma actuators can significantly change the flow pattern (for example, a linear-stabilized discharge) and, in particular, reduce their resistance and thermal loads on them (especially at supersonic and hypersonic flow speeds).
Despite the noticeable progress in the research of plasma actuators, a number of problems should be noted that have yet to be solved in the future. Here, we mention only the most important of them. The first problem includes an insufficient understanding of the physics of processes in plasma actuators as well as their interaction with an aerodynamic flow or a combustible mixture. For example, we would like to have a number of clearly defined criteria that indicate the degree of efficiency of using various types of actuators in a particular practical situation. The second technical problem is the need to develop a powerful, reliable, compact energy source with a high response frequency (in particular, this is necessary to avoid the development of various types of plasma instabilities in the flow).
The review considers the physics of processes in high-current pulse discharges (magnetoplasma compressor, capillary discharge, etc.) and the main mechanisms for generating highly uneven plasma in high-speed gas flows.
In the case of a magnetoplastic compressor, the main parameter determining the interaction of plasma jets with supersonic air flows is the power emitted in the discharge. At a power of ~20 MW, the speed of propagation of the jet from the magnetoplast compressor is several times faster than supersonic flow at M = 2, so the flow practically does not affect the plasma jet. When the power is reduced to ~0.8 mW, the plasma practically does not penetrate into the flow because its speed becomes less than the flow rate. When the discharge power is further reduced to ~3 kW, the plasma jet follows the flow and spreads along it.
These types of discharges can create areas of heated plasma away from their main gas flow area. Such discharges can provide a volumetric ignition mode by heating with thermal conductivity and UV radiation. Thus, MPC pulse plasma can be used for volumetric ignition of supersonic fuel mixtures, while capillary, longitudinal transverse and linearly stationary discharge can be used for emergency ignition along the flow.
This paper considers the use (at high and ultra-high surges) of non-equilibrium plasma from pulsed nanosecond «barrier» and «sliding» surface discharges as plasma actuators. Note that for any of these discharges, the main factor determining their applicability for gas plasma flow control is that due to the impulse-localized energy output, it is possible to create a relatively dense plasma in the flow cm−3 (at a typical specific energy input of 0.05–0.5 eV per molecule in electronic degrees of gas freedom) with less cooling time (for example, due to gas-dynamic expansion) in the plasma region.
In these nanosecond discharges, the significant excess of the amplitude of the electric field over the threshold («penetration») value allows the electron ensemble to be rapidly heated. At a fixed direction of the electric field vector (for example, in high-voltage discharges with pulse durations in the nanosecond range), this results in the rapid achievement of the ionization threshold by electrons and the effective formation of highly uneven plasma. In this way, the highest efficiency and speed of energy relaxation are achieved precisely at high and ultra-high values of electric fields, when the preferred type of gas excitation is the creation of highly excited states of molecules and ionization. In this case, rapid quenching of highly excited particles and recombination of plasma lead to the formation of atoms and molecules with high energy in progressive degrees of freedom, which can exchange their energy with the rest of the gas in several collisions. This situation is quite different from the excitation of oscillating degrees of molecular freedom under moderate electric fields, when the relaxation of the excitation and an increase in the temperature of the gas can take a long time in terms of gas dynamics.
For the microwave and laser discharge conditions considered in the overview, the gas-plasma flow has comparable (depending on the conditions) free time paths for the electron and time of field direction change. Thus, to achieve the electron energy (ionization) necessary for the development of electronic avalanches, it may require a large number of cycles of electromagnetic field change. In this case, the stresses of electric fields in these discharges should be significantly higher than in the case of a pulsed high-voltage discharge with a pulse duration in the nanosecond range. The need for an allocated spatial direction of energy input (which goes mainly to the excitement of highly energetic states) is dictated by the need to quickly convert the excitation of the internal and chemical degrees of gas freedom into thermal energy, which can be used for flow control.
As a result of experimental and theoretical studies of microwave discharge, it is shown that both rich and poor combustible mixtures ignite, and the combustion intensity is maximum for stoichiometric mixtures under low-temperature plasma surface microwave discharge. It has been shown that the induction period decreases from 1 ms to 5 μs with an increase in E/p from 40 to 200 Tds. The propagation rate of the front edge of the combustion region, dependent on the equivalent ratio of mixture and microwave feed, reaches its maximum in the stoichiometric mixture and reaches 160 m/s at E/p = 150 Td. The combustion temperature in these conditions is about 3000 K.
The above examples point to aerodynamic quality management (at both subsonic and supersonic speeds), by non-stationary currents with the help of small influences, by flow in short-term inseparable modes, ignition and combustion and other characteristics of AA.
Author Contributions
Conceptualization, V.V.K.; formal analysis, S.V.R.; data curation, V.V.K.; writing—original draft preparation, V.V.K. and S.V.R.; writing—review and editing, S.V.R. and A.Y.V.; visualization, V.V.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bletzinger, P.; Ganguly, B.N.; VanWie, D.; Garscadden, A.J. Plasmas in high speed aerodynamics. Phys. D Appl. Phys. 2005, 38, R33. [Google Scholar] [CrossRef]
- Moreau, E.J. Airflow control by non-thermal plasma actuators. Phys. D Appl. Phys. 2007, 40, 605. [Google Scholar] [CrossRef]
- Miles, R.B. Lecture Series Notes for Von Karman Institute Lectures; Von Karman Institute: Sint-Genesius-Rode, Belgium, 2011. [Google Scholar]
- Boiko, A.V.; Dovgal, A.V.; Zanin, Y.B.; Kozlov, V.V. Three-dimensional structure of separated flows on wings. Thermophys. Aeromech. 1996, 3, 1–13. [Google Scholar]
- Mhitaryan, A.M.; Labinov, S.D.; Fridland, V.Y. Some Problems of Aerodynamics and Electro-Hydrodynamics; Kiev Institute of Civil Aviation Engineers: Kiev, Ukraine, 1964; Volume 1, p. 9397. [Google Scholar]
- Mhitaryan, A.M.; Maksimov, V.S.; Flidland, V.Y.; Labinov, S.D. Technology of boundary layer investigation with a new type work panel. J. Eng. Phys. Thermophys. 1961, 4, 237. [Google Scholar]
- Klimov, A.I.; Koblov, A.N.; Mishin, G.I.; Serov, Y.L.; Yavor, I.P. Shock wave propagation in a glow discharge. Sov. Tech. Phys. Lett. 1982, 8, 192. [Google Scholar]
- Roth, J.R. Aerodynamic flow acceleration using paraelectric and peristaltic electrohydrodynamic effects of a one atmosphere uniform glow discharge plasma. Phys. Plasmas. 2003, 10, 2117. [Google Scholar] [CrossRef]
- Roth, J.R. 25th Anniversary, IEEE Conference Record—Abstracts. In Proceedings of the 1998 IEEE International Conference on Plasma Science (Cat. No.98CH36221), Raleigh, NC, USA, 1–4 June 1998; p. 291. [Google Scholar]
- Roth, J.R.; Dai, X. Paper AIAA 2006-1203. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006. [Google Scholar]
- Roth, J.R.; Sherman, D.M.; Wilkinson, S.P. Paper AIAA 1998-0328. In Proceedings of the AIAA Meeting, Reno, NV, USA, 12–15 January 1998. [Google Scholar]
- Roth, J.R.; Sherman, D.M.; Wilkinson, S.P. Electrohydrodynamic flow control with a glow-discharge surface plasma. AIAA J. 2000, 38, 1172. [Google Scholar] [CrossRef]
- Bedin, A.P.; Mishin, G.I. Pis’ma v JTF. Sov. Phys. Tech. Phys. Lett. 1995, 24, 719. [Google Scholar]
- Caruana, D. Plasmas for aerodynamic control. Plasma Phys. Control. Fusion 2010, 52, 124045. [Google Scholar] [CrossRef]
- Wang, L.; Luo, Z.; Xia, Z.; Liu, B.; Deng, X. Review of actuators for high speed active flow control. Sci. China Technol. Sci. 2012, 55, 2225. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V. Numerical Simulation of Pulsed Jets of a High-Current Pulsed Surface Discharge. Comput. Therm. Sci. 2021, 13, 45–56. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Surzhikov, S.T.; Grishin, Y.М. Radiative gas dynamic of linear-stabilized surface discharge in atmospheric gases. In Proceedings of the 36th AIAA Plasmadynamics and Lasers Conference, Toronto, ON, Canada, 6 June 2005. Volume AIAA 2005-4929, 11p. [Google Scholar]
- Kuzenov, V.V.; Surzhikov, S.T.; Sharikov, I.V. Numerical simulation of linear-stabilized surface discharge in rare air. In Proceedings of the Fifteenth International Conference on MHD Energy Conversion and Sixth International Workshop on Magnetoplasma Aerodynamics, Moscow, Russia, 24–27 May 2005; Volume 2, p. 650. [Google Scholar]
- Zabaykin, V.A. Quality of High-Enthalpy Flow upon Electric-Arc Heating of Air in a Facility for In-vestigation Supersonic Combustion. Combust. Explos. Shock. Waves 2003, 39, 23–30. [Google Scholar] [CrossRef]
- Tretyakov, P.K. Organization of a pulsed mode of combustion in scramjets. Combust. Explos. Shock. Waves 2012, 48, 677. [Google Scholar] [CrossRef]
- Liu, Q.; Baccarella, D.; Lee, T. Review of Combustion Stabilization for Hypersonic Airbreathing Propulsion. Prog. Aerosp. Sci. 2020, 119, 100636. [Google Scholar] [CrossRef]
- Jacobsen, L.S.; Carter, C.D.; Jackson, T.A.; Williams, S.; Barnett, J. Plasma-Assisted Ignition in Scramjets. J. Propuls. Power 2008, 24, 641–654. [Google Scholar] [CrossRef]
- Lebouvier, S.A.; Kramer, N.J.; van Veldhuizen, E.M. Speed of streamers in argon over a flat surface of a dielectric. J. Phys. D Appl. Phys. 2009, 42, 015211. [Google Scholar]
- Timatkov, V.V.; Pietsch, G.J.; Saveliev, A.B.; Sokolova, M.V.; Temnikov, A.G. Influence of solid dielectric on the impulse discharge behaviour in a needle-to-plane air gap. J. Phys. D Appl. Phys. 2005, 38, 877–886. [Google Scholar] [CrossRef]
- Mursenkova, I.V.; Znamenskaya, I.A.; Lutsky, A.E. Influence of shock waves from plasma actuators on transonic and supersonic airflow. J. Phys. D Appl. Phys. 2018, 51, 105201. [Google Scholar] [CrossRef]
- Leger, L.; Sellam, M.; Barbosa, E.; Depussay, E. Visualization by discharge illu-mination technique and modification by plasma actuator of rarefied Mach 2 airflow around a cylinder. Meas. Sci. Technol. 2013, 24, 065401. [Google Scholar] [CrossRef]
- Ju, Y.; Sun, W. Plasma assisted combustion: Dynamics and chemistry. Prog. Energy Combust. Sci. 2015, 48, 21–83. [Google Scholar] [CrossRef]
- Znamenskaya, I.A.; Latfullin, D.F.; Mursenkova, I.V. Laminar-Turbulent Transition in a Supersonic Boundary Layer during Initiation of a Pulsed Surface Discharge. Tech. Phys. Lett. 2008, 34, 668–670. [Google Scholar] [CrossRef]
- Znamenskaya, I.; Mursenkova, I.; Kuli-Zade, T.; Kolycheva, A. Vizualization of 3D non-stationary flow in shock tube using nanosecond volume discharge. Shock. Waves 2009, 1, 533–538. [Google Scholar]
- Aulchenko, S.M.; Zamuraev, V.P.; Kalinina, A.P. Nonlinear effects of pulsed periodic energy supply on shock wave structure of transonic flow around airfoils. J. Appl. Mech. Tech. Phys. 2006, 47, 359–365. [Google Scholar] [CrossRef]
- Aulchenko, S.M.; Zamuraev, V.P.; Kalinina, A.P. Effect of asymmetric pulsed periodic energy supply on aerodynamic characteristics of airfoils. J. Appl. Mech. Tech. Phys. 2007, 48, 834–839. [Google Scholar] [CrossRef]
- Georgievsky, P.Y.; Levin, V.A. Unsteady effects for a supersonic flow past a pulsing energy source of high power. In Proceedings of the International Conference on the Methods of Aerophysical Research(ICMAR’98), Novosibirsk, Russia, 29 June–3 July 1998; p. 58. [Google Scholar]
- Asada, A.K.; Ninomiya, Y. Airfoil flow experiment on the duty cycle of dbd plasma actuator. In Proceedings of the 47th AIAA Aerospace Sciences Meeting including The New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009. AIAA-2009-531. [Google Scholar]
- Saveliev, A.; Sechenov, V.; Golub, V.; Son, E.; Aksenov, V.; Gubin, S. Sliding discharge for aircraft control. In Proceedings of the 47th AIAA Aerospace Sciences Meeting including The New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009. AIAA-2009-696. [Google Scholar]
- Jolibois, J.; Forte, M.; Moreau, E. Flow control and mems. In Proceedings of the IUTAM Symposium held at the Royal Geographical Society, London, UK, 19–22 September 2006. [Google Scholar]
- Opaits, D.; Roupassov, D.; Starikovskaia, S.; Starikovskii, A.; Zavialov, I.; Saddoughi, S. Plasma control of boundary layer using low-temperature non equilibrium plasma of gas discharge. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005. AIAA-2005-1180. [Google Scholar]
- Zavialov, I.; Opaits, D.; Roupassov, D.; Starikovskaia, A.Y.; Saddoughi, S.G. Boundary layer control for naca-0015 airfoil in subsonic regime. Proc. 15th ICMHD 2005, 2005, 186–191. [Google Scholar]
- Roupassov, D.; Zavyalov, I.; Starikovskii, A. Boundary layer separation plasma control using low-temperature non-equilibrium plasma of gas discharge. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006. AIAA-2006-373. [Google Scholar]
- Cybik, В.; Wilkerson, J.; Grossman, K. Performance characteristics of the sparkjet flow control actuator. In Proceedings of the 2nd AIAA Flow Control Conference, Portland, OR, USA, 28 June–1 July 2004. AIAA-2004-2131. [Google Scholar]
- Pavon, S.; Ott, P.; Leyland, P.; Dorier, J.-L.; Hollenstein, C. Effects of surface dielectric barrier discharge on transonic flows around an airfoil. In Proceedings of the 47th AIAA Aerospace Sciences Meeting including The New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2004. AIAA-2009-649. [Google Scholar]
- Balcon, B.; Moreau, E. Electric wind produced by a surface dbd operating over a wide range of relative humidity. In Proceedings of the 47th AIAA Aerospace Sciences Meeting including The New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2004. AIAA-2009-488. [Google Scholar]
- Son, E.E.; Tereshonok, D.V. Supersonic gas flow control by thermal vortices. High Temp. 2010, 48, 3–8. [Google Scholar]
- Golub, V.V.; Saveliev, A.S.; Sechenov, V.A.; Son, E.E.; Tereshonok, D.V. Plasma aerodynamics in a supersonic gas flow. High Temp. 2010, 48, 903–909. [Google Scholar] [CrossRef]
- Znamenskaya, I.A.; Latfullin, D.F.; Mursenkova, I.V.; Sysoev, N.N. Experimental Study of the Interaction of a Decaying Plasma of a Pulsed Volume Discharge with a Shock Layer. Vestnik Moskovskogo Universita. Ser. 3. Fiz. Astron. 2006, 3, 57–61. [Google Scholar]
- Znamenskaya, I.A.; Latfullin, D.F.; Lutskiĭ, A.E.; Mursenkova, I.V. Energy deposition in boundary gas layer during initiation of nanosecond sliding surface discharge. Tech. Phys. Lett. 2010, 36, 795. [Google Scholar] [CrossRef]
- Znamenskaya, I.A.; Latfullin, D.F.; Lutsky, A.E.; Mursenkova, I.V.; Sysoev, N.N. Development of gasdynamic perturbations propagating from a distributed sliding surface discharge. Tech. Phys. 2009, 52, 546–554. [Google Scholar] [CrossRef]
- Znamenskaya, I.A.; Ivanov, I.E.; Orlov, D.M.; Sysoev, N.N. Pulsed action on a shock wave in the case of self-localized high-current surface discharge in front of the shock-wave front. Dokl. Phys. 2009, 54, 107–110. [Google Scholar] [CrossRef]
- Patel, M.P.; Ng, T.T.; Vasudevan, S.; Corke, T.C.; Post, M.L.; McLaughlin, T.E.; Suchomel, C.F. Scaling Effects of an Aerodynam-icPlasma Actuator. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2007. Paper AIAA 2007-635. [Google Scholar]
- Starikovskaia, S.M.; Starikovskiy, A.Y. Runaway Electrons Preionized Diffuse Discharges; NOVA Publishers: Hauppauge, NY, USA, 2014. [Google Scholar]
- Starikovskiy, A.Y.; Nikipelov, A.A.; Nudnova, M.M.; Roupassov, D.V. SDBD plasma actuator with nanosecond pulse-periodic discharge. Plasma Sources Sci. Technol. 2009, 18, 034015. [Google Scholar] [CrossRef]
- Roupassov, D.V.; Nikipelov, A.A.; Nudnova, M.M.; Starikovskiy, A.Y. Flow separation control by plasma actuator with nanosecond pulsed-periodic discharge. AIAA J. 2009, 47, 168. [Google Scholar] [CrossRef]
- Aleksandrov, N.L.; Kindysheva, S.V.; Kirpichnikov, A.A.; Kosarev, I.N.; Starikovskaia, S.M.; Starikovskiy, A.Y. Plasma decay in N2, CO2 and H2O excited by high-voltage nanosecond discharge. J. Phys. D Appl. Phys. 2007, 40, 4493. [Google Scholar] [CrossRef]
- Roupassov, D.V.; Starikovskiy, A.Y. Development of nanosecond surface discharge in ‘ctuator’ geometry. IEEE Trans. Plasma Sci. 2008, 36, 1312. [Google Scholar] [CrossRef]
- Anikin, N.B.; Zavialova, N.A.; Starikovskaia, S.M.; Starikovskiy, A.Y. Nanosecond-discharge development in long tubes. IEEE Trans. Plasma Sci. 2008, 36, 902. [Google Scholar] [CrossRef]
- Raizer, Y.P. Gas Discharge Physics; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Nudnova, M.M.; Aleksandrov, N.L.; Starikovskiy, A.Y. Influence of Polarity on the Properties of a Nanosecond Surface Barrier Discharge in Air at Atmospheric Pressure. Plasma Phys. Rep. 2010, 36, 90–98. [Google Scholar] [CrossRef]
- Xu, D.A.; Shneider, M.N.; Lacoste, D.A.; Laux, C.O. Thermal and hydrodynamic effects of nanosecond discharges in atmospheric pressure air. J. Phys. D Appl. Phys. 2014, 47, 235202. [Google Scholar] [CrossRef]
- Aleksandrov, N.L.; Starikovskiy, A. Plasma-Assisted Ignition and Combustion. Prog. Energy Combust. Sci. 2011, 39, 61–110. [Google Scholar] [CrossRef]
- Meyer, R.; Palm, P.; Ploenjes, E.; Rich, J.W.; Adamovich, I.V. Nonequilibrium Radio Frequency Discharge Plasma Effect on Conical Shock Wave: M = 2.5 Flow. AIAA J. 2003, 41, 465. [Google Scholar]
- Starikovskiy, A.; Miles, R.B. Experimental Investigation of Dynamic Stall in a Wide Range of Mach Numbers by Plasma Actuators with Combined Energy/Momentum Action. In Proceedings of the 47th AIAA Plasmadynamics and Lasers Conference, Washington, DC, USA, 13–17 June 2016. Paper AIAA 2016-4017. [Google Scholar]
- Macheret, S.O.; Ionikh, Y.Z.; Chernysheva, N.V.; Yalin, A.P.; Martinelli, L.; Miles, R.B. Shock wave propagation and dispersion in glow discharge plasmas. Phys. Fluids 2001, 13, 2693. [Google Scholar] [CrossRef]
- Khorunzhenko, V.I.; Roupassov, D.V.; Starikovskiy, A.Y. Hypersonic Flow and Shock Wave Structure Control by Low Tem-perature Nonequilibrium Plasma of Gas Discharge. In Proceedings of the 38th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibition, Indianapolis, IN, USA, 7–10 July 2002. Paper AIAA 2002-2497. [Google Scholar]
- Nudnova, M.; Starikovskiy, A. Ozone formation in pulsed SDBD at wide pressure range. In Proceedings of the 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012. Paper AIAA 2012-407. [Google Scholar] [CrossRef]
- Khorunzhenko, V.I.; Roupassov, D.V.; Starikovskaia, S.M.; Starikovskiy, A.Y. Hypersonic Shock Wave—Low Temperature Nonequilibrium Plasma Interaction. In Proceedings of the 39th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Huntsville, AL, USA, 20–23 July 2003. Paper AIAA 2003-5048. [Google Scholar]
- Montello, A.; Nishihara, M.; Takashima, K.; Rich, J.W.; Adamovich, I.V.; Lempert, W. Picosecond CARS Measurements of Vi-brational Distribution Functions in a Nonequilibrium Mach 5 Flow. In Proceedings of the 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2011. Paper AIAA 2011-1322. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V. Approximate calculation of convective heat transfer near hypersonic aircraft surface. J. Enhanc. Heat Transf. 2018, 25, 181–193. [Google Scholar] [CrossRef]
- Sidorenko, A.A.; Zanin, B.Y.; Postnikov, B.V.; Budovsky, A.D.; Starikovskiy, A.Y.; Roupassov, D.V.; Zavialov, I.N.; Malmuth, N.D.; Smereczniak, P.; Silkey, J.S. Pulsed discharge actuators for rectangular wing separation control. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2007. AIAA 2007-941. [Google Scholar]
- Sidorenko, A.A.; Budovsky, A.D.; Pushkarev, A.V.; Maslov, A.A. Flight Testing of DBD plasma separation control system. In Proceedings of the 48th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 7–10 January 2008. Paper AIAA 2008-373. [Google Scholar]
- Surzhikov, S.T.; Shang, J.S. Plasmadynamics of Glow Discharge in Hypersonic Internal Flows. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2007. 26p, AIAA Paper 07-0994. [Google Scholar]
- Shang, J.S.; Menart, J.; Kimmel, R.; Hayes, J. Hypersonic Inlet with Plasma Induced Compression. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006. 12p, AIAA 2006-0764. [Google Scholar]
- Shang, S.; Chang, C.; Surzhikov, S. Simulating Hypersonic Magneto-Fluid Dynamic Compression in Rectangular Inlet. AIAA J. 2007, 45, 2710–2720. [Google Scholar] [CrossRef]
- Hayes, W.D.; Probstein, R.F. Hypersonic Flow Theory; Academic Press: New York, NY, USA, 1959; 464p. [Google Scholar]
- Shang, J.S.; Surzhikov, S.T. Magneto-fluid-dynamics interaction for hypersonic flow control. In Proceedings of the 42nd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 5–8 January 2004. 11p, AIAA 2004-0508. [Google Scholar]
- Loitsyansky, L.G. Mechanics of Liquids and Gases; Pergamon: Bakel, Senegal, 1966; 816p. [Google Scholar]
- Surzhikov, S.T. Hypersonic Rarefied Gas Flow around a Surface Glow Discharge with an External Magnetic Field; IPMech RAS: Moscow, Russia, 2011; 273p. [Google Scholar]
- Mesyats, G.A.; Bychkov, Y.I.; Kremnev, V.V. Pulsed nanosecond electric discharges in gases. Sov. Phys. Usp. 1972, 15, 282. [Google Scholar] [CrossRef]
- Zarin, A.S.; Kuzovnikov, A.A.; Shibkov, V.M. Freely Localized Microwave—Discharge in the Air. M. Oil and Gas; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Ershov, A.P.; Kalinin, A.V.; Lodinev, V.V.; Shibkov, V.M. Kinetics of gas heating in pulse discharge in air. Proc. XX ICPIG 1991, 2, 379–380. [Google Scholar]
- Anokhin, E.M.; Kuzmenko, D.N.; Kindysheva, S.V.; Soloviev, V.R.; Aleksandrov, N.L. Flow control: Non-thermal and thermal effects. Plasma Sources Sci. Technol. 2015, 24, 045014. [Google Scholar] [CrossRef]
- Bityurin, V.A.; Bocharov, A.N. Magnetohydrodynamic interaction in hypersonic flow around a blunt body. Fluid Gas Mech. 2006, 5, 188. [Google Scholar]
- Filimonova, E.A. Discharge effect on the negative temperature coefficient behaviour and multistage ignition in C3H8-air mixture. J. Phys. D Appl. Phys. 2015, 48, 015201. [Google Scholar] [CrossRef]
- Bityurin, V.A.; Bocharov, A.N. On the features of the electromagnetic thermal protection of the descent vehicle. PZhTF 2011, 37, 70–74. [Google Scholar]
- Bocharov, A.N.; Bityurin, V.A.; Lineberry, J. Study of MHD Interaction in Hypersonic Flows. In Proceedings of the 15th International Conference on MHD Energy Conversion, Moscow, Russia, 24–27 May 2005; pp. 399–416. [Google Scholar]
- Bityurin, V.A.; Bocharov, A.N. MHD Flow Control in Hypersonic Flight. In Proceedings of the 15th International Conference on MHD Energy Conversion, Moscow, Russia, 24–27 May 2005; Volume 2, pp. 429–433. [Google Scholar]
- Bityurin, V.A.; Bocharov, A.N. MHD Parachute in ReEntry Flight. Induced Electric Field Effects in Hypersonic MHD Flow. In Proceedings of the 2nd International ARA Days, Arcachon, France, 21–23 October 2008. Paper AA-3-2008-61. [Google Scholar]
- Bityurin, V.A.; Bocharov, A.N.; Popov, N.A. Non-Equilibrium Effects in MHD Parachute Concept: Induced Electric Field Effects. In Proceedings of the 47th AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 5–8 January 2009. AIAA Paper 2009-1230. [Google Scholar]
- Aleksandrov, N.L.; Bazelyan, A.E.; Bazelyan, E.M.; Kochetov, I.V. Modeling of long streamers in atmospheric-pressure air. Plasma Phys. Rep. 1995, 21, 57. [Google Scholar]
- Hagelaar, G.J.; Pitchford, L.C. Solving the Boltzmann equation to obtain electron transport coefficients and rate coefficients for fluid models. Plasma Sources Sci. Technol. 2005, 14, 722. [Google Scholar] [CrossRef]
- Kossyi, I.A.; Kostinsky, A.Y.; Matveev, A.A.; Silakov, V.P. Kinetic scheme of the non-equilibrium discharge in nitrogen-oxygen mixtures. Plasma Sources Sci. Technol. 1992, 1, 207. [Google Scholar] [CrossRef]
- Raiser, Y.P. Laser Spark and Discharge Propagation; Nauka: Moscow, Russia, 1974. [Google Scholar]
- Morgan, C.G. Laser-induced breakdown of gases. Rep. Progress Phys. 1975, 38, 621. [Google Scholar] [CrossRef]
- Radziemski, L.J.; Cremers, D. Lasers-Induced Plasmas and Applications; Marcel Dekker: New York, NY, USA, 1989. [Google Scholar]
- Mashek, I.C.; Lashkov, V.A.; Khoronzhuk, R.S.; Potapenko, D.P.; Brovkin, V.G. Microwave energy deposition in supersonic flows on laser-initiated dipile structures. In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MD, USA, 13–17 January 2014. AIAA-2014-0487. [Google Scholar]
- Khoronzhuk, R.S.; Karpenko, A.G.; Lashkov, V.A.; Potapenko, D.P.; Mashek, I.C. Microwave discharge initiated by double laser spark in supersonic airflow. J. Plasma Phys. 2015, 81, 905810307. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Ryzhkov, S.V. Turbulence in two-phase flows with macro-, micro- and nanoparticles: A review. Symmetry 2022, 14, 2433. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Ryzhkov, S.V. Particle-laden and droplet-laden two-phase flows past bodies (a review). Symmetry 2023, 15, 388. [Google Scholar] [CrossRef]
- Kolesnichenko, Y.F.; Brovkin, V.G.; Khmara, D.V.; Lashkov, V.A.; Mashek, I.C.; Ryvkin, M.I. In Proceedings of the 41st AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 2003; Paper AIAA 2003-362.
- Lashin, A.M.; Starikovskiy, A.Y. Shock and detonation waves interaction with entropy layers. Tech. Phys. 1995, 65, 11. [Google Scholar]
- Lashin, A.M.; Starikovskiy, A.Y. Stability of interaction between shock waves and entropy layers. High Temp. 1996, 34, 94–104. [Google Scholar]
- Starikovskiy, A.; Limbach, C.; Miles, R.B. Trajectory Control of Small Rotating Projectiles by Laser Discharges. In Proceedings of the 47th AIAA Plasmadynamics and Lasers Conference, Washington, DC, USA, 13–17 June 2016. Paper AIAA 2016-4308. [Google Scholar]
- Georgievsky, P.Y.; Levin, V.A. Mechanics: Contemporary Issues; Moscow State University: Moscow, Russia, 1987. [Google Scholar]
- Briesclienk, S.; O’Byrne, S.; Kleine, H. Laser-induced plasma ignition studies in a model scramjet engine. Combust. Flame 2013, 160, 145–148. [Google Scholar] [CrossRef]
- Katsnelson, S.S.; Pozdnyakov, G.A. Initiation of combustion processes in a hydrogen-oxygen mixture under the action of a low-energy strong-current electron beam. Combust. Explos. Shock. Waves 2007, 43, 132–138. [Google Scholar] [CrossRef]
- Bezgin, L.V.; Kopchenov, V.I.; Starik, A.M.; Titova, N.S. Initiation of a detonation wave in a supersonic flow of a hydrogen-oxygen mixture around a wedge by resonant laser radiation. J. Tech. Phys. 2007, 77, 39–46. [Google Scholar] [CrossRef]
- Chinitz, W. On the use of shock-induced combustion in hypersonic engines. In Proceedings of the Space Plane and Hypersonic Systems and Technology Conference, Norfolk, VA, USA, 18–22 November 1996. N 96-4536. [Google Scholar]
- Li, C.; Kailasanath, K.; Oran, E.S. Detonation structures generated by multiple shocks on ram-accelerator projectiles. Combust. Flame 1997, 108, 173–186. [Google Scholar] [CrossRef]
- Bezgin, L.; Canzhelo, A.; Gouskov, O.; Kopchenov, V.; Yarunov, Y. Some estimations of a possibility to utilize shock-induced combustion in propulsion systems. In Gaseous and Heterogeneous Detonations: Science to Applications; Roy, G., Frolov, S., Kailasanath, K., Smirnov, N., Eds.; ENAS Publishers: Moscow, Russia, 1999; pp. 285–300. [Google Scholar]
- Starik, A.M.; Titova, N.S. Numerical analysis of the kinetics of combustion of hydrogen-air mixtures with the addition of NH3, CH4 and C2Hb behind shock waves. Combust. Explos. Shock. Waves 2000, 36, 31–38. [Google Scholar] [CrossRef]
- Da Silva, F.L.F.; Deshaies, B. Stabilization of an oblique detonation wave by a wedge: A parametric numerical study. Combust. Flame 2000, 121, 152–166. [Google Scholar] [CrossRef]
- Varatharajan, B.; Williams, F.A. Ethylene ignition and detonation chemistry, part 1: Detailed modeling and experimental comparison. J. Propuls. Power 2002, 18, 344–351. [Google Scholar] [CrossRef]
- Bezgin, L.V.; Smoked, V.I.; Starik, A.M.; Titova, N.S. On the initiation of combustion of a CH4-O2 mixture in a supersonic flow when O2 molecules are excited by an electric discharge. Combust. Explos. Shock. Waves 2008, 44, 3–16. [Google Scholar]
- Starik, A.M.; Titova, N.S. On the kinetics of detonation initiation in a supersonic flow of an H2 + O2 (air) mixture when O2 molecules are excited by resonant laser radiation. Kinet. Catal. 2003, 44, 35–46. [Google Scholar] [CrossRef]
- Starik, A.M.; Titova, N.S.; Lukhovitsky, B.I. Kinetics of low-temperature initiation of combustion of H2+O2+H2O mixtures upon excitation of H2O molecular vibrations by laser radiation. ZhTP 2004, 74, 77–83. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V. Evaluation of the possibility of ignition of a hydrogen–oxygen mixture by erosive flame of the impulse laser. Laser Phys. 2019, 29, 096001. [Google Scholar] [CrossRef]
- Anisimov, S.I.; Imas, Y.A.; Romanov, G.S.; Khodyko, Y.V. Effect of High Power Radiation on Metals; National Technical Information Service: Moscow, Russia, 1970. [Google Scholar]
- Vedenov, A.A.; Gladush, G.G. Physical Processes in Laser Processing of Materials; Energoatomizdat: Moscow, Russia, 1985. [Google Scholar]
- Vorobyov, V.S. Breakdown of an erosion torch during quasi-stationary irradiation of metals by a laser. Quantum Electron. 1986, 13, 1909–1911. [Google Scholar]
- Kamrukov, A.S.; Kashnikov, G.N.; Kozlov, N.P.; Kondratenko, M.M.; Lebedev, E.F.; Orlov, V.K.; Ostashev, V.E.; Protasov, Y.S.; Semenov, A.M. Experimental investigation of the effectiveness of the matching of a magneto plasma compressor with an explosive magnetohydrodynamic generator. High Temp. 1984, 22, 313–318. [Google Scholar]
- Kuzenov, V.V.; Ryzhkov, S.V.; Varaksin, A.Y. Numerical Modeling of Individual Plasma Dynamic Characteristics of a Light-Erosion MPC Discharge in Gases. Appl. Sci. 2022, 12, 3610. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V.; Varaksin, A.Y. Simulation of Parameters of Plasma Dynamics of a Magneto Plasma Compressor. Appl. Sci. 2023, 13, 5538. [Google Scholar] [CrossRef]
- Alekseev, A.I.; Chernikov, V.A.; Vaulin, D.N. The effect of a magnetic field on longitudinal-transverse discharge in the high-speed flow of an air-hydrocarbon mixture. Mosc. Univ. Phys. Bull. 2015, 70, 251–257. [Google Scholar] [CrossRef]
- Alekseev, A.I.; Vaulin, D.N.; Deshko, K.I.; Chernikov, V.A. Study of the possibility to use a magnetoplasma compressor for plasma-assisted combustion in a high-speed flow. Plasma Phys. Rep. 2018, 44, 766–774. [Google Scholar] [CrossRef]
- Alekseev, A.I.; Vaulin, D.N.; Stepanov, A.I.; Chernikov, V.A. The influence of an external magnetic field on the burning of a high-speed air-carbon mixture. High Temp. 2018, 56, 20–24. [Google Scholar] [CrossRef]
- Ershov, A.P.; Kamenshchikov, S.A.; Logunov, A.A.; Chernikov, V.A. Initiation of Combustion of a Supersonic Propane-Air Flow by a Discharge of a Magnetoplasma Compressor. High Temp. 2009, 47, 822–829. [Google Scholar] [CrossRef]
- Aleksandrov, A.F.; Ershov, A.P.; Kamenshchikov, S.A. Ignition of a supersonic propane-air mixture using pulsed plasma. Bull. Mosc. Univ. Ser. 3. Physics. Astron. 2008, 2, 63–65. [Google Scholar]
- Vinogradov, V.; Chernikov, V.; Timofeev, I.; Kolesnikov, E. Preliminary Study Of Different Plasma Discharges At M=2 Air Flow. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2006. AIAA-2005-0988. [Google Scholar]
- Aleksandrov, A.; Bychkov, V.; Chernikov, V.; Ershov, A.; Gromov, V.; Kolesnikov, E.; Levin, V.; Shibkov, V.; Vinogradov, V. Arc Discharge as a Means for Ignition and Combustion of Propane-AirMixture Supersonic Flow. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006. AIAA 2006-1462. [Google Scholar]
- Ershov, A.P.; Kolesnikov, E.B.; Timofeev, I.B.; Chernikov, V.A.; Chuvashev, S.N.; Shibkov, V.M. Plasma-dynamic discharges in transverse supersonic air flows. High Temp. 2006, 44, 477–486. [Google Scholar] [CrossRef]
- Ershov, A.P.; Kolesnikov, E.B.; Timofeev, I.B.; Chernikov, V.A.; Chuvashev, S.N.; Shibkov, V.M. The interaction between plasma jet of a capillary discharge and transverse supersonic air flow. High Temp. 2007, 45, 580–587. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V.; Starostin, A.V. Pulsed jets for dense plasma generation in an external magnetic field. Russ. Phys. J. 2020, 62, 2041–2045. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V. Mathematical Modeling of Plasma Dynamics for Processes in Capillary Discharges. Russ. J. Nonlinear Dyn. 2019, 15, 543–550. [Google Scholar] [CrossRef]
- Rudinskii, A.V.; Yagodnikov, D.A.; Ryzhkov, S.V.; Onufriev, V.V. Features of Intrinsic Electric Field Formation in Low-Temperature Oxygen–Methane Plasma. Tech. Phys. Lett. 2021, 47, 520–523. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V.; Varaksin, A.Y. Calculation of heat transfer and drag coefficients for aircraft geometric models. Appl. Sci. 2022, 12, 11011. [Google Scholar] [CrossRef]
- Shumeiko, A.I.; Telekh, V.D.; Ryzhkov, S.V. Probe Diagnostics and Optical Emission Spectroscopy of Wave Plasma Source Exhaust. Symmetry 2022, 14, 1983. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V. Estimation of the neutron generation in the combined magneto-inertial fusion scheme. Phys. Scr. 2021, 96, 125613. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V. The Qualitative and Quantitative Study of Radiation Sources with a Model Configuration of the Electrode System. Symmetry 2021, 13, 927. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V.; Varaksin, A.Y. The Adaptive Composite Block-Structured Grid Calculation of the Gas-Dynamic Characteristics of an Aircraft Moving in a Gas Environment. Mathematics 2022, 10, 2130. [Google Scholar] [CrossRef]
- Ryzhkov, S.V. Magneto-Inertial Fusion and Powerful Plasma Installations (A Review). Appl. Sci. 2023, 13, 6658. [Google Scholar] [CrossRef]
- Anokhin, E.M.; Popov, M.A.; Kochetov, I.V.; Starikovskii , A.Y.; Aleksandrov, N.L. Plasma Decay in the Afterglow of High-Voltage Nanosecond Discharges in Unsaturated and Oxygenated Hydrocarbons. Plasma Phys. Rep. 2017, 43, 1198–1207. [Google Scholar] [CrossRef]
- Starikovskiy, A.Y.; Aleksandrov, N.L. Gasdynamic Flow Control by Ultrafast Local Heating in a Strongly Nonequilibrium Pulsed Plasma. Plasma Phys. Rep. 2021, 47, 148–209. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).