Can the Orbital Debris Disease Be Cured Using Lasers?
Abstract
1. Introduction
2. Methods
2.1. High-Energy Laser Ground Station
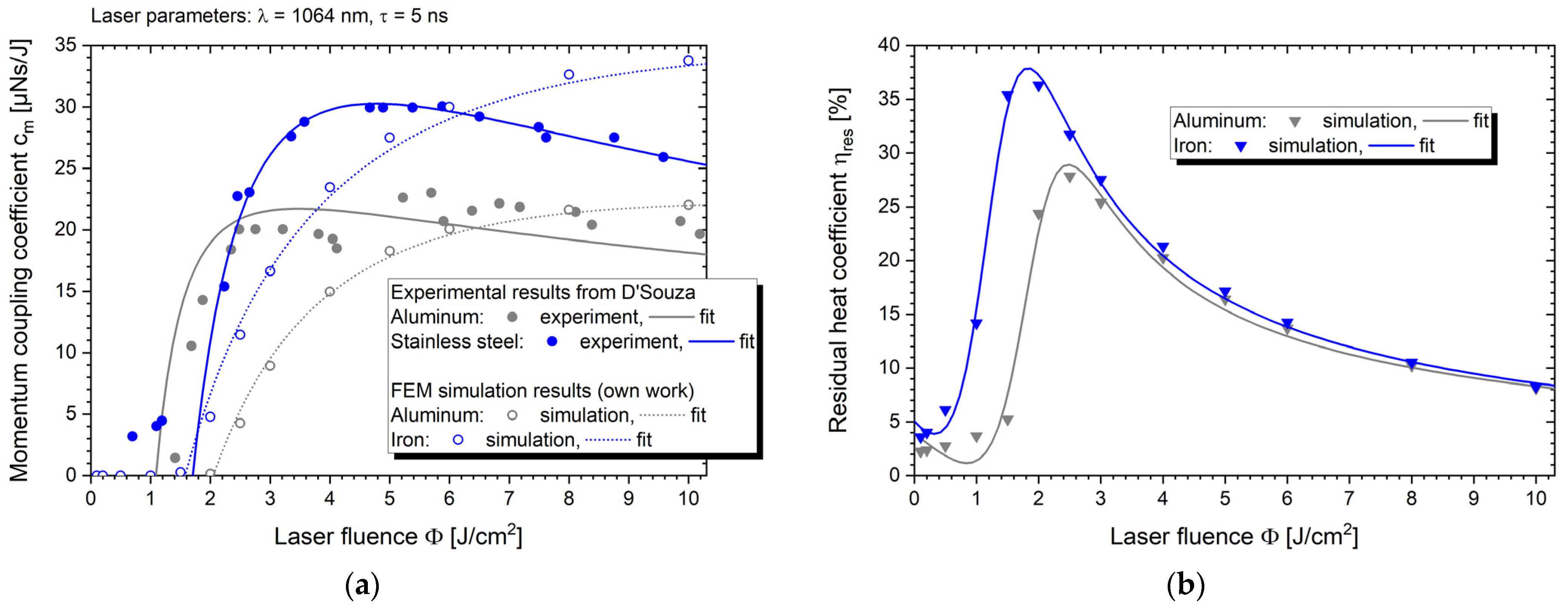
2.2. Laser–Matter Interaction
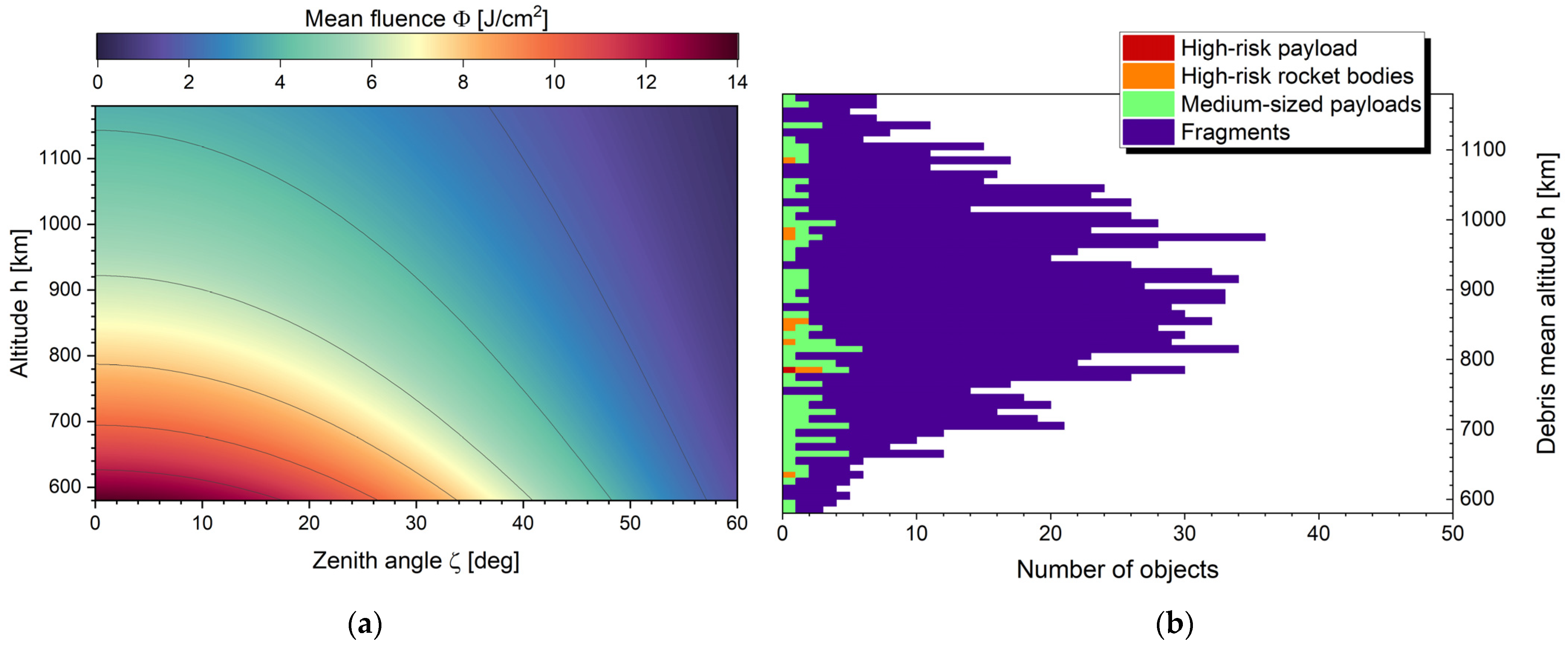
2.3. Space Debris Simulation Targets
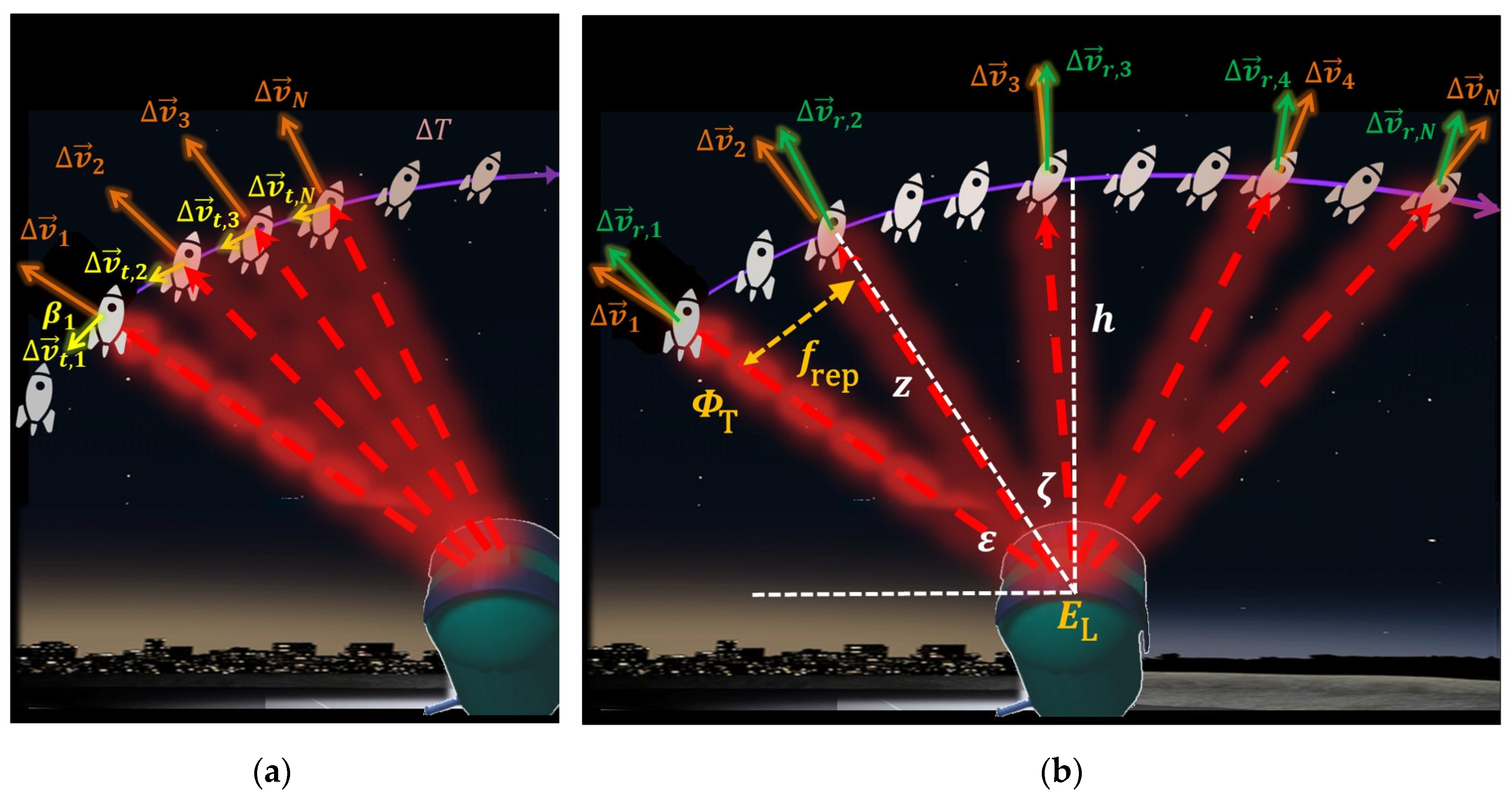
2.4. Laser-Imparted Momentum and Heat
2.5. Prediction of Orbit Modification
3. Results
3.1. Laser Irradiation Settings
3.1.1. Laser Fluence
3.1.2. Irradiation Interval
3.1.3. Laser Pulse Repetition Rate
3.2. Orbit Modification
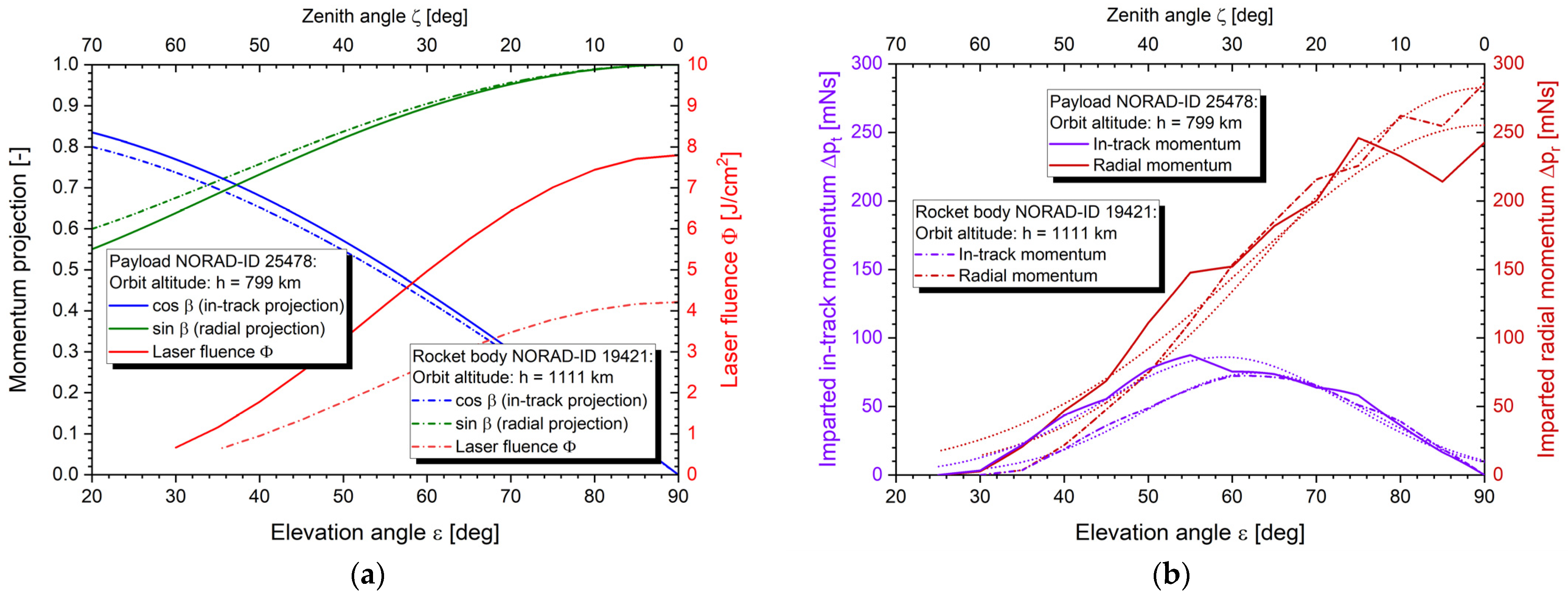
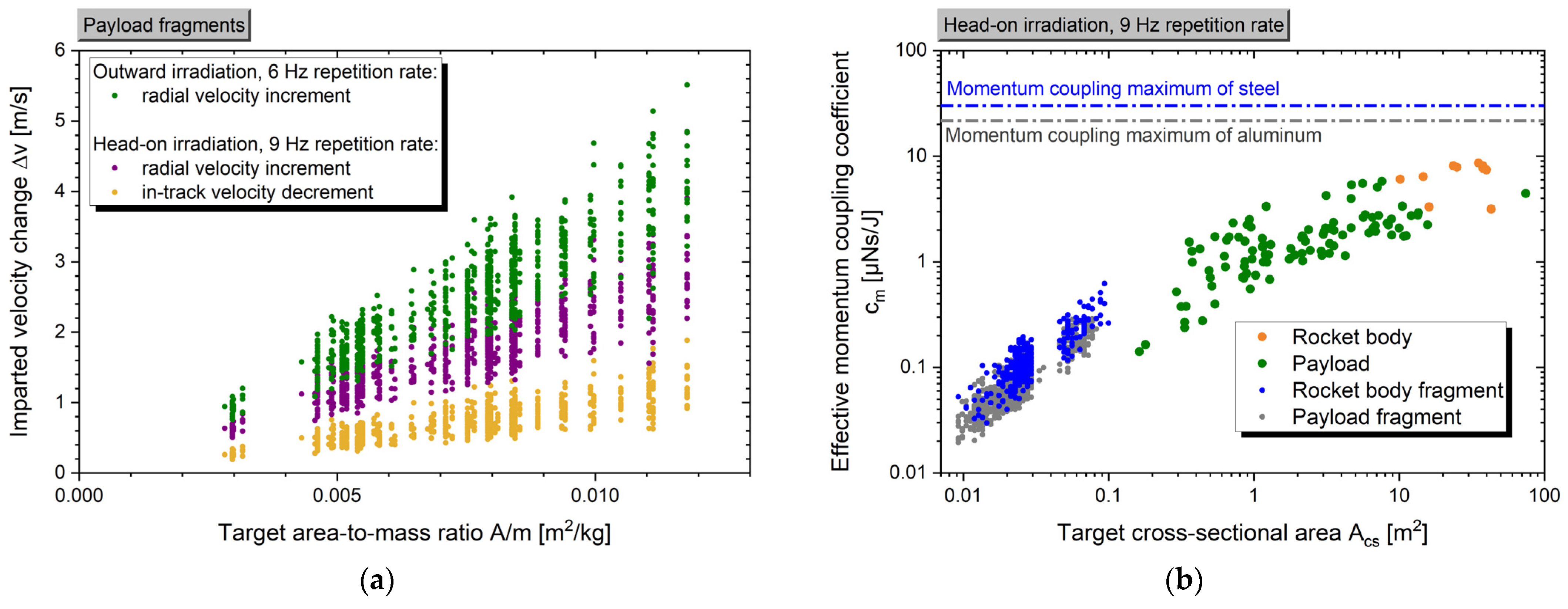
3.2.1. Orbital Velocity Changes
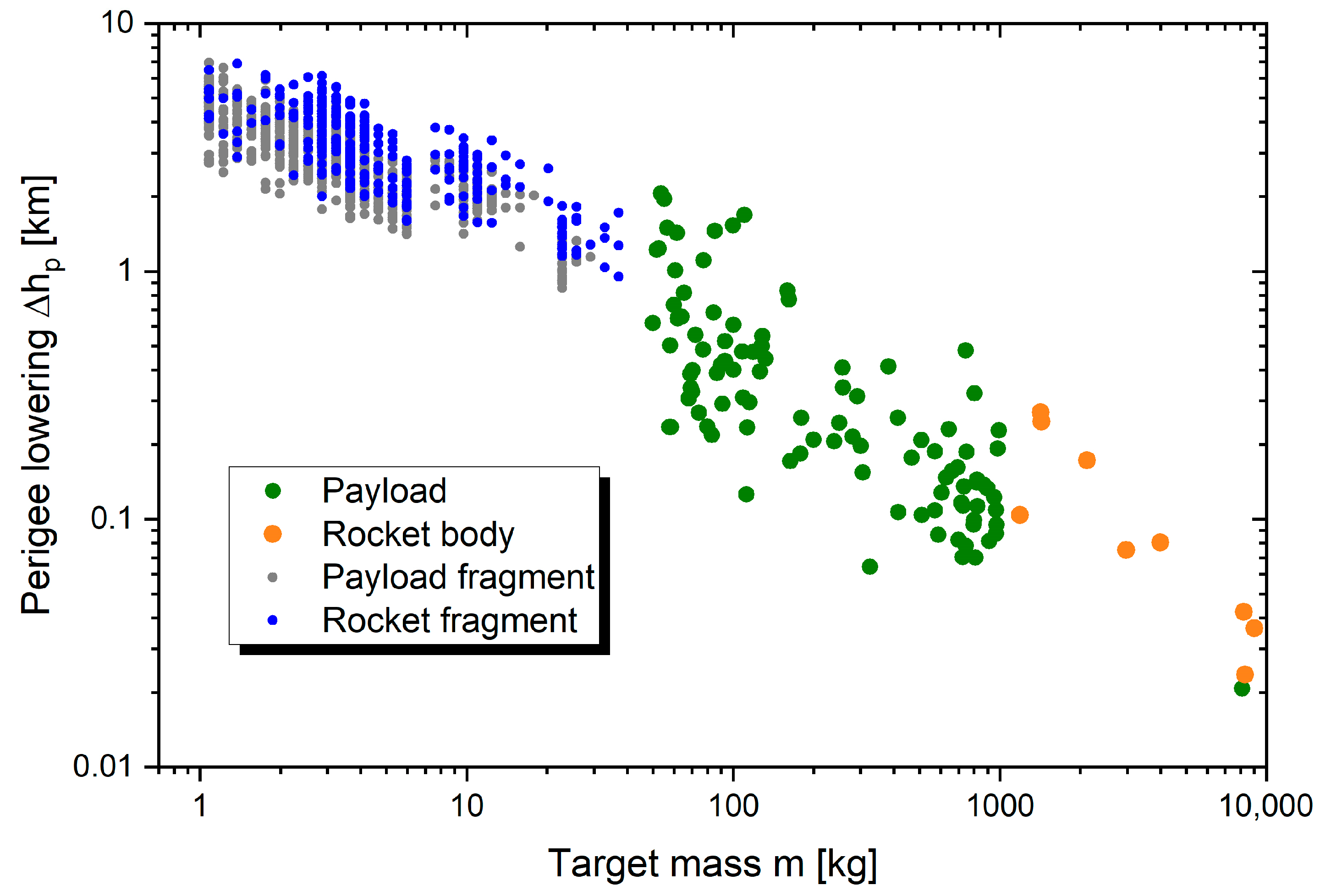
3.2.2. Perigee Lowering Method
3.2.3. Multi-Pass Removal
4. Discussion
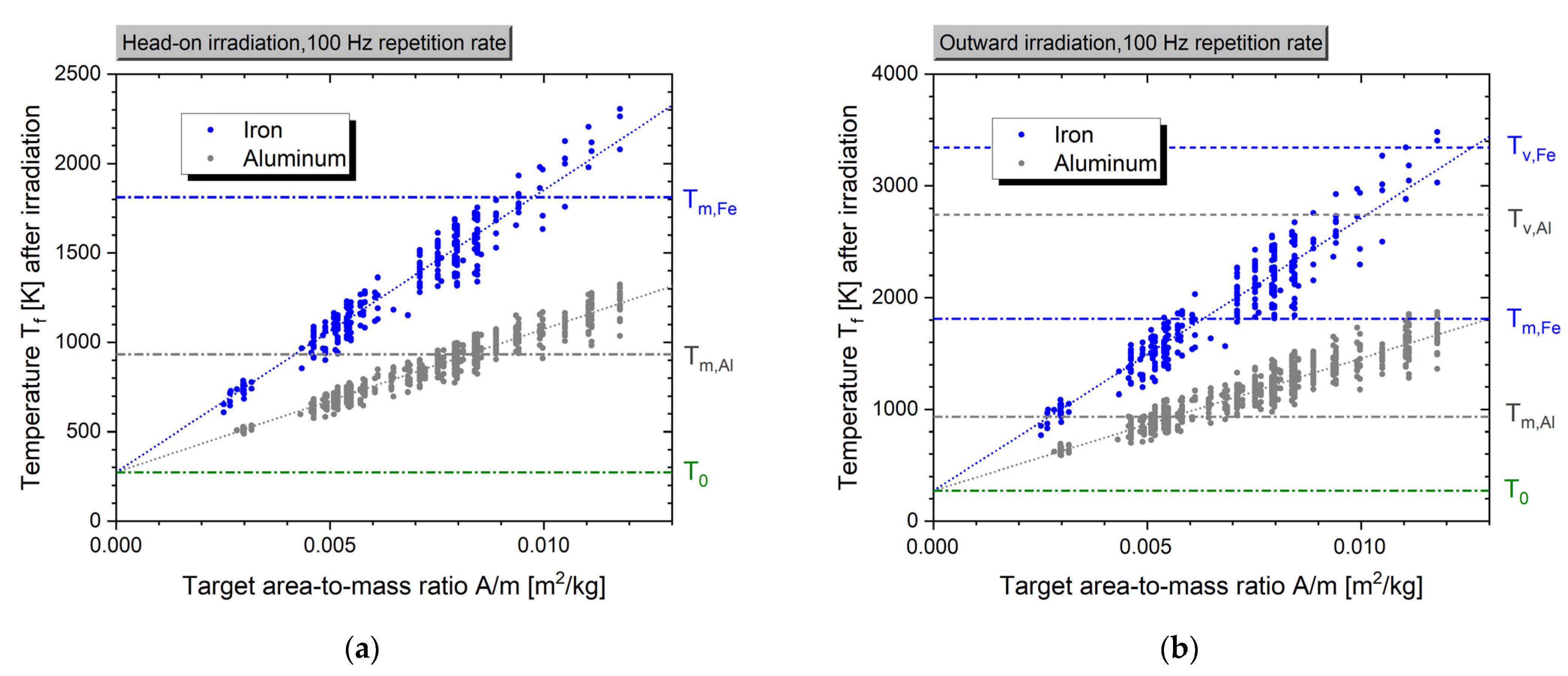
4.1. Thermo—Mechanical Integrity
4.2. Momentum Prediction
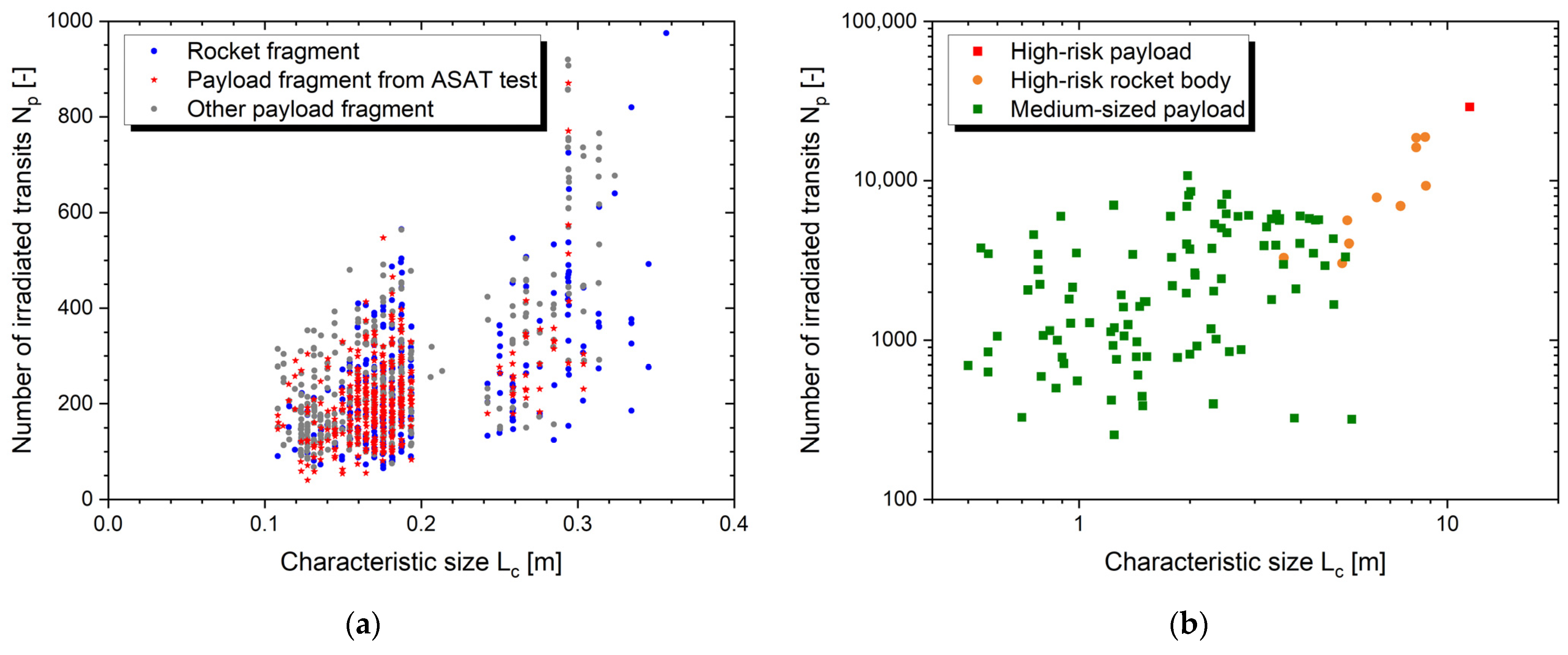
4.3. Removal Efficiency of Laser Station Networks
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kessler, D.J.; Cour-Palais, B.G. Collision Frequency of Artificial Satellites: The Creation of a Debris Belt. J. Geophys. Res. 1978, 83, 2637–2646. [Google Scholar] [CrossRef]
- Phipps, C.; Bonnal, C. Laser Ranging and Nudging in Space Debris Traffic Management. Sens. Transducers J. 2022, 255, 17–23. Available online: https://www.sensorsportal.com/HTML/DIGEST/P_3254.htm (accessed on 17 March 2023).
- Colvin, T.J.; Karcz, J.; Wusk, G. Cost and Benefit Analysis of Orbital Debris Remediation; NASA Headquarters, Office of Technology, Policy, and Strategy: Washington, DC, USA, 10 March 2023. [Google Scholar]
- Clearspace-1. Available online: https://www.esa.int/Space_Safety/ClearSpace-1 (accessed on 17 March 2023).
- Astroscale Selects Rocket Lab to Launch Phase I of JAXA’s Debris Removal Demonstration Project. Available online: https://astroscale.com/astroscale-selects-rocket-lab-to-launch-phase-i-of-jaxas-debris-removal-demonstration-project/ (accessed on 17 March 2023).
- Liou, J.-C. An active debris removal parametric study for LEO environment remediation. Adv. Space Res. 2011, 47, 1865–1876. [Google Scholar] [CrossRef]
- Johnson, N.L.; Krisko, P.H.; Liou, J.-C.; Anz-Meador, P.D. NASA’s new breakup model of Evolve 4.0. Adv. Space Res. 2001, 28, 1377–1384. [Google Scholar] [CrossRef]
- Acciarini, G.; Baresi, N.; Bridges, C.; Felicetti, L.; Hobbs, S.; Günes Baydin, A. Observation Strategies and Megaconstellations Impact on Current LEO Population. In Proceedings of the 2nd NEO and Debris Detection Conference, Darmstadt, Germany, 24–26 January 2023. [Google Scholar]
- Hakima, H.; Emami, M.R. Assessment of active methods for removal of LEO debris. Acta Astronaut. 2018, 144, 225–243. [Google Scholar] [CrossRef]
- Phipps, C.R.; Albrecht, G.; Friedman, H.; Gavel, D.; George, E.V.; Murray, J.; Ho, C.; Priedhorsky, W.; Michaelis, M.M.; Reilly, J.P. ORION: Clearing near-Earth space debris using a 20 kW, 530 nm, Earth-based, repetitively pulsed laser. Laser Part. Beams 1996, 14, 1–44. [Google Scholar] [CrossRef]
- Schall, W. Orbital Debris Removal by Laser Radiation. Acta Astronaut. 1991, 24, 343–351. [Google Scholar] [CrossRef]
- Phipps, C.R. L’ADROIT—A spaceborne ultraviolet laser system for space debris clearing. Acta Astronaut. 2014, 104, 243–255. [Google Scholar] [CrossRef]
- Soulard, R.; Quinn, M.N.; Tajima, T.; Mourou, G. ICAN: A novel laser architecture for space debris removal. Acta Astronaut. 2014, 105, 192–200. [Google Scholar] [CrossRef]
- Rubenchik, A.M.; Erlandson, A.C.; Liedahl, D. Laser system for space debris cleaning. AIP Conf. Proc. 2012, 1464, 448–455. [Google Scholar] [CrossRef]
- Esmiller, B.; Jacquelard, C.; Eckel, H.-A.; Wnuk, E. Space debris removal by ground-based lasers: Main conclusions of the European project CLEANSPACE. Appl. Opt. 2014, 53, I45–I54. [Google Scholar] [CrossRef] [PubMed]
- Scharring, S.; Lorbeer, R.-A.; Eckel, H.-A. Heat Accumulation in Laser-Based Removal of Space Debris. AIAA J. 2018, 56, 2506–2508. [Google Scholar] [CrossRef]
- Loktionov, E.; Phipps, C.; Sharaborova, E. Unintended consequences with laser nudging or re-entry of satellites. Acta Astronaut. 2021, 181, 439–444. [Google Scholar] [CrossRef]
- Weeden, B.; Samson, V. (Eds.) Global Counterspace Capabilities: An Open Source Assessment; Secure World Foundation: Broomfield, CO, USA, 2023. [Google Scholar]
- Handmer, A. Lighting Up Down Under: A Science and Technology Studies examination of policy, legal and organizational challenges encountered during the development of Active Debris Removal technology in Australia. In Proceedings of the 73rd International Astronautical Congress (IAC), Paris, France, 18–22 September 2022. [Google Scholar]
- Speiser, J.; Ewers, B.; Kästel, J.; Lorbeer, R.-A.; Oberbeckmann, D.; Sauder, D.; Weichelt, B. Thin Disk Laser Development for Space Debris Monitoring and Mitigation. In Proceedings of the 2022 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 15–20 May 2022. [Google Scholar]
- Kästel, J.; Speiser, J. Turbulence Mitigation by Tiled Aperture Coherent Coupling of Laser Emitters. In Proceedings of the Laser Congress 2019 (ASSL, LAC, LS&C), Vienna, Austria, 29 September–3 October 2019; OSA Technical Digest, paper JW2A.44. Optica Publishing Group: Washington, DC, USA, 2019. [Google Scholar] [CrossRef]
- Scharring, S.; Dreyer, H.; Wagner, G.; Kästel, J.; Wagner, P.; Schafer, E.; Riede, W.; Bamann, C.; Hugentobler, U.; Lejba, P.; et al. LARAMOTIONS: A conceptual study on laser networks for near-term collision avoidance for space debris in the low Earth orbit. Appl. Opt. 2021, 60, H24–H36. [Google Scholar] [CrossRef] [PubMed]
- Deng, Y.; Ji, X.; Li, X.; Wang, T.; Yu, H. Optimal momentum coupling between the ground-based laser impulse and space debris. Appl. Phys. B 2022, 128, 138. [Google Scholar] [CrossRef]
- Tyson, R.K. Principles of Adaptive Optics, 4th ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Olivier, S.S.; Gavel, D.T. Tip–tilt compensation for astronomical imaging. J. Opt. Soc. Am. A 1994, 11, 368–378. [Google Scholar] [CrossRef]
- McClatchey, R.A.; Fenn, R.W.; Selby, J.; Volz, F.; Garing, J. Optical Properties of the Atmosphere; Air Force Cambridge Research Laboratories: Bedford, MA, USA, 1972. [Google Scholar]
- Opiela, J.N. A study of the material density distribution of space debris. Adv. Space Res. 2009, 43, 1058–1064. [Google Scholar] [CrossRef]
- D’Souza, B.C. Development of Impulse Measurement Techniques for the Investigation of Transient Forces due to Laser-Induced Ablation. Ph.D. Thesis, University of Southern California, Los Angeles, CA, USA, 2007. [Google Scholar]
- Scharring, S.; Wagner, G.; Kästel, J.; Riede, W.; Speiser, J. Ablative collision avoidance for space debris in the Low Earth Orbit by a single multi-kJ pulse from a ground-based laser. In Proceedings of the 2021 AMOS Conference Proceedings, Maui, HI, USA, 14–17 September 2021. [Google Scholar]
- Scharring, S.; Eisert, L.; Lorbeer, R.-A.; Eckel, H.-A. Momentum predictability and heat accumulation in laser-based space debris removal. Opt. Eng. 2019, 58, 011004-1–011004-12. [Google Scholar] [CrossRef]
- Klein, E.M. Simulation of Space Debris Heating in Laser-Ablative Orbit Modification Manouvers. Master’s Thesis, Technical University of Braunschweig, Braunschweig, Germany, 2021. [Google Scholar]
- Raciukaitis, G.; Brikas, M.; Gecys, P.; Gedvilas, M. Accumulation effects in laser ablation of metals with high-repetition-rate lasers. Proc. SPIE 2008, 7005, 725–735. [Google Scholar] [CrossRef]
- Scharring, S.; Karg, S.; Lorbeer, R.-A.; Dahms, N.; Eckel, H.-A. Low-Noise Thrust Generation by Laser-Ablative Micropropulsion. In Proceedings of the 30th International Electric Propulsion Conference (IEPC), Kobe, Japan, 4–10 July 2015. paper IEPC-2015-143. [Google Scholar]
- Orzi, D.J.O.; Alvira, F.C.; Bilmes, G.M. Determination of femtosecond ablation thresholds by using laser ablation induced photoacoustics (LAIP). Appl. Phys. A 2013, 110, 735–739. [Google Scholar] [CrossRef]
- McKnight, D.; Witner, R.; Letizia, F.; Lemmens, S.; Anselmo, L.; Pardini, C.; Rossi, A.; Kunstadter, C.; Kawamoto, S.; Aslanov, V.; et al. Identifying the 50 statistically-most-concerning derelict objects in LEO. Acta Astronaut. 2021, 181, 282–291. [Google Scholar] [CrossRef]
- United States Strategic Command (USSTRATCOM). Two-Line Element Orbital Data, USSTRATCOM 2019. Available online: https://www.space-track.org/ (accessed on 20 April 2023).
- European Space Agency-European Space Operations Center (ESA/ESOC), Space Debris User Portal (DISCOS Database, Master-8 Model), ESA/ESOC. 2019. Available online: https://sdup.esoc.esa.int/ (accessed on 20 April 2023).
- Krisko, P.H.; Horstman, M.; Fudge, M.L. SOCIT4 collisional-breakup test data analysis: With shape and materials characterization. Adv. Space Res. 2008, 41, 1138–1146. [Google Scholar] [CrossRef]
- Liedahl, D.A.; Rubenchik, A.; Libby, S.B.; Nikolaev, S.; Phipps, C.R. Pulsed laser interactions with space debris: Target shape effects. Adv. Space Res. 2013, 52, 895–915. [Google Scholar] [CrossRef]
- Phipps, C.R.; Baker, K.L.; Libby, S.B.; Liedahl, D.A.; Olivier, S.S.; Pleasance, L.D.; Rubenchik, A.; Trebes, J.E.; George, E.V.; Marcovici, B.; et al. Removing orbital debris with lasers. Adv. Space Res. 2012, 49, 1283–1300. [Google Scholar] [CrossRef]
- Wen, Q.; Yang, L.; Zhao, S.; Fang, Y.; Wang, Y. Removing small scale space debris by using a hybrid ground and space based laser system. Optik 2017, 141, 105–113. [Google Scholar] [CrossRef]
- Bloembergen, N.; Patel, C.K.N.; Avizonis, P.; Clem, R.G.; Hertzberg, A.; Johnson, T.H.; Marshall, T.; Miller, R.B.; Morrow, W.E.; Salpeter, E.E.; et al. Beam Material Interactions and Lethality. In Report to The American Physical Society of the study group on science and technology of directed energy weapons. Rev. Mod. Phys. 1987, 59 Pt II, S119–S143. [Google Scholar] [CrossRef]
- Jumper, G.Y.; Holladay, J.J.; Wiechert, M.K.; Seggel, W.A. Impact of Thrust Alignment on Orbital Debris Removal by Ground-Based Lasers. J. Spacecr. Rocket. 2012, 49, 261–267. [Google Scholar] [CrossRef]
- Nussbaum, M.; Schafer, E.; Yoon, Z.; Keil, D.; Stoll, E. Spectral Light Curve Simulation for Parameter Estimation from Space Debris. Aerospace 2022, 9, 403. [Google Scholar] [CrossRef]
- Dianetti, A.D.; Crassidis, J.L. Space Object Material Determination from Polarized Light Curves. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. paper AIAA 2019-0377. [Google Scholar] [CrossRef]

| Category | ||||||
|---|---|---|---|---|---|---|
| Payload | 59.9 | −0.0145 | 17.4 | −0.0052 | 41.1 | −0.0105 |
| Rocket Body | 68.7 | −0.0253 | 22.9 | −0.0099 | 54.2 | −0.0237 |
| Payload fragment | 55.7 | −0.0113 | 13.1 | −0.0024 | 34.6 | −0.0056 |
| Rocket fragment | 57.0 | −0.0158 | 14.9 | −0.0046 | 36.5 | −0.0092 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scharring, S.; Kästel, J. Can the Orbital Debris Disease Be Cured Using Lasers? Aerospace 2023, 10, 633. https://doi.org/10.3390/aerospace10070633
Scharring S, Kästel J. Can the Orbital Debris Disease Be Cured Using Lasers? Aerospace. 2023; 10(7):633. https://doi.org/10.3390/aerospace10070633
Chicago/Turabian StyleScharring, Stefan, and Jürgen Kästel. 2023. "Can the Orbital Debris Disease Be Cured Using Lasers?" Aerospace 10, no. 7: 633. https://doi.org/10.3390/aerospace10070633
APA StyleScharring, S., & Kästel, J. (2023). Can the Orbital Debris Disease Be Cured Using Lasers? Aerospace, 10(7), 633. https://doi.org/10.3390/aerospace10070633





