Abstract
In this paper, a novel guidance algorithm based on adaptive convex optimization is proposed to ensure robustness in the uncertainty of a lunar lander’s parameters and satisfy the constraints of terminal position, velocity, attitude, and thrust. To address the problem of parameter uncertainty in the landing process, the parameter-adaptive method is used to achieve online real-time optimal estimations of specific impulse and mass by the optimal observer, and the estimated parameters are used to realize optimal trajectory programming. To overcome the difficulty in constraining the attitude and the thrust level at the final stage in the convex optimization process, a rapid adjustment phase is added to meet the final attitude and thrust constraints; the target-adaptive method is used to adjust the target adaptively at the same time. Therefore, the position and velocity deviations caused by the rapid adjustment phase can be eliminated by the target offset. Finally, the results of numerical experiments demonstrate the effectiveness of the proposed algorithm.
1. Introduction
In this paper, an adaptive convex optimization algorithm is presented for the application of lunar surface pinpoint landings. Unlike the classical method that directly convexifies the lunar landing dynamics model with the corresponding constraints into a second-order cone programming (SOCP) problem, the proposed approach introduces parameter-adaptive and target-adaptive algorithms to improve the adaptability of the method for parameter uncertainties and constraints on the final attitude and thrust magnitude of the lander.
To successfully implement autonomous obstacle avoidance and ensure an accurate and safe landing, the lunar landing process is usually divided into three phases: powered descent, approach, and landing, as shown in Figure 1 [1,2,3,4]. In the powered descent phase, the lander’s altitude and velocity will be greatly reduced. In the subsequent approach phase, various sensors on the lander will start to work actively to avoid obstacles and select the landing site, and a soft landing will be achieved in the final landing phase. These phases can be subdivided further depending on the mission. Taking Chang’e-3 [2,5,6,7,8] as an example, the lunar lander is in a transfer orbit with an apocynthion of 100 km and pericynthion of 15 km before the powered descent phase. From near the pericynthion, it enters the powered descent phase. The main goal of the powered descent phase is to reduce the altitude and velocity of the lander as much as possible. During the powered descent phase, the altitude is reduced from 15 km to 2.4 km and the velocity is reduced from 1.7 km/s to approximately 50 m/s [9,10]. This phase typically consumes approximately 80% of the lander’s fuel, so the guidance algorithm for this phase requires minimizing fuel consumption with the initial lander state error and model uncertainty and achieving the entrance state requirements for the subsequent approach phase at the end.
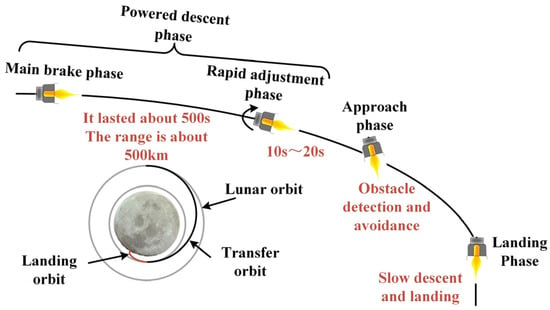
Figure 1.
Typical lunar landing process.
To save as much fuel as possible during the powered descent phase, the linear tangent guidance law with suboptimal fuel characteristics was adopted for the Chang’e-3 probes. However, the linear tangent guidance law cannot control the flight distance; in fact, the allowable landing area of Chang’e-3 is a rectangle area, 356 km long and 91 km wide, in Sinus Iridum [11]. This clearly does not meet the mission requirements of future lunar exploration for high-precision landings.
China plans to establish a manned lunar base in the future, which requires the lander to be able to land with pinpoint accuracy near the base [12]. In addition, as the exploration of the moon progresses further, lunar landers need the ability to land precisely near high-science-value targets with complex terrain [13,14].
All of these goals require the next-generation lunar lander to have the capability of precision pinpoint landing. The quality of trajectory planning and the accuracy of the guidance algorithm have a direct impact on the final landing accuracy and fuel consumption during the powered descent phase, where most of the lander’s kinetic and potential energy are dissipated. Due to their critical importance, these algorithms have received extensive attention from various institutions and individuals [15].
Current lunar surface landing guidance algorithms are divided into explicit and trajectory optimization algorithms. Explicit guidance algorithms are typically represented by augmented Apollo powered-descent guidance (A2PDG) [16], fractional-polynomial powered descent guidance [17], and zero-effort-miss/zero-effort-velocity (ZEM/ZEV) guidance [18,19,20]. These algorithms have good autonomy for real-time adjustments and anti-interference capabilities and can guarantee terminal guidance accuracy.
Compared to explicit guidance algorithms, numerical optimization algorithms based on optimization principles design nominal trajectories according to certain objectives and constraints. These methods typically consume less fuel and are more robust. In particular, convex optimization algorithms have been widely studied and applied owing to their polynomial computational complexity and theoretical global optimality [21,22].
The method presented in [22] transforms the Mars landing problem into a convex optimization problem, ensuring convergence to the optimal solution within a limited number of iterations. As a result, subsequent research has focused on extending this method to more complex dynamics, constraints, free-final-time problems, and other related areas. These improvements aim to enhance the robustness and applicability of the algorithm [23,24]. The determination of the optimal time-of-flight required for convex optimization was further specified in [23]. As reported in [24], by combining convex optimization with the pseudo-spectral method, the number of nodes and CPU time is reduced, and the accuracy of the operation is improved by reasonably selecting the set of nodes.
Furthermore, other improvements have been investigated to extend the applicability of the method under different conditions, such as complex dynamics environments, or to add functions, such as hazard avoidance. In [25], convex optimization and curvature adjustment strategies were combined to ensure obstacle avoidance while reducing fuel consumption. In [26], an approach to optimal trajectory design with uncertainty was considered. The uncertainty was further considered in [27], where a convex optimization method was proposed to achieve precise landing of the rocket under different initial states and various disturbances. An optimal control approach based on learning and theoretical support was proposed to solve the problem of the on-board fuel-optimal guidance law in the powered descent phase in [28]. The dimension of the learning space was significantly reduced by guiding the learning process with the necessary conditions derived from Pontryagin’s minimum principle, and supervised learning (SL) and optimal control theory were combined. In [29], a learning-based six-DOF planetary powered descent and landing method was introduced using reinforcement learning theory. The thrust command of each engine was mapped to the estimated state of the lander by learning a policy, achieving precise positioning and soft landing with robustness to noise and parameter uncertainty. Different discount rates were also introduced to calculate shape and terminal rewards, significantly improving performance.
In [30], a convex optimal trajectory programming algorithm was improved for application to landing on asteroids with irregular shapes and gravitational fields. In [31], an effective solution for powered-descent guidance was proposed, which considered multiple constraint conditions, such as attitude and state-triggered constraints. The authors of [32] utilized a dual-quaternion-based approach to simultaneously handle attitude and thrust constraints, achieving an integrated design of guidance and control. Building upon these works, the non-convex trajectory optimization problem, which is difficult to handle, was solved in real-time by combining continuous convex programming and first-order cone optimization in [33]. Multiple constraint conditions, including attitude, thrust, and state-triggered constraints, can be simultaneously handled by this algorithm, which achieves higher computational efficiency and faster convergence rates.
In this study, we first considered that landers usually fly with uncertainties such as specific impulse and initial mass [34,35], which can affect convex optimization and reduce the optimality of the lander trajectory and increase fuel consumption. In addition, various lunar surface sensors, such as cameras and lidars, typically do not work when the lander is further away from the moon, which means that the lander has no attitude constraints at this time. However, as the powered descent phase comes to an end and the lander gets close enough to the moon, it is usually desired that the lander has a specific attitude so that it can obtain images and measurements from various sensors for obstacle avoidance and navigation [9,35,36,37,38] and a specific thrust magnitude for a smooth transition to the subsequent phase [10,39].
On this basis, an adaptive convex optimization algorithm for lunar landing guidance is proposed. In the proposed algorithm, we first consider the effect of parameter uncertainty during the flight of the powered descent phase. Thus, an optimal observer using accelerometric measurements was designed to estimate the specific impulse and real-time mass of the lander and eliminate uncertainty. After this observer convergence is reached, the lander’s trajectory is replanned online on the basis of the new parameter values. This algorithm utilizes the optimal observer to obtain the optimal estimation of the system state and parameters, compensating for parameter uncertainty. In contrast to learning-based methods, this algorithm does not require training datasets and can provide more precise estimations due to its mathematical model-based nature. Furthermore, the optimal observer-based approach can offer error quantification and correction for estimations, thereby improving the robustness of the algorithm. Additionally, unlike the approach in [31,32,33] that introduces attitude constraints throughout the entire flight, this paper inserts a rapid adjustment phase at the end of the trajectory generated by the classical convex optimization algorithm. This method does not introduce attitude constraints in the convex optimization process, nor does it require integrated guidance and control design. Instead, the rapid adjustment phase at the end of the trajectory, generated by the classical convex optimization algorithm, is used to constrain the lander’s attitude (primarily pitch angle) and thrust magnitude. The deviation of the position and velocity caused by the rapid adjustment of the attitude and thrust is eliminated by adaptively adjusting the power descent phase target to meet the requirement of approaching the phase entrance window. Compared with classical methods, the proposed approach in this paper, which incorporates a rapid adjustment phase and a target-adaptive algorithm, only requires the lander to have a specific attitude at the end of the powered descent phase, rather than imposing unnecessary constraints on attitude range throughout the entire flight. This provides the lander with greater flexibility for adjusting attitude during flight, leading to more efficient fuel consumption. Moreover, it avoids the need for six-DOF guidance and a control-integrated design, which reduces the design complexity and system complexity, as well as the state dimension. This results in a smaller computational load and better real-time performance of the guidance system.
The remainder of this paper is organized as follows. Section 2 presents the lunar landing process and phase division as well as the dynamics model and briefly describes how to transform the lunar landing optimal trajectory planning problem into a finite-dimensional convex optimization problem. Section 3 presents the design of an optimal estimator to estimate the uncertainties in the lunar landing process to achieve parameter adaption. Section 4 presents a target-adaptive algorithm that allows the lander to make rapid adjustments to meet the approach phase entrance requirements without causing position and velocity deviations. Section 5 presents the numerical results using only parameter adaption, only target adaption, and integrated simulation. Finally, Section 6 summarizes the conclusions of this study.
2. Problem Formulation
2.1. Guidance System Scheme
The convex optimization algorithm, which is used to plan the optimal trajectory, can transfer from the given initial state to a predetermined target state on the premise of saving as much fuel as possible. However, two problems remain.
On the one hand, it is difficult to add the final attitude constraints to the guidance process, which causes uncertainty in the final attitude. However, when the lander is close enough to the lunar surface, to navigate and avoid hazards, the sensors and detection elements usually require the lander to have a certain attitude. Furthermore, the lander requires a specific thrust for a smooth transition to the subsequent phase. To achieve the attitude and thrust constraints at the end of the powered descent phase, the powered descent phase is divided into the main breaking phase and rapid adjustment phase. The thrust and attitude are smoothly transferred to meet the requirements of the subsequent phase during the rapid adjustment phase. However, the trajectory generated by convex optimization depends on the specific impulse, initial mass, and other parameters of the engine. The uncertainty of the parameters affects the optimality of the trajectory formed by the convex optimization and the accuracy of the final state. Simultaneously, the rapid adjustment process also affects the final state. Therefore, it is necessary to adopt an adaptive convex optimization algorithm to achieve the entrance condition of the approach phase by automatically adjusting the powered descent phase target and estimating the guidance parameters in real time to improve guidance accuracy and reduce fuel consumption.
The sequence of the guidance system is shown in Figure 2. The powered descent phase is divided into the main breaking phase and the rapid adjustment phase. A closed-loop feedback system is implemented along the optimal trajectory generated by convex optimization. The nominal trajectory is generated twice: The trajectory generated for the first time is offline, and only the target-adaptive algorithm is considered. After the online parameter estimation converges, the adaptive convex optimization is performed according to the current lander state. Both the target adaption and parameter adaption are considered during this convex optimization. The lander then carries closed-loop feedback guidance according to the nominal trajectory. Before the end of the powered descent phase, the lander enters the rapid adjustment phase. In this phase, the lander adjusts its attitude and thrust rapidly. In this phase, the lander performs open-loop guidance. As the target-adaptive adaption has been carried out previously, after the guidance of the rapid adjustment phase is completed, the lander reaches the target state of the power descent phase.
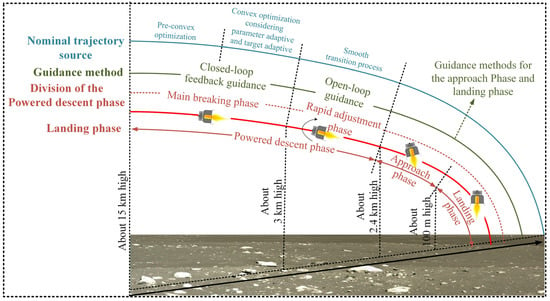
Figure 2.
Sequence of the lunar lander guidance system.
2.2. Dynamic Model
As the inertial force does not exist in the lunar center inertial coordinate system, and to simplify the problem, a dynamic model is established in this coordinate system. Under this condition, the dynamic model is given by:
where and are the position and velocity of the lander at time, respectively; is the thrust; is the mass; is the vacuum specific impulse; is the nominal gravity acceleration constant of the Earth; is the gravitational acceleration; and denotes the mass flow coefficient.
As this paper adopts the inverse-square gravity model, and the coordinate system of the model is in the inertial frame, the gravitational acceleration varies with the position during flight. On the one hand, as the flight altitude decreases, the magnitude of the gravitational acceleration changes. On the other hand, as the latitude and longitude of the lander change, the direction of the in the inertial frame also changes. Therefore, in this paper, the gravitational acceleration is assumed to be a time-varying quantity that changes along the nominal trajectory of the lander during the approach phase before powered descent guidance.
The state of the lander must be constrained to ensure vehicle safety during the landing process. In the landing process, to prevent the lander from hitting the lunar surface, a height constraint should be introduced:
where denotes the height of the lander, and denotes the minimum allowable height. The thrust constraint can also be introduced as:
where , are the minimum and maximum thrusts, respectively, provided by the thruster.
where is the mass of the lander without fuel in the powered descent phase, and is the final mass of the lander.
Finally, the constraints on the initial and final states of the lander are given as:
where and are the initial and target positions, respectively, and and are the initial and target velocity, respectively.
The trajectory planning problem for lunar landing can be formulated as a two-point boundary fuel-optimal control problem. By taking the fuel consumption as the landing performance index and maximizing the final mass , the following objective function must be minimized:
By combining the dynamic model, constraints, and objective functions in Formulas (1)–(6), the optimization problem referred to as Problem 1 is expressed as follows.
Problem 1:
Continuous-time minimum fuel optimization problem
2.3. Trajectory Planning Algorithm Based on Convex Optimization
For Problem 1, as shown in Formula (7), because in the dynamic model appears in the denominator and the thrust constraint is a nonconvex constraint, Problem 1 is a non-convex problem. To use the convex optimization method to solve the problem the model needs to be convexified and converted into a convex problem, specifically, the SOCP problem. First, logarithmic mass is introduced [22]:
Second, new control variables are introduced:
From Formulas (8) and (9), the dynamic model becomes:
The objective function becomes:
Furthermore, the thrust constraint and mass constraint also become:
The remaining mass constraint becomes:
where denotes the logarithmic dry mass.
Furthermore, the control variable constraint must be introduced:
When the optimal solution is obtained, the control variable must satisfy [40]:
where the superscript asterisks indicate the optimal control variables.
To avoid the exponential nonconvex constraint, Taylor expansion can be performed using Formula (12):
where satisfies:
where denotes the initial mass of the lander.
The logarithmic mass must also satisfy the following constraints:
From the preceding convexification of the dynamics and constraints, the fuel-optimal continuous-time convex optimization problem represented as Problem 2 can be described as follows.
Problem 2:
Continuous-time minimum fuel SOCP problem
Problem 2 is an SOCP problem obtained by lossless convexification from Problem 1. This must be discretized before solving. The state and augmented control variables are defined as follows:
Accordingly, the dynamic model of Formula (10) becomes:
where
To discretize the problem, the time interval is divided into intervals with time increment ; the temporal nodes are , , . In the time interval , the control variables satisfy:
where denotes a specific primary function. In the proposed algorithm, the primary function is taken as a constant function, which means that the control variables remain unchanged in each interval. The discrete dynamic model is [28,41]:
where , , and are , , , and is the solution of the linear matrix ordinary differential equation:
and are defined as:
Problem 3 can be obtained after discretization:
Problem 3:
Convex finite-dimensional fuel-optimal lunar landing problem
where , , , and .
In this way, the lunar landing problem becomes a discrete SOCP problem. If a feasible solution exists for Problem 3, then this solution also defines a feasible solution for Problem 1 [22], and simultaneously, Problem 3 can be solved globally optimally in polynomial time [42]. Further discussion on the speed of convergence can be found in [23].
3. Parameter-Adaptive Algorithm
Parameters such as mass and specific impulse must be used in the convex optimization process of the lander. If the parameters used are inconsistent with reality, the parameter error will affect the optimality of the landing trajectory and then affect the landing error and fuel consumption. Therefore, a parameter-adaptive algorithm is proposed in this paper to estimate the parameters of the lander by constructing an observer, using these parameters in the convex optimization process to ensure optimality.
3.1. Model of the Uncertainty
During landing, some uncertainties exist in the engine working conditions, processing technology, oxidant, and fuel state; therefore, some uncertainty exists in the specific impulse of the lander. At the same time, owing to the volatility of the fuel carried by the lander and the weight of the crew and materials, the initial mass also has uncertainty; therefore, the mass in the flight process also has uncertainty. Therefore, the proposed algorithm uses the online measured value of the accelerometer to estimate the contrast impulse and mass.
Assuming that the specific impulse remains constant during flight, the mass flow coefficient is also constant. Subsequently, the mass and mass flow coefficients of the lander satisfy the following differential equations:
where .
Taking the measurement of the accelerometer as an observation, the observation equation is:
Let ; then, Formulas (28) and (29) can be written as:
where
3.2. Observer Design
The system (30) is nonlinear, and more precisely, its measurement equation is nonlinear. In this study, considering that the steady-state behavior of the Kalman filter is unbiased and optimal [43], an optimal observer based on an extended Kalman filter was designed. Considering the optimal observer designed for the system (30), the model of the observers is:
The Jacobian matrix of and in is:
The observation gain matrix is set as:
where is the solution to the Riccati equation:
where , , and are positive-definite symmetric matrices. By combining the differential Formulas (32) and (35), converges to .
To avoid drastic changes in the parameters, which leads to the drastic fluctuation of guidance parameters and the loss of smoothness in the guidance process, the second component is smoothed by the integral sliding window:
4. Target-Adaptive Algorithm
It is usually necessary for the lander to have a specific thrust and attitude at the end of the powered descent phase to facilitate the operation of various lunar surface sensors and to transition smoothly to the subsequent approach phase. The classical convex optimization algorithm typically imposes constraints on the thrust range and attitude throughout the entire flight process, rather than requiring the lander to have a specific thrust magnitude and direction at the end of the powered descent phase. To address this issue, this paper proposes a target-adaptive algorithm based on convex optimization for real-time trajectory planning. During most of the powered descent phase, the lander’s control system adjusts the attitude in real time based on the thrust direction commanded by the guidance system to ensure that the lander’s thrust direction is consistent with the command. In the last several seconds of the powered descent phase (generally 10~20 s), the lander switches to open-loop guidance and rapidly adjusts its attitude and thrust to smoothly transition to the desired thrust and attitude in a linear manner over time.
Due to the fact that the lander switches to open-loop guidance in the final seconds of the powered descent phase, adjusting the attitude and thrust rapidly to achieve the desired values, it naturally deviates from the nominal values in terms of thrust direction and magnitude. Consequently, the lander’s final state at the end of the powered descent phase deviates from the desired position and velocity. To address this issue, the target offset technique is proposed in this paper, which intentionally shifts the constraints on the final target state of the convex optimization to enable the lander to reach the original ideal target state, which has not been offset, after the rapid adjustment phase of open-loop guidance.
The flight process of the lander is shown in Figure 3. Assuming that the lander flies along the initial nominal trajectory, as indicated by the black line in Figure 3 at the beginning, after entering the rapid adjustment phase, because the attitude and thrust no longer refer to the nominal command designed by the nominal convex optimization algorithm, the position and velocity of the lander inevitably deviate from the ideal position and velocity along the black dotted line. The actual lander final state also deviates from the target state, . The target-adaptive algorithm adopts the target offset technology. After setting the target to , the convex optimization trajectory is re-planned. The final nominal trajectory is indicated by the blue line in Figure 3. The lander flies along the nominal trajectory through closed-loop guidance during the main breaking phase. In the rapid adjustment phase, owing to the rapid adjustment of attitude and thrust, the lander also deviates from the nominal trajectory along the blue dotted line. However, owing to the target offset technology, the lander reaches the target state after rapid adjustment.
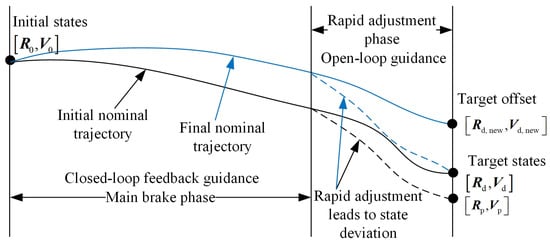
Figure 3.
Target-adaptive algorithm.
The specific algorithm for target adaption is as follows: the target position and velocity of the lander are and , respectively. Then, are considered as the target values of the convex optimization for trajectory programming. On the basis of the current optimal trajectory, it is assumed that the last s will enter the rapid-adjusted phase so that the final attitude and thrust of the lander meet the constraints. However, the final position and velocity of the lander deviate from the nominal state owing to the insertion of a rapid adjustment phase compared with the nominal trajectory. Assuming that the times before and after the rapid adjustment are and , the ideal initial and end thrust values are and , and the initial and end pitch angles are and , respectively. As the lander generally does not exhibit lateral movement during landing, its yaw angle changes little; therefore, the yaw angle is assumed to change along the original yaw angle profile. Simultaneously, the roll angle is independent of the thrust direction and can be set arbitrarily. Therefore, the effect of roll angle is not considered in this process. During the rapid adjustment phase, the thrust and pitch angles change uniformly according to the program instructions:
where represents the nondimensional time, and , represent the change values of thrust and pitch angle, respectively, to be adjusted in the rapid adjustment phase.
According to Formula (36) the output thrust vector of the lander is given by:
According to the thrust vector output , the position , velocity , and mass of the lander in the initial stage of the rapid adjustment phase, the predicted position , and velocity can be obtained.
As the process of the rapid adjustment phase lasts only 10~20 s, the mass of the lander changes little during this process. Consider a typical 7500 N variable-thrust engine with a specific impulse of 309 s as an example. Its full-thrust output is 20 s, and the fuel consumption is approximately 50 kg. If the initial mass of the lander is 5000 kg, the mass change is only 1%. Therefore, in the prediction process, the mass of the lander is regarded as unchanged and is calculated using the average mass of the rapid adjustment phase. First, the average mass is predicted as follows.
As the mass satisfies:
the final mass can be obtained as:
and the average mass is:
Therefore, the predicted position and velocity changes of the lander are:
If the nominal target states without any offset are and , the position and velocity deviations caused by the rapid adjustment are:
In the proposed algorithm, the target bias method is used to adjust the target-state deviation; that is, the new landing target is set as:
where and are feedback correction coefficients for the target position and target velocity, respectively.
According to the new landing targets and obtained previously, convex optimization is performed again to obtain the optimal trajectory. After the optimal trajectory is obtained, the position and velocity deviations are recalculated. This process is repeated until the final position and velocity deviations are less than certain values.
According to the preceding discussion, a closed-loop guidance system is shown in Figure 4. Its main guidance loop compares the nominal trajectory generated by convex optimization with the trajectory generated by guidance and carries out position and speed feedback on the basis of the nominal guidance command so that the lander does not leave the nominal trajectory in the presence of interference force and output uncertainty and successfully reaches the target state.
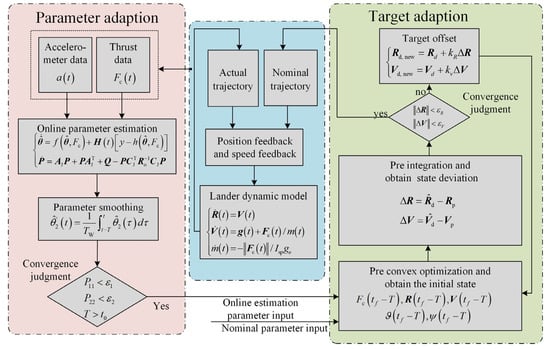
Figure 4.
Guidance system structure.
Simultaneously, the parameter-adaptive module uses the information measured by the accelerometer and the output data of the thruster to estimate the online parameters through a nonlinear optimal observer. The estimated parameters converge to the real value with the accumulation of acceleration measurement data. To avoid violent oscillation of the estimated parameters, the estimated parameters are smoothed by the sliding-window integral smoother, and then the parameters are transmitted to the convex optimization system to generate a new nominal trajectory. In the subsequent guidance process, the lander uses a new nominal trajectory for closed-loop feedback guidance. This module improves the adaptability of the guidance to mass and specific impulse uncertainty.
In addition, the target-adaptive module first performs pre-convex optimization in the convex optimization process, and according to the convex optimization trajectory, the final state of the main breaking phase is obtained, namely, the state of the lander at the moment. It is assumed that the attitude and thrust of the lander linearly and smoothly transit to the target attitude and thrust. This transition leads to deviation and of the target state of the lander. Therefore, the target of the lander deviates according to Formula (44), and convex optimization is performed again until the final state deviation of the lander is less than the given value. The trajectory formed at this time is the nominal trajectory, and the lander conducts closed-loop feedback guidance according to this trajectory. This module ensures the terminal attitude and thrust-constraint ability of the lander.
5. Simulation Results and Discussion
This section describes the three numerical simulations that were conducted to verify the effects of parameter adaption and target adaption and the integrated guidance effect.
5.1. Parameter-Adaptive Algorithm
Owing to the existence of many uncertainties, the flight parameters of the lander may be inconsistent with the nominal parameters, which can degrade the optimality of the convex optimal trajectory and consume additional fuel. The parameters are set as shown in Table 1 with references from [10,39,44]. Due to the ignition of the descent engine at perilune, the initial vertical velocity of the lander is zero.

Table 1.
Lander parameters in parameter-adaptive simulation.
The estimation results of the optimal observer for the mass and specific impulse are shown in Figure 5 and Figure 6. As the measurements are directly related to the mass, the convergence of the mass estimates is rapid, as shown in Figure 5, converging to the true value within 0.5 s, and then tracking the gradual decrease in the true value as the fuel is consumed. By contrast, because the integration of the mass flow coefficient (specific impulse) is related only to the measured value, the convergence rate of the specific impulse is slower than that of the mass. As shown in Figure 6 and Table 2, convergence can be completed in approximately 10 s. Under the initial conditions of this simulation example, the mean value of the final mass estimation error is −0.0059 kg, and the standard deviation of the error is 0.2333 kg; the mean value of the final specific impulse estimation error is −0.0315 s, and the standard deviation of the error is 0.601 s. Furthermore, note that there is a fluctuation of approximately ±5 s in the estimated specific impulse curve after 500 s. This result was due to a sudden change in the thrust curve at this time, as shown in Figure 7. Thus, the matrix in Formula (35) changed, and accordingly, the matrix changed, which according to Formula (35) affected the corresponding observed gain matrix and thus caused an unexpected change in the observed value.
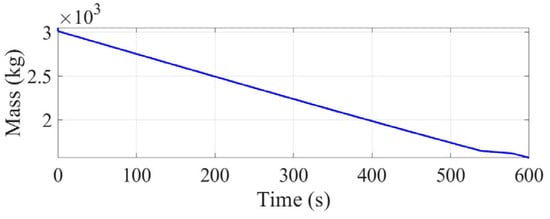
Figure 5.
Mass estimation curve.
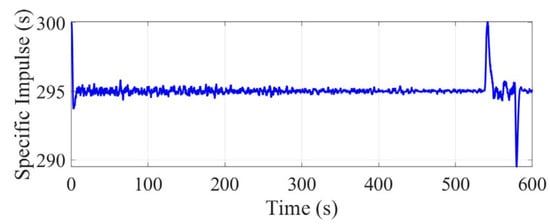
Figure 6.
Specific impulse curve.

Table 2.
Parameter estimation error.
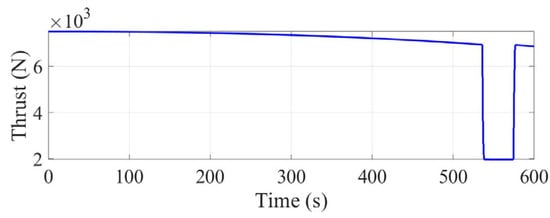
Figure 7.
Thrust curve.
Depending on the convergence rate, it takes approximately 10 s for the parameter estimation to reach convergence. Therefore, matrix was tested from the beginning of the estimation to 10 s later. In addition, if the abrupt thrust change point occurs before convergence, it should be re-regarded as the start time, leaving 10 s at the abrupt change point to allow the parameter estimation to converge. The matrix is checked 10 s after the start time, and if the matrix satisfies and , the observer is considered to have achieved convergence on the parameter estimates. After convergence, the onboard computer uses this parameter estimation result to re-plan the optimal trajectory and uses this trajectory as the basis for closed-loop feedback guidance.
Comparisons of whether to use the parameter-adaptive algorithm are shown in Figure 8, Figure 9 and Figure 10. It can be seen that with either feedback guidance with the optimal trajectory formed by convex optimization based on nominal parameters or online estimated parameters, the lander can reach the predetermined target state. In the case where the parameter-adaptive algorithm is not used, the actual parameters are different from the nominal parameters used for convex optimization. The uncertainties in the thrusters and output devices cause the lander to deviate from the nominal trajectory, and the velocity and position feedback loops correct the deviation so that the lander finally reaches the intended target. When the parameter-adaptive algorithm is used, the lander actively estimates each parameter with uncertainties and re-inputs the parameter estimates into the onboard computer to form a nominal trajectory again, thereby reducing the uncertainty in the landing process, improving the landing accuracy, and simultaneously ensuring the optimality of the landing trajectory.
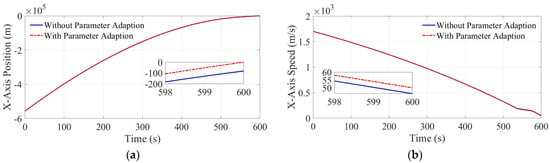
Figure 8.
X-axis flight curve: (a) X-axis position; (b) X-axis speed.
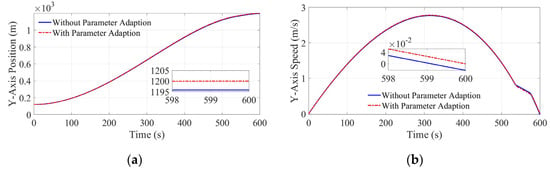
Figure 9.
Y-axis flight curve: (a) Y-axis position; (b) Y-axis speed.
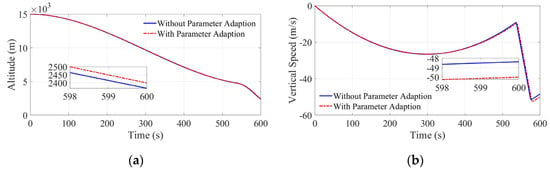
Figure 10.
Z-axis flight curve: (a) altitude; (b) vertical speed.
The simulation results are listed in Table 3. In this simulation, when no parameter adaption was adopted, the final X-direction position error, Y-direction position error, and altitude errors of the lander were 0.8568 m, −0.0373 m, and −1.172 m, respectively, and the final X-axis speed error, Y-axis speed error, and vertical speed error were −0.5780 m/s, −0.2046 m/s, and 0.2805 m/s, respectively. In the case of adopting parameter adaption, the three-axis position error of the lander trajectory was −0.01574 m, −0.067 m, and 0.051 m, and the three-axis speed error was −0.013 m/s, −0.073 m/s, and 0.0058 m/s. The uncertainty of the end state of the lander was greatly reduced. With respect to fuel consumption, the final remaining mass was 0.34 kg more with the parameter-adaptive algorithm than without it because the parameters used for optimal trajectory planning by convex optimization are closer to the actual parameters when the parameter-adaptive algorithm is used. In conclusion, the parameter-adaptive algorithm can improve the accuracy of the final state while also resulting in a slight reduction in fuel consumption.

Table 3.
Final state of lander.
5.2. Target-Adaptive Algorithm
The target-adaptive algorithm places the state of the lander exactly at the predetermined target state after the rapid adjustment phase by actively performing the target offset. The relevant simulation parameters are presented in Table 4 [10,39,44].

Table 4.
Lander parameters in target-adaptive simulation.
The simulation results are shown in the following figures, and the three-axis thrust curves are shown in Figure 11. As shown in the figures, compared to the original optimal trajectory without the rapid adjustment phase, the two curves with the rapid adjustment phase exhibit a rapid change in thrust in the last 10 s, in addition to the typical max-min-max thrust switch caused by the convex optimization. This rapid change was due to the rapid linear adjustment of the attitude angle and thrust magnitude. The total thrust curve is shown in Figure 12a. It can be seen that the total thrust of the original optimal trajectory ended near 6800 N, and the final thrust was approximately 3500 N after rapid adjustment, which is conducive to the subsequent phase. Figure 12b further shows the fuel consumption and lander mass. As the proposed algorithm adds a rapid adjustment phase to ensure that the lander meets the final attitude and thrust constraints, the trajectory must not be optimal, and the algorithm inevitably consumes more fuel compared to the original optimal trajectory formed by convex optimization. As depicted in Figure 12b, the addition of a rapid adjustment phase to the original trajectory for the purpose of uniformly reducing the thrust magnitude at the end resulted in the lowest fuel consumption and a final mass of 1584.1 kg. However, at this point, the lander had already deviated from the desired state and failed to achieve the desired position and velocity. Nonetheless, the fuel consumption of the original trajectory and the target-adaptive adjustment trajectory were nearly equivalent, with respective final masses of 1578.8 kg and 1578.7 kg. This observation highlights that the target-adaptive algorithm can effectively ensure that the lander conforms to the final attitude and thrust constraints with a minimal additional fuel cost (i.e., only 0.1 kg) in comparison to the original trajectory.
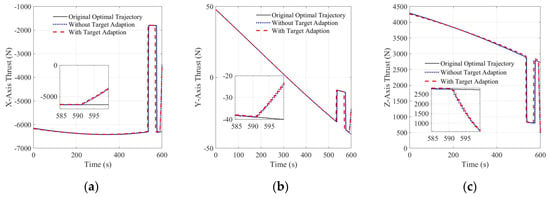
Figure 11.
Three−axis thrust curve (a) X-axis thrust curve; (b) Y-axis thrust curve; (c) Z-axis thrust curve.
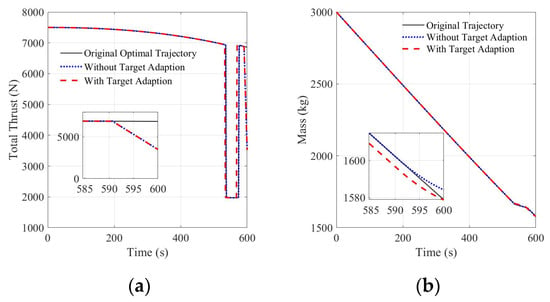
Figure 12.
Thrust curve and mass curve: (a) thrust curve; (b) mass curve.
The change in the attitude angle is shown in Figure 13. Figure 13a shows the change in the yaw angle. As the rapid adjustment phase does not adjust the yaw angle, the three curves in Figure 13a almost coincide, and the yaw angle itself changes less under the calculation example shown in this paper and can be maintained at approximately 180°. Figure 13b shows the pitch angle curve; according to the original optimal trajectory, the pitch angle was adjusted from 55° to 66° at an almost uniform speed in the last 10 s. After inserting the rapid adjustment phase, the lander quickly adjusted the pitch angle from approximately 66° to approximately 82° in the last 10 s, reaching the target attitude angle, which can meet the requirements of sensor alignment to the ground for navigation, obstacle avoidance, and autonomous landing site selection in the next flight phase.
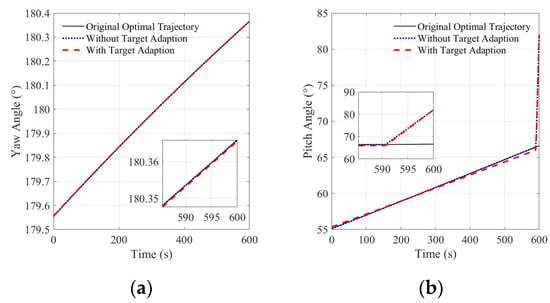
Figure 13.
Attitude curve (a) yaw angle curve; (b) pitch angle curve.
As the rapid adjustment phase is inserted at the end of the main braking phase, it inevitably causes the state to deviate from its target state. To avoid this situation, the proposed algorithm adopts a target offset to correct it. The speed curves are shown in Figure 14. As seen in the figure, the original optimal trajectory without the rapid adjustment phase reaches the expected target state, that is, the X-axis speed is 50 m/s, the Y-axis speed is 0 m/s, and the vertical speed is −50 m/s. The speed curve after adding the rapid adjustment phase coincides with the original curve at first, but after the rapid adjustment begins, the speed curves gradually deviate from the original curve, and after finishing the rapid adjustment phase, all the speeds deviate from the desired target state; the X-axis speed is 60 m/s, Y-axis speed is 0.05 m/s, and vertical speed is −57 m/s. After the target-adaptive adjustment, because the landing target state used in the convex optimization is not the predetermined target state at this time, the deviation of the speed curve is generated at the beginning compared to the original nominal curve. However, after the rapid adjustment phase, the final speed is exactly the predetermined target speed, so the final speed error is eliminated by the target-adaptive technique. The position curves are presented in Figure 15; for the same reason as that for the speed curve, the original optimal curve could successfully reach the intended landing position of [0, 1200, 2400] m. However, the state of the lander gradually deviated from the nominal value in the rapid adjustment phase, so the lander finally reached the position of [23.89, 1200.2, 2376] m. After target adaption, the lander finally reached the target position.
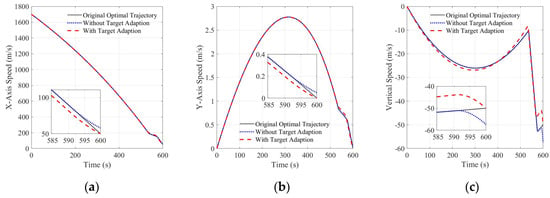
Figure 14.
Three-axis speed curve (a) X-axis speed curve; (b) Y-axis speed curve; (c) vertical speed curve.
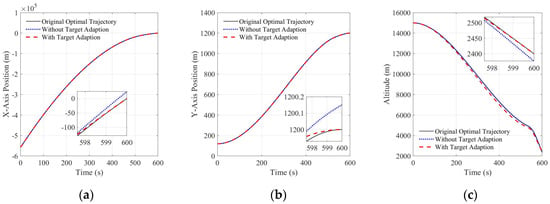
Figure 15.
Three-axis position curve (a) X-axis position curve; (b) Y-axis position curve; (c) altitude curve.
5.3. Integrated Simulation Verification
In this experiment, 1000 Monte Carlo shooting simulations were performed to verify the deviations caused by the parameter uncertainties and rapid adjustment phase, with the simulation parameters listed in Table 5 [10,39,44].

Table 5.
Monte Carlo shooting simulation parameters.
The statistics of the simulation results are shown in Figure 16, Figure 17, Figure 18 and Figure 19. Figure 16a, Figure 17a and Figure 18a show the distribution of the position error, and it can be seen that the error is largest in the X direction and smallest in the Y direction. It can also be seen that the position error with adaptions is almost unbiased, that is, its mean value is zero, whereas its position error without adaptions is biased. This result is due to the addition of the rapid adjustment phase after the main braking phase, which performs the rapid adjustment of attitude and thrust causing the position to deviate from its target. In contrast, the adaptive convex optimization algorithm uses a target-adaptive algorithm that actively performs a target offset to compensate for this part of the violation, such that the position error can be unbiased. In addition, because the adaptive convex-optimized guidance uses a parametric adaptive algorithm that compensates for the specific impulse and initial mass uncertainty, the variance in the landing position error is smaller when the convex-optimized algorithm is used, and the three-axis position error is within 11.23 m with a more concentrated distribution.
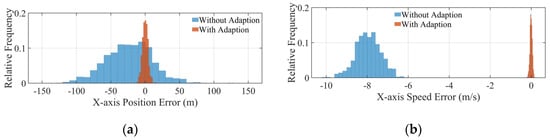
Figure 16.
X-axis error distribution: (a) position error; (b) speed error.
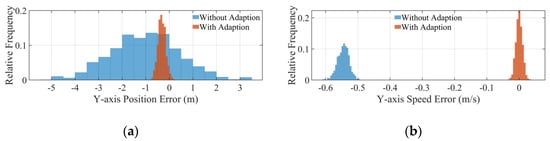
Figure 17.
Y-axis error distribution: (a) position error; (b) speed error.
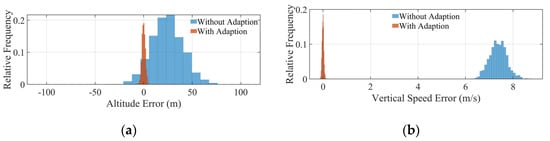
Figure 18.
Z-axis error distribution: (a) position error; (b) speed error.
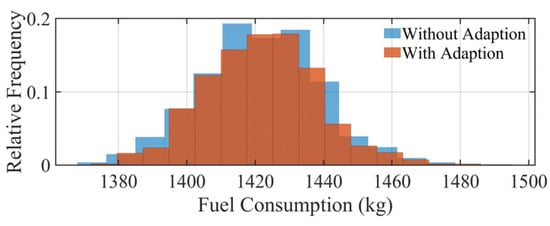
Figure 19.
Fuel consumption error distribution.
Figure 16b, Figure 17b and Figure 18b show the lander velocity error distribution, which has a smaller variance and less bias for the same reasons as the position distribution with the adaptive convex optimization algorithm. Its three-axis velocity error was within 0.05 m/s.
Figure 19 shows the distribution of fuel consumed by the lander. It can be observed that the fuel consumption distribution is almost the same with and without the adaptive convex optimization. In fact, the fuel consumption distribution during flight depends mainly on the optimality of the trajectory and distribution of the specific impulse. In the case of the adaptive convex optimization algorithm, the adaptive algorithm optimizes the planned trajectory by estimating the specific impulse and lander mass online, which saves fuel. However, the trajectory is out of the optimal trajectory owing to the insertion of the rapid adjustment phase to satisfy the target thrust magnitude and attitude, which increases fuel consumption. From the simulation results, the fuel consumption with and without adaptive convex optimization were almost the same for the simulation conditions used in this example.
6. Conclusions
In this paper, an adaptive convex optimization-based trajectory planning method is proposed to address the problem in which the optimality of the planned trajectory is impaired by the difference in specific impulse and mass from the nominal value when the conventional landing optimization algorithm is applied to lunar surface landing guidance, and it is difficult to constrain the terminal attitude and thrust magnitude. Parameters such as specific impulse and mass are estimated online by parameter adaption, and these parameters are used in the convex optimization process to ensure the optimality of the planned trajectory. The target state, such as lander position and velocity, does not deviate when the attitude and thrust magnitude of the lander are constrained at the end moment by inserting a rapid adjustment phase through the target-adaptive algorithm. The simulation results show that the parameter-adaptive algorithm can improve the optimality of the planned trajectory and save fuel, and the target-adaptive algorithm can satisfy the target thrust magnitude and attitude constraints through rapid adjustment without causing deviation of position and velocity. The integrated verification shows that the proposed algorithm can improve the landing accuracy without increasing fuel consumption; the final position error was less than 11.23 m, and the velocity error was less than 0.05 m/s.
Author Contributions
Conceptualization, Y.D. and P.W.; methodology, Y.D.; software, Y.D.; validation, P.W.; formal analysis, R.M.; writing—original draft preparation, Y.D.; writing—review and editing, R.M. and P.W.; visualization, Y.D.; supervision, R.M.; project administration, R.M.; funding acquisition, R.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Fourth Batch of Pre-research on Manned Spaceflight, grant number 18123060201.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sostaric, R.R. Powered descent trajectory guidance and some considerations for human lunar landing. In Proceedings of the 30th Annual AAS Rocky Mountain Guidance and Control Conference, Breckenridge, CO, USA, 3–7 February 2007. [Google Scholar]
- Paschall, S.; Brady, T.; Sostaric, R. Lunar landing trajectory design for onboard hazard detection and avoidance. In Proceedings of the 32nd Annual AAS Guidance and Control Conference, Breckenridge, CO, USA, 31 January–4 February 2009. [Google Scholar]
- Barbee, B.W.; Gaylor, D.E. Automated real-time targeting and guidance (ARTGUID) for lunar descent and precision landing. In Proceedings of the 33rd Annual AAS Rocky Mountain Guidance and Control Conference, Breckenridge, CO, USA, 5–10 February 2010. [Google Scholar]
- Kwon, J.W.; Lee, D.; Bang, H. Virtual trajectory augmented landing control based on dual quaternion for lunar lander. J. Guid. Control Dynam. 2016, 39, 2044–2057. [Google Scholar] [CrossRef]
- Huang, X.; Wang, D.; He, Y.; Guan, Y. Autonomous navigation and control for pin point lunar soft landing. In Proceedings of the 7th International ESA Conference on Guidance, Navigation & Control Systems, Tralee, County Kerry, Ireland, 2–5 June 2008. [Google Scholar]
- Epp, C.D.; Robertson, E.A. Autonomous precision landing and hazard detection and avoidance technology (ALHAT). In Proceedings of the 2008 IEEE Aerospace Conference, Big Sky, MT, USA, 1–8 March 2008. [Google Scholar]
- Paschall, S.C.; Brady, T.; Cohanim, B.E.; Sostaric, R. A self contained method for safe & precise lunar landing. In Proceedings of the 2008 IEEE Aerospace Conference, Big Sky, MT, USA, 1–8 March 2008. [Google Scholar]
- Epp, C.D.; Smith, T.B. Autonomous precision landing and hazard detection and avoidance technology (ALHAT). In Proceedings of the 2007 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2007. [Google Scholar]
- Sun, Z.Z.; Jia, Y.; Zhang, H. Technological advancements and promotion roles of chang’e-3 lunar probe mission. Sci. China Technol. Sci. 2013, 56, 2702–2708. [Google Scholar] [CrossRef]
- Li, S.; Jiang, X.Q.; Tao, T. Guidance summary and assessment of the chang’e-3 powered descent and landing. J. Spacecr. Rocket. 2016, 53, 258–277. [Google Scholar] [CrossRef]
- Sun, Z.Z.; Zhang, T.; Zhang, H.; Jia, Y.; Zhang, H.; Chen, J.; Wu, X.; Shen, Z. The technical design and achievements of chang’e-3 probe. Sci. Sin. Technol. 2014, 44, 331–343. [Google Scholar]
- Li, C.L.; Wang, C.; Wei, Y.; Lin, Y.T. China’s present and future lunar exploration program. Science 2019, 365, 238–239. [Google Scholar] [CrossRef] [PubMed]
- Mu, R.J.; Li, Y.T.; Luo, R.B.; Su, B.Z.; Shan, Y.Z. A distributed radio beacon/imu/altimeter integrated localization scheme with uncertain initial beacon locations for lunar pinpoint landing. Sensors 2020, 20, 19. [Google Scholar] [CrossRef] [PubMed]
- Ito, T.; Sakai, S. Throttled explicit guidance to realize pinpoint landing under a bounded thrust magnitude. J. Guid. Control Dynam. 2021, 44, 854–861. [Google Scholar] [CrossRef]
- Song, Z.Y.; Wang, C.; Theil, S.; Seelbinder, D.; Sagliano, M.; Liu, X.F.; Shao, Z.J. Survey of autonomous guidance methods for powered planetary landing. Front. Inf. Technol. Electron. Eng. 2020, 21, 652–674. [Google Scholar] [CrossRef]
- Lu, P. Augmented apollo powered descent guidance. J. Guid. Control Dynam. 2019, 42, 447–457. [Google Scholar] [CrossRef]
- Lu, P. Theory of fractional-polynomial powered descent guidance. J. Guid. Control Dynam. 2020, 43, 398–409. [Google Scholar] [CrossRef]
- Wang, P.Y.; Guo, Y.N.; Ma, G.F.; Wie, B. Two-phase zero-effort-miss/zero-effort-velocity guidance for mars landing. J. Guid. Control Dynam. 2021, 44, 75–87. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, Y.; Ma, G.; Zeng, T. Collision avoidance zem/zev optimal feedback guidance for powered descent phase of landing on mars. Adv. Space Res. 2017, 59, 1514–1525. [Google Scholar] [CrossRef]
- Furfaro, R.; Scorsoglio, A.; Linares, R.; Massari, M. Adaptive generalized zem-zev feedback guidance for planetary landing via a deep reinforcement learning approach. Acta Astronaut. 2020, 171, 156–171. [Google Scholar] [CrossRef]
- Liu, X.; Li, S.; Xin, M. Comparison of powered descent guidance laws for planetary pin-point landing. Acta Astronaut. 2021, 187, 101–114. [Google Scholar] [CrossRef]
- Acikmese, B.; Ploen, S.R. Convex programming approach to powered descent guidance for mars landing. J. Guid. Control Dynam. 2007, 30, 1353–1366. [Google Scholar] [CrossRef]
- Acikmese, B.; Scharf, D.; Blackmore, L.; Wolf, A. Enhancements on the convex programming based powered descent guidance algorithm for mars landing. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008. [Google Scholar]
- Sagliano, M. Pseudospectral convex optimization for powered descent and landing. J. Guid. Control Dynam. 2018, 41, 320–334. [Google Scholar] [CrossRef]
- Cui, P.Y.; Zhao, D.Y.; Zhu, S.Y. Obstacle avoidance guidance for planetary landing using convex trajectory and adaptive curvature regulation. Acta Astronaut. 2022, 199, 313–326. [Google Scholar] [CrossRef]
- Benedikter, B.; Zavoli, A.; Wang, Z.B.; Pizzurro, S.; Cavallini, E. Convex approach to covariance control with application to stochastic low-thrust trajectory optimization. J. Guid. Control Dynam. 2022, 45, 2061–2075. [Google Scholar] [CrossRef]
- Benedikter, B.; Zavoli, A.; Wang, Z.B.; Pizzurro, S.; Cavallini, E. Convex Approach to Stochastic Control for Autonomous Rocket Pinpoint Landing. In Proceedings of the AAS/AIAA Astrodynamics Specialist Conference, Charlotte, NC, USA, 8–11 August 2022. [Google Scholar]
- You, S.; Wan, C.; Dai, R.; Rea, J.R. Learning-based onboard guidance for fuel-optimal powered descent. J. Guid. Control Dynam. 2021, 44, 601–613. [Google Scholar] [CrossRef]
- Gaudet, B.; Linares, R.; Furfaro, R. Deep reinforcement learning for six degree-of-freedom planetary landing. Adv. Space Res. 2020, 65, 1723–1741. [Google Scholar] [CrossRef]
- Pinson, R.M.; Lu, P. Trajectory design employing convex optimization for landing on irregularly shaped asteroids. J. Guid. Control Dynam. 2018, 41, 1243–1256. [Google Scholar] [CrossRef]
- Szmuk, M.; Reynolds, T.P.; Acikmese, B. Successive convexification for real-time six-degree-of-freedom powered descent guidance with state-triggered constraints. J. Guid. Control Dynam. 2020, 43, 1399–1413. [Google Scholar] [CrossRef]
- Reynolds, T.P.; Szmuk, M.; Malyuta, D.; Mesbahi, M.; Açıkmeşe, B.; Carson, J.M., III. Dual quaternion-based powered descent guidance with state-triggered constraints. J. Guid. Control Dynam. 2020, 43, 1584–1599. [Google Scholar] [CrossRef]
- Kamath, A.G.; Elango, P.; Kim, T.; Mceowen, S.; Yu, Y.; Carson, J.M.; Mesbahi, M.; Acikmese, B. Customized real-time first-order methods for onboard dual quaternion-based 6-dof powered-descent guidance. In Proceedings of the AIAA SciTech 2023 Forum, National Harbor, MD, USA, 23–27 January 2023. [Google Scholar]
- Wang, H.F.; Zhang, H.H.; Wang, Z.G.; Wang, Z.W. Downrange estimation based on powered explicit guidance for pinpoint lunar landing. J. Aerosp. Eng. 2022, 35, 04021129. [Google Scholar] [CrossRef]
- Zhao, H.Q.; Dai, H.H.; Dang, Z.H. Optimal guidance for lunar soft landing with dynamic low-resolution image sequences. Adv. Space Res. 2022, 69, 4013–4025. [Google Scholar] [CrossRef]
- Wu, P.; Mu, R.J.; Deng, Y.P. Robust crater detection algorithm based on maximum entropy threshold segmentation. Int. J. Aerosp. Eng. 2022, 2022, 4872248. [Google Scholar] [CrossRef]
- Mu, R.J.; Wu, P.; Deng, Y.P.; Song, H.F. Optical navigation method and error analysis for the descending landing phase in planetary exploration. Aerospace 2022, 9, 28. [Google Scholar] [CrossRef]
- Latorre, F.; Spiller, D.; Curti, F. Imbalanced Data Handling for Deep Learning-Based Autonomous Crater Detection Algorithms in Terrain Relative Navigation. In Proceedings of the International Conference on Applied Intelligence and Informatics, Reggio Calabria, Italy, 1–3 September 2022. [Google Scholar]
- Zhu, X.Y.; Su, Y.; Ji, Y.C.; Zhang, H.B.; Zhao, B.; Li, J.D.; Dai, S.; Xue, X.P.; Li, C.L. Ground experiments and performance evaluation of the low-frequency radio spectrometer onboard the lander of chang’e-4 mission. Res. Astron. Astrophys. 2021, 21, 8–16. [Google Scholar] [CrossRef]
- Blackmore, L.; Acikmese, B.; Carson, J.M. Lossless convexification of control constraints for a class of nonlinear optimal control problems. Syst. Control. Lett. 2012, 61, 863–870. [Google Scholar] [CrossRef]
- Malyuta, D.; Reynolds, T.; Szmuk, M.; Mesbahi, M.; Acikmese, B.; Carson, J.M. Discretization performance and accuracy analysis for the rocket powered descent guidance problem. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2022. [Google Scholar]
- Sturm, J.F. Implementation of interior point methods for mixed semidefinite and second order cone optimization problems. Optim. Method Softw. 2002, 17, 1105–1154. [Google Scholar] [CrossRef]
- Possieri, C.; Sassano, M. Deterministic optimality of the steady-state behavior of the kalman-bucy filter. IEEE Control Syst. Lett. 2019, 3, 793–798. [Google Scholar] [CrossRef]
- Zhang, H.H.; Li, J.; Wang, Z.G.; Guan, Y.F. Guidance navigation and control for chang’e-5 powered descent. Space Sci. Technol. 2021, 2021, 15–29. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).