Abstract
Highly porous open-cell carbon materials have great potential for use as high-temperature thermal insulation for space vehicles due to a unique combination of properties: low density, high rigidity, sufficient compressive strength, and low thermal conductivity. The physical properties of these materials essentially depend on their microstructure. This implies the possibility of constructing a new advanced technique for the optimal design of multilayer thermal protection systems for aerospace vehicles, taking into account the dependence of materials’ thermal properties on microstructure. The formulation of the optimization problem traditional to thermal design implies the determination of the layer thicknesses that provide a minimum specific mass of the thermal protection, subject to the specified constraints on the maximum temperatures in the layers. The novelty of this work lies in the fact that, along with the thickness of the layers, the design parameters include the cell diameter and porosity, which characterize the structure of highly porous cellular materials. The innovative part of the presented paper lies in the determination of cell diameter and the porosity of open-cell carbon foam together with the thickness of the layers for multilayer thermal insulation, ensuring the required operational temperature on the boundaries of the layers and a minimum of the total mass of the system. This article reveals new possibilities for using the numerical optimization method to determine the geometric parameters of the thermal protection system and the morphology of the materials used. A new methodology for designing heat-loaded structures based on the simultaneous selection of macro- and micro-parameters of the system is proposed. The basic principles of constructing an algorithm for designing a multilayer thermal protection system are outlined, taking into account the possibility of choosing the parameters of the highly porous materials’ structure. The reliability of the developed optimization method was verified by comparing the results of mathematical modeling with experimental data obtained for highly porous cellular materials with known microstructure parameters.
1. Introduction
The study of the Sun, the planets, and the small bodies of the Solar System with the help of automatic interplanetary stations and descent vehicles is one of the priority areas of fundamental space research, for which the purpose is to develop the theoretical basis of key scientific disciplines about space. The thermal protection of space vehicles operates under significant thermal loads [1,2,3,4], which requires an optimal design both in terms of technological and mass characteristics. The mass of thermal protection makes a significant contribution to the total mass of the spacecraft bus comparable to the mass of the payload. One of the promising directions to reduce the relative weight of multilayer thermal protection systems for spacecraft is linked to the use of ultra-light heat-insulating materials in their construction [5,6,7,8,9]. Highly porous open-cell carbon materials have great potential here due to their low density, high rigidity, sufficient compressive strength, and low thermal conductivity [10].
The manufacturing technology of highly porous open-cell carbon materials is based on the process of thermal destruction of polyurethane foam previously impregnated with phenol-formaldehyde resin. The maximum use temperature for open-cell carbon foams obtained in this way reaches 350 °C in air and 3500 °C in an inert atmosphere or in a vacuum. In addition to being used in their original form, these materials can serve as the basis for the production of composite materials with unique thermal, mechanical, spectral, and chemical properties obtained by deposition from the gas phase of graphite, refractory metals (niobium, tantalum, tungsten, molybdenum, and rhenium) or ceramic compounds (oxides, nitrides, carbides, borides, and silicides of any metal) [10].
Reticulated carbon foams are produced with a porosity of 98–82% and have sufficient mechanical strength for practical applications (compression strength 0.3–4.0 MPa and modulus of elasticity 25–350 MPa) [10]. The results of compression tests carried out for carbon foams with different porosities are well-interpolated by the polynomial dependence discussed previously in [11]. The tensile strength is lower than in the compression test, which is typical for brittle materials. The open-cell carbon foams’ specific surface area is comparable to the corresponding characteristic of the polyurethane foam used as a structure-forming matrix. It depends less on the absolute values of porosity in the range of 80–98% than on the diameter of the cells. The specific surface area changes in the range of 5–300 cm−1. The biggest values correspond to materials with the smallest cell diameter. Despite the variety of possible structural modifications of carbon contained in highly porous carbon materials, they are characterized by isotropic properties. The thermal expansion of the materials has the almost linear nature of its temperature dependence in the range of 850–2400 °C. In the range of 850–2400 °C, the thermal expansion is 3.7 × 10−6 K−1 [10]. The melting point, specific heat, and expansion coefficient of open-cell foams are the same as those of the base material forming their microstructure [12]. The thermal conductivity depends not only on the thermal and optical properties of the solid phase but also on the materials’ morphology. The highly porous cellular materials inherit a three-dimensional spatial microstructure of the structure-forming organic matrix with open pores. Heat transfer in the highly porous open-cell carbon materials is described by four processes: thermal conductivity of solid struts forming the foam structure, thermal conductivity of the gas contained within cells, heat exchange due to gas convection, and radiative heat transfer through the porous structure of the foam.
At low temperatures, the main mechanism of heat transfer is conduction through the solid material forming the cell [8]. The solid material conductivity is calculated as the inverse of the total thermal resistances of the struts and struts’ junctures with different geometry [13]. Experimental results have determined a functional relationship between the conductivity of the solid phase and porosity [14]. At high temperatures, the radiative conductivity significantly exceeds the conductivity of the solid phase. To simulate the radiation component of the thermal conductivity of highly porous cellular materials, the complex structure of the material, consisting of individual particles—struts and strut junctures—is considered as some continuous semitransparent medium that emits, absorbs, and scatters radiation [14,15,16,17,18,19,20].
The physical properties of open-cell foams significantly depend on many factors: temperature, operating conditions, material composition, microstructure parameters, raw material properties, and production technology. On the one hand, this makes it possible to control the properties of the obtained materials during the manufacturing process at a wide range, thereby creating materials with desirable properties that have an optimal structure for specific operating conditions [11]. On the other hand, such a multifactorial nature makes it difficult to determine, model, and predict the properties of materials, and increases the spread of their values.
For the practical application of promising highly porous open-cell carbon materials in the design of effective heat-shielding structures, it is necessary to develop adequate heat transfer mathematical models that allow for predicting with sufficient accuracy the influence of materials’ morphology on their thermal properties [8,21,22]. High-quality mathematical models of the materials’ physical properties are necessary to determine the design parameters of structural elements and obtain the maximum information about their characteristics using experimental data. The study of radiative-conductive heat transfer in highly porous materials with a complex structure is a problem of great theoretical and practical interest [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29], because it allows for significantly reducing the amount of experimental research in the creation of new samples of aviation and space technology due to the widespread use of mathematical modeling methods.
One of the most traditional problems in thermal design involves determining the parameters of multilayer thermal protection systems that will satisfy formulated constraints and optimization criteria. In most cases, the layers’ thicknesses for multilayer thermal insulation, ensuring the required operational temperature on the boundaries of the layers and a minimum of the total mass of the system, are determined. Optimization techniques imply that the thermophysical properties of materials are obtained through experimental studies in a wide temperature range. In cases where multilayer thermal protection includes a highly porous layer, the structure parameters of the material (cell diameter and porosity) can be chosen along with the thicknesses of the layers, thereby contributing to a more efficient solution to the problem of optimizing multilayer thermal protection.
This paper presents a new advanced technique for the optimal design of multilayer thermal protection systems for aerospace vehicles, taking into account the dependence of materials’ thermal properties on microstructure. In addition to layer thicknesses, design parameters include cell diameter and the porosity of the foam. The new formulation of the thermal design problem presented in this paper allows for expanding the search for the optimal parameters of thermal insulation based on open-cell carbon foams and, therefore, increasing the efficiency of its solving.
The aim of this work is to develop a method and algorithm for the optimal design of a multilayer thermal protection for high-temperature applications, taking into account the possibility of choosing the microstructure parameters of highly porous open-cell materials. To construct such an algorithm, it is necessary to develop a high-quality mathematical model of heat transfer in the structure of a highly porous material. It is desirable that this model be simple enough for use in engineering applications, and, at the same time, accurate for design calculations. To develop such a model, this paper uses a methodology based on solving inverse heat transfer problems, i.e., verification of the developed theoretical method using the experimental results obtained under conditions close to the operating conditions of the thermal protection for a real spacecraft.
The proposed aim is achieved as a result of the consistent solution of the following main tasks:
- To develop a method and algorithm for the optimal design of a multilayer thermal protection, taking into account the dependence of thermal properties on the foam’s morphology.
- To study the heat transfer in a flat layer of highly porous open-cell carbon material and to verify the heat transfer mathematical model by means of experimental–computational research.
- To evaluate the efficiency of the developed algorithm by comparing the results of computational experiments with experimental data.
2. Materials and Methods
The designed system operating in a vacuum consists of L layers made of different materials with density ρl, l = 1, 2, …, L and thickness dl. It is assumed that the layer n consists of a highly porous open-cell carbon material and that it is semitransparent, while layers are opaque. A temperature distribution Tl(x,τ) in multilayer thermal protection is one-dimensional by the spatial coordinate and is described by the quasi-linear heat conduction with coefficients Cl, λl depending on the temperature:
The heat equation is supplemented with initial and boundary conditions:
where B, E, and F are parameters characterizing the boundary conditions. Boundary conditions of the first kind correspond to the values B = 0, E = 1, and F = T(τ); boundary conditions of the second kind are B = 1, E = 0, and F = q(τ); boundary conditions of the third kind are B = 1, E = α, and F = α·Te(τ), where α is the heat transfer coefficient and Te is the flow temperature. At both sides of the system, the boundary conditions can be set by taking into account the heat flux radiated by the surface of the thermal protection:
where qA(τ) is the absorbed heat flux and is the heat flux emitted by the heated surface of the thermal protection.
Thermal contact conditions are set at the layer boundaries:
Radiative-conductive heat transfer in a porous layer n is described by the equation with coefficients Cn, λn depending on the temperature and the microstructure parameters of the highly porous open-cell carbon material:
The coefficient 1/3 in the simplified relation (7) takes into account the average number of struts oriented in each of the orthogonal x, y, and z directions.
Highly porous open-cell carbon materials are considered semi-transparent media that absorb, emit, and scatter radiation [14,15,16,17,18,19,20]. The thermal protection systems in engineering applications, such as aerospace vehicles, are usually optically thick, with no fewer than several photon mean free paths. Due to this circumstance, the radiative flux in highly porous materials can be approximated by the Rosseland equation [30]:
The scattering anisotropy is taken into account by a weighted scattering coefficient with the asymmetry factor :
The solid struts forming the foam structure have a random orientation, and they are thick enough to be considered opaque. Using numerical Monte Carlo methods, it was found that the scattering phase function of the highly porous cellular materials closely matches the scattering phase function of large convex diffusely reflecting particles with random orientation [31], and that it is identical to the scattering phase function for opaque large spheres with the same physical and optical properties. It is assumed that reflection is complete, diffuse, and that it obeys the Lambert law. The scattering phase function in this case can be described by the expression for large spherical particles with the asymmetry factor :
The solid struts forming the carbon foam structure are assumed to be opaque, scattering is limited to the diffuse reflection, and reflectivity is independent of the incidence angle. Under these assumptions, the scattering albedo is equal to the reflectivity [16]: .
So, the spectral extinction coefficient is calculated by:
The extinction coefficient mainly depends on the average equivalent diameter a, the porosity δ, the ratio of the minimum and maximum strut diameters t = bmin/bmax, and the normalized curvature k [20]:
where k = R1/R2 is a parameter that takes into account the concave triangle shape of the strut’s cross-section, R1 is the radius of a circle circumscribed around an equilateral triangle modeling the strut’s cross-section, and R2 is the curvature radius of the concave side surface of the strut (Figure 1).
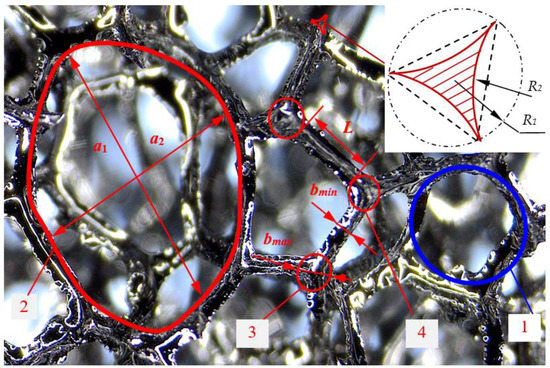
Figure 1.
Structure parameters of open-cell carbon foam: 1—pore, 2—cell, 3—strut juncture, 4—strut, a1—larger cell diameter, a2—smaller cell diameter, bmax—strut juncture diameter, L—strut length, bmin—strut diameter.
For the boundary value problem solution (1), (5), the implicit and monotone finite-difference scheme of second-order approximation, developed by A. Samarskii [32], is used.
The design parameters vector consists of the thickness of layers k = 1, 2, …, N, N ≤ L and porosity δ and cell diameter a of the highly porous open-cell carbon material, thus forming layer n. As the minimization criterion, the local mass functional is considered:
The density of the porous layer depends on the density ρs of the base material, forming the foam microstructure, and porosity δ:
The constraints in the optimization problem are:
The upper and lower bounds amin, amax, and δmax take into account the structure parameters available for the manufactured materials.
The optimization problem (14)–(17) is solved using the algorithm based on the projected Lagrangian method with the quadratic subproblem [33]:
with linear constraints chosen so that the space of minimization would be restricted within the subspace of vectors orthogonal to the active constraints’ gradients:
The next approximation of the optimal vector of design parameters is calculated as:
A search direction is found as the solution of the quadratic subproblem [33]:
Minimize
subject to linear constraints , obtained by expanding the functions (19) about p in a Taylor series and neglecting the nonlinear term [34]:
The quadratic approximation to the Lagrangian function is found as . The Jacobian matrix of first derivatives of constraints is calculated using the sensitivity functions [34].
The step length is determined by minimizing the augmented Lagrangian merit function with a penalty parameter r, thereby ensuring the realization of an unconstrained minimum at a stationary point, found from a sufficient condition for optimality [35]:
The conditions for terminating the iterative process are:
where εo is an accuracy of optimization problem solution, εc is the maximum acceptable absolute violation in nonlinear constraints, and is a vector composed of the components of the Lagrangian function gradient corresponding to the free variables.
3. Results
To introduce the developed method into the practice of designing spacecraft thermal protection systems, it is necessary to confirm the reliability of the heat transfer model in an open-cell structure. The necessary verification has been carried out by comparing the results of mathematical modeling with experimental data obtained for the highly porous open-cell carbon materials with known microstructure parameters (Figure 2).

Figure 2.
Structure of open-cell foam samples RVC-20; RVC-60; RVC-80.
The object of research in the conducted thermal tests was a three-layer sandwich panel (Figure 3) simulating the operation of a multilayer thermal protection system.
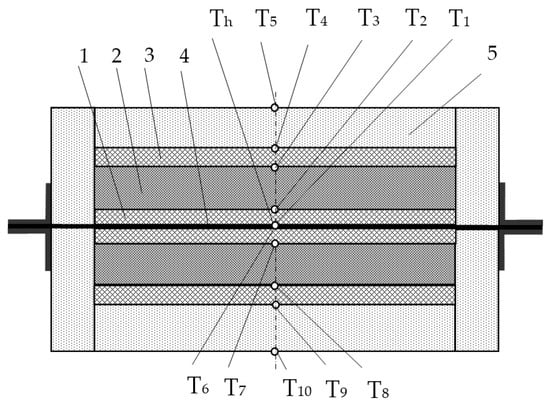
Figure 3.
Scheme of tests with symmetrical heating of two experimental assemblies: 1—high-temperature ceramic plate (d1 = 2.95 mm), 2—high-porous cellular material specimen (d2), 3—high-temperature ceramic plate (d3 = 7.15 mm), 4—heating element (h), 5—heat insulating plate, Th, T1–T10—thermocouples.
The three-layer sandwich panel used in the tests consisted of the open-cell carbon foam layer (d2 = 13.0 mm) located between the layers of the high-temperature ceramic material (d1 = 2.95 mm; d3 = 7.15 mm). The ceramic material contained silicon nitride, whose physical properties are known in a wide temperature range [36]. A core in the sandwich panel was made of vitreous carbon foam samples with a different structure determined by the number of pores per 1 cm of 8, 24, and 32, hereinafter referred to as RVC-20, RVC-60, and RVC-80 (ERG Aerospace Corporation (USA)) (Figure 2). The porosity of the materials was 0.97. The average values of the structure parameters of vitreous carbon foam samples with various numbers of pores per 1 cm were determined as a result of studies of the structure of these materials using a stereoscopic microscope equipped with a digital video camera (Table 1).

Table 1.
Average values of the structure parameters of open-cell foam samples with various numbers of pores per 1 cm.
Thermal tests were carried out under conditions of unsteady radiation-conductive heating at a pressure of ~0.01 Pa in the temperature range of 297–1273 K. Experimental data included the thermal state parameters (unsteady one-dimensional temperature field) of a three-layer sandwich panel and the electrical parameters of a heating element.
The implementation of the specified thermal regime of the panel was provided by the experimental module EM-2B used in the high-temperature thermovacuum stand TVS-1M. A methodical approach for the investigation of highly porous cellular materials’ thermal properties has been reported previously in [37,38].
Thermal tests were carried out in three stages:
- Stage 1—Preparation and thermal testing of a sandwich panel with the RVC-20 core;
- Stage 2—Preparation and thermal testing of a sandwich panel with the RVC-60 core;
- Stage 3—Preparation and thermal testing of a sandwich panel with the RVC-80 core.
At each stage, the following tasks were solved:
- (1)
- A methodology of thermal tests was developed;
- (2)
- Experimental samples, thermal sensors, and elements of the experimental module (EM) were made in accordance with the requirements for them;
- (3)
- The geometric parameters and the density of the vitreous carbon foam samples were determined;
- (4)
- The structure parameters of vitreous carbon foam samples were studied;
- (5)
- The control and measuring lines of the automated system for scientific research of thermophysical processes and the systems of the thermal vacuum stand TVS-1M were checked and prepared for thermal tests;
- (6)
- The experimental module EM-2V was assembled and installed in the vacuum chamber of the stand;
- (7)
- Preliminary thermal tests were carried out to check the operability of the stand systems, to select the heating modes, to debug the three-layer panel heating program, and to remove the adsorbed water;
- (8)
- Thermal tests were carried out, during which the temperatures on the surface of the heating element and at the given points of the investigated three-layer panel were determined;
- (9)
- The results of the thermal tests were processed and analyzed.
The processing of the obtained experimental information was carried out using the experimental–computational system, developed at the Thermal Laboratory of the Department of Space Systems Engineering, Moscow Aviation Institute.
All tests were carried out under the same conditions (heating modes and pressure in the vacuum chamber of the stand) and with the identical samples of the ceramic material and the heat-insulating elements. In addition, carbon foam samples used in tests had similar thicknesses (Table 2). Thus, the results of the thermal tests make it possible to compare the heat-insulating properties of vitreous carbon foam samples with different microstructures and to evaluate the effect of the materials’ morphologies on their physical properties.

Table 2.
Geometrical and mass characteristics of experimental specimens.
The investigated materials RVC-20, RVC-60, and RVC-80 had a three-dimensional spatial microstructure with open pores (Figure 1). The unit cell of the material structure had a shape close to a pentagondodecahedron, consisting of twelve pentagonal faces, at the vertices of which there were junctures, and the edges were formed by struts connecting the junctures. In one juncture, as a rule, four struts were connected, but there were junctures that combined more struts (up to six). The thickness of the strut was variable along the length and increased in the vicinity of the juncture. The sectional shape of the struts was close to an equilateral triangle with concave sides. The elements of the cellular structure (cells, pores, struts, and strut junctures) had different sizes and were arbitrarily oriented in space. There were various defects in the structure of the material, and, as a result, the structure of a real high-porous cellular material could differ significantly from its mathematical model.
The structural element dimensions of the studied materials samples decreased with an increase in the number of pores per 1 cm (Table 1). The dimensions of the cells depended on the number of pores per linear size more than the dimensions of the struts and strut junctures. The influence of the number of pores per linear size on the dimensions of the material structure elements decreased with an increase in the considered parameter. The materials’ microstructure parameters obtained as a result of statistical processing were taken into account when calculating the conductive λc and radiative λR components of thermal conductivity.
Taking into account the mechanical and electrical properties of the materials RVC-20, RVC-60, and RVC-80, as well as the significant hardness of the ceramic plates, microthermocouples with a diameter of 0.1 mm were installed on the heated and reverse surfaces of the ceramic plates in specially cut grooves that were 170 μm deep. Grooves with thermocouples were filled with a specially prepared composition based on ceramic material powder (90%) with a working temperature of 1573 K. Outside the plates, thermocouple wires were electrically insulated.
During thermal tests, a symmetrical scheme was implemented (Figure 3) with conductive-radiation heating of two identical experimental assemblies, A and B, including a high-porous cellular material core (Table 2) and layers of high-temperature ceramic material. This test scheme allowed for the determination of heat flux on the surface of the heating element (Figure 4) by its electrical parameters [38]:
where I(τ) is the current in the heating element circuit; U(τ) is the voltage at the boundaries of the heating element operating zone; S = 0.005 m2 is the heating element operating zone area; δh = 0.0001 m is the heating element thickness; Th(τ) is the heating element temperature; τ is time; τe is the end time of the measurements (tests); and ρh and ch are the density and heat capacity of the heating element’s material: ρh = (7902 − 0.0584 × Th) kg/m3; ch (T) = (500 + 0.1744 × Th) J/(kg·°C).

Figure 4.
Stages of thermal tests preparation: (a) Experimental module EM-2V with installed heating element 4; (b) Ceramic plate 1 with thermocouples T1 and T2 was installed on the heating element; (c) The side elements of the heat-insulating holder 5 and the vitreous carbon foam specimen 2 were installed; (d) Ceramic plate 3 with thermocouples T3 and T4 was installed in a heat-insulating holder; (e) Heat-insulating plate was installed; (f) Experimental module EM-2V with assemblies A and B in the vacuum chamber of the TVS-1M stand.
Experimental assemblies A (upper) and B (lower) with installed thermocouples T1, T2, T3, and T4 and T6, T7, T8, and T9 were located on the heating element of the experimental module EM-2V (Figure 3). Experimental assemblies were installed in heat-insulating holders 5 made of high-temperature ceramic heat-insulating material based on SiO2 fibers (Figure 4). The assembled experimental module was installed on the water-cooled working table of the thermal vacuum stand TVS-1M vacuum chamber (Figure 4).
The results of the thermal tests showed that:
- (1)
- The temperature changing program specified for the heating element was successfully implemented in the temperature range from room temperature to 1273 K.
- (2)
- In the thermal tests of stage 1, a good agreement of the temperatures was obtained at the corresponding symmetrical points T1 and T6 and T2 and T7, indicating a good implementation of the symmetrical heating scheme of the experimental assemblies. However, a significant (up to 100 K) divergence of the temperatures was observed at the corresponding symmetrical points T3 and T8 and T4 and T9, which increased with increasing temperature. This discrepancy is explained by a significant difference (up to 10%) in the densities of RVC-20 samples A and B. At high temperatures, radiation becomes the dominant heat transfer mechanism in a highly porous carbon material, and sample A with greater density heats up more slowly.
In the thermal tests of stages 2 and 3, the temperatures at the symmetrical points of the experimental assemblies A and B had similar values, indicating a good implementation of the symmetrical heating scheme of the three-layer model panels. Because the densities of samples A and B for materials RVC-60 and RVC-80 were practically the same, it can be assumed that the values of the thermophysical properties of these materials also coincide.
- (3)
- Highly porous open-cell carbon foam specimens did not have noticeable signs of destruction after repeated heating (including heating, preliminary, and standard tests) up to a temperature of ~1273 K in vacuum.
- (4)
- During the preliminary tests of experimental assemblies, a significant change in pressure in the vacuum chamber of the TVS-1M stand was observed, which was associated with the release of adsorbed water from open-cell carbon foam samples and heat-insulating elements, as well as volatile components from the technological materials used.
The time dependences of the heat flux on the heating element coincided in all three tests of experimental assemblies with high-porous cellular materials samples RVC-20, RVC-60, and RVC-80 (Figure 5). On the heated surface of the RVC-20 sample, lower values of temperature T2 were realized; however, this sample heated up much faster than the others (especially at high temperatures), as evidenced by the nature of the change in temperature T3 on the back surface of the sample (Figure 6). Thus, the material RVC-20 with the largest average cell diameter exhibited the worst thermal insulation properties.
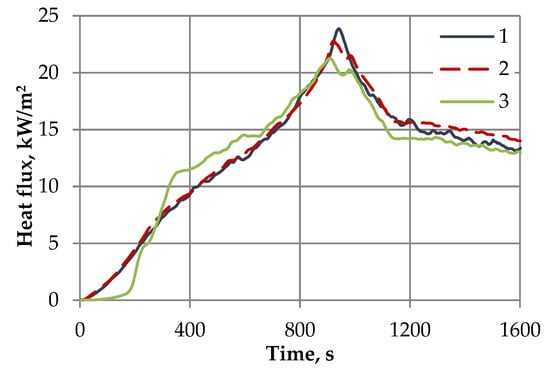
Figure 5.
Heat flux on heating element in thermal tests of experimental assemblies with vitreous carbon foam samples RVC-20 (1), RVC-60 (2), and RVC-80 (3).
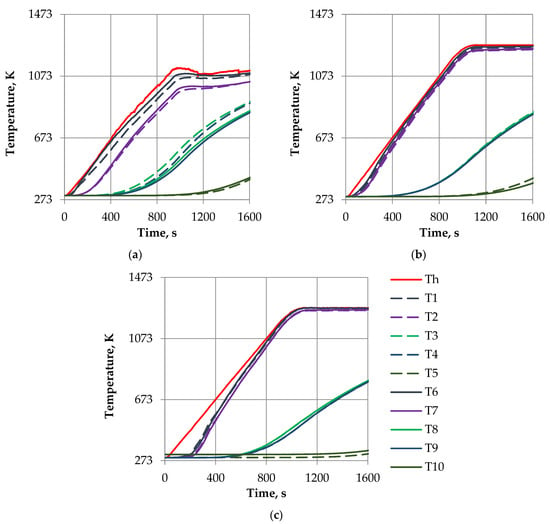
Figure 6.
Thermal tests results for experimental assemblies A and B with high-porous cellular materials samples RVC-20 (a), RVC-60 (b), and RVC-80 (c).
The heated surface temperature T2 of the highly porous open-cell carbon material sample increased with an increase in the number of pores per 1 cm (decrease in the material’s average cell diameter) at temperatures exceeding ~800 °C.
The back surface temperature of the highly porous open-cell carbon material sample T3 at high temperatures dropped significantly with an increase in the number of pores by 1 cm. Thus, high-porous cellular materials with the smallest cell size demonstrated the best thermal insulation properties at high temperatures, and the radiation component of thermal conductivity increased significantly.
The thermal tests results obtained for two experimental assemblies can be considered the results of two separate (independent) tests of highly porous materials samples A and B. At the same time, in order to build a more accurate mathematical model of heat transfer in a highly porous materials structure, this experimental information should be supplemented with the results of thermal tests carried out under the other conditions (heating modes and pressure in the vacuum chamber of the stand).
The results of the tests are the source data for solving the test optimal design problem. A statement implies the determination of the open-cell carbon foam layer thickness together with the cell diameter [35]. The design parameters should ensure allowable maximum temperature on the back surface of the panel and a minimum of the total mass of the system (Figure 7).
Figure 7.
The scheme of a model sandwich panel: 1—silicon nitride, 2—vitreous carbon foam, 3—silicon nitride.
The allowable temperature of the back surface of the sandwich panel was limited to 766 K, which was implemented in the tests of the RVC-80 vitreous carbon foam sample. The minimum cell diameter was limited to 0.656 mm, corresponding to a sample of RVC-80. As the initial condition in the boundary-value problem, the temperature distribution in the three-layer panel at the initial time moment was set. The boundary condition on the heated surface of the sandwich panel was the heat flux on the heating element obtained in thermal tests (Figure 5). It was assumed that the heat flux on the panel’s back surface was equal to 0.
The results of mathematical modeling demonstrate a good agreement with the experimental data (Figure 8, Figure 9 and Figure 10). The results of the comparison of the obtained experimental and calculated temperatures confirm that the presented method of mathematical modeling of radiative-conductive heat transfer can be used in the algorithm of optimal design of a multilayer thermal protection, taking into account the morphology of highly porous cellular materials. The noticeable difference between the theoretical and experimental results for the RVC-20 sample can be explained by the fact that this material is not an optically thick medium, so the Rosseland approximation used for the conductivity radiative component calculation leads to significant inaccuracy.
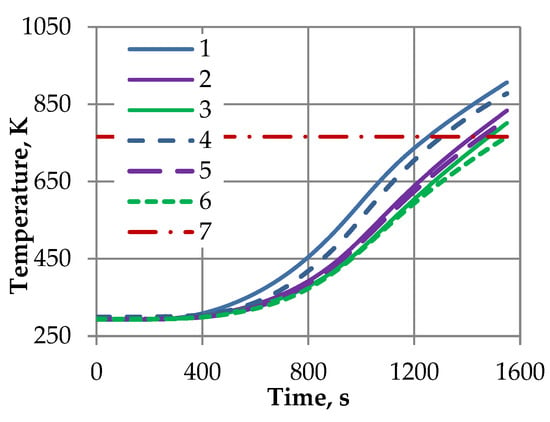
Figure 8.
Temperature on the back surface of the three-layer sandwich panel: calculation for samples RVC-20 (1), RVC-60 (2), and RVC-80 (3); experiment for samples RVC-20 (4), RVC-60 (5), and RVC-80 (6); (7)—allowable temperature.
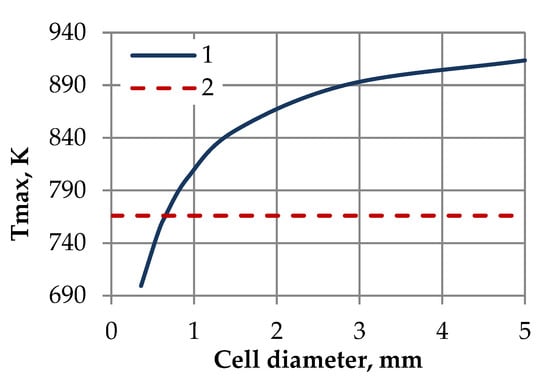
Figure 9.
Maximum temperature on the back surface of a three-layer sandwich panel (1); allowable temperature (2).
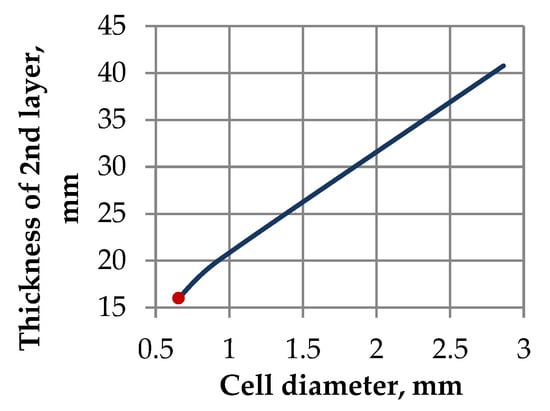
Figure 10.
Thickness of vitreous carbon foam layer as a function of cell diameter.
The experimental and calculated temperatures are almost the same at temperatures below 1000 K, while at higher temperatures, the difference between them increases significantly. Thus, for the design of heat protection systems operating at temperatures above 1000 K, a more accurate analysis of radiative heat transfer in porous media is required.
In this problem, the optimal thickness of the porous layer is 15.9 mm, and the cell diameter is 0.656. The obtained optimal parameters of the porous layer closely correspond to the parameters of the vitreous carbon foam sample RVC-80 used in the experiment. These results fully correspond to the experimental data, according to which the material with the minimum dimensions of the microstructure has the best thermal insulation properties. Thus, the thermal experiment conducted allows for justification of the efficiency and reliability of the developed optimization technique and the software implementing this algorithm.
4. Conclusions
A new method has been developed to select the optimal parameters for multilayer thermal insulation including highly porous materials. The porosity and cell diameter of the foam can be determined along with the thickness of the layers as the component of the design parameters vector. The reliability of the developed optimization method was verified by comparing the mathematical modelling results with experimental data obtained for highly porous cellular materials with known microstructure parameters. The calculated optimal parameters of the vitreous carbon foam layer are in good agreement with the experimental data, according to which the material with a smaller cell diameter has the best thermal insulation properties. These results confirmed that the developed optimization method can be used to solve the practical thermal design problems. An important result of the work is the algorithm for the designing of thermal insulation based on carbon foam, which makes it possible to determine the structural properties of materials optimal for specific operating conditions. It is established that the optimum is achieved on the bounds specified for the variables describing the carbon foam structure. This fact indicates the absence of the contradictory influence of the optimized parameters on the objective function. In further studies, it is advisable to introduce corrections into the formulation of the optimization problem by supplementing a number of constraints with the parameters of the structure’s stress–strain state and expanding the range of variation of independent variables, without limiting research to the properties of existing materials. This would make it possible to indicate directions for the creation of new materials. In general, the developed method has good prospects for improvement. An interesting direction for further research is the study of composite materials based on carbon foams filled with ultra-light carbon or silica aerogels, which can be used as effective heat insulation in many practical applications.
Author Contributions
Conceptualization, supervision, project administration, funding acquisition, O.M.A.; methodology, writing—review and editing, A.V.N.; software, writing—original draft preparation, data curation, visualization, M.O.S.; validation, formal analysis, investigation, resources, S.A.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Russian Science Foundation, grant number 18-19-00492.
Data Availability Statement
Data available on request due to restrictions.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| A | Jacobian matrix of constraints; |
| B | Parameter characterized a boundary condition; |
| C | Volumetric heat capacity, J/(m3·K); |
| E | Parameter characterized a boundary condition; |
| F | Parameter characterized a boundary condition; |
| H | Hessian matrix; |
| I | Radiative emissive power, W/(m2 sr); |
| J | Minimized function, kg/m2; |
| L | Number of layers in system; |
| Nτ | Number of steps by time; |
| T | Temperature, K; |
| X | Coordinate of layer boundary, m; |
| a | Cell diameter, m; |
| bmin | Minimum strut diameter, m; |
| bmax | Maximum strut diameter, m; |
| c | Specific heat capacity, J/(kg·K); |
| dl | Layer thickness, m; |
| p | Vector of parameters; |
| q | Heat flux, W/m2; |
| r | Solid surface reflectivity; |
| s | Search direction; |
| α | Absorption coefficient, m−1; |
| β | Extinction coefficient, m−1; |
| βR | Rosseland mean extinction coefficient, m−1; |
| γ | Step length; |
| δ | Porosity; |
| ε | Emissivity; |
| λ | Conductivity, W/(m K); |
| ρ | Density, kg/m3; |
| σ | Scattering coefficient, m−1; |
| τ | Time, s; |
| Φ(θ) | Scattering phase function; |
| Vector of Lagrange multiplier; | |
| Stefan–Boltzmann constant, W/(m2·K4); | |
| ω | Scattering albedo. |
| Subscripts | |
| R | radiative; |
| b | blackbody; |
| c | conductive; |
| s | solid phase; |
| λ | wavelength. |
References
- Chang, B.; Huang, J.; Yao, W.-X. Thermal Protection Mechanism of a Novel Adjustable Non-Ablative Thermal Protection System for Hypersonic Vehicles. Aerospace 2023, 10, 1. [Google Scholar] [CrossRef]
- Alekseev, S.V.; Aksenova, I.V.; Ivanova, E.K.; Kharitonova, E.V.; Lokhov, A.A. On developing the design of the protective heat shield for the Interhelio-Zond spacecraft. Sol. Syst. Res. 2018, 52, 680–683. [Google Scholar] [CrossRef]
- Suzuki, T.; Aoki, T.; Ogasawara, T.; Fujita, K. Nonablative lightweight thermal protection system for Mars Aeroflyby Sample collection mission. Acta Astronaut. 2017, 136, 407–420. [Google Scholar] [CrossRef]
- Venkatapathy, E.; Laub, B.; Hartman, G.J.; Arnold, J.O.; Wright, M.J.; Allen, G.A., Jr. Thermal protection system development, testing, and qualification for atmospheric probes and sample return missions: Examples for Saturn, Titan and Stardust-type sample return. Adv. Space Res. 2009, 44, 138–150. [Google Scholar] [CrossRef]
- Liu, J.; Xu, M.; Zhang, R.; Zhang, X.; Xi, W. Progress of Porous/Lattice Structures Applied in Thermal Management Technology of Aerospace Applications. Aerospace 2022, 9, 827. [Google Scholar] [CrossRef]
- Kubota, Y.; Miyamoto, O.; Aoki, T.; Ishida, Y.; Ogasawara, T.; Umezu, S. New thermal protection system using high-temperature carbon fibre-reinforced plastic sandwich panel. Acta Astronaut. 2019, 160, 519–526. [Google Scholar] [CrossRef]
- Wang, X.; Wei, K.; Tao, Y.; Yang, X.; Zhou, H.; He, R.; Fang, D. Thermal protection system integrating graded insulation materials and multilayer ceramic matrix composite cellular sandwich panels. Compos. Struct. 2019, 209, 523–534. [Google Scholar] [CrossRef]
- Alifanov, O.M.; Cherepanov, V.V. Identification of models and prediction of physical properties of highly porous heat-shielding materials. J. Eng. Phys. Thermophys. 2010, 83, 770–782. [Google Scholar] [CrossRef]
- Venkataraman, S.; Haftka, R.T.; Sankar, B.V.; Zhu, M.; Blosser, M.L. Optimal functionally graded metallic foam thermal insulation. AIAA J. 2004, 42, 2355–2363. [Google Scholar] [CrossRef]
- Shchurik, A.G. Iskusstvennye Uglerodnye Materialy [Artificial Carbon Materials]; PGU Publ.: Perm’, Russia, 2009; pp. 297–314. [Google Scholar]
- Alifanov, O.M.; Budnik, S.A.; Nenarokomov, A.V.; Salosina, M.O. Design of thermal protection based on open cell carbon foam structure optimization. Appl. Therm. Eng. 2020, 173, 115252. [Google Scholar] [CrossRef]
- Ashby, M.F.; Evans, A.G.; Fleck, N.A.; Gibson, L.J.; Hutchinson, J.W.; Wadley, H.N.G. Metal Foams: A Design Guide; Butterworth Heinemann: Woburn, MA, USA, 2000; pp. 181–187. [Google Scholar]
- Alifanov, O.M.; Cherepanov, V.V.; Shchurik, A.G.; Mironov, R.A. Calculation of characteristics of reticular materials based on a glassy carbon by its optical constants determined experimentally. J. Eng. Phys. Thermophys. 2020, 93, 710–718. [Google Scholar] [CrossRef]
- Baillis, D.; Coquard, R. Radiative and Conductive Thermal Properties of Foams. In Cellular and Porous Materials: Thermal Properties Simulation and Prediction; Ochsner, A., Murch, G.E., de Lemos, M.J.S., Eds.; WILEY-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2008; pp. 343–382. [Google Scholar]
- Doermann, D.; Sacadura, J.F. Heat transfer in open cell foam insulation. J. Heat Transf. 1996, 118, 88–93. [Google Scholar] [CrossRef]
- Coquard, R.; Rochais, D.; Ballis, D. Conductive and Radiative Heat Transfer in Ceramic and Metal Foams at Fire Temperatures. Fire Technol. 2012, 48, 699–732. [Google Scholar] [CrossRef]
- Baillis, D.; Raynaud, M.; Sacadura, J.F. Determination of spectral radiative properties of open cell foam. Model validation. J. Thermophys. Heat Transf. 2000, 14, 137–143. [Google Scholar] [CrossRef]
- Cunsolo, S.; Coquard, R.; Baillis, D.; Bianco, N. Radiative properties modeling of open cell solid foam: Review and new analytical law. Int. J. Therm. Sci. 2016, 104, 122–134. [Google Scholar] [CrossRef]
- Loretz, M.; Coquard, R.; Baillis, D.; Maire, E. Metallic foams: Radiative properties/comparison between different models. J. Quant. Spectrosc. Radiat. Transf. 2008, 109, 16–27. [Google Scholar] [CrossRef]
- Cunsolo, S.; Coquard, R.; Baillis, D.; Chiu, W.K.S.; Bianco, N. Radiative properties of irregular open cell solid foams. Int. J. Therm. Sci. 2017, 117, 77–89. [Google Scholar] [CrossRef]
- Wang, M.; Pan, N. Modeling and prediction of the effective thermal conductivity of random open-cell porous foams. Int. J. Heat Mass Transf. 2008, 51, 1325–1331. [Google Scholar] [CrossRef]
- Reznik, S.V.; Prosuntsov, P.V.; Mikhailovskii, K.V. Prediction of thermophysical and thermomechanical characteristics of porous carbon–ceramic composite materials of the heat shield of aerospace craft. J. Eng. Phys. Thermophys. 2015, 88, 594–601. [Google Scholar] [CrossRef]
- Gusarov, A.V.; Poloni, E.; Shklover, V.; Sologubenko, A.; Leuthold, J.; White, S.; Lawson, J. Radiative transfer in porous carbon-fiber materials for thermal protection systems. Int. J. Heat Mass Transf. 2019, 144, 118582. [Google Scholar] [CrossRef]
- Corasaniti, S.; De Luca, E.; Gori, F. Effect of structure, porosity, saturating fluid and solid material on the effective thermal conductivity of open-cells foams. Int. J. Heat Mass Transf. 2019, 138, 41–48. [Google Scholar] [CrossRef]
- Samudre, P.; Kailas, S.V. Thermal performance enhancement in open-pore metal foam and foam-fin heat sinks for electronics cooling. Appl. Therm. Eng. 2022, 205, 117885. [Google Scholar] [CrossRef]
- Marri, G.K.; Balaji, C. Experimental and numerical investigations on the effect of porosity and PPI gradients of metal foams on the thermal performance of a composite phase change material heat sink. Int. J. Heat Mass Transf. 2021, 164, 120454. [Google Scholar] [CrossRef]
- Liu, H.; Zhao, X. Thermal Conductivity Analysis of High Porosity Structures with Open and Closed Pores. Int. J. Heat Mass Transf. 2022, 183, 122089. [Google Scholar] [CrossRef]
- Niu, D.; Hongtao, G. Thermal Conductivity of Ordered Porous Structures Coupling Gas and Solid Phases: A Molecular Dynamics Study. Materials 2021, 14, 2221. [Google Scholar] [CrossRef]
- Kim, M.; Kim, Y. A Thermo-Mechanical Properties Evaluation of Multi-Directional Carbon/Carbon Composite Materials in Aerospace Applications. Aerospace 2022, 9, 461. [Google Scholar] [CrossRef]
- Ozisik, M.N. Radiative Transfer and Interactions with Conduction and Convection; Wiley: New York, NY, USA, 1973; pp. 340–352. [Google Scholar]
- Hulst, H.C.; van de Hulst, H.C. Light Scattering by Small Particles; Wiley–Chapman: New York, NY, USA, 1957; pp. 132–135. [Google Scholar]
- Samarskii, A.A. The Theory of Difference Schemes; Marcel Dekker Inc.: New York, NY, USA, 2001; pp. 33–67. [Google Scholar]
- Gill, P.E.; Murray, W.; Wright, M.H. Practical Optimization; Academic Press: London, UK, 1981; pp. 233–251. [Google Scholar]
- Nenarokomov, A.V. Design of a System of Multilayer Heat Insulation of Minimum Mass. High Temp. 1997, 35, 453–457. [Google Scholar]
- Salosina, M.O.; Alifanov, O.M.; Nenarokomov, A.V. An optimal design of thermal protection based on materials morphology. Comput. Assist. Methods Eng. Sci. 2019, 26, 47–60. [Google Scholar]
- Peletskii, V.E. The investigation of thermal conductivity of silicon nitride. High Temp. 1993, 31, 668–670. [Google Scholar]
- Alifanov, O.M. Mathematical and experimental simulation in aerospace system verification. Acta Astronaut. 1997, 41, 43–51. [Google Scholar] [CrossRef]
- Alifanov, O.M.; Budnik, S.A.; Mikhaylov, V.V.; Nenarokomov, A.V.; Titov, D.M.; Yudin, V.M. An experimental–computational system for materials thermal properties determination and its application for spacecraft structures testing. Acta Astronaut. 2007, 61, 341–351. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).