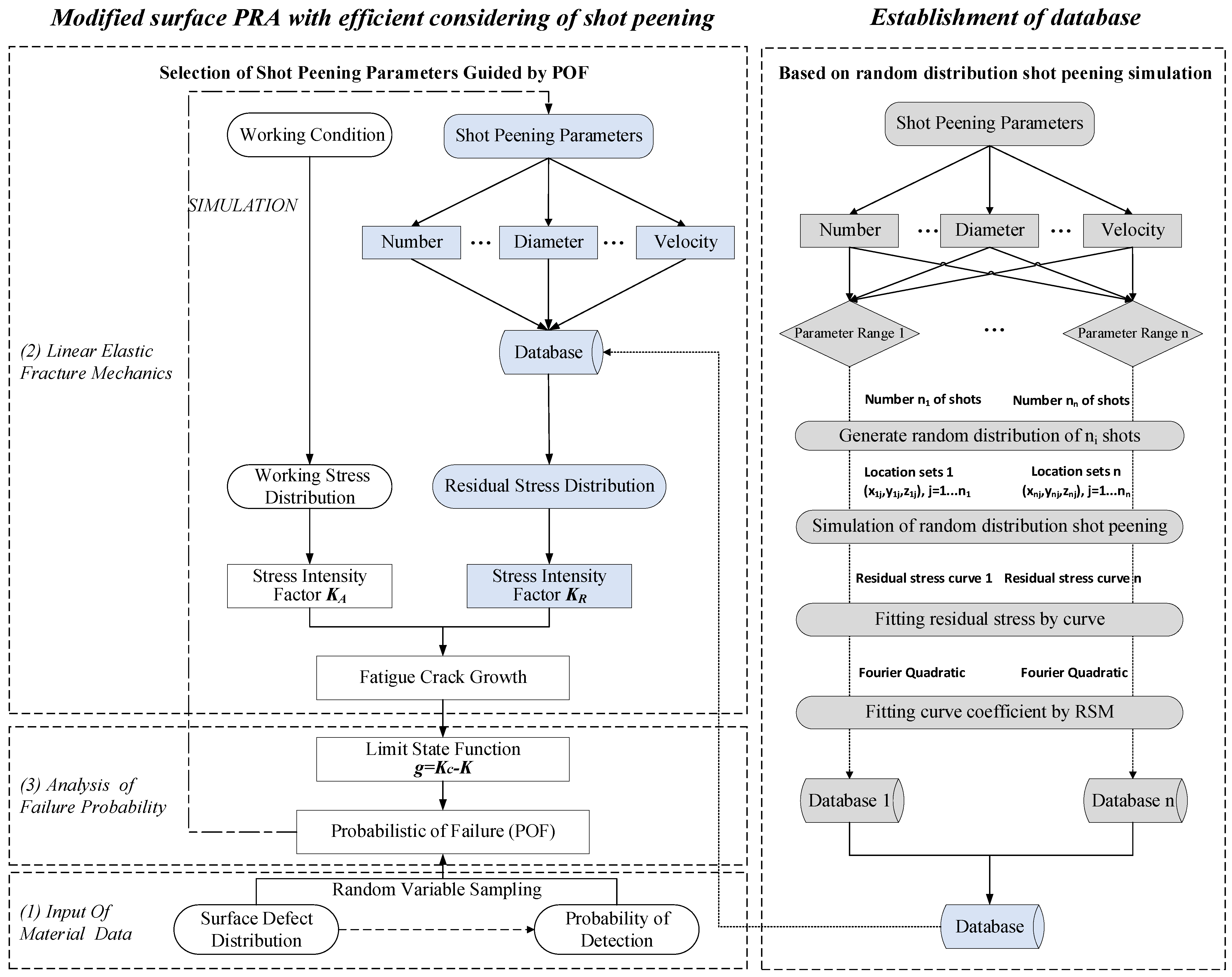
2.2.1. Input of Material Data
As can be seen from the modified surface PRA in
Figure 1, the material data that is input consists of two parts, including surface defect distribution and the probability of detection, which characterize the probability of an anomaly being introduced during manufacturing and processing and the likelihood of the defect being detected, respectively. Specifically, the distribution of defects and the probability of defect detection when employing specific techniques can be quantitatively analyzed [
22] by accumulating material data. The FAA has published data on the induction of surface defects during the machining process of titanium, steel, nickel (alloy), or powdered nickel (alloy) round hole features that was gathered by the US industry during the early 21st century [
4], as shown in
Figure 2 (defect distribution), and
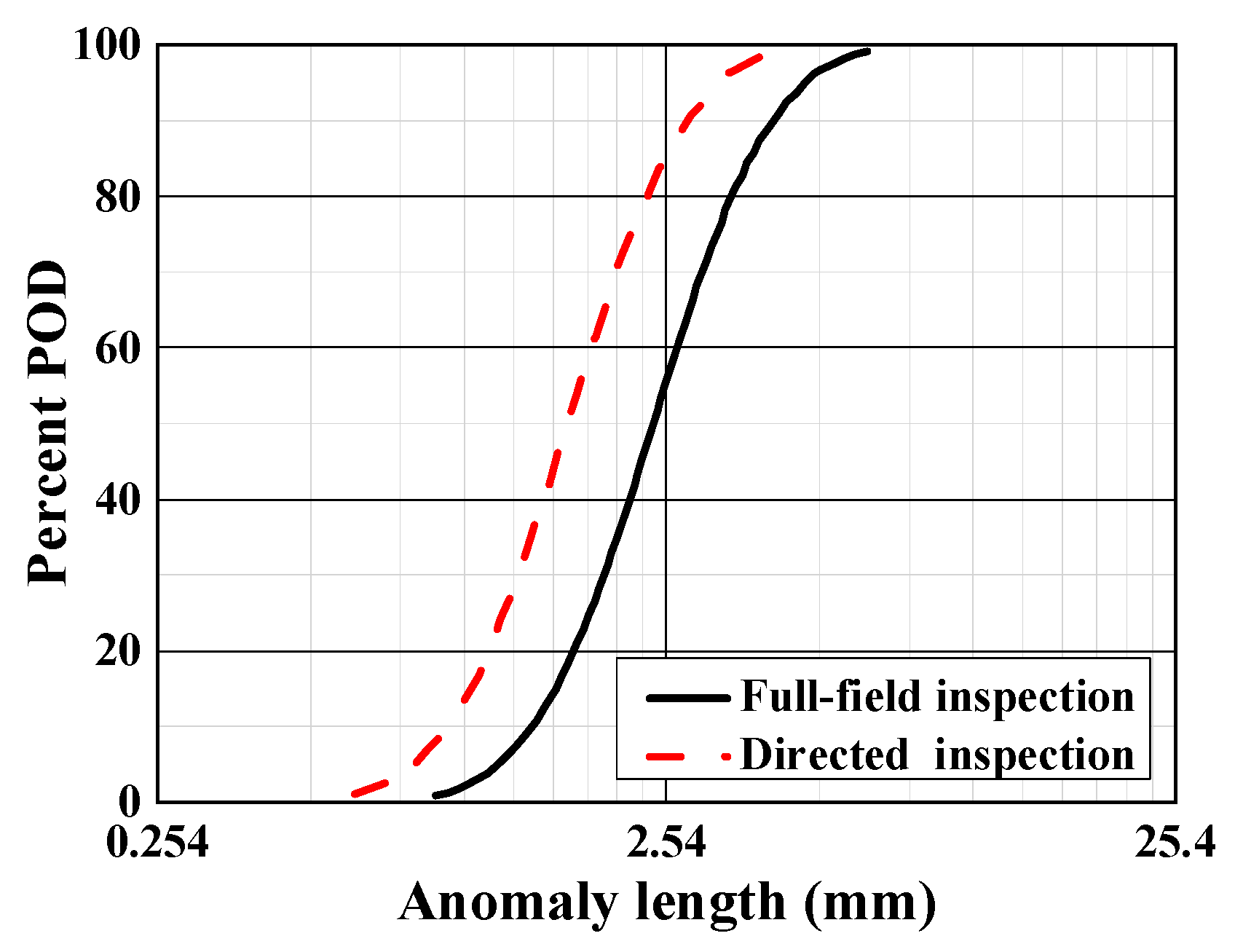
Figure 3 (detection probability). Defects described quantitatively as having an extremely low probability of occurring served as the initial size distribution of the cracks. Similar data collections have been performed in other countries [
23] to realistically characterize the status of field services in the context of local conditions. Publicly available data [
4] were chosen to provide input for the surface PRA to analyze the fracture mechanics and probabilities, while taking into consideration the fact that the purpose of this paper is to present a method of research. Specifically, a crack size of 0.0254 mm to 2.54 mm was considered as the initial value for the purposes of crack growth calculation.
2.2.2. Linear Elastic Fracture Mechanics
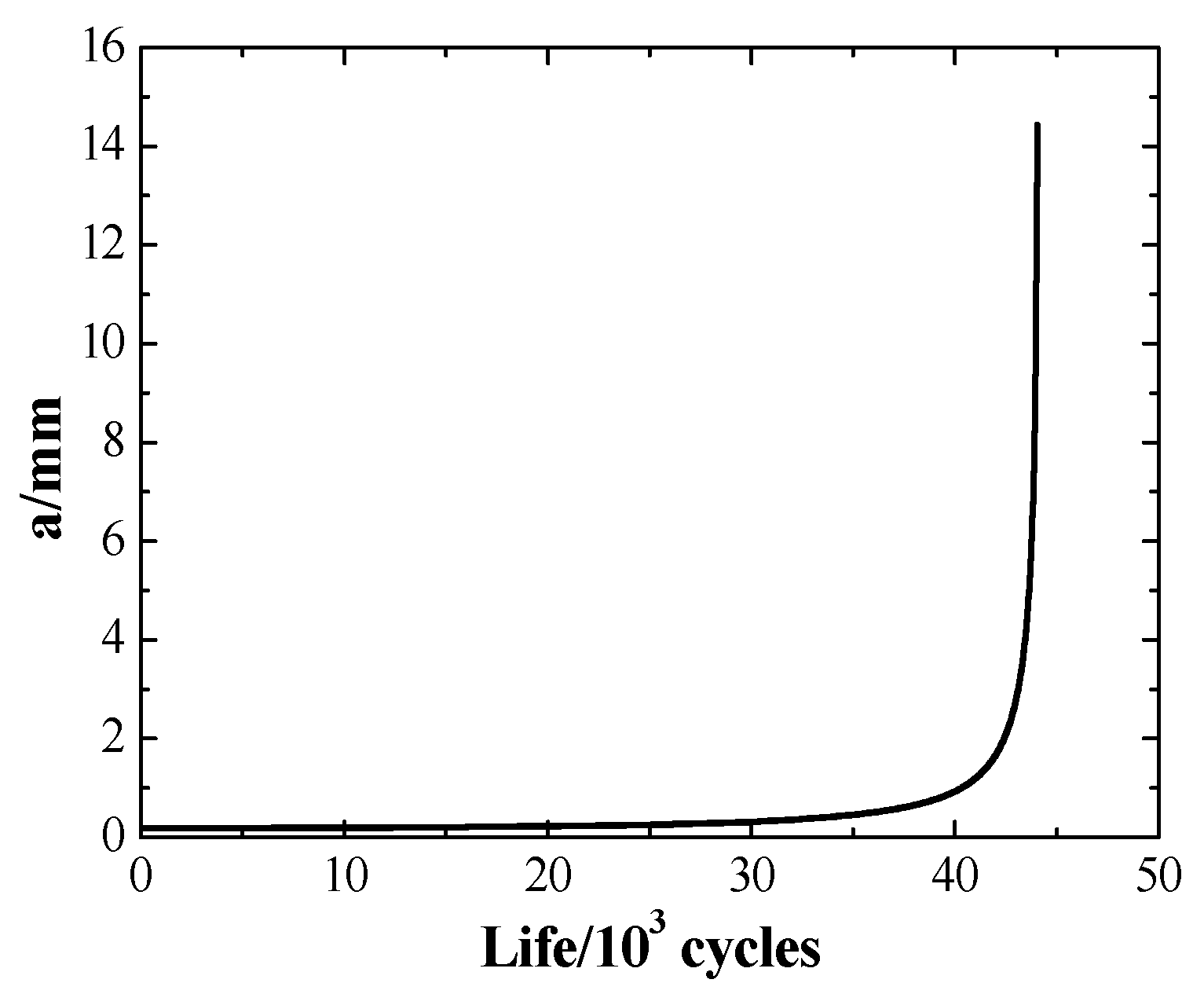
After efficiently obtaining the shot peening residual stress from the database, the linear elastic fracture mechanics is used to analyze whether defects appearing with an extremely small probability can cause life-limited parts to fail. Specifically, the defect is analyzed on the basis of the low-cycle fatigue crack growth of the cracked bodies in order to determine the failure of the life-limited part during its lifetime. Based on a considerable number of studies, it can be stated that crack length
a increases with accumulating numbers of load cycles, and fatigue crack growth rates are usually obtained by the empirical law. The most common form of the empirical law is
where Δ
K is the stress intensity factor range, and
R is the stress ratio. A series of models [
24] have been proposed to calculate
K. Notably, the purpose of this paper is to identify the key sensitive process parameters based on failure risk, and therefore, the issue of residual stress relaxation due to factors such as the temperature during service is disregarded, as the sensitivity ranking of different process parameters is not affected [
25]. The prediction of the fatigue crack growth rate and the calculation of the stress intensity factors considering the residual stress obtained by shot peening will be described in detail below.
Residual stress from shot peening affects the failure risk in the surface area by affecting fatigue crack propagation [
26]. Many studies have been performed that address the effect of residual stress on fatigue crack growth. In these, superposition techniques [
27] have often been adopted to assess the effect of a known residual stress field on fatigue crack propagation. Additionally, for linear elastic materials, the applicability of the superposition method has been mathematically demonstrated by Bueckner [
28]. Moreover, for the TC4 material analyzed in this paper, the superposition method has also been applied in order to consider the effect of residual stress on crack growth [
29]. Therefore, the combination of the stress intensity factor superposition method with the weight function method is employed in this paper due to its general applicability and simplicity compared to the integral stress intensity factor calculation using the finite element method.
Specifically, the superposition involves the computation of a stress intensity factor
KR that is associated with the initial pre-existing residual stress field. This factor is then superposed onto the stress intensity factor resulting from the applied loading
KA in order to give the total resultant stress intensity factor for the maximum and minimum loads [
30,
31]:
where
KT,max and
KT,min are the total stress intensity factors for the maximum and minimum loads, including the contribution of the residual stress intensity factor to the applied loading stress intensity factor in a compensated manner. The stress intensity factor range and the effective stress ratio are then respectively calculated as shown below.
The stress ratio is mainly affected by residual stress. Therefore, the calculation of the crack growth rate needs to reflect the influence of the stress ratio in the empirical law, for example, the Walker [
32], Harter T-method [
33], or NASGRO [
34] equations. The NASGRO equation, which takes the effect of plasticity-induced crack closure into consideration, is used here. Notably, the nominal stress ratio
RA should be replaced with the effective stress ratio
Reff in the original equation in order to calculate the crack growth rate. The NASGRO equation can be expressed as follows:
where Δ
Kth is the threshold below which the Δ
K values are too low to cause crack growth;
KC denotes the toughness of the fracture;
C,
n,
p, and
q are constants determined by experiments; and
f is the ratio of the crack opening stress intensity factor and the maximum stress intensity factor. The crack size obtained from the defect distribution sampling is considered to be the initial value of
a in Equation (5), thereby influencing the calculation of crack growth. The material constants used in the NASGRO equation are listed in
Table 1.
KA and
KR are used to calculate superposition-based crack growth, and are obtained from two separate analyses.
KA results from applied loading, whereas
KR is associated with the initial residual stress field. Both can be determined by the weight function stress intensity factor algorithm [
24], which can be expressed as follows:
where
ah is the crack half length,
σ is the stress distribution when the region does not contain any cracks,
F is the geometric correction coefficient of the cracked body,
W is the width of the cracked body geometry, and
L is the length of the cracked body geometry. Then, the total stress intensity factor is obtained by adding the stress intensity factors due to the applied load and residual stress.
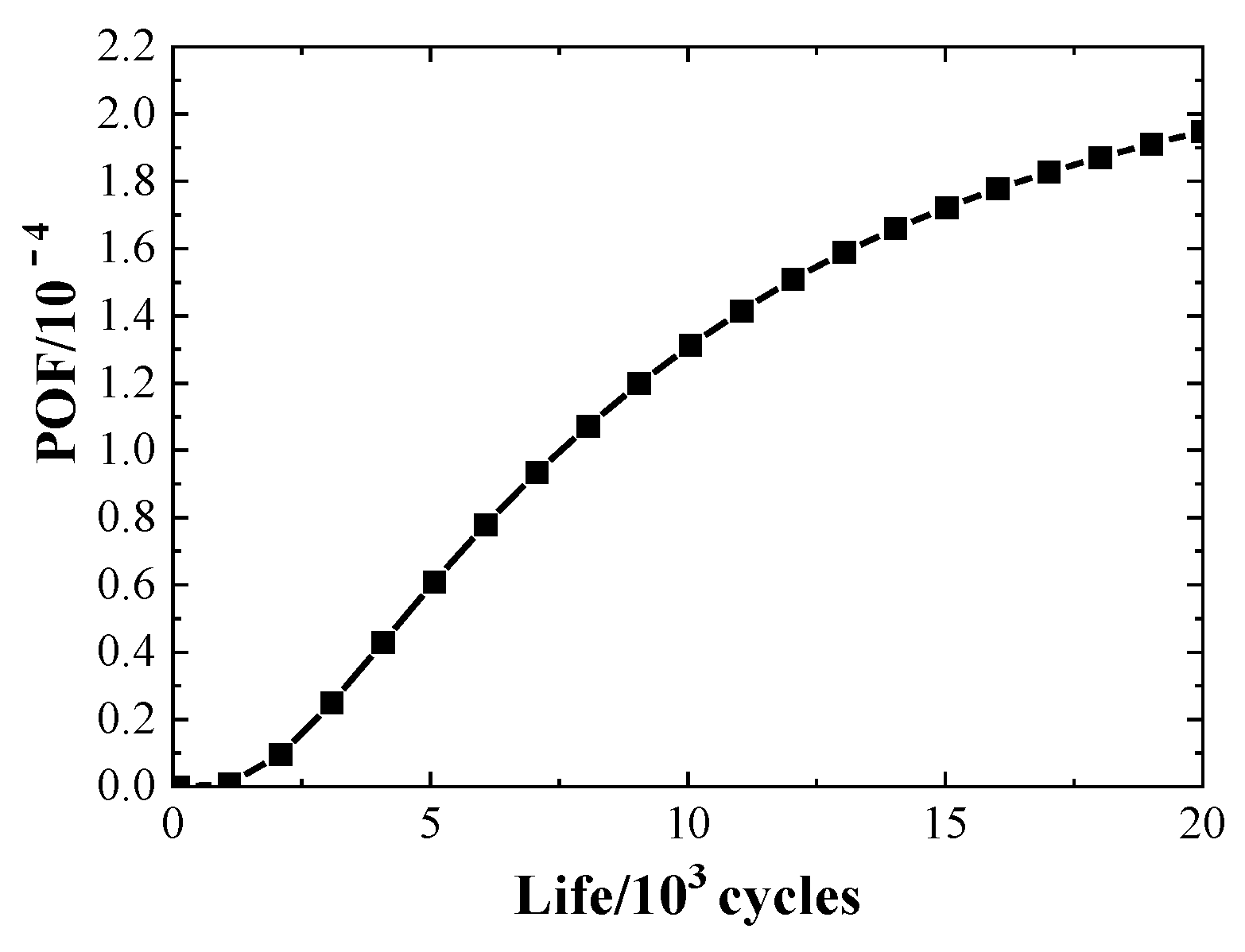
2.2.3. Analysis of the Probability of Failure
Surface PRA is based on generalized stress–strength interference theory, with the stress intensity factor
K denoting generalized stress and the fracture toughness
KC denoting generalized strength. The limit state function is obtained by calculating the difference between the fracture toughness of the material and the stress intensity factor, as follows:
where
KC is the fracture toughness of the material,
K is the stress intensity factor of the component, and
g is the limit state function.
For failure, the stress–strength interference model describes the probability of the generalized stress amplitude being greater than the generalized strength amplitude. Correspondingly, crack destabilization can occur, and fatigue fracture is judged as occurring when the stress intensity factor at the tip of the crack is greater than or equal to the fracture toughness, that is, when
g ≤ 0; in such cases, the component is considered to fail, as shown by shading in
Figure 4b. If the probability density functions of the generalized stress amplitude
K and the generalized intensity amplitude
KC are known to be
f(
K), and
h(
KC), respectively, the probability that
KC is less than
K for any stress amplitude
K is given by the following equation:
Since the generalized intensity is normally positive, the lower limit of integration can be taken as 0. From statistical theory,
F(
K) is a monotonic function of
K and a random variable with the probability of occurrence
f(
K)
dK. Therefore, the differential of the failure risk can be expressed using the following equation:
The risk of failure is obtained by bringing Equation (8) into Equation (9) and integrating, as shown below.
where
h(
KC) and
f(
K) are the probability density distribution functions of fracture toughness and the stress intensity factor, respectively. The equation is usually solved via Monte Carlo simulation or numerical integration [
35]. Simultaneously, the probability failure risk is calculated by combining the crack growth rate equation and stress intensity factor equation. In this study, via an integral-based method called the fast NI method [
27,
36], the probability of disk failure is computed while taking multiple variables into consideration, e.g., the initial defect size, the load, the crack growth velocity, and the fracture toughness. Since the research method in this study connects the manufacturing plan directly with the engineering plan, the analysis of random variables can be ignored here. In summary, the effect of potential defects on the safety of life-limited parts is assessed on the basis of the probabilistic failure risk. Specifically, the probabilistic risk assessment is adopted to address the low-cycle fatigue failure of life-limited parts with initial cracks introduced by surface features during manufacturing.