NARX-Elman Based Mach Number Prediction and Model Migration of Wind Tunnel Conditions
Abstract
:1. Introduction
2. Methodology
2.1. Key Parameters for Continuous Wind Tunnel Experiments
2.2. Wind Tunnel Flow Field Model Structure Selection
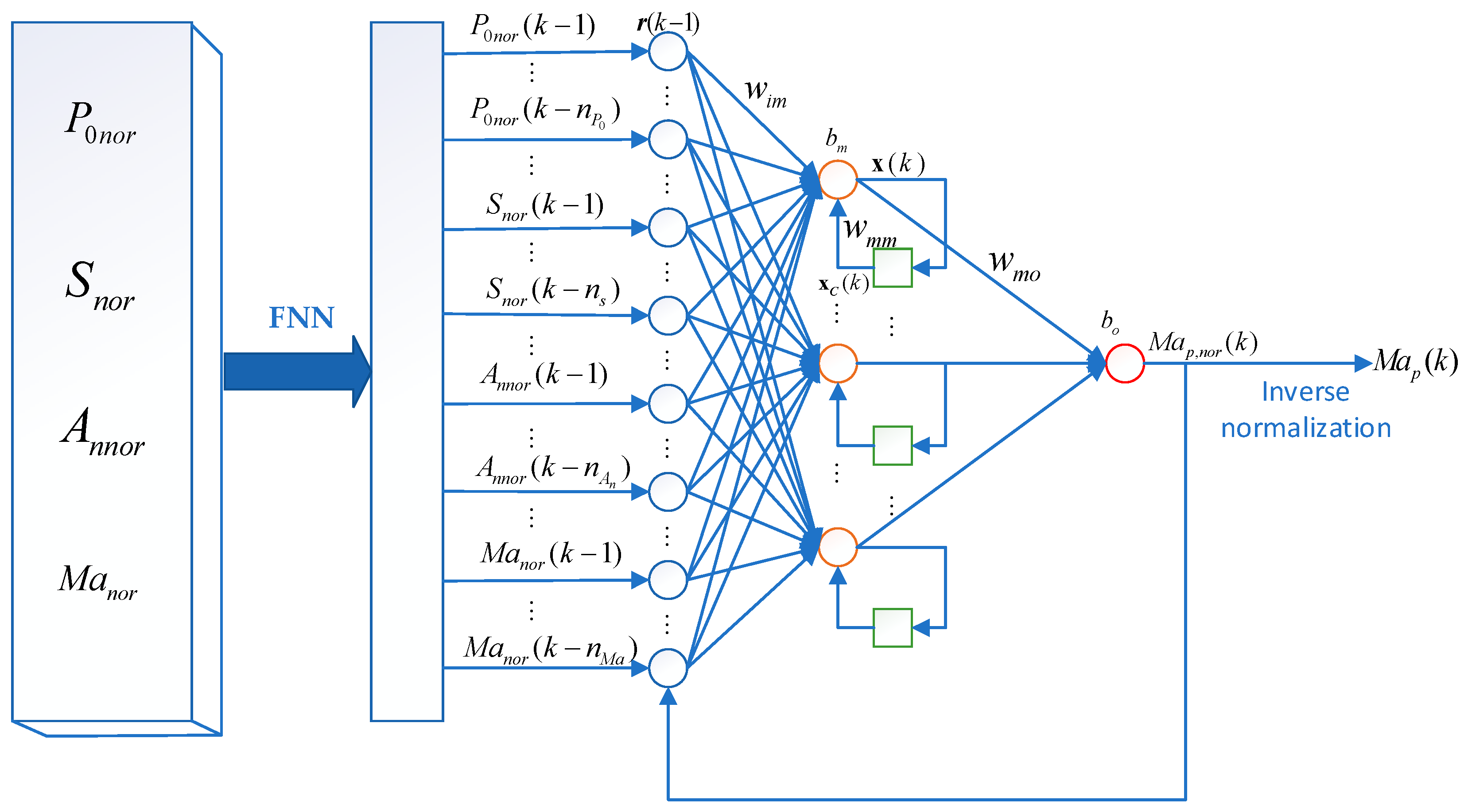
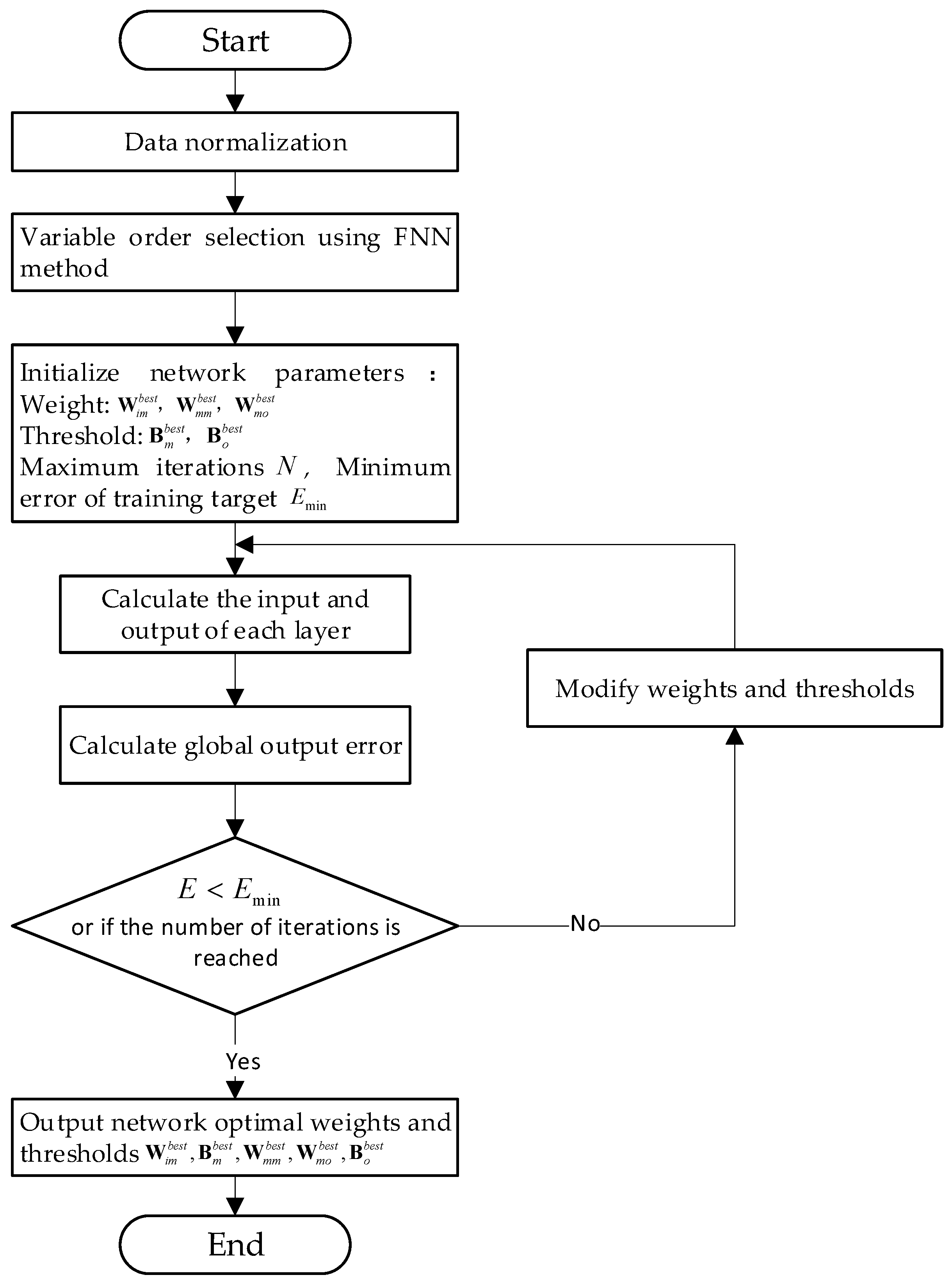
2.3. NARX-Elman Mach Number Prediction Model Establishment
2.3.1. Variable Order Selection Using FNN Method
2.3.2. Determination of Non-Linear Fitting Function Using Elman Network
2.4. IOSBC-GA Mach Number Migration
2.4.1. Similarity Analysis among Different Modes
2.4.2. Mode Migration Using IOSBC Model
2.4.3. Parameter Optimization Using Genetic Algorithm
3. Illustration and Discussion
3.1. Experimental Conditions and Settings
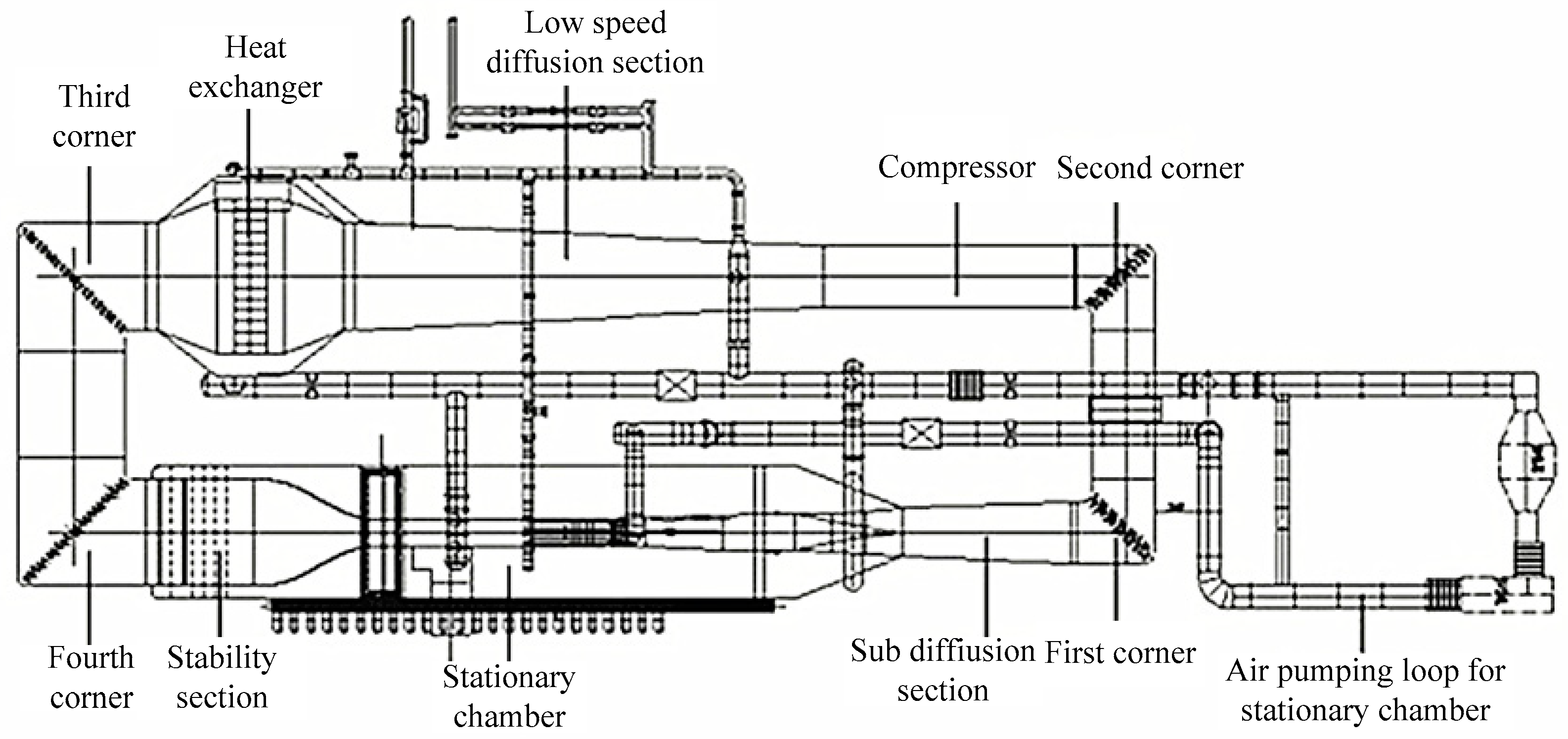
3.1.1. Continuous Wind Tunnel Blowing System Pneumatic Structure
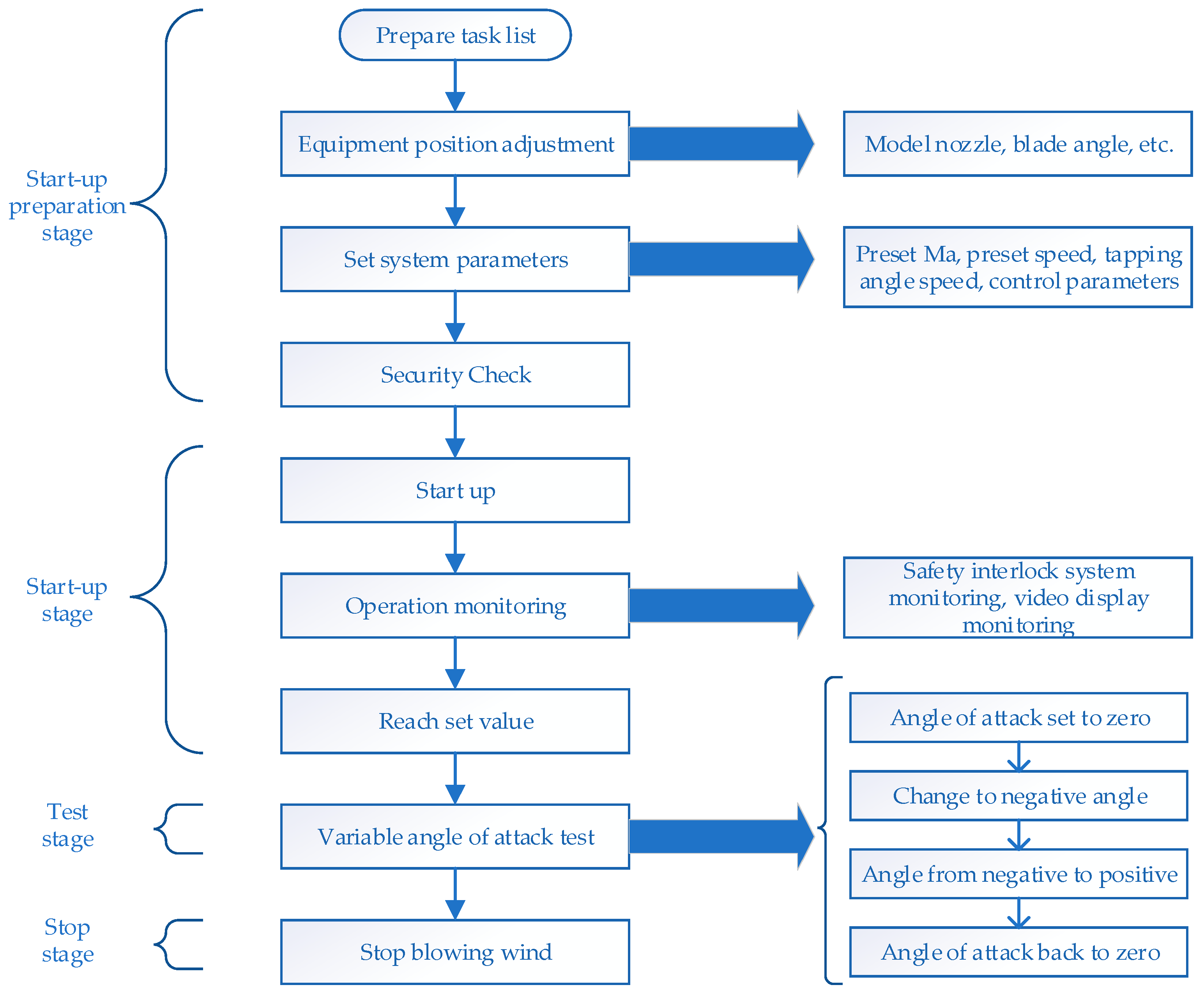
3.1.2. Continuous Wind Tunnel Blowing Test Process
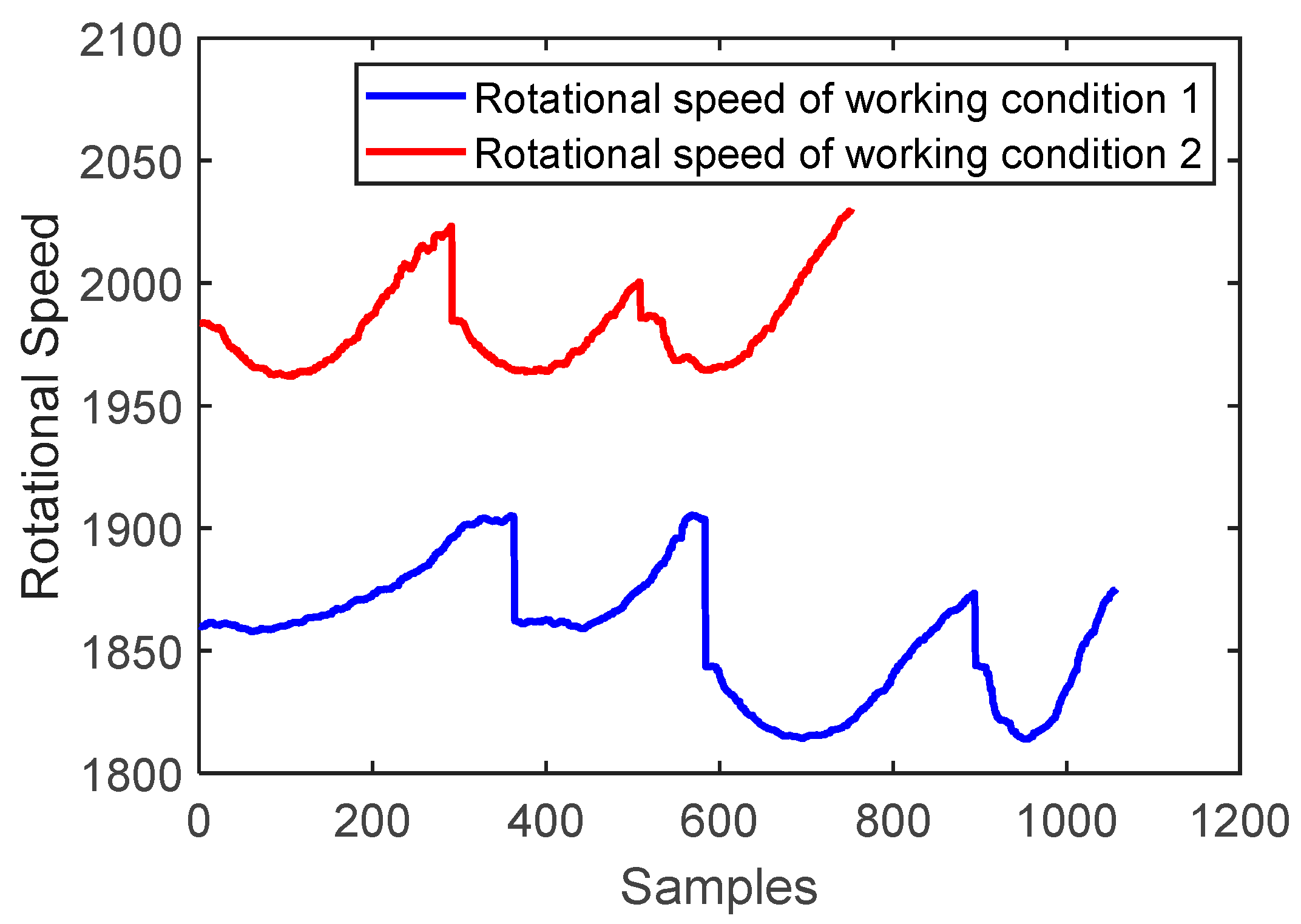
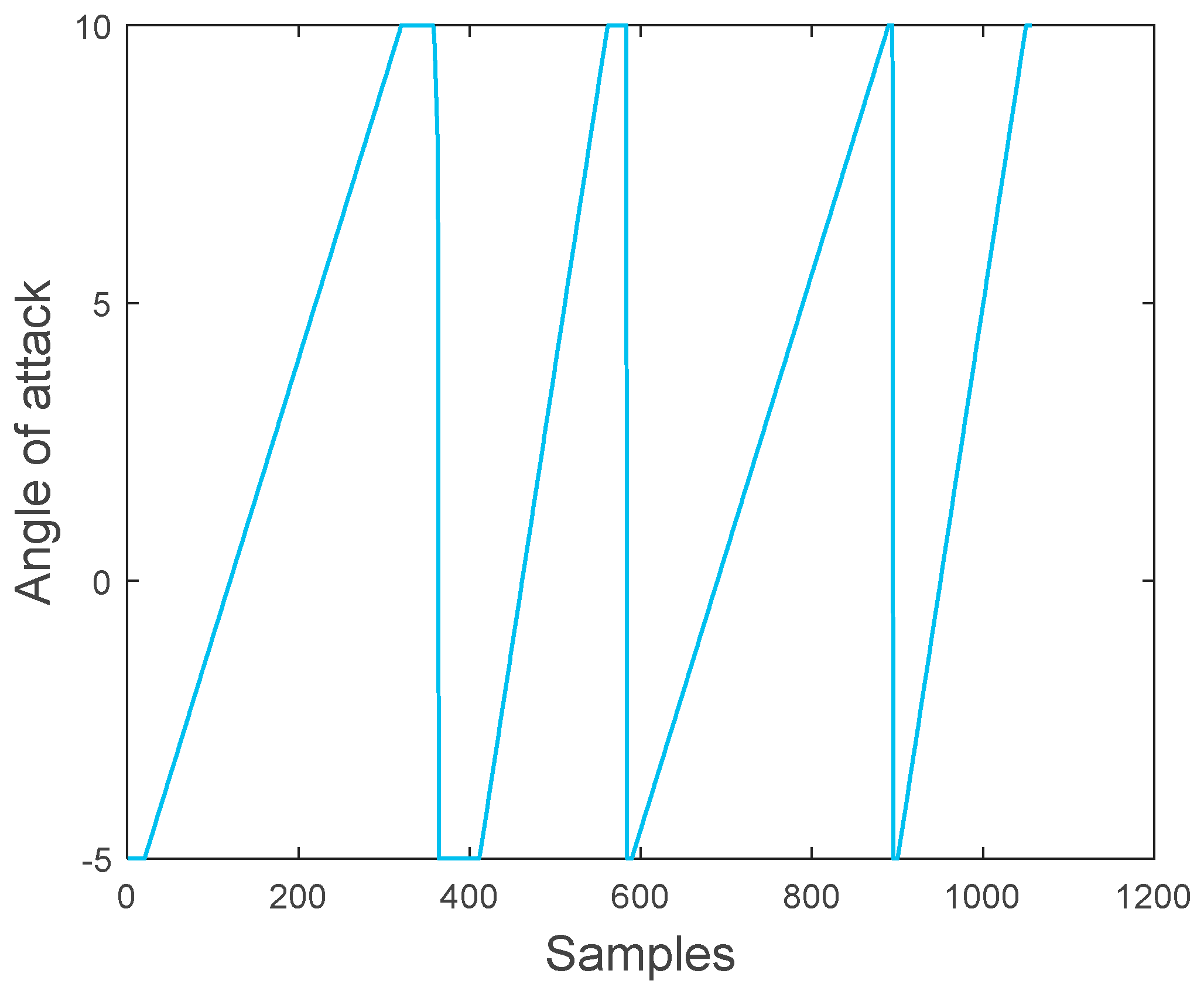
3.1.3. Analysis of Variables and Selection of Working Conditions for the Modeling Process
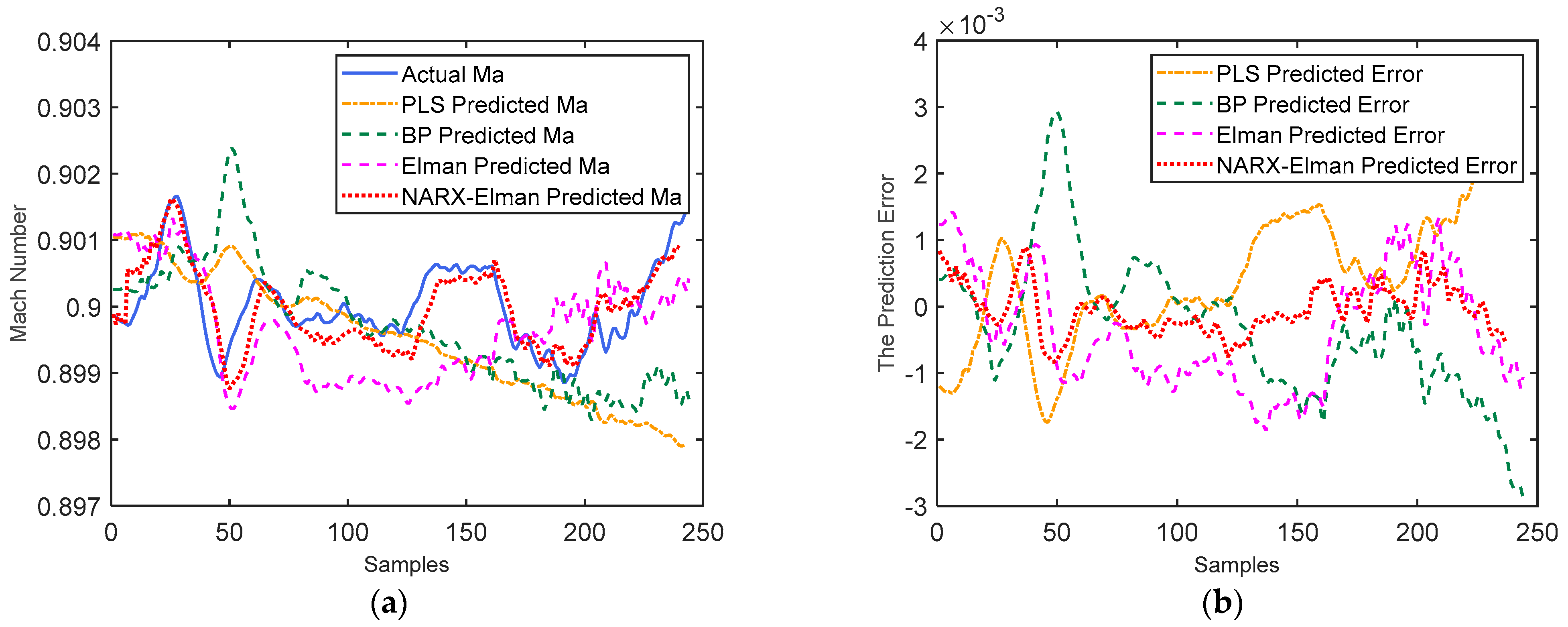
3.2. Mach Number Prediction for a Single Mode
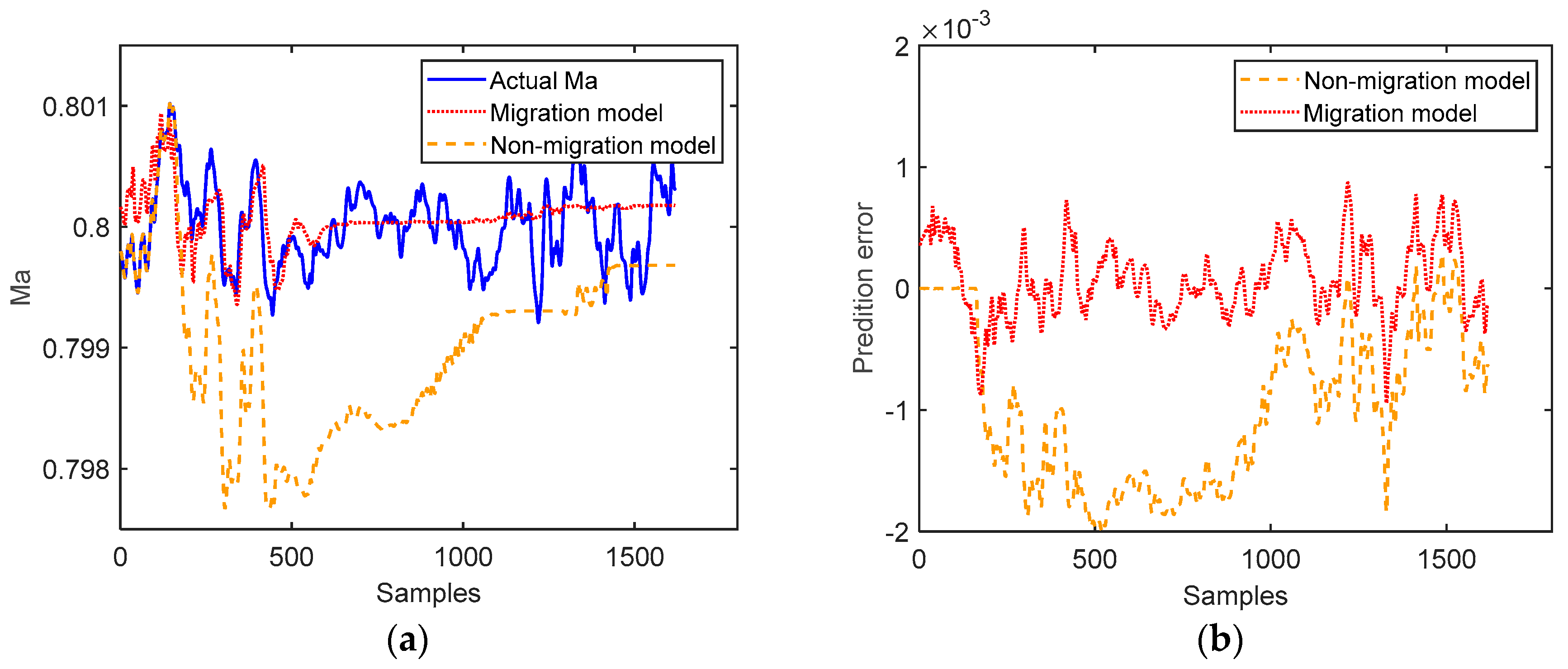
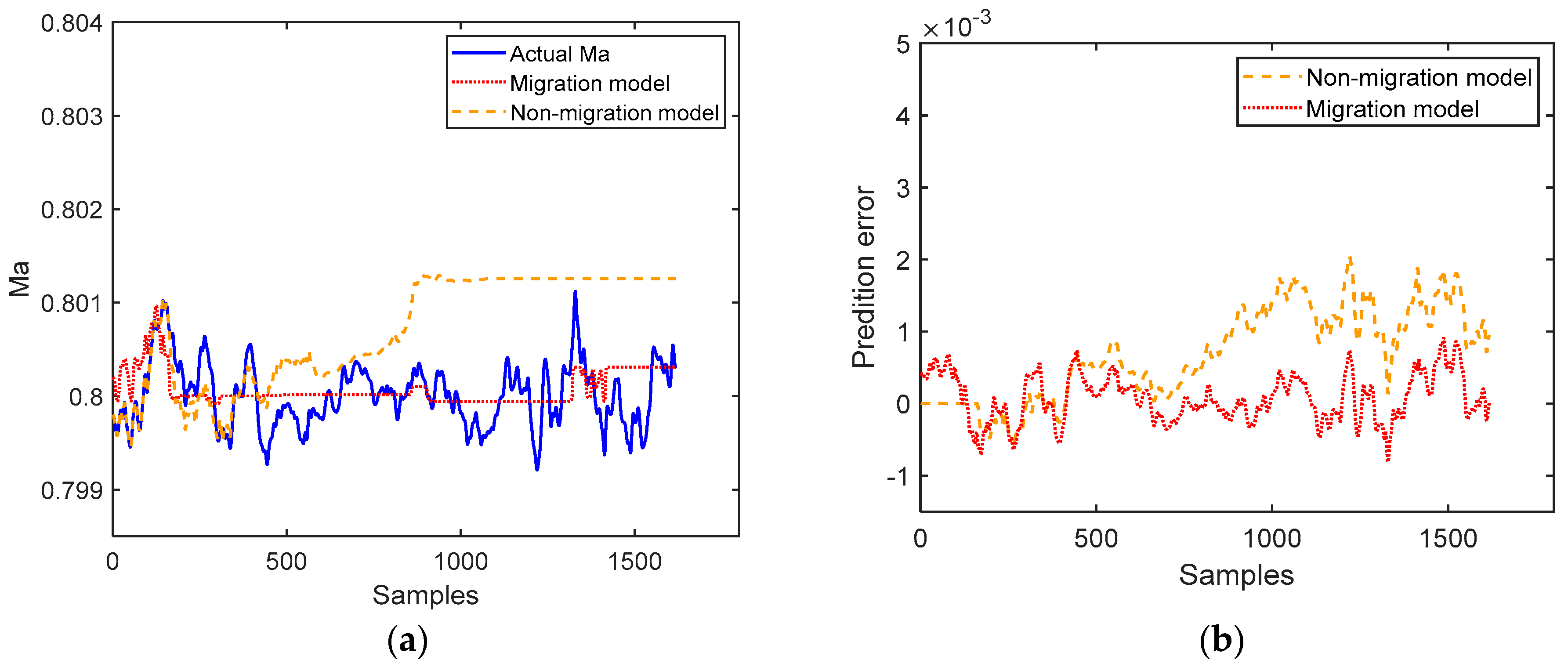
3.3. Mach Number Prediction for Multiple Modes
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Desai, S.S. Relative roles of computational fluid dynamics and wind tunnel testing in the development of aircraft. Curr. Sci. 2003, 84, 49–64. [Google Scholar]
- Haley, P.; Soloway, D. Generalized predictive control for active flutter suppression. IEEE Control Syst. Mag. 1997, 17, 64–70. [Google Scholar] [CrossRef]
- Shahrbabaki, A.N.; Bazazzadeh, M.; Manshadi, M.D.; Shahriari, A. Designing a fuzzy logic controller for the Reynolds number in a blowdown supersonic wind tunnel. In Proceedings of the 2014 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2014. [Google Scholar]
- Luo, Y.; Xing, S.; Song, W.; Chen, T.; Gao, Q. Fuzzy and PID compound control of Mach number for 0.6 meters supersonic wind tunnel. In Proceedings of the 2011 2nd International Conference on Artificial Intelligence, Management Science and Electronic Commerce (AIMSEC), Dengleng, China, 8–10 August 2011. [Google Scholar]
- Guo, J.; Zhang, R.; Cui, X.; Huang, X.; Zhao, L. Mach number prediction and analysis of multi-mode wind tunnel system. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020; pp. 6895–6900. [Google Scholar]
- Zhang, T.; Mao, Z.; Yuan, P. Decoupled PID controller for wind tunnel system. In Proceedings of the 26th Chinese Control and Decision Conference (2014 CCDC), Changsha, China, 31 May–2 June 2014; pp. 3547–3550. [Google Scholar]
- Ng, W.F.; Popernack, T.G. Combination probe for hi-frequency unsteady aerodynamic measurements. IEEE Trans. Aerosp. Electron. Syst. 1988, 24, 76–84. [Google Scholar] [CrossRef]
- Tang, Y.; Li, H.; Cai, Y. State space description based predictive control for normal temperature continuous transonic wind tunnel. In Proceedings of the 2016 Chinese Control and Decision Conference (CCDC), Yinchuan, China, 28–30 May 2016. [Google Scholar]
- Zhang, J.; Yuan, P.; Chin, K. Model predictive control for the flow field in an intermittent transonic wind tunnel. IEEE Trans. Aerosp. Electron. Syst. 2017, 54, 324–338. [Google Scholar] [CrossRef]
- Triplett, W.E. Wind tunnel correlation study of aerodynamic modeling for F/A-18 wing-store tip-missile flutter. J. Aircr. 1984, 21, 329–334. [Google Scholar] [CrossRef]
- Müller, D.; Reichert, M.; Herbst, J. Data-driven modeling and coordination of large process structures. In Proceedings of the Move to Meaningful Internet Systems 2007: CoopIS, DOA, ODBASE, GADA, and IS: OTM Confederated International Conferences CoopIS, DOA, ODBASE, GADA, and IS 2007, Vilamoura, Portugal, 25–30 November 2007; Proceedings, Part I. Springer: Berlin/Heidelberg, Germany, 2007; pp. 131–149. [Google Scholar]
- Mark, A.; Jose, C.P. Classification and prediction of wind tunnel Mach number responses using both competitive and gamma neural networks. Assoc. Comput. Mach. 2007, 1, 252–260. [Google Scholar]
- Tang, X.; Liu, K.; Wang, X.; Gao, F.; Macro, J.; Widanage, W.D. Model migration neural network for predicting battery aging trajectories. IEEE Trans. Transp. Electrif. 2020, 6, 363–374. [Google Scholar] [CrossRef]
- Park, J.; Lee, S.Y.; Choi, L.Y.; Jeong, H.; Noh, H.H.; Yu, S.H.; Song, H.; Hong, S.W. Analyzing drift patterns of spray booms with different nozzle types and working pressures in wind tunnel. J. Korean Soc. Agric. Eng. 2021, 63, 39–47. [Google Scholar]
- Li, Z.; Qin, Y.; Hou, S.; Zhang, R.; Sun, H. Renewable energy system based on IFOA-BP neural network load forecast. Energy Rep. 2020, 6, 1585–1590. [Google Scholar] [CrossRef]
- Huang, M.; Hong, C.; Chen, J.; Ma, C.; Li, C.; Huang, Y. Prediction of peak shear strength of rock joints based on back-propagation neural network. Int. J. Geomech. 2021, 21, 04021085. [Google Scholar] [CrossRef]
- Elman, J.L. Finding structure in time. Cogn. Sci. 1990, 14, 179–211. [Google Scholar] [CrossRef]
- Leontaritis, I.; Billings, S. Input-output parametric models for non-linear systems part I: Deterministic non-linear systems. Int. J. Control 1985, 41, 303–328. [Google Scholar] [CrossRef]
- Leontaritis, I.; Billings, S. Input-output parametric models for non-linear systems part II: Stochastic non-linear systems. Int. J. Control 1985, 41, 329–344. [Google Scholar] [CrossRef]
- Mohd, N.; Aziz, N. Performance and robustness evaluation of Nonlinear Autoregressive with Exogenous input model predictive control in controlling industrial fermentation process. J. Clean. Prod. 2016, 136, 42–50. [Google Scholar] [CrossRef]
- Broomhead, D.; King, P. Extracting qualitative dynamics from experimental data. Phys. D Nonlinear Phenom. 1986, 20, 217–236. [Google Scholar] [CrossRef]
- Mathew, B.K.; Brown, R. Determing embedding dimension for phase-space reconstruction using a geometrical construction. Phys. Rev. A 1992, 45, 3403–3411. [Google Scholar]
- Aksamit, N.; Whitfield, P. Examining the pluvial to nival river regime spectrum using nonlinear methods: Minimum delay embedding dimension. J. Hydrol. 2019, 572, 851–868. [Google Scholar] [CrossRef]
- Lu, J.; Gao, F. Process modeling based on process similarity. Ind. Eng. Chem. Res. 2008, 47, 1967–1974. [Google Scholar] [CrossRef]
- Wang, J.; Yang, Y.; Sun, S. SFLA-WNN Soft-Sensor Modeling and Reconfiguration of Grinding Process Based on Model Migration. J. Shanghai Jiaotong Univ. 2012, 46, 1951–1955. [Google Scholar]
- Tang, C.; Yang, O. Modeling of scramjet combustors based on model migration and process similarity. Energies 2019, 12, 2516. [Google Scholar]
- Holland, J. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
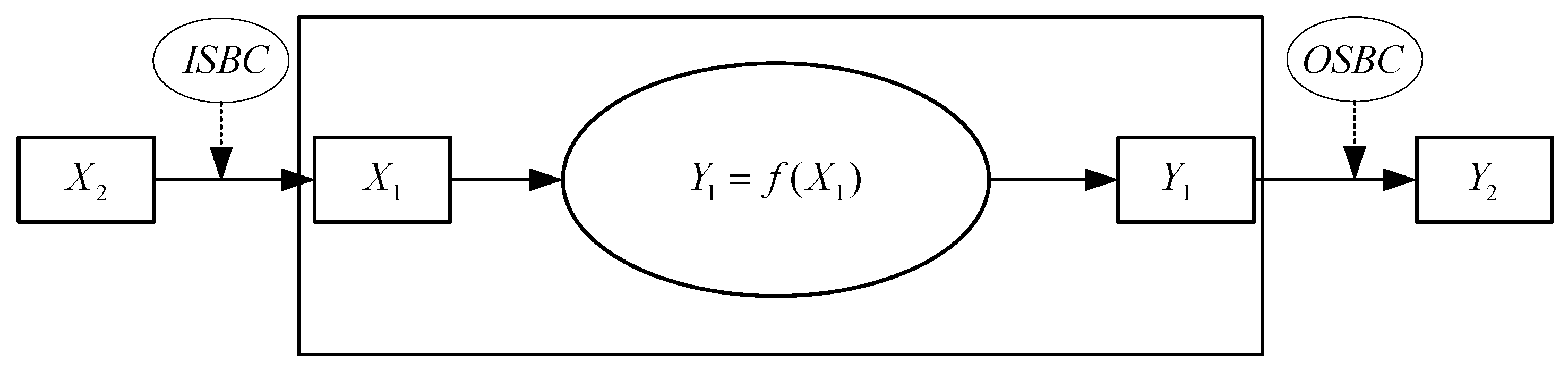





| Test Conditions | Ma | Blade Angle (°) | Total Sample | ||
|---|---|---|---|---|---|
| 1 | 0.85 | 100 | 56.3 | 0.1 | 1057 |
| 2 | 0.90 | 100 | 76.5 | 0.2 | 752 |
| 3 | 0.80 | 100 | 76.5 | 0.1 | 1626 |
| Variables | Total Pressure | Rotational Speed | Angle of Attack | Mach Number |
|---|---|---|---|---|
| Best Order | 4 | 5 | 6 | 5 |
| PLS | BP | ||||
|---|---|---|---|---|---|
| RMSE | A | MD | RMSE | A | MD |
| 0.0013 | 0.0011 | 0.0027 | 0.0008 | 0.0003 | 0.0027 |
| Elman | NARX-Elman | ||||
| RMSE | A | MD | RMSE | A | MD |
| 0.0006 | 0.0002 | 0.0024 | 0.00016 | 0.00001 | 0.00089 |
| PLS | BP | ||||
|---|---|---|---|---|---|
| RMSE | A | MD | RMSE | A | MD |
| 0.0012 | 0.0004 | 0.0036 | 0.0011 | 0.0003 | 0.0029 |
| Elman | NARX-Elman | ||||
| RMSE | A | MD | RMSE | A | MD |
| 0.0009 | 0.0003 | 0.0019 | 0.00037 | 0.00002 | 0.00089 |
| Parameter | Value |
|---|---|
| Number of groups | 80 |
| Termination of evolutionary algebra | 100 |
| Crossover probability | 0.6 |
| Mutation probability | 0.01 |
| Base Working Condition | Non-Migration Model | Migration Model | ||||
|---|---|---|---|---|---|---|
| RMSE | A | MD | RMSE | A | MD | |
| 1 | 0.00120 | 0.00098 | 0.00200 | 0.00032 | 0.00008 | 0.00094 |
| 2 | 0.00130 | 0.00041 | 0.00270 | 0.00034 | 0.00008 | 0.00092 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, L.; Shao, Y.; Jia, W. NARX-Elman Based Mach Number Prediction and Model Migration of Wind Tunnel Conditions. Aerospace 2023, 10, 498. https://doi.org/10.3390/aerospace10060498
Zhao L, Shao Y, Jia W. NARX-Elman Based Mach Number Prediction and Model Migration of Wind Tunnel Conditions. Aerospace. 2023; 10(6):498. https://doi.org/10.3390/aerospace10060498
Chicago/Turabian StyleZhao, Luping, Yawen Shao, and Wei Jia. 2023. "NARX-Elman Based Mach Number Prediction and Model Migration of Wind Tunnel Conditions" Aerospace 10, no. 6: 498. https://doi.org/10.3390/aerospace10060498
APA StyleZhao, L., Shao, Y., & Jia, W. (2023). NARX-Elman Based Mach Number Prediction and Model Migration of Wind Tunnel Conditions. Aerospace, 10(6), 498. https://doi.org/10.3390/aerospace10060498







