Abstract
Discovering and mitigating potential risks in advance is essential for preventing aviation accidents on routine flights. Although anomaly detection-based explanation techniques have successfully uncovered potential risks for proactive flight safety management, explaining group-scale precursors using these methods is challenging due to the assumption that risky flights are significantly fewer in number than normal flights, as well as the reliance on non-domain knowledge for hyperparameter adjustment. To characterize the group-scale precursors more accurately, we propose a novel technique called Catalyst Mass-Based Clustering Analysis (CMCA), which employs a composite entropy-energy dissipation index during approach to evaluate the energy management performance. On this basis, an optimization objective is constructed to identify clusters exhibiting significant energy management differences during the approach phase. We successfully identify group-scale precursors with energy management issues by applying CMCA to a combination of minority-labeled and majority-unlabeled flights. Comparative experiments show that these precursors have energy levels that deviate from normal flights by 5.83% and 10.93%, respectively, 1000 ft above touchdown, demonstrating the effectiveness of our method. The analysis suggests that poor energy management awareness on the part of pilots could be responsible for these group-scale precursors. Notably, the results obtained using CMCA are comprehensible for Subject Matter Experts, making the method a valuable tool for proactive flight safety management.
1. Introduction
Compared to post hoc incidence investigation, proactive risk management has attracted significantly more attention from airlines than ever before [1]. The Federal Aviation Administration (FAA) has called on airlines to play a more proactive role in managing risks by developing protocols to address them [2]. Proactive risk management is a forward-thinking method that focuses on anticipating risks to prevent damage, instead of simply reacting to risks. One effective method utilized in proactive risk management is flight data-based flight safety management. Fortunately, in routine FOQA (Flight Operation Quality Assurance) projects, a large number of flight data are collected [3], providing ample data for flight data-based flight safety management. For example, to prevent safety incidents caused by a decline in driving skills, pilots are trained based on accident, routine flight, and training data, which is known as EBT (Evidence-Based Training). Although the ED (Exceedance Detection) used in commercial airlines can detect abnormal flights (which are known as exceedances), when the variables exceed the SME (Subject Matter Expert)-defined limitations, it is hard to identify potential risks.
Various data science techniques such as machine learning have been employed to identify potential risks in aviation. Most of these techniques rely on the theory of anomaly detection. However, these methods have a fundamental limitation: they assume that abnormal data instances should be significantly fewer in number than normal data instances. This assumption leads to difficulties in detecting group-scale precursors [4], which consist of a larger number of flights with similar potential risks. Moreover, data-driven methods often adopt hyperparameter adjustment criteria based on anomaly detection rates, making it challenging to explain risky flight conditions.
Recently, there has been a growing interest in identifying precursors that could lead to abnormal flight conditions. Precursor mining is regarded as a weakly-supervised learning problem that can estimate the likelihood of a safety incident occurring and determine when precursors are likely to appear. Deep learning tools, such as DT-MIL (Deep Temporal Multiple Instance Learning) [5] and IM-DoPE (Intelligent Methodology for the Discovery of Precursors of Adverse Events), ref. [6] have shown remarkable performance in identifying precursors in individual flight time series. However, the issue of group-scale precursors that have similar potential risks has yet to be fully explored. Unlike the precursors studied in individual flights or novelty detection, the group-scale precursor mining problem aims to identify and explain patterns that exhibit potential risks consisting of multiple flights.
We propose a novel method for identifying potential risks in routine commercial aircraft using group-scale precursors. The precursors in the approach phase are the focus of this research. They are considered to be induced by factors such as manipulation habits and training, resulting in the degradation of nominal flight conditions. Unlike traditional anomaly detection, these precursors are not represented as outliers but as groups of flights exhibiting similar characteristics. By focusing on these high-risk flight scenarios, we can develop a more targeted method for detecting and addressing potential safety events, thus contributing to improved flight safety and reducing potential risks.
As a powerful technique for knowledge discovery, machine learning techniques have shown great performance in extracting valuable information from large complex accident datasets in aviation safety [7] such as anomaly detection from flight data [8,9], human factor discovery from safety incident reports [10,11], and go-around flight detection from ADS-B data [12]. The research that is most relevant to discovering and explaining safety incidents based on flight data is summarized below.
Anomaly detection tools are commonly used to identify potential risks in aviation due to the substantial number of nominal flights relative to the number of fatal accidents. Typically, these tools establish classifiers based on an assumption of unbalanced data to identify potential risks. For example, OC-SVM (One Class-Support Vector Machine), which utilizes multiple kernel functions as the measurement to evaluate the abnormal behaviors described through continuous and discrete variables, has been adopted to identify abnormal operations [13]. Another typical example is the IMS (Inductive Monitoring System) [14], in which a flight is assigned to the nearest cluster and given the same label as the cluster. Clustering shows remarkable performance in aviation anomaly detection due to its natural grouping ability and the need for unlabeled data [15,16,17]. Density segmentation-based clustering has been used to detect different areas and flight data in sparse areas were defined as anomalies [18]. Further, to evaluate the anomaly degree of each outlier, the LOP (Local Outlier Probability) has been applied to obtain the outlier scores [19]. Researchers have also attempted to develop nominal behavior classifiers using deep learning technologies. Thanks to their powerful feature-capturing ability, deep temporal neural networks have performed well in detecting adverse events [5]. For instance, an AE (Auto-Encoder) and a CVAE (Convolutional Variation Auto-Encoder) have been utilized to discover adverse events by reconstructing flights in a lower-dimensional space [8,20,21]. However, restricted by the need for a large amount of training data, these methods did not perform well in discovering potential risks. It is evident that general anomaly detection tools struggle to identify group-scale precursors because of the fundamental data assumption of anomaly detection and the unexplainable results obtained from non-domain-related hyperparameter adjustment criteria.
Empirically setting hyperparameters can result in incomplete information and results that are difficult to understand. In practice, adjusting the hyperparameters according to anomaly detection rates of 1%, 3%, and 5% is common [18,19,22,23], as the precursors lack a clear definition. This strategy is practical because the clustering results are sensitive to hyperparameters. However, the results obtained with these detection rates are unreliable because the clusters and outliers are adjusted empirically. For example, when the anomaly detection rate is increased, a flight that was originally identified as normal might be considered an anomalous flight. This change is hard to explain from a flight safety perspective. Furthermore, focusing only on outliers will overlook clusters with similar risks such as flights within a cluster exhibiting specific deviations in energy states. In addition, utilizing these detection rates overlooks important safety information because the data distribution and domain knowledge are not considered, and the strategy may fail when the data are not substantial. To address these limitations, specific methods have been utilized to obtain natural clustering results to guide the adjustment of hyperparameters. In [24], a Bayesian Information Criterion (BIC) was used to determine the number of components in a Gaussian Mixture Model (GMM), and the DBSCAN method was then utilized to merge similar flights. The hyperparameters of DBSCAN were set according to the GMM test results. However, using such hyperparameter adjustment criteria lacks domain guidance, leading to hard-to-explain clusters and outliers in the analysis.
Moreover, efforts have been made to emphasize the precursors so they can be detected. To achieve this, specific methods, such as PCA (Principal Component Analysis), t-SNE (t-Distributed Stochastic Neighbor Embedding), and AE [18,21,25], have been used to extract the features of high-dimensional flight data to highlight the differences between nominal and abnormal flights. Nevertheless, these techniques generated unexplainable features, leading to results that were difficult to comprehend. Methods combining flight theories have been used to characterize anomaly flights to address this issue. For example, the energy-related coefficients derived from additional performance models [4] have been applied to explore flight performance during approach. Moreover, statistical methods, such as the mean and variance of key flight variables, have been widely used to identify potential risks [26,27].
Enhancing the dissimilarity between nominal and precursory flights is another way to highlight the precursors. Euclidean distance has been widely used in the aviation industry to measure the similarity between flights [14]. Additionally, to describe the distance between heterogeneous flight data, nLCS (Longest Common Subsequence) [28] and VAR (Vector Autoregression) [29] models have been applied to measure the discrete variables and continuous variables, respectively. However, using traditional similarity measurements to identify small clusters was challenging because the “data background” was not considered, resulting in a weak ability to distinguish clusters with similar densities [30]. To address this issue, Mahalanobis distance was used to measure the dissimilarity in [31], taking into account the data background. Considering the data background, the distance between two flights increases when they are in a high-density area and decreases when they are in a low-density area [32]. Such data-independent measurements are useful for identifying flights with group-scale precursors.
Catalyst Mass Clustering Analysis (CMCA) is proposed to discover the group-scale precursors. The main contributions of this paper are as follows: (1) A clustering method is developed to capture the group-scale precursors. (2) A domain-knowledge-based hyperparameter adjustment criterion is proposed to find clusters with different performances during approach. (3) Labels for majority-unlabeled flight group-scale precursors are generated from minority-labeled flight data.
Exploring group-scale precursors can assist domain experts in characterizing the abnormal behavior of flights while also providing targeted training suggestions for different types of pilots, making the proposed method valuable for stakeholders. The rest of the paper is organized as follows. Section 2 outlines the steps involved in CMCA. Then, in Section 3, the experimental results are compared, and in Section 4, the method’s performance is discussed. Finally, our method’s key benefits and main innovations are summarized in the conclusion.
2. Methodology
The process of performing CMCA is shown in Figure 1. First, the continuous and discrete flight variables are selected using various methods based on the energy analysis. Second, the dissimilarity matrix is obtained by calculating the isolation dissimilarity of N flights and P catalysts. Then, the mass-based clustering is implemented, in which the hyperparameters are adjusted until the optimization goal is satisfied and the labeled group-scale precursors can be acquired.
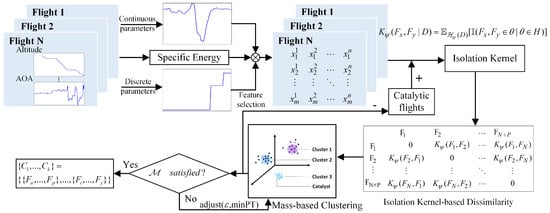
Figure 1.
Process of using CMCA to identify group-scale precursors.
2.1. Energy-Based Feature Selection
Before implementing the clustering algorithm, it is necessary to eliminate redundant variables because they can not only seriously affect the performance of machine learning algorithms but also result in the failure of similarity measurements due to dimension explosion. The flight variables that are available in the data can be divided into three categories: data related to the performance of the aircraft such as the aircraft’s weight and ground speed; environmental data such as the atmospheric temperature; and attitude configuration data such as the angle of attack and Euler angles.
The variables are selected based on the energy change because the energy variation is closely linked to flight safety during approach. Continuous variables describing the aircraft’s state such as the altitude and speed can be extracted through their correlations with energy changes. Discrete variables contain practical safety information about pilots’ maneuvers; however, the correlation between the discrete control variables and energy is not significant in mathematical terms. For example, changing the flaps from 0 to 5 degrees will increase the aircraft drag, leading to slower airspeed and higher energy consumption. Correlations such as the Pearson index between energy and variables such as the flap angle may not be significant because the flap angle is just a step signal. However, according to the mechanism analysis, the change of flaps is very important for the energy state. As a result, various methods have been proposed to select continuous and discrete variables separately.
The process of continuous variable selection is shown in Algorithm 1. The complete set contains all the continuous variables. The set represents the features selected by the algorithm. In step 1, set S extracts one element once from , not returning it until all the variables closely related to energy are obtained. Every time a new variable is upgraded, the energy is derived, as shown in Equation (1)
| Algorithm 1: Continuous feature selection |
 |
In the equation, V represents the airspeed, H denotes the altitude, and g represents the acceleration of gravity. In this research, we adopted the Maximal Information Coefficient (MIC) , which can capture both linear and nonlinear associations. is derived from Equation (2).
where represents the correlation coefficient of and represents the joint probability of variables .
Once all the elements in the complete set have been processed, Step 2 is augmented to remove features with high collinearity in S. First, the new set is constructed using a randomly chosen element from S. Then, the correlation coefficients between elements f and set are calculated as . Next, the element f with the weakest correlation is merged into until all elements in S are traversed.
Focusing on the variations rather than the values is more effective in capturing discrete features. However, the algorithm used for continuous variables cannot be applied to discrete variables such as the flap position because the correlation between these variables and energy is insignificant. Discrete variable changes are recorded as step signals, representing a flight state switch. Therefore, the variables whose own changes can affect the decreased speed of aircraft energy are considered significant during approach. Energy leaps induced by the variables are sought within two seconds of the step change to detect their influence.
An example of discrete variable selection is depicted in Figure 2, where the variation in the specific total energy during the 300 s flight is presented. Figure 2a,b show the energy response in more detail during the 90–110 s and 130–150 s intervals. The black line represents the total specific energy, and the red and green dotted lines depict the fitted lines based on data from the 0–140 s and 140–300 s periods, respectively. At 140 s, the flap angle changed from 0 degrees to 15 degrees, as shown in Figure 2d, followed by a decrease in the energy-reducing rate. Additionally, the influence of the slat angle, which changed at about 100 s, as shown in Figure 2c, was almost negligible in energy.
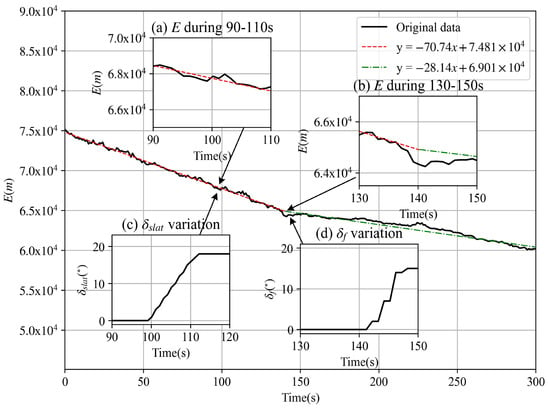
Figure 2.
Influence of flap and slat angles on specific energy.
2.2. Catalyst Mass Cluster Analysis
Given a flight dataset comprising n flight records F, the catalyst clustering approach involves designing a metric to improve the clustering quality from an energy management perspective. The metric is also used to measure the clustering quality. The more significant the differences between clusters, the higher the quality of clustering. To accurately distinguish flights with different energy performances during the approach phase, is constructed based on the specific total energy, as described in detail in Section 2.3. Therefore, the objective of Catalyst Mass-based Clustering is to satisfy by identifying a set of clusters , where .
In Figure 3, we illustrate the differences between the general and catalyst clustering methods. Solid dots of the same color represent the same class data, whereas hollow dots represent the catalysts. Under general clustering, the same dataset C1 and C2 was misclassified into two distinct categories, and some blue dots were mistakenly grouped into C3. Furthermore, the red dots were identified as outliers due to their sparse data distribution. In contrast, in catalyst mass clustering, the density of data within the outlier group is increased through the introduction of catalysts. The scattered similar points can then be aggregated, enhancing the clustering quality. Finally, the catalysts are removed to produce the final clustering results. Further, the hyperparameters are adjusted according to optimization goal , which means that all the clusters are significantly different and can be used for further safety analysis.
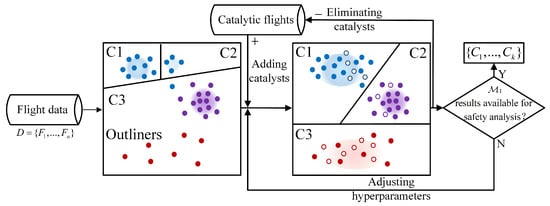
Figure 3.
The differences between catalyst clustering and standard clustering, where the blue solid points belong to the C1 cluster, the purple ones belong to C2, and the red ones belong to C3. In addition, the hollow dots that represent the catalytic flights added.
In this study, the labeled flight data identified by Exceedance Detection are regarded as the catalysts. They provide the label information of the clustering results and improve local densities [33]. In addition, the isolation kernel is used to measure the dissimilarity because it has been proven to be minimally affected by the dimensions.
2.3. Composite Entropy-Energy Dissipation Index
Improper energy management during approach can increase the risk of safety incidents. To differentiate flights with varying levels of performance during approach, we constructed a composite entropy-energy dissipation index for the approach phase, which is denoted as . The index is defined as follows:
where is used to determine whether the energy-reducing velocity is centered around the typical values observed across most flights and quantifies the stability of the energy variation. can be acquired from Equation (4)
The component of the composite entropy-energy dissipation index during approach refers to the energy-reducing velocity. This is defined as the difference between the specific total energy at 10 nm away from the runway and the energy at 1000 ft above touchdown . To assess the deviation of from the typical values observed across most flights, z-score centralization is utilized. We also calculate from Equation (5), which represents the stability of the energy variation
To reduce the overreaction to minor energy fluctuations, we decompose the energy-reducing acceleration into several states using the SAX (Symbolic Aggregate Approximation) representation. In this method, each state is assigned a probability based on the SAX representation.
Once the evaluation index has been constructed, the optimization issue regarding mentioned in Section 2.2 is defined by
where is the indicator function, denotes the results of the significance test, and T represents the threshold of passing the test. This optimization aims to find clustering results where all clusters exhibit significant differences in approaching energy management levels, which reflect distinct approaching performance characteristics.
2.4. Isolation Kernel-Based Dissimilarity
The isolation kernel is utilized in this research as it can mitigate the issue of distance concentration that has affected some traditional methods. Moreover, as a data-dependent measurement, the Isolation Kernel-Based Dissimilarity enhances the distance between different flights, which is vital in identifying group-scale precursors.
In addition, the isolation kernel can transform density-based clustering into mass-based clustering, which can help to overcome some of the limitations of density-based clustering in distinguishing clusters with similar densities [30,34]. The Isolation Kernel-Based Dissimilarity function is defined as follows:
where represents the expectation. The Isolation Kernel-Based Dissimilarity between two flights and , denoted as , is defined as the probability that and belong to the same isolating area . Here, a specific isolating area is defined as a subset of , and represents different partitions of the set D.
To utilize the isolation kernel for measuring the dissimilarity between flights, we start by selecting random elements from the dataset D to construct a set of center points , as shown in Algorithm 2. This operation splits the dataset into two parts, Z and . Then, every element is assigned to the hypersphere space corresponding to by identifying the nearest center point . This assigns each element to a specific hypersphere based on the center point it is closest to. Elements that are in the same hypersphere are assigned a distance of 1, whereas elements that are not in the same hypersphere are assigned a distance of 0. Then, a distance matrix is obtained in Step 10 in Algorithm 2. By repeating Steps 3–9 for t times, t distance matrices are obtained. Finally, the Isolation Kernel-Based Dissimilarity matrix is calculated by taking the mathematical expectation of the distance matrices.
| Algorithm 2: Isolation Kernel-Based Dissimilarity |
 |
This measure provides an objective way to compare the dissimilarity between different flights, which is vital for detecting adverse events. Isolation Kernel-Based Dissimilarity is robust because it is a mathematical expectation-based ensemble algorithm.
Furthermore, the data background is considered in the spaces partition step using Voronoi-based nearest neighbor partition [35], thereby enhancing the dissimilarity between nominal and abnormal flights. As shown in Figure A1, the partitions on the left are sparser, whereas the data density on the right is significantly higher than on the left. The different partitions increase the dissimilarity between two flights in high-density areas and decrease the dissimilarity in low-density areas, making the Isolation Kernel-Based Dissimilarity a data-dependent measure.
After the distance matrix is obtained, DBSCAN is performed, which is known for its superior performance in automatically determining the number of clusters and identifying irregular clusters. The DBSCAN algorithm involves the calculation of a density function that measures the density around each sample, denoted as . The expression for this density function, calculated as Equation (8), is given by
where the function denotes the norm of the vector . Here, is the threshold of density, and represents the cardinality of a set. The value of the density function for flight is the number of flights within a neighborhood of in the data space D that lie within the threshold .
By using data-dependent dissimilarity, the mass-based clustering method can improve the accuracy of identifying clusters with varying densities [36]. The mass function that forms the core of the clustering process is obtained by transforming Equation (9), as shown below:
where is the IKD (Isolation Kernel-Based Dissimilarity) between and , and is the preset threshold of mass.
3. Experiments
To assess the performance of CMCA, data from 3604 flights that used the same approach mode for landing on a single runway were collected. A total of 31 flights with high energy and 22 with low energy in approach labeled by Exceedance Detection were used as catalytic flights. The flights were routine flights operated by an airline in China that followed the same approach pattern, which reduced the potential for confounding factors to affect the results. The experiments were conducted using Python 3.9, and the scikit-learn==1.0.2, numpy==1.20.3, and pandas==1.5.0 modules were utilized. The experiments were carried out on an HP workstation with 16 GB of RAM and an i7-9700 CPU @ 3.00 GHz.
3.1. Preprocessing
To extract the feature vector, the sampling rates were first standardized to 1 Hz. Then, the flight data were processed using z-score normalization. By sampling every 0.25 nm starting from a distance of 10 nm away from the runway, feature vector was formed according to Equation (10).
where represents the value of the ith variable at distance j.
Algorithm 1 and the discrete parameter selection method described in Section 2.1 were applied to select the most relevant variables first. As a result, 23 continuous and 4 discrete features were extracted from an original number of 78 variables recorded in the flight data. As shown in Figure 4a, there was high collinearity among the 78 variables, with the axis representing the parameter index ranging from 0 to 77. However, after decorrelation, significant improvements were observed, as shown in Figure 4b, where the axis represents the new variable index ranging from 0 to 22.
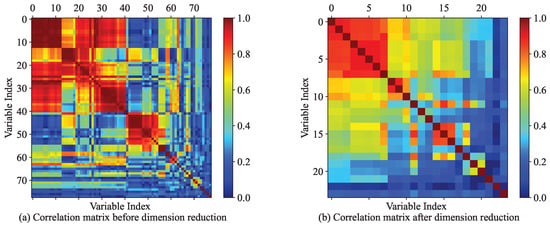
Figure 4.
Correlation matrix: (a) original parameters, (b) selected features.
3.2. Selection of Catalytic Flights
For the purposes of identifying potential safety events, 31 high-energy approaching flights and 22 low-energy approaching flights were selected as representative examples of high-risk flight conditions. High-energy flights pose a greater risk of speed exceedances and other dangerous mishaps, whereas low-energy flights can seriously impact the aircraft’s maneuverability, making it more difficult to recover from potential accidents. The catalyst flights were selected according to the FOQA monitoring standards from CAAC (Civil Aviation Administration of China). We focused on the airspeed at around 1000 ft above touchdown . When , a flight is regarded as having a low-energy approach, and when , it is regarded as having a high-energy approach, where represents the final approach speed.
Figure 5 shows the results of our analysis for two catalytic flights used as representative examples of high-risk flight scenarios. For both cases, the light-blue areas represent 50% of all flights, whereas the dark-blue areas represent 90% of all flights.
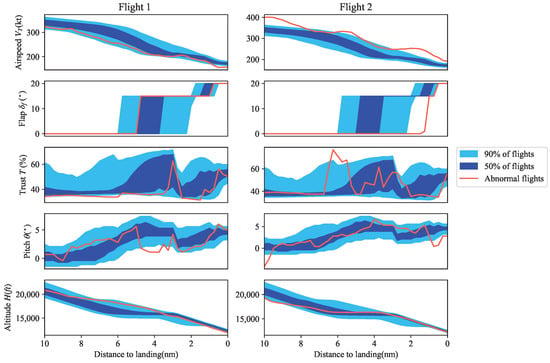
Figure 5.
The airspeed, flap, thrust, pitch, and altitude of the flights, where the light-blue areas represent 50% of all flights and the dark-blue areas represent 90% of all flights. In this figure, abnormal flights are indicated by red lines.
For Flight 1, it can be observed that certain parameters deviated from nominal flight conditions, which resulted in a lower speed at 1000 ft above touchdown (shown on the right-hand side of the horizontal axis). This deviation from typical flight conditions could potentially indicate an issue with the aircraft’s power, altitude, or other critical parameters. In contrast, Flight 2 exhibited significant deviations from typical flight conditions, with the parameters exceeding the boundaries of 90% of all flights. Specifically, improper operation of the thrust, flap, and pitch angle occurred around 2 nm from the runway, causing a high-energy approach and a typical high-risk event.
3.3. on Different Flights
To evaluate the effectiveness of our proposed metric in distinguishing between different flights during approach, four flights were analyzed, and the results are presented in Figure 6. Figure 6a shows the specific total energy and Figure 6b shows the differential value of the acceleration of energy .
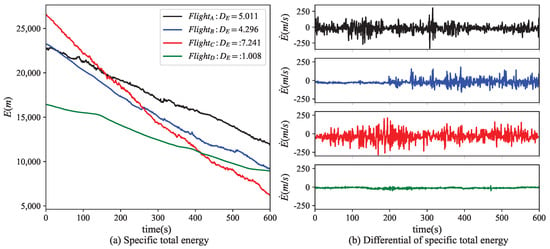
Figure 6.
Energy variation analysis of flights with different values.
The distribution of the values for each flight is illustrated in Figure 6. In general, most flights with stable and well-managed energy exhibited relatively lower values, whereas higher values indicated poorer approaching performance. Among the four analyzed flights, exhibited the highest level of stability but the lowest energy consumption, resulting in the lowest value of 1.008. In contrast, and both experienced noticeable vibrations and exhibited a moderate rate of energy dissipation, leading to moderate values of 5.011 and 4.296, respectively. showed the most pronounced fluctuations and a significant energy dissipation, resulting in the highest value among the four flights. These findings suggest that can serve as a useful tool for identifying flights with poor approaching performance and supporting early intervention to address potential safety events.
Overall, our proposed metric is a valuable new tool for characterizing the stability of the approach and has wide-ranging implications for improving flight safety and enhancing the effectiveness of safety interventions.
3.4. Comparative Experiments
In this section, the performance of CMCA in discovering adverse events is verified through comparative experiments. The following algorithms commonly used in the aviation industry are used as the baselines:
(1) Algorithm 1 (IKD K-means): As one of the most widely used partition-based clustering algorithms, K-means groups similar objects into one cluster by minimizing the distance between samples. IKD (Isolation Kernel-Based Dissimilarity) is used to replace the Euclidian distance, and the elbow curve determines the number of clusters. By applying IKD to the task of event detection in flight data, we aim to evaluate its effectiveness in identifying patterns of behavior that may indicate group-scale precursors.
(2) Algorithm 2 (GMM): The Gaussian Mixture Model uses probability values to express the affiliation between a sample and clusters. The GMM is particularly effective in identifying clusters that exhibit different variances and covariances, making it well-suited for identifying complex relationships among flight data variables. In the GMM, each sample point is assigned a probabilistic affiliation with clusters based on the posterior probability of the sample’s membership in each cluster. The number of clusters is determined using the Bayesian Information Criterion (BIC).
(3) Algorithm 3 (DBSCAN): DBSCAN is a popular clustering algorithm that is widely used in aviation research to detect potential safety events [18]. It works by identifying regions of high density in the data using a user-defined radius (eps ) and a minimum number of points required to form a cluster (min_samples ). Data points that are not part of any cluster are considered noise points. In our experiment, we use the Euclidean distance measure to test the performance of the Isolation Kernel-Based Dissimilarity (IKD) technique in identifying potential adverse events. We also analyze the sensitivity of the algorithm to and to better understand the process of identifying group-scale precursors.
To determine the number of clusters for Algorithms 1 and 2, the elbow method and BIC were utilized. For Algorithm 3, the radius and the minimum sample number were selected based on a 5% anomaly detection rate. In addition, the hyperparameters of CMCA were determined with the optimization goal .
The clustering results of the baseline algorithms and CMCA are presented in Figure 7. Specifically, we reduced the high-dimensional flight data to two dimensions (named Embedding1 and Embedding2) using t-SNE for better presentation while preserving as many of the pairwise similarities between the data points as possible. The axes correspond to the values of the two features extracted through t-SNE.
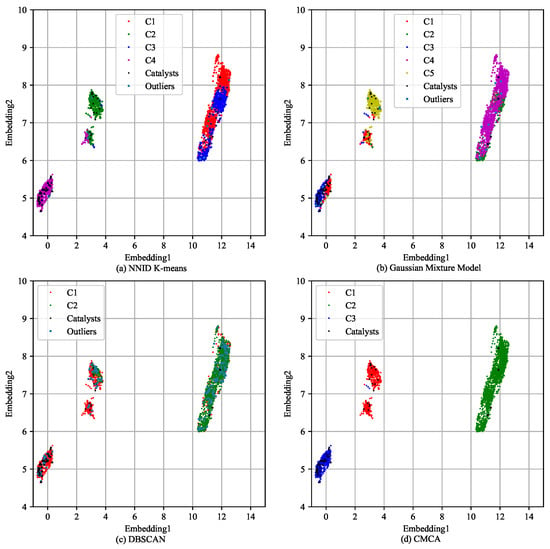
Figure 7.
Clustering results of the comparative experiments in a 2-dimensional space.
The different clusters are indicated by different colored dots and the black pentagons indicate the catalyst flights. Figure 7a–d correspond to the clustering results obtained using Algorithms 1–3 and CMCA. As shown in Figure 7, Algorithms 1 and 2 produced 4 and 5 clusters, respectively, but the cluster boundaries shown in Figure 7a,b are fuzzy and difficult to interpret. In addition, Algorithm 3 identified two clusters, C1 marked in red and C2 marked in green, that were less clearly separated, whereas CMCA detected three distinct clusters with obvious boundaries.
By leveraging the catalyst flights, the labels of the catalysts were propagated to the unlabeled flights within their respective clusters. Flights in C1 were labeled as precursors of low-energy approaches, whereas flights in C3 were labeled as precursors of high-energy approaches. The results were further confirmed by comparing the average specific total energy values of C1 and C3, which were, respectively, 5.83% lower and 10.93% higher than those of C2 at 1000 ft above touchdown.
Of particular interest is that most of the low-energy catalytic flights were clustered in C1 and most of the high-energy catalytic flights were clustered in C3, as shown in Figure 7d. Specifically, 17 flights classified as having low-energy approaches were assigned to C1 and 32 flights classified as having high-energy approaches were assigned to C3. These findings highlight the potential of CMCA for detecting and predicting safety events in flight data and showcase its potential impact on aviation safety research and practice. It is worth mentioning that by incorporating the characteristics of other flight stages, selecting the appropriate features, and constructing an applicable , this method can be easily extended to other flight phases.
To better validate the clustering quality of CMCA, a statistical analysis of the of each cluster was carried out. The statistical results of the algorithms mentioned above are shown in Figure 8.
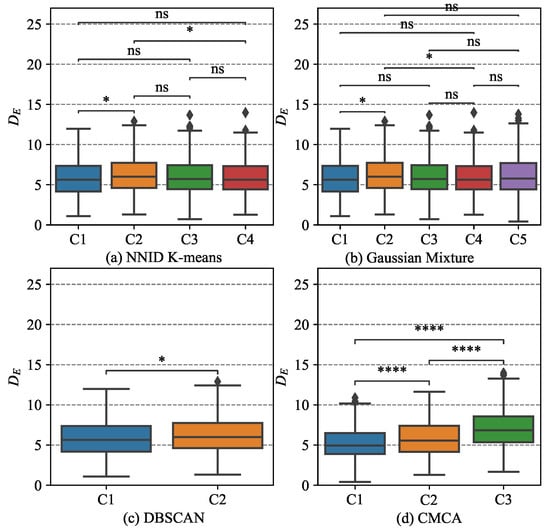
Figure 8.
Statistical analysis of on the clustering results. Where the symbols * (p < 0.05) and **** (p < 0.00) indicate that the differences between the clusters were significant, whereas indicates that they were not.
As shown in Figure 8, the results reveal that the three clusters identified by CMCA exhibited significant differences (p < 0.00) in terms of , indicating that they may correspond to different levels of performance during approach. As for the other methods, it is evident from Figure 8a that only the indices between C1 and C2, and C2 and C4 demonstrated significant differences (p < 0.05) in performance during approach according to further non-parametric Mann–Whitney testing. This implies that other clusters could not be distinguished based on performance during approach. Similarly, only the differences between C1 and C2 and C2 and C4 were remarkable, which can be seen in Figure 8b. As seen in Figure 8c, although the two clusters in Algorithm 3 differed, the substantial data imbalance between C1 (3357) and C2 (101) significantly influenced the test results. These findings suggest that CMCA can provide reliable insights into the safety implications of different flight states and can be a valuable tool for identifying group-scale precursor issues.
To further analyze the influence of the hyperparameters, a sensitivity analysis of Algorithm 3 and CMCA was carried out, and the results are shown in Figure 9, where the horizontal axis represents the value of and the vertical axis represents the number of clusters corresponding to a certain and . The number of flights in the top four clusters and the outliers are shown in Table 1.
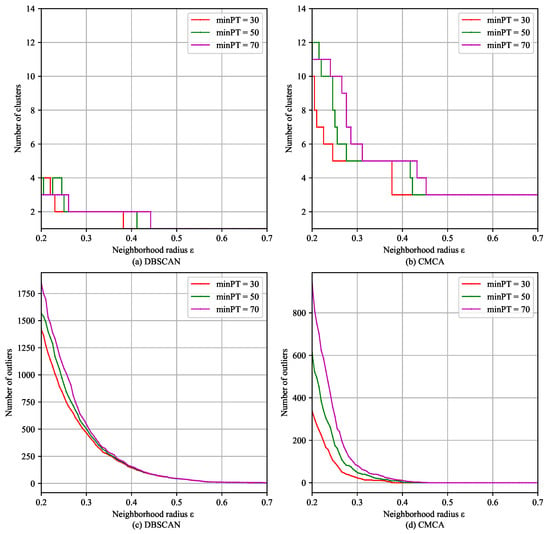
Figure 9.
Sensitivity of DBSCAN and CMCA to and .

Table 1.
The number of flights within clusters.
It can be observed in Figure 9 and Table 1 that adjusting had little effect on the number of outliers and clusters identified by Algorithm 3 and CMCA. As gradually increased, both methods identified fewer clusters and detected fewer outliers. The main difference was that Algorithm 3 could identify up to 4 clusters and CMCA could identify up to 12 clusters. When the number of clusters was stable, the number of outliers continued to vary for Algorithm 3, whereas for CMCA, both the number of clusters and outliers tended to stabilize when was around 0.4. Furthermore, CMCA outperformed the other methods in identifying smaller clusters, likely due to the unique sensitivity of the number of clusters identified by Isolation Kernel Dissimilarity to .
4. Discussion
The findings demonstrate that the proposed CMCA method is highly effective in identifying group-scale precursors, particularly for flights that experience abnormal energy management during approach. In this section, the unique features that make CMCA effective are discussed, including its ability to detect minor differences between clusters. Another critical characteristic of CMCA is that the hyperparameters are fine-tuned using the composite entropy-energy dissipation index, which is developed specifically for the approach phase using domain knowledge. Finally, CMCA is designed to produce easy-to-interpret clustering results, which can help stakeholders make informed decisions quickly based on the safety implications associated with each cluster.
4.1. Advantages of CMCA
Adopting energy metrics in aircraft can help detect abnormal patterns, such as high- and low-energy approaches, by analyzing raw variables, which are often related to safety incidents [37]. Consistent with these results, we found that 90% of flights exhibited variables such as airspeed that were associated with risky flight behavior. Unlike other techniques used to detect outliers [14,18] and individual flight precursors [5], our experiments show that CMCA can identify group-scale precursors with similar risks in energy management. This may be due to the sensitivity provided by IKD, which increases the distance between nominal flights and those with precursors, resulting in more compact clusters. With more compact clusters, the number of clusters becomes more sensitive to the hyperparameters. In addition, based on the sensitivity analysis of the cluster number to , clustering using IKD may primarily merge or split clusters when adjusting the hyperparameters. Explaining and verifying these hypotheses may be the goals of future studies.
Tuning the hyperparameters is a crucial aspect of discovering precursory flights in aviation safety research. To determine the appropriate hyperparameters, the BIC criterion, elbow curve criterion, and anomaly detection rate [18,19,22,23] are often utilized. Although these methods have been proven to be effective in aviation safety research, it has been suggested that the clusters obtained using these criteria do not show noticeable differences, as shown in Figure A3, Figure A4 and Figure A5. Through our experiments, we found that using resulted in certain parameters that deviated significantly for most flights, as shown in Figure A2, which is consistent with previous research on safety incidents [37]. Therefore, we conclude that using can help identify clusters with significant differences in energy states. Although the captured risks of precursor flights may vary, the underlying mechanisms of these precursors can still be explored and better understood through statistical analysis.
4.2. Explanation Analysis of CMCA Results
Figure A2, Figure A3, Figure A4 and Figure A5 illustrate the results obtained from CMCA and Algorithms 1–3. In CMCA, the orange area represents the data distribution of 90% of the cluster, and the red line represents the average value. The light-blue area represents 90% of the total data, and the dark-blue line depicts the mean value. In addition, the horizontal axis depicts the distance from landing.
By comparing the results from CMCA with those from NNID K-means, GMM, and DBSCAN [18,24], it is evident that CMCA can provide a more intuitive understanding of SMEs. To further illustrate the explainability of the results from CMCA, we use the pilots’ operation during approach as an example. Pilots in C2 had a moderate workload with . The crew adjusted the aircraft configuration at 8 nm, gradually pulled up to further decrease speed, set the flap at 15 degrees, and increased engine thrust to maintain airspeed. Finally, they set the flap to 20 degrees at 1 nm to further reduce energy. In contrast, pilots in C1 had a more significant workload, as they operated more frequently from 9 nm, resulting in a , which was 10.91% lower than in C2. Flights in C1 had lower-than-average airspeed because the pilots reduced it in advance. To achieve a stable reduction in airspeed, they increased engine power at 8 nm and set the flap at 15 degrees earlier. Pilots in C3 conducted most of their operations after 4 nm and in a shorter time, with a , which was 23.64% higher than in C2, suggesting a weak energy-state awareness.
5. Conclusions
This study proposes a catalytic clustering-based precursor discovery method that combines labeled and unlabeled data to effectively identify group-scale precursors caused by pilot operation habits. The method addresses the limitation of traditional empirical adjustment-based anomaly or precursor discovery tools that rely on fixed threshold values, making it ideal for identifying subtle and cluster-wide precursor risks. The innovative contributions of this work are:
(1) Development of catalytic mass-based clustering that is sensitive to hyperparameters for identifying small clusters and propagating weak labels to unlabeled flights with similar risks in the same cluster for analysis.
(2) Construction of a composite entropy-energy dissipation index for the approach phase, which provides a criterion for adjusting the hyperparameters of the clustering algorithm and helps to identify clusters with different performances during approach.
In summary, the proposed CMCA method is a new approach to detecting group-scale precursors caused by pilot operation habits or training that provides SMEs with deeper insights into aircraft energy states during the approach phase. As a potential avenue for improvement of this study, further research could focus on exploring the internal distribution of group-scale precursors, including the likelihood of inducing anomalies and potential safety measures to minimize precursor risks. One promising direction could be to combine the precursor analysis tools for individual flights and conduct multi-stage potential risk analysis during the approach phase.
Author Contributions
Z.X. was responsible for writing the paper and conducting the experiments; Z.G. was the research director; J.L. was responsible for analyzing the results; Y.Z. was responsible for the data processing. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the National Natural Science Foundation of China (52272351).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Restrictions apply to the availability of these data. Data were obtained from the China Academy of Civil Aviation Science and Technology and are available from the authors with the permission of the China Academy of Civil Aviation Science and Technology.
Acknowledgments
The authors would like to thank the reviewers and the editors for their valuable comments and constructive suggestions that helped to improve the paper significantly. The authors acknowledge the flight data provided by the China Academy of Civil Aviation Science and Technology.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| FOQA | Flight Operation Quality Assurance |
| CMCA | Catalyst Mass-Based Cluster Analysis |
| nLCS | Longest Common Subsequence |
| VAR | Vector Autoregressive |
| VARX | Vector Autoregressive Process with Exogenous Variable |
| NASA | National Aeronautics and Space Administration |
| MKAD | Multiple Kernel Anomaly Detection |
| OC-SVM | One Class-Support Vector Machine |
| IMS | Inductive Monitoring System |
| HDBSCAN | Hierarchical Density-Based Spatial Clustering of Applications with Noise |
| DBSCAN | Density-Based Spatial Clustering of Applications with Noise |
| GMM | Gaussian Mixture Model |
| AD | Anomaly Detection |
| MIC | Maximal Information Coefficient |
| SAX | Symbolic Aggregate Approximation |
| IKD | Isolation Kernel-Based Dissimilarity |
| BIC | Bayesian Information Criterion |
Appendix A
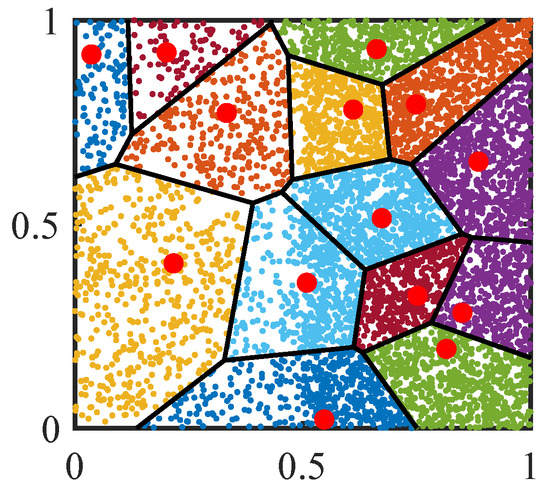
Figure A1.
Space partitions of isolation kernel.
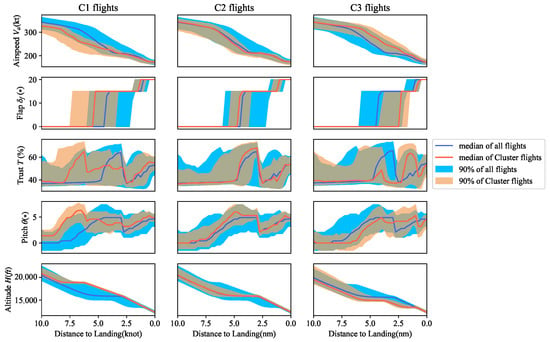
Figure A2.
Distributions of airspeed, flap, thrust, pitch, and altitude in 3 clusters using CMCA.
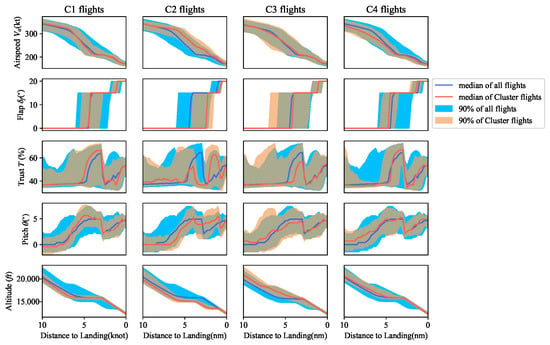
Figure A3.
Flight parameter analysis of clusters using the NNID K-means method.
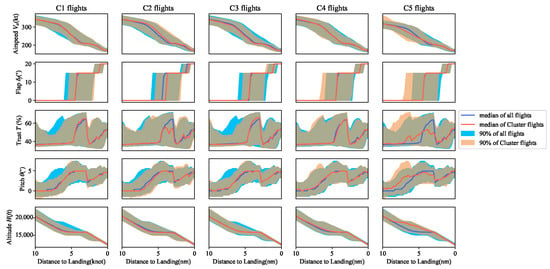
Figure A4.
Flight parameter analysis of clusters using the GMM method.
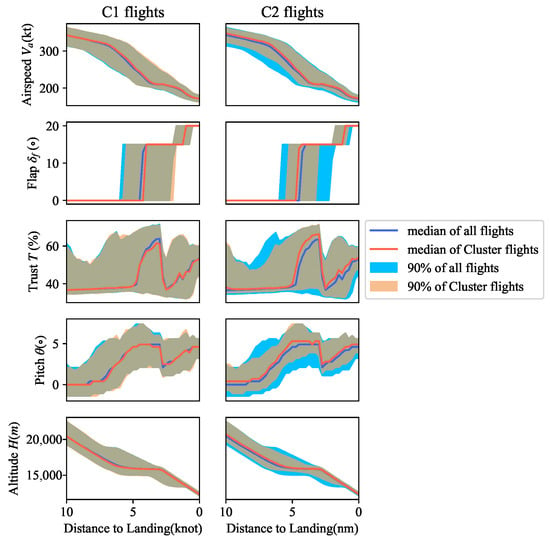
Figure A5.
Flight parameter analysis of clusters using the DBSCAN method.
References
- Ackley, J.L.; Puranik, T.G.; Mavris, D.N. A supervised learning approach for safety event precursor identification in commercial aviation. In Proceedings of the AIAA Aviation 2020 Forum, Virtual Conference, 15–19 June 2020. [Google Scholar]
- FAA. Out Front on Airline Safety: Two Decades of Continuous Evolution. Available online: https://www.faa.gov/newsroom/out-front-airline-safety-two-decades-continuous-evolution (accessed on 14 May 2023).
- IATA. World Air Transportation Statistics; Plus Edition; IATA: Montreal, QC, Canada, 2021. [Google Scholar]
- Puranik, T.G.; Mavris, D.N. Identification of instantaneous anomalies in general aviation operations using energy metrics. J. Aerosp. Inf. Syst. 2019, 17, 51–65. [Google Scholar] [CrossRef]
- Janakiraman, V.M. Explaining aviation safety incidents using deep temporal multiple instance learning. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, London, UK, 19–23 August 2018. [Google Scholar]
- Bleu-Laine, M.; Puranik, T.G.; Carman, M.; Mavris, D.N.; Matthews, B. Predicting adverse events and their precursors in aviation using multi-class multiple-instance learnin. In Proceedings of the AIAA Scitech 2021 Forum, Virtual Event, 11–21 January 2021. [Google Scholar]
- Badri, A.; Boudreau-Trudel, B.; Souissi, A.S. Occupational health and safety in the Industry 4.0 era: A cause for major concern? Saf. Sci. 2018, 109, 403–411. [Google Scholar] [CrossRef]
- Memarzadeh, M.; Matthews, B.; Avrekh, I. Unsupervised anomaly detection in flight data using convolutional variational auto-encoder. Aerospace 2020, 7, 115. [Google Scholar] [CrossRef]
- Memarzadeh, M.; Asanjan, A.A.; Matthews, B. Robust and Explainable Semi-Supervised Deep Learning Model for Anomaly Detection in Aviation. Aerospace 2022, 9, 437. [Google Scholar] [CrossRef]
- Madeira, T.; Melicio, R.; Valério, D.; Santos, L. Machine Learning and Natural Language Processing for Prediction of Human Factors in Aviation Incident Reports. Aerospace 2021, 8, 47. [Google Scholar] [CrossRef]
- Nogueira, R.P.R.; Melicio, R.; Valério, D.; Santos, L. Learning Methods and Predictive Modeling to Identify Failure by Human Factors in the Aviation Industry. Appl. Sci. 2023, 13, 4069. [Google Scholar] [CrossRef]
- Kumar, S.G.; Corrado, S.J.; Puranik, T.G.; Mavris, D.N. Classification and Analysis of Go-Arounds in Commercial Aviation Using ADS-B Data. Aerospace 2021, 8, 291. [Google Scholar] [CrossRef]
- Das, S.; Matthews, B.; Srivastava, A.N.; Ozca, N.C. Multiple kernel learning for heterogeneous anomaly detection: Algorithm and aviation safety case study. In Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 25–28 July 2010. [Google Scholar]
- Iverson, D.L.; Martin, R.; Schwabacher, M.; Spirkovska, L.; Taylor, W.; Mackey, R.; Castle, J.P. General purpose data-driven system monitoring for space operations. J. Aerosp. Comput. Inf. Commun. 2012, 9, 26–44. [Google Scholar] [CrossRef]
- Rose, R.L.; Puranik, T.G.; Mavris, D.N. Natural Language Processing Based Method for Clustering and Analysis of Aviation Safety Narratives. Aerospace 2020, 7, 143. [Google Scholar] [CrossRef]
- Zhang, X.C. Data Clustering; Science Press: Beijing, China, 2017; pp. 68–86. [Google Scholar]
- Angadi, B.M.; Kakkasageri, M.S.; Manvi, S.S. Recent Trends in Computational Intelligence Enabled Research; Academic Press: New York, NY, USA, 2021; pp. 23–40. [Google Scholar]
- Li, L.; Das, S.; Hansman, R.J.; Palacios, R.; Srivastava, A.N. Analysis of flight data using clustering techniques for detecting abnormal operations. J. Aerosp. Inf. Syst. 2015, 12, 587–598. [Google Scholar] [CrossRef]
- Oehling, J.; Barry, D.J. Using machine learning methods in airline flight data monitoring to generate new operational safety knowledge from existing data. Saf. Sci. 2019, 114, 89–104. [Google Scholar] [CrossRef]
- Memarzadeh, M.; Matthews, B.; Templin, T. Multi-class anomaly detection in flight data using semi-supervised explainable deep learning model. J. Aerosp. Inf. Syst. 2021, 19, 83–97. [Google Scholar]
- Basora, L.; Olive, X.; Dubot, T. Recent advances in anomaly detection methods applied to aviation. Aerospace 2019, 6, 117. [Google Scholar] [CrossRef]
- Cokorilo, O.; Luca, M.D.; Dell’Acqua, G. Aircraft safety analysis using clustering algorithms. J. Risk Res. 2014, 17, 1325–1340. [Google Scholar] [CrossRef]
- Sheridan, K.; Puranik, T.G.; Mangortey, E.; Pinon, O.; Kirby, M.; Mavris, D.M. An application of DBSCAN clustering for flight anomaly detection during the approach phase. In Proceedings of the AIAA SciTech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Zhao, W.; Li, L.; Alam, S.; Wang, Y. An incremental clustering method for anomaly detection in flight data. Transp. Res. Part C Emerg. Technol. 2021, 132, 103406. [Google Scholar] [CrossRef]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef]
- Wang, L.; Wu, C.; Sun, R. An analysis of flight Quick Access Recorder(QAR) data and its applications in preventing landing incidents. Reliab. Eng. Syst. Saf. 2014, 127, 86–96. [Google Scholar] [CrossRef]
- Wang, L.; Ren, Y.; Wu, C. Effects of flare operation on landing safety: A study based on ANOVA of real flight data. Saf. Sci. 2018, 102, 14–25. [Google Scholar] [CrossRef]
- Budalakoti, S.; Srivastava, A.N.; Otey, M.E. Anomaly detection and diagnosis algorithms for discrete symbol sequences with applications to airline safety. IEEE Trans. Syst. Man Cybern. Part C 2009, 39, 101–113. [Google Scholar] [CrossRef]
- Melnyk, I.; Matthews, B.; Valizadegan, H. Semi-Markov switching vector autoregressive model-based anomaly detection in aviation systems. In Proceedings of the 22th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Ting, K.M.; Washio, T.; Zhu, Y.; Xu, Y. Breaking the curse of dimensionality with Isolation Kernel. arXiv 2021, arXiv:2109.14198. [Google Scholar]
- Khalastchi, E.; Kalech, M.; Kaminka, G.A. Online data-driven anomaly detection in autonomous robots. Knowl. Inf. Syst. 2015, 43, 657–688. [Google Scholar] [CrossRef]
- Aryal, S.; Ting, K.M.; Washio, T.; Haffari, G. Data-dependent dissimilarity measure: An effective alternative to geometric distance measures. Knowl. Inf. Syst. 2017, 53, 479–506. [Google Scholar] [CrossRef]
- Andreeva, O.; Li, W.; Ding, W.; Kuijjer, M.; Quackenbush, J.; Chen, P. Catalysis clustering with GAN by incorporating domain knowledge. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Virtual Conference, 23–27 August 2020. [Google Scholar]
- Ting, K.M.; Xu, B.C.; Washio, T.; Zhou, Z.H. Isolation distributional kernel: A new tool for kernel based anomaly detection. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Virtual Conference, 23–27 August 2020. [Google Scholar]
- Qin, X.; Ting, K.M.; Zhu, Y.; Lee, V.C. Nearest-neighbour-induced isolation similarity and its impact on density-based clustering. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019. [Google Scholar]
- Ting, K.M.; Zhu, Y.; Carman, M.; Zhu, Y.; Zhou, Z.H. Overcoming key weaknesses of distance-based neighbourhood methods using a data dependent dissimilarity measure. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Puranik, T.P.; Jimenez, H.; Mavris, D.N. Energy-Based Metrics for Safety Analysis of General Aviation Operations. J. Aircr. 2017, 54, 2285–2297. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).