Buckling Analysis and Structure Improvement for the Afterburner Cylinder of an Aero-Engine
Abstract
1. Introduction
2. Buckling Theory
3. Buckling Analysis of the Afterburner Cylinder
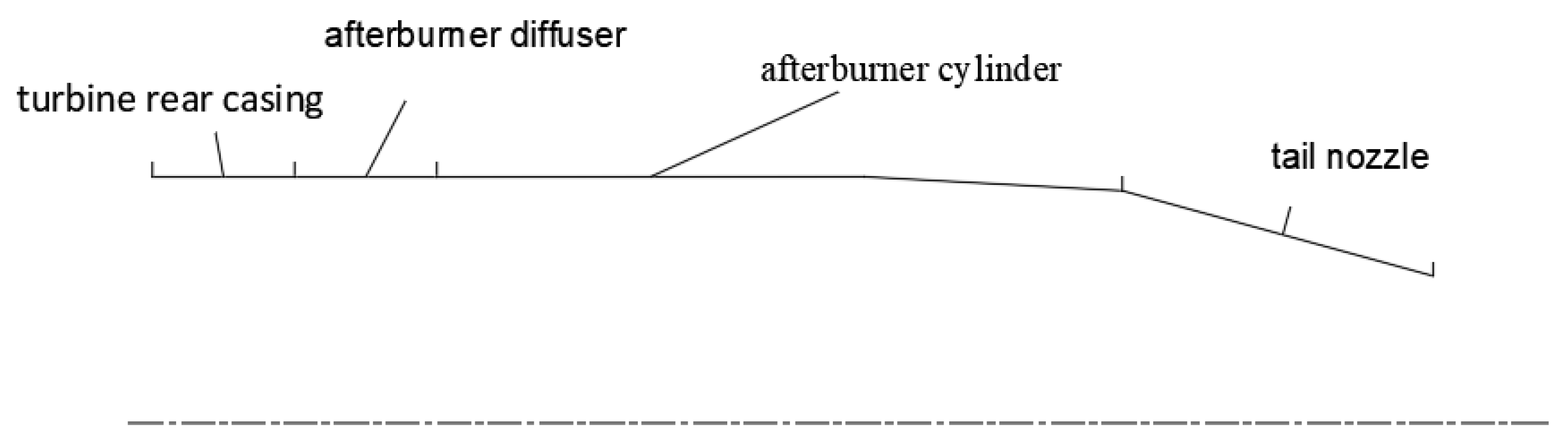
3.1. Structure and Loads
3.1.1. Structure Description
3.1.2. The Loads
3.2. The Buckling Analysis of the Afterburner Cylinder
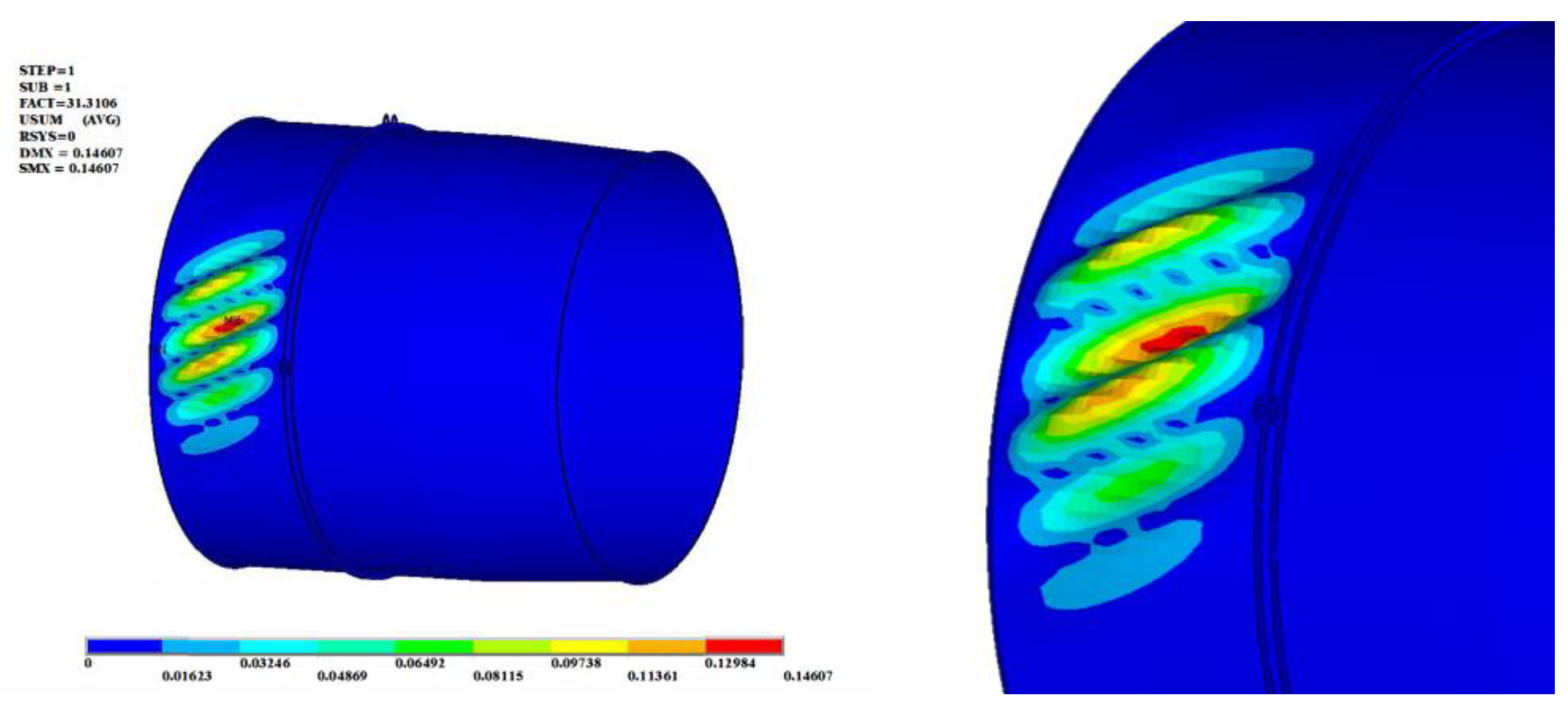
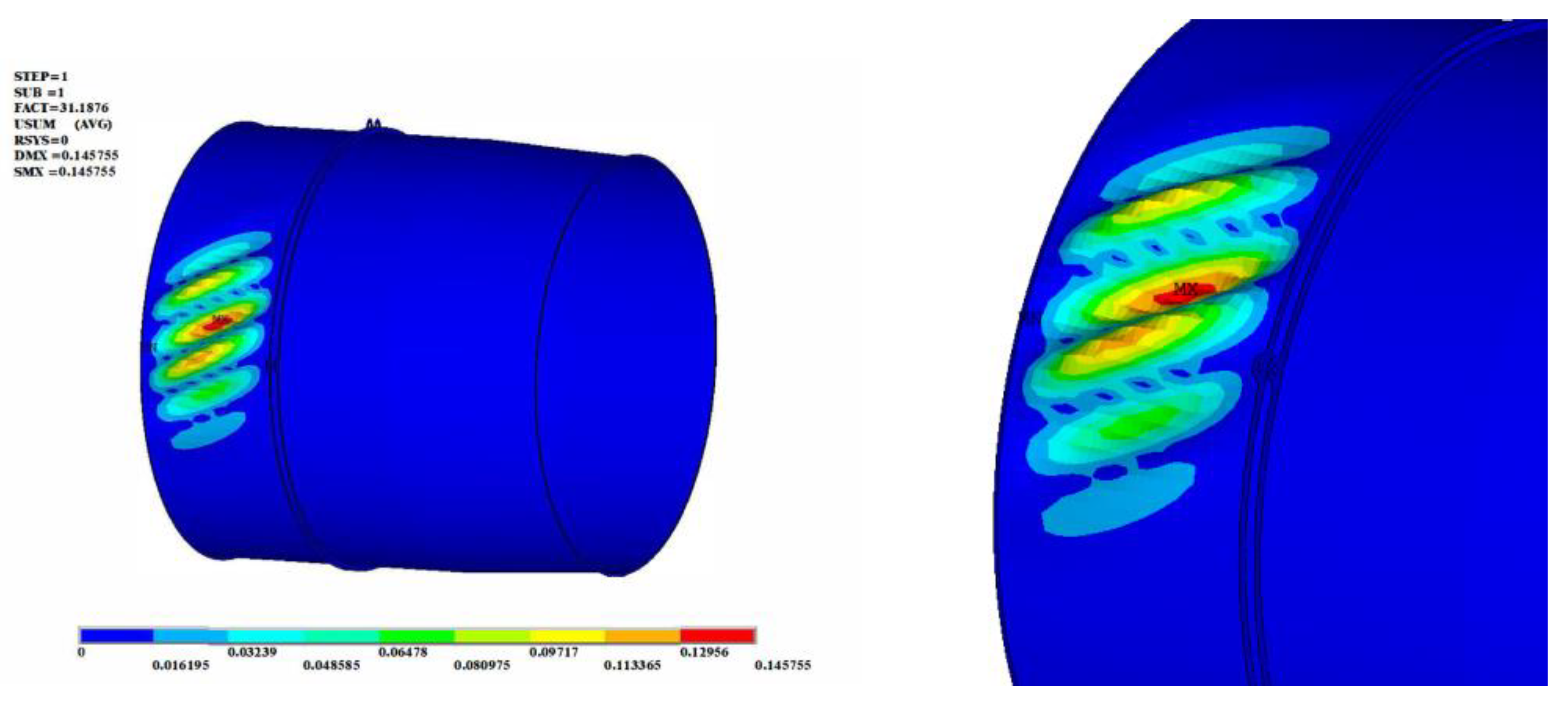
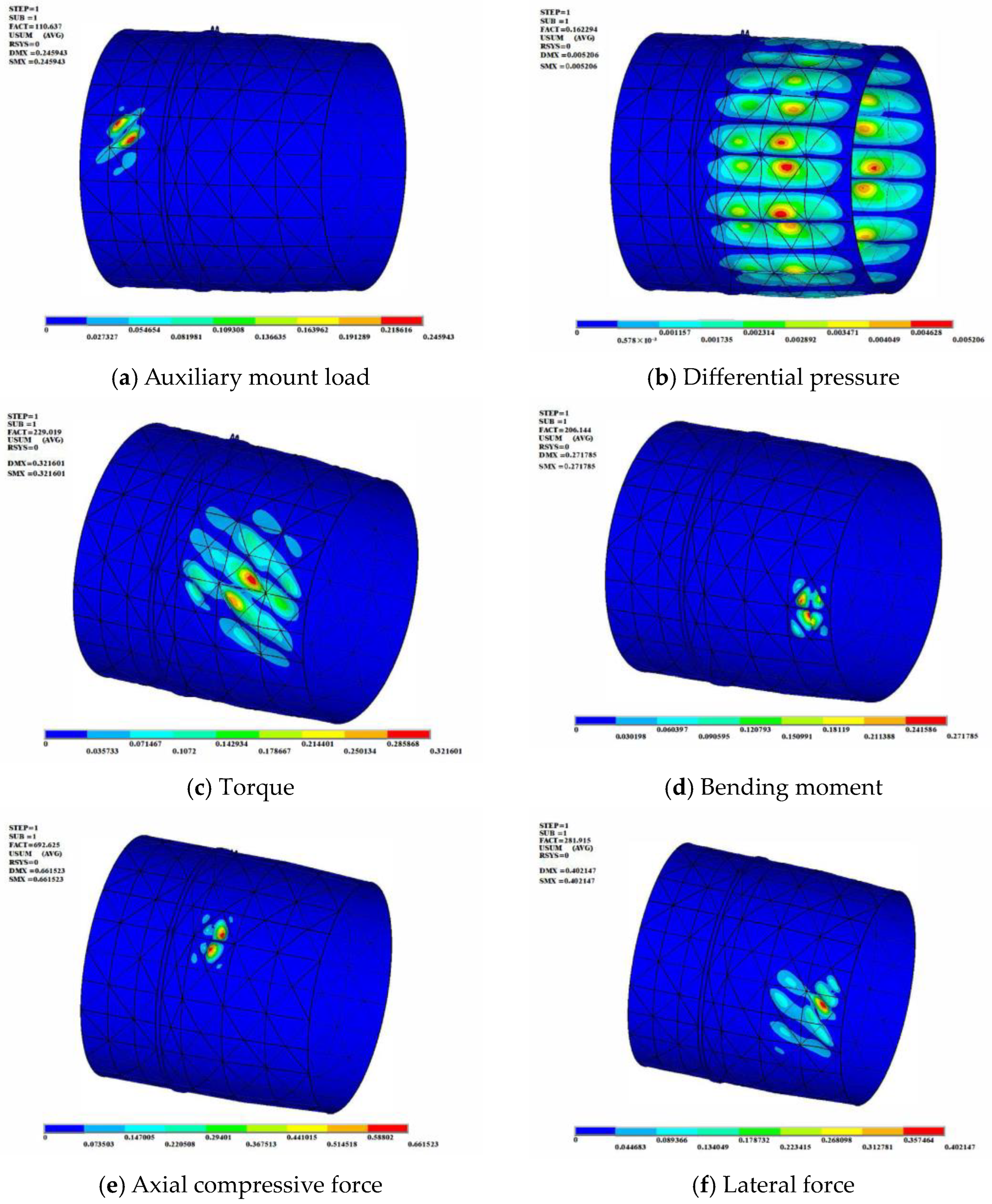
3.2.1. The Buckling Analysis under Auxiliary Mount Loads
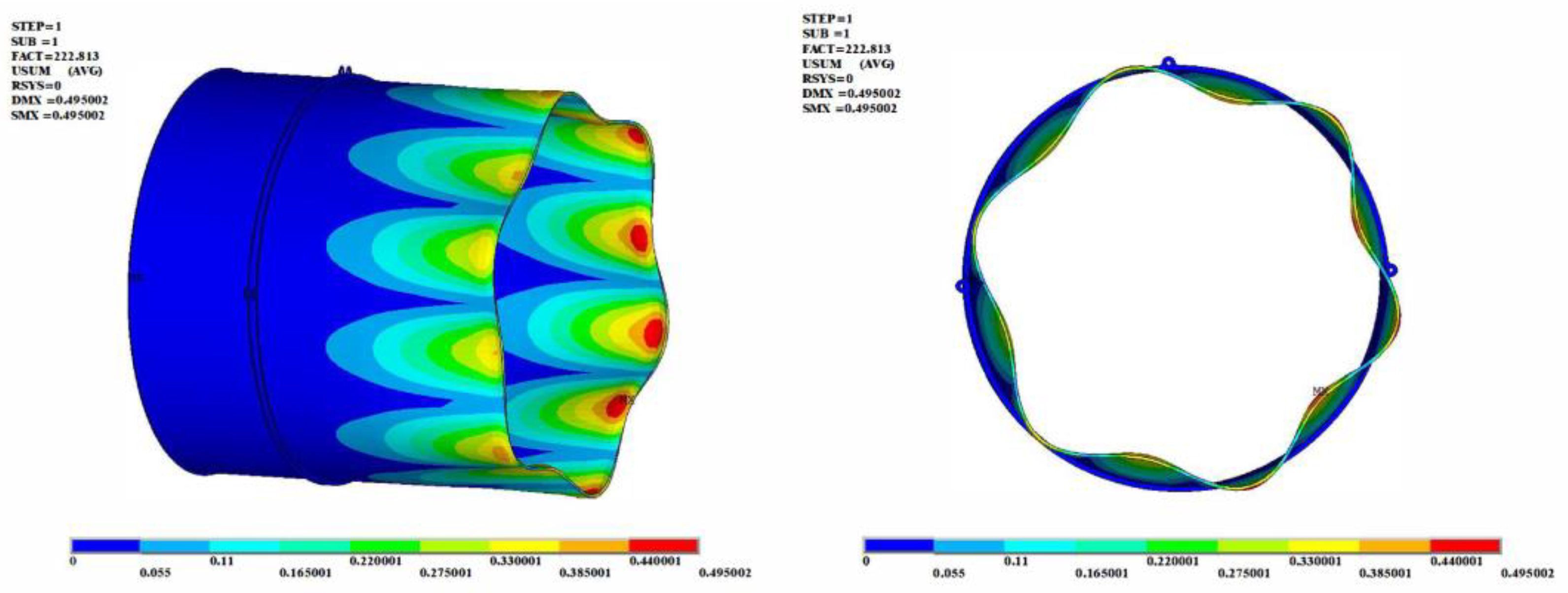
3.2.2. Buckling Analysis under Loads of the Rear Flange
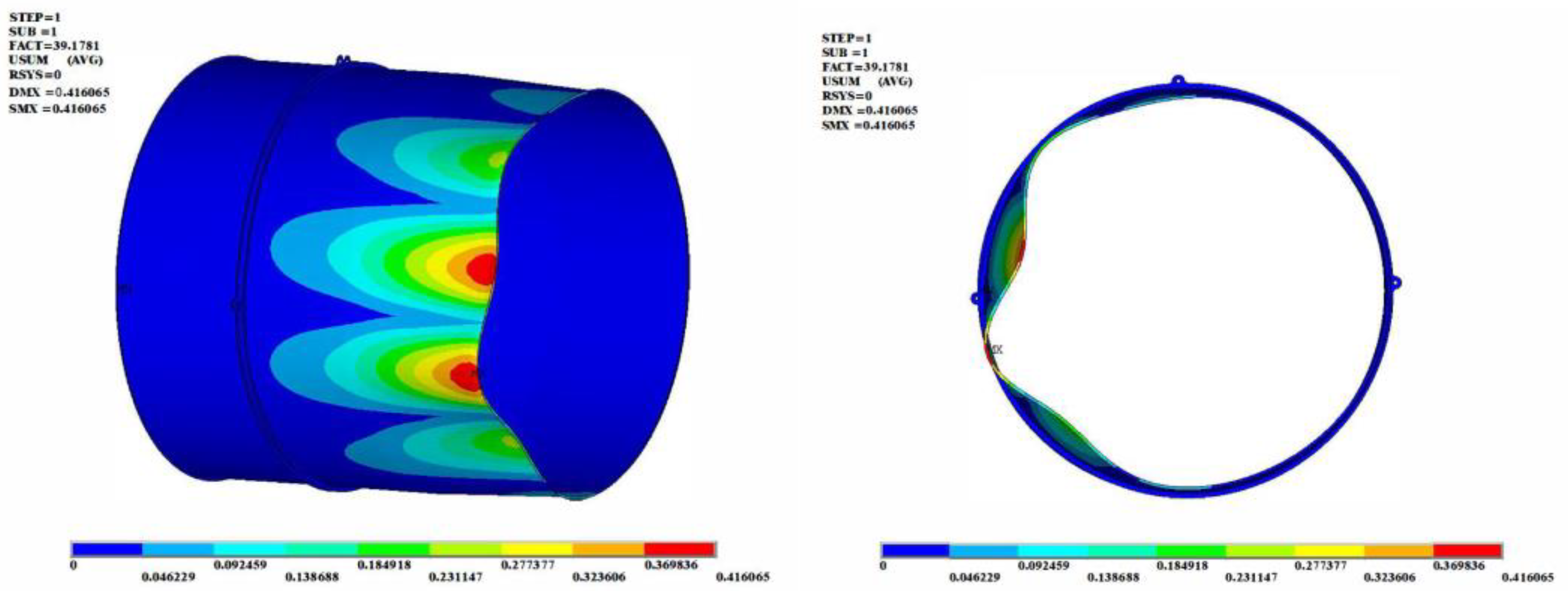
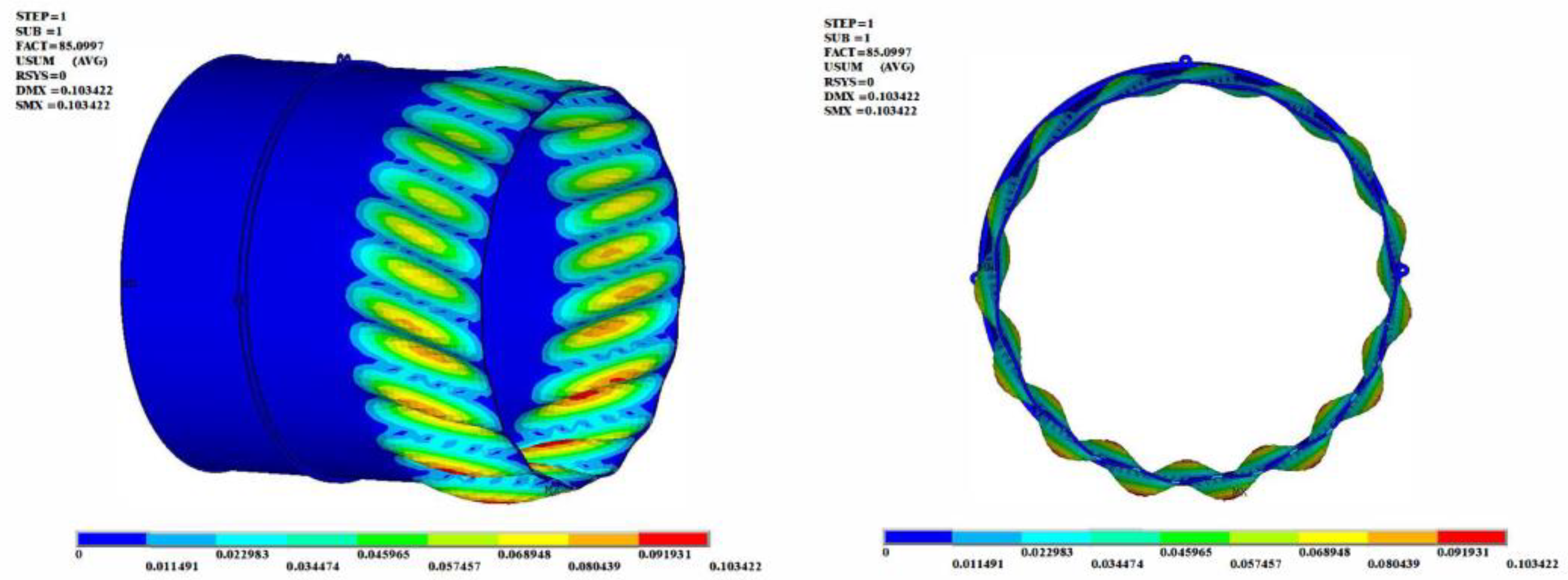
- Under the loads of the axial compressive force or torque, the buckling modes of the afterburner cylinder showed a regular wavy distribution, with an axial half-wave number of n = 1. The circumferential wave number was dense under the load of the torque, with a wave number of m = 15, but under the axial compressive force, the circumferential wave number was m = 6.
- Under the load of the axial compressive force, the critical buckling load of the cylinder was 222.8 kN. The load value was relatively small, compared to the axial load at the flange, indicating that the cylinder was prone to buckling under the axial compressive force of the rear flange.
- Under the load of the lateral force, the critical buckling load was 39.2 kN. This load value was also small, which indicated the cylinder was prone to buckling.
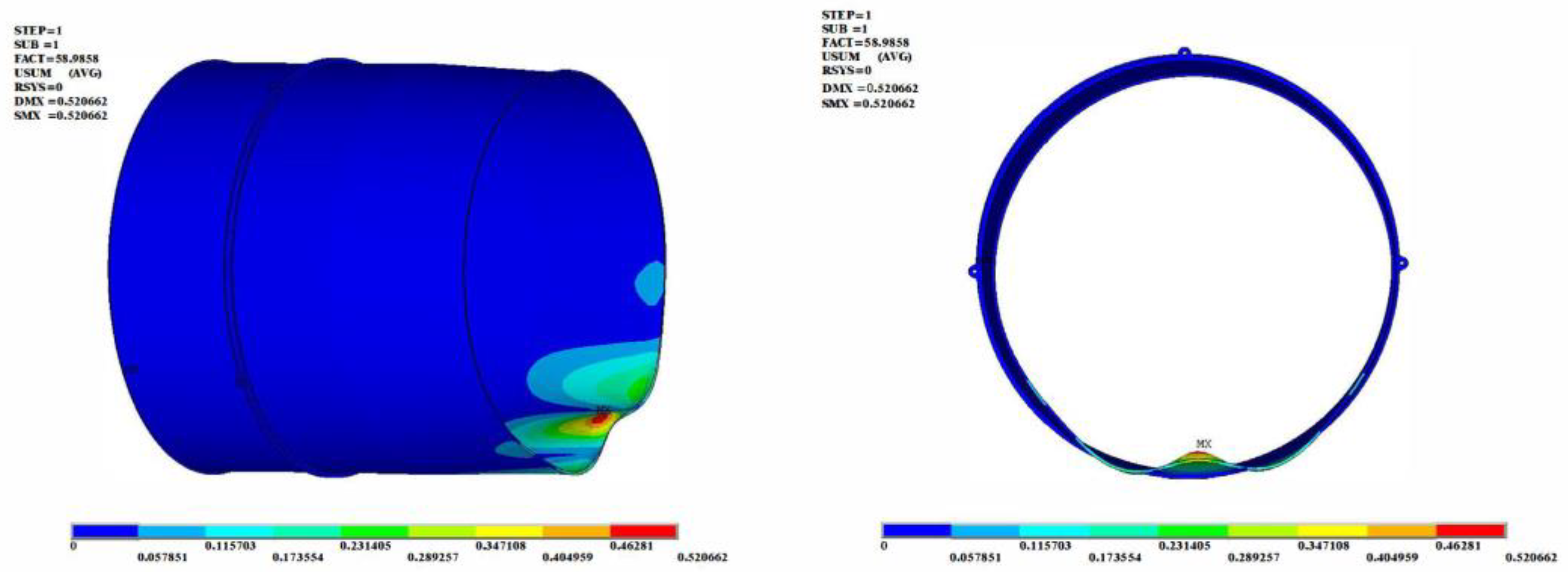
- Buckling only occurred near the rear flange under the load of the bending moment or the lateral force, and the buckling deformation was closely related to the direction of the loads.
- The buckling occurred in the rear section of the cylinder under various loads of the rear flange.
3.2.3. Buckling Analysis under Differential Pressure
3.3. Buckling Analysis and Summary
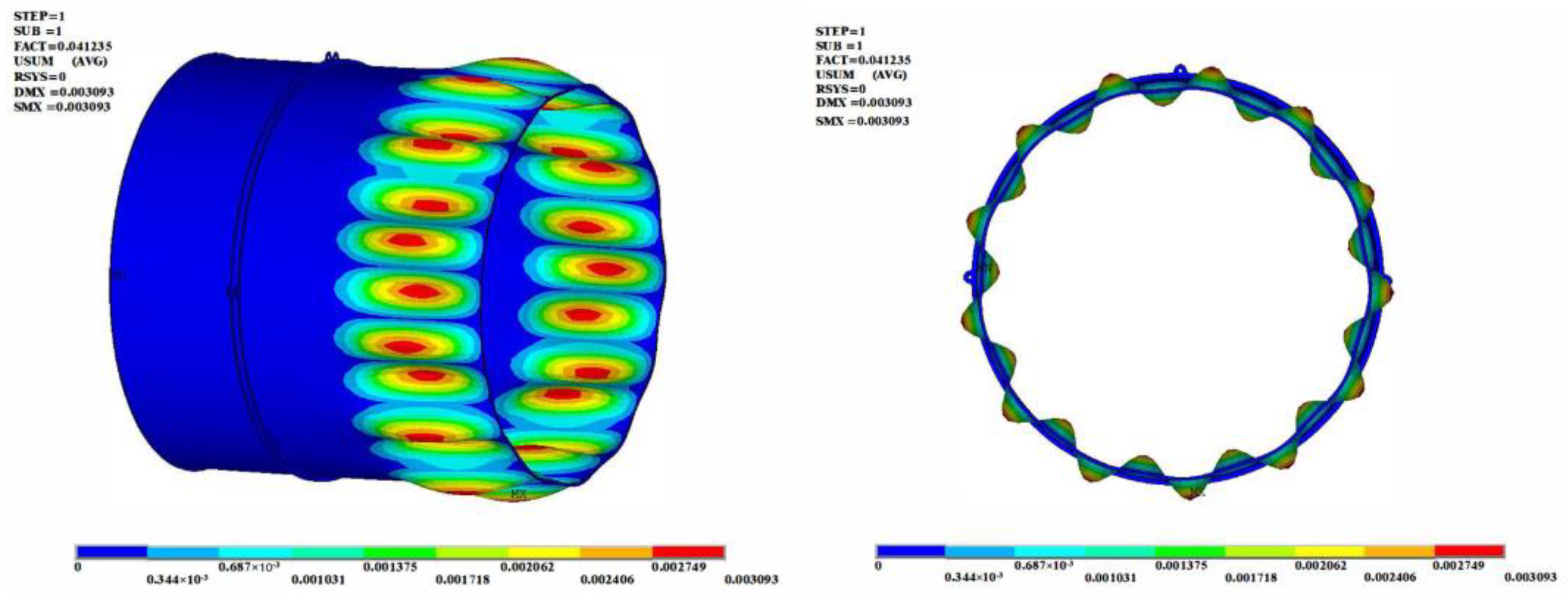
- Under the load of a single auxiliary mount, local buckling occurred in the front section of the cylinder corresponding to the location of the load, with buckling displacement distributed along the oblique direction. The buckling was caused by the torque generated by the load of the mount in the front section of the cylinder.
- Under the loads of the auxiliary mounts on both the left and right sides, the casing would still occur buckling. If the loads on both sides were equal, buckling would occur randomly in the front cylinder corresponding to one side of the mount. If the loads on both sides were not equal, buckling would occur in the cylinder corresponding to the larger load of the mount.
- Under the loads of one or two auxiliary mounts, the critical buckling load of the afterburner cylinder was very close.
- Under the loads of the rear flange, buckling occurred near the rear flange, and buckling mode was closely related to the load form.
- Under the loads of axial compressive force or torque on the rear flange, the buckling displacement of the cylinder showed a regular wave distribution, with an axial half-wave number of n = 1. The circumferential wave number under the load of the torque was much bigger than that under the load of the axial compressive force.
- Under the load of the bending moment or the lateral force on the rear flange, buckling only occurred in the local casing near the rear flange, with buckling deformation closely related to the direction of the load.
- The buckling of the afterburner cylinder was highly likely to occur under external pressure bigger than the internal pressure or under axial compressive force.
4. Improvement and Discussion
4.1. Cylinder Wall-Thickening Scheme
- The critical buckling load increased linearly as the wall thickness increased under all loads.
- Under the load of the torque or the auxiliary mount, increasing the wall thickness of the cylinder resulted in a relatively higher increase in the critical buckling load.
- Under the load of differential pressure or lateral force, increasing the wall thickness of the cylinder resulted in a relatively smaller increase in the critical buckling load.
4.2. Grille Reinforcement Scheme
- Under the loading conditions of the auxiliary mount or differential pressure, the buckling mode remained largely consistent with the original design, while the critical buckling load increased significantly.
- Under various rear flange loading conditions, the buckling modes of the reinforced cylinder exhibited considerable deviation from the original design. The critical buckling loads increased by 169% to 619%, signifying a substantial enhancement in the structure’s load-bearing capacity.
4.3. Discussion
- Compared with the original scheme, the wall-thickening scheme could not alter the buckling mode of the cylinder. As the wall thickness increased, the critical buckling load under all loading conditions exhibited a linear growth. With a 0.3 mm increase in wall thickness, the critical buckling load increased by 17.86% to 66.4%, but the increase in wall thickness would result in a significant increase in structural weight, which would affect the engine’s thrust-to-weight ratio.
- For the grille reinforcement scheme, the buckling modes under the auxiliary mount load and the differential pressure load remained similar to the original scheme. However, the buckling modes under the rear flange loads exhibited substantial differences, compared to the original design. Under various loading conditions, the critical buckling load of the cylinder increased by 169% to 619%, with a more significant increase in critical buckling load compared to the wall-thickening approach.
5. Conclusions
- Under the auxiliary mount load, buckling occurred in the front section of the cylinder corresponding to the mount load, manifesting as local buckling. Under the load of the auxiliary mounts on the left and right sides, buckling occurred in the front cylinder section corresponding to the loading of the one-side mount.
- Under the load of differential pressure (external pressure exceeding internal pressure) or the axial compressive force of the rear flange, the afterburner cylinder was highly susceptible to buckling.
- Under various rear flange loads, buckling deformation occurred near the rear flange. Under axial compressive force or torque, the buckling mode of the cylinder exhibited a regular wavy distribution. Under bending moment or lateral force, buckling occurred only in the local cylinder area near the rear flange, with the buckling deformation being closely related to the direction of the load application.
- Regarding the wall-thickening scheme, the buckling mode remained unchanged. As the wall thickness increased, the critical buckling load under all loading conditions grew linearly. An increase in the critical buckling load of 17.78% to 59.46% was observed when the wall thickness was augmented by 0.3 mm.
- For the grille reinforcement scheme, the buckling modes under the auxiliary mount load and differential pressure load were similar to the original design, but the buckling modes under the rear flange loads exhibited significant differences, compared to the original design. The critical buckling load increased by 169% to 619%, representing a substantial enhancement in load-bearing capacity.
- Although the wall thickness scheme could increase the critical buckling load and was relatively simple to implement, the increased wall thickness would result in a higher cylinder weight, negatively affecting the specific thrust-to-weight performance of the aero-engine. The grille reinforcement scheme effectively improved the rigidity and stability of the overall aero-engine while significantly increasing the critical buckling load. Therefore, the grille reinforcement scheme was deemed superior.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Blachut, J. Buckling of sharp knuckle torisphere under external pressure. Thin Walled Struct. 1998, 30, 55–77. [Google Scholar] [CrossRef]
- Lu, Z. Imperfection sensitivity of elastic and elastic-plastic torispherical pressure vessel heads. Thin Walled Struct. 1995, 23, 21–39. [Google Scholar] [CrossRef]
- Stanley, S.S., III. Buckling design studies of inverted, oblate bulkheads for a propellant tank. In Proceedings of the 43rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Denver, CO, USA, 22–25 April 2002. [Google Scholar]
- Corona, E. Dome reversal of metal beverage containers. J. Press. Vessel Technol. 1998, 120, 456–461. [Google Scholar] [CrossRef]
- Elishakoff, I. Probabilistic resolution of the twentieth century conundrum in elastic stability. Thin Walled Struct. 2012, 59, 35–57. [Google Scholar] [CrossRef]
- Einafshar, N.; Lezgy-Nazargah, M.; Beheshti-Aval, S.B. Buckling, post-buckling and geometrically nonlinear analysis of thin-walled beams using a hypothetical layered composite cross-sectional model. Acta Mech. 2021, 232, 2733–2750. [Google Scholar] [CrossRef]
- Li, X.F.; Lee, K.Y. Effects of engesser’s and haringx’s hypotheses on buckling of timoshenko and higher-order shear-deformable columns. J. Eng. Mech. 2018, 144, 04017150. [Google Scholar] [CrossRef]
- Yang, H.; Lo, S.H.; Sze, K.Y.; Leung, A.Y. Coupled static and dynamic buckling of thin walled beam by spline finite element. Thin Walled Struct. 2012, 60, 118–126. [Google Scholar] [CrossRef]
- He, B.; Zhang, Y.; Ge, W.Y.; An, Y.; Liu, D. Buckling analysis of thin-walled members with open-branched cross section via semi-analytical finite strip transfer matrix method. Thin Walled Struct. 2018, 124, 20–31. [Google Scholar] [CrossRef]
- Bourihane, O.; Ed-Dinari, A.; Braikat, B.; Jamal, M.; Mohri, F.; Damil, N. Stability analysis of thin-walled beams with open section subject to arbitrary loads. Thin Walled Struct. 2016, 105, 156–171. [Google Scholar] [CrossRef]
- Jiao, P.; Chen, Z.; Tang, X.; Su, W.; Wu, J. Design of axially loaded isotropic cylindrical shells using multiple perturbation load approach-Simulation and validation. Thin Walled Struct. 2018, 133, 1–16. [Google Scholar] [CrossRef]
- Vasilikis, D.; Karamanos, S. Closure to “more on mechanics of confined thin-walled cylinders subjected to external pressure”. Appl. Mech. Rev. 2014, 66, 010801. [Google Scholar] [CrossRef]
- Tafreshi, A. Buckling and post-buckling analysis of composite cylindrical shells with cutouts subjected to internal pressure and axial compression loads. Int. J. Press. Vessel. Pip. 2002, 79, 351–359. [Google Scholar] [CrossRef]
- Carvelli, V.; Panzeri, N.; Poggi, C. Buckling strength of GFRP under-water vehicles. Compos. Part B Eng. 2001, 32, 89–101. [Google Scholar] [CrossRef]
- Ouellette, P.; Hoa, S.V.; Sankar, T.S. Buckling of composite cylinders under external pressure. Polym. Compos. 1986, 7, 363–374. [Google Scholar] [CrossRef]
- Khot, N.S. Buckling and postbuckling behavior of composite cylindrical shells under axial compression. AIAA J. 1970, 8, 229–235. [Google Scholar] [CrossRef]
- Maali, M.; Bayrak, B.; Kiliç, M.; Sagiroglu, M.; Aydin, A.C. Buckling behavior of double-layered composite cylindrical shells. Int. J. Press. Vessel. Pip. 2021, 191, 104328. [Google Scholar] [CrossRef]
- Shen, K.C.; Yang, Z.Q.; Jiang, L.L.; Pan, G. Buckling and post-buckling behavior of perfect/perforated composite cylindrical shells under hydrostatic pressure. J. Mar. Sci. Eng. 2022, 10, 278. [Google Scholar] [CrossRef]
- Bin Kamarudin, M.N.; Mohamed Ali, J.S.; Aabid, A.; Ibrahim, Y.E. Buckling analysis of a thin-walled structure using finite element method and design of experiments. Aerospace 2022, 9, 541. [Google Scholar] [CrossRef]
- Zhang, G.; Zhu, H.; Wang, Q.; Zhang, X.; Ren, M.; Xue, S.; Li, G. Buckling analysis of thin-walled metal liner of cylindrical composite overwrapped pressure vessels with depressions after autofrettage processing. Sci. Eng. Compos. Mater. 2021, 28, 540–554. [Google Scholar] [CrossRef]
- Ehsani, A.; Rezaeepazhand, J. Stacking sequence optimization of laminated composite grid plates for maximum buckling load using genetic algorithm. Int. J. Mech. Sci. 2016, 119, 97–106. [Google Scholar] [CrossRef]
- Donnell, L.H. Effect of Imperfections on Buckling of Thin Cylinders Under External Pressure. J. Appl. Mech. 1956, 23, 569–575. [Google Scholar] [CrossRef]
- Karman, V.; Tsien, H.S. The buckling of thin cylinders under axial compression. J. Aeron Sci. 1941, 8, 303–312. [Google Scholar] [CrossRef]
- Argyridi, A.K.; Sapountzakis, E.J. Higher order beam theory for linear local buckling analysis. Eng. Struct. 2018, 177, 770–784. [Google Scholar] [CrossRef]
- Baiz, P.M.; Natarajan, S.; Rabczuk, T. Linear buckling analysis of cracked plates by sfem and xfem. J. Mech. Mater. Struct. 2011, 6, 1213–1238. [Google Scholar] [CrossRef]
- Mesnil, R.; Douthe, C.; Leger, B. Linear buckling of quadrangular and kagome gridshells: A comparative assessment. Eng. Struct. 2017, 132, 337–348. [Google Scholar] [CrossRef]



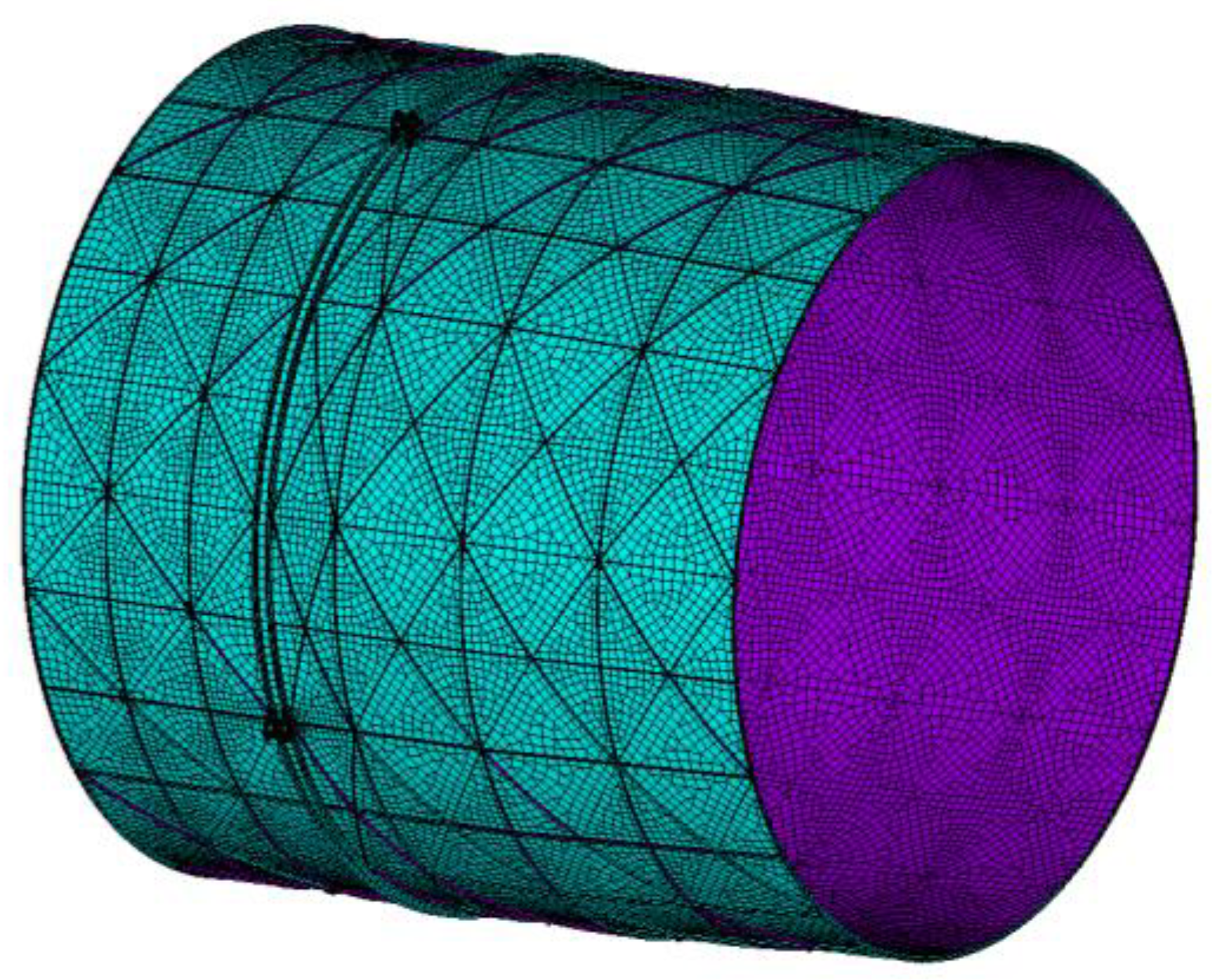

| Load Types | Description |
|---|---|
| Auxiliary mount | One or two mounts are loaded |
| Rear flange | Axial force, vertical force, lateral force, bending moment, torque |
| Differential pressure | External pressure is greater than internal pressure |
| Load Condition | Load Types | Load Value 1 | |
|---|---|---|---|
| 1 | Auxiliary mount loads | One mount is loaded | Fz1 = −1000 N |
| 2 | Two mounts are loaded | Fz1 = −1000 N, Fz3 = −1000 N | |
| 3 | Rear flange loads | Axial compressive force | Fx = 1000 N |
| 4 | Lateral force | Fy = 1000 N | |
| 5 | Torque | Mx = 1000 N m | |
| 6 | Bending moment | My = 1000 N m | |
| 7 | Differential pressure | q = 1 MPa | |
| Load Types | Load Value | Critical Buckling Eigenvalue (λ) | Critical Buckling Loads | Buckling Modes |
|---|---|---|---|---|
| Axial compressive force | Fx = 1000 N | 222.8 | 222.8 kN | Buckling in the rear section of the cylinder 2, m = 6, n = 1 |
| Lateral force | Fy = 1000 N | 39.2 | 39.2 kN | The rear part of the cylinder is unstable, and the buckling deformation is related to the load direction. |
| Torque | Mx = 1000 N m | 85.1 | 85.1 kN m | Buckling in the rear section of the cylinder, m = 15, n = 1 |
| Bending moment | My = 1000 N m | 59 | 59 kN m | The rear part of the cylinder is buckling, and the buckling deformation is related to the load direction. |
| Load Types | Auxiliary Mount | Differential Pressure | |||
|---|---|---|---|---|---|
| Wall Thickness | λ | Increment (%) 3 | λ | Increment (%) | |
| t = 1.2 mm (Original scheme) | 31.31 | — | 0.041235 | — | |
| t = 1.3 mm | 37.58 | 20 ↑ | 0.0434 | 5.25 ↑ | |
| t = 1.4 mm | 44.49 | 42.1 ↑ | 0.046 | 11.56 ↑ | |
| t = 1.5 mm | 52.1 | 66.4 ↑ | 0.049 | 18.83 ↑ | |
| Load Types | Axial Compressive Force | Lateral Force | |||
|---|---|---|---|---|---|
| Wall Thickness | λ | Increment (%) | λ | Increment (%) | |
| t = 1.2 mm (Original scheme) | 222.8 | — | 39.2 | — | |
| t = 1.3 mm | 249 | 11.76 ↑ | 41.4 | 5.61 ↑ | |
| t = 1.4 mm | 276.8 | 24.24 ↑ | 43.7 | 11.48 ↑ | |
| t = 1.5 mm | 307.4 | 37.97 ↑ | 46.2 | 17.86 ↑ | |
| Load Types | Torque | Bending Moment | |||
|---|---|---|---|---|---|
| Wall Thickness | λ | Increment (%) | λ | Increment (%) | |
| t = 1.2 mm (Original scheme) | 85.1 | — | 59 | — | |
| t = 1.3 mm | 103.4 | 21.50 ↑ | 66.7 | 13.05 ↑ | |
| t = 1.4 mm | 118.8 | 39.60 ↑ | 75.1 | 27.29 ↑ | |
| t = 1.5 mm | 135.7 | 59.46 ↑ | 84.1 | 42.54 ↑ | |
| Load Types | Original Scheme λ | Grille Reinforcement λ | Increment (%) |
|---|---|---|---|
| Auxiliary mount | 31.31 | 110.6 | 253 ↑ |
| Axial compressive force | 222.8 | 692.6 | 211 ↑ |
| Differential pressure | 0.04123 | 0.162 | 293 ↑ |
| Torque | 85.1 | 229.0 | 169 ↑ |
| Bending moment | 59 | 206.1 | 249 ↑ |
| Lateral force | 39.2 | 281.9 | 619 ↑ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, X.; Zou, Y.; He, B.; Xiang, J.; Li, Z.; Yang, Q. Buckling Analysis and Structure Improvement for the Afterburner Cylinder of an Aero-Engine. Aerospace 2023, 10, 484. https://doi.org/10.3390/aerospace10050484
Zheng X, Zou Y, He B, Xiang J, Li Z, Yang Q. Buckling Analysis and Structure Improvement for the Afterburner Cylinder of an Aero-Engine. Aerospace. 2023; 10(5):484. https://doi.org/10.3390/aerospace10050484
Chicago/Turabian StyleZheng, Xiaoxia, Yu Zou, Bohan He, Jixin Xiang, Zhiqiang Li, and Qiao Yang. 2023. "Buckling Analysis and Structure Improvement for the Afterburner Cylinder of an Aero-Engine" Aerospace 10, no. 5: 484. https://doi.org/10.3390/aerospace10050484
APA StyleZheng, X., Zou, Y., He, B., Xiang, J., Li, Z., & Yang, Q. (2023). Buckling Analysis and Structure Improvement for the Afterburner Cylinder of an Aero-Engine. Aerospace, 10(5), 484. https://doi.org/10.3390/aerospace10050484





