Abstract
This paper shows a series of tools that help in the research of morphing micro air vehicles (MAVs). These tools are aimed at generating parametric CAD models of wings in a few seconds that can be used in aerodynamic studies, either via CFD directly using the model obtained or via wind tunnel through rapid prototyping with 3D printers. It also facilitates the analysis of morphing wings by allowing for the continuous parametric deformation of the airfoils and the wing geometry. In addition, one of the tools greatly simplifies the purely experimental design of this type of vehicle, allowing the transfer of experimental measurements to the computer, generating virtual models with the same deformation as the physical model. This software has two fundamental parts. The first one is the parameterization of the airfoils, for which the CST (Class-Shape Transformation) method will be used. CST coefficients can be modified according to the actuator variable that changes the wing geometry. The second part is the generation of a three-dimensional parametric model of the wing. We used OpenCASCADE technology in its Python version called PythonOCC, which enables the generation of geometries with good surface quality for typical and non-standard wing shapes. Finally, the use of this software for the study of a morphing aircraft will be shown, as well as improvements that could be incorporated in the future to increase its capabilities for the design and analysis of MAVs.
1. Introduction
In recent years, the increase in computing power has made possible many of the advances that exist in the field of engineering, especially in aeronautics, because of the multidisciplinary nature associated with it. Specifically, this improvement in computing has made it possible to solve problems involving many variables, which used to be solved thanks to the knowledge of engineers, in a mathematical way by finding optimums that meet one or more objectives that the design group wants to achieve. Under this growing use of optimisation tools, the need to generate parametric mathematical models that can be used in this process is implicit. Among other things that can be parameterized in aircraft design, one of the most important is the geometry itself, whose parameterization is useful not only for following an optimisation process but also for testing different aircraft concepts without requiring long design times. This geometry parameterization is especially relevant in the RPAS (Remotely Piloted Aircraft System) sector. This is because, by not having the constraints of having to carry a human being, unusual geometries can be used which are subordinated to the correct fulfilment of the mission for which they were designed. One of the areas of aeronautical engineering that directly affects geometry and is increasingly being studied is that of the adaptive wing concept for RPAS.
A morphing can vary the geometry of its wing to adapt to each aerodynamic condition required by the mission [1]. The advantage of these aircraft over traditional ones is that they can be more aerodynamically efficient as they do not generate discontinuities in their surface to control the aircraft. The use of these technologies is closely related to RPAS due to their cost, the variety of missions for which they are designed, their low aerodynamic load, and their easier certification process compared to a passenger aircraft [2]. In the particular case of a morphing aircraft, having a parametric model of the geometry becomes essential, to vary the shape of the aircraft.
Computer-aided engineering (CAx) techniques (CAD, CAM, CAE, etc.) are increasingly vital in the process of designing an RPA. In particular, they are highly relevant for generating new designs and testing prototypes with the aid of 3D virtual models, thus reducing costs and expediting the development of the final product [3,4]. The design space of a UAV is large and multidimensional, with numerous geometric solutions for the aircraft that can fulfil the mission(s) for which it was designed. Although commercial CAD applications provide the opportunity to create complex designs and high-quality virtual models, these software programs are intended for use in various engineering areas and require extensive training for proper use [5,6]. Therefore, it is necessary to have tools that enable the creation of conceptual RPA designs based on the knowledge that can be used for CFD/FEM calculations or even the manufacture of real prototypes using Rapid Prototyping, without the need for in-depth knowledge of 3D design tools.
In the last decade, interest in parametric aircraft design software has increased significantly due to the clear advantages it offers. A selection of the most relevant tools to obtain parametric geometry focused on aircraft conceptual design can be found in [7,8,9]. Some tools of special interest will be mentioned below. OpenVSP [10,11] is the most widely used aircraft parametric design tool developed by NASA whose main objective is to quickly generate different aircraft configurations without the need to have experience in CAD tools. In 2019, they introduced the possibility to program macros that provide further automation in design. GENUS [12] is an aircraft conceptual design software programmed by the Cranfield University aircraft design group that allows the generation of preliminary 3D aircraft geometries in a modular way. TiGL [13] is a software developed by the German Aerospace Research Centre (DLR). It can be used to create high-fidelity models of aircraft based on their CPACS parametric description and can generate both moving control surfaces and internal structures within components. GENEAIR [14] is an application designed to generate and optimise unconventional aircraft geometries. These applications are intended for the preliminary design of aircraft that have a fixed geometry. In contrast to these tools, the software described in this paper provides a series of applications that facilitate the design and analysis of morphological aircraft, both in the conceptual phase, generating parametric CAD models in only a few seconds, and in the laboratory experimentation phase, using the geometry for rapid prototyping [15,16] or transferring the information from the physical prototype to the virtual model.
This paper is organised as follows. Section 2 introduces the mathematical core behind the geometrical kernel. Section 3 describes the software architecture, with Section 3.1 dedicated to airfoil parameterization and Section 3.2 to wing geometry parameterization. Section 4 shows the usefulness of this software in a real scenario. Section 5 includes a brief explanation about bioinspired configurations. Finally, Section 6 draws conclusions and outlines the future steps to be taken to extend the software functionalities.
2. Geometric Kernel
The Python programming language has been chosen for the development of this software because it is the open source object-orientated language that has expanded the most in recent years in the research community due to the large number of scientific libraries available. For geometry generation, the OpenCASCADE technology kernel [17] in its Python version, called PythonOCC [18], is used. The main reason for using Python coupled to this geometry kernel is that enables great flexibility when generating applications that can be improved and extended in the future. In addition, since Python’s functionalities are not restricted, it is possible to adapt the software to very specific studies, being able to interrelate the generated geometry with physical analysis applications and automate processes.
OpenCASCADE technology is a collection of libraries that make up the core of professional computer-aided design. OpenCASCADE geometry is based on NURBS (non-uniform rational B-spline), so curves and surfaces are defined by B-Splines. NURBS geometry is widely used in CAD design and industry standards, such as IGES, STEP, ACIS, and PHIGS, are based on this type of geometry. The B-Spline curves of order k and degree k − 1 are defined by Equation (1):
where are the control points, are the nodes and are the basic functions of the B-Splines defined by Equation (2):
The usual way to use this type of curve is to generate B-Splines that pass through a set of points by interpolating them. The B-Spline surfaces are defined as the tensor product shown in Equation (3):
OpenCASCADE technology enables the generation of surfaces by interpolating different curves. This method has several problems when it is used to generate aerodynamic surfaces. The first problem comes from the fact that it is not possible to use guide curves, so it is not possible to have proper control of the final contour of the geometry. The other problem is that there is no control over the quality and continuity of the surface, which can produce insufficient quality surfaces by aeronautical standards. What has been done to avoid these problems is to use Gordon Surfaces [19] which allows the use of guides and generates curves with better continuity. The surfaces generated with Gordon’s method are based on the superposition of three interpolated surfaces. The simplified equation of this surface can be seen in Equation (4):
The surface interpolates the profiles introduced to generate the surface. The surface is a surface that arises from the interpolation of the guide curves. Finally, the curve interpolates a network of intersection points of the two mentioned surfaces. Figure 1 shows the construction of these surfaces.
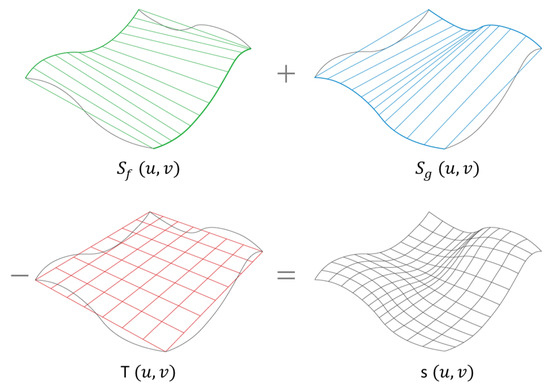
Figure 1.
Interpolations necessary to obtain a Gordon surface, . interpolates the profiles, is the interpolation of the guide curves and interpolates a network of intersection points of and .
This surface formulation provides greater control over the surface by incorporating guide curves. Furthermore, the result provides a better surface quality, which is crucial when designing aerodynamic surfaces. To use Gordon surfaces, we have applied the algorithm implemented by the open-source software TiGL. An in-depth explanation of the mathematical theory underlying Gordon surfaces and their implementation is given in [13].
3. Software Architecture
The designed software has two differentiated parts that are then interrelated. On the one hand, there is the package related to airfoil geometry, for which functions have been developed to generate airfoils using the CST method; read airfoils stored by coordinates ensuring that they are in Selig format and the trailing edge is sharp; adapt airfoils introduced by points to the CST method; and automatically parameterize airfoil shape deformations based on data extracted from laboratory tests. On the other hand, there is the wing generation package, for which a series of functions have been developed to generate different wing geometries.
3.1. Airfoil Parameterization
For the parameterization of airfoils, the CST (Class-Shape function Transformation) method developed by Brenda Kulfan in her paper [20] has been used. This method has been selected for several reasons, including its flexibility in being able to sweep the entire airfoil design space with a relatively small number of variables and being a robust method that does not produce degenerate airfoil shapes. Furthermore, it meets the desirable properties for an airfoil parameterization technique introduced in [21]. Another interesting feature of this project is that both the fuselages and the axisymmetric nacelles can be generated with the same method, which is very useful for future software extensions with relative ease.
3.1.1. CST Method Theory
The CST method is based on two functions introduced by the author, the class function and the shape function. The equation for the generic class function is given in Equation (5)
where and the coefficients N1 and N2 are in the range between 0 and 1. Depending on this value, arbitrary shapes are obtained [22]. For the case of airfoils with rounded leading edge and sharp trailing edge, the value of these coefficients will be and . The root of the first term of the class function ensures that a rounded leading edge is generated in addition to imposing an intersection with the abscissa at the origin, while the term forces an intersection to exist at x = 1, generating a sharp trailing edge. The shape functions of this method are the Berstein polynomials
where N is the Bernstein polynomial degree, are the coefficients of the method, and the term K is the Binomial Coefficient defined as
In these equations there are the coefficients that will be the design variables. When these coefficients are modified, the entire airfoil design space is swept. The first term of the shape function defines the radius of the leading edge, and the last term defines the bottleneck angle. The remaining terms affect the rest of the airfoil, so that lower-order polynomials affect the forward region while higher-order polynomials affect the rear region. Thus, the equations for the upper and lower airfoil will be as follows.
where the letter U corresponds to the upper surface and the letter L corresponds to the lower surface, and the term is the thickness of the trailing edge of the airfoil dimensioned with the chord.
This is the basic definition of the CST method; however, Kulfan herself modified their method to give it more flexibility in describing the leading edges of the airfoils [23]. This modification introduces an additional term that gives the equations as follows:
Adding this term is very relevant when high-curvature airfoils and sharp leading edges are involved. This is especially important for MAVs (Micro Air Vehicles) that use high-curvature configurations to carry out some missions at low speeds. In addition, this extra term means that fewer terms of the CST method are needed to reproduce a high-quality airfoil, which will reduce optimisation times.
3.1.2. CST as a Filter
Although the CST method can be used directly, there is a more useful way to start from an airfoil already known to the designer. To perform this adaptation in this software, it is necessary to enter the airfoil by points in the Selig format [24] with a .dat file, starting from the trailing edge moving along the upper surface to the leading edge and returning to the trailing edge along the inner surface. The application will store these points and, by least squares minimisation, the coefficients of the CST method that make the squared difference between the values of the z coordinates of the points of the original airfoil and the created airfoil minimum. Figure 2 shows the adaptation of an Eppler 61 airfoil with this method, together with the error made in the adaptation superimposed on the typical wind tunnel tolerance for airfoils [20].
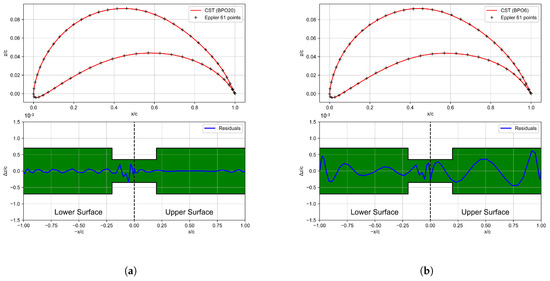
Figure 2.
Comparison between the original CST method and the modified CST method. The green band represents the typical manufacturing accuracy of a wind tunnel model [20]. Subfigure (a) shows how fitting an Eppler 61 airfoil, within tolerances, requires Bernstein polynomials of order 20 (BPO20) for upper and lower surfaces for the original CST method, while subfigure (b) shows that with the modified CST method Bernstein polynomials of order 6 (BPO6) are required to be within tolerances. (a) CST without modification (BPO20); (b) CST with modification (BPO6).
In Figure 2, the importance of having introduced the additional Kulfan term can be also seen. Without this term, 20 coefficients are needed for the upper and lower to be within tolerances, while with the leading edge term only 6 coefficients are needed for each surface, which means a great improvement in the calculation time when adapting the airfoil, being reduced up to 35 times.
Another advantage of this method within this software is that it can be used to filter the sets of coordinates obtained in laboratory tests. A typical way to work with morphing RPAS is to test the deformation produced in the airfoils when the built-in actuator is operated. Once the test has been performed, it is useful to save the airfoil coordinates for use in aerodynamic studies; however, when these airfoils are measured, errors are made that result in poor continuity when plotting the airfoil. Using this method, these coordinates can be filtered, ensuring a smooth airfoil without shape errors derived from measurement and approximation errors [25].
3.1.3. Actuator Effect Parameterization
Several studies use the adaptive wings CST method to optimise the shape of the airfoil depending on the circumstance of the flight. In [26], this parameterization is used to optimise the endurance of a wing. In reference [27], Gaspari proposes an algorithm to optimise the shape of the CST airfoil taking into account both aerodynamics and the wing structure. After seeing these examples, it can be concluded that this parameterization method is useful when applied to airfoil geometry optimisation.
In addition to designing the optimal airfoil shapes for each flight condition, another interesting thing is being able to modify the shape of an airfoil continuously by varying the actuator parameter. This is especially interesting for a purely experimental design of an adaptive wing because it is necessary to have a way to transfer the measurement data to the computer and to be able to continuously modify the airfoil in order to perform the necessary calculations. A case of experimental design would be the micro-RPAS studied in [28], in which a piezoelectric actuator was installed and the deformation of an already fabricated airfoil was measured. To achieve this continuous change in airfoil shape, a function is programmed to adjust the coefficients of the CST method using polynomial curves dependent on the actuator parameter. To find these functions, the only thing to do is introduce a vector with the name of the .dat files (file path) that include the coordinates of the airfoils measured or calculated, and another vector showing the value of the actuator parameter at which these airfoils are determined. It will also be necessary to choose the degree of the polynomial that best fits the entered coefficients. The output of the function will return the coefficients of the polynomial curves that adapt the coefficients of the CST method.
3.2. Wing Parameterization
The second part of this software generates the wetted surface of the wing. As mentioned above, the geometric kernel selected for this was OpenCascade together with the Gordon surface creation function of TiGL. Building upon the aforementioned software as the geometric foundation, functions are developed to enable the fully parametric generation of the right half-wing, encompassing both its overall shape and airfoils. The coordinate system has the origin at the leading edge of the root airfoil, the x-axis is directed towards the trailing edge of the root airfoil, the y-axis is directed towards the tip of the right half-wing, and the z-axis is such that it forms a right-hand coordinate system.
The function that generates the three-dimensional wing geometry works as follows. Start by selecting the type of wing to be generated among single-tapered wings, double-tapered wings, and elliptical wings have been chosen. Once a wing type has been selected, the most relevant parameters for its geometry, such as wingspan (b), root chord (), tip chord (), sweep angles (), dihedrals (), and twist () are entered. These parameters are shown in Figure 3, for a simple tapered wing. With these data, enough points are generated to plot the leading and trailing edges using B lines, as shown in Figure 4a. These edges will be the future guides to generate the wetted surface of the wing. Another way to obtain these curves is by entering the leading and trailing edge points by coordinates. These points can be interpolated with a B-Spline of degree 1 or 3, depending on whether a straight section or a continuous curved wing is desired.
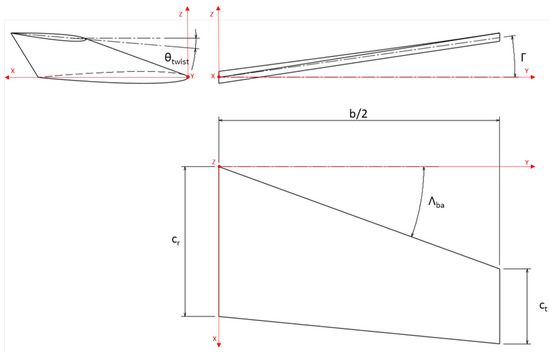
Figure 3.
Simple tapered wing parameters.
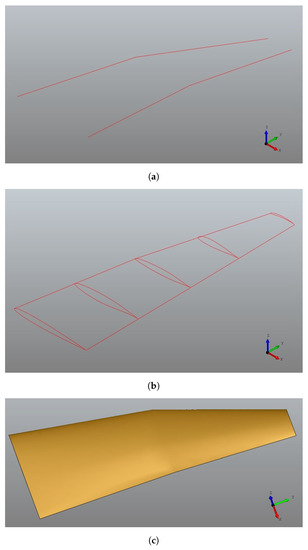
Figure 4.
Generation process of a double tapered wing surface. Subfigure (a) shows the leading and trailing edge lines. In subfigure (b), the airfoils are placed along the wingspan. Finally, in subfigure (c) the wing surface is generated. (a) Leading and trailing edges; (b) airfoils along the span; and (c) finished wing.
The next step is to place the desired airfoils along the wing span. The user must enter information about the airfoils and their location along the wing span. With respect to airfoils, it is necessary to introduce a vector of the same length as the number of airfoils to be introduced. The way to enter these vectors is by typing the name of the .dat file where its coordinates are stored in a folder called Airfoils in the software directory. For example, if one wanted to enter three NACA 0008 airfoils the vector will be of the form:
The coordinates of these airfoils may be obtained from a database or from airfoils generated by the CST method. In order to use the CST airfoils, their coordinates are extracted and stored in Selig format into a .dat file. The next step is to enter the position of the airfoils along the semi-span of the wing (y-axis), in millimetres. It is important to note that there must be at least two airfoils, one at the root and one at the tip. For the above example of the NACA 0008 airfoil a possible vector would be:
The next step is to place each airfoil in position. The process for achieving this is as follows. The first step is to read the .dat files where the airfoil coordinates are stored. The next task is to find the intersection between the y-coordinate where the airfoil will be located with the curves of the leading and trailing edge. To accomplish this, a surface parallel to the xz plane of sufficient size is generated so that the intersection always occurs. With these intersection points, the distance between them and the angle formed by the line joining them with the xy is calculated. Then the coordinates of the airfoils are rotated by the angle calculated above and multiplied by the distance between the intersection points so that the airfoil has the proper chord. Finally, the airfoil nose coordinate is placed at the leading edge intersection point and, once placed, the airfoil curve is generated by a B-Spline of order 3. Figure 4b shows an example of the placement on the wingspan of different airfoils.
Once the leading and trailing edge curves and airfoils are in place, the wing surface is made. A Gordon surface is used, employing the airfoils as profile curves and the leading and trailing edges as guides. The last step is to close the surface. An algorithm analyses the edges of the created surface and searches for the curves of the root and tip airfoils. Then, the inner surfaces of these airfoils are generated. With these two surfaces plus the outer surface of the wing, a closed outer shell is generated, which can remain a surface or become a solid.
Once the wing geometry is completed, it can be inspected with the OpenCascade viewer (Figure 4c) or export the created geometry in .stp or .stl formats.
Figure 5 shows the algorithm used to generate the wing geometries. The first thing to do is choose the airfoils that you want to use. Existing airfoils have to be entered using a .dat file where their coordinates are stored in Selig format. The coordinates of these airfoils can be filtered by fitting the airfoil to the CST method. On the other hand, if the objective is to optimise new airfoils, the CST method can be used. In the case of airfoils whose shape varies parametrically, the function that modifies the parameters of the CST airfoil will be defined to obtain the change of shape. If airfoil variation has been obtained by laboratory tests, the measured airfoils and actuator values can be entered to generate polynomial functions that allow the CST parameters to be varied to obtain continuous deformation of the airfoils. Once the airfoils are well defined, the wings function can be used to generate the 3D geometry. To create the wing, it is necessary to select one of the four types of geometries available in the software, which are simple tapered, double tapered, elliptical, and free form. For the first three types, it is necessary to select their geometrical parameters to define the leading and trailing edges; furthermore, the selected airfoils and their position in the wingspan must be specified. In the case of the free-form wing, the shape of the leading and trailing edges is defined by coordinates. With this information, the openCASCADE kernel is used to generate the three-dimensional model of the wing. In the case of morphing vehicles, the wing must be generated each time any parameters that modify its geometry change. Finally, with the 3D model created, there is an option to save the generated geometry storing all its parameters or generate a .stp or .stl file that can be used in external tools.
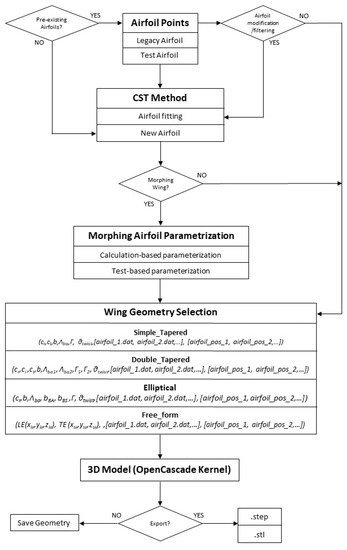
Figure 5.
Software box diagram.
4. Software Application
The design of this tool is part of the study of adaptive wing micro air vehicles (MAVs) at the School of Aeronautics and Space Engineering (ETSIAE) belonging to the Universidad Politécnica de Madrid (UPM).
To validate the software, we will focus on the MAV concept shown in Figure 6. This model presents a low wing aspect ratio (AR = 2.5) and a low operating range (low Reynolds number). The geometry of this MAV consists of a Zimmerman wing platform with Eppler 61 airfoils. The Zimmerman wing is made up of two half-ellipses joined at 25% of the chord, as shown in Figure 7. The fuselage is designed with Whitcomb airfoils. These characteristics were selected according to the main aerodynamic parameters, maximum lift-to-drag ratio, maximum lift coefficient, and minimum drag coefficient [29].

Figure 6.
Micro-RPA model made of composite.
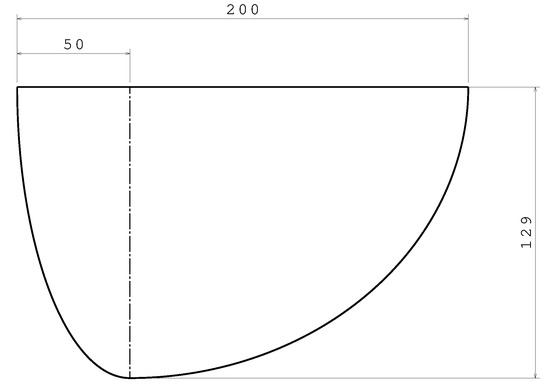
Figure 7.
Zimmerman wing platform. Dimensions in mm.
The wings of this MAV can modify their curvature and thickness depending on flight conditions to maximise endurance. This variation is achieved using MFC actuators (Macro Fibre Composite) actuators installed in the lower surface of the airfoil and centered at 40% of the chord. In Figure 8, it is possible to see a detailed view of the MFC installation inside the lower surface of the wing. This actuator modifies the shape of the airfoil depending on its voltage, which operating range is from −500 to 1500 V. To reach this voltage, a 12 V DC power source has been attached to the power supply board and the applied voltage has been varied using a control pin with voltages ranging from 0 to 5 V.

Figure 8.
A detailed view of the MFC installation.
To verify the advantages of the programmed software, it is intended to replicate the wing of their experimental MAV [28].
The baseline airfoil selected for this aircraft is the Eppler 61. This airfoil has adequate performance at low Reynolds [30] and a mostly turbulent boundary layer that makes the stall more predictable [31]. In addition, it has a concave lower surface, which is necessary to achieve continuous curvature variations. The shape variation of this airfoil was experimentally tested. It is important to note that this variation in airfoil shape has been carried out without taking into account the aerodynamic loads that the MAV would experience in flight. For this purpose, a semi-wing with curing composites on mould was fabricated and the deformation of the airfoil root produced at different voltages by the MFC was measured, Figure 9.
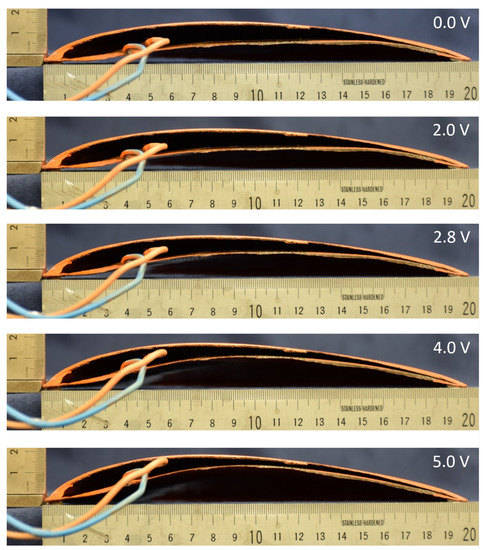
Figure 9.
Stages of airfoil deformation from 0 V to 5 V range of the control pin signal voltage.
From these tests, the airfoil coordinates are extracted and adapted to the CST method, using six terms for each surface. In this way, not only the airfoil is parameterized with a relatively small number of variables, but the filtering property of this method is also applied. Figure 10 shows the airfoil with a control pin voltage of 5 V. It can be seen that the adaptation to the CST method captures the trend of the measured points while correcting for small deviations related to measurement error and providing a smooth surface.
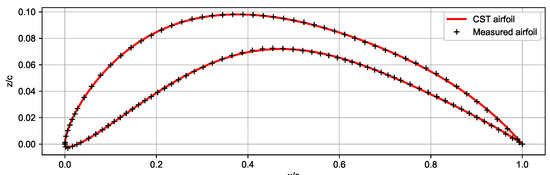
Figure 10.
MAV airfoil with voltage of 5 V. Figure shows the points measured on test (black) and the CST airfoil adaptation (red).
The next step is to fit the CST coefficients with a polynomial function. Therefore, the airfoil surface depends only on the MFC tension. The function designed for this purpose, explained above, is used. Figure 11 shows the adjustment of the CST coefficients of the upper surface and Figure 12 shows those of the lower surface.
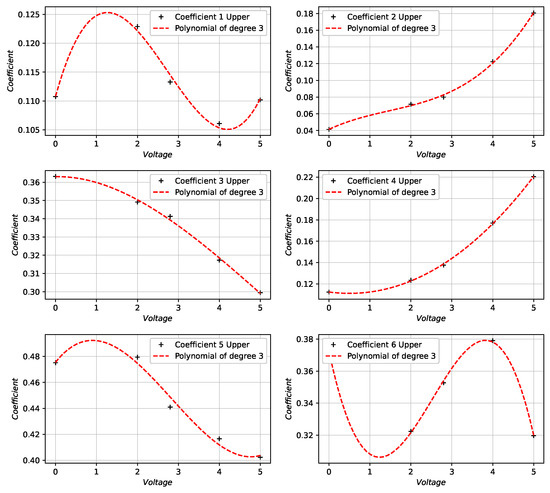
Figure 11.
Fitting of the CST coefficients for the upper surface of the test airfoils using a polynomial of degree 3.
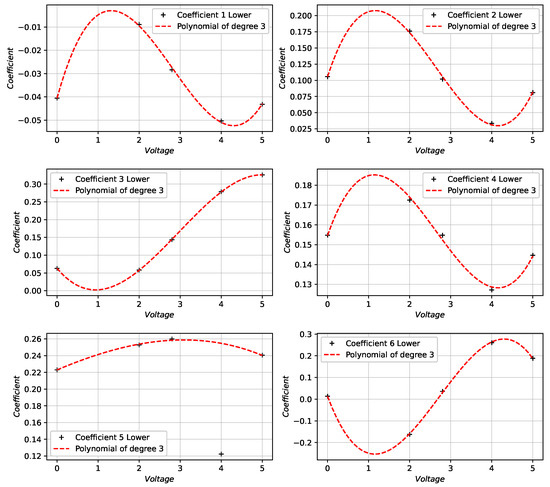
Figure 12.
Fitting of the CST coefficients for the lower surface of the test airfoils using a polynomial of degree 3.
Figure 11 and Figure 12 show that a cubic function is capable of recording the variation of the CST coefficients with the MFC actuator voltage. The mean relative error and the mean absolute error between the z/c coordinates of the airfoils obtained with the polynomial curve coefficients and the original coefficients are calculated to check the accuracy of this cubic function in fitting the coefficients.
Table 1 shows that the highest error occurs in the airfoil at 2.8 V, its mean relative error being less than 1.5% and its mean absolute error being within the tolerances for aerodynamic airfoils. Once the airfoil geometry is parameterized with the control pin tension, the wing is generated.

Table 1.
Mean relative error and mean absolute error between the z/c coordinates of the airfoils obtained with the polynomial curve coefficients and the CST coefficients of the test aerofoils.
The programmed elliptical wing input is used, which is also capable of double elliptical wings. In the aerodynamic studies carried out on this aircraft [32,33], it has been assumed that all wing airfoils are modified equally. Therefore, the MFC tension at which the wing is desired to be generated will be selected, which modifies the shape of the airfoils. Once the airfoil is modified, its coordinates are automatically stored in a .dat file. With this file created, the only necessary thing is to input the distribution of the airfoils along the span and then generate the wing.
As can be seen (Figure 13a–c) it is possible to modify the global shape of the wing only by modifying the MFC tension. Regarding the time it takes to generate the geometry once the airfoils are parameterized with voltage, it depends on the options that are introduced within the application that generates the wings, as shown in Table 2.
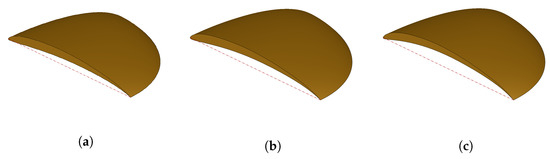
Figure 13.
Wing model at 0 V (a), 2.8 V (b) and 5 V (c).

Table 2.
Execution times to visualize and generate the wing geometry. The .stl file is generated with a linear deviation of 0.005 mm and an angular deviation of 0.5 degrees. These times are calculated on a computer with an Intel Core i5-4210U processor.
Finally, the quality of the generated surfaces is analysed. Figure 14 shows a curvature analysis of the airfoils obtained with this software. The airfoil presents a continuous curvature along its entire chord, this being especially important at the leading edge, where the curvature is shown to grow without abruptness. The absence of noise in the curvature is important when analysing the subsonic flow around the airfoil, since the pressure is governed by the curvature [25].

Figure 14.
Airfoil curvature analysis.
Figure 15 shows a zebra stripe evaluation on the wing surface. The surface quality is adequate, showing curvature continuity throughout the surface.
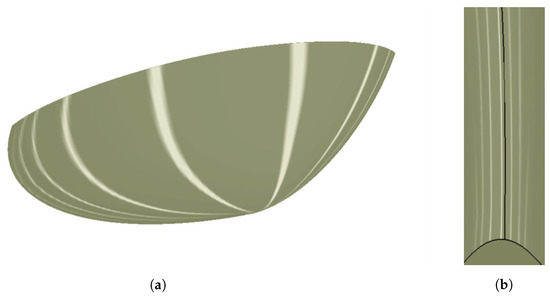
Figure 15.
Zebra stripe evaluation on the wing surface. (a) Upper surface; (b) leading edge.
5. Bioinspired Configurations
Standard wing geometries have been shown throughout this paper; however, this application can adequately generate more complex wing geometries. There is currently growing interest in bioinspired MAVs. These types of vehicles typically have wings with unconventional and complex geometries. Bioinspired flight systems cover different types, including those with deformation-motion modes, flapping, or a combination of both. An example of a flight system with deformation motion modes is the MAV, which was analysed in Section 4. These types of aircraft are based on the concept that the high-efficiency aerodynamic performance of birds’ wings is highly dependent on their complex deformation. During non-flapping flight states, birds can dynamically alter their wing postures to optimise adaptability to a wide range of flight behaviours and conditions. Concerning flapping wing aircraft, current bird-like aircraft primarily replicate the flapping movement to generate lift and thrust for flight, but their aerodynamic efficiency is still markedly inferior to that of birds. Therefore, extensive research is urgently needed to allow birdlike aircraft to achieve the exceptional flying ability of birds [34]. In the future, by combining flapping wing motion with alterations in wing profile shape, these aircraft can achieve good aerodynamic performance, strong manoeuvrability, and high flight efficiency. These variations in wing shape have a strong impact on aerodynamic characteristics and performances, making geometry optimisation crucial in this class of vehicles [35]. Therefore, the tools designed in this work are very useful for the study of this type of MAV. Figure 16 is an example of what can be achieved with the software developed, with a wing of a corvid with airfoils of the Ananda–Selig family [36], which are bird-shaped sectional airfoils designed to fly at low Reynolds.
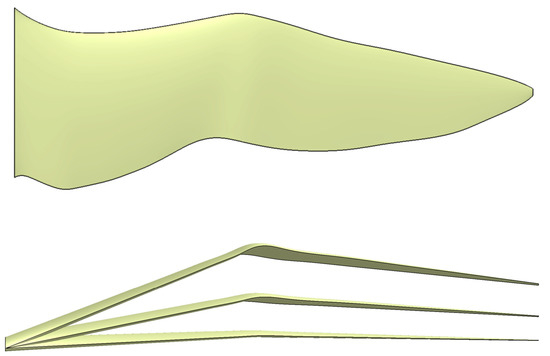
Figure 16.
Corvid wing generated with the application.
To simulate the change in wing shape in Figure 16, a motion law has been programmed to modify the coordinates of the points at the leading and trailing edges according to a parameter. Once the value of this parameter has been set, the points corresponding to the leading and trailing edges are obtained. These will be introduced in the free form wing type, and developed taking into account these kinds of geometries. With the edges, the next step is to choose the airfoils, which can be morphing or not. The only thing to do is specify the position of the airfoils along the wingspan, and they will be automatically positioned, no matter how complex the wing geometry is. In this way, the software presented can be an easy and versatile tool to study wings with a complex plan shape and that can completely modify its geometry in a parametric way.
6. Conclusions
In this work, parametric wings design software specifically focused on the study of morphing MAVs has been presented. The use of CST airfoils and Gordon surfaces produces a wing surface quality suitable for CFD and 3D printing of prototypes. The usefulness of this software has been proven when performing studies of vehicles with adaptive wings, due to the parameterization of all relevant characteristics of the wing. In addition, it has been shown that the use of the CST method to characterise the airfoils is useful for this application, since the coefficients of this method can be modified parametrically to generate the change in the geometry of the airfoils by modifying the control parameter. In Table 1, it is shown that modifying these coefficients using polynomials to allow for continuous camber variation of airfoils is well suited. This simple method provides good accuracy in the representation of the geometry change; for the case studied, the maximum relative error between airfoil coordinates is 1.419%.
The above features make this CAx tool suitable for preliminary design, rapid prototyping, and reverse engineering of morphing wings. It is ideal for preliminary design because of its high degree of automation, which allows it to be used without extensive knowledge of computer-aided design programs, being able to generate complex geometries based mainly on aeronautical design knowledge. In addition, the time required to generate geometries is relatively short, less than one second for the tested cases, allowing designers to quickly generate a large number of design solutions for the wings. As for rapid prototyping, once the most relevant models have been selected from the preliminary design, they can be 3D printed and tested thanks to the quality of the generated surfaces and the possibility of saving in stl format. Finally, as demonstrated in Section 4, this tool is useful for reverse engineering morphing wing aircraft, as it provides automatic parameterization tools to deform laboratory-tested wings. These features, combined with the fact that the environment is highly programmable, make this application suitable for iterative processes, such as geometry optimisation.
Author Contributions
Conceptualization, Á.A.R.-S., M.J.C.-C., R.B.-M. and J.N.-C.; methodology, Á.A.R.-S., M.J.C.-C. and J.N.-C.; software, J.N.-C.; validation, Á.A.R.-S., M.J.C.-C., R.B.-M. and J.N.-C.; formal analysis, Á.A.R.-S., M.J.C.-C., R.B.-M., J.N.-C., J.C.M.-G. and E.B.-B.; investigation, Á.A.R.-S., M.J.C.-C., R.B.-M., J.N.-C., J.C.M.-G. and E.B.-B.; resources, Á.A.R.-S., M.J.C.-C., R.B.-M., J.N.-C., J.C.M.-G. and E.B.-B.; data curation, Á.A.R.-S.; writing—original draft preparation, Á.A.R.-S., M.J.C.-C., R.B.-M., J.N.-C., J.C.M.-G. and E.B.-B.; writing—review and editing, Á.A.R.-S., M.J.C.-C., R.B.-M., J.N.-C., J.C.M.-G. and E.B.-B.; visualization, Á.A.R.-S. and J.N.-C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ACIS | Geometric modelling kernel developed by Spatial Corporation |
| BPO | Bernstein Polynomials Order |
| CAD | Computer Aided Design |
| CFD | Computational Fluid Dynamics |
| CPACS | Common Parametric Aircraft Configuration Schema |
| CST | Class-Shape Transformation |
| DLR | Deutsches Zentrum für Luft- und Raumfahrt |
| IGES | Initial Graphics Exchange Specification |
| MAV | Micro Air Vehicle |
| MFC | Macro Fibre Composite |
| NASA | National Aeronautics and Space Administration |
| NURBS | Non-Uniform Rational Basis Spline |
| PHIGS | Programmer’s Hierarchical Interactive Graphics System |
| RPAS | Remotely Piloted Aircraft System |
| STEP | Standard for the Exchange of Product Model Data |
| STL | Standard Tessellation Language |
| b | Wingspan |
| c | Local chord |
| Sweep Angle | |
| Dihedral | |
| Wing twist | |
| C | B-Spline curve |
| B-Spline basis functions | |
| B-Spline control points | |
| s | B-Spline surface |
| Profiles interpolation surface | |
| Guide curves interpolation surface | |
| T | Surface that interpolates intersection points between and |
| S | Shape function |
| Shape function coefficients | |
| Binomial coefficients | |
| Class function | |
| Class function coefficients | |
| Relative to upper surface | |
| Relative to lower surface | |
| Non-dimensional airfoil station | |
| Non-dimensional airfoil ordinate | |
| Non-dimensional trailing edge thickness | |
| Leading edge coefficient |
References
- Lampton, A.; Niksch, A.; Valasek, J. Morphing airfoils with four morphing parameters. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008; p. 7282. [Google Scholar]
- Barbarino, S.; Bilgen, O.; Ajaj, R.M.; Friswell, M.I.; Inman, D.J. A review of morphing aircraft. J. Intell. Mater. Syst. Struct. 2011, 22, 823–877. [Google Scholar] [CrossRef]
- Łukaszewicz, A.; Szafran, K.; Józwik, J. CAx techniques used in UAV design process. In Proceedings of the 2020 IEEE 7th International Workshop on Metrology for AeroSpace (MetroAeroSpace), Pisa, Italy, 22–24 June 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 95–98. [Google Scholar]
- Shokirov, R.; Abdujabarov, N.; Takhirov, J.; Bobomurodov, S. Automated design of the appearance of an unmanned aerial vehicle. In Proceedings of the AIP Conference Proceedings, Adelaide, Australia, 11–16 December 2022; AIP Publishing LLC: Melville, NY, USA, 2022; Volume 2432, p. 030088. [Google Scholar]
- Dankwort, C.W.; Weidlich, R.; Guenther, B.; Blaurock, J.E. Engineers’ CAx education—It’s not only CAD. Comput.-Aided Des. 2004, 36, 1439–1450. [Google Scholar] [CrossRef]
- Łukaszewicz, A.; Skorulski, G.; Szczebiot, R. The main aspects of training in the field of computer-aided techniques (CAx) in mechanical engineering. In Proceedings of the 17th International Scientific Conference on Engineering for Rural Development, Jelgava, Latvia, 23–25 May 2018; pp. 865–870. [Google Scholar]
- De Marco, A.; Di Stasio, M.; Della Vecchia, P.; Trifari, V.; Nicolosi, F. Automatic modeling of aircraft external geometries for preliminary design workflows. Aerosp. Sci. Technol. 2020, 98, 105667. [Google Scholar] [CrossRef]
- Chambers, P.; Sóbester, A. Aircraft Topology Generation via Recursive Component Fitting Operators. In Proceedings of the 18th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Denver, CO, USA, 5–9 June 2017; p. 4327. [Google Scholar]
- Soulat, M.E. Parametric geometry representation to support aircraft design. In Proceedings of the 2012 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–17. [Google Scholar]
- Hahn, A. Vehicle sketch pad: A parametric geometry modeler for conceptual aircraft design. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010; p. 657. [Google Scholar]
- McDonald, R.A.; Gloudemans, J.R. Open vehicle sketch pad: An open source parametric geometry and analysis tool for conceptual aircraft design. In Proceedings of the AIAA SciTech 2022 Forum, San Diego, CA, USA, 3–7 January 2022; p. 4. [Google Scholar]
- Smith, H.; Sziroczák, D.; Abbe, G.; Okonkwo, P. The GENUS aircraft conceptual design environment. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 2932–2947. [Google Scholar] [CrossRef]
- Siggel, M.; Kleinert, J.; Stollenwerk, T.; Maierl, R. TiGL: An open source computational geometry library for parametric aircraft design. Math. Comput. Sci. 2019, 13, 367–389. [Google Scholar] [CrossRef]
- Gagnon, H.; Zingg, D.W. Geometry generation of complex unconventional aircraft with application to high-fidelity aerodynamic shape optimization. In Proceedings of the 21st AIAA Computational Fluid Dynamics Conference, San Diego, CA, USA, 24–27 June 2013; p. 2850. [Google Scholar]
- Bardera, R.; Rodríguez-Sevillano, Á.; Barderas, E.B.; Casati, M.J. Rapid prototyping by additive manufacturing of a bioinspired micro-RPA morphing model for a wind tunnel test campaign. In Proceedings of the AIAA AVIATION 2022 Forum, Chicago, IL, USA, 27 June–1 July 2022; p. 4130. [Google Scholar]
- Larsson, R.; Ringertz, U.; Lundström, D.; Sobron, A. Rapid prototyping in aircraft design using cfd, wind tunnel and flight testing. In Proceedings of the 33rd Congress of the International Council of the Aeronautical Sciences, Stockholm, Sweden, 4–9 September 2022. [Google Scholar]
- OpenCASCADE Technology. 2021. Available online: https://www.opencascade.com/ (accessed on 19 December 2022).
- PythonOCC. 2021. Available online: https://github.com/tpaviot/pythonocc (accessed on 19 December 2022).
- Gordon, W.J. Spline-blended surface interpolation through curve networks. J. Math. Mech. 1969, 18, 931–952. [Google Scholar]
- Kulfan, B.; Bussoletti, J. Fundamental Parameteric Geometry Representations for Aircraft Component Shapes. In Proceedings of the 11th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Portsmouth, VA, USA, 6–8 September 2006; p. 6948. [Google Scholar]
- Padulo, M.; Maginot, J.; Guenov, M.; Holden, C. Airfoil design under uncertainty with robust geometric parameterization. In Proceedings of the 50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference 17th AIAA/ASME/AHS Adaptive Structures Conference 11th AIAA No, Palm Springs, CA, USA, 4–7 May 2009; p. 2270. [Google Scholar]
- Kulfan, B.M. Universal parametric geometry representation method. J. Aircr. 2008, 45, 142–158. [Google Scholar] [CrossRef]
- Kulfan, B. Modification of CST Airfoil Representation Methodology. 2009. Available online: http://www.brendakulfan.com/docs/CST8.pdf (accessed on 19 December 2022).
- Site, U.A.D. 2021. Available online: https://m-selig.ae.illinois.edu/ads.html (accessed on 19 December 2022).
- Sóbester, A.; Forrester, A.I. Aircraft Aerodynamic Design: Geometry and Optimization; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Li, H.; Ang, H. Preliminary airfoil design of an innovative adaptive variable camber compliant wing. J. Vibroeng. 2016, 18, 1861–1873. [Google Scholar] [CrossRef]
- De Gaspari, A.; Ricci, S. Knowledge-based shape optimization of morphing wing for more efficient aircraft. Int. J. Aerosp. Eng. 2015, 2015, 325724. [Google Scholar] [CrossRef]
- Barcala-Montejano, M.; Rodríguez-Sevillano, A.; Crespo-Moreno, J.; Bardera-Mora, R.; Silva-González, A. Optimized performance of a morphing micro air vehicle. In Proceedings of the 2015 International Conference on Unmanned Aircraft Systems (ICUAS), Denver, CO, USA, 9–12 June 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 794–800. [Google Scholar]
- Bardera, R.; Rodríguez-Sevillano, Á.A.; Barroso, E. Numerical and Experimental Study of Aerodynamic Performances of a Morphing Micro Air Vehicle. Appl. Mech. 2021, 2, 442–459. [Google Scholar] [CrossRef]
- Burns, T.; Mueller, T. Experimental studies of the Eppler 61 airfoil at low Reynolds numbers. In Proceedings of the 20th Aerospace Sciences Meeting, Orlando, FL, USA, 11–14 January 1982; p. 345. [Google Scholar]
- Thipyopas, C.; Moschetta, J.M. A fixed-wing biplane MAV for low speed missions. Int. J. Micro Air Veh. 2009, 1, 13–33. [Google Scholar] [CrossRef]
- Bardera-Mora, R.; Garcia-Magariño, A.; Barroso, E.; Rodriguez-Sevillano, A. Study of Aerodynamic Performances of a Biologically Inspired Micro-UAV by Wind Tunnel Testing. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019; p. 3581. [Google Scholar]
- Bardera, R.; Rodríguez-Sevillano, Á.; García-Magariño, A. Aerodynamic Investigation of a Morphing Wing for Micro Air Vehicle by Means of PIV. Fluids 2020, 5, 191. [Google Scholar] [CrossRef]
- Jiakun, H.; Zhe, H.; Fangbao, T.; Gang, C. Review on bio-inspired flight systems and bionic aerodynamics. Chin. J. Aeronaut. 2021, 34, 170–186. [Google Scholar]
- Hassanalian, M.; Throneberry, G.; Abdelkefi, A. Investigation on the planform and kinematic optimization of bio-inspired nano air vehicles for hovering applications. Meccanica 2018, 53, 2273–2286. [Google Scholar] [CrossRef]
- Ananda, G.K.; Selig, M.S. Design of bird-like airfoils. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018; p. 0310. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).